Variable Effects of Temperature and Relative Humidity on Rhipicephalus sanguineus s.l. (Acari: Ixodidae) Development

Abstract

Rhipicephalus sanguineus s.l. (Latreille, 1806) can establish populations in residences and may lead to severe domestic and peridomestic infestations. Detection in the early infestation stage is challenging because of their small body size and the lack of visibility when ticks stay in sheltered refugia. The residents may believe that the infestation has been eliminated when no ticks are observed until ticks reappear when seeking hosts. Thus, it is necessary to improve our understanding of tick phenology to achieve more effective infestation management. In this study, the relationships between environmental conditions and tick development were explored in laboratory and using linear and nonlinear models. Three R. sanguineus s.l. strains, from one colony of the temperate lineage and two of the tropical lineage, were evaluated for the development of all life stages and conversion efficiency index (CEI) under five temperatures and four relative humidities (RHs). The development times differed between the three tick strains across stages and were primarily dependent on temperature. The CEIs had little variance explained by temperature, RH, or strains. Compared with the linear and exponential models with temperature as the only variable, the Brière-1 model was the best approximating model for most of the developmental rates. The developmental temperature thresholds for R. sanguineus s.l. development estimated by the Brière-1 model varied inconsistently across strains and life stages. We developed a more predictive relationship between environmental factors and R. sanguineus s.l. development, which can be utilized to predict tick development using temperature and develop appropriate control strategies.

The brown dog tick, Rhipicephalus sanguineus s.l. (Latreille, 1806), has a worldwide distribution, often associated with humans and their canine companions. The taxonomy of R. sanguineus s.l. has been reassessed repeatedly in recent years based on both morphological and molecular analyses (Moraes-Filho et al. 2011; Nava et al. 2012, 2018; Zemstova et al. 2016; Chitimia-Dobler et al. 2017; Hornok et al. 2017; Bakkes et al. 2020). While a consensus has yet to be reached for many of the taxonomic issues within the R. sanguineus s.l. complex of species, there is strong evidence that two main genotypes occur in the United States, the so-called ‘temperate’ and ‘tropical’ lineages, which may sometimes be found in sympatry (Eremeeva et al. 2011, Tucker et al. 2021). The temperate lineage corresponds to R. sanguineus s.s. as redescribed by Nava et al. (2018), a tick that is known to inhabit Western Europe, Chile, Uruguay, Argentina, and part of the United States. Slapeta et al. (2021) has proposed a name of Rhipicephalus linnaei (Audouin, 1826) for the ‘tropical’ lineage, which corresponds to a tick species known to occur in South Africa, Mozambique, Brazil, Paraguay, Colombia, Australia, Fiji, Laos, and part of the United States. While the choice of name for this tick remains debatable, as there is no evidence that the description of Audouin would best fit the tropical lineage more than any other Rhipicephalus species known from the Old World, the evidence proving that this is a separate species is quite conclusive.

Rhipicephalus sanguineus s.l. is primarily an ectoparasite of dogs, although other animals, including humans, have been recorded as hosts (Yakhchali and Hosseine 2006, Schuster et al. 2009, Kabir et al. 2011, Mentz et al. 2016). It is one of the most important tick vectors of disease-causing pathogens that parasitize dogs and humans, serving as the primary vector of Ehrlichia canis (Rickettsiales: Ehrlichiaceae) (Groves et al. 1975) for dogs and is a vector of Rickettsia rickettsii (Rickettsiales: Rickettsiaceae) (Demma et al. 2005) in certain parts of its distribution for dogs and humans. In addition to the veterinary and medical importance of R. sanguineus s.l., the tick is recognized for its ability to thrive in indoor environments, which can result in severe residential infestations (Uspensky and Ioffe-Uspensky 2002). A domestic infestation with R. sanguineus s.l. is most likely initiated by a few engorged female ticks that are brought inside while attached to dogs (Uspensky and Ioffe-Uspensky 2002). Those female ticks then detach in the residence and oviposit. Due to the high reproductive rate of ticks (Koch 1982), the tick population can increase rapidly within a short period resulting in a severe infestation. Furthermore, R. sanguineus s.l. are difficult to detect during the early stages of infestation because of their small body size, especially in larval and nymphal stages, and the lack of visibility during development in sheltered refugia, ultimately, resulting in a delay in the implementation of tick control efforts. Early detection of ticks may also depend on the coat type of dogs’ breed that inhabits the residence as the dog hair length could affects human tick-detecting efficiency (Uspensky and Ioffe-Uspensky 2002). After an acaricide treatment, the lack of visibility of ticks during certain developmental periods while inhabiting refugia could lead one to believe that the elimination of ticks has been achieved, resulting in discontinuation of control measures. Therefore, it is critical to understand R. sanguineus s.l. phenology to effectively manage its residential infestations.

Tick development is highly dependent on environmental conditions and can be variable in its expression (Koch and Tuck 1986, Jacobs et al. 2004, Labruna et al. 2017). Koch and Tuck (1986) evaluated R. sanguineus s.l. developmental time using a colony originally collected in Oklahoma (lineage was not assessed at the time). They reported that larval and nymphal molting time ranged from 6.2–20. 1 d and 9.3–32. 3 d, respectively, at a temperature range of 20–35°C and a relative humidity (RH) range of 15–95%. All engorged larvae and nymphs failed to molt at 10°C during an observation period of 34 wk. The authors identified that temperature was the primary effect on larval and nymphal molting time. Humidity only affected larval molting time at 35°C, where larvae required a shorter time to reach their molt when held at 90% RH (6.2 d) than those held at 35% RH (8. 2 d). Using a South African-colonized R. sanguineus s.l. strain, Jacobs et al. (2004) examined tick development at five temperatures (10–30°C) and three RHs (40–90%). The authors documented that preoviposition and egg incubation periods were the shortest under higher temperature and higher humidity conditions (25°C with 90% RH for preoviposition and 30°C with 90% RH for egg incubation). No engorged larvae or nymphs molted at 10°C, which is consistent with Koch and Tuck (1986). However, only the minimum and the maximum developmental times and their conditions were reported. Therefore, it is difficult to accurately compare development across conditions with other studies. Labruna et al. (2017) simulated different seasonal conditions by varying photoperiods (10:14–14:10 L:D) and temperatures (10–29°C) while maintaining R. sanguineus s.l. colonies at a constant RH (76%). They compared development times for the tropical and temperate lineages. Their results suggested that development time generally decreased as temperature increased. At low temperatures (10, 13, and 16°C), the tropical lineage either failed or required a longer time to develop as compared to the temperate species.

To achieve more efficient management and elimination of residential infestations by R. sanguineus s.l., predictive relationships between environmental conditions and tick development are necessary. Linear and nonlinear models have been used to explore the relationships between environmental factors and development, particularly temperature, for other arthropod species. For example, Tran et al. (2012) documented that the Brière-1 model best described the relationship between Bactericera cockerelli (Šulc) (Hemiptera: Triozidae) development and temperature. The Brière-1 model is a nonlinear temperature-dependent development model. As temperature increases, the development rate increases from zero at the minimum development temperature until reaches the optimal temperature, then decreases dramatically to zero at the maximum developmental temperature (Brière et al. 1999). However, it is difficult to identify whether the developmental rate changes or whether mortality occurs when temperature exceeds the optimal temperature. This model has been used to estimate temperature thresholds and describe the development of multiple arthropod species, such as Thrips hawaiiensis (Morgan) (Thysanoptera: Thripidae) (Lin et al. 2021) and Anoplophora chinensis (Forster) (Coleoptera: Cerambycidae) (Keena et al. 2021).

Ogden et al. (2004) fit an exponential model to Ixodes scapularis Say (Acari: Ixodidae) development over different temperatures and demonstrated that developmental time decreased as temperature increased. McCalla et al. (2019) evaluated multiple linear and nonlinear models on temperature-dependent development of Diaphorina citri Kuwayama (Hemiptera: Liviidae) and all models provided good fits to observed data within the temperature range evaluated. Jacobs et al. (2004) used linear or nonlinear models to estimate the minimum developmental temperature for R. sanguineus s.l. in different life stages, with temperatures ranging from 10.1 to 12.3°C. However, Jacobs et al. (2004) used different models for each life stage and did not explicitly compare the ability of different models to estimate the minimum developmental temperature within each life stage. In our study, developmental time of each stage for three colonized R. sanguineus s.l. strains representing two lineages was evaluated under 20 combinations of five temperatures and four RHs. The results were fit to linear and nonlinear models to determine the best model to describe the relationship between abiotic environmental factors and R. sanguineus s.l. development.

Materials and Methods

Ticks

Three R. sanguineus s.l. strains were evaluated in this study, differing in origin and time in colony: one laboratory-reared strain from Ecto Services Inc. (Henderson Co., NC), one CDC strain, and one field-collected strain from Florida. Ecto Services, Inc. established their laboratory-reared strain in 2008 with ticks obtained from Professional Laboratory and Research Service Inc. (Corapeake, NC) and it has been annually replenished with several hundred ticks collected from dogs. The CDC strain was originally collected from Imperial County, California in 2018 and has been laboratory-reared at the CDC using rabbits as hosts without replenishment. The Florida-collected strain was established from a single collection of several hundred adults and nymphs at a residential property in Port St. Lucie, Florida in 2018 and has been reared in the Veterinary Entomology laboratory at the University of Florida using cattle as hosts without replenishment from field. These strains are referred to as NC, CA, and FL in the following text, respectively. All engorged larvae, nymphs, and adults of the NC and CA strains were purchased and shipped to the University of Florida overnight with a temperature logger (HOBO U23-001 pro v2, Onset Computer Corporation, Bourne, MA) inside the package to record temperature every 10 min. The FL strain was reared by feeding the collected adult FL ticks (F₁ generation) on cattle (IACUC#201702142, #202011034) to obtain engorged individuals. Hosts were used for three feedings at maximum with an interval of at least 2 wk between feedings. Off-host ticks were held under standard conditions (25°C, 92% relative humidity, 12:12 [L:D]) until placement on cattle for blood feeding. For the FL strain, developmental rate estimations were begun using ticks from F₂ or later generation to minimize the colonization effects on tick performance. Samples of engorged nymphs from each strain were held until molting and the resulting flat adults were sent to Georgia Southern University to identify their lineage using the molecular protocol described in Eremeeva et al. (2011) and Tucker et al. (2021), as they are not morphologically distinct. Ticks from the FL and CA colonies were identified as belonging to the tropical lineage, while the NC colony included only ticks of the temperate lineage.

Tick Rearing—FL Colony

For adult tick feeding, an area (30 × 30 cm) along the topline of a calf (136–317 kg) starting from the mid-back to hip was shaved and a stockinet sleeve (40 cm long, 10 cm diameter, Comfort Products Inc., Croydon, PA) was fitted to the shaved skin using an adhesive (ACCRAbond, Memphis, TN). To fit the sleeve, a 10-cm-diameter circle was traced onto the shaved area as a reference. The adhesive was applied in an approximately 5-cm-wide ring around the outer perimeter of the traced area, as well as around a similarly sized width of the inner side of one end of the sleeve. The sleeve then was adhered to the adhesive-coated skin, and the adhesive was allowed to dry for 24 h before placing ticks into the sleeve. Up to 40 females and 40 males were placed into the sleeve, and the loose end of the sleeve was knotted to prevent tick escape. Ticks were checked daily until all females had engorged and detached from the host, which required up to 14 d. Detached, engorged females were removed from the sleeve daily using soft forceps and placed in glass petri dishes in groups of up to six females to oviposit. Males in the sleeve were removed after the last female detached from the host.

Following oviposition, eggs from up to six females were mixed gently and divided into 0.5-g groups. Each egg group was placed into a 25.9-ml (7-dram) glass vial covered with a piece of organdy cloth and sealed using a cap with center removed. When hatched larvae were at least 14 d old, they were placed on a calf for feeding.

For larval and nymphal feeding, a rectangular area (32 × 38 cm) was shaved along the topline of the calf starting from the shoulder to the middle of the back. A 5-cm-wide cardboard frame template with an external perimeter of 27 × 33 cm and internal perimeter of 22 × 28 cm was prepared. A frame was drawn on the shaved area of the calf using both the inner and outer edges of the cardboard frame as references. Adhesive (Hiptag cement, Ruscoe Co., Akron, OH) was applied to the 5-cm area between the two reference lines and spread evenly using a paint brush. A cotton patch (27 × 33 cm, Organic Cotton Plus) was adhered to the adhesive-treated skin area and allowed to dry for 24 h before larvae or nymphs were transferred inside.

A 4-cm slit was cut into the cloth patch near the highest point on the calf and approximately 10,000 emergent larvae from a 0.5-g egg mass, or up to 3,000 nymphs were tapped from the vial into the patch. A surgical suture (4/0, Your Design Medical, Brooklyn, NY) was used to sew the slit on the patch closed to prevent tick escape. The patch integrity was inspected daily without opening it. Starting from the fourth day after ticks were placed into the patch, the suture was opened to allow collection of the engorged ticks that had detached from the calf by using a mouth aspirator with HEPA filter and/or forceps. The patch was sewn closed after collecting detached ticks. Engorged ticks were collected daily until all ticks detached from the calf.

Developmental Times

Ticks were evaluated for developmental rates under the paired combinations of five constant temperatures, 20, 23, 27, 30, and 35°C, and four RH, 33, 52, 75, and 92%. Expected variation in temperatures and humidities was ±1°C and ±10%, respectively, except for 92% RH, where the upper limit was 100%. The environmental conditions were selected based on the range of expected conditions in residential environments. Magnesium chloride hexahydrate, magnesium nitrate hexahydrate, sodium chloride, and potassium nitrate were obtained from Thermo Fisher Scientific (Hampton, NH), and their saturated solutions were used to provide nominal fixed RH of 33, 52, 75, and 92%, respectively (Greenspan 1977). Saturated salt solutions were prepared by adding salt into 600-ml tap water at room temperature until the salt no longer dissolved at 30-min postaddition and then stirring the solution for an additional 24 h to ensure the solution was saturated. The saturated salt solution was placed in a glass aquarium (9.5 L, United Pet Group Inc. Blacksburg, VA) that was sealed with a foam weatherstrip seal (0.95 cm wide) and a removable lid to produce the fixed humidities. The humidity was monitored for 1 wk before tick evaluations started to ensure the correct humidity level. Salt solutions in the chambers were replenished or replaced with new solution when RH continuously exceeded ±10% from nominal. These humidity chambers were held in incubators (I30VL, Percival Scientific Inc., Perry, IA) with one of the five temperature settings. This arrangement provided 20 temperature–humidity combinations for tick developmental time evaluations. Each chamber contained an electronic thermo-hygrometer (HOBO U23-001 pro v2, Onset Computer Corporation, Bourne, MA) to record the temperature and humidity every 10 min. Environmental conditions were checked every 2–5 mo by examining the data from the electronic thermo-hygrometer.

Ticks were held inside 25.9-ml (7-dram) glass vials covered with a piece of organdy cloth and closed using a cap with the center removed during experimental evaluations. Each glass vial contained 10 engorged nymphs or 10 engorged larvae or one engorged female. For each environmental condition of each tick stage, there were three replicate glass vials. The tick-containing vials were placed into the humidity chambers with one of the four saturated salt solutions and the chambers were placed in the forementioned incubators set at specified temperatures. Ticks were checked daily to record the date of biological events: preoviposition time of engorged females (POT, number of days between female detachment from host to the day the first egg was observed); egg incubation time (EIT, number of days between the first egg was observed to the first larva was observed); molting time of engorged larvae and nymphs (LMT and NMT respectively, number of days between detachment from host to molting to the next life stage). These time periods will be referred to as developmental times. However, the POT and EIT of CA strain were not evaluated at 35°C due to insufficient engorged females from this colony. Ticks were considered successfully hatched or molted when the larva, nymph, or adult could walk freely in the vial. A tick was considered dead when it did not molt within a 2-wk period after the previous tick molted in the same vial. Analysis was conducted on the development times for successfully molted, oviposited, or hatched ticks. Ticks were kept in the vials after hatching or molting under the same conditions for further study. Engorged females were allowed 2 wk to complete oviposition after the first egg was observed and then removed from the vial. The egg masses laid by those females were kept in the same vial at same condition for larval hatching. The engorged females and egg masses were weighed to calculate the conversion efficiency index (CEI), which is the percentage of female weight converted to weight of the resultant eggs. All the evaluations of tick development were conducted in a 0:24 L:D environment.

Statistics

Developmental times were the days between two biological events as described above. Developmental rates were calculated as the inverse of developmental times. The mean and standard error of developmental times were calculated for each environmental condition, strain, and stage. Linear regression was used to explore the relationship between CEI and female preoviposition weight. Model selections were conducted on each developmental time or developmental rate using corrected Akaike information criterion (AIC_c) in three levels. The first model selection examined the difference between replications and between strains using generalized linear models. In total, 18 linear models were generated by the variables of temperature (T), RH (R), strain (S), and their interactions (Table 1). The developmental times were fit to the 18 models with and without having replication (K) included as a variable (Supp Table 5 [online only]). Variations in developmental times were considered relatively small between replications if more than half of the models from the model set without replication had smaller AIC_c values than the model set with replication as a variable, and replicates were then combined for further analysis. Otherwise, subsequent model selections would be performed including replicate as a variable. The difference between strains was determined by examining the top ranked models (ΔAIC_c < 10) from the 18-model set chosen above (lower AIC_c values with or without replication). If the top ranked models had strain as a variable, the developmental times were considered to have large variation between strains and each strain was analyzed separately for the subsequent model selections. Otherwise, strains would be combined as described above for replicates.

Table 1.

The comparisons of ΔAICc and R² values between the models with and without strain as a variable for Rhipicephalus sanguineus s.l. developmental times. The models with lowest AIC_c values (ΔAIC_c =0) are bolded

Model	POT		EIT		LMT		NMT		CEI
	ΔAICc	R 2	ΔAICc	R 2	ΔAICc	R 2	ΔAICc	R 2	ΔAICc	R 2
Model with strain
S + T + R + ST + SR + TR + STR	1.05	0.751	12.79	0.796	0.00	0.822	5.57	0.849	4.33	0.235
S + T + R + ST + SR + TR	5.06	0.738	8.21	0.796	1.66	0.821	3.04	0.849	1.27	0.228
S + T + R + ST + SR	4.17	0.736	6.11	0.796	0.29	0.821	6.96	0.848	0.00	0.224
S + T + R + ST + TR	2.15	0.735	3.75	0.796	2.24	0.821	0.00	0.849	2.57	0.201
S + T + R + SR + TR	62.76	0.620	20.35	0.774	181.89	0.799	430.45	0.807	2.02	0.203
S + T + R + ST	1.94	0.732	1.68	0.796	0.82	0.821	3.91	0.848	2.21	0.192
S + T + R + SR	61.54	0.617	18.29	0.774	179.87	0.799	433.33	0.807	0.86	0.198
S + T + R + TR	59.44	0.617	15.98	0.774	182.53	0.799	427.38	0.807	3.18	0.176
S + T + ST	0.00	0.732	0.00	0.795	0.19	0.820	4.77	0.848	9.48	0.144
S + R + SR	192.69	0.150	258.16	0.020	2714.99	0.021	3357.58	0.003	9.08	0.146
S + T + R	58.71	0.614	13.96	0.774	180.52	0.799	430.24	0.807	2.95	0.167
S + T	56.76	0.614	12.23	0.773	178.83	0.799	430.87	0.806	10.27	0.118
S + R	189.04	0.147	253.89	0.019	2715.86	0.018	3353.92	0.003	10.88	0.115
S	187.04	0.146	251.81	0.019	2714.25	0.017	3352.82	0.002	17.38	0.068
Model without strain
T + R + TR	90.73	0.526	47.42	0.719	293.08	0.784	448.28	0.805	10.61	0.116
T + R	89.81	0.523	45.39	0.719	291.21	0.784	451.22	0.804	10.11	0.107
T	87.89	0.523	43.70	0.719	289.85	0.784	451.85	0.804	16.77	0.059
R	211.31	0.001	252.92	<0.001	2739.48	<0.001	3353.96	0.001	19.04	0.046

SSE of each model was included in Supp Table S7 (online only). S, strain; T, temperature; R, RH; ST, strain × temperature; SR, strain × RH; TR, temperature × RH; STR, strain × temperature × RH. POT, preoviposition time; EIT, egg incubation time; LMT, larval molting time; NMT, nymphal molting time; CEI, conversion efficiency index.

The second model selection was performed to identify the effects on developmental times from temperature and RH. In total, four models for each strain and developmental phase were generated using temperature, RH, and their interaction and were fit to the developmental times (Table 2). The model with the lowest AIC_c value was considered the best approximating model to describe the data, and the variables in this model were considered the primary variables for the developmental times.

Table 2.

Model selection results with temperature, RH, and their interactions as variables for Rhipicephalus sanguineus s.l. development times. Models with the smallest AICc (ΔAICc = 0) for each variable within strain shown in bold

Strain/models	POT		EIT		LMT		NMT
	ΔAICc	R 2	ΔAICc	R 2	ΔAICc	R 2	ΔAICc	R 2
FL
T + R + TR	4.34	0.688	4.34	0.760	0.00	0.836	1.78	0.835
T + R	2.08	0.687	2.08	0.759	2.81	0.835	1.14	0.835
T	0.00	0.687	0.00	0.759	3.34	0.834	0.00	0.835
R	68.46	<0.001	82.50	<0.001	955.24	0.002	1066.51	0.001
NC
T + R + TR	4.41	0.842	4.29	0.799	2.02	0.788	3.41	0.893
T + R	2.14	0.842	2.01	0.792	0.72	0.788	1.93	0.893
T	0.00	0.842	0.00	0.795	0.00	0.787	0.00	0.893
R	110.73	<0.001	95.93	<0.001	888.16	<0.001	1328.45	<0.001
CA
T + R + TR	0.00	0.749	3.12	0.940	2.24	0.817	0.00	0.845
T + R	3.29	0.717	1.63	0.939	0.25	0.817	3.78	0.844
T	5.19	0.691	0.00	0.938	0.00	0.816	4.48	0.844
R	60.34	0.026	130.92	<0.001	834.22	0.007	1110.29	<0.001

SSE of each model was included in Supp Table S8 (online only). T, temperature; R, RH; TR, temperature × RH. POT, preoviposition time; EIT, egg incubation time; LMT, larval molting time; NMT, nymphal molting time.

In previous studies of arthropod development, nonlinear models are often good descriptions of the data (Tran et al. 2012, McCalla et al. 2019). These nonlinear models often are fit to developmental rate rather than time. Therefore, the third model selection evaluated the ability of nonlinear models to describe the developmental rates (D, developmental time⁻¹) using the primary variables identified in the previous model selection. The developmental rates were referred as POR, EIR, LMR, and NMR for preoviposition rate, egg incubation rate, larval molting rate, and nymphal molting rate, respectively. According to previous studies (Koch and Tuck 1986, Jacobs et al. 2004), temperature appears to be the primary variable for tick development. Thus, we anticipated that temperature would be our most important variable in the second model selection, and the third model selection was planned to be conducted with three models that include only temperature as variable. Nonlinear models including RH would be considered if this was not the case. The models considered were the best linear model $(D=b_1+b_{2}T)$ for each strain from the second model selection and two nonlinear models: exponential model $(D=b_1{e}^{b_{2}T})$ and Brière-1 model $(D=b_{1}T(T-T_{min})\sqrt{(T_{max}-T)})$ (Brière et al. 1999). Additionally, other nonlinear, temperature-dependent development models, including Brière-2 (Brière et al. 1999), Lactin (Lactin et al. 1995), Lobry-Rosso-Flandrois (Rosso et al. 1993), Ratkowsky (Ratkowsky 1983), and performance models (Wang et al. 2013; Supp Table 5 [online only]), were evaluated for their ability to describe the data during preliminary screening for potential nonlinear models for developmental rate. However, many of these model fits were ill-conditioned due to the narrow temperature range tested in this study. Thus, they were not included in the third model selection. All model selections were performed using Matlab with functions of fitglm and fitnlm (2020a, MathWorks).

Results

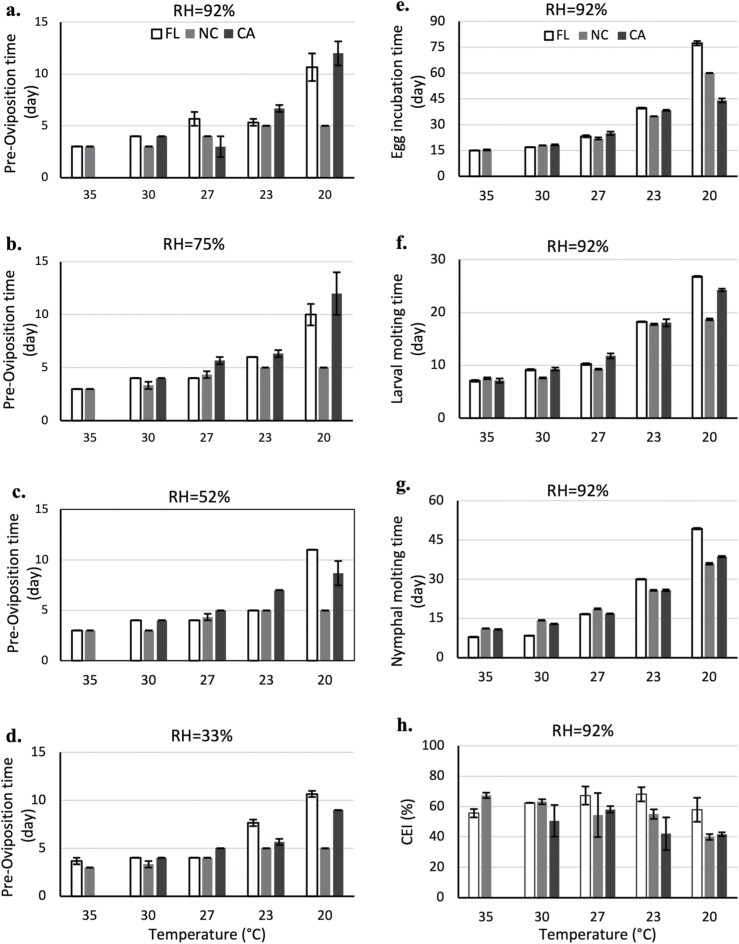
The realized temperature and RH were within the expected variation during the evaluations. The success of oviposition and larval hatch was high across conditions (Supp Tables S1 and S2 [online only]). Larval molting success varied from 33 to 100% with lower success levels at high temperatures (Supp Table 3 [online only]), while nymphal molting success was greater than 90% for all conditions and strains (Supp Table 4 [online only]). Selected developmental times and CEI values of each strain under various conditions of temperatures and RHs are displayed in Fig. 1, with remaining conditions shown in the supplement (Supp Fig. 1 [online only]). Overall, development times were more sensitive to temperature than RH (Fig. 1a–g, Supp Fig. 1 [online only]), while CEI was relatively insensitive to both (Fig. 1h, Supp Fig. 1j–l [online only]). An outlier (916.67%) from the CEI of the FL strain at 35°C and 92% RH was removed before analysis, as it was outside possible biological bounds (maximum possible CEI could be 100%). This may have been caused by a failure of the scale used, condensation in the vial, or an incorrect data recording. Similar patterns were observed across all RHs for each developmental time (e.g., Fig. 1a–d, Supp Fig. 1 [online only]). Developmental times generally decreased as temperature increased. CEI did not exhibit a clear pattern with either temperature or RH. Greater variability was observed between three R. sanguineus s.l. strains at 20°C than at other evaluated temperatures. Among the three strains, the NC strain developed the fastest at 20°C for all stages (Fig. 1, Supp Fig. 1 [online only]), except egg incubation where the CA strain developed the fastest (Fig. 1e, Supp Fig. S1a–c [online only]).

Fig. 1.

The mean ± SE of developmental times and conversion efficiency index (CEI) of three Rhipicephalus sanguineus s.l. strains at different relative humidities with five temperatures. (a) Preoviposition time at 92% RH; (b) preoviposition time at 75% RH; (c) preoviposition time at 52% RH; (d) preoviposition time at 33% RH; (e) egg incubation time at 92% RH; (f) larval molting time at 92% RH; (g) nymphal molting time at 92% RH; (h) CEI at 92% RH. The preoviposition time, egg incubation time, and CEI were not evaluated for CA strain due to insufficient tick females. Figure was created using Excel (Microsoft 365).

For all developmental times and CEI, the models without replication as a variable had lower AIC_c values than the models with replication as a variable (Supp Table 6 [online only]). Therefore, replicates were combined for further analysis. To assess whether developmental times differed between strains, models were constructed with and without strain as a variable using combined replications. All top ranked models (ΔAIC_c < 10) contained strain as a variable, while the models without strain all ranked at the bottom (ΔAIC_c > 43, Table 1). The highest R² values for POT, EIT, LMT, and NMT were 0.751, 0.796, 0.822, and 0.849, respectively, while the highest R² value for CEI was only 0.235 (Table 1). Therefore, CEI was not further analyzed using model selection due to the limited variance explained by strain, temperature, RH, or their interaction. For developmental times, model selection was then conducted for each strain separately using combined replications and considering temperature, RH, and interactions.

With replications combined, the developmental times for each strain were fit to four linear models generated by variables of temperature, RH, and their interaction. The model with temperature as the only variable (Table 2) was the best model to describe the four developmental times for all tick strains, except the POT and NMT of the CA strain and LMT of the FL strain, which were best described by the model with temperature, RH, and their interaction (Table 2). The R² values of the best models for the developmental times ranged from 0.687 to 0.938. The models that best described the developmental times consistently included temperature as a variable. Therefore, temperature was used as the primary variable for further model selection considering nonlinear model approaches.

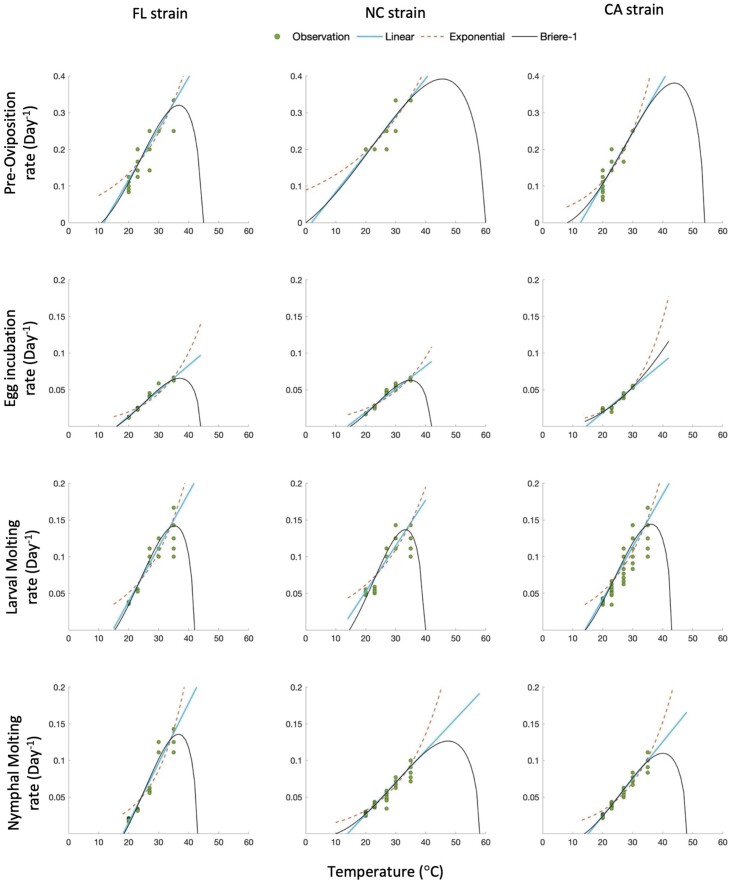
The relationship between temperature and developmental rate were estimated using linear, exponential, and Brière-1 models (Table 3, Fig. 2). In Fig. 2, fitted curves were extrapolated beyond the observational temperature range, to observe the shape of the Brière-1 model. The R. sanguineus s.l. developmental rates were positively related to temperature within the tested temperature range (20–35°C). Compared with the linear and exponential models, the Brière-1 model better described the developmental times of FL and NC strains, with the lowest AIC_c and the highest R². For the CA strain, the Brière-1 model was the best approximating model only for LMR and NMR, while POR and EIR were best described by the linear model and the exponential model, respectively. However, the ΔAIC_c value of the Brière-1 model for POR was small (ΔAIC_c = 0.24), indicating that both exponential and Brière-1 models provide good descriptions of the data. For EIR, ΔAIC_c of Brière-1 model was larger, suggesting that the linear model better described the data. Based on the Brière-1 model, the estimated minimum and maximum temperatures for R. sanguineus s.l. development varied inconsistently across strains and life stages (Table 3, Fig. 2). The estimates of minimum temperature of POR of the NC strain and the maximum temperature of EIR of the CA strain were not reliable because they are unsuitable for R. sanguineus s.l.

Table 3.

Estimated parameters of linear and nonlinear models including only temperature for describing the development of three Rhipicephalus sanguineus s.l. strains. Models with the smallest AIC_c (ΔAIC_c = 0) for each development rate within strain shown in bold

Strain	Parametersa	POR	EIR	LMR	NMR
FL	Linear
	b 1 (Intercept)	−0.164	−0.055	−0.109	−0.148
	b 2 (Slope)	0.014	0.003	0.007	0.008
	AICc	−249.00	−514.42	−3,328.80	−3,403.20
	ΔAICc	4.07	18.80	186.96	95.86
	R 2	0.87	0.98	0.93	0.91
	SSE	0.047	<0.001	0.058	0.111
	Exponential
	b 1	0.041	0.004	0.012	0.005
	b 2	0.060	0.081	0.073	0.098
	AICc	−232.90	−439.82	−2,965.17	−3,078.37
	ΔAICc	20.16	93.39	550.59	420.69
	R 2	0.82	0.92	0.86	0.84
	SSE	0.064	0.002	0.116	0.193
	Brière-1
	b 1	1.232 × 10–4	3.242 × 10–5	7.981 × 10–5	8.261 × 10–5
	T min	10.94	15.94	15.38	18.47
	T max	44.29	43.78	41.71	42.73
	AICc	−253.06	−533.21	−3,515.76	−3,499.06
	ΔAICc	0.00	0.00	0.00	0.00
	R 2	0.88	0.98	0.95	0.92
	SSE	0.045	<0.001	0.041	0.095
NC	Linear
	b 1 (intercept)	−0.020	−0.044	−0.072	−0.061
	b 2 (slope)	0.010	0.003	0.006	0.004
	AICc	−269.87	−507.49	−3,154.82	−4,690.95
	ΔAICc	0.45	63.99	319.01	28.90
	R 2	0.83	0.96	0.81	0.96
	SSE	0.036	0.001	0.137	0.013
	Exponential
	b 1	0.089	0.006	0.019	0.007
	b 2	0.039	0.068	0.058	0.073
	AICc	−269.82	−448.13	−2,970.60	−4,470.85
	ΔAICc	0.50	123.35	503.22	249.00
	R 2	0.82	0.89	0.74	0.94
	SSE	0.038	0.002	0.189	0.019
	Brière-1
	b 1	3.333 × 10–5	3.539 × 10–5	9.009 × 10–5	2.197 × 10–5
	T min	−23.99	14.82	14.56	10.00
	T max	59.35	41.36	39.24	57.95
	AICc	−270.32	−571.48	−3,473.82	−4,719.85
	ΔAICc	0.00	0.00	0.00	0.00
	R 2	0.83	0.99	0.89	0.96
	SSE	0.036	<0.001	0.079	0.012
CA	Linear
	b 1 (Intercept)	−0.178	−0.049	−0.100	−0.077
	b 2 (Slope)	0.014	0.003	0.071	0.005
	AICc	−252.11	−405.83	−2,957.48	−4,555.49
	ΔAICc	0.00	30.59	73.53	32.04
	R 2	0.91	0.95	0.90	0.96
	SSE	0.013	<0.001	0.073	0.017
	Exponential
	b 1	0.022	0.003	0.013	0.007
	b 2	0.080	0.098	0.070	0.078
	AICc	−248.84	−436.42	−2,733.31	−4,138.53
	ΔAICc	3.27	0.00	297.70	449.00
	R 2	0.90	0.97	0.85	0.92
	SSE	0.015	<0.001	0.115	0.034
	Brière-1
	b 1	7.748 × 10–5	1.811 × 10–6	6.979 × 10–5	3.728 × 10–5
	T min	8.20	8.08	14.23	13.90
	T max	53.76	2070.75	42.96	47.96
	AICc	−251.87	−422.77	−3,031.01	−4,587.54
	ΔAICc	0.24	13.65	0.00	0.00
	R 2	0.91	0.96	0.92	0.96
	SSE	0.014	<0.001	0.063	0.016

POR, preoviposition rate; EIR, egg incubation rate; LMR, larval molting rate; NMR, nymphal molting rate.

^a The SE of estimated parameters are included in Supp Table S9 (online only).

Fig. 2.

The developmental rates of three Rhipicephalus sanguineus s.l. strains at different temperatures with fitted curves of linear, exponential, and Brière-1 models. Data points for each individual tick are not visible due to overlap when estimated rates were similar.

Discussion

Management of R. sanguineus s.l. residential infestations has been challenging. Multiple issues plague elimination of an infestation, including the lack of infestation recognition and the reduced visibility resulting from small size and cryptic tick behavior during some stages or phases. One of our hypotheses is that immediately following an infestation, tick phenology may generate synchronicity in stages due to a limited age structure at an infestation and relatively equivalent indoor environmental conditions, especially temperature, such that only one stage is questing or feeding at a time. Unnoticed cryptic populations may most often occur under scenarios when only larvae are questing or feeding, resulting in ticks not being noticed by residents. Should this occur during later infestation periods, residents may be misled into believing that control efforts have been successful, and the tick infestation has been eliminated when it has not, resulting in a larger infestation when control is stopped. Therefore, understanding R. sanguineus s.l. phenology, especially environmental impacts on tick developmental time, is critical to establishment of an effective management plan resulting in the elimination of R. sanguineus s.l. infestations. The results of this study suggest that tick developmental times or rates primarily were affected by strain and temperature. By identifying the Brière-1 model as the best approximating model compared with the linear and exponential models, we provide a foundation for tick development prediction, which can be used for future work.

CEI was poorly explained by all models generated with variables of strain, temperature, RH, and their interactions. This indicated that CEI was only slightly affected by strain, temperature, and humidity. In this study, the minimum CEI (20.1%) and the maximum CEIs (69.5%) were observed at 33% RH and 52% RH, respectively, at 27°C from the NC strain (Supp Fig. 2 [online only]). Jacobs et al. (2004) reported that the minimum CEI (31.0%) and the maximum CEI (65.7%) were observed at 40% and 90% RH, respectively, at 15°C. However, CEI values at other temperature and RH conditions were not reported. The environmental conditions in which minimum and maximum CEIs were observed in the present study are different from Jacobs et al. (2004). This may be due to different tick strains used in the evaluations. The relationships between CEIs and environmental conditions were also examined for other tick species. For example, Davey (1988) documented no observed difference in CEI of R. (Boophilus) annulatus Say (Acari: Ixodidae) within a temperature range of 20–30°C, while CEI began decreasing at 35°C and a lower CEI was observed at both 15 and 40°C. In the present study, the highest R² is less than 0.24, indicating that the variables considered did not explain much of the variance in CEI, and other factors may be more important. Lopes et al. (2000) reported that the CEI of Amblyomma cajennense (Fabricius) (Acari: Ixodidae) was not significantly different between laboratory and field conditions, but was related to female weight before oviposition. A negative correlation between CEI and female preoviposition weights was documented for Dermacentor marginatus (Sulzer) and Haemaphysalis punctata Canestrini and Fanzago (Acari: Ixodidae) (Chitimia and Cosoroabǎ 2007). However, no clear relationship between CEI and female preoviposition weight in the three R. sanguineus s.l. strains was observed in this study (Supp Fig. 2 [online only]). Thus, whether female preoviposition weight affects CEI, or what other factors may influence CEI, requires future exploration.

Developmental times were affected by environmental conditions. At higher temperatures, all strains exhibited similar developmental times. However, as temperature decreased, NC strains took less time to develop than the other strains. This difference between strains could be due to the different lineage (tropical or temperate linage) of the strains as the FL and CA strains are tropical lineage while the NC strain is a temperate lineage. Similar results were reported in Labruna et al. (2017) where at the same environmental conditions, R. sanguineus of tropical and temperate linages exhibited slightly different developmental times. The differences expanded when the temperature decreased below 20°C, where tropical lineage ticks developed more slowly than temperate lineage ticks. For the temperatures that are in the range evaluated in our study, the developmental time from Labruna et al. (2017) generally was similar with our results. However, important differences (e.g., photoperiod and measurement interval) existed between our two studies, which may impact the precision of this comparison.

The models indicated that temperature was the primary factor affecting R. sanguineus s.l. development, while RH had a lesser effect, a result consistent with Koch and Tuck (1986). Similar results were observed with Dermacentor nitens Neumann (Acari: Ixodidae) (Despins 1992). The Brière-1 model was the best approximating model, within the evaluated temperature range, for most of the relationships between development rates and temperature. The temperature range studied did not extend up into the region where development rates would strongly decline (above optimum) for the estimated Brière-1 models, limiting the predictive ability under higher temperature. It estimated the upper and lower temperature thresholds for tick development, which were relatively consistent across all developmental rates. However, the models did generate some curious results. The maximum temperature for EIR of the CA strain, as estimated by the Brière-1 model, was extremely high compared to estimates from the other developmental rates. The exceptionally high rate observed in the CA strain is biologically unrealistic and would imply functionally an always-increasing development rate with temperature. This estimate was likely due to the lack of data at and above 35°C, as there were insufficient engorged CA strain females available in the study. As a result, the Brière-1 model was not the best fit for EIR of the CA strain and the parameter estimates may not be accurate. An extremely low minimum temperature was estimated for POR of the NC strain, which may also be due to the limited temperature range tested in this study, that did not cover a range sufficient to support the accurate model prediction of the minimum temperature. The range of temperatures studied here focused on temperatures likely to occur in a residence. As a result, the three models were often very similar over the temperature range studied (Fig. 2), and the models showed equally good fits for some strains and stages (Table 3).

The developmental thresholds of R. sanguineus s.l. that were estimated by the models in this study have been explored previously. No larvae hatched when eggs were held at 8 ± 2°C for more than 75 d (Dantas-Torres et al. 2010) and no engorged larvae or engorged nymphs molted at 10°C within a study period of 34 wk (Koch and Tuck 1986). Jacobs et al. (2004) estimated that the overall low temperature threshold for R. sanguineus s.l. development in the laboratory was approximately 10–12°C. The lower developmental threshold reported from these studies overlapped with the estimated temperature from Brière-1 models presented in this study (8.077–18.466°C). However, no clear upper developmental threshold has previously been reported for R. sanguineus s.l. development. Here, successful development was observed at 35°C for all stages, with a shorter developmental period than at lower temperatures, which is consistent with Koch and Tuck (1986). In addition, the maximum developmental temperatures were estimated in this study using a Brière-1 model and ranged from 39.238 to 59.353°C, which enhanced our knowledge of R. sanguineus s.l. development limits. Although tick development at 59°C seems unlikely, and our studies did not extend to temperatures near these development limits, these results provide guidance for future studies.

Our findings indicated that during residential infestations, tick development will likely vary due to different microclimates, especially temperature, in different indoor areas. Ticks can be found inside homes and the peridomestic environment, including adjacent habitats such as porches, garages, and attics. These habitats may have environmental conditions quite different than living areas within the residence. Depending on the local climate, living spaces also may vary in environmental conditions over time, dependent on residents’ use of heating and cooling. This can result in variable tick development and resulting changes in tick phenology over time as not all ticks will develop simultaneously, affecting molting and subsequent host-seeking. As a result, the periods when ticks are not visible to residents may increase. Such a scenario can mislead residents into believing that the tick infestation has been eliminated until ticks undergoing development suddenly appear to residents when host-seeking. Thus, these differences in experienced environments generating variable development times could extend an infestation that results in the need to apply control tactics for longer periods.

In addition to linear, exponential, and Brière-1 models, more complex developmental models (Supp Table 5 [online only]), such as the Lactin model (Lactin et al. 1995) and Performance model (Wang et al. 2013), have been used to describe temperature-dependent development of other arthropods. However, our data encompassing a limited temperature range were not sufficient to support such complex models. To improve the accuracy of a tick population model, extended environmental conditions should be considered. For instance, fluctuating temperatures, wider range of temperatures, and the incorporation of cooling and heating at different areas of a residence should be evaluated to extend our knowledge. Additional data will also improve the model fit as well as enabling exploration of more extensive models, which may provide a more accurate relationship between temperature and developmental rates. As the species complex is better understood, further differences between species or populations should be considered. In addition, there was no replication of incubators that held the ticks at different temperature due to constraints of space, time, and labor. Thus, it is unknown if there was any variation between incubators, such as air circulation, which may have affected differences in tick developmental time between temperatures.

This study has estimated a predictive relationship between R. sanguineus s.l. development and environmental factors. These R. sanguineus s.l. development models will allow researchers to better understand tick developmental patterns and to better estimate and consider ticks that may not be currently visible when making management decisions. It can also provide guidance for pest control personnel to appropriately develop control strategies based on the prediction of tick development time using temperature. For instance, if the temperature of an attic in a Florida summer routinely exceeds 40°C, which is approaching the maximum developmental temperature estimated in this study, this attic may be a less viable habitat for ticks to develop during summer months. If this is confirmed, pest control should focus on more viable tick habitat in the residence when temperatures are high. If the residents keep the living room temperature relatively low, tick development may require a longer time than those areas at higher temperature. Therefore, the pest control may need to be extended to achieve the best results. This study has extended our knowledge of environmental effects on R. sanguineus s.l. development and provided a foundation for estimating tick populations during a residential infestation, which could improve pest control strategies for more efficient tick elimination.