Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Jul 12;9(8):2748–2755. doi: 10.1021/acsphotonics.2c00505

Computational Photon Counting Using Multithreshold Peak Detection for Fast Fluorescence Lifetime Imaging Microscopy

Janet E Sorrells †,‡, Rishyashring R Iyer ‡,§, Lingxiao Yang ‡,§, Elisabeth M Martin †,‡, Geng Wang ‡, Haohua Tu ‡,§, Marina Marjanovic †,‡, Stephen A Boppart †,‡,§,∥,⊥,*
PMCID: PMC9389606  PMID: 35996369

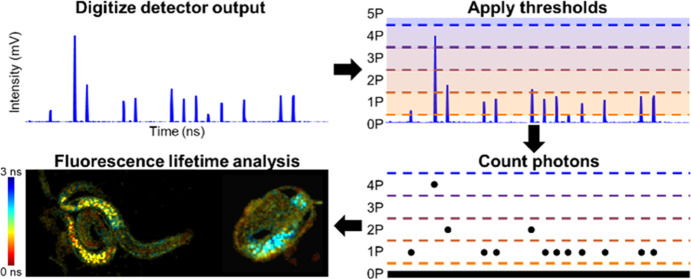
Abstract

graphic file with name ph2c00505_0007.jpg

Time-resolved photon counting methods have a finite bandwidth that restricts the acquisition speed of techniques like fluorescence lifetime imaging microscopy (FLIM). To enable faster imaging, computational methods can be employed to count photons when the output of a detector is directly digitized at a high sampling rate. Here, we present computational photon counting using a hybrid photodetector in conjunction with multithreshold peak detection to count instances where one or more photons arrive at the detector within the detector response time. This method can be used to distinguish up to five photon counts per digitized point, whereas previous demonstrations of computational photon counting on data acquired with photomultiplier tubes have only counted one photon at a time. We demonstrate in both freely moving C. elegans and a human breast cancer cell line undergoing apoptosis that this novel multithreshold peak detection method can accurately characterize the intensity and fluorescence lifetime of samples producing photon rates up to 223%, higher than previously demonstrated photon counting FLIM systems.

Keywords: FLIM, fluorescence lifetime, single-photon detection, multiphoton microscopy, photon counting

Many optical technologies rely on time-resolved photon counting such as time of flight (ToF) imaging,1 light detection and ranging (LiDAR),2 and optical microscopy. Specifically, multiphoton fluorescence lifetime imaging microscopy (FLIM) often uses time-resolved photon counting to compute and spatially map fluorescence lifetime. The time between excitation and emission in the fluorescence process follows an exponential decay probability density function, and the mean time between excitation and emission is the fluorescence lifetime.3 Fluorescence lifetime can be used to investigate various properties within biological samples. Notably, FLIM can be used to examine metabolism in biological samples via reduced nicotinamide adenine dinucleotide and nicotinamide adenine dinucleotide phosphate (NAD(P)H)4,5 because protein-bound NAD(P)H has a longer fluorescence lifetime than “free” NAD(P)H.6

Presently, most photon counting FLIM systems use time-correlated single photon counting (TCSPC), in which analog electronics are used to count and time-tag incident photons relative to the pulsed laser source used for excitation.7,8 However, TCSPC systems experience a dead time: the amount of time after a photon is counted that a subsequent photon cannot be counted. This is due to both the detector response function and the limited bandwidth of the additional analog electronics. When many photons arrive close together in time, it becomes more likely that photons will arrive while the system is “dead” and these additional informative photons will not be counted, biasing the fluorescence intensity and lifetime measurements, termed the “pile-up effect”. Thus, the dead time of the system determines the maximum acceptable photon rate (photon rate is the percentage of laser excitation pulses resulting in a photon count), above which the distortion due to pile-up in fluorescence lifetime and intensity becomes significant. Many standard TCSPC systems have a maximum acceptable photon rate of around 5–10%, meaning that the fluorescence signal must be attenuated so that 90–95% of laser pulses on average do not result in a photon count.7,9

One way to combat dead time is to use array detectors, such as silicon photomultipliers (SiPMs)10 and single-photon avalanche diode (SPAD) arrays,11 which are made up of many small single-pixel detectors that can work independently, though each individual pixel detector has a dead time. These detectors can suffer from lower quantum efficiency due to the geometrical limitation on fill factor, which is one barrier to autofluorescence imaging, which generally has a much lower intensity than fluorescent dyes. Regardless, high photon-rate-capable SPAD array systems have been developed and will be important for the future of fast FLIM.12 As an alternative to multi-pixel detectors, pulse pile-up inspectors can be used to reject data when multiple photons arrive at the detector within a short period, providing a way to combat pile-up, but are still limited by system dead time.13,14 An additional demonstrated strategy matched the dead time of a SPAD array TCSPC FLIM system to the laser repetition period to improve performance.15 While these improvements have all contributed to enabling faster imaging, they all still are inherently limited by the dead time of the photon counting hardware employed. Direct pulse sampling, where the output of the detector is directly digitized and used to approximate photon counts,16 can be used for rapid acquisition of FLIM but has poorer accuracy than photon counting methods due to the lack of single-photon resolution.17 Time-gated methods, where fluorescence intensity is collected in varying time windows with respect to the laser pulse, can provide fast fluorescence lifetime contrast but has poorer temporal resolution and must employ either multiple detectors or use multiple acquisitions to acquire multiple time-gates.18−20

Recent advances in time to digital conversion (TDC)- and field-programmable gate array (FPGA)-based technologies have achieved dead times as low as 0.650 ns, and enabled fast TCSPC21,22 and digital frequency domain23 FLIM. However, thus far, the fastest single-detector dead time in a photon counting FLIM system (0.625 ns) has been demonstrated by our research group using computational photon counting on directly digitized photomultiplier tube (PMT) output by implementing a simple thresholded peak detection algorithm called Single-photon PEak Event Detection (SPEED).17

This demonstration used a high-bandwidth PMT, transimpedance amplifier, and fast digitization at 3.2 GS/s to collect data, and classified any local maxima (a digitized data point with a voltage greater than the points immediately before and after it) that was above the empirically determined single-photon threshold as a photon count using GPU-accelerated real-time processing. Similar approaches using fast digitization have previously been demonstrated for FLIM24−26 and secondary electron counting in scanning electron microscopy.27

Here, we expand upon previous methods with higher bandwidth detection electronics and explore the implications of using a hybrid photodetector (HPD) versus using a PMT. PMTs have high gain variability due to the multiple dynode amplification, in which the randomness associated with signal amplification at each dynode is compounded. HPDs have a two-step amplification process consisting of electron bombardment and then avalanche gain, which leads to low gain variability and a more linear dependence of signal on the number of incident photons.28,29 The signal created by a PMT when a single photon arrives at the detector is highly variable and cannot be easily distinguished from the signal created when multiple photons arrive nearly simultaneously; however, when using an HPD, single- and multiphoton responses can be distinguished.28−31 Although this principle is known, to our knowledge, it has not previously been utilized in computational photon counting methods to count multiple photons arriving at the HPD within the detector response time.

Results and Discussion

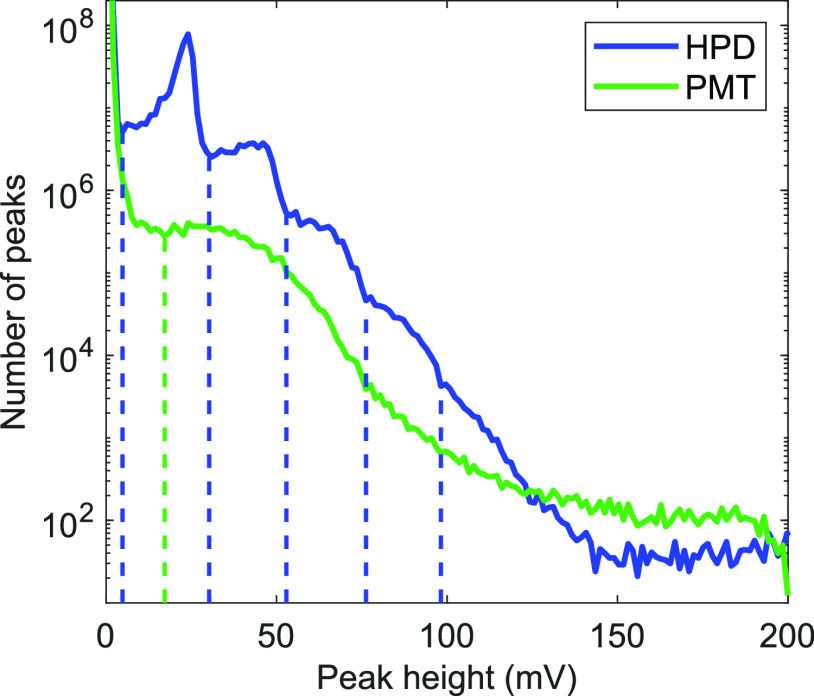
In response to the arrival of one or more photons, HPDs and PMTs produce waveforms that have peaks of various heights. To examine the differences between HPD (R10467U-40, Hamamatsu) and PMT (H10721-210, Hamamatsu) photon peak height distribution, we examined two-photon fluorescence of NADH in concentrations from 1 to 5 mM on our custom FLIM system (similar to our previously published system;17,32 see Figure S1) using both detectors and digitizing the amplified output at 5 GS/s. The peak height distributions (Figure 1) match well with previously experimental28,31 and theoretical29 comparisons of HPD and PMT performance. By examining the local minima of the HPD and PMT peak height distributions, thresholds for one to five photons were set for the HPD and a threshold for a single photon was set for the PMT (dashed vertical lines, Figure 1). These lines delineate whether a peak will be counted as 0, 1, 2, etc. photons. Inevitably there is some overlap between expected peak heights for different numbers of incident photons on the detector, which is one source of error for this method that is not present in traditional single-photon counting systems when photon rates are kept very low.

Figure 1.

Figure 1

Open in a new tab

Peak height distribution for hybrid photodetector (HPD, blue) and photomultiplier tube (PMT, green) for 1–5 mM NADH using 30 mW of power incident on the sample. Dashed lines delineate between peak heights that arise from different numbers of incident photons on the detectors. The negative PMT output values were inverted for easier comparison.

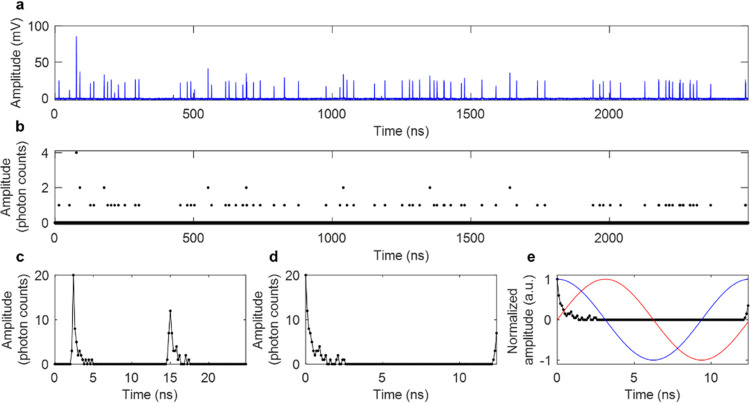
To acquire time-resolved photon counts using computational photon counting, a standard optical setup for a two-photon fluorescence microscope was used and the fluorescence was collected in the epi-direction by an HPD (Figure S1). The detector output is amplified and directly sampled at 5 GS/s (Figure 2a), computationally converted into photon counts using GPU-accelerated processing17,32,33 (Figure 2b), compressed into one 25 ns time block for each pixel composing of the average photon counts over two laser periods (Figure 2c), and then interleaved and shifted based on the time bin within the line of data that has the maximum value (Figure 2d). Digitization at 5 GS/s leads to interleaved sampling since the laser period (12.5 ns) is not a multiple of the sampling period (0.2 ns), so data can be averaged into a time period of twice the laser period (25 ns) and then interleaved to have 0.1 ns time bins over a 12.5 ns period. Interleaved sampling has similarly been applied for direct pulse sampling FLIM.34 For fast and convenient lifetime calculation, phasor analysis35 is applied to photon counts to determine fluorescence lifetime and phasor components g and s (Figure 2e).

Figure 2.

Figure 2

Open in a new tab

Data processing steps for a single pixel of data using Single- and multiphoton PEak Event Detection (SPEED). (a) Raw data: HPD output that was amplified and then directly digitized at 5 GS/s. (b) Photon counts based on the multiple threshold model for the HPD. (c) Photon counts averaged into twice the laser period, 25 ns. (d) Photon counts interleaved and circularly shifted to have the maximum value at t = 0 ns. (e) Photon counts (black), and sine (red) and cosine (blue) multiplication factors that are used to calculate g and s components for phasor analysis.

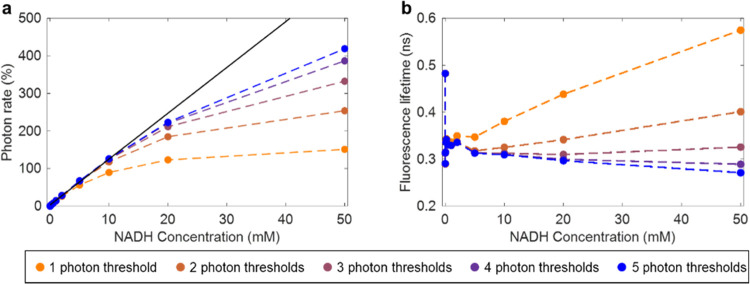
The intensity linearity and fluorescence lifetime accuracy at different concentrations of NADH were examined using one to five photon thresholds for the HPD (Figure 3) to determine the optimal number of thresholds. Using five photon thresholds provided the best intensity linearity (Figure 3a) and consistent lifetime estimation from 0.005 to 50 mM NADH (Figure 3b). Using five photon thresholds also provided accurate lifetime estimation for fluorescent dyes such as Rhodamine B and Fluorescein (Figure S2) and provided a better fit to a Poisson distribution of photon arrivals than a single photon threshold (Figure S3).

Figure 3.

Figure 3

Open in a new tab

Intensity linearity and fluorescence lifetime consistency acquired using HPD for different concentration of NADH with constant excitation power. (a) Intensity linearity given in calculated photon rate as a function of NADH concentration. The black line represents a linear fit for NADH concentrations 0–10 mM and associated photon rates. (b) Calculated fluorescence lifetime of NADH over the same range of concentrations.

Our previous characterization of the performance of the SPEED algorithm using a PMT calculated the maximum acceptable photon rate as the upper limit where less than 10% of photon counts appear to be missed, and fluorescence lifetime was consistently estimated within 10% error.17 Using the same metric, accurate intensity results are acquired using the HPD at a maximum NADH concentration of 20 mM, which had a counted photon rate of 223% with an estimated 9.75% loss of photon counts from a linear fit (black solid line, Figure 3a) calculated based on photon rate from lower concentrations. This is higher than our previously published maximum photon rate calculated using a PMT, of around 206%.17 Using the HPD, we can confidently classify high-amplitude peaks as multiple photon counts. However, there is still pile-up experienced due to the nature of peak detection, which requires unique peaks, meaning that if the directly acquired signal does not decrease in the digitized point immediately after a photon arrives at the detector due to a high photon rate, photons will still be missed. The dead time is approximately twice the sampling period: 0.4 ns (Figure S4), as opposed to the previously achieved dead time of 0.625 ns achieved using digitization at 3.2 GS/s.17 The theoretical maximum possible measurable photon count rate is the inverse of the dead time, which is 2.5 giga counts per second, though of course this is not practical and the performance of the system to characterize fluorescence lifetime at a rate that high would be poor. Future work could incorporate dead time corrections and compensations36−38 to further improve results and achieve better accuracy at high photon rates.

In contrast to the small improvement in maximum acceptable photon rate, the fluorescence lifetime consistency across a wide range of photon rates is substantially improved compared to previous results. Our previously published system accurately estimated NADH fluorescence lifetime for photon rates of approximately 6–206%.17 Now, with improved bandwidth and the multithreshold model for HPD photon counts, NADH fluorescence lifetime is accurately estimated for photon rates from 0.03 to 419% (Figure 3b) using five photon thresholds. Interestingly, using three photon thresholds showed more consistent lifetime estimation at high photon rates, likely due to both underestimating the maximum number of photons arriving within a time bin and underestimating subsequent photons due to pile-up. Finer temporal resolution and slightly shorter dead time are highly impactful in fluorescence lifetime estimation since the fluorescence lifetime of NADH in solution is short. With a fluorescence lifetime of only ca. 0.3–0.4 ns,6 the probability that multiple photons will arrive in consecutive time bins is larger for 0.3125 ns time bins than for 0.200 ns time bins, leading to the superior performance in lifetime estimation for our higher bandwidth system. Additionally, fluorescence lifetime estimation at low photon rates is drastically improved using all of the data acquired in each line of the image (instead of each pixel of the image, as in previous demonstration17) to determine the time bin that is synchronized with the excitation pulse (Supplementary Note 1, Figure S5).

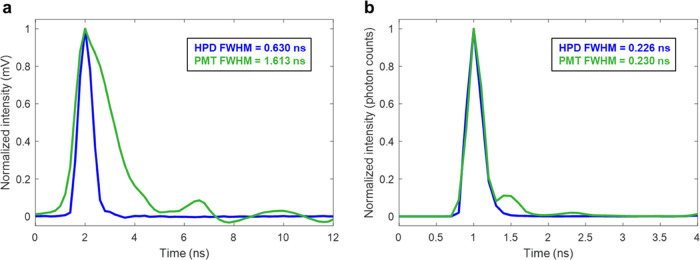
To characterize detector performance, we compared the single-photon temporal response by averaging the directly digitized signal of thousands of single- and multiphoton waveforms (Figure 4a), and the impulse response function in photon counts (Figure 4b) as the resultant timecourse of second harmonic generation (SHG), which unlike fluorescence is an instantaneous process. The waveform of the HPD response to photons had a full width at half-maximum (FWHM) of 0.630 ns (Figure 4a), which corresponds well to the manufacturer-specified 0.6 ns pulse width. The waveform of the PMT response had an FWHM of 1.613 ns (Figure 4a), similar to our previous estimation of 1.617 ns, which was collected using slightly lower bandwidth electronics.17 However, when comparing the impulse response function using counted photons (Figure 4b), computed as the incident photon counts obtained over time for SHG, the HPD and PMT performed similarly, with FWHM values of 0.226 and 0.230 ns, respectively. The PMT had a small number of counts after the main response, which could be due to some signal reflection between the PMT, amplifier, and digitizer, although it was not observed in the HPD data, or could be due to afterpulsing of the PMT.39,40 These results were obtained at relatively low photon rates, with a mean pixel photon rate of 0.32% (max 13.5%) for the HPD and 0.33% (max 7.5%) for the PMT to eliminate the effect pile-up would have on the estimated response functions; similar values were obtained using both detectors with higher photon rate data as well. Both the HPD and PMT are thus good detector candidates for computational photon counting using peak detection. Many traditional photon counting methods rely on discriminators, which have reduced capability when the detector waveform is longer. However, when using peak detection, the temporal impulse response computed using photon counts is only 0.04 ns different for these two detectors since peaks can be discriminated even if two photons arrive within the FWHM of the detector waveform. Though as previously stated, the HPD has the benefit of better performance due to the ability to clearly characterize arrivals of multiple photons within one time bin.

Figure 4.

Figure 4

Open in a new tab

Impulse response functions using both an HPD (blue) and a PMT (green). (a) Average single-photon waveform, calculated using direct pulse sampling methods. (b) Impulse response function using computational photon counting, determined as the resultant temporal spread of signal from SHG, which should produce an instantaneous response.

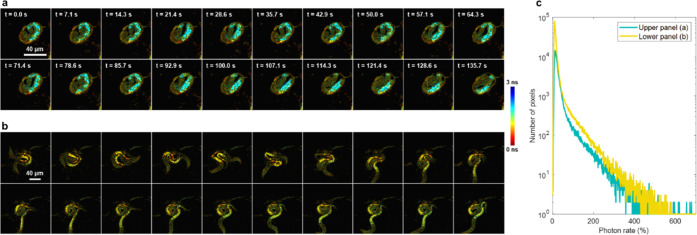
To demonstrate the capabilities of a fast FLIM system equipped with high maximum photon rate detection, we acquired label-free images of live, nonimmobilized C. elegans at room temperature using 2.5 μs pixel dwell times, with only 200 laser pulses per pixel per frame and no frame averaging (Figure 5). With 10–15 mW of incident power on the sample and two-photon excitation at 750 nm, live C. elegans produced photon rates up to over 600% within a single pixel with approximately 3% of pixels within the C. elegans producing photon rates over 100% (Figure 5c). Fluorescence was acquired within a 75 nm spectral band centered at 450 nm to target NAD(P)H autofluorescence. Additional videos show the motion of a mature C. elegans egg (Figure 5a, Video 1) and two C. elegans moving around (Figure 5b, Video 2). The NAD(P)H two-photon autofluorescence lifetime in C. elegans has been previously imaged and characterized using FLIM systems with significantly slower acquisition, such as with 160 μs pixel dwell time and using the average of eight images where C. elegans were immobilized by the addition of polystyrene beads.41 In addition, human breast cancer cells produced measured photon rates that increased almost 10-fold in seconds during apoptosis (Figure S6, Supplementary Note 2), which shows that high maximum photon rate imaging capabilities are useful for high-dynamic-range processes in living samples.

Figure 5.

Figure 5

Open in a new tab

NAD(P)H autofluorescence in live C. elegans over 135.7 s. Single frames acquired with 2.5 μs pixel dwell time are shown with no frame averaging. (a) Mature egg in its final stages before hatching (256 × 256 pixels). (b) Two C. elegans in motion (512 × 512 pixels). Scale bar: 40 μm. (c) Histogram of nonzero photon rates within pixels of all frames of both the mature egg from (a) (teal) and the two hatched C. elegans from (b) (yellow).

Although useful frames can be acquired with just 2.5 μs pixel dwell time, the transferring, processing, and saving of multiple gigabytes of raw data acquired for each frame presently limit the imaging speed. GPU-accelerated processing enables saving processed data (∼0.15 Hz) 2.5 times faster than saving raw data (∼0.06 Hz). FPGA-based peak detection methods could be used in future work to reduce the volume of data and enable higher frame rates that can fully utilize the capability to collect many photon counts with only 2.5 μs pixel dwell time. Another consideration is the number of imaging channels. Due to the limitation on data transfer speed, we only performed computational photon counting on one channel from a single detector, although a few digitizers exist that can acquire multiple channels of data at sufficiently high rates for accurate computational photon counting that could enable the use of two channels simultaneously. The use of multiple detectors has been employed previously to improve the FLIM throughput of TCSPC systems.22,26,42 Furthermore, there are many more detectors than just HPDs and PMTs that could potentially be used in future work with similar fast digitization and computational photon counting such as electron-bombarded CCDs,43 SiPMs,10 SPAD arrays,11 and ultrafast CMOS cameras.44

Faster photon counting technologies enable the ability to study fast biological dynamics and ameliorate some of the challenges and limitations associated with the translation of multiphoton microscopy to clinical imaging, such as long image acquisition times. Presently, portable multiphoton systems have been used for clinical imaging of autofluorescence and multiharmonic imaging.45,46 Notably, the JenLab MPTflex system has been used for two-photon FLIM of NAD(P)H for in vivo human studies,45 yet the image acquisition time is significantly longer than what could be achieved using computational photon counting methods and multiple photon thresholds, depending on the emitted photon rate distribution. Samples that only produce low (<5–10%) photon rates would optimally be imaged using TCSPC systems with good temporal resolution, but when the maximum photon rate emitted by a sample is higher, the presented methods allow for faster acquisition while maintaining photon counting accuracy. Thus, enabling photon counting in FLIM for photon rates up to 223% using fast electronics, an HPD, and computational photon counting with a multithreshold model can open up new research, commercial, and clinical possibilities for FLIM.

Methods

FLIM System

The microscopy system used for imaging is described in Figure S1 and is similar to previous setups.12,19 Briefly, the tunable output of an 80 MHz pulsed laser source (InSight X3+, Spectra-Physics) was used in a laser scanning setup with two galvanometer mirrors (6230H, Cambridge Technologies) and a water immersion, 1.05 NA multiphoton excitation imaging objective lens (XLPLN25XWMP2, Olympus) to excite two-photon fluorescence and SHG, which were collected in the epi-direction using a dichroic mirror (FF665-Di01, Semrock) to separate excitation and emission. Another removable dichroic mirror was used to direct the emitted fluorescence or SHG to either an HPD (R10467U-40, Hamamatsu) or an analog output PMT (H10721-210, Hamamatsu). The signal was amplified by a 20 dB, 2.5 GHz bandwidth amplifier (HSA-X-2-20, Femto) and digitized by a high-speed digitizer (ADQ7WB, Teledyne SP Devices). For the determination of photon thresholds, raw data was saved and later analyzed in MATLAB 2021a (MathWorks). Real-time GPU-accelerated processing (using a GeForce RTX 2080, NVIDIA) was used to save processed compressed data after threshold analysis was completed. A custom LabVIEW software and GUI were used to control acquisition. Unless otherwise specified, a laser pulse centered at 750 nm with a 240 fs pulse duration at the sample plane was used for excitation, the FOV was 512 × 512 pixels (180 × 180 μm), and pixel dwell time was 2.5 μs.

Fluorophore and Standard Preparations

NADH powder was dissolved in a 1 M HEPES buffer to maintain a stable pH. Rhodamine B was dissolved in sterile water, and Fluorescein was dissolved in 100% ethanol. SHG was imaged using urea crystals.

C. elegans Sample Preparation

C. elegans growing on agar plates seeded with E. coli were obtained (Carolina Biological Supply Company) and left to grow for 2–4 days. For imaging, a small (<1 cm diameter) portion was cut out of the agar plate and placed in an imaging dish (P35G-0-10-C, MatTek). An average power of 10–15 mW was incident on the sample for imaging.

Acknowledgments

The authors thank Darold Spillman for his administrative and technical support and Eric Chaney and Dr. Edita Aksamitiene for help with the mammalian cell culture.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.2c00505.

  • Motion of a matureC. elegans egg (Video 1) (AVI)

  • TwoC. elegans moving around (Video 2) (AVI)

  • Custom two-photon FLIM setup for implementing SPEED (Figure S1); fluorescence decay curves of fluorescent standards using SPEED and TCSPC (Figure S2); photon counting histograms and fit to Poisson model (Figure S3); demonstration of 0.4 ns dead time using SPEED with HPD (Figure S4); inferring laser pulse temporal alignment with digitized data (Supplementary Note 1); inferring laser pulse temporal alignment using each pixel or each line of data (Figure S5); description of mammalian cell culture and treatment (Supplementary Note 2); and apoptosis dynamics in human breast cancer cells imaged using SPEED (Figure S6) (PDF)

Author Contributions

J.E.S., R.R.I., L.Y., and S.A.B. designed the research. J.E.S., R.R.I., and L.Y. designed the microscopy system with significant guidance from G.W., H.T., M.M., and S.A.B. J.E.S., R.R.I., L.Y., and E.M.M. built the microscopy system. J.E.S. prepared samples, acquired images, and analyzed the data. J.E.S. and S.A.B. wrote the paper. S.A.B. obtained funding to conduct the research.

This work was partially supported by grants from the National Institutes of Health, U.S. Department of Health and Human Services (R01CA213149, R01CA241618, R43MH119979, and R41GM139528), and the Air Force Office of Scientific Research (FA9550-17-1-0387). J.E.S. was supported by the National Science Foundation Graduate Research Fellowship Program (DGE-1746047). Additional information can be found at http://biophotonics.illinois.edu.

The method and apparatus reported here have been disclosed as intellectual property by J.E.S., R.R.I., and S.A.B. to the Office of Technology Management at the University of Illinois at Urbana-Champaign.

The authors declare the following competing financial interest(s): The method and apparatus reported here has been disclosed as intellectual property by J.E.S., R.R.I, and S.A.B. to the Office of Technology Management at the University of Illinois at Urbana-Champaign.

Notes

Data presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request and through a collaborative research agreement. The GPU code for real-time processing will be made available upon publication at: https://github.com/Biophotonics-COMI.

Supplementary Material

ph2c00505_si_001.avi (516.4KB, avi)
ph2c00505_si_002.avi (551.2KB, avi)
ph2c00505_si_003.pdf (578.7KB, pdf)

References

  1. Li B.; Bartos J.; Xie Y.; Huang S.-W. Time-magnified photon counting with 550-fs resolution. Optica 2021, 8, 1109–1112. 10.1364/OPTICA.420816. [DOI] [Google Scholar]
  2. Fu C.; Zheng H.; Wang G.; Zhou Y.; Chen H.; He Y.; Liu J.; Sun J.; Xu Z. Three-dimensional imaging via time-correlated single-photon counting. Appl. Sci. 2020, 10, 1930. 10.3390/app10061930. [DOI] [Google Scholar]
  3. Berezin M. Y.; Achilefu S. Fluorescence lifetime measurements and biological imaging. Chem. Rev. 2010, 110, 2641–2684. 10.1021/cr900343z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bower A. J.; Sorrells J. E.; Li J.; Marjanovic M.; Barkalifa R.; Boppart S. A. Tracking metabolic dynamics of apoptosis with high-speed two-photon fluorescence lifetime imaging microscopy. Biomed. Opt. Express 2019, 10, 6408–6421. 10.1364/BOE.10.006408. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Gómez C. A.; Sutin J.; Wu W.; Fu B.; Uhlirova H.; Devor A.; Boas D. A.; Sakadžić S.; Yaseen M. A. Phasor analysis of NADH FLIM identifies pharmacological disruptions to mitochondrial metabolic processes in the rodent cerebral cortex. PLoS One 2018, 13, e0194578 10.1371/journal.pone.0194578. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Lakowicz J. R.; Szmacinski H.; Nowaczyk K.; Johnson M. L. Fluorescence lifetime imaging of free and protein-bound NADH. Proc. Natl. Acad. Sci. U.S.A. 1992, 89, 1271–1275. 10.1073/pnas.89.4.1271. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Datta R.; Heaster T. M.; Sharick J. T.; Gillette A. A.; Skala M. C. Fluorescence lifetime imaging microscopy: fundamentals and advances in instrumentation, analysis, and applications. J. Biomed. Opt. 2020, 25, 071203 10.1117/1.JBO.25.7.071203. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Hirvonen L. M.; Suhling K. Fast timing techniques in FLIM applications. Front. Phys. 2020, 8, 161. 10.3389/fphy.2020.00161. [DOI] [Google Scholar]
  9. Gerritsen H. C.; Agronskaia A. V.; Bader A. N.; Esposito A.. Time Domain FLIM: Theory, Instrumentation, and Data Analysis. In Laboratory Techniques in Biochemistry and Molecular Biology; van der Vliet P. C.; Pillai S., Eds.; North Holland Publishing Co., 2009; Vol. 33, pp 95–132. [Google Scholar]
  10. Klanner R. Characterisation of SiPMs. Nucl. Instrum. Methods Phys. Res., Sect. A 2019, 926, 36–56. 10.1016/j.nima.2018.11.083. [DOI] [Google Scholar]
  11. Bruschini C.; Homulle H.; Antolovic I. M.; Burri S.; Charbon E. Single-photon avalanche diode imagers in biophotonics: review and outlook. Light: Sci. Appl. 2019, 8, 87. 10.1038/s41377-019-0191-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Krstajić N.; Poland S.; Levitt J.; Walker R.; Erdogan A.; Ameer-Beg A.; Henderson R. K. 0.5 billion events per second time correlated single photon counting using CMOS SPAD arrays. Opt. Lett. 2015, 40, 4305–4308. 10.1364/OL.40.004305. [DOI] [PubMed] [Google Scholar]
  13. Schuyler R.; Isenberg I. A monophoton fluorometer with energy discrimination. Rev. Sci. Instrum. 1971, 42, 813. 10.1063/1.1685237. [DOI] [Google Scholar]
  14. van Meurs B.; van der Werf R. A circuit for rejecting multiple events detected during a timing cycle in single photon counting experiments. J. Phys. E: Sci. Instrum. 1976, 9, 437. 10.1088/0022-3735/9/6/005. [DOI] [Google Scholar]
  15. Farina S.; Labanca I.; Acconcia G.; Ghezzi A.; Farina A.; D’Andrea C.; Rech I. Above pile-up fluorescence microscopy with a 32 Mc/s single-channel time-resolved SPAD system. Opt. Lett. 2022, 47, 82–85. 10.1364/OL.444815. [DOI] [PubMed] [Google Scholar]
  16. Bower A. J.; Li J.; Chaney E. J.; Marjanovic M.; Spillman D. R.; Boppart S. A. High-speed imaging of transient metabolic dynamics using two-photon fluorescence lifetime imaging microscopy. Optica 2018, 5, 1290–1296. 10.1364/OPTICA.5.001290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Sorrells J. E.; Iyer R. R.; Yang L.; Chaney E. J.; Marjanovic M.; Tu H.; Boppart S. A. Single-photon peak event detection (SPEED): a computational method for fast photon counting in fluorescence lifetime imaging microscopy. Opt. Express 2021, 29, 37759–37775. 10.1364/OE.439675. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. de Grauw C. J.; Gerritsen H. C. Multiple time-gate module for fluorescence lifetime imaging. Appl. Spectrosc. 2001, 55, 670–678. 10.1366/0003702011952587. [DOI] [Google Scholar]
  19. Yang W.; Chen S.-L. Time-gated fluorescence imaging: advances in technology and biological applications. J. Innovative Opt. Health Sci. 2020, 13, 2030006 10.1142/S1793545820300062. [DOI] [Google Scholar]
  20. Liu C.; Wang X.; Zhou Y.; Liu Y. Timing and operating mode design for time-gated fluorescence lifetime imaging microscopy. Sci. World J. 2013, 2013, 801901 10.1155/2013/801901. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Loidolt-Krüger M.; Jolmes F.; Patting M.; Wahl M.; Sisamakis E.; Devaux A.; Erdman R. PicoQuant Photonics North America, Inc.: using rapidFLIMHiRes to visualize dynamic processes with ultra fast FLIM imaging and outstanding time resolution. Proc. SPIE 2021, 11715, 117150D 10.1117/12.2595993. [DOI] [Google Scholar]
  22. Wahl M.; Röhlicke T.; Kulish S.; Rohilla S.; Krämer B.; Hocke A. C. Photon arrival time tagging with many channels, sub-nanosecond deadtime, very high throughput, and fiber optic remote synchronization. Rev. Sci. Instrum. 2020, 91, 013108 10.1063/1.5121412. [DOI] [PubMed] [Google Scholar]
  23. Colyer R. A.; Lee C.; Gratton E. A novel fluorescence lifetime imaging system that optimizes photon efficiency. Microsc. Res. Tech. 2008, 71, 201–213. 10.1002/jemt.20540. [DOI] [PubMed] [Google Scholar]
  24. Moon S.; Park B.; Won Y. Digital implementation of TCSPC. Opt. Lett. 2020, 45, 1615–1618. 10.1364/OL.384461. [DOI] [PubMed] [Google Scholar]
  25. Hwang W.; Kim D.; Moon S.; Kim D. Y. Achieving a high photon count rate in digital time-correlated single photon counting using a hybrid photodetector. Opt. Express 2021, 29, 9797–9804. 10.1364/OE.419896. [DOI] [PubMed] [Google Scholar]
  26. Alvarez L. A. J.; Widzgowski B.; Ossato G.; van den Broek B.; Jalink K.; Kuschel L.; Roberti M. J.; Hecht F. SP8 FALCON: a novel concept in fluorescence lifetime imaging enabling video-rate confocal FLIM. Nat. Methods 2019, 16, 1069–1071.31619775 [Google Scholar]
  27. Agarwal A.; Simonaitis J.; Goyal V. K.; Berggren K.. Secondary electron count imaging in SEM. ArXiv (Physics, Instrumentation and Detectors). arXiv:2111.01862v1. arXiv.org e-Print archive. https://arxiv.org/abs/2111.01862 (accessed Aug 3, 2022).
  28. Kim D.; Hwang W.; Won Y.; Moon S.; Lee S. Y.; Kang M.; Han W. S.; Kim D. Y. Enhancement of performance in time-domain FLIM with GaAsP hybrid detectors. Proc. SPIE 2019, 10882, 108821J 10.1117/12.2510959. [DOI] [Google Scholar]
  29. Photomultiplier Tubes: Basics and Applications, 3rd ed.; Hamamatsu Photonics, 2007. [Google Scholar]
  30. Michalet X.; Cheng A.; Antelman J.; Suyama M.; Arisaka K.; Weiss S. Hybrid photodetector for single-molecule spectroscopy and microscopy. Proc. SPIE 2008, 6862, 68620F 10.1117/12.763449. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Fukasawa A.; Haba J.; Kageyama A.; Nakazawa H.; Suyama M. High speed HPD for photon counting. IEEE Trans. Nucl. Sci. 2008, 55, 758–762. 10.1109/TNS.2008.918736. [DOI] [Google Scholar]
  32. Iyer R. R.; Sorrells J. E.; Yang L.; Chaney E. J.; Spillman D. R. Jr.; Tibble B. E.; Renteria C. A.; Tu H.; Žurauskas M.; Marjanovic M.; Boppart S. A. Label-free metabolic and structural profiling of dynamic biological samples using multimodal optical microscopy with sensorless adaptive optics. Sci. Rep. 2022, 12, 3438 10.1038/s41598-022-06926-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Sorrells J. E.; Iyer R. R.; Yang L.; Bower A. J.; Spillman D. R.; Chaney E. J.; Tu H.; Boppart S. A. Real-time pixelwise phasor analysis for video-rate two-photon fluorescence lifetime imaging microscopy. Biomed. Opt. Express 2021, 12, 4003–4019. 10.1364/BOE.424533. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Dow X. Y.; Sullivan S. Z.; Muir R. D.; Simpson G. J. Video-rate two-photon excited fluorescence lifetime imaging system with interleaved digitization. Opt. Lett. 2015, 40, 3296–3299. 10.1364/OL.40.003296. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Digman M. A.; Caiolfa V. R.; Zamai M.; Gratton E. The phasor approach to fluorescence lifetime imaging analysis. Biophys. J. 2008, 94, L14–L16. 10.1529/biophysj.107.120154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Coates P. B. The correction for photon ‘pile-up’ in the measurement of radiative lifetimes. J. Phys. E: Sci. Instrum. 1968, 1, 878. 10.1088/0022-3735/1/8/437. [DOI] [Google Scholar]
  37. Isbaner S.; Karedla N.; Ruhlandt D.; Stein S. C.; Chizhik A.; Gregor I.; Enderlein J. Dead-time correction of fluorescence lifetime measurements and fluorescence lifetime imaging. Opt. Express 2016, 24, 9429–9445. 10.1364/OE.24.009429. [DOI] [PubMed] [Google Scholar]
  38. Rapp J.; Ma Y.; Dawson R. M. A.; Goyal V. K. Dead time compensation for high-flux ranging. IEEE Trans. Signal Process. 2019, 67, 3471–3486. 10.1109/TSP.2019.2914891. [DOI] [Google Scholar]
  39. Coates P. B. The origins of afterpulses in photomultipliers. J. Phys. D: Appl. Phys. 1973, 6, 1159–1166. 10.1088/0022-3727/6/10/301. [DOI] [Google Scholar]
  40. Morton G. A.; Smith H. M.; Wasserman R. Afterpulses in photomultipliers. IEEE Trans. Nucl. Sci. 1967, 14, 443–448. 10.1109/TNS.1967.4324452. [DOI] [Google Scholar]
  41. Stringari C.; Abdeladim L.; Malkinson G.; Mahou P.; Solinas X.; Lamarre I.; Brision S.; Galey J.-B.; Supatto W.; Legouis R.; Pena A.-M.; Beaurepaire E. Multicolor two-photon imaging of endogenous fluorophores in living tissues by wavelength mixing. Sci. Rep. 2017, 7, 3792 10.1038/s41598-017-03359-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. McLoskey D.; Birch D. J. S.; Sanderson A.; Suhling K.; Welch E.; Hicks P. J. Multiplexed single-photon counting. I. A time-correlated fluorescence lifetime camera. Rev. Sci. Instrum. 1996, 67, 2228–2237. 10.1063/1.1147041. [DOI] [Google Scholar]
  43. Hirvonen L. M.; Jiggins S.; Sergent N.; Zanda G.; Suhling K. Photon counting imaging with an electron-bombarded CCD: towards a parallel-processing photoelectric time-to-amplitude converter. Rev. Sci. Instrum. 2014, 85, 123102 10.1063/1.4901935. [DOI] [PubMed] [Google Scholar]
  44. Sergent N.; Levitt J.; Green M.; Suhling K. Rapid wide-field photon counting imaging with microsecond time resolution. Opt. Express 2010, 18, 25292–25298. 10.1364/OE.18.025292. [DOI] [PubMed] [Google Scholar]
  45. Weinigel M.; Breunig H. G.; Uchugonova A.; König K. Multipurpose nonlinear optical imaging system for in vivo and ex vivo multimodal histology. J. Med. Imaging 2015, 2, 016003 10.1117/1.JMI.2.1.016003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Yang L.; Park J.; Marjanovic M.; Chaney E. J.; Spillman D. R. Jr.; Phillips H.; Boppart S. A. Intraoperative label-free multimodal nonlinear optical imaging for point-of-procedure cancer diagnostics. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 6801412 10.1109/JSTQE.2021.3054578. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ph2c00505_si_001.avi (516.4KB, avi)
ph2c00505_si_002.avi (551.2KB, avi)
ph2c00505_si_003.pdf (578.7KB, pdf)

Articles from ACS Photonics are provided here courtesy of American Chemical Society

RESOURCES