Quantitative Acoustophoresis

Abstract

Studying cellular mechanics allows important insights into its cytoskeletal composition, developmental stage, and health. While many force spectroscopy assays exist that allow probing of mechanics of bioparticles, most of them require immobilization of and direct contact with the particle and can only measure a single particle at a time. Here, we introduce quantitative acoustophoresis (QAP) as a simple alternative that uses an acoustic standing wave field to directly determine cellular compressibility and density of many cells simultaneously in a contact-free manner. First, using polymeric spheres of different sizes and materials, we verify that our assay data follow the standard acoustic theory with great accuracy. We furthermore verify that our technique not only is able to measure compressibilities of living cells but can also sense an artificial cytoskeleton inside a biomimetic vesicle. We finally provide a thorough discussion about the expected accuracy our approach provides. To conclude, we show that compared to existing methods, our QAP assay provides a simple yet powerful alternative to study the mechanics of biological and biomimetic particles.

Introduction

Being able to measure the mechanical properties of a biological material is key for understanding the molecular basis and biological function of these properties. For example, the eukaryotic cytoskeleton is a composition of intertwined networks of microtubules as well as actin and intermediate filaments. Together, these structures play a crucial role in cell motility, division, and shape maintenance and dictate the mechanical properties of the cell. A wide variety of experimental techniques have been applied to study cell mechanics, including atomic force microscopy,^1,2 pipette aspiration,^3,4 optical tweezers,⁵⁻⁷ and others.^8,9 Most of these methods can, however, probe only one cell at a time, making it time-consuming to generate sufficient statistics. Moreover, these techniques usually require direct contact with the target surface, which allows access to only a small portion of the cell, thus decreasing the sensitivity for elucidating the interior structural responses. In addition, contact with the surface might also give rise to distortions of the cellular response. To circumvent these issues, we introduce here a contact-free and multiplexed quantitative method to measure the mechanical properties of biological particles based on acoustic manipulation.^10,11

It has long been appreciated that compressible particles immersed in a liquid experience a force when placed in an acoustic standing wave (ASW) field.^12,13 As has been established more than five decades ago,¹⁴ this acoustic radiation force (referred to as force in the following) depends on the particle volume and density/compressibility ratios between the particle and liquid; thus, its use does not require any labels or contact with the sample. Over the years, ASW-based methods have found a wide range of applications, for example, spawning a whole research field called acoustofluidics. Some of the notable applications of acoustofluidics include applying forces in order to efficiently mix fluids inside a microfluidic chip^15,16 (which is normally a challenge at the very low Reynolds numbers characteristic for these devices); manipulating microscopic particles such as cells using acoustic tweezers;¹⁷⁻¹⁹ using sonoporation for gene delivery into cells;²⁰ enriching nanoparticles,²¹ and filtering/sorting biological particles based on the difference in their sizes and mechanical properties²²⁻²⁴ (often referred to as acoustophoresis). These methods use acoustic force solely in a qualitative manner, that is, to manipulate particles and/or their environment and are consequently not adapted for quantitative characterization of the particles. While acoustic force spectroscopy (AFS) has recently been established as a powerful tool to exert and measure forces on bioparticles tethered between a surface and a microparticle with piconewton precision,^10,11,25,26 the ASW field serves only as a manipulation tool for the microparticle and is therefore not used to directly extract mechanical information from the bioparticle itself. In contrast, acoustic scattering has been employed to reveal important aspects of cellular mechanics in size-normalized acoustic scattering (SNACS).²⁷ Thus, even though SNACS measures relative changes and is not optimized to determine quantifiable parameters of cell mechanics such as Young’s modulus, this technique is able to sense different steps in the cell cycle based on relative changes in cell stiffness.

Here, we build upon a different approach, quantitative acoustophoresis (QAP), which uses the fact that the applied force acting on a particle in an ASW field depends on the volume, density, and compressibility of the particle. In the case that the particle volume and density can be measured independently, quantifying the particle force in an ASW field of known intensity thus enables determination of the particle compressibility. In turn, the force can be calculated from measured particle trajectories, making use of the balance between the acoustic force, Stokes drag, and buoyance force.²⁸ While other versions of this method have been proposed before²⁹⁻³¹ (sometimes integrated with other biophysical techniques^32,33), a thorough investigation of important aspects such as measurement precision, data variability, and error sources has so far been lacking. This has greatly limited its use as a general multiplexed and quantitative tool to probe and characterize biological material in a contact-free manner.

In the current study, we present a QAP design that can be used to independently determine the radius, density, and compressibility from multiple particles of an unknown sample simultaneously. Compared to existing methods, our approach not only is very simple (both in its experimental implementation and data analysis) but also allows us to study dynamic changes in the mechanics of the same particles over time. Starting with commercially available spherical particles, we first verified that our measurement data depend on these particle parameters as the standard acoustic theory predicts. Next, we extended our measurements to biomimetic giant unilamellar vesicles (GUVs) and biological samples (eukaryotic cells), and, also here, we found that determined compressibilities are in good agreement with expected values. Finally, we conducted a thorough discussion of potential error sources, which allowed us to conclude that our instrument should be capable of measuring compressibilities of biological samples with an accuracy of better than 90%.

Results and Discussion

Acoustic Force Response of Single Particles Follows the Acoustic Theory

Acoustophoresis takes advantage of the fact that particles immersed in a compressible medium will experience a force when exposed to an ASW field. In addition to an instrument-characteristic term Q (see eq 8 in the Materials and Methods section for the full version), this force F_ac depends on one input parameter (squared voltage U) and three particle-specific parameters: radius R_p, density ρ_p, and compressibility β_p

1

Here, φ_p(ρ_p,β_p) is generally referred to as the acoustic contrast factor (ACF), which is given by

2

where ρ_m and β_m are the density and compressibility of the immersion medium, respectively. The idea behind QAP is that the instrument-characteristic term Q can be deduced from measuring the force response of a known sample where the three above-mentioned particle parameters are known. If one then measures an unknown sample where both density and radius can be determined via different means, the compressibility can accordingly be deduced from the acoustic fore generated.

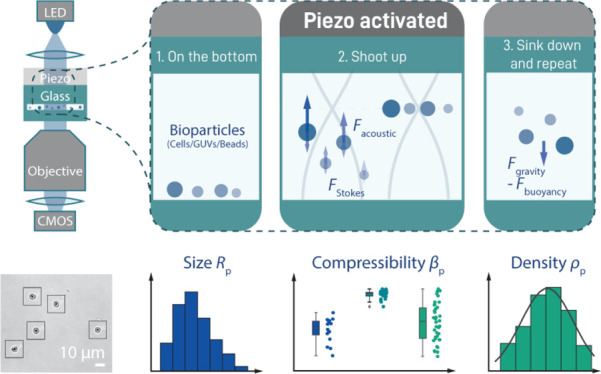
Employing a similar setup to that used for conducting AFS (which uses a piezoelectric actuator to generate an ASW inside a flow cell),^10,11 we are able to determine the radius, density, and compressibility of particles. The main difference between our assay and other implementations of acoustophoresis^28,30,31 is that we create an ASW in a flow cell in the vertical direction (Figure 1A). This means that experiments start with sedimented particles located at the bottom of the flow cell and that the application of an ASW field elevates them into the solution (here denoted as “shooting up”, Figure 1B). This approach provides three advantages compared to a conventional horizontal ASW: (1) measurement of particle translocation in the z-direction allows us to distribute particles over two dimensions (as opposed to one for horizontal acoustophoresis), which enables us to probe a far larger number of particles in a given field of view (FOV), improving statistics (Figure 1B); (2) since particles sediment to the bottom after application of the acoustic force, the same particle can be measured multiple times (Figure 1C); and finally, (3) the sedimentation trajectory of a particle allows straightforward quantification of the density of this particle, independent of its compressibility. In addition, we take advantage of the capability of our assay to remeasure the same particle repeatedly by recording shooting up trajectories over a wide variety of different ASW field intensities. This not only improves the measurement precision but also serves as an important control for a proper acoustic response (see below).

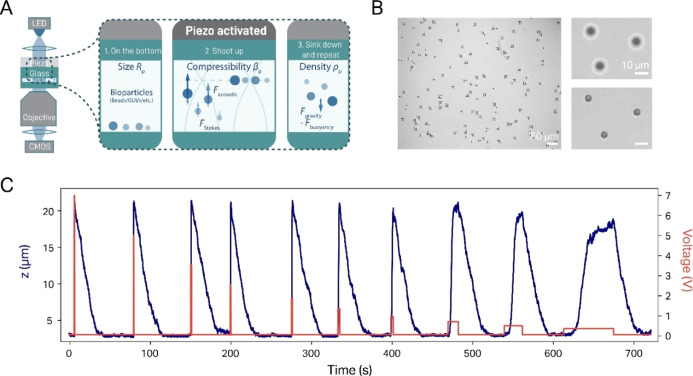
Figure 1.

Setup and general procedure of a QAP measurement. (A) General scheme of the AFS setup (left) and the experimental procedure for QAP (right). (B) Typical brightfield image (left, ∼750 × 600 μm) during a measurement of 5.31 μm PS particles, showing more than 115 trackable beads in the FOV. Since the application of an ASW field induces the particles to rise up toward the node, the corresponding bead translocation is visible and can be tracked by following the change of the bead diffraction pattern. This is visualized in two exemplary brightfield images (right), which show three particles first sedimented at the bottom of the flow cell (top) and then lifted to the node after application of the ASW field (bottom). (C) Exemplary trajectory of a single 5.31 μm PS particle over a full measurement. In this case, we start at a maximum voltage of 7 V and end at the lowest voltage of 0.5 V, yielding a range of >100-fold in ASW field strength. The duration of the field application is increased with decreasing voltage, in order to give the particle sufficient time to levitate to the node (note that at low voltages, the particles do not fully reach the node).

As a proof of concept for the method, we first characterize commercial spherical polystyrene (PS) particles (ρ ≃ 1050 g/L), which are available in a rather narrow size distribution (SD < 5%), in order to check for data consistency in practice (Figure 1C). Generally, every measurement was conducted by applying a voltage signal to the piezo, which induced the particles to travel to the node, located some 20 μm above the bottom surface. After the particles settled in the node, the voltage was shut off until the particle had subsided back to the surface. This procedure is—depending on the particle radius—rather quick (on the minute scale) and thus allows us to remeasure the same particles repeatedly at different voltages and over long timescales (Figure 1C). It should be noted here that this procedure also works if the particles in question are lighter than the immersion medium. In this case, the particles will just rise to the top of the flow cell in the absence of force but will be pushed down (since the acoustic node is in this case below the particles) when an ASW field is applied and is described by the same physics as that discussed below.¹⁰

While the radius of a spherical particle can be measured directly from brightfield images (Figure 1B; note, however, that for commercial samples, we do not measure the size of the particle but take the manufacturer value), the particle density can be deduced from the sedimentation rate (Figure 2A). Two factors have to be considered here: first, we noticed that diffusion is significant for particles smaller than 5 μm and a density close to that of water (<1100 g/L). Therefore, the trajectory of such particles does not follow a monotonous sedimentation course but includes random undulations, which renders fitting of sedimentation trajectories more difficult (Figure 2B). A second feature is that the sedimentation rate is not constant but slows down notably when the particle approaches the surface. This is caused by a relative viscosity increase close to the flow cell walls and can be corrected for using Brenner’s law³⁴ (see the Materials and Methodssection).

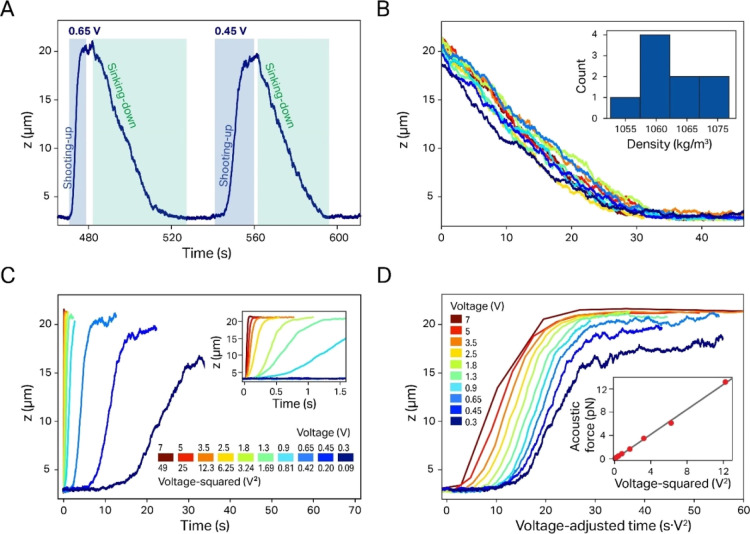
Figure 2.

Exemplary data display and analysis for a single 5.31 μm PS particle (same particle as shown in Figure 1C). (A) The sedimented particle moves to the node when the voltage signal is applied to the piezo and sediments back to the surface when the signal is switched off. (B) The particle density can be determined from sedimentation trajectories. The resulting density distribution from the different sedimentation events is shown in the inset. (C) During shooting up, the particle velocity increases strongly (quadratic dependence) with the applied voltage (an enlarged plot for the higher voltages is shown in the inset). (D) The quadratic dependence of the force on the applied voltage is visualized by generating voltage-adjusted z-trajectories (the same trajectories as those in C). Here, the timescale is normalized by multiplication with the quadratic voltage and reproduces virtually the same shape independent of the applied voltage. (Inset) The quadratic dependence can be better appreciated by plotting the corresponding forces vs the squared voltage, which can be described by a linear fit (black line).

While the average sedimentation rate for a given particle is constant, the shooting up rate in an ASW field changes as a function of the applied voltage (Figure 2C and the inset). In particular, eq 1 predicts that the force acting on the particle scales linearly with the square of the voltage. This prediction holds true over a wide range of forces and can be qualitatively demonstrated by plotting shooting up trajectories at different voltages using a timescale normalized by the squared voltage (Figure 2D), when virtually all curves map onto each other with remarkable precision. Nevertheless, two complication factors have to be considered when deducing the force from the shooting up trajectories. First, the force is not simply a linear function of the shooting up rate since even then, gravity and buoyancy still act on the particles, and thus, the sedimentation has to be taken into account as an additional correction factor. Second, the ASW field and accordingly the force are not constant over the height of the flow cell, which is the reason why we determine the shooting up rate from the “linear” portion of the particle trajectory (see the Materials and Methods section). When we accordingly calculated the forces for a single particle with all the corrections implemented, the obtained force values follow the predicted scaling with the squared voltage with remarkable precision (inset of Figure 2D) except for the data points at the extreme voltages. These deviations are most likely caused by data undersampling (at high voltages) or noise due to diffusion (at the lowest voltages; see the inset of Figure S1 for the full data range). Therefore, our measurements over a wide range of ASW field strengths provide better statistics and serve as an important control regarding data robustness. The plot in the inset of Figure 2D also helps identify the voltage-normalized (VN) force f_ac, that is, the slope of F_ac versus U, as an important parameter for the particle characterization.

Heat Map Calibration Reduces Data Variance Caused by Local Field Heterogeneity

In order to check for reproducibility, we next compared the variance of forces measured for different particles in the same batch. Figure 3A shows the force plotted against the voltage squared for all particles in a single FOV (∼750 × 600 μm, N = 28). In agreement with the results in Figure 2D, all plots reproduced the linear dependency between the exerted force and the voltage squared. However, a substantial particle-to-particle variance is evident in the slope (SD ∼ 20–30%), much larger than what would be expected from either the particle size variation (<5%, as reported by the manufacturer) or the measured variance of the calculated particle density (<1%, inset of Figure 3A). A closer investigation of this phenomenon revealed that for a given FOV, the VN force of individual particles shows a strong spatial correlation, that is, in some areas, significantly stronger forces are exerted on particles than in others. A local heterogeneity of the acoustic field strength of comparable magnitude has been reported for similar experimental setups before and was attributed to the geometry of the flow cell,²⁶ while in another work, the ASW field distribution was shown to be dependent on the dimension of the channel.³⁵ We therefore sought to reduce the resulting measured force variance by accounting for local variations in the ASW field. To this end, we generated “heat maps” by plotting the local relative VN force δf_ac as a function of the position in the flow cell. This map is compiled from the local acoustic response of several hundred particles distributed randomly over a given FOV (Figure 3B). If we then measure the variance of the VN force of a different batch of particles and afterward apply a local correction factor predicted by the heat maps in the same FOV (see the Materials and Methods section), we found that the standard deviation of the relative VN force variance is typically reduced by a factor of 3 (from a SD of ∼20–30% down to ∼ 5–10%, Figure 3C and Table S1).

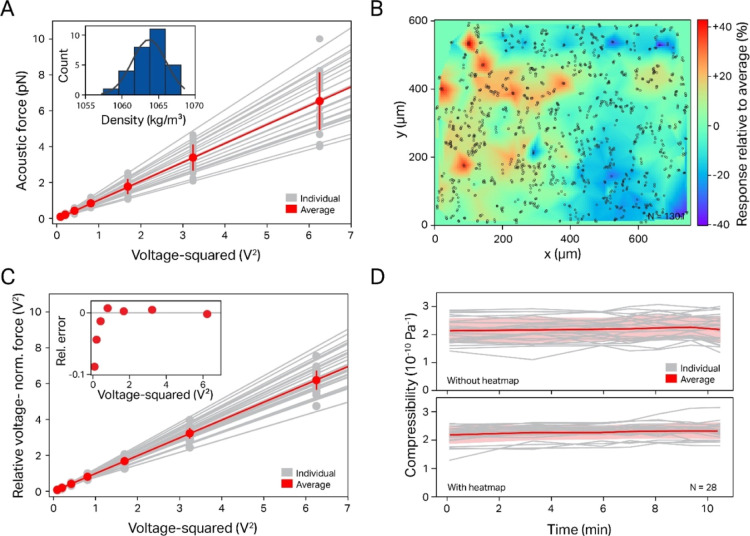
Figure 3.

Experimental data for different 5.31 μm PS particles from the same batch, including heat map calibration. (A) For all particles, the forces scale quadratically with the voltage; however, significant particle-to-particle variation is observed. (Inset) The calculated density distribution for the same batch of PS particles shows a very narrow distribution of <1% variance. (B) The calculated local VN force (here, accumulated over 469 beads) yields a “heat map” of this particular FOV (rel. field variance δf_ac = 0.35). Red/blue spots indicate strong/weak response of the local ASW field. (C) Reanalyzing the same data as that in (A) using the heat map calibration results in a significantly reduced particle-to-particle variation. (D) Showcase of heat map usage for continuous tracking of PS compressibility over time, where it decreases the error both for the total population (red) as well as that of individual particles (gray lines).

The reduction in the VN force variance can also be beneficial when following the compressibility of individual particles over time. While this experimental approach is not expected to be particularly insightful for particles such as PS, whose mechanics are expected to be stable over time, such an experiment could be valuable for living cells whose mechanics change during the cell cycle, as has recently been demonstrated using the related SNACS technique.²⁷ In Figure 3D, the compressibility of individual 5.31 μm PS particles is plotted as a function of time with and without correction using the heat map, demonstrating that the correction reduces the variance in compressibility by 50% (0.25 vs 0.38 × 10^–10 Pa^–1). This improvement can be explained by particle diffusion, which results in a change of their location even in the absence of any flow; nevertheless, since the resulting displacement is rather small, the improvement due to the heat map is lower than what is observed for an ensemble of particles. We also found that the heat map force correction procedure yielded only modest improvements when measuring particles in a compressibility range closer to that of water (>3.5 × 10^–10 Pa^–1, see below). For this reason, the results below were conducted without employing this precalibration procedure.

QAP Measurement of Different Samples Reproduces Expected Results

Once we had verified that eq 1 properly describes the expected force dependence on the input voltage, we set out to check that the same equation accurately describes the dependence of force on particle-specific parameters. To this end, we first determined how the VN force changes when using batches of PS particles over a range of different sizes (from 1.76 to 5.09 μm in diameter). When plotting the average VN force versus the cube of the particle radius, the experimental data follow the linear dependence predicted by the theory with very good agreement (Figure 4A, blue line; R² = 0.9995).

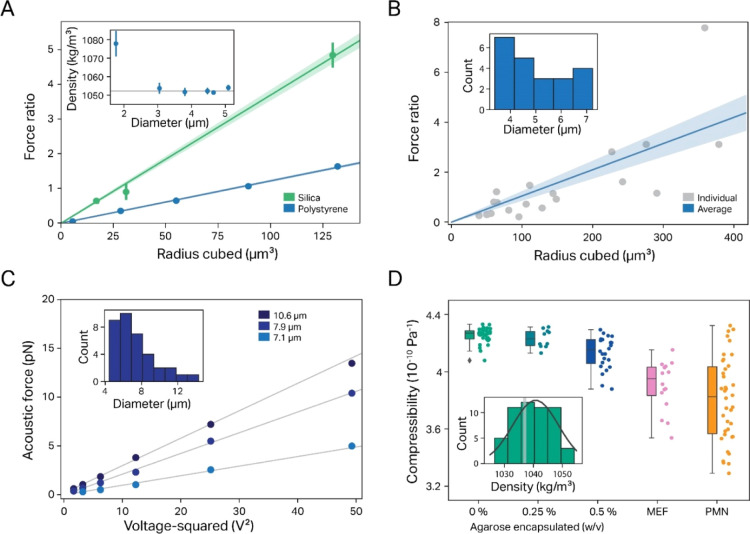
Figure 4.

Determination of the ACF and compressibility for different particle samples. (A) The relative VN force response depends linearly on the particle size for PS (blue) and silica beads (green); (inset) the measured density of different batches of PS beads agrees very well with the published value (gray line), with only small beads showing a significant deviation. Note that we display here the VN force as the calibrated force ratio, which constitutes the measured VN force of the particle normalized by the VN force of the calibration particle (eq 11a in the Materials and Methods section). Since here as well as in all other cases, we use as calibration particle PS beads 4.47 μm in diameter, the calibrated force ratio of these particles (radius cubed ≈ 90 μm³) is by definition 1. (B) A polydisperse sample of PMMA particles also shows a linear dependence of the relative acoustic force on the particle size. The inset shows the measured size dispersion of the sample. (C) Acoustic forces measured for three exemplary GUVs show the expected linear dependence on the square voltage. The inset shows the measured SD of the sample. (D) Compressibility values for different biomimetic/biological samples: GUVs (the inset shows the measured density distribution, with the light bar indicating the expected density value of 1037 g/L), GUVs with a cytoskeleton-mimicking agarose meshwork, and two different cell lines (MEFs: mouse fibroblasts with vimentin KO and PMN: human neutrophil cells).

Next, we also investigated how the ACF depends on the choice of the material. We choose silica here since (a) it differs significantly from PS both in density (1960 g/L vs 1050 g/L, respectively) and compressibility (0.306 × 10^–10 Pa^–1 vs 2.2 × 10^–10 Pa^–1, respectively), and (b) spherical silica particles of similarly narrow size ranges to that of PS beads are commercially available. We also found here that the average VN force scales linearly with the cube of particle radius with very good agreement (R² = 0.9975). The slope of the curves in Figure 4A, that is, the voltage-/radius-normalized force, constitutes an important particle parameter since according to eq 1, it should only depend on the particle ACF, apart from the instrument-specific Q-factor. Therefore, the ratio between the two slopes should equal the ratio of the ACF of silica and PS particles. Fitting the data in Figure 4A between silica and PS particles 0.0367/0.0121 = 3.03 ± 0.32 indeed matched the ratio predicted by the ACF very well (φ_silica/φ_PS = 1.51/0.55 = 2.75), once more confirming that our approach yields accurate results. However, the case of silica is somewhat problematic with regard to compressibility measurements since here the density constitutes the dominating contribution to the ACF (φ_{density term} ≃ 1.58 and φ_{compressibility term} ≃ 0.07) over the compressibility (<5%). This large disparity means that in this case, the ACF is quite insensitive to the particle compressibility, and therefore, the latter cannot be deduced with satisfactory precision for this type of material, at least not under the given experimental conditions. Nevertheless, this does not necessarily preclude compressibility measurements for this kind of material but rather requires better optimized experimental conditions, for example, choosing a liquid medium with a higher density than that of water-based solutions. Moreover, we currently envision the main potential of QAP to lie in the application to biological samples, in particular eukaryotic cells. For these samples, the density is only slightly higher than that of the medium, and thus, the compressibility term contributes significantly to the ACF, which ensures that both parameters should always be discernible with good precision (see the Results and Discussion below).

The tests we presented so far demonstrate the robustness of the data; however, they stem from samples of not only a known particle size but also a very narrow SD. This contrasts to most real-life applications (e.g., when measuring either living cells or particles produced bvia chemical means), where the size may vary significantly from particle to particle. Therefore, we next checked how accurately our technique is able to determine compressibilities under conditions when the particle size is not known a priori but has to be measured in situ using our instrument. To this end, we employed a sample of polydisperse spherical polymethyl methacrylate (PMMA) particles with a large SD (1–10 μm). As expected, we observed in this case for the force versus size plot a larger data variance from the expected linear relationship; still, even in this case, we were able to determine a compressibility value of 2.715 ± 0.43 × 10^–10 Pa^–1, within an experimental error to the known value (2.44 × 10^–10 Pa^–1), showing that our approach is also applicable to heterogeneous samples (Figure 4B).

Mechanical Characterization of Artificial Vesicles and Cells Using QAP

The above tests of QAP were conducted on hard spheres made out of a homogeneous material for which the acoustic response has been well established. This is in contrast to a biological cell that, even in a simplified picture, constitutes a heterogeneous water mixture separated from the extracellular environment only by a very thin and highly flexible lipid bilayer membrane.³⁶ We therefore sought to first measure on a cell-mimetic system that can be produced under well-controlled in vitro conditions in order to obtain a well-defined particle density and compressibility.

For this reason, we conducted experiments on GUVs produced using an inverted emulsion method.³⁷⁻³⁹ We first generated a significant ACF solely by choosing buffers of different densities between interior and exterior solutions (sucrose and glucose solutions with densities of 1037 and 1017 g/L, respectively). Measurements on GUVs in these buffers (Figure 4C) demonstrate that even this primitive test system faithfully reproduces the linear dependence of the force with the voltage squared. The compressibility extracted from these data, 4.25 ± 0.01 (SEM) × 10^–10 Pa^–1, compares very well with the published compressibility data of aqueous glucose and sucrose solutions,⁴⁰ from which we calculate an expected compressibility range of 4.22–4.28 × 10^–10 Pa^–1.

Nevertheless, the reduced compressibility of biological samples such as cells compared to water is not only caused by the dissolved material but also, and probably to a large extent, by the stiffening action of the cytoskeleton. While faithful mimicking of these structures is in principle possible in vitro,⁴¹ it would be too difficult to integrate this into our GUV production method, and we instead chose to emulate a primitive cytoskeletal network by encapsulating a 3D crosslinked agarose gel in the GUVs. We indeed found that the compressibility measured on GUVs containing 0.5% agarose decreased significantly to 4.13 ± 0.02 (SEM) × 10^–10 Pa^–1, while a sample containing 0.25% agarose showed no notable decrease with a value of 4.23 ± 0.02 (SEM) × 10^–10 Pa^–1, the employed agarose concentration might in this case have been too low for gelling. On the other hand, encapsulation of agarose with higher concentrations than 0.5% did not result in a successful GUV production method.

Importantly, we determined GUV densities of around 1040.2 ± 0.9 (SEM) g/L, independent of the presence or absence of agarose inside the vesicles. These values not only are very close to the expected density of 1037 g/L (Figure 4D, inset) for a 300 mM sucrose solution⁴² but also rule out that the increase in the ACF is caused by a change in density. Therefore, our results indicate that the rigidity of the encapsulated agarose is the main cause for the decrease of the compressibility observed in the case of GUVs encapsulated with 0.5% agarose.

After this important control, we finally conducted compressibility measurements of living cells using QAP (Materials and Methods). To this end, we first used mouse embryonic fibroblasts (MEFs) featuring a knockout of the cytoskeletal protein vimentin, for which we determined density and compressibility values of 1052.4 ± 3.5 (SEM) g/L and 3.96 ± 0.05 (SEM) × 10^–10 Pa^–1, respectively. This was higher than a previously reported compressibility value for wild-type mouse fibroblasts (3.78 ± 0.17 × 10^–10 Pa^–1),²⁸ therefore indicating that QAP has the ability to “sense” the impaired cytoskeletal structure of our mutant cells. In a second set of measurements, we characterized a batch of human neutrophil cells (PMN cells, raw data shown in Figure S2A–D)⁴³ and found density and compressibility to be 1080.6 ± 4.7 (SEM) g/L and 3.81 ± 0.05 × 10^–10 (SEM) Pa^–1, respectively. This matched the available literature data on similar cell lines⁴⁴ and thus demonstrated that the method can be successfully applied to live biological systems.

QAP Is Especially Precise when Used for Biological Samples

The aim of this work is not only to present a new method for measuring compressibilities of bioparticles but also to thoroughly discuss the capabilities and limits of this technique. To this end, we considered the main potential error sources and, based on these, estimated the expected accuracy of our assay. In this regard, we note that the samples in Figure 4D reveal a notable increase in their relative error that seems to correlate with a decrease in the measured absolute compressibility. We therefore set out to estimate what experimental errors would be expected in our measurements and how they compare to the observed data variance in the measured compressibility in Figure 4D.

For this estimation, we consider three principal error sources: these are the uncertainties in the measurement of both particle size and density (ΔR_p and Δρ_p, respectively), as well as the relative variance in the local ASW field strength, resulting in a relative force variance δf_ac (compare Figure 3B). Here, we consider typical error values of ΔR_p = 200 nm, Δρ_p = 10 g/L, and δf_ac = 30% (Methods and Materials). We then calculate the impact of these errors on the compressibility determination considering the standard error propagation theory, assuming a medium compressibility of 4.5 × 10^–10 Pa^–1 (Materials and Methods).

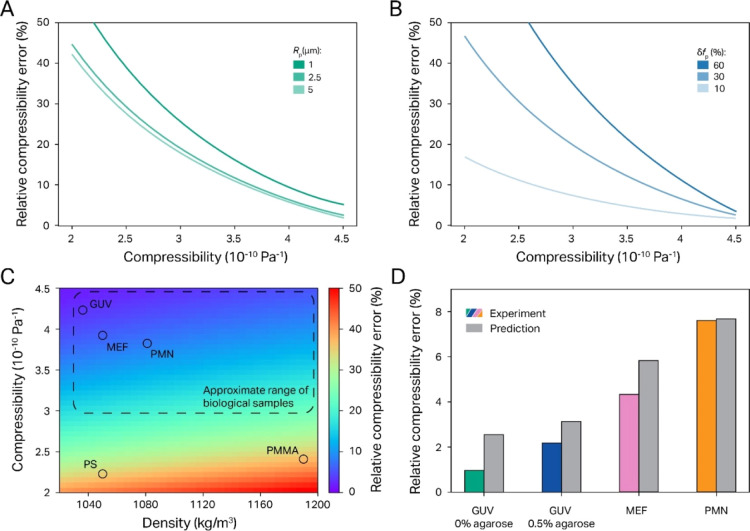
This analysis revealed that the absolute value of the particle compressibility is the dominating factor in governing the relative compressibility error of QAP measurements. Thus, Figure 5A predicts that the relative compressibility error is at a minimum when the compressibilities of the particle and medium are identical (i.e., 4.5 × 10^–10 Pa^–1) but increases strongly as the particle compressibility becomes lower than that of the medium. In comparison, the variance of either the particle size (Figure 5A) or the density (Figure S3) has overall a much smaller effect on the measurement precision. Another important role in the expected accuracy of our compressibility measurements is played by the local force variance δf_ac, as can be appreciated from Figure 5B. Nevertheless, it is also here quite noteworthy how much smaller its effect becomes when the particle compressibility is close to that of the medium. This dependency explains why we did not apply the heat map correction for the biosample data shown in Figure 4.

Figure 5.

Expected and measured experimental error of our QAP assay. (A) Plot of predicted rel. compressibility error δβ_p vs the absolute compressibility value β_p for three different particle sizes shows a strong increase of δβ_p with β_p (note, however, that relative errors remain <20% for compressibilities >3 × 10^–10 Pa^–1, which is the range expected for eukaryotic cells) (B) Plot of predicted δβ_p vs β_p for three different variances in the ASW field. These curves demonstrate that the field heterogeneity has a much lower influence on the relative error when the particles compressibility is close to that of water. (C) δβ_p dependency on the density and compressibility of the sample for a range commonly found for biological samples (dotted line), as well as PS and PMMA particles (circles). (D) Comparison of the experimentally measured standard deviation with the predicted error for the biological sample data shown in Figure 4D demonstrates that the error estimates obtained above are not only realistic but even rather conservative.

In order to give a general idea on the expected accuracy of our approach for the compressibility determination, Figure 5C displays an error heat map that considers both particle density and compressibility, with a particular focus on the biorelevant range^{28,31−33,44−47} (indicated by the dotted rectangle). This not only highlights again that the absolute compressibility value has a much larger influence on the measurement accuracy than on the density but also demonstrates that for biomimetic and biological samples, our method should be able to determine compressibilities with an SD error of better than 20%, even in the absence of the heat map calibration. This can furthermore be appreciated from Figure 5D, which compares observed data SD variance with values estimated from our prediction and shows in all cases that the measured data spread is actually lower than predicted. This demonstrates that our precision estimates made in Figure 5C are still fairly conservative such that our method yields for all investigated samples a compressibility variance of less than 10% SD.

Outside of the error caused by stochastic variance, we might expect a limited amount of systematic deviations. These should be mainly caused by the fact that the medium density and compressibility values must be known for a proper measurement, and thus, some variance caused, for example, by a slight inaccuracy in the buffer composition might be expected. However, the fact that all our measurement results fairly accurately match the expected values indicates that this should in practice not cause much concern. In addition, it should be considered that our method should perform even better if we consider assays where we map the change of compressibility for individual bioparticles (either caused by drug treatment or when measuring over the whole cell cycle) over time (Figure 3D). In these cases, we would remeasure the same particles repeatedly and determine relative changes in the compressibility, and thus, most of the above discussed errors should have less relevance than what we predicted in Figure 5, at least if we assume that neither particle size nor density will significantly change. This is quite important, since, for example, the SNACS technique verified that during the cell cycle, relative acoustic scattering changes of >30% occur,²⁷ which is much larger than the observed variance for living cells (Figure 4D). Since we expect the acoustic scattering (on which SNACS is based) to be dominated by the ACF, our technique should thus be equally suited to resolve different mechanical states during cellular growth and division.

Conclusions

In conclusion, we present here an acoustophoresis assay that allows us to extract quantitative mechanical information such as size, density, and compressibility from micrometer-sized particles while not requiring direct contact with either a surface or a probe particle. In addition, our measurement procedure is quite simple since it is just based on recording and analyzing particle trajectories in the z-direction. Finally, it also permits the determination of particle compressibilities over a wide range of parameters with good precision. While many applications for QAP could be found in nanotechnology and material science, the method seems particularly promising for studying the effects of cellular processes or externally administered drugs on the cytoskeletal network of eukaryotic cells. One such application would be the assessment of the reconstituted cytoskeleton in the bottom-up artificial cells, which, as our GUV data demonstrated, lies in the optimal range of the technique’s applicability.

The capabilities of our acoustophoresis approach are summarized together with that of other methods in Table 1. Notable is the capacity of QAP to measure samples in two dimensions, which should allow massive multiplexing of quantitative measurements of particles. On the other hand, while flow-based methods might allow for an even larger sample throughput in a given amount of time, these techniques cannot remeasure the same particle multiple times and thus are expected to be less precise than our approach. Moreover, the possibility to remeasure particles allows us to, for example, follow cellular dynamics over time, either during the cell cycle or as a response to drug treatment, similar to what has been accomplished using the SNACS method. We therefore believe that QAP will in the future provide an appealing technique to study the mechanics of biological particles.

Table 1. Comparison of Existing Acoustophoresis Assays Used to Measure Particle Compressibilties^a.

method	density	dynamics	dimension	fitting	requirement
Hartono 201128	–	–	1D	simulation	translucent transducer
Yang 201632	–	+	1D	equation	flow, specific chip translucent transducer
Wang 201829	+	–	1D	simulation	triple wave, translucent transducer
Wu 201931	–	–	0D	equation	flow, surface acoustic wave, specific chip
Bogatyr 2022	+	+	2D	linear	translucent transducer

^aThe different fields list whether the technique allows the measurement of particle densities and dynamics, how many dimensions particles can be freely distributed in for measurement (note that 0D means a lack of multiplexing), what kind of fit it requires (“simulation”: measured curves have to be overlayed with computer-simulated trajectories), and whether there are special hardware requirements.

Materials and Methods

Buffers and Measured Samples

Synthetic PS particles were obtained from either Spherotech GmbH (1.76, 3.05, 3.8, 4.47, and 5.09 μm) or Microparticles GmbH (5.31 μm). Silica particles with diameters of 2.56, 3.14 μm (Spherotech GmbH), or 5.06 μm (Bangs Laboratories Inc.) were used, as well as PMMA particles in a diameter range of 1–10 μm (Polysciences Europe GmbH). QAP measurements of all these particles were conducted in a buffer of phosphate-buffered saline (Sigma) supplemented with 0.01% casein.

GUVs were produced using the inverted emulsion method.³⁷⁻³⁹ Different solutions were used in the interior (300 mM sucrose, 50 mM NaCl, and 20 mM HEPES) and exterior (300 mM glucose, 50 mM NaCl, and 20 mM HEPES) to create a density difference and ensure that the particles move down. 0.01% casein was added to the exterior solution (1017 g/L) for the measurement.

PMN cells were collected from patients at Sanquin, Amsterdam, and measured 4 h after reception in an HEPES buffer (pH 7.5, 1013 g/L) containing 5 g/L albumin, 1 mM Ca, and 1 g/L glucose.

MEF Vim −/– cells were grown in T-75 flasks at 37 °C in a 5% CO₂ environment. Cells were cultured in Dulbecco’s modified Eagle medium, supplemented with high glucose, sodium pyruvate, 10% FBS, 25 mM HEPES (pH 7.2), 1% penicillin/streptomycin, and 1% non-essential amino acids (Gibco, Life Technologies). Culture medium was exchanged every 3 days, and cells were passaged after reaching ∼80/90% confluence. On the day of the experiment, cells were detached from the surface after 4 min incubation in 3 mL of TrypLE Express (Gibco, Life Technologies), harvested via centrifugation (200g × 5 min), and resuspended in 2 mL of culture medium (estimated medium density: 1007 g/L).

AFS Setup

All the QAP experiments were performed on a custom-built AFS described previously.^10,11 The setup consisted of an inverted microscope equipped with a 20× objective (CFI Plan Fluor 20×, Nikon). Experiments were started by flushing the sample particles into a reusable glass flow cell (AFS G1, LUMICKS B.V.) with two piezoelectric actuators glued on the top and connected to a frequency generator (SDG830, Siglent). The flow cell was mounted on an inverted microscope via the specially designed holder (MICRONIT B.V.). The sample was illuminated using a light-emitting diode (M660L4, Thorlabs Inc.), and particles were tracked at a 60 Hz frame rate using a CMOS camera (DCC3240M, Thorlabs Inc.).

Prior to the experiments, passivation of the flow cell surfaces was accomplished with either casein or bovine serum albumin (BSA) and Pluronics F127 (Sigma). To this end, the channel was first incubated for 30 min in 0.2% protein solution, which in the case of BSA was followed by a second incubation with 0.5% Pluronics F127. This passivation significantly lowered the fraction of the particles sticking to the bottom and, in the case of the GUVs, prevented them from bursting and spreading over the surface. After this step, the sample particles were flushed in at a concentration low enough to ensure that tracking was not impaired. Typically, this corresponded to 50–100 per FOV for the 20× objective (∼750 × 600 μm). All QAP measurements were conducted at room temperature.

Custom-written LabView software was used to control the frequency generator and camera and record the sample particles’ sizes and movement in all three directions. The lateral motion was monitored using a quadrant interpolation algorithm.⁴⁸ For vertical tracking, a stack of images over a range of 30 μm were recorded at a 150 nm step size using a nanometer piezo translation stage (PI, P-517.2CL) driven by a digital piezo controller (PI, E-710.4CL) and saved as a look-up table (LUT). The bead profile during the experiments could then be compared to those stored in the LUT to determine the z-position at each frame.⁴⁹ Importantly, the choice of an objective with a larger magnification allows for more precise tracking and size measurement of the particle.

Sedimentation and Density Determination

Particles with a density ρ_p greater than that of the medium ρ_m will sediment to the bottom of the flow cell. As is demonstrated below, we can use this to determine the value of ρ_p from the sedimentation trajectory of the particle. This is especially useful for the measurements of the biological samples for which prior knowledge of their density is normally absent. Even more importantly, these density values can later be used to characterize the sample without any prior mechanical information about it (see below).

Following each shooting up event (described in the section “Shooting Up”), the sample particles sediment to the bottom of the flow cell (Figure 1A). This process is driven by the combined action of gravity F_grav and buoyancy F_buoy forces (eq 3), counteracted by the velocity-dependent Stokes’ drag F_Stokes that a particle experiences when moving though a liquid (eq 4), thus giving

3

4

here, R_p is the sample particle radius, g = 9.81 m/s² is the gravity of the earth, v_down is the measured sedimentation speed, 6π is the value of a shape-dependent drag force prefactor for a spherical particle, and η_m is the viscosity of the medium. Importantly, the particles do not sediment within an infinite reservoir of liquid with a constant viscosity. Instead, the presence of the flow cell wall nearby leads to a viscosity that depends on and increases with the shortening distance (in this case, height) from the cell wall, which results in a notable slowing down of the particle velocity when approaching the bottom surface of the channel (see Figure 2B). The effective viscosity as a function of the particle height is then given according to Brenner’s correction by the following equation, eq 5

5

here, we use the 12th-order polynomial approximation as in previously published studies^10,11

6

It depends on the ratio of the particle radius R_p and the distance from the bottom to the particle center z. Consequently, the sedimentation trajectory of the larger particles (>5 μm) is affected to a greater extent. In contrast, the smaller ones (<3 μm) only experience a significant contribution of the effective viscosity change close to the bottom of the flow cell.

The force balance that fully describes the sedimentation of a sample particle can now finally be combined into eqs 3 and 4

7

7a

Since all the other variables in eq 7a are known, we can solve the equation for the particle density to give eq 8

8

To calculate the density of the sample particle, the full sedimentation trajectory was simulated by calculating the force balance (eq 7a), the velocity, and the next position at each time point, while the sample density was varied to optimize the fitting of the raw data with the model. This, in essence, is similar to the approach discussed before, where the third-order polynomial approximation of Brenner’s correction was tested against other correction forms and proved to produce a poor fit of the experimental data.²⁶ Here, however, the difference was in the 12th-order polynomial approximation, which successfully reproduced the trajectory with its unique features, most importantly, the significant velocity reduction close to the bottom surface of the flow cell.

Shooting Up

This work mainly focuses on demonstrating that the ASW field formed in the channel could be used to reliably measure the mechanical properties of the sample particles contact- and label-free. To understand the exact methodology, certain theoretical and experimental details are due to be explained in detail in the sections below.

The piezoelectric actuator glued on the top of the flow cell was connected to the frequency generator, which can supply it with an alternating voltage U at a frequency ν of choice, thus generating an acoustic wave that propagates into the flow cell. In this work, a resonance frequency of ν_res = 14.96 MHz was used, which produced a standing wave node at z_node = 20 μm above the bottom.

A particle located in the ASW field experiences the acoustic pressure and velocity gradient, which results in a force F_ac acting on the particle, given by eq 9

9

where β_p and β_m are the compressibilities of the particle and the surrounding medium, respectively, which characterize how the volume changes in response to the isotropic pressure change. The density- and compressibility-dependent term φ_p is called the ACF. Depending on the sign of φ, the acoustic force is either pushing the particle toward (φ_p > 0) or away from (φ_p < 0) the node. For example, here, we are investigating particles with a positive ACF, and thus, the particles were pushed toward the node, that is, lifted from the bottom into the solution, referred to here as “shooting up.” The other terms define the ASW field and are thus strongly dependent on the specific setup: E_ac^* is the voltage-independent field intensity, k_ac is the wavenumber, and ϕ_ac is the phase delay. Because the ASW field generated in the flow cell is a standing wave, the force is distributed as a sinusoidal function of z: its amplitude is maximal in the antinode and decreases down to zero at the node. Finally, the voltage term U² is quadratic because the ASW field intensity scales with the second power of the voltage supplied to the piezo. Since we consistently used the same flow cell and FOV in the experiments and the field-generating piezo was shown to work robustly for an extended period of time, these last few terms that characterize the ASW field and the setup did not change from experiment to experiment. In addition, the temperature in the room was maintained at T = 20 °C to prevent the viscosity changes as well as the density changes of both the medium and the samples. Apart from these terms, the acoustic force exerted on different sample particles depends then only on the particle size cubed R_p, voltage squared U², and the acoustic factor of the sample particle φ_p (eq 1).

This dependency can be simplified even further by remarking that the applied voltage value can be varied in a range of 0 to 10 V. This upper limit is set out of the precaution of preventing the ungluing of the piezo from the flow cell. However, in principle, even greater voltage amplitudes could be applied. Since according to eq 9, the acoustic force on a particle depends on the electric field density, which in turn depends on the voltage squared, it makes sense here to define the VN force f_ac described by eq 10 below, which then is not voltage-dependent

10

Using this equation (where Q denotes the instrument-specific factor introduced in eq 1), the response of calibration particles with known properties and the response of sample particles of interest can be related to finding the missing value of the sample’s contrast factor and its compressibility, as discussed below.

Force Balance and Determination

The next step toward understanding how the ASW field can be used to mechanically characterize sample particles involves writing down the force balance that describes their motion when the ASW field is turned on. In this case, all the forces previously described for the sedimentation (eq 3 and 4) are still acting. This time, however, there is the additional acoustic force F_ac, which pushes the particles upward toward the acoustic node. The only difference is that now F_Stokes is pointing in the opposite direction of this upward motion. The force balance in short and expanded forms can then be written below, respectively, as 11 and 11a

11

11a

The effect of the different terms above can be best explained by discussing their influence on the shape of a typical shooting up trajectory (Figure 2A). Its features can be explained by the interplay of different terms in eq 11a. The shooting up starts slowly and exhibits a curvature close to the bottom, which is caused by the effective viscosity change, described by λ(z) (eq 6). Further away from the bottom, it is followed by a relatively linear region, which starts to curl as the particle approaches the acoustic node. The sinusoidal dependency of the force on the z-position manifests itself in the upper segment and also explains the slight decrease of the shooting up height z_max observed at lower voltages. There, acoustic force is compensated completely by gravity and buoyancy even before reaching the node, where F_ac = 0.

To measure the force acting on a particle, the velocity v_mid of the particle is determined as the slope of a small 5 μm segment of the shooting up trajectory around its mid-height z_mid (10 μm). This was performed with a linear fit of z(t). The following expression based on eq 11a is then used to calculate the acoustic force

12

To calculate this, the viscosity correction λ(z_mid) is also calculated at the mid-height, the particle size is measured from the camera image, and the sample’s density is determined from the sedimentation. Thus, only the prior knowledge of the medium viscosity η_m and density ρ_m is needed, as opposed to a more precise but complicated modeling of the expected particle trajectory.²⁴

Average Response Flow Cell Calibration and Compressibility Determination

Generally speaking, the ASW field intensity and the force depend on the flow cell’s selected FOV/region. An average calibration of the flow cell FOV had to be performed before the sample measurement to account for that. For this, PS beads of known size R_cal were flushed into the flow cell and shot up using a series of at least five different voltages in the range of 0.2 to 10 V. The voltages were chosen in the way that they differed by a factor of 1.4–1.5 (ca. √2), corresponding to an acoustic force difference of a factor of approximately 2. The acoustic forces exerted on all the calibration beads at different voltages were calculated using eq 11, averaged among all the beads, and plotted against U² to give a VN acoustic force. The linear fit was performed with a fixed interception point (0,0), and the resulting slope was taken as the calibration value f_cal that described the average acoustic force in the selected FOV. Apart from offering higher data robustness, the voltage series enabled us to determine the proper ASW field range in order to achieve maximum sensitivity. Thus, too low/high ASW fields result in noisy trajectories/insufficient tracking resolution in order to properly determine v_mid. Therefore, a wide voltage range ensured the acquisition of reliable data, where none of these issues mentioned above cause problems.

The procedure described above yielded the VN force of the calibration particle f_cal (for all our measurements presented here, a sample of 4.47 μm diameter PS particles served as the calibration sample). The same measurement was then repeated for the particles to be characterized to obtain the corresponding VN force f_ac. Calculating the ratio of the two forces helps eliminate the unknown instrument Q-factor in eq 10 and yields the calibrated force ratio

13

Since both f_cal and f_p are known as well as the sizes of all the particles and the acoustic factor of the calibration beads φ_cal, φ_p remains the only unknown value in this proportion. It can be calculated using eq 12

14

Finally, considering the physical definition of the contrast factor (eq 2) and having prior knowledge of the medium density ρ_m and compressibility β_m, the compressibility of the sample of interest is expressed through them as shown below

15

Note that the Q-factor can not only vary from flow cell to flow cell but also change for the same flow cell slightly over the course of days. For this reason, we typically conduct for every day that a new particle sample is probed a fresh calibration.

ASW Field Heat Map Calibration

Since we found that the ASW field is not homogeneous within a given FOV, an additional calibration procedure was used in some cases (Figure 3B–D) and is further referred to as ASW field heatmap calibration. The idea of this approach is to map out local differences in the ASW field that are caused by the flow cell geometry.²⁶ By considering these heterogeneities of the ASW field as a function of the x and y positions in the FOV, the particle-to-particle variance was effectively decreased by a factor of 3–4, and the mechanical properties of individual particles could be tracked over time (see the Results and Discussion section).

For an exemplary ASW field heat map calibration, 5.31 μm PS particles with a very narrow SD (SD < 0.1 μm) were shot up at 0.5, 1, and 2 V. Their trajectories in z and their x–y movements were tracked. Similar to the average response flow cell calibration, the acoustic force acting on the particles was calculated using eq 11. However, it was performed with the range of the shooting up trajectory between 0.1 and 0.9 of the final height. Since the acoustic force is distributed sinusoidally in the flow cell (see eq 9), the resulting acoustic force as a function of z could be fitted using a simple sine function for each bead. The wavelength and the phase delay were calculated from the known properties of the medium, node position, and frequency, thus becoming the fixed parameters of the fit and leaving the amplitude as the only variable. The VN force at 7 μm from the flow cell bottom was then calculated for each bead and voltage using the fit results and saved together with the corresponding x and y positions. New particles were flushed in, and this measurement was repeated in the same manner until at least 1000 shooting up events covering all regions of the FOV were recorded. All these data were then smoothened by averaging forces recorded at the points 30 μm to each or closer, linearly interpolated on a coordinate grid with 5 μm steps, and plotted (Figure 3B).

During the actual measurement, the force values were obtained at 7 μm from the flow cell bottom (around the antinode of the acoustic wave at this frequency) for each sample particle at least for five different voltages in the range of 0.2–10 V. The analysis steps to determine the compressibility were the same as those for the average response calibration, except for one difference, which is that for each shooting up event, the measured acoustic force was divided by the calibration value of the VNAC (calculated using linear interpolation to the exact same x–y position). These were then linearly fitted as a function of voltage squared. The resulting slope was equal to f_p/f_cal and was then used to obtain the compressibility of each sample particle.

Data Analysis

All the analyses following the data acquisition were performed using a custom-written Python script, which employed a series of filters at each step. These filtering conditions are listed below, along with the rationale for their use.

Filtering

Shooting up events for a particular bead and voltage were filtered out if any of the following conditions were fulfilled:

• At any point during the voltage application, data points gave a z-position being exactly equal to either 0.00 or −40.00 μm (absolute max and min z-values that the tracking software can record), which were indicative of a tracking error.

• The particle moved down by 1 μm or more after the voltage was turned on, another indicator of a further tracking error.

• The shooting up height z_max was lower than 10 μm or higher than 25. This sorted out irresponsive particles and the potential shifts of the tracking region of interest from one bead to another.

• The z-position changed by more than 7 μm between two adjacent time points. This is a yet another loss of a tracking indicator, which alternatively was characteristic for very fast-moving particles, for which the trajectory could not be fitted due to the insufficient number of data points.

• The central segment of the shooting up trajectory contained less than six points in the fitting range of the height z. While the threshold could be lowered to three points without compromising the quality of the fit, this usually led to underestimating the shooting up velocity as the trajectories were too rugged and often lacked a well-resolved linear region around their mid-height.

• In addition, when measuring particles with known sizes (the case for both PS and silica particles), we excluded data that indicated sizes that deviated more than 10% from the average values. This procedure helped filter out particle aggregates and dirt.

Similar filters were also applied to exclude data artifacts from the sedimentation trajectories:

• Any sedimentation event was filtered out if it followed the shooting up event that met any of the conditions mentioned above.

• At any point during the sedimentation, the z-position of the bead was equal exactly to 0.00 or −40.00 μm.

• The sedimentation depth, the difference between the starting position and the position on the bottom, was smaller than the preceding shooting up the height by 2 μm or more: z_depth < z_max – 2 μm.

• The z-position changed by more than 7 μm between two adjacent time points.

Error Propagation Calculations

We measure particle compressibilities β_p by first determining the ACF φ_p using eq 12 and then calculate β_p from this via eq 13. We accordingly first consider principal error sources determining the ACF error δφ_p and subsequently use that value to deduce the compressibility error δβ_p. This is performed using the standard error propagation theory, and accordingly, eqs 12 and 13 are calculated to yield the errors eqs 16 and 17, respectively. We then consider four different error sources contributing to δφ_p (eq 14); these constitute the estimated precision to determine the particle force δf_p and radius δR_p, the local field heterogeneity causing the force variance δf_ac, and finally the radius variance of the calibration particles ΔR_cal as reported by the manufacturer. Regarding the compressibility calculation, there are in addition to δφ_p three additional error sources: the error of the particle density determination Δρ_p as well as the potential variances of the medium density Δρ_m and compressibility Δβ_m. For the data shown in Figure 5, we used the following standard values: unless otherwise stated, we consider particles with a radius of R_p = 5 μm, a density of ρ_p = 1060 g/L, and compressibilities of β_p > 3 × 10^–10 Pa^–1 since this is a value range reported for many eukaryotic cells.^{28,31−33,44−47} We then use the following assumptions regarding the various error contributions: δf_cal = 1%, δf_ac = 30%, ΔR_p = 0.1 μm (Δd_p = 0.2 μm), ΔR_cal = 0.025 μm, R_p = 5 μm, R_cal = 2.655 μm, δβ_m = 0.05 × 10^–10 Pa^–1, β_m = 4.5 × 10^–10 Pa^–1, Δρ_p = 10 g/L, and ρ_m = 1006 g/L. Equations 16 and 17 are then used to estimate the precision of compressibility measurement for nearly all cases; the sole exception is the case when we estimate the error dependence on the radius for particles smaller than 5 μm (Figure 5A). In this particular case, we additionally consider that the density determination will be less precise because of the increased particle diffusion (Figure 2B), and for this reason, we assume in eq 17a that the density error will increase linearly with the inverse of the particle radius.

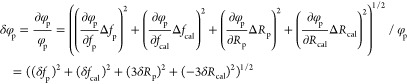16

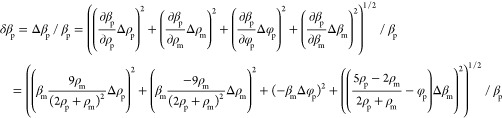17

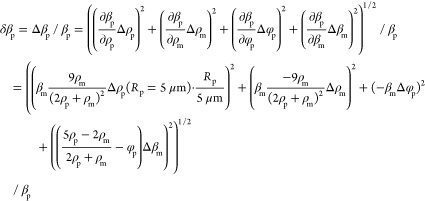17a

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnanoscienceau.2c00002.

• Additional experimental data including improvements regarding the use of the heat map for calibration and the full voltage–force range for PS particles, raw PMN cell data, and the compressibility effect on the experimental error (PDF)

Author Contributions

^† V.B. and A.S.B. contributed equally.

The authors declare the following competing financial interest(s): V.B., A.S.B., G.J.L.W. and E.J.G.P. have been granted a patent covering the quantitative acoustophoresis method which is licensed to LUMICKS. G.J.L.W. and E.J.G.P. own shares of LUMICKS.