Abstract
The ongoing COVID-19 pandemic has created an unprecedented predicament for global supply chains (SCs). Shipments of essential and life-saving products, ranging from pharmaceuticals, agriculture, and healthcare, to manufacturing, have been significantly impacted or delayed, making the global SCs vulnerable. A better understanding of the shipment risks can substantially reduce that nervousness. Thenceforth, this paper proposes a few Deep Learning (DL) approaches to mitigate shipment risks by predicting ”if a shipment can be exported from one source to another”, despite the restrictions imposed by the COVID-19 pandemic. The proposed DL methodologies have four main stages: data capturing, de-noising or pre-processing, feature extraction, and classification. The feature extraction stage depends on two main variants of DL models. The first variant involves three recurrent neural networks (RNN) structures (i.e., long short-term memory (LSTM), Bidirectional long short-term memory (BiLSTM), and gated recurrent unit (GRU)), and the second variant is the temporal convolutional network (TCN). In terms of the classification stage, six different classifiers are applied to test the entire methodology. These classifiers are SoftMax, random trees (RT), random forest (RF), k-nearest neighbor (KNN), artificial neural network (ANN), and support vector machine (SVM). The performance of the proposed DL models is evaluated based on an online dataset (taken as a case study). The numerical results show that one of the proposed models (i.e., TCN) is about 100% accurate in predicting the risk of shipment to a particular destination under COVID-19 restrictions. Unarguably, the aftermath of this work will help the decision-makers to predict supply chain risks proactively to increase the resiliency of the SCs.
Keywords: Supply chain risk, COVID-19, Deep learning, Convolutional network, Temporal convolutional network, Classifiers
1. Introduction
A supply chain (SC) is a coordinated network of man, machine, activities, resources, and technology involved in manufacturing and delivering a product to end-users. It encompasses everything from the delivery of raw materials or semi-finished products from the suppliers to the manufacturer through the transformation and shipment of the completed service or product to the end-user or customers (Khan, Yu, Golpîra, Sharif, & Mardani, 2020). To ensure the smooth flow of materials and products, management of supply chain operations is important (Kohl, Henke, & Daus, 2021). In that regard, the decision-makers have to plan various activities related to the acquisition and movement of the raw materials and product shipment and the distribution of the materials and products at the right place and at the right time. However, due to the ongoing uncertain situations created by the COVID-19 pandemic (e.g., border closure, lockdown, social distancing), the efficient flow of materials and all sorts of products, including life-saving items, such as personal protective equipment, face masks, oxygen supply, and ventilators have significantly impacted (Iyengar et al., 2020, Rowan and Laffey, 2020, Singh et al., 2021). Such predicaments may disrupt the movement of products across multiple tiers. Therefore, having a better understanding of those predicaments can unarguably help to manage them. To run a business efficiently, it is very essential to deal with supply chain risk (Dechprom and Jermsittiparsert, 2019, Ho et al., 2015, Tang, 2006) and disruption at the early stage (i.e., the planning stage of SCs). To be better equipped with the ongoing pandemic and to reduce the impact of overall supply chain disruptions, the merit of proactively identifying risks is undeniable. The sooner the decision-makers can identify or predict imminent supply chain risk, the better they can minimize the impact by designing a proper mitigation plan (Singh et al., 2021). Both external (e.g., demand risk, supply risk, environmental risks, business risks) and internal risks (e.g., manufacturing risks, planning and control risks, mitigation and contingency risks) should be identified at the rudimentary phase of the risk identification and assessment plan (Shekarian & Mellat Parast, 2020). A range of methodologies can be applied to identify risks in the supply chain risk management (SCRM) plan. These methodologies can be divided into two main types, which are — the quantitative and qualitative types. The qualitative types are those studies and theories that are empirical and conceptual, while the quantitative types are the approaches that are based on statistics, simulation, and mathematical optimization (Pournader, Kach, & Talluri, 2020). Strategies that fall in the supply chain risk identification and assessment plan (SCRI&AP) are mostly either reactive or proactive, and both strategies aim to reduce the risk as much as possible. However, at different times, the reactive strategy is applied after the risk is materialized, while the proactive strategy is applied to identify and determine the risks before they happen (Chu, Park, & Kremer, 2020). Most existing studies focus more on proactive techniques to facilitate efficient mitigation and contingency plans. However, proactive strategies depend on the capability of predicting the probability of occurrence of risks and their potential impacts. Prediction approaches of SCRI&AP can be categorized into six classes: (1) approaches that depend on mathematical formulation (Escobar et al., 2020, Tat et al., 2020); (2) approaches that rely on network structures that represent the problem in the form of states and transitions between them (Hosseini & Ivanov, 2020); (3) approaches that are agent-based and multi-agent communications (Perez, Henriet, Lang, & Philippe, 2020); (4) approaches that depend on the fuzzy logic and reasoning methodology (Díaz-Curbelo, Espin Andrade, & Gento Municio, 2020); (5) approaches that rely on machine learning (ML) and big data or sometimes called data analytics (Brintrup et al., 2020, Liu et al., 2020, Sharma, Kamble et al., 2020); and (6) approaches that depend on deep learning (DL) (Wichmann, Brintrup, Baker, Woodall, & McFarlane, 2020). Among many prediction approaches available in the literature, artificial intelligence (AI) techniques have been considered widely as the most successful approaches (Ketchen & Craighead, 2020). Hence, proper implementation of AI techniques can bolster proactive strategies to mitigate risks in SCs (Ketchen and Craighead, 2020, Mollenkopf et al., 2020).
Artificial intelligence (AI) (Kraus, Feuerriegel, & Oztekin, 2020) has shown great interest recently, which has led to the rapid growth of science known as machine learning (ML). Deep learning (DL) is a class of machine learning that uses multiple neural network layers to extract high-level features from raw data input (Saxe et al., 2021, Wang, Xizhao and Zhao et al., 2020). Fundamentally, three structures act as the backbone of a DL model: deep neural network (DNN), conventional neural network (CNN), and recurrent neural network (RNN) (LeCun, Bengio, & Hinton, 2015). The DNN is sometimes called a dense neural network, and it depends on the artificial neural networks (ANN), while the CNN structure deals with high-dimensional data and local dependencies between them, and its parameters can be tuned based on the number and width of the convolution filters. RNN is based on long short-term memory (LSTM), and gated recurrent unit (GRU) (Nguyen, Tran, Thomassey, & Hamad, 2021).
Due to the COVID-19 restrictions and their aftermath on the global SC, such as border closures, exporting goods or emergency items from one source to a destination is now highly uncertain. In this post-pandemic time, the decision-makers often do not have prior knowledge of whether the shipments (carrying both raw materials and finished goods) will be delivered at the right time to the right body or not. Unarguably, a delayed shipment will result in delayed production or lost sales, which eventually will increase the overall supply chain costs. Therefore, a proper prediction of shipment status (whether that will be delayed or not due to COVID-19 restrictions) can reduce future losses and aid in devising a better risk management plan. Although the undeniable merit of ML and DL approaches, only 2% of the total studies in SCRI&AP applied ML approaches for risk identification (Baryannis, Validi, Dani, & Antoniou, 2019). Reportedly, a few of those existing AI-based approaches are Artificial Neural Network (ANN), Support vector machine (SVM), and decision trees. Whilst there exist many classifiers that can be used for predicting (i.e., random forests (RF), random trees (RT) k-nearest neighbors (KNN), SoftMax, logistic, and many others), which can enhance the predicting accuracy. Moreover, nearly 1% of the studies presented the DL approaches in risk identification. DL models can be applied with different ML classifiers to provide accuracy or a predicated result (Baryannis et al., 2019).
Based on these research gaps and the relevancy of DL/Ml models, this paper proposes a DL methodology based on four main phases to predict if the shipment can be exported from one city to another city, and this was based on a data set collected online that holds information about the shipment status during the COVID-19 restriction. This kind of prediction can prevent potential risks and allows the evaluation of economic impacts from commodity flow to and from cities under quarantine orders. The first phase is acquiring the data, and this is done by picking up an online data set: “US Supply chain Information for COVID19”. The second phase is the de-noising phase, in which some unnecessary and incomplete data are removed, and some data are reshaped to act as input for the next layers. The third phase is extracting features from four different models that depend on RNN and a combination of RNN and CNN. RNN models are the Long short term memory (LSTM), Bi-directional long short term memory (BiLSTM), and gated recurrent unit (GRU), while the combined model relies on the temporal convolutional network (TCN). The fourth phase is the classification phase which depends on six classifiers: ANN, SVM, KNN, SoftMax, RT, and RF. Finally, different statistical measurements are used to evaluate the performance of the proposed methodology. Overall, the main contributions stemming from this work are four-fold:
-
(i)
Proposal of a wide range of DL approaches based on RNN models which are LSTM, BiLSTM, and GRU to predict shipment delays/status (i.e., supply chain risks) in SCRI&AP.
-
(ii)
Introducing a temporal convolutional network (TCN) by combining RNN and CNN models.
-
(iii)
Identification of the most promising DL approach in terms of performance while training among a few advanced DL approaches.
-
(iv)
Performance demonstration of the selected classifiers on the advanced DL networks while dealing with supply chain data.
The remaining parts of the study are arranged as follows: Section 2 explains a few existing works on SCRI&AP with and without DL approaches. Section 3 illustrates the proposed DL approaches with all phases for shipment export prediction. Section 4 presents the experimental results with associated discussion. Section 4.1 highlights a few managerial implications of this study, which is followed by the conclusion in Section 5.
2. Literature review
Based on the research scope, this section highlights traditional methods, ML approaches, and DL methodologies to predict risks and disruptions in the SCRI&AP domain. A literature review summary is also compiled at the bottom of this section.
2.1. Traditional methods to predict supply chain risks
Traditional methods to predict supply chain risks are mostly based on stochastic programming, which stands on some stochastic parameters to model a specific risk. The main core of this methodology is the mathematical model. A study to cope with supply chain disruptions was proposed by Khalilabadi, Zegordi, and Nikbakhsh (2020). That work is intended to substitute a vulnerable or risk-prone product in case of a product shortage. The data were collected from livestock-drug distribution companies in Iran. Their proposed model was based on multi-stage stochastic integer programming and was solved by a customized progressive hedging algorithm. Their results showed that their proposed stochastic model could increase the profit of the company by 3.27%. To design a second-generation bio-diesel SC network under risk, Babazadeh, Razmi, Pishvaee and Rabbani (2017) proposed a probability programming model which was solved using a fused solution based on flexible lexicographic and augmented constraint. The proposed model was evaluated using data obtained from reliable historical data and scientific reports of different cities in Iran. The results were able to reduce the total costs of bio-diesel SC.
Recently, another study proposed by Sharma, Shishodia, Kamble, Gunasekaran and Belhadi (2020) considered different risks that occurred in the agricultural supply chains (ASCs) because of this pandemic. Their survey obtained supply, demand, financial, logistics, infrastructure, management, operation, policy, biological, and environmental risks. A fuzzy linguistic quantifier order weighted aggregation (FLQ-QWAO) strategy was implemented to mitigate the unprecedented risks following COVID-19 in the field of ASCs. The data were obtained from micro, small, medium, and multinational types of companies. Results from the FLQ-QWAO concluded that most micro companies would suffer from high financial risks, while the small enterprises will suffer from the demand side, logistics and infrastructural, and even financial risks. In the case of medium companies, most of them will suffer from the demand side, policy and regulatory, financial, biological, environmental, and weather-related risks, whereas, in the multinational companies, the biggest risk that will influence their progress is the logistics and infrastructure.
2.2. ML methods to predict supply chain risks
Due to the rapid growth of AI, several studies have been applying ML concepts in predicting risks to devise a better SCRI&AP. The common ML techniques that exist in the literature are ANN, Bayesian learning, big data, and SVM. ANN was applied by Cai, Qian, Bai, and Liu (2020) to examine the factors that affect the risk evaluation of SC. A model was built based on the back-propagation neural network (BPNN). BPNN has the merits of solving highly non-linear or complex problems. This model was used to build a risk evaluation index system, which was able to provide enterprises with an effective decision support system to carry out the risk management of their SC. Notably, they claimed that their proposed model also can act as a guide to financial institutions to expand their business. Another study proposed by Rezaei, Shokouhyar, and Zandieh (2019) applied an ANN for better classification of the retailers based on their specified risk levels known by experts and risk managers. The model was based on an unsupervised learning type known as a self-organizing map (SOM). They had collected data from a leading distributor of spare parts for all motor vehicles. The data entered to the SOM was about 3292 records regarding that distributor’s retailers and their purchases in the period from May2012–May2014. Each record holds several features such as “type of retailer”, “work experience”, “recency”, “frequency”, and “the returned product”. Obtained results from that model provided an informed guideline to managers about any future disruption or risk level, which helped them to formulate a risk mitigation method.
SVM is one of the most important classifiers as it is known for its highest performance in prediction and forecasting over other classifiers. A study proposed by Tang, Dong, and Shi (2019) for financial data prediction based on a combination of piece-wise linear representation (PLR) and weighted support vector machine (PLS-WSVM). Their objective was to predict the turning points whether if the stock market falls or rises to a point or a for a long time. Twenty stock market data were obtained to test their proposed method. Their results proved the supremacy of PLS-WSVM against other ML models. Recently, Liu and Huang (2020) proposed an ensemble SVM to solve the risk assessment of the SC finance problem. The model was applied to the SC financial analysis of China’s listed companies. The data obtained from the companies hold a large number of noisy examples. Therefore, a noise filtering schema was implemented based on fuzzy clustering and principal component analysis to reduce those noises and achieve optimal clean data sets. Five different classifiers based on SVM were proposed relying on cross-validation SVM (CSVM), particle swarm optimization SVM (PSVM), ensemble cross-validation SVM (EN-CSVM), ensemble particle swarm optimization SVM (EN-PSVM), and the ensemble AdaBoost particle swarm optimization SVM (EN-AdaPSVM), whereas the EN-AdaPSVM showed the highest performance.
2.3. DL methods to predict supply chain risks
A study was subjected by Xu, Ji, and Liu (2018) to develop a deep learning model for dynamic demand forecasting for station-free bike-sharing. The deep learning model was based on LSTM neural network (LSTM-NN) to forecast the trip productions of bike-sharing and attractions for various time intervals. The data were obtained from a downtown area of Nanjing city. The performance of the LSTM-NN was compared with different statistical models and different machine learning algorithms. The results showed that the LSTM-NN had a reasonable and good forecasting accuracy surpassing the former methods. Meanwhile, Vo, He, Liu, and Xu (2019) built a deep responsible investment portfolio (DRIP) model based on multivariate bidirectional long short term memory (BiLSTM) combined with reinforcement learning to forecast the stock for the reconstruction of the investment portfolio. Data on financial, stock prices and ESG rating data were obtained from Yahoo finance. The results of their proposed DRIP proved to have a better financial performance compared to any LSTM, GRU, and standard BiLSTM. Nikolopoulos, Punia, Schäfers, Tsinopoulos, and Vasilakis (2021) proposed a DL model based on the LSTM architecture to predict the growth rates of supply chains in the days of the COVID-19 pandemic. Excess demand for products and services was predicted based on the data obtained from google trends and governmental decisions regarding the lockdown. Several techniques were applied for prediction based on time-series, ML, and DL. Their results showed that the DL model based on the LSTM proved to have the highest forecasting accuracy compared to classical ML and time-series forecasting approaches.
Table 1.
Summary of the Literature Review.
| Reference | Problem | Data | Mechanism | Algorithm | Results |
|---|---|---|---|---|---|
| Khalilabadi et al. (2020) | Predicting product shortage risk | Drug distribution company in Iran | Stochastic approach | Multi-stage stochastic integer programming progressive hedging algorithm | Their model helped to enhance the company profit by nearly 3.27% |
| Babazadeh, Razmi, Rabbani and Pishvaee (2017) | Model a second-generation Biodiesel SC network under risk | Two main biodiesel production in Iran known as JCL and UCO | Fuzzy logic approach | Probabilistic fuzzy logic programming method | Reduction in the total cost of Biodiesel SC |
| Jabbarzadeh, Fahimnia, and Sabouhi (2018) | Random disruptions in SC | Plastic pipe industry | Hybrid approach | Stochastic (bi-objective optimization based on fuzzy-means clustering) | Maximize the overall sustainability performance in disruptions |
| Haddadsisakht and Ryan (2018) | Accommodation of carbon tax with tax rate uncertainty |
Data obtained from carbon factories, warehouses, and collection centers | Hybrid approach | Hybrid robust stochastic combined with probabilistic scenario | Product flows adjustment to tax rates shows a small benefit |
| Qazi, Dickson, Quigley, and Gaudenzi (2018) | Capture the interdependence between risks | Global manufacturing SC | Network approach | BBN | Prioritizing risks and strategies |
| Blos, da Silva, and Wee (2018) | Risks in the production and delivery of goods from a source to a destination | Shipping goods from China to Brazil | Agent approach | Agent-based model | Enabling the ability to model, analyze, control, and monitor the shipment of goods |
| Paul (2015) | Selection of supplier during a set of risk factors | Hypothetical data for five different suppliers | Reasoning approach | A rule-based fuzzy inference engine | Helped to obtain the best supplier |
| Cai et al. (2020) | Risks and factors affect the SC | Some Financial enterprises |
Machine learning | BPNN | Provide good references for enterprise effective decision system |
| Rezaei et al. (2019) | Classification of the retailers based on risk levels | ISACO: a leading distributor for motor vehicles | Machine learning | SOM | Formulation of the risk mitigation methods based on the level of risks |
| Shang, Dunson, and Song (2017) | Transport time risks in air cargo SC | Leading forwarder on routes served by airlines | Machine learning | Bayesian parametric model | Assist the forwarder to offer reasonable service and price, enable fair supplier evaluation |
| Ojha, Ghadge, Tiwari, and Bititci (2018) | Factors and occurrence of risk propagation | Leading automotive organization in India | Machine learning | Bayes network | Detection of the mean service level at maximum or minimum when disruption occurs |
| Papadopoulos et al. (2017) | Achieve resilience in case of disasters | Data collected from tweets, news, Facebook, WordPress | Machine learning | Big data model (CFA) | Concluded that Swift trust, information sharing, public–private partnership are the important factors for resilience SC |
| Tang et al. (2019) | Prediction of financial data | 20 market stocks | Machine learning | (PLS-WSVM) | Able to detect the turning points if the market falls or rises to a point for a long time |
| Liu and Huang (2020) | Risk assessment of SC finance | Financial companies from China | Machine learning |
CSVM, PSVM, EN-CSVM, EN-PSVM, En-AdaPSVM |
Enhancing the credit assessment accuracy |
| Punia, Nikolopoulos, Singh, Madaan, and Litsiou (2020) | Forecasting multi-channel retail demand | Data obtained from a multi-channel retailer | Deep learning |
RF LSTM LSTM RF |
Ranked the explanatory variable according to the relative importance |
| Xu et al. (2018) | Dynamic demand for station-free bike-sharing | Data obtained from downtown area of Nanjing city | Deep learning | LSTM-NNs | Forecast the gap between inflow and outflow of sharing bike trip so a re-balance can be formed during sharing bikes |
| Yu, Guo, Asian, Wang, and Chen (2019) | Practical flight delay prediction | Real data of arrival and departure flights from PEK airport | Deep learning | DBN SVR | An efficient handling of large data to obtain main factors of flight delays. |
| Vo et al. (2019) | Reconstruction of the investment portfolio | Data obtained from Yahoo finance | Deep learning | LSTM GRU BiLSTM DRIP |
Achieved competitive financial performance and social influence |
| Nikolopoulos et al. (2021) | Predicting the growth rates, demand for products and services during the COVID-19 pandemic | Data obtained from google trends and governmental decision of the lockdown | DL with other approaches | Time-series, ML, DL using LSTM |
Helped the policy makers and planners to make better decisions during the next pandemics |
| Sharma, Shishodia et al. (2020) | Risks occurred in the agricultural SC during COVID-19 pandemic | Data obtained from 20 companies from their investment in plants | Fuzzy logic approach | FLQ-QWAO | Efficient prediction of different risks in all companies whether micro, small, medium, and multi-national |
| Our proposed method | Prediction of shipments delivered to different countries during the COVID pandemic | Data taken from US supply chain information for COVID-19 | Different DL models with classifiers |
LSTM, BiLSTM, GRU, TCN |
TCN showed the highest performance. The model is capable of deciding the types of shipments that can be delivered |
2.4. Summary of literature review
Table 1 shows a summary of the related works in terms of the SCRI&AP problems. Data, mechanism, algorithm, or the model applied, and the results achieved from each related work are compiled in different columns of that Table 1. Based on the literature review and Table 1, there exist a set of gaps and limitations related to methodologies applied in the SCRI&AP and the risks emanating from the COVID-19 pandemic. On the one hand, the gaps related to the first type of methodologies which are based on mathematical reasoning, single and multi-agents, network structures, fuzzy logic, and hybrid, have a lot of limitations. These methods cannot provide accurate decision-making in case of risks. In addition to this, the former methods cannot handle a huge amount of data sets and problems of big size. Moreover, the network approaches do not concentrate on a set of uncertain risks, and the agent-based method focuses on a small number of parameters, making it hard to support many policies. In addition, the hybrid approaches increase the computational complexity, and the reasoning approaches in SCRI&AP are focused on only one type of reasoning, which is case-based reasoning, even though there exist different types of reasoning that can show higher performance in mitigating risks.
The limitation related to the second type of methodologies (i.e., ML) is that only a limited number of classifiers are applied. The techniques used are the ANN, Bayesian network, and SVM. Many different techniques, such as decision tables, random forests, and many others, exist that can better predict risk and increase the performance of risk classification. Finally, the third type of methodologies in the SCRI&AP is DL, considered the most suitable one for risk prediction in SCRI&AP. DL methods can deal with huge data and achieve high accuracy compared to other methods, especially ML. On the other hand, this pandemic creates huge demand and supply issues for the SCM, transportation challenges during nationwide lockdowns, international border closures and supply shortages, panic buying, and stocking. Moreover, the transportation of shipments from one country to another in this pandemic is a critical issue. This pandemic has affected the transportation of different types of shipping, such as oil shipping, container shipping, and dry bulk shipping. Activities of transportation of shipments (such as preparing shipping items and distributing at the right quantity, place, and time) are significantly impacted. Therefore, better risk prediction models such as DL must exist to deal with these risks.
3. Methodology
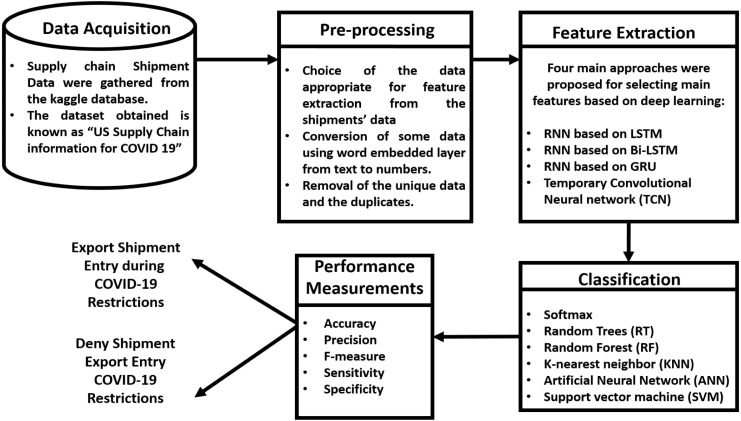
This section is dedicated to the methodology and implementation phases. The deep learning models are implemented by using three recurrent neural networks (RNNs) and one convolutional neural network (CNN). The RNNs are based on the stacked LSTM, stacked BiLSTM, and the stacked gated recurrent unit, whereas the CNN applied was based on the TCN. Then, six main classifiers were used to test the performance of the deep learning models, and these classifiers are Softmax, RT, RF, KNN, ANN, and SVM. Finally, depending on these deep learning models and classifiers, we can predict whether a shipment will be exported to the destination or not under this pandemic situation. Our methodology consists of five main phases which are data acquisition or exploration, pre-processing or filtering phase, feature extraction or selecting the most important and potential features, and finally, the outcome step is prediction and classification as shown in Fig. 1.
Fig. 1.
The proposed methodology for predicting shipment data during the COVID restrictions.
3.1. Data acquisition
The data was collected from a public database available online known as Kaggle (Chain, 2000), which is a common platform for ML and a data science community. This database has tons of data sets available online. The data set chosen is called “US Supply Chain Information for COVID19” (Keller, 2020). This data set has shipments that can be transferred from a source to a destination. In this data set, 4 547 661 shipments are classified into mining (except oil and gas), food manufacturing, textile mills, paper, wood product manufacturing, and many others as shown in the excel sheet about the North American industry classification system that can be obtained from Keller (2020). Each shipment has 20 red attributes that represent the details of the shipment, such as the “shipment ID”, “origin state”, “origin metro”, “concatenation of origin state and metro area”, “destination state”, “destination metro area”, “concatenation of the destination metro and state”, “industry classification of shipper”, “quarter in which the shipment occurred”, “code of the shipment”, “mode of transportation of the shipment”, “shipment value”, “weight”, “great circle distance between the shipment origin and destination”, “routed distance between shipment origin and destination”, “temperature-controlled shipment”, “export entry”, “export final destination” and this column represent three main destinations which are Canada, Mexico and others”, “hazardous material if it flammable liquid, other hazmat or not hazmat at all”, and finally the “weight factor”. Each row or shipment in the data set has 20 columns as they represent its attributes.
3.2. Pre-processing
Our filtration process depends on two main steps. The first step is the removal of the columns that represent the same attributes and the unique identifiers’ columns. The selected columns that follow the former criteria are removed. The eliminated columns are the “shipment id”, “concatenation of the original state and metro area”, “concatenation of the destination state and metro area”. The remaining number of columns now is 17 and this is the result of the first step. Then, the second step starts by converting the text columns to numeric columns, and this is done for 4 columns which are the “temperature-controlled shipment”, “export entry”, “export final destination” and finally the “hazardous material”. The embedded sequence layer was applied to convert these columns from text to numeric columns. Finally, the number of columns for each shipment that can be progressed to the next step are the remaining 17 columns.
3.3. Feature extraction
This stage is one of the most important stages because the most discriminant features are extracted using four main models based on RNN and CNN. Three models were based on stacked LSTM, stacked BiLSTM, stacked GRU layers. The last model is based on a temporal neural network (TCN) that is formed based on a mix of RNN and CNN. In this step, the features are extracted from the 16 columns selected because the column of “export entry” will be predicted. These columns represent the main attributes of the shipment.
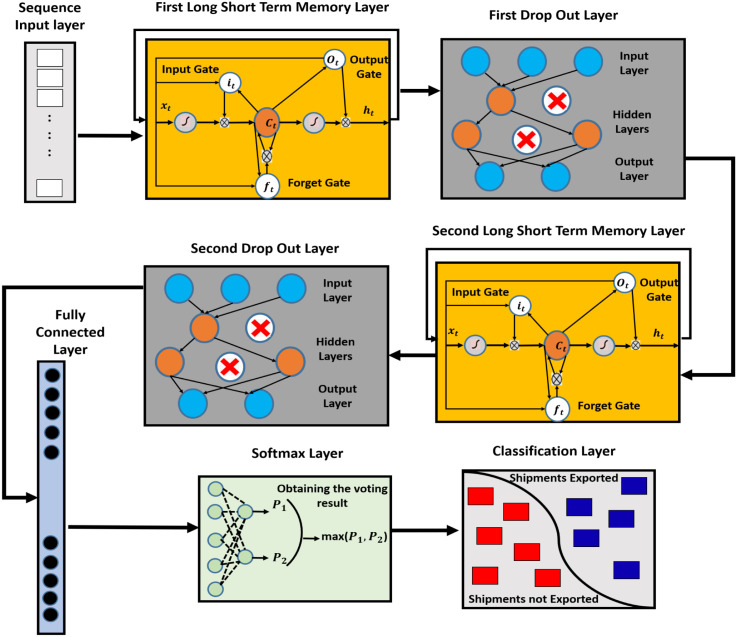
3.3.1. RNN model based on the stacked LSTM
The first model proposed is based on the LSTM to train the 16 columns obtained from the pre-processing stages. The model is composed of eight layers, and these layers are one sequence input layer, two LSTM layers, two dropout layers, one fully connected layer, one SoftMax layer, and one classification layer. Fig. 3 shows the layer-by-layer description of the stacked LSTM. The layers of the model are explained in detail as follows (see Fig. 2):
Fig. 3.
Deep learning model based on the BiLSTM layers.
Fig. 2.
Deep learning model based on the LSTM Layers.
Sequence Input Layer: This is the starting layer of the model. This layer takes the input data obtained from the pre-processing step, and the data acts as an input sequence to the network. In this layer, the data are normalized automatically.
LSTM function Layer: LSTM is one of the RNN types that permits the network to keep long-term dependencies between the data at a specific time based on various time steps proposed before. It is considered to be a chain of repeated components of neural networks. Each module consists of three main gates, and these gates are the input gate, forget gate, and output gate. Each gate has sigmoid layers and piece-wise multiple operations. The output of each sigmoid layer are numbers that fall in range intervals from [0,1]. This interval represents a portion of the input information. The LSTM works on the time-series data based on RNN (Nguyen, Tran, Thomassey, & Hamad, 2020). The LSTM begins by reading an input sequence of vectors known by , where and it express an m-dimensional vector of readings for variables at a specific time-instance . Since that the LSTM can operate on a large time-series, its performance is not always the same, but it depends on the input.
Based on the new information in the state , the LSTM modules operates in three main steps as follows. The first step, the LSTM module decides what kind of old information that should be forgotten by producing an output of a number in range from [0, 1]. The forgotten information will be defined by with
| (1) |
where, is the output in-state ; and are known as the weights and bias matrices of the forget gate, and is defined as the logistic non-linearity. Then in the second step, is processed before the storage in the cell state. The value is known as the input gate along with a vector of candidate values that is generated by a tanh layer at the same time known as:
| (2) |
| (3) |
is updated in a new cell state known by as follows:
| (4) |
where ( and ( are known as the weight and the bias of the input and the memory cell gates respectively. In the third step, the output gate is represented by:
| (5) |
| (6) |
and are known as the weight and bias of the output layer, and represents a part of the cell state that is produced as output. The cell state aims to run straight down the entire chain, and it maintains the sequential information in the inner state, and it allows the LSTM to persist the knowledge obtained from subsequent time steps (Tran, Du Nguyen, & Thomassey, 2019).
Dropout Layer: It is a layer that focuses on preventing the over-fitting of the model and it was proposed by Srivastava, Hinton, Krizhevsky, Sutskever, and Salakhutdinov (2014) and it is a very simple and effective methodology. The data collected in most of the practices performed are not pure; they sometimes hold some noisy data (Goodfellow, Bengio, Courville, & Bengio, 2016). The proposed RNN models can have some difficulty dealing with separating the normal data from the noisy ones. In contrast, the RNN model learns on these noisy data as normal ones, and this could allow the model to be over-fitted and confused (Wang et al., 2020). The over-fitting model has high accuracy on the training data, but a low accuracy on the test data and other generalization applications. It is also important to know that in most of the applications, the noisy data are less in quantity and much less in occurrence than the normal data entered. This layer quits a specific proportion of neurons in the network randomly. This operation can reduce the probability of occurrence of noisy data and its influence on the model. The mini-batch is trained in a different network because the neurons are randomly discarded. This leads the total training parameters of the model to become unchanged. The drop-out layer works during the training stage only, and all the neurons of the model still operate in the testing stage even the discarded one. After applying the operation of the dropout, each unit of the neural network in the training stage must require the addition of a probability process. The equation of the feed-forward for the standard network based on a drop out operation is defined as follows:
| (7) |
where is known as the Bernoulli random variables in a probabilistic term known as . When the is equal to 0, the neuron is discarded, but if the is equal to 1 the neuron is trained. is known as the input values of the th neuron in the th layer; is determined to be the final output value of the th neuron of the (l 1) the layer; express the linear combined output value of the th neuron of the (l 1) the layer; and are deemed to be the weight and the bias values between the th neurons of the th layer and the th neuron of the (l 1) the layer and is the activation function.
IW: Initial Weight, RW : Recurrent weight
Fully connected Layer: This layer is always applied in the stage of the classification in the conventional RNN. The main aim of the fully connected layer is to extract the features of the output data of the RNN and to connect the stages of the feature extraction with SoftMax classifier (Lin, Chen, & Yan, 2013). A fully connected layer is usually composed of 2–3 layers fully connected to the feed-forward neural network. The final output of the feature map of the RNN is transformed into a one-dimensional array by applying a flatten function. This one-dimensional array is deemed to be the input of the full connection layer, and the output of the full connection layer is a one-dimensional vector. Each value in this vector is a quantitative value of n classifications. Moreover, in the fully connected network, all the neurons between the layers are interconnected with each other using the following equation:
| (8) |
where is known as the activation function, is the fully-connected layer input, is the fully connected layer output, and and are known to be weights and biases of the fully connected network respectively.
SoftMax function layer: The SoftMax function is an extension of the logistic regression and it solves single and multi-class classification problems (Jiang et al., 2018). The output result of the fully connected layer is a form of a quantization matrix Known as of rows and columns. The is known as the samples, while the is known as the quantized value that corresponds to categories. , where represents that the th sample belongs to the probability value of the first-class category. The different element value in as variant magnitudes do not conform to the probability distribution. This problem can be solved by applying the SoftMax function to normalize the calculation. The output value starts to conforms to the probability distribution after the SoftMax normalization. If the training input sample is and the corresponding label is , the sample is forecasted to be the probability of category that is defined as .
Classification Layer: It is the final layer of the first model. The layer calculates the loss function, and it is performed by a match operation between the forecasted result and the target label. The most widely used loss functions are the mean square error (MSE) (Köksoy, 2006) and the cross-entropy function (CE) (Ho & Wookey, 2019). CE function is applied because the input data belongs to a binary classification category of two classes only. The cost function of CE is evaluated using the following equation as follows: This is the final layer, and it computes the loss function, and it is calculated by matching the normalized prediction result with the targeted actual label. The most commonly used loss functions are the mean square error (MSE) and the cross-entropy (CE). In this method, the CE is applied because the input data belong to a classification binary value. The CE cost function is obtained using the following equation:
| (9) |
where is the th training sample, is the th category, is the logical indication function. if the value of is true, then I 1 otherwise I 0. is the actual label of th sample. is the probability value calculation function normalized, and it represents the probability value of the th sample belongs to the th category, and is the CE loss function. The parameters of each layer in the LSTM model are defined in Table 2. This table shows the number of layers, the name of each layer, and the main parameters of each layer.
Table 2.
Parameters of the RNN LSTM network layers.
| Layer no. | Layer name | Parameters of each layer | Activations | Learnables |
|---|---|---|---|---|
| 1 | Sequence input layer | Number of Inputs 16 | 16 | – |
| 2 | First LSTM layer | Number of hidden units 100 Output mode “Sequence” State activation function “tanh” Gate activation function “Sigmoid” |
150 | IW 600 × 16 RW 600 × 150 Bias 600 × 1 |
| 3 | First drop out layer | Drop out Quantity 0.3 | 150 | |
| 4 | Second LSTM layer | Number of hidden units 200 Output mode “Last” State activation function “tanh” Gate activation function “Sigmoid” |
200 | IW 800 × 150 RW 800 × 200 Bias 800 × 1 |
| 5 | Second drop out layer | Drop Out Quantity 0.2 | 200 | W 2 × 200 Bias 2 × 1 |
| 6 | Fully connected layer | Output size 2 | 2 | – |
| 7 | SoftMax Layer | Number of Outputs 1 | 2 | – |
| 8 | Classification layer | Loss function “Cross Entropy” | – | – |
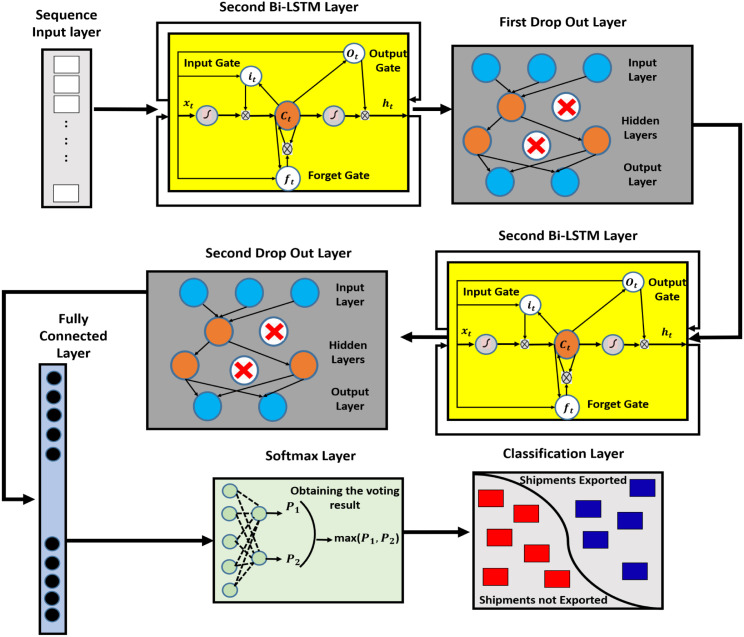
3.3.2. RNN model based on the stacked BiLSTM
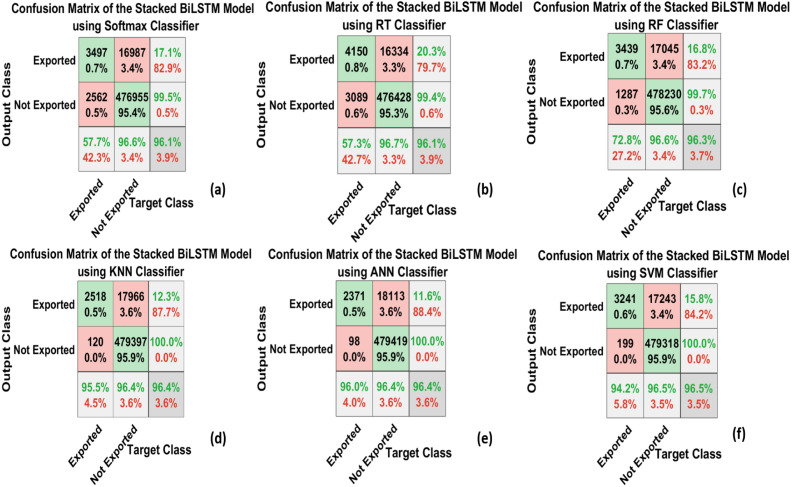
The second model proposed is based on the BiLSTM and it is composed of eight layers:
Bi-directional LSTM function Layer: The neural network model adopted is based on the BiLSTM. BiLSTM depends on the LSTM and the bidirectional current network (Zhang, Zhang, Zhao, & Lian, 2020). The model consists of one sequence input layer, two BiLSTM layers, two dropout layers, one fully connected layer, one SoftMax layer, and one classification layer. The only difference between this model and the previous one is replacing two LSTM layers with another two BiLSTM layers. Fig. 4 shows the description of the layers based on the BiLSTM model and it is shown as follows: The main objective of the LSTM is to overcome the vanishing gradient problem of the RNN, and it also depends on the memory cell to express the past timestamp. In this layer, the BiLSTM is used instead of the LSTM as the bidirectional can provide a better understanding of the time series data in two main directions. The previous time-series data can impact the current forecasting, while the future time series data will also impact the current forecasting to a certain extent. The process of learning features from the previous and future data can provide more accurate forecasting. Moreover, the trained parameters used for the BiLSTM layer in the training process can be used in forecasting (Hao, Long, & Yang, 2019).
Fig. 4.
Deep learning model based on the GRU layers.
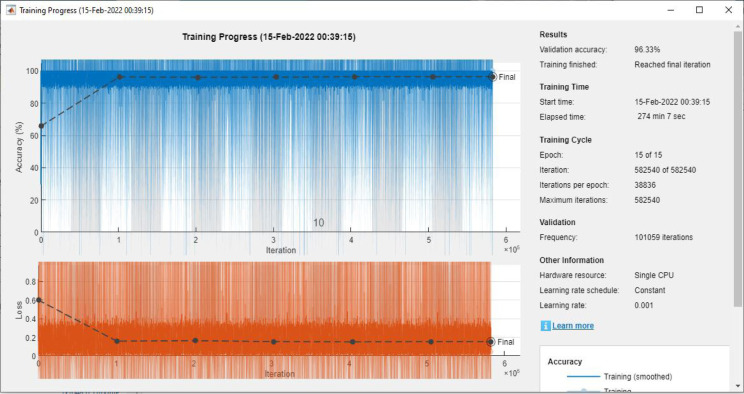
It is called bi-directional because the information recorded in the last forward vector the LSTM is improved from front to back, and the information recorded in the last backward vector, the LSTM is improved from back to front. The fusion between these records together can complete the information. In addition to this, more accurate results can be predicted based on the obtained information, and it can cause less forecasting error than the one-way LSTM. Table 3 shows the parameters of the BiLSTM model. The difference between this model and the previous model in parameters is that the number of hidden neurons applied in the first LSTM layer is 100 and the second LSTM layer is 200, while in this model the notion is to increase the number of hidden neurons in the bi-directional LSTM layers for more training on the past and future data. Therefore, the parameters of hidden units in the bi-directional layers are set to 300 neurons.
Table 3.
Parameters of the stacked BiLSTM network layers.
| Layer no. | Layer name | Parameters of each layer | Activations | Learnables |
|---|---|---|---|---|
| 1 | Sequence input layer | Number of Inputs 16 | 16 | – |
| 2 | First BiLSTM layer | Number of hidden units 300 Output mode “Sequence” State activation function “tanh” Gate activation function “Sigmoid” |
300 | IW 1200 × 16 RW 1200 × 150 Bias 1200 × 1 |
| 3 | First drop out layer | Drop out Quantity 0.3 | 300 | – |
| 4 | Second BiLSTM layer | Number of hidden units 300 Output mode “Last” State activation function “tanh” Gate activation function “Sigmoid” |
300 | IW 1200 × 300 RW 1200 × 150 Bias 1200 × 1 |
| 5 | Second drop out layer | Drop Out Quantity 0.2 | 300 | W 2 × 300 Bias 2 × 1 |
| 6 | Fully connected layer | Output size 2 | 2 | – |
| 7 | SoftMax Layer | Number of Outputs 1 | 2 | – |
| 8 | Classification layer | Loss function “Cross Entropy” | – | – |
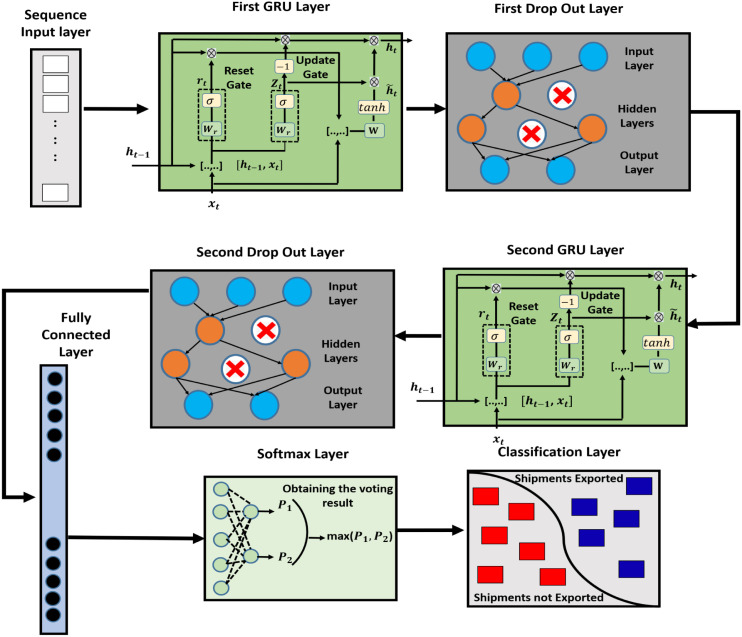
3.3.3. RNN model based on the stacked GRU
The third model proposed is based on the deep gated recurrent unit (GRU) layers and it is the same as the previous models in that this model consists of eight layers, and the LSTM and BiLSTM are replaced by two GRU layers. The main reason for introducing the GRU is that, it has proved as more efficient than the basic RNN, LSTM, and BiLSTM in all tasks except in the field of the language modeling (Basiri, Nemati, Abdar, Cambria, & Acharya, 2021). The GRU controls the flow of information like the LSTM unit, but without the need for any memory unit. It only exposes the hidden content without any control. Moreover, GRU is new and its performance is on par with LSTM, and it is computationally more efficient and has a less complex structure. In addition to this, GRU trains faster and performs better than the LSTM on less training data. GRU is simple and easy to maintain, and the process of adding new gates in case of additional input to the network is a simple process for GRU (Jiao, Wang, & Qiu, 2020). Fig. 5 shows the full of the third model that is based on GRU layers.
Fig. 5.
(a) Overall TCN model (b) Structure of residual block (c) Structure of dilated casual convolutional layer.
GRU function Layer: This layer is a type of the feedback recurrent neural network (RNN) with a memory unit. The hidden layer is a gated recurrent unit, and it is deemed to be an enhancement on the hidden layer of the traditional RNN. The GRU consist of two main gates which are the update gate, reset gate and a temporary output. The function of the gate in the GRU is the process of information gathering and screening, and this is performed by the multiplication of the corresponding elements in gate vector . has the information vector, and the information in or is selected, therefore if the element in is 1, the corresponding element in is selected, otherwise the corresponding element in and is discarded. and are the gate vectors and they represent the outputs of the reset and update gates at instant time respectively. and are deemed to be the information vectors and they express the temporary output and the hidden layer output at instant time respectively. The feed forward operation of the GRU is defined as follows:
| (10) |
| (11) |
| (12) |
| (13) |
is the input of the network at instant time , while , and , is known to be the weight matrices of the reset, update, and temporary output respectively, and the , , and formulate the biases corresponding to these weights. GRU has tons of advantages as it can avoid the phenomenon of gradient explosion and disappearance, and it can solve the problem of long-term dependence as well as realize a truly infinite loop compared to LSTM. Table 4 shows the main parameters of the GRU model, and these parameters involve the values that are introduced to the GRU layer and other layers in the model.
Table 4.
Parameters of the stacked GRU network layers.
| Layer No. | Layer name | Parameters of each layer | Activations | Learnables |
|---|---|---|---|---|
| 1 | Sequence input layer | Number of Inputs 16 | 16 | – |
| 2 | First GRU layer | Number of hidden units 150 Output mode “Sequence” State activation function “tanh” Gate activation function “Sigmoid” |
150 | IW 450 × 16 RW 450 × 150 Bias 450 × 1 |
| 3 | First drop out layer | Drop out Quantity 0.2 | 150 | – |
| 4 | Second GRU layer | Number of hidden units 300 Output mode “Last” State activation function “tanh” Gate activation function “Sigmoid” Reset Gate Mode “After- Multiplication” |
300 | IW 900 × 150 RW 900 × 300 Bias 900 × 1 |
| 5 | Second drop out layer | Drop Out Quantity 0.2 | 300 | W 2 × 300 Bias 2 × 1 |
| 6 | Fully connected layer | Output size 2 | 2 | – |
| 7 | SoftMax layer | Number of Outputs 1 | 2 | – |
| 8 | Classification layer | Loss function “Cross Entropy” | – | – |
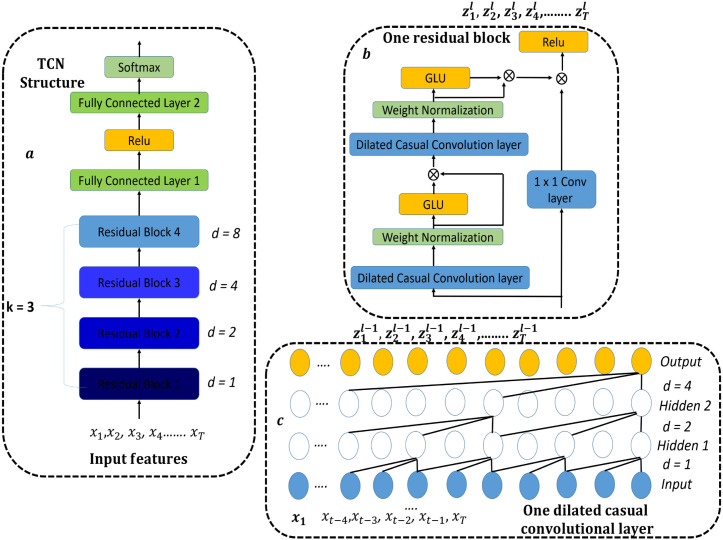
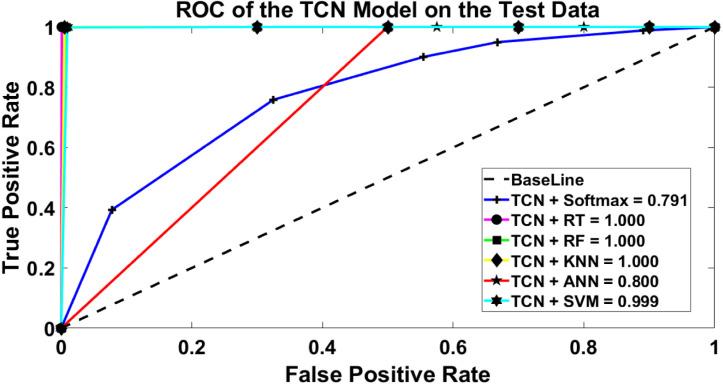
3.3.4. TCN deep learning model
The last and the fourth implemented model was based on a temporary convolutional network (TCN). The TCN model has proved its advantages against any conventional approaches such as the CNN and RNN. TCN was applied in many different applications such as improving traffic prediction, sound event localization and detection, probabilistic forecasting, and many other applications (Chen, Kang, Chen, & Wang, 2020), and the TCN proved the highest accuracy performance in those applications. TCN was first proposed by Lea, Vidal, Reiter, and Hager (2016) with the aim of segmentation of video-based actions. TCN consists of two main steps based on conventional processes. The first step is to compute the low-level features using CNN that encodes spatial–temporal information, and the second step is to input these low-level features into a classifier that captures the high-level temporal information usually using RNN or CNN.
TCN provides a unified approach to capture all two levels of information hierarchically. The overall architecture of the proposed TCN is manifested in Fig. 5(a). The proposed TCN models sequential features from the input data and map them to probability distributions of bases appearing at each time point. The proposed model is formed of 4 stacked residual blocks, two fully connected layers, a RELU activation function, and a SoftMax layer as shown in Fig. 5(a) (Bai, Kolter, & Koltun, 2018). The residual block has two main stacked dilated casual convolutional layers, except the first block has three dilated casual layers. The weight normalization is performed on each dilated casual layer followed by a gate linear unit as an activation function. The main notion of the TCN can be simplified to stacking a group of dilated casual convolution layers of the same length as illustrated in Fig. 5(c).
Dilated casual convolutional Layer: TCN can take a series of any length of input and then can produce output as the same length. For a given input sequence and a filter , the dilated casual convolution operation on the th point of is defined by:
| (14) |
where is the dilation factor and is the filter size. The output result of the dilated casual convolution layer is expressed by . For the first layer, manifests the input sequence, while for a higher layer it represents the output of the former layer. Each dilation layer has a dilation factor and this factor increases exponentially by 2. The index is the number of the layers. The TCN stacks residual blocks to form a deeper structure, rather than simply stacking layers. Each residual block consists of two stacked dilated casual convolutional layers. The word “casual” means that the activation obtained for a specific time step cannot depend on the activation from future time steps. Each of the two stacked dilated layers has the same dilation factor , filter size , and some filters .
Weight normalization layer: A weight normalization layer (Salimans & Kingma, 2016) is applied for each dilated casual convolutional layer. It is a substitute way to the batch normalization methodology. The main notion of the WN is to separate the direction of the weight away from their norm, therefore, this will enhance the case of the optimization problem. The weights have to be normalized and multiplied by a specific learning scaled parameter. The equation of the weight normalization layer is defined as follows:
| (15) |
is defined as the input of WN, is the output, is known as the scale, represents the bias, and is a small constant value used for numerical stability, while represent the layer weight, is defined as the Frobenius norm of the weights for output channel and finally * determines the convolution. Moreover, when the weights is near to orthogonal and the input is normalized, then for each layer the total layer dimension is then , and this means that WN will propagate the normalization through the convolutional layers.
Gated linear unit (GLU): They are preserved to be feed-forward networks as they are composed of many different layers of geometric gated mixing units and it acts as an activation function. Each unit in a specific layer produces a combination of the forecasting obtained from the previous layer, and the final layer consists of only a single neuron that explains the output of the full network. The main advantages of this layer are that the main information is spread to every single neuron on which each gating function will work on. The gating function is fixed, and each neuron tries to forecast the same target with an attached loss per-neuron, and finally, all the learning phases happen during each neuron (Dauphin, Fan, Auli, & Grangier, 2017). The equation of the GLU is , where is known as the piece-wise multiplication. The GLU allows the selection of what features is more essential in forecasting the correct export shipment.
Next, a residual connection is performed to activate the output produced from the second convolutional layer, and the input of the block is followed by a RELU activation function. The input to each block is added to the output of the block. A 1-by-1 convolution is applied on the input when the number of channels between the input and the output does not match, and a final activation function is applied. The same is performed for the remaining residual blocks. Finally, two fully connected layers are applied after the last residual block and a SoftMax function transforms the output of the last fully connected layer into a matrix of probabilities. Table 5 represents the parameters used in each layer during the training phase in terms of the number of blocks, filters, input channels. The filter size and the dropout factor are also specified. The number of block layers is presented as experimental, and block weights, bias, strides, dilation factor, and padding are determined. Finally, the parameters of the fully connected layer and the optional 1 1 convolutional layers are illustrated.
Table 5.
Parameters of the TCN network layers.
| Layers parameters | Values assigned experimentally | |||
|---|---|---|---|---|
| Number of blocks | 4 | |||
| Number of filters | 175 | |||
| Filter size | 3 | |||
| Drop out factor | 0.05 | |||
| Number of input channels | 16 | |||
| Blocks | ||||
| Block 1 | Conv1: Weights 3 × 16 × 175 Conv1: Bias 175 × 1 Stride 1 Dilation Factor 1 Padding [2; 0] |
Conv2: Weights 3 × 175 × 175 Conv2: Bias 175 × 1 Stride 1 Dilation Factor 1 Padding [2; 0] |
Conv3: Weights 3 × 175 × 175 Conv3: Bias 175 × 1 Stride 1 Dilation Factor 1 Padding [2; 0] |
|
| Block 2 | Conv1: Weights 3 × 175 × 175 Conv1: Bias 175 × 1 Stride 1 Dilation Factor 2 Padding [4; 0] |
Conv1: Weights 3 × 175 × 175 Conv1: Bias 175 × 1 Stride 1 Dilation Factor 2 Padding [4; 0] |
||
| Block 3 | Conv1: Weights 3 × 175 × 175 Conv1: Bias 175 × 1 Stride 1 Dilation Factor 4 Padding [8; 0] |
Conv1: Weights 3 × 175 × 175 Conv1: Bias 175 × 1 Stride 1 Dilation Factor 4 Padding [8; 0] |
||
| Block 4 | Conv1: Weights 3 × 175 × 175 Conv1: Bias 175 × 1 Stride 1 Dilation Factor 8 Padding [16; 0] |
Conv1: Weights 3 × 175 × 175 Conv1: Bias 175 × 1 Stride 1 Dilation Factor 8 Padding [16; 0] |
||
| Optional 1 × 1 convolutional layer | Weights: 1 × 16 × 175 Bias 175 × 1 |
|||
| Fully connected layer | Weights: 2 × 175 Bias 2 × 1 |
|||
3.4. Classification
3.4.1. ML classifiers
Six main ML classifiers are applied on the features obtained from proposed deep learning models. In most of the deep learning methodologies applied for classification are based on convolutional and fully connected layers. Among them, the most widely used classifier is firstly the SoftMax classifier. The notion of this classifier is to learn as much from the lower level parameters (Jiang et al., 2018). Secondly, support vector machine (SVM) is deemed to be a conventional two-class model. It has several merits in solving small samples, multi-class, high-dimensional pattern recognition. It has the ability to solve non-linear multi-classification problems by transforming linear indivisible into linear divisible problems using soft interval maximization methodologies (Vapnik, 2013). Thirdly, Artificial neural networks (ANN) is a classifier that is composed of various neurons to convert the input vector to an output vector. The main functionality of the ANN is that each neuron takes an input, and then it applies an activation function on it (Haykin & Network, 2004). The output produced from the activation act as an input to the next layer. Moreover, the network can be designed in two main forms which are the feed-forward or feedback networks. The main connection between one neuron and the other is the weight, and this weight is updated and used on the features from one neuron to another (Haykin et al., 2009). The weights are used in the training phase so that they can classify vectors based on sufficient neurons found in the hidden layer. The classification function of the ANN begins with the summation of the multiplication of weight summed by the bias of the neuron. If the addition is positive, the output values of the neuron fire, otherwise it does not fire. The neural network was applied widely in pattern classification tasks.
Fourthly, random trees (RT) or sometimes called perfect random tree ensemble (PERT) are random tree classifiers, which can fit the training data perfectly (Cutler & Zhao, 2001). The main construction of the trainer is based on firstly placing all the features in the root mode. Then, each non-terminal node is splitted randomly at each step of the construction of the tree (Jagannathan, Pillaipakkamnatt, & Wright, 2009). This process is performed by choosing two features from the node until these two belong to different classes. If all the features in the data did not come from the same class, then this node is considered to be terminal. The next step is to randomly choose a feature in order to split. The operation of the split is repeated until a definitive split is reached. Fifthly, random forest (RF) is a classifier that is composed of a combination of the random tree classifiers. Each classifier is obtained by applying a random feature that is sampled separately from the input features. Each tree in the forest adjusts a new vote for the recent popular class to classify the input features (Breiman, 1999). This classifier used randomly selected features or a combination of them at each node to build the tree. One of the methods that are used in generating the training set is the bagging method. Every time the tree is grown to a depth on a new training data based on a combination of features. These grown trees to the maximum are not pruned. This is the main advantage of the random forest over the decision tree methods (Pal, 2005). Finally, k-nearest neighbor (KNN) is one of the simplest and mostly used for classification tasks. It operates by obtaining the main distance between two samples and this can be in the form of Euclidean, Manhattan, city block and Chebyshev distances. Finally, the decision rule that explains the maximum similarity in the KNN represent which class does this sample belong to. The main distance applied using KNN is the Euclidean distance. Table 6 shows the main parameters used by each classifier.
Table 6.
Parameters of each classifier applied on the methodologies.
| Classifiers | Parameters |
|---|---|
| SoftMax | Loss function “Cross Entropy Function” |
| Support vector machine (SVM) | Batch Size 100, Calibrators “Logistic” Epsilon 1 × , Kernel Function “Polynomial” |
| Artificial neural network (ANN) | Learning Rate 0.3, Momentum 0.2 Training Time 1000, Validation Threshold 20 |
| Random trees (RT) | Batch Size 100, Max Depth 0 Seed 1, MinVarienceProp 0.001 |
| Random Forest (RF) | Batch Size 100, Max Depth 0 Seed 1, MinVarienceProp 0.001 Number of iterations 300, Number of features 0 |
| k-nearest neighbor (KNN) | KNN 1, Batch Size 100 Nearest neighbor (NN) Search Algorithm “Linear NN Search” Distance function “Euclidian distance” |
4. Experimental results
This section represents the results of the four proposed DL feature extraction methods on the six classifiers verified. The whole experiments were carried out on a laptop with Intel Core i7-8565U @1.80 GHz 1.99 GHz, 12 GB RAM, and NVIDIA GeForce GTX 310M 4 GB graphics card. The deep learning models and classifiers were developed using MATLAB Software. The total number of shipments in the dataset is 4 547 661. 2 048 577 out of 4 547 661 shipments are selected to verify the performance of the proposed models in forecasting and predication. The main aim is to determine if the shipment is going to be exported or not based on the information provided with each shipment and this will be with a great benefit in the COVID-19 pandemic. The selected shipments are divided into 50% training, 25% validation, and 25% for test. This division leads to creation of 1 048 576 in the training set, while 500 001 shipments in each of the validation and the test sets. The experiment is verified using the stacked LSTM, stacked BiLSTM, stacked GRU, and TCN models. The performance is illustrated based on the training options of the model, various statistical performance measurements, receiver operating characteristic (ROC), and the confusion matrices. Finally, each DL model is verified using six machine learning classifiers.
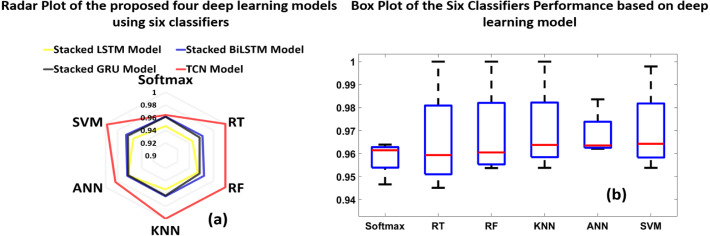
4.1. Performance measurements and main findings
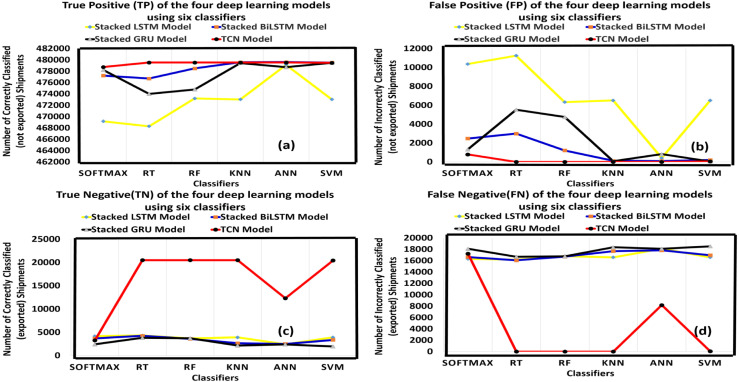
To validate and to demonstrate the supremacy of one DL model among others, this paper has considered different performance measures. These measurements depend mainly on statistical calculations and probabilities. They are: true positive (TP), false positive (FP), true negative (TN), false negative (FN), precision (P), accuracy (A), sensitivity (SEN), specificity (SPEC), false-positive rate (FPR), False negative rate (FNR), F-measure (F1), Error (E), Matthews correlation coefficient (MCC) and Cohen’s kappa coefficient (K) (Ratner, 2017).
Each of these measurements is explained in terms of definition, purpose, and formula. These measurements show how the DL methods vary in performance and accuracy. The four main terms that describe the entire process of the correctly classified or the incorrectly classified instances are the TP, TN, FP, and FN. All the measurements provided are explained as follows:
TP: It represents the number of shipments that will not be exported due to uncertainties and the proposed system predicted it correctly.
TN: It represents the number of shipments that will be exported and the proposed system predicted it correctly.
FP: It represents the number of shipments that will not be exported and the proposed system predicted it as exported.
FN: It represents the number of shipments that will be exported and the proposed system predicted it as not exported.
Precision (P) is defined as the number of correctly classified instances of the shipment not exported over the summation of the correctly and incorrectly not exported shipments. It is expressed in terms of TP and FP by:
| (16) |
Accuracy is estimated as the percentages of the correctly classified instances (here, shipments not exported or shipments exported) overall the total numbers of test instances and it is represented as follows:
| (17) |
The sensitivity (SEN), detection rate, sometimes called the recall refers to the capability of the system to positively detect the shipments that are not exported based on a condition. It is defined using the following formula: -
| (18) |
The specificity (SPEC), detection rate, sometimes called the recall refers to the ability of the system to correctly determine the absence of the number of shipments that are exported and it is defined as follows:
| (19) |
Two important terms that are useful in building decisions and taking action are the false positive rate (FPR) or sometimes known as the fall-out ratio and the false-negative rate (FNR) or sometimes called the miss-out ratio. FPR is represented as the main ratio between the absence of shipments exported wrongly classified as shipments not exported over the total number of shipments that are exported, but the FNR is defined as the ratio between the number of the wrongly classified instance as shipments exported over the total number of shipments that are not exported. Both FPR and FNR are defined using the following equations:
| (20) |
| (21) |
F-measure or sometimes called F1-score depends on the precision and recall of its main calculations. It is defined using the following formula:
| (22) |
Another simple known measurement is called the Error (E), and it is defined as:
| (23) |
Mathews correlation coefficient (MCC) is used to define the value of classification. To calculate the value of this coefficient; TP, TN, FN, and FP are used. This measurement can be also used even if the classes vary in size. It is also defined as the correlation between the target and the predicted values obtained from the classification methods. MCC is defined using the following equation:
| (24) |
Finally, the last measurement used is Cohen’s kappa coefficient (K) or sometimes known as Kappa statistic (Donner & Klar, 1996). It is a statistical measurement that determines the agreement for a qualitative class. This measurement indicates the prediction of each classifier to features in C classes that are mutually exclusive as shown in the following equation:
| (25) |
where is the probability of an instance agreement among different classifiers, and the is a probability that describes the instance agreement probability.
4.2. Training options for the proposed DL models
In the DL methodologies, parameters need to be adjusted to the network during the training phases. These parameters must be adjusted carefully and sometimes based on the trial and error methods. Various parameters are adjusted such as network solver optimizer, mini-batch size, initially learn rate, learning rate (schedule, period, factor), maximum (epochs and iterations), number of iterations in each epoch, L2 regularization, gradient (decay factor, function, threshold value), validation frequency, verbose, and the verbose frequency. The network solver is a solver for training the DL network. There are three main types of solver optimizers which are: adaptive moment estimation (adam), stochastic gradient descent momentum (SGDM), root mean square propagation (RMSProp). Adam is an update to the RMSProp optimizer as it combines the best properties of the adaptive gradient algorithm (AdaGrad) and RMSProp algorithms. Adam is much faster than SGD and it can handle sparse gradients on noisy problems. Therefore, Adam is used in the four DL models. A parameter related to the Adam solver is known as gradient decay factor is adjusted for the DL models with different values from 0 to 1. The next parameter is the “mini-batch size” and it is considered to be the amount of data included in each sub-epoch weight and it defines the number of samples to work through before updating the internal model parameters. In the RNNs, the mini-batch size is larger, because, in the RNN model, it is required to make larger gradient steps. After all, with larger batch sizes in the RNN models, they can converge faster and give better performance by improving the effectiveness of the optimization steps leading to a rapid convergence of the model parameters. On the contrary, it is necessary to provide a small mini-batch size for the TCN model because it leads to a small number of iterations for the training algorithm and higher accuracy is achieved in the overall performance.
The next parameter is the initial learning rate. The learning is defined with average values for the model to achieve an average training time and optimal results. If the learning rate is high, the training might reach a sub-optimal result and it will not converge. If the learning rate is too low, the training will take a long time to converge. It is defined with a value of 0.001 for all the RNN models, while in the TCN model the learning rate is defined with 0.1. Another common parameter is the learning rate schedule. There are two options for the learning rate schedule which are “none” or “piece-wise”. The first option means that the learning rate keeps constant during the whole training stage, while the second option means that the training is updated every learning rate by a certain factor. The first option was applied for the RNN models, while the second option was applied for the TCN model, as it showed better accuracy performance in the classification. In addition to this, for the TCN there are two related parameters which are the learning rate drop factor and learning rate drop period. The drop period is the number of epochs used for dropping the learning rate. The global learning rate is multiplied by the drop factor every time number of epochs passes and it is defined by the drop factor. Therefore, the drop period and factor are assigned as 0.9 and multiplied by the learning rate every 5 epochs. The next parameters are the number of epochs, iterations, and the maximum number of iterations. Each epoch holds a set of iterations and the multiplication of the number of iterations by the number of epochs produces the maximum number of iterations. In the RNN models, it can be seen that a large number of iterations are performed to obtain a normal convergence, while the TCN model, relies on a small number of iterations achieving a high convergence in the validation accuracy. The next parameter is the “L2 regularization” and it is a term for the weights as it is sometimes called weight decay. This parameter is used to reduce over-fitting.
Another important parameter is the “gradient threshold method”. In the RNN models, the gradient method is known as l2norm, and if the l2norm of the gradient is larger than the gradient threshold, then the gradient is scaled so that the l2norm equals the gradient threshold. The gradient threshold in the RNN models is infinity so that the l2norm will never be greater than the infinity. In the TCN model, the gradient method is the global-l2norm and it is defined by L and if L is greater than the gradient threshold, then all the gradients are scaled by a factor of gradient threshold divided by L. An important parameter is the validation frequency its value represents after how many iterations a validation accuracy will be computed. Finally, there exist two optional parameters which are the verbose and verbose frequency. If the verbose parameter is assigned to 1, the training process will be plotted. Otherwise, it will not. The verbose frequency shows the number of iterations between printing to the command window.
Table 7, Table 8 show the training parameters for the RNN models and the TCN model. The tables clarify the values tested for the model and the last values that showed the highest validation accuracy. The performance of the proposed DL models is illustrated in the following sections. Each DL model is evaluated using three main measures. The first measure depends on the calculation of various statistical variables based on the validation and test data of shipments. The second measure relies on the receiver operator characteristic (ROC) of the model on six main classifiers. Finally, the last measure is the computation of the confusion matrices to verify the final results of the DL models.
Table 7.
Parameters of the training options for the proposed RNN Models.
| Training parameters | Values tested before reaching the final model | Stacked LSTM model | Stacked BiLSTM model | Stacked GRU model |
|---|---|---|---|---|
| Optimizer | Sgdm, Adam, Rmsprop | Adam | Adam | Adam |
| Gradient decay factor | 0.5, 0.7, 0.9, 0.95 0.99 | 0.95 | 0.7 | 0.95 |
| Mini batch size | 1, 8, 16, 32, 64 | 64 | 16 | 32 |
| Initial learning rate | 0.01, 0.001, 0.0001 | 0.001 | 0.001 | 0.001 |
| learning rate schedule | “Constant”, “Piece wise” | “Constant” | “Constant” | “Constant” |
| Max epochs | 10, 15, 20, 25, 30 | 15 | 10 | 15 |
| Iterations per epochs | 38 836 | 38 836 | 38 836 | 38 836 |
| Total number of iterations | 388 360,582 540,776 720, 970 900,1 165 080 | 582 540 | 388 360 | 582 540 |
| L2 Regularization | 0.1, 0.01, 0.001, 0.0001 | 0.001 | 0.1 | 0.0001 |
| Gradient threshold method | “l2-norm”, “global-l2norm” | “l2-norm” | “l2-norm” | “l2-norm” |
| Gradient threshold value | 1, 2, 3, 4, 5, Inf | Inf | Inf | Inf |
| Validation frequency | 50 000, 101 059, 150 000 | 101 059 | 101 059 | 101 059 |
Table 8.
Parameters of the training options for the proposed TCN Model.
| Training parameters | Values tested before reaching the final model | TCN Model |
|---|---|---|
| Optimizer | Sgdm, Adam, Rmsprop | Adam |
| Gradient decay factor | 0.5, 0.7, 0.9, 0.95, 0.99 | 0.99 |
| Mini batch size | 1, 8, 16, 32, 64 | 1 |
| Initial learning rate | 0.01, 0.001, 0.0001 | 0.1 |
| Learning rate schedule | “Constant”, “Piece wise” | “Piecewise” |
| Learning rate drop period | 2, 5, 7, 9 | 5 |
| Learning rate drop factor | 0.2, 0.4, 0.5, 0.7 0.9 | 0.9 |
| Max epochs | 100, 200, 300, 400, 500 | 400 |
| Iterations per epochs | 1 | 1 |
| Total number of iterations | 100, 200, 300, 400, 500 | 400 |
| L2 Regularization | 0.1, 0.01, 0.001, 0.0001 | 0.0001 |
| Gradient threshold method | “l2-norm”, “global-l2norm” | “global-l2norm” |
| Gradient threshold value | 1, 2, 3, 4, 5, Inf | 1 |
| Validation frequency | 20, 50, 70 100 | 70 |
4.3. Performance of the stacked LSTM model
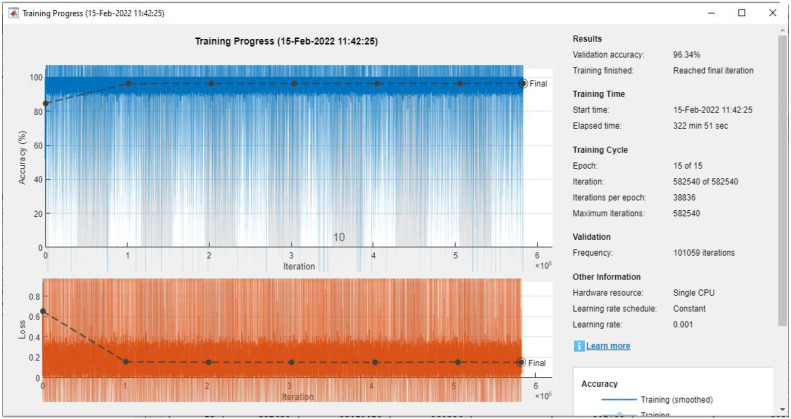
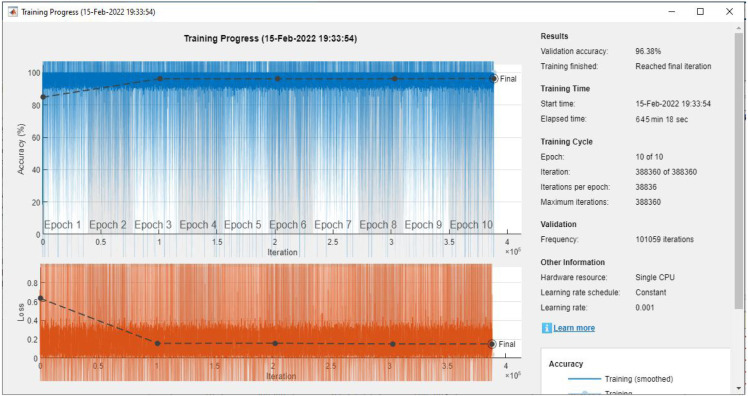
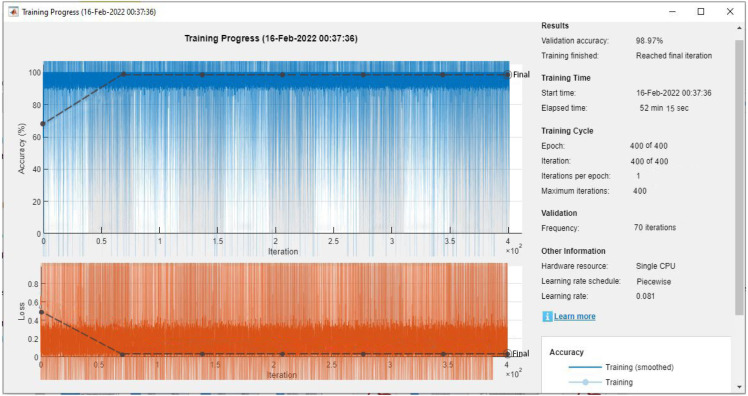
It is essential to evaluate the performance of the stacked LSTM model based on the computation of the validation accuracy obtained from the model. Fig. 6 shows the training and loss curves obtained from the Stacked LSTM model based on the parameters mentioned in Table 7. In addition to this, the validation accuracy of the proposed Stacked LSTM model is identified with an accuracy value of 96.23%. It can be seen that several training parameters and their values are defined clearly in the Fig. 6 such as learning rate, epochs, iterations, maximum iterations, and their values are 0.001, 15, 38 836, and 582 540 respectively.
Fig. 6.
Training and loss curves of the stacked LSTM model for shipments prediction.
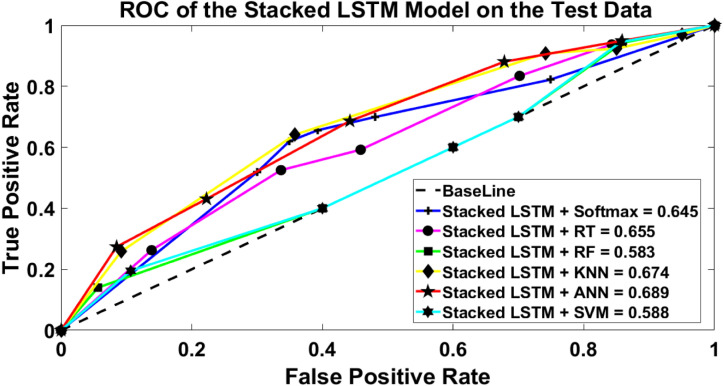
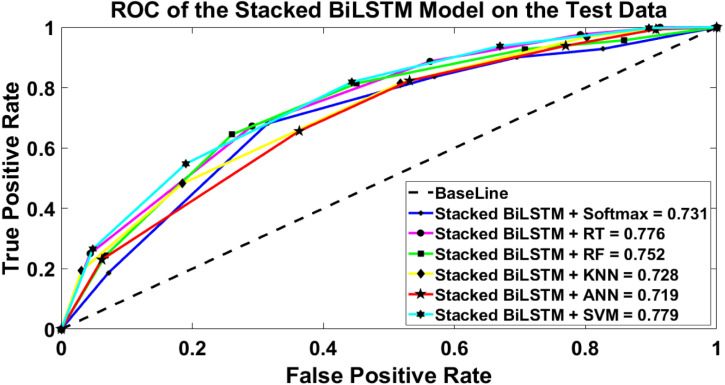
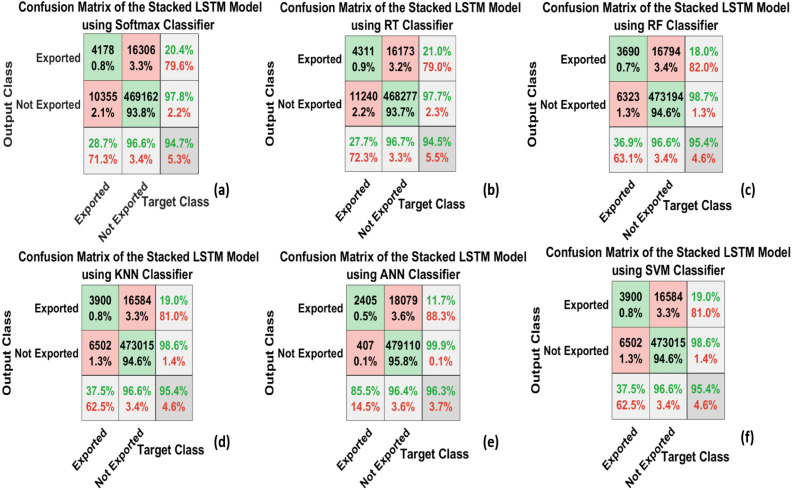
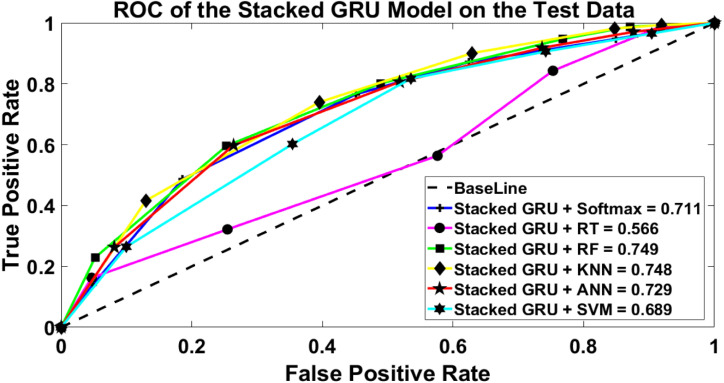
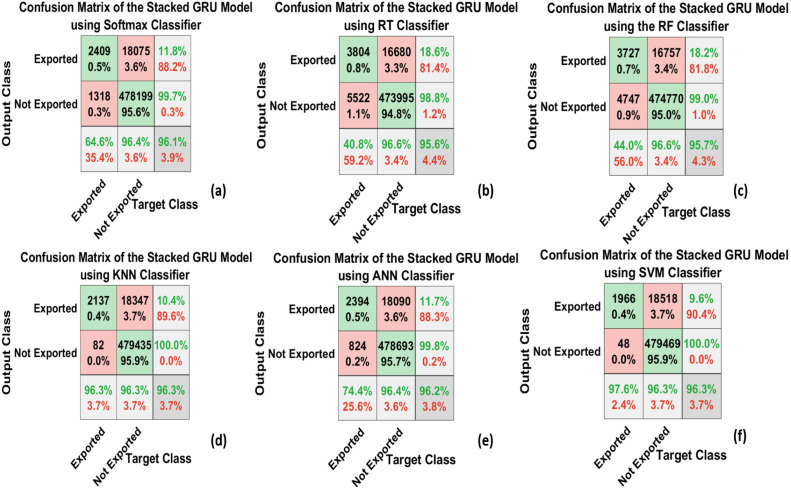
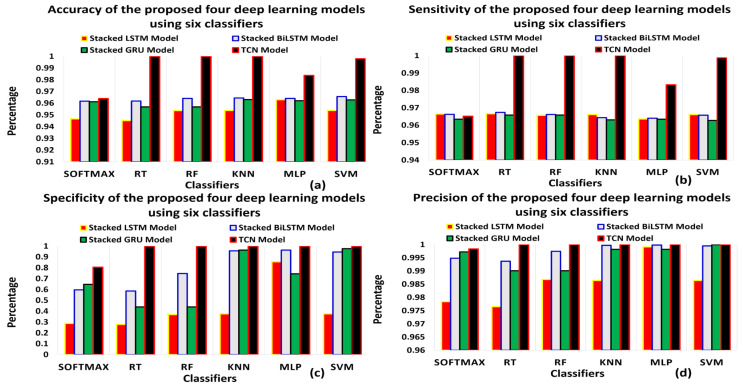
Table 9, Table 10 show the performance measurements calculated for the stacked LSTM methodology using six main ML classifiers on the validation and the testing sets. The rows of the table represent the classifiers, while the columns of the table present the performance measurements illustrated. These measurements are calculated to assist the SC in determining the average number of correct shipments to be exported in the “TP” column and the average number of the correct shipments that should not be exported in the “TN” column. The FN and FP represent the average number of incorrectly classified shipments based on the performance of each classifier. It can be observed that KNN and SVM had the highest performance measurements with the same accuracy values, whereas SoftMax and RT had the lowest accuracy performance using stacked LSTM methodology on the validation and test sets. It can be seen that all the classifiers have a nearly equal average SEN and FNR. Finally, it can be realized that the maximum accuracy achieved using stacked LSTM on the validation and the test sets are 0.9545 and 0.9538 respectively.
Table 9.
The results of the stacked LSTM model on the validation data in terms of various statistical performance measurements.
| Classifiers | TP | FP | FN | TN | SEN | SPEC | P | A | FPR | FNR | F1 | MCC | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Softmax | 469 437 | 10 262 | 16 104 | 4198 | 0.966 | 0.290 | 0.978 | 0.947 | 0.709 | 0.033 | 0.972 | 0.218 | 0.215 |
| RT | 468 528 | 11 171 | 15 895 | 4407 | 0.967 | 0.282 | 0.976 | 0.945 | 0.717 | 0.032 | 0.971 | 0.220 | 0.218 |
| RF | 473 440 | 6259 | 16 539 | 3763 | 0.966 | 0.375 | 0.986 | 0.954 | 0.624 | 0.033 | 0.976 | 0.242 | 0.227 |
| KNN | 473 290 | 6409 | 16 340 | 3962 | 0.966 | 0.382 | 0.986 | 0.954 | 0.617 | 0.033 | 0.976 | 0.251 | 0.237 |
| ANN | 479 263 | 436 | 17 740 | 2562 | 0.964 | 0.854 | 0.999 | 0.963 | 0.145 | 0.035 | 0.981 | 0.320 | 0.211 |
| SVM | 473 290 | 6409 | 16 340 | 3962 | 0.966 | 0.382 | 0.986 | 0.954 | 0.617 | 0.033 | 0.976 | 0.251 | 0.237 |
Table 10.
The results of the stacked LSTM model on the test data in terms of various statistical performance measurements.
| Classifiers | TP | FP | FN | TN | SEN | SPEC | P | A | FPR | FNR | F1 | MCC | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Softmax | 469 162 | 10 355 | 16 306 | 4178 | 0.966 | 0.287 | 0.978 | 0.946 | 0.712 | 0.033 | 0.972 | 0.215 | 0.211 |
| RT | 468 277 | 11 240 | 16 173 | 4311 | 0.966 | 0.277 | 0.976 | 0.945 | 0.722 | 0.033 | 0.054 | 0.213 | 0.211 |
| RF | 473 194 | 6323 | 16 794 | 3690 | 0.986 | 0.180 | 0.967 | 0.953 | 0.819 | 0.013 | 0.976 | 0.236 | 0.221 |
| KNN | 473 015 | 6502 | 16 584 | 3900 | 0.966 | 0.374 | 0.986 | 0.953 | 0.625 | 0.033 | 0.976 | 0.245 | 0.231 |
| ANN | 479 110 | 407 | 18 079 | 2405 | 0.963 | 0.855 | 0.9991 | 0.963 | 0.144 | 0.036 | 0.9810 | 0.308 | 0.198 |
| SVM | 473 015 | 6502 | 16 584 | 3900 | 0.9661 | 0.374 | 0.986 | 0.953 | 0.625 | 0.033 | 0.976 | 0.245 | 0.231 |
Another important figure to illustrate the performance of a classification model at all various classification thresholds is the receive operator characteristic (ROC). ROC has two main parameters which are the true positive rate (TPR) and False positive Rate (FPR). Fig. 7a shows the ROC curves of the Stacked-LSTM model on the test data. The -axis represents the FPR and the -axis represents the TPR. The figure has 6 main ROC curves. The blue line with plus markers represents the ROC curve of the Softmax Model, while the magenta line with a black circle marker shows the ROC curve of the RT. In addition to this, the green and the yellow lines with square and diamond markers represent the ROC of RF and KNN respectively. Finally, the red and the cyan lines with pentagon and hexagon markers represent the ANN and SVM ROC curves. The value assigned to each ML model in the legend represents the area under the curve (AUC). On one hand, it can be manifested from the ROC figure that the classifiers based on the stacked LSTM model that showed the lowest AUC are RT, SVM, and Softmax on the test data. On the other hand, it can be seen that the classifiers based on the stacked LSTM model that showed the highest (AUC) on the test data are ANN, and SVM.
Fig. 7.
ROC of the stacked LSTM model using various classifiers on the shipments test data prediction.
The confusion matrix is a specific table layout that permits the visualization of the performance of a certain methodology, and it is sometimes called the heat map or the error matrix. The confusion matrix is obtained on the highest performance classifiers using the four proposed DL methodologies. It can be seen from the results that ANN with stacked LSTM had shown the highest classification accuracy. Fig. 10(a, b, c, d, e, and f) represent the confusion matrix for the stacked LSTM based on Softmax, RT, RF, KNN, ANN, and SVM respectively, and each row of the matrix illustrates the instance in the predicated classes. Therefore, the -axis is called the output class, and the -axis is called the target class. The green orders represent the average correctly classified instances, while the red indicates the average incorrectly classified instances. For example, the first row for the confusion matrix in Fig. 8(a) has three cells and a number beside it on the -axis. The number beside the -axis is the class number, while the first cell is colored in green and has two main values; the first value is an integer, and the other one is a percentage. The integer values represent the number of the correctly classified instances from exported shipments class which means that 4178 shipments from 20 425 are classified correctly, and this is defined as the value of the TP. The percentage value is 0.8% which means that 0.8% of the test data are classified correctly. To illustrate, 4178 is divided over 500 001 to obtain the 8.35%percentage. The second cell in the first row has a red color which means that the integer value which is 16 306 is the number of incorrectly classified instances from the not exported shipments and are classified to be shipment exported. The percentage under the 16 306 value in the cell is deduced by dividing 16 306 over 500 001 to obtain 3.3%. The last cell in the first row has two main percentages, one with a green color and the other one with a red color. The green one represents the SEN and the red percentage express the average FNR.
Fig. 10.
ROC of the stacked BiLSTM model using various classifiers on the shipments test data prediction.
Fig. 8.
Confusion matrix of the stacked LSTM model using various classifiers on the shipments test data prediction.
The second row in the first sub-figure has also three main cells. The first cell has two main values, the first is an integer and the second one is a percentage. The integer value is the number of the shipments that were exported and incorrectly classified as not exported, whereas the percentage value is the integer value divided over the test set. The same is for the second cell in the second row. The third cell in the second row has two values, the first one is the SPEC and the second one is the FPR. The last row in the confusion matrix has also three main cells: the first percentage in the first cell is the average precision, the second percentage in that same cell is the average false discovery rate. The false discovery rate is a measurement that is calculated by dividing the average FP over the summation of the average FP and TP. The values of the second cell two percentages, the first percentage are the average negative predictive value, and it is the division of the average TN over the summation of average TN and FN, while the second percentage is the average false omission rate, and it is calculated by the division of the average FN over the summation of average FN and average TN. The last cell in the last row has two percentages; the first percentage is the summation of the percentages in the green areas, while the second percentage is the summation of the percentages in the red areas.
4.4. Performance of the stacked BiLSTM model
In this subsection, the same experiment is performed using a stacked BiLSTM model. The aim is to illustrate if the stacked BiLSTM model can improve the performance of the results obtained from the stacked-LSTM. To visualize the performance of the stacked BiLSTM the same performance measurements described above are calculated and the roc and the confusion matrices are computed. Fig. 9 represents the training and the loss curves of the stacked BiLSTM model. The blue line represents the training, while the red line represents the loss curves, whereas, the black line describes the calculated validation accuracy and loss during the training progress. It can be visualized also from the figure that the number of epochs is equal to 10 which is less than that of the stacked LSTM and the total number of iterations are 388 360.
Fig. 9.
Training and loss curves of the stacked BiLSTM model for shipments prediction.
Table 11, Table 12 represent the performance of the stacked-BiLSTM using six classifiers based on various statistical measurements on the validation and test data sets. It can be manifested from the table that stacked BiSLTM based on SVM had the highest classification performance, while stacked BiLSTM based on Softmax followed by RT has the lowest classification results, whereas, the stacked Bi LSTM based on RF, KNN, and ANN had the same accuracy performance on both sets.
Table 11.
The results of the stacked-BiLSTM model on the validation data in terms of various statistical performance measurements.
| Softmax | 476 955 | 2562 | 16 987 | 3497 | 0.965 | 0.577 | 0.994 | 0.960 | 0.422 | 0.034 | 0.979 | 0.299 | 0.249 |
| RT | 476 428 | 3089 | 16 334 | 4150 | 0.966 | 0.573 | 0.993 | 0.9611 | 0.426 | 0.033 | 0.980 | 0.325 | 0.284 |
| RF | 478 230 | 1287 | 17 045 | 3439 | 0.965 | 0.727 | 0.997 | 0.963 | 0.272 | 0.034 | 0.981 | 0.338 | 0.261 |
| KNN | 479 397 | 120 | 17 966 | 2518 | 0.963 | 0.954 | 0.999 | 0.963 | 0.045 | 0.036 | 0.981 | 0.335 | 0.210 |
| ANN | 479 419 | 98 | 18 113 | 2371 | 0.963 | 0.960 | 0.999 | 0.963 | 0.039 | 0.036 | 0.981 | 0.326 | 0.199 |
| SVM | 479 318 | 199 | 17 242 | 3241 | 0.965 | 0.942 | 0.999 | 0.965 | 0.057 | 0.034 | 0.982 | 0.378 | 0.262 |
Table 12.
The results of the stacked-BiLSTM model on the test data in terms of various statistical performance measurements.
| Classifiers | TP | FP | FN | TN | SEN | SPEC | P | A | FPR | FNR | F1 | MCC | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Softmax | 477 224 | 2475 | 16 633 | 3669 | 0.966 | 0.597 | 0.994 | 0.961 | 0.402 | 0.033 | 0.980 | 0.314 | 0.263 |
| RT | 476 707 | 2992 | 16 062 | 4240 | 0.967 | 0.586 | 0.993 | 0.961 | 0.413 | 0.032 | 0.980 | 0.334 | 0.292 |
| RF | 478 484 | 1215 | 16 704 | 3598 | 0.966 | 0.747 | 0.997 | 0.964 | 0.252 | 0.033 | 0.981 | 0.353 | 0.275 |
| KNN | 479 578 | 121 | 17 665 | 2637 | 0.964 | 0.956 | 0.999 | 0.964 | 0.043 | 0.035 | 0.981 | 0.345 | 0.221 |
| ANN | 479 604 | 95 | 17 810 | 2492 | 0.964 | 0.963 | 0.999 | 0.964 | 0.036 | 0.035 | 0.981 | 0.337 | 0.210 |
| SVM | 479 503 | 196 | 16 947 | 3355 | 0.965 | 0.944 | 0.999 | 0.965 | 0.055 | 0.034 | 0.982 | 0.387 | 0.272 |
Fig. 10 shows the roc curves of the stacked BiLSTM model based on the six classifiers. It can be visualized that stacked Bi LSTM SVM had the highest AUC value, while the stacked BiLSTM based on ANN had the lowest AUC value. In comparison with AUC, it is be seen that the stacked BiLSTM model had higher values for AUC than the stacked LSTM based on the same classifiers. Fig. 11(a,b,c,d,e, and f) represent the confusion matrices of stacked BiLSTM based on Softmax, RT, RF, KNN, ANN, and SVM. Then, based on the confusion matrices the performance of the stacked BiLSTM is higher than stacked LSTM using all the classifiers.
Fig. 11.
Confusion matrix of the stacked BiLSTM model using various classifiers on the shipments test data prediction.
4.5. Performance of the stacked GRU model
A deep model based on gated recurrent unit layers is applied to verify its performance on the shipments of the test and the validation sets. GRU layers are considered to be faster than LSTM because they use two gates which are then reset and the forget, while LSTM uses three gates which are the input, forget, and output. This makes GRU faster and less expensive. It also uses fewer training parameters and memory. Therefore, the same experiment is applied on the stacked GRU model to visualize the achieved accuracy and to compare between the stacked GRU model and the stacked LSTM and BiLSTM models. Fig. 12 shows the validation accuracy obtained from the stacked GRU model after training based on 15 epochs forming about 582 540 iterations. It can be seen that the validation accuracy obtained from the stacked GRU model is slightly lower than the stacked LSTM and the stacked BiLSTM models.
Fig. 12.
Training and loss curves of the stacked GRU model for shipments prediction.
On one hand, in Table 13 it can be seen that the results of the stacked GRU based on KNN and SVM showed the highest performance, while the stacked GRU based on ANN and Softmax showed an average performance, whereas, the stacked GRU based on RT and RF showed the same and the lowest statistical results performance on the validation data. On the other hand, in Table 13 it can be seen that the results of the stacked GRU based on KNN showed the highest performance, while the stacked GRU based on ANN and SVM showed the same performance and the stacked GRU based on RT and RF showed the same performance, while the stacked GRU model based on Softmax showed the lowest statistical results performance on the test data.
Table 13.
The results of the stacked-GRU model on the validation data in terms of various statistical performance measurements.
| Classifiers | TP | FP | FN | TN | SEN | SPEC | P | A | FPR | FNR | F1 | MCC | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Softmax | 468 261 | 1438 | 17 747 | 2555 | 0.963 | 0.639 | 0.996 | 0.960 | 0.360 | 0.036 | 0.979 | 0.272 | 0.199 |
| RT | 474 314 | 5385 | 16 379 | 3923 | 0.966 | 0.451 | 0.990 | 0.957 | 0.548 | 0.033 | 0.978 | 0.274 | 0.245 |
| RF | 474 993 | 4706 | 16 436 | 3866 | 0.966 | 0.451 | 0.990 | 0.957 | 0.548 | 0.033 | 0.978 | 0.274 | 0.249 |
| KNN | 479 602 | 97 | 18 017 | 2285 | 0.963 | 0.959 | 0.999 | 0.963 | 0.040 | 0.036 | 0.981 | 0.322 | 0.194 |
| ANN | 481 349 | 864 | 17 788 | 2514 | 0.964 | 0.744 | 0.998 | 0.962 | 0.025 | 0.035 | 0.980 | 0.294 | 0.203 |
| SVM | 479 644 | 55 | 18 188 | 2114 | 0.963 | 0.974 | 0.999 | 0.963 | 0.025 | 0.036 | 0.981 | 0.312 | 0.181 |
Fig. 13 shows the roc curves of the stacked GRU model based on Softmax, RT, RF, KNN, ANN, and SVM classifiers. It can be visualized that stacked GRU based on RF had the highest AUC value, while the stacked GRU based on RT had the lowest AUC value. Fig. 14(a,b,c,d,e, and f) represent the confusion matrices of stacked GRU based on Softmax, RT, RF, KNN, ANN, and SVM. Then, based on the confusion matrices the performance of the stacked GRU is higher than stacked LSTM using all the classifiers and slightly lower than the Stacked BiLSTM (see Table 14).
Fig. 13.
ROC of the stacked GRU model using various classifiers on the shipments test data prediction.
Fig. 14.
Confusion matrix of the stacked GRU model using various classifiers on the shipments test data prediction.
Table 14.
The results of the stacked-GRU model on the test data in terms of various statistical performance measurements.
| Classifiers | TP | FP | FN | TN | SEN | SPEC | P | A | FPR | FNR | F1 | MCC | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Softmax | 478 199 | 1318 | 18 075 | 2409 | 0.963 | 0.646 | 0.997 | 0.961 | 0.353 | 0.035 | 0.980 | 0.264 | 0.188 |
| RT | 473 995 | 5522 | 16 680 | 3804 | 0.9659 | 0.439 | 0.990 | 0.956 | 0.560 | 0.034 | 0.977 | 0.264 | 0.235 |
| RF | 474 770 | 4747 | 16 757 | 3727 | 0.965 | 0.439 | 0.990 | 0.956 | 0.560 | 0.034 | 0.977 | 0.264 | 0.239 |
| KNN | 479 435 | 82 | 18 347 | 2137 | 0.963 | 0.963 | 0.998 | 0.963 | 0.036 | 0.036 | 0.981 | 0.310 | 0.181 |
| ANN | 478 693 | 824 | 18 090 | 2394 | 0.963 | 0.743 | 0.998 | 0.962 | 0.256 | 0.036 | 0.980 | 0.285 | 0.193 |
| SVM | 479 469 | 48 | 18 518 | 1966 | 0.962 | 0.976 | 0.999 | 0.962 | 0.023 | 0.037 | 0.981 | 0.300 | 0.168 |
4.6. Performance of the TCN model
TCN model has experimented on the shipments data for enhancing the performance of the results obtained from the stacked LSTM, GRU, and BiLSTM models. It can be found from the former results that the performance of the three RNN architectures is nearly similar to each other in performance with a slight difference between them. Also, it is seen that the three RNN models fail to predict a large number of shipments that can be exported and this is due to the small number of shipments that can be exported compared to the shipment that cannot be exported.
Therefore, TCN overcomes all the former problems and can deal with the unbalanced number of classes. Fig. 15 shows the training performance based on TCN. It can be seen that it had the highest validation accuracy compared to the RNN models. It is also visualized that TCN uses a small number of epochs and iterations compared to the RNN models.
Fig. 15.
Training and loss curves of the TCN model for shipments prediction.
Table 15, Table 16 represent the TCN model performance on the validation and the test data. It can be manifested that TCN based on RF and KNN showed a perfect performance on the validation set, and the TCN model based on RT, RF, and KNN presented the maximum classification accuracy on the test data. It can be identified from the tables that the TCN based on the Softmax had a similar performance equivalent to that of the RNN models on the validation and the test data. Fig. 16 presents the roc curves of the TCN model relying on the test data. It can be seen that the highest AUC achieved was based on the TCN depending on RT, RF, and KNN classifiers. The lowest AUC was reached using TCN based on Softmax, ANN, and SVM. Fig. 17(a,b,c,d,e, and f) represent the confusion matrices of stacked TCN based on Softmax, RT, RF, KNN, ANN, and SVM. Then, it can be found that the performance of the TCN model is higher than the stacked LSTM, BiLSTM, and GRU in the prediction of the shipments. Finally, all these measurements, plots, and graphs are designed and analyzed to assist the practitioners to build statistical percentages to support SCRI&AP, which will help in taking decisions related to the export of the shipments during this pandemic of COVID.
Table 15.
The results of the TCN model on the validation data in terms of various statistical performance measurements.
| Classifiers | TP | FP | FN | TN | SEN | SPEC | P | A | FPR | FNR | F1 | MCC | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Softmax | 478 931 | 768 | 17 008 | 3294 | 0.965 | 0.810 | 0.998 | 0.964 | 0.189 | 0.034 | 0.981 | 0.353 | 0.260 |
| RT | 479 662 | 37 | 54 | 20 248 | 0.999 | 0.998 | 0.999 | 0.999 | 0.001 | 0.000 | 0.999 | 0.997 | 0.997 |
| RF | 479 699 | 0 | 0 | 20 302 | 1.000 | 1.000 | 1.000 | 1.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1 |
| KNN | 479 699 | 0 | 0 | 20 302 | 1.000 | 1.000 | 1.000 | 1.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1 |
| ANN | 468 794 | 10 905 | 1271 | 19 031 | 0.997 | 0.635 | 0.977 | 0.975 | 0.364 | 0.002 | 0.987 | 0.750 | 0.745 |
| SVM | 479 699 | 0 | 8104 | 12 198 | 0.983 | 1.000 | 1.000 | 0.983 | 0.000 | 0.016 | 0.991 | 0.768 | 0.742 |
Table 16.
The results of the TCN model on the test data in terms of various statistical performance measurements.
| Classifiers | TP | FP | FN | TN | SEN | SPEC | P | A | FPR | FNR | F1 | MCC | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Softmax | 478 726 | 791 | 17 223 | 3261 | 0.965 | 0.804 | 0.998 | 0.963 | 0.195 | 0.034 | 0.981 | 0.348 | 0.255 |
| RT | 479 517 | 0 | 0 | 20 484 | 1.000 | 1.000 | 1.000 | 1.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1 |
| RF | 479 517 | 0 | 0 | 20 484 | 1.000 | 1.000 | 1.000 | 1.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1 |
| KNN | 479 517 | 0 | 0 | 20 484 | 1.0000 | 1.000 | 1.000 | 1.000 | 0.000 | 0.000 | 1.000 | 1.000 | 1 |
| ANN | 479 517 | 0 | 8179 | 12 305 | 0.983 | 1.000 | 1.000 | 0.983 | 0.000 | 0.016 | 0.991 | 0.768 | 0.742 |
| SVM | 479 473 | 44 | 59 | 20 425 | 0.998 | 0.997 | 0.999 | 0.997 | 0.002 | 0.000 | 0.999 | 0.997 | 0.997 |
Fig. 16.
ROC of the TCN model using various classifiers on the shipments test data prediction.
Fig. 17.
ROC of the TCN model using various classifiers on the shipments test data prediction.
4.7. Overall performance
It is essential to visualize the performance of the proposed DL models together to determine the efficiency of the models compared to each other. Fig. 18(a, b, c, and d) manifest the average sensitivity, specificity, precision, and accuracy of the proposed DL methodologies using six classifiers. Each sub-figure consists of bars that present the level of the performance and how they are compared with other classifiers. The red and the white bars describe the performance of the stacked LSTM and stacked BiLSTM DL models respectively, while the green and the black bars represent the performance of the stacked GRU and TCN models respectively. The -axis represents the six classifiers and the -axis represents the percentage values. On one hand, Fig. 18(a, b, and d) represent the accuracy, sensitivity, and specificity measurements, and the -axis is determined with minimum and maximum values from 0.9 to 1 to have a better visualization of the performance. In the first sub-figure it can be visualized that the values of accuracy are nearly equal with all the DL models using all the classifiers. It can also be visualized in sub-figure b that the three RNN models had a sensitivity value that did not exceed 0.97, while the TCN model reached the maximum sensitivity using RT, RF, and KNN. Meanwhile, in sub-figure (c), the values of the -axis are range from 0 to 1, for better visualization of the specificity performance. In sub-figure d, it can be seen that the RNN models had a high precision competing with the TCN model. It can be from Fig. 18 that the stacked LSTM showed the lowest performance, while the TCN showed the highest performance based on the presented bar sub-figures.
Fig. 18.
Representation for the average sensitivity, specificity, precision and accuracy for the four proposed DL methodologies on the proposed experiment.
Fig. 19(a,b,c, and d) shows a visual representation of the performance of the TP, FP, TN, and FN measurements calculated from the six classifiers on the four proposed DL methods. Each sub-figure has the number of shipments on the -axis and the classifiers on the -axis. The yellow curve represents the performance of the stacked LSTM and the blue curve expresses the performance of the stacked BiLSTM, while the black and the red curves illustrate the performance of the stacked GRU and the TCN model respectively. In Fig. 19(a), the TCN model showed the highest average TP over all other classifiers, while the stacked LSTM model showed low average TP performance using SoftMax and RT classifiers. The stacked LSTM, stacked BiLSTM, and the TCN had an equivalent TP performance using KNN, ANN, and SVM classifiers. It can be seen that the stacked LSTM cannot compete with other models in the TP except using the ANN classifier. In Fig. 19(b), it can be manifested that the TCN model showed zero average FP value using RF, KNN, and SVM classifiers, while the stacked BiLSTM and the stacked GRU showed an equivalent FP using KNN and SVM. However, the FP performance using LSTM was the worst using Softmax, RT, RF, KNN, and SVM. In Fig. 19(c), it is visualized that TCN has the highest TN values using classifiers starting from RT, RF, KNN, ANN, and SVM. It can be seen that there is a big gap in the TN performance using TCN than any other proposed DL methodologies. This can prove that the TCN is superior in performance. Finally, in Fig. 19(d), it can be seen that the TCN has the lowest average FN values over other DL methodologies.
Fig. 19.
Visual representation of the average TP, TN, FP and FN measurements for shipments exported based on the DL methods.
For better visualization two different diagrams are added which are the spider plot and the box plots. The spider plot presents a visual tool that can be used to organize the data logically. It can be used as a tool that organizes different concepts relying on color, space, and images. Fig. 20(a) is a spider plot in the form of a hexagon shape that illustrates the performance of the deep learning models. It can be manifested that the TCN is higher in performance than other RNN models especially using RT, RF, KNN, and SVM. Fig. 20(b) presents the ranges of the classifiers’ accuracies in terms of the proposed DL models in the form of a box plot. The box plot represents each classifier in a form of a box with lower and upper bounds presenting the range and the medium of the accuracy values obtained from this classifier.
Fig. 20.
(a) represents the radar plot for the proposed DL models based on the six classifiers (b) describes the box plot for the classifiers values obtained from the DL models.
Finally, the same experiment was developed using the 16 attributes based on the ML classifiers only and without using any of the proposed deep learning models. The results showed an average accuracy of 76.32%, 80.54%, 83.42%, 82.10%, 85.23% and 84.56% using Softmax, RT, RF, ANN, KNN, and SVM respectively.
4.8. Result summary
This paper presents a novel case study based on several DL methodologies to predict whether the shipments can be exported or not during the COVID-19 pandemic. Following the lack of case studies in the application of deep learning approaches in supply chain management, the main aim is to shed light on the development and application of DL methodologies in the analysis of supply chain data. Banking on the results depicted in earlier tables, the stacked LSTM, stacked BiLSTM, and stacked GRU approaches showed an acceptable performance, the stacked BiLSTM was higher inaccuracy with a small number of decimals concerning the stacked LSTM and stacked GRU, while the TCN model showed superior performance than others. This proves that the combination of RNN and CNN layers led to a great enhancement in the performance. Finally, the last stage is the classification stage, where classifiers were used to classify the test data and a set of performance measurements were used to evaluate the performance to obtain a final accuracy value. The performance is illustrated in the result tables, curves, bars, and confusion charts. It can be deduced from the classification stage that the highest performance classifiers were the RT, RF, KNN, and SVM. In comparison with ML classifiers without any DL approaches, it can be seen that the DL models improved the prediction accuracy by 14.46%. The results show the strength and the robustness of DL models. This also proves that the automatic feature extraction provided by the DL models assisted the ML classifiers to produce an accurate forecasting result. It also can be seen based on the accuracies obtained from the ML approaches that they misclassified a huge number of shipments even if they exported or not, while the application of the RNN models which are based on LSTM, BiLSTM, GRU improved the classification performance of the number of shipments that are not exported and achieved accuracies higher than that of the ML approaches. Finally, the proposed TCN model that is based on a combination of RNN and CNN enhanced the performance of both classes of shipments even when dealing with a small number of shipments on one of the two classes.
4.9. Complexity
The complexity of the proposed methods is defined based on two metrics. The first metric is the time during the training, and the second metric is the complexity of each DL methodology in terms of Big O notation. The training time required for the stacked LSTM, stacked BiLSTM, stacked GRU are approximately 322 min and 51 s, 274 min and 7 s, 645 min and 18 s respectively, while the training time required for the TCN is only 52 min and 15 s for each trial training. The computational complexity of a simple single-recurrent layer such as the stacked LSTM or GRU is linear depending on the length of the input sequence. It is also linear during the training and inference time, taking into account that the internal steps of the LSTM and GRU are based on the multiplication by constant operation. Therefore, the complexity of the LSTM or GRU is O(N), where is the length of the sequence. In the case of the BiLSTM, the complexity will be O (2N) because two LSTMs are trained instead of one on the input sequence. The complexity of the TCN model depends on the residual blocks, and the main core of the residual block is the dilated causal convolutional layer. The complexity of the dilated convolution layer is O(N). TCN is considered to be a high paralleled, and this gives an advantage to this model in which it can be accelerated by technologies such as parallel computing. The main merit that led TCN to become better in the time complexity is that it took a small number of epochs to converge and its parallelization has led to a small amount of computational time, in contrast with the RNNs.
5. Conclusion and discussion
The benefit of the TCN model is the ability to predict and forecast the shipments to be exported with high accuracy and in a reasonable computational time. TCN is preserved to be the next revolution for the time-series data. It proved that it outperforms the classical CNN and RNNs for time-series tasks. It performs well in the prediction tasks with time series. The computations of the TCN are performed layer-wise. In other words, every time step, the computations are updated simultaneously instead of updating sequentially like the RNNs. The convolutions performed are computed across time, and the prediction obtained is a function of a fixed-length period. In addition to this, fourteen performance measurements are used to evaluate the model’s performance. The measurements obtained can assist company owners in making smart decisions before exporting their products because these measurements are based on probabilistic calculations. The aftermath of this work will be laid an excellent platform for practitioners to predict better if a shipment will be exported or not, given the uncertainties imposed by the COVID-19 pandemic. Thanks to the digital revolution, particularly with the emergence of Industry 4.0 and 5.0, industries can archive all supply chain data in a single platform. Before implementing these proposed DL methodologies, one common assumption was the company’s data-richness. If a company has a sufficient data management strategy and a platform to retrieve historical data, implementing these proposed DL methodologies will not be difficult. Since DL models are data-focused and software-oriented, implementation of such models may also prerequisite sufficient parallel computing resources.
Nevertheless, this work can still be enhanced in many different ways. The amount of shipments chosen in this paper for training is 1 048 576, 500 001 for the test, and 500 001 for the validation. It can be tried to extend or increase the number of shipments in the testing phase. The TCN layers can be changed by replacing the dilated casual convolutional layer with other convolutional layers, applying different normalization layers, increasing the number of residual blocks, and adding drop-out or spatial drop-out layers. The gated linear unit can be replaced with LSTM or other RNN layers. These changes in the TCN layers can lead to the existence of a few new versions of TCN. Different types of classifiers can also be applied, such as the decision tables and sparse representation classifier (SRC), rather than the conventional and traditional classifiers. The training can be optimized using heuristic or meta-heuristic techniques. Hybridization between different DL approaches for better performance can be another legit consideration.
This work presents four DL methodologies to predict whether a shipment will be exported from a source to a destination or not, which is very useful during the COVID-19 pandemic. The presented DL methods comprise various supporting classifiers such as SoftMax, RT, RF, KNN, ANN, and SVM. The prime aim of this work is to shed light on the development of DL and ML concepts in the context of supply chain risk identification and assessment plan. The proposed approach involves capturing data, filtering the attributes, extracting features, and then classifying them by using a different classifier. Results have shown a significant improvement in predicting if a shipment is to be exported or not compared to many other existing ML approaches. The highest accuracies obtained based on the stacked LSTM, stacked BiLSTM, stacked GRU, and the stacked TCN are 96.3%, 96.50%,96.30%, and 100.0%, respectively. It can be concluded that the TCN has significantly improved performance over other DL methods. In regards to computational complexity, the proposed TCN model also outperforms others.
CRediT authorship contribution statement
Mahmoud M. Bassiouni: Problem conceptualization, Data curation, Formal analysis, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing – original draft. Ripon K. Chakrabortty: Problem conceptualization, Formal analysis, Investigation, Methodology, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. Omar K. Hussain: Validation, Visualization, Writing – review & editing. Humyun Fuad Rahman: Validation, Visualization, Writing – original draft, Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data availability
Data will be made available on request.
References
- Babazadeh R., Razmi J., Pishvaee M.S., Rabbani M. A sustainable second-generation biodiesel supply chain network design problem under risk. Omega. 2017;66:258–277. [Google Scholar]
- Babazadeh R., Razmi J., Rabbani M., Pishvaee M.S. An integrated data envelopment analysis–mathematical programming approach to strategic biodiesel supply chain network design problem. Journal of Cleaner Production. 2017;147:694–707. [Google Scholar]
- Bai S., Kolter J.Z., Koltun V. 2018. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv preprint arXiv:1803.01271. [Google Scholar]
- Baryannis G., Validi S., Dani S., Antoniou G. Supply chain risk management and artificial intelligence: state of the art and future research directions. International Journal of Productions Research. 2019;57(7):2179–2202. [Google Scholar]
- Basiri M.E., Nemati S., Abdar M., Cambria E., Acharya U.R. ABCDM: An attention-based bidirectional CNN-RNN deep model for sentiment analysis. Future Generation Computer Systems. 2021;115:279–294. [Google Scholar]
- Blos M.F., da Silva R.M., Wee H.-M. A framework for designing supply chain disruptions management considering productive systems and carrier viewpoints. International Journal of Productions Research. 2018;56(15):5045–5061. [Google Scholar]
- Breiman, L. (1999). Random forests: UC Berkeley TR567.
- Brintrup A., Pak J., Ratiney D., Pearce T., Wichmann P., Woodall P., et al. Supply chain data analytics for predicting supplier disruptions: a case study in complex asset manufacturing. International Journal of Productions Research. 2020;58(11):3330–3341. [Google Scholar]
- Cai X., Qian Y., Bai Q., Liu W. Exploration on the financing risks of enterprise supply chain using back propagation neural network. Journal of Computational and Applied Mathematics. 2020;367 [Google Scholar]
- Chain S. 2000. Kaggle. https://www.kaggle.com/datasets?search=Supply+chain [Online; accessed 29-Jan-2020] [Google Scholar]
- Chen Y., Kang Y., Chen Y., Wang Z. Probabilistic forecasting with temporal convolutional neural network. Neurocomputing. 2020;399:491–501. [Google Scholar]
- Chu C.-Y., Park K., Kremer G.E. A global supply chain risk management framework: An application of text-mining to identify region-specific supply chain risks. Advanced Engineering Informatics. 2020;45 [Google Scholar]
- Cutler A., Zhao G. Pert-perfect random tree ensembles. Computing Science and Statistics. 2001;33:490–497. [Google Scholar]
- Dauphin Y.N., Fan A., Auli M., Grangier D. International conference on machine learning. PMLR; 2017. Language modeling with gated convolutional networks; pp. 933–941. [Google Scholar]
- Dechprom S., Jermsittiparsert K. Sustainability related supply chain risks: A case of multiple organizational strategic networks. International Journal of Innovation, Creativity and Change. 2019;5(2):769–785. [Google Scholar]
- Díaz-Curbelo A., Espin Andrade R.A., Gento Municio A.M. The role of fuzzy logic to dealing with epistemic uncertainty in supply chain risk assessment: Review standpoints. International Journal of Fuzzy Systems. 2020:1–23. [Google Scholar]
- Donner A., Klar N. The statistical analysis of kappa statistics in multiple samples. Journal of Clinical Epidemiology. 1996;49(9):1053–1058. doi: 10.1016/0895-4356(96)00057-1. [DOI] [PubMed] [Google Scholar]
- Escobar J.W., Marin A.A., Lince J.D. Multi-objective mathematical model for the redesign of supply chains considering financial criteria optimisation and scenarios. International Journal of Mathematics in Operational Research. 2020;16(2):238–256. [Google Scholar]
- Goodfellow I., Bengio Y., Courville A., Bengio Y. MIT press; Cambridge: 2016. Deep learning, Vol. 1. [Google Scholar]
- Haddadsisakht A., Ryan S.M. Closed-loop supply chain network design with multiple transportation modes under stochastic demand and uncertain carbon tax. International Journal of Production Economics. 2018;195:118–131. [Google Scholar]
- Hao S., Long J., Yang Y. International conference on security and privacy in new computing environments. Springer; 2019. Bl-ids: Detecting web attacks using bi-lstm model based on deep learning; pp. 551–563. [Google Scholar]
- Haykin S., Network N. A comprehensive foundation. Neural Networks. 2004;2(2004):41. [Google Scholar]
- Haykin S.S., et al. Prentice Hall; New York: 2009. Neural networks and learning machines/Simon Haykin. [Google Scholar]
- Ho Y., Wookey S. The real-world-weight cross-entropy loss function: Modeling the costs of mislabeling. IEEE Access. 2019;8:4806–4813. [Google Scholar]
- Ho W., Zheng T., Yildiz H., Talluri S. Supply chain risk management: a literature review. International Journal of Productions Research. 2015;53(16):5031–5069. [Google Scholar]
- Hosseini S., Ivanov D. Bayesian networks for supply chain risk, resilience and ripple effect analysis: A literature review. Expert Systems with Applications. 2020;161 doi: 10.1016/j.eswa.2020.113649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iyengar K., Bahl S., Vaishya R., Vaish A. Challenges and solutions in meeting up the urgent requirement of ventilators for COVID-19 patients. Diabetes & Metabolic Syndrome: Clinical Research & Reviews. 2020;14(4):499–501. doi: 10.1016/j.dsx.2020.04.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jabbarzadeh A., Fahimnia B., Sabouhi F. Resilient and sustainable supply chain design: sustainability analysis under disruption risks. International Journal of Productions Research. 2018;56(17):5945–5968. [Google Scholar]
- Jagannathan G., Pillaipakkamnatt K., Wright R.N. 2009 IEEE international conference on data mining workshops. IEEE; 2009. A practical differentially private random decision tree classifier; pp. 114–121. [Google Scholar]
- Jiang M., Liang Y., Feng X., Fan X., Pei Z., Xue Y., et al. Text classification based on deep belief network and softmax regression. Neural Computing and Applications. 2018;29(1):61–70. [Google Scholar]
- Jiao M., Wang D., Qiu J. A GRU-RNN based momentum optimized algorithm for SOC estimation. Journal of Power Sources. 2020;459 [Google Scholar]
- Keller S. 2020. US supply chain information for COVID19. https://www.kaggle.com/skeller/us-supply-chain-information-for-covid19 [Online; accessed 29-Jan-2020] [Google Scholar]
- Ketchen D.J., Jr., Craighead C.W. Research at the intersection of entrepreneurship, supply chain management, and strategic management: Opportunities highlighted by COVID-19. Journal of Management. 2020;46(8):1330–1341. [Google Scholar]
- Khalilabadi S.M.G., Zegordi S.H., Nikbakhsh E. A multi-stage stochastic programming approach for supply chain risk mitigation via product substitution. Computers & Industrial Engineering. 2020;149 [Google Scholar]
- Khan S.A.R., Yu Z., Golpîra H., Sharif A., Mardani A. A state-of-the-art review and meta-analysis on sustainable supply chain management: Future research directions. Journal of Cleaner Production. 2020 [Google Scholar]
- Kohl H., Henke M., Daus D. 02 The importance of supply chain management for sustainability in global value chains. Sustainability in Global Value Chains: Measures, Ethics and Best Practices for Responsible Businesses. 2021:3. [Google Scholar]
- Köksoy O. Multiresponse robust design: Mean square error (MSE) criterion. Applied Mathematics and Computation. 2006;175(2):1716–1729. [Google Scholar]
- Kraus M., Feuerriegel S., Oztekin A. Deep learning in business analytics and operations research: Models, applications and managerial implications. European Journal of Operational Research. 2020;281(3):628–641. [Google Scholar]
- Lea C., Vidal R., Reiter A., Hager G.D. European conference on computer vision. Springer; 2016. Temporal convolutional networks: A unified approach to action segmentation; pp. 47–54. [Google Scholar]
- LeCun Y., Bengio Y., Hinton G. Deep learning. Nature. 2015;521(7553):436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- Lin M., Chen Q., Yan S. 2013. Network in network. arXiv preprint arXiv:1312.4400. [Google Scholar]
- Liu J., Chen M., Liu H. The role of big data analytics in enabling green supply chain management: a literature review. Journal of Data, Information and Management. 2020:1–9. [Google Scholar]
- Liu Y., Huang L. Supply chain finance credit risk assessment using support vector machine–based ensemble improved with noise elimination. International Journal of Distributed Sensor Networks. 2020;16(1) [Google Scholar]
- Mollenkopf D.A., Ozanne L.K., Stolze H.J. A transformative supply chain response to COVID-19. Journal of Service Management. 2020 [Google Scholar]
- Nguyen H., Tran K.P., Thomassey S., Hamad M. Forecasting and anomaly detection approaches using LSTM and LSTM autoencoder techniques with the applications in supply chain management. International Journal of Information Management. 2020 [Google Scholar]
- Nguyen H., Tran K.P., Thomassey S., Hamad M. Forecasting and anomaly detection approaches using LSTM and LSTM autoencoder techniques with the applications in supply chain management. International Journal of Information Management. 2021;57 [Google Scholar]
- Nikolopoulos K., Punia S., Schäfers A., Tsinopoulos C., Vasilakis C. Forecasting and planning during a pandemic: COVID-19 growth rates, supply chain disruptions, and governmental decisions. European Journal of Operational Research. 2021;290(1):99–115. doi: 10.1016/j.ejor.2020.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ojha R., Ghadge A., Tiwari M.K., Bititci U.S. Bayesian network modelling for supply chain risk propagation. International Journal of Productions Research. 2018;56(17):5795–5819. [Google Scholar]
- Pal M. Random forest classifier for remote sensing classification. International Journal of Remote Sensing. 2005;26(1):217–222. [Google Scholar]
- Papadopoulos T., Gunasekaran A., Dubey R., Altay N., Childe S.J., Fosso-Wamba S. The role of Big Data in explaining disaster resilience in supply chains for sustainability. Journal of Cleaner Production. 2017;142:1108–1118. [Google Scholar]
- Paul S.K. Supplier selection for managing supply risks in supply chain: a fuzzy approach. International Journal of Advanced Manufacturing Technology. 2015;79(1–4):657–664. [Google Scholar]
- Perez B., Henriet J., Lang C., Philippe L. 2020. Multi-agent model for risk prediction in surgery. arXiv preprint arXiv:2005.10738. [DOI] [PubMed] [Google Scholar]
- Pournader M., Kach A., Talluri S. A review of the existing and emerging topics in the supply chain risk management literature. Decision Sciences. 2020;51(4):867–919. doi: 10.1111/deci.12470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Punia S., Nikolopoulos K., Singh S.P., Madaan J.K., Litsiou K. Deep learning with long short-term memory networks and random forests for demand forecasting in multi-channel retail. International Journal of Productions Research. 2020;58(16):4964–4979. [Google Scholar]
- Qazi A., Dickson A., Quigley J., Gaudenzi B. Supply chain risk network management: A Bayesian belief network and expected utility based approach for managing supply chain risks. International Journal of Production Economics. 2018;196:24–42. [Google Scholar]
- Ratner B. CRC Press; 2017. Statistical and machine-learning data mining:: techniques for better predictive modeling and analysis of big data. [Google Scholar]
- Rezaei S., Shokouhyar S., Zandieh M. A neural network approach for retailer risk assessment in the aftermarket industry. Benchmarking: An International Journal. 2019 [Google Scholar]
- Rowan N.J., Laffey J.G. Challenges and solutions for addressing critical shortage of supply chain for personal and protective equipment (PPE) arising from coronavirus disease (COVID19) pandemic–case study from the Republic of Ireland. Science of the Total Environment. 2020;725 doi: 10.1016/j.scitotenv.2020.138532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salimans T., Kingma D.P. 2016. Weight normalization: A simple reparameterization to accelerate training of deep neural networks. arXiv preprint arXiv:1602.07868. [Google Scholar]
- Saxe A., Nelli S., Summerfield C. If deep learning is the answer, what is the question? Nature Reviews Neuroscience. 2021;22(1):55–67. doi: 10.1038/s41583-020-00395-8. [DOI] [PubMed] [Google Scholar]
- Shang Y., Dunson D., Song J.-S. Exploiting big data in logistics risk assessment via bayesian nonparametrics. Operations Research. 2017;65(6):1574–1588. [Google Scholar]
- Sharma R., Kamble S.S., Gunasekaran A., Kumar V., Kumar A. A systematic literature review on machine learning applications for sustainable agriculture supply chain performance. Computers & Operations Research. 2020;119 [Google Scholar]
- Sharma R., Shishodia A., Kamble S., Gunasekaran A., Belhadi A. Agriculture supply chain risks and COVID-19: mitigation strategies and implications for the practitioners. International Journal of Logistics Research and Applications. 2020:1–27. [Google Scholar]
- Shekarian M., Mellat Parast M. An integrative approach to supply chain disruption risk and resilience management: a literature review. International Journal of Logistics Research and Applications. 2020:1–29. [Google Scholar]
- Singh S., Kumar R., Panchal R., Tiwari M.K. Impact of COVID-19 on logistics systems and disruptions in food supply chain. International Journal of Productions Research. 2021;59(7):1993–2008. [Google Scholar]
- Srivastava N., Hinton G., Krizhevsky A., Sutskever I., Salakhutdinov R. Dropout: a simple way to prevent neural networks from overfitting. Journal of Machine Learning Research. 2014;15(1):1929–1958. [Google Scholar]
- Tang C.S. Perspectives in supply chain risk management. International Journal of Production Economics. 2006;103(2):451–488. [Google Scholar]
- Tang H., Dong P., Shi Y. A new approach of integrating piecewise linear representation and weighted support vector machine for forecasting stock turning points. Applied Soft Computing. 2019;78:685–696. [Google Scholar]
- Tat R., Heydari J., Rabbani M. A mathematical model for pharmaceutical supply chain coordination: Reselling medicines in an alternative market. Journal of Cleaner Production. 2020;268 [Google Scholar]
- Tran K.P., Du Nguyen H., Thomassey S. Anomaly detection using long short term memory networks and its applications in supply chain management. IFAC-PapersOnLine. 2019;52(13):2408–2412. [Google Scholar]
- Vapnik V. Springer science & business media; 2013. The nature of statistical learning theory. [Google Scholar]
- Vo N.N., He X., Liu S., Xu G. Deep learning for decision making and the optimization of socially responsible investments and portfolio. Decision Support Systems. 2019;124 [Google Scholar]
- Wang S.-H., Muhammad K., Hong J., Sangaiah A.K., Zhang Y.-D. Alcoholism identification via convolutional neural network based on parametric ReLU, dropout, and batch normalization. Neural Computing and Applications. 2020;32(3):665–680. [Google Scholar]
- Wang X., Zhao Y., Pourpanah F. Springer; 2020. Recent advances in deep learning. [Google Scholar]
- Wichmann P., Brintrup A., Baker S., Woodall P., McFarlane D. Extracting supply chain maps from news articles using deep neural networks. International Journal of Productions Research. 2020;58(17):5320–5336. [Google Scholar]
- Xu C., Ji J., Liu P. The station-free sharing bike demand forecasting with a deep learning approach and large-scale datasets. Transportation Research Part C (Emerging Technologies) 2018;95:47–60. [Google Scholar]
- Yu B., Guo Z., Asian S., Wang H., Chen G. Flight delay prediction for commercial air transport: A deep learning approach. Transportation Research Part E: Logistics and Transportation Review. 2019;125:203–221. [Google Scholar]
- Zhang B., Zhang H., Zhao G., Lian J. Constructing a PM2. 5 concentration prediction model by combining auto-encoder with Bi-LSTM neural networks. Environmental Modelling & Software. 2020;124 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.