Abstract
In the study, a multi-purpose reverse logistics network has been designed to create effectual management of medical waste (MW) generated in 39 districts of Istanbul, a heavily populated city, during the COVID-19 pandemic as well as that to be generated in the next decade. With the model, the medical waste management system in Istanbul is analyzed during the pandemic and for the next 10 years. The model attempts to integrate economic, environmental, and social objectives within the sustainable development goals. It aims to maximize the number of personnel and government earnings for the estimated MW of a megacity while minimizing the total fixed cost and the cost of carbon emissions and transportation. The results indicated that the existing facilities are sufficient for the treatment and disposal of MW generated even under pandemic conditions. However, the capacity of the sterilization facility could be insufficient to treat the estimated amount of MW in the next decade. Opening a sterilization facility near the sanitary landfill in Komurcuoda with a total management cost of 62,450,332 €/year would be an optimum solution for Istanbul MW. In comparison to the single-purpose model results, the multi-purpose model resulted in approximately 42,000 € more in total cost. Sensitivity analyses show that the amount of MW has the most significant effect on the total cost. This simple model created an effective MW management proposal for Istanbul, which can be a model for megacities.
Supplementary Information
The online version contains supplementary material available at 10.1007/s10669-022-09873-z.
Keywords: Medical waste, Medical waste management, COVID-19, Reverse logistics, Mixed-integer linear programming model
Introduction
Increasing population and rapid industrialization are the main causes of the increasing generation of solid waste in the world, the pandemic and its duration had an extra impact on the medical part of solid waste. Medical waste (MW) generated by health institutions such as hospitals, research centers, and laboratories associated with medical procedures, is listed in the special waste category of solid waste (Baveja et al. 2000; Yong et al. 2009). Approximately 85% of the total amount of MW is non-hazardous waste containing inert materials such as paper, glass, and food residues, while the remaining 15% may contain chemicals, sharp objects, pharmaceuticals, and high concentrations of heavy metals, pathogens, and/or genotoxic substances are classified as hazardous waste (WHO 2018). MW with non-hazardous materials can be disposed of regularly without any special handling (WHO 2017). Treatment of MW is performed by applying various methods alone or in the combination with several methods such as thermal processes, chemical processes, irradiation technologies, and biological and mechanical processes. Turkey has a regulation on control of medical waste (MWCR) that outlines the responsibilities of municipalities as being the governing authorities for medical waste management (MWM), including the establishment of management plans and processing facilities, transportation of waste from the health institutions, and safe disposal of waste at the provincial level (Republic of Turkey Ministry of Health 2021). According to this regulation, MW consists of pathological, infectious, and cutting-piercing waste. The MW collected in Turkey has been distributed as 0.1% pathological, 96.4% infectious, and 3.5% cutting-piercing waste (Kesici 2016). Segregation of all MW at the point of generation, and appropriate treatment and safe disposal of MW are very important. This is because improper separation, collection, and disposal of MW may impair air, water, and soil quality while causing the spread of hazardous substances and infectious diseases (AIDS, Hepatitis-A and B, and COVID-19, etc.) (WHO 2017). MWCR requires a separate collection of MW at a source of generation without harming the environment and human health.
Today, there is an unusual increase in MW produced in health institutions due to the COVID-19 epidemic. As the volume and complexity of MW increase worldwide during the COVID-19 epidemic, the risk of disease transmission increases through unsafe transportation and disposal practices. For instance, it is reported that the daily generation of MW increased six times in hospitals in China during the months when the number of COVID-19 cases peaked (Calma 2020). Hence, China had to construct new MW disposal centers and mobile waste facilities to increase the waste disposal treatment from 50 to 263 tons daily (Mandy 2020; Sarkodie and Owusu 2020). Not only in China but also all around the world, the implementation of proper MW management with special regulations is of critical importance to mitigate the risks to humans and the environment.
Reverse logistics or reverse supply chain is a whole process of the product movement including recovering products and/or disposing of them appropriately (Pokharel and Mutha 2009; Zhang et al. 2011). Reverse logistics practices determine the configuration and operational strategy of the reverse logistics system, which has a significant impact on long-term performance (Yu et al. 2020). Today, these practices have become important in the management of various types of waste, primarily electrical and electronic devices (Shih 2001; Achillas et al. 2012; Dat et al. 2012), computers (Ahluwalia and Nema 2006), paper (Pati et al. 2008), and vehicles (Balci and Ayvaz 2017). To improve the decision-making on reverse logistics practices at both strategic and operational levels, quantitative optimization models and various computational techniques have been used. The implementation of these practices with the optimization models and computational techniques is also vital in designing an effective system for the recovery and disposal of this kind of waste, and in minimizing adverse effects on humans and the environment, and creating potential job opportunities (Demirel et al. 2016; Govindan et al. 2016; Rahimi and Ghezavati 2018; Gao 2019). The effectiveness of these techniques has been validated in a wide variety of industries and business sectors (Yu and Solvang 2016; Alhamsi and Diabat 2017; John et al. 2018; Trochu et al. 2020). There have been many studies on reverse logistics practices in MWM, either in the supply chain design of materials in industrial applications or waste management in the literature. A review of the most up-to-date and relevant research in MWM using mathematical programming models and quantity techniques is provided here. Shih and Lin (2003) used dynamic programming and integer linear programming methods to minimize transportation cost and risk and ensure a daily payload balance for workers for the management planning of infectious medical waste (IMW). Chaerul et al. (2008) also used a goal programming model to resolve complexities such as the selection of technology for the timely removal of waste, controlling the risk of infection, and legal and budget restrictions. Shi et al. (2009) developed a Mixed-Integer Linear Programming (MILP) model that aims to decrease the costs of MW in reverse logistics networks using a genetic algorithm with a hybrid-coding rule. The effectiveness and feasibility of the model were confirmed using an exemplary application of a recycled MW sent from a specific hospital to a particular material manufacturer. Rolewicz-Kalińska (2016) studied the MWM procedure in Poland, considering logistic constraints and economic perspectives. They emphasized that the most significant potential for change in MWM system logistics is related to the activities designed to improve waste separation at generation sites and maintain the balance between the amount of waste produced and disposal capacity. Budak and Ustundag (2016) applied basic reverse logistics for optimal location-allocation decisions related to waste collection, transportation, and disposal in health institutions in Turkey and verified the effectiveness and feasibility of their model by applying a single-objective MILP model of a reverse logistics network to optimize only the total cost. He et al. (2016) investigated the material flow and the structure of MW collection systems in China using reverse logistics practices to minimize the transportation risk of MW. Mantzaras and Voudrias (2017) developed an optimization model to decrease the total cost of collection, transport, and disposal process for MW in the Region of East Macedonia-Thrace, Greece, using a genetic algorithm and Monte Carlo simulation. They determined the optimal locations of transfer stations, their design capacities, the number of treatment facilities, and the cost of IMW in the management system. Alshraideh and Qdais (2017) developed a model to optimize the collection of the MW generated in Northern Jordan. The model which was solved with a genetic algorithm aimed to minimize the transportation distance and transportation costs and reduce toxic gas emissions. Wang et al. (2019) proposed a dynamic approach for the MW reverse logistics network by combining the Grey GM (1,1) prediction method with a multi-objective optimization model. Firstly, they predicted the amount of MW generated a in multi-period of target hospitals based on the Grey GM (1,1) method. Then a multi-objective and multi-period model was developed to optimize the selection of locations with minimal operating costs and the least possible effect on the environment. Kargar et al. (2020a) used a tri-objective MILP model for the safe disposal of MW. Their purpose was to minimize the total cost and risk by selecting five main levels of the network, including 20 medical centers, seven storages, seven treatment centers, one transfer station, and one disposal center. More recent studies have used reverse logistics network design with multiple objectives and outputs for various countries and cities during COVID-19 (Table 1). As seen in the literature, many mixed-integer linear models with different optimization techniques have been applied by researchers, based on their specific problems. The simple models could also give more understandable and interpretable solutions for MWM to decision-makers. In addition, there is a limited number of studies that have proposed a future-oriented approach for planning the need for MWM including both the data before and after the pandemic for megacities. Istanbul, with over 15.4 million inhabitants, is one of Turkey's most important cities with its history, social culture, and economy. It has an important geographic location as a bridge between Asia and Europe. Currently, there are more than 8000 health institutions in the city (Korkut 2018). The health institutions serve not only the people living in the city, and but the whole country and patients from abroad, including the Middle East, Caucasus, and Europe. The amount of waste from these health institutions constitutes an important part of the total waste produced in this megacity. Therefore, the MW poses the greatest risk among all waste groups (Bdour et al. 2007; Budak and Ustundag 2016). Birpinar et al. (2009) researched the collection, and temporary storage of MW generated in 192 hospitals in Istanbul in the light of the MWCR. They found that approximately 77% of the hospitals had sufficient equipment to collect MW and 63% had temporary storage warehouses. In general, although they focused on the current situation of the hospitals in terms of MWCR, they did not explore the issues of treatment and disposal of MW. Eren and Tuzkaya (2021) focused on the vehicle routing problem and they developed a model for transporting MW generated in 15 health institutions in Istanbul to the sterilization and incineration facilities under the COVID-19 pandemic conditions using only one vehicle.
Table 1.
Summary of reverse logistics network design studies on COVID-19 pandemic
| References | Objective | Multi-objective | Multi-period | Multi- product | Approach | Uncertainty | Location of case |
|---|---|---|---|---|---|---|---|
| Kargar et al. (2020b) |
Reduction of overall cost Reduction of risk associated with the collection and treatment of IMWC |
X | X | – | Dynamic programming MILP | X | Babol, Iran |
| Yu et al. (2020) |
Determining the best locations of temporary facilities Creating the transportation strategies |
X | X | – | MILP | X | Wuhan, China |
| Govindan et al. (2021) | Reduction of overall cost and risks | Bi-objective | X | X | MILP | – | Tehran, Iran |
| Shadkam (2022) | Reduction of the costs associated with fixed costs, material flow costs, and the costs of building potential centers | – | – | – | MILP | X | – |
Research conducted by the American Public Health Association reported that the collection, treatment, and landfilling of the US healthcare system waste contributes to 9–10% of all national greenhouse gas emissions (Erickson 2021). Optimizing transportation and minimizing waste amount is important to reduce the carbon footprint from MW. Turkey submitted its Statement of Intended National Contribution to the Secretariat of the United Nations Framework Convention on Climate Change (UNFCCC) on 30 September 2015 and ratified Paris Agreement in 2021. According to Turkey’s national contribution statement, it is foreseen that greenhouse gas emissions will be reduced by 21% in 2030 compared to the reference value (CSB 2022). Therefore, it is essential to minimize CO2 emissions in every activity.
Considering the problems that occur with MW, this study attempts to integrate various aspects of sustainable development by presenting a simple reverse logistics network design based on economic, environmental, and social objectives within the framework of the sustainable development goals. In this study, a multi-purpose sustainable reverse logistics network design is proposed to minimize the total fixed cost, cost of transportation and operation of MW, CO2 emissions occur during the opening of facilities, transportation of waste between facilities, and to maximize the earnings of the state from the minimum paid tax cost by maximizing the number of employees in the next decade in Istanbul as an example of a megacity. The model analyzes the future need for extra facilities in the treatment and disposal stages of MW generated in health institutions. This study aims to create effectual management of MW, both generated during the COVID-19 pandemic and to be generated in 39 districts of Istanbul in the next decade using actual data from 7 years, including the duration of the COVID-19 pandemic. Sensitivity analyses have also been conducted to observe the effect of each parameter on model results and to increase the awareness of decision-makers and other stakeholders.
Methodology
Problem definition
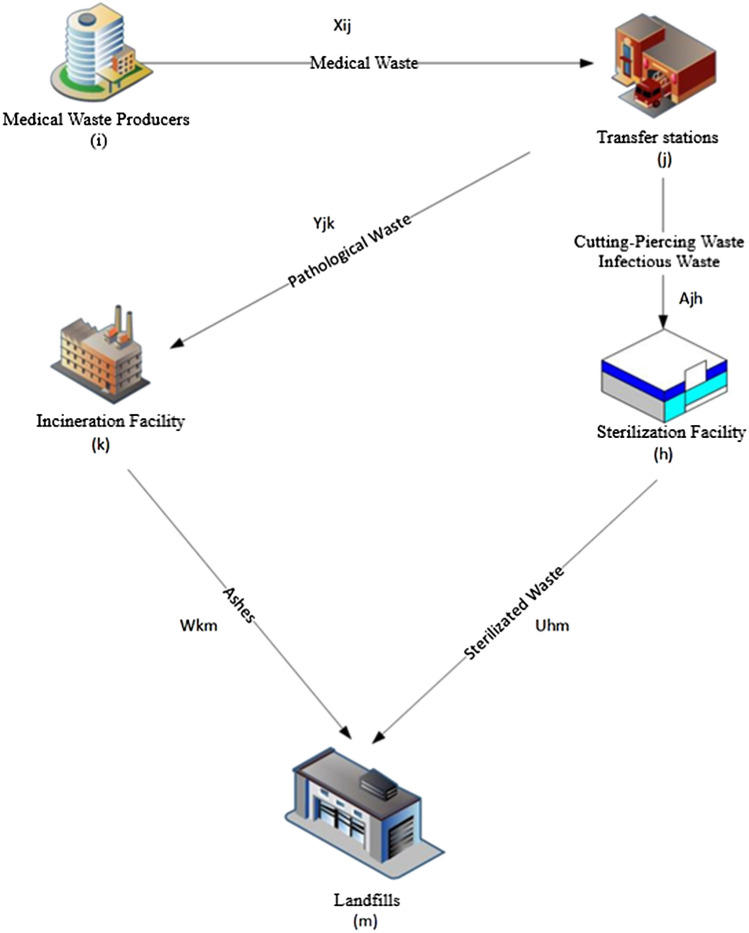
A multi-purpose sustainable reverse logistics network design problem that covers economic, environmental, and social purposes for the MW is discussed in this study. The disposal process of MW is shown in Fig. 1. The reverse logistics network begins with the transport of MW (pathological waste, cutting-piercing waste, and infectious waste) collected from authorized MW producers (i) to the transfer stations (j). While MW transported to the transfer stations is kept separately based on their characteristics without any treatment, cutting-piercing and infectious MW is transferred to the sterilization facility (h), and pathological MW is processed at the incineration facility (k). The cutting-piercing and infectious MW from the transfer stations (j) to the sterilization facility (h) are transformed into harmless products by subjecting them to the sterilization process. After the sterilization process, the waste is transported to the landfill (m) and disposed of. Incineration is considered to be the safest method for MW disposal. Pathological MW transferred from the transfer stations (j) to the incineration facility (k) is combusted and converted into a harmless product. The ashes that form due to the incineration process are transported to the landfill (m) and disposed of. The use of the National Waste Transportation form is mandatory when MW is being transferred from a transfer station to a sterilization or incineration facility and then to a landfill.
Fig. 1.
MW disposal process
The problem is formulated as a multi-purpose, single-product, MILP model. The multi-purpose analysis has many advantages over the single-purpose analysis. It provides a systematic methodology to analyze the effects of strategic decisions. It offers alternative solutions for a set of targets and balances the targets and allows decision-makers to make more appropriate decisions by considering different and important factors (Chang 2011).
The proposed model should explain the flow of MW to minimize the fixed cost of opening facilities, the operational cost, and the transportation cost of waste transported between facilities. At the same time, the model should minimize the cost of the carbon emission that occurs during the opening of the facilities and the transport of materials between facilities. Finally, it should maximize the number of personnel to be employed in the facilities to be opened and maximize the state's earnings from the minimum paid tax cost. In addition, all the cost was calculated in local currency (Turkish Lira (₺)). Then, the price in ₺ currency was converted to Euro (€), taking into account the estimated 3-year exchange rates on USDforecast (USDforecast 2020).
MILP model
While some of the variables in the model are integer, the others are continuous variables. Therefore, the model to be established is the MILP model. It was formulated as a multi-purpose optimization problem; consequently, it could be used to investigate the trade-offs between different conflicting objectives (e.g., minimization of the cost and carbon emission while maximizing the number of personnel) (Samsatli and Samsatli 2018). The goal programming approach, one of the most frequently used methods to solve problems, has been used. In the goal programming method, the decision-makers determine a mathematical value for each goal they want to achieve. The solution that minimizes deviations from mathematical values has been defined as the accepted solution.
In the solution of the goal programming problem, the weighting method in which a large number of objective functions are based on a single-objective function has been used. With the weighting method, a single-objective function has been converted into a weighted sum of functions that represent the goals of the problem.
Model assumptions
The proposed mathematical model includes the following assumptions:
-
(i)
All MW generated in health institutions must be collected (It is mandatory by law).
-
(ii)
The segregation of MW is completed at a source of generation using suitable color-coded containers (It is also mandatory by law).
-
(iii)
The capacities of all present facilities and landfills are limited and stable.
-
(iv)
CO2 emissions are considered to occur during the transportation of MW to each facility.
-
(v)
CO2 emission from transport depends on the distance traveled.
-
(vi)
Vehicles used to transport the MW have a limited number and capacity.
-
(vii)
The coefficients of the goal function are deterministic and are known.
-
(viii)
39 districts of Istanbul province are assumed as MW producers.
-
(ix)
Percentage distribution of each type of MW is known.
-
(x)
The locations of potential sterilization and incineration facilities to be opened in the future are considered candidate areas.
-
(xi)
The selection of the final location is made among the potential locations.
Model representation
Indices:
| i: | MW producers | i: 1,2,3…I |
| j: | Transfer stations | j: 1,2,3…J |
| k: | Incineration facility | k: 1,2,3…K |
| h: | Sterilization facility | h: 1,2,3…H |
| m: | Landfills | m: 1,2,3…M |
Parameters:
| : | The amount of MW generated by MW producers (i) (ton) |
| The fixed opening cost | |
| The fixed cost of opening an incineration facility (k) (€) | |
| The fixed cost of opening a sterilization facility (h) (€) | |
| The collection cost | |
| Collection cost of MW per ton (€/ton) | |
| The process cost | |
| The unit cost of incineration at an incineration facility (k) (€/ton) | |
| The unit cost of sterilization at a sterilization facility (h) (€/ton) | |
| The unit cost of disposal at a landfill (m) (€/ton) | |
| The transportation cost | |
| The unit cost of transportation of MW from MW producers (i) to transfer stations (j) (€/ton*km) | |
| The unit cost of transportation of pathological waste from transfer stations (j) to incineration facility (k) (€/ton*km) | |
| The unit cost of transportation of cutting-piercing waste and infectious waste from transfer stations (j) to sterilization facility (h) (€/ton*km) | |
| The unit cost of transportation of ashes from incineration facility (k) to landfills (m) (€/ton*km) | |
| The unit cost of transportation of sterilized waste from sterilization facility (h) to landfills (m) (€/ton*km) | |
| The transportation distances | |
| : | Distance between MW producers (i) and transfer stations (j) (km) |
| : | Distance between transfer stations (j) and incineration facility (k) (km) |
| : | Distance between transfer stations (j) and sterilization facility (h) (km) |
| : | Distance between incineration facility (k) and landfills (m) (km) |
| : | Distance between sterilization facility (h) and landfills (m) (km) |
| Carbon emission | |
| Average CO2 emission factor per ton*km (g CO2/ton*km) | |
| cop: | Carbon emission cost per ton (€/ton) |
| The amount of CO2 that occurs when the sterilization facility (h) is opened | |
| The amount of CO2 that occurs when the incineration facility (k) is opened | |
| Employment | |
| cemp: | Employment cost in the Social Security Institution (SSI) (€) |
| The number of personnel to be employed when the sterilization facility (h) is opened | |
| The amount of personnel to be employed when the incineration facility (k) is opened | |
| Capacities | |
| : | The capacity of transfer stations (j) (ton) |
| : | The capacity of incineration facility (k) (ton) |
| : | The capacity of the sterilization facility (h) (ton) |
| : | The capacity of landfills (m) (ton) |
| Other parameters | |
| : | The weight percentage of pathological waste in MW |
| : | The weight percentage of cutting-piercing waste and infectious waste in MW |
| : | The amount of sterilized cutting-piercing waste and infectious waste (ton) |
| : | The amount of incinerated pathological waste (ton) |
| w1: | The goal weight for cost minimization |
| w2: | The goal weight for CO2 minimization |
| w3: | The goal weight for employment maximization |
Decision variables:
| : | The amount of MW shipped from MW producers (i) to transfer stations (j) |
| : | The amount of pathological waste shipped from transfer stations (j) to incineration facility (k) |
| : | The amount of cutting-piercing waste and infectious waste shipped from transfer stations (j) to sterilization facility (h) |
| : | The amount of ashes shipped from incineration facility (k) to landfills (m) |
| : | The amount of sterilized waste shipped from sterilization facility (h) to landfills (m) |
| : | The sum of the amount of ashes sent from incineration facility (k) to landfills (m) and the amount of sterilized waste sent from sterilization facility (h) to landfills (m) |
| : | If sterilization facility (h) is opened 1; otherwise, 0 |
| : | If incineration facility (k) is opened 1; otherwise, 0 |
Model formulation
Objective function
Generally, the goals contradict each other in multi-purpose decision models. There may not be an optimal solution for the three goals of this study. However, the interactions of the objectives with each other in the model can be examined, and the obtained results can help decision-makers. Within the scope of the model, three goals are considered as follows:
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
The first goal is to minimize the total cost, and the objective function built-in in line with this goal has six components. The first component indicates the fixed installation cost of the sterilization and the incineration facilities, while the second, the third, and the fourth components represent the transportation cost at each stage of the network, the cost of collecting MW, and the sterilization cost of cutting-piercing, and infectious MW, respectively. Then, the fifth component represents the incineration cost of pathological MW transported to the incineration facility. Finally, the sixth component is the disposal cost of ash and sterilized waste transported to the landfill.
The second goal is to minimize the cost of carbon emissions during the opening of the facilities and the transportation of waste from MW producers to landfills.
| 7 |
| 8 |
The objective function of this goal includes two components. The first component represents the cost of carbon emission resulting from the opening of the designated sterilization facility and incineration facility, while the second component is the cost of carbon emission during the transport of MW at each stage of the network. The carbon emission resulting from the incineration process and other processes are ignored in this objective function.
The third goal is to maximize the profit of the state arising from the tax cost by keeping the number of employees working at minimum wage in sterilization and incineration facilities likely to be opened at a maximum.
| 9 |
The objective function for the third goal has a single component. This component represents the net tax cost of personnel working at the facility with minimum wage when the designated sterilization and incineration facilities are opened.
Constraints
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
| 15 |
| 16 |
| 17 |
| 18 |
| 19 |
| 20 |
Constraint (10) is that the amount of MW transported from MW producers (i) to transfer stations (j) is equal to the total amount of MW generated by MW producers. Constraint (11) provides that the amount of MW transported to transfer stations (j) is equal to the amount of pathological waste transported to the incineration facility (k). Constraint (12) states that the amount of MW containing the cutting-piercing waste and infectious waste transported to transfer stations has the same content as the MW transported to the sterilization facility (h). Constraint (13) is that the amount of sterilized waste sent to the landfill sites (m) is equal to the amount of sterilized waste in the sterilization facility (h). Constraint (14) is that the amount of ashes carried to the landfill sites (m) is equal to the amount of ashes resulting from the processes in the incineration facility (k). Constraints (15–18) are that the capacity of the transfer stations (j), sterilization (h) and incineration (k) facility, and landfill sites (m) should not be exceeded. Constraint (19) is that decision variables are not negative. Finally, constraint (20) ensures that the values that indicate the decision to open the facility can be 0 or 1.
Application
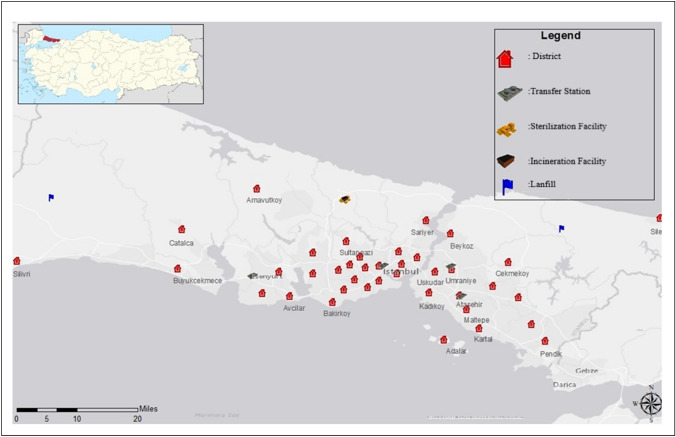
The model is developed as the reverse logistics network design for the disposal of MW generated or to be generated in Istanbul. Within the scope of MW regulation, it is expected to be resolved at minimum cost by defining the network parameters for the disposal of the MW generated in 39 districts of Istanbul. According to Istanbul Environment Management Industry and Trade Company (ISTAC J.S.Co.), which is a subsidiary company of Istanbul Metropolitan Municipality (IBB), presently, there are four transfer stations (in Kucukbakkalkoy, Hekimbasi, Silahtaraga, and Kirac), one sterilization and one incineration facility (in Odayeri) and two landfill sites (Komurcuoda, and Seymen) in Istanbul. There was a landfill site in Odayeri used for the disposal of MW until 2018, but it was closed due to its filled capacity (IBB 2020a). The locations were displayed on the map using ArcGIS 10.5, a scalable integrated geographic information system software (Fig. 2). In addition, the locations of 39 districts, transfer stations, sterilization and incineration facilities, and landfill sites of the network are shown in Fig. 2. The coordinates of the 39 districts, transfer stations, existing sterilization and incineration facilities, and landfill sites are given in SM (Table SM-1–4). The MW amount and the population of the 39 districts in 2020, and the predicted values for the year 2030 are given in Table SM-1. If the capacity of the present treatment facilities is insufficient within the next 10 years due to an increase in the amount of MW, it may be appropriate to establish two sterilization and two incineration facilities in Komurcuoda village of Sile district (Anatolian region) and Seymen village of Silivri district (European region). The locations of these potential facilities for future projection have been selected considering their proximity to landfill sites and are given in Table SM-5.
Fig. 2.
Locations of 39 districts, transfer stations, sterilization facilities, incineration facilities, and landfill sites in Istanbul
Application data
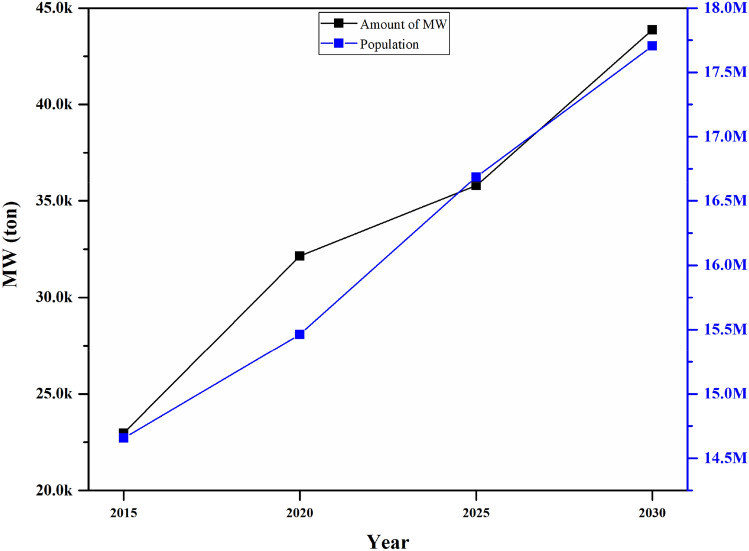
The population and amount of MW in the districts of Istanbul were obtained through the Turkish Statistical Institute (TURKSTAT) and ISTAC J.S.Co. (Table SM-6). The amount of MW to be generated in the next 10 years has been estimated based on the relation between the population and MW amounts in the previous years (2014–2020) using Pearson correlation. The correlation coefficient was found to be 0.95 (p < 0.05) (in Fig. SM-1), which results in a statistically significant positive correlation. Soysal et al. (2010) also reported a positive correlation between the population and the amount of MW collected in Izmir, Turkey (r = 0.79, p < 0.001). Besides, Wei et al. (2021) underlined that there is a significant positive correlation between population and production of MW (p < 0.01). After 2020, the population and MW amount was estimated considering the rate of increase over the previous years (Table SM-7). MW of 0.0013 ton/capita was collected in Istanbul in the year 2015 (a population of 14.5 million), while it was 0.0021 ton/capita in 2020 (a population of 15.4 million). As shown in Fig. 3, in addition to the increasing population, there has been an unexpected increase (deviation from the increasing trend in the previous years) in the amount of MW in 2020. About the data obtained from IBB (2020b), the increase rate of MW in Istanbul over the years is calculated to be approximately 5.5%. Due to the COVID-19 pandemic, this rate in the year 2020 is found to be 10.6%. This unexpected increase rate for the following years has been attributed to the expected increase in the MW amount in Istanbul due to the uncertainty about the future of the pandemic. Therefore, the sufficiency of facilities’ capacity in case of any increase such as 5%, 10%, and 15% in the amount of MW was investigated with sensitivity analysis. It is foreseen that the amount of MW will be ~ 35,799 and 43,866 tons for a population of 16.6 million (in 2025) and 17.7 million (in 2030), respectively (Table SM-7).
Fig. 3.
Correlation between amount of MW and population in Istanbul (2014–2030)
In Istanbul, MW is collected and sent to disposal by 43 licensed vehicles (trucks) with specially equipped units under the criteria specified in MWCR. These vehicles with a volume of 23 m3 constitute the majority of the fleet. The collected MW has been distributed as 0.1% pathological, 96.4% infectious, and 3.5% cutting-piercing waste (Kesici 2016). Based on this information, the distribution of MW amount (43,866 tons) estimated in connection with the population in 2030 was determined to be 43.8; 1,531; and 42,291 tons for pathological, cutting-piercing, and infectious waste, respectively.
Even though the amount of MW sent to the incineration facility decreases by 95% in volume, and 75% on mass bases (Demir et al. 2002), the MW sent to the sterilization facility decreases by approximately 70% by volume before reaching the landfill (IBB 2018). To perform the cost calculation correctly for the disposal process of MW, some information was collected from TURKSTAT, ISTAC J.S.Co., and the literature.
The cost of transporting and collecting waste in Turkey is approximately 30 €/ton (Ozturk 2017). Based on this information, transportation and collecting cost was assumed to be 30 €/ton. In Turkey, the average operational cost of the incineration facility for k1, k2, and k3 was determined as 443.7 €/ton, while this cost in the sterilization facility for h1, h2, and h3 was 388.3 €/ton (CSB 2019). Furthermore, the average cost in landfills for m1 and m2 was determined to be 221.9 €/ton (CSB 2019). This information was used to run the model. Considering the economic aspects of this study, road transportation has relatively small fixed costs. This is because it operates on publicly operated high-speed and often free road networks (Sadjady 2011). Road transportation is best suited for high-value products for short distances. In the absence of energy data, the carbon footprint of a transportation operation can be estimated using the activity-based approach, which is a more general method (McKinnon and Piecyk 2010). Hence, CO2 emission from road transportation has been calculated using the activity-based approach. The method has calculated CO2 emission from road transportation, taking into account the average CO2 emission factor (g CO2/ton*km) per transport volume of the MW (ton) and transportation distance (km). The average carbon emission factor is 62 g CO2/ton*km for road transportation (McKinnon and Piecyk 2010). Both potential sterilization and incineration facilities are planned to be built on an area of 7000 m2. According to Hong et al. (2015), the amount of CO2 emission during the construction of facilities was calculated to be 5000 tons. The amount of CO2 emission released during transportation of MW in 2030 has been found to be approximately 2031 tons in the model. Energy and carbon taxes play a crucial role in meeting international climate targets in many countries. The pricing of these taxes varies considerably among nations. According to the information provided by OECD in 2012, effective carbon tax rates ranged from 2.8 € to 107 € per ton of CO2. In early 2021, the European Union Emissions Trading System (EU ETS) set a price of around 30 € per ton of CO2 (OECD 2021a). There is no direct carbon tax or emissions trade tax for CO2 in Turkey. The priced emissions are mainly from road transport. The most of unpriced emissions originate from the electricity sector and the industrial sector (OECD 2021b). For this reason, only road transportation is taken into account when calculating the prices due to CO2 emission within the model. The OECD effective carbon rate of mid-value (60 €), an estimated value for the year 2030, is considered for the conversion of CO2 emission to a money-based value in the model (OECD 2021a).
The number of personnel to be employed in k1, k2, and k3 incineration facilities is 10, 16, and 17, respectively. It was determined as 10, 16, and 15 for h1, h2, and h3 sterilization facilities, respectively. The tax to be paid to the SSI for the personnel employed has been assumed as 388.3 €. The annual capacities of existing transfer stations (j1), incineration facility (k1), sterilization facility (h1), and landfill sites (m1 and m2) are reported as 15,000; 8650; 40,000; 1,440,000; and 1,620,000 tons, respectively (ISTAC 2019). The annual capacities of k2 and k3 potential incineration facilities are considered to be 8640 tons, while those of h2 and h3 potential sterilization facilities are assumed to be 40,000 tons. The goal weights of the model were assumed to be 0.334, 0.333, and 0.333. The distances between facilities were calculated using the Euclidean correlation method.
Results and discussion
Model solution
The reverse logistics network design model has been developed as a multi-purpose, single-product MILP model. The model was encoded, and an optimal solution was achieved using the Generalized Algebraic Modelling System (GAMS 23.5.1) solver with a 2.40 GHz Intel Core Processor and 8 GB of RAM. In the model solution, goal programming and weighting methods were used. The calculation time required for the optimal solution was found to be 62 CPU seconds.
The non-complex representation of the model is as follows.
| Goal: | The minimum fixed cost, transportation cost, and operational cost (z1(x)) |
| The minimum cost of carbon emission (z2(x)) | |
| The maximum income of the state with minimum tax cost (z3(x)) | |
| Constraints: | Balance constraints |
| Capacity constraints | |
| Logic constraints |
In the first step of the goal programming method, solutions were achieved by setting up optimization models for three-objective functions separately. Thus, deviations were kept to a minimum. The results for z1, z2, and z3 were 61,754,191; 640,593; and 13,591 €, respectively. The weighting method was used in the second step of the goal programming method, which allows multiple-objective functions to be represented as a single-objective function. Thus, each weighted goal was indicated in the objective function as a single-objective and then took its place in the multi-purpose model. In addition to the constraints mentioned in the previous section, goal equations were specified in the model as separate constraints, and deviation variables of each goal equation were added to the constraint. While , and represent a negative deviation from the objective, , , and are a positive deviation from the objective.
The first goal equation mentioned as z1 has been converted into a constraint as follows and has taken its place in the model.
The second goal equation (z2) is shown in the model by converting it into a constraint as follows.
Then, the third goal equation mentioned as z3 in the previous section was also transformed into a constraint and placed in the model.
The optimal cost solution value of the problem was determined to be 62,450,332 €. As the most appropriate solution, it is proposed that a sterilization facility (h3) be opened in Komurcuoda, Sile in addition to the existing incineration (k1) and sterilization facility (h1) in Odayeri, Eyup. Based on the optimal values of the decision variables, the amounts of MW transported through the processes from collection to disposal and the procedures applied to MW are shown in Table 2.
Table 2.
Optimal values of decision variables (optimal routes) in the next decade for Istanbul
| Variable | Value | Variable | Value | Variable | Value |
|---|---|---|---|---|---|
| 2 | 438 | 552 | |||
| 260 | 1601 | 1164 | |||
| 1488 | 147 | 1876 | |||
| 0.04 | 3409 | 2894 | |||
| 471 | 975 | 767 | |||
| 2265 | 216 | 11.2 | |||
| 1241 | 1147 | 20 | |||
| 587 | 646 | 8.9 | |||
| 54 | 1796 | 3.8 | |||
| 254 | 1910 | 11097 | |||
| 879 | 1788 | 19980 | |||
| 4224 | 2390 | 8922 | |||
| 268 | 645 | 3822 | |||
| 961 | 1545 | 32.9 | |||
| 605 | 17 | 3822 | |||
| 137 | 310 | 40000 | |||
| 86 | 3179 | ||||
| 217 | 455 |
In the study conducted by Mantzaras and Voudrias (2017), the locations of potential treatment facilities, transfer stations, and landfill sites were determined with the aim of minimizing the cost of collecting, transporting, and disposing of IMW produced in East Macedonia-Thrace in Greece. As the optimal solution, they suggested that it would be appropriate to build a treatment plant in Chrysoupolis's landfill site without the need for any transfer station to be built. The total cost based on the optimum result was calculated as 465,600 €/year (38,800 €/month). In the study conducted by Kargar et al. (2020a) on the management of MW in the city of Babol (Iran), the total cost, including the collection and transportation, processing, and disposal of waste was found to be 22,024 €/year for 20 medical, seven storage and seven treatment centers with one transfer station and one disposal centers were taken into a consideration in the model. It has been observed that the cost based on the amount of waste produced is also lower than the minimum cost obtained in our study. Since Istanbul has a larger population than both the East Macedonia-Thrace region and Babol city, it seems quite normal that the amount of waste produced in Istanbul is higher, and as a result, it has a higher cost. In addition, the fact that only IMW management was taken into account in the study conducted in Greece also affects the total cost amount in that study.
An estimated 43,866 tons of MW to be generated in 2030 are transported to transfer stations. According to optimal results, temporary MW storage in transfer stations is sorted according to their types (pathological, cutting-piercing, and infectious). While 11,109 tons of waste come from 11 districts to the transfer station (j1) located in Kucukbakkalkoy, Atasehir, the MW from 11 districts taken to the transfer station (j2) located in Hekimbasi, Umraniye is 20,000 ton and that transported from 12 districts to the transfer station (j3) located in Silahtaraga, Eyup, is 8931 ton. Lastly, 3826 tons of MW are transported from seven districts to the transfer station (j4) in Esenyurt, Kirac. A total of 43.8 tons of pathological MW from all transfer stations is transferred to the k1 incineration facility. While 40,000 tons of cutting-piercing and infectious MW are transferred from j1, j2, and j3 transfer stations to the h3 sterilization facility, only 3822 tons of MW from the j4 transfer station are transferred to the h1 facility. This may be due to the h1 and h3 facilities being closer to transfer stations than the other facilities, thus reducing the cost. Then, the treated waste in incineration facility, and in the h1, h3 sterilization facilities is sent to the landfill. The ash with a weight of 32.9 tons from the k1 incineration facility, the treated waste weighing 3822 tons from the h1 sterilization facility, and 40,000 tons of treated waste from the h3 sterilization facility are sent to the m1 landfill.
In the three-goal objective function, the optimal result offers the balancing of different criteria. Therefore, conciliatory results have been obtained for single-purpose objectives (Table 3). The result, which includes minimizing the total fixed costs of the opening facilities, the operational cost of the facilities, and the total cost of the transportation of the waste between the facilities, is 3,090,993 € more than the expected optimal result for a single-purpose objective. Another result with the goal of minimizing the cost of carbon emission released during the opening of the facilities and the transportation of waste between the facilities is 14,920 € less than the optimal result of the single-purpose objective. Lastly, there was no deviation from the optimal result of the goal, which maximizes the number of personnel to be employed in the facilities to be opened and the state's earnings from the minimum tax cost.
Table 3.
Deviations amounts of single-purpose objectives for the next decade
| Positive deviation | Negative deviation |
|---|---|
| 0 | |
| 14,920 | |
The model output, which includes the optimum routing from the collection facilities to the disposal of 32,146 tons of MW generated in 39 districts of Istanbul in 2020 under the COVID-19 pandemic conditions regardless of the cost factor, is given in Table 4. MW of 3553 tons from three districts, 6182 tons from nine districts, 20,001 tons from 21 districts, and 2410 tons from seven districts are transported to j1, j2, j3, and j4 transfer stations, respectively. Depending on the content of MW, 32.1 tons and 32,113 tons from all transfer stations are transferred to k1 and h1, respectively, and then, the ashes (24.1 tons) and the treated waste (32,112 tons) are sent to m1. According to the model output, Istanbul has sufficient facilities for all processes ranging from the collection to the disposal of the MW generated in 2020, and the capacity of the existing facilities meets the need for the disposal of MW.
Table 4.
Optimal values of decision variables (optimal routes) in 2020 under the COVID-19 pandemic conditions for Istanbul
| Variable | Value | Variable | Value | Variable | Value |
|---|---|---|---|---|---|
| 4.5 | 142 | 1094 | |||
| 170 | 2490 | 1835 | |||
| 954 | 1375 | 237 | |||
| 406 | 181 | 802 | |||
| 1990 | 1565 | 3.5 | |||
| 1313 | 287 | 6.2 | |||
| 1222 | 1428 | 20 | |||
| 548 | 1560 | 2.4 | |||
| 568 | 1171 | 3550 | |||
| 539 | 1475 | 6176 | |||
| 266 | 563 | 19980 | |||
| 572 | 1001 | 2407 | |||
| 395 | 19 | 24.1 | |||
| 244 | 298 | 32112 | |||
| 54 | 2758 | ||||
| 164 | 309 | ||||
| 323 | 701 | ||||
| 666 | 457 |
Sensitivity analyses
Sensitivity analysis, a measurement of the sensitivity of models, indicates the effects of variables on the model. It could give decision-makers insight into trade-offs. To observe the possible changes in the values of objective functions, sensitivity analyses were performed on some of the decision factors and the critical parameters of the model that may impact the decision-makers. The different analyses and their effects on the objective function value are presented below.
Sensitivity analysis on the weight given to objective functions
A sensitivity analysis was carried out to provide a basis to decision-makers by considering various parameters (amount of MW, cost of the carbon emission, and tax rate paid to SSI for working personnel), and to examine the behavior of the model. Three objectives of this study (minimizing the total cost, cost of minimizing CO2 emission, and maximizing the number of employees) are equally important within the framework of sustainability goals. The goal weight of the first, second, and third objectives was assumed to be 0.334, 0.333, and 0.333, respectively. In addition to our scenario, 14 other scenarios were considered with different combinations to observe the effects of these changes on the objective function value. Table SM-8 illustrates the scenarios and objective function values. Final computations present a schematic diagram of the Pareto frontier and the non-dominated solutions (Fig. SM-2). When a small change was made in the weights given to the objective functions, generally, the objective function values did not significantly change. The results indicated that the solution approach of the proposed model is correct and its behavior is reasonable (Table SM-8). The Pareto frontier, which offers optimal decisions according to the requirements of the real world, also pointed out the same results. Decision-makers can choose the best solution concerning their objectives using the given Pareto frontier.
Sensitivity analysis on the generated waste amount
It is found that the rate of MW increases by approximately 5.5% every year, depending on the population in Istanbul. However, this rate has reached 10.6% in 2020 due to the COVID-19 pandemic. Therefore, the analyses were deliberately conducted with variations of 5%, 10%, and 15% for each of the critical parameters in case of an extraordinary situation. The effects of these changes on incineration and sterilization facilities’ capacity and total cost were investigated. With 5%, 10%, and 15% increase rates in the estimated amount of MW for the year 2030, an increase in the optimum value of the objective function was observed at the rates of 4.3%, 8.5%, and 12.2%, respectively (Table 5). Furthermore, these changes in rates on MW did not affect the original number of needed incineration and sterilization facilities stated in the optimum solution (in 2030). Mantzaras and Voudrias (2017) reported that a sensitivity analysis with a 25% increase in the amount of IMW and 15% in the fuel cost resulted in a 5.61% and 0.98% increase in the total management cost, respectively, and no need for extra facilities to be opened. Kargar et al. (2020a) conducted a sensitivity analysis to evaluate the impact of a 5% and 10% increase in the amount of MW produced per capita on the total cost. Increasing the amount of MW per capita by 5% and 10% resulted in an increase of 28.5% and 31.6%, respectively, in the total cost. As a result, any increase in the quantity of MW significantly affects the total cost.
Table 5.
Sensitivity analysis of MW amount (2030) on the objective function value
| Rate (%) | Incineration facility | Sterilization facility | Objective function value |
|---|---|---|---|
| 5 | k1 | h1, h3 | 65,135,696 |
| 10 | k1 | h1, h3 | 67,758,610 |
| 15 | k1 | h1, h3 | 70,069,272 |
Sensitivity analysis on the cost of carbon emission
In the model, CO2 emissions that occur during the opening of a new facility or the transportation of the MW from the MW producers to the landfills were specified as the source of the emission cost. This is because the carbon emission is reflected as a cost in the model and it is related to the amount of MW generated. Therefore, an increase in the amount of MW will increase carbon emissions. Assuming that the existing facilities are operated and the proposed ones are opened in the year 2030, increasing the cost of carbon emission per ton by 5%, 10%, and 15% are seen not to have affected the optimum value (Table 6).
Table 6.
Sensitivity analysis of the carbon emission cost (2030) on the objective function value
| Rate (%) | Incineration facility | Sterilization facility | Objective function value |
|---|---|---|---|
| 5 | k1 | h1, h3 | 62,450,332 |
| 10 | k1 | h1, h3 | 62,450,332 |
| 15 | k1 | h1, h3 | 62,450,332 |
Sensitivity analysis on the tax rate of the personnel to be employed
Finally, when it is assumed that the needed sterilization and incineration facilities are operated for the next 10 years, there has been no change in the optimum value of the objective function, in case of a 5%, 10%, and 15% increase in the tax rate of the personnel working with minimum wage (Table 7). This is because the estimated number of personnel to be employed at the facilities for the next decade is certain. However, this number can vary depending on the increase in the amount of MW and the number of facilities to be opened. Therefore, simply increasing the tax rate does not have a noticeable effect on the model. Eventually, it can be concluded that a rise in the amount of MW affects the model results more than the other key parameters.
Table 7.
Sensitivity analysis of the tax rate value (2030) of the personnel working with the minimum wage on the objective function value
| Rate (%) | Incineration Facility | Sterilization facility | Objective function value |
|---|---|---|---|
| 5 | k1 | h1, h3 | 62,450,332 |
| 10 | k1 | h1, h3 | 62,450,332 |
| 15 | k1 | h1, h3 | 62,450,332 |
Conclusion
A mixed-integer linear programming (MILP) model is used to determine the adequacy of existing facilities and minimize the total cost and CO2 emissions while maximizing state earnings. The model offers a different solution for each purpose, operating the reverse logistics network with GAMS 23.5.1 solver. The model's result indicates that the existing facilities' number and capacity are sufficient in the treatment of MW even under current COVID-19 pandemic conditions. Furthermore, the model has demonstrated that the capacity of the sterilization facility will be insufficient in 2030, and it has suggested opening a new sterilization facility at a location close to the sanitary landfill in Komurcuoda, Sile which could be a potential area. It is found that z1 accounts for the most significant portion of the total cost. The single-purpose model resulted in a total cost of 62,408,375 €, which is less than that of the multi-purpose model (62,450,332 €). A slightly higher value has been obtained in the multi-objective model. The multi-objective model has a higher number of limitations; therefore, it shows trade-offs among objectives and gives a better idea to decision-makers. The model provides several implications for megacities with similar scenarios and can be used for an integrated medical waste management (MWM) evaluation framework developed with minor adjustments by the municipalities. The primary goal of this study is to create a management plan within the framework of sustainability goals for the present and the future, thus every goal was equally important. That is, the limitation of this method is that the allocation of weights to each criterion is subjective; therefore, it is thought that reaching a consensus among stakeholders depends on the prioritization of attributes. However, this research could be a basis to determine which objective could be an optimum solution using sensitivity analyses. At the same time, government authorities responsible for economic and environmental issues can also use sensitivity analyses to objectively introduce appropriate and robust legislation on waste management, while dealing with the costs and flows of reverse logistics activities. The sensitivity analyses on key parameters of the model have revealed that the capacity of existing facilities and the new sterilization facility proposed to be opened in 2030 will be sufficient to meet the treatment needs, even if the amount of MW increases by 15% more than the predicted amount in the next 10 years. For future planning, the management of MW could be organized using this simple network to determine specific locations of present or newly opened processing facilities and the flow rates between facilities. Therefore, the model could give managers insight into waste management systems.
Further studies can develop a multi-purpose and multi-product mixed-integer linear model with limited capacity by considering the risks as well as the costs due to the increasing amount of waste generated or to be generated by health institutions. In addition, the entire model has been developed in a deterministic way which cannot detect the uncertainties at some points of waste management. Future research may focus on advanced methods (Stochastic programming and Robust modeling) by defining and controlling the uncertainty of some parameters to make robust decisions on reverse logistic network design for MWM.
Supplementary Information
Below is the link to the electronic supplementary material.
Funding
Not applicable.
Declarations
Conflict of interest
The authors declare that they have no competing interests.
References
- Achillas C, Aidonis D, Vlachokostas C, Moussiopoulos N, Banias G, Triantafillou D. A multi-objective decision-making model to select waste electrical and electronic equipment transportation media. Resour Conserv Recycl. 2012;68:76–84. doi: 10.1016/j.resconrec.2012.01.004. [DOI] [Google Scholar]
- Ahluwalia PK, Nema AK. Multi-objective reverse logistics model for integrated computer waste management. Waste Manage Res. 2006;24(6):514–527. doi: 10.1177/0734242X06067252. [DOI] [PubMed] [Google Scholar]
- Alhamsi A, Diabat A. A genetic algorithm for reverse logistics network design: a case study from the GCC. J Clean Prod. 2017;151:652–669. doi: 10.1016/j.jclepro.2017.02.096. [DOI] [Google Scholar]
- Alshraideh H, Qdais HA. Stochastic modeling and optimization of medical waste collection in Northern Jordan. J Mater Cycles Waste Manag. 2017;19:743–753. doi: 10.1007/s10163-016-0474-3. [DOI] [Google Scholar]
- Balci S, Ayvaz B. A mixed-integer linear programming model for end of life vehicles recycling network design. Southeast Eur J Soft Comput. 2017;6(1):20–31. doi: 10.21533/scjournal.v6i1.130. [DOI] [Google Scholar]
- Baveja G, Muralidhar S, Aggarwal P. Medical Waste Management-an Overview Hospital Today. 2000;5(9):485–486. [Google Scholar]
- Bdour A, Altrabsheh B, Hadadin N, Al-Shareif M. Assessment medical wastes management practice: a case study of the northern part Jordan. Waste Manage. 2007;27:746–759. doi: 10.1016/j.wasman.2006.03.004. [DOI] [PubMed] [Google Scholar]
- Birpinar ME, Bilgili MS, Erdogan T. Medical waste management in Turkey: a case study of Istanbul. Waste Manage. 2009;29:445–448. doi: 10.1016/j.wasman.2008.03.015. [DOI] [PubMed] [Google Scholar]
- Budak A, Ustundag A. Reverse logistics optimization for waste collection and disposal in health institutions: the case of Turkey. Int J Logist Res Appl. 2016;20(4):322–341. doi: 10.1080/13675567.2016.1234595. [DOI] [Google Scholar]
- Calma J (2020) The COVID-19 pandemic is generating tons of medical waste. https://buff.ly/2Ui4K7s. Accessed 15 Sept 2020
- Chaerul M, Tanaka M, Shekdar AV. Resolving complexities in healthcare waste management: a goal programming approach. Waste Manage Res. 2008;26(3):217–232. doi: 10.1177/0734242X07076939. [DOI] [PubMed] [Google Scholar]
- Chang CT. Multi-choice goal programming with utility functions. Eur J Oper Res. 2011;215(2):439–445. doi: 10.1016/j.ejor.2011.06.041. [DOI] [Google Scholar]
- CSB (2019) 2019 yili MCK tibbi atik bedelleri. https://webdosya.csb.gov.tr/db/cygm/duyurular/mck_tur_20191210-20191210095135.xlsx. Accessed 7 April 2022
- CSB (2022) Paris Anlasmasi. https://iklim.csb.gov.tr/paris-anlasmasi-i-98587. Accessed 7 April 2022
- Dat LQ, Linh DTT, Chou SY, Vincent FY. Optimizing reverse logistic costs for recycling end-of-life electrical and electronical products. Expert Syst Appl. 2012;39(7):6380–6387. doi: 10.1016/j.eswa.2011.12.031. [DOI] [Google Scholar]
- Demir A, Bilal Ş, Ozkaya B (2002) The management of medical wastes in Istanbul. ISWA World Environment Congress 283–287
- Demirel E, Demirel N, Gokcen H. A mixed integer linear programming model to optimize reverse logistics activities of end-of-life vehicles in Turkey. J Clean Prod. 2016;112:2101–2113. doi: 10.1016/j.jclepro.2014.10.079. [DOI] [Google Scholar]
- Eren E, Tuzkaya UR. Safe distance-based vehicle routing problem: medical waste collection case study in COVID-19 pandemic. Comput Ind Eng. 2021 doi: 10.1016/j.cie.2021.107328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erickson S (2021) Environmental impact of medical waste part I: high carbon footprint. https://www.onsitewaste.com/post/environmental-impact-of-medical-waste-part-i-high-carbon-footprint. Accessed 7 April 2022
- Gao X. A novel reverse logistics network design considering multi-level investments for facility reconstruction with environmental considerations. Sustainability. 2019;11(9):270. doi: 10.3390/su11092710. [DOI] [Google Scholar]
- Govindan K, Paam P, Abtahi AR. A fuzzy multi-objective optimization model for sustainable reverse logistics network design. Ecol Indic. 2016;67:753–768. doi: 10.1016/j.ecolind.2016.03.017. [DOI] [Google Scholar]
- Govindan K, Nasr A, Mostafazadeh P, Mira H. Medical waste management during coronavirus disease 2019 (COVID-19) outbreak: a mathematical programming model. Comput Ind Eng. 2021 doi: 10.1016/j.cie.2021.107668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He ZG, Li Q, Fang J. The solutions and recommendations for logistic problems in the collection of medical waste in China. Proc Environ Sci. 2016;31:447–456. doi: 10.1016/j.proenv.2016.02.099. [DOI] [Google Scholar]
- Hong J, Shen GQ, Feng Y, Lou WST, Mao C. Greenhouse gas emissions during the construction phase of a building: a case study in China. J Clean Prod. 2015;103:249–259. doi: 10.1016/j.jclepro.2014.11.023. [DOI] [Google Scholar]
- IBB (2018) Tons of medical waste in Istanbul turn into energy. https://www.ibb.istanbul/en/News/Detail/1245. Accessed 06 Aug 2020
- IBB (2020a) Landfill areas. https://atikyonetimi.ibb.istanbul/hizmetlerimiz/duzenli-depolama-alanlari/. Accessed 6 Aug 2020a
- IBB (2020b) Ilce, yil ve atik turu bazinda atik miktari. https://data.ibb.gov.tr/dataset/ilce-yil-ve-atik-turu-bazinda-atik-miktari/resource/50036dfd-aea5-4f06-832f-f7020fdaaa5a. Accessed 06 Aug 2020b
- ISTAC (2019) Medical waste management. https://www.istac.istanbul/en/clean-istanbul/our-services/istanbul-medical-waste-management. Accessed 06 Aug 2020
- John ST, Sridharan R, Kumar PR. Reverse logistics network design: a case of mobile phones and digital cameras. Int J Adv Manuf Technol. 2018;954(1):615–631. doi: 10.1007/s00170-017-0864-2. [DOI] [Google Scholar]
- Kargar S, Paydar MM, Safei AS. A reverse supply chain for medical waste: a case study in Babol healthcare sector. Waste Manag. 2020;113:197–209. doi: 10.1016/j.wasman.2020.05.052. [DOI] [PubMed] [Google Scholar]
- Kargar S, Pourmehdi M, Paydar M. Reverse logistics network design for medical waste management in the epidemic outbreak of the novel coronavirus (COVID-19) Sci Total Environ. 2020 doi: 10.1016/j.scitotenv.2020.141183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kesici S (2016) Reverse logistics network design for medical waste: a case study for Izmir. Dissertation, Gazi University
- Korkut EN. Estimations and analysis of medical waste amounts in the city of Istanbul and proposing a new approach for the estimation of future medical waste. Waste Manage. 2018;81:168–176. doi: 10.1016/j.wasman.2018.10.004. [DOI] [PubMed] [Google Scholar]
- Mandy Z (2020) Coronavirus leaves China with mountains of medical waste. https://www.scmp.com/news/china/society/article/3074722/coronavirus-leaves-china-mountains-medical-waste. Accessed 15 Sept 2020
- Mantzaras G, Voudrias EA. An optimization model for collection, haul, transfer, treatment, and disposal of infectious medical waste: application to a Greek region. Waste Manage. 2017;69:518–534. doi: 10.1016/j.wasman.2017.08.037. [DOI] [PubMed] [Google Scholar]
- McKinnon AC, Piecyk M. Measuring and managing CO2 emissions of European chemical transport. Logistic Res Centre Heriot-Watt Univ. 2010;2011:22. [Google Scholar]
- OECD (2021a) Effective carbon rates. https://www.oecd.org/tax/tax-policy/effective-carbon-rates-2021a-brochure.pdf. Accessed 1 April 2022
- OECD (2021b) Supplement to effective carbon rates. https://www.oecd.org/tax/tax-policy/effective-carbon-rates-turkey.pdf. Accessed 1 April 2022
- Ozturk (2017) Atik Toplama Miktari ve Maliyeti %50 Dusurulebilir. http://www.cevresehirkutuphanesi.com/assets/files/slider_pdf/PNAVvqKEjOtl.pdf. Accessed 7 April 2022
- Pati RK, Vrat P, Kumar P. A goal programming model for paper recycling system. Omega. 2008;36(3):405–417. doi: 10.1016/j.omega.2006.04.014. [DOI] [Google Scholar]
- Pokharel S, Mutha A. Perspectives in reverse logistics: a review. Resour Conserv Recycl. 2009;53(4):175–182. doi: 10.1016/j.resconrec.2008.11.006. [DOI] [Google Scholar]
- Rahimi M, Ghezavati V. Sustainable multi-period reverse logistics network design and planning under certainty utilizing conditional value at risk (CVar) for recycling construction and demolition waste. J Clean Prod. 2018;172:1567–1581. doi: 10.1016/j.jclepro.2017.10.240. [DOI] [Google Scholar]
- Republic of Turkey Ministry of Health (2021) Health system strengthening and support project restructuring (P152799) environmental and social management framework. https://pydb.saglik.gov.tr/Eklenti/42149/0/esmf-hssspmoh16122021pdf.pdf. Accessed 2 April 2022
- Rolewicz- Kalińska A. Logistic constraint as part of a sustainable medical waste management system. Transp Res Proc. 2016;16:473–482. doi: 10.1016/j.trpro.2016.11.044. [DOI] [Google Scholar]
- Sadjady H. Physical flows. In: Farahani RZ, Rezapour S, Kardar L, editors. Logistics operations and management: concepts and models. London: Elsevier; 2011. pp. 11–42. [Google Scholar]
- Samsatli S, Samsatli NJ. A Multi-objective MILP for the design and operation of future integrated multi-vector energy networks capturing detailed spatial-temporal dependencies. Appl Energy. 2018;220:893–920. doi: 10.1016/j.apenergy.2017.09.055. [DOI] [Google Scholar]
- Sarkodie SA, Owusu PA. Global assessment of environment, health and economic impact of novel coronavirus (COVID-19) Environ Cev Sustain. 2020 doi: 10.1007/s10668-020-00801-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadkam E. Cuckoo optimization algorithm in reverse logistics: a network design for COVID-19 waste management. Waste Manage Res. 2022;40(4):458–469. doi: 10.1177/0734242X211003947. [DOI] [PubMed] [Google Scholar]
- Shi L, Fan H, Gao P, Zhang H. Network model and optimization of medical waste reverse logistics by improved genetic algorithm. Adv Comput Intell. 2009 doi: 10.1007/978-3-642-04843-2_6. [DOI] [Google Scholar]
- Shih LH. Reverse logistics system planning for recycling electrical appliances and computers in Taiwan. Resour Conserv Recycl. 2001;32(1):55–72. doi: 10.1016/S0921-3449(00)00098-7. [DOI] [Google Scholar]
- Shih LS, Lin YT. Multicriteria optimization for infectious medical waste collection system planning. Period Pract Period Hazard Toxic Radioact Waste Manage. 2003;7(2):78–85. doi: 10.1061/(ASCE)1090-025X(2003)7:2(78). [DOI] [Google Scholar]
- Soysal A, Simsek H, Soysal D, Alyu F. Management of health-care waste in Izmir Turkey. Annali dell'Istituto superiore di sanità. 2010;46(3):299–302. doi: 10.4415/ANN_10_03_13. [DOI] [PubMed] [Google Scholar]
- Trochu J, Chaabane A, Ouihimmou M. A carbon-constrained stochastic model for eco-efficient reverse logistics network design under environmental regulations in the CRD industry. J Clean Prod. 2020 doi: 10.1016/j.jclepro.2019.118818. [DOI] [Google Scholar]
- USDforecast (2020) Euro rate forecast. http://usdforecast.com/tr/euro-tahmini.html. Accessed 6 Aug 2020
- Wang Z, Huang L, He CX. A multi-objective and multi-period optimization model for urban healthcare waste’s reverse logistics network design. J Comb Optim. 2019 doi: 10.1007/s10878-019-00499-7. [DOI] [Google Scholar]
- Wei Y, Cui M, Ye Z, Guo Q. Environmental challenges from the increasing medical waste since SARS outbreak. J Clean Prod. 2021 doi: 10.1016/j.jclepro.2020.125246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization (WHO) (2017) Safe Management of Wastes from Health-care activities. https://apps.who.int/iris/bitstream/handle/10665/259491/WHO-FWC-WSH-17.05-eng.pdf. Accessed 22 July 2020
- World Health Organization (WHO) (2018) Health-care waste. https://www.who.int/en/news-room/fact-sheets/detail/health-care-waste. Accessed 22 July 2020
- Yong Z, Gang X, Guanxing W, Tao Z, Dawei J. Medical waste management in China: a case study of Nanjing. Waste Manage. 2009;29:1376–1382. doi: 10.1016/j.wasman.2008.10.023. [DOI] [PubMed] [Google Scholar]
- Yu H, Solvang WD. An improved multi-objective programming with augmented ε-constraint method for hazardous waste location-routing problems. Int J Environ Res Public Health. 2016;13(6):548. doi: 10.3390/ijerph13060548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H, Sun X, Solvang WD, Zhao X. Reverse logistics network design for effective management of medical waste in epidemic outbreaks: Insights from the coronavirus disease 2019 (COVID-19) outbreak in Wuhan (China) Int J Environ Res Public Health. 2020;17(5):1770. doi: 10.3390/ijerph17051770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang YM, Huang GH, Li He. An inexact reverse logistics model for municipal solid waste management systems. J Environ Manage. 2011;92:522–530. doi: 10.1016/j.jenvman.2010.09.011. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.