Abstract
This paper examines the diversification role of socially responsible investments (SRI) during the COVID-19 pandemic. To assess the contribution to risk diversification and improved financial performance of SRI we analyze the effect of including clean energy equities in portfolios of conventional equities and other assets commonly considered as safe havens. We construct minimum variance portfolios for different rebalancing frequencies and by considering or restricting short positions. Two approaches are applied: AR-GARCH models to fit the marginal distributions of individual assets and DCC skew Student copula specifications to model the conditional dependencies among pairs via the Kendall’s tau correlation measure. We provide evidence of the important role that SRI have played in diversifying and improving the financial performance of portfolios based on different securities such as traditional equities, Treasury bonds, gold, crude oil and Bitcoin.
Keywords: SRI, ESG, Diversification, Dependence, Safe haven, DCC-copula, COVID-19
1. Introduction
The field of socially responsible investments (SRI), which incorporates environmental, social, and governance (ESG) considerations beyond simply financial ones, in the study, analysis, and allocation of securities, has grown exponentially over the last years, driven by demand from institutional and retail investors, and regulatory pressure. The global crisis caused by the COVID-19 pandemic has brought to the fore the enormous vulnerability of economies worldwide and has reinforced the relevance of SRI in the transition towards a more balanced economy and society. Actually, sustainable investing has seen a significant increase since the pandemic outbreak in 2020. According to Morningstar, US sustainable funds gathered $51.1 billion of net inflows in 2020 and a record of $69.2 billion in 2021, more than double and triple, respectively, the inflows of $21.4 billion in 2019. Furthermore, investors poured $45.6 billion into ESG funds globally in the first quarter of 2020, which sharply contrasts with global outflows of $384.7 billion for the overall fund universe. Growing cumulative flows in sustainable funds evidence the higher resilience of SRI during the COVID-19 crisis in comparison to its conventional counterpart.
In times of financial instability such as the associated with the onset of the COVID-19 pandemic, investors need to thoroughly evaluate different strategies that can help minimize risks and improve their overall performance. The term diversification then comes into play. Broadly speaking, diversification enables investors to reduce their overall risk exposure by combining financial assets that have a weakly positive correlation on average so that potential losses in one asset can be (at least partially) offset by gains in other asset classes (Grauer and Shen, 2000, Joost and Laeven, 2007). In the case of an asset that is uncorrelated or negatively correlated with another asset or portfolio in periods of economic downturns or crisis, it becomes a so-called safe haven (Baur and McDermott, 2010, Baur and Lucey, 2010).1 Traditionally considered safe havens, such as gold and crude oil, or potential new safe havens, such as Bitcoin, have performed differently over the course of the COVID-19 crisis. Diverse studies reveal that crude oil is not making as much of a dent in risk mitigation as originally expected (Conlon and McGee, 2020, Corbet et al., 2020b, Sharif et al., 2020), whereas cryptocurrencies are still too risky due to their high intrinsic volatility to be effectively considered a safe haven (Kristoufek, 2013, Li and Wang, 2017). Thus, relevant and updated studies in the field of financial allocation, such as Ji et al. (2020), consider that the concept of safe haven securities should be re-evaluated and perhaps, disruptive assets such as those that meet ESG criteria – which appear to be performing better and exhibiting low risk exposure during the pandemic2 – should be considered.
Despite the higher resilience of SRI during the COVID-19 crisis both in terms of demand and performance, the hedging properties of ESG assets have been explored only marginally (Ferrer et al., 2018, Arif et al., 2021, Sharma et al., 2022, Yousaf et al., 2022). Moreover, most of the existing studies restrict their analysis at the identification of the potential role of ESG securities as diversifiers or hedges without quantifying the diversification and hedging benefits of ESG investments against conventional investments through risk management analysis and portfolio performance assessment. Thus, the present paper extends the previous literature by raising two research questions. First, to what extent has ESG investing acted as a diversifier, a hedge or even as a safe haven since the COVID-19 outbreak? Second, beyond contributing to risk reduction, does the performance of conventional assets and potential safe haven assets improve when they are combined with ESG securities? To account for the performance of ESG and conventional investments, recent literature uses mutual funds or stock/fixed-income indices (Elie et al., 2019, Dutta et al., 2020, Broadstock et al., 2021, Tareq et al., 2021). However, since the use of exchange-traded-funds (ETFs) offers several advantages, to address our research questions we rely on daily data for six ETFs linked to different assets over the period 2019–2021.3 First, traditional equities and Treasury bonds are used as proxies for conventional investments in the equity and fixed-income markets, respectively. Second, gold, oil and cryptocurrencies are employed to track the performance of traditionally considered safe havens or, at least, hedges. Third, from the wide ESG investment spectrum, the target investor in this research is one with investment preferences towards the equity market and involved with environmental concerns. Thus, we focus on green equities.4 In particular, as we analyze the Environmental component of the ESG label, we consider the ETF with one of the highest MSCI ESG scores (7.61 in 2019) among those with a “Leader” tag based on MSCI ESG ranking as a proxy for the clean energy equity market. This score considers the categories of sustainable impact solutions, carbon intensity, and green revenues.
To achieve the goal of this study, our methodological approach consists of examining the dynamic correlation behavior of optimal portfolios of considered alternative assets when ESG assets are incorporated. Using novel and particularly suitable techniques, we examine the significant ability of SRI to diversify and improve the performance of different portfolios in which clean energy equities are combined with either conventional equities, conventional Treasury bonds, gold, crude oil, or Bitcoin. The left tail of the return distribution is the focus of these techniques, which are essential for inferring diversification and safe haven implications. In concrete terms, we apply different frequency portfolio rebalancing based on the minimum variance optimization method, allowing us to evaluate the ESG results both in terms of risk and return during the pandemic period. In order to model the conditional co-moments between each pair of asset returns, a DCC skew Student copula is used to fit the time-varying covariance matrix. Unlike other correlation approaches, this Student copula gives an overall view and characterization of the joint distribution. The marginals follow a standard GARCH (1,1) model under the assumption of skew Student’s t distributions, which is mainly selected for the widely proven high convergence properties of the model and the good fit of this theoretical distribution to leptokurtic and left skewed empirical distributions, like those of financial series. A sufficiently consistent period to make GARCH and copula estimates is analyzed, including a first part of relative calm in the markets corresponding to 2019, and a second subperiod characterized by the pandemic spanning from 2020 to 2021.
Initial results for the time-varying volatilities and Dependences among security pairs indicate high volatility for individual assets and strong evidence of interdependence among assets during the early stages of the pandemic. However, in subsequent shocks of the crisis, the correlation between clean energy equities and considered assets is much lower. This provides diversifying evidence in favor of SRI. As a result of the portfolio rebalancing exercise, we observe that overall, the active management of ESG portfolios yields higher performance than the passive investment in single securities. In other words, SRI provide a hedge for most of the single asset classes and improves the risk-return relationship of individual investments. In light of these findings, it appears that SRI have the potential to reduce risk, as well as increase portfolio performance during times of crisis, such as the recent pandemic caused by the SARS-CoV-2 virus.
The present work makes several contributions to the existing literature. First, a number of existing studies investigate the diversifying properties of clean energy equities when they are combined with dirty energy equities or with funds/indices that track the performance of the overall equity market (Ferrer et al., 2018, Arif et al., 2021, Kuang, 2021, Tareq et al., 2021). Unlike the previous literature, we assess the performance of single investments in conventional equities and Treasury bonds and in commonly considered safe haven assets (i.e., gold, crude oil and cryptocurrencies) against portfolios including ESG assets. Thus, our approach allows one to compare the performance of the active management of each ESG portfolio against (1) the passive strategy of investing in the corresponding asset and holding this position (2) the active management of a set of competing ESG portfolios that involve very diverse asset classes from the equity, Treasury, commodity and cryptocurrency markets. Second, studies on the performance of ESG assets mostly rely on the widely employed Sharpe ratio (Alexopoulos, 2018, Omura et al., 2021, Yousaf et al., 2022), whereas we assess the performance of our different investment strategies by employing downside risk performance measures in addition to the former. The advantage of the downside risk performance measures over the Sharpe ratio is that the returns are not adjusted by the standard deviation, which considers both negative and positive deviations from the mean return, but by the negative deviations of returns from a minimal acceptable return or threshold. Third, most of the literature examines whether ESG assets exhibit diversifying or hedging features based on the analysis of their dependence or correlation with other asset classes through different methodological approaches (Elie et al., 2019, Dutta et al., 2020, Umar et al., 2020, Tareq et al., 2021). Thus, these studies merely report on the potential ability of ESG assets to act as a diversifier or a hedge when there exists evidence of low positive correlation or no significant correlation with other assets. However, results in the present study, which goes beyond correlation analysis, reveal that ESG-diversified portfolios outperform passive investments in individual assets, thus indicating the benefits of hedges with ESG assets despite reported evidence of strong interdependence with the rest of considered assets in the early stages of the sanitary crisis. Fourth, our results contribute to better understanding the reasons why investors would keep supporting sustainable financing through the demand of green financial instruments in the presence of an external shock, such as the COVID-19 sanitary crisis, which is essential for the implementation of policy actions that promote the role of sustainable financing in the transition to a greener economy.
The remainder of this paper proceeds as follows. Section 2 provides a brief review of the relevant literature. Section 3 introduces the conditional univariate and multivariate methodology to be implemented in the calibration of the minimum variance portfolios. Section 4 describes the dataset employed. Empirical findings related to portfolio weighting, performance assessment and risk management are reported in Section 5. Section 6 concludes.
2. Literature review
This paper relates to two strands of literature. The first one is devoted to assessing the performance of SRI during episodes of financial instability. Based on the estimation of risk-adjusted abnormal returns by means of different factor models, Nofsinger and Varma (2014) find that among SRI equity funds, the environmental, social and governance categories significantly outperform conventional funds in crisis periods. Becchetti et al. (2015) further show that socially responsible funds outperform conventional funds during the 2008 global financial crisis (GFC), but not in the course of the prior 2001 dotcom crisis. Alexopoulos (2018) assesses the performance of a broad set of clean energy and conventional energy ETFs under two shocks of different nature – the 2008 GFC and the 2014 oil crisis – and document that the former shock affected more the performance of clean energy ETFs than the latter did in conventional energy ETFs. Broadstock et al. (2021) and Omura et al. (2021) contribute to this body of literature by offering evidence in the context of the COVID-19 pandemic. Using a comprehensive dataset that comprises ESG scores for China’s CSI300 stock index constituents, Broadstock et al. (2021) show that overall high-ESG portfolios outperform low-ESG portfolios. In turn, the results in Omura et al. (2021) indicate the outperformance of SRI stock indices against their conventional counterparts during the sanitary crisis.
The second strand of literature addresses the analysis of the diversifying or hedging properties of several assets including commodities, such as crude oil and gold, and more recently, cryptocurrencies, in times of market turmoil. In the face of the oil price collapse triggered by the coronavirus outbreak, the research in the field has mostly concentrated on the role of gold and cryptocurrencies as safe haven assets during the pandemic.5 With a focus on gold, Akhtaruzzaman et al. (2021) find that gold only served as a safe haven asset for international equity markets during the early stages of the pandemic (i.e., until mid-March 2020). Based on data before and after the announcement of the COVID-19 disease on December 31, 2019, Ji et al. (2020) shows that the role of safe haven for gold remains robust during the pandemic, whereas Salisu et al. (2021) document that the effectiveness of gold hedging properties depends upon market conditions, being more limited after the announcement of the disease. In turn, the ability of cryptocurrencies to minimize the risk of investment strategies during the current pandemic has also deserved wide research attention, often in comparison to gold. Conlon and McGee (2020) offer evidence that adding Bitcoin to a portfolio containing S&P 500 stocks yields increased downside risk relative to holding the stock portfolio alone, thus suggesting that Bitcoin does not act as a safe haven during the COVID-19 crisis. Based on the DCC-GARCH methodology, Mariana et al. (2021) further show that both Bitcoin and Ethereum exhibit safe haven properties for the S&P 500 during the pandemic, although these are not investigated through portfolio performance assessment. A related study by Dutta et al. (2020) extends the findings of Mariana et al. (2021) by showing under a similar methodological approach that Bitcoin is a diversifying asset for global crude oil markets. Based on the asymmetric DCC approach, Chemkha et al. (2021) document that Bitcoin cannot be considered a safe haven for major international equity markets and currencies during the pandemic due to its increased volatility.
In comparison to gold and cryptocurrencies, evidence on the diversifying or hedging properties of ESG assets within the context of the ongoing pandemic crisis is far more limited. Existing studies infer on the potential role of ESG assets to serve as diversifiers, hedges or safe havens from correlation and dependence analyses under different econometric approaches. Concentrating on clean energy equity investments, the results in Arif et al. (2021) reveal weak dynamic interconnectedness between green and conventional stock indices in the long run, which suggests diversifying opportunities for investors with long investment horizons. Using the frequency-domain Granger causality test suggested by Breitung and Candelon (2006) and Sharma et al. (2022) confirm the findings in Arif et al. (2021) by offering evidence of bidirectional causality between sustainable and conventional indices in the short term, but not in the long run. Ferrer et al. (2021) rely on the wavelet-based network approach to show that strategies combining clean energy stock indices and general stocks do not offer diversifying or hedging benefits, whereas portfolios including clean energy stocks and green bonds may offer interesting diversification opportunities. Finally, Yousaf et al. (2022) does not find robust empirical evidence across the different quantiles defined to capture extreme S&P 500 downturns to support the safe haven property of clean energy stocks when these are combined with positions in the S&P 500.
Overall, the literature review reveals the existence of a research gap that consists of going one step further in the identification of the hedging properties of ESG assets in the context of the COVID-19 sanitary crisis by assessing empirically whether investment portfolios incorporating ESG assets effectively contribute not only to reduce risk exposure but also to outperform investments restricted only to conventional assets.
3. Methodology
A four-step process is followed in order to determine the conditional portfolio weights on a monthly basis. First, we estimate the different time-varying volatilities and Kendall dependencies for the full sample period. Second, the conditional covariance matrix is conducted as a cross product of prior deviations and correlations. Third, year 2019 represents the training period for the statistical models and is not considered for the rest of the analysis. Fourth, we calculate the dynamic portfolio rebalancing weights that minimize the variance of the respective portfolios made up of each asset class and the ESG shares. In order to increase robustness, multiple rebalancing frequencies are considered.
This section describes the optimal problem to be used for our empirical assessment. Section 3.1. details the particularities of the time-varying minimum variance problem, while Section 3.2. examines in further detail the dynamics of the copula correlation to be introduced in the optimal problem. Specifically, in this paper we rebalance our investment strategies on different frequency basis from the information suggested in a prior DCC skew Student copula estimation.
3.1. Minimum variance portfolio optimization
The construction of optimal investment portfolios that minimize risk and also allow obtaining the highest expected return from asset diversification has been a widely discussed topic by the academic community (Markowitz, 1959a, Markowitz, 1959b, Santos and Moura, 2014, Bertrand and Lapointe, 2015, Sahamkhadam et al., 2018, Aziz et al., 2019, Brauneis and Mestel, 2019).6 Formally, the minimum variance portfolio choice can be established as a dynamic optimization problem in which the investment’s risk exposure is minimized as:
| (1) |
where is the dynamic covariance matrix and is the vector of time-varying portfolio weights. Note that two different portfolio compositions are considered, allowing and constraining short sells. No additional constraints are needed to conduct the former optimization, while the non-negativity condition of the weights must be included in the latter .
The calculation of the time-varying portfolio variance () requires the estimation of the conditional covariance matrix, :
| (2) |
where the main diagonal is based on the return’s variance of each of the selected assets and the remaining components are covariances between pairs of asset returns. We model these conditional moments by way of the GARCH (1,1) specification for the case of the variance, and DCC Student copula for the correlation terms.7 We estimate each of the univariate GARCH (1,1) models from the innovations or residuals of prior AR (1) models.8
From the estimated conditional correlations, the conditional covariance matrix is obtained as follows:
| (3) |
where is the conditional deviation matrix, which is expressed as a diagonal matrix with the diagonal elements as conditional volatilities obtained from the GARCH (1,1) model. On the other hand, is the dynamic correlation matrix obtained through the application of the multivariate DCC skew Student copula specification. This matrix has its main diagonal composed by ones, and conditional Kendall’s correlations out of the diagonal.
3.2. Copulas and the optimal problem
An n-dimensional copula is an n-dimensional distribution in the unit hypercube with uniform marginals. Sklar (1959) demonstrate that the joint distribution, , of a random vector, , with marginals, , can be expressed as:
| (4) |
Where C, which is solely determined in the interval for under continuous marginals:
| (5) |
The density function can be interpreted as follows:
| (6) |
where are the marginal densities and is the density function of the copula given by:
| (7) |
Where is the quantile function of the marginals.
Then, considering the skewed and heavy-tailed patterns of most financial time series (Demarta and McNeil, 2007), we implement a DCC Student Copula approach as it exhibits desirable properties in modeling asset returns. In this regard, let the n-dimensional random vector of asset returns follow a copula GARCH model with joint distribution given by:
| (8) |
where is the conditional distribution of the i marginal series density and is the n-dimensional Copula. The conditional mean , where is the -field generated by the past realization of , and the conditional variance, , follows an AR (1)-GARCH (1,1) process:
| (9) |
| (10) |
where are . random variables which conditionally follow a standardized skew Student distribution, , of Fernández and Steel (1998) with skew and shape parameters and , respectively. is the slope in the AR(1) model and the lag-1 autocorrelation, and measures how volatility reacts to new information, while represents the persistence in volatility. .
Then, we assume a Skew Student Copula to model the dependence structure of the marginal distributions with conditional correlation, , and constant shape parameter . The conditional density of the copula can be summarized as:
| (11) |
Where is the Probability Integral Transformed (PIT) transformation of the return series by via the first stage GARCH, depicts the quantile transformation of the uniform marginals constraint to the common shape parameter of the multivariate density, and are each of the univariate marginals of the multivariate Student distribution with common shape parameter .
The joint density of this second stage estimation is written as:
| (12) |
where the likelihood is composed of a part due to the joint DCC copula dynamics and a part due to the first stage univariate GARCH dynamics:
| (13) |
where , and the sample correlation with of is given by .
Under elliptical distributions as the student’s t, making time-varying the correlation matrix of the copula is an extension of the 2-stage DCC model, and allows the fitting of a Student copula with disparate shape parameters for the first stage, which unless estimated jointly is not considered in the standard DCC-GARCH. Thus, to estimate the dynamic conditional correlations via the DCC Copula, first we must construct some instrumental variables, which play the role of covariances between pairs:
| (14) |
Where is the constant Pearson’s correlation between pairs and are the standardized innovations resulting from the GARCH (1,1) fitting.
Then, the dynamic Pearson’s correlations coefficients, , result from the standardization of the former auxiliary variables, :
| (15) |
As initial condition to initialize the calculus of the correlation coefficients, we impose:
| (16) |
Notwithstanding, under the assumption of the joint multivariate Student distribution, the Pearson’s correlation coefficient cannot capture tail dependence and thus, it is not invariant under monotone transformations of the original returns. Therefore, we implement the Kendall’s approach (Kruskal, 1958), based on rank correlations and depending just on the copula, :
| (17) |
which for elliptical distributions as the student’s t it is proved a one to one relation against the Pearson’s coefficient (Lindskog et al., 2003):
| (18) |
3.3. Portfolio returns and performance measures
Similarly to Díaz and Esparcia (2021), we conduct a realized performance analysis in which we build different portfolios from historical data but examine their returns one day ahead. Then, the overall performance over the entire period under study is examined from prior daily returns. Thus, we test how well the technique used in the construction of the portfolio has really worked.
First, from the time-varying optimization process described in Section 3.2., we calibrate the dynamic optimal asset weights, . Then, the portfolio return obtained over the next day, , can be characterized by:
| (19) |
where depicts the transpose vector of weights resulting from portfolio rebalancing at each given point in time, while is the dynamic column vector of asset returns obtained one day ahead of portfolio formation.
Second, to assess which investment alternative yields the greatest risk-adjusted value in current pandemic markets, we examine the ex-post performance of both, single assets and ESG-assets combined strategies. We implement two different performance measures: the Sharpe ratio (SR) and downside risk measures. First, the SR (Sharpe, 1966, Sharpe, 1975, Sharpe, 1994) measures the mean-excess return per unit of total risk as follows:
| (20) |
where and are the mean and the standard deviation of portfolio returns over the period under examination. is the risk-free rate, which is calculated from non-seasonally adjusted 3-month Treasury Bill rates retrieved from the Federal Reserve Bank of St. Louis.9
Second and clearly opposed to the classical , there is a vein of the literature specially concerned about losses and so, considering just the left-tail risk (Roy, 1952, Markowitz, 1959a). Thus, Fishburn (1977) defines the Lower Partial Moments () to account for the negative deviations of returns from a minimal acceptable return or threshold, .10 Kaplan and Knowles (2004) defines a set of Kappa indices with regard to a variety of orders:
| (21) |
where is the mean return over the period under examination and is the LPM of order and threshold .11
4. Data
The full data sample spans from January 2019 to December 2021, including 756 observations of daily closing market prices of ETFs linked to renewable energy equities, conventional equities, Treasury bonds, gold, crude oil, and cryptocurrencies. All the data are gathered from Yahoo Finance. The First Trust Global Wind Energy ETF is used as a proxy for the clean energy equity market. This ETF offers exposure to the global wind power industry by tracking the performance of the ISE Clean Edge Global Wind Energy Index (GWE), which includes both pure play wind power companies and firms with more broad-based activities that keep some focus on wind power. Also used in recent literature (Alexopoulos, 2018, Miralles-Quirós and Miralles-Quirós, 2019, Çelik et al., 2022), this ETF is rated AA by MSCI ESG fund ratings.12 In addition, this ETF is particularly suitable for our analysis because it provides exposure to a particularly well-recognized segment of the green energy market.
As for the conventional asset classes, the iShares MSCI World ETF and the SPDR Bloomberg Barclays International Treasury Bond ETF are used to characterize the global performance of the overall stock market and Treasury bond markets, respectively. iShares MSCI World ETF tracks a market cap-weighted index of large- and mid-cap developed market stocks worldwide, whereas SPDR Bloomberg Barclays International Treasury Bond offers exposure to bonds issued by governments outside the US. In turn, the behavior of the prices of gold and crude oil are proxied by the ETFs SPDR Gold Shares and the United States Oil Fund, LP, respectively. In addition, the Grayscale Bitcoin Trust, which enables investors to gain exposure to the price movements of Bitcoin, is employed as a proxy for the cryptocurrency market. Table 1 offers some descriptive features for selected ETFs as well as information on ESG metrics for the equity and bond ETFs as provided by MSCI.
Table 1.
Investment opportunity set.
| First Trust Global Wind Energy | iShares MSCI World | SPDR Bloomberg Barclays International Treasury Bond | SPDR Gold Shares | United States Oil Fund, LP | Grayscale Bitcoin Trust | |
|---|---|---|---|---|---|---|
| Descriptive features | ||||||
| Ticker | FAN | URTH | BWX | GLD | USO | GBTC |
| Exposure | Global | Global | Global | Global | Global | Global |
| Asset class | Equity | Equity | Bond | Commodity | Commodity | Cryptocurrency |
| Currency | USD | USD | USD | USD | USD | USD |
| MSCI ESG fund ratings | ||||||
| ESG rating | Leader | Average | Average | |||
| ESG score | 7.31 | 5.92 | 5.99 | |||
| MSCI supplemental fund metrics | ||||||
| Sustainable Impact Solutions (%). A weighted average of each issuer’s percent of revenues generated from Sustainable Impact Solutions goods and services with positive impact on the society and the environment. | 41.67 | 6.08 | 0.00 | NA | NA | NA |
| Carbon Intensity (tCO2e/$m sales). A weighted average of the carbon intensity of the fund’s holdings. | 736.40 | 139.80 | 38.10 | NA | NA | NA |
| Green Revenues (%). A weighted average of each issuer’s percent of revenue generated by goods and services, including alternative energy, energy efficiency, green building, pollution prevention and sustainable water. | 56.90 | 5.00 | 0.00 | NA | NA | NA |
| Board Independence (%). A weighted average percentage of issuers in the fund that have an independent board of directors. | 77.20 | 78.80 | 70.00 | NA | NA | NA |
| Board Diversity (%). A weighted average percentage of women on the board of the fund’s holdings. | 25.50 | 31.00 | 32.50 | NA | NA | NA |
| UNGC Violations (%). A sum of the weight of issuers in the fund that are in violation of the UN Global Compact principles according to MSCI ESG Research methodology. | 0.00 | 1.40 | 0.00 | NA | NA | NA |
| Very Severe Controversies (OECD) (%). A sum of the weight of issuers in the fund that are facing one or more very severe controverse related to the environment, product quality, human rights, labor rights and governance based on OECD guidelines. | 0.00 | 1.80 | 0.00 | NA | NA | NA |
| Controversial Weapons (%). A sum of the weight of issuers in the fund that have any tie to landmines, cluster munitions, biological, chemical, depleted uranium, or nuclear weapons. | 0.00 | 0.50 | 0.00 | NA | NA | NA |
| Tobacco (%). A sum of the weight of the issuers in the fund that are tobacco producers that derive 5%, as well as tobacco distributors, suppliers, and retailers if the combined revenue is 15% of total revenues. | 0.00 | 0.70 | 0.00 | NA | NA | NA |
This table reports on the considered components of the investment opportunity set. NA denotes not available information because ESG criteria do not apply to the underlying assets of specific ETFs, such as commodities or cryptocurrencies, due to their nature.
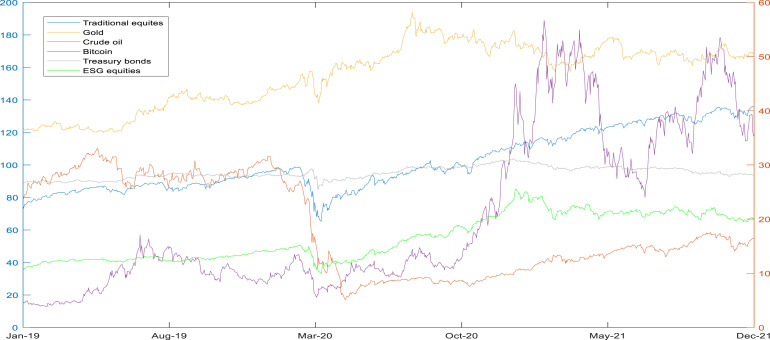
Fig. 1 plots the evolution over time of the daily closing prices for the six selected ETFs. We can observe that all the ETFs share a common pattern, the collapse in their trading prices in mid-March 2020 due to the exponential growth in the COVID-19 spread worldwide and the first global confinements. According to this Figure, assets that had traditionally been considered safe havens or hedge assets ceased to be so during the period in which all correlations between assets increased dramatically. This is a clear example of the increased interconnectedness among financial markets during periods of heightened financial turmoil (Liu et al., 2013, Ferrer et al., 2018, Gong et al., 2019). However, except for crude oil, it seems that the rest of the ETFs have followed an upward trend from the beginning of April until the end of December 2020, coinciding with the relaxation of the health restriction measures and the first green shoots at the economic level.13 At the econometric level, we report that all series behave as random walks with stochastic trend or unit root, so in order to carry out a study of statistical guarantees, a total of 755 daily continuous returns are computed from the first log-differences of the daily ETF closing prices.
Fig. 1.
Daily evolution of closing prices for considered ETFs. This figure reports on the daily closing prices of the different ETF types under study. Gold, crude oil and traditional equity ETF prices are labeled on left -axis and ESG equities, Bitcoin and Treasury bonds ETF prices are labeled on right -axis. Prices are expressed in dollars.
Table 2 provides the summary statistics of the daily continuous returns computed for the different ETF asset classes. We find that Bitcoin exhibits the highest annualized average daily return and standard deviation (volatility) over the sample period, where the high volatility is mainly associated to the sharp price swings observed during the year 2021. As expected, the lowest volatility is related to Treasury bonds, while the lowest average daily return corresponds to crude oil, which is consistent with the daily abrupt falls in price during the first months of 2020. Additionally, ESG stocks reach the second highest average return and the fourth lowest risk exposure in terms of volatility, which undoubtedly confers them a risk-return ratio to be considered and that will be the starting point of our research. Kurtosis coefficients report clear evidence of leptokurtic empirical distributions. The Jarque–Bera test confirms the non-normal distribution of the series by rejecting the null hypothesis of normality for all asset types. The absence of normality in returns will be considered in subsequent sections by assuming the skewed Student’s t distribution in the model fitting. Except for gold and Treasury bonds (for the case of 1 and 2 lags), we find evidence of high autoregressive presence or weak autocorrelation based on the Ljung–Box test for 1, 2 and 5 lags. The Lagrange Multiplier test confirms the presence of strongly significant autocorrelation in squared returns for all the assets under study across different lag orders. Consequently, the estimation of several asymmetric GARCH models is required in the empirical analysis to account for these volatility patterns. The DCC skew Student copula is used to properly adjust the tail dependence. This is consistent with the results of Elie et al. (2019), who highlight the need of examining the tail dependence of gold and crude oil with clean energy stock indices following the financial turmoil, although no major differences are observed when using different copula models.
Table 2.
Descriptive statistics for the log-returns of ETFs over the period January 2019–December 2021.
| ESG equities | Traditional equities | Gold | Crude oil | Bitcoin | Treasury bonds | |
|---|---|---|---|---|---|---|
| Mean | 0.2095 | 0.1996 | 0.1122 | −0.1194 | 0.6796 | 0.0170 |
| Std. Dev. | 0.2478 | 0.2155 | 0.1535 | 0.5005 | 0.8678 | 0.0800 |
| Skewness | −1.1597 | −1.5998 | −0.5615 | −2.4575 | −0.0567 | −2.3093 |
| Kurtosis | 16.6558 | 24.4124 | 7.1785 | 26.4180 | 5.2235 | 32.1727 |
| JB | 5897.23 | 14418.04 | 572.87 | 17618.47 | 150.49 | 26845.58 |
| (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | |
| Q (1) | 6.1233 | 49.5286 | 4.1137 | 7.0031 | 3.4348 | 0.0066 |
| (0.0133)⁎⁎ | (0.0000)⁎⁎⁎ | (0.0425)⁎⁎ | (0.0081)⁎⁎⁎ | (0.0638)⁎ | (0.9353) | |
| Q (2) | 39.1540 | 89.7310 | 4.4068 | 7.1959 | 6.5610 | 6.8129 |
| (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.1104) | (0.0274)⁎⁎ | (0.0376)⁎⁎ | (0.0332)⁎⁎ | |
| Q (5) | 53.3010 | 105.7165 | 15.1863 | 14.2391 | 7.5644 | 23.5130 |
| (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0096)⁎⁎⁎ | (0.0142)⁎⁎ | (0.1819) | (0.0003)⁎⁎⁎ | |
| LM (3) | 228.0688 | 292.3104 | 33.8334 | 60.0007 | 26.5230 | 265.6606 |
| (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | |
| LM (5) | 230.6026098 | 302.0409 | 44.8828 | 79.5120 | 30.4490 | 266.4361 |
| (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | |
| LM (7) | 237.5733 | 333.0872 | 69.1927 | 108.9584 | 30.5883 | 334.0919 |
| (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0000)⁎⁎⁎ | (0.0001)⁎⁎⁎ | (0.0000)⁎⁎⁎ |
This table provides information on the main descriptive statistics of the continuous log-returns for the different assets. The average return (Mean) and the standard deviation (Std. Dev.) of the series are presented in annualized terms, while skewness and kurtosis remain in their daily standard format. Additionally, three tests are conducted to assess the common properties of most financial time-series, namely, non-normality by the Jarque–Bera test (JB), and autocorrelation in the first and second moments by the Ljung–Box () and Lagrange-Multiplier () test statistics, respectively. Note that different lag orders are evaluated, and p-values are presented in parentheses.
Statistical significance at the 10%.
Statistical significance at the 5%.
Statistical significance at the 1%.
5. Empirical analysis
In this section, the minimum variance selection criterion from the DCC skew Student copula approach is applied to obtain the optimal portfolio weights for the combination of clean energy stocks with each asset class: traditional equities, gold, crude oil, Bitcoin and Treasury bonds. The dependence structure between asset returns is completely determined by the dependence structure of the generated uniform variables describing the relationship between the returns according to a given specification. The dependence patterns discussed in this paper are characterized by means of Student’s t-copula that captures the dependence at the center and tails of the distribution. A comprehensive and comparative analysis is then performed between the ESG portfolios and the investment in the aforementioned assets in order to show whether diversification benefits are obtained from the inclusion of clean energy equities in the portfolios. We propose three different portfolio rebalancing strategies, changing the asset allocation every 1, 5 or 22 days by using the conditional covariance matrix estimated in those periods. Section 5.1. details the copula estimation process and its main economic and empirical findings, while Sections 5.2, 5.3 deal with the particularities of portfolio formation and subsequent assessment.
5.1. Model fitting and time-varying copula analysis
To conduct the dependence analysis using the copula approach, it is necessary to know the marginal distribution functions of the returns for the different asset types. For this purpose, we start the process by conducting a time series AR (1) fitting for the returns of the various asset pairs and then we extract the standardized residuals from the resulting GARCH (1,1) models (see Eqs. 9 and 10). From Panel A of Table 3, the estimated parameters of the marginal distributions are analyzed in three steps, namely, mean process, variance equations and distribution fitting.
Table 3.
DCC-skew. Student copula parameters and statistics.
| Panel A: Univariate parameters and statistics | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| assets | ESG equities | Traditional equities | Gold | Crude oil | Bitcoin | Treasury bonds | ||||||
| 0.0011 | (3.2195)⁎⁎⁎ | 0.0009 | (4.0898)⁎⁎⁎ | 0.0004 | (1.2161) | 0.0013 | (1.8101)⁎ | 0.0018 | (0.9911) | 0.0001 | (0.8145) | |
| 0.0102 | (0.2698) | −0.0978 | (−2.8631)⁎⁎⁎ | 0.0429 | (1.4335) | −0.0097 | (−0.2694) | −0.0574 | (−1.523) | −0.0518 | (−1.3301) | |
| 0.0000 | (1.2072) | 0.0000 | (1.469) | 0.0000 | (0.5948) | 0.0000 | (2.9088)⁎⁎⁎ | 0.0002 | (1.725)⁎ | 0.0000 | (0.2379) | |
| 0.1561 | (4.8226)⁎⁎⁎ | 0.2011 | (4.928)⁎⁎⁎ | 0.0767 | (2.7506)⁎⁎⁎ | 0.1214 | (3.6116)⁎⁎⁎ | 0.0596 | (3.2192)⁎⁎⁎ | 0.1341 | (1.3222) | |
| 0.8298 | (24.9766)⁎⁎⁎ | 0.7747 | (19.053)⁎⁎⁎ | 0.8920 | (27.0151)⁎⁎⁎ | 0.8367 | (24.0797)⁎⁎⁎ | 0.8836 | (18.8337)⁎⁎⁎ | 0.7623 | (8.6039)⁎⁎⁎ | |
| 0.8960 | (16.8107)⁎⁎⁎ | 0.7523 | (19.2075)⁎⁎⁎ | 0.8619 | (20.4865)⁎⁎⁎ | 0.8302 | (18.2308)⁎⁎⁎ | 1.0339 | (15.3629)⁎⁎⁎ | 0.9674 | (18.2962)⁎⁎⁎ | |
| 7.0496 | (4.2947)⁎⁎⁎ | 6.5698 | (4.5847)⁎⁎⁎ | 4.4171 | (5.5924)⁎⁎⁎ | 4.7179 | (5.8324)⁎⁎⁎ | 7.3273 | (4.7305)⁎⁎⁎ | 9.4945 | (1.8756)⁎ | |
| Q (1) | 0.7502 | (0.3864) | 2.0610 | (0.1511) | 0.9364 | (0.3332) | 4.6100 | (0.0318)⁎⁎ | 0.3045 | (0.5811) | 0.2374 | (0.6261) |
| Q (2) | 3.4519 | (0.014)⁎⁎ | 2.4590 | (0.0979)⁎ | 1.0993 | (0.6791) | 4.9750 | (0.0005)⁎⁎⁎ | 0.682 | (0.9053) | 0.2867 | (0.9952) |
| Q (5) | 6.1968 | (0.0393)⁎⁎ | 3.2650 | (0.3675) | 2.6763 | (0.5169) | 6.0070 | (0.0463)⁎⁎ | 1.0437 | (0.9401) | 1.0269 | (0.9427) |
| LM (3) | 2.7670 | (0.0962)⁎ | 0.1007 | (0.751) | 0.4107 | (0.5216) | 0.3443 | (0.5573) | 2.2540 | (0.1333) | 7.1460 | (0.0075)⁎⁎⁎ |
| LM (5) | 2.7890 | (0.3219) | 0.5016 | (0.8832) | 0.8539 | (0.7768) | 0.4179 | (0.9076) | 2.6720 | (0.3411) | 7.6230 | (0.0247)⁎⁎ |
| LM (7) | 3.4500 | (0.4329) | 0.7382 | (0.952) | 1.0224 | (0.9099) | 0.4733 | (0.9807) | 3.3050 | (0.4579) | 8.4910 | (0.0408)⁎⁎ |
| Panel B: Joint multivariate parameters and statistics | ||||||||||||
| Traditional equities | Gold | Crude oil | Bitcoin | Treasury bonds | ||||||||
| 0.0225 | (1.7976)⁎ | 0.0125 | (0.7826) | 0.0187 | (2.2352)⁎⁎ | 0.0022 | (0.1069) | 0.0381 | (2.1863)⁎⁎ | |||
| ESG equities - | 0.9322 | (26.4195)⁎⁎⁎ | 0.9128 | (8.2988)⁎⁎⁎ | 0.9666 | (66.8766)⁎⁎⁎ | 0.9106 | (8.9262)⁎⁎⁎ | 0.8875 | (25.2576)⁎⁎⁎ | ||
| 0.0327 | (1.0225) | 0.0270 | (0.5031) | 0.0002 | (0.0279) | 0.0275 | (0.5595) | 0.0109 | (0.4001) | |||
| 9.2256 | (3.2737)⁎⁎⁎ | 11.3598 | (2.3615)⁎⁎ | 20.2953 | (1.7785)⁎ | 10.9250 | (2.3354)⁎⁎ | 21.2065 | (0.6919) | |||
This table provides information about the estimation of the volatility and dependence structure between assets for the period 2019–2021. Panel A reports on the parameter estimation and residual summary statistics for the marginal distributions, the mean and the variance equations of each of the individual assets. Regarding the mean, refers to the unconditional mean the process, whereas denotes the persistence in returns. With respect to the parametrization of the variance process of the different assets, measures the mean reversion of the model, while () refers to persistence in volatility. and are the Ljung–Box and the Lagrange-Multiplier statistics, conducted using and lags to test for the presence of serial correlation in residuals and and lags for squared residuals. Parameters and report on the shape of the skewed Student’s t distribution. Panel B reports on the parameter estimation for the DCC skew Student copula. t-values, presented in parentheses, are computed using robust standard errors.
Statistical significance at the 10%.
Statistical significance at the 5%.
Statistical significance at the 1%.
The estimation results indicate that the model adequately represents the marginal distribution for the returns of the assets. We observe high persistence in volatility, , and low impact of contemporaneous shocks, , which evidences that the selected models accurately reflect the conditional heteroscedasticity of the series. Skewed Student’s t distributions can be used to model the non-normality of asset returns, as the skewness () and kurtosis () parameters are significant in every case. These parameters properly capture the negative asymmetric behavior () of the series under study and the shape parameter, , properly fits the existing jumps and tail dependence. The Ljung–Box () and Lagrange multiplier () tests conducted on standardized and standardized squared innovations, respectively, confirm that the AR (1) and GARCH (1,1) specifications efficiently capture the dynamics and particularities of the marginal distribution of the selected asset classes.14
Given that the dependence structure between assets may change over time, we estimate the copula parameters every day using Eqs. (11), (12), (13), (14), (15), (16), (17), (18). The estimation and PIT transformation of the marginals provide for a great deal of flexibility. Specifically, for estimation purposes we follow the empirical approach, also called pseudo-likelihood (Genest et al., 1995) in which asymptotic properties are established under the assumption that the sequence of is .. The use of this methodology allows us to approximate a distribution with a better fit of the heavy tails of the standardized innovations. Based on the above assumptions, the copula correlation measures are fitted, and the estimated distributions are transformed into uniform distributions through the probability functions obtained to provide the estimates of the copula parameters. From Panel B of Table 3, we report on a positive and statistically significant persistence in the copula parameter, , whereas the Student’s t copula model is mostly negative. Additionally, except for the case of Treasury bonds, we find high statistical significance of the parameters measuring the degree of dependence of ESG and other asset types in the tail of the distribution, , which highlights the adequacy of the selected model and distribution to fit the empirical multivariate connectedness structure between pairs.
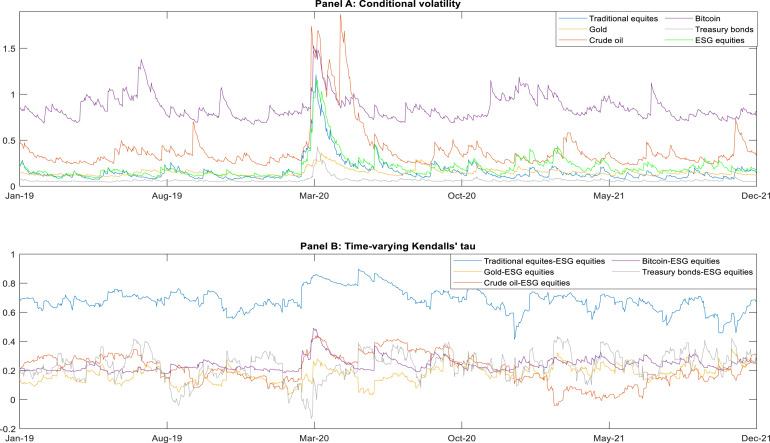
In Panel A of Table 4 we provide the summary statistics of the conditional volatilities for the different asset classes, whereas Panel A of Fig. 2 further depicts the evolution of the time varying heteroscedasticity series over the period 2019–2021. A generally stable trend is observed for most of the assets during the pre-COVID sample period, except for a few notable volatility peaks for Bitcoin in mid-June 2019 and some further rallies by crude oil in mid-September 2019. The WHO’s declaration of the pandemic in March 2020 triggers a surge in volatility for all assets, including the more stable and less risky ones, such as Treasury bonds and gold. Actually, for most of the selected assets, the highest peaks over the sample period are reached in March 2020. Since May 2020 volatility in financial markets starts to recover average pre-pandemic levels as a result of the relaxation of global restrictions and the reactivation of economic activity. However, some remarkable spikes in volatility are experienced by Bitcoin and crude oil during the successive months that can be related to specific market events rather than an external shock affecting all financial markets.15 Volatility for the rest of assets remains relatively stable until the end of the sample in December 2021.
Table 4.
Statistics for the time-varying volatilities and correlations.
| Panel A: Univariate marginals’ distributions. Conditional volatilities | ||||||
|---|---|---|---|---|---|---|
| ESG equities | Traditional equities | Gold | Crude oil | Bitcoin | Treasury bonds | |
| Mean | 0.2096 | 0.1635 | 0.1521 | 0.4006 | 0.8552 | 0.0650 |
| Std. Dev. | 0.1370 | 0.1311 | 0.0405 | 0.2591 | 0.1333 | 0.0340 |
| Max | 1.1543 | 1.2121 | 0.3597 | 1.8701 | 1.5286 | 0.4297 |
| Min | 0.0905 | 0.0720 | 0.1037 | 0.2197 | 0.6723 | 0.0437 |
| Q1 | 0.1371 | 0.0994 | 0.1245 | 0.2775 | 0.7622 | 0.0528 |
| Q2 | 0.1740 | 0.1264 | 0.1437 | 0.3214 | 0.8181 | 0.0581 |
| Q3 | 0.2350 | 0.1757 | 0.1635 | 0.4029 | 0.9236 | 0.0657 |
| Panel B: Multivariate distribution. Time-varying Kendall’s tau | ||||||
| Traditional equities | Gold | Crude oil | Bitcoin | Treasury bonds | ||
| Mean | ESG equities correlation with | 0.6856 | 0.1761 | 0.2131 | 0.2400 | 0.2338 |
| Std. Dev. | 0.0781 | 0.0580 | 0.1034 | 0.0454 | 0.0966 | |
| Max | 0.8971 | 0.3480 | 0.4394 | 0.4903 | 0.4346 | |
| Min | 0.4136 | 0.0300 | −0.0412 | 0.1734 | −0.1295 | |
| Q1 | 0.6418 | 0.1349 | 0.1467 | 0.2067 | 0.1769 | |
| Q2 | 0.6845 | 0.1767 | 0.2149 | 0.2279 | 0.2433 | |
| Q3 | 0.7271 | 0.2137 | 0.2907 | 0.2609 | 0.2961 | |
This table reports on the summary statistics of the trends and patterns described by each of the single asset volatilities (Panel A) and the different dependence structures among asset-ESG pairs in terms of Kendall’s tau (Panel B).
Fig. 2.
Modeling the marginal and multivariate dynamics. This figure presents the outputs of the multivariate model. Panel A reports on the time-varying volatilities obtained from modeling the marginal distributions of the different assets via AR-GARCH specifications. All considered patterns are expressed in annual terms. Panel B represents the time-varying Kendall’s tau dependences resulting from the DCC skew Student copula estimations.
In Panel B of Table 4, we present a summary of the main descriptive statistics for the Kendall’s tau conditional correlations between ESG stocks and the rest of assets. Interestingly, the mean correlation between renewable energy equities and traditional equities is moderate (0.69), which indicates that equity SRI offer some room for diversification for investments in the overall equity market. This result suggests that ESG equities and conventional equities are perceived by investors to some extent as different asset classes despite they belong to the same market. Our findings further extend the studies of Sharma et al. (2022) and Arif et al. (2021), who report on the potential diversifying role of clean energy stocks for conventional stocks during the pandemic by using equities that track the performance of the broad renewable energy sector rather than of a specific clean energy source as we do. In turn, the average correlation between ESG equities and the other asset classes (i.e., gold, crude oil, Bitcoin and Treasuries) is clearly lower (approximately 0.20). This low correlation over the sample period suggests that clean energy equities can serve as a hedge for investments in the commodity, cryptocurrency, and Treasury markets. Panel B of Fig. 2 further details the evolution of the conditional correlations between ESG equities and the rest of assets over the sample period. We find that after the onset of the pandemic, correlations between SRI and some of the assets, such as gold or Treasury bonds, come to fall sharply. However, the opposite occurs subsequently, i.e., a bullish rebound in terms of dependencies is observed for all the asset pairs under investigation, which reflects the increased interconnectedness among financial markets when a global external shock occurs. We observe that the correlation between traditional and ESG equities increases substantially following the pandemic outbreak and returns to its pre-pandemic value of around 0.6 by mid-2020. Interestingly, crude oil and Treasury bonds display occasional negative values in the tau, which is especially evident in March 2020, thus indicating the potential role of clean energy equities as a hedge, or even as a safe haven, during the most acute stages of the pandemic.16 Additionally, this punctual ESG-Treasury negative correlation is particularly compelling given that it indicates a flight-to-safety phenomenon from equities to Treasury bonds during times of crisis.
These findings are consistent with those obtained by Ren and Lucey (2021) from their study of dependence relationships between clean wind energy indices and cryptocurrencies up to October 2020, and those obtained by Kuang (2021) for clean energy indices with other equity assets also for the year 2020. Hence, our results complement the findings reported in these two studies regarding the behavior of ESG equities in comparison to other assets during the COVID-19 outbreak: (1) they are weak diversifiers against traditional equity assets; (2) they represent hedging assets for investors in crypto assets.
5.2. Portfolio construction
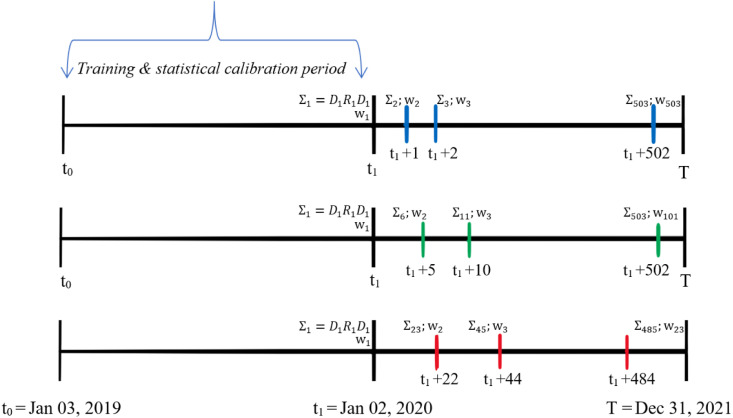
As described in the Methodology section, we conduct two types of conditional portfolio optimization problems (allowing for or constraining short sells) over different frequencies (daily, weekly or monthly). Fig. 3 details the steps to be followed at each frequency to obtain the minimum variance portfolio composition according to the optimization problem type. For the daily rebalancing portfolios, the weights are calculated every business day from January 2020 to December 2021, yielding 503 minimum variance optimizations for each portfolio.17 For the weekly rebalancing portfolio, the weights are rebalanced every 5 workdays, achieving a total of 101 rebalances. Finally, in the monthly rebalancing portfolio the weights are computed every 22 working days, reporting a total of 23 rebalances.
Fig. 3.
Time-varying covariances & portfolio construction. This figure illustrates the three processes associated with portfolio rebalancing in accordance with their frequency: daily, weekly, or monthly. For all cases, our initial training and statistical calibration period is from January 3, 2019, to December 31, 2019, which is designed to ensure consistency and precise estimates for our different GARCH and copula specifications. The rebalancing approaches are driven over the period that spans from January 02, 2020,to December 31, 2021. The upper panel shows the daily rebalancing frequency (blue color) with 503 daily minimum variance optimizations. The middle panel shows the weekly portfolio rebalancing approach (green color) with 101 portfolio optimizations, that is, an optimization every five working days. Finally, the lower panel displays the monthly rebalancing frequency (red color) with 23 time-varying optimization problems, i.e. every 22 working days.. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
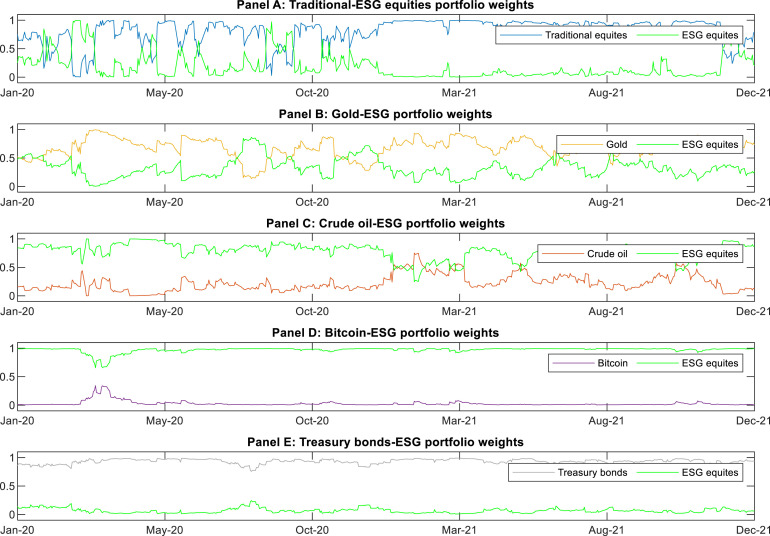
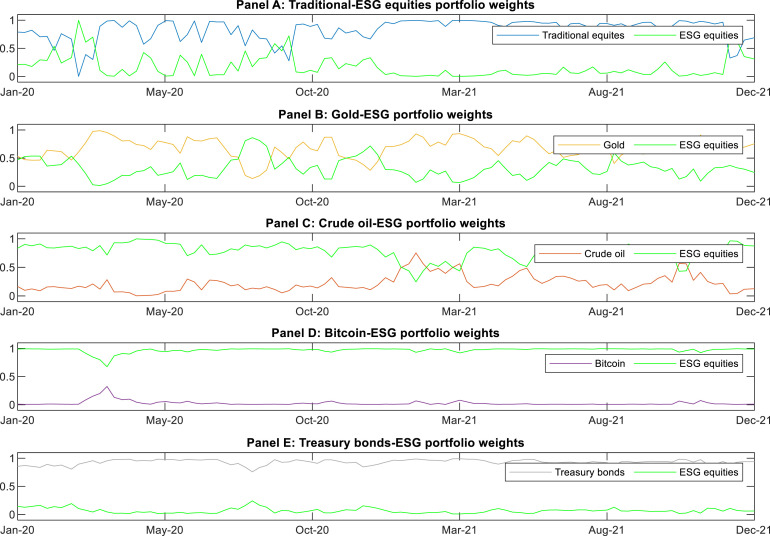
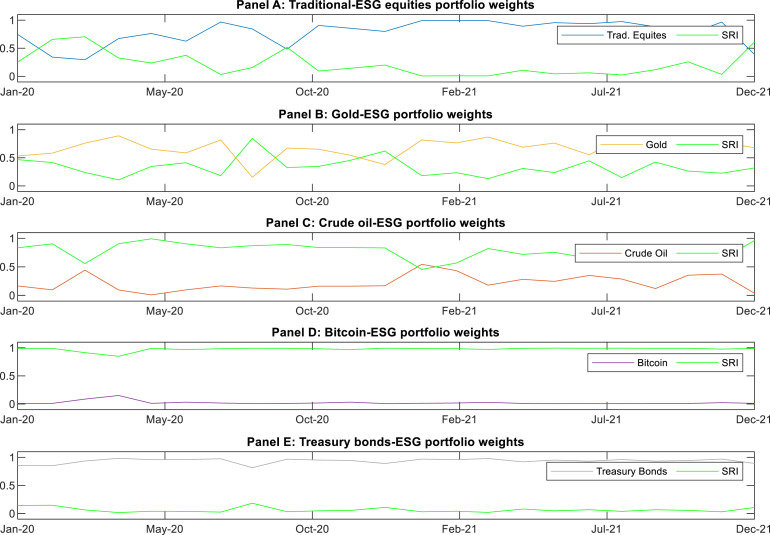
Fig. 4 shows the evolution of portfolio weights in the daily rebalancing optimization problem without short selling in which ESG equities are included, and this is also shown in Appendix A, Appendix B for the weekly and monthly rebalancing exercises, respectively.18 In the case of portfolios containing Bitcoin and Treasury bonds, the relative weights seem to be more clearly established and hardly vary throughout the sample, whereas portfolios including the other three asset classes seem to experience greater variation and even reversals. Portfolios composed of traditional and ESG equities stand out, where the majority of funds are allocated to traditional portfolios, but the situation reverses several times in 2020 and at the end of the sample period. Reversals and the high fluctuations observed in the weights occur less frequently with more realistic rebalancing strategies. By rebalancing the portfolio daily, the portfolio’s composition can be more quickly adjusted to new information, but it is associated with higher transaction costs and justifying portfolio changes becomes more difficult.
Fig. 4.
Dynamic portfolio weights: 1 day rebalance This Figure presents the weight evolution for minimum variance portfolios constructed by combining the ETFs of each asset class and the ETF of ESG equities over the years 2020 and 2021 for the 1 day rebalance under constrained portfolios.
Table 5 presents the summary statistics relating to the dynamic rebalancing of different portfolio weightings. In each panel, information is provided regarding the different rebalancing frequencies of each pair of asset classes, both in the case of short selling restrictions as well as in the case that short positions are allowed. The differences in weights between the constrained portfolios and those that allow for short sales are small in average terms. Short positions in ESG equities occur with some frequency in portfolios that include both traditional and ESG equities, however, affecting the first quartile of cases. It is during such periods of high positive correlation that it becomes necessary to take short positions in one of the two assets in order to minimize portfolio risk.
SRI play a critical role in reducing portfolio risk exposure, which is best demonstrated when paired with gold, crude oil, or Bitcoin. With gold, ESG equities make up approximately one third of the minimum variance portfolios; with crude oil, almost 80%; and with Bitcoin, almost all of the portfolio (roughly 97%). Conversely, the lowest average weightings for SRI are allocated to traditionally safe assets such as Treasury bonds, where SRI will act not so much to reduce their risk, but to improve the risk-return ratio of the overall portfolio. According to the standard deviation, the very high weights in the portfolio with Bitcoin and very low weights in the portfolios with Treasuries are also very stable over time. Portfolio compositions with gold, crude oil, and in particular traditional equities, are observed to be the most unstable, as shown in Fig. 4. Overall, there are very small differences in the average weights across rebalancing frequencies, which supports the robustness of these results.
Table 5.
Descriptive statistics for the dynamic minimum variance-DCC copula portfolio weights.
| Panel A: 1 day rebalance | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stat. | Traditional + ESG equities |
Gold + ESG equities |
Crude oil + ESG equities |
Bitcoin + ESG equities |
Treasury bonds + ESG equities |
|||||||||||||||
| Constrained |
Short selling |
Constrained |
Short selling |
Constrained |
Short selling |
Constrained |
Short selling |
Constrained |
Short selling |
|||||||||||
| Equity | ESG | Equity | ESG | Gold | ESG | Gold | ESG | Oil | ESG | Oil | ESG | Bitcoin | ESG | Bitcoin | ESG | T. bonds | ESG | T. bonds | ESG | |
| Mean | 0.81 | 0.19 | 0.88 | 0.12 | 0.68 | 0.32 | 0.68 | 0.32 | 0.22 | 0.78 | 0.22 | 0.78 | 0.03 | 0.97 | 0.02 | 0.98 | 0.93 | 0.07 | 0.97 | 0.03 |
| Std. Dev. | 0.23 | 0.23 | 0.29 | 0.29 | 0.17 | 0.17 | 0.17 | 0.17 | 0.14 | 0.14 | 0.15 | 0.15 | 0.05 | 0.05 | 0.05 | 0.05 | 0.04 | 0.04 | 0.05 | 0.05 |
| Max. | 1.00 | 0.99 | 1.39 | 1.22 | 1.00 | 0.86 | 1.01 | 0.87 | 0.75 | 1.00 | 0.75 | 1.03 | 0.34 | 1.00 | 0.34 | 1.02 | 0.99 | 0.24 | 1.05 | 0.22 |
| Min. | 0.01 | 0.00 | −0.22 | −0.39 | 0.14 | 0.00 | 0.13 | −0.01 | 0.00 | 0.25 | −0.03 | 0.25 | 0.00 | 0.66 | −0.02 | 0.66 | 0.76 | 0.01 | 0.78 | −0.05 |
| Q1 | 0.71 | 0.03 | 0.71 | −0.09 | 0.58 | 0.20 | 0.58 | 0.19 | 0.12 | 0.70 | 0.12 | 0.70 | 0.01 | 0.97 | −0.01 | 0.98 | 0.91 | 0.03 | 0.95 | −0.01 |
| Q2 | 0.90 | 0.10 | 0.95 | 0.05 | 0.69 | 0.31 | 0.70 | 0.30 | 0.19 | 0.81 | 0.19 | 0.81 | 0.01 | 0.99 | 0.00 | 1.00 | 0.94 | 0.06 | 0.98 | 0.02 |
| Q3 | 0.97 | 0.29 | 1.09 | 0.29 | 0.80 | 0.42 | 0.81 | 0.42 | 0.30 | 0.88 | 0.30 | 0.88 | 0.03 | 0.99 | 0.02 | 1.01 | 0.97 | 0.09 | 1.01 | 0.05 |
| Panel B: 5 days rebalance | ||||||||||||||||||||
| Stat. | Traditional + ESG equities |
Gold + ESG equities |
Crude oil + ESG equities |
Bitcoin + ESG equities |
Treasury bonds + ESG equities |
|||||||||||||||
| Constrained |
Short selling |
Constrained |
Short selling |
Constrained |
Short selling |
Constrained |
Short selling |
Constrained |
Short selling |
|||||||||||
| Equity | ESG | Equity | ESG | Gold | ESG | Gold | ESG | Oil | ESG | Oil | ESG | Bitcoin | ESG | Bitcoin | ESG | T. bonds | ESG | T. bonds | ESG | |
| Mean | 0.83 | 0.17 | 0.91 | 0.09 | 0.68 | 0.32 | 0.68 | 0.32 | 0.22 | 0.78 | 0.22 | 0.78 | 0.03 | 0.97 | 0.02 | 0.98 | 0.93 | 0.07 | 0.97 | 0.03 |
| Std. Dev. | 0.20 | 0.20 | 0.26 | 0.26 | 0.17 | 0.17 | 0.18 | 0.18 | 0.15 | 0.15 | 0.15 | 0.15 | 0.04 | 0.04 | 0.05 | 0.05 | 0.04 | 0.04 | 0.05 | 0.05 |
| Max. | 1.00 | 1.00 | 1.39 | 1.19 | 0.99 | 0.86 | 0.99 | 0.87 | 0.75 | 1.00 | 0.75 | 1.01 | 0.32 | 1.00 | 0.32 | 1.02 | 0.99 | 0.24 | 1.05 | 0.23 |
| Min. | 0.00 | 0.00 | −0.19 | −0.39 | 0.14 | 0.01 | 0.13 | 0.01 | 0.00 | 0.25 | −0.01 | 0.25 | 0.00 | 0.68 | −0.02 | 0.68 | 0.76 | 0.01 | 0.77 | −0.05 |
| Q1 | 0.74 | 0.03 | 0.75 | −0.10 | 0.58 | 0.20 | 0.58 | 0.19 | 0.12 | 0.72 | 0.12 | 0.72 | 0.01 | 0.97 | −0.01 | 0.97 | 0.92 | 0.03 | 0.95 | −0.01 |
| Q2 | 0.91 | 0.09 | 0.98 | 0.02 | 0.69 | 0.31 | 0.70 | 0.30 | 0.19 | 0.81 | 0.19 | 0.81 | 0.01 | 0.99 | 0.00 | 1.00 | 0.94 | 0.06 | 0.98 | 0.02 |
| Q3 | 0.97 | 0.26 | 1.10 | 0.25 | 0.80 | 0.42 | 0.81 | 0.42 | 0.28 | 0.88 | 0.28 | 0.88 | 0.03 | 0.99 | 0.03 | 1.01 | 0.97 | 0.08 | 1.01 | 0.05 |
| Panel C: 22 days rebalance | ||||||||||||||||||||
| Stat. | Traditional + ESG equities |
Gold + ESG equities |
Crude oil + ESG equities |
Bitcoin + ESG equities |
Treasury bonds + ESG equities |
|||||||||||||||
| Constrained |
Short selling |
Constrained |
Short selling |
Constrained |
Short selling |
Constrained |
Short selling |
Constrained |
Short selling |
|||||||||||
| Equity | ESG | Equity | ESG | Gold | ESG | Gold | ESG | Oil | ESG | Oil | ESG | Bitcoin | ESG | Bitcoin | ESG | T. bonds | ESG | T. bonds | ESG | |
| Mean | 0.79 | 0.21 | 0.85 | 0.15 | 0.67 | 0.33 | 0.67 | 0.33 | 0.22 | 0.78 | 0.21 | 0.79 | 0.02 | 0.98 | 0.01 | 0.99 | 0.94 | 0.06 | 0.98 | 0.02 |
| Std. Dev. | 0.21 | 0.21 | 0.27 | 0.27 | 0.17 | 0.17 | 0.17 | 0.17 | 0.14 | 0.14 | 0.14 | 0.14 | 0.03 | 0.03 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 |
| Max. | 0.99 | 0.70 | 1.20 | 0.71 | 0.89 | 0.85 | 0.89 | 0.85 | 0.54 | 0.99 | 0.55 | 1.00 | 0.15 | 0.99 | 0.15 | 1.01 | 0.98 | 0.18 | 1.04 | 0.16 |
| Min. | 0.30 | 0.01 | 0.29 | −0.20 | 0.15 | 0.11 | 0.15 | 0.11 | 0.01 | 0.46 | 0.00 | 0.45 | 0.01 | 0.85 | −0.01 | 0.85 | 0.82 | 0.02 | 0.84 | −0.04 |
| Q1 | 0.67 | 0.03 | 0.67 | −0.08 | 0.58 | 0.23 | 0.58 | 0.22 | 0.11 | 0.65 | 0.10 | 0.65 | 0.01 | 0.98 | −0.01 | 0.98 | 0.92 | 0.03 | 0.96 | −0.01 |
| Q2 | 0.86 | 0.14 | 0.89 | 0.11 | 0.68 | 0.32 | 0.68 | 0.32 | 0.17 | 0.83 | 0.16 | 0.84 | 0.01 | 0.99 | 0.00 | 1.00 | 0.95 | 0.05 | 0.99 | 0.01 |
| Q3 | 0.97 | 0.33 | 1.08 | 0.33 | 0.77 | 0.42 | 0.78 | 0.42 | 0.35 | 0.89 | 0.35 | 0.90 | 0.02 | 0.99 | 0.02 | 1.01 | 0.97 | 0.08 | 1.01 | 0.04 |
5.3. Performance assessment
We determine the performance of our strategies over the years 2020 and 2021 based on the returns resulting from holding minimum variance portfolios until the time of the next rebalancing, i.e. the next day, the next week, or the next month. Subsequently, once we have obtained all the series of portfolio returns calculated at one point in time (see Eq. (19)), we calculate the different performance measures for the overall 2020–2021 period and analyze them in a simple way multiplying by the relevant factors due to the well-proven properties of log-returns.
In Table 6, the summary statistics for the observed returns are shown in the top four rows of each panel and the most common performance measures are shown in the lower six rows of each panel. Three columns provide the information of each asset class, depicting the case for holding the asset separately, the case for combining that asset with SRI and constraining short selling, and the case for combining that asset with ESG stocks in portfolios allowing for short selling. Each panel discloses the information according to the rebalancing frequency of the optimal portfolios.
Table 6.
In-sample pandemic performance assessment.
| Panel A: 1 day rebalance | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stat. | Tradicional equities | Traditional + ESG equities |
Gold | Gold + ESG equities |
Crude oil | Crude oil + ESG equities |
Bitcoin | Bitcoin + ESG equities |
Treasury bonds | Treasury bonds + ESG equities |
|||||
| Constr. | Short S. | Constr. | Short S. | Constr. | Short S. | Constr. | Short S. | Constr. | Short S. | ||||||
| Mean | 0.1716 | 0.1959 | 0.2036 | 0.0827 | 0.1172 | 0.1172 | −0.3109 | 0.1405 | 0.1408 | 0.7462 | 0.2053 | 0.2025 | −0.0014 | 0.0050 | −0.0086 |
| Std. Dev. | 0.2510 | 0.2512 | 0.2517 | 0.1691 | 0.1521 | 0.1520 | 0.5730 | 0.3054 | 0.3059 | 0.8748 | 0.2960 | 0.2959 | 0.0916 | 0.0907 | 0.0901 |
| Skewness | −1.4741 | −1.7205 | −1.7100 | −0.6114 | −0.3897 | −0.3853 | −2.4479 | −2.7767 | −2.7860 | −0.1032 | −1.3821 | −1.3796 | −2.2972 | −2.4496 | −2.4691 |
| Kurtosis | 19.8228 | 21.0097 | 20.9547 | 6.8633 | 6.8938 | 6.9130 | 22.6506 | 25.4899 | 25.5349 | 5.3912 | 14.8262 | 14.8285 | 28.0057 | 29.1648 | 29.8328 |
| Sharpe | 0.6767 | 0.7729 | 0.8022 | 0.4791 | 0.7590 | 0.7596 | −0.5456 | 0.4543 | 0.4546 | 0.8511 | 0.6877 | 0.6783 | −0.0340 | 0.0364 | −0.1151 |
| Kappa 1 | 0.1554 | 0.1820 | 0.1903 | 0.0911 | 0.1447 | 0.1449 | −0.1092 | 0.1008 | 0.1009 | 0.1495 | 0.1422 | 0.1400 | −0.0031 | 0.0114 | −0.0195 |
| Kappa 2 | 0.9031 | 1.0221 | 1.0623 | 0.6614 | 1.0634 | 1.0646 | −0.6568 | 0.5704 | 0.5706 | 1.2509 | 0.9274 | 0.9152 | −0.0191 | 0.0703 | −0.1207 |
| Kappa 3 | 1.2678 | 1.4143 | 1.4692 | 1.1074 | 1.8117 | 1.8132 | −0.9253 | 0.7747 | 0.7747 | 2.1864 | 1.3522 | 1.3339 | −0.0255 | 0.0939 | −0.1608 |
| Kappa 4 | 1.3886 | 1.5486 | 1.6087 | 1.3430 | 2.2093 | 2.2111 | −1.0135 | 0.8365 | 0.8366 | 2.6152 | 1.4904 | 1.4703 | −0.0270 | 0.0987 | −0.1691 |
| Omega | 1.1554 | 1.1820 | 1.1903 | 1.0911 | 1.1447 | 1.1449 | 0.8908 | 1.1008 | 1.1009 | 1.1495 | 1.1422 | 1.1400 | 0.9969 | 1.0114 | 0.9805 |
| Panel B: 5 days rebalance | |||||||||||||||
| Stat. | Tradicional equities | Traditional + ESG equities |
Gold | Gold + ESG equities |
Crude oil | Crude oil + ESG equities |
Bitcoin | Bitcoin + ESG equities |
Treasury bonds | Treasury bonds + ESG equities |
|||||
| Constr. | Short S. | Constr. | Short S. | Constr. | Short S. | Constr. | Short S. | Constr. | Short S. | ||||||
| Mean | 0.1716 | 0.1935 | 0.1960 | 0.0827 | 0.1041 | 0.1037 | −0.3109 | 0.2094 | 0.2099 | 0.7462 | 0.2082 | 0.2040 | −0.0014 | −0.0012 | −0.0137 |
| Std. Dev. | 0.2510 | 0.2509 | 0.2512 | 0.1691 | 0.1573 | 0.1572 | 0.5730 | 0.2839 | 0.2838 | 0.8748 | 0.2962 | 0.2959 | 0.0916 | 0.0905 | 0.0899 |
| Skewness | −1.4741 | −1.6064 | −1.5883 | −0.6114 | −0.6009 | −0.6057 | −2.4479 | −1.8855 | −1.8823 | −0.1032 | −1.2578 | −1.2460 | −2.2972 | −2.5340 | −2.5498 |
| Kurtosis | 19.8228 | 20.2632 | 20.1673 | 6.8633 | 7.6933 | 7.6790 | 22.6506 | 17.2420 | 17.2181 | 5.3912 | 14.0910 | 14.0497 | 28.0057 | 29.9647 | 30.5309 |
| Sharpe | 0.6767 | 0.7645 | 0.7735 | 0.4791 | 0.6508 | 0.6487 | −0.5456 | 0.7313 | 0.7335 | 0.8511 | 0.6971 | 0.6833 | −0.0340 | −0.0324 | −0.1714 |
| Kappa 1 | 0.1554 | 0.1793 | 0.1824 | 0.0911 | 0.1240 | 0.1236 | −0.1092 | 0.1578 | 0.1582 | 0.1495 | 0.1441 | 0.1406 | −0.0031 | −0.0027 | −0.0306 |
| Kappa 2 | 0.9031 | 1.0153 | 1.0284 | 0.6614 | 0.8997 | 0.8964 | −0.6568 | 0.9523 | 0.9553 | 1.2509 | 0.9454 | 0.9275 | −0.0191 | −0.0166 | −0.1904 |
| Kappa 3 | 1.2678 | 1.4141 | 1.4331 | 1.1074 | 1.4959 | 1.4903 | −0.9253 | 1.3583 | 1.3628 | 2.1864 | 1.3901 | 1.3643 | −0.0255 | −0.0222 | −0.2536 |
| Kappa 4 | 1.3886 | 1.5529 | 1.5739 | 1.3430 | 1.7729 | 1.7667 | −1.0135 | 1.5124 | 1.5174 | 2.6152 | 1.5403 | 1.5116 | −0.0270 | −0.0233 | −0.2664 |
| Omega | 1.1554 | 1.1793 | 1.1824 | 1.0911 | 1.1240 | 1.1236 | 0.8908 | 1.1578 | 1.1582 | 1.1495 | 1.1441 | 1.1406 | 0.9969 | 0.9973 | 0.9694 |
| Panel C: 22 days rebalance | |||||||||||||||
| Stat. | Traditional equities | Traditional + ESG equities |
Gold | Gold + ESG equities |
Crude oil | Crude oil + ESG equities |
Bitcoin | Bitcoin + ESG equities |
Treasury bonds | Treasury bonds + ESG equities |
|||||
| Constr. | Short S. | Constr. | Short S. | Constr. | Short S. | Constr. | Short S. | Constr. | Short S. | ||||||
| Mean | 0.1716 | 0.2081 | 0.2244 | 0.0827 | 0.1252 | 0.1240 | −0.3109 | 0.1187 | 0.1209 | 0.7462 | 0.2035 | 0.1984 | −0.0014 | 0.0058 | −0.0056 |
| Std. Dev. | 0.2510 | 0.2515 | 0.2516 | 0.1691 | 0.1632 | 0.1634 | 0.5730 | 0.3070 | 0.3069 | 0.8748 | 0.2956 | 0.2954 | 0.0916 | 0.0904 | 0.0899 |
| Skewness | −1.4741 | −1.6000 | −1.6114 | −0.6114 | −0.4574 | −0.4639 | −2.4479 | −2.7531 | −2.7520 | −0.1032 | −1.3450 | −1.3410 | −2.2972 | −2.5171 | −2.5023 |
| Kurtosis | 19.8228 | 20.5453 | 20.5747 | 6.8633 | 8.4552 | 8.4491 | 22.6506 | 25.6910 | 25.6939 | 5.3912 | 14.5685 | 14.5794 | 28.0057 | 30.0559 | 30.2000 |
| Sharpe | 0.6767 | 0.8203 | 0.8852 | 0.4791 | 0.7563 | 0.7485 | −0.5456 | 0.3812 | 0.3883 | 0.8511 | 0.6825 | 0.6659 | −0.0340 | 0.0448 | −0.0819 |
| Kappa 1 | 0.1554 | 0.1922 | 0.2093 | 0.0911 | 0.1464 | 0.1449 | −0.1092 | 0.0844 | 0.0860 | 0.1495 | 0.1410 | 0.1372 | −0.0031 | 0.0130 | −0.0126 |
| Kappa 2 | 0.9031 | 1.0888 | 1.1752 | 0.6614 | 1.0609 | 1.0492 | −0.6568 | 0.4819 | 0.4909 | 1.2509 | 0.9189 | 0.8967 | −0.0191 | 0.0808 | −0.0787 |
| Kappa 3 | 1.2678 | 1.5170 | 1.6359 | 1.1074 | 1.7501 | 1.7304 | −0.9253 | 0.6515 | 0.6635 | 2.1864 | 1.3470 | 1.3143 | −0.0255 | 0.1076 | −0.1049 |
| Kappa 4 | 1.3886 | 1.6660 | 1.7967 | 1.3430 | 2.0639 | 2.0414 | −1.0135 | 0.7009 | 0.7137 | 2.6152 | 1.4926 | 1.4564 | −0.0270 | 0.1127 | −0.1099 |
| Omega | 1.1554 | 1.1922 | 1.2093 | 1.0911 | 1.1464 | 1.1449 | 0.8908 | 1.0844 | 1.0860 | 1.1495 | 1.1410 | 1.1372 | 0.9969 | 1.0130 | 0.9874 |
This table reports on the summary statistics of the observed returns (top four rows) and different performance measures (low six rows) for the various strategies under study. Portfolio assessment is divided into constrained (Constr.) and not constrained short selling (short S.). The information regarding the different rebalancing frequencies is clearly divided into three sections: Panel A describes the daily evaluation, while Panels B and C detail the weekly and monthly assessments, respectively. By rows the information could be divided into three categories: statistics of the four order moments of the distribution, classical performance ratios (Sharpe) and downside risk measures (Kappa and Omega indices).
We find that even the statistics of the raw returns for the ESG portfolios show some relevant results. Interestingly, the combination of ESG equities with almost all the asset class increases the mean return and reduces the risk, as measured by the standard deviation. In the case of Bitcoin, the behavior is quite different. By combining Bitcoin portfolios with ESG stocks, the portfolio return is reduced to a third of what it would be if you invested exclusively in Bitcoin, but the associated risk is also reduced to a third. It is also noteworthy that, when combining crude oil with ESG stocks, the average return is substantially higher, and the risk can be cut in half. Consequently, SRI become an important means of diversification during the pandemic turmoil and subsequent period since it can be used to reduce risk exposure in every asset combination. These results are consistent, regardless of the rebalancing frequency being considered.
The performance metric analysis considers the classic Sharpe ratio that is based on standard deviation as the risk measure, and Kappa and Omega downside risk measures which only consider deviations towards the left tail as risk, i.e., losses above the threshold.19 In terms of Sharpe ratios, large enhancements in terms of the risk-return relationship are observed almost in all cases. The exception is to include ESG stocks in a Bitcoin or Treasury bond portfolio that allows short selling since these portfolios do not improve performance. For all other cases, the relevant improvements are remarkably high with respect to gold and crude oil. Despite being more discreet in the case of traditional equities (Sharpe ratio increases by 15%), are especially relevant. Traditional equity portfolios are not a single asset, they are a well-diversified portfolio, where reducing risks and increasing returns is a very complex task that ESG stocks contribute to achieve.
The performance results offered by the downside risk measures are consistent with those obtained for the Sharpe ratio. By calculating the risk associated to negative returns, we find that the inclusion of ESG equities can improve the performance of the portfolios. For all asset classes, the results are similar to those obtained when using traditional performance measures; however, the result in the case of Bitcoin stands out. While according to the Sharpe ratio, Bitcoin’s performance deteriorates when combined with ESG equities, no differences are observed in terms of performance for Bitcoin before and after it is combined with clean energy equities for several measures of downside risk. Therefore, once extreme negative returns are considered, our results reveal that SRI cannot only serve to reduce the risk of investing in Bitcoin, but also to maintain its financial performance.
Overall, the empirical findings in this study support the fact that, beyond providing diversification and hedge protection, the inclusion of ESG assets increases the portfolio performance significantly. Our findings on the role of ESG equities as diversifiers and hedge assets are consistent with previous studies that consider some of the assets that we examine (Elie et al., 2019, Kuang, 2021, Tareq et al., 2021, Gustafsson et al., 2022). Additionally, our results based on portfolio performance analysis are also in line with those obtained by Kuang (2021) and Gustafsson et al. (2022). Kuang (2021) compares the performance of ESG assets against dirty energy stocks and international equity indices from passive portfolios with constant weights, analyzing downside risk measures. In turn, Gustafsson et al. (2022) examine energy metals and precious metals as potential safe havens for clean energy assets by examining optimal hedge ratios and risk. Therefore, our study extends the previous literature’s analysis of the role of SRI during times of crisis. Considering clean energy equities and paying particular attention to tail risks, we examine both risk reduction and portfolio performance through active management and rebalancing with different frequencies. Incorporating ESG equities to portfolios with very diverse asset classes improves their financial performance in a significant way.
6. Conclusions and remarks
Our study evaluates the diversification benefits in terms of risk reduction and performance improvement associated with combining renewable energy equities with a variety of asset classes. As the COVID-19 pandemic unfolds, the potential role of ESG stocks as diversifiers, hedges, and even safe havens is examined from the perspective of extreme tail dependence. We also analyze the impact of including SRI in actively managed portfolios with different rebalancing frequencies. These portfolios contain other asset classes, including conventional equities, Treasury bonds, crude oil, gold, and cryptocurrencies. By analyzing the case of clean energy equities in market periods of exceptional volatility, this paper contributes to the literature on the hedging properties of ESG assets across a variety of asset classes and on the downside risk measure behavior of portfolios that include these assets. As a result of the shortage of related empirical research covering the COVID-19 outbreak, this study employs an AR (1)-GARCH (1,1) approach to model the marginal distributions, and a DCC skew Student copula method to fit the conditional dependencies via Kendall’s tau. The conditional covariances for each ESG-asset combination are used to calculate a minimum variance portfolio rebalancing process that alternately allows and restricts short positions. In this study, we measure the benefits of combining clean energy stocks with individual assets in terms of overall risk-return (Sharpe ratio) and downside risk-return (Kappa ratio and Omega ratio).
First, from the perspective of risk, high individual risk and dependence between different asset classes are evident on the ongoing of the pandemic, which supports the expanded view of greater interconnectedness between financial markets during times of high market volatility. However, clean energy stocks may be able to provide a relevant degree of diversification in the overall equity market over the whole period 2020–2021. Moreover, clean energy stocks can be used as a diversifier and a hedge for investments in commodities, cryptocurrencies, and Treasury securities, since the correlation with them is very low (roughly 0.20). According to the minimum variance portfolio analysis, SRI can be used for diversification during the pandemic turmoil and subsequent period since it can be used as a tool to reduce risk exposure across all asset combinations and for every frequency of rebalancing.
Second, from the point of view of performance, adding ESG stocks improves portfolio performance for almost all asset classes, particularly with regard to gold and crude oil. Although the relative improvement in traditional equities (the Sharpe ratio increases by 15%) is more subtle, it is especially relevant since the proxy of traditional equities is per se a widely diversified portfolio. Downside risk measures also provide results that support those obtained for the Sharpe ratio. In addition, although Bitcoin’s performance deteriorates when combined with ESG stocks according to the Sharpe ratio, when considering negative extreme returns, SRI are not only able to mitigate the risks of investing in Bitcoin, but also to preserve its performance.
The results on the diversifying benefits of clean energy assets may help to design optimal policies to accelerate the transition to a more sustainable economy. Policy actions are essential to achieving global environmental and climate targets in the sense of promoting renewable energy systems and supporting capital mobilization for sustainable investments. Policy makers must understand the impact that external shocks, like the ongoing sanitary crisis, may have on the demand for green financial instruments in order to reinforce the relevance of supportive policies in the field of sustainable financing. Beyond environmental concerns, the results of this study suggest that in times of financial turmoil investors are likely to demand renewable energy assets for diversification or hedging purposes. Moreover, the methodological approach we follow amplifies the relevance of our results to policy makers and investors because the correlation and portfolio performance analysis considers the presence of extreme down movements in the selected assets, which is especially suitable in a period of financial instability such as the COVID-19 crisis.
Finally, this study leaves open several avenues for future research. In particular, it urges further insight into the performance of ESG portfolios by considering other green assets. For instance, clean energy stocks that provide broader exposure to the renewable energy sector, green bonds that account for the performance of the ESG fixed income market or even the brand-new green cryptocurrencies, which offer exposure to the speculative market of digital currencies but with a focus on reducing energy consumption in the mining process. Recent events have brought the need to accelerate the green energy transition to the forefront, so it also encourages investigating the effects of these events on the diversifier properties of renewable energy equities.
Footnotes
This work was supported by Ministerio de Economía, Industria y Competitividad (ECO 2017-89715-P), Universidad de Castilla-La Mancha 2020-GRIN-28832, co-financed with FEDER funds) and Excma. Diputación Provincial de Albacete – UCLM (DIPUAB-2021-4, Proyectos de I + D + i para jóvenes investigadores 2021).
Alternatively, a strong (weak) hedge is an asset that is negatively correlated on average (uncorrelated) with the other asset but does not necessarily reduce losses in extreme market conditions.
On the one hand, unlike ETF shares, open-end fund shares are not traded on an exchange and, hence, cannot be bought and sold continuously through the trading day at market prices. Additionally, Pavlova and de Boyrie (2022) argue that ETFs not only provide higher transparency and flexibility to all day trading than conventional open-end funds, but also often have lower costs and provide higher tax-efficiency. The stock indices, on the other hand, cannot be directly invested in.
Based on the EU Taxonomy, environmentally sustainable economic activities are those that make a substantial contribution to or do no significant harm to any of the six EU environmental objectives, namely, climate change mitigation, climate change adaptation, sustainable use and protection of water and marine resources, transition to a circular economy, pollution prevention and control, and protection and restoration of biodiversity and ecosystems.
In order to provide a more focused review of the relevant literature on the safe haven role of considered assets, we concentrate on studies circumscribed to the COVID-19 pandemic period. With reference to other periods encompassing other crisis episodes, some of the following studies offer insights into the hedging benefits of investments involving crude oil (Aloui et al., 2013, Junttila et al., 2018, Corbet et al., 2020a), gold (Baur and McDermott, 2010, Agyei-Ampomah et al., 2014, Mensi et al., 2018, Talbi et al., 2021), cryptocurrencies (Kristoufek, 2013, Chowdhury, 2016, Bouri et al., 2017a, Bouri et al., 2017b, Ji et al., 2020) SG assets (Sadorsky, 2014, Ferrer et al., 2018, Elie et al., 2019, Dutta et al., 2020, Iglesias-Casal et al., 2020, Umar et al., 2020, Tareq et al., 2021) against diverse securities. Please note that although some studies on SRI are focused from the perspective of reducing the risk of investments in ESG assets by combining them with other assets instead of the other way round (Elie et al., 2019, Dutta et al., 2020), inferences from the dependence and correlation analyses are equally valid.
Specifically, studies as Sahamkhadam et al. (2018) focus on the minimum variance problem under the assumption of copula models to fit the conditional covariances between asset pairs.
These and other models are explained more in detail in Appendix.
Several studies show that simple and traditional models, such as ARCH (1) or GARCH (1,1), provide better results than more complex extensions of these basic models for different purposes and data samples (Bollerslev, 1987, Hansen and Lunde, 2005, Harvey et al., 1994).
The series are quoted in internal rates of return (IRR). Then, zero-coupon bond prices are calculated from the former time series. Finally, the risk-free rate is approximated from the average of the daily returns calculated from zero-coupon bond prices.
The of order is computed as: , where is the return of the considered portfolio over the sample period and is the probability density function of portfolio returns.
The Kappa index of order 2 is extensively evidenced to coincide with the Sortino ratio (Sortino and Van der Meer, 1991), while Omega corresponds to Kappa index of order 1 plus one (Bertrand and Prigent, 2011).
MSCI ESG fund ratings range from leader (AAA, AA), average (A, BBB, BB) to laggard (B, CCC) based on the exposure of funds’ holdings to ESG risk and its management by issuer companies in comparison to peers. See https://www.msci.com/our-solutions/esg-investing/esg-fund-ratings.
In previous crisis periods, crude oil was considered a safe haven asset. It behaves differently during these turbulent times since severe geographical and mobility restrictions influenced the generalized decline in crude oil prices during several months of 2020.
Note that both for the case of standardized residuals and standardized squared residuals, we hardly find autocorrelation for some lag orders and for very few assets.
Regarding Bitcoin, evidence of increased volatility in the first half of 2021 can be associated with the Tesla’s announcement in February, in which Elon Musk made public a strong investment of $1.5 billion in Bitcoin along with the acceptance of this digital currency as a method of payment for his vehicles, and China’s ban on Bitcoin as a means of payment since late June. Also contributing to a gloomy mood in the crypto markets is the emerging ESG narrative surrounding bitcoin’s proof-of-work consensus mechanism and the negative regulatory undertones from the Financial Action Task Force, the intergovernmental watchdog on anti-money laundering. As for the crude oil market, the steep surge in volatility observed at the end of the sample period is partially driven by supply and price shocks in competing resources and damages in oil infrastructures caused by Hurricanes Ida and Nicholas.
To be classified as a safe haven against other securities, an asset should be evaluated based on the observation of negative correlations over successive crisis intervals (Baur and Lucey, 2010).
We discard 2019 for our portfolio formation, understanding that this year only plays the role of training and calibration period to properly fit the econometric models. As suggested by Hwang and Valls Pereira (2006), parameter estimation of GARCH and copula specifications can be biased in small samples and thus, a window as the one conducted in the present research of more than 500 workdays is recommended.
For the sake of brevity, dynamic portfolio weights that allow for short positions are not plotted in the current study but can be provided upon request.
We consider zero as threshold for the Kappa indices.
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.eap.2022.05.001.
Appendix A. Dynamic portfolio weights: 5 day rebalance
This Fig. A.1 presents the weight evolution for minimum variance portfolios constructed by combining the ETFs of each asset class and the ETF of ESG equities over the years 2020 and 2021 for the 5 day rebalance under constrained portfolios.
Fig. A.1.
Appendix B. Dynamic portfolio weights: 22 day rebalance
This Fig. B.1 presents the weight evolution for minimum variance portfolios constructed by combining the ETFs of each asset class and the ETF of ESG equities over the years 2020 and 2021 for the 22 day rebalance under constrained portfolios.
Fig. B.1.
Appendix C. Supplementary data
The following is the Supplementary material related to this article.
We provide the Rstudio codes for downloading data sample and estimating the DCC time-varying MVT copula approach. We also provide the Matlab codes for the Minimum Variance (MV) minimization problem.
References
- Agyei-Ampomah Sam, Gounopoulos Dimitrios, Mazouz Khelifa. Does gold offer a better protection against losses in sovereign debt bonds than other metals? J. Bank. Financ. 2014;40(1):507–521. doi: 10.1016/j.jbankfin.2013.11.014. [DOI] [Google Scholar]
- Akhtaruzzaman Md, Boubaker Sabri, Lucey Brian M., Sensoy Ahmet. Is gold a hedge or a safe-haven asset in the COVID–19 crisis? Econ. Model. 2021;102 doi: 10.1016/J.ECONMOD.2021.105588. [DOI] [Google Scholar]
- Alexopoulos Thomas A. To trust or not to trust? A comparative study of conventional and clean energy exchange-traded funds. Energy Econ. 2018;72:97–107. doi: 10.1016/J.ENECO.2018.03.013. [DOI] [Google Scholar]
- Aloui Riadh, Hammoudeh Shawkat, Nguyen Duc Khuong. A time-varying copula approach to oil and stock market dependence: The case of transition economies. Energy Econ. 2013;39:208–221. doi: 10.1016/j.eneco.2013.04.012. [DOI] [Google Scholar]
- Arif Muhammad, Hasan Mudassar, Alawi Suha M., Naeem Muhammad Abubakr. COVID-19 and time-frequency connectedness between green and conventional financial markets. Glob. Finance J. 2021;49 doi: 10.1016/J.GFJ.2021.100650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aziz Nor Syahilla Abdul, Vrontos Spyridon, Hasim Haslifah M. Evaluation of multivariate GARCH models in an optimal asset allocation framework. N. Am. J. Econ. Finance. 2019;47:568–596. doi: 10.1016/J.NAJEF.2018.06.012. [DOI] [Google Scholar]
- Baur Dirk G., Lucey Brian M. Is gold a hedge or a safe haven? An analysis of stocks, bonds and gold. Financial Rev. 2010;45(2):217–229. doi: 10.1111/j.1540-6288.2010.00244.x. [DOI] [Google Scholar]
- Baur Dirk G., McDermott Thomas K. Is gold a safe haven? International evidence. J. Bank. Financ. 2010;34(8):1886–1898. doi: 10.1016/j.jbankfin.2009.12.008. [DOI] [Google Scholar]
- Becchetti Leonardo, Ciciretti Rocco, Dalò Ambrogio, Herzel Stefano. Socially responsible and conventional investment funds: Performance comparison and the global financial crisis. Appl. Econ. 2015;47(25):2541–2562. doi: 10.1080/00036846.2014.1000517. [DOI] [Google Scholar]
- Bertrand Philippe, Lapointe Vincent. How performance of risk-based strategies is modified by socially responsible investment universe? Int. Rev. Financ. Anal. 2015;38:175–190. doi: 10.1016/j.irfa.2014.11.009. [DOI] [Google Scholar]
- Bertrand Philippe, Prigent Jean luc. Omega performance measure and portfolio insurance. J. Bank. Financ. 2011;35(7):1811–1823. doi: 10.1016/J.JBANKFIN.2010.12.001. [DOI] [Google Scholar]
- Bollerslev Tim. A conditionally heteroskedastic time series model for speculative prices and rates of return. Rev. Econ. Stat. 1987;69(3):542–547. [Google Scholar]
- Bouri Elie, Jalkh Naji, Molnár Peter, Roubaud David. Bitcoin for energy commodities before and after the 2013 crash: Diversifier, hedge or safe haven? Appl. Econ. 2017;49(50):5063–5073. doi: 10.1080/00036846.2017.1299102. [DOI] [Google Scholar]
- Bouri Elie, Molnár Peter, Azzi Georges, Roubaud David, Hagfors Lars Ivar. On the hedge and safe haven properties of bitcoin: Is it really more than a diversifier? Finance Res. Lett. 2017;20:192–198. doi: 10.1016/j.frl.2016.09.025. [DOI] [Google Scholar]
- Brauneis Alexander, Mestel Roland. Cryptocurrency-portfolios in a mean–variance framework. Finance Res. Lett. 2019;28:259–264. doi: 10.1016/j.frl.2018.05.008. [DOI] [Google Scholar]
- Breitung Jörg, Candelon Bertrand. Testing for short- and long-run causality: A frequency-domain approach. J. Econometrics. 2006;132(2):363–378. doi: 10.1016/J.JECONOM.2005.02.004. [DOI] [Google Scholar]
- Broadstock David C., Chan Kalok, Cheng Louis T.W., Wang Xiaowei. The role of ESG performance during times of financial crisis: Evidence from COVID-19 in China. Finance Res. Lett. 2021;38 doi: 10.1016/J.FRL.2020.101716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Çelik Ismail, Sak Ahmet Furkan, Höl Arife Özdemir, Vergili Gizem. The dynamic connectedness and hedging opportunities of implied and realized volatility: Evidence from clean energy ETFs. N. Am. J. Econ. Finance. 2022;60 doi: 10.1016/J.NAJEF.2022.101670. [DOI] [Google Scholar]
- Chemkha Rahma, BenSaïda Ahmed, Ghorbel Ahmed. Connectedness between cryptocurrencies and foreign exchange markets: Implication for risk management. J. Multinatl. Financ. Manag. 2021;59 doi: 10.1016/J.MULFIN.2020.100666. [DOI] [Google Scholar]
- Chowdhury Abdur. Is bitcoin the Paris hilton of the currency world? Or are the early investors onto something that will make them rich? J. Invest. 2016;25(1):64–72. doi: 10.3905/joi.2016.25.1.064. [DOI] [Google Scholar]
- Conlon Thomas, McGee Richard. Safe haven or risky hazard? Bitcoin during the Covid-19 bear market. Finance Res. Lett. 2020;35(May) doi: 10.1016/j.frl.2020.101607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbet Shaen, Goodell John W., Günay Samet. Co-movements and spillovers of oil and renewable firms under extreme conditions: New evidence from negative WTI prices during COVID-19. Energy Econ. 2020 doi: 10.1016/j.eneco.2020.104978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbet Shaen, Larkin Charles, Lucey Brian. The contagion effects of the COVID-19 pandemic: Evidence from gold and cryptocurrencies. Finance Res. Lett. 2020;35 doi: 10.1016/j.frl.2020.101554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demarta Stefano, McNeil Alexander J. The t copula and related copulas. Internat. Statist. Rev. 2007;73(1):111–129. doi: 10.1111/j.1751-5823.2005.tb00254.x. [DOI] [Google Scholar]
- Díaz Antonio, Esparcia Carlos. Dynamic optimal portfolio choice under time-varying risk aversion. Int. Econ. 2021 doi: 10.1016/j.inteco.2021.02.002. [DOI] [Google Scholar]
- Dutta Anupam, Das Debojyoti, Jana R.K., Vo Xuan Vinh. COVID-19 and oil market crash: Revisiting the safe haven property of gold and bitcoin. Resour. Policy. 2020;69 doi: 10.1016/J.RESOURPOL.2020.101816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elie Bouri, Naji Jalkh, Dutta Anupam, Uddin Gazi Salah. Gold and crude oil as safe-haven assets for clean energy stock indices: Blended copulas approach. Energy. 2019;178:544–553. doi: 10.1016/J.ENERGY.2019.04.155. [DOI] [Google Scholar]
- Fernández Carmen, Steel Mark F.J. On bayesian modeling of fat tails and skewness. J. Amer. Statist. Assoc. 1998;93(441):359–371. doi: 10.1080/01621459.1998.10474117. [DOI] [Google Scholar]
- Ferrer Román, Benítez Rafael, Bolós Vicente J. Interdependence between Green financial instruments and major conventional assets: A wavelet-based network analysis. Mathematics. 2021;9(8):900. doi: 10.3390/MATH9080900. [DOI] [Google Scholar]
- Ferrer Román, Shahzad Syed Jawad Hussain, López Raquel, Jareño Francisco. Time and frequency dynamics of connectedness between renewable energy stocks and crude oil prices. Energy Econ. 2018;76:1–20. doi: 10.1016/J.ENECO.2018.09.022. [DOI] [Google Scholar]
- Fishburn P. Mean-risk analysis with risk associated with below-target returns. Am. Econ. Rev. 1977;67(2):116–126. http://www.jstor.org/stable/1807225. [Google Scholar]
- Genest C., Ghoudi K., Rivest L.P. A semiparametric estimation procedure of dependence parameters in multivariate families of distributions. Biometrika. 1995;82(3):543–552. doi: 10.1093/biomet/82.3.543. [DOI] [Google Scholar]
- Gong Chen, Tang Pan, Wang Yutong. Measuring the network connectedness of global stock markets. Physica A. 2019;535 doi: 10.1016/j.physa.2019.122351. [DOI] [Google Scholar]
- Grauer Robert R., Shen Frederick C. Do constraints improve portfolio performance? J. Bank. Financ. 2000;24(8):1253–1274. doi: 10.1016/S0378-4266(99)00069-2. [DOI] [Google Scholar]
- Gustafsson Robert, Dutta Anupam, Elie Bouri. Are energy metals hedges or safe havens for clean energy stock returns? Energy. 2022;244 doi: 10.1016/J.ENERGY.2021.122708. [DOI] [Google Scholar]
- Hansen Peter R., Lunde Asger. A forecast comparison of volatility models: Does anything beat a GARCH(1, 1)? J. Appl. Econometrics. 2005;20(7):873–889. doi: 10.1002/jae.800. [DOI] [Google Scholar]
- Harvey A., Ruiz E., Shephard N. Multivariate stochastic variance models. Rev. Econom. Stud. 1994;61(2):247–264. doi: 10.2307/2297980. [DOI] [Google Scholar]
- Hwang Soosung, Valls Pereira Pedro L. Small sample properties of GARCH estimates and persistence. Eur. J. Finance. 2006;12(6–7):473–494. doi: 10.1080/13518470500039436. [DOI] [Google Scholar]
- Iglesias-Casal Ana, López-Penabad María Celia, López-Andión Carmen, Maside-Sanfiz José Manuel. Diversification and optimal hedges for socially responsible investment in Brazil. Econ. Model. 2020;85:106–118. doi: 10.1016/J.ECONMOD.2019.05.010. [DOI] [Google Scholar]
- Ji Qiang, Zhang Dayong, Zhao Yuqian. Searching for safe-haven assets during the COVID-19 pandemic. Int. Rev. Financ. Anal. 2020;71 doi: 10.1016/j.irfa.2020.101526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joost Driessen, Laeven Luc. International portfolio diversification benefits: Cross-country evidence from a local perspective. J. Bank. Financ. 2007;31(6):1693–1712. doi: 10.1016/j.jbankfin.2006.11.006. [DOI] [Google Scholar]
- Junttila Juha, Pesonen Juho, Raatikainen Juhani. Commodity market based hedging against stock market risk in times of financial crisis: The case of crude oil and gold. J. Int. Financial Mark. Inst. Money. 2018;56:255–280. doi: 10.1016/j.intfin.2018.01.002. [DOI] [Google Scholar]
- Kaplan Paul D., Knowles James A. Kappa: A generalized downside risk-adjusted performance measure. J. Perform. Meas. 2004;8:42–54. http://w.performance-measurement.org/KaplanKnowles2004.pdf. [Google Scholar]
- Kristoufek Ladislav. BitCoin meets Google trends and Wikipedia: Quantifying the relationship between phenomena of the internet era. Sci. Rep. 2013;3(1):3415. doi: 10.1038/srep03415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruskal William H. Ordinal measures of association. J. Amer. Statist. Assoc. 1958;53(284):814–861. doi: 10.1080/01621459.1958.10501481. [DOI] [Google Scholar]
- Kuang Wei. Are clean energy assets a safe haven for international equity markets? J. Cleaner Prod. 2021;302 doi: 10.1016/J.JCLEPRO.2021.127006. [DOI] [Google Scholar]
- Li Xin, Wang Chong Alex. The technology and economic determinants of cryptocurrency exchange rates: The case of Bitcoin. Decis. Support Syst. 2017;95:49–60. doi: 10.1016/j.dss.2016.12.001. [DOI] [Google Scholar]
- Lindskog Filip, McNeil Alexander, Schmock Uwe. Kendall’s tau for elliptical distributions. Contrib. Econ. 2003;14:9–156. doi: 10.1007/978-3-642-59365-9_8. [DOI] [Google Scholar]
- Liu Ming-Lei, Qiang Ji, Ying Fan. How does oil market uncertainty interact with other markets? an empirical analysis of implied volatility index. Energy. 2013;55:860–868. doi: 10.1016/j.energy.2013.04.037. [DOI] [Google Scholar]
- Mariana Christy Dwita, Ekaputra, Adi Irwan, Husodo, Ananto Zaäfri. Are bitcoin and ethereum safe-havens for stocks during the COVID-19 pandemic? Finance Res. Lett. 2021;38 doi: 10.1016/J.FRL.2020.101798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markowitz Harry. 1959. Portfolio selection. Investment under uncertainty. [Google Scholar]
- Markowitz Harry. first ed. John Wiley and Sons; 1959. Portfolio Selection. [Google Scholar]
- Mensi Walid, Hkiri Besma, Al-Yahyaee Khamis H., Kang Sang Hoon. Analyzing time–frequency co-movements across gold and oil prices with BRICS stock markets: A VaR based on wavelet approach. Int. Rev. Econ. Finance. 2018;54:74–102. doi: 10.1016/j.iref.2017.07.032. [DOI] [Google Scholar]
- Miralles-Quirós José Luis, Miralles-Quirós María Mar. Are alternative energies a real alternative for investors? Energy Econ. 2019;78:535–545. doi: 10.1016/J.ENECO.2018.12.008. [DOI] [Google Scholar]
- Nofsinger John, Varma Abhishek. Socially responsible funds and market crises. J. Bank. Financ. 2014;48:180–193. doi: 10.1016/J.JBANKFIN.2013.12.016. [DOI] [Google Scholar]
- Omura Akihiro, Roca Eduardo, Nakai Miwa. Does responsible investing pay during economic downturns: Evidence from the COVID-19 pandemic. Finance Res. Lett. 2021;42 doi: 10.1016/J.FRL.2020.101914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlova Ivelina, de Boyrie Maria E. ESG ETFs and the COVID-19 stock market crash of 2020: Did clean funds fare better? Finance Res. Lett. 2022;44 doi: 10.1016/J.FRL.2021.102051. [DOI] [Google Scholar]
- Ren Boru, Lucey Brian M. A clean, green haven? Examining the relationship between clean energy, clean and dirty cryptocurrencies. SSRN Electron. J. 2021 doi: 10.2139/SSRN.3963957. [DOI] [Google Scholar]
- Roy A.D. Safety first and the holding of assets. Econometrica. 1952;20(3):431–449. doi: 10.2307/1907413. [DOI] [Google Scholar]
- Sadorsky Perry. Modeling volatility and conditional correlations between socially responsible investments, gold and oil. Econ. Model. 2014;38:609–618. doi: 10.1016/J.ECONMOD.2014.02.013. [DOI] [Google Scholar]
- Sahamkhadam Maziar, Stephan Andreas, Östermark Ralf. Portfolio optimization based on GARCH-EVT-Copula forecasting models. Int. J. Forecast. 2018;34(3):497–506. doi: 10.1016/J.IJFORECAST.2018.02.004. [DOI] [Google Scholar]
- Salisu Afees A., Raheem Ibrahim D., Vo Xuan Vinh. Assessing the safe haven property of the gold market during COVID-19 pandemic. Int. Rev. Financ. Anal. 2021;74 doi: 10.1016/J.IRFA.2021.101666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santos André A.P., Moura Guilherme V. Dynamic factor multivariate GARCH model. Comput. Statist. Data Anal. 2014;76:606–617. doi: 10.1016/J.CSDA.2012.09.010. [DOI] [Google Scholar]
- Sharif Arshian, Aloui Chaker, Yarovaya Larisa. COVID-19 pandemic, oil prices, stock market, geopolitical risk and policy uncertainty nexus in the US economy: Fresh evidence from the wavelet-based approach. Int. Rev. Financ. Anal. 2020;70 doi: 10.1016/j.irfa.2020.101496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma Deep Gagan, Sarker Tapan, Rao Amar, Talan Gaurav, Jain Mansi. Revisiting conventional and green finance spillover in post-COVID world: Evidence from robust econometric models. Glob. Finance J. 2022;51 doi: 10.1016/J.GFJ.2021.100691. [DOI] [Google Scholar]
- Sharpe William F. Mutual fund performance. J. Bus. 1966;39(1):119–138. https://www.jstor.org/stable/2351741?seq=1#metadata_info_tab_contents. [Google Scholar]
- Sharpe William F. Adjusting for risk in portfolio performance measurement. J. Portfolio Manag. 1975;1(2):29–34. doi: 10.3905/jpm.1975.408513. [DOI] [Google Scholar]
- Sharpe William F. The sharpe ratio. J. Portfolio Manag. 1994;21(1):49–58. doi: 10.3905/jpm.1994.409501. [DOI] [Google Scholar]
- Sklar M. Fonctions de repartition an dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris. 1959;8:229–231. [Google Scholar]
- Sortino Frank A., Van der Meer Robert. Downside risk. J. Portf. Manag. 1991;17(4):27. doi: 10.3905/jpm.1991.409343. [DOI] [Google Scholar]
- Talbi Marwa, Bedoui Rihab, de Peretti Christian, Belkacem Lotfi. Is the role of precious metals as precious as they are? A vine copula and BiVaR approaches. Resour. Policy. 2021;73 doi: 10.1016/J.RESOURPOL.2021.102140. [DOI] [Google Scholar]
- Tareq Saeed, Bouri Elie, Alsulami Hamed. Extreme return connectedness and its determinants between clean/green and dirty energy investments. Energy Econ. 2021;96 doi: 10.1016/J.ENECO.2020.105017. [DOI] [Google Scholar]
- Umar Zaghum, Kenourgios Dimitris, Papathanasiou Sypros. The static and dynamic connectedness of environmental, social, and governance investments: International evidence. Econ. Model. 2020;93:112–124. doi: 10.1016/J.ECONMOD.2020.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yousaf Imran, Suleman Muhammad Tahir, Demirer Riza. Green investments: A luxury good or a financial necessity? Energy Econ. 2022;105 doi: 10.1016/J.ENECO.2021.105745. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
We provide the Rstudio codes for downloading data sample and estimating the DCC time-varying MVT copula approach. We also provide the Matlab codes for the Minimum Variance (MV) minimization problem.