Skip to main content
PMC home page
Elsevier - PMC COVID-19 Collection logoLink to Elsevier - PMC COVID-19 Collection
. 2022 Aug 21;22:100231. doi: 10.1016/j.mran.2022.100231

Strain wars 5: Gibbs energies of binding of BA.1 through BA.4 variants of SARS-CoV-2

Marko Popovic 1
PMCID: PMC9392893  PMID: 36034590

Abstract

This paper reports, for the first time, standard Gibbs energies of binding of the BA.1, BA.2, BA.3, BA.2.13, BA.2.12.1 and BA.4 Omicron variants of SARS-CoV-2, to the Human ACE2 receptor. Variants BA.1 through BA.3 exhibit a trend of decreasing standard Gibbs energy of binding and hence increased infectivity. The BA.4 variant exhibits a less negative standard Gibbs energy of binding, but also more efficient evasion of the immune response. Therefore, it was concluded that all the analyzed strains evolve in accordance with expectations of the theory of evolution, albeit using different strategies.

Keywords: Omicron variant, Binding constant, Dissociation constant, Antigen-receptor binding, Evolution

"The virus is mankind's ultimate predator."

R. Cook, Formula for death, 1995

1. Introduction

Living organisms represent open thermodynamic systems with the property of growth (von Bertalanffy, 1950; Popovic, 2019; Popovic et al., 2021, Popovic, 2018, 2017). SARS-CoV-2, except for being a biological system, also represents a chemical system, characterized by an empirical formula (Popovic and Minceva, 2020b; Degueldre, 2021; Popovic, 2022c). Moreover, SARS-CoV-2 represents an open thermodynamic system, with the property of growth (Popovic and Minceva, 2020a). Thus, thermodynamics has proved itself to be a powerful tool in analysis of infections caused by SARS-CoV-2 (Lucia et al., 2021, 2020a). It was shown that thermodynamic property - entropy can be used in analysis and prediction of development of the COVID-19 pandemic (Lucia et al., 2020b; Kaniadakis et al., 2020). Moreover, thermodynamics can be used in deeper analysis of fundamental life functions (Lucia and Grisolia, 2020, Lucia, 2015).

SARS-CoV-2 has evolved into a great number of variants, each characterized by specific chemical and thermodynamic properties (Popovic and Popovic, 2022; Popovic, 2022a, 2022b]. Newer variants differ from earlier ones in genetic sequence and information content. Change in information acquired through mutations can be analyzed using equations similar to those of thermodynamics (Hansen et al., 2018) and leads to change of elemental composition and thermodynamic properties. The host organism (human) represents an open thermodynamic system, characterized by an empirical formula and thermodynamic properties (Popovic and Minceva, 2020c). Various strains of SARS-CoV-2 compete with each other in the human population, leading to domination of new mutants, from Hu-1 to BA.5 (Popovic and Minceva, 2021a).

The first step in SARS-CoV-2 infection is antigen-receptor binding. The antigen of SARS-CoV-2 is the spike glycoprotein trimer (SGP), while the host cell receptor is the human angiotensin-converting enzyme 2 (hACE2) (Scialo et al., 2020; Cao et al., 2022). SGP-hACE2 binding represents a chemical equilibrium, characterized by a dissociation constant, binding constant, as well as standard thermodynamic properties: standard reaction enthalpy, entropy and Gibbs energy (Gale 2022, 2020, 2019, 2018). Thermodynamic properties play an important role in research on SGP-hACE2 interaction (Head et al., 2022). The energetics of virus-host interactions are important for understanding the infection process (Şimşek et al., 2021). All chemical processes have a thermodynamic driving force in the form of Gibbs energy (Demirel, 2014; Atkins and de Paula, 2011, 2014). Gibbs energy of growth represents the driving force for multiplication of microorganisms (von Stockar, 2013a, 2013b, 2010; Demirel, 2014; Hellingwerf et al., 1982; Westerhoff et al., 1982), including viruses (Popovic and Minceva, 2022a).

Virus-host interactions occur at two levels: at the membrane and in the cytoplasm (Popovic and Minceva, 2021a). The interaction at the membrane represents the antigen-receptor binding. The interaction in the cytoplasm represents virus multiplication. Both processes are driven by Gibbs energy (Popovic and Minceva, 2021a). The goal of this paper is to, starting from dissociation constant of various variants of SARS-CoV-2, calculate binding constants and Gibbs energies of binding for Omicron variants BA.1 through BA.4, using thermodynamic methodology.

2. Methods

The calculation starts from dissociation constants, KD, for SGP of the BA.1, BA.2, BA.3, BA.2.13, BA.2.12.1 and BA.4 Omicron variants of SARS-CoV-2, to the Human ACE2 receptor. The KD values were taken from (Cao et al., 2022) and are shown in Table 1 . They have been measured using surface plasmon resonance, at room temperature (Cao et al., 2022).

Table 1.

Standard thermodynamic properties of SGP-hACE2 binding for the variants BA.1 through BA.4 of SARS-CoV-2. The KD data were taken from (Cao et al., 2022). The KB and ΔbG values were calculated, as described in the Methods section.

Variant KD (M) KB (M−1) ΔbG (kJ/mol)
BA.1 3.05E-09 3.28E+08 −48.60
BA.2 1.56E-09 6.41E+08 −50.27
BA.3 2.62E-09 3.82E+08 −48.98
BA.2.13 1.61E-09 6.21E+08 −50.19
BA.2.12.1 1.77E-09 5.65E+08 −49.95
BA.4 1.67E-08 5.99E+07 −44.39
Open in a new tab

Antigen-receptor binding represents a chemical process. The rate of this process is given by the phenomenological equation

rB=−LBTΔBG (1)

Where rB is the rate of SGP-hACE2 binding, LB a constant (known as binding phenomenological coefficient), T temperature and ΔBG Gibbs energy of SGP-hACE2 binding (Popovic and Popovic, 2022; Popovic, 2022a, 2022b von Stockar, 2013a; Demirel, 2014). The rate of binding is proportional to the absolute value of the Gibbs energy of binding.

Eq. (1) considers binding of one hACE2 receptor to one virus SGP antigen. However, Gale (2022) suggested a more realistic model that considers virus-cell binding and takes into account the fact that a single virus can bind to multiple receptors. The equation has the form Gale (2022)

FB=11+1Ka_virus_T·Cfree(1+[I]KVI) (2)

Where FB is the fraction of viruses bound to host cells, Ka_virus_T association constant for binding of the virus to host cells at temperature T, Cfree total number of cells in the host tissue that have hACE2 receptors and can bind to SARS-CoV-2 but have no bound virus, [I] concentration of a virus inhibitor (if present), KVI dissociation constant of virus-inhibitor complex (if an inhibitor is present) Gale (2022).

The process of binding of the virus to its receptor can be analyzed at two levels. The first is the binding process of a single virus antigen (SGP) to a single receptor (hACE2), described by a dissociation constant. However, in reality, a virus attaches to the host cell using multiple receptors. This process is characterized by its own specific dissociation constant. Eqs. (1) and (2) are complementary. However, the first is based on a mechanistic model that assumes antigen-receptor binding, while the second is more realistic and describes virus-cell binding.

It is well documented that mutations lead to change in Gibbs energy of binding (Barton et al., 2021). The ability of coronaviruses to infect humans is related to their binding strengths to human receptor proteins (Zou et al., 2020). Mutation may induce significant conformational transitions in the spike glycoprotein (Istifli et al., 2021). Natural selection promotes mutations that increase the SGP-hACE2 binding affinity (Istifli et al., 2021). Binding affinity is quantified by Gibbs energy of binding (Gale 2022, 2020, 2019, 2018). Gibbs energy of binding can be calculated from dissociation constants, through the equation

ΔBG0=−RgTln(KB) (3)

Where Rg is the universal gas constant and T temperature (Popovic and Popovic, 2022; Du et al., 2016). KB represents the binding constant, which is the reciprocal of the dissociation constant KD (Du et al., 2016).

KB=1KD (4)

The dissociation constant is the equilibrium constant of the dissociation reaction of the antigen-receptor complex into the free receptor and antigen

GP−Cr⇄GP+Cr (5)

where Cr represents the host cell receptor (hACE2), GP the virus antigen (SGP) and GP-Cr the antigen- receptor complex (Popovic and Popovic, 2022; Du et al., 2016). Thus, KD is defined as the ratio of concentrations of the free receptor [Cr] and antigen [GP] to the receptor antigen complex [GP-Cr] (Popovic and Popovic, 2022; Du et al., 2016)

KD=[GP][Cr][GP−Cr] (6)

Therefore, Gibbs energy of binding is the driving force for the antigen-receptor binding process.

3. Results

Starting from SGP-hACE2 dissociation constants for the BA.1, BA.2, BA.3, BA.2.13, BA.2.12.1 and BA.4 variants of SARS-CoV-2, published in (Cao et al., 2022), binding constants and standard Gibbs energies of SGP-hACE2 binding were calculated, as described in the Methods section. They are given in Table 1. Standard Gibbs energies of binding for BA.1 and BA.3 are very similar (−48.60 kJ/mol and −48.98 kJ/mol, respectively). On the other hand, standard Gibbs energies of binding of BA.2, BA.2.13 and BA.2.12.1 also have similar values (−50.27 kJ/mol, −50.19 kJ/mol and −49.95 kJ/mol, respectively). The BA.4 strain is characterized by the least negative standard Gibbs energy of binding (−44.39 kJ/mol). A similar trend can be seen with the binding constants. BA.1 and BA.3 have similar binding constant values (3.28 ∙ 108 M−1 and 3.82 ∙ 108 M−1, respectively). The variants BA.2, BA.2.13. and BA.2.12.1 are also characterized by similar binding constant values (6.41 ∙ 108 M−1, 6.21 ∙ 108 M−1 and 5.65 ∙ 108 M−1, respectively). The BA.4 variant has a much lower binding constant compared to the other variants (5.99 ∙ 107 M−1).

4. Discussion

SARS-CoV-2 has evolved many times since 2019, through acquisition of mutations in various locations, and many variants were registered (Sun et al., 2022, Magazine et al., 2022). The latest variants have been recorded in 2022 (Cao et al., 2022). Dissociation constants have been reported for binding of spike glycoprotein trimer (SGP) to human angiotensin-converting enzyme 2 (hACE2), for practically all major SARS-CoV-2 variants (Cao et al., 2022; Wu et al., 2022; Han et al., 2022; Barton et al., 2021; Laffeber et al., 2021; Augusto et al., 2021). Using the SGP-hACE2 dissociation constants, in this paper, binding constants and standard Gibbs energies of binding have been determined (Table 1). For comparison, the binding constant for the Hu-1 variant (wild type) was found to be 5.88 ∙ 107 M−1, which gives a Gibbs energy of binding of −44.35 kJ/mol (Popovic, 2022a). Notice that the virus has evolved towards a more negative Gibbs energy of binding. More negative Gibbs energy of binding influences, according to Eq. (1), the antigen-receptor binding rate. The more negative Gibbs energy of binding leads to greater binding rate. The greater binding rate leads to increased infectivity and decreased incubation period.

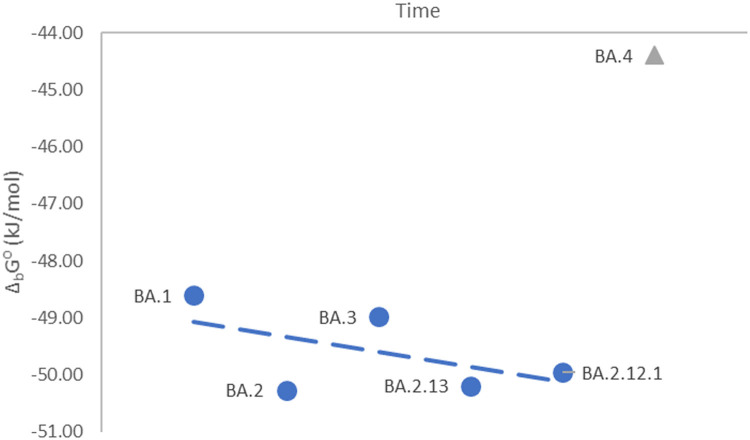
The BA.2 variant is characterized by a dissociation constant of 1.56 ∙ 10−9 M (Cao et al., 2022). This gives a binding constant of 6.41 ∙ 108 M−1 and a Gibbs energy of binding of −50.27 kJ/mol. The trend of decreasing Gibbs energy of binding during evolution of SARS-CoV-2 variants continues in the case of BA.2 (Fig. 1 ).

Fig. 1.

Fig. 1

Open in a new tab

Standard Gibbs energies of SGP-hACE2 binding of SARS-CoV-2 variants, isolated from November 2021 to January 2022.

The SGP-hACE2 binding constant for BA.3 was calculated to be 3.82 ∙ 108 M−1, which gives a standard Gibbs energy of binding of −48.98 kJ/mol. The SGP-hACE2 binding constant of BA.2.13 was found to be 6.21 ∙ 108 M−1, while its standard Gibbs energy of binding was found to be −50.19 kJ/mol. Variant BA.2.12.1 was found to have a SGP-hACE2 binding constant of 5.65 ∙ 108 M−1 and standard Gibbs energy of binding of −49.95 kJ/mol. The calculated values for the variants BA.1 through BA.3 exhibit a decreasing trend in standard Gibbs energy of SGP-hACE2 binding, as can be seen from Fig. 1. This means that binding rate and infectivity of the mentioned variants have increased through evolution, in the period from November 2021 to January 2022. This is in agreement with the predictions of the theory of evolution. Virus evolution is expected to proceed towards better adaptation, meaning an increased infectivity. A possible reason for the increase in infectivity is faster entrance of the virus into the host cell. This could be a consequence of a greater SGP-hACE2 binding rate. The increase in SGP-hACE2 binding rate is, according to Eq. (1), a consequence of a more negative Gibbs energy of binding.

The BA.4 variant is characterized by a SGP-hACE2 binding constant of 5.99 ∙ 107 M−1 and standard Gibbs energy of binding of −44.39 kJ/mol. It is represented by the gray triangle in Fig. 1. It can be noticed that BA.4 is characterized by a less negative Gibbs energy of binding. This implies that BA.4 has a lower SGP-hACE2 binding rate, which should lead to a decreased infectivity. Indeed, (Cao et al., 2022) reported that BA.4 and BA.5 variants have a decreased binding affinity. At the first glance, it seems that evolution of BA.4 and BA.5 opposes the expectations of the theory of evolution and observed trends. However, mutations on BA.4 that led to less negative Gibbs energy of binding and consequent decreased binding affinity, have also led to more efficient evasion of immune response (Barton et al., 2021; Cao et al., 2022). More effective evasion of immune response (Khan et al., 2022; Tuekprakhon et al., 2022) allows better accommodation of the virus to its environment (Barton et al., 2021; Cao et al., 2022). All this can finally result in increased infectivity. It seems that infectivity is a complex phenomenon, which depends on Gibbs energy of binding, binding rate and evading immune response (Harvey et al., 2021).

5. Conclusions

Evolution of SARS-CoV-2 variants from BA.1 to BA.3 exhibits a tendency towards more negative Gibbs energy of SGP-hACE2 binding and hence increased SGP-hACE2 binding rate. The goal of this process is in agreement with the expectations of the theory of evolution, in the sense of increased virus infectivity.

BA.4 variant deviates from the trend, in the sense of evolution towards less negative Gibbs energy of SGP-hACE2 binding, which is followed by more effective evasion of the immune response.

When predictions of the direction of viral evolution are made, it is necessary to have in mind changes in Gibbs energy of binding, binding affinity and evasion of the immune system.

CRediT authorship contribution statement

Marko Popovic: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Writing – original draft, Writing – review & editing, Visualization.

Declaration of Competing Interest

The author declares no conflict of interest.

References

  1. Atkins P.W., de Paula J. 2nd edition. W. H. Freeman and Company; 2011. Physical Chemistry for the Life Sciences. [Google Scholar]
  2. Atkins P.W., de Paula J. 10th Edition. W. H. Freeman and Company; New York: 2014. Physical Chemistry: Thermodynamics, Structure, and Change. [Google Scholar]
  3. Augusto G., Mohsen M.O., Zinkhan S., Liu X., Vogel M., Bachmann M.F. In vitro data suggest that Indian delta variant B.1.617 of SARS-CoV-2 escapes neutralization by both receptor affinity and immune evasion. Allergy. 2021 doi: 10.1111/all.15065. 10.1111/all.15065. Advance online publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Barton M.I., MacGowan S.A., Kutuzov M.A., Dushek O., Barton G.J., van der Merwe P.A. Effects of common mutations in the SARS-CoV-2 Spike RBD and its ligand, the human ACE2 receptor on binding affinity and kinetics. Elife. 2021;10:e70658. doi: 10.7554/eLife.70658. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cao Y.R., Yisimayi A., Jian F., Song W., Xiao T., Wang L.…Xie X.S. BA. 2.12. 1, BA. 4 and BA. 5 escape antibodies elicited by Omicron infection. bioRxiv. 2022 doi: 10.1101/2022.04.30.489997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Degueldre C. Single virus inductively coupled plasma mass spectroscopy analysis: a comprehensive study. Talanta. 2021;228 doi: 10.1016/j.talanta.2021.122211. [DOI] [PubMed] [Google Scholar]
  7. Demirel Y. 3rd ed. Elsevier; Amsterdam: 2014. Nonequilibrium Thermodynamics: Transport and Rate Processes in Physical, Chemical and Biological Systems. [Google Scholar]
  8. Du X., Li Y., Xia Y.-.L., Ai S.-.M., Liang J., Sang P., Ji X.-.L., et al. Insights into protein–ligand interactions: mechanisms, models, and methods. Int. J. Mol. Sci. 2016;17(2):144. doi: 10.3390/ijms17020144. MDPI AG. Retrieved from. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Gale P. How virus size and attachment parameters affect the temperature sensitivity of virus binding to host cells: predictions of a thermodynamic model for arboviruses and HIV. Microb. Risk Analy. 2020;15 doi: 10.1016/j.mran.2020.100104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Gale P. Towards a thermodynamic mechanistic model for the effect of temperature on arthropod vector competence for transmission of arboviruses. Microb. Risk Analy. 2019;12:27–43. doi: 10.1016/j.mran.2019.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gale P. Using thermodynamic parameters to calibrate a mechanistic dose-response for infection of a host by a virus. Microb. Risk Analy. 2018;8:1–13. doi: 10.1016/j.mran.2018.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gale P. Using thermodynamic equilibrium models to predict the effect of antiviral agents on infectivity: Theoretical application to SARS-CoV-2 and other viruses. Microbial risk analysis. 2022;21:100198. doi: 10.1016/j.mran.2021.100198. [DOI] [PMC free article] [PubMed] [Google Scholar]; https://doi.org/10.1016/j.mran.2021.100198
  13. Han P., Li L., Liu S., Wang Q., Zhang D., Xu Z., Han P., Li X., Peng Q., Su C., Huang B., Li D., Zhang R., Tian M., Fu L., Gao Y., Zhao X., Liu K., Qi J., Gao G.F.…Wang P. Receptor binding and complex structures of human ACE2 to spike RBD from omicron and delta SARS-CoV-2. Cell. 2022 doi: 10.1016/j.cell.2022.01.001. S0092-8674(22)00001-0. Advance online publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hansen L.D., Popovic M., Tolley H.D., Woodfield B.F. Laws of evolution parallel the laws of thermodynamics. J. Chem. Thermodyn. 2018;124:141–148. doi: 10.1016/j.jct.2018.05.005. [DOI] [Google Scholar]
  15. Harvey W.T., Carabelli A.M., Jackson B., et al. SARS-CoV-2 variants, spike mutations and immune escape. Nat. Rev. Microbiol. 2021;19:409–424. doi: 10.1038/s41579-021-00573-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Head R.J., Lumbers E.R., Jarrott B., Tretter F., Smith G., Pringle K.G., Islam S., Martin J.H. Systems analysis shows that thermodynamic physiological and pharmacological fundamentals drive COVID-19 and response to treatment. Pharmacol. Res. Perspect. 2022;10(1):e00922. doi: 10.1002/prp2.922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hellingwerf K.J., Lolkema J.S., Otto R., Neijssel O.M., Stouthamer A.H., Harder W., van Dam K., Westerhoff H.V. Energetics of microbial growth: an analysis of the relationship between growth and its mechanistic basis by mosaic non-equilibrium thermodynamics. FEMS Microbiol. Lett. 1982;15(1):7–17. doi: 10.1111/j.1574-6968.1982.tb00028.x. [DOI] [Google Scholar]
  18. Istifli E.S., Netz P.A., Sihoglu Tepe A., Sarikurkcu C., Tepe B. Understanding the molecular interaction of SARS-CoV-2 spike mutants with ACE2 (angiotensin converting enzyme 2) J. Biomol. Struct. Dyn. 2021:1–12. doi: 10.1080/07391102.2021.1975569. Advance online publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kaniadakis G., Baldi M.M., Deisboeck T.S., Grisolia G., Hristopulos D.T., Scarfone A.M., Sparavigna A., Wada T., Lucia U. The κ-statistics approach to epidemiology. Sci Rep. 2020;10(1):19949. doi: 10.1038/s41598-020-76673-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Khan K., Karim F., Ganga Y., et al. Omicron BA.4/BA.5 escape neutralizing immunity elicited by BA.1 infection. Nat. Commun. 2022;13:4686. doi: 10.1038/s41467-022-32396-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Laffeber C., de Koning K., Kanaar R., Lebbink J. Experimental evidence for enhanced receptor binding by rapidly spreading SARS-CoV-2 variants. J. Mol. Biol. 2021;433(15) doi: 10.1016/j.jmb.2021.167058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lucia U., Grisolia G., Deisboeck T.S. Thermodynamics and SARS-CoV-2: neurological effects in post-Covid 19 syndrome. Atti della Accademia Peloritana dei Pericolanti. 2021;99(2):A3. doi: 10.1478/AAPP.992A3. [DOI] [Google Scholar]
  23. Lucia U., Grisolia G., Deisboeck T.S. Seebeck-like effect in SARS-CoV-2 bio-thermodynamics. Atti della Accademia Peloritana dei Pericolanti-Classe di Scienze Fisiche. Matematiche e Naturali. 2020;98(2):6. doi: 10.1478/AAPP.982A6. [DOI] [Google Scholar]
  24. Lucia U., Deisboeck T.S., Grisolia G. Entropy-based pandemics forecasting. Front. Phys. 2020;8:274. doi: 10.3389/fphy.2020.00274. [DOI] [Google Scholar]
  25. Lucia U., Grisolia G. How life works—A continuous Seebeck-Peltier transition in cell membrane? Entropy. 2020;22(9):960. doi: 10.3390/e22090960. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lucia U. Bioengineering thermodynamics of biological cells. Theor. Biol. Med. Model. 2015;12:29. doi: 10.1186/s12976-015-0024-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Magazine N., Zhang T., Wu Y., McGee M.C., Veggiani G., Huang W. Mutations and Evolution of the SARS-CoV-2 Spike Protein. Viruses. 2022;14(3):640. doi: 10.3390/v14030640. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Popovic M., Popovic M. Strain Wars: competitive interactions between SARS-CoV-2 strains are explained by Gibbs energy of antigen-receptor binding. Microb. Risk Analy. 2022 doi: 10.1016/j.mran.2022.100202. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Popovic M. Strain wars 2: binding constants, enthalpies, entropies, Gibbs energies and rates of binding of SARS-CoV-2 variants. Virology. 2022;570:35–44. doi: 10.1016/j.virol.2022.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Popovic M. Strain wars 3: differences in infectivity and pathogenicity between Delta and Omicron strains of SARS-CoV-2 can be explained by thermodynamic and kinetic parameters of binding and growth. Microb. Risk Analy. 2022 doi: 10.1016/j.mran.2022.100217. Advance online publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Popovic M. Atom counting method for determining elemental composition of viruses and its applications in biothermodynamics and environmental science. Comput. Biol. Chem. 2022;96 doi: 10.1016/j.compbiolchem.2022.107621. [DOI] [PubMed] [Google Scholar]
  32. Popovic M., Stenning G., Göttlein A., Minceva M. Elemental composition, heat capacity from 2 to 300 K and derived thermodynamic functions of 5 microorganism species. J. Biotechnol. 2021;331:99–107. doi: 10.1016/j.jbiotec.2021.03.006. [DOI] [PubMed] [Google Scholar]
  33. Popovic M., Minceva M. Coinfection and interference phenomena are the results of multiple thermodynamic competitive interactions. Microorganisms. 2021;9(10):2060. doi: 10.3390/microorganisms9102060. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Popovic M., Minceva M. A thermodynamic insight into viral infections: do viruses in a lytic cycle hijack cell metabolism due to their low Gibbs energy? Heliyon. 2020;6(5):e03933. doi: 10.1016/j.heliyon.2020.e03933. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Popovic M., Minceva M. Thermodynamic insight into viral infections 2: empirical formulas, molecular compositions and thermodynamic properties of SARS, MERS and SARS-CoV-2 (COVID-19) viruses. Heliyon. 2020;6(9):e04943. doi: 10.1016/j.heliyon.2020.e04943. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Popovic M., Minceva M. Thermodynamic properties of human tissues. Therm. Sci. 2020;24(6B):4115–4133. doi: 10.2298/TSCI200109151P. [DOI] [Google Scholar]
  37. Popovic M. Thermodynamic properties of microorganisms: determination and analysis of enthalpy, entropy, and Gibbs free energy of biomass, cells and colonies of 32 microorganism species. Heliyon. 2019;5(6):e01950. doi: 10.1016/j.heliyon.2019.e01950. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Popovic M. Living organisms from Prigogine's perspective: an opportunity to introduce students to biological entropy balance. J. Biol. Educ. 2018;52(3):294–300. doi: 10.1080/00219266.2017.1357649. [DOI] [Google Scholar]
  39. Popovic, M. (2017). Researchers in an entropy wonderland: A review of the entropy concept. arXiv preprint arXiv:1711.07326.
  40. Scialo F., Daniele A., Amato F., Pastore L., Matera M.G., Cazzola M., Castaldo G., Bianco A. ACE2: the major cell entry receptor for SARS-CoV-2. Lung. 2020;198(6):867–877. doi: 10.1007/s00408-020-00408-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Şimşek B., Özilgen M., Utku F.Ş. How much energy is stored in SARS-CoV-2 and its structural elements? Energy Storage. 2021:e298. doi: 10.1002/est2.298. [DOI] [Google Scholar]
  42. Sun Y., Lin W., Dong W., Xu J. Origin and evolutionary analysis of the SARS-CoV-2 Omicron variant. J. Biosaf. Biosecur. 2022;4(1):33–37. doi: 10.1016/j.jobb.2021.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Tuekprakhon A., Nutalai R., Dijokaite-Guraliuc A., Zhou D., Ginn H.M., Selvaraj M., Liu C., Mentzer A.J., Supasa P., Duyvesteyn H., Das R., Skelly D., Ritter T.G., Amini A., Bibi S., Adele S., Johnson S.A., Constantinides B., Webster H., Temperton N.…Screaton G.R. Antibody escape of SARS-CoV-2 Omicron BA.4 and BA.5 from vaccine and BA.1 serum. Cell. 2022;185(14) doi: 10.1016/j.cell.2022.06.005. 2422–2433.e13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. von Bertalanffy L. The theory of open systems in physics and biology. Science. 1950;111(2872):23–29. doi: 10.1126/science.111.2872.23. [DOI] [PubMed] [Google Scholar]
  45. Von Stockar U. In: Biothermodynamics: The Role of Thermodynamics in Biochemical Engineering. Urs von Stockar., editor. EPFL Press; Lausanne: 2013. Live cells as open non-equilibrium systems; pp. 475–534. [Google Scholar]
  46. Von Stockar U. In: Biothermodynamics: the Role of Thermodynamics in Biochemical Engineering. von Stockar U., editor. EPFL Press; Lausanne: 2013. Biothermodynamics of live cells: energy dissipation and heat generation in cellular structures; pp. 475–534. [Google Scholar]
  47. Von Stockar U. Biothermodynamics of live cells: a tool for biotechnology and biochemical engineering. J. Non-Equilib. Thermodyn. 2010;35(4):415–475. doi: 10.1515/jnetdy.2010.024. [DOI] [Google Scholar]
  48. Westerhoff H.V., Lolkema J.S., Otto R., Hellingwerf K.J. Thermodynamics of growth. Non-equilibrium thermodynamics of bacterial growth: the phenomenological and the Mosaic approach. Biochimica et Biophysica Acta (BBA) - Reviews on Bioenergetics. 1982;683(3–4):181–220. doi: 10.1016/0304-4173(82)90001-5. [DOI] [PubMed] [Google Scholar]
  49. Wu L., Zhou L., Mo M., Liu T., Wu C., Gong C., Lu K., Gong L., Zhu W., Xu Z. SARS-CoV-2 Omicron RBD shows weaker binding affinity than the currently dominant Delta variant to human ACE2. Signal Transduct. Target. Ther. 2022;7(1):8. doi: 10.1038/s41392-021-00863-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Zou J., Yin J., Fang L., Yang M., Wang T., Wu W.…Zhang P. Computational prediction of mutational effects on SARS-CoV-2 binding by relative free energy calculations. J. Chem. Inf. Model. 2020;60(12):5794–5802. doi: 10.1021/acs.jcim.0c00679. [DOI] [PubMed] [Google Scholar]

Articles from Microbial Risk Analysis are provided here courtesy of Elsevier

RESOURCES