Comparison of different scoring methods based on latent variable models of the PHQ-9: an individual participant data meta-analysis

Abstract

Background

Previous research on the depression scale of the Patient Health Questionnaire (PHQ-9) has found that different latent factor models have maximized empirical measures of goodness-of-fit. The clinical relevance of these differences is unclear. We aimed to investigate whether depression screening accuracy may be improved by employing latent factor model-based scoring rather than sum scores.

Methods

We used an individual participant data meta-analysis (IPDMA) database compiled to assess the screening accuracy of the PHQ-9. We included studies that used the Structured Clinical Interview for DSM (SCID) as a reference standard and split those into calibration and validation datasets. In the calibration dataset, we estimated unidimensional, two-dimensional (separating cognitive/affective and somatic symptoms of depression), and bi-factor models, and the respective cut-offs to maximize combined sensitivity and specificity. In the validation dataset, we assessed the differences in (combined) sensitivity and specificity between the latent variable approaches and the optimal sum score (⩾10), using bootstrapping to estimate 95% confidence intervals for the differences.

Results

The calibration dataset included 24 studies (4378 participants, 652 major depression cases); the validation dataset 17 studies (4252 participants, 568 cases). In the validation dataset, optimal cut-offs of the unidimensional, two-dimensional, and bi-factor models had higher sensitivity (by 0.036, 0.050, 0.049 points, respectively) but lower specificity (0.017, 0.026, 0.019, respectively) compared to the sum score cut-off of ⩾10.

Conclusions

In a comprehensive dataset of diagnostic studies, scoring using complex latent variable models do not improve screening accuracy of the PHQ-9 meaningfully as compared to the simple sum score approach.

Background

The Patient Health Questionnaire (PHQ) was developed to screen and assess for the presence and severity of eight mental and behavioral disorders (Spitzer, Kroenke, & Williams, 1999). The depression scale constitutes the short-form PHQ-9 and consists of nine items derived from the Diagnostic and Statistical Manual of Mental Disorders (DSM-IV) diagnostic criteria for major depressive disorder (Kroenke, Spitzer, & Williams, 2001). Respondents are asked how often they were bothered by each of the nine symptoms of depression in the past 2 weeks, and items are rated using four response categories (not at all, several days, more than half the days, nearly every day). Total scores range from 0 to 27, with higher scores indicating more severe symptoms of depression. The PHQ-9 was developed for screening for major depression as well as for the dimensional assessment of depression severity (Kroenke et al., 2001). It is considered a valid instrument for the evaluation of depressive symptoms in medical care (Löwe et al., 2004; Löwe, Kroenke, Herzog, & Gräfe, 2004; Löwe, Unützer, Callahan, Perkins, & Kroenke, 2004) and is available in many languages.

The PHQ-9 sum score is typically used as a measure of depression symptom severity and depression screening. A recent individual participant data meta-analysis (IPDMA), with data from 17,357 participants from 58 primary studies, evaluated screening accuracy of the PHQ-9 to detect major depression. This study found that a cut-off sum score of ⩾10 maximized combined sensitivity and specificity but had less than ideal positive and negative predictive values when depression prevalence was low (Levis, Benedetti, & Thombs, 2019). Diagnostic accuracy could not be improved by the use of the diagnostic algorithm of the PHQ-9 (He et al., 2020) nor by omitting the potentially problematic item operationalizing suicidal ideation (Wu et al., 2019).

Although a latent variable approach has been utilized to shorten the scale to four items (Ishihara et al., 2019), no studies have investigated whether utilizing latent variable-based scoring may improve the screening accuracy of the PHQ-9. In latent variable approaches such as confirmatory factor analysis (CFA), one or more unobservable (latent) variables are modelled to describe the variation of the observed item responses. In contrast to the sum score, a factor score empirically weights item responses to maximize the likelihood of the observed data and might therefore rank individuals differently based on their specific response pattern compared to the sum score.

The appropriate structure of latent variable models underlying the PHQ-9 is contested. Some studies suggest that the PHQ-9 is a unidimensional measure, i.e. all item responses can be best explained by a single latent variable (Arrieta et al., 2017; Choi, Schalet, Cook, & Cella, 2014; Harry & Waring, 2019; Kocalevent, Hinz, & Brähler, 2013; Merz, Malcarne, Roesch, Riley, & Sadler, 2011; Wahl et al., 2014), whereas others suggest that it is necessary to differentiate between a cognitive/affective and somatic factor to appropriately represent the observed data (Beard, Hsu, Rifkin, Busch, & Björgvinsson, 2016; Chilcot et al., 2013; Elhai et al., 2012; Forkmann, Gauggel, Spangenberg, Brähler, & Glaesmer, 2013; Miranda & Scoppetta, 2018; Patel et al., 2019). More recently, bi-factor modeling has been increasingly used to establish ‘sufficient’ unidimensionality of the PHQ-9 (Arnold et al., 2020; Chilcot et al., 2018; Doi, Ito, Takebayashi, Muramatsu, & Horikoshi, 2018), acknowledging that minor deviations from a unidimensional model may be clinically irrelevant.

These studies investigating the factorial structure of the PHQ-9 have commonly relied on the assessment of approximate fit indices using rules of thumb (e.g. CFI >0.95, RMSEA <0.08) to determine the most appropriate model in their respective samples. They have not investigated whether the use of latent variable models to weight item responses and account for possible violations of unidimensionality had a clinically relevant advantage compared to the use of simple sum scores. However, such an assessment would be needed to distinguish whether such models pick up real and relevant deviations from model assumptions such as unidimensionality or are a result of overfitting, as more complex models can fit the observed data more precisely.

We know of only one study that has compared depression screening accuracy as a measure of predictive validity between different latent variable models of the PHQ-9 and the sum score (Xiong et al., 2014). That study found that unidimensional, two-dimensional, and bi-factor modeling yielded only small and potentially negligible increases in screening accuracy compared to the use of sum scores. The generalizability of this finding, however, is unclear as the study included only 491 participants (116 major depression cases), using the Chinese version of the PHQ-9 and we, therefore, replicate this analysis in a comprehensive data set.

Severity scores from latent variable models may more accurately identify cases of major depression than a sum score approach. Therefore, this study aimed to investigate the degree to which diagnostic accuracy may be improved by employing latent variable models in depression screening compared to sum scores. To answer this question, we estimated unidimensional, two-dimensional, and bi-factor models for the PHQ-9 using data collected for an IPDMA on the diagnostic accuracy of the PHQ-9 (Levis, Benedetti & Thombs, 2019). We then identified optimal cut-offs that maximized combined sensitivity and specificity in each of the latent models and compared their accuracy to the standard sum score approach (cut-off of ⩾10) to determine whether gains achieved by using complex latent factor methods were clinically relevant.

Methods

This study is a secondary analysis of data accrued for an IPDMA of the diagnostic accuracy of the PHQ-9 for screening to detect major depression (Levis, Benedetti & Thombs, 2019; Levis et al., 2020; Thombs et al., 2014). We divided the IPDMA database into calibration and validation samples to first calibrate models, and, second, test model accuracy against the sum score approach.

The main IPDMA was registered in PROSPERO (CRD42014010673) and a protocol was published (Thombs et al., 2014). The present analysis was not part of the original IPDMA protocol, but a protocol was prespecified and published on Open Science Framework (https://osf.io/ytpez/). Results of the study are reported following PRISMA-DTA (McInnes et al., 2018) and PRISMA-IPD (Stewart et al., 2015) reporting guidelines.

Identification of eligible studies

In the main IPDMA, datasets from articles in any language were eligible for inclusion if (1) they included PHQ-9 item data; (2) they included diagnostic classification for current major depressive disorder (MDD) or major depressive episode (MDE) using DSM (American Psychiatric Association, 1987, 1994, 2000) or International Classification of Diseases (ICD) (World Health Organization, 1992) criteria based on a validated semi-structured or fully structured interview; (3) the diagnostic interview and PHQ-9 were administered within 2 weeks of each other, because DSM (American Psychiatric Association, 1987, 1994, 2000) and ICD (World Health Organization, 1992) criteria specify that symptoms must have been present in the last 2 weeks; (4) participants were ⩾18 years and not recruited from youth or college settings; and (5) participants were not recruited from psychiatric settings or because they were identified as having symptoms of depression, since screening is done to identify previously unrecognized cases (Thombs et al., 2011). Datasets, where not all participants were eligible, were included if primary data allowed the selection of eligible participants.

Database searches and study selection

A medical librarian searched Medline, Medline In-Process & Other Non-Indexed Citations via Ovid, PsycINFO, and Web of Science (January 1, 2000 – February 7, 2015), using a peer-reviewed (McGowan et al., 2016) search strategy (see supplementary material 1). We limited our search to these databases based on research showing that adding other databases when the Medline search is highly sensitive does not identify additional eligible studies (Rice et al., 2016; Sampson et al., 2003).

The search was initially conducted from 1 January 2000 to 7 February 2015, then updated to 9 May 2018. We limited the search to the year 2000 forward because the PHQ-9 was published in 2001 (Kroenke et al., 2001). We also reviewed reference lists of relevant reviews and queried contributing authors about non-published studies. Search results were uploaded into RefWorks (RefWorks-COS, Bethesda, MD, USA). After de-duplication, remaining citations were uploaded into DistillerSR (Evidence Partners, Ottawa, Canada) for processing review results. Two investigators independently reviewed titles and abstracts for eligibility. If either deemed a study potentially eligible, the full-text review was done by two investigators, independently, with disagreements resolved by consensus, consulting a third investigator when necessary. Translators were consulted for languages other than those for which team members were fluent.

Data extraction, contribution and synthesis

Authors of eligible datasets were invited to contribute de-identified primary data, including PHQ-9 item data and major depression status. We emailed corresponding authors of eligible primary studies at least three times, as necessary, with at least 2 weeks between each email. If there was no response, we emailed co-authors and attempted phone contact. Individual participant data were converted to a standard format and synthesized into a single dataset with study-level data. We compared published participant characteristics and diagnostic accuracy results with results from raw datasets and resolved any discrepancies in consultation with the original investigators.

For defining major depression, we considered MDD or MDE based on the DSM. If more than one was reported, we prioritized MDE over MDD, since screening would attempt to detect depressive episodes and further interview would determine if the depressive episode is related to MDD, bipolar disorder, or persistent depressive disorder (dysthymia).

When datasets included statistical weights to reflect sampling procedures, we used the provided weights for latent variable model estimation and assessment of diagnostic accuracy. For studies where sampling procedures merited weighting, but the original study did not weight, we constructed weights using inverse selection probabilities. Weighting occurred, for instance, when all participants with positive screens and a random subset of participants with negative screens were administered a diagnostic interview.

Data used in this study

For the present study, we only included primary studies that classified major depression using the Structured Clinical Interview for DSM Disorders (SCID) (First, 1995). The SCID is a semi-structured diagnostic interview intended to be conducted by an experienced diagnostician; it requires clinical judgment and allows rephrasing questions and probes to follow-up responses. The reason for including only studies that administered the SCID is that in recent analyses using three large IPDMA databases (Levis et al., 2018; Levis et al., 2019; Wu et al., 2020) we found that fully structured interviews identify more patients with low-level symptoms as depressed but fewer patients with high-level symptoms compared to semi-structured interviews. These results are consistent with the idea that semi-structured interviews most closely replicate clinical interviews done by trained professionals, whereas fully structured interviews are less rigorous reference standards. They are less resource-intensive options that can be administered by research staff without diagnostic skills but hence may misclassify major depression in substantial numbers of patients (Brugha, Bebbington, & Jenkins, 1999; Brugha, Jenkins, Taub, Meltzer, & Bebbington, 2001; Kurdyak & Gnam, 2005; Nosen & Woody, 2008).

In our main PHQ-9 IPDMA database, most (44 of 47, 94%) primary studies that used semi-structured interviews to classify major depression status used the SCID, thus we limited our analysis on these to ensure comparability of the outcome as much as possible. Furthermore, we excluded an additional three studies which did not provide PHQ-9 item-level data necessary for this analysis and were able to include 41 studies (87%) in the analysis.

We split available data into two datasets used for calibration of models and validation. Eligible studies from the search conducted in February 2015 were used as the calibration dataset, whereas additional eligible studies from the May 2018 search were used as the validation dataset. This mimics the necessity to establish a scoring algorithm prior to its use in screening. We replicated the analysis based on a random-split of the data as a sensitivity analysis.

Statistical analyses

Estimation of latent factor models

In the calibration sample, a unidimensional (all items load on a single factor), two-dimensional (two correlated factors for cognitive/affective [items 1, 2, 6, 7, 8, 9] and somatic [items 3, 4, 5] symptoms of depression), and bi-factor model (a general factor and specific factors accounting for cognitive/affective and somatic symptoms of depression) were fitted using all available PHQ-9 item scores from study participants. For each study, factor means, and covariances were modelled separately, whereas we assumed invariance of measurement parameters across studies to calibrate latent scores on the same scale. Each of the models was identified by constraining the latent factor means and variances of one group to 0 and 1, respectively.

We fitted each of the three models in the calibration sample and descriptively assessed the measurement parameters such as item loadings and factor covariances as well as exact (chi-square) and approximate (comparative fit index CFI <0.95, root mean squared error of approximation RMSEA <0.08, standardized root mean residual SRMR <0.06) measures of fit (Brown, 2006; Hu & Bentler, 1999). As the models are nested, we compared fit of the models using scaled likelihood ratio tests (Satorra & Bentler, 2010). Furthermore, we reported the correlation between latent factor scores and the sum scores.

We then estimated individual factor scores for all participants in the calibration dataset from each of the three models using the Empirical Bayes Modal approach. We used the following estimates of depression severity from each model in subsequent analyses:

1. Factor scores from the unidimensional model

2. Cognitive/affective factor scores from the two-dimensional model (since the main diagnostic criteria of MDD are cognitive-affective symptoms)

3. General factor scores from the bi-factor model.

For all confirmatory factor analyses, we treated the observed item responses as four level ordinally scaled variable and therefore used a diagonally weighted least squares estimator with a mean- and variance-adjusted test statistic. This approach estimates a model equivalent to that of a graded response model from the item-response theory framework (Forero & Maydeu-Olivares, 2009). The analysis was conducted in R (R Development Core Team, 3.0.1., 2013) with the Lavaan package (Rosseel, 2012).

Identification of optimal cut-offs for scores from latent factor models in the calibration sample

For each of the three latent score estimates, we calculated overall screening accuracy for a range of potential cut-offs in the calibration dataset. Given that the continuous scale of the latent variables has a substantially larger number of potential thresholds compared to the sum score, we imposed a grid with step width = 0.01 over the observed range of the scale as potential cut-offs. For each potential cut-off, we used a bivariate model fitted via Gauss-Hermite adaptive quadrature (Riley, Dodd, Craig, Thompson, & Williamson, 2008) to estimate sensitivity and specificity, accounting for the clustered nature of the data in the IPDMA. This 2-stage meta-analytic approach models sensitivity and specificity simultaneously, accounting for the inherent correlation between them and for the precision of estimates within studies. For each analysis, this model provides estimates of pooled sensitivity and specificity. Bivariate models were fitted using glmer in lme4 (Bates, Mächler, Bolker, & Walker, 2014). For each of the three latent scores, we then chose the cut-off that maximized combined sensitivity and specificity as the optimal cut-off. For the sum score, we used the standard optimal cut-off of ⩾10 (Levis et al., 2018), which was also optimal in the calibration dataset.

To investigate heterogeneity, we assessed forest plots of sensitivities and specificities for each included study at the optimal cut-offs from each of the three models and the sum score. We reported estimated variances of the random effects for sensitivity and specificity (τ²) and R, the ratio of the estimated standard deviation of the pooled sensitivity or specificity from the random-effects model to that from the corresponding fixed-effects model (Higgins & Thompson, 2002). We also compared the heterogeneity in diagnostic accuracy between the latent variable models and the sum score to investigate whether the more complex latent variable models show stronger heterogeneity.

Comparison of accuracy of latent models and sum score in the validation sample

The respective factor scores in the validation sample were calculated using the model parameters obtained in the calibration sample and a standard normal prior. We estimated pooled sensitivity and specificity using the bivariate model for the latent scores along the grid of potential thresholds and for each sum score in the validation sample to construct empirical receiver operator characteristic (ROC) plots in the validation sample. We compared the overall diagnostic accuracy of each method by estimating the difference and the respective 95% confidence intervals of the area under the curve (AUC) to the sum score ROC plot.

We furthermore estimated the differences (along with their respective 95% confidence intervals) of sensitivity and specificity between the PHQ-9 sum score cut-off of ⩾10 and the optimal cut-off identified for each method in the calibration sample. Following previous studies (Ishihara et al., 2019; Wu et al., 2019), a difference of 5% in sensitivity or specificity was set as the criterion for clinical relevance. Percentile-based confidence intervals were sampled using the cluster bootstrap approach (van der Leeden, Meijer, & Busing, 2008), resampling at study and subject levels. For each comparison, we used 1000 bootstrap iterations.

Results

Data

A flowchart of the search and inclusion process can be found as supplementary material 2. From the 41 studies included, 24 studies with 4,378 participants (652 depression cases) were used as the calibration set, and 17 studies with 4,252 participants (568 depression cases) as the validation set. The calibration and validation set differed in multiple characteristics (see Table 1). Participants in the calibration set were, on average, older and more likely to be male. Study characteristics including country, language, and general setting, as well as the method of administration of diagnostic interview and PHQ-9 questionnaire also differed. The mean PHQ-9 score did not differ significantly between calibration and validation sets, whereas participants in the validation set were slightly less likely to be classified with major depressive disorder according to the SCID.

Table 1.

Characteristics of the included participants stratified by sample.

	Calibration sample	Validation sample	p value
N	4378	4252
Age [mean (s.d.)]	50.44 (19.21)	46.69 (16.17)	<0.001
Male sex [N (%)]	1805 (41.2)	1324 (31.2)	<0.001
Country (%)			<0.001
Canada	372 (8.5)	889 (20.9)
USA	1675 (38.3)	518 (12.2)
UK	126 (2.9)	135 (3.2)
Germany	804 (18.4)	160 (3.8)
Netherlands	260 (5.9)	0 (0.0)
Australia	270 (6.2)	0 (0.0)
Brazil	347 (7.9)	0 (0.0)
Israel	151 (3.4)	0 (0.0)
Singapore	113 (2.6)	0 (0.0)
Iran	122 (2.8)	0 (0.0)
Italy	138 (3.2)	0 (0.0)
South Africa	0 (0.0)	679 (16.0)
Mexico	0 (0.0)	280 (6.6)
Kenya	0 (0.0)	192 (4.5)
Zimbabwe	0 (0.0)	264 (6.2)
Spain	0 (0.0)	1003 (23.6)
Myanmar	0 (0.0)	132 (3.1)
Language [N (%)]			<0.001
English	2443 (55.8)	1542 (36.3)
German	804 (18.4)	160 (3.8)
Dutch	260 (5.9)	0 (0.0)
Portuguese	347 (7.9)	0 (0.0)
Hebrew	151 (3.4)	0 (0.0)
Italian	138 (3.2)	0 (0.0)
Farsi	122 (2.8)	0 (0.0)
South African languages	0 (0.0)	679 (16.0)
Spanish	0 (0.0)	1283 (30.2)
Malay, Chinese or Tamil	113 (2.6)	0 (0.0)
Kiswahili	0 (0.0)	192 (4.5)
Shona	0 (0.0)	264 (6.2)
Burmese	0 (0.0)	132 (3.1)
Method of PHQ-9 administration [N (%)]			<0.001
Face to face	1462 (33.4)	1693 (39.8)
Internet	198 (4.5)	176 (4.1)
Self-administered (mail)	873 (19.9)	164 (3.9)
Self-administered (in research setting)	1845 (42.1)	2219 (52.2)
Method of SCID administration [N (%)]			<0.001
Face to face	3180 (72.6)	3477 (81.8)
Computerized (no interviewer)	147 (3.4)	0 (0.0)
Phone	1051 (24.0)	775 (18.2)
Participant recruitment setting [N (%)]			<0.001
Primary Care	1085 (24.8)	1399 (32.9)
Outpatient care	2093 (47.8)	1591 (37.4)
Inpatient care	633 (14.5)	1262 (29.7)
Non-medical setting	567 (13.0)	0 (0.0)
SCID major depression = yes [N (%)]	652 (14.9)	568 (13.4)	0.044
PHQ-9 total score [mean (s.d.)]	6.81 (5.93)	6.84 (5.96)	0.801

For categorical variables, chi-square tests were performed, for continuous variables independent t tests. M = mean, s.d. = standard deviation, N = sample size.

Estimation of latent factor models

Table 2 shows the loadings of the three latent factor models as well as their fit indices and the correlations of factor scores with the PHQ-9 sum score. Overall, in each model, we observed high loadings of the main factors, indicating that the variance within items can be well explained by the imposed latent variables. Loadings of the specific factors in the bi-factor model were low, indicating that most of the observed variance can be explained by the general factor. Likelihood ratio tests indicated that compared to the bi-factor model, the two-dimensional model had significantly worse fit to the data (robust delta chi-square = 238.2, df = 27, p < 0.001). The unidimensional model fitted the data as well as the two-dimensional model (robust delta chi-square = 0.843, df = 1, p = 0.36). Fit indices also suggest that the bi-factor model fitted the data best, with RMSEA (<0.08) and CFI (>0.95) meeting rule of thumb thresholds. The correlations between latent factor scores from all models and the PHQ-9 sum score were all >0.97, except for the specific factors in the bi-factor model.

Table 2.

Loadings, correlation with sum score and fit indices of the three latent variable models in the calibration sample

		Unidimensional model	Two-dimensional model		Bi-factor model
	Item		Cognitive-affective	Somatic factor	General factor	Cognitive-affective	Somatic factor
Loadings	PHQ-9 1	0.88 (0.01)	0.86 (0.01)		0.84 (0.01)	0.11 (0.02)
	PHQ-9 2	0.91 (0.01)	0.89 (0.01)		0.88 (0.01)	0.35 (0.03)
	PHQ-9 3	0.70 (0.03)		0.67 (0.01)	0.60 (0.01)		0.33 (0.02)
	PHQ-9 4	0.81 (0.02)		0.82 (0.01)	0.73 (0.01)		0.34 (0.02)
	PHQ-9 5	0.73 (0.03)		0.72 (0.01)	0.64 (0.01)		0.33 (0.02)
	PHQ-9 6	0.85 (0.02)	0.81 (0.01)		0.79 (0.01)	0.17 (0.03)
	PHQ-9 7	0.81 (0.02)	0.75 (0.01)		0.77 (0.01)	−0.18 (0.03)
	PHQ-9 8	0.77 (0.02)	0.72 (0.01)		0.75 (0.01)	−0.28 (0.03)
	PHQ-9 9	0.82 (0.02)	0.76 (0.01)		0.75 (0.01)	0.12 (0.03)
	correlation with PHQ-9 Sum Score	0.97	0.97	0.97	0.97	0.18	0.42
Model Fit	Robust chi-square	3447.80	2971.95		2720.10
	Degree of freedom	1186	1185		1158
	p value	<0.001	<0.001		<0.001
	CFI	0.940	0.953		0.959
	RMSEA (95% CI)	0.092 (0.088; 0.095)	0.082 (0.078; 0.085)		0.077 (0.073; 0.081)
	SRMR	0.083	0.100		0.097

CFI: comparative fit index, RMSEA: root mean square error of approximation, SRMR: standardized root mean square residual.

A graphical representation and the full specification of the models including thresholds and scaling factors, which we used for scoring, can be found in the supplementary material 3.

Identification of optimal cut-offs and comparison of diagnostic accuracy

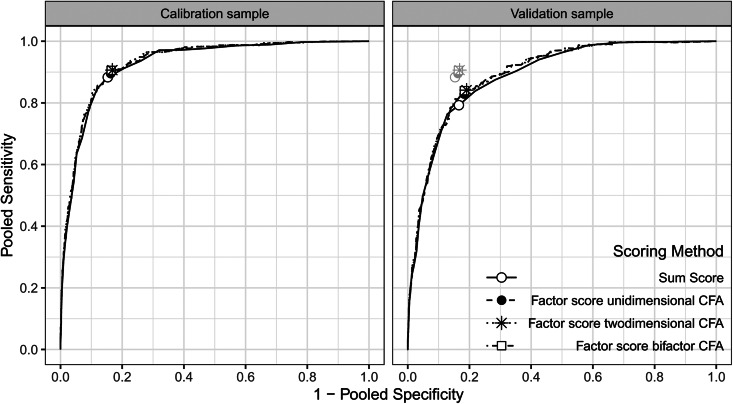
Figure 1 shows the ROC plots for the different scoring methods in the calibration and validation samples. In the calibration sample, the curves almost perfectly overlap, suggesting no meaningful difference between the scoring methods in terms of diagnostic accuracy. Given that there are substantially more potential thresholds in the latent variable models, these showed an irrelevant increase in AUC (0.927 for the sum score, 0.931 for the unidimensional, 0.932 for the two-dimensional and 0.933 for the bi-factor model). In the validation sample, overall screening accuracy was lower for all scoring methods than in the calibration sample (AUC = 0.890, 0.896, 0.897 and 0.898, respectively).

Fig. 1.

ROC Curves comparing diagnostic accuracy of the sum score and the latent variable models in the calibration and validation sample.

Table 3 shows the results of the meta-analysis and the optimal cut-offs identified in the calibration sample. The optimal cut-offs for the two-dimensional and the bi-factor model yielded a 0.01 larger combined sensitivity and specificity compared to the sum score and the unidimensional model in the calibration sample (see Table 3). Across scoring methods, estimates of heterogeneity (τ², R, see Table 3) were similar. Examination of forest plots (Supplementary Material 4) indicated that there was no apparent difference in heterogeneity of sensitivity and specificity between studies under the different scoring approaches.

Table 3.

Estimates from the IPD meta-analyses for each model's cut-off maximizing combined sensitivity and specificity

Outcome	Threshold	TP	FP	TN	FN	Pooled Sensitivity	Pooled Specificity	Combined Sensitivity Specificity	Measures of heterogeneity
									τ2 (Sensitivity)	τ2 (Specificity)	R (Sensitivity)	R (Specificity)
Sum score	10.00	554	607	3279	102	0.88 (0.81; 0.93)	0.85 (0.81; 0.88)	1.73	1.08	0.31	2.59	2.81
Single factor from unidimensional model	0.58	560	645	3241	96	0.90 (0.83; 0.94)	0.84 (0.80; 0.87)	1.73	1.11	0.33	2.61	2.92
Cognitive-affective factor from two-dimensional model	0.58	567	644	3242	89	0.91 (0.84; 0.94)	0.84 (0.80; 0.87)	1.74	1.04	0.30	2.55	2.82
General factor from bi-factor model	0.57	569	668	3218	87	0.91 (0.85; 0.94)	0.83 (0.80; 0.86)	1.74	1.02	0.30	2.51	2.83

TP = true positives, FP = false positives, TN = true negatives, FN = false negatives, τ² = tau squared.

Bootstrapping indicated that observed differences in the area under the curve were very small [_ΔAUC_{onedimensional – sum score} = 0.006 (95%-CI: 0.000–0.013, p = 0.044), _ΔAUC_{two−dimensional – sum score} = 0.007 (0.000–0.015, p = 0.050), _ΔAUC_{bi−factor – sum score} = 0.007 (0.000–0.015, p = 0.054)]. Bootstrapping the differences of sensitivity, specificity and combined sensitivity and specificity in the validation sample showed that the optimal cut-off of the two-dimensional model had a 0.0503 (0.0000–0.1048) point higher sensitivity when compared to the sum score's optimal cut-off (Table 4). This gain in sensitivity was achieved at the expense of a 0.0257 (0.0059–0.0506) point loss in specificity. The bootstrapped confidence intervals indicated that these differences were not statistically significant as the confidence intervals covered 0. However, despite the very large dataset, the CI does not allow us to exclude the possibility of a 5% advantage as well.

Table 4.

Mean differences of (combined) sensitivity, specificity between optimal cut-offs of latent factor models and sum score along with bootstrapped 95% confidence interval in parentheses

	ΔAUC	Difference in sensitivity	Difference in specificity	Difference in combined sensitivity and specificity
Unidimensional model – Sum Score	0.006 (0.000–0.013)	0.0356 (−0.0116; 0.0886)	−0.0174 (−0.0328; −0.0029)	0.0182 (−0.0303; 0.0717)
Two-dimensional model – Sum Score	0.007 (0.000–0.015)	0.0503 (0.0000; 0.1048)	−0.0257 (−0.0506; −0.0059)	0.0246 (−0.0301; 0.0836)
Bi-factor model – Sum Score	0.007 (0.000–0.015)	0.0486 (−0.0041; 0.1041)	−0.0185 (−0.0414; 0.0009)	0.0300 (−0.0253; 0.0919)

Discussion

We compared the screening accuracy of scores predicted with commonly used confirmatory factor analysis models of the PHQ-9 to the sum score. Overall, there was no clinically meaningful gain in screening accuracy from employing such scoring methods in screening for major depression. Most of the observed increase in sensitivity when using the two-dimensional or bi-factor model was obtained at the expense of a decrease in specificity and combined sensitivity and specificity did not significantly differ between scoring methods. Therefore, the use of latent variable modeling does not improve the less than ideal positive and negative predictive values of the PHQ-9 sum score (Levis et al., 2018).

We fitted three different factor models, all of which have been previously found to fit observed PHQ-9 data reasonably well in various samples (Arnold et al., 2020; Arrieta et al., 2017; Beard et al., 2016; Chilcot et al., 2018, 2013; Choi et al., 2014; Doi et al., 2018; Elhai et al., 2012; Forkmann et al., 2013; Harry & Waring, 2019; Kocalevent et al., 2013; Merz et al., 2011; Miranda & Scoppetta, 2018; Patel et al., 2019; Wahl et al., 2014). Overall, we found that the bifactor model fitted the data best and that neither the one- nor the two-dimensional model met common thresholds for approximate model fit. However, the observed differences in model fit came with trivial model changes – e.g. the correlation between cognitive/affective and somatic factors in the two-dimensional is 0.89, suggesting that these factors are hardly different. Also, the high correlation with the sum score indicates very modest differences between the models. Importantly, the observed differences in model fit did not reflect a meaningful difference in diagnostic accuracy.

Across samples we constrained the measurement parameters to be the same, essentially imposing measurement invariance. Despite the large number of equality constraints imposed across studies, fit indices of the models were above or close to commonly used cut-offs indicating appropriate goodness of fit. Hence, the assumption of complete measurement invariance across studies seems justifiable and is in line with earlier research on the PHQ-9, which showed only small deviations from measurement invariance in various samples (Baas et al., 2011; Cook et al., 2017; Harry & Waring, 2019; Keum, Miller, & Inkelas, 2018; Patel et al., 2019; Tibubos et al., 2018). In principle, violations of measurement invariance between samples could be responsible for less than ideal diagnostic accuracy of factor scores. The assumption of measurement invariance was, however, considered necessary, as in any screening setting, there would be no way to concurrently estimate sample-specific measurement parameters for the specific sample and use a predetermined cut-off at the same time.

Our findings also suggest that, over a large number of studies, neither accounting for potential violations of unidimensionality of the PHQ-9 nor weighting of item responses leads to a substantial increase in the predictive validity of the PHQ-9. The above-mentioned studies investigating latent factor models of the PHQ-9 relied heavily on approximate goodness of fit measures and did not incorporate external measures of validity. It remains unclear whether in these single studies there was indeed meaningfully different measurement parameters or if a better fit of more complex models was due to overfitting. It seems advisable to investigate whether the use of complex latent factor models leads to an improved validity in view of some external criterion.

We found that the calibration and validation sets differed significantly in terms of participant and study characteristics, except for the mean PHQ-9 scores. The size of the observed sample differences was clinically meaningful; e.g., the percentage of male participants was about 10% higher in the calibration sample. Also, age and language of PHQ-9 administration showed substantial differences between both samples. It is possible that these differences might be responsible for the overall lower diagnostic accuracy in the validation sample, although a simple alternative explanation is that accuracy in the calibration sample was explicitly maximized, and the same model parameters were then used in the validation sample. The differences between calibration and validation samples can be explained due to the fact that we did not randomly split the data, but used data accrued at different times. Given that screening tools are commonly developed in a calibration sample and then subsequently applied in different populations, our approach resembles common research practice and adds to the external validity of our findings. Analysis based on a random split replicates that use of latent variable scores instead of the sum score does not improve diagnostic accuracy (see supplementary material 6).

A major strength of this study is the large number of studies and participants included. The collected data covers a wide variety of potential settings for depression screening. Furthermore, data collection (Thombs et al., 2014) and this specific analysis (https://osf.io/ytpez/) were prespecified. We deviated from the prespecified analysis plan only in two respects. First, we imposed a narrower grid of potential thresholds for the latent factor models than originally planned. Second, to account for the fact that higher sensitivity may come at the expense of lower specificity, we also bootstrapped combined sensitivity and specificity as an overall measure of diagnostic accuracy for a given cut-off.

Although not observed in this study, there are cases where the performance of sum scores and factor scores may differ more considerably. It is often noted that sum scores and factor scores have a very strong correspondence, often correlating above 0.95 (Embretson & Reise, 2000) and diverging mostly in the case of extreme scores. If given a unidimensional model, these two scoring approaches would tend to diverge more if loadings (and thresholds) are very heterogeneous across items. With nine items, the PHQ-9 also represents a relatively short assessment tool. If typical assumptions underlying latent variable models were to hold, it is possible that a larger item pool coupled with appropriate test assembly (a short-form or computer adaptive test) could provide better measurement precision for individual respondents or around a potential cut score on the latent variable. Thus, improvement of screening accuracy beyond the PHQ-9, with potentially fewer or a similar number of administered items, is still theoretically possible.

A limitation of this study is that we did not investigate whether scores from latent variable models have better screening accuracy in specific subgroups. For example, it is reasonable to assume that symptoms of depression manifest differently across the lifespan, cultural background or health status. Separating cognitive/affective and somatic symptoms of depression might in particular warranted in participants with severe somatic illnesses. However, it was not possible to explore this question due to variation between included studies in whether, and how such information was collected. Overall, the literature search might not be exhaustive, since it did not cover all potentially relevant databases. However, earlier research has shown that the large majority of eligible studies can be identified through a specific Medline search. A further potential limitation is that not all potentially eligible studies could be included in the IPDMA database and that we included only the subset of studies which used the SCID as reference standards given the different performance of interview reference standards (Levis et al., 2018; Levis et al., 2019; Wu et al., 2020), and provided item-level data.

In conclusion, the choice between different measurement models did not affect the diagnostic accuracy of the PHQ-9 and scoring based on latent factor models of the PHQ-9 did not improve diagnostic accuracy clinically meaningful when screening for depression. Although the underlying factorial structure of the PHQ-9 has been contested and given the simplicity of calculation, the PHQ-9 sum score is preferable in an applied setting, although its measurement model might be considered unrealistic.

Author contributions

BLevis, JPAI, PC, IS, SBP, RCZ, SM (DEPRESSD Steering Committee Members), ABenedetti, and BDT (DEPRESSD Directors) were responsible for the conception, design and oversight of the main IPDMA project of which the present study is a part. FF, CF, BLevis, JPAI, PC, IS, ABenedetti, and BDT were responsible for the conception and design of the present study. JB and LAK designed and conducted database searches to identify eligible studies. SBP, DA, LA, HRB, ABeraldi, CNB, CHB, GC, MHC, DC, KC, YC, CDQ, JRF, LJG, EPG, CGG, NJ, MEK, YK, MAL, SRL, BLöwe, RAM, LM, BPM, LN, FLO, AP, SLP, TJQ, AGR, EHS, ASidebottom, ASimning, LS, PLLT, MTR, AT, HCvW, LIW, and JW contributed primary datasets that were included in this study. BLevis, YS, BDT, CH, AK, YW, ZN, PMB, DN, DBR, KER, NS, MA, and MI contributed to data extraction and coding for the meta-analysis.

FF, CF, BLevis, ABenedetti, and BDT contributed to data analysis and interpretation. FF, CF, BLevis, ABenedetti, and BDT contributed to drafting the manuscript. All authors provided a critical review and approved the final manuscript. ABenedetti and BDT are the guarantors; they had full access to all the data in the study and took responsibility for the integrity of the data and the accuracy of the data analyses.

Acknowledgements

This study was funded by the Canadian Institutes of Health Research (CIHR; KRS-134297, PCG-155468). Felix Fischer was supported by Deutsche Forschungsgemeinschaft (Fi 1999/6-1). The primary study by Fischer et al. was funded by the German Federal Ministry of Education and Research (01GY1150). Dr. Levis was supported by a Fonds de recherche du Québec - Santé (FRQS) Postdoctoral Training Fellowship. Drs. Benedetti and Thombs were supported by FRQS researcher salary awards. Dr. Wu was supported by a FRQS Postdoctoral Training Fellowship. Mr. Bhandari was supported by a studentship from the Research Institute of the McGill University Health Centre. Ms. Neupane was supported by G.R. Caverhill Fellowship from the Faculty of Medicine, McGill University. Ms. Rice was supported by a Vanier Canada Graduate Scholarship. Ms. Riehm and Ms. Saadat were supported by CIHR Frederick Banting and Charles Best Canada Graduate Scholarship master's awards. The primary studies by Fiest et al., Patten et al., Amoozegar et al., and Prisnie et al. were supported by the Cumming School of Medicine, University of Calgary, and Alberta Health Services through the Calgary Health Trust, as well as the Hotchkiss Brain Institute. Dr. Patten was supported by a Senior Health Scholar Award from Alberta Innovates Health Solutions. Dr. Jetté was supported by a Canada Research Chair in Neurological Health Services Research and an AIHS Population Health Investigator Award. The primary study by Amtmann et al. was supported by a grant from the Department of Education (NIDRR grant number H133B080025) and by the National Multiple Sclerosis Society (MB 0008). Data collection for the study by Ayalon et al. was supported by a grant from Lundbeck International. The primary study by Khamseh et al. was supported by a grant (M-288) from Tehran University of Medical Sciences. The primary studies by Marrie et al. and Bernstein et al. were supported by CIHR (THC-135234) and Crohn's and Colitis Canada. Dr. Bernstein was supported in part by the Bingham Chair in Gastroenterology. Dr. Marrie was supported by the Waugh Family Chair in Multiple Sclerosis and the Research Manitoba Chair, and CIHR grants, during the conduct of the study. The primary study by Bhana et al. was the output of the PRogramme for Improving Mental health carE (PRIME) and was supported by the UK Department for International Development (201446). The views expressed do not necessarily reflect the UK Government's official policies. The primary study by Bombardier et al. was supported by the Department of Education, National Institute on Disability and Rehabilitation Research, Spinal Cord Injury Model Systems: University of Washington (grant no. H133N060033), Baylor College of Medicine (grant no. H133N060003), and University of Michigan (grant no. H133N060032). The primary study by Chibanda et al. was supported by a grant from Grand Challenges Canada (0087-04). Dr. Conwell received support from NIMH (R24MH071604) and the Centers for Disease Control and Prevention (R49 CE002093). The primary study by Martin-Subero et al. was supported in part by a grant from the Spanish Ministry of Health's Health Research Fund (Fondo de Investigaciones Sanitarias, project 97/1184). Collection of data for the primary study by Gjerdingen et al. was supported by grants from the NIMH (R34 MH072925, K02 MH65919, P30 DK50456). The primary study by Green et al. (2018) was supported by a grant from the Duke Global Health Institute (453-0751). The primary study by Eack et al. was funded by the NIMH (R24 MH56858). The primary study by Haroz et al. was supported by the United States Agency for International Development Victims of Torture Fund: AID-DFD A-00-08-00308. The primary study by Lara et al., was supported by the Consejo Nacional de Ciencia y Tecnología/National Council for Science and Technology (CB-2009-133923-H). The primary studies by Osório et al. (2012) were funded by Reitoria de Pesquisa da Universidade de São Paulo (grant number 09.1.01689.17.7) and Banco Santander (grant number 10.1.01232.17.9). Dr. Osório was supported by Productivity Grants (PQ-CNPq-2 -number 301321/2016-7). Dr. Löwe received research grants from Pfizer, Germany, and from the medical faculty of the University of Heidelberg, Germany (project 121/2000) for the study by Gräfe et al. Collection of data for the primary study by Williams et al. was supported by a NIMH grant to Dr Marsh (RO1-MH069666). Dr. Marx was supported by the Department of Defense (W81XWH-08-2- 0100/W81XWH-08-2-0102 and W81XWH-12- 2-0117/W81XWH-12-2-0121). The primary study by Picardi et al. was supported by funds for current research from the Italian Ministry of Health. The primary study by Wagner et al. was supported by grants U10CA21661, U10CA180868, U10CA180822, and U10CA37422 from the National Cancer Institute. The study was also funded in part by a grant from the Pennsylvania Department of Health. The department specifically declaims responsibility for any analyses, interpretations, or conclusions of the primary study. The primary study by Rooney et al. was funded by the United Kingdom National Health Service Lothian Neuro-Oncology Endowment Fund. The primary study by Shinn et al., was supported by grant NCI K07 CA 093512 and the Lance Armstrong Foundation. The primary study by Sidebottom et al. was funded by a grant from the United States Department of Health and Human Services, Health Resources and Services Administration (grant number R40MC07840). Simning et al.'s research was supported in part by grants from the NIH (T32 GM07356), Agency for Healthcare Research and Quality (R36 HS018246), NIMH (R24 MH071604), and the National Center for Research Resources (TL1 RR024135). The primary study by Spangenberg et al. was supported by a junior research grant from the medical faculty, University of Leipzig. Collection of data for the studies by Turner et al. (2012) were funded by a bequest from Jennie Thomas through the Hunter Medical Research Institute. The study by Wittkampf et al. was funded by The Netherlands Organization for Health Research and Development (ZonMw) Mental Health Program (nos. 100.003.005 and 100.002.021) and the Academic Medical Center/University of Amsterdam. No other authors reported funding for primary studies or for their work on this study. No funder had any role in the design and conduct of the study; collection, management, analysis, and interpretation of the data; preparation, review, or approval of the manuscript; and decision to submit the manuscript for publication.

Conflict of interest

All authors have completed the ICJME uniform disclosure form at www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare no support from any organisation for the submitted work other than that described above; no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years with the following exceptions: Dr Bernstein declares that he has consulted to Abbvie Canada, Amgen Canada, Bristol Myers Squibb Canada, Roche Canada, Janssen Canada, Pfizer Canada, Sandoz Canada, Takeda Canada, and Mylan Pharmaceuticals. He has also received unrestricted educational grants from Abbvie Canada, Janssen Canada, Pfizer Canada, and Takeda Canada; as well as been on speaker's bureau of Abbvie Canada, Janssen Canada, Takeda Canada and Medtronic Canada, all outside the submitted work. Dr Pugh declares that she received salary support from Pfizer-Astella and Millennium, outside the submitted work. Dr Wagner declares that she receives personal fees from Celgene, outside the submitted work. No other relationships or activities that could appear to have influenced the submitted work.