Abstract
Understanding how to catalytically break the C–H bond of aromatic molecules, such as polycyclic aromatic hydrocarbons (PAHs), is currently a big challenge and a subject of study in catalysis, astrochemistry, and planetary science. In the latter, the study of the breakdown reaction of PAHs on mineral surfaces is important to understand if PAHs are linked to prebiotic molecules in regions of star and planet formation. In this work, we employed a periodic density functional theory along with Grimme’s D4 (DFT-D4) approach for studying the adsorption of a sample of PAHs (naphthalene, anthracene, fluoranthene, pyrene, coronene, and benzocoronene) and fullerene on the [010] forsterite surface and its defective surfaces (Fe-doped and Ni-doped surfaces and a MgO-Schottky vacancy) for their implications in catalysis and astrochemistry. On the basis of structural and binding energy analysis, large PAHs and fullerene present stronger adsorption on the pristine, Fe-doped, and Ni-doped forsterite surfaces than small PAHs. On a MgO-Schottky vacancy, parallel adsorption of the PAH leads to the chemisorption process (C–Si and/or C–O bonds), whereas perpendicular orientation of the PAH leads to the catalytic breaking of the aromatic C–H bond via a barrierless reaction. Spin density and charge analysis show that C–H dissociation is promoted by electron donation from the vacancy to the PAH. As a result of the undercoordinated Si and O atoms, the vacancy acts as a Frustrated Lewis Pair (FLP) catalyst. Therefore, a MgO-Schottky vacancy [010] forsterite surface proved to have potential catalytic activity for the activation of C–H bond in aromatic molecules.
Keywords: periodic DFT-D4, PAHs, fullerene, forsterite, astrochemistry, cosmochemistry, catalysis
Introduction
The study of the reactivity of organic molecules as feedstock for the formation of precursors of complex molecular species is the focus of organic chemistry, materials science, catalysis, astrochemistry, and planetary science.1−4 The orbital interaction of an sp2 carbon with an s orbital of a hydrogen atom forms a strong C–H bond with a bonding energy of about 4.6 eV, which we can find in aromatic species such as benzene5 and polycyclic aromatic hydrocarbons (PAHs).6 Shedding light on the activation of the aromatic C–H bond is the first step to understand the reactivity of aromatic molecules.7 PAHs lock up about 20% of carbon in the universe, whereas 80% is locked up in other species. PAHs might be linked to other organic molecules because they can act as a carbon feedstock; therefore, studying their reactivity is also important for understanding the chemical evolution of our universe.4
Finding Earth-abundant materials that are able to activate and catalyze the C–H bond breaking of aromatic species is still a big challenge because of its high bond energy and high stability. Synthetic transition-metal catalysts such as Wilkinson’s (rhodium-based),8 palladium,9,10 and iridium catalysts11 are able to break the aromatic C–H bond. However, these catalysts are harmful to human health and, moreover, very expensive.12 Recently, metal-free catalysts such as frustrated Lewis pairs13 (FLPs), formed by a Lewis acid and bases that cannot bind together as a result of steric hindrances, have been studied because they can activate aromatic hydrocarbons.14
Mineral-bearing materials are organized periodic systems and have been considered as cheap and safe alternatives to synthetic catalysts.15 In fact, mineral surfaces have active inorganic interfaces that can host molecular species and possibly activate them.16 Hence, minerals catalyze processes that are thermodynamically favorable but kinetically hindered by high energy barriers.17
Forsterite (Mg2SiO4) is one of the most abundant olivinic minerals available on Earth and in space.18,19 Experimental studies have reported the potential catalytic role of forsterite and Fe-doped forsterite for the conversion of methanol to olefine and PAHs.20,21 However, theoretical and mechanistic studies on the catalytic activity of forsterite are currently lacking. Only a few studies have addressed the interaction of organic species with a forsterite surface using first-principle methods.22−24
In this work, we use periodic density functional theory (DFT) along with Grimme’s D4 method25 (DFT-D4) to study the adsorption and C–H activation of PAHs (naphthalene, anthracene, fluoranthene, pyrene, coronene, and benzocoronene) on the pristine [010] forsterite surface ([010]-fo).19,22,26,27 Along with the pristine [010]-fo surface, we also study the defective surfaces of [010] forsterite28 containing Fe dopant (Fe-[010]-fo),29,30 Ni dopant (Ni-[010]-fo),22 and MgO-Schottky vacancy (VMgO-[010]-fo).31 Defects are ubiquitous, at different concentrations, in all crystalline mineral structures.32 They are often promoted by the radiation of isotopic decay, or by high temperatures during crystal growth, and can be of different natures, that is, bulk, planar, line, and point defects.32 A small amount of Fe and Ni in olivine is generally present,28,33,34 whereas the presence of a MgO-Schottky vacancy might have been the result of the reaction of olivine with a small amount of water.35
We also include the adsorption of C60 onto forsterite as this molecule is abundant in space.36,37 We analyze the geometrical parameters and adsorption energies for the adsorption of PAHs and C60 as well as the energy barriers and the electronic structure associated with the C–H bond dissociation of PAHs only on the vacancy forsterite surface. As it is not fully understood whether astronomically PAHs might be formed in situ on forsterite or adsorbed on forsterite after they are formed in the gas phase,18 we report, along with the adsorption energies, the binding energies that might be used for astronomical modeling to predict their abundance and formation. This study aims to understand the surface chemistry of aromatic molecules in interstellar space and on solar system bodies as well as the role of minerals as potential catalysts.
Theoretical Methods
Forsterite and PAH Structures
In this study, we model the crystalline nonpolar [010]-fo surface (Mg96O192Si48) and its defective surfaces under dry conditions, shown in Figure 1.
Figure 1.

Optimized slab models of [010] forsterite at two different orientations: (a) [010]-fo, (b) Fe-[010]-fo, (c) Ni-[010]-fo, and (d) VMgO-[010]-fo (the location of the vacancy is indicated by the Si and O labels reported on the corresponding undercoordinated atoms). The vacuum region is located along the z-axis, and the atomic labels of the corresponding atoms (Si, Mg, O, Ni, and Fe) are reported.
All models have a 19 × 17.94 × 35.20 Å (α = β = γ = 90°) supercell (4 × 3 × 1) with a slab thickness of 9.25 Å. The [010] slab surfaces were generated by cutting the optimized bulk of forsterite from a prior study22 using the METADISE code.38 The bottom layers (about 4 Å thickness) have been constrained during the whole optimization procedure, whereas the topmost layers were allowed to relaxed unconstrainedly. The presence of defects has proved to increase the reactivity and catalytic activity of several materials.39−41 Therefore, we decided to model the defective surfaces of [010]-fo by replacing an undercoordinated Mg atom on the surface with only one transition metal (e.g., Fe and Ni for this work) and optimizing the resulting slab model. Furthermore, VMgO-[010]-fo is created by removing a MgO unit from the [010]-fo surface, again followed by a reoptimization of the slab. Hence, the pristine surface is characterized by 12 Mg atoms facing the vacuum region, whereas the defective surfaces are characterized by only 11 Mg atoms facing the vacuum region.
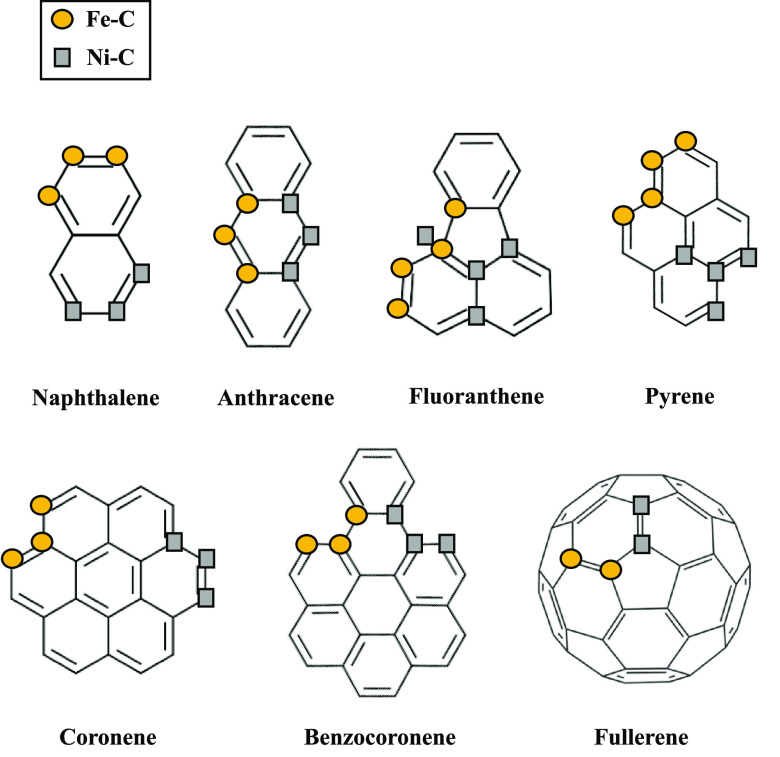
The PAHs taken into consideration in this study are naphthalene, anthracene, pyrene, fluoranthene, coronene, benzocoronene, and fullerene. These species (Figure 3 as well as Figures S7–S13 in the Supporting Information) are characterized by honeycomb structures of fused hexagonal carbon rings bound with hydrogen atoms on their edges. Fluoranthene is the only PAH with a five-membered ring. The fullerene, C60, is characterized by a spherical shape (buckyball) with hexagonal and pentagonal rings bound together, forming [6,6] and [5,6] ring junctions (Figure S13), which are bridge C atoms of two hexagonal rings and hexagonal-pentagonal rings, respectively. The gas-phase model of PAHs has been optimized in a cubic unit cell with sides of 15 Å.
Figure 3.
The skeleton structure of PAHs and the location of carbon–transition-metal interactions less than 3 Å (see the Supporting Information), on the PAH structure, when they adsorb on the Fe and Ni-[010]-fo. The legend shows the symbol related to C–Fe (circles) and C–Ni (squares) interactions.
Calculation Setup
The slab models were optimized using periodic density functional theory implemented in the SIESTA code,42 which makes use of localized atomic orbitals basis sets (LCAO). The details of the method have been described as well as benchmarked in a prior work22 and are summarized here.
The Perdew–Becke–Ernzerhof43 (PBE) exchange-correlation functional has been employed along with the DZP basis set using the core pseudopotentials and setting the radii of the split valence type for the hydrogen atoms to 0.5. The counterpoise correction44,45 is taken into account for all calculations to correct for the basis set superposition error.
The dispersion energy is taken into account a posteriori, on the optimized geometry at the PBE/DZP level, employing Grimme’s DFT-D4 code.25,46,47 The Brillouin zone is sampled using a 2 × 2 × 1 Monkhorst–Pack48k-point grid for all surfaces with a unit cell of 18.996 × 17.938 Å and 1 × 1 × 1 Monkhorst–Pack k-point grid for the gas-phase models (reagents). The mesh cutoff is set to 200 Ry (see the Supporting Information of our previous work22). All calculations are run with the spin-unrestricted formalism, and convergence is reached when the forces are lower than 0.01 eV Å –1. All structures are optimized using the limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) algorithm.49 An electric field along the z-axis is set to override the resulting dipole moment along the z-axis of the slabs during the optimization procedure. In a prior study,22 PBE-D4/DZP was proven to be a robust theory level to study the interaction of aromatic molecules on mineral surfaces.
We analyzed the electronic structure of the vacancy surface with the spin-density isosurfaces and the population analysis charge based on the Voronoi scheme.50 These techniques allow us to define the spin-up and spin-down population (spin density) of each atom as well as the electronic donation and acceptance between the atoms (partial atomic charges). The spin density and charge analysis have been calculated at the PBE+U level of theory with a single-point calculation using TZP on the optimized DZP geometry with supplementary 4 × 4 × 1 Monkhorst–Pack’s k-points. The Hubbard U value, using the LDA+U method,51 is set to 15.3 eV to describe the strong on-site Coulomb interaction of the localized electrons of the 2p orbitals of the oxygen atoms to reproduce the experimental band gap (8.4 eV).52 A threshold tolerance of 10–2 and a tolerance population of 4 × 10–4 are selected for the LDA+U method. The radii for the split-valence type of TZP for all atoms, excluding hydrogen, are set up to be 0.30. The reaction barriers (e.g., the characterization of a saddle point) and the minimum energy path are calculated using the climbing-image nudged elastic band method53 (CI-NEB) implemented in the atomistic simulation environment54,55 python module employing SIESTA as a calculator. The minimum energy path is optimized through linear interpolation of the reagent and the product by six images. Each image can be thought of as a representation along the reaction path with all images interconnected by springs. The optimization focuses on finding the lowest energy possible for each image, and the maximum one only for one image, while maintaining the constraint that they are equally spaced with respect to neighboring images. Note that, after optimization of the CI-NEB path, the energies of the images represent the minimum energy path from the initial to the final geometry. The path is optimized using the Fast Inertial Relaxation Engine (FIRE)56 algorithm, which provides robust results compared to those from quasi-Newton methods.57 The spring constant is set to 0.1 eV/Å, and the six images between the reagent and the product are considered optimized when the forces are lower than 0.025 eV/Å.
In this work, the binding energy (Ebind) is defined as
| 1 |
Emol is the energy of the optimized molecule in the gas phase, Eslab is the energy of the optimized forsterite slab, and Emol–slab is the energy of the optimized adsorbed molecule on the forsterite slab. Positive and negative binding energy values show exoergic and endoergic adsorption processes, respectively.
The adsorption energy (Eads) is defined as
| 2 |
Eproduct is the energy of the optimized product. For this definition, Eads= −Ebind. Therefore, negative and positive values of Eads show exoergic and endoergic processes, respectively.
Harmonic frequencies of PAHs adsorbed onto a vacancy surface are computed to compare different adsorption configurations that differ from the position of an H atom. The zero-point energy correction (EΔZP) is calculated as
| 3 |
EZPads is the zero-point energy correction of PAH adsorbed onto a vacancy forsterite surface where only the PAH was allowed to vibrate and EZPmol is the zero-point energy of the PAH in the gas phase. The resulting corrected zero-point adsorption energy is the sum of Eads and EΔZP.
We define contact points (C.P.) as the sum of orbital interactions between the p orbital of a C atom with the 3p orbital of an Mg atom and 3d orbital of Fe and Ni atoms. The surface area of each PAHs is calculated as the sum of the area of the single hexagons and/or pentagons using the carbon backbone, that is, excluding the bound H atoms.
Results and Discussion
Structure of the [010] Forsterite Surfaces
The [010]-fo surface has an orthorhombic structure with the Pbnm space group, and differs from the bulk because of the presence of undercoordinated Mg atoms bound with three neighboring O atoms on the external layer that faces the vacuum region.
The surface structure of [010]-fo is characterized by undercoordinated Mg atoms (M1) shown in Figure 2 and fully coordinated Mg atoms (M2) located in the underlying layer. The Si (Si1) atoms on the surface are fully coordinated (tetrahedral structures). The bond distances, only for the atoms located on the surface, are reported in the table included in Figure 2 and show Mg–O and Si–O distances ranging between 1.63 and 1.90 Å. Mg, O, and Si atoms, on the surface, form zigzag edges following an alternating unit scheme: −O–Si–O–Mg–O–. The Mg–O bond lengths of the undercoordinated Mg atoms on the surface (M1) are shorter than those of the octahedral Mg–O (M2–O2) with a bond distance that ranges between 2 and 2.16 Å. All calculated bond lengths are in agreement with the DFT study carried out by Navarro-Ruiz et al.58 using LCAO methods and by Brodholt using plane wave methods.59
Figure 2.
Side-view figure that shows the labels of the atomic positions of the [010]-fo forsterite. M shows the location of an Mg, Fe, and Ni atoms or MgO vacancy. The table reports distances (d), in Angstrom (Å), and angles, in degrees (°), of the atoms found in the top figure.
We also studied the presence of point defects on the [010]-fo surface, shown in Figure 1b–d. The Fe-[010]-fo surface is characterized by an undercoordinated Fe2+ atom bound to three oxygen atoms. When the Fe is located in the M1 site, it is more stable by 0.30 eV with respect to the M2 site and 0.22 eV with respect to the M3 site. Hence, M1 is the preferred site (Figure 2). The table reported in Figure 2 shows the bond distances and angles of the Fe-[010]-fo, which are in close agreement with the geometrical parameters of the pristine surface.
Along with Fe-[010]-fo, we considered the presence of undercoordinated Ni as a point defect on the surface, Ni-[010]-fo (Figure 1 c). The location of the Ni point defect in the M1 site is slightly more stable by about 0.04 and 0.01 eV compared to those of M2 and M3, respectively. However, this difference is not significant considering the accuracy of the functional used.22 Once the transition metal coordinates with an aromatic molecule such as naphthalene, the Ni point defect in the M1 site is stabilized by 0.30 and 1.61 eV with respect to M2 and M3. The table in Figure 2 shows bond distances and angles for Ni-[010]-fo, which are in close agreement with those for Fe-[010]-fo and [010]-fo. Overall, the presence of transition metals does not significantly change the forsterite structure as compared to the pristine [010]-fo structure. The stability of the transition metals on the surface, as reported by the study of Navarro-Ruiz et al.,29 is due to the need to stabilize the high-spin state (quintet for Fe and triplet for Ni), reducing the Fe or Ni–O electronic repulsion in the bulk caused by the size of these atoms.
Another type of defect occurring in crystalline structures is the MgO-Schottky defect, which can be formed when a cation–anion pair is removed, resulting in a vacancy.60 The energy required to form the Schottky-MgO vacancy defect is about 7 eV for the bulk35 and 11.85 eV on the surface, as computed by us. For comparison, SiO2 vacancies are less favorable because the formation energy is about 20 eV for the bulk35 and 14.23 eV for SiO removed from the surface, as computed by us. As the formation energies of these vacancies are large, we expect that the abundance must be low, which justifies the choice of modeling only one MgO vacancy on the surface (further discussion is reported in “Astrochemical and Cosmochemical Implications”). The presence of the Schottky MgO vacancy (VMgO-[010]-fo), shown in Figure 1d, causes an interruption of the zigzag units, resulting in the formation of a SiO32– unit and O atoms that bridge an Mg and Si atom. The absence of an MgO unit does not allow the formation of a bond between the two distant Si and O atoms on the surface. The distance between the unbound Si and O atoms, the two labeled atoms in Figure 1d, in the vacancy is about 5.12 Å, causing the formation of a cavity. The table in Figure 2 shows that the Si–O distances are slightly shorter than those of other surfaces. Instead, the O atom that lacks a neighboring Mg atom because of the vacancy (Figure 1d) binds with a second neighbor, Si (Si1), which has a distance of 1.61 and 1.97 Å with the Mg located in the M2 site. Therefore, the cavity formation (see the structure in Figure 10a) causes a bond length reorganization to compensate for the absence of an Mg atom. The MgO vacancy is more stable when located on the surface in the M1 site by about 2.90 eV with respect to the M2. Hence, M1 is the most favorable site for all three defects considered in this study.
Figure 10.
Spin-density isosurface (isovalue 0.007 e/A3) of VMgO-[010]-fo (a) and the dissociation of the C−H bond of naphthalene on the VMgO-[010]-fo (b). Yellow density indicates the spin-up population and red density the spin-down one.
Interaction of PAHs and C60 with [010] Forsterite
Structural Analysis
Previous theoretical studies have shown that forsterite strongly binds with aromatic molecules on its surfaces.22−24
Therefore, we have selected a sample of PAHs that span a range in the surface area (Table 1) and that contain catacondensed PAHs (e.g., acenes, naphthalene, and anthracene), pericondensed PAHs (pyrene and coronene), and irregular PAHs (benzocoronene). In addition, we also selected the nonalternant aromatic species fluoranthene and fullerene. The skeleton structure of the mentioned PAHs is reported in Figure 3.
Table 1. Surface Area of PAHs and the [010] Forsterite Surfaces ([010]-fo, Fe-[010]-fo, Ni-[010]-fo, and VMgO-[010]-fo) Optimized in This Studya.
| surface area (Å2) | |
|---|---|
| naphthalene | 10.18 |
| anthracene | 15.28 |
| fluoranthene | 18.34 |
| pyrene | 20.37 |
| coronene | 35.64 |
| benzocoronene | 40.73 |
| forsterite surfaces (4 × 3 × 1) | 340.74 |
The average sizes of the hexagons and pentagons are 1.40 Å, which is the distance of a single C–C bond.
We optimized all structures for a parallel adsorption of the molecular plane with respect to the surface. The adsorption of PAHs on the [010] forsterite surfaces causes a slight deviation of the PAH structure from their planarity (Figure 4).
Figure 4.
Side views using two different perspectives (second perspective in thumbnail) of the optimized geometries of benzocoronene adsorbed on (a) [010]-fo, (b) VMgO-[010]-fo, (c) Fe-[010]-fo, and (d) Ni-[010]-fo. Atomic labels are reported on the corresponding atoms.
This is in-line with the average dihedral angles
of the C atoms
of the PAH skeleton, reported in Table 2. The average dihedral angles do not show characteristic
planar structures of 180°. With the exception of pyrene, PAH
adsorption on [010]-fo and Fe-[010] causes a larger deviation from
planarity than that on Ni-[010]-fo in which the adsorbed molecules
have dihedral angles close to 180°. The average angles indicate
a perfect 120°, characteristic of sp2 carbons for
all PAHs with the exception of fluoranthene. The latter show larger
angle deviation from 120° with respect to the other PAHs because
of the presence of a five-membered ring that causes major bending
of its structure. The major flexibility due to the presence of a five-membered
ring has been identified also in other materials with PAH-like structures.39 The 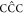 and dihedral Θ angles reported in Table 2 indicate that PAHs
adsorbed on the surface have the 120° angles expected for planar
PAHs, whereas the fullerene (C60) deviates from this by
about 6°, as expected for a buckyball-like structure (Figure 5a,b,c).61 Thus, we conclude that the adsorption process
does not induce significant changes in the conformational structure
of the PAHs relative to the gas phase, apart from a moderate loss
in planarity.
and dihedral Θ angles reported in Table 2 indicate that PAHs
adsorbed on the surface have the 120° angles expected for planar
PAHs, whereas the fullerene (C60) deviates from this by
about 6°, as expected for a buckyball-like structure (Figure 5a,b,c).61 Thus, we conclude that the adsorption process
does not induce significant changes in the conformational structure
of the PAHs relative to the gas phase, apart from a moderate loss
in planarity.
Table 2. Geometrical Parameters of PAHs Adsorbed on Forsterite Surfacesa.
|
|
|
[nC–nMg] | [nC–nM] | C.P. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| naphthalene: | |||||||||||
| [010]-fo22 | 2.61 | 120.21 | 176.18 | 5–2 | 5 | ||||||
| Fe-[010]-fo22 | 2.51 | 2.43 | 120.02 | 172.04 | 2–1 | 3–1 | 5 | ||||
| Ni-[010]-fo22 | 2.64 | 2.42 | 120.04 | 178.14 | 2–1 | 3–1 | 5 | ||||
| anthracene: | |||||||||||
| [010]-fo | 2.65 | 120.82 | 173.06 | 6–2 | 6 | ||||||
| Fe-[010]-fo | 2.70 | 2.40 | 120.47 | 176.65 | 3–2 | 3–1 | 6 | ||||
| Ni-[010]-fo | 2.73 | 2.41 | 120.38 | 177.05 | 3–2 | 3–1 | 6 | ||||
| fluoranthene: | |||||||||||
| [010]-fo | 2.68 | 125.34 | 174.68 | 7–3 | 7 | ||||||
| Fe-[010]-fo | 2.62 | 2.56 | 125.73 | 176.99 | 3–2 | 4–1 | 7 | ||||
| Ni-[010]-fo | 2.52 | 2.62 | 126.02 | 177.83 | 2–1 | 4–1 | 6 | ||||
| pyrene: | |||||||||||
| [010]-fo | 2.72 | 120.79 | 179.15 | 5–2 | 5 | ||||||
| Fe-[010]-fo | 2.64 | 2.61 | 121.19 | 175.30 | 3–1 | 4–1 | 7 | ||||
| Ni-[010]-fo | 2.66 | 2.50 | 120.86 | 177.64 | 3–1 | 4–1 | 7 | ||||
| coronene: | |||||||||||
| [010]-fo | 2.73 | 120.92 | 175.63 | 11–4 | 11 | ||||||
| Fe-[010]-fo | 2.63 | 2.51 | 120.97 | 174.78 | 7–3 | 3–1 | 10 | ||||
| Ni-[010]-fo | 2.68 | 2.46 | 120.80 | 177.90 | 5–3 | 3–1 | 8 | ||||
| benzocoronene: | |||||||||||
| [010]-fo22 | 2.71 | 120.61 | 176.29 | 11–4 | 11 | ||||||
| Fe-[010]-fo22 | 2.66 | 2.47 | 120.46 | 178.90 | 8–4 | 3–1 | 11 | ||||
| Ni-[010]-fo22 | 2.67 | 2.48 | 120.43 | 179.18 | 8–4 | 3–1 | 11 | ||||
| fullerene: | |||||||||||
| [010]-fo | 2.74 | 113.49 | 139.00 | 4–2 | 4 | ||||||
| Fe-[010]-fo | 2.10 | 106.82 | 133.63 | 2–1 | 2 | ||||||
| Ni-[010]-fo | 2.81 | 2.09 | 111.65 | 143.19 | 1–1 | 2–1 | 3 |
Reported are the average distances 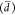 in Angstrom (Å), average angles
in Angstrom (Å), average angles 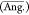 and dihedral angles
and dihedral angles 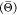 in degrees (deg), number (n) of atoms (C, Mg, or M) interacting with each other (e.g., [ nC–nMg
]), and the number of contact points (C.P.), which is the sum of C
atoms interacting with either an Mg or transition metal. The average
values are calculated from the geometrical parameters reported in
the Supporting Information. M is the transition
metal (e.g., Fe or Ni) of the corresponding surface (e.g., Fe for
Fe-[010]-fo). Missing values shows no interaction between the atoms.
in degrees (deg), number (n) of atoms (C, Mg, or M) interacting with each other (e.g., [ nC–nMg
]), and the number of contact points (C.P.), which is the sum of C
atoms interacting with either an Mg or transition metal. The average
values are calculated from the geometrical parameters reported in
the Supporting Information. M is the transition
metal (e.g., Fe or Ni) of the corresponding surface (e.g., Fe for
Fe-[010]-fo). Missing values shows no interaction between the atoms.
Figure 5.
Side views using two different perspectives (second perspective in thumbnail) of the optimized geometries of fullerene adsorbed on (a) [010]-fo, (b) Fe-[010]-fo, (c) Ni-[010]-fo, and (d) VMgO-[010]-fo. Atomic labels are reported on the corresponding atoms.
The larger the surface area of the PAHs (Table 1), the larger the number of interactions of the C atoms either with an Mg or with transition-metal dopant atoms (contact points), as shown in Table 2. Although pyrene has a larger surface area than fluoranthene, the number of contact points in pyrene is roughly the same as that in fluoranthene. This could be attributed to the more compact structure of the pyrene skeleton as compared to that of fluoranthene. With the exception of pyrene and fullerene, the number of Mg atoms interacting with the C atoms at a distance less than 3 Å increases with increasing surface area of the PAH. Therefore, the larger the surface area, the higher the number of contact points. Distances larger than 3 Å do not present orbital interactions (see Population Analysis section in the Supporting Information).
Interaction of PAHs and C60 with Doped Forsterite
Figure 3 shows the preferred carbon sites of PAHs and fullerene that interact with Fe or Ni on the surface. Naphthalene, anthracene, coronene, and benzocoronene have three transition-metal interactions located in the edge carbons of the PAHs. Fluoranthene and pyrene, instead, have four C–Fe and C–Ni interactions. Furthermore, for fluoranthene and pyrene, we noticed a different behavior from the Ni–C interactions because the optimization of the geometry led to a structure in which the inner carbon of these PAHs can interact with Ni atoms at distances smaller than 3 Å (see Geometrical Parameters section in the Supporting Information for details). Instead, fullerene has two Fe–C and Ni–C interactions located in the [6,6] ring junction.
PAHs do not adsorb with the center of the π-ring on the transition-metal-doped surfaces (Fe and Ni-[010]-fo), as seen for benzene–cation complexes (gas-phase configuration) with the same spin configuration of the surfaces (quintet for Fe2+ and triplet for Ni2+). The gas-phase configuration shows carbon–transition-metal (C–M) bond distances of about 2.28 Å for Fe2+ and 2.17 Å for Ni2+ (values calculated from the optimized geometries reported in a prior study22 and in agreement with published theoretical studies of Fe–PAH complexes in the gas phase62). The PAHs on forsterite surfaces have, as shown in Table 2, slightly larger C–M bond distances with respect to the gas-phase configuration. On a regular forsterite surface, the PAH will orient itself on the surface to interact closely with as many Mg atoms as possible. For doped surfaces, binding of PAHs is a competition of favorable orientations to interact with as many Mg atoms as possible and to optimize the interaction with the transition metal. Table 2 summarizes this competition, illustrating that, on doped surfaces, the number of C–Mg interactions decreases relative to the pristine surface but this is compensated for by the interactions with the transition metal. In general, but not always, the number of contact points remains the same. We note that the difference between the Fe–C and Ni–C bond distances of the PAHs on forsterite surfaces with respect to the gas-phase configuration, considering the optimized distance, is about 0.12–0.33 Å for Fe and 0.24–0.45 Å for Ni. Hence, PAHs can optimize the Fe–C distance on an Fe-doped surface better than that on a Ni-doped surface.
Fullerene shows smaller (Table 2) C–Fe and C–Ni distances than PAHs, resulting in a stronger interaction.
Interaction of PAHs and C60 with a Vacancy
The geometrical structures of all species adsorbed on VMgO-[010]-fo are reported separately in a table in Figure 6. The vacancy has peculiar
structures with respect to the pristine and transition-metal-doped
ones. Specifically, the adsorption of naphthalene, anthracene, fluoranthene,
benzocoronene, and fullerene have characteristic 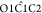 angles for the rehybridization of the C
atoms of PAHs from sp2 to sp3 (about 109°).
The C–Si bond has a short distance, about 1.9 Å, and the
angles for the rehybridization of the C
atoms of PAHs from sp2 to sp3 (about 109°).
The C–Si bond has a short distance, about 1.9 Å, and the 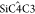 angles, about 118–120°, are
close to the geometrical parameters of silane complexes (about 120°).63 Therefore, the adsorption of these species on
the vacancy surface causes the breaking of one aromatic ring (i.e.,
a chemisorption process). The
angles, about 118–120°, are
close to the geometrical parameters of silane complexes (about 120°).63 Therefore, the adsorption of these species on
the vacancy surface causes the breaking of one aromatic ring (i.e.,
a chemisorption process). The  angles, in the table in Figure 6, show a perfect 109°
for anthracene, whereas the other PAHs slightly diverge from this
value. Hence, the surface area of anthracene allows a perfect interaction
with the vacancy. Pyrene and coronene do not show covalent bond formation.
In fact, species only with a terminal aromatic ring with four hydrogen
atoms (naphthalene, anthracene, fluoranthene, and benzocoronene) and
the six-membered ring of fullerene form covalent bonds with the undercoordinated
Si and O atoms (see C.N. in the table in Figure 6). This occurs as a result of their large
structural flexibility with respect to more compact structures such
as pyrene and coronene. The coordination number of O and Si increases
once PAHs adsorb on the vacancy forsterite surface, in-line with the
formation of C–O and C–Si bonds. For the case of pyrene,
the molecule binds only with the Si atom, leaving the O atom with
a lower coordination number (2) with respect to the adsorption of
the other PAHs and C60. However, the Si–C distance,
for the case of pyrene, is larger by about 0.25 Å as compared
to that for the other PAHs chemisorbed on the vacancy. The adsorption
structure of pyrene on the vacancy is shown in Figure 6b. All species have O–C and Si–C
bond distances in good agreement with the average experimental values
(1.40 and 1.87 Å, respectively).64
angles, in the table in Figure 6, show a perfect 109°
for anthracene, whereas the other PAHs slightly diverge from this
value. Hence, the surface area of anthracene allows a perfect interaction
with the vacancy. Pyrene and coronene do not show covalent bond formation.
In fact, species only with a terminal aromatic ring with four hydrogen
atoms (naphthalene, anthracene, fluoranthene, and benzocoronene) and
the six-membered ring of fullerene form covalent bonds with the undercoordinated
Si and O atoms (see C.N. in the table in Figure 6). This occurs as a result of their large
structural flexibility with respect to more compact structures such
as pyrene and coronene. The coordination number of O and Si increases
once PAHs adsorb on the vacancy forsterite surface, in-line with the
formation of C–O and C–Si bonds. For the case of pyrene,
the molecule binds only with the Si atom, leaving the O atom with
a lower coordination number (2) with respect to the adsorption of
the other PAHs and C60. However, the Si–C distance,
for the case of pyrene, is larger by about 0.25 Å as compared
to that for the other PAHs chemisorbed on the vacancy. The adsorption
structure of pyrene on the vacancy is shown in Figure 6b. All species have O–C and Si–C
bond distances in good agreement with the average experimental values
(1.40 and 1.87 Å, respectively).64
Figure 6.
For
the PAHs adsorbed on the VMgO-[010]-fo surface,
we report a schematic representation of the atomic labels of the hexagonal
rings chemisorbed with the undercoordinated Si and O for (a) naphthalene,
anthracene, fluoranthene, benzocoronene, and fullerene, (b) pyrene,
and (c) coronene. A table reporting the average distance 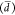 and distance (d) in Angstrom
(Å), angles
and distance (d) in Angstrom
(Å), angles 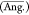 and average dihedral angles
and average dihedral angles 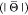 , in degrees (deg), coordination number
(C.N.) for the specified atom, and the number (n)
of atoms (C and Mg) interacting with each other ([nC–nMg ]) for the vacancy surface, PAHs, and
C60. Missing values indicate no interaction between the
atoms. The average values are calculated from the geometrical parameters
reported in the Supporting Information.
, in degrees (deg), coordination number
(C.N.) for the specified atom, and the number (n)
of atoms (C and Mg) interacting with each other ([nC–nMg ]) for the vacancy surface, PAHs, and
C60. Missing values indicate no interaction between the
atoms. The average values are calculated from the geometrical parameters
reported in the Supporting Information.
The distance of the undercoordinated Si and O atoms on the vacancy structure is reduced once their coordination is completed by the chemisorption of the PAHs (see the O1–Si1 distance in the table reported in Figure 6). However, for the case of coronene, the distance O1–Si1 increases with respect to the noncoordinated surface. Angles and dihedral values of coronene adsorbed on the vacancy do not show the formation of C sp3, but a quasi-planar structure, in agreement with the values shown in the adsorption on the pristine and transition-metal-doped surfaces. The coordination number of O and Si of the vacancy, when coronene is adsorbed on it, is completed. Nevertheless, for the case of coronene adsorbed on the vacancy, there is no covalent bond formation; the vacancy enlarged its structure to accommodate the large surface area of coronene, which in turn causes the formation of a Si reconstruction, as shown in Figure 7.
Figure 7.
Vacancy reconstruction caused by the adsorption of coronene on VMgO-[010]-fo. In the thumbnail is reported the close-up perspective of the reconstruction. The atomic labels on the corresponding atoms indicate the reconstructed atoms.
The vacancy reconstruction, caused by the adsorption of coronene on the vacancy, is characterized by the formation of the Si–O bond located in the underlying surface, moving the Si atom between the surface layer and the layer below the surface, completing the coordination of the Si atom. Also, the O atom on the vacancy completes the coordination with a Si located in the underlying surface.
Because of the interaction of the PAHs with the vacancy, the number of Mg atoms interacting with C atoms is much lower with respect to those of the pristine and metal-doped surfaces, comparing the values between the Table 2 and the table reported in Figure 6, respectively.
Binding Energy Analysis
Figure 8 summarizes the binding energies for the PAHs adsorbed on the four different surfaces considered in this study. Disregarding for the moment the interaction with the Schottky defect, there is a general trend of increasing binding energy with the PAH size/surface area, but those of pyrene and the fullerene form an exception to this, not surprising, given their geometries.
Figure 8.

Binding energies of the adsorption of PAHs on [010] forsterite surfaces modeled in this study. The surfaces follow the order shown in the legend for all PAHs. Numerical values are reported in the Supporting Information. The asterisks (*) on the bars show data reported from a prior work.22
The general increase of the binding energy is attributed to the increasing number of contact points (see Table 2), which is related to the size of the surface area (see Table 1). All PAHs are slightly more stabilized (larger binding energy) on Fe-[010]-fo than on Ni-[010]-fo, which is opposite these species (Fe2+ and Ni2+) on benzene in the gas phase (gas-phase configuration).22 As discussed in the “Interaction of PAHs and C60 with Doped Forsterite” section, this reflects subtle geometrical differences in the balance between Mg–PAH and Ni–PAH interactions. PAH adsorption on Fe-doped forsterite shows consistently higher binding energies than that on a pure surface, reflecting that PAHs can optimize their interaction on this surface better than on a Ni-doped surface. The binding energy trend between Fe and the pristine surface is, instead, in agreement with the binding energy trend observed for the binding of Fe2+ and Mg2+ with benzene in the gas phase.65
As shown in Figure 8, all molecules bind strongly on the vacancy
surface with binding
energies larger than 2 eV. We note that anthracene has larger binding
energies than naphthalene, in-line with the reactivity studies conducted
by Bonfanti et al.66 and Rasmussen.67 Anthracene adsorbs on the vacancy surface with
the formation of perfect C–Si and C–O bonds and  and
and  angles of 109° and 120°, respectively. Table 3 shows the binding
energy of PAHs and fullerene as a function of the
angles of 109° and 120°, respectively. Table 3 shows the binding
energy of PAHs and fullerene as a function of the 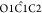 and
and  angles (see labels in Figure 6). Excluding the special case
of fullerene, the binding energy of PAHs decreases as a function of
the angle deviations from 109° and 120°, for
angles (see labels in Figure 6). Excluding the special case
of fullerene, the binding energy of PAHs decreases as a function of
the angle deviations from 109° and 120°, for  and
and 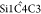 , respectively. Therefore, anthracene is
the PAH that benefits the most from the adsorption process on the
vacancy surface. Here, we focus only on the localized effect on the
vacancy site as the latter is responsible for chemisorption processes
of PAHs, and we will study the effect of the binding of PAHs on the
pristine part of the vacancy surface in a follow-up study.
, respectively. Therefore, anthracene is
the PAH that benefits the most from the adsorption process on the
vacancy surface. Here, we focus only on the localized effect on the
vacancy site as the latter is responsible for chemisorption processes
of PAHs, and we will study the effect of the binding of PAHs on the
pristine part of the vacancy surface in a follow-up study.
Table 3. Binding Energies (Ebind), at PBE-D4/DZP and PBE/DZP Levels, Dispersion Energy (D4), and Angles (^) Only for the Chemisorbed Molecules, of the Interaction of PAHs with the VMgO-[010]-fo Surface.
Fullerene is an exception because it benefits from the formation of covalent bonds with the O and Si atoms on the vacancy and, therefore, from the rehybridization of the C atoms (from tensioned sp2 to sp3 carbons)61 that break the symmetry of the icosahedral structure. Despite the fact that benzocoronene has larger geometrical deviations than other PAHs (see angles in Table 3), its binding energy is closer to the anthracene one because of the higher dispersion energy (see Table 3).
The binding energy of pyrene and coronene deviates with respect to the other PAHs because of their physisorption state (see the discussion in the “Structural Analysis” section and the table in Figure 6).
The difference in binding energies between the vacancy surface and the pristine surfaces is much larger for naphthalene, anthracene, and fullerene than for the other PAHs. The smaller number of contact points for naphthalene and anthracene as compared to other PAHs makes the contribution from the covalent bond formation on the vacancy surface relatively more important. The propensity of fullerenes for addition reactions through the carbons of the six-membered ring facilitates covalent bond formation on the vacancy surface and results in a relatively high binding energy.
Adsorption Mechanism
In the previous section, we saw that PAHs strongly bind onto the vacancy surface with the formation of C–O and C–Si bonds. To evaluate the possible presence of activation barriers associated with the formation of covalent bonds (see the “Structural Analysis” section), we calculated the minimum energy path by employing the CI-NEB approach to locate possible saddle points (transition states); see section “C–H Activation” in the Supporting Information. Because of technical and computational difficulties in optimizing these large molecular interactions with CI-NEB, we considered only the adsorption of naphthalene and benzocoronene on the vacancy surface to address potential differences between small and large PAHs in the chemisorption process. For the PAH approaching the surface in parallel (Figure 9a), the adsorption is studied for both naphthalene and benzocoronene. For a perpendicular orientation (Figure 9b), we studied only naphthalene because of technical difficulties.
Figure 9.
A schematic representation of the (a) parallel and (b) perpendicular adsorption of naphthalene on VMgO-[010]-fo. Atomic labels depict the bond formation due to the adsorption.
Parallel Adsorption
When the molecule is oriented parallel to the surface (Figure 9a), the adsorption process is barrierless and has large exoergic adsorption energy of about −2.2 eV for naphthalene. We also reported the minimum energy path for benzocoronene (red curve in Figure S3 in Supporting Information) to check how the path changes for large surface area molecules. Benzocoronene also has a large adsorption energy of about −2.59 eV with a barrierless and exoergic adsorption.
Perpendicular Adsorption
When the molecule is oriented perpendicular to the surface (Figure 9b), the adsorption on the VMgO-[010]-fo leads, during the optimization process, to the dissociation of the C–H bond of the PAH. In contrast, this process on the pristine and transition-metal surfaces does not lead to dissociation but only adsorption (see Figure 4). On the vacancy, the optimized minimum energy path (Figure S4), with the CI-NEB method, shows a barrierless and exoergic reaction of −3.5 eV. Therefore, the dissociation (perpendicular adsorption) is more favorable than the adsorption (parallel adsorption) by about −1.3 eV.
The electron donation of the C–Si interaction causes, at the same time, the transposition of the hydrogen to the neighboring oxygen atom on the vacancy, forming an O–H bond with a distance of about 0.99 Å, typical for hydroxyl groups.64 The last step implies the adsorption of the remaining carbon skeleton on the surface (Figure 9b).
The spin-density isosurfaces show a large population of spin down localized on the Si atoms and spin up localized on the O atoms of the VMgO-[010]-fo surface (Figure 10). The Voronoi charge analysis shows a partial positive charge on the Si atom (0.897) and a partial negative charge on the O atom (−0.625). After the dissociation, the partial electronic charge is reduced to 0.625 for the Si atoms, gaining electrons, and −0.356 for the O atom, donating electrons. The Voronoi charge analysis shows a donation of the electrons from the 2p orbital of the C atom of naphthalene to the 3p orbital of the undercoordinated Si atom on the vacancy, whereas the O atom donates electron density to the proton (H) dissociated from the PAH. This behavior is similar to the catalytic effect of frustrated Lewis pairs (FLPs), which are a Lewis acid and base that are not able to bind because of geometrical hindrance. Therefore, the geometrical hindrance causes the increase of the strength of the Lewis acid and base. The simultaneous electron transfer is responsible for the cleavage of the C–H bond through a barrierless reaction promoted by an O and undercoordinated Si atoms, similar to the electron-transfer mechanism of the FLPs.68 The formation of a polar cavity, caused by the electric field generated by the presence of FLPs, polarizes the C–H bond (see “C–H Activation” section in the Supporting Information,) allowing the cleavage of the bond. This activation mechanism was first suggested by Grimme et al.69 for the cleavage of molecular hydrogen, which goes through a barrierless process once the molecule is inside the cavity and is subjected to the electric field caused by the presence of the FLPs. The presence of a barrier is caused only by the entrance of the molecule into the cavity because of steric hindrance.69 As the cavity space between Si and O atoms is almost 5 Å, a terminal C–H bond of a PAH has enough space to enter the cavity. Hence, the C–H cleavage is a barrierless process for this case study. In addition, the O has higher electronic affinity (1.46 eV)70 than C (1.26 eV)71 with respect to the H (0.75 eV),72 and Si has higher electronic affinity (1.39 eV)70 than H. Hence, the loss of stability caused by the cleavage of the C–H bond is compensated by the formation of stable C–Si and H–O bonds.
Table 4 reports the zero-point energy corrected adsorption energy for all PAHs on the VMgO-[010]-fo based on the two studied mechanisms (perpendicular and parallel). For the parallel adsorption, naphthalene, anthracene, fluoranthene, and benzocoronene show comparable adsorption energies, whereas pyrene show smaller exoergic adsorption energies than other PAHs as discussed in “Binding Energy Analysis” section. For the perperndicular adsorption, the exoergicity of benzocoronene is even larger (−5.48 eV) with respect to those of all PAHs. Anthracene has a slightly lower adsorption energy with respect to naphthalene and fluoranthene. This might reflect the electron density is mainly localized in the central ring of anthracene and is lower in the terminal ring (the ring bound with the surface).67,73,74 However, on the vacancy surface, anthracene prefers to bind with the terminal ring, not with the central one, as the latter would require major structural changes. As a result, the perpendicular adsorption energy of anthracene is not as large as those for naphthalene and fluoranthene.
Table 4. Zero-Point Energy Corrected Adsorption Energies for the Adsorption of PAHs on VMgO-[010]-fo through a Perpendicular (Eads⊥) and Parallel (Eads) Adsorption.
| Eads⊥ (eV) | Eads= (eV) | |
|---|---|---|
| naphthalene | –3.73 | –2.44 |
| anthracene | –3.51 | –2.97 |
| fluoranthene | –3.84 | –2.33 |
| pyrene | –4.18 | –1.49 |
| coronene | –4.19 | –2.43 |
| benzocoronene | –5.48 | –2.83 |
The adsorption energy trend, for the perpendicular adsorption, is the reverse of the parallel adsorption, in which anthracene is more stabilized with respect to other PAHs because of the perfect geometrical fit with the vacancy surface (see the discussion in the “Interaction of PAHs and C60 with a Vacancy” section and Table 3).
The C–H dissociation through a perpendicular adsorption mechanism is more energetically favorable and, therefore, more likely to happen with respect to the parallel adsorption (Table 4). On the basis of the Bell–Evans–Polanyi principle,75,76 higher adsorption energies are associated with low energy barriers, and because of the large exoergicity, we would expect a barrierless process also for anthracene, fluoranthene, pyrene, and coronene. Furthermore, a perpendicular adsorption does not lead to aromaticity loss as this effect occurs only for the parallel adsorption. The C atom of the PAH bound with a Si atom loses an H atom, which is bound with the neighboring O atom, maintaining the sp2 hybridization of the C.
Astrochemical and Cosmochemical Implications
The study of the interaction of silicate minerals with PAHs in star-forming regions is important because it may relate to the organic composition of comets and asteroids. The latter locks up a variety of organic molecules including the prebiotic building blocks of life as well as PAHs.18 During the star formation evolution, silicate dust grains surrounding the protostar coagulate to form planetesimals and cometesimals that eventually will lead to planet formation. Therefore, the cometary and asteroidal composition locks up valuable information about the processes that form molecules in space.4,18
In this study, we focused on crystalline forsterite as the main component of silicate grains, asteroids, and meteorites.77,78 Silicate minerals in protoplanetary disks and the solar system often have a crystalline nature, as revealed by observations of dust disks around young stellar objects, comets, and asteroids.79 In the interstellar medium (ISM), silicates have strong infrared Si–O stretching mode and O–Si–O bending mode absorption features around 9.7 and 18 μm, respectively.80 Although IR observations reveal that interstellar silicate grains lack large-scale order,81 X-ray absorption studies reveal short-scale crystalline structures.82 Possibly, interstellar silicates are polycrystalline, and in that case, their adsorption behavior would be well described by the study presented here. However, in the ISM, there is no direct evidence of the presence of crystalline silicate, and thus, this issue is still under investigation.77,81
The composition of the dust, asteroids, and meteorites (silicate materials) is largely dominated by silicate structures belonging to the olivine and pyroxene’s families with stoichiometric formulas Mg2xFe2–2xSiO4 and MgxFe1–xSiO3, respectively. The composition of silicate materials in the universe is usually very rich in Mg and poor in Fe (Mg/Fe ratios less than a few percent).83 The trace of transition metals is embedded in forsterite as point defects28 (the presence of one single atom per surface area), distortionary rearrangement of a perfect crystal lattice, and Mg-, Si-, and MgO-Schottky vacancy.27,31 Point defects might already have formed in the envelope of asymptotic giant branch (AGB) stars or may reflect energetic processing of silicate grains in the ISM by, for example, cosmic rays,84,85 whereas thermal annealing and irradiation by the stars are the processes taking place in protoplanetary disks.86 Molecular dynamics simulations suggest the vacancy formation has been preferentially formed around the AGB stars through O-loss or Schottky defect creation.31
Part of the condensed dust in the ISM is formed by PAHs along with other aromatic carbonaceous molecules because of the formation of cluster agglomerates by the π-stacking of their aromatic skeleton.87,88 In space, PAHs are important for maintaining the energy and ionization balance in some regions of the interstellar medium as well as for producing the most important molecule in the universe, H2.40,73 In carbonaceous meteorites, PAHs were hypothesized to be formed by the conversion of aliphatic compounds to aromatic ones through post-Fischer–Tropsch synthesis at low temperature catalyzed by minerals at 360–400 K. However, because of the large abundance of nonalkylated PAHs with temperatures between 400 and 800 K, the hypothesis of PAH formation post-Fischer–Tropsch synthesis was rejected.89 Therefore, the origin of PAHs in asteroidal settings is still to be clarified, whereas it is clear that circumstellar regions and the ISM are the most likely places for the formation of these aromatic compounds.90
The silicates found in meteorites, specifically carbonaceous chondrites, have a characteristic composition of nonvolatile elements, for example, Fe, Ni, and Mg, in which the abundance is comparable to the abundance of elements observed in the Sun.91,92
The abundance of PAHs in the Murchinson carbonaceous meteorite is about 1.82 mmol/g with a large abundance of PAHs with four aromatic units.93 PAHs with more than six aromatic units such as coronene (C24H12) and benzocoronene (C28H14) have not yet been identified in meteorites. The presence of fullerene in meteorites is suspected and still needs further clarifications.94 Therefore, we have considered studying the interaction of coronene and an analogous molecule with an extra hexagonal ring (benzocoronene) along with fullerene to clarify as to why large organic species have not yet been detected.
The potential catalytic activity of forsterite and its defective surfaces, revealed by this study, provides a new view on why large PAHs might not be present in carbonaceous meteorites. The degradation of PAHs, as we saw for the C−H activation on the vacancy surface, is favorable for PAHs up to seven aromatic units. In the ISM the barrier for H-loss from PAHs in the gas phase is 4.7 eV,95 and it can be easily promoted by energetic UV-photons (about 12 eV). Astronomical models imply that photodestruction is more rapid for small PAHs than for large PAHs.6,96 In our calculations based on the binding and adsorption energies, on a solid surface, we see the opposite trend, and the dissociation rate is more favorable for large PAHs, suggesting that defects in crystalline olivine might catalyze the dissociation of the C–H bond of PAHs in an asteroidal setting. Therefore, this work provides the basis for future astronomical modeling and experimental studies. In particular, the dissociation sequence of each C–H bond of PAHs as well as the estimation of energy barriers for the pristine and metal-doped surfaces needs to be clarified in future works.
Conclusions
In summary, we present a comprehensive
dispersion-corrected density
functional theory (DFT-D4) investigation of PAHs with the pristine
[010] forsterite surface and its defective surfaces, containing Fe
and Ni dopants or an MgO-Schottky vacancy. The lowest-energy adsorption
geometries and their binding energetics of naphthalene, anthracene,
fluoranthene, pyrene, coronene, benzocoronene, and fullerene on these
four [010] forsterite surfaces are unraveled. With the exception of
fullerene, all species adsorb on the surfaces maintaining angles and
dihedral angles close to the gas-phase configuration. A large surface
area allows large contact points (number of atomic interactions) with
the surface. Excluding the vacancy surface, we found that all organic
species, in this study, present larger binding energy on the Fe-[010]-fo
surface with respect to Ni and the pristine surface, which shows the
opposite behavior of benzene–cation complexes in the gas phase.
These small differences in the binding energy for the adsorption of
PAHs on pristine and transition-metal surfaces are caused by differences
in the number of contact points. The vacancy surface shows different
behaviors with respect to pristine and transition-metal surfaces because
of the formation of covalent C–O and C–Si bonds with
PAHs. Anthracene has a larger binding energy with respect to other
PAHs as a result of the formation of perfect 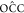 and
and  angles of 109° and 120° characteristic
of silane complexes. Deviations from these angles are reflected in
the differences in binding energy of PAHs on the vacancy surface.
Pyrene and coronene physisorb on the vacancy without covalent bond
formation. For the case of coronene, the physisorption causes the
reconstruction of Si–O bonds on the vacancy. Fullerene adsorption
occurs through the formation of C–O and C–Si bonds on
the six-membered ring analogous to PAHs chemisorption. The larger
binding energy of the chemisorption of fullerene on the vacancy reflects
the formation of covalent bonds that break the icosahedral symmetry
of the buckyball.
angles of 109° and 120° characteristic
of silane complexes. Deviations from these angles are reflected in
the differences in binding energy of PAHs on the vacancy surface.
Pyrene and coronene physisorb on the vacancy without covalent bond
formation. For the case of coronene, the physisorption causes the
reconstruction of Si–O bonds on the vacancy. Fullerene adsorption
occurs through the formation of C–O and C–Si bonds on
the six-membered ring analogous to PAHs chemisorption. The larger
binding energy of the chemisorption of fullerene on the vacancy reflects
the formation of covalent bonds that break the icosahedral symmetry
of the buckyball.
We found that a barrierless adsorption is possible for a parallel orientation of the PAH with respect to the vacancy surface, and a barrierless C−H dissociation is possible in the perpendicular orientation. The latter is energetically more favorable than the parallel adsorption. Therefore, the vacancy has potential catalytic activity for the dissociation of the C−H bond of PAHs. For the C−H dissociation process, the charge analysis has shown an electron donation of the O atoms to the C atoms and electron attraction of the H to the Si atom. This causes splitting of the C–H bond and the formation of C–Si and O–H bonds on the surface. This mechanism is similar to the electron-transfer mechanism of FLPs catalysts.
Hence, forsterite surfaces with a vacancy show potential catalytic activity for the dissociation of aromatic CH. Furthermore, the catalytic potential of forsterite might shed light on the formation of the so-called organic inventory of star-forming regions in space. This study will be followed up with future studies on addressing the selectivity of the vacancy for the dissociation of the hydrogen bound with different carbon sites of the PAHs as well as clarifying the catalytic activity of the pristine surfaces and how to release the fragmented PAH strongly bound to the catalytic site.
Acknowledgments
D.C. and I.L.t.K. thank M. Wolthers, S. E. Ruiz Hernandez, and N. de Leeuw for the comments and suggestions that helped to develop this study. D.C. thanks the Gagliardi group for fruitful discussions. D.C., R.M., and A.G.G.M.T. acknowledge the E.U. under the Horizon 2020 Marie Skłodowska-Curie ITN EUROPAH (Grant No. 722346) and SurfSara and CINECA, under the ISCRA initiative, for the availability of high-performance computing resources and support. T.L. acknowledges NWO for funding via a VENI fellowship (722.017.008). N.Y.D. acknowledges the UK Engineering and Physical Sciences Research Council (EPSRC) for funding (Grant No. EP/S001395/1). Studies on interstellar chemistry at Leiden Observatory are supported by a Spinoza award by the Dutch Research Council (NWO).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsearthspacechem.2c00084.
Binding energies, population analysis, C–H activation, geometrical parameters, and cartesian coordinates (PDF)
Author Present Address
▲ Department of Chemistry, The University of Chicago, 5735 S. Ellis Ave., Chicago, IL 60637, USA
Author Present Address
■ John and Willie Leone Family Department of Energy and Mineral Engineering, The Pennsylvania State University, 212 Hosler Building, University Park, PA 16802, USA.
The authors declare no competing financial interest.
Supplementary Material
References
- Parshall G. W. Organometallic Chemistry in Homogeneous Catalysis. Science 1980, 208, 1221–1224. 10.1126/science.208.4449.1221. [DOI] [PubMed] [Google Scholar]
- Nakao Y.; Kashihara N.; Kanyiva K. S.; Hiyama T. Nickel-Catalyzed Alkenylation and Alkylation of Fluoroarenes via Activation of CH Bond over CF Bond. J. Am. Chem. Soc. 2008, 130, 16170–16171. 10.1021/ja807258m. [DOI] [PubMed] [Google Scholar]
- Segawa Y.; Stephan D. W. Metal-Free Hydrogenation Catalysis of Polycyclic Aromatic Hydrocarbons. Chem. Commun. 2012, 48, 11963–11965. 10.1039/c2cc37190a. [DOI] [PubMed] [Google Scholar]
- Tielens A. G. G. M. The Molecular Universe. Rev. Mod. Phys. 2013, 85, 1021–1081. 10.1103/RevModPhys.85.1021. [DOI] [Google Scholar]
- Davico G. E.; Bierbaum V. M.; DePuy C. H.; Ellison G. B.; Squires R. R. The C-H Bond Energy of Benzene. J. Am. Chem. Soc. 1995, 117, 2590–2599. 10.1021/ja00114a023. [DOI] [Google Scholar]
- Andrews H.; Candian A.; Tielens A. G. G. M. Hydrogenation and Dehydrogenation of Interstellar PAHs: Spectral Characteristics and H2 Formation. Astron. Astrophys. 2016, 595, A23. 10.1051/0004-6361/201628819. [DOI] [Google Scholar]
- Arndtsen B. A.; Bergman R. G.; Mobley T. A.; Peterson T. H. Selective Intermolecular Carbon-Hydrogen Bond Activation by Synthetic Metal Complexes in Homogeneous Solution. Acc. Chem. Res. 1995, 28, 154–162. 10.1021/ar00051a009. [DOI] [Google Scholar]
- Thalji R. K.; Ahrendt K. A.; Bergman R. G.; Ellman J. A. Annulation of Aromatic Imines via Directed CH Activation with Wilkinson’s Catalyst. J. Am. Chem. Soc. 2001, 123, 9692–9693. 10.1021/ja016642j. [DOI] [PubMed] [Google Scholar]
- Jia C.; Piao D.; Oyamada J.; Lu W.; Kitamura T.; Fujiwara Y. Efficient Activation of Aromatic C-H Bonds for Addition to C-C Multiple Bonds. Science 2000, 287, 1992–1995. 10.1126/science.287.5460.1992. [DOI] [PubMed] [Google Scholar]
- Gorelsky S. I. Origins of Regioselectivity of the Palladium-Catalyzed (Aromatic) CH Bond Metalation–Deprotonation. Coord. Chem. Rev. 2013, 257, 153–164. 10.1016/j.ccr.2012.06.016. [DOI] [Google Scholar]
- Cho J.-Y.; Tse M. K.; Holmes D.; Maleczka R. E.; Smith M. R. Remarkably Selective Iridium Catalysts for the Elaboration of Aromatic C-H Bonds. Science 2002, 295, 305–308. 10.1126/science.1067074. [DOI] [PubMed] [Google Scholar]
- Egorova K. S.; Ananikov V. P. Which Metals are Green for Catalysis? Comparison of the Toxicities of Ni, Cu, Fe, Pd, Pt, Rh, and Au Salts. Angew. Chem., Int. Ed. 2016, 55, 12150–12162. 10.1002/anie.201603777. [DOI] [PubMed] [Google Scholar]
- Stephan D.; Erker G. Frustrated Lewis Pairs: Metal-free Hydrogen Activation and More. Angew. Chem., Int. Ed. 2010, 49, 46–76. 10.1002/anie.200903708. [DOI] [PubMed] [Google Scholar]
- Légaré M.-A.; Courtemanche M.-A.; Rochette É.; Fontaine F.-G. Metal-free Catalytic C-H Bond Activation and Borylation of Heteroarenes. Science 2015, 349, 513–516. 10.1126/science.aab3591. [DOI] [PubMed] [Google Scholar]
- Abu El-Rub Z.; Bramer E. A.; Brem G. Review of Catalysts for Tar Elimination in Biomass Gasification Processes. Ind. Eng. Chem. Res. 2004, 43, 6911–6919. 10.1021/ie0498403. [DOI] [Google Scholar]
- Rimola A.; Sodupe M.; Ugliengo P.. Role of Mineral Surfaces in Prebiotic Chemical Evolution. In Silico Quantum Mechanical Studies; Life: Basel, Switzerland, 2019; Vol. 9, p 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James Cleaves H. II; Michalkova Scott A.; Hill F. C.; Leszczynski J.; Sahai N.; Hazen R. Mineral–Organic Interfacial Processes: Potential Roles in the Origins of Life. Chem. Soc. Rev. 2012, 41, 5502–5525. 10.1039/c2cs35112a. [DOI] [PubMed] [Google Scholar]
- Ehrenfreund P.; Charnley S. B. Organic Molecules in the Interstellar Medium, Comets, and Meteorites: A Voyage from Dark Clouds to the Early Earth. Annu. Rev. Astron. Astrophys. 2000, 38, 427–483. 10.1146/annurev.astro.38.1.427. [DOI] [Google Scholar]
- Zamirri L.; Corno M.; Rimola A.; Ugliengo P. Forsterite Surfaces as Models of Interstellar Core Dust Grains: Computational Study of Carbon Monoxide Adsorption. ACS Earth Space Chem. 2017, 1, 384–398. 10.1021/acsearthspacechem.7b00041. [DOI] [Google Scholar]
- Li Q.; Dai W.; Liu B.; Sarre P.; Xie M.; Cheung A.-C. Catalytic Conversion of Methanol to Larger Organic Molecules Over Crystalline Forsterite: Laboratory Study and Astrophysical Implications. Mol. Astrophys. 2018, 13, 22–29. 10.1016/j.molap.2018.09.002. [DOI] [Google Scholar]
- Ferrante R.; Moore M.; Nuth J.; Smith T. Laboratory Studies of Catalysis of CO to Organics on Grain Analogs. Icarus 2000, 145, 297–300. 10.1006/icar.2000.6350. [DOI] [Google Scholar]
- Campisi D.; Lamberts T.; Dzade N. Y.; Martinazzo R.; ten Kate I. L.; Tielens A. G. G. M. Interaction of Aromatic Molecules with Forsterite: Accuracy of the Periodic DFT-D4Method. J. Phys. Chem. A 2021, 125, 2770–2781. 10.1021/acs.jpca.1c02326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rimola A.; Trigo-Rodríguez J. M.; Martins Z. Interaction of Organic Compounds with Chondritic Silicate Surfaces. Atomistic Insights from Quantum Chemical Periodic Simulations. Phys. Chem. Chem. Phys. 2017, 19, 18217–18231. 10.1039/C7CP03504G. [DOI] [PubMed] [Google Scholar]
- Asaduzzaman A.; Zega T.; Laref S.; Runge K.; Deymier P.; Muralidharan K. A Computational Investigation of Adsorption of Organics on Mineral Surfaces: Implications for Organics Delivery in the Early Solar System. Earth Planet. Sci. Lett. 2014, 408, 355–361. 10.1016/j.epsl.2014.10.029. [DOI] [Google Scholar]
- Caldeweyher E.; Mewes J.-M.; Ehlert S.; Grimme S. Extension and Evaluation of the D4 London-Dispersion Model for Periodic Systems. Phys. Chem. Chem. Phys. 2020, 22, 8499–8512. 10.1039/D0CP00502A. [DOI] [PubMed] [Google Scholar]
- Watson G. W.; Oliver P. M.; Parker S. C. Computer Simulation of the Structure and Stability of Forsterite Surfaces. Phys. Chem. Miner. 1997, 25, 70–78. 10.1007/s002690050088. [DOI] [Google Scholar]
- de Leeuw N. H. Density Functional Theory Calculations of Hydrogen-Containing Defects in Forsterite, Periclase, and α-Quartz. J. Phys. Chem. B 2001, 105, 9747–9754. 10.1021/jp0109978. [DOI] [Google Scholar]
- Fei H.; Katsura T. Si and O Self-Diffusion in Hydrous Forsterite and Iron-Bearing Olivine from the Perspective of Defect Chemistry. Phys. Chem. Miner. 2016, 43, 119–126. 10.1007/s00269-015-0779-0. [DOI] [Google Scholar]
- Navarro-Ruiz J.; Ugliengo P.; Rimola A.; Sodupe M. B3LYP Periodic Study of the Physicochemical Properties of the Nonpolar (010) Mg-Pure and Fe-Containing Olivine Surfaces. J. Phys. Chem. A 2014, 118, 5866–5875. 10.1021/jp4118198. [DOI] [PubMed] [Google Scholar]
- Navarro-Ruiz J.; Ugliengo P.; Sodupe M.; Rimola A. Does Fe2+ in Olivine-Based Interstellar Grains Play Any Role in the Formation of H2? Atomistic Insights from DFT Periodic Simulations. Chem. Commun. 2016, 52, 6873–6876. 10.1039/C6CC02313D. [DOI] [PubMed] [Google Scholar]
- Quadery A. H.; Pacheco S.; Au A.; Rizzacasa N.; Nichols J.; Le T.; Glasscock C.; Schelling P. K. Atomic-Scale Simulation of Space Weathering in Olivine and Orthopyroxene. J. Geophys. Res. Planets 2015, 120, 643–661. 10.1002/2014JE004683. [DOI] [Google Scholar]
- Schwartz K.; Lang M. In Encyclopedia of Geochemistry: A Comprehensive Reference Source on the Chemistry of the Earth; White W. M., Ed.; Springer International Publishing: Cham, 2016; pp 1–5. [Google Scholar]
- Palme H.; Lodders K.; Jones A. In Treatise on Geochemistry, 2nd ed.; Holland H. D., Turekian K. K., Eds.; Elsevier: Oxford, 2014; pp 15–36. [Google Scholar]
- Westphal A. J.; et al. Evidence for Interstellar Origin of Seven Dust Particles Collected by the Stardust Spacecraft. Science 2014, 345, 786–791. 10.1126/science.1252496. [DOI] [PubMed] [Google Scholar]
- Brodholt J. P.; Refson K. An ab Initio Study of Hydrogen in Forsterite and a Possible Mechanism for Hydrolytic Weakening. J. Geophys. Res. Solid Earth 2000, 105, 18977–18982. 10.1029/2000JB900057. [DOI] [Google Scholar]
- Cami J. Can Fullerene Analogues be the Carriers of the Diffuse Interstellar Bands?. Proc. Int. Astron. Union 2013, 9, 370–374. 10.1017/S1743921313016141. [DOI] [Google Scholar]
- Maier J. P.; Campbell E. K. Fullerenes in Space. Angew. Chem., Int. Ed. 2017, 56, 4920–4929. 10.1002/anie.201612117. [DOI] [PubMed] [Google Scholar]
- Watson G. W.; Kelsey E. T.; de Leeuw N. H.; Harris D. J.; Parker S. C. Atomistic Simulation of Dislocations, Surfaces and Interfaces in MgO. J. Chem. Soc., Faraday Trans. 1996, 92, 433–438. 10.1039/ft9969200433. [DOI] [Google Scholar]
- Cortese R.; Campisi D.; Duca D. Hydrogen Arrangements on Defective Quasi-Molecular BN Fragments. ACS Omega 2019, 4, 14849–14859. 10.1021/acsomega.9b01445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campisi D.; Candian A. Do Defects in PAHs Promote Catalytic Activity in Space? Stone–Wales Pyrene as a Test Case. Phys. Chem. Chem. Phys. 2020, 22, 6738–6748. 10.1039/C9CP06523G. [DOI] [PubMed] [Google Scholar]
- Radzig V.In Physico-Chemical Phenomena in Thin Films and at Solid Surfaces; Trakhtenberg L. I., Lin S. H., Ilegbusi O. J., Eds.; Thin Films and Nanostructures; Academic Press, 2007; Vol. 34; pp 231–345. [Google Scholar]
- Soler J. M.; Artacho E.; Gale J. D.; García A.; Junquera J.; Ordejón P.; Sánchez-Portal D. The SIESTA Method for Ab Initio Order-N Materials Simulation. J. Phys.: Condens. Matter 2002, 14, 2745. 10.1088/0953-8984/14/11/302. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Boys S.; Bernardi F. The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors. Mol. Phys. 1970, 19, 553–566. 10.1080/00268977000101561. [DOI] [Google Scholar]
- Sordo J. A.; Chin S.; Sordo T. L. On the Counterpoise Correction for the Basis Set Superposition Error in Large Systems. Theor. Chem. Acc. 1988, 74, 101–110. 10.1007/BF00528320. [DOI] [Google Scholar]
- Caldeweyher E.; Ehlert S.; Hansen A.; Neugebauer H.; Spicher S.; Bannwarth C.; Grimme S. A Generally Applicable Atomic-Charge Dependent London Dispersion Correction. J. Chem. Phys. 2019, 150, 154122. 10.1063/1.5090222. [DOI] [PubMed] [Google Scholar]
- Caldeweyher E.; Bannwarth C.; Grimme S. Extension of the D3 Dispersion Coefficient Model. J. Chem. Phys. 2017, 147, 034112. 10.1063/1.4993215. [DOI] [PubMed] [Google Scholar]
- Monkhorst H. J.; Pack J. D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
- Liu D. C.; Nocedal J. On the Limited Memory BFGS Method for Large Scale Optimization. Math. Program. 1989, 45, 503–528. 10.1007/BF01589116. [DOI] [Google Scholar]
- Fonseca Guerra C.; Handgraaf J.-W.; Baerends E. J.; Bickelhaupt F. M. Voronoi Deformation Density (VDD) Charges: Assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD Methods for Charge Analysis. J. Comput. Chem. 2004, 25, 189–210. 10.1002/jcc.10351. [DOI] [PubMed] [Google Scholar]
- Dudarev S. L.; Botton G. A.; Savrasov S. Y.; Humphreys C. J.; Sutton A. P. Electron-Energy-loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study. Phys. Rev. B 1998, 57, 1505–1509. 10.1103/PhysRevB.57.1505. [DOI] [Google Scholar]
- Shankland T. J. Band Gap of Forsterite. Science 1968, 161, 51–53. 10.1126/science.161.3836.51. [DOI] [PubMed] [Google Scholar]
- Henkelman G.; Uberuaga B. P.; Jónsson H. A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. J. Chem. Phys. 2000, 113, 9901–9904. 10.1063/1.1329672. [DOI] [Google Scholar]
- Larsen A. H.; et al. The Atomic Simulation Environment-A Python Library for Working with Atoms. J. Phys.: Condens. Matter 2017, 29, 273002. 10.1088/1361-648X/aa680e. [DOI] [PubMed] [Google Scholar]
- Bahn S. R.; Jacobsen K. W. An Object-Oriented Scripting Interface to a Legacy Electronic Structure Code. Comput. Sci. Eng. 2002, 4, 56–66. 10.1109/5992.998641. [DOI] [Google Scholar]
- Bitzek E.; Koskinen P.; Gähler F.; Moseler M.; Gumbsch P. Structural Relaxation Made Simple. Phys. Rev. Lett. 2006, 97, 170201. 10.1103/PhysRevLett.97.170201. [DOI] [PubMed] [Google Scholar]
- Garrido Torres J. A.; Jennings P. C.; Hansen M. H.; Boes J. R.; Bligaard T. Low-Scaling Algorithm for Nudged Elastic Band Calculations Using a Surrogate Machine Learning Model. Phys. Rev. Lett. 2019, 122, 156001. 10.1103/PhysRevLett.122.156001. [DOI] [PubMed] [Google Scholar]
- Navarro-Ruiz J.; Ugliengo P.; Rimola A.; Sodupe M. B3LYP Periodic Study of the Physicochemical Properties of the Nonpolar (010) Mg-Pure and Fe-Containing Olivine Surfaces. J. Phys. Chem. A 2014, 118, 5866–5875. 10.1021/jp4118198. [DOI] [PubMed] [Google Scholar]
- Brodholt J. Ab Initio Calculations on Point Defects in Forsterite (Mg2SiO4) and Implications for Diffusion and Creep. Am. Mineral. 1997, 82, 1049–1053. 10.2138/am-1997-11-1201. [DOI] [Google Scholar]
- Stoneham A. M. The Theory of Defects in Solids. Contemp. Phys. 1979, 20, 535–545. 10.1080/00107517908210920. [DOI] [Google Scholar]
- Rodríguez-Fortea A.; Irle S.; Poblet J. M. Fullerenes: Formation, Stability, and Reactivity. WIREs Comput. Mol. Sci. 2011, 1, 350–367. 10.1002/wcms.21. [DOI] [Google Scholar]
- Simon A.; Joblin C. Thermochemistry and Infrared Spectroscopy of Neutral and Cationic IronPolycyclic Aromatic Hydrocarbon Complexes of Astrophysical Interest: Fundamental Density Functional Theory Studies. J. Phys. Chem. A 2007, 111, 9745–9755. 10.1021/jp072506a. [DOI] [PubMed] [Google Scholar]
- Schwieger S.; Wagner C.; Bruhn C.; Schmidt H.; Steinborn D. Synthesis and Structures of Zeise-type Complexes with Vinylsilane Ligands and Quantum Chemical Analysis of the Platinum–Vinylsilane Bonding. Z. Anorg. Allg. Chem. 2005, 631, 2696–2704. 10.1002/zaac.200500110. [DOI] [Google Scholar]
- Johnson R. D., III. NIST Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 101, Release 21. 2020.
- Kolakkandy S.; Pratihar S.; Aquino A. J. A.; Wang H.; Hase W. L. Properties of Complexes Formed by Na+, Mg2+, and Fe2+ Binding with Benzene Molecules. J. Phys. Chem. A 2014, 118, 9500–9511. 10.1021/jp5029257. [DOI] [PubMed] [Google Scholar]
- Bonfanti M.; Casolo S.; Tantardini G. F.; Ponti A.; Martinazzo R. A few simple rules governing hydrogenation of graphene dots. J. Chem. Phys. 2011, 135, 164701. 10.1063/1.3650693. [DOI] [PubMed] [Google Scholar]
- Rasmussen J. A. Polycyclic Aromatic Hydrocarbons: Trends for Bonding Hydrogen. J. Phys. Chem. A 2013, 117, 4279–4285. 10.1021/jp400287h. [DOI] [PubMed] [Google Scholar]
- Rokob T. A.; Bakó I.; Stirling A.; Hamza A.; Pápai I. Reactivity Models of Hydrogen Activation by Frustrated Lewis Pairs: Synergistic Electron Transfers or Polarization by Electric Field?. J. Am. Chem. Soc. 2013, 135, 4425–4437. 10.1021/ja312387q. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Kruse H.; Goerigk L.; Erker G. The Mechanism of Dihydrogen Activation by Frustrated Lewis Pairs Revisited. Angew. Chem., Int. Ed. 2010, 49, 1402–1405. 10.1002/anie.200905484. [DOI] [PubMed] [Google Scholar]
- Chaibi W.; Peláez R. J.; Blondel C.; Drag C.; Delsart C. Effect of a Magnetic Field in Photodetachment Microscopy. Eur. Phys. J. D 2010, 58, 29–37. 10.1140/epjd/e2010-00086-7. [DOI] [Google Scholar]
- Bresteau D.; Drag C.; Blondel C. Isotope Shift of the Electron Affinity of Carbon Measured by Photodetachment Microscopy. Phys. Rev. A 2016, 93, 013414. 10.1103/PhysRevA.93.013414. [DOI] [Google Scholar]
- Lykke K. R.; Murray K. K.; Lineberger W. C. Threshold Photodetachment of H–. Phys. Rev. A 1991, 43, 6104–6107. 10.1103/PhysRevA.43.6104. [DOI] [PubMed] [Google Scholar]
- Campisi D.; Simonsen F. D. S.; Thrower J. D.; Jaganathan R.; Hornekær L.; Martinazzo R.; Tielens A. G. G. M. Superhydrogenation of Pentacene: the Reactivity of Zigzag-Edges. Phys. Chem. Chem. Phys. 2020, 22, 1557–1565. 10.1039/C9CP05440E. [DOI] [PubMed] [Google Scholar]
- Fukui K.; Yonezawa T.; Shingu H. A Molecular Orbital Theory of Reactivity in Aromatic Hydrocarbons. J. Chem. Phys. 1952, 20, 722–725. 10.1063/1.1700523. [DOI] [Google Scholar]
- Bell R. P. The Theory of Reactions Involving Proton Transfers. Proc. R. Soc. London A 1936, 154, 414–429. 10.1098/rspa.1936.0060. [DOI] [Google Scholar]
- Evans M. G.; Polanyi M. Inertia and Driving Force of Chemical Reactions. Trans. Faraday Soc. 1938, 34, 11–24. 10.1039/tf9383400011. [DOI] [Google Scholar]
- Brucato J. R.; Strazzulla G.; Baratta G.; Colangeli L. Forsterite Amorphisation by Ion Irradiation: Monitoring by Infrared Spectroscopy. Astron. Astrophys. 2004, 413, 395–401. 10.1051/0004-6361:20031574. [DOI] [Google Scholar]
- Reddy V.; Dunn T. L.; Thomas C. A.; Moskovitz N. A.; Burbine T. H.. Asteroids IV; University of Arizona Press, 2015; pp 43–63. [Google Scholar]
- Draine B. Interstellar Dust Grains. Annu. Rev. Astron. Astrophys. 2003, 41, 241–289. 10.1146/annurev.astro.41.011802.094840. [DOI] [Google Scholar]
- Draine B. T.Interstellar Extinction in the Infrared. In Infrared Spectroscopy in Astronomy; European Space Agency: 1989; p 93.
- Kemper F.; Vriend W. J.; Tielens A. G. G. M. The Absence of Crystalline Silicates in the Diffuse Interstellar Medium. Astrophys. J. 2004, 609, 826–837. 10.1086/421339. [DOI] [Google Scholar]
- Zeegers S. T.; Costantini E.; Rogantini D.; de Vries C. P.; Mutschke H.; Mohr P.; de Groot F.; Tielens A. G. G. M. Dust Absorption and Scattering in the Silicon K-Edge. Astron. Astrophys. 2019, 627, A16. 10.1051/0004-6361/201935050. [DOI] [Google Scholar]
- Molster F.; Kemper C. Crystalline Silicates. Space Sci. Rev. 2005, 119, 3–28. 10.1007/s11214-005-8066-x. [DOI] [Google Scholar]
- Bringa E. M.; Kucheyev S. O.; Loeffler M. J.; Baragiola R. A.; Tielens A. G. G. M.; Dai Z. R.; Graham G.; Bajt S.; Bradley J. P.; Dukes C. A.; Felter T. E.; Torres D. F.; Breugel W. v. Energetic Processing of Interstellar Silicate Grains by Cosmic Rays. Astrophys. J. 2007, 662, 372–378. 10.1086/517865. [DOI] [Google Scholar]
- Carrez P.; Demyk K.; Cordier P.; Gengembre L.; Grimblot J.; D’hendecourt L.; Jones A. P.; Leroux H. Low-Energy Helium Ion Irradiation-Induced Amorphization and Chemical Changes in Olivine: Insights for Silicate Dust Evolution in the Interstellar Medium. Meteorit. Planet. Sci. 2002, 37, 1599–1614. 10.1111/j.1945-5100.2002.tb00814.x. [DOI] [Google Scholar]
- Henning T. Cosmic Silicates. Annu. Rev. Astron. Astrophys. 2010, 48, 21–46. 10.1146/annurev-astro-081309-130815. [DOI] [Google Scholar]
- Rapacioli M.; Calvo F.; Spiegelman F.; Joblin C.; Wales D. J. Stacked Clusters of Polycyclic Aromatic Hydrocarbon Molecules. J. Phys. Chem. A 2005, 109, 2487–2497. 10.1021/jp046745z. [DOI] [PubMed] [Google Scholar]
- Rapacioli M.; Joblin C.; Boissel P. Spectroscopy of Polycyclic Aromatic Hydrocarbons and Very Small Grains in Photodissociation Regions. Astron. Astrophys. 2005, 429, 193–204. 10.1051/0004-6361:20041247. [DOI] [Google Scholar]
- Wing M. R.; Bada J. L. The Origin of the Polycyclic Aromatic Hydrocarbons in Meteorites. Orig. Life Evol. Biosph. 1991, 21, 375–383. 10.1007/BF01808308. [DOI] [Google Scholar]
- Cherchneff I. The formation of Polycyclic Aromatic Hydrocarbons in evolved circumstellar environments. EAS Publ. Ser. 2011, 46, 177–189. 10.1051/eas/1146019. [DOI] [Google Scholar]
- Lodders K. Solar System Abundances and Condensation Temperatures of the Elements. Astrophys. J. 2003, 591, 1220–1247. 10.1086/375492. [DOI] [Google Scholar]
- Anders E.; Grevesse N. Abundances of the Elements: Meteoritic and Solar. Geochim. Cosmochim. Acta 1989, 53, 197–214. 10.1016/0016-7037(89)90286-X. [DOI] [Google Scholar]
- Huang Y.; Aponte J. C.; Zhao J.; Tarozo R.; Hallmann C. Hydrogen and Carbon Isotopic Ratios of Polycyclic Aromatic Compounds in Two CM2 Carbonaceous Chondrites and Implications for Prebiotic Organic Synthesis. Earth Planet. Sci. Lett. 2015, 426, 101–108. 10.1016/j.epsl.2015.06.027. [DOI] [Google Scholar]
- Hammond M. R.; Zare R. N. Identifying the Source of a Strong Fullerene Envelope Arising from Laser Desorption Mass Spectrometric Analysis of Meteoritic Insoluble Organic Matter. Geochim. Cosmochim. Acta 2008, 72, 5521–5529. 10.1016/j.gca.2008.08.008. [DOI] [Google Scholar]
- Wiersma S. D.; Candian A.; Bakker J. M.; Martens J.; Berden G.; Oomens J.; Buma W. J.; Petrignani A. Photolysis-Induced Scrambling of PAHs as a Mechanism for Deuterium Storage. Astron. Astrophys. 2020, 635, A9. 10.1051/0004-6361/201936982. [DOI] [Google Scholar]
- Allain T.; Leach S.; Sedlmayr E. Photodestruction of PAHs in the Interstellar Medium. I. Photodissociation Rates for the Loss of an Acetylenic Group. Astron. Astrophys. 1996, 305, 602–615. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Johnson R. D., III. NIST Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 101, Release 21. 2020.