Fixed-Effect vs Random-Effects Models for Meta-Analysis: 3 Points to Consider

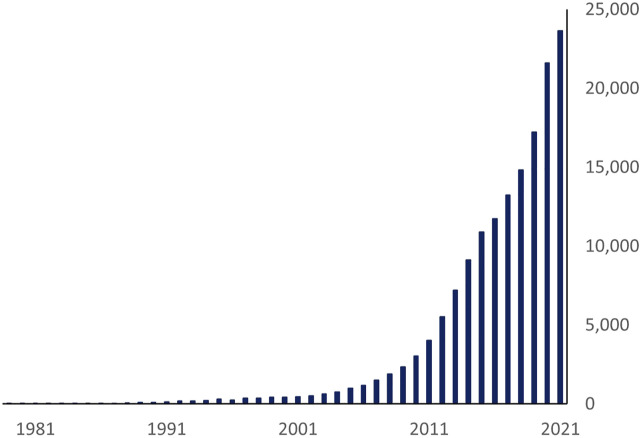
Meta-analysis is the statistical procedure for combining data from multiple studies. Meta-analyses are being conducted with increasing frequency (Figure 1). Compared to a single clinical study, they can increase statistical power, improve accuracy, and provide a summary of findings with respect to key clinical questions. Understanding the statistical models underlying the analysis is important.

Figure 1.

The number of PubMed articles over time with “meta-analysis” in the title.

Most meta-analyses are based on 1 of 2 statistical models, the fixed-effect model or the random-effects model.

• 1. Understand that the assumptions for each model are different. ¹

The fixed-effect model assumes 1 true effect size underlies all the studies in the meta-analysis, thus the term “fixed effect”. Any differences in observed effects are due to sampling error. Investigators use the singular (effect) since there is only 1 true effect.

The random-effects model assumes that the true effect could vary from study to study due to the differences (heterogeneity) among studies. For example, the effect size might be higher or lower in trials where the participants’ demographics vary (eg, older vs younger, or lower vs higher socioeconomic status, or less vs higher educated), or when a different surgical technique of an intervention is used. Because studies will differ in the mixes of participants and in the implementation of surgical interventions, (among other reasons), each study may have a different effect size. If it were possible to perform an infinite number of studies, the effect estimates of all the studies would follow a normal distribution. The pooled estimate would be the mean or average effect. The effect sizes in the studies that are performed are assumed to represent a random sample of all possible effect sizes, hence the term “random effects”. Investigators use the plural (effects) since there is a range of true effects.

• 2. Understand that the statistics for each model are different.

We know that in a meta-analysis, a pooled estimate is calculated as a weighted average of the effect estimates within the individual studies. Weights are assigned to each study based on the inverse of the overall error variance (ie, 1/variance). Generally, more weight is given to studies with larger sample sizes.

In the fixed-effect model, all observed differences reflect sampling error. Therefore, any variance would come from within each study. The pooled estimate is calculated as a weighted average, where the weight assigned to each study is the inverse of that study’s variance. Larger studies have much more weight than smaller studies in the fixed-effect models. Common methods used for fixed-effect models include the Peto odds ratio and the Mantel-Haenszel method.

In the random-effects model , 2 sources contribute to the variance, that which arises from within each study and the variance that occurs between studies. Both need to be taken into account. While larger studies still have larger weights, in the random effects models, smaller studies have relatively greater weight than in fixed-effect models. The method frequently used to account for both sources of variance is the DerSimonian and Laird method.

• 3. Understand that the results under each model may be similar or different.

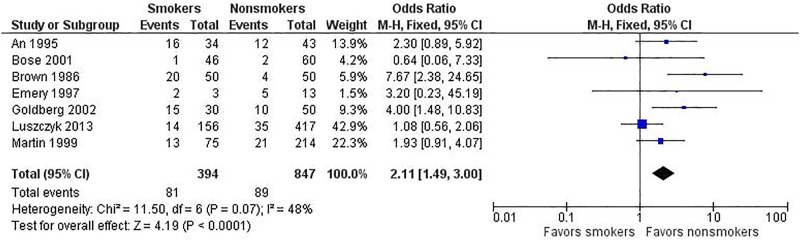
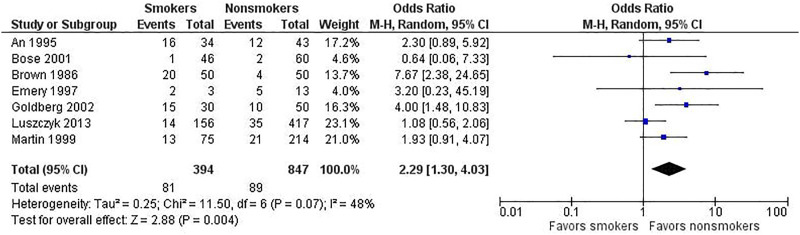
By way of example, we use selective data from a meta-analysis on the risk of nonunion in smokers undergoing spinal fusion. ² We present the same data for the fixed-effect (Figure 2) and random-effects (Figure 3) models to underscore how the different analyses affect the results. Note the following differences. ³ First, the study weights listed in the metaanalysis table and represented by the size of each study’s point estimate (box) are more similar under the random-effects model. Specifically, note the size of the boxes for the largest study (Luszczyk 2013) vs the smallest study (Emery 1997) under the 2 models. Second, the estimate of the effect size differs between the 2 models. In this case, the random-effects model results in a larger effect size, 2.39 vs 2.11 for the fixed-effect model. The results generated from fixed-effect and random-effects models can be the same or different, with either model yielding a higher estimate of the effect size. Third, the confidence interval for the summary effect is wider under the random-effects model. This will always be the case because the model accounts for 2 sources of variation.

Figure 2.

Example of a fixed-effect analysis.

Figure 3.

Example of a random-effects analysis.

Which model to use depends on the circumstances. Generally, the random-effects model is often the appropriate model, capturing uncertainty resulting from heterogeneity among studies. When there are too few studies to obtain an accurate estimate of the between-studies variance, one may consider a fixed-effect model. Likewise, in the scenario of a high-quality study with a large sample size and a low-quality study with a small sample size, a fixed-effect model will provide a greater weight to the larger, better-quality study. ⁴