Neural trajectories in the supplementary motor area and motor cortex exhibit distinct geometries, compatible with different classes of computation

Abstract

The supplementary motor area (SMA) is believed to contribute to higher-order aspects of motor control. We considered a key higher-order role: tracking progress throughout an action. We propose that doing so requires population activity to display ‘low trajectory divergence’: situations with different future motor outputs should be distinct, even when present motor output is identical. We examined neural activity in SMA and primary motor cortex (M1) as monkeys cycled various distances through a virtual environment. SMA exhibited multiple response features that were absent in M1. At the single-neuron level these included ramping firing rates and cycle-specific responses. At the population level they included a helical population-trajectory geometry with shifts in the occupied subspace as movement unfolded. These diverse features all served to reduce trajectory divergence, which was much lower in SMA versus M1. Analogous population-trajectory geometry, also with low divergence, naturally arose in networks trained to internally guide multi-cycle movement.

eTOC Blurb

The supplementary motor area is believed to guide action by ‘looking ahead’ in time. Russo et al. formalize this idea, and predict a basic property that neural activity must have to serve that purpose. That property is present, explains diverse features of activity, and distinguishes higher from lower-level motor areas.

Introduction

The supplementary motor area (SMA) is implicated in higher-order aspects of motor control (Eccles, 1982; Penfield and Welch, 1951; Roland et al., 1980). SMA lesions cause motor neglect (Krainik et al., 2001; Laplane et al., 1977), unintended utilization (Boccardi et al., 2002), deficits in bimanual coordination (Brinkman, 1984), and difficulty performing sequences (Shima and Tanji, 1998). Relative to primary motor cortex (M1), SMA activity is less coupled to actions of a specific body part (Boudrias et al., 2006; Tanji and Kurata, 1982; Tanji and Mushiake, 1996; Yokoi et al., 2018). Instead, SMA computations appear related to learned sensory-motor associations (Nachev et al., 2008; Tanji and Kurata, 1982), reward anticipation (Sohn and Lee, 2007), internal initiation and guidance of movement (Eccles, 1982; Romo and Schultz, 1992; Thaler et al., 1995), timing (Merchant and de Lafuente, 2014; Remington et al., 2018b; Wang et al., 2018) and sequencing (Kornysheva and Diedrichsen, 2014; Mushiake et al., 1991; Nakamura et al., 1998; Tanji and Shima, 1994). SMA neurons show abstracted but task-specific responses, such as selective bursts during sequences (Shima and Tanji, 2000) and continuous ramping and rhythmic activity during a timing task (Cadena-Valencia et al., 2018). This suggests that SMA computations are critical when pending action must be guided by abstract “contextual” factors; e.g., knowing the overall action and one’s moment-by-moment progress within it (Tanji and Shima, 1994). Such guidance may be important both when performing movements from memory and for appropriately leveraging sensory cues (Gamez et al., 2019).

Tracking of context is presumably particularly important during temporally extended actions, of which sequences are the most commonly studied (Kornysheva and Diedrichsen, 2014; Mushiake et al., 1991; Nakamura et al., 1998; Rhodes et al., 2004; Shima and Tanji, 2000; Tanji and Shima, 1994; Yokoi and Diedrichsen, 2019). During sequences, SMA neurons respond phasically with various forms of sequence selectivity (Shima and Tanji, 2000; Tanji and Mushiake, 1996). Such selectivity is proposed to reflect a key computation: arranging multiple distinct movements in the correct order, out of many possible orders (Tanji, 2001). Importantly, not all movements require sequencing (Krakauer et al., 2019; Wong and Krakauer, 2019). E.g., a tennis swing lacks discrete elements that can be arbitrarily arranged, and SMA is proposed not to be critical for movements of this type (Tanji, 2001). Yet there exist many actions that, while not meeting the strict definition of a sequence, last longer than a tennis swing and may require computations regarding ‘what comes next’ beyond what can be accomplished by M1 alone. A unifying hypothesis is that SMA computations relate to that general need: guiding action by internally tracking context. What properties should one expect of a neural population performing that class of computation?

Inquiring whether neural responses are consistent with a hypothesized computation is a common goal (e.g., Gallego et al., 2018; Pandarinath et al., 2018; Saxena and Cunningham, 2019). Standard approaches include decoding hypothesized signals (e.g., via regression; Morrow and Miller, 2003), and/or direct comparisons between empirical and simulated population activity (e.g., via canonical correlation; Sussillo et al., 2015). An emerging approach is to consider the geometry of the population response: the arrangement of population states across conditions (DiCarlo et al., 2012; Diedrichsen and Kriegeskorte, 2017; Gallego et al., 2018; Saez et al., 2015; Schaffelhofer and Scherberger, 2016; Stringer et al., 2019) and/or the time-evolving trajectory of activity in neural state-space (Ames et al., 2014; Foster et al., 2014; Hall et al., 2014; Henaff et al., 2019; Michaels et al., 2016; Raposo et al., 2014; Remington et al., 2018a; Remington et al., 2018b; Stopfer and Laurent, 1999; Sussillo and Barak, 2013; Sussillo et al., 2015). A given geometry may be consistent with some computations but not others (Driscoll et al., 2018). An advantage of this approach is that certain geometric properties are expected to hold for a broad class of computations, regardless of the specific computation deployed during a particular task. For example, we recently characterized M1 activity using a metric, trajectory tangling, that assesses whether activity is consistent with noise-robust dynamics (Russo et al., 2018). This approach revealed a population-level property – low trajectory tangling – that was conserved across tasks and species.

Here we consider the hypothesis that SMA guides movement by tracking contextual factors, and derive a prediction regarding population trajectory geometry. We predict that SMA trajectories should avoid ‘divergence’; trajectories should be structured, across time and conditions, such that it is never the case that two trajectories follow the same path and then separate. Low trajectory divergence is essential to ensure that neural activity can distinguish situations with different future motor outputs, even if current motor output is similar. We hypothesize that the need to avoid divergence shapes the population trajectory, and thus the response features observed within a particular task.

We employed a cycling task that shares some features with sequence tasks but involves continuous motor output and thus provides a novel perspective on SMA response properties. We found that the population response in SMA, but not M1, exhibits low trajectory divergence. The major features of SMA responses, at both the population and single-neuron levels, could be understood as serving to maintain low divergence. Simulations confirmed that low divergence was necessary for a network to guide action based on internal / contextual information. Furthermore, artificial networks naturally adopted SMA-like trajectories when they had to internally track contextual factors. Thus, a broad hypothesis regarding the class of computations performed by SMA accounts for population activity in a novel task.

Results

Task and behavior

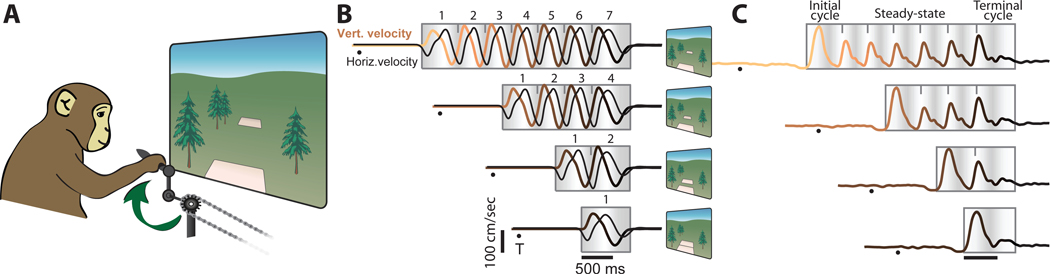
We trained two rhesus macaque monkeys to grasp a hand-pedal and cycle through a virtual landscape (Figure 1A; Russo et al., 2018). Each trial required cycling between two targets. The trial began with the monkey’s virtual position stationary on the first target, with the pedal orientated either straight up (‘top-start’) or down (‘bottom-start’). After a 1000 ms hold period, the second target appeared. Its distance determined the required number of revolutions: 1, 2, 4, or 7 cycles. After a 500–1000 ms randomized delay period, a go cue (brightening of the second target) was delivered. The monkey cycled to that target and remained stationary to receive juice reward. Because targets were separated by an integer number of cycles, the second target was acquired with the same pedal orientation as the first. Landscape color indicated whether forward virtual motion required cycling forward or backward (forward is defined as the hand moving away from the body at the cycle’s top). Using a block-randomized design, monkeys performed all combinations of two cycling directions, two starting orientations, and four cycling distances. Averages of hand kinematics, muscle activity and neural activity were computed after temporal alignment.

Figure 1.

Illustration of task, behavior, and muscle activity

A) Monkeys grasped a hand pedal and cycled through a virtual environment. The schematic illustrates forward cycling, instructed by a green environment. Backward cycling was instructed by an orange, desert-like environment.

B) Trial-averaged hand velocity for seven-cycle, four-cycle, two-cycle and one-cycle movements. Data are for forward cycling, starting at cycle’s bottom (monkey C). Vertical velocity traces are colored from tan to black to indicate time with respect to the end of movement. Black dots indicate target appearance. Gray box with shading indicates the epoch when the pedal was moving (preceding go cue not shown). Shading indicates vertical hand position; light shading indicates cycle apex. Ticks show cycle divisions used for analysis. Small schematics at right illustrate relationship between number of cycles and target distance.

C) Muscle activity, recorded from the medial head of the triceps (monkey D). Intra-muscularly recorded voltages were rectified, filtered, and trial averaged. Data are shown for backward cycling, starting at cycle’s top.

Vertical and horizontal hand velocity had nearly sinusoidal temporal profiles (Figure 1B). Muscle activity patterns (Figure 1C) were often non-sinusoidal. Initial-cycle and terminal-cycle muscle patterns often departed from the middle-cycle pattern, an expected consequence of accelerating / decelerating the arm (e.g., the initial-cycle response is larger in Figure 1C). Muscle activity and hand kinematics differed in many ways, yet shared the following property: the response when cycling a given distance was a concatenation of an initial-cycle response, middle cycles with a repeating response, and a terminal-cycle response. We refer to the middle cycles as ‘steady-state’, reflecting the repetition of kinematics and muscle activity across such cycles, both within a cycling distance and across distances. Seven-cycle movements had ~5 steady-state cycles and four-cycle movements had ~2 steady-state cycles. Two- and one-cycle movements involved little or no steady-state cycling.

Cycling is not strictly speaking a sequence. Muscle activity during a four-cycle movement roughly follows an ABBC pattern, but these elements lack well-defined boundaries and are neither discrete nor orderable (C can’t be performed before A). Nevertheless, cycling seems likely to require ‘temporal structuring of movement’ (Tanji and Shima, 1994) beyond what M1 alone can contribute. Our motivating hypothesis – that SMA tracks contextual factors for the purpose of guiding action – predicts that the SMA population response should be structured to distinguish situations with different future actions, even when current motor output is identical. The cycling task produced multiple instances of this scenario, both within and between conditions. Consider the second and fifth cycles of a seven-cycle movement (Figure 1B,C). Motor output is essentially identical, but will differ in two more cycles. The same is true when comparing the second cycle of seven-cycle and four-cycle movements. Distinguishing between such situations requires tracking context via some combination of ‘dead-reckoning’ and interpretation of visual cues (optic flow and the looming target). Does the need to track context account for the geometry of the SMA population response? While this is fundamentally a population-level question, we begin by examining single-neuron responses. We then document specific features of the population response. Finally, we consider a general property of population trajectory geometry that is necessary for tracking context. We ask whether the data have this general property, and whether it explains the specific response features observed during cycling.

Single-neuron responses

Well-isolated single neurons were recorded consecutively from SMA and M1. M1 recordings spanned sulcal and surface primary motor cortex and the immediately adjacent aspect of dorsal premotor cortex (Russo et al., 2018). In both SMA and M1, neurons were robustly modulated during cycling. Of neurons that spiked often enough to be noticed and isolated, nearly all were task modulated. Isolations that were not task modulated were abandoned and not considered further (a total of 6 SMA and 4 M1 isolations across both monkeys). All other isolated neurons were analyzed regardless of their response properties. This included 77 and 70 SMA neurons (monkeys C and D) and 116 and 117 M1 neurons. Firing rate modulation (maximum minus minimum rate) averaged 52 and 57 spikes/s for SMA (monkey C and D) and 73 and 64 spikes/s for M1.

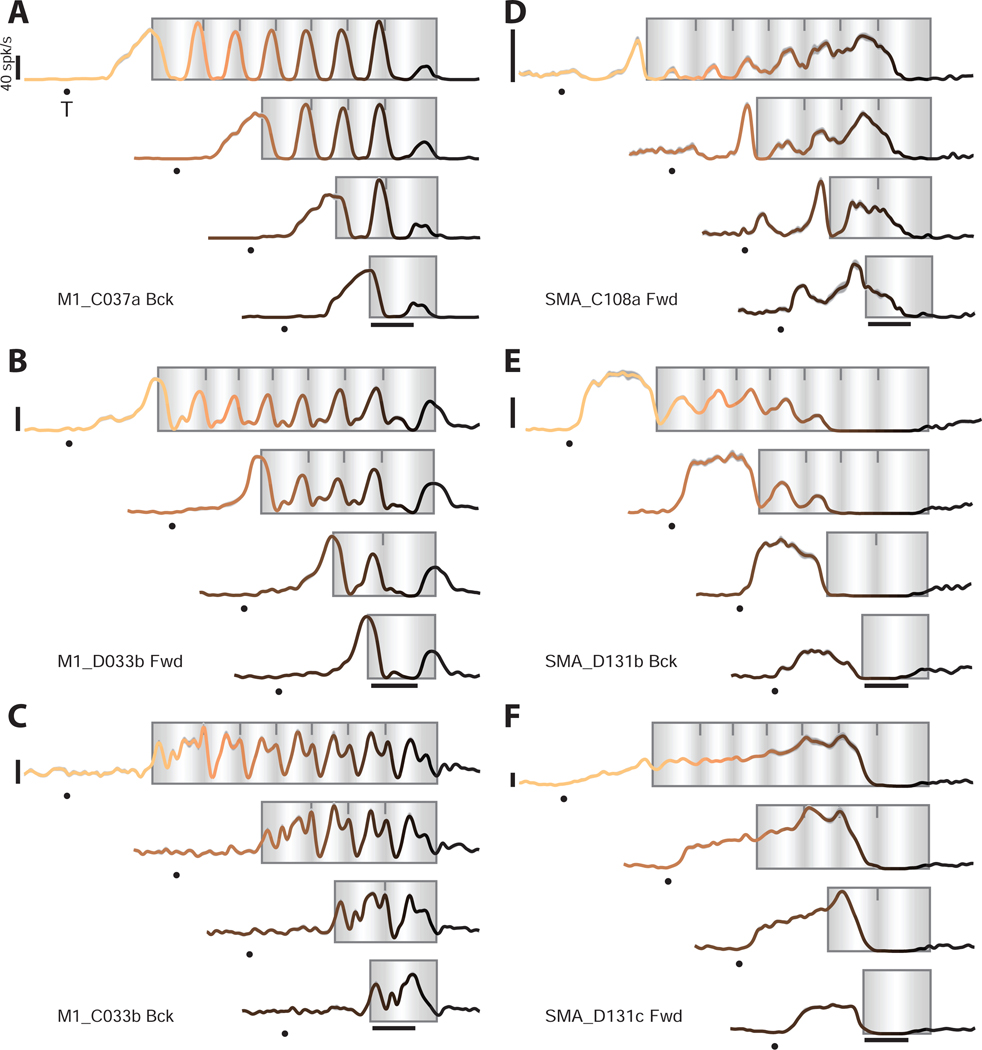
In M1, single-neuron responses (Figure 2A–C) were typically complex, yet showed two consistent features. First, for a given cycling distance, responses repeated across steady-state cycles. For example, for a seven-cycle movement, the firing rate profile was very similar across cycles 2–6 (Russo et al., 2018). Second, response elements – initial-cycle, steady-state, and terminal-cycle responses – were conserved across distances. Thus, although M1 responses rarely matched patterns of muscle activity or kinematics, they shared the same general structure: responses were essentially a concatenation of an initial-cycle response, a steady-state response, and a terminal-cycle response. Even complex responses that might be mistaken as ‘noise’ displayed this structure (Figure 2C).

Figure 2.

Responses of example neurons

A-C) Firing rates for three example M1 neurons. Plotting conventions as in Figure 1C. Each panel’s label indicates the region, monkey (C or D), and cycling direction for which data were recorded. Cycling started from the bottom position. All calibrations are 40 spikes/s. Gray envelopes around each trace (typically barely visible) give the standard error of the mean.

D-F) Firing rates for three SMA neurons.

Neurons in SMA (Figure 2D–F) displayed different properties. Responses were typically a mixture of rhythmic and ramp-like features. As a result, during steady-state cycling, single-neuron responses in SMA had a greater proportion of power well below the ~2 Hz cycling frequency (Figure 3A,B). Due in part to these slow changes in firing rate, a clear ‘steady-state’ response was rarely reached. Furthermore, the initial-cycle response in SMA often differed across cycling distances (e.g., compare seven-cycle and two-cycle responses in Figure 2E) even when muscle and M1 responses were similar. In contrast, terminal-cycle responses were similar across distances. For example, in Figure 2E, the response during a four-cycle movement resembles that during the last four cycles of a seven-cycle movement.

Figure 3.

SMA responses show greater cycle-to-cycle differences

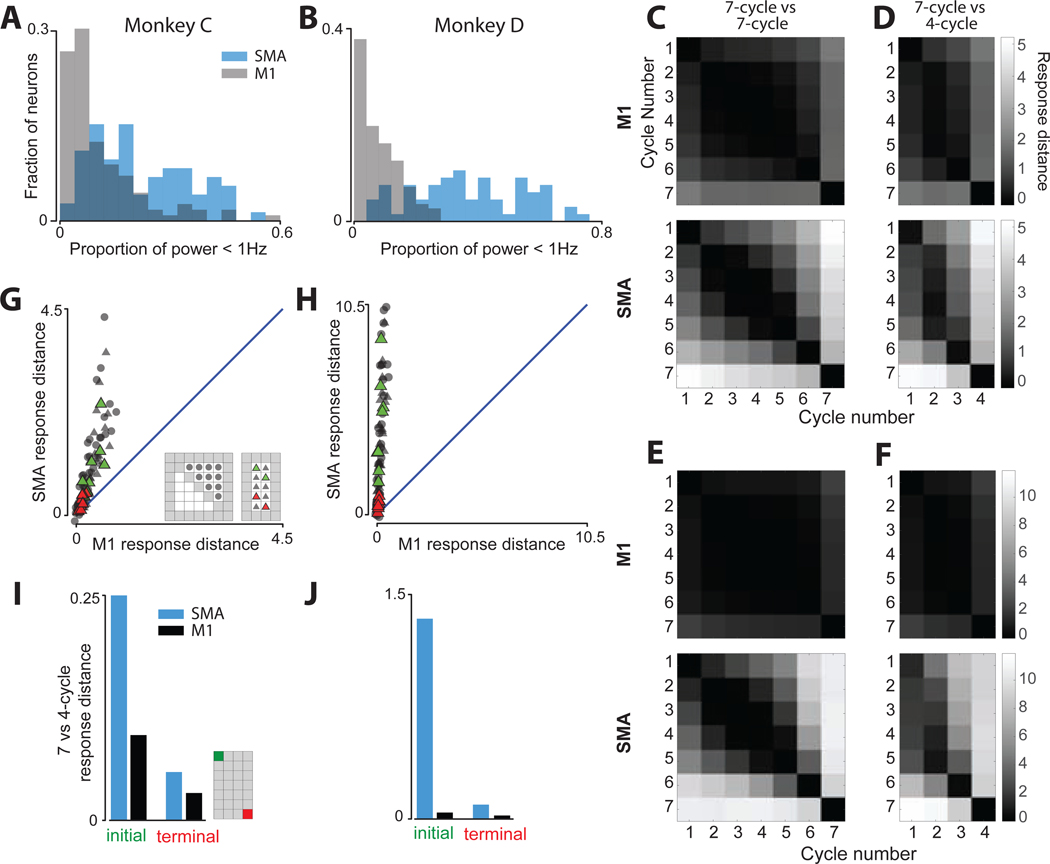
A) Histogram of the proportion of low-frequency (< 1 Hz) power in the trial-averaged firing rate. Right-shifted histograms indicate more low-frequency power. For each neuron, power was computed for each seven-cycle condition after mean centering (ensuring no power at 0 Hz). Proportion of power < 1 Hz was averaged across conditions to yield one value per neuron. Data for monkey C.

B) Same for monkey D.

C) Matrices of response distances when comparing cycles within a seven-cycle movement. For each comparison (e.g., cycle two versus three) normalized response distance was computed for each condition (two directions and starting locations) and averaged. The matrix is symmetric because the distance metric is symmetric. The diagonal is not exactly zero due to cross-validation. Data for monkey C.

D) Matrices of response distances comparing seven-cycle and four-cycle movements. Data for monkey C.

E) Same as panel C, but for monkey D.

F) Same as panel D, but for monkey D.

G) SMA versus M1 response distance for comparisons among steady-state cycles within seven-cycle movements (circles) and between seven- and four-cycle movements (triangles). For each of the four conditions, there are ten within-seven-cycle comparisons (square inset) and ten seven-versus-four-cycle comparisons (rectangular inset). Red triangles highlight comparisons between cycles equidistant from movement end: e.g., six-of-seven versus three-of-four. Green triangles highlight comparisons between cycles equidistant from movement beginning. Data for monkey C.

H) Same for monkey D.

I) Response distance when comparing initial cycles (one-of-seven verses one-of-four) and terminal cycles (seven-of-seven verses four-of-four). These are the same values as in panel D (comparisons highlighted in inset), plotted here for direct comparisons.

J) Same for monkey D.

Individual-cycle responses are more distinct in SMA

We compared the response on each cycle with that on every other cycle, both within seven-cycle movements and between seven- and four-cycle movements. For each neuron, we compared time-varying firing rates for the two cycles of interest. The ‘response distance’ between these two firing rates, averaged across all neurons, was computed using the crossnobis estimator (Diedrichsen and Kriegeskorte, 2017; Yokoi et al., 2018), providing an unbiased estimate of squared distance. Response distance was normalized based on the typical intra-cycle firing-rate modulation for that condition. This analysis thus assesses the degree to which responses are different for two cycles, relative to the response magnitude within a single cycle. Response distance for a given comparison was averaged across the two cycling directions and starting positions (Figure 3C–F,I,J), or shown independently for each (Figure 3G,H).

Figure 3C–F plot response distances in matrix form. For M1, responses were similar among all steady-state cycles, resulting in a central dark block of low distances. This block is square for within-seven-cycle comparisons and rectangular for seven-versus-four-cycle comparisons. Outer rows and columns are lighter (higher response distances) because initial- and terminal-cycle responses differed from one another and from steady-state responses. This analysis confirms that M1 responses involve a distinct initial-cycle response, a repeating steady-state response, and a distinct terminal-cycle response. These results agree with the finding that M1 activity relates to execution of the present movement (Hatsopoulos et al., 2003; Lara et al., 2018; Yokoi et al., 2018). Motor output (muscle activity and hand kinematics) is similar across steady-state cycles. M1 activity was correspondingly similar.

For SMA, the central block of high similarity was largely absent. Instead, response distance grew steadily with temporal separation. For example, within a seven-cycle movement, the second-cycle response was modestly different from the third-cycle response, fairly different from the fifth-cycle response, and very different from the seventh-cycle response. Average response distance was larger for SMA versus M1, both across all comparisons (p<10⁻¹⁰ for each monkey; resampling test) and for comparisons among steady-state cycles (p<10⁻⁸ for each monkey).

Steady-state comparisons are particularly relevant because motor output is essentially identical across steady-state-cycles. If activity within an area primarily reflects the present motor output, distances among steady-state cycles should be small. If activity tracks motor context, distances should be larger, especially when comparing cycles with different future motor outputs (e.g., three-of-seven versus three-of-four). We plotted response distance for SMA versus M1 for all steady-state comparisons (Figure 3G,H) both within seven-cycle movements (circles) and between seven- and four-cycle movements (triangles). Comparisons were made independently for each condition (the two directions and starting positions). Results agreed with the analyses in panels C-F (which averaged across conditions): response distance was always low for M1 but was often high for SMA.

Intriguingly, when comparing seven- and four-cycle movements, SMA response distance reflected whether steady-state cycles shared the same future motor output. Response distance was modest when comparing cycles equidistant from movement end (red triangles) and higher (p<0.05 for both monkeys, t-test) for cycles equidistant from the beginning (green triangles). The task affords a further comparison of this type: seven- and four-cycle movements share initial-cycle motor outputs, but become different in ~3 cycles (~1500 ms). In contrast, terminal-cycle motor output is similar and remains so as the monkey becomes stationary. Thus, if activity tracks motor context, response distance should be greater when comparing initial versus terminal cycles. This was indeed the case: SMA response distance was much larger between initial cycles than between final cycles (Figure 3I,J). Initial-cycle responses tended to share some structure; response distance was not as large as for some other comparisons (e.g., cycle one versus four). Yet initial-cycle responses were much more dissimilar than final-cycle responses, reflecting what can be seen in Figure 2D–F. This asymmetry was present in both areas but was larger for SMA (p<0.05 and p<10⁻¹⁰, monkey C and D; resampling test).

Cycle-to-cycle response specificity in SMA somewhat resembles contingency-specific activity during movement sequences (e.g., a neuron that bursts only when pulling will be followed by turning; Shima and Tanji, 2000). Yet specificity during cycling is manifested differently, by responses that evolve continuously rather than burst at a key moment. The ramping activity we observed was more reminiscent of pre-movement responses in a timing task (Cadena-Valencia et al., 2018). That said, ramping activity was not the only source of cycle-to-cycle response differences. To further explore such differences, we consider the evolution of population trajectories.

SMA and M1 display different population trajectories

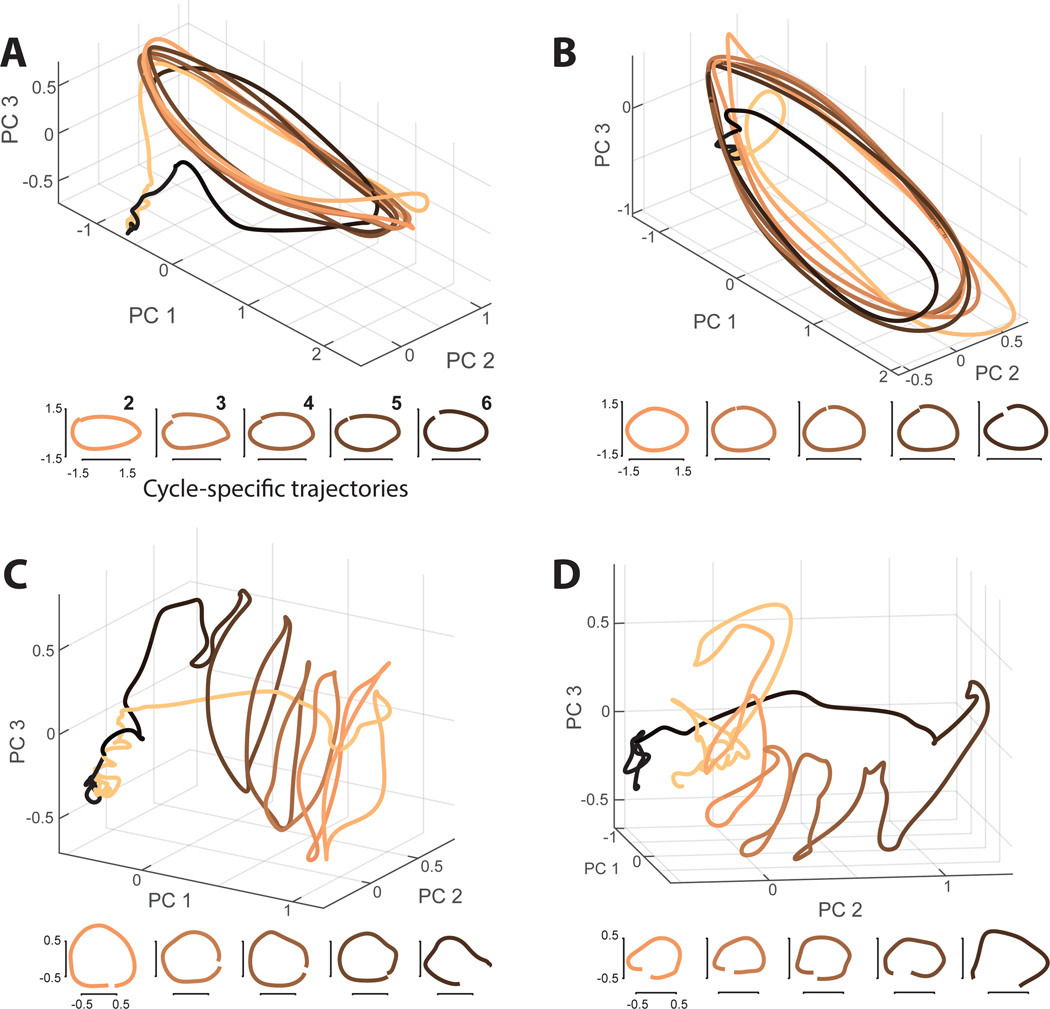
To gain intuition, we first visualized population trajectories in three dimensions. Projections onto the top three PCs are shown for one seven-cycle condition for M1 (Figure 4A,B) and SMA (Figure 4C,D), shaded light to dark to denote the passage of time. For M1, trajectories exited a baseline state just before movement onset, entered a periodic orbit during steady-state cycling, and remained there until settling back to baseline as movement ended. To examine within-cycle structure, we also applied PCA separately for each cycle (bottom of each panel). For M1, this revealed little new; the dominant structure on each cycle was an ellipse, as was seen in the projection of the full response.

Figure 4.

Visualization of population trajectories

A) M1 population trajectory during a seven-cycle movement (cycling forward from the bottom). Top trajectory is the projection onto the top three PCs, from 1500 ms before movement onset until 500 after, shaded from tan (movement beginning) to black (movement end). PCs were found using all four seven-cycle conditions and data from 200 ms before movement onset until 200 ms after movement offset (narrower than the plotted range, to prioritize dimensions that capture movement-related activity). Small plots at bottom show projections of each steady-state cycle (2–6) onto the first two PCs found using data from that cycle only.

B) Same for monkey D, data are from the seven-cycle, forward, top-start condition.

C) SMA population trajectory for monkey C. Same condition as in A.

D) SMA population trajectory for monkey D. Same condition as in B.

In SMA, the dominant geometry was quite different and also more difficult to summarize in three dimensions. We first consider data for monkey C (Figure 4C). Just before movement onset, the population trajectory moved sharply away from baseline (from left to right in the plot). The trajectory returned to baseline in a rough spiral, with each cycle separated from the last. The population trajectory for monkey D was different in some details (Figure 4D) but it was again the case that a translation separated cycle-specific features.

SMA population trajectories appear to have a ‘messier’ geometry than M1 trajectories; e.g., cycle-specific loops appear non-elliptical and kinked. Yet it should be stressed that a three-dimensional projection is necessarily a compromise. The view is optimized to capture the largest features in the data; smaller features can be missed or partially captured and distorted. We thus employed cycle-specific PCs to visualize the trajectory on each cycle separately. Doing so revealed near-circular trajectories, much as in M1. Thus, individual-cycle orbits are present in SMA, but are a smaller feature relative to the large translation.

In summary, M1 trajectories are dominated by a repeating elliptical orbit while SMA trajectories are better described as helical. Each cycle involves an orbit, but these are separated by a translation. This translation reflects ramp-like responses in single-neurons. Yet the translation does not account for all the cycle-to-cycle differences in SMA. Unlike an idealized helix, individual-cycle orbits in SMA occur in somewhat different subspaces. This property is explored below.

The SMA population response occupies different dimensions across cycles

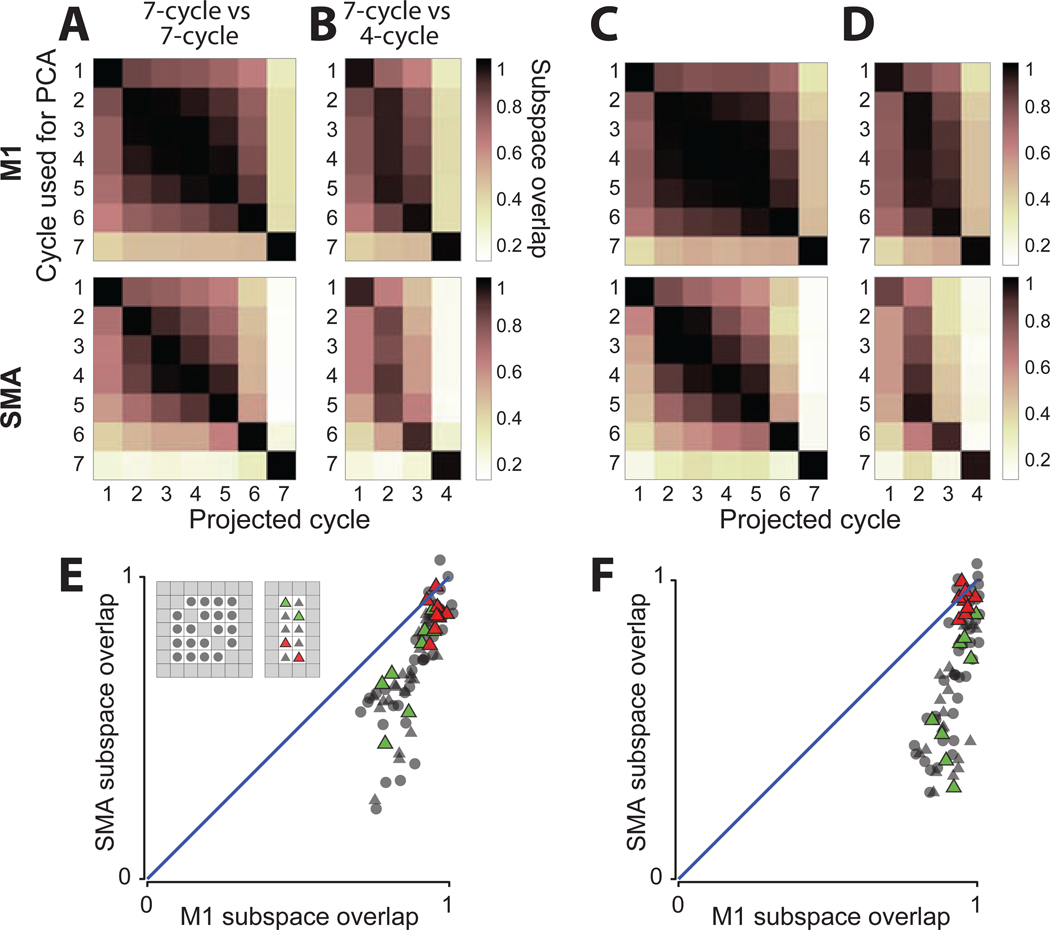
To ask whether activity on different cycles occupies the same dimensions, we computed subspace overlap (Elsayed et al., 2016). For example, to compare cycle one and two, we computed PCs from activity during cycle one, projected activity during cycle two, and computed the variance explained. We employed six PCs, which captured most of the response variance for a given cycle. Essentially identical results were obtained using fewer or more PCs (Figure S1). Variance was normalized so that unity indicates that two cycles occupy the same subspace. We employed cross-validation so that sampling error did not bias overlap toward lower values. As in Figure 3C–F, we compared within seven-cycle movements (Figure 5A,C) and between seven- and four-cycle movements (Figure 5B,D).

Figure 5.

Subspace overlap between responses on different cycles

A) Subspace overlap, comparing cycles within seven-cycle movements. Each matrix entry shows subspace overlap for one comparison. Rows indicate the cycle used to find the PCs, and columns indicate the cycle for which variance captured is computed. Overlap is not symmetric. Data are averaged across conditions (pedaling directions and starting positions). Diagonal entries are not exactly unity due to cross-validation. Data for monkey C.

B) Cross-validated subspace overlap comparing seven-cycle with four-cycle movements. Data for monkey C.

C) Same as panel A but for monkey D.

D) Same as panel B but for monkey D.

E) Subspace overlap for SMA versus M1 for comparisons among steady-state cycles within seven-cycle movements (circles) and between seven- and four-cycle movements (triangles). For each of the four conditions there are twenty within-seven-cycle comparisons (square inset) and ten seven-versus-four-cycle comparisons (rectangular inset). Red triangles highlight comparisons between cycles equidistant from movement end. Green triangles highlight comparisons between cycles equidistant from movement beginning. Data for monkey C.

F) Same for monkey D.

See also Figure S1.

For M1, subspace overlap was high among steady-state cycles, producing a central block structure (Figure 5A–D, top row). That block was square when comparing within seven-cycle movements (cycles 2–6 versus 2–6) and rectangular when comparing between seven- and four-cycle movements (cycles 2–6 versus 2–3). Thus, in M1, the subspace found for any steady-state cycle overlapped heavily with that for all other steady-state cycles.

For SMA (bottom row) the central block was less well-defined. Comparing within seven-cycle movements, SMA subspace overlap declined steadily as cycles became more distant from one another. For example, for monkey D, overlap declined from 0.97 when comparing cycle two versus three, to 0.39 when comparing two versus six (monkey C: from 0.91 to 0.49). A similar effect was present when comparing seven- and four-cycle movements. For example, overlap was only 0.54 (monkey C) and 0.38 (monkey D) when comparing cycle two-of-seven with three-of-four, even though these cycles had similar motor output. Overall, subspace overlap among steady-state cycles was lower for SMA versus M1: p<10⁻⁷ for both monkeys for within-seven-cycle comparisons, and p<10⁻¹⁰ for both monkeys for seven-versus-four-cycle comparisons (resampling test).

The analyses in Figure 5A–D average across the four conditions. Figure 5E,F considers each condition separately for all comparisons among steady-state cycles, both within seven-cycle and between seven- and four-cycle movements. M1 subspace overlap was reasonably high for all comparisons (always >0.71 for monkey C and >0.79 for D). SMA subspace overlap was significantly lower overall (p<10⁻¹⁰ for each monkey, paired t-test) with minima of 0.23 and 0.29. Yet SMA subspace overlap was not always low. It was typically high when comparing cycles equidistant from movement end (red triangles). In contrast, overlap was lower (p<0.05 and p<0.005; monkey C and D, paired t-test) when comparing cycles equidistant from movement beginning (green triangles ). Thus, subspace overlap was high when two situations shared a similar future, and low otherwise.

Population trajectories in artificial networks

‘Motor context’ – i.e., abstract information that guides future action – may be remembered (e.g., “I am performing a particular sequence”; Shima and Tanji, 2000), internally estimated (“it has been 800 ms since the last button press”; Gamez et al., 2019), or derived from abstract cues (“this color means reach quickly”; Lara et al., 2018). In the cycling task, salient contextual information arrives when the target appears, specifying the number of cycles to be produced. The current motor context (how many cycles remain) can then be updated throughout the movement, based on both visual cues and internal knowledge of the number of cycles already produced.

Our hypothesis is that the helical SMA population trajectory is a natural solution to the problem of internally tracking motor context during multi-cycle rhythmic movement. Is this hypothesis sufficient to explain the helical structure, or are additional assumptions (regarding parameters that are represented or other computations that are performed) necessary? Conversely, are the elliptical M1 trajectories indeed what is expected if a network does not internally track motor context?

To address these questions, we trained artificial recurrent networks that did, or did not, need to internally track motor context. We considered simplified inputs (pulses at specific times) and simplified outputs (pure sinusoids lasting four or seven cycles). We trained two families of recurrent networks. A family of ‘context-naïve’ networks received one input pulse indicating that output generation should commence, and a different input pulse indicating that output should be terminated. These pulses were separated by four or seven cycles, corresponding to the desired output. Thus, context-naïve networks had no information regarding context until the second input. Nor did they need to track context; the key information was provided at the critical moment. In contrast, a family of ‘context-tracking’ networks received only an initiating input pulse, which differed depending on whether a four- or seven-cycle output should be produced. Context-tracking networks then had to generate a sinusoid with the appropriate number of cycles, and terminate with no further external guidance. For each family, we trained 500 networks that differed in their initial connection weights (Methods).

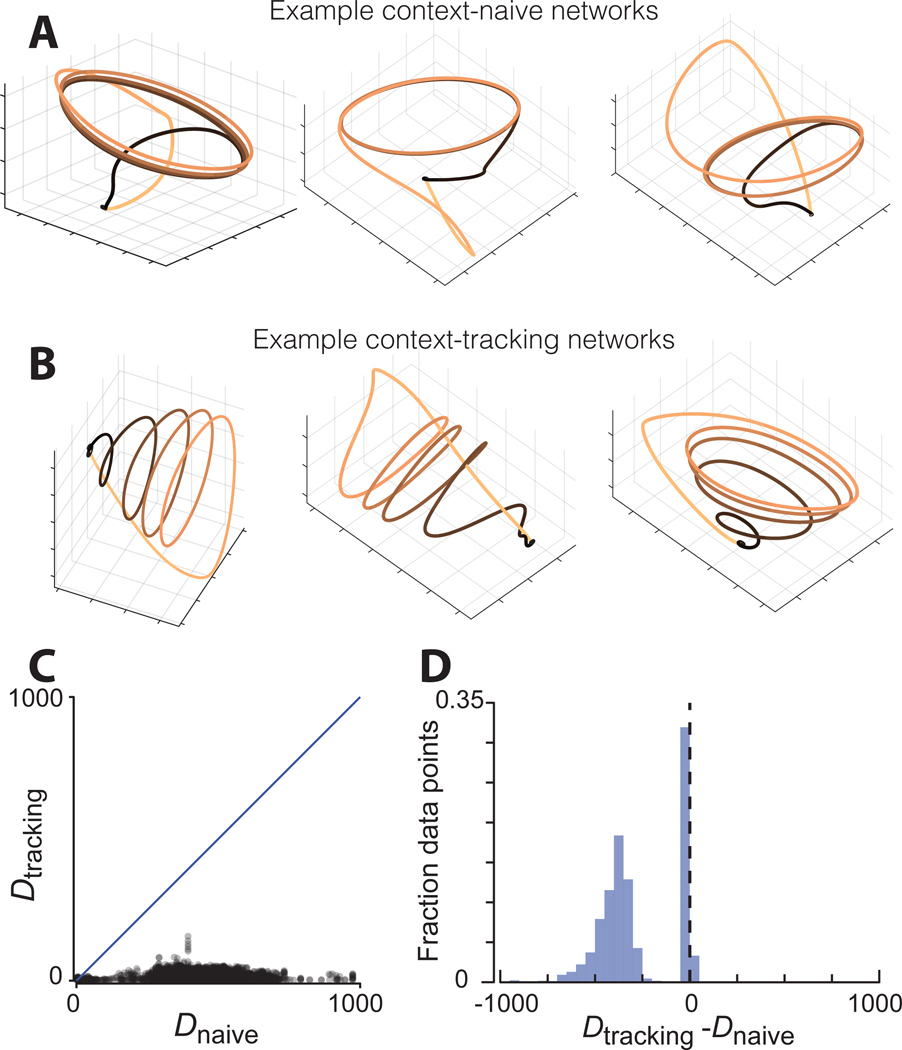
The two network families learned qualitatively different solutions involving population trajectories with different geometries. Context-naïve networks employed an elliptical limit cycle (Figure 6A). The initiating input caused the trajectory to enter an orbit, and the terminating input prompted the trajectory to return to baseline. This solution was not enforced but emerged naturally. There was network-to-network variation in how quickly activity settled into the limit cycle (Figure S2) but all networks that succeeded in performing the task employed a version of this strategy.

Figure 6.

Trajectory geometry in simulated networks.

A) Population trajectories for three example context-naïve networks during the four-cycle condition. Left, right, and vertical axes correspond to PC 1, 2, and 3.

B) Population trajectories for three example context-tracking networks.

C) Trajectory divergence for context-tracking versus context-naïve networks. Comparison involves 500 networks of each type, paired arbitrarily. Each dot plots D_tracking versus D_naïve for one time during one pairing. Diagonal line indicates unity.

D) Distribution of differences in trajectory divergence between context-naïve and context tracking networks. D_tracking – D_naïve was computed for every time and all possible pairings (every context-tracking network with every context-naïve network).

See also Figures S2–S4

Context-tracking networks utilized population trajectories that were more helical; the trajectory on each cycle was separated from the others by an overall translation (Figure 6B). While there was network-to-network variation (Figure S3), all successful context-tracking networks employed some form of helical or spiral trajectory. This solution is intuitive: context-tracking networks do not have the luxury of following a repeating orbit. If they did, information regarding context would be lost, and the network would have no way of ‘knowing’ when to terminate its output.

For context-tracking networks, trajectories could also occupy somewhat different subspaces on different cycles. Projected onto three dimensions, this geometry resulted in individual-cycle trajectories of seemingly different magnitude (Figure 6B, first and third examples). As with the helical structure, this geometry creates separation between individual-cycle trajectories. There was considerable variation in the degree to which this strategy was employed. Some context-tracking networks used nearly identical subspaces for every cycle while others used quite different subspaces. Context-naïve networks never employed this strategy.

The population geometry adopted by context-naïve and context-tracking networks bears obvious similarities to the empirical population geometry in M1 and SMA, respectively. That said, we stress that neither family is intended to faithfully model the corresponding area. Furthermore, reasonable alternative modeling choices exist. For example, rather than asking context-tracking networks to track progress using internal dynamics alone, one can provide a ramping input. Providing an external input respects the fact that, during cycling, tracking of context can and presumably does benefit from visual inputs (optic flow and the looming of the target). Interestingly, context-tracking networks trained in the presence / absence of ramps employed similar population trajectories (Figure S4). The slow translation that produces helical structure is a useful computational tool – one that networks produced on their own if needed, but were also content to inherit from upstream sources. For these reasons, we focus not on the details of individual network trajectories, but rather on the geometric features that differentiate context-tracking from context-naïve trajectories, and that might similarly differentiate M1 and SMA trajectories.

Trajectory divergence

Trajectories displayed by context-tracking networks reflect specific solutions to a general problem: ensuring that two trajectory segments never trace the same path and then diverge. Avoiding such divergence is critical when network activity must distinguish situations that have the same present motor output but different future outputs. Rather than assessing the specific paths of individual-network solutions, we developed a general metric of trajectory divergence. We note that trajectory divergence differs from trajectory tangling (Russo et al., 2018), which was very low in both SMA and M1 (Figure S5). Trajectory tangling assesses whether trajectories are consistent with a locally smooth flow-field. Trajectory divergence assesses whether similar paths eventually separate, smoothly or otherwise. A trajectory can have low tangling but high divergence, or vice versa (Figure S6).

To construct a metric of trajectory divergence, we consider times t and t′, associated population states ${\mathit{x}}_t$ and ${\mathit{x}}_{t^{\prime }}$, and future population states ${\mathit{x}}_{t+\text{Δ}}$ and ${\mathit{x}}_{t^{\prime }+\text{Δ}}$. We consider all possible pairings of t and t′ across both times and cycling distances. Thus, t and t′ might occur during different cycles of the same movement or during different distances. We compute the ratio $\frac{{\Vert x_{t+\text{Δ}}-x_{t^{\prime }+\text{Δ}}\Vert }^2}{{\Vert x_t-x_{t^{\prime }}\Vert }^2+\alpha }$, which becomes large if ${\mathit{x}}_{t+\text{Δ}}$ differs from ${\mathit{x}}_{t^{\prime }+\text{Δ}}$ despite ${\mathit{x}}_t$ and ${\mathit{x}}_{t^{\prime }}$ being similar. The constant α is small and proportional to the variance of x, and prevents hyperbolic growth.

Given that the difference between two random states is typically sizeable, the above ratio will be small for most values of t′. As we are interested in whether the ratio ever becomes large, we take the maximum, and define divergence for time t as:

$$D(t)=\underset{t^{\prime },\text{Δ}}{\max }\frac{{\Vert x_{t+\text{Δ}}-x_{t^{\prime }+\text{Δ}}\Vert }^2}{{\Vert x_t-x_{t^{\prime }}\Vert }^2+\alpha }.$$ 1

We consider only positive values of Δ. Thus, D (t) is large if similar trajectories diverge but not if dissimilar trajectories converge. Divergence was assessed using a twelve-dimensional neural state. Results were similar for all reasonable choices of dimensionality.

D (t) differentiated between context-tracking and context-naïve networks. To compare, we considered pairs of networks, one context-tracking and one context-naïve. For each time, we plotted D (t) for the context-tracking network versus that for the context-naïve network. Trajectory divergence was consistently lower for context-tracking networks (Figure 6C, p<0.0001, rank sum test). This was further confirmed by taking the difference in D (t) for every time and all network pairs (Figure 6D). Both context-tracking and context-naïve trajectories contained many moments when divergence was low, resulting in a narrow peak near zero. However, context-naïve trajectories (but not context-tracking trajectories) also contained moments when divergence was high, yielding a large set of negative differences.

Trajectory divergence is lower for SMA

The roughly helical structure of the empirical SMA population response (Figure 4) suggests low trajectory divergence, as does the finding that SMA responses differ across cycles (Figures 3 and 5). Yet the complex shape of the empirical trajectories makes it impossible to ascertain, via inspection, whether divergence is low. Furthermore, it is unclear whether cycle-to-cycle response differences ensure low divergence across both time and cycling distances. We therefore directly measured trajectory divergence for the empirical trajectories.

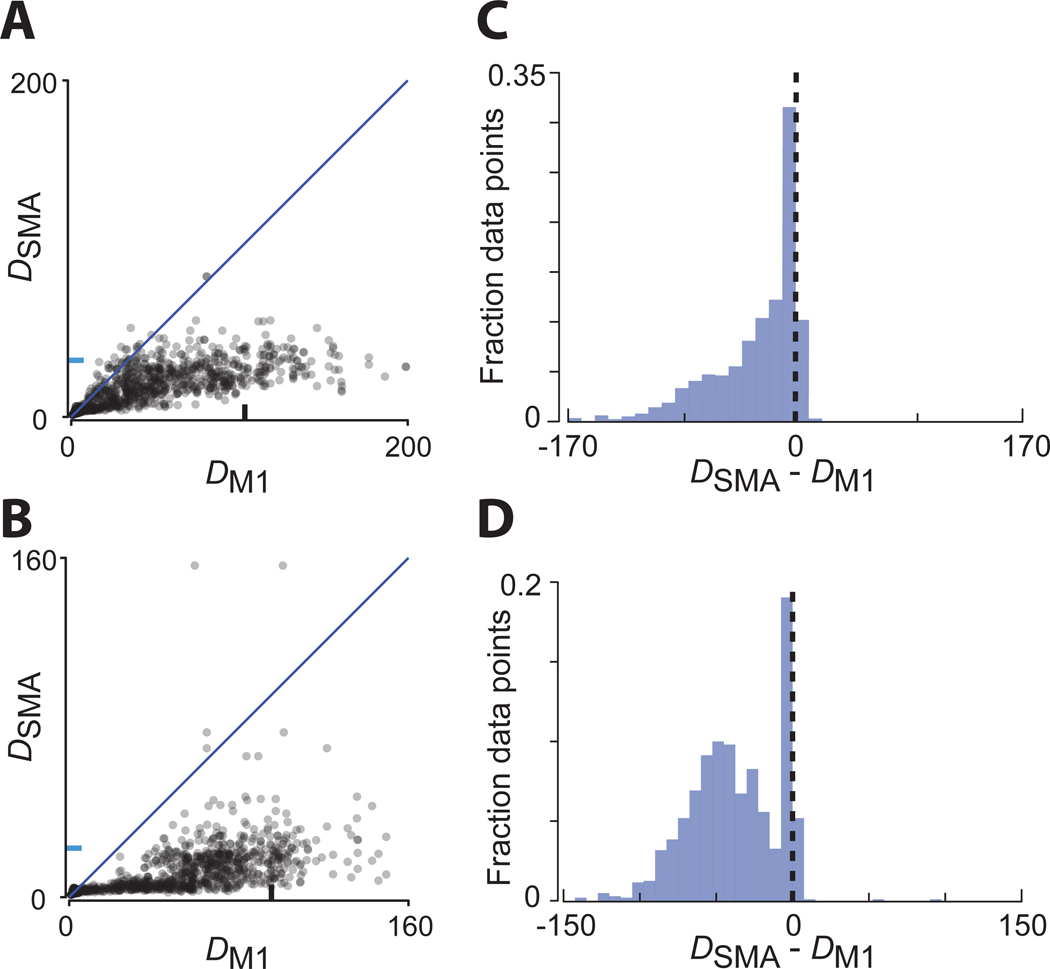
Plotting SMA versus M1 trajectory divergence for each time (Figure 7A,B) revealed that divergence was almost always lower in SMA. We next computed the difference in divergence, at matched times, between SMA and M1 (Figure 7C,D). There was a narrow peak at zero (moments where divergence was low for both) and a large set of negative values, indicating lower divergence for SMA. Strongly positive values (lower divergence for M1) were absent (monkey C) or very rare (monkey D; 0.13% of points > 20). Distributions were significantly negative (p<0.00001 for monkey A and B, bootstrap). The overall scale of divergence was smaller for the empirical data than for the networks. Specifically, divergence reached higher values for context-naïve networks than for the empirical M1 trajectories. This occurs because simulated trajectories can repeat almost perfectly, yielding very small values of the denominator in equation 1. Other than this difference in scale, trajectory divergence for SMA and M1 differed in much the same way as for context-tracking and context-naïve networks (compare Figure 7C,D with Figure 6D).

Figure 7.

Trajectory divergence in M1 and SMA

A) Trajectory divergence for SMA versus M1 (monkey C). Each dot corresponds to one time during one condition. Divergence was computed considering all times for all distances that shared a direction and starting position. Data for all conditions is then plotted together. Blue and black tick mark denotes 90th percentile trajectory divergence for SMA and M1 respectively.

B) Same for monkey D.

C) Distribution of the differences in trajectory divergence between SMA and M1 (monkey C). Same data as in panel A, but for each time / condition we computed the difference in divergence.

D) Same for monkey D.

See also Figures S5–S7

The ability to consider both network and neural trajectories (despite differences across networks and across monkeys) underscores that the divergence metric describes trajectory geometry at a useful level of abstraction. Multiple features can contribute to low divergence, including ramping activity, cycle-specific responses, and different subspaces on different cycles. Different network instantiations may use these different ‘strategies’ to different degrees. Trajectory divergence provides a useful summary of a computationally-relevant property, regardless of the specifics of how it was achieved.

Because trajectory divergence abstracts away from the details of specific trajectories, it can be readily applied in new situations. For example, the cycling task involved not only different cycling distances, but also different cycling directions and different starting positions. The latter is particularly relevant, because movements ended at the same position (cycle top or bottom) as they started. Thus, how a movement will end depends on information present at the beginning. Dowa SMA distinguish between movements that will end in one position versus the other? One could address this using a traditional approach, perhaps assessing the presence and timing of ‘starting-position-tuning.’ However, it is simpler, and more relevant to the hypothesis being considered, to ask whether divergence remains low when comparisons are made across all conditions including starting positions. This was indeed the case (Figure S7).

Computational implications of trajectory divergence

We considered trajectory divergence because of its expected computational implications. A network with a high-divergence trajectory can accurately and robustly generate its output on short timescales. Yet unless guided by external inputs at key moments, such a network may be susceptible to errors on longer timescales. For example, if a trajectory approximately repeats, a likely error would be the generation of extra cycles or the skipping of a cycle.

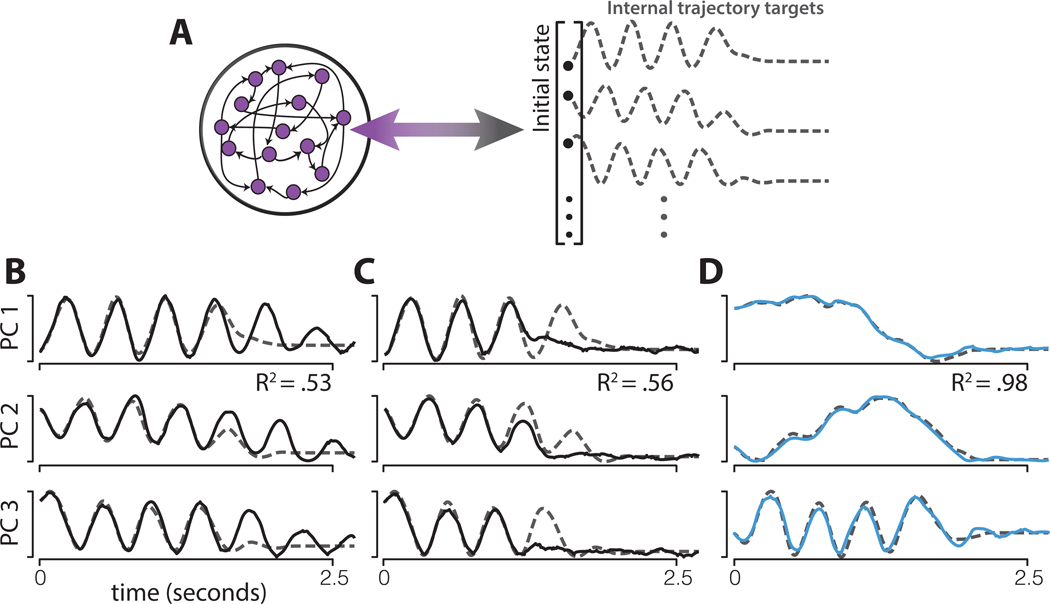
To test these intuitions, we employed a new set of simulations using an atypical training approach that enforced an internal network trajectory (Russo et al., 2018), as opposed to the usual approach of training a target output. We trained networks to precisely follow the empirical M1 trajectory, recorded during a four-cycle movement, without any input indicating when to stop (Figure 8A). Networks were trained in the presence of additive noise. Using data from each monkey, we trained forty networks: ten for each of the four four-cycle conditions. Networks were able to reproduce the cyclic portion of the M1 trajectory. However, without the benefit of a stopping pulse, these networks failed to consistently complete the trajectory. For example, networks sometimes erroneously produced extra cycles (Figure 8B) or skipped cycles and stopped early (Figure 8C).

Figure 8.

Networks trained to follow empirical population trajectories.

A) Networks were trained to autonomously follow a target trajectory defined by the top six PCs of the empirical population trajectory for a four-cycle movement, including stopping at the end. Dashed lines show the target trajectory for three PCs for one example: monkey D, M1, cycling backward starting at the bottom. The activity of every neuron in the network was trained to follow a random combination of the projection onto the top six PCs. This ensured that the simulated population trajectory matched the empirical trajectory.

B) Example network (solid) and target (dashed) trajectories on one trial, for a network trained to produce the empirical M1 trajectory. The network trajectory initially matches the target, but continues ‘cycling’ when it should have ended. This resulted in an R² (variance in the target accounted for by the network trajectory) well below unity.

C) As in panel B, but for an example trial where the opposite error was made: the network trajectory stops early. This trajectory is produced by the same network as in B; the only difference is the additive noise on that particular trial.

D) Example network (blue) and target (dashed) trajectories on one trial, for a network trained to produce the empirical SMA trajectory. The level of additive noise was the same as for the network in panels B and C, but the network succeeds in following the trajectory to the end.

We also trained networks to follow the empirical SMA trajectories. Those trajectories contained a rhythmic component and lower-frequency ‘ramping’ signals (Figure 8D) related to the translation seen in Figure 4C,D. In contrast to the high-divergence M1 trajectories, which were never consistently followed for the full trajectory, the majority of network initializations resulted in good solutions where the low-divergence SMA trajectory was successfully followed from beginning to end. Thus, in the absence of a stopping pulse, SMA trajectories could be reliably produced and terminated but M1 trajectories could not.

Discussion

Many studies argue that SMA contributes to the guidance of action based on internal, abstract, or contextual factors (Cadena-Valencia et al., 2018; Kornysheva and Diedrichsen, 2014; Merchant and de Lafuente, 2014; Mushiake et al., 1991; Nakamura et al., 1998; Remington et al., 2018b; Romo and Schultz, 1992; Shima and Tanji, 2000; Sohn and Lee, 2007; Tanji and Kurata, 1982; Tanji and Shima, 1994; Thaler et al., 1995; Wang et al., 2018). We translated this hypothesis into a prediction regarding the geometry of population activity. As predicted, trajectory divergence was low in SMA, and provided a cohesive explanation for diverse response features. Slowly ramping firing-rates are, at the surface level, a very different feature from changes in the occupied subspace. Yet both contribute to low divergence. Other features (which we did not attempt to isolate) maintained low divergence across cycling directions and starting positions. This raises a broader point: the features that subserve low divergence will almost certainly be task and situation specific. For example, during sequences of reaches, SMA neurons exhibit burst-like responses with various forms of selectivity. Such selectivity presumably produces low divergence, although this remains to be explicitly tested. Thus, a reasonable hypothesis is that, during a given task, SMA responses will exhibit some of the dominant response features seen in M1 (transient responses when reaching, rhythmic activity during cycling, etc.) combined with additional response features that ensure low divergence.

An essential strategy is to focus on specific features that relate to how a network might perform a particular task (Churchland et al., 2012; Driscoll et al., 2018; Gallego et al., 2017; Kaufman et al., 2014; Mante et al., 2013; Remington et al., 2018b; Stopfer and Laurent, 1999). A complementary strategy is to quantify general properties that may be preserved across a class of computations. Our divergence metric was designed with this goal. We recently considered a different geometric property, trajectory tangling (Russo et al., 2018), which is necessary for a network to robustly generate an output via internal dynamics. Low trajectory tangling was observed in M1 across a range of tasks, in both monkeys and mice. As another example, studies of the visual system have employed linear separability (a different definition of ‘untangled’) to assess whether population geometry is consistent with a class of computation having been performed (DiCarlo and Cox, 2007; Pagan et al., 2013).

The advantages of this approach come with a limitation: geometry may strongly suggest a class of computations, yet do little to delineate the specific computation. For example, low trajectory divergence in SMA is consistent with internal tracking of context, but does not specify the input-output relationship the network is trying to accomplish. Indeed, we observed low-divergence trajectories regardless of whether context-tracking networks received a ramping input or internally generated their own ramp. Similarly, it remains unclear what signals SMA conveys to downstream areas. Possibilities include start/stop signals, a ‘keep moving’ signal that remains high during movement, or a rhythmic signal that entrains downstream pattern generation (Schoner and Kelso, 1988). Deciphering the computation used to perform a particular task will typically require a level of detail below that captured by measures of population geometry.

A goal of assessing population geometry is to find general properties. At the same time, exceptions may be informative. For example, during grasping, trajectory tangling becomes high in M1, suggesting a shift in the balance of input-driven versus internally driven activity (Suresh et al., 2019). We expect that, in SMA, there will be situations where divergence becomes revealingly high. For example, there are presumably limits on the timescales across which SMA can track context, which may be revealed in the timescales over which divergence stays low. Trajectory divergence is also likely to become high when action is guided by sudden, unpredictable cues.

Given the benefits of low divergence, why employ separate areas – SMA and M1 – with low and high divergence? Why not unify context tracking and pattern generation? Allowing high divergence in M1 may be useful for two reasons. First, dispensing with divergence-avoiding signals frees dynamic range for other computations, such as generating fine-grained aspects of the outgoing motor command. Second, low divergence may interfere with adaptation; learning on one cycle would have no clear way of transferring to other cycles (Sheahan et al., 2016).

The concepts in the present study are informed by our field’s understanding of how recurrent networks perform computations (Mante et al., 2013; Michaels et al., 2016; Remington et al., 2018b; Russo et al., 2018; Stringer et al., 2019). Because recurrent-network-based computations are commonly described via flow-fields governing a neural state (Maheswaranathan, 2019; Sussillo and Barak, 2013), this perspective has been termed a ‘dynamical systems view’ (Shenoy et al., 2013). This view intersects with ideas regarding how dynamical systems can perform computations (van Gelder, 1998) or describe behavior (Kelso, 2012). It has been argued that dynamics-based explanations should supplant ‘representational’ explanations (van Gelder, 1998). This view is extreme; dynamical systems may involve representations (Bechtel, 2012). Yet it is true that purely representational thinking can be limiting. For example, the question of whether M1 is more concerned with ‘muscles versus movements’ is poorly addressed by inquiring whether neural activity is a function of muscle activity versus movement kinematics (Fetz, 1992; Scott, 2008). M1 is dominated by signals that are neither muscle-like nor kinematic-like, but are readily understood as necessary for low trajectory tangling (Russo et al., 2018).

Correspondingly, multiple aspects of the SMA population response are readily understood as aiding low trajectory divergence. It is tempting to apply representational interpretations to some of those properties. For example, there is a dimension in which activity is ramp-like during cycling, which might be thought of as a representation of ‘time’, ‘distance’, or ‘progress within the overall movement’. While it is conceivable that this dimension might consistently represent these things during other tasks, there is presently no evidence for this. Furthermore, low divergence is aided by additional features that lack a straightforward representational interpretation, such as occupancy of different subspaces across cycles. The dynamical perspective helps one to see the connection between these seemingly disjoint response features, in a way that a purely representational perspective does not.

STAR Methods

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Dr. Mark M. Churchland (mc3502@columbia.edu).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

Datasets are provided at https://data.mendeley.com/datasets/tfcwp8bp5j/1. Code is provided at https://github.com/aarusso/trajectory-divergence.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Main experimental datasets

Subjects were two adult male rhesus macaques (monkeys C and D). Animal protocols were approved by the Columbia University Institutional Animal Care and Use Committee. Experiments were controlled and data collected under computer control (Speedgoat Real-time Target Machine). During experiments, monkeys sat in a customized chair with the head restrained via a surgical implant. Stimuli were displayed on a monitor in front of the monkey. A tube dispensed juice rewards. The left arm was loosely restrained using a tube and a cloth sling. With their right arm, monkeys manipulated a pedal-like device. The device consisted of a cylindrical rotating grip (the pedal), attached to a crank-arm, which rotated upon a main axel. That axel was connected to a motor and a rotary encoder that reported angular position with 1/8000 cycle precision. In real time, information about angular position and its derivatives was used to provide virtual mass and viscosity, with the desired forces delivered by the motor. The delay between encoder measurement and force production was 1 ms.

Horizontal and vertical hand position were computed based on angular position and the length of the crank-arm (64 mm). To minimize extraneous movement, the right wrist rested in a brace attached to the hand pedal. The motion of the pedal was thus almost entirely driven by changes in shoulder and elbow angle, with the wrist moving only slightly to maintain a comfortable posture.

METHOD DETAILS

Task

Monkeys performed the ‘cycling task’ as described previously (Russo et al., 2018). The monitor displayed a virtual landscape, generated by the Unity engine (Unity Technologies, San Francisco). Surface texture and landmarks provided visual cues regarding movement through the landscape along a linear ‘track’. One rotation of the pedal produced one arbitrary unit of movement. Targets on the track indicated where the monkey should stop for juice reward.

Each trial began with the monkey stationary on top of an initial target. After a 1000 ms hold period, the final target appeared at a prescribed distance. Following a randomized (500–1000 ms) delay period, a gocue (brightening of the final target) was given. The monkey then had to cycle to acquire the final target. After remaining stationary in the final target for 1500 ms, the monkey received a reward. The full task included 20 conditions distinguishable by final target distance (half-, one-, two-, four-, and seven-cycles), initial starting position (top or bottom of the cycle), and cycling direction (forward or backward). Half-cycle distances evoked quite brief movements. Because of the absence of a full-cycle response, they are not amenable to many of the analyses we employ, and were thus not analyzed.

Salient visual cues (landscape color) indicated whether cycling must be ‘forward’ (the hand moved away from the body at the top of the cycle) or ‘backward’ (the hand moved toward the body at the top of the cycle) to produce forward virtual progress. Trials were blocked into forward and backward cycling. Other trials types were interleaved, randomly, within those blocks.

Neural recordings during cycling

After initial training, we performed a sterile surgery during which monkeys were implanted with a head restraint and recording cylinders (Crist Instruments, Hagerstown, MD). Cylinders were located based on magnetic resonance imaging scans. For M1 recordings, the cylinder was placed surface normal to the cortex and centered over the border between caudal PMd and primary motor cortex. After recording in M1, we performed a second sterile surgery to move the cylinder over the SMA. SMA cylinders were angled at ~20° degrees to avoid the superior sagittal sinus. The skull within the cylinders was left intact and covered with a thin layer of dental acrylic. Electrodes were introduced through small (3.5 mm diameter) burr holes drilled by hand through the acrylic and skull, under ketamine / xylazine anesthesia. Neural recordings were made using conventional single electrodes (Frederick Haer Company, Bowdoinham, ME) driven by a hydraulic microdrive (David Kopf Instruments, Tujunga, CA). The use of conventional electrodes, as opposed to electrode arrays, allowed recordings to be made from the medial bank (where most of the SMA is located) and from both surface and sulcal M1.

Recording locations were guided via microstimulation, light touch, and muscle palpation protocols to confirm the trademark properties of each region. For motor cortex, recordings were made from primary motor cortex (both surface and sulcal) and the adjacent (caudal) aspect of dorsal premotor cortex. These recordings are analyzed together as a single motor cortex population. All recordings were restricted to regions where microstimulation elicited responses in shoulder and arm muscles.

Neural signals were amplified, filtered, and manually sorted using Blackrock Microsystems hardware (Digital Hub and 128-channel Neural Signal Processor). On each trial, the spikes of the recorded neuron were filtered with a Gaussian (25 ms standard deviation; SD) to produce an estimate of firing rate versus time. These were then temporally aligned and averaged across trials(Russo et al., 2018) (details below).

EMG recordings

Intra-muscular EMG was recorded from the major shoulder and arm muscles using percutaneous pairs of hook-wire electrodes (30mm x 27 gauge, Natus Neurology) inserted ~1 cm into the belly of the muscle for the duration of single recording sessions. Electrode voltages were amplified, bandpass filtered (10–500 Hz) and digitized at 1000 Hz. To ensure that recordings were of high quality, signals were visualized on an oscilloscope throughout the duration of the recording session. Recordings were aborted if they contained significant movement artifact or weak signal. Offline, EMG records were high-pass filtered at 40 Hz and rectified. Rectified EMG voltages were smoothed with a Gaussian (25 ms SD, same as neural data) and trial averaged (see below). Recordings were made from the following muscles: the three heads of the deltoid, the two heads of the biceps brachii, the three heads of the triceps brachii, trapezius, latissimus dorsi, pectoralis, brachioradialis, extensor carpi ulnaris, extensor carpi radialis, flexor carpi ulnaris, flexor carpi radialis, and pronator. Recordings were made from 1–8 muscles at a time, on separate days from neural recordings. We often made multiple recordings for a given muscle, especially those that we previously noted could display responses that vary with recording location (e.g., the deltoid). We made 29 (monkey C) and 35 (monkey D) total muscle recordings.

Trial alignment and averaging

To preserve response features, it was important to compute the average firing rate across trials with nearly identical behavior. This was achieved by 1) training to a high level of stereotyped behavior, 2) discarding rare aberrant trials, and 3) adaptive alignment of individual trials prior to averaging. Because of the temporally extended nature of cycling movements, standard alignment procedures (e.g., locking to movement onset) often misalign responses later in the movement. For example, a seven-cycle movement lasted ~3500 ms. By the last cycle, a trial 5% faster than normal and a trial 5% slower than normal would be misaligned by 350 ms, or over half a cycle.

To ensure response features were not lost to misalignment, we adaptively aligned trials within a condition (Russo et al., 2018). First, trials were aligned on movement onset. Individual trials were then scaled so that all trials had the same duration (set to be the median duration across trials). Because monkeys usually cycled at a consistent speed (within a given condition) this brought trials largely into alignment: e.g., the top of each cycle occurred at nearly the same time for each trial. An adaptive alignment procedure was used to correct any remaining slight misalignments. To do so, the time-base for each trial was scaled so that the position trace on that trial closely matched the average position of all trials. This involved a slight non-uniform stretching, and resulted in the timing of all key moments – such as when the hand passed the top of the cycle – being nearly identical across trials. This ensured that high-frequency temporal response features were not lost to averaging.

Neural firing rates and EMG activity were computed on each trial before adaptive alignment. Thus, the above procedure never alters the magnitude of these variables, but simply aligns when those values occur across trials. The adaptive procedure was used once to align trials within a condition on a given recording session, and again to align data across recording sessions. A similar alignment procedure was used within the response distance analysis to ensure all cycles were of the same duration. For all datasets, averages were made across a median of ~15 trials.

Data Preprocessing

We standardly (Churchland et al., 2012; Russo et al., 2018; Seely et al., 2016) use soft normalization to balance the desire for analyses to explain the responses of all neurons with the desire that weak responses not contribute on an equal footing with robust responses. For example, many of our analyses employ PCA. Because PCA seeks to capture variance, it can be disproportionately influenced by differences in firing rate range (e.g., a neuron with a range of 100 spikes/s has 25 times the variance of a similar neuron with a range of 20 spikes/s). The response of each neuron was thus normalized prior to application of PCA. Neural data were ‘soft’ normalized: response ≔ response/(range(response) +5). Soft normalization is also helpful for non-PCA-based analyses (e.g., of response distance) to avoid results being dominated by a few high-firing-rate neurons.

QUANTIFICATION AND STATISTICAL ANALYSIS

Response distance

Response distance assesses the degree to which the population response is different on two different cycles (either within a seven-cycle movement, or between seven-cycle and four-cycle movements of the same type). Consider r_i(t), a vector containing the trial-averaged firing rate of every neuron at time t within cycle i. The simplest definition of response distance between cycles i and j is equivalent to ${\sum }_t\sqrt{{\text{Δ}}_{i,j}(t)\cdot {\text{Δ}}_{i,j}(t)}$ where ${\text{Δ}}_{i,j}(t)={\mathit{r}}_i(t)-{\mathit{r}}_j(t)$ and ‘∙’ indicates the dot product. However, this approach allows distance to be increased by sampling error in r. We therefore employed the crossnobis estimator(Diedrichsen and Kriegeskorte, 2017; Yokoi et al., 2018), which provides an unbiased estimate of squared distance. We randomly divided trials into two non-overlapping partitions, and computed two trial-averaged firing rate vectors: ${\mathit{r}}_i^{(1)}(t)$ and ${\mathit{r}}_i^{(2)}(t)$. (Partitioning was done separately for each neuron as most neurons were not recorded simultaneously). The crossnobis estimator was then the average, across twenty random partitions, of ${\sum }_t{\text{Δ}}_{i,j}^{(1)}(t)\cdot {\text{Δ}}_{i,j}^{(2)}(t)$. Virtually identical results were obtained if we employed a different method to combat sampling error: denoising the average firing rate of each neuron by reconstructing it based on the top twelve population-level principal components.

We employed temporal alignment to ensure that response distance was not inflated if two cycles had similar responses but different durations. This is of little concern when comparing among steady-state cycles (duration was highly stereotyped) but becomes a concern when comparing an initial-cycle response with a steady-state cycle response. To avoid misalignment, the response on each cycle was scaled both to have the same duration and such that the angular position matched at all times. After alignment, response distance is zero if two responses are the same except for their time-course.

Comparisons were made within a given seven-cycle condition and between seven-cycle and four-cycle conditions. Comparisons were always made between conditions of the same type (i.e., the same cycling direction and starting position). Response distances were normalized by response magnitude within a steady-state cycle of the same condition type. For simplicity, we chose the fourth cycle of the seven-cycle movement. Response magnitude was the squared distance of the firing rate from its mean (computed in a cross-validated fashion).

We used resampling, across neurons, to assess the statistical significance of differences between SMA and M1. For example, we found that response distance, averaged across steady-state cycles, was higher in SMA. A key question is whether this difference is reliable, or might simply have occurred between any two random populations of neurons. To address this, we pooled all neurons for both areas, and created two resampled ‘areas’ by random partition. We computed the key metric (e.g., average response distance across steady-state cycles) for both resampled areas, and took the difference. The distribution of such differences, across 100 random partitions, is an estimate of the sampling distribution of measured differences if there is no true difference between the two populations. This distribution was approximately Gaussian, and p-values were thus based on a Gaussian fit.

Subspace overlap

Subspace overlap was used to measure the degree to which the population response occupied different neural dimensions on different cycles (different cycles within a distance, or between distances). Subspace overlap was always computed for a pair of cycles: a reference cycle and a comparison cycle. The population response for the reference cycle was put in matrix form, R_ref, of size t x n where t is the number of times within that cycle and n is the number of neurons. Analogously, the population response during the comparison cycle was R_comp. We applied PCA to R_ref, yielding W_ref, an n x k matrix of principal components. We similarly applied PCA to R_comp, yielding W_comp. We define variance captured as $V(R,W)=1-\frac{{\Vert R-RW{W}^T\Vert }_F}{\parallel R{\parallel }_F}$. Subspace overlap was then computed as: $\frac{V\left(R_{\text{comp}},W_{\text{ref}}\right)}{V\left(R_{\text{comp}},W_{\text{comp}}\right)}$.

The subspace overlap should be unity if the population response on reference and comparison cycles occupies the same dimensions (i.e., are spanned by the same PCs). However, subspace overlap can be diluted by sampling error (i.e., two responses that are in truth identical, but appear slightly different because average firing rates were computed for a finite number of trials). We thus computed subspace overlap using cross validation. To do so we partitioned the data (by randomly partitioning the trials recorded for each neuron) to produce $R_{\text{ref}}^{(1)}$, $R_{\text{ref}}^{(2)}$, $R_{\text{comp }}^{(1)}$ and $R_{\text{comp}}^{(2)}$. Cross-validated subspace overlap was then the average (over 20 partitions) of:

$$\frac{1}{2}\left[\frac{V\left(R_{\text{comp}}^{(1)},W_{\text{ref}}^{(2)}\right)}{V\left(R_{\text{comp}}^{(1)},W_{\text{comp}}^{(2)}\right)}+\frac{V\left(R_{\text{comp}}^{(2)},W_{\text{ref}}^{(1)}\right)}{V\left(R_{\text{comp}}^{(2)},W_{\text{comp}}^{(1)}\right)}\right]$$

Cross-validation was helpful in reducing the impact of sampling error. However, similar results were obtained if we did not employ cross-validation and simply computed the uncorrected subspace overlap as above. To test for statistical significance, we used the resampling procedure described in the previous section.

Trajectory Divergence

Consider times t and t′. These times could occur within the same movement. E.g., t could be a time near the middle of the movement and t′ could be a time near the end. The two times could also occur for different distances within the same condition type. E.g., if we consider forward cycling that starts at the top, t could occur during a two-cycle movement and t′ could occur during a seven-cycle movement.

Consider the associated neural states x_t and x_t′. The squared distance between these states is $\parallel {\mathit{x}}_t-{\mathit{x}}_{t^{\prime }}{\parallel }^2$ The squared distance between the corresponding states, some time Δ in the future, is $\parallel {\mathit{x}}_{t+\text{Δ}}-{\mathit{x}}_{t^{\prime }+\text{Δ}}{\parallel }^2$ Divergence assess whether this future distance ever becomes large despite the present distance being small. We define the divergence for a given time, during a given condition, as:

$$D(t)=\underset{t^{\prime },\text{Δ}}{\max }\frac{{\Vert {\mathit{x}}_{t+\text{Δ}}-{\mathit{x}}_{t^{\prime }+\text{Δ}}\Vert }^2}{{\Vert {\mathit{x}}_t-{\mathit{x}}_{t^{\prime }}\Vert }^2+\alpha }$$

Where t′ indexes across all times within all movements of the same type, and Δ indexes from one to the largest time that can be considered: $\min \left(T-t,T^{\prime }-t^{\prime }\right)$where T is the duration of the condition associated with time t and T′ is the duration of the condition associated with time t′ For our primary analysis, divergence was measured separately for each of the four condition types. For example, if the condition type is forward cycling starting at the top, t′ indexes across times and across distances of that type. The same effect was observed (SMA divergence lower than M1 divergence) if t′ indexed across all conditions regardless of type (Figure S7).

The state vectors x_t were found by applying PCA to the population response across all times (starting 100 ms before movement onset and ending 100 ms after movement offset) and across all conditions considered by the analysis. We term this full dimensional matrix X^full. Every column of X^full contains the data for one neuron. We used PCA to reduce the dimensionality of the data to twelve, yielding a matrix X with twelve columns. The state vector x_t was then the appropriate row (corresponding to the time and condition in question) of X. Twelve PCs captured an average of 89% and 87% of the data variance in M1 and SMA respectively. Results were not sensitive to the choice of dimensionality; divergence was always much lower for SMA versus M1. This was also true if we did not employ PCA, but simply used X^full. That said, we still preferred to use PCA as a preprocessing step. Reducing dimensionality makes analysis much faster, and the accompanying denoising of the data reduces concerns that sampling error might impact the denominator in the divergence computation. To ensure that denominator was well behaved (e.g., did not become too close to zero) we also included the constant α, set to 0.01 times the variance of X. Results were essentially identical across a range of reasonable values of α

We used a bootstrap procedure to assess the statistical significance of differences in trajectory divergence between SMA and M1. For each region for each monkey, neurons were resampled with replacement before application of PCA. Trajectory divergence was then analyzed for the resampled populations. The difference was taken between trajectory divergence in the resampled SMA population and the resampled M1 population and we assessed whether the resulting distribution of differences had a negative mean (i.e., whether divergence tends to be lower for SMA). This bootstrap procedure was repeated for 1000 iterations.

Recurrent Neural Networks

We trained recurrent neural networks to produce four and seven cycles of a sinusoid in response to external inputs. A network consisted of N = 50 firing-rate units with dynamics:

$$\tau \frac{d\mathbf{\text{r}}}{dt}=-\mathbf{\text{r}}(t)+f(Ar+\mathbf{\text{I}}(t)+\mathbf{\text{b}})$$

$$z={\mathbf{\text{w}}}_{\text{out }}^{\text{T}}\mathit{r}$$

where τ is a time-constant, r represents an N-dimensional vector of firing rates, f ≔tanh is a nonlinear input-output function, A is an N × N matrix of recurrent weights, I(t) represents time-varying external input, and b is a vector of constant biases. The network output z is a linear readout of the rates. Components of both A and w_out were initially drawn from a normal distribution of zero mean and variance 1/N. b was initialized to zero. Throughout training, A, w_out, and b were modified.

Context-tracking networks were trained to generate a four-cycle versus seven-cycle output after receiving a short go pulse (a square pulse lasting half a cycle prior to the start of the output) without the benefit of a stopping pulse. For context-tracking networks only, go pulses were different depending on whether four or seven cycles should be produced. The two go pulses were temporally identical, but entered the network through different sets of random input weights; $I(t)=w_{4}I(t)$ or $I(t)=w_{7}I(t)$, where I(t) is a square pulse of unit amplitude.

Context-naïve networks received both a go pulse and a stop pulse. Go and stop pulses were distinguished by entering the network through different sets of random input weights; $I(t)=w_{{\text{g}}_0}I(t)$ or $I(t)=W_{\text{stop }}I(t)$. Go and stop pulses were separated by an appropriate amount of time to complete the desired number of cycles. We analyzed network activity only when go and stop pulses were separated by four or seven cycles. Yet we did not wish context-naïve networks to learn overly specific solutions. Thus, during training, we also included trials where the network had to cycle continuously in the absence of a stop-pulse. This ensured that context-naïve networks learned a general solution; e.g., they could cycle for six cycles and stop if the go and stop pulses were separated by six cycles.

We also considered a modification of context-tracking networks that received a downward ramping input through another set of weights, w_ramp. The ramping input has a constant slope but different starting values for different numbers of desired cycles. The end of the cycling period was indicated by the ramp signal reaching zero. Thus, such networks received explicit and continuous information about time to the end of movement, and could inherit this information rather than constructing it through their own internal dynamics.

Networks were trained using back-propagation-through-time (Werbos, 1988) using TensorFlow and an Adam optimizer to adjust A, w_out and b to minimize the squared difference between the network output z and the sinusoidal target function. Input weights, w₄, w₇, w_go, w_stop and w_ramp, were drawn from a zero-mean unit-variance normal distribution and remain fixed throughout training. The amplitude of pulses and cycles were set to a value that produced a response but avoided saturating the units. The maximum height of the ramp signal was set to the same amplitude as the input pulses for the seven-cycle condition. For each condition, we trained 500 networks, each initialized with a different realization of A and w_out

Trajectory-constrained Neural Networks

To test the computational implications of trajectory divergence, we trained recurrent neural networks with an atypical approach. Rather than training networks to produce an output, we trained them to autonomously follow a target internal trajectory (DePasquale et al., 2018; Russo et al., 2018). We then asked whether networks were able to follow those trajectories from beginning to end, without the benefit of any inputs indicating when to stop.

Target trajectories were derived from neural recordings (M1, and SMA) during the four-cycle movements for each of the four condition types (forward-bottom-start, forward-top-start, backward-bottom-start, backward-top-start). Target trajectories spanned the time period from movement onset until 250 ms after movement offset. To emphasize that the network should complete the trajectory and remain in the final state, we extended the final sample of the target trajectory for an additional 500 ms. To obtain target trajectories, neural data were mean-centered and projected onto the top six PCs (computed for that condition). Each target trajectory was normalized by its greatest norm (across times). We trained a total of 160 networks, each with a different weight initialization. The eighty networks for each monkey included ten each for the two cortical areas and four condition types (two starting positions by two cycling directions).

Network dynamics were governed by:

$$\mathit{v}(t+\text{Δ}t)=\mathit{v}(t)+\text{Δ}t/\tau (-\mathit{v}(t)+Af(\mathit{v}(t))+\mathit{w}(t))$$

where f ≔tanh and $\mathit{w}\sim \mathcal{N}\left(0,{\sigma }_W^{2}I\right)$ adds noise. $V$ can be thought of as the membrane voltage and $f(v(t))$ as the firing rate. $Af(\mathit{v}(t))$is then the vector of inputs to each unit: i.e., the firing rates weighted by the connection strengths. Network training attempted to minimize the difference between this input vector and a target trajectory: ${\mathit{s}}_{targ}(t)$Training focused on the vector of inputs, rather than the vector of outputs (firing rates) purely for technical purposes. The end result is much the same as inputs and outputs are related by a monotonic function. A was trained using recursive least squares. The target trajectory was constructed as ${\mathit{s}}_{targ}(t)=G{\mathit{y}}_{targ}(t)\cdot y_{targ}$ is the six-dimensional trajectory derived from the physiological data. G is an N × 6 matrix of random weights, sampled from $\mathcal{U}[-.5,.5]$, that maps the global target trajectory onto a target input of each model unit. This construction ensures that the target network trajectory is isomorphic with the physiological trajectory, with each unit having random ‘tuning’ for the underlying factors. The entries of A were initialized by draws from a centered normal distribution with variance 1/N (where N = 50, the number of network units). Simulation employed 4 ms time steps.

To begin a given training epoch, the initial state was set with $v(0)$ based on $s_{targ}(0)$ and A. The network was simulated, applying recursive least squares (Sussillo and Abbott, 2009) with parameter α =1 to modify A as time unfolds. After 1000 training epochs, stability was assessed by simulating the network 100 times, and computing the mean squared difference between the actual and target trajectory. That error was normalized by the variance of the target trajectory, yielding an R² value. An average (across the 100 simulated trials) R² < 0.9 was considered a failure.

Because the empirical population trajectories never perfectly repeated, it was trivially true that networks could follow the full trajectory, for both M1 and SMA, in the complete absence of noise (i.e., for ${\sigma }_w=0$). For the larger value of ${\sigma }_W$ used for our primary analysis, all networks failed to follow the M1 trajectories while most networks successfully followed the SMA trajectories (although there were still some network initializations that never resulted in good solutions). It is of course unclear what value of ${\sigma }_W$ is physiologically relevant. We therefore also performed an analysis where we swept the value of ${\sigma }_W$ until failure. The level of noise that was tolerated was much greater when networks followed the SMA trajectories. Indeed, some M1 trajectories (for particular conditions) could never be consistently followed even at the lowest noise level tested.

To visualize network activity (Figure 8B–D) we ‘decoded’ the network population. To do so, we reconstructed the first three dimensions of the trajectory (which should match the first three dimensions of the target trajectory) by pseudo-inverting G.

Highlights.

• Guiding action across time necessitates population activity with ‘low divergence’.

• The supplementary motor area, but not motor cortex, exhibits low divergence.

• Low divergence explains diverse single-neuron and population-level features.