Abstract
In this study, we use the sample data from Jan 22, 2020 to Jan 21, 2022 to investigate the impacts of added infection number on the volatility of BDI. Under this structure, the control variables (freight rate, Brent crude oil price, container idle rate, port congestion level, global port calls) are added to test whether the information contained in the added infection number is covered. In the GARCH-MIDAS model, we divide the volatility of BDI into the long-term and short-term components, then employ in the least squares regression to empirically test the influences of added infection number on the volatility. From the analysis, we find the added infection numbers effectively impact the BDI volatility. In addition, whether the freight rate, Brent crude oil price, container idle rate, port congestion level, global port calls and other variables are considered alone or at the same time, further the added infection number still significantly influences the volatility of BDI. By studying the ability of the confirmed number to explain the volatility of BDI, a new insight is provided for the trend prediction of BDI that the shipping industry can take the epidemic development of various countries as a reference to achieve the purpose of cost or risk control.
Keywords: Shipping market, COVID-19 epidemic, BDI volatility, GARCH-MIDAS model
1. Introduction
The business sector of many publications is usually filled with a series of indexes such as S&P, ZEW and CPI, which are adopted by investment professionals as a powerful tool to measure the economy health (Lin et al., 2019; Xu et al., 2021a). For the shipping industry, which is responsible for shipping the vast majority of the world's trade goods overseas, the index is the best way to evaluate the market performances (Xu et al., 2022a). Based on the type, size, age of ships, many shipping indexes have been generated. Behind each index, there are different backgrounds and different purposes. Additionally, there are many types of indexes reflecting the level of freight and charter rate in the container sector. For example, Shanghai Airlines exchange release CCFI (China Container Freight Rate Index) and SCFI (Shanghai Container Freight rate Index), Guangzhou Airlines exchange released PSI (Pearl river Shipping freight rate Index). Drury, a well-known shipping consultancy, developed Drury Containerized Freight Index. At the same time, the Dow Jones global shipping index is like a typical stock index because it mainly tracks the stock performance of 25 companies in the shipping industry. Among all these shipping indexes, the Baltic dry bulk freight rate index (BDI) is of particular significance in measuring the health of the world economy (Gu et al., 2020; Chen et al. 2021, 2022c; Xu et al., 2022b). The trend of BDI index indeed reflects the market demands for commodities such as metals, minerals, grains and building materials. Since these “BDI materials” are the basic raw materials for manufacturing final products, the index is regarded by many as a leading economic indicator of industrial production and economic activities, laying the foundation for economic decision-making (Zeng et al., 2015; Makridakis et al., 2020; Katris and Kavussanos, 2021; Chen et al., 2022a, 2022b).
However, the trend is often affected by many uncertain factors (e.g., war, disease). So far, the Covid-19 epidemic is one of the most serious infectious diseases and serious global crisis in past hundred years (Aktar et al., 2021; Kane et al., 2021; Uddin et al., 2021; Zhang et al., 2021). Specially, the epidemic has sharply reversed the expectation of moderate growth which caused the huge losses to related industries and international shipping trades (Vo et al., 2021; Zhang and Zhang, 2021). For example, the global shipping volume has decreased over 600 million tons (Xu et al., 2021a; Narasimha et al., 2021). In particular, the volume of commodity trade declined by 32% in 2021; thus, the panic among global investors triggers turmoil in financial and capital markets (Kamal et al., 2021; Khan et al., 2021; Nam and Kim, 2021). Although the Covid-19 epidemic hasn't dissipated, the demand for bulk commodity will continue to increase, while the amount of new ship is relatively limited, which ensures the scarcity of transport capacity, and BDI further rises. On the one hand, influenced by Covid-19 epidemic, the port congestion caused by the shortage of labor and customs quarantine has led to a significant increase in the BDI (Chen et al., 2020; Wang et al., 2021). Because of loose fiscal and monetary policies to promote the economic development, with the rise of infrastructure construction, the global demand for iron, coal and steel has increased significantly. Therefore, the Covid-19 epidemic has the multi-stage complexity characteristics for the change of BDI.
Hence, it is necessary to find out the mechanism of Covid-19 epidemic in the change of shipping industry. Previous scholars investigated this issue, Yang et al. (2008) analyzed the uncertainty between BDI and CCFI in the shipping industry via the method of support vector machine. Further, Lin et al. (2019) used a GRACH model to show the influences of BDI on commodity market and stock market. Meanwhile, Zhang et al. (2019) discussed the effect of BDI on the shipping market to forecast the freight rate with the AI technology. On this basis, Yang et al. (2021) investigated the stock market and crude oil market to describe the changes of BDI, further evaluate the shipping risk from VAR approach. To sum up, the above-mentioned studies presented the impact of BDI change on the shipping industry, yet few scholars paid attention to the influences under the emergencies (financial crisis, natural disaster, major epidemic). Although Gu et al. (2020) reported the relation between the international and domestic shipping market to observe the factors influencing BDI, the regression outcomes are limited by the short sample and single factor of shipping market. Most of the common literatures on BDI volatility used the same frequency data to build models for research, and BDI volatility is a variable of high-frequency volatility like stock market, so using the same frequency data to build models is easy to lose high-frequency information. However, the GARCH-MIDAS model can solve this problem well. It allows low-frequency influencing factors to explain high-frequency variables, and makes full use of the effective information brought by mixing variables to make the research results more accurate.
Since the Covid-19 epidemic, the international shipping capacity significantly declines, leading to the rise in freight rate. In the context of tight logistics capacity, the phenomena of cabinet dumping occur frequently in the shipping industry. Xu et al. (2021) analyzed which factors affect port operation through constructing a panel regression model from 14 major ports in China. Beyond that, Narasimha et al. (2021) discussed the impacts of Covid-19 on Indian ports and related industries through quantitative performance sources before and during the Covid-19 epidemic. Furthermore, Xu et al. (2021b) observed that there are significant difference in the results of different regions and times by the regression analysis of shipping trade volume between China and major regions. In addition, Kamal et al. (2021) discussed the interactive mechanism between stock market and Covid-19 epidemic. Hence, the Covid-19 epidemic undoubtedly affects the volatility of shipping market. Liu et al. (2021) mainly studies the prediction effect of SVR-GARCH model and SVR-GJR model on the fluctuation of shipping market index. From the previous research, few studies adopted GARCH models to analyze the change of BDI, so as to discuss the fluctuation of shipping market. Furthermore, from the perspective of affecting factors and constructing model of market volatility, few literature incorporated Covid-19 epidemic and BDI into the same research framework to test the difference in the predictive power.
The rest of our study is organized as follows. In Section 2, we present the methodology in this research. Section 3 shows the data source and gives the empirical analysis. Finally, we conclude the observations and provide the future research in Section 4.
2. Methodology
In this study, we decompose the volatility of BDI, takes the long-term and short-term components of volatility as the research object. Since the action cycle of fundamental and behavioral factors on volatility is different, the release frequency of relevant information on fundamental factor is low (e.g., mostly monthly or quarterly). If we want to explore its relationship with volatility, the traditional method is to establish with the same frequency data. When the interpolation method is employed to convert low-frequency data into high-frequency data, it will inevitably add noise artificially; otherwise, it is easy to convert high-frequency data into low-frequency data by summing and averaging where the important information can be ignored. Hence, in this case, it is necessary to study the BDI volatility separately. Although the previous discussed the volatility decomposition that focuses on the long-term (Ghysels et al., 2007; Engle et al., 2013), further we investigate the short-term component of volatility on emergency outbreak. Considering that there exist many factors affecting stock price, we firstly employ the GARCH-MIDAS model based on the realized volatility, a low-frequency variable, which is adopted to decompose the volatility into the long-term and short-term components. Next, we introduce Ordinary Least Squares (OLS) to regress and investigate control variables to the volatilities of long-term and short-term components, which can avoid directly introducing variables into GARCH-MIDAS model resulting in the omission of information contained in other variables. Further, we bring the variables into the GARCH-MIDAS model to get the impact of the confirmed number on the volatility of BDI. Hence, the specific model of realized BDI volatility is
| (1) |
where m is the month frequency to depict the volatility of long-term BDI, N m indicates the valid number of days, r d,m means the variation of BDI. In particular, the distribution form of r d,m is composed of the average value E() and volatility value as follow
| (2) |
where and are the long-term and short-term components, respectively. Further, is a stochastic process obeying the conditional standard normal distribution, namely , where indicates the information from the d 1 day in the mth month. Thus, we employ the standard GARCH(1,1) to describe the short-term component as
| (3) |
where () are the positive constant terms and . Thus, we introduce the lagging period K into the long-term component, which can be described as
| (4) |
where is a constant term, means the aggregate effect that shows the lagging impact of on . Based on the latent phase, we suppose that the lag period is 14; thus, indicates the weight of lag period on , which is mainly decided by and as
| (5) |
In this study, we employ the method of OLS to take BDI into the long-term and short-term component as explaining variables, infection number of Covid-19 as the explanatory, then add the related control variables to discuss the relationship (Takeda and Tomozawa, 2006). On this basis, we build the benchmark model as
| (6) |
where is a constant term, is the coefficient of infection number in the lagging period i, is parameter of BDI volatility in the lagging period i, is random error term, respectively. Because we adopt the daily data as research object, in order to consider the continuous influences of infection number, the benchmark combine with information criteria to avoid endogenous problem. In the following, we discuss two parts of regression for BDI volatility in the long-term and short components. Beyond that, to observe whether the infection number is still effective if adding control variables, we expand the benchmark as
| (7) |
where and are control variable and corresponding coefficient in the lagging period i, is random error term. Hence, we aim at the model is to test whether infection number are significant if introducing five typical factors (e.g., average freight rate, Brent crude oil price, container idle rate, port congestion level, global port calls) in the following research. Namely, whether the information contained in the infection number plays a role independently of the existing variables, further infection number and existing variables on the BDI volatility is different.
In order to quantitatively compare the sample accuracy of the prediction model, firstly, based on MSE(Mean Square Error), MAE(Mean Absolute Error), RMSE(Root Mean Square Error), we evaluate the prediction influences of GARCH-MIDAS model, further verify the reliability and direction test. In particular, the reliability tests whether there are significant statistical differences in the sample impact of prediction model (Hansen et al., 2011). Under the given confidence level, the prediction model with better performance is selected, which does not specify the specific prediction model as the real, and valuable information leads to more than one optimal model contained in MCS (Model Confidence Set). Denote as the loss function n in dth day, where is the loss value between two forecasting models in the set of M. Hence, we have . Thus, from the equivalence test and elimination rules, the model rejecting the original hypothesis is eliminated, and the process is repeated until no model can be removed from the set. The statistics used in this test include absolute statistics and quadratic statistics as
| (8) |
| (9) |
where is the average loss value between two forecasting models. When each statistical value from two models is greater than the critical value, the original hypothesis is rejected and the model is eliminated. Meanwhile, DOC (Direction-of-Change) test is the core of market timing, which can measure the proportion the prediction model correctly estimates the change direction (rise or fall) of actual volatility. Assuming that is a dummy variable, if the model correctly predicts the movement direction of volatility on tth day, the value is 1; otherwise it is 0. Therefore, we introduce the total volatility to describe the dummy variable can be expressed as
| (10) |
Hence, DOC , where t indicates the number of sample predicted values. The DOC value of prediction model is less than or equal to that of random walk, which is contrary to the assumption. Obviously, the prediction model with large DOC value means high prediction accuracy.
3. Empirical results and discussion
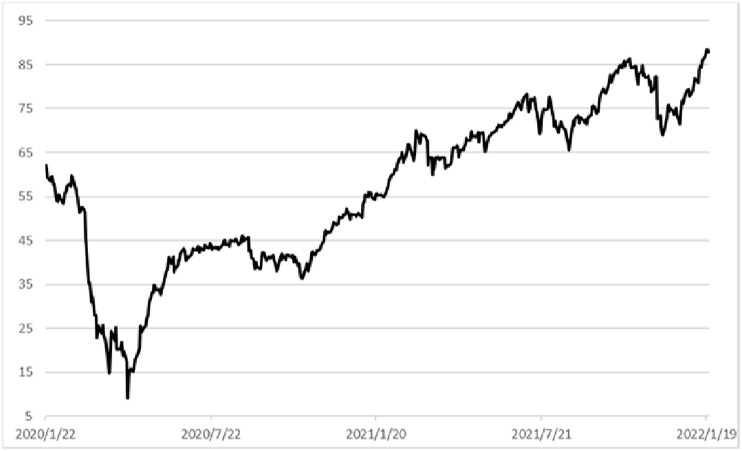
Our dataset consists of average freight rate, Brent crude oil price, container idle rate, infection number and port congestion level during the period from Jan 22, 2020 to Jan 21, 2022, which contains a total of 3138 observations (except for weekends and holidays). From ourworldindata.com, the added infection number is available to associate with the data from WHO (World Health Organization) in Fig. 1 , which can be published by Johns Hopkins University at https://github.com/CSSEGISandData/COVID-19 where the complete Covid-19 dataset is a collection of the Covid-19 data maintained by Our World in Data. It is updated daily and includes data on confirmed cases, deaths, hospitalizations, and testing.
Fig. 1.
Number of newly confirmed cases during the epidemic.
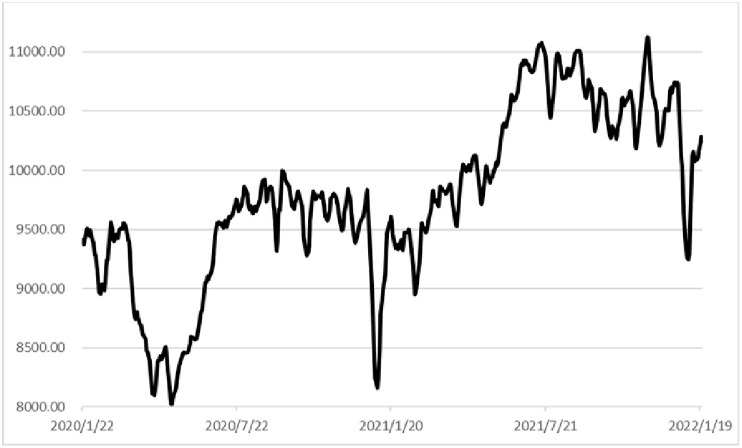
In order to test the model, we use the database from Clarksons Research Intelligence for BDI, where the volatility is decomposed from the above model in Fig. 2 . As can be seen from Fig. 2, the trend of long-term component of volatility is basically the same as that of short-term component, but there are still differences. In early July, early October in 2020, late January and early May in 2021, it exists a small peak in the short-term component, at this time, the long-term component of volatility is basically stable. Generally speaking, the long-term component smoothens the noise in the short-term component to a certain extent, but still reflects the basic trend of BDI volatility.
Fig. 2.
The trend of long- and short-term components of spread volatility based on realized volatility.
Beyond that, we further select the control variables to join the least squares regression. On the one hand, it can be to prevent information redundancy, that is, to ensure that the information contained in the confirmed case of Covid-19 epidemic is not covered by BDI. On the other hand, it is also to explore whether it exists any difference between the Covid-19 epidemic and BDI on the action cycle of spread volatility. Thus, some classical variables are considered for analysis as shown in Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7 : (1) The freight rate directly impacts the rise and fall of BDI. The increased demand for raw materials indicates that the demand for cargo ship transportation in various countries also increases. In this case, if the increase of freight can be greater than the increase of oil price cost, of course, its profit is maintained. On this premise, the BDI rises, the share prices of transportation stocks also increase. (2) Brent crude oil is light & low sulfur crude oil produced in Brent oil fields in the North Sea where its price is the benchmark of market oil price. So, its price fluctuation can accurately and timely reflect the wind direction of oil price market; thus, it can result in a significant effect on the BDI trend. (3) The container idle rate is important significantly to the shipping market. The low container idle rate is not conducive to the cargo owners and terminals to accurately predict the arrival time of ships and goods, make corresponding arrangements, and achieve a high degree of coordination among shipping company, terminal and cargo owner, resulting in vicious interaction. (4) Port congestion not results in a negative impact on the port itself and shipping companies, but also affects its upstream and downstream industries. When the port congestion is serious, it causes the backlog of goods, even miss the goods sales time leading to food decay and additional transportation costs. (5) Global containership port calls represents the operation efficiency of berthing port and loading efficiency affected by the epidemic, which results in the shipping companies having to extend the voyage time, and the cost of ships berthing at the port increases. So, it not only bears the higher risk of cargo loss, but also aggravates the port pollution.
Fig. 3.
The trend of average freight rate.
Fig. 4.
The trend of Brent crude oil price.
Fig. 5.
The trend of container idle rate.
Fig. 6.
The trend of port congestion level.
Fig. 7.
The trend of global port calls.
4. Empirical analysis
4.1. Benchmark model
The empirical regression outcomes of the benchmark model are shown in Table 1 , in which column 2 and column 4 are the regression values of the short-term component and long-term component of the daily added confirmation for BDI. It is not difficult to find that the added infection number has a significant impact on both the long-term and short-term components of volatility.
Table 1.
The regression result in Benchmark model.
| Short-term component |
Long-term component |
|||
|---|---|---|---|---|
| Regression Val | Standard Dev | Regression Val | Standard Dev | |
| Infection(-1) | 0.00071*** | 0.00011 | 0.00083*** | 0.00011 |
| Infection(-2) | 0.00080*** | 0.00012 | 0.00087*** | 0.00012 |
| Infection(-3) | 0.00090*** | 0.00012 | 0.00092*** | 0.00012 |
| Infection(-4) | 0.00092*** | 0.00013 | 0.00097*** | 0.00012 |
| Infection(-5) | 0.00096*** | 0.00013 | 0.0010*** | 0.00012 |
| Infection(-6) | 0.0011*** | 0.00013 | 0.0011*** | 0.00013 |
| Infection(-7) | 0.0012*** | 0.00014 | 0.0012*** | 0.00013 |
| Infection(-8) | 0.0014*** | 0.00015 | 0.0013*** | 0.00014 |
| Infection(-9) | 0.0015*** | 0.00015 | 0.0014*** | 0.00014 |
| Infection(-10) | 0.0016*** | 0.00016 | 0.0015*** | 0.00015 |
| Infection(-11) | 0.0018*** | 0.00017 | 0.0017*** | 0.00015 |
| Infection(-12) | 0.0021*** | 0.00017 | 0.0019*** | 0.00016 |
| Infection(-13) | 0.0024*** | 0.00018 | 0.0022*** | 0.00017 |
| Infection(-14) | 0.0025*** | 0.00018 | 0.0026*** | 0.00017 |
| BDI(-1) | 104.15*** | 16.84 | 115.73*** | 15.91 |
| BDI(-2) | 106.43*** | 16.82 | 117.27*** | 15.89 |
| BDI(-3) | 108.06*** | 16.80 | 118.81*** | 15.86 |
| BDI(-4) | 109.35*** | 16.78 | 120.35*** | 15.84 |
| BDI(-5) | 110.36*** | 16.77 | 121.89*** | 15.81 |
| BDI(-6) | 111.65*** | 16.76 | 123.42*** | 15.79 |
| BDI(-7) | 112.84*** | 16.74 | 124.96*** | 15.76 |
| BDI(-8) | 113.40*** | 16.74 | 126.50*** | 15.74 |
| BDI(-9) | 113.54*** | 16.74 | 128.04*** | 15.71 |
| BDI(-10) | 113.25*** | 16.74 | 129.58*** | 15.68 |
| BDI(-11) | 113.47*** | 16.74 | 131.12*** | 15.65 |
| BDI(-12) | 113.93*** | 16.73 | 132.66*** | 15.63 |
| BDI(-13) | 114.42*** | 16.73 | 134.21*** | 15.60 |
| BDI(-14) | 115.10*** | 16.72 | 135.75*** | 15.57 |
| Constant term | 1735.93*** | 69.74 | 1671.78*** | 69.29 |
| R2 | 0.066 | 0.090 | ||
Note: * means rejections of null hypothesis at the 10% significance level, ** indicates rejections of null hypothesis at the 5% significance level, *** means rejections of null hypothesis at the 1% significance level.
From the perspective of short-term component, the coefficient of the added infection number lagging from phase 1 to phase 14 are significantly positive, that is, when the added infection number increases, the shore-term component of BDI also increases. On the other hand, from the long-term component, the coefficient of added infection number lagging from phase 1 to phase 14 are also significantly positive, where the long-term component is greater and more persistent than that of short-term component. Therefore, we not only consider the added infection number, but also combine some macro fundamental variables.
4.2. Adding average freight rate as control variable
The regression results after adding average freight rate into the benchmark model are shown in Table 2 . Here, we introduce the average freight rate as control variable to explore the regression results. Whether the long-term component or short-term component, after adding the average freight rate as control variable, the significance and symbol of added infection number are not affected. In particular, the value of significant item has not change, indicating the information contained in the added infection number has not been covered. At present, the added infection number has not influenced obviously the average freight rate to predict the BDI volatility. Further, with the increase of average freight rate and the decrease of lag period, the BDI volatility also increases.
Table 2.
The regression result for after adding average freight rate as control variable.
| Short-term component |
Long-term component |
|||
|---|---|---|---|---|
| Regression Val | Standard Dev | Regression Val | Standard Dev | |
| Infection(-1) | −0.00062*** | 4.98E-05 | −0.00067*** | 4.36E-05 |
| Infection(-2) | −0.00064*** | 5.34E-05 | −0.00067*** | 4.54E-05 |
| Infection(-3) | −0.00067*** | 5.77E-05 | −0.00068*** | 4.74E-05 |
| Infection(-4) | −0.00067*** | 5.90E-05 | −0.00068*** | 4.96E-05 |
| Infection(-5) | −0.00068*** | 6.09E-05 | −0.00068*** | 5.21E-05 |
| Infection(-6) | −0.00071*** | 6.54E-05 | −0.00069*** | 5.48E-05 |
| Infection(-7) | −0.00073*** | 7.09E-05 | −0.00069*** | 5.79E-05 |
| Infection(-8) | −0.00078*** | 7.96E-05 | −0.00070*** | 6.14E-05 |
| Infection(-9) | −0.00078*** | 8.22E-05 | −0.00071*** | 6.55E-05 |
| Infection(-10) | −0.00079*** | 8.60E-05 | −0.00072*** | 7.03E-05 |
| Infection(-11) | −0.00082*** | 9.40E-05 | −0.00074*** | 7.62E-05 |
| Infection(-12) | −0.00085*** | 0.00011 | −0.00077*** | 8.35E-05 |
| Infection(-13) | −0.00087*** | 0.00012 | −0.00081*** | 9.32E-05 |
| Infection(-14) | −0.00084*** | 0.00012 | −0.00088*** | 0.00011 |
| Freight(-1) | 1.05*** | 0.02 | 1.06*** | 0.02 |
| Freight(-2) | 1.04*** | 0.02 | 1.06*** | 0.02 |
| Freight(-3) | 1.04*** | 0.02 | 1.05*** | 0.02 |
| Freight(-4) | 1.03*** | 0.02 | 1.05*** | 0.02 |
| Freight(-5) | 1.03*** | 0.02 | 1.04*** | 0.02 |
| Freight(-6) | 1.02*** | 0.02 | 1.04*** | 0.02 |
| Freight(-7) | 1.02*** | 0.02 | 1.04*** | 0.02 |
| Freight(-8) | 1.01*** | 0.02 | 1.03*** | 0.02 |
| Freight(-9) | 1.01*** | 0.02 | 1.03*** | 0.02 |
| Freight(-10) | 1.00*** | 0.02 | 1.02*** | 0.02 |
| Freight(-11) | 1.00*** | 0.02 | 1.02*** | 0.02 |
| Freight(-12) | 1.00*** | 0.03 | 1.02*** | 0.02 |
| Freight(-13) | 1.00*** | 0.03 | 1.01*** | 0.02 |
| Freight(-14) | 1.00*** | 0.03 | 1.01*** | 0.02 |
| BDI(-1) | −413.14*** | 32.30 | −481.21*** | 31.22 |
| BDI(-2) | −425.53*** | 33.22 | −469.04*** | 31.69 |
| BDI(-3) | −439.80*** | 34.05 | −456.80*** | 32.16 |
| BDI(-4) | −451.49*** | 34.77 | −444.46*** | 32.61 |
| BDI(-5) | −459.96*** | 35.39 | −432.03*** | 33.06 |
| BDI(-6) | −462.73*** | 36.02 | −419.51*** | 33.50 |
| BDI(-7) | −459.68*** | 36.53 | −406.89*** | 33.93 |
| BDI(-8) | −454.46*** | 36.82 | −394.17*** | 34.35 |
| BDI(-9) | −446.97*** | 36.93 | −381.11*** | 34.77 |
| BDI(-10) | −438.96*** | 36.89 | −367.94*** | 35.18 |
| BDI(-11) | −425.41*** | 36.89 | −354.66*** | 35.58 |
| BDI(-12) | −407.68*** | 36.85 | −341.26*** | 35.97 |
| BDI(-13) | −388.28** | 36.75 | −327.74*** | 36.36 |
| BDI(-14) | −368.02*** | 36.66 | −314.09*** | 36.75 |
| Constant term | 17.61 | 41.21 | 21.84 | 33.52 |
| R2 | 0.86 | 0.90 | ||
Note: * means rejections of null hypothesis at the 10% significance level, ** indicates rejections of null hypothesis at the 5% significance level, *** means rejections of null hypothesis at the 1% significance level.
4.3. Brent crude oil price as control variable
The regression results after adding Brent crude oil price into the benchmark model are shown in Table 3 . Here, we introduce the average freight rate as control variable to explore the regression result. From the following results, we find that the added infection number is independent of Brent crude oil price. Further, whether the long-term component or short-term component, the symbols of added infection number are consistent with those before adding Brent crude oil price, but the value only changes slightly, where indicating that the added infection number effectively influences the BDI volatility. Additionally, the increase of Brent crude oil price will improve the BDI volatility, but we also observe that the impact of long-term component is slightly weaker than that of short-term component. Further, both the short- and long-term component of added infection number have become negative, and the value of the coefficient has also changed. It can be seen the information contained in the added infection number overlaps with the price of Brent crude oil. The short-term and long-term component in Brent crude oil price affects the prediction ability of the added infection number to the BDI volatility.
Table 3.
The regression result for after adding Brent crude oil price as control variable.
| Short-term component |
Long-term component |
|||
|---|---|---|---|---|
| Regression Val | Standard Dev | Regression Val | Standard Dev | |
| Infection(-1) | −0.00047*** | 8.26E-05 | −0.00053*** | 7.89E-05 |
| Infection(-2) | −0.00048*** | 8.78E-05 | −0.00053*** | 8.10E-05 |
| Infection(-3) | −0.00050*** | 9.39E-05 | −0.00053*** | 8.34E-05 |
| Infection(-4) | −0.00051*** | 9.56E-05 | −0.00052*** | 8.61E-05 |
| Infection(-5) | −0.00052*** | 9.80E-05 | −0.00052*** | 8.91E-05 |
| Infection(-6) | −0.00051*** | 0.00010 | −0.00052*** | 9.25E-05 |
| Infection(-7) | −0.00050*** | 0.00011 | −0.00051*** | 9.64E-05 |
| Infection(-8) | −0.00049*** | 0.00013 | −0.00051*** | 0.00010 |
| Infection(-9) | −0.00049*** | 0.00013 | −0.00050*** | 0.00011 |
| Infection(-10) | −0.00047*** | 0.00013 | −0.00049*** | 0.00011 |
| Infection(-11) | −0.00041*** | 0.00014 | −0.00047*** | 0.00012 |
| Infection(-12) | −0.00033** | 0.00016 | −0.00045*** | 0.00013 |
| Infection(-13) | −0.00022 | 0.00018 | −0.00042*** | 0.00015 |
| Infection(-14) | −0.00021 | 0.00018 | −0.00038*** | 0.00016 |
| Brent(-1) | 60.88*** | 2.19 | 63.30*** | 2.03 |
| Brent(-2) | 60.60*** | 2.19 | 62.98*** | 2.04 |
| Brent(-3) | 60.32*** | 2.19 | 62.68*** | 2.04 |
| Brent(-4) | 60.09*** | 2.19 | 62.38*** | 2.05 |
| Brent(-5) | 59.95*** | 2.20 | 62.09*** | 2.06 |
| Brent(-6) | 59.83*** | 2.20 | 61.82*** | 2.06 |
| Brent(-7) | 59.57*** | 2.20 | 61.55*** | 2.07 |
| Brent(-8) | 59.31*** | 2.20 | 61.29*** | 2.07 |
| Brent(-9) | 59.18*** | 2.20 | 61.05*** | 2.08 |
| Brent(-10) | 59.08*** | 2.21 | 60.82*** | 2.08 |
| Brent(-11) | 58.92*** | 2.21 | 60.59*** | 2.08 |
| Brent(-12) | 58.64*** | 2.21 | 60.38*** | 2.09 |
| Brent(-13) | 58.30*** | 2.22 | 60.17*** | 2.09 |
| Brent(-14) | 58.08*** | 2.23 | 59.98*** | 2.09 |
| BDI(-1) | −141.01*** | 23.48 | −159.77*** | 23.08 |
| BDI(-2) | −142.34*** | 23.78 | −160.98*** | 23.29 |
| BDI(-3) | −144.33*** | 24.03 | −162.26*** | 23.50 |
| BDI(-4) | −146.54*** | 24.26 | −163.60*** | 23.73 |
| BDI(-5) | −149.41*** | 24.48 | −165.03*** | 23.96 |
| BDI(-6) | −152.00*** | 24.72 | −166.54*** | 24.20 |
| BDI(-7) | −154.39*** | 24.96 | −168.14*** | 24.44 |
| BDI(-8) | −158.05*** | 25.16 | −169.83*** | 24.70 |
| BDI(-9) | −161.49*** | 25.32 | −169.82*** | 24.95 |
| BDI(-10) | −165.53*** | 25.44 | −169.81*** | 25.20 |
| BDI(-11) | −167.86*** | 25.57 | −169.82*** | 25.46 |
| BDI(-12) | −169.26*** | 25.70 | −169.84*** | 25.74 |
| BDI(-13) | −170.33*** | 25.83 | −169.87*** | 26.02 |
| BDI(-14) | −170.35*** | 25.96 | −169.91*** | 26.31 |
| Constant term | −1275.12*** | 116.53 | −1397.96*** | 105.87 |
| R2 | 0.63 | 0.69 | ||
Note: * means rejections of null hypothesis at the 10% significance level, ** indicates rejections of null hypothesis at the 5% significance level, *** means rejections of null hypothesis at the 1% significance level.
4.4. Container idle rate as control variable
The regression results after adding container idle rate as control are shown in Table 4 . It can be found that the container idle rate is significantly negative in both the short- and long-term component, indicating that with the increase of container idleness rate, the BDI volatility decreases, which is opposite to the impact of the added infection number on BDI volatility. At the same time, the container idle rate decreases with the increase of lag period, meaning that the effect of container idleness rate will gradually decrease. The significance and symbol of the short-term and long-term component of added infection number are not influenced, namely the information contained in the added infection number is not fully covered, and the container idle rate doesn't affect the prediction ability of added infection to the BDI volatility.
Table 4.
The regression result for after adding container idle rate as control variable.
| Short-term component |
Long-term component |
|||
|---|---|---|---|---|
| Regression Val | Standard Dev | Regression Val | Standard Dev | |
| Infection(-1) | 0.00026** | 0.00011 | 0.00033*** | 0.00011 |
| Infection(-2) | 0.00030** | 0.00012 | 0.00035*** | 0.00011 |
| Infection(-3) | 0.00036*** | 0.00012 | 0.00038*** | 0.00012 |
| Infection(-4) | 0.00036*** | 0.00013 | 0.00042*** | 0.00012 |
| Infection(-5) | 0.00038*** | 0.00013 | 0.00046*** | 0.00013 |
| Infection(-6) | 0.00044*** | 0.00014 | 0.00050*** | 0.00013 |
| Infection(-7) | 0.00053*** | 0.00015 | 0.00056*** | 0.00014 |
| Infection(-8) | 0.00071*** | 0.00016 | 0.00062*** | 0.00014 |
| Infection(-9) | 0.00075*** | 0.00017 | 0.00071*** | 0.00015 |
| Infection(-10) | 0.00083*** | 0.00017 | 0.00082*** | 0.00016 |
| Infection(-11) | 0.0010*** | 0.00019 | 0.00097*** | 0.00017 |
| Infection(-12) | 0.0013*** | 0.00020 | 0.0012*** | 0.00018 |
| Infection(-13) | 0.0016*** | 0.00022 | 0.0014*** | 0.00019 |
| Infection(-14) | 0.0017*** | 0.00022 | 0.0018*** | 0.00021 |
| Idle(-1) | −416.72*** | 38.55 | −425.25*** | 38.70 |
| Idle(-2) | −413.43*** | 38.60 | −421.38*** | 38.81 |
| Idle(-3) | −409.98*** | 38.66 | −417.51*** | 38.92 |
| Idle(-4) | −406.23*** | 38.65 | −413.66*** | 39.03 |
| Idle(-5) | −402.32*** | 38.61 | −409.80*** | 39.14 |
| Idle(-6) | −398.30*** | 38.63 | −405.96*** | 39.24 |
| Idle(-7) | −394.46*** | 38.72 | −402.12*** | 39.35 |
| Idle(-8) | −390.03*** | 38.89 | −398.29*** | 39.45 |
| Idle(-9) | −385.24*** | 38.97 | −394.54*** | 39.55 |
| Idle(-10) | −380.48*** | 39.04 | −390.80*** | 39.64 |
| Idle(-11) | −374.92*** | 39.21 | −387.06*** | 39.74 |
| Idle(-12) | −369.04*** | 39.42 | −383.33*** | 39.83 |
| Idle(-13) | −363.22*** | 39.70 | −379.61*** | 39.92 |
| Idle(-14) | −356.86*** | 39.89 | −375.90*** | 40.01 |
| BDI(-1) | 42.17** | 18.49 | 51.53*** | 17.60 |
| BDI(-2) | 44.34** | 18.54 | 53.23*** | 17.62 |
| BDI(-3) | 45.69** | 18.59 | 54.94*** | 17.64 |
| BDI(-4) | 46.64** | 18.65 | 56.67*** | 17.66 |
| BDI(-5) | 47.41** | 18.69 | 58.41*** | 17.67 |
| BDI(-6) | 48.86*** | 18.72 | 60.17*** | 17.69 |
| BDI(-7) | 50.46*** | 18.73 | 61.94*** | 17.71 |
| BDI(-8) | 51.30*** | 18.74 | 63.72*** | 17.72 |
| BDI(-9) | 51.58*** | 18.75 | 66.10*** | 17.73 |
| BDI(-10) | 51.36*** | 18.75 | 68.50*** | 17.73 |
| BDI(-11) | 51.97*** | 18.75 | 70.90*** | 17.73 |
| BDI(-12) | 52.89*** | 18.74 | 73.32*** | 17.73 |
| BDI(-13) | 54.04*** | 18.72 | 75.74*** | 17.73 |
| BDI(-14) | 55.55*** | 18.70 | 78.17*** | 17.72 |
| Constant term | 3928.34*** | 210.71 | 3933.58*** | 212.72 |
| R2 | 0.24 | 0.26 | ||
Note: * means rejections of null hypothesis at the 10% significance level, ** indicates rejections of null hypothesis at the 5% significance level, *** means rejections of null hypothesis at the 1% significance level.
4.5. Port congestion level as control variable
The regression results after adding port congestion level as control variable are shown in Table 5 . Through analysis and comparison, the port congestion is significantly positive in both short-term and long-term components. On the one hand, with the increase of port congestion level, the BDI volatility increases. On the other hand, with the increase of lag period, the impact of port congestion level on BDI volatility decreases. As the above shown, the impact of long-term component on BDI volatility is also greater than that of short-term component. Obviously, the short-term component of added infection number is negative in the lag period of 1–7, and then positive. However, for long-term component, it becomes positive in the lag period of 10. Therefore, the information contained in the added infection number overlaps with the port congestion level in the short period, yet the impact of port congestion on the added infection number gradually disappears with the increase of lag period.
Table 5.
The regression result for after adding container idle rate as control variable.
| Short-term component |
Long-term component |
|||
|---|---|---|---|---|
| Regression Val | Standard Dev | Regression Val | Standard Dev | |
| Infection(-1) | −0.0003*** | 0.00011 | −0.00051*** | 0.00010 |
| Infection(-2) | −0.00027** | 0.00012 | −0.00047*** | 0.00011 |
| Infection(-3) | −0.00023* | 0.00012 | −0.00043*** | 0.00011 |
| Infection(-4) | −0.00022* | 0.00013 | −0.00039*** | 0.00011 |
| Infection(-5) | −0.00019 | 0.00013 | −0.00034*** | 0.00012 |
| Infection(-6) | −0.00012 | 0.00014 | −0.00028** | 0.00012 |
| Infection(-7) | −3.26E-05 | 0.00015 | −0.00022* | 0.00013 |
| Infection(-8) | 0.00012 | 0.00016 | −0.00015 | 0.00013 |
| Infection(-9) | 0.00018 | 0.00016 | −7.19E-05 | 0.00013 |
| Infection(-10) | 0.00027 | 0.00017 | 2.48E-05 | 0.00015 |
| Infection(-11) | 0.00046 | 0.00018 | 0.00015 | 0.00015 |
| Infection(-12) | 0.00072*** | 0.00019 | 0.00030* | 0.00016 |
| Infection(-13) | 0.0010*** | 0.00020 | 0.00052*** | 0.00018 |
| Infection(-14) | 0.0011*** | 0.00021 | 0.00083*** | 0.00019 |
| Congestion(-1) | 142.31*** | 8.40 | 174.88*** | 8.21 |
| Congestion(-2) | 140.49*** | 8.47 | 172.63*** | 8.29 |
| Congestion(-3) | 138.46*** | 8.52 | 170.43*** | 8.36 |
| Congestion(-4) | 136.48*** | 8.57 | 168.26*** | 8.44 |
| Congestion(-5) | 134.82*** | 8.61 | 166.12*** | 8.51 |
| Congestion(-6) | 133.39*** | 8.67 | 164.02*** | 8.59 |
| Congestion(-7) | 132.05*** | 8.73 | 161.95*** | 8.66 |
| Congestion(-8) | 130.48*** | 8.78 | 159.91*** | 8.73 |
| Congestion(-9) | 128.88*** | 8.83 | 157.88*** | 8.80 |
| Congestion(-10) | 127.22*** | 8.88 | 155.87*** | 8.87 |
| Congestion(-11) | 125.60*** | 8.94 | 153.90*** | 8.93 |
| Congestion(-12) | 124.12*** | 9.00 | 151.94*** | 9.00 |
| Congestion(-13) | 122.74*** | 9.06 | 150.02*** | 9.07 |
| Congestion(-14) | 121.30*** | 9.11 | 148.11*** | 9.13 |
| BDI(-1) | −59.91*** | 18.82 | −98.54*** | 18.35 |
| BDI(-2) | −61.19*** | 19.07 | −98.47*** | 18.52 |
| BDI(-3) | −63.46*** | 19.31 | −98.40*** | 18.68 |
| BDI(-4) | −65.99*** | 19.55 | −98.34*** | 18.85 |
| BDI(-5) | −68.88*** | 19.80 | −98.29*** | 19.03 |
| BDI(-6) | −71.03*** | 20.04 | −98.24*** | 19.21 |
| BDI(-7) | −72.77*** | 20.27 | −98.20*** | 19.40 |
| BDI(-8) | −75.04*** | 20.46 | −98.17*** | 19.59 |
| BDI(-9) | −77.37*** | 20.62 | −98.78*** | 19.80 |
| BDI(-10) | −79.86*** | 20.75 | −99.43*** | 20.01 |
| BDI(-11) | −80.85*** | 20.86 | −100.10*** | 20.23 |
| BDI(-12) | −80.93*** | 20.97 | −100.82*** | 20.46 |
| BDI(-13) | −80.82*** | 21.07 | −101.57*** | 20.70 |
| BDI(-14) | −80.22*** | 21.18 | −102.36*** | 20.95 |
| Constant term | −15397.55*** | 992.85 | −19315.62*** | 964.13 |
| R2 | 0.41 | 0.52 | ||
Note: * means rejections of null hypothesis at the 10% significance level, ** indicates rejections of null hypothesis at the 5% significance level, *** means rejections of null hypothesis at the 1% significance level.
4.6. Global port calls as control variable
The regression results after adding global container port calls as control variable are shown in Table 6 . From the regression results, we can see that the coefficient of port calls is significantly positive, whether it is the regression of short-term or long-term component. Further, the coefficient changes from lag period 1 to 14 is not obvious, which indicates that port calls has basically the same influence on the short-term and long-term components of BDI. However, the coefficient of long-term component is greater than that of short-term component. Both short-term and long-term components of confirmed number are positive from lag 1 to 14. The lag of short-term components in lag 6 becomes significant, and the lag of long-term components in lag 4 becomes significant, indicating that port calls has no impact on the volatility prediction ability of the number of confirmed covid-19, and the information contained in the number of confirmed covid-19 is not covered by port calls.
Table 6.
The regression result for after adding global port calls as control variable.
| Short-term component |
Long-term component |
|||
|---|---|---|---|---|
| Regression Val | Standard Dev | Regression Val | Standard Dev | |
| Infection(-1) | 8.08E-05 | 7.47E-05 | 8.36E-05 | 6.52E-05 |
| Infection(-2) | 0.00010 | 7.92E-05 | 9.47E-05 | 6.70E-05 |
| Infection(-3) | 0.00013 | 8.44E-05 | 0.00011 | 6.89E-05 |
| Infection(-4) | 0.00012 | 8.60E-05 | 0.00012* | 7.11E-05 |
| Infection(-5) | 0.00013 | 8.83E-05 | 0.00014* | 7.35E-05 |
| Infection(-6) | 0.00016* | 9.35E-05 | 0.00016** | 7.61E-05 |
| Infection(-7) | 0.00021** | 9.97E-05 | 0.00018** | 7.92E-05 |
| Infection(-8) | 0.00029*** | 0.00011 | 0.00021** | 8.26E-05 |
| Infection(-9) | 0.00032*** | 0.00011 | 0.00025*** | 8.66E-05 |
| Infection(-10) | 0.00036*** | 0.00012 | 0.00029*** | 9.14E-05 |
| Infection(-11) | 0.00047*** | 0.00012 | 0.00035*** | 9.70E-05 |
| Infection(-12) | 0.00062*** | 0.00013 | 0.00043*** | 0.00010 |
| Infection(-13) | 0.00081*** | 0.00014 | 0.00053*** | 0.00011 |
| Infection(-14) | 0.00085*** | 0.00014 | 0.00069*** | 0.00012 |
| Port calls(-1) | 1.27*** | 0.046 | 1.41*** | 0.040 |
| Port calls(-2) | 1.27*** | 0.046 | 1.41*** | 0.041 |
| Port calls(-3) | 1.26*** | 0.046 | 1.41*** | 0.042 |
| Port calls(-4) | 1.26*** | 0.046 | 1.41*** | 0.042 |
| Port calls(-5) | 1.26*** | 0.046 | 1.41*** | 0.042 |
| Port calls(-6) | 1.26*** | 0.046 | 1.41*** | 0.043 |
| Port calls(-7) | 1.26*** | 0.046 | 1.41*** | 0.043 |
| Port calls(-8) | 1.26*** | 0.046 | 1.41*** | 0.043 |
| Port calls(-9) | 1.26*** | 0.046 | 1.41*** | 0.044 |
| Port calls(-10) | 1.26*** | 0.046 | 1.41*** | 0.044 |
| Port calls(-11) | 1.26*** | 0.047 | 1.41*** | 0.044 |
| Port calls(-12) | 1.26*** | 0.047 | 1.41*** | 0.044 |
| Port calls(-13) | 1.27*** | 0.048 | 1.42*** | 0.045 |
| Port calls(-14) | 1.28*** | 0.048 | 1.42*** | 0.045 |
| BDI(-1) | 31.14 | 27.29 | 41.41 | 30.21 |
| BDI(-2) | 37.48 | 27.45 | 47.93 | 30.25 |
| BDI(-3) | 42.30 | 27.60 | 54.51* | 30.30 |
| BDI(-4) | 46.11 | 27.75 | 61.15** | 30.34 |
| BDI(-5) | 49.24* | 27.89 | 67.84** | 30.38 |
| BDI(-6) | 53.28* | 28.00 | 74.60** | 30.42 |
| BDI(-7) | 57.28** | 28.04 | 81.42*** | 30.45 |
| BDI(-8) | 59.46** | 28.04 | 88.31*** | 30.49 |
| BDI(-9) | 60.64** | 28.02 | 95.79*** | 30.48 |
| BDI(-10) | 60.65** | 27.98 | 103.29*** | 30.46 |
| BDI(-11) | 62.22** | 27.92 | 110.83*** | 30.44 |
| BDI(-12) | 64.54** | 27.86 | 118.40*** | 30.42 |
| BDI(-13) | 66.91** | 27.79 | 126.01*** | 30.39 |
| BDI(-14) | 70.17** | 27.68 | 133.64*** | 30.36 |
| Constant term | −10485.21*** | 442.48 | −11787.47*** | 389.21 |
| R2 | 0.62 | 0.73 | ||
Note: * means rejections of null hypothesis at the 10% significance level, ** indicates rejections of null hypothesis at the 5% significance level, *** means rejections of null hypothesis at the 1% significance level.
5. Robustness analysis
5.1. Add all variables into the benchmark model
Here we consider all control variables into the regression model to test the robustness. In order to avoid the effect of explanatory variables on the freedom degree, we expand the original model with a 7th lag to regress all control variables
| (11) |
In order to further investigate whether it exists a coupling impact between the added influence number and all control variables, we consider the interaction terms on the basic of Equation (11) as follows
| (12) |
where , , , and are the coefficients of first-order lag in the interaction terms. As observed in Table 7 , for Equation (11), in the short-term component, the significance and symbol of each control variable have no change. Whether it is the long-term component and short-term component of the BDI volatility, the symbols and significances of coefficients in control variables have not changed. Comparing Table 1, Table 7, the results are basically consistent. In particular, the significance in the short-term component of container idle rate is gradually stronger from lag 1 to 5, whereas that of port calls is gradually weaker from lag 5 to 7. However, for Equation (12) in the short-term component, it's obvious significantly of the added infection number in the lag 5 and 6. Meanwhile, it shows some differences that the significance of short-term component in container idle rate gradually becomes stronger, while that of port calls gradually becomes weaker, furthermore the significance of long-term component in port congestion gradually becomes stronger. On this basis, we find that the influences of container idle rate and port congestion on the BDI volatility has a certain lag, and the impact of short-term component in port calls on the BDI volatility is more significant that of long-term component.
Table 7.
The regression result for after adding the above as control variables.
| Short-term component |
Long-term component |
|||||||
|---|---|---|---|---|---|---|---|---|
| Equation (11) |
Equation (12) |
Equation (11) |
Equation (12) |
|||||
| Regression Val | Standard Dev | Regression Val | Standard Dev | Regression Val | Standard Dev | Regression Val | Standard Dev | |
| Infection(-1) | −0.00041*** | 5.12E-05 | −3.96E-05 | 0.00013 | −0.00042*** | 4.47E-05 | −2.98E-06 | 0.00015 |
| Infection(-2) | −0.00042*** | 5.49E-05 | −0.00012 | 0.00010 | −0.00042*** | 4.62E-05 | −1.55E-05 | 0.00011 |
| Infection(-3) | −0.00043*** | 5.94E-05 | −0.00014 | 0.00010 | −0.00041*** | 4.78E-05 | −2.10E-05 | 9.06E-05 |
| Infection(-4) | −0.00043*** | 6.06E-05 | −5.82E-05 | 0.00013 | −0.00040*** | 4.97E-05 | −2.51E-05 | 8.18E-05 |
| Infection(-5) | −0.00044*** | 6.22E-05 | 0.00086*** | 0.00025 | −0.00040*** | 5.17E-05 | −2.88E-05 | 7.65E-05 |
| Infection(-6) | −0.00046*** | 6.67E-05 | 0.00025* | 0.00015 | −0.00039*** | 5.40E-05 | −3.27E-05 | 7.34E-05 |
| Infection(-7) | −0.00047*** | 7.23E-05 | −4.79E-06 | 0.00012 | −0.00039*** | 5.67E-05 | −3.71E-05 | 7.17E-05 |
| BDI(-1) | −309.01*** | 36.53 | 0.22 | 0.68 | −352.30*** | 37.20 | −0.17 | 0.66 |
| BDI(-2) | −318.85*** | 37.30 | −0.13 | 0.69 | −333.96*** | 36.96 | −0.53 | 0.64 |
| BDI(-3) | −332.42*** | 37.99 | −0.43 | 0.70 | −317.31*** | 36.76 | −0.86 | 0.62 |
| BDI(-4) | −344.95*** | 38.50 | −0.79 | 0.71 | −302.14*** | 36.59 | −1.16* | 0.60 |
| BDI(-5) | −354.99*** | 38.80 | −1.20* | 0.72 | −288.25*** | 36.46 | −1.43** | 0.58 |
| BDI(-6) | −358.91*** | 39.02 | −1.67** | 0.72 | −275.46*** | 36.35 | −1.68*** | 0.57 |
| BDI(-7) | −357.50*** | 39.02 | −2.10*** | 0.72 | −263.65*** | 36.27 | −1.91*** | 0.55 |
| Freight(-1) | 1.17*** | 0.044 | 1.22*** | 0.068 | 1.13*** | 0.041 | 0.89*** | 0.072 |
| Freight(-2) | 1.16*** | 0.046 | 1.17*** | 0.070 | 1.10*** | 0.043 | 0.77*** | 0.070 |
| Freight(-3) | 1.14*** | 0.048 | 1.11*** | 0.072 | 1.07*** | 0.045 | 0.67*** | 0.069 |
| Freight(-4) | 1.12*** | 0.050 | 1.04*** | 0.073 | 1.05*** | 0.046 | 0.59*** | 0.067 |
| Freight(-5) | 1.09*** | 0.051 | 0.98*** | 0.074 | 1.01*** | 0.048 | 0.53*** | 0.066 |
| Freight(-6) | 1.06*** | 0.053 | 0.91*** | 0.076 | 0.98*** | 0.049 | 0.48*** | 0.065 |
| Freight(-7) | 1.03*** | 0.055 | 0.84*** | 0.077 | 0.95*** | 0.051 | 0.43*** | 0.064 |
| Brent(-1) | −12.06*** | 2.64 | −19.53*** | 3.31 | −14.96*** | 2.30 | −24.46*** | 2.67 |
| Brent(-2) | −12.60*** | 2.65 | −20.03*** | 3.30 | −15.20*** | 2.30 | −23.67*** | 2.64 |
| Brent(-3) | −13.15*** | 2.66 | −20.76*** | 3.31 | −15.47*** | 2.29 | −23.09*** | 2.61 |
| Brent(-4) | −13.49*** | 2.67 | −21.31*** | 3.32 | −15.75*** | 2.29 | −22.69*** | 2.58 |
| Brent(-5) | −13.72*** | 2.68 | −21.74*** | 3.35 | −16.07*** | 2.28 | −22.46*** | 2.57 |
| Brent(-6) | −13.65*** | 2.70 | −21.24*** | 3.37 | −16.40*** | 2.28 | −22.37*** | 2.57 |
| Brent(-7) | −13.88*** | 2.71 | −21.76*** | 3.41 | −16.77*** | 2.28 | −22.42*** | 2.57 |
| Idle(-1) | 32.86* | 19.53 | 52.37 | 33.73 | 46.84*** | 16.61 | 77.00** | 35.19 |
| Idle(-2) | 37.99** | 19.24 | 61.02* | 31.98 | 49.89*** | 16.35 | 68.23** | 32.04 |
| Idle(-3) | 42.37** | 18.94 | 68.28** | 31.05 | 52.81*** | 16.11 | 62.65** | 29.75 |
| Idle(-4) | 46.40** | 18.63 | 77.44*** | 29.90 | 55.62*** | 15.88 | 58.95** | 28.01 |
| Idle(-5) | 51.34*** | 18.35 | 89.44*** | 29.00 | 58.34*** | 15.68 | 56.47** | 26.64 |
| Idle(-6) | 55.63*** | 18.14 | 96.52*** | 28.00 | 60.99*** | 15.49 | 54.85** | 25.54 |
| Idle(-7) | 59.64*** | 17.97 | 101.99*** | 27.13 | 63.57*** | 15.31 | 53.86** | 24.64 |
| Congestion(-1) | −38.27*** | 5.50 | −28.15*** | 9.65 | −31.39*** | 5.39 | 0.31 | 9.56 |
| Congestion(-2) | −39.85*** | 5.46 | −30.87*** | 8.68 | −34.64*** | 5.30 | −11.45 | 8.46 |
| Congestion(-3) | −41.50*** | 5.42 | −32.69*** | 7.73 | −37.81*** | 5.22 | −19.22** | 7.68 |
| Congestion(-4) | −43.13*** | 5.39 | −34.47*** | 6.99 | −40.91*** | 5.14 | −24.92*** | 7.09 |
| Congestion(-5) | −44.23*** | 5.36 | −35.56*** | 6.45 | −43.94*** | 5.05 | −29.44*** | 6.63 |
| Congestion(-6) | −45.52*** | 5.33 | −37.16*** | 6.09 | −46.92*** | 4.96 | −33.23*** | 6.25 |
| Congestion(-7) | −46.84*** | 5.29 | −39.27*** | 5.82 | −49.85*** | 4.88 | −36.55*** | 5.94 |
| Port calls(-1) | 0.27*** | 0.05 | 0.36*** | 0.08 | 0.35*** | 0.05 | 0.75*** | 0.09 |
| Port calls(-2) | 0.24*** | 0.05 | 0.28*** | 0.08 | 0.33*** | 0.05 | 0.62*** | 0.08 |
| Port calls(-3) | 0.21*** | 0.05 | 0.21*** | 0.07 | 0.31*** | 0.05 | 0.53*** | 0.08 |
| Port calls(-4) | 0.18*** | 0.05 | 0.16** | 0.06 | 0.29*** | 0.05 | 0.48*** | 0.07 |
| Port calls(-5) | 0.15*** | 0.05 | 0.14** | 0.06 | 0.27*** | 0.05 | 0.44*** | 0.07 |
| Port calls(-6) | 0.13** | 0.05 | 0.12* | 0.06 | 0.25*** | 0.05 | 0.41*** | 0.07 |
| Port calls(-7) | 0.12** | 0.05 | 0.10* | 0.06 | 0.24*** | 0.05 | 0.39*** | 0.07 |
| Infection·Freight | −6.67E-07*** | 1.34E-07 | −5.78E-09 | 1.55E-07 | ||||
| Infection·Brent | 3.86E-05*** | 9.87E-06 | 1.88E-05*** | 6.68E-06 | ||||
| Infection·Idle | 0.00044*** | 0.00012 | 0.00051*** | 0.00014 | ||||
| Infection·Congestion | −4.46E-05** | 2.08E-05 | −7.25E-05*** | 1.81E-05 | ||||
| Infection·Port calls | −1.81E-07 | 1.29E-07 | −5.37E-07*** | 1.52E-07 | ||||
| Constant term | 1808.05** | 798.07 | −1064.70 | 1445.76 | 83.63 | 827.54 | −11220.25*** | 1838.12 |
| R2 | 0.88 | 0.89 | 0.92 | 0.95 | ||||
Note: * means rejections of null hypothesis at the 10% significance level, ** indicates rejections of null hypothesis at the 5% significance level, *** means rejections of null hypothesis at the 1% significance level.
5.2. GARCH-MIDAS model based on BDI volatility
From the empirical results in Section 4, it can be seen that the added infection number not only has a significant effect on the short-term component of BDI volatility, but also has a certain impact on the long-term component. Thus, the added infection number is directly included in GARCH-MIDAS model for robustness test. Here we modify Equation (4) to obtain
| (13) |
where are the variables of ln(Infection m-k), Freight m-k, Brent m-k, Idle m-k, Congestion m-k and ln(Port calls m-k). Here we depict the long-term component of BDI volatility; thus, the added infection number can be taken as the logarithm to calculate. Therefore, the result is shown in Table 8 , where the effect of added infection number on the long-term component of BDI volatility is reflected. For coefficient θ, it is positive at the significance level of 10%, meaning that in the long-term component, the increase of the added infection number will improve the BDI volatility, which is consistent with the regression result of the least square method. In the control variables, only the values of θ in container idle rate and port calls are positive at the 10% significance level. Besides, the coefficient of fright rate is negative, which means the freight rate slightly reduces the BDI volatility in the long-term component; further, the coefficients of Brunt crude oil and port congestion are positive but significantly greater than 10%, which indicates the two control variables increase the volatility of BDI but the effect is not obvious in the long-term component.
Table 8.
Parameter estimates results for GARCH-MIDAS model based on the added infection number.
| ln(Infection) | Freight | Brent | Idle | Congestion | ln(Port calls) | |
|---|---|---|---|---|---|---|
| 2246.71** | 3031.17* | 2244.95* | 2240.12* | 2350.71* | 2240.10* | |
| (4.71) | (13.68) | (6.62) | (1.14) | (9.69) | (1.15) | |
| 0.84*** | 0.76* | 0.75* | 0.96* | 0.97* | 0.36* | |
| (0.06) | (0.06) | (0.05) | (0.04) | (0.03) | (0.04) | |
| 0.15*** | 0.24* | 0.25* | 0.04* | 0.00 | 0.64* | |
| (0.06) | (0.06) | (0.04) | (0.02) | (0.03) | (0.04) | |
| −81.35** | 0.74 | −2.41* | −24.03* | −161.40 | −414.32* | |
| (33.65) | (1.74) | (1.04) | (10.62) | (174.96) | (110.32) | |
| 6.19* | −0.00 | 0.02 | 5.15* | 1.38 | 0.31* | |
| (2.63) | (0.00) | (0.02) | (2.44) | (1.39) | (0.08) | |
| 4.07*** | 64.84 | 1.00 | 3.75* | 1.58* | 1.24* | |
| (0.80) | (140.51) | (2.11) | (0.58) | (0.83) | (0.16) | |
| LLF | −1838.04 | −1805.01 | −1839.21 | −1836.37 | −1846.80 | −1819.96 |
| AIC | 7.05 | 6.93 | 7.06 | 7.05 | 7.09 | 6.98 |
| BIC | 7.10 | 6.97 | 7.11 | 7.09 | 7.13 | 7.03 |
Note: * means rejections of null hypothesis at the 10% significance level, ** indicates rejections of null hypothesis at the 5% significance level, *** means rejections of null hypothesis at the 1% significance level.
6. Conclusions
From the sample data from Jan 22, 2020 to Jan 21, 2022, this study uses the fluctuation decomposition method and least squares regression method to study the effect of the added infection number on the volatility of BDI. In this model, the control variables (freight rate, Brent crude oil price, container idle rate, port congestion level) are added to test whether the information contained in the added infection number is covered by the above variables. From the analysis, we observe the following results. First, the added infection number can effectively affect the volatility of BDI. Whether it is a long-term component or a short-term component, the added infection number increase the volatility of BDI, but the effect on the short-term component is slightly stronger than that of the long-term component. Further, whether the freight rate, Brent crude oil price, container idle rate, port congestion level and other control variables are considered alone or at the same time, then the added infection number still significant influences the volatility of BDI. However, after introducing the freight rate, Brent crude oil price and port congestion level, the regression coefficient of added infection number becomes negative, indicating the added infection number doesn't not fully contain the information contained in traditional economic variables. Then, in the long-term component, the added infection number will indirectly affect the volatility of BDI via the coupling effect with some control variables, which is different from the short-term mechanism. Finally, the result of GARCH-MIDAS model is still significant when the long-term component is directly described from added infection number, which supports the conclusion that the added infection number in the benchmark model effectively affects the long-term trend.
With the arrival of the post epidemic period, the BDI volatility more frequently and is affected by more factors, including freight rate, Brent crude oil price, container idle rate, port congestion caused by the epidemic and the rise of commodity prices. In this context, it is of practical significance to study the long-term component of epidemic and the impact of various influencing factors on the volatility of BDI. For example, the shipping industry is blocked by the COVID-19 epidemic, the efficiency of maritime supply chain is reduced, and the demand for industrial raw materials is reduced, which results in the BDI volatility. Since the COVID-19 epidemic cannot be completely eliminated in short term, the shipping industry needs to assess the additional risk brought by the epidemic, prepare for uncertain events such as geopolitical changes, reduce the cost of maritime supply chain and improve the transportation efficiency.
The limitation of this research is that the time of the selected variables is short. In the process of selecting variables, the data is searched via various channels as much as possible, but it is still not comprehensive. Although the GARCH-MIDAS model has just been put forward, the content of the model is very rich, and the improvement and innovation of the model still need to be studied.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data availability
Data will be made available on request.
References
- Aktar M.A., Alam M.M., Al-Amin A.Q. Global economic crisis, energy use, CO2 emissions, and policy roadmap amid COVID-19. Sustain. Prod. Consum. 2021;26:770–781. doi: 10.1016/j.spc.2020.12.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J.H., Di Z.J., Shi J., et al. Marine oil spill pollution causes and governance: a case study of Sanchi tanker collision and explosion. J. Clean. Prod. 2020;273 [Google Scholar]
- Chen J.H., Xiong W.J., Xu L., et al. Evolutionary game analysis on supply side of the implement shore-to-ship electricity. Ocean Coast Manag. 2021;215 [Google Scholar]
- Chen J.H., Zhuang C.L., Xu H., et al. Collaborative management evaluation of container shipping alliance in maritime logistics industry: CKYHE case analysis. Ocean Coast Manag. 2022;225 [Google Scholar]
- Chen J.H., Ye J., Zhuang C.L., et al. Liner shipping alliance management: overview and future research directions. Ocean Coast Manag. 2022;219 [Google Scholar]
- Chen J.H., Ye J., Liu A.T., et al. Robust optimization of liner shipping alliance fleet scheduling with consideration of sulfur emission restrictions and slot exchange. Ann. Oper. Res. 2022 doi: 10.1007/s10479-022-04590-x. [DOI] [Google Scholar]
- Engle R.F., Ghysels E., Sohn B. Stock market volatility and macroeconomic fundamentals. Rev. Econ. Stat. 2013;95(3):776–797. [Google Scholar]
- Ghysels E., Sinko A., Valkanov R. MIDAS regressions: further results and new directions. Econom. Rev. 2007;26(1):53–90. [Google Scholar]
- Gu Y., Dong X., Chen Z. The relation between the international and China shipping markets. Res. Transport. Bus. Manag. 2020;34 [Google Scholar]
- Hansen P.R., Lunde A., Nason J.M. The model confidence set. Econometrica. 2011;79(2):453–497. [Google Scholar]
- Kamal M.R., Chowdhury M.A.F., Hosain M.M. Stock market reactions of maritime shipping industry in the time of COVID-19 pandemic crisis: an empirical investigation. Marit. Pol. Manag. 2021:1–16. [Google Scholar]
- Kane B., Zajchowski C., Allen T.R., et al. Is it sager at the beach? Spatial and temporal analysis of beachgoer behaviors during the COVID-19 pandemic. Ocean Coast Manag. 2021;205 doi: 10.1016/j.ocecoaman.2021.105533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katris C., Kavussanos M.G. Time series forecasting methods for the baltic dry index (bdi) J. Forecast. 2021;40(8):1540–1565. [Google Scholar]
- Khan K., Su C.W., Tao R., et al. How do geopolitical risk affect oil prices and freight rates? Ocean Coast Manag. 2021;215 [Google Scholar]
- Lin A.J., Chang H.Y., Hsiao J.L. Does the Baltic Dry Index drive volatility spillovers in the commodities, currency, or stock markets? Transport. Res. E Logist. Transport. Rev. 2019;127:265–283. [Google Scholar]
- Liu J., Li Z., Sun H., Yu L., Gao W. Maritime Policy & Management; 2021. Volatility Forecasting for the Shipping Market Indexes: an Ar-Svr-Garch Approach; pp. 1–18. [Google Scholar]
- Makridakis S., Merikas A., Merika A., et al. A novel forecasting model for the baltic dry index utilizing optimal squeezing. J. Forecast. 2020;39(1):56–68. [Google Scholar]
- Nam D., Kim M. Implication of COVID-19 outbreak on ship survey and certification. Mar. Pol. 2021;131 doi: 10.1016/j.marpol.2021.104615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narasimha P.T., Jena P.R., Majhi R. Impact of COVID-19 on the Indian seaport transportation and maritime supply chain. Transport Pol. 2021;110:191–203. doi: 10.1016/j.tranpol.2021.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takeda F., Tomozawa T. An empirical study on stock price responses to the release of the environmental management ranking in Japan. Econ. Bull. 2006;13(5):1–4. [Google Scholar]
- Uddin M., Chowdhury A., Anderson K., et al. The effect of COVID–19 pandemic on global stock market volatility: can economic strength help to manage the uncertainty? J. Bus. Res. 2021;128:31–44. doi: 10.1016/j.jbusres.2021.01.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vo T.A., Mazur M., Thai A. 2021. The Impact of COVID-19 Economic Crisis on the Speed of Adjustment toward Target Leverage Ratio: an International Analysis; p. 102157. Finance Research. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z., Wu X., Lo K.L., et al. Assessing the management efficiency of shipping company from a congestion perspective: a case study of Hapag-Lloyd. Ocean Coast Manag. 2021;209 [Google Scholar]
- Xu L., Shi J., Chen J., et al. Estimating the effect of COVID-19 epidemic on shipping trade: an empirical analysis using panel data. Mar. Pol. 2021;133 doi: 10.1016/j.marpol.2021.104768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu L., Yang S., Chen J., et al. The effect of COVID-19 pandemic on port performance: evidence from China. Ocean Coast Manag. 2021;209 doi: 10.1016/j.ocecoaman.2021.105660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu L., Shi J., Chen J.H. Maritime Policy & Management; 2022. Agency Encroachment and Information Sharing: Cooperation and Competition in Freight Forwarding Market. [DOI] [Google Scholar]
- Xu L., Zhao X.Y., Chen J.H. Exploring the governance dilemma of nuclear wastewater in Fukushima: a tripartite evolutionary game model. Ocean Coast Manag. 2022;225 [Google Scholar]
- Yang H., Dong F., Ogandaga M. Forewarning of freight rate in shipping market based on support vector machine. Traffic Transport. Stud. 2008:295–303. [Google Scholar]
- Yang J., Zhang X., Ge Y.E. Measuring risk spillover effects on dry bulk shipping market: a value-at-risk approach. Marit. Pol. Manag. 2021:1–19. [Google Scholar]
- Zeng Q., Qu C., Ng A.K.Y., et al. A new approach for Baltic Dry Index forecasting based on empirical mode decomposition and neural networks. Marit. Econ. Logist. 2015;18(2):192–210. [Google Scholar]
- Zhang R., Zhang J. Long-term pathways to deep decarbonization of the transport sector in the post-COVID world. Transport Pol. 2021;110:28–36. doi: 10.1016/j.tranpol.2021.05.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X., Chen M.Y., Wang M.G., et al. A novel hybrid approach to Baltic Dry Index forecasting based on a combined dynamic fluctuation network and artificial intelligence method. Appl. Math. Comput. 2019;361:499–516. [Google Scholar]
- Zhang S.C., Mu Y.T., Sun Y. Early impact of COVID-19 pandemic on the molluscan shellfish supply chain in China. Ocean Coast Manag. 2021;213 doi: 10.1016/j.ocecoaman.2021.105852. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.