Advancements in Sustainable Manufacturing Supply Chain Modelling: a Review

Abstract

Managers at various echelons of supply chains are continuously faced with problems of examining and improving supply chain processes with the aim of improving productivity and customer service level, while reducing emissions and total costs simultaneously. This study is aimed at presenting the trends in sustainable manufacturing supply chain modelling in order to establish the modelling approaches which have predominantly been used for improving manufacturing supply chains from years 2010 to 2020. The study employs the systematic literature review methodology for reviewing articles published within the 11-year period. We proffer a classification approach for manufacturing supply chain models, grouping these models into mathematical models, simulation models, hybrid models, and their subcategories. The results showed that though there is a rising trend in the use of simulation and hybrid models, mathematical models have been used more for sustainable manufacturing supply chain modelling. The rise in the use of simulation and hybrid models can be explained by the fact that these models tend to handle uncertain and stochastic data better than mathematical models, which perform better with deterministic data. This research will aid other researchers in recognising the current gaps in manufacturing supply chain modelling in order to identify future research directions.

Introduction

Manufacturing is the transformation of raw materials to finished products with the aid of human labour, machines, methods, and money. It is basically the process by which new products are made from raw materials. Moreover, a supply chain links producers and consumers in a network for producing and distributing specific products. Therefore, manufacturing supply chain networks are responsible for the efficient distribution of manufactured products from producers to customers around the world. To this end, researchers have developed various models for analysing and improving these supply chain networks. However, to the best of our knowledge, there is no recent literature that classifies the manufacturing supply chain models in order to highlight the differences as well as the similarities between the models. In the context of this research, modelling refers to the act of developing a model which is a representation of a theoretical or actual system (Birta and Arbez 2019). It differs from simulation which is the utilisation of a model to analyse the performance or behaviour of the theoretical or actual system in response to different inputs to the system (Birta and Arbez 2019).

Shekarian and Parast (2020), Vishnu et al. (2019), as well as Rajagopal et al. (2017) conducted reviews of models and methods for handling supply chain risk. Mula et al. (2010a) reviewed only mathematical models for supply chain planning. Barbosa and Azevedo (2017) reviewed only hybrid simulation models for improving manufacturing supply chain performance. Similarly, Abideen and Mohammad (2019) reviewed only discrete event simulation and agent-based simulation models, while Clausen et al. (2019) focused on only agent-based simulation models. Moreover, the reviews by Beamon (1998) and Min and Zhou (2002) are quite obsolete.

The aim of this research is to provide a classification and review of sustainable manufacturing supply chain models in order to appropriately group the models and highlight the differences and similarities between the models. From the research, the recently developed manufacturing supply chain models can be conveniently classified into mathematical, simulation and hybrid models. The mathematical models can be further classified by nature, type, and objectives. By nature, the mathematical models can be classified as linear programming (LP), mixed integer linear programming (MILP), nonlinear programming (NLP), or mixed integer nonlinear programming (MINLP) models. By type, the mathematical models can be classified as deterministic and non-deterministic models. The deterministic models are the linear and nonlinear models while the non-deterministic models are the stochastic and fuzzy models. By objectives, the mathematical models can be classified as single objective and multi-objective models. On the other hand, the simulation models can be further broken down into agent-based, discrete event, Monte Carlo, and system dynamics simulation models.

Therefore, this paper is aimed at answering the research question: What are the most prevalent techniques for modelling and analysing sustainable supply chains of the manufacturing industry? The answer to this research question is provided by means of a systematic literature review (SLR) of articles published between 2010 and 2020, on the subject matter. The purpose of an SLR is the identification, selection, and critical appraisal of research articles so as to answer precisely formulated research questions. This study proposes a scheme for classifying existing research on manufacturing supply chain modelling and simulation. The following section describes the research methodology employed, providing details of how the SLR was conducted.

Research Methodology

The research methodology utilised in this study is a systematic literature review (SLR) of peer-reviewed scholarly articles published between 2010 and 2020, which are related to the topic of ‘Advancements in Sustainable Manufacturing Supply Chain Modelling: A Review’. The SLR process is a methodology that is utilised in identifying, selecting, and critically assessing research with the aim of providing an answer to formulated research questions. This study adopts the SLR development procedure of five stages provided in Denyer and Tranfield (2009). Basically, the stages of creating an SLR are formulation of research questions, locating research articles, selection and evaluation of the articles, analysis and synthesis of the articles, and finally, usage and reporting of the results. These five stages are discussed in the following subsections.

Formulation of a Research Question

This is the first stage of the SLR process as outlined by Denyer and Tranfield (2009). In this stage, a research question was developed in order to provide a focus and guidance for the study, thereby preventing ambiguity in reporting of results. Hence, the aim of the study is to provide answers to the research question formulated. Therefore, the research question developed during this stage is as follows:

• What are the most prevalent techniques for modelling and analysing sustainable supply chains of the manufacturing industry?

The research question was formulated this way in order to focus the study on reviewing only articles that develop models suitable for analysing sustainable manufacturing supply chains. It was chosen over other research questions because its answers provide knowledge on the techniques and trends in sustainable manufacturing supply chain modelling, which is the main point of the research. The question seeks to understand and classify the various techniques for modelling of sustainable manufacturing supply chains, in order to determine the trends in modelling and analysis of manufacturing supply chains. Obtaining a good understanding of the modelling techniques would help in ascertaining the effectiveness of the techniques, as well as the trends in usage of these techniques.

Locating Research Articles

This is the second stage of the SLR process where research articles relevant to answering the research questions were located. In this stage, a literature search of published articles was conducted by searching online databases such as Google Scholar, ResearchGate, Taylor & Francis Online, ScienceDirect, IEEE Xplore, Wiley Online Library, Emerald Insight, and SpringerLink databases. The keywords and search terms that were used for the search include ‘linear manufacturing supply chain models’, ‘nonlinear manufacturing supply chain models’, ‘stochastic manufacturing supply chain models’, ‘multi-objective manufacturing supply chain models’, ‘fuzzy manufacturing supply chain models’, ‘agent-based simulation manufacturing supply chain models’, ‘Monte Carlo simulation manufacturing supply chain models’, ‘discrete event simulation manufacturing supply chain models’, ‘system dynamics simulation manufacturing supply chain models’, ‘hybrid manufacturing supply chain models’, and ‘manufacturing supply chain optimisation model using predictive machine learning’. These keywords were chosen because they were specific enough to return only articles related to the topic of the research from the search engines. Moreover, the keywords were also broad enough to represent the main concepts of the study. They were chosen in such a way that mainly articles related to manufacturing supply chain models were generated by the search engines; this was to avoid generating articles which were out of scope of the research. Moreover, as this study is concerned with only the recent advancements in modelling manufacturing supply chains, studies were selected from between year 2010 and 2020, a period of 11 years.

Selection and Evaluation of Articles

This is the third stage of the SLR process where the articles were selected and evaluated based on certain inclusion criteria. The first criterion utilised is that the articles must be peer-reviewed studies, this is because peer-reviewed articles tend to be of higher quality. Another criterion utilised is that the research must have been published between 2010 and 2020 because this study is concerned with only the recent advancements and trends in manufacturing supply chain modelling. Yet another criterion used is that the articles must be published in English language because English is the main research language utilised across the globe (Giannakoulopoulos et al. 2020; Nunan 2003). Another criterion used is that articles must deal with manufacturing supply chain models; therefore, articles dealing with service, construction, waste, pharmaceutical/healthcare, petroleum, energy, and agricultural supply chains were excluded. Also, only articles that develop one or more supply chain optimisation or simulation models were considered. A total of 503 papers were identified by applying these inclusion criteria. Furthermore, 235 articles were identified to be duplicates and were excluded from the study, leaving a total of 268 papers.

Analysis and Synthesis of Articles

This is the fourth stage of the SLR process where the papers selected were analysed and synthesised. According to Denyer and Tranfield (2009), analysis deals with breaking down specific studies into individual parts, while describing how these parts relate to each other, while synthesis is aimed at finding associations between constituent parts of different selected studies. In this stage, to analyse the articles, each article was evaluated based on the modelling and optimisation technique used, year of publication, and journal of publication of the article. On the other hand, during synthesis of the articles an attempt was made to identify the associations between the individual characteristics of the different studies selected.

Usage and Reporting of Results

This is the final stage of the SLR process. In this stage, a summary of all selected articles is provided, taking cognizance of the data extracted from the articles (Denyer and Tranfield 2009). Furthermore, they also explained that all knowledge and unknowns concerning the research questions addressed is brought to bear in this stage, by presenting this information in the form of statistics, graphs, tables, and discussions. Therefore, in this stage, the concluding results of the analysis and synthesis of the literature review were presented.

Results of the Systematic Literature Review

The result of the SLR was the identification of three classifications of manufacturing supply chain optimisation models grouped into mathematical models, simulation models, and hybrid models. Therefore, each article reviewed can be grouped into one of these three broad classifications of manufacturing supply chain models. Furthermore, the mathematical models can be grouped by nature, type, and objectives. By nature, the mathematical models can be classified as linear programming (LP), mixed integer linear programming (MILP), nonlinear programming (NLP), or mixed integer nonlinear programming (MINLP) models. By type, the mathematical models can be classified as deterministic and non-deterministic models. The deterministic models are the linear and nonlinear models while the non-deterministic models are the stochastic and fuzzy models. By objectives, the mathematical models can be classified as single objective and multi-objective models, while the simulation models can be grouped into agent-based, Monte Carlo, discrete event, and system dynamics simulation models. Figure 1 shows the various type classifications and subcategories of manufacturing supply chain models.

Fig. 1.

Type classifications and subcategories of manufacturing supply chain models

Mathematical Models

Mathematical models represent a theoretical or actual system by using mathematical concepts such as variables, equations, and inequalities, which are then solved analytically in order to study the effects of different components of the system and predict the behaviour of such systems (Giordano et al. 2013). A large portion of the articles reviewed proposed a mathematical/analytical model for optimising manufacturing supply chains. These models could be linear, nonlinear, stochastic, fuzzy, and multi-objective models or a combination of them. Mathematical models can be classified according to nature, type, and objectives. The following subheadings describe these classifications of mathematical models.

Classification of Mathematical Models by Nature

One of the ways of classifying a mathematical model is by the nature of the model. By this, mathematical models can be classified based on the structure of both the objective function and constraints, which are involved in the optimisation problem (Dutta 2016). Therefore, by this classification, mathematical models can be LP models, MILP models, NLP models, or MINLP models.

According to Dutta (2016), LP models are those models that utilise a linear objective function as well as linear constraints. He further explained that MILP models are basically LP models with the addition of the restriction that some of the model variables are integers. Moreover, he explained that NLP models are those models that utilise a nonlinear objective function and/or nonlinear constraints, while MINLP models are basically NLP models with the added restriction that some of the model variables are integers.

Classification of Mathematical Models by Type

Another way of classifying a mathematical model is by the type of the model. By this, mathematical models can be classified based on being deterministic or non-deterministic. Deterministic models are models which have unique variable states and will always generate the same optimum solution for a given set of initial conditions, while non-deterministic models incorporate randomness and uncertainty in the states of variables, and as such depend on retrials to better sample the parameter space in search of the optimum solution (Dutta 2016).

Deterministic Models

As earlier described, deterministic models will generate the same optimum solution for a given set of initial conditions. In the context of this research, the deterministic models are the linear models and nonlinear models.

Linear Models

Linear models refer to those mathematical models that utilise a linear objective function and linear constraints, for modelling and optimisation of manufacturing supply chains (Dutta 2016). Dondo et al. (2011) presented an optimisation framework based on a mixed integer linear programming (MILP) formulation to solve the multi-echelon vehicle routing problem utilising cross-docking in supply chain management, in order to satisfy customer demands and minimise total transportation cost. Melo et al. (2011) developed a large-scale MILP model to study a multi-period supply chain network redesign problem encountered in strategic supply chain planning. Naraharisetti and Karimi (2010) developed a MILP model for redesigning supply chains with multi-purpose production facilities, handling multi-tiered distribution of products, where distributors distribute products between themselves before reaching the customers. Kunnumkal and Topaloglu (2011) developed a dynamic programming model for inventory distribution systems aiming to minimise total holding, replenishment, and backlogging cost throughout a specific planning horizon. Sitek and Wikarek (2015) developed an approach involving MILP modelling to model and optimise decision problems related to timely order execution, environmental costs, fleet size needs, distribution centre capacity, and recycling in sustainable supply chain and green supply chain management.

Some researchers have developed MILP models for closed-loop supply chain networks aiming to simultaneously optimise the forward and reverse chains of the supply network in order to maximise profit in various manufacturing industries (Amin and Zhang 2014; Hashemi et al. 2014; Kannan et al. 2010; Nallusamy et al. 2018; Özceylan et al. 2017; Özkır and Başlıgıl 2012; Paksoy et al. 2011; Pant et al. 2018; Pedram et al. 2017; Pourjavad and Mayorga 2018; Prakash et al. 2017; Sadeghi et al. 2020; Sasikumar and Haq 2011; Yi et al. 2016; Zhang et al. (2010). Chatzikontidou et al. (2017) and Li et al. (2011) presented MILP models for decision-making at the strategic, tactical level, and inventory management aiming to of minimise total supply chain network cost. Lalmazloumian et al. (2013), Arampantzi et al. (2018), and Wang et al. (2011) proposed MILP models considering procurement, manufacturing, and delivery costs with the aim of minimising supply chain costs while improving customer service level. Altmann (2014) proposed a MILP model considering product demand affected by environmental sustainability requirements. Shukla et al. (2011) formulated a MILP model for optimising a supply chain network aiming to maximise both robustness and efficiency of the network. Longinidis and Georgiadis (2011) developed a MILP model which could be utilised as a strategic decision tool for integrating financial statement analysis with decisions concerning supply chain design under uncertain demand. Wu (2010) proposed a MILP model to handle the problem of production loading having import limits aiming to minimise total supply chain network costs.

Some researchers have proposed linear supply chain optimisation models for optimising supply chain networks of the pulp and paper manufacturing industry (Ouhimmou et al. 2019; Safaei et al. 2017). Duong and Bui (2018) formulated deterministic, multi-product, multi-echelon, and multi-period MILP models for the delocalization supply chain problem and the capacitated facility location problem, respectively. Cintron et al. (2010) presented a multi-criteria MILP model for determining the best configuration of the manufacturing plants and distribution centres that improve flow of products to consumers in the distribution network. Sadjady and Davoudpour (2012) proposed a MILP model aiming to minimise total costs of two-echelon deterministic, single-period, multi-commodity supply chain networks. Shu et al. (2013) developed a linear optimisation model for a distribution network constituted by a supplier, set of warehouses and set of retailers considering two commodity categories and formulation of the optimisation problem as the uncapacitated facility location problem. Cortinhal et al. (2019) proposed a MILP model of supply chain networks for identifying the network configuration having lowest total cost based on constraints such as technological conditions, resource availability, and customer service level requirements. Khalifehzadeh and Fakhrzad (2019) proposed a MILP model to handle the multi-stage production–distribution planning problem with multiple suppliers, producers, retailers, and customers in uncertainty. Tóth et al. (2017) proposed a mathematical model to optimise the operation parameters of blending technologies manufacturing supply chains with the objective of profit maximisation. Aalaei and Davoudpour (2017) developed a mathematical model for optimising cellular manufacturing system aiming to minimise total holding cost, material handling costs, transportation costs, as well as fixed costs of production.

Nonlinear Models

Nonlinear models refer to those mathematical models that utilise a nonlinear objective function and/or nonlinear constraints for modelling and optimisation of manufacturing supply chains (Dutta 2016). Some other researchers have developed nonlinear models to solve manufacturing supply chain problems. Nasiri et al. (2010) developed a mixed integer nonlinear programming (MINLP) model for locating warehouses, allocating retailers to opened warehouses, obtaining the perfect inventory control policy, and managing order quantity and safety stock level. Kaur and Singh (2018) developed a supply chain logistics procurement model which is environmentally sustainable and of a MINLP type. Benyoucef et al. (2013) developed a nonlinear optimisation model to handle the decisions concerning supplier selection and integrated facility location for supply chain network design such as facility/supplier selection and facility location/supplier reliability, in order to minimise supply chain network costs. Xu et al. (2020) and Göksu et al. (2015) presented synchronization and control methods for managing nonlinear, chaotic, and dynamic behaviours of multi-echelon supply chain systems having disturbances and perturbations. Spiegler et al. (2016) proposed simplification methods for aiding supply chain analysts in representing complex nonlinear supply chain models as accurate linear models. Ghasemy (2019) developed a non-linear programming model to manage the problem of aggregate production planning in a multi-period, multi-product, multi-site, multi-sales channel, two-echelon supply chain of a garment manufacturing supply chain. Manupati et al. (2019) developed a MINLP model for monitoring performance of supply chains and optimising emission levels as well as operational costs, using a blockchain approach. Also, Manupati et al. (2018) developed a bi-objective MINLP model for minimisation of total cost as well as minimisation of carbon emissions, considering a three-level supply chain network. Aminzadegan et al. (2019) as well as Taxakis and Papadopoulos (2016) presented MINLP and MILP models for handling the problem of transportation, production scheduling, inventory planning, and resource allocation in a supply chain aiming to minimise delivery cost, resource allocation, and lost sale cost. Amirtaheri et al. (2017) developed two nonlinear bi-level programming models for investigating a decentralised production–distribution supply chain.

Some researchers have formulated MINLP models for analysing a multi-echelon joint inventory-location problem aiming to simultaneously determine warehouse locations as well as warehouse and retailer inventory policies that minimise total operational costs (Diabat et al. 2011; Keskin and Üster 2012; Zhao et al. (2016);;. Hariga et al. (2017) proposed a MINLP for a closed-loop supply chain aiming to minimise the entire supply chain cost by optimising production cycle length, batch number and sequence, as well as inventory levels. Esmaeilikia et al. (2014) developed a MINLP model incorporating various flexibility options in manufacturing, sourcing, and distribution functions for flexibility analysis of supply chains. Al-Salem et al. (2016) proposed a MINLP model that captures the forward and reverse flow of a single product type, through a set of warehouses dealing with products from the two directions, aiming to minimise total costs. Petridis (2013) developed a MINLP model aiming to minimise total cost in a supply chain network having multiproduct warehouses, production facilities, and distribution centres, considering capacity and facility selection decisions. Nasiri et al. (2014) developed MINLP and MILP models for handling the capacitated facility location problem of a supply chain having three echelons of suppliers, production sites, and distribution centres. Longinidis and Georgiadis (2014) developed a MINLP model for strategic planning of a supply chain, considering sale and leaseback in the supply chain network design. Fahimnia et al. (2011) proposed a MINLP model for a two-echelon production–distribution supply chain network for handling the optimisation of the aggregate production–distribution planning problem considering warehouse storage assignments, transport routings, and inventory management issues. Taleizadeh et al. (2011) developed a MINLP model for determining the reorder points, safety stock, and amount of shipments that minimise total supply chain costs.

Non-deterministic Models

As earlier described, non-deterministic models incorporate randomness and uncertainty in the states of variables and as such depend on retrials to better sample the parameter space in search of the optimum solution (Dutta 2016). In the context of this research, the non-deterministic models are the stochastic models and fuzzy models.

Stochastic Models

Stochastic models refer to those mathematical models that are used in representing randomness and uncertainty in modelling and optimisation of manufacturing supply chains, by allowing for random variation in one or more inputs over time (Dutta 2016). Another group of researchers have developed stochastic models for analysing manufacturing supply chains. Zanjani and Nourelfath (2014) developed stochastic mathematical programming models while considering the operations planning and spare-part logistics problem for third party maintenance providers. Baghalian et al. (2013) proposed a mixed integer stochastic model with a nonlinear objective function and linear constraints for designing a network of multi-products supply chains comprising several capacitated retailers, distribution centres, and production facilities, in markets under uncertainty. Azad and Davoudpour (2012) presented a stochastic supply chain network optimisation model for controlling risks in supply chain networks containing three-tier decision makers namely suppliers, distribution centres, and customers. Soleimani et al. (2013) proposed a MILP formulation for planning multi-product, multi-period closed-loop supply chain networks having stochastic demand and price.

Some researchers have proposed stochastic programming models for handling multi-product, multi-period closed-loop supply chains structured as a multi-layer network, having raw material supplies and customer demands uncertainty (Amin and Zhang 2013; Jeihoonian et al. 2017; Zeballos et al. 2014). Al-e-hashem et al. (2013) developed a stochastic model for handling the multi-period, multi-site, multi-product aggregate production planning problem in a sustainable supply chain with uncertainty in demand. Feng et al. (2012) developed a stochastic model for investigating the capacity allocation and contract selection problem of a three-level manufacturing supply chain, aiming to maximise profit. Cardona-Valdés et al. (2011) proposed a stochastic optimisation model for finding the optimal supply chain network configuration and transportation modes assignment that simultaneously minimise total cost and service time, under demand uncertainty. Sarkar and Giri (2018) developed a stochastic two-echelon supply chain model for supply chains having a single-buyer and a single-vendor and stochastic demand. Tolooie et al. (2020) developed a two-stage stochastic MILP model to handle the multi-period capacitated facility location and allocation problem and minimise establishing and transportation costs.

Fuzzy Models

Fuzzy models refer to those mathematical models that utilise fuzzy set theory for modelling and optimisation of manufacturing supply chains (Pasi 2009). Some researchers have developed fuzzy supply chain optimisation models for investigating manufacturing supply chain problems having uncertain, vague, or imprecise data. Kocamaz et al. (2016) presented an approach for controlling chaotic supply chains using adaptive neuro-fuzzy inference system–based controllers, in order to handle the control and synchronization of supply chain networks that are chaotic using various artificial intelligence techniques. Jindal et al. (2015) developed a fuzzy MILP model to optimally decide on the products or parts location and allocation per facility, quantity of remanufacture products, number of purchased parts from external suppliers, and level of inventory of products or parts, in order to maximise profit. Dotoli et al. (2016) as well as Bai and Liu (2014) presented fuzzy optimisation models for maximising entire supply chain network efficiency, while satisfying product demand and considering capacity at each node of the supply chain. Alimoradi et al. (2014) proposed a fuzzy MILP model to handle uncertainty in customer product returns in closed-loop supply chains.

Some researchers have developed fuzzy models for handling closed-loop supply chain networks aiming to minimise the total supply chain costs and maximise profit (Amin and Zhang 2012; Dai and Li 2017; Darbari et al. 2017; Farrokh et al. 2018; Jindal and Sangwan 2013; Özceylan and Paksoy 2013; Pishvaee and Torabi 2010; Pourmehdi et al. 2020; Ramezani et al. 2014; Subulan et al. 2015; Talaei et al. 2016; Vahdani et al. 2013; Wu et al. 2018). Tabrizi and Razmi (2013) developed a fuzzy MINLP model of a supply chain network, representing uncertain risk sources by the fuzzy set theory. Paksoy and Pehlivan (2012) developed a fuzzy MILP model aiming to determine the fuzzy capacities of supply chain facilities and provide a minimum cost network configuration design. Pathak and Mondal (2012) presented a fuzzy MILP model for handling the aggregate production–distribution planning problem in multi-echelon, multi-stage, multi-product, multi-period, multi-distribution centre supply chain networks aiming to maximise profit of all products handled by the supply chain network. Peidro et al. (2010) and Mula et al. (2010b) presented fuzzy MILP models for tactically planning supply chain networks having multiple echelons, products, levels, and periods, aiming to obtain optimal use of available resources, and meeting customer demands at minimum cost. Bilgen (2010) developed an integrated fuzzy optimisation model for handling the problem of production–distribution planning, aiming to optimally manage interrelated logistics decisions considering uncertainty in capacity.

Classification of Mathematical Models by Objectives

One other way of classifying mathematical models is by the number of objective functions the model possesses. By this, mathematical models can be grouped into single objective models and multi-objective models. When the mathematical model contains a sole objective function, it is a single objective model, while when the model contains more than one objective function, it is a multi-objective model (Dutta 2016).

All of the models described in previous sections of this paper are single objective models; therefore, they utilised only one objective function for optimisation of manufacturing supply chains. The following subheading describes the multi-objective models that have been used for sustainable manufacturing supply chain modelling within the period of review.

Multi-objective Models

As described earlier, multi-objective models refer to those mathematical models that utilise more than one objective function for modelling and optimisation of manufacturing supply chains (Dutta 2016). Some of the optimisation models developed by researchers actually have multiple objective functions. Ivanov et al. (2013) developed a formulation to provide a solution to a multi-objective, multi-commodity, and multi-period production–distribution planning problem for a centralised multi-stage upstream network, considering structure dynamics. Das and Lashkari (2015) formulated a multi-objective model which can be utilised to plan and control specific internal business factors in order to create a risk-resilient supply chain. Banyai et al. (2014) developed a multi-objective mathematical model to find the optimal spare part make-or-buy solution. Cakici et al. (2012) developed a multi-objective optimisation model to handle the integrated production–distribution planning decisions in a supply network at a detailed scheduling level. Similarly, Jamili et al. (2016), Rafiei et al. (2018), and Gholami et al. (2019) developed multi-objective optimisation models to handle the integrated production–distribution planning problem of four-echelon supply chains, aiming for total supply chain cost minimisation and service level maximisation. Ramudhin et al. (2010), Vafaei et al. (2020), and Yadav et al. (2018) developed multi-objective mixed integer linear programming (MOMILP) models for multi-product, multi-echelon, and multi-transportation mode supply chains, with the objectives of transportation, purchasing vehicles and building warehouses cost minimisation, carbon dioxide emission minimisation, and job opportunities maximisation. Hiremath et al. (2012) proposed a multi-objective model for outbound logistics aiming for minimising total cost, maximising unit fill rates and maximising resource utilization of facilities in the network.

Some researchers have developed MOMILP models for optimising multi-level closed-loop supply chain networks of the tyre manufacturing industry aiming to minimise total cost and environmental impacts of the supply chain networks (Abdolazimi et al. 2020; Amin et al. 2017; Sahebjamnia et al. 2018). Ahmadi and Amin (2019) presented MOMILP formulation for maximising total profit in a closed-loop supply chain network of mobile phones having stochastic demand, while simultaneously maximising eligible suppliers’ weights. Jabbarzadeh et al. (2018) proposed a bi-objective optimisation model for minimising cost and greenhouse gas emissions in a supply chain. Vafaeenezhad et al. (2019) and Arampantzi and Minis (2017) presented multi-objective linear programming models for sustainably optimising multi-product, multi-echelon, multi-period supply chains considering environmental, social, and economic performance. Kadambala et al. (2017) developed a MOMILP for maximising profit, optimising customer surplus, and minimising energy use in closed-loop supply chain networks. Trivedi et al. (2017) developed a multi-objective integer linear program (MOILP) for product mix optimisation, order allocation, and supplier selection in order to optimise profit, considering constraints of machine and capacity. Chen et al. (2017) developed a MOMILP model utilised in optimising the total cost and total CO₂ emissions of a supply chain, in order to handle the multi-stage closed-loop supply chain design problem. Yildiz et al. (2015) developed a multi-objective nonlinear model for examining the impact of upstream entities on individual entities’ reliability, in order to measure the total reliability of the network. Entezaminia et al. (2016) and Jakhar (2014) proposed multi-objective models for green supply chain networks considering reverse logistics aiming to minimise total losses and maximise profit and total product environmental scores. Sarrafha et al. (2015) presented a bi-objective MINLP model whose objectives were to minimise total supply chain costs and minimise the average delay incurred in transporting products to distribution centres. Pasandideh et al. (2015) presented a multi-objective mixed integer nonlinear programming (MOMINLP) model for a multi-product, multi-period supply chain having three echelons with the aim of determining manufacturing plants production quantity in different periods, warehouse number and locations, as well as products quantities transported across supply chain nodes. Pazhani et al. (2013) presented a bi-objective MILP model for a multi-product, multi-period closed-loop supply chain aiming to minimise total cost and maximise service level of warehouses and supply chain facilities. Venkatesan and Kumanan (2012) proposed a multi-objective model for optimising a supply chain network, aiming to minimise supply chain cost, maximise flexibility of volume, and minimise demand fulfilment lead time. Al-e-hashem et al. (2011) developed a MOMINLP model to handle the multi-period, multi-site, multi-product aggregate production planning problem, aiming to minimise total supply chain losses and maximise customer satisfaction by minimising shortages at customer zones in all periods. Kamali et al. (2011) presented a MOMINLP to handle a supply chain system consisting of a solitary buyer and many vendors, under an all-unit vendor quantity discount policy. Ma et al. (2016) developed a multi-objective MINLP model to handle an environmental closed-loop supply chain having two conflicting objectives of minimising the economic cost and minimising environmental influence, while also handling supply chain uncertainty.

Ali et al. (2020b) developed a fuzzy MOMILP model for optimisation of a multi-stage reverse logistics network of an air conditioner manufacturer. While considering the multi-product, multi-site, and multi-period manufacturing environment, Badhotiya et al. (2019) developed a fuzzy MOMILP model for minimising total cost, time of delivery, and level of backorders in the automobile manufacturing industry. Nemati and Alavidoost (2018) developed a fuzzy MOMILP model for the sales and operations planning process of a multi-site manufacturing company, having various suppliers of raw material, distribution centres, customers, and a broad product family range. Kumar et al. (2016) proposed a fuzzy multi-objective model for optimisation of order allocation among suppliers, considering sustainability of the supply chain network. Jindal and Sangwan (2013) developed fuzzy MOMILP models for closed-loop supply chains having various customer zones, disassembly centres, collection centres, external suppliers, refurbishing centres, and product recovery processes aiming to minimise costs under capacity constraints. Gholamian et al. (2015) developed a fuzzy MOMILP for supply chain production planning under demand uncertainty. Similarly, Taran and Roghanian (2013) proposed a fuzzy MOMILP model aiming to minimise manufacturing and distribution costs, considering supply chain costs and customer demand as uncertain quantities which were modelled using fuzzy sets theory. Shaw et al. (2012) developed a fuzzy MOMILP model for selecting the most appropriate supplier in supply chain networks, considering the carbon emission issue. Peidro et al. (2012) proposed a fuzzy MOMILP model to manage the centralised replenishment and production–distribution problem in a ceramic tile supply chain, aiming to maximise the fuzzy gross margin as well as minimise the fuzzy idle time and fuzzy quantity of backorders in the network. Lee et al. (2012) developed a fuzzy multi-level multi-objective production planning for supply chains in a fuzzy environment, aiming to maximise the total profit of the supply chain and customer satisfaction level. Haleh and Hamidi (2011) proposed a fuzzy MOMILP model aiming to optimise price, quality, and risk, while satisfying constraints such as logistics costs, capacity, and demand. Similarly, Nagar et al. (2012) developed a multi-objective stochastic model aiming to maximise supply chain profit and minimise financial risk, in order to achieve an optimal service level.

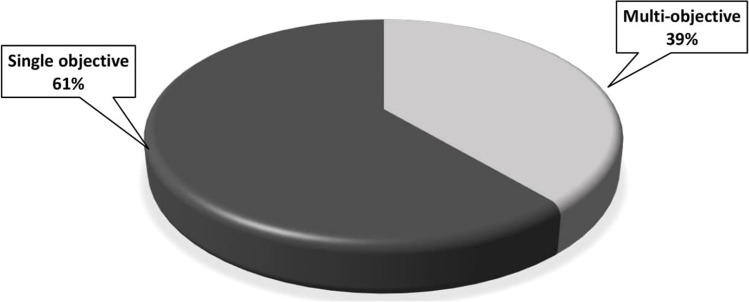
Figure 2 displays the percentage of mathematical models reviewed that are single objective and the percentage that are multi-objective.

Fig. 2.

Percentage of mathematical models reviewed that are single objective versus multi-objective

Simulation Models

Simulation models utilise logic developed in a computer program to represent a theoretical or actual system, obtaining results about the system by statistical analysis (Birta and Arbez 2019). Some of the articles reviewed proposed simulation models for optimising manufacturing supply chains. These models could be agent-based simulation (ABS) models, Monte Carlo simulation (MCS) models, discrete event simulation (DES) models, or system dynamics simulation (SDS) models.

Agent-Based Simulation Models

Agent-based models refer to those simulation models that are utilised in studying and understanding the relationships between components of a supply chain system by representing these components as autonomous entities or agents and simulating their interactions (Pereda et al. 2017). Mizgier et al. (2012) developed an ABS model for representing the economic environment in which supply chain networks operate. Pu et al. (2018) proposed an ABS approach for coordinating and dynamic allocation planning of smart manufacturing enterprises supply chains. Lohmer et al. (2020) and Dulam et al. (2020) utilised ABS models for investigating the effect of resilience on a complex supply chain network affected by uncertainties and disruptions. Terrada et al. (2020) presented an ABS model for handling decision-making problems involving information systems in management of supply chains. Haddad et al. (2019) developed an ABS model for managing repair and maintenance supply chain network activities aiming to shorten the supply chain and decrease total cost. Sergeyev and Lychkina (2019) proposed an agent-based model for managing inter-organizational coordination and integration between supply chain network participants.

Researchers have proposed ABS models for optimising supply chains of the clothing manufacturing industry (Gold et al. 2020; Ma et al. 2017). Papakostas et al. (2020) proposed an agent-based approach for choosing an additive manufacturing service provider in a situation where there are multiple appropriate technologies and resources. Hajmohammad and Shevchenko (2020) proposed an ABS model for managing sustainability risk in supply chains and assessing the evolutionary processes effect on the presence of sustainable or unsustainable business practices among suppliers. Again, researchers have developed agent-based models for handling supply chain inventory and facility disruptions (Blos et al. 2018; Kessentini et al. 2018; Kim et al. 2010; Li et al. 2018; Nair and Vidal 2011; Okada et al. 2015; Ponte et al. 2017; Saberi et al. 2012). Zheng et al. (2019) developed a multi-agent-based simulation model aiming to investigate the benefits of introducing the physical Internet into existing supply chain networks. Long (2018) conducted an agent-based computational experiment for aiding decision-making in a manufacturing supply chain network having five echelons.

Researchers have developed agent-based modelling systems for supply chain transportation and distribution optimisation in terms of product flows and vehicle routing (Alho et al. 2017; Becker et al. 2016; Böhnlein et al. 2011; Holmgren et al. 2012; Li and Chan 2012; Li and Epureanu 2020; Roorda et al. 2010; Rouzafzoon and Helo 2018; Sakai et al. 2020; Serrano-Hernandez et al. 2018). Drakaki et al. (2019) presented a multi-agent-based approach for handling decision-making concerning sustainability, supplier selection, routing, and order allocation. ABS has been utilised in examining the effect of multiple out-of-stock situations on different supply chain network scenarios (Rosales et al.; Wu et al. 2013). Ribino et al. (2017) proposed an ABS approach for determining the effect of specific factors on automatic logistic warehouses during performance improvement. Ballouki et al. (2017) utilised multi-agent-based simulation for selecting the cheapest product among alternatives, based on supplying and production costs, under capacity constraints.

Researchers have presented ABS approaches for evaluating risk linked to supply chain disruptions as a result of failures at supply chain nodes (Blos and Miyagi 2014; Giannakis and Louis 2011; Seck et al. 2015). Long and Zhang (2014) proposed an integrated agent-based framework for inventory-production–transportation modelling and simulation of supply chains. Agent-based models have been utilised in investigating the bullwhip effect considering varying demand patterns, ordering policies, and supply chain structures (Chinh et al. 2013; Tang and Pan 2014). Hernández et al. (2013) presented a multi-agent collaborative solution for multi-level decision-making in automotive supply chains. Medini and Rabénasolo (2014) utilised ABS for determining the optimal configuration, by investigating the performance of various supply chain configurations. Amini et al. (2012) used ABS for examining the effect of various production-sales policies on product distribution and profit. Mustapha et al. (2010) developed an agent-based framework for modelling and simulating the organisational aspects of supply chains at different levels. Wang (2010) proposed a multi-agent-based model for collaborative negotiation in supply chain network. Golroudbary et al. (2019) developed a framework combining ABS and SD models for complex logistics systems, considering interactions effects and dynamic feedback in assessing the supply chain network reliability.

Some researchers have applied machine learning (ML) together with ABS models for optimising manufacturing supply chains. Aghaie and Heidary (2018) applied reinforcement learning, an ML training method, in optimizing the simulation procedure for finding the best risk-sensitive retailer based on a profit function. Pereira et al. (2018) developed a predictive and adaptive manufacturing supply chain management approach for omnichannel retailing supply chains which combines ML for minimising uncertainty and ABS for handling synchronisation of supply and demand in the supply chain. Zhou et al. (2015) combined ABS with Q-learning for evaluating trade-offs between satisfying demand service levels and cost goals for manufacturing supply chains with multiple products.

Monte Carlo Simulation Models

Monte Carlo simulation models refer to those simulation models utilised in analysing and predicting the behaviour of supply chain systems at a particular point in time, relying on repeated random sampling to predict the probability of different outcomes of uncertain events (Klug 2011). Olson and Wu (2011) utilised a data envelopment analysis (DEA) simulation model and MCS for analysing the international outsourcing problem, in order to measure, evaluate, and assess the risk of outsourcing. Tao et al. (2019) built an MCS model for investigating procurement and distribution decisions in a three-tier supply chain experiencing uncertainty in demand and supply. Thomas and Mahanty (2020) presented an MCS model for analysing emergency sourcing prevention strategies of two-echelon supply chains experiencing supply disruptions, evaluating the impacts of rare-but-long disruptions and frequent-but-short disruptions on long-term profit and backlog of manufacturing supply chains. Ozkan and Kilic (2019) utilised MCS for handling logistics network design problems by approximating the reliability of candidate supply chain networks. Similarly, Mikhail et al. (2019) used MCS in testing the disruption resistibility of supply chain networks. Alvarado-Vargas and Kelley (2019) as well as Lei and MacKenzie (2019) used MCS for generating uncertainty conditions and scenarios while analysing the risks in regional and global supply chains.

Samson and Gloet (2018) used MCS for evaluating alternative supply chain designs considering uncertain quantities such as cost, service level, quality, and delivery reliability. Mönch et al. (2017) utilised MCS for strategic supply chain network design and simulation in the semiconductor manufacturing industry. Diaz and Marsillac (2016) used MCS for assessing performance and extent of commitment to strategic remanufacturing operations of a supply chain. Mangla et al. (2014) used MCS for evaluating the impacts of delay and disruption risks on management of green supply chains. Dotoli et al. (2014) used a combination of cross-efficiency DEA and MCS for handling the supplier selection problem under uncertainty. Belvárdi et al. (2012) have utilised MCS with sensitivity analysis for optimising supply chains for handling the stochastic nature of the processes and visualising the relationships among decision variables and performance indicators. Cáceres-Cruz et al. (2012) combined MCS with heuristics to solve a single-period inventory routing problem having demand uncertainty. Klug (2011) and Zhang et al. (2011) used MCS for container demand planning and production planning in an automotive supply chain, respectively. Huang et al. (2010) presented an MCS inventory model for investigating the effect of product substitution on profit and inventory level.

Discrete Event Simulation Models

Discrete event simulation models refer to those simulation models utilised in analysing and predicting the behaviour of supply chain systems that can be broken down into groups of logically independent processes which autonomously evolve over time (Birta and Arbez 2019). Carvalho et al. (2012) presented a simulation study for evaluating various scenarios in order to improve supply chain resilience and understand the effect of mitigation strategies on performance of supply chain entities. Bottani and Montanari (2010) developed a discrete event simulation (DES) model for assessing the 30 supply chain configurations on the bullwhip effect and total supply chain costs in a fast-moving consumer goods supply chain. Jayant et al. (2014) presented a DES model which enables the user to analyse the performance of reverse logistics networks for a company that manufactures commercial acid batteries, thereby providing a better understanding of interrelationships between parties in the network. Yoo et al. (2010) proposed a DES model and hybrid algorithm, which combines nested partitioning with optimal computing budget allocation methods, for optimising the efficiency of supply chains. Patil et al. (2011) proposed a DES approach for planning and control of inventory throughout the multi-echelon supply chain from suppliers to consumers.

Sharma et al. (2019) designed a simulation-based production and distribution multi-echelon supply chain network for gear shop manufacturing in order to determine effective resource utilization and improve productivity of the existing network. Chan and Prakash (2012) developed DES models for analysing the effect of lateral collaboration on performance measures such as total supply chain costs. Blanco et al. (2011) developed a DES model for investigating the interrelation between non-linear supply chain phenomena such as uncertainty, congestion, waste, vulnerability, and the bullwhip effect. Mousavi et al. (2019) combined discrete event and agent-based simulation modelling for investigating the internal nervousness of demand fulfilment in a semiconductor supply chain which is as a result of uncertainties in the network. Di Febbraro et al. (2016) developed a DES model for optimising supply chains considering intermodal freight transportation operations dynamics. Von Cube et al. (2016) proposed a DES model for monetarily quantifying risks irrespective of depth of information, thereby allowing the model to be suitable for a wide variety of use-cases. Ali et al. (2020a) utilised DES for investigating the effect of lead time uncertainty on the bullwhip effect in a multi-product, multi-echelon decentralised and centralised supply chain. Vieira et al. (2020) and Vieira et al. (2019) developed DES models for aiding decision-making by testing various supply chain risk and disruption scenarios. Rachih et al. (2019) utilised DES for evaluating the performance of a supply chain system by determining the impact of inventory level on costs. Rabe et al. (2016) presented a DES model for collaborative route planning in supply chains in order to reduce transportation distance. Rabe et al. (2015) utilised DES for strategically designing supply chain distribution for minimisation of emissions and costs, while improving service level. Miranzadeh et al. (2015) utilised DES for simulating a three-echelon supply chain aiming to determine the echelon having the longest waiting time and number of requests. Nasab et al. (2014) proposed a DES model for handling the facility location problem in a three-echelon supply chain with stochastic demand.

System Dynamics Simulation Models

System dynamics simulation models refer to those simulation models that are used in studying manufacturing supply chains by exploring the behaviour of these supply chains over a particular period and evaluating the structure of supply chain elements and their interactions, including causal relationships, reaction delays, feedback loops, and environmental influences (Mutanov et al. 2020). The system dynamics simulation (SDS) model developed by Mutanov et al. (2020) was utilised in evaluating measures of consumer satisfaction and improving the distribution logistics processes of manufacturing supply chains. Sinha et al. (2020) developed an SDS model for aiding policy experimentation in manufacturing supply chains by evaluating the impact of demand-side and supply-side incentives. Alamerew and Brissaud (2020) used an SDS model to optimise a manufacturing supply chain considering dynamics of cost, revenue, as well as strategic decisions and regulatory decisions for a reverse supply chain. Yan and Liu (2017) utilised SDS for investigating the impact of single, double, triple, and four chain inventory transhipment models on average stock level, supply chain stability, average customer requirement, and average customer satisfaction of manufacturing supply chains. Langroodi and Amiri (2016) developed an SDS model for choosing the appropriate region for order placement within a manufacturing supply chain in order to minimise the cost of order placement and product shipment within the supply chain.

Some researchers have applied SDS models to optimise inventory replenishment in manufacturing supply chains experiencing disruptions, in order to reduce annual total logistics costs (Kiisler and Hilmola 2020; Abdullah et al. 2019; Botha et al. 2017; Georgiadis 2013; Patel et al. 2010). Sayyadi and Awasthi (2018) utilised SDS for evaluating various sustainable transport policies against criteria such as congestion level, fuel consumption, and emission in the transportation system of manufacturing supply chains. Alglawe et al. (2017) applied SDS in analysing the effect of cost of quality and opportunity cost on an automobile manufacturing supply chain in order to derive a general relationship between cost of quality factors and quality level. Mehrjoo and Pasek (2015) proposed an SDS model for analysing the behaviour and relationships of manufacturing supply chains, quantifying the risks associated with the products in the supply chain and determining their expected value and probabilities of losses. Sadeghiamirshahidi et al. (2014) developed an SDS model for improving the efficiency of manufacturing supply chains by studying the production rate, inventory levels, and backlog orders of the supply chain, under different operational conditions such as fixed and varied capacity policies and comparing the supply chain efficiency, under these conditions, in terms of total cost. Similarly, Wang and Murata (2011) proposed an SDS model for evaluating various capacity planning policies for remanufacturing facilities in closed-loop manufacturing supply chains. Lehr et al. (2013) developed an SDS model which allows an original equipment manufacturer to analyse different value recovery strategies for business-to-business products in a closed-loop manufacturing supply chain setting.

Hybrid Models

A good number of articles presented a hybrid framework for manufacturing supply chain optimisation. These frameworks are usually a combination of any of the mathematical or simulation modelling techniques.

Smew et al. (2013) presented a hybrid framework combining multi-objective optimisation and DES modelling for accurately evaluating the suitability of several production control strategies to the supply chain system, aiming to maximise customer service level and minimise work-in-process. Dai and Zheng (2015) proposed a hybrid framework that integrates MCS, embedded hybrid genetic algorithm, fuzzy programming, and chance-constrained programming approaches for profit maximisation and computational time minimisation in a multi-period, multi-product, multi-echelon, closed-loop supply chain under uncertainty. Memari et al. (2013) combined the use of Arena simulation software with MILP to evaluate and select the best network configuration of a supply chain considering cost of transportation and time of transportation as the performance criteria. Similarly, Senyigit and Soylemez (2012) proposed a framework which utilised MILP and discrete event simulation for solving the lot sizing with supplier selection problem in multi-echelon, multi-product supply chain network experiencing stochastic demand. Shukla et al. (2010) developed a hybrid approach composing of simulation, Taguchi method, multiple non-linear regression analysis and psychoclonal algorithm for handling the complications encountered during dynamic interactions between multi-facilities and multi-locations in a supply chain. Yazdekhasti and Mehrjardi (2017) presented a hybrid procedure for optimizing a warranty two-echelon distribution network, composing of MCS for simulating random failures and obtaining the optimal solutions to the nonlinear programming formulation using the branch and bound algorithm.

Some researchers have combined mathematical and simulation-based optimisation for planning and maximising profit of multi-period, multi-echelon, and multi-product supply chain networks (Chiadamrong and Piyathanavong 2017; Ji and Chiadamrong 2019; Pires et al. 2018; Sitek et al. 2014). Salem and Haouari (2016) developed a hybrid simulation-optimisation framework for studying a three-echelon stochastic supply chain network having uncertain demand and supply, aiming to minimise total cost. Moghaddam (2015) presented a hybrid simulation-optimisation procedure combining a multi-objective optimisation model with MCS for best supplier selection, optimal parts, and products configuration of manufacturing and refurbishing facilities in a closed-loop supply chain network. Mula et al. (2013) proposed a hybrid framework that combines fuzzy multi-objective programming with SDS, aiming to find the optimal number of truck shipments and inventory level for a supply chain. Nikolopoulou and Ierapetritou (2012) developed a hybrid approach which combines MILP and ABS modelling in order to provide a realistic representation of the supply chain network, aiming to minimise total costs subject to capacity and inventory constraints. Similarly, Venkatesan and Kumanan (2011) presented a hybrid optimisation and simulation approach for minimising total cost, maximising the reliability of supplier delivery using the multi-objective optimisation model and evaluation of the robustness of sourcing strategies considering price, demand risks, and exchange rate using a DES model of the supply chain network. Kiuchi et al. (2020) proposed a Bayesian optimisation approach together with an agent-based supply chain simulator for handling the constrained multi-echelon inventory optimisation problem. Drakaki and Tzionas (2015) combined Coloured Petri nets and agent-based control system for evaluating performance of warehouses in a supply chain.

Some researchers have utilised hybrid modelling approaches which combined MILP and DES models for integrated production scheduling and transportation within supply chains (Frazzon et al. 2016, 2017; Sel and Bilgen 2014). Aqlan and Lam (2016) proposed an optimisation-simulation approach combining multi-objective optimisation and DES modelling for aiding decision makers in selecting best risk mitigation strategies and conducting customer orders and inventory allocation. Kabirian et al. (2013) utilised a hybrid approach composing of LP and DES models for optimising raw materials ordering policies, finished goods inventory, product manufacturing capacity, and prices. Orji and Liu (2018) combined fuzzy modelling and SDS for investigating the effect of the dynamic behaviour of the key drivers of lean supply chain management on the sustainable performance of manufacturing supply chains. Poornikoo and Qureshi (2019) combined fuzzy modelling with SDS for decreasing the bullwhip effect in single-product, multi-echelon, multi-period manufacturing supply chains. Aslam et al. (2014) combined multi-objective optimisation with SDS for minimising total inventory, backlog costs, and demand fluctuations in manufacturing supply chains.

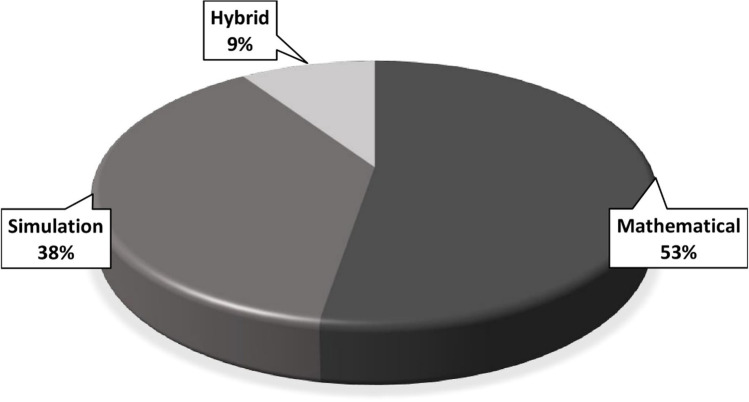
Figure 3 displays the percentage of reviewed articles that utilised either mathematical, simulation, or hybrid models for improving manufacturing supply chains. From Fig. 3, mathematical models, constituting 53% of articles reviewed, have been used the most for improving manufacturing supply chains, followed by simulation models and hybrid models which constitute 38% and 9%, respectively.

Fig. 3.

Percentage of reviewed articles that utilised either mathematical, simulation, or hybrid models for improving manufacturing supply chains

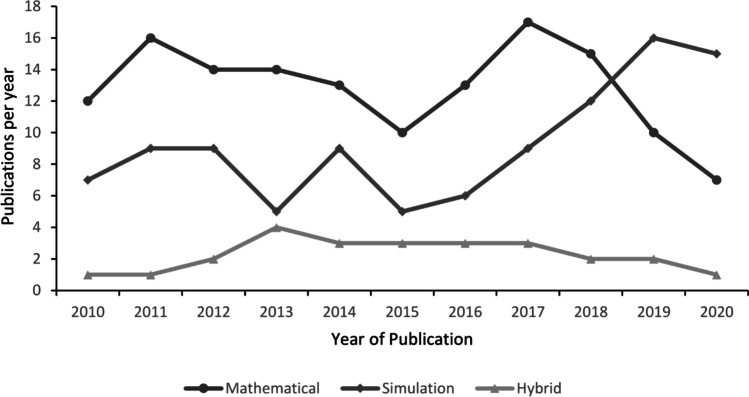
Figure 4 is a line chart that shows the evolution of manufacturing supply chain models from 2010 to 2020. From Fig. 4, there is an increasing trend in the usage of simulation and hybrid models. This upward trend can be explained by the fact that simulation and hybrid models tend to handle stochastic and uncertain data better than mathematical models, which perform better with deterministic data.

Fig. 4.

Evolution of manufacturing supply chain models from 2010 to 2020

Figure 5 is a stacked bar chart that shows the total quantity of manufacturing supply chain modelling publications per year from 2010 to 2020. Figure 5 supports the fact that mathematical models have been used the most for improving manufacturing supply chains.

Fig. 5.

Total quantity of manufacturing supply chain modelling publications per year from 2010 to 2020

Table 1 shows the classification and subcategories of articles based on the optimisation technique utilised. Articles which are cited in more than one sub-category utilise a combination of the modelling techniques of those sub-categories.

Table 1.

Classification of articles based on optimisation technique utilised

Technique	Category	Articles
Mathematical	Linear	Dondo et al. (2011), Melo et al. (2011), Naraharisetti and Karimi (2010), Kunnumkal and Topaloglu (2011), Sitek and Wikarek (2015), Li et al. (2011), Ouhimmou et al. (2019), Duong and Bui (2018), Cintron et al. (2010), Sadeghi et al. (2020), Arampantzi et al. (2018), Pourjavad and Mayorga (2018), Kannan et al. (2010), Nallusamy et al. (2018), Cortinhal et al. (2019), Khalifehzadeh and Fakhrzad (2019), Aminzadegan et al. (2019), Pant et al. (2018), Pedram et al. (2017), Tóth et al. (2017), Safaei et al. (2017), Aalaei and Davoudpour (2017), Özceylan et al. (2017), Chatzikontidou et al. (2017), Prakash et al. (2017), Taxakis and Papadopoulos (2016), Lalmazloumian et al. (2013), Altmann (2014), Hashemi et al. (2014), Nasiri et al. (2014), Amin and Zhang (2014), Özkır and Başlıgıl (2012), Paksoy et al. (2011), Shukla et al. (2011), Sasikumar and Haq (2011), Longinidis and Georgiadis (2011), Zhang et al. (2010), Wang et al. (2011), Wu (2010)
	Nonlinear	Nasiri et al. (2010), Kaur and Singh (2018), Benyoucef et al. (2013), Diabat et al. (2011), Xu et al. (2020), Göksu et al. (2015), Spiegler et al. (2016), Ghasemy (2019), Manupati et al. (2019), Manupati et al. (2018), Aminzadegan et al. (2019), Amirtaheri et al. (2017), Hariga et al. (2017), Taxakis and Papadopoulos (2016), Zhao et al. (2016), Esmaeilikia et al. (2014), Al-Salem et al. (2016), Ma et al. (2016), Yildiz et al. (2015), Sarrafha et al. (2015), Petridis (2013), Pasandideh et al. (2015), Nasiri et al. (2014), Özceylan, and Paksoy (2013), Amin and Zhang (2013), Fahimnia et al. (2011), Taleizadeh et al. (2011), Kamali et al. (2011)
	Stochastic	Zanjani and Nourelfath (2014), Baghalian et al. (2013), Azad and Davoudpour (2012), Zeballos et al. (2014), Ahmadi and Amin (2019), Soleimani et al. (2013), Nagar et al. (2012), Amin and Zhang (2013), Feng et al. (2012), Cardona-Valdés et al. (2011), Sarkar and Giri (2018), Tolooie et al. (2020), Jeihoonian et al. (2017)
	Fuzzy	Kocamaz et al. (2016), Jindal et al. (2015), Ali et al. (2020b), Pourmehdi et al. (2020), Badhotiya et al. (2019), Nemati and Alavidoost (2018), Darbari et al. (2017), Farrokh et al. (2018), Wu et al. (2018), Kumar et al., (2016), Jindal and Sangwan (2013) , Dai and Li (2017), Dotoli et al. (2016), Bai and Liu (2014), Gholamian et al. (2015), Talaei et al. (2016), Subulan et al. (2015), Alimoradi et al. (2014), Ramezani et al. (2014), Özceylan, and Paksoy (2013), Pishvaee and Torabi (2010), Tabrizi and Razmi (2013), Taran and Roghanian (2013), Vahdani et al. (2013), Paksoy and Pehlivan (2012), Shaw et al. (2012), Amin and Zhang (2012), Peidro et al. (2012), Mula et al. (2010b), Lee et al. (2012), Pathak and Mondal (2012), Haleh and Hamidi (2011), Peidro et al. (2010), Bilgen (2010)
	Multi-objective	Ivanov et al. (2013), Das and Lashkari (2015), Banyai et al. (2014), Cakici et al. (2012), Rafiei et al. (2018), Vafaei et al. (2020), Yadav et al. (2018), Hiremath et al. (2012), Abdolazimi et al. (2020), Ali et al. (2020b), Pourmehdi et al. (2020), Badhotiya et al. (2019), Manupati et al. (2018), Nemati and Alavidoost (2018), Gholami et al. (2019), Ahmadi and Amin (2019), Jabbarzadeh et al. (2018), Vafaeenezhad et al. (2019), Arampantzi and Minis (2017), Sahebjamnia et al. (2018), Kumar et al., (2016), Kadambala et al. (2017), Trivedi et al. (2017), Jindal and Sangwan (2013), Dai and Li (2017), Chen et al. (2017), Amin et al. (2017), Ma et al. (2016), Jamili et al. (2016), Yildiz et al. (2015), Entezaminia et al. (2016), Sarrafha et al. (2015), Subulan et al. (2015), Pasandideh et al. (2015), Ramezani et al. (2014), Nagar et al. (2012), Özceylan and Paksoy (2013), Jakhar (2014), Taran and Roghanian (2013), Vahdani et al. (2013), Pazhani et al. (2013), Shaw et al. (2012), Amin and Zhang (2012), Peidro et al. (2012), Lee et al. (2012), Venkatesan and Kumanan (2012), Al-e-hashem et al. (2011), Haleh and Hamidi (2011), Cardona-Valdés et al. (2011), Kamali et al. (2011), Pishvaee and Torabi (2010), Ramudhin et al. (2010)
Simulation	Agent-based	Mizgier et al. (2012), Giannakis and Louis (2011), Pu et al. (2018), Lohmer et al. (2020), Dulam et al. (2020), Gold et al. (2020), Papakostas et al. (2020), Sakai et al. (2020), Li and Epureanu (2020), Hajmohammad and Shevchenko (2020), Terrada et al. (2020), Haddad et al. (2019), Sergeyev and Lychkina (2019), Drakaki et al. (2019), Zheng et al. (2019), Long (2018), Rosales et al. (2018), Kessentini et al. (2018), Rouzafzoon and Helo (2018), Ribino et al. (2017), Li et al. (2018), Blos et al. (2018), Ma et al. (2017), Serrano-Hernandez et al. (2018), Ponte et al. (2017), Ballouki et al. (2017), Alho et al. (2017), Okada et al. (2015), Di Febbraro et al. (2016), Becker et al. (2016), Seck et al. (2015), Long and Zhang (2014), Blos and Miyagi (2014), Tang and Pan (2014), Hernández et al. (2013), Medini and Rabénasolo (2014), Chinh et al. (2013), Wu et al. (2013), Saberi et al. (2012), Holmgren et al. (2012), Li and Chan (2012), Amini et al. (2012), Böhnlein et al. (2011), Nair and Vidal (2011), Mustapha et al. (2010), Roorda et al. (2010), Kim et al. (2010), Wang (2010), Golroudbary et al. (2019), Aghaie and Heidary (2018), Pereira et al. (2018), Zhou et al. (2015)
	Monte Carlo	Olson and Wu (2011), Tao et al. (2019), Thomas and Mahanty (2020), Ozkan and Kilic (2019), Mikhail et al. (2019), Lei and MacKenzie (2019), Alvarado-Vargas and Kelley (2019), Samson and Gloet (2018), Mönch et al. (2017), Diaz and Marsillac (2016), Mangla et al. (2014), Dotoli et al. (2014), Belvárdi et al. (2012), Cáceres-Cruz et al. (2012), Klug (2011), Zhang et al. (2011), Huang et al. (2010)
	Discrete event	Carvalho et al. (2012), Bottani and Montanari (2010),Jayant et al. (2014), Yoo et al. (2010), Patil et al. (2011), Sharma et al. (2019), Chan and Prakash (2012), Blanco et al. (2011), Mousavi et al. (2019), Von Cube et al. (2016), Ali et al. (2020a), Vieira et al. (2020), Vieira et al. (2019), Rachih et al. (2019), Rabe et al. (2016), Rabe et al. (2015), Miranzadeh et al. (2015), Nasab et al. (2014)
	System dynamics	Golroudbary et al. (2019), Mutanov et al. (2020), Sinha et al. (2020), Alamerew and Brissaud (2020), Kiisler and Hilmola (2020), Sayyadi and Awasthi (2018), Alglawe et al. (2017), Abdullah et al. (2019), Yan and Liu (2017), Botha et al. (2017) , Langroodi and Amiri (2016), Mehrjoo and Pasek (2015), Sadeghiamirshahidi et al. (2014), Lehr et al. (2013), Georgiadis (2013), Wang and Murata (2011), Patel et al. (2010)
Hybrid	Mathematical-simulation	Smew et al. (2013), Dai and Zheng (2015), Memari et al. (2013), Senyigit and Soylemez (2012), Shukla et al. (2010), Yazdekhasti and Mehrjardi (2017), Salem and Haouari (2016), Moghaddam (2015), Mula et al. (2013), Nikolopoulou and Ierapetritou (2012), Venkatesan and Kumanan (2011), Kiuchi et al. (2020), Drakaki and Tzionas (2015), Aqlan and Lam (2016), Kabirian et al. (2013), Ji and Chiadamrong (2019), Pires et al. (2018), Frazzon et al. (2017), Frazzon et al. (2016), Chiadamrong and Piyathanavong (2017), Sitek et al. (2014), Sel and Bilgen (2014), Orji and Liu (2018), Poornikoo and Qureshi (2019), Aslam et al. (2014)

Table 2 shows a summary of the simulators used within the simulation and hybrid modelling works and the corresponding articles in which they were used. The simulators which have been used for simulation and hybrid modelling are NetLogo, Java Agent Development Framework (JADE), SimMobility, AnyLogic, AgentSpeak, MATLAB, Multiagent Simulation of Networks (MASON), Transportation and Production Agent-based Simulator (TAPAS), VenSim, C programming language, Microsoft Excel, SIMWARE, Arena, Simul8, SIMIO, SimChain, iThink, Powersim, ExtendSim, and Witness.

Table 2.

Summary of simulators used in simulation and hybrid modelling articles

Simulator	Articles
C	Mizgier et al. (2012), Ponte et al. (2017), Shukla et al. (2010),
NetLogo	Gold et al. (2020), Hajmohammad and Shevchenko (2020), Seck et al. (2015, Tang and Pan (2014), Wu et al. (2013), Nair and Vidal (2011), Aghaie and Heidary (2018), Zhou et al. (2015)
JADE	Papakostas et al. (2020), Terrada et al. (2020), Drakaki et al. (2019), Kessentini et al. (2018), Blos et al. (2018), Long and Zhang (2014), Blos and Miyagi (2014), Medini and Rabénasolo (2014), Saberi et al. (2012), Li and Chan (2012), Böhnlein et al. (2011), Nikolopoulou and Ierapetritou (2012)
SimMobility	Sakai et al. (2020), Alho et al. (2017)
AnyLogic	Haddad et al. (2019), Sergeyev and Lychkina (2019), Rouzafzoon and Helo (2018), Li et al. (2018), Serrano-Hernandez et al. (2018), Mustapha et al. (2010), Golroudbary et al. (2019), Pereira et al. (2018), Golroudbary et al. (2019),
AgentSpeak	Ribino et al. (2017)
MATLAB	Di Febbraro et al. (2016), Ozkan and Kilic (2019), Von Cube et al. (2016), Poornikoo and Qureshi (2019),
MASON	Chinh et al. (2013)
TAPAS	Holmgren et al. (2012)
VenSim	Mutanov et al. (2020), Alvarado-Vargas and Kelley (2019), Sinha et al. (2020), Alamerew and Brissaud (2020), Kiisler and Hilmola (2020), Sayyadi and Awasthi (2018), Alglawe et al. (2017), Abdullah et al. (2019), Yan and Liu (2017), Langroodi and Amiri (2016), Mehrjoo and Pasek (2015), Sadeghiamirshahidi et al. (2014), Georgiadis (2013), Patel et al. (2010), Mula et al. (2013), Orji and Liu (2018), Poornikoo and Qureshi (2019), Aslam et al. (2014)
Microsoft Excel	Olson and Wu (2011), Mangla et al. (2014), Klug (2011), Kabirian et al. (2013),
SIMWARE	Belvárdi et al. (2012)
Arena	Carvalho et al. (2012), Jayant et al. (2014), Patil et al. (2011), Sharma et al. (2019), Chan and Prakash (2012), Blanco et al. (2011), Ali et al. (2020a), Rachih et al. (2019), Miranzadeh et al. (2015), Nasab et al. (2014), Memari et al. (2013), Senyigit and Soylemez (2012), Aqlan and Lam (2016), Ji and Chiadamrong (2019), Chiadamrong and Piyathanavong (2017), Sel and Bilgen (2014),
Simul8	Bottani and Montanari (2010),
SIMIO	Vieira et al. (2020), Vieira et al. (2019)
SimChain	Rabe et al. (2015),
iThink	Botha et al. (2017), Georgiadis (2013),
Powersim	Georgiadis (2013), Wang and Murata (2011),
ExtendSim	Smew et al. (2013),
Witness	Venkatesan and Kumanan (2011)

Table 3 shows the most prevalent journals for publication of articles on manufacturing supply chain modelling. From Table 2, the most prevalent journal for publication is the International Journal of Production Research constituting a percentage of 11.94% of all papers reviewed.

Table 3.

Most prevalent journal of publication

Journal	Articles	% of total
International Journal of Production Research	32	11.94
Computers & Industrial Engineering	22	8.21
International Journal of Production Economics	16	5.97
Journal of Cleaner Production	10	3.73
European Journal of Operational Research	9	3.36
Expert Systems with Applications	8	2.99
Annals of Operations Research	6	2.24
Journal of Manufacturing Systems	6	2.24
Computers & Operations Research	4	1.49
Procedia CIRP	4	1.49
Journal of Industrial and Production Engineering	4	1.49
International Journal of Logistics Systems and Management	3	1.12
Procedia Engineering	3	1.12
Transportation Research Part E: Logistics and Transportation Review	3	1.12
Computers & Chemical Engineering	3	1.12
Procedia Computer Science	3	1.12
The International Journal of Advanced Manufacturing Technology	3	1.12
International Journal of Management Science and Engineering Management	3	1.12
IFAC-PapersOnline	3	1.12
Simulation Modelling Practice and Theory	3	1.12
Conference Articles	33	12.31
Others (76)	87	32.46
Total	268	100

The values in bold are the total papers reviewed

Conclusions and Future Research Directions

Supply chains facilitate the manufacturing and distribution of products around the world. However, the challenges encountered in manufacturing and distribution have given rise to the need for various attempts at managing and controlling these difficulties. Therefore, researchers have proposed various models in the form of mathematical, simulation, and hybrid models for handling supply chain network disruptions and risks.

This research has provided a review and classification scheme for sustainable manufacturing supply chain models, organising the models into groups, and highlighting the similarities as well as the differences between the models. From the research, the recently developed manufacturing supply chain models can be conveniently classified into mathematical, simulation, and hybrid models. Furthermore, the mathematical models can be grouped by nature, type, and objectives. By nature, the mathematical models can be classified as linear programming (LP), mixed integer linear programming (MILP), nonlinear programming (NLP), or mixed integer nonlinear programming (MINLP) models. By type, the mathematical models can be classified as deterministic and non-deterministic models. The deterministic models are the linear and nonlinear models while the non-deterministic models are the stochastic and fuzzy models. By objectives, the mathematical models can be classified as single objective and multi-objective models. On the other hand, the simulation models can be further broken down into agent-based, discrete event, Monte Carlo, and system dynamics simulation models. The research also showed that though there is a growing trend in the use of simulation and hybrid models, mathematical models have been used more for manufacturing supply chain modelling. The rise in the use of simulation and hybrid models can be explained by the fact that these models tend to handle stochastic and uncertain data better than mathematical models, which perform better with deterministic data.

From the foregoing, based on prior research in manufacturing supply chain modelling, some areas for future research are:

The development of simulation-based multi-echelon supply chain inventory planning models, for evaluating various performance measures such as service level and fill rate, at specific echelons of a supply chain network.

The COVID-19 pandemic is currently causing disruptions in supply chain operations across the world and various researchers are developing models and strategies to aid supply chains cope with these disruptions. Therefore, a comprehensive review of the models that have been developed to aid supply chain managers and analysts cope with supply chain disruptions in the COVID-19 era is necessary.

Also, a study that compares the efficacy of various sub-categories of supply chain modelling techniques is required. This will enable researchers determine the most effective sub-category technique for supply chain optimisation based on each major classification described in this study.

Additionally, there is the need for a recent classification and review of existing supply chain models in other areas such as service, construction, waste, pharmaceutical/healthcare, petroleum, energy, and agricultural supply chains. This is in order to discover the modelling trends and determine the prevalent optimisation techniques in these areas.

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Declarations

Competing Interests

The authors declare no competing interests.