Online Gambling Disorder Questionnaire (OGD-Q): An item r‘esponse theory examination

Highlights

• •Gambling disorder behaviours differ in their diagnostic weight/importance.
• •OGD-Q reliably differentiates between individuals at different trait levels.
• •Salience is indicated as the most representative symptom of problematic gambling.

Abstract

Gambling disorder behaviours, such as one’s preoccupation with gambling and/or mood modification due to gambling, have been proposed to differ in their diagnostic weight/importance, especially when informing diagnostic scales. Such potential differences are imperative to be considered to improve assessment accuracy. The latter is particularly important in the light of the rapidly increasing gambling opportunities offered online. To contribute to this area of knowledge, the current study assessed an online adult community sample (N = 968, M_age = 29.5 years, SD_age = 9.36 years) regarding their responses on the Online Gambling Disorder Questionnaire (OGD-Q). Item response theory (IRT) procedures examined the psychometric properties of the instrument, at both the item and the scale level. Results indicated that the OGD-Q demonstrated good capacity to reliably assess problem gambling and differentiate between individuals at similar levels of the trait, particularly between 1 and 3 SDs above the mean. The findings also showed OGD-Q components/items possess varying discrimination capacities, whilst they also differ in reliability across respondents with different levels of disordered gambling behaviours. Thus, it is supported that consideration is required regarding the differential weighting of one’s item responses in the assessment procedure, taking concurrently into account their severity of disordered gambling behaviours.

1. Introduction

Gambling has become increasingly accessible and novel online gambling platforms are potentially capturing a new generation of young gamblers (King et al., 2020). In addition to traditional offline activities (e.g., casino gambling, in-person agency betting), gamblers are now faced with increased online gambling opportunities like esports and online sports betting, online casinos, smartphone/device games, and loot boxes/crates (i.e., randomised rewards unlocked during video game play, usually by payment; King et al., 2020). In Australia, where the current study is conducted, there are approximately 6.8 million regular gamblers each year, and around 1.1 million are estimated to be at risk of gambling-related problems (Armstrong & Carroll, 2017). Given the high proportion of gambling involvement in Australia (∼25 % of the general population), and the increased access to online gambling activities, accurate assessment of disordered gambling behaviours in the community is crucial (King et al., 2020).

1.1. Gambling disorder

Gambling disorder is defined as problematic and persistent gambling resulting in clinically significant impairment or distress (American Psychiatric Association [APA], 2013). The Diagnostic and Statistical Manual for Mental Disorders, fifth edition (DSM-5; APA, 2013) defines disordered gambling as being a combination of at least four of the following nine criteria in a 12-month period: (1) increased spending to achieve desired excitement; (2) experiences of unpleasant symptoms when attempting to limit gambling behaviour; (3) repeated and unsuccessful attempts to stop or cut down gambling; (4) preoccupation with gambling; (5) gambling when feeling distressed; (6) returning to gamble to recoup previous losses; (7) deception about gambling; (8) compromising or losing relationship, employment or other opportunities because of gambling; and (9) relying on others for financial aid because of gambling losses (APA, 2013). Although chasing losses is likely more idiosyncratic of gambling, most of these criteria align with those defining other forms of addictive behaviours, such as disordered gaming (King et al., 2020). Griffiths (2019) refers to this as the confirmatory approach, which emphasises the importance of shared components when classifying behavioural addictions.

1.2. Components model of addiction

Griffiths (2019) has proposed that in order to distinguish a behavioural addiction from excessive behaviour, one must meet the following criteria, which align with the DSM-5 definition (APA, 2013): salience, mood modification, tolerance, withdrawal symptoms, conflict, and relapse (Griffiths, 2019). Salience refers to the amount of engagement in the behaviour and the extent to which it consumes the individual, e.g., constantly thinking about when they can next gamble (DSM-5 criterion A5); mood modification is the engagement in behaviour to cope with negative feelings, e.g., experiencing a rush, or feeling of escape (A6); tolerance is the amount of the behaviour required to achieve the same effects, e.g., requiring increased gambling to feel the same ‘high’ (A1); withdrawal symptoms include unpleasant feelings and physiological effects when unable to engage in the behaviour, e.g., irritability when attempting to stop gambling (A2); conflict can be intrapsychic or interpersonal, or conflicts with other activities caused by excessive engagement or preoccupation with the activity, e.g., experiencing a loss of control, compromising important relationships or job prospects due to consequences of gambling (A3, A4, A7); and relapse is the typical reverting to excessive engagement in the activity after successful periods of inactivity, e.g., not gambling for some months and then gambling excessively (Griffiths, 2019).

1.3. The online gambling disorder Questionnaire (OGD-Q)

The components model has been used to develop scales measuring a range of behavioural addictions, including gaming, social media, shopping (Griffiths, 2019) and even the proposed construct of food addiction (Kircaburun et al., 2020). Recently, the OGD-Q was developed to capture online gambling disorder in young people, based on current diagnostic criteria and the components model of addiction (González-Cabrera et al., 2020). The 11-item questionnaire uses a 5-point scale for item responses, ranging from 1 (never) to 5 (every day), where higher scores indicate higher level of online gambling behaviour. The scale developers dichotomised responses to be > 3 = “problem” and item scores < 3 to be “no problem”. If a problem exists in 4 or more items in a 12-month period, then “online gambling disorder” is considered established (González-Cabrera et al., 2020).

The OGD-Q, being based on the DSM-5 criteria, presents with high construct validity and can be clinically useful for both prevention and intervention purposes. Specifically, it may be applied as a screening instrument in the community for the identification of individuals at risk or to monitor the progress of treatment in clinical populations via repeated measures (González-Cabrera et al., 2020). For such processes to be effective and reliable, a more specific examination of how the different OGD-Q items perform when assessing problem gambling behaviour, aside of the scale as a whole, could be particularly informative.

1.4. Item response theory

Item response theory (IRT) offers an alternative approach to classical test theory (CTT), which is typically used in scale development and psychometric assessment (Sharp et al., 2012). Whereas CTT relies upon the sum of items to observe the latent trait (in this case one’s level of disordered gambling), IRT can estimate latent trait amount based upon an individual item response (Kircaburun et al., 2020). IRT also provides an item level estimation of reliability by considering latent trait level, item parameters and overall scale reliability, whereas with CTT only the latter would be possible (Kircaburun et al., 2020). Because IRT is based upon individual responses and psychometric properties are not sample-dependent as they are in CTT, they are group invariant and therefore more generalisable (Gomez et al., 2019).

In essence, IRT examines the probability of item endorsement based on latent trait level, item difficulty (β) and item discrimination (α), and displays the logistic regression lines, or item characteristic curve, on a graph defined by those item parameters (i.e., β and α; Zarate et al., 2021). Item difficulty is the level of latent trait when there is a 0.5 median probability of item endorsement, that is, lower β values represent items that are ‘easier’ to endorse and vice versa. Item discrimination refers to the steepness of the regression line, that is, the item’s ability to discriminate between people with varying trait levels in relation to item difficulty (Gomez et al., 2019). IRT can also include an additional parameter, called pseudo-guessing (c), which refers to the probability that individuals low in trait level will endorse items by guessing, e.g., the OGD-Q uses a 5-point rating scale, so there is a 1 in 5 chance that a person would endorse the item randomly, or by ‘guessing’ (Zarate et al., 2021).

1.5. Study aims

Other IRT studies have demonstrated that different components/criteria of behavioural addiction function differently psychometrically when operating as instruments in diagnostic scales, such as in food addiction (Kircaburun et al., 2020), and internet gaming disorder (Gomez et al., 2019), as well as problem gambling (Anselmi et al., 2021, Sharp et al., 2012). However, past IRT studies emphasizing on gambling scales to assess the differential psychometric functioning of disordered gambling criteria/ behaviours invite further investigation due to: a) in some cases exclusively examining adolescent and or specific national populations (e.g. South Africans) and; b) not reporting/examining pseudo-guessing indices (Anselmi et al., 2021, Sharp et al., 2012). Therefore, examining the OGD-Q using and advanced three parametric (3-PL) IRT analysis model seems promising, as it could determine a) which items (i.e., components) are more likely to be endorsed based on differing trait levels; b) which are more reliable or precise at measuring disordered gambling behaviours and; c) how pseudo-guessing effects could differentially effect one’s assessment. This would enable further exploration of item ranking and item selection when it comes to assessing problem gambling across various prevention, diagnostic and intervention settings.

2. Method

2.1. Participants

The current study was part of a larger project investigating addictive behaviours among adults in the community. Following ethics approval from the University Ethics Committee, a sample of 968 participants were recruited via online channels (e.g., email, website, and social media advertising) and word-of-mouth during 2019 and 2020. Participants were aged between 18 and 64 years (M = 29.5, SD = 9.36). The sample included predominantly males (64.3 %) of Caucasian descent (61.5 %), that were single (61.2 %), and employed full time (34.2 %). The random sampling error for a sample of 968 approximated 3 % with a 95 % confidence interval, which is acceptable based upon the literature (Hill, 1998). Research additionally suggests that a sample sized ≥ 750 is adequately powered to accurately estimate all item parameters in a 3-parameter IRT analysis of a 10-item test (Faul et al., 2007, Şahin and Anıl, 2017).

2.2. Measures

The OGD-Q measures gambling behaviour severity based on established diagnostic criteria for gambling disorder (e.g., “Do you feel the need to spend more and more money to get the high you desire?”). The 11-item OGD-Q captures responses using a 5-point Likert-type scale, and in the current study these options were: 1 (never), 2 (once in a while), 3 (sometimes), 4 (often), and 5 (every day). Overall scores range from a possible 11 up to 55, the total score being the sum of all item responses, where a higher score indicates higher level of problem gambling behaviour. The OGD-Q was found to have high internal consistency in the present study (Cronbach’s α = 0.95 and McDonald’s ω = 0.95).

2.3. Statistical analyses

The first step of data analysis was to assess missing values and then perform the IRT analysis. Model fit was assessed using the log likelihood index of fit (de Ayala, 2013); the root-mean-square error of approximation (RMSEA < 0.05 indicates good fit; Hu & Bentler, 1999); and the Bayesian and Akaike information criterion (BIC and AIC, respectively), where smaller values indicate better fit (de Ayala, 2013). Item fit was assessed using the S-χ² statistic, which indicates the amount of likeness between the predicted and observed response frequencies. Poor fit is indicated by a significant p value, which in this case was set at p =.01 due to the test’s inherent sensitivity to large sample size (Stone & Zhang, 2003).

Item performance and reliability were assessed by examining the item characteristic curves (ICC; α, β) and item information function (IIF) respectively, using IRTPRO software (Version 3.1; Cai et al., 2011). Test reliability was likewise assessed by assessing the test information function (TIF), while the overall performance of the OGD-Q was indicated by the test characteristic curve (TCC).

3. Results

The current dataset had between 1 and 6 missing cases for each item but given the sample size (N = 968), the proportion of missing values was well below the recommended threshold of 5 % (Schafer, 1999). A Little’s missing completely at random (MCAR) test showed that all missing values were missing completely at random (χ² = 88.112, p =.082).

IRT assumptions were tested before proceeding with the analyses. Firstly, the sample was randomly split in halves and R Studio (Lavaan package; Rosseel, 2012) was used to fit a principal component analysis (PCA) and confirmatory factor analysis (CFA) with both tests showing unidimensionality (see supplementary material). Secondly, local independence was assessed by examining the residual covariance between all different item pairs via the standardised LDχ² statistic, where values < 10 are considered as indication of local independence (Chen & Thissen, 1997). Thirdly, monotonicity was assessed by the ‘monotonous’ increment of OGD scores as latent trait levels increased (i.e. difficulty parameters for successive Likert responses are ordered in all the items; Reeve et al., 2007). Last, before calculating the 3PL graded model (see results below), the 1PL (-2loglikelihood = 7848.81, AIC = 7938.81, BIC = 8158.20), the 2PL (-2loglikelihood = 457303.48, AIC = 457327.48, BIC = 457385.98) and the partial credit (-2loglikelihood = 7917.08, AIC = 8027.08, BIC = 8295.22) models were calculated and indicated lower fit, supporting the 3PL model as the optimum model.

3.1. IRT analyses

The items’ local independence was assessed using the LDχ² statistic in the context of the IRT analysis. This tests the independence of each item’s residuals to ensure they are not related, to rule out any additional latent factors. Among all item pairs, the highest LDχ² value was 4.0, which occurred between items 5 and 8 (see Table 1). This indicated local independence as no values were above the recommended cut-off value of 10 (Chen & Thissen, 1997).

Table 1.

Local independence values by OGD-Q item.

Item	1	2	3	4	5	6	7	8	9	10
1
2	–0.2
3	0.8	–0.1
4	–0.9	0.2	0.1
5	–0.3	–1.4	0.3	0.7
6	–0.2	0.9	0.5	–0.1	–0.6
7	0.5	0.4	1.4	0.6	2.9	3.2
8	–1.2	0.0	1.6	–1.2	4.0	1.4	0.6
9	0.8	2.0	0.4	–0.1	0.8	0.8	0.2	0.4
10	–0.6	–0.9	1.7	0.3	0.2	–0.2	0.5	–0.3	–0.2
11	–0.5	1.2	1.3	1.4	1.4	1.5	0.4	0.5	1.0	0.2

Note: Local independence represented by standardised LD χ^{2 statistic} for each item.

The 3PL model estimation was processed and showed good fit (M₂[8 6 9] = 1139.60; p <.001; χ^{2Loglikelihood} = 7772.77; RMSEA = 0.02; BIC = 8150.91; AIC = 7882.77). At the item level, there were no significant S-χ² statistics (at p <.01), which indicated good fit for all items independently (see Table 2).

Table 2.

3PL IRT item properties and fit statistics for all OGD-Q items.

Item	Component	α		β 1		β2		β3		β4		λ	S-χ2
													Value	df	p
1	Tolerance	2.93	(0.35)	0.90	(0.09)	1.80	(0.19)	2.17	(0.23)	2.90	(0.33)	0.87	52.00	47	0.285
2	Withdrawal	4.71	(0.67)	1.31	(0.13)	1.82	(0.19)	2.18	(0.24)	2.57	(0.30)	0.94	42.49	35	0.179
3	Intrapsychic Conflict	4.33	(0.61)	1.23	(0.12)	1.75	(0.18)	2.18	(0.24)	2.72	(0.33)	0.93	41.27	36	0.251
4	Interpersonal	4.00	(0.58)	1.23	(0.12)	1.68	(0.17)	2.10	(0.23)	2.69	(0.32)	0.92	44.87	43	0.395
5	Salience	3.20	(0.44)	0.87	(0.09)	1.60	(0.16)	2.10	(0.22)	2.79	(0.33)	0.88	59.36	47	0.106
6	Mood Modification	4.03	(0.69)	1.21	(0.12)	1.68	(0.18)	2.01	(0.22)	3.02	(0.35)	0.92	48.67	42	0.222
7	Intrapsychic Conflict	4.29	(0.79)	1.24	(0.12)	1.76	(0.19)	2.13	(0.24)	2.48	(0.30)	0.93	49.37	38	0.102
8	Gambling through behaviours	2.88	(0.38)	0.75	(0.08)	1.52	(0.15)	2.08	(0.22)	2.59	(0.29)	0.86	64.11	52	0.121
9	Deception	4.88	(0.86)	1.27	(0.12)	1.71	(0.18)	2.12	(0.23)	2.50	(0.29)	0.94	46.01	35	0.101
10	Borrowing due to gambling	4.66	(1.12)	1.61	(0.17)	1.98	(0.23)	2.26	(0.27)	2.57	(0.33)	0.94	31.35	29	0.348
11	Salience	6.31	(1.15)	1.42	(0.13)	1.84	(0.19)	2.18	(0.23)	2.46	(0.28)	0.97	34.24	28	0.193

Note: Standard errors are in parentheses. α = item discrimination, i.e., the ability of an item to discriminate between varying levels of the underlying trait (θ), gambling behaviour. β = item difficulty, i.e., the level of gambling behaviour intensity, where subsequent response rates are more likely to be increasingly positive. λ = item loadings, i.e., the amount of variance of an item explained by the latent factor. S-χ² = the item fit statistic for each item, which behaves similarly to χ² in CFA, with non-significant rates showing no deviation of the item modelling from the data.

3.2. Item discrimination

As shown in Table 2, factor loadings were high and ranged between λ = 0.86 (item 8) and λ = 0.97 (item 11; Thompson, 2004), while the discrimination values ranged between α = 2.88 (item 8) and α = 6.31 (item 11). Although items differed in discrimination strength, they overall indicated very high discrimination capacity (Baker, 2001). From highest discrimination (α) and loading (λ) values to lowest, the items were ordered as such: item 11 (“salience”); item 9 (related to lying); item 2 (“withdrawal”); item 10 (related to borrowing); item 3 (“intrapsychic conflict”); item 7 (“intrapsychic conflict”); item 6 (“mood modification”); item 4 (“interpersonal conflict”); item 5 (“salience”); item 1 (“tolerance”); and item 8 (related to chasing losses; see Table 2).

3.3. Item difficulty

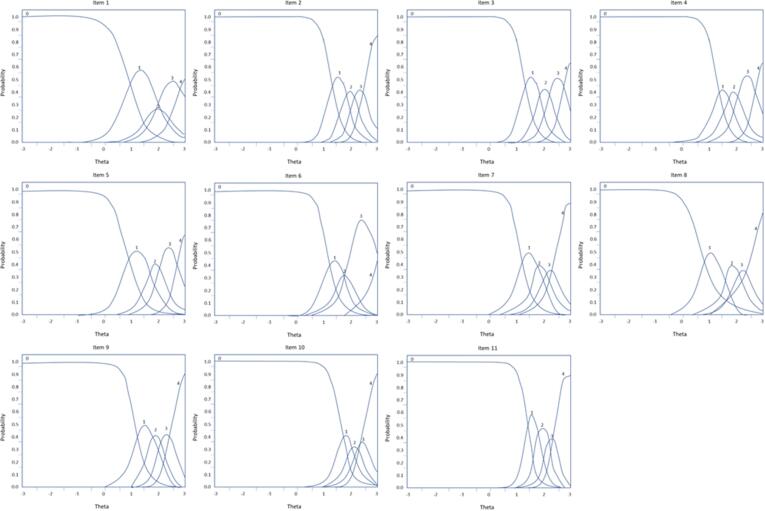
For item difficulty, items varied with each other and also across their respective thresholds (or response categories; see Table 2). Item difficulty refers to the point at which the item response curves intersect, indicating the likelihood of a specific response based on one’s trait level. As shown in Fig. 1, for a trait (θ) score below 0.90, there was a 46 % chance that the response “never” would be endorsed for item 1 (e.g., “Do you feel the need to spend more and more money to get the high you desire?”), indicating no problematic gambling behaviour.

Fig. 1.

OGD-Q item characteristic curves. Note Fig. 1: Theta = latent trait level. Probability = the likelihood of item endorsement based on difficulty and latent trait level.

At the first threshold, the descending sequence of items was: item 10; item 11 (“salience”); item 2 (“withdrawal”); item 9 (lying); item 7 (“intrapsychic conflict”); item 3 (“intrapsychic conflict”); item 4 (“interpersonal conflict”); item 6 (“mood modification”); item 1 (“tolerance”); item 5 (“salience”); and item 8 (see Table 2). At the last threshold, the descending sequence of items was item 11 (“salience”); item 7 (“intrapsychic conflict”); item 9 (lying); item 2 (“withdrawal”); item 10 (borrowing); item 8 (chasing losses); item 4 (“interpersonal conflict”); item 3 (intrapsychic conflict”); item 5 (“salience”); item 1 (“tolerance”); and item 6 (“mood modification”). Interestingly, endorsing more difficult categories (always vs almost always) required higher latent trait levels. This indicates that all items showed appropriate functionality to assess OGD-Q levels.

3.4. Pseudo-guessing

The pseudo-guessing parameters showed that as the item difficulty and latent trait level increased, guessing values decreased, indicating lower probability of endorsing a more difficult response with lower level of trait (see Table 3). That is, someone with a low level of problem gambling behaviour would have a lower chance of responding in the way that someone with a higher trait level would. At the first threshold, items were ordered from highest pseudo-guessing probability to lowest as such: item 8 (chasing losses), item 1 (“tolerance”), item 5 (“salience”), item 6 (“mood modification”), item 4 (“interpersonal conflict”), item 3 (“intrapsychic conflict”), item 7 (“intrapsychic conflict”), item 2 (“withdrawal”), item 9 (lying), item 10 (borrowing), and item 11 (“salience”). Although there were some slight variations in pseudo-guessing values across the thresholds, they mostly followed the same pattern, apart from item 6 (“mood modification”), which showed a marked decrease in pseudo-guessing probability between thresholds 3 (–8.09) and 4 (–12.16).

Table 3.

3PL IRT pseudo-guessing parameters for all OGD-Q items.

Item	Component	α		c1		c2		c3		c4
1	Tolerance	2.93	(0.35)	–2.64	(0.21)	–5.27	(0.32)	–6.35	(0.38)	–8.50	(0.59)
2	Withdrawal	4.71	(0.67)	–6.18	(0.55)	–8.55	(0.69)	–10.28	(0.81)	–12.08	(0.98)
3	Intrapsychic Conflict	4.33	(0.61)	–5.32	(0.44)	–7.55	(0.56)	–9.44	(0.67)	–11.79	(0.91)
4	Interpersonal	4.00	(0.58)	–4.93	(0.41)	–6.73	(0.50)	–8.41	(0.60)	–10.79	(0.81)
5	Salience	3.20	(0.44)	–2.80	(0.23)	–5.13	(0.33)	–6.72	(0.41)	–8.92	(0.61)
6	Mood Modification	4.03	(0.69)	–4.89	(0.47)	–6.77	(0.58)	–8.09	(0.66)	–12.16	(1.28)
7	Intrapsychic Conflict	4.29	(0.79)	–5.32	(0.57)	–7.54	(0.72)	–9.14	(0.84)	–10.62	(0.96)
8	Gambling through behaviours	2.88	(0.38)	–2.17	(0.19)	–4.37	(0.28)	–5.99	(0.35)	–7.46	(0.46)
9	Deception	4.88	(0.86)	–6.21	(0.66)	–8.32	(0.79)	–10.36	(0.95)	–12.20	(1.11)
10	Borrowing due to gambling	4.66	(1.12)	–7.50	(1.12)	–9.22	(1.29)	–10.50	(1.44)	–11.98	(1.61)
11	Salience	6.31	(1.15)	–8.93	(1.03)	–11.63	(1.26)	–13.74	(1.45)	–15.50	(1.61)

Note: Standard errors are in parentheses. α = item discrimination, i.e., the ability of an item to discriminate between varying levels of the underlying trait (θ), problem gambling behaviour. c = pseudo-guessing parameter, i.e., decreasing probability of response based on lower latent trait level.

Overall, the OGD-Q items were good at discriminating between responses based on underlying trait level (problem gambling behaviour), as shown by the steepness of the ICC slopes. Higher trait level also reflected increased probability for degree of endorsement as well as lower probability of pseudo-guessing when considered with item discrimination. The results indicated that the items had good capacity for measuring varying levels of problematic gambling severity, and that the items function differently when doing so (see Fig. 1).

3.5. Item information function

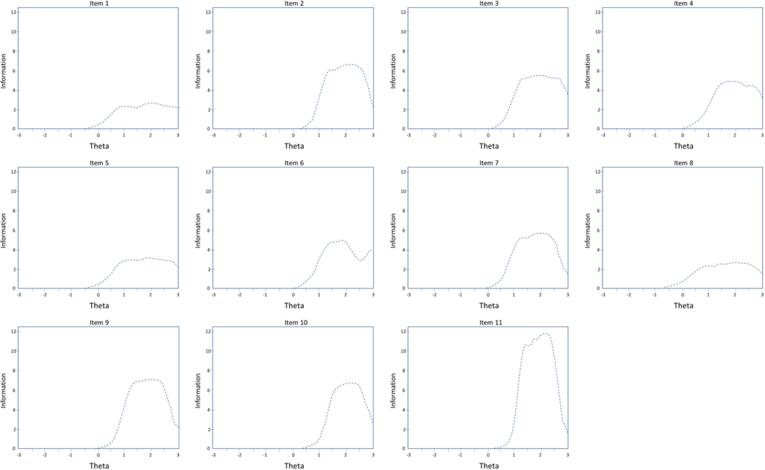
The item information function (IIF) offers a measure of reliability and precision of each scale item, represented by a curve that is shaped by the item’s difficulty and discrimination, spanning a continuum of latent trait level. As shown in Fig. 2, the current data showed differences in reliability across the items, with item information ranging between approximately 0.5 and 3 SDs above the mean. Item 11 (“salience”) had the highest amount of information between around 1.2 and 2.8 SDs above the mean, demonstrating that it offered better precision at predicting responses based on higher trait level, as well as differentiating between response options when trait level is similar. Items 9 and 10 both had relatively high information, peaking at around 1 to 3 SDs above the mean. Items 2 (“withdrawal”), 7, 3 (both “intrapsychic conflict”), 4 (“interpersonal conflict”) and 6 (“mood modification”), all showed moderately high information. Items 5 (“salience”), 1 (“tolerance”) and 8 (chasing losses) all showed lower information, ranging between approximately 1 SD below to 3 SDs above the mean and are demonstrated by considerably flatter item information curves that are lower than those of other items (see Fig. 2).

Fig. 2.

OGD-Q item information function curves. Note Fig. 3: Theta = latent trait level. Information = the precision of an item presented as a curve that is shaped by its difficulty and discrimination across latent trait level.

3.6. Overall scale performance

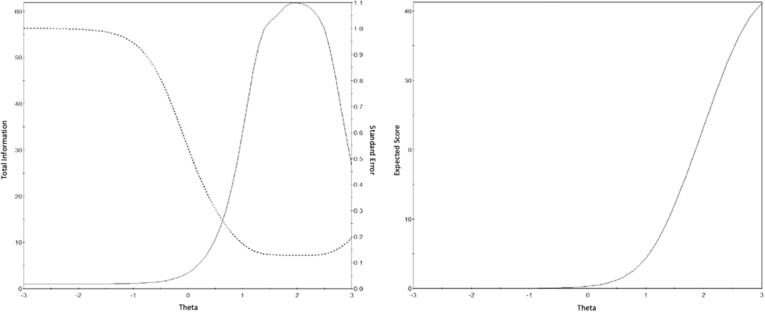
Overall, the scale provided the most information when scores were approximately 0.8 to 3 SDs above the mean, as shown by the test information curve (TIC) in Fig. 3A. Test information is the inverse of its variance, thus with increased information there is less error and overall greater test precision. The test characteristic curve (TCC) showed a sharp, monotonic, incline in the problem gambling behaviour trait as scores increased, particularly between approximately 10 and 40 (see Fig. 3b). The TIC and TCC indicate that the OGD-Q is a reliable instrument for assessing problem gambling behaviour especially for those above the mean (although may not differentiate effectively varying levels of not at risk gambling behaviours; those below the mean).

Fig. 3.

OGD-Q test information curve (a) and test characteristic curve (b). Note Figure 4: Theta = latent trait level. Information = the overall precision of the scale presented as a solid curve that is shaped by its difficulty and discrimination across latent trait level. Standard error, the inverse of information variance, is represented by a broken curve. Expected score is the expected overall score on the OGD-Q based on latent trait level.

4. Discussion

The aim of the current study was to assess the psychometric properties of the OGD-Q and to determine if its items function differently in disordered gambling assessment. Using a large sample (N = 968) and advanced IRT procedures, OGD-Q item discrimination, difficulty, pseudo-guessing, and reliability parameters were investigated. The results showed that the OGD-Q adequately captured a measure of the unidimensional problem gambling construct. The IRT showed that the OGD-Q items varied across the psychometric parameters in relation to the level of problem gambling behaviour, indicating that some items are more capable of capturing a measure of problem gambling than others, and that a specific order of items could be considered.

The overall reliability of the scale was better at higher levels of problem gambling behaviour (at around 2 SDs above the mean) but was not as precise at measuring problem gambling among those at lower trait levels (around and below the mean). This may be important when considering the use of the OGD-Q as a screening tool in the general population with lower trait levels, or where different components exist differently in specific gambling activities (e.g., loot boxes in video games, or online casinos).

4.1. Item discrimination

The OGD-Q items were psychometrically sound, with high difficulty values (>2 SDs from the mean) and sufficient discrimination values. Most of the items had discrimination values ranging between 4 and 5, indicating they capably differentiate between those with different trait levels. However, item 11 (“salience”) had considerably higher discrimination capacity (α = 6.31), which indicates that it is especially robust at differentiating between individual disordered gambling behaviours. In a 2PL IRT analysis of the SOGS-RA, the highest performing item of the scale was arguably similar to OGD-Q item 11, (e.g., SOGS-RA Item 11: “In the past 12 months, have you ever skipped or been absent from school or work due to betting activities?”; λ = 0.82, α = 3.70, β = 1.97; Anselmi et al., 2021). Although no DSM-5 criterion directly relates to item 11 (as proposed by González-Cabrera et al.), the relevant ICD-11 criterion, “Increasing priority given to gambling to the extent that gambling takes precedence over other life interests and daily activities” (World Health Organization, 2019) indicates that salience, or increased priority, is an important characteristic of disordered gambling. Interestingly, the other OGD-Q “salience” item (item 5) did not perform as well (α = 3.20) as item 11, nor most other items in the scale.

Item 1 (“tolerance”) was the second-lowest performing item of the OGD-Q in the present study, with a discrimination value of 2.93 (β values ranged between 0.9 and 2.90, λ = 0.87). During development of the OGD-Q, researchers found item 1 (“tolerance”) to have the lowest item-total correlation (r = 0.62) and factor loading (λ = 0.63) of all the items (González-Cabrera et al., 2020). However, previous IRT research found a similar item on the PGSI related to tolerance (e.g., “Did you need to gamble with larger amounts of money to get the same feeling of excitement?”) performed moderately well compared to other items (α = 1.52; Sharp et al., 2012).

Item 8 (chasing losses) performed the lowest among all OGD-Q items, with a discrimination value of 2.88. During the scale development, researchers found item 8 had strong item-total correlation (r = 0.72) and good factor loading (λ = 0.73; González-Cabrera et al., 2020). The current findings are in line with the Sharp et al. (2012) IRT of the PGSI, which showed that chasing one’s losses had the lowest discriminating ability compared to other items (α = 1.07). However, the SOGS-RA (which did not have a similar “tolerance” item), was found to perform moderately well at discriminating between individual responses with a yes/no response format when participants were asked about chasing their losses (λ = 0.65, α = 1.61; Anselmi et al., 2021).

When measuring problem gambling, tolerance and chasing losses may not be as important, particularly when differentiating between people at similar trait level. The items that relate to increasing demands from gambling, such as prioritising gambling over important areas of functioning, withdrawal symptoms, and lack of control, appear to be better at discriminating between individuals with differing levels of the problem gambling trait and could therefore be prioritised when assessing problem gambling.

4.2. Item difficulty

Threshold 1 (once in a while). The results indicated variation in the difficulty of the OGD-Q items, meaning that there was a difference in how much of the latent problem gambling trait was needed to endorse a response option (i.e., higher trait = more frequent gambling behaviour). At the first threshold, the results indicate that people lower in the problem gambling trait would be less likely to endorse items 8 and 5 than items 10 and 11, meaning that lower risk gamblers are less likely to chase their losses (item 8) and think about gambling (item 5) but may prioritise gambling (item 11) and borrow money (item 10). In the current study, item 10 was more likely to be endorsed at lower and higher problem gambling trait levels (rather than moderate levels). This is partially in line with the SOGS-RA IRT analysis, which found that the two items related to borrowing money (e.g., “Have you borrowed money to bet and not paid it back?” and “Have you borrowed money or stolen something in order to bet or to cover gambling debts?”) were more likely to be endorsed with higher trait level (Anselmi et al., 2021). However, in their IRT of the PGSI, Sharp et al. (2012) found that borrowing money was more likely with a moderate amount of the problem gambling severity trait. Additionally, a CFA of the PGSI using a Spanish sample found that 64.5 % of low-risk gamblers endorsed the chasing losses item, a proportion much higher than for any other item (Lopez-Gonzalez et al., 2018).

Thresholds 2 (sometimes) and 3 (often). These thresholds yielded similar patterns of results in terms of difficulty, where the items with lowest difficulty were items 2 (“withdrawal”), 11 (“salience”), and 10 (borrowing), indicating that those items were less likely to be endorsed at moderate levels of the problem gambling trait. Interestingly, items 8 and 5 (the least discriminating items) were more likely to be endorsed with moderate levels of the trait. This was in line with the SOGS-RA IRT study, which revealed that the chasing losses item was more likely to be endorsed “yes” with a moderate level of trait (β = 1.86; Anselmi et al., 2021), and in the PGSI IRT study, the same was true for responding with sometimes (β = 1.59) and most of the time (β = 2.38; Sharp et al., 2012). In the CFA of the PGSI, 78.4 % of moderate-risk sports bettors indicated that they chased their losses, which was the highest endorsed item (Lopez-Gonzalez et al., 2018). They also found that moderate-risk gamblers endorsed “borrowing money” the least, with only 14.7 % of the sample endorsing this item.

Threshold 4 (every day). At threshold 4, the results indicate that those higher in the problem gambling trait would be more likely to endorse items 11, 7, and 9 but least likely to endorse items 1 and 6. In other words, those higher in the problem gambling trait would probably prioritise gambling (item 11), feel that their gambling is out of control (item 7), and hide their gambling behaviour from others (item 9). However, they would be less likely to spend increasing amounts to get the same high (item 1) and their gambling would be less related to modifying unpleasant mood states (item 6).

In the SOGS-RA IRT study, the item that appears to be similar to OGD-Q item 11, (i.e., “Have you ever skipped or been absent from school or work due to betting activities?”) had the second highest difficulty level (β = 1.86; Anselmi et al., 2021), indicating that a moderate amount of the trait would be required to endorse “yes” to the item. However, it may not represent the same aspect of problem gambling as the OGD-Q item 11. The PGSI does not have an item that aligns with prioritising gambling over other important functions, so a further comparison cannot be made. In relation to the second-highest ranked OGD-Q item for difficulty (i.e., item 7), the SOGS-RA has one item that may also conceptualise perceived lack of control (e.g., “Have you felt that you would like to stop betting money but didn’t think you could?”), which indicated that a moderate level of trait would be needed to endorse “yes” to the item (β = 1.71; Anselmi et al., 2021).

For the most part, the current findings were reflective of the literature, although some differences were notable, particularly that borrowing money (endorsed with lower trait levels in the current study) was more likely to be endorsed with moderate to high levels of the trait when using the PGSI (Sharp et al., 2012) and SOGS-RA (Anselmi et al., 2021). Nonetheless, the current study indicated that prioritising gambling is more likely to be endorsed at the high ends of the trait continuum, whereas it is less likely to be an everyday occurrence for people with moderate trait level. Overall, the results indicated that individuals who place gambling before other important areas of their life and feel they have little control are more likely to have more severe gambling problems and psychometric assessment should take this into account.

4.3. Pseudo-guessing parameter

Pseudo-guessing is a third parameter that assesses the likelihood of a guessed response, that is, the probability of a response when the trait is low (and items too difficult). The results indicated that, as would be expected, the pseudo-guessing values decreased as the trait level increased. The results showed that items 11 and 10 had the lowest pseudo-guessing probability, meaning that individuals low in the underlying trait would be least likely to randomly endorse those items.

4.4. Item and scale reliability

At the item level, there was variability in the reliability indices in relation to differing trait level, item difficulty and guessing parameters. The IIFs of items 1 (“tolerance”), 5 (“salience”) and 8 (chasing losses) were low and yielded flat curves, providing the most information at the mean trait level up to around 3 SDs above the mean. This indicates that these items lower in information are not as precise or reliable at capturing an accurate measure of problem gambling as other items in the scale.

Several items produced a moderately high amount of information and were therefore more reliable than those with the flatter curves. Items 2 (“withdrawal”), 3 (“intrapsychic conflict”), 4 (“interpersonal conflict”), and 7 (“intrapsychic conflict”) provided the highest amount of information between 0.5 SDs and 3SDs above the mean. Items 2 (“withdrawal”) and 7 (“intrapsychic conflict”) were technically more precise, indicated by their slightly taller and narrower curves that both peaked at around 2 SDs above the mean. These items appear to capture a reliable measure of problem gambling at higher levels of the trait. Nevertheless, items 3 (“intrapsychic conflict”), and 4 (“interpersonal conflict”) were somewhat superior to items 2 and 7 when the trait level is slightly higher.

Item 6 (“mood modification”) was similar but had a dip in information at around 2.5 SDs above the mean, before increasing again at around 3 SDs. Interestingly, this dip occurred with a peak in response option often, which was the highest endorsement of that item, indicating that it is less likely for someone higher in the problem gambling trait to engage in everyday (compared to often) gambling to try and improve their mood.

Items 9 (lying) and 10 (borrowing) provided the most amount of information between approximately 1 and 3 SDs above the mean, peaking at around 2 SDs above the mean trait level, indicating that these items performed well when the trait level was higher. The IIF of item 11 (“salience”) was considerably higher than other items and demonstrated the most amount of information for respondents in the range between 1.2 and 2.8 SDs above the mean trait level. This indicates that the item is especially reliable when respondents are higher in problem gambling behaviour.

Overall, the items appeared to be more reliable when the trait level is average to high, with most items performing well at higher trait level. The items with more information at lower trait levels (items 1, 5 and 8) were less reliable than others (indicated by wide, flat curves situated below difficulty intercepts), and those higher in information provided the most information at higher trait levels in general. This was reflected by the total information curve (TIC), which showed that overall, the OGD-Q provided the most reliable information between 1 and 3 SDs above the mean. This indicates that the scale is more reliable at measuring problem gambling in people with higher levels of disordered gambling behaviour and somewhat less reliable around the mean, which is understandable as the scale was developed as a diagnostic tool for online gambling disorder.

4.5. Implications, limitations and future research

A key strength of the current study was that it provided additional support for the use of the OGD-Q as an assessment of problem gambling. The use of IRT also extended previous findings by examining psychometric properties at the item and scale level, considering item difficulty, discrimination capacity, and pseudo-guessing probability.

The current IRT confirmed the reliability of the OGD-Q at the scale level and assessed reliability, or precision, of each item. Of note, item 8 performed considerably worse than other items, indicating that chasing losses may not be indicative of problem gambling, therefore the weight of the DSM-5 “chasing losses” criterion (A6) should be reconsidered. Similarly, item 1 (criterion A1) had low precision, indicating that tolerance may not indicate an important component of gambling addiction. It could also be concluded that these items are not needed on the OGD-Q or could be omitted if a brief tool was designed for use in clinical and acute settings. On the other hand, item 11 (“salience”) appears to be most representative of problem gambling, and it could be concluded that prioritising gambling over important areas of one’s life is potentially more diagnostically accurate. However, these findings should be interpreted cautiously as the current sample was community based, and clinical implications would require confirmation using a clinical sample.

Overall, items 11 (“salience”), 10 (borrowing) and 7 (“intrapsychic conflict”) were the highest performing items and therefore most representative of problem gambling. In terms of the components model of behavioural addiction (Griffiths, 2019), the current findings indicated that salience and intrapsychic conflict (particularly in relation to feelings of control) are most important to the experience of problem gambling, whereas tolerance is not.

Despite the strengths and potential diagnostic implications of the current study, limitations were present. First, the OGD-Q was originally designed to measure online gambling behaviour among adolescents and thus age-related limitations may occur when it is used in adult samples. Although the current findings indicated that the scale and items reliably measured problem gambling in a community sample (for the most part), future research could focus more sharply on clinical populations, which may present with different components’ weighting and diagnostic features. Second, the data used in the current study was collected without following any specific stratification method, which could also limit generalisability. Third, given the wider research project implemented online collection, the current findings may not be comparable with that of face-to-face respondents warranting cautiousness when extrapolating our conclusions. Future research should consider addressing these limitations to test/confirm the present findings. In particular, the examination of potential age-related and culture-related differential functioning of the distinct OGD-Q items may need to be prioritized in line with recent literature recommendations (Stavropoulos et al., 2022; Zarate et al., 2022).

Compliance with Ethical Standards.

5. Ethical standards – Animal Rights:

All procedures performed in the study involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards. This article does not contain any studies with animals performed by any of the authors. Ethics approval was received from the Victoria University, Melbourne, Australia, Ethics Committee HRE20-169.

6. Informed consent:

Informed consent was obtained from all individual participants included in the study.

7. Confirmation Statement:

Authors confirm that this paper has not been either previously published or submitted simultaneously for publication elsewhere.

8. Copyright:

Authors assign copyright or license the publication rights in the present article.

9. Data and syntax availability:

The data of the current study is available on the following github link https://github.com/Vas08011980/Online-Gambling-Disorder-Questionnaire-OGD-Q-An-Item-Response-Theory-Examination/blob/main/OGDQ_IRT.sav and the syntax of the current study is available on the following github link https://github.com/Vas08011980/Online-Gambling-Disorder-Questionnaire-OGD-Q-An-Item-Response-Theory-Examination/blob/main/OGDQ%20IRTpro%20Syntax.

Funding.

vS.has received the Australian Research Council, Discovery Early Career Researcher Award 2021. Grant Award Number: DE210101107.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.