Abstract
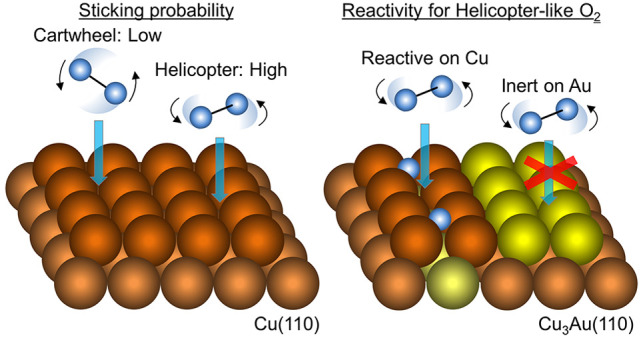
The orientation and motion of reactants play important roles in reactions. The small rotational excitations involved render the reactants susceptible to dynamical steering, making direct comparison between experiments and theory rather challenging. Using space-quantized molecular beams, we directly probed the (polar and azimuthal) orientation dependence of O2 chemisorption on Cu(110) and Cu3Au(110). We observed polar and azimuthal anisotropies on both surfaces. Chemisorption proceeded rather favorably with the O–O bond axis oriented parallel (vs perpendicular) to the surface and rather favorably with the O–O bond axis oriented along [001] (vs along [1̅10]). The presence of Au hindered the surface from further oxidation, introducing a higher activation barrier to chemisorption and rendering an almost negligible azimuthal anisotropy. The presence of Au also prevented the cartwheel-like rotations of O2.
Keywords: metal surface, oxidation, copper, copper−gold alloy, steric effect
Introduction
Activation of molecular oxygen (O2) constitutes an important step in oxidative processes, including heterogeneous catalysis, electrocatalysis, and corrosion of metals.1−7 The interaction of O2 with various metal surfaces induces changes in its chemical stability and reactivity. It follows that the ability to control such processes bears on the chemical economic world. Alloying of pristine metals provides one of the simplest ways to do so. Understanding the microscopic mechanism behind O2 chemisorption entails unraveling the stereochemistry of the processes involved.8−14
O2 dissociative adsorption on Cu(110) provides a model system for understanding the oxidation processes on Cu surfaces.15−32 The pristine Cu(110) surface possesses an anisotropic surface structure, on which anisotropic Cu–O chains grow as a precursor to oxide formation.28−32 Early molecular beam experiments observed initial sticking probabilities (S0) increasing with translational energy (Et), approaching 0.8 at a high enough Et.24
At low Et, two competing mechanisms could account for the observed O2 dissociative adsorption. A precursor-mediated channel (a weakly bound, physisorbed trapping molecular state) dominates at low Et and low surface temperatures (TS). Activated dissociative chemisorption becomes important as Et increases, which occurs directly and/or via a short-lived molecularly chemisorbed state. One could also think of a three-well potential33 that ascribes transient molecularly chemisorbed states to negatively ionized O2–, e.g., the peroxo state, as suggested by high-resolution electron energy loss spectroscopy (HREELS) measurements17,18 and -density functional theory (DFT)-based calculations.19 Such negatively charged states could account for the high sticking probability and the well-known efficient catalytic activity of Cu for oxidation.
At high Et, hyperthermal molecular oxygen beam (HOMB) experiments14 report effective formation of Cu2O precursor on Cu(110), that exhibits dependence on the azimuthal orientation at which O2 impinges the surface. This demonstrates another important feature that comes from the inherent orientation dependence of reactions. The stereodynamics of reactant molecules (the orientation and the movement of molecules in 3D space) plays an important role in reactions. The small rotational energy excitations involved (ca. less than a few meV) render the reactants susceptible to dynamical steering(1,34−36) and make direct verification of calculated potential energy surfaces (PES) rather challenging.1,10−14,25,37 Helicopter-like rotating O2 (with dominant rotational angular momentum J parallel along the surface normal) adsorbs more effectively than cartwheel-like rotating O2 (with J perpendicular to the surface normal).19,20,22 As mentioned earlier, a possible candidate for transient molecularly chemisorbed state would be an adsorbed O2 exhibiting peroxo-like character (O2–), with azimuthal orientation-dependent stability.19,20,22 As expected from previous discussions,34−36 at high Et (ca. 500 meV), the impinging O2 does not have enough time to reorient (be steered) and the favorable helicopter-like rotating O2 dominantly account for chemisorption.19 On the other hand, at low Et (ca. 50 meV), the impinging O2 have enough time to reorient (be steered) to more favorable orientations toward reactive sites.19
Ancient people know that alloying with inert gold (Au) protects Cu from further corrosion, and we observe several ancient products enduring in rather pristine condition.38 Now, we know that the deeper d-band center induced by Au alloying prevents the strong bonding–antibonding interaction with the antibonding state of the impinging O2, resulting in the inertness of the alloy surface.33,39,40 Moreover, the presence of Au changes the electron distribution (electronic corrugation) on the Cu surface. Thus, one would expect different dynamical processes (e.g., translational to rotational energy transfer effects) occurring when O2 impinges on a Cu–Au alloy surface as compared to a Cu surface.
In this study, we clarify the alignment dependence of O2 chemisorption on Cu(110) and Cu3Au(110). We do this by using a single-quantum-state-selected (space quantized, following the 1922 Stern-Gerlach experiment41,42) O2 beam developed at NIMS (for which both the molecular alignment and the spin state are well-defined).10 On Cu(110), as in previous studies, we observed both polar and azimuthal anisotropies. O2 chemisorption proceeds rather favorably with the O–O bond axis oriented parallel (vs perpendicular) to the surface and rather favorably with the O–O bond axis oriented along [001] (vs along [1̅10]). O2 chemisorption on Cu3Au(110) shows similar polar and azimuthal anisotropies. However, the presence of Au hinders the surface from further oxidation via a higher activation barrier to chemisorption and an almost negligible azimuthal anisotropy.
Results and Discussion
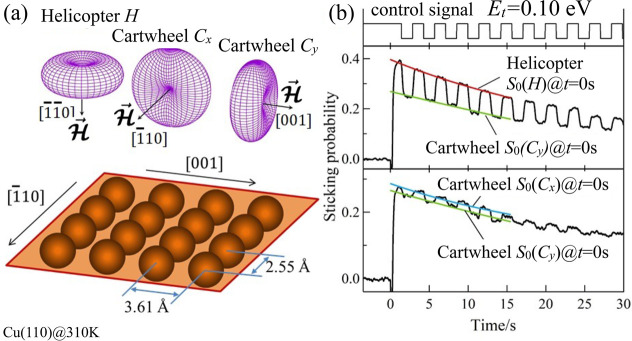
In Figure 1, we
show the measured alignment-dependent O2 initial sticking
probabilities (S0) on Cu(110). O2 in a spin rotational state [(J, M) = (2,2)] exhibit a sin2 θ-dependent O–O
bond axis (angular) distribution, where θ gives the polar angle
subtended by the O–O bond axis with a predetermined defining
magnetic field (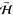 ). Thus, helicopter-like and cartwheel-like
rotating O2 (vide ante) can be generated, achieved by directing
). Thus, helicopter-like and cartwheel-like
rotating O2 (vide ante) can be generated, achieved by directing 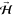 perpendicular or parallel to the surface
(Figure 1a). Helicopter-like
rotating O2 have O–O bond axes oriented dominantly
parallel to the surface. On the other hand, for cartwheel-like rotating
O2, the O–O bond axes can assume both parallel and
perpendicular configurations. We can further prepare two types of
cartwheel-like rotating O2 depending on their azimuthal
orientation, e.g., by aligning
perpendicular or parallel to the surface
(Figure 1a). Helicopter-like
rotating O2 have O–O bond axes oriented dominantly
parallel to the surface. On the other hand, for cartwheel-like rotating
O2, the O–O bond axes can assume both parallel and
perpendicular configurations. We can further prepare two types of
cartwheel-like rotating O2 depending on their azimuthal
orientation, e.g., by aligning 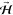 along [1̅10] (Cartwheel (x), Cx) or
along [001] (Cartwheel (y), Cy) (see Figure 1a).
along [1̅10] (Cartwheel (x), Cx) or
along [001] (Cartwheel (y), Cy) (see Figure 1a).
Figure 1.
(Space quantized) O2 sticking probabilities
on Cu(110).
(a) Angular distributions (upper panel) of the molecular axis (O–O
bond axis) of an O2 (in the triplet electronic ground state 3Σg– and spin-rotational state (J = 2, M = 2)) with respect to Cu(110) (schematically depicted in the lower
panel) and corresponding defining magnetic fields 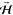 . Orienting
. Orienting 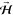 perpendicular to the surface, i.e., along
[1̅ 1̅0], results in helicopter-like rotating O2. Two types of cartwheel-like rotating O2 can also be
realized by orientating
perpendicular to the surface, i.e., along
[1̅ 1̅0], results in helicopter-like rotating O2. Two types of cartwheel-like rotating O2 can also be
realized by orientating 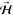 parallel to the surface, i.e., either along
[1̅10] or [001]. (b) Time evolution of the sticking probability
for a space-quantized O2 impinging on Cu(110) (at a surface
temperature of ca. 310 K) with translational energy Et = 0.10 eV. Time t =
0 corresponds to the time the beam shutter is opened to allow the
molecular beam to impinge on the surface. Following the control signal
shown (topmost right panel), the
parallel to the surface, i.e., either along
[1̅10] or [001]. (b) Time evolution of the sticking probability
for a space-quantized O2 impinging on Cu(110) (at a surface
temperature of ca. 310 K) with translational energy Et = 0.10 eV. Time t =
0 corresponds to the time the beam shutter is opened to allow the
molecular beam to impinge on the surface. Following the control signal
shown (topmost right panel), the 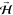 direction can be modulated to alternately
produce helicopter-like (high signal) and cartwheel-like (low signal)
rotating O2 that impinge on Cu(110). Numerical fits to
the corresponding sticking probability data points (using exponentially
decaying functions extrapolated to t = 0) also shown
to guide the eye. The values at t = 0 correspond
to the initial sticking probabilities S0(H), S0(Cx), and S0(Cy).
direction can be modulated to alternately
produce helicopter-like (high signal) and cartwheel-like (low signal)
rotating O2 that impinge on Cu(110). Numerical fits to
the corresponding sticking probability data points (using exponentially
decaying functions extrapolated to t = 0) also shown
to guide the eye. The values at t = 0 correspond
to the initial sticking probabilities S0(H), S0(Cx), and S0(Cy).
In Figure 1b, we
show the time evolution of the sticking probability for O2 on Cu(110), measured while modulating 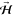 to alternately produce helicopter-like
and cartwheel-like O2 at E0 = 0.10 eV. We determined the sticking probability curves by fitting
the data points corresponding to each geometry to an exponential decay
function (see smooth curves), and the values extrapolated to t = 0 (beam shutter removed) correspond to initial sticking
probabilities S0(H) and S0(Cy), respectively. Because we are discussing the very early stage of
oxidation, Cu segregation40,43,44 induced by oxygen adsorption need not be considered in S0. We see that S0(H) > S0(Cy) and S0(H) > S0(Cx), in general, indicating
that more reactive
parallel-oriented O2 as compared to perpendicular-oriented
O2. This is consistent with previous XPS studies on Cu(111).45) From Figure 1b, we can also see from the time evolution of the sticking
probabilities that S0(Cx) > S0(Cy), indicating that
O2 with O–O bond axes oriented along [001] are more
reactive
than those with O–O bond axes oriented [1̅10].
to alternately produce helicopter-like
and cartwheel-like O2 at E0 = 0.10 eV. We determined the sticking probability curves by fitting
the data points corresponding to each geometry to an exponential decay
function (see smooth curves), and the values extrapolated to t = 0 (beam shutter removed) correspond to initial sticking
probabilities S0(H) and S0(Cy), respectively. Because we are discussing the very early stage of
oxidation, Cu segregation40,43,44 induced by oxygen adsorption need not be considered in S0. We see that S0(H) > S0(Cy) and S0(H) > S0(Cx), in general, indicating
that more reactive
parallel-oriented O2 as compared to perpendicular-oriented
O2. This is consistent with previous XPS studies on Cu(111).45) From Figure 1b, we can also see from the time evolution of the sticking
probabilities that S0(Cx) > S0(Cy), indicating that
O2 with O–O bond axes oriented along [001] are more
reactive
than those with O–O bond axes oriented [1̅10].
In Figure 2, we show the corresponding results on Cu3Au(110)-(4 × 1). Low-energy electron diffraction (LEED) patterns (Figure 2a) indicate Au atom segregation, forming a (4 × 1) restructured surface46 (see Figure 2b). A detailed layer profile of the surface analyses43 found that 50% of surface Cu atoms on Cu(110) were replaced by Au atoms. This results in a reduction in the O2 sticking probability to 15% of that on Cu(110). The reduced sticking probability indicates effects from the second-layer Au atoms and/or the nonlocalized contribution of the first-layer Au atoms to the reactive sites. Although we expect the existence of transient molecular states similar to that on Cu(110), the deeper d-states of Au interact weakly with the antibonding states of O2 without filling them with electrons, rendering it more difficult to form intermediate O2δ− states. Moreover, the expected larger work function of Cu3Au(110) compared to Cu(110) (ca. 4.48 eV, and ca. 5.37 eV for Au(110))47,48 renders negatively charged states unstable. As on Cu(110), we see that S0(H) > S0(Cy) and S0(H) > S0(Cx), in general. Again, this indicates more reactive parallel-oriented O2 as compared to perpendicular-oriented O2. However, in contrast to the case on Cu(110), we find negligible azimuthal anisotropy on Cu3Au(110)-(4 × 1), as now we have S0(Cx) ∼ S0(Cy).
Figure 2.
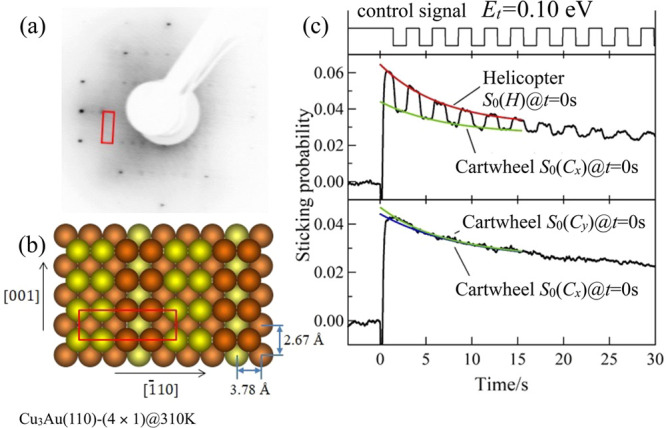
(Space quantized) O2 sticking probabilities
on Cu3Au(110)-(4 × 1). (a) LEED patterns for a clean
Cu3Au(110)-(4 × 1). (b) Schematic depiction of Cu3Au(110)-(4 × 1) (Cu, reddish balls; Au, yellowish balls).
(c)
Time evolution of the sticking probability for a space-quantized O2 impinging on Cu3Au(110)-(4 × 1) (at a surface
temperature of ca. 310 K) with translational energy Et = 0.10 eV. Time t =
0 corresponds to the time the beam shutter is opened to allow the
molecular beam to impinge on the surface. Following the control signal
shown (topmost right panel), the direction of the defining magnetic
field 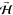 can be modulated to alternately produce
helicopter-like (high signal) and cartwheel-like (low signal) rotating
O2 that impinge on Cu3Au(110)-(4 × 1).
Numerical fits to the corresponding sticking probability data points
(using exponentially decaying functions extrapolated to t = 0) also shown to guide the eye. The values at t = 0 correspond to the initial sticking probabilities S0(H), S0(Cx), and S0(Cy).
can be modulated to alternately produce
helicopter-like (high signal) and cartwheel-like (low signal) rotating
O2 that impinge on Cu3Au(110)-(4 × 1).
Numerical fits to the corresponding sticking probability data points
(using exponentially decaying functions extrapolated to t = 0) also shown to guide the eye. The values at t = 0 correspond to the initial sticking probabilities S0(H), S0(Cx), and S0(Cy).
To determine how the translational/beam energy Et affects the steric effect, in Figure 3a, we plot the ratios S0(H)/S0(Cx) and S0(H)/S0(Cy), determined from S0(H) and S0(C) obtained simultaneously by a single modulation measurement, as a function of Et. Theoretically, when O2 with O–O bond axes oriented parallel the surface adsorb, we have S0(H)/S0(Cx) = 2 (or S0(H)/S0(Cy) = 2). And when O2 can adsorb regardless of O–O bond axes orientations, we have S0(H)/S0(Cx) = 1 (or S0(H)/S0(Cy) = 1). Experimentally, on Cu(110), we find S0(H)/S0(Cx) = 1.35 and S0(H)/S0(Cy) = 1.5 at Et = 0.10 eV, and S0(H)/S0(Cx) ∼ S0(H)/S0(Cy) ∼ 1.0 for Et ≥ 0.33 eV. This indicates the importance of steric effects at small Et, becoming negligible for translational/beam energies Et ≥ 0.33 eV. On Cu3Au(110)-(4 × 1), the Et-dependence of S(H)/S(C) follows a trend similar to that observed on Pt(111),49 i.e., initial increase in S0(H)/S0(Cx) and S0(H)/S0(Cy) at Et ≤ 0.26 eV, and then a gradual decrease from E0 ≥ 0.26 eV.
Figure 3.
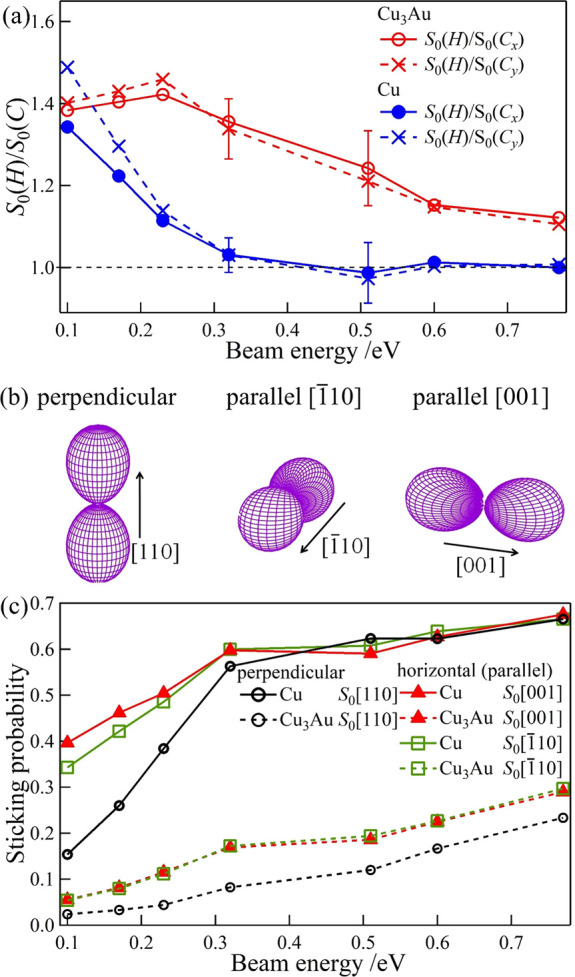
Translational energy dependence of (space quantized) O2 initial sticking probabilities on Cu(110) and Cu3Au(110). (a) Initial sticking probability ratio S0(H)/S0(C) for helicopter-like and cartwheel-like rotating O2 on Cu(110) and Cu3Au(110) at 310 K. (b) Angular distributions of the O2 molecular axis (O–O bond axis) oriented perpendicular (along [110]) and parallel (along [1̅10] and [001]) to the corresponding surfaces. (c) Initial sticking probability contributions from the O–O bond axis oriented perpendicular and parallel to Cu(110) and Cu3Au(110) as indicated in panel b.
To determine how the O–O bond axes orientation with respect to the surface normal affects the sticking probability on Cu(110) and Cu3Au(110), we plot in Figure 3c the Et-dependent orientation-resolved sticking probabilities S0[001] and S0[1̅10] for O2 with O–O bond axes oriented parallel to the surface (along [001] and [1̅10], respectively) and S0[110] for O2 with O–O bond axes oriented perpendicular to the surface (along [110]). (For details on how to determine the orientation resolved sticking probabilities, we refer the readers to the Experimental and Theoretical Methods.)
On Cu(110), S0[110], S0[1̅10], and S0[001] all increase gradually with increasing Et (see Figure 3c). Again, we observe an orientational dependence favoring O–O bond axes oriented parallel to the surface (see S0[1̅10] > S0[110] and S0[001] > S0[110] for Cu(110) in Figure 3c). We also observe an in-plane azimuthal orientation dependence favoring O–O bond axes oriented parallel to the surface along [001] (see S0[001] > S0[1̅10] for Cu(110) in Figure 3c). And, as we have observed earlier, we also see that both polar and azimuthal orientational dependence becomes negligible at Et > 0.3 eV.
On Cu3Au(110)-(4 × 1), we also see that S0[110], S0[1̅10], and S0[001] all increase gradually with increasing incident translational (beam) energy (see Figure 3c). Again, we observe an orientational dependence favoring O–O bond axes oriented parallel to the surface (see S0[1̅10] > S0[110] and S0[001] > S0[110] for Cu3Au(110)-(4 × 1) in Figure 3c), which persists throughout the incident translational (beam) energy range of the experiment, i.e., Et[eV]: [0.1, 0.8]. And, as we have observed earlier, we find negligible in-plane azimuthal orientation dependence.
Upon further examination of the ratios of the corresponding initial sticking probabilities (see Figure 6), we see that the presence of Au considerably decreases the adsorption of O2 with O–O bond axes oriented perpendicular to the surface (i.e., O–O bond axes parallel to [110]). We also see a negligible effect on the adsorption of O2 with O–O bond axes oriented parallel to the surface (i.e., O–O bond axes parallel to [001] and [1̅10]).
Figure 6.
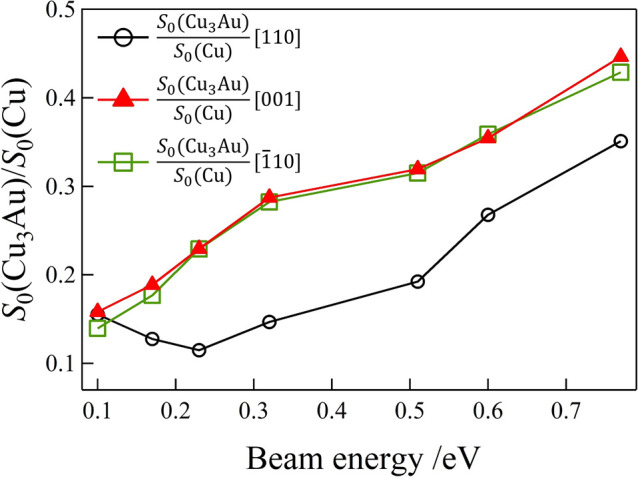
Ratios of (space quantized) O2 initial sticking probabilities on Cu(110) and Cu3Au(110). Initial sticking probability ratios for O2 adsorption on Cu3Au(110)-(4 × 1) and Cu(110), with the O–O bond axis oriented along [110], [001], and [1̅10] (S0(Cu3Au)/S0(Cu)[110], S0(Cu3Au)/S0(Cu)[001], and S0(Cu3Au)/S0(Cu)[1̅10], respectively).
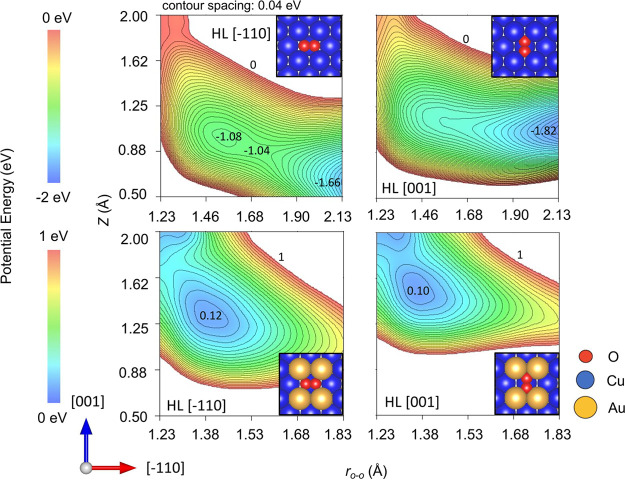
In the following, we discuss the origin of the different energy dependence of S0 and its steric effects for Cu(110) and Cu3Au(110). As has been shown in the previous study on Cu(110),24 a barrier exists before O2 enters the chemisorption well of O2δ−. The magnitude of the barrier depends on the angle of O2 axis relative to the surface plane and on the impact position in the surface unit cell. Molecularly adsorbed O2 is stable in the geometry with its molecular axis parallel to the surface.16,19,20 Thus, it is reasonable to expect that the activation barrier to the O2δ− state is lower if O2 approaches with its molecular axis parallel to the surface. We show that the potential energy curves (PEC) of O2 on Cu(110) manifest such preference (see Figure 4). Moreover, the preferential orientation of O22– is parallel to the [001] direction.19,20 Therefore, the azimuthal dependence of S0 appeared at Et ≤ 0.20 eV, possibly revealing the azimuthal dependence of O2δ− stability. Considering bond dissociation, we also plot the potential energy surface (PES) for O2 in Figure 5. Here, the collisions on the on-top site and the bridge site are not considered because the high activation barrier of such sites cannot be overcome at the experimental incident energy. The adsorption energies of O2 on Cu(110), at [001] and [1̅10] bond orientations, are −1.82 and −1.66 eV, respectively. Moreover, the activation barrier appears in the entrance channel. By tracing the minimum energy path, we found a relatively higher energy barrier for O2 dissociation at the [1̅10] orientation than at the [001] bond orientation on Cu(110). The energy difference between the barriers is about 40 meV. These comparative results agree well with previous calculations on Cu(110).18,19S0 increasing with increasing Et can be explained by the widened range of impact parameters at which incident O2 molecules surmount the barrier. At Et ≥ 0.33 eV, S0(H)/S0(C) ∼ 1.0 and sticking probability saturates at ∼0.65. The lower saturation of sticking probability compared to the previously reported value ∼0.823 may be caused by the single rotational state in the beam. On the other hand, the continued S0 increase upon increasing Et could be expected because incident O2 molecules surmount the higher barrier at the bridge and/or on-top sites, but the saturation of S0 is different from such expectation. Moreover, S0(H)/S0(C) ∼ 1.0 at Et ≥ 0.33 eV indicates no steric preference in O2 sticking. However, the potential landscape and the corresponding energy dissipation process is expected to be quite different for both geometries. To explain the difference between the results and expectation, we speculate the following. The experimental result of S0(H)/S0(C) ∼ 1.0 suggests the contribution of charge transfer50,51 into O2δ− state after overcoming the activation barrier at Et ≥ ∼ 0.4 eV.51 The high-energy O2 comes over the seam between the physisorption state and molecularly adsorbed state. Charge transfer occurs, the short-lived excited O2δ− state couples with substrate excitations, and then de-excited, trapped, and finally O2 dissociates. Although the ground-state interaction potential of O2δ− depends on the alignment of the molecular axis against the surface, the trapping process into the excited O2δ− state may not strongly depend on the molecular orientation of O2 because various excited states coupling with the surface are available after the first activation seam into the molecularly adsorbed state is overcome. The steering effects after overcoming the activation barrier also smear out the orientation dependence of charge transfer. The saturation of the sticking probability suggests that the impact condition (location of O2 and the reaction site at the surface) at which the O2δ− state is stable enough for the dissociative adsorption is limited.
Figure 4.
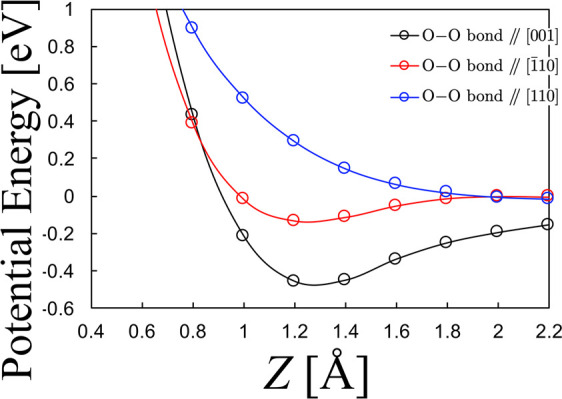
Orientation dependent potential energy curves (PECs) for O2/Cu(110). PECs shown as a function of the O2 center-of-mass distance Z (Å) above a 4-fold hollow site on Cu(110). PECs calculated with the O–O bond length fixed at a gas phase equilibrium distance of 1.23 Å, and the O–O bond axis orientations fixed parallel to [1̅10], [001], and [110] on Cu(110). Energies (eV) given with respect to O2 sufficiently far (ca. 5.0 Å) from Cu(110). Structures and related figures drawn using the VESTA package.66
Figure 5.
Potential energy surfaces (PESs) for O2 on Cu(110) and Cu3Au(110)-(4 × 1). Potential energy surfaces (PESs) for O2 and Cu3Au(110)-(4 × 1). PESs shown as functions of the O2 center-of-mass distance Z (Å) (from the 4-fold hollow site (HL) of Cu on Cu(110) (upper panels) and Au on Cu3Au(110)-(4 × 1) (lower panels)) and the O2 bond length rO–O (Å). PESs calculated with the O2 bond axis fixed either parallel to [1̅10] (left panels) or parallel to [001] (right panels). Energies (eV) given with respect to O2 sufficiently far (ca. 5.0 Å) from the surface, in increments of ca. 0.04 eV.
Cu3Au(110) has a work function larger than Cu(110).47 We can thus expect a rather correspondingly less stable O2δ− state. This renders it more difficult for charge transfers to occur, requiring higher Et as compared to that on Cu(110). Note that there are more stable molecularly chemisorbed O2 states on Cu than on Au.1 Consistent with that, Figure 5 shows an endothermic molecularly adsorbed O2 state, with adsorption energies of 0.10 and 0.12 eV, respectively. The ground state O2 becomes unstable (ca. > 1 eV) by Au alloying.
The increase in S0(H)/S0(C) at Et ≤ 0.26 eV on Cu3Au(110) can be accounted for by the decreasing contribution of the trapping-mediated process in the physisorption well with increasing Et. This means that the value of S0(H)/S0(C) for the directly activated process would be higher than the observed value and be close to 2, suggesting that for the direct process to occur at low Et conditions, the O–O bond axes must be parallel to the surface. The azimuthal dependence observed on Cu(110) disappears on Cu3Au(110) because of the absence of a stable O2δ− state (see Figure 5). Note that the stability of the O2 depends on its azimuthal orientation on Cu3Au(110), and also susceptible to ensemble effect of interaction potentials. The 3% larger lattice constant of Cu3Au than Cu renders the active sites for the dissociation of the horizontal molecules practically azimuthally isotropic. The steering effect, which redirects the impinging O2 to the preferred geometry becomes insufficient at high energies, e.g., Et > 0.26 eV. At higher Et, O2 with O–O bond axes oriented perpendicular to the surface can also overcome the activation barrier. The angular distribution of the O–O bond axes could also smear out the steric effect, with the reaction occurring at a finite range of orientations depending on Et.
In Figure 6, we show the translational energy dependence of the initial sticking probability ratios S0(Cu3Au)/S0(Cu) for S0[001], S0[1̅10], and S0[110]. S0(Cu3Au)/S0(Cu) for S0[110] exhibits the least value compared to the rest and indicates that Au alloying effectively reduces the sticking of O2 with O–O bond axes oriented perpendicular to the surface. Au alloying filters the molecular orientation and permeates only O2 with O–O bond axes oriented horizontal to the surface and supply the O atoms. This filtering effect may lead to the selective surface chemical reactions and selective oxidative catalytic reactions. Reduction in corrosion of Au alloyed Cu may be attributed to the reduction in the presence (if not complete absence) of intermediate short-lived O2δ− that increases reactivity but reduces the steric preference in processes at higher Et.
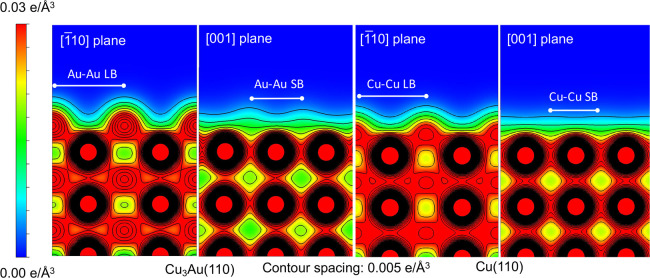
Charge population analyses of adsorbed O2 on Cu3Au(110) and Cu(110) indicate electron gain (O2δ− states, see Table 1). Hence, a shallow potential for molecularly chemisorbed O2 on Cu3Au suggests that dissociation via the transiently trapped O2δ− will be difficult, and the dissociative adsorption may occur over the high adiabatic activation barrier in the (approximately) usual two-well potential. Unstable molecular chemisorbed O2 states on Cu3Au results in weakened orientation dependence of the O2 sticking probability. In addition, the large atomic radii of surface Au atoms lessen the anisotropy of the surface charge distribution on Cu3Au(110) (see Figure 7). Correspondingly, the electron surface corrugation as seen by an impinging O2 on Cu(110) varies more between [001] and [1̅10] bond orientations, having a relatively smooth electron surface distribution along the [1̅10] direction or the [001] plane. Collectively, these results confirm the azimuthal dependence of O2 adsorption on Cu(110) and its inertness toward Cu3Au(110).
Table 1. Electron Gain (e-Gain) of O2 Adsorbed on Cu3Au(110)-(4 × 1) and Cu(110)a.
| surface | O–O bond axis orientated along | O–O bond length (Å) | e-gain (e) |
|---|---|---|---|
| Cu3Au(110)–(4 × 1) | [001] | 1.33 | 0.61 |
| Cu3Au(110)–(4 × 1) | [1̅10] | 1.43 | 0.78 |
| Cu(110) | [001] | 2.13 | 1.58 |
| Cu(110) | [1̅10] | 2.13 | 1.72 |
e-gain (e) given with respect to O2 sufficiently far (ca. 5.0 Å) from the corresponding surfaces.
Figure 7.
Electron distribution on Cu3Au(110) and Cu(110). 2D cut through the long bridge (LB) and short bridge (SB) sites of the electron distributions as viewed along [1̅10] and [001] on the corresponding surfaces. Note the more pronounced orientation-dependent contour difference observed on Cu(110) than on Cu3Au(110)-(4 × 1). Electron distributions (e/Å3) given with respect to distances sufficiently far (ca. 5.0 Å) from the surface, in increments of 0.005 e/Å3.
Conclusion
In conclusion, we demonstrate the effect of alloying on the steric effects in O2 dissociative adsorption. At low beam energies, the dissociative adsorption of O2 occurs on the adiabatic potential landscape on Cu(110). O2 with O–O bond axes parallel to the surface exhibit higher reactivity as compared to those oriented normal to the surface. The reactivity also depends on the O–O bond orientations along the surface. At high beam energies, the O2 in all orientations overcome the activation barrier and steric effects become negligible. Reactions via charge transfer into short-lived O2δ− state also smear out the steric effects and reduce initial sticking probability saturations to ca. 0.7. On Cu3Au(110), the overall initial sticking probabilities reduce to ca. 15% that of on Cu(110). Except for the negligible azimuthal orientation dependence, the reactivity also shows similar dependence on the O–O bond axes orientations with respect to the surface, as on Cu(110). Alloying with Au increases the activation barrier in the entrance channel, increases the work function, and renders the molecularly chemisorbed O2 (O2) state unstable.
Experimental and Theoretical Methods
Sample Preparation
We cleaned the Cu(110) and Cu3Au(110) samples by 1.0 eV Ar+ sputtering and annealing at 773 K. We repeated this procedure until we could no longer detect the impurities by Auger electron spectroscopy (AES).
Space-Quantized, State-Selected O2(3Σ–g) Molecular Beam
For details regarding the experimental apparatus, we refer the readers to previous reports.10,13 Briefly, we generated O2 molecular beams by the free expansion of seeded gas of O2/He. We then used hexapole magnets to filter the (J, M) state from the O2 molecular beam. We could also control the translational energy of the state-selected O2(J, M) beam by adjusting the number of the hexapole magnets and the O2/He mixing ratio of the seeded O2 beam. Note that we use the following notations:
J = K + S: O2 total angular momentum with corresponding quantum number J;
K: O2 rotational angular momentum with corresponding quantum number K;
S: O2 total electron spin angular momentum with corresponding quantum number S;
M = MK + MS: projection of J along the external field direction;
MK and MS: projection of K and S along the external field direction, respectively;
Thus, we are able to prepare O2(J = 2, M = 2), which corresponds to O2(K = 1, MK = 1, S = 1), with rotational energy EK = BK(K + 1) ≈ (0.18 meV)(1)(1 + 1) = 0.36 meV, and translational energy Et. An O2 in state (K = 1, Et = 100 meV) would have traveled a distance of 15 Å by the time it rotates 90°.
The angular distribution
of the O2(J = 2, M =
2) molecular axis orientation approximately
follows a sin2 θ distribution, where θ is the
polar angle of the O2 molecular axis relative to the direction
of the defining magnetic field 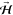 . Depending on the orientation of the defining
magnetic field
. Depending on the orientation of the defining
magnetic field 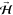 , i.e., perpendicular or parallel to the
surface, we could have helicopter- or cartwheel-like rotating O2(J = 2, M = 2). Helicopter-like
rotating O2(J = 2, M =
2) have an O–O bond axis oriented parallel to the surface.
Cartwheel-like rotating O2(J = 2, M = 2) can also have O–O bond axis orientations other
than parallel to the surface (i.e., perpendicular and in between).
By aligning
, i.e., perpendicular or parallel to the
surface, we could have helicopter- or cartwheel-like rotating O2(J = 2, M = 2). Helicopter-like
rotating O2(J = 2, M =
2) have an O–O bond axis oriented parallel to the surface.
Cartwheel-like rotating O2(J = 2, M = 2) can also have O–O bond axis orientations other
than parallel to the surface (i.e., perpendicular and in between).
By aligning 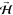 parallel to [1̅10] or [001], we can
prepare two types of cartwheel-like rotating O2, which
we label as cartwheels Cx and Cy, respectively.
Thus, we can prepare a space-quantized, state-selected O2(3Σ–g) molecular beam, in which nearly all (ca. 100%) of the molecules
are in the spin-rotational state (J = 2, M = 2).
parallel to [1̅10] or [001], we can
prepare two types of cartwheel-like rotating O2, which
we label as cartwheels Cx and Cy, respectively.
Thus, we can prepare a space-quantized, state-selected O2(3Σ–g) molecular beam, in which nearly all (ca. 100%) of the molecules
are in the spin-rotational state (J = 2, M = 2).
Initial Sticking Probabilities for Helicopter-like and Cartwheel-like Rotating O2(J = 2, M = 2)
We express the initial sticking probability S0(H) for helicopter-like rotating O2(J = 2, M = 2) as10
| 1 |
For the two types of cartwheel-like rotating O2(J = 2, M = 2), viz., S0(Cx) and S0(Cy), we have
| 2 |
and
| 3 |
(θ, ϕ) give the polar and azimuthal orientation of the O2 molecular axis with respect to the surface. Rave(θ, ϕ) gives the reaction rate averaged over the surface unit cell. From eqs 1–3, we then determine the initial sticking probability S0(R) for a random distribution, i.e.,
| 4 |
For initial sticking probabilities S0[110], S0[001], and S0[1̅10], which correspond to O2 with molecular axis parallel to [110], [001], and [1̅10], respectively, we have
| 5 |
| 6 |
| 7 |
Computational Details
We performed spin-polarized density functional theory52,53 (DFT) based total energy calculations,54−57 using the projector augmented wave (PAW) formalism.58 We employed plane wave basis set, with a cutoff energy of 700 eV. We used the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) for the exchange correlation functional.59,60 We adopt the Monkhorst and Pack method to perform Brillouin zone integrations, with 10 × 10 × 1 special k-points,61 and conduct frozen lattice calculations with energy convergence of less than 1 × 10–5 eV. To model the Cu(110) and Cu3Au(110), we used a periodic slab, six atomic layers thick with eight atoms per layer, separated by 15 Å of vacuum along [110]. To obtain the optimized geometry after surface cleaving, we relaxed the first 2 atomic layers of the surface slabs until Hellmann–Feynman forces are less than 0.01 eV/Å. We used a (4 × 2) surface unit cell of Cu(110) and Cu3Au(110) as the supercell for O2 adsorption. This takes care of the unwanted interaction between periodic images of O2. In the case of Cu3Au(111), we adopt the (4 × 1) reconstructed structure for the first two atomic layers. To have a better comparison of the relative strength of adsorption on Au surface atoms of Cu3Au(110) and on Cu surface atoms of pristine Cu(110), we chose the 4-fold coordinated Au/Cu hollow site as O2 adsorption site. We determined the adsorption energies from the change in the total energy of the system with respect to the case with O2 sufficiently far (ca. 5 Å) from the surface. To determine the charge population of O2 upon adsorption, we used Bader charge analyses.62−65 We used the VESTA package66 to draw the structures and related figures.
Acknowledgments
We thank MEXT (Ministry of Education, Culture, Sports, Science and Technology-Japan) for Grants-in-Aid for Scientific Research (JP20H02623, JP20K21148, JP20K21171, JP15KT0062, JP26248006, JP20H02638) and the NIMS Joint Research Hub Program. Structures and related figures appearing in the manuscript were drawn using the VESTA package.66
Author Present Address
|| Institute of Laser Engineering, Osaka University, Suita, Osaka 565–0871, Japan
Author Present Address
# Advanced Science Research Center, Japan Atomic Energy Agency, Tokai, Ibaraki 319–1195, Japan
The authors declare no competing financial interest.
References
- Montemore M. M.; van Spronsen M. A.; Madix R. J.; Friend C. M. O. O2 activation by metal surfaces: implications for bonding and reactivity on heterogeneous catalysts. Chem. Rev. 2018, 118, 2816–2862. 10.1021/acs.chemrev.7b00217. [DOI] [PubMed] [Google Scholar]
- Huang W.; Sun G.; Cao T. Surface Chemistry of group IB metals and related oxides. Chem. Soc. Rev. 2017, 46, 1977–2000. 10.1039/C6CS00828C. [DOI] [PubMed] [Google Scholar]
- Stampfl C.; Soon A.; Piccinin S.; Shi H.; Zhang H. Bridging the temperature and pressure gaps: close-packed transition metal surfaces in an oxygen environment. J. Phys.: Condens. Matter 2008, 20, 184021. [Google Scholar]
- Lundgren E.; Mikkelsen A.; Andersen J. N.; Kresse G.; Schmid M.; Varga P. Surface oxides on close-packed surfaces of late transition metals. J. Phys.: Condens. Matter 2006, 18, R481. [Google Scholar]
- Libuda J.; Freund H.-J. Molecular beam experiments on model catalysts. Surf. Sci. Rep. 2005, 57, 157–298. 10.1016/j.surfrep.2005.03.002. [DOI] [Google Scholar]
- Jones F. Teeth and bones: applications of Surface Science to dental Materials and related bioMaterials. Surf. Sci. Rep. 2001, 42, 75–205. 10.1016/S0167-5729(00)00011-X. [DOI] [Google Scholar]
- Roberts M. Chemisorption and reaction pathways at metal surfaces: the role of surface oxygen. Chem. Soc. Rev. 1989, 18, 451–475. 10.1039/cs9891800451. [DOI] [Google Scholar]
- Kurahashi M.; Yamauchi Y. Steric effect in O2 sticking on Al(111): Preference for parallel geometry. Phys. Rev. Lett. 2013, 110, 246102. 10.1103/PhysRevLett.110.246102. [DOI] [PubMed] [Google Scholar]
- Kurahashi M.; Yamauchi Y. Spin correlation in O2 chemisorption on Ni(111). Phys. Rev. Lett. 2015, 114, 016101. 10.1103/PhysRevLett.114.016101. [DOI] [PubMed] [Google Scholar]
- Kurahashi M. Oxygen adsorption on surfaces studied by a spin-and alignment-controlled O2 beam. Prog. Surf. Sci. 2016, 91, 29–55. 10.1016/j.progsurf.2016.03.001. [DOI] [Google Scholar]
- Gerbi A.; Savio L.; Vattuone L.; Pirani F.; Cappelletti D.; Rocca M. Role of Rotational Alignment in Dissociative Chemisorption and Oxidation: O2 on Bare and CO-Precovered Pd (100). Angew. Chem., Int. Ed. 2006, 45, 6655–6658. 10.1002/anie.200602180. [DOI] [PubMed] [Google Scholar]
- Vattuone L.; Gerbi A.; Cappelletti D.; Pirani F.; Gunnella R.; Savio L.; Rocca M. Selective production of reactive and nonreactive oxygen atoms on Pd(001) by rotationally aligned oxygen molecules. Angew. Chem. 2009, 121, 4939–4942. 10.1002/ange.200900870. [DOI] [PubMed] [Google Scholar]
- Vattuone L.; Savio L.; Pirani F.; Cappelletti D.; Okada M.; Rocca M. Interaction of rotationally aligned and of oriented molecules in gas phase and at surfaces. Prog. Surf. Sci. 2010, 85, 92–160. 10.1016/j.progsurf.2009.12.001. [DOI] [Google Scholar]
- Moritani K.; Tsuda M.; Teraoka Y.; Okada M.; Yoshigoe A.; Fukuyama T.; Kasai T.; Kasai H. Effects of Vibrational and Rotational Excitations on the Dissociative Adsorption of O2 on Cu Surfaces. J. Phys. Chem. C 2007, 111, 9961–9967. 10.1021/jp0718496. [DOI] [Google Scholar]
- Wendelken J. The chemisorption of oxygen on Cu(110) studied by EELS and LEED. Surf. Sci. 1981, 108, 605–616. 10.1016/0039-6028(81)90568-9. [DOI] [Google Scholar]
- Briner B.; Doering M.; Rust H.-P.; Bradshaw A. M. Mobility and trapping of molecules during oxygen adsorption on Cu(110). Phys. Rev. Lett. 1997, 78, 1516. 10.1103/PhysRevLett.78.1516. [DOI] [Google Scholar]
- Prabhakaran K.; Sen P.; Rao C. N. R. Studies of molecular oxygen adsorbed on Cu surfaces. Surf. Sci. 1986, 177, L971–L977. 10.1016/0039-6028(86)90130-5. [DOI] [Google Scholar]
- Rajumon M.; Prabhakaran K.; Rao C. Adsorption of oxygen on (100), (110) and (111) surfaces of Ag, Cu and Ni: an electron spectroscopic study. Surf. Sci. 1990, 233, L237–L242. 10.1016/0039-6028(90)90169-9. [DOI] [Google Scholar]
- Liem S.; Clarke J.; Kresse G. Pathways to dissociation of O2 on Cu (110) surface: first principles simulations. Surf. Sci. 2000, 459, 104–114. 10.1016/S0039-6028(00)00451-9. [DOI] [Google Scholar]
- Liem S.; Clarke J.; Kresse G. Dissociation pathways of oxygen on copper (110) surface: a first principles study. Comput. Mater. Sci. 2000, 17, 133–140. 10.1016/S0927-0256(00)00010-0. [DOI] [Google Scholar]
- Diao Z. Y.; Han L. L.; Wang Z. X.; Dong C. C. The adsorption and dissociation of O2 on Cu low-index surfaces. J. Phys. Chem. B 2005, 109, 5739–5745. 10.1021/jp0457803. [DOI] [PubMed] [Google Scholar]
- Ge J.-Y.; Dai J.; Zhang J. Z. Dissociative adsorption of O2 on Cu(110) and Cu(100): Three-dimensional quantum dynamics studies. J. Phys. Chem. 1996, 100, 11432–11437. 10.1021/jp960776f. [DOI] [Google Scholar]
- Nesbitt A.; Lewin A.; Hodgson A. Adsorption of oxygen on Cu(110). J. Phys.: Condens. Matter 1991, 3, S71. [Google Scholar]
- Hodgson A.; Lewin A.; Nesbitt A. Dissociative chemisorption of O2 on Cu(110). Surf. Sci. 1993, 293, 211–226. 10.1016/0039-6028(93)90315-B. [DOI] [Google Scholar]
- Ertl G. Untersuchung von oberflächenreaktionen mittels beugung langsamer elektronen (LEED): I. Wechselwirkung von O2 und N2O mit (110)-, (111)- und (100)-Kupfer-Oberflächen. Surf. Sci. 1967, 6, 208–232. 10.1016/0039-6028(67)90005-2. [DOI] [Google Scholar]
- Jensen F.; Besenbacher F.; Laegsgaard E.; Stensgaard I. Surface reconstruction of Cu(110) induced by oxygen chemisorption. Phys. Rev. B 1990, 41, 10233. 10.1103/PhysRevB.41.10233. [DOI] [PubMed] [Google Scholar]
- Sun L.; Hohage M.; Denk R.; Zeppenfeld P. Oxygen adsorption on Cu(110) at low temperature. Phys. Rev. B 2007, 76, 245412. 10.1103/PhysRevB.76.245412. [DOI] [Google Scholar]
- Döbler U.; Baberschke K.; Haase J.; Puschmann A. Azimuthal-and Polar-Angle-Dependent Surface Extended X-Ray–Absorption Fine-Structure Study:(2 × 1) O on Cu (110). Phys. Rev. Lett. 1984, 52, 1437. 10.1103/PhysRevLett.52.1437. [DOI] [Google Scholar]
- Coulman D. J.; Wintterlin J.; Behm R.; Ertl G. Novel mechanism for the formation of chemisorption phases: The (2 × 1) O-Cu (110) “added row” reconstruction. Phys. Rev. Lett. 1990, 64, 1761. 10.1103/PhysRevLett.64.1761. [DOI] [PubMed] [Google Scholar]
- Feidenhans R.; Grey F.; Nielsen M.; Besenbacher F.; Jensen F.; Laegsgaard E.; Stensgaard I.; Jacobsen K. W.; Nørskov J. K.; Johnson R. Oxygen chemisorption on Cu (110): A model for the c(6 × 2) structure. Phys. Rev. Lett. 1990, 65, 2027. 10.1103/PhysRevLett.65.2027. [DOI] [PubMed] [Google Scholar]
- Liu W.; Wong K.; Zeng H.; Mitchell K. What determines the structures formed by oxygen at low index surfaces of copper?. Prog. Surf. Sci. 1995, 50, 247–257. 10.1016/0079-6816(95)00059-3. [DOI] [Google Scholar]
- Lian X.; Xiao P.; Liu R.; Henkelman G. Calculations of the (2 × 1)-O reconstruction kinetics on Cu(110). J. Chem. Phys. 2017, 146, 111101. 10.1063/1.4978578. [DOI] [PubMed] [Google Scholar]
- Holloway S.; Gadzuk J. Charge transfer, vibrational excitation, and dissociative adsorption in molecule-surface collisions: Classical trajectory theory. J. Chem. Phys. 1985, 82, 5203–5215. 10.1063/1.448645. [DOI] [Google Scholar]
- Diño W. A.; Kasai H.; Okiji A. Orientational effects in dissociative adsorption/associative desorption dynamics of H2(D2) on Cu and Pd. Prog. Surf. Sci. 2000, 63, 63–134. 10.1016/S0079-6816(99)00019-2. [DOI] [Google Scholar]
- Kasai H.; Diño W. A.; Muhida R. Surface science-based reaction design: increasing the ortho-para hydrogen conversion yield via molecular orientation, a case study. Prog. Surf. Sci. 2003, 72, 53–86. 10.1016/S0079-6816(03)00009-1. [DOI] [Google Scholar]
- Diño W. A. Can we probe local surface reactivity with hydrogen molecules?. J. Phys.: Condens. Matter 2002, 14, 4379–4384. [Google Scholar]
- Ertl G. Reactions at well-defined surfaces. Surf. Sci. 1994, 299–300, 742–754. 10.1016/0039-6028(94)90694-7. [DOI] [Google Scholar]
- Shimada I.; Wagner U. Peruvian Black Pottery Production and Metalworking: A Middle Sicán CraftWorkshop at Huaca Sialupe. MRS Bull. 2001, 26, 25–30. 10.1557/mrs2001.15. [DOI] [Google Scholar]
- Okada M.; Teraoka Y. Active oxidation of Cu3Au(110) using hyperthermal O2 molecular beam. Appl. Surf. Sci. 2010, 256, 5676–5680. 10.1016/j.apsusc.2010.03.020. [DOI] [Google Scholar]
- Okada M.; Tsuda Y.; Oka K.; Kojima K.; Diño W. A.; Yoshigoe A.; Kasai H. Experimental and theoretical studies on oxidation of Cu-Au alloy surfaces: effect of bulk Au concentration. Sci. Rep. 2016, 6, 1–8. 10.1038/srep31101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerlach W.; Stern O. Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld. Zeitschrift für Physik 1922, 9, 349–352. 10.1007/BF01326983. [DOI] [Google Scholar]
- Hershbach D. In Molecular Beams in Physics and Chemistry: From Otto Sternas Pioneering Exploits to Present-Day Feats; Friedrich B., Schmidt-Boecking H., Eds.; Springer, 2021; pp 1–22. [Google Scholar]
- Tsuda Y.; Oka K.; Makino T.; Okada M.; Diño W. A.; Hashinokuchi M.; Yoshigoe A.; Teraoka Y.; Kasai H. Initial stages of Cu3Au (111) oxidation: oxygen induced Cu segregation and the protective Au layer profile. Phys. Chem. Chem. Phys. 2014, 16, 3815–3822. 10.1039/c3cp54709d. [DOI] [PubMed] [Google Scholar]
- Trinh Q. T.; Yang J.; Lee J. Y.; Saeys M. Computational and experimental study of the Volcano behavior of the oxygen reduction activity of PdM@PdPt/C (M = Pt, Ni, Co, Fe, and Cr) core-shell electrocatalysts. J. Catal. 2012, 291, 26–35. 10.1016/j.jcat.2012.04.001. [DOI] [Google Scholar]
- Moritani K.; Okada M.; Sato S.; Goto S.; Kasai T.; Yoshigoe A.; Teraoka Y. Photoemission study of the translational energy induced oxidation processes on Cu(111). Journal of Vacuum Science and Technology. A 2004, 22, 1625–1630. 10.1116/1.1743254. [DOI] [Google Scholar]
- Over H.; Gilarowski G.; Niehus H. The composition and structure of Cu3Au(110)-(4 × 1): a low-energy electron diffraction analysis. Surf. Sci. 1997, 381, L619–L622. 10.1016/S0039-6028(97)00086-1. [DOI] [Google Scholar]
- Fain S. Jr; McDavid J. Work-function variation with alloy composition: Cu-Au. Phys. Rev. B 1976, 13, 1853. 10.1103/PhysRevB.13.1853. [DOI] [Google Scholar]
- Lide D.CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, 1998. [Google Scholar]
- Ueta H.; Kurahashi M. Dynamics of O2 Chemisorption on a Flat Platinum Surface Probed by an Alignment-Controlled O2 Beam. Angew. Chem., Int. Ed. 2017, 56, 4174–4177. 10.1002/anie.201612281. [DOI] [PubMed] [Google Scholar]
- Citri O.; Baer R.; Kosloff R. The role of non adiabatic mechanisms in the dissociation dynamics of O2 on silver surfaces. Surf. Sci. 1996, 351, 24–42. 10.1016/0039-6028(95)01269-9. [DOI] [Google Scholar]
- Katz G.; Zeiri Y.; Kosloff R. Nonadiabatic charge transfer processes of oxygen on metal surfaces. Isr. J. Chem. 2005, 45, 27–36. 10.1560/TFF4-Y5JM-3LPQ-D2FJ. [DOI] [Google Scholar]
- Kohn W.; Sham L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- Hohenberg P.; Kohn W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
- Kresse G.; Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Hafner J. Ab initio simulation of the metal/nonmetal transition in expanded fluid mercury. Phys. Rev. B 1997, 55, 7539. 10.1103/PhysRevB.55.7539. [DOI] [Google Scholar]
- Kresse G.; Hafner J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251. 10.1103/PhysRevB.49.14251. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- Perdew J. P.; Chevary J. A.; Vosko S. H.; Jackson K. A.; Pederson M. R.; Singh D. J.; Fiolhais C. Atoms molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671. 10.1103/PhysRevB.46.6671. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Monkhorst H. J.; Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
- Tang W.; Sanville E.; Henkelman G. A grid-based Bader analysis algorithm without lattice bias. J. Phys.: Condens. Matter 2009, 21, 084204. [DOI] [PubMed] [Google Scholar]
- Sanville E.; Kenny S. D.; Smith R.; Henkelman G. Improved grid-based algorithm for Bader charge allocation. J. Comput. Chem. 2007, 28, 899–908. 10.1002/jcc.20575. [DOI] [PubMed] [Google Scholar]
- Henkelman G.; Arnaldsson A.; Jónsson H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. 10.1016/j.commatsci.2005.04.010. [DOI] [Google Scholar]
- Yu M.; Trinkle D. R. Accurate and efficient algorithm for Bader charge integration. J. Chem. Phys. 2011, 134, 064111. 10.1063/1.3553716. [DOI] [PubMed] [Google Scholar]
- Momma K.; Izumi F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. 10.1107/S0021889811038970. [DOI] [Google Scholar]