First‐Principles Studies on the Atomistic Properties of Metallic Magnesium as Anode Material in Magnesium‐Ion Batteries

Abstract

Rechargeable magnesium‐ion batteries (MIBs) are a promising alternative to commercial lithium‐ion batteries (LIBs). They are safer to handle, environmentally more friendly, and provide a five‐time higher volumetric capacity (3832 mAh cm⁻³) than commercialized LIBs. However, the formation of a passivation layer on metallic Mg electrodes is still a major challenge towards their commercialization. Using density functional theory (DFT), the atomistic properties of metallic magnesium, mainly well‐selected self‐diffusion processes on perfect and imperfect Mg surfaces were investigated to better understand the initial surface growth phenomena. Subsequently, rate constants and activation temperatures of crucial diffusion processes on Mg(0001) and Mg(10$\bar{1}$ 1) were determined, providing preliminary insights into the surface kinetics of metallic Mg electrodes. The obtained DFT results provide a data set for parametrizing a force field for metallic Mg or performing kinetic Monte‐Carlo simulations.

Magnesium anode: In a density functional theory study, we investigate the fundamental surface and diffusion properties of metallic magnesium, which is used as anode material in magnesium‐ion batteries. Our work provides deep insights into the ongoing surface growth mechanism by discussing the energy barriers and the activation temperatures of various diffusion processes on Mg(0001) and Mg(10$\bar{1}$ 1).

Introduction

Rechargeable batteries are of outstanding importance in achieving global climate goals as they play a key role in electronic applications, in the mobility sector for the electrification of cars, or stationary grid energy storage systems for surplus wind and solar power. The most prominent representatives are Lithium‐ion batteries (LIBs),[ ¹ , ² , ³ , ⁴ , ⁵ ] which are facing controversy due to the use of critical raw materials such as lithium, cobalt, nickel, or graphite. ^[6] Metallic lithium anodes have a high theoretical capacity (3861 mAh g⁻¹), the lowest negative electrochemical potential (−3.04 V vs. standard hydrogen electrode (SHE)), and a low density (0.59 g cm⁻³), however, are prone to form dendrites. ^[7] Dendrites are needle‐shaped structures leading to short circuits, thermal runaways, and even battery failures, although promising approaches such as the electrostatic shielding of the lithium surface through additives have been proposed to tackle this problem. ^[8] Due to these safety concerns, graphite with intercalated lithium ions is still used as anode material in commercial LIBs, reducing its theoretical capacity by roughly one order of magnitude to 372 mAh g⁻¹ in present day commercial LIBs. ^[9]

Therefore, rechargeable multivalent magnesium‐ion batteries (MIBs) have emerged as a promising alternative, mainly due to the bivalency of the magnesium atom, which allows it to carry twice the charge resulting in a higher volumetric capacity (3833 mAh cm⁻³ vs. 777 mAh cm⁻³ of graphite anodes in commercial LIBs). ^[10] Additionally, magnesium has a low electrochemical potential (−2.37 V vs. SHE), is highly abundant, of low cost, and is environmentally friendly. These benefits are reflected in the exponentially increasing number of publications that have recently been dedicated to the topic of MIBs, as shown in Figure 1 from the publication by Li et al. ^[11] On the other hand, a great deal of effort is required to find suitable electrolytes that allow reversible magnesium deposition while at the same time providing a broad electrochemical window.[ ⁹ , ¹² ] Conventional carbonate electrolytes cannot be used for rechargeable MIBs because the solid‐electrolyte interface (SEI) formed by decomposition products of the electrolyte is not permeable to magnesium cations, in contrast to lithium cations.[ ¹⁰ , ¹³ ] Proposed solutions are electrolytes based on Grignard reagents, Mg(TFSI)₂ salts or ionic liquids, as well as the use of polymeric interlayers as artificial SEI.[ ¹³ , ¹⁴ ] Nevertheless, the structure and growth mechanism of SEI formation remains poorly understood due to its high complexity, highlighting the need for adequate theoretical modeling on different time and length scales. ^[15]

Figure 1.

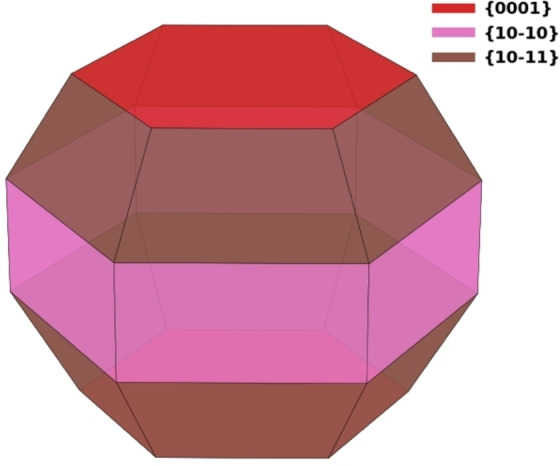
Thermodynamic equilibrium shape of a magnesium crystal as determined by the calculated Wulff construction. All surface energies (PBE) from Table S5 were included in the evaluation of the Wulff shape.

The second controversial issue is whether dendrite formation is possible on metallic magnesium anodes. On the one hand, the tendency of occurrence is significantly lower than for the lithium equivalent, ^[16] yet dendrites have been demonstrated under harsh deposition conditions, as shown by the Banerjee group. ^[17] As a result, there have been requests to conduct experiments to determine critical current densities ^[18] and to define precise voltage windows ^[19] for dendrite‐free regions. In a recently published study, the critical overpotential of dendrite formation on lithium, sodium, and magnesium was calculated using a grand‐canonical density functional theory (DFT) approach, indicating a combination of high surface tension, low surface capacitance, and low potential of zero charge (PZC) as indicators for mitigated dendrite growth. ^[20] Another explanation for enhanced dendrite growth on lithium compared to magnesium surfaces includes the accumulation of negative excess charges at the peaks of protrusions of the lithium electrodes inducing a strong electric field that attracts further lithium cations. ^[21] In addition, lower step‐down and terrace self‐diffusion barriers of magnesium compared to lithium are considered responsible for the reduced dendrite growth.[ ²² , ²³ ]

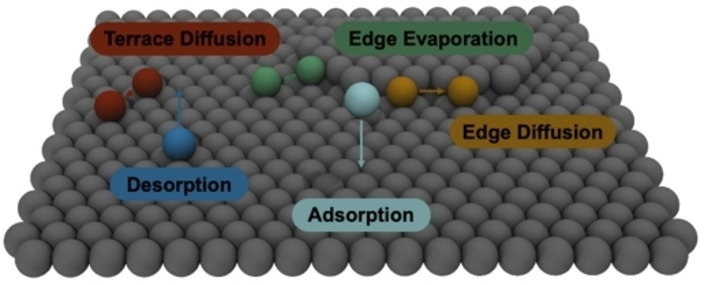
In this work, periodic DFT calculations have been performed to determine the atomistic properties of magnesium and to explain the initial stages of surface growth. This technique has previously been applied for lithium ^[24] and sodium ^[25] in our group. For this purpose, the bulk, surface, and adsorption properties of magnesium were first calculated. Based on the obtained surface energies, the corresponding equilibrium shape of a magnesium crystal was determined within the framework of the Wulff construction. ^[26] Subsequently, a wide variety of two‐ and three‐dimensional diffusion processes on perfect and imperfect Mg(0001) and Mg(10$\bar{1}$ 1) surfaces were investigated and analyzed concerning surface growth phenomena. Finally, the obtained DFT results provide a data set for parametrizing a force field for metallic Mg or performing kinetic Monte‐Carlo studies.[ ²⁷ , ²⁸ ]

Results and Discussion

Surface properties and Wulff construction of a magnesium crystal

The surface energy [Eq. (1)] is regarded as a measure for the stability of a surface and determines the equilibrium shape of a crystal. ^[29] In agreement with literature,[ ³⁰ , ³¹ , ³² ] Mg(0001) is the most stable crystal surface, followed by Mg(10$\bar{1}$ 0)A and Mg(10$\bar{1}$ 1), which differ in our calculations by less than 1 meV Å⁻² (Table 1). Mg(0001) lies in the basal plane of the hcp unit cell, which is characterized by a particularly high packing density, resulting in thermodynamic stabilization. ^[33] At this point, we refer to the work of Tang et al., who established a model to predict the relative stability of magnesium surfaces based on the number of broken basal and non‐basal bonds. ^[34] They also showed that Friedel oscillations are especially present on low‐index Mg surfaces, influencing surface relaxation. On the other hand, on high index surfaces, relaxation is driven by charge depletion and charge smoothing effects. In an embedded atom method (EAM) potential study, Mg (10$\bar{1}$ 1) was considered to be the second most stable surface, which is not the case according to our DFT calculations. ^[35] Caution is required for Mg(10$\bar{1}$ 0) since there are two possible surface terminations Mg(10$\bar{1}$ 0)A and Mg (10$\bar{1}$ 0)B, which are shown in Figure S2. Mg(10$\bar{1}$ 0)B differs from Mg(10$\bar{1}$ 0)A by one missing row and is characterized by parallel atomic lines making deep channels. Mg(10$\bar{1}$ 0)A also has channels, but not as distinct as in Mg(10$\bar{1}$ 0)B. Surface energies calculated with the BEEF‐vdW functional are generally lower but have the same stability sequence. All PBE results are within the error range of the BEEF‐vdW functional. Further surface energies (that also entered the following Wulff construction) and a literature data summary are provided in Table S5. In addition, we refer to the adsorption properties chapter in the Supporting Information for a detailed adsorption energy study of Mg on Mg(0001), Mg(10$\bar{1}$ 0)A, Mg(10$\bar{1}$ 0)B and Mg(10$\bar{1}$ 1).

Table 1.

Surface energies γ for selected magnesium surfaces calculated with Equation (1) and from literature. For the BEEF‐vdW functional, the calculated standard deviations of the surface energies are given in parenthesis.

Surface	$\gamma$ [meV Å−2]
	this work		other work
	PBE	BEEF‐vdW	experiment [38]
Mg(0001)	33.9	38.7 (9)	51.0
Mg(10$\stackrel{-}{1}$ 0)A	40.3	44.9 (9)
Mg(10$\stackrel{-}{1}$ 1)	40.9	45.8 (8)
Mg(10$\stackrel{-}{1}$ 0)B	55.5	59.4 (11)

Interestingly, and as already shown in literature,[ ³⁰ , ³¹ ] the Wulff construction (Figure 1) reveals for both functionals (PBE, BEEF‐vdW) a reverse order of the area fractions versus surface energies. Our calculations confirm that Mg(10$\bar{1}$ 1) has the largest area share with 48.6 % (Table 2), although it is only the third most stable surface, followed by Mg(10$\bar{1}$ 0)A (27.9 %) and Mg(0001) (23.7 %) as shown in Table 2. Other publications also assign Mg(11$\bar{2}$ 0) area fractions in the Wulff construction, which was not observed in our case.[ ³⁵ , ³⁶ ] It is important to mention that even over a wide potential range, the shape of the magnesium crystal behaves almost constant, which suggests that in the working potential range of magnesium batteries, our calculated surface area fractions are still valid. ^[37] The calculated area fractions emphasize the need to study the diffusion properties of all three surfaces collectively, rather than looking at one surface termination individually.

Table 2.

Calculated (PBE and BEEF‐vdW) and literature area fractions of the magnesium surface Mg(0001), Mg(10$\bar{1}$ 0)A, and Mg(10$\bar{1}$ 1) from the calculated Wulff construction shown in Figure 1.

Functional	Area fraction [%]			Ref.
	Mg(0001)	Mg(10$\bar{1}$ 0)A	Mg(10$\bar{1}$ 1)
PBE	23.7	27.9	48.6	this work
BEEF‐vdW	22.4	25.8	50.5	this work
PBE	22.5	27.2	49.5	[30]
PBE	25.0	33.0	42.0	[31]

Terrace self‐diffusion on Mg(0001), Mg(10$\bar{1}$ 0)A, and Mg(10$\bar{1}$ 1)

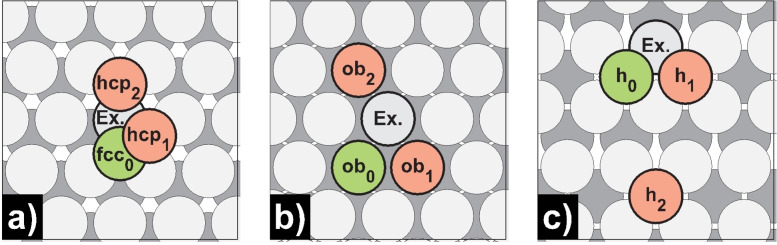
To understand the mobility of Mg atoms on defect‐free surfaces, we examined the terrace self‐diffusion barriers on the three thermodynamic most stable surfaces Mg(0001), Mg(10$\bar{1}$ 0)A, and Mg(10$\bar{1}$ 1). A schematic illustration of the initial (atoms marked in green) and final (atoms marked in red) positions is shown in Figure 2. The respective barriers were calculated with Equation (2) and are summarized in Table 3. Additionally, estimated prefactors and room‐temperature reaction rates, calculated with Equation (5), are provided for the PBE and the BEEF‐vdW functionals in the Supporting Information, as well as the energy profiles of the respective processes (Table S7, Table S8, Figure S4).

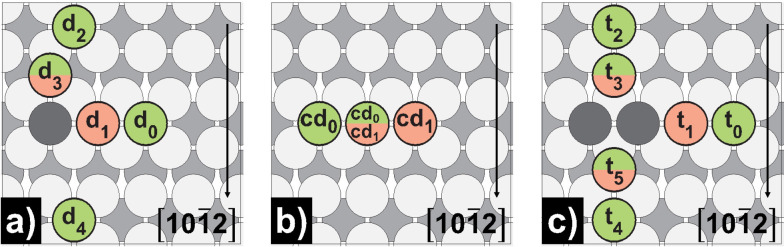
Figure 2.

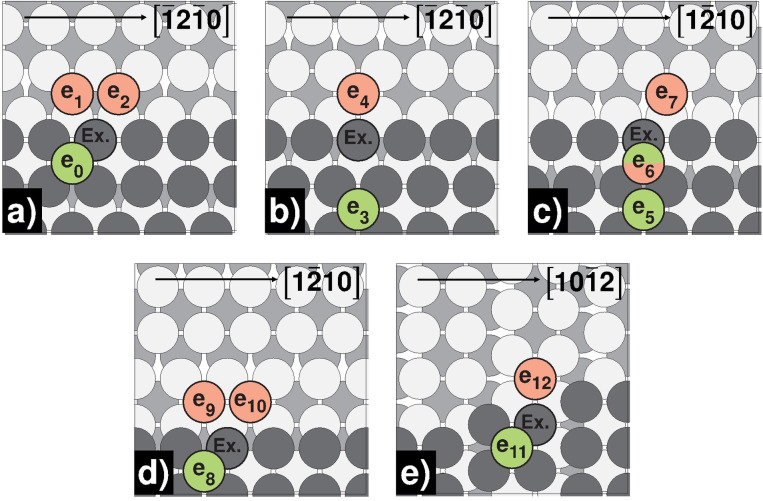
Schematic representation of terrace self‐diffusion processes on a) Mg(0001), b) Mg(10$\bar{1}$ 0)A, and c) Mg(10$\bar{1}$ 1). Green‐colored atoms mark the initial, while red‐colored atoms mark the final positions.

Table 3.

Activation energies E _a for forward and backward terrace self‐diffusion processes calculated with Equation (2) (PBE and BEEF‐vdW) and from literature. For the BEEF‐vdW functional the calculated standard deviations of the activation energies are given in parentheses.

Terrace	Pathway	E a for [eV]			E a rev [eV]
		this work		other work	this work		other work
		PBE	BEEF‐vdW	PBE	PBE	BEEF‐vdW	PBE
Mg(0001)	fcc0↔hcp1	0.02	0.02 (0.02)	0.02[ 23 , 30 , 39 ], 0.03 [36]	0.01	0.01 (0.01)	0.02[ 23 , 30 , 39 ], 0.03 [36]
	fcc0↔hcp2 (Ex.)	0.74	0.79 (0.23)	0.79 [30]	0.72	0.77 (0.23)	0.79 [30]
Mg(10$\bar{1}$ 0)A	ob0↔ob1	0.02	0.02 (0.04)	0.02 [30]	0.02	0.02 (0.04)	0.02 [30]
	ob0↔ob2	0.42	0.35 (0.15)	0.45 [30]	0.42	0.35 (0.15)	0.45 [30]
	ob0↔ob2 (Ex.)	0.46	0.47 (0.14)	0.56 [30]	0.46	0.47 (0.14)	0.56 [30]
Mg(10$\bar{1}$ 1)	h0↔h1	0.30	0.27 (0.06)	0.29 [30]	0.30	0.27 (0.06)	0.29 [30]
	h0↔h1 (Ex.)	0.59	0.62 (0.16)	0.57 [30]	0.59	0.62 (0.16)	0.57 [30]
	h0↔h2	0.42	0.38 (0.08)	0.41 [30]	0.42	0.38 (0.08)	0.41 [30]

Diffusion of a single Mg adatom on Mg(0001) occurs almost barrier‐free from the thermodynamic most stable fcc to the slightly increased hcp position in a hopping mechanism [fcc₀→hcp₁, E _a=0.02 eV]. Roe et al. justified the low terrace self‐diffusion barrier on Mg(0001) with the small coordination number of 3 of the migrating atom, an intrinsic property of the hexagonally close‐packed {0001}‐facet. ^[39] A possible exchange process for Mg(0001) seems highly unfavorable [fcc₀→hcp₂ (Ex.), E _a=0.74 eV], which is also true for all investigated Mg surfaces in contrast to the alkali metal Na(100) in which the exchange process is dominating. ^[25] The morphology of Mg(10$\bar{1}$ 0)A is characterized, as mentioned earlier, by channels running parallel to each other. Diffusion within a channel has a minor barrier [ob₀↔ob₁, E _a=0.02 eV], while transitions across channels have approximately 20‐fold higher barriers for hopping and exchange processes [ob₀↔ob₂, E _a=0.42 eV; ob₀↔ob₂ (Ex.), E _a=0.46 eV]. In the case of Mg(10$\bar{1}$ 1), diffusion between adjacent and opposite hollow positions was studied. Adjacent diffusion [h₀↔h₁, E _a=0.30 eV] is more likely than diffusion between opposing sites [h₀↔h₂, E _a=0.42 eV]. The PBE and BEEF‐vdW calculations are consistent and in agreement with literature.[ ²³ , ³⁰ , ³⁶ , ³⁹ ] Recently, Jäckle et al. suggested that the low terrace self‐diffusion barrier of magnesium on Mg(0001) may indicate the lack of dendrite growth. ^[23] This statement should be evaluated considering that the barriers on Mg(10$\bar{1}$ 1), the surface with the largest area fraction of the Wulff particle, are several times higher than for Mg(0001), which is also valid on Mg(10$\bar{1}$ 0)A for diffusion across a channel.

Dimer interaction energies on Mg(0001), Mg(10$\bar{1}$ 0)A, and Mg(10$\bar{1}$ 1)

The formation of polyatomic clusters represents the first stage of island formation. Here the question arises if attractive or repulsive interactions between adatoms are at play, resulting in a uniform distribution of the adsorbates or the formation of dimer, trimer, or cluster structures. Thus, we calculated the interaction energies E _int with Equation (3) for merged and more distant dimer configurations, as shown in Figure 3. Our calculations reveal high negative interaction energies between two merged Mg adsorbates (second atom placed at position 1 or 6 for Mg(0001), 1 for Mg(10$\bar{1}$ 0), and 1 or 4 for Mg(10$\bar{1}$ 1)) and an interaction energy sequence given by E _{int„Mg(0001)}>E _int,Mg(10 ${}_{\bar{1}}$ ₁₎>E _int,Mg(10 ${}_{\bar{1}}$ _0)A, as shown in detail in Tables 4, 5, and 6. The differences in interaction energies may be related directly to the number of nearest surface atoms of the adsorbates following the opposite order (3_Mg(0001)<4_Mg(10 ${}_{\bar{1}}$ ₁₎<5_Mg(10 ${}_{\bar{1}}$ _0)A). The two possible merged dimer conformations on Mg(0001) are shown in Figure 4. Notice the final configuration in Figure 4a, which results from placing the second atom at position 1. Interestingly, both atoms are no longer in their initial fcc‐ but moved to bridge‐like positions after relaxation. Moreover, the dimer relaxes to the same final configuration when both atoms are initially placed in the neighboring hcp positions with an interaction energy of 0.51 eV. In the thermodynamically more stable merged dimer conformation (E _int=0.54 eV), one atom is located in an fcc or hcp position above a surface atom, as shown in Figure 4b. One should note that on Mg(0001), the more distant dimer configurations (second atom at position 2, 3, 5, or 8) also exhibit negative interaction energies for the PBE functional (E _int<−0.03 eV), which are on the order of the terrace self‐diffusion barrier. If the second Mg adsorbate is initially placed in positions 4 and 7, in the relaxed geometry, the atom moves to position 6 (same geometry as in Figure 4b). Two conformations with noticeable interaction energies are also present on Mg(10$\bar{1}$ 1). In the thermodynamically more stable conformation, both adsorbates are in adjacent hollow positions (0 & 3) and have an interaction energy of −0.31 eV. In the thermodynamic less stable conformation, one atom sits in a hollow‐ and the other in an fcc‐like position (0 & 1). Since the atom sitting in fcc position coordinates to only three surface atoms, the interaction to the second adsorbate is slightly higher (−0.35 eV). For the BEEF‐vdW functional, the differences in interaction energies are less pronounced for the two dimer conformations on Mg(10$\bar{1}$ 1) and drop at greater atom distances for all investigated surfaces to negligible values (|E _int|≤0.02 eV). Nevertheless, the PBE interaction energy sequence is consistent with the BEEF‐vdW calculations and literature but differs in representing the long‐range attraction.[ ²³ , ³⁰ ]

Figure 3.

Schematic illustration of dimer configuration sites for the interaction energies E _int given in Table 4, Table 5, and Table 6 for a) Mg(0001), b) Mg(10$\bar{1}$ 0)A, and c) Mg(10$\bar{1}$ 1). The first atom is always located at the green position 0, while the second adatom is initially placed on the red positions.

Table 4.

Calculated (PBE/BEEF‐vdW) and theoretical reference dimer interaction energies E _int of two Mg adatoms adsorbed on (6×6) Mg(0001). E _int was calculated with Equation (3) and the adatoms were initially placed at positions 0 & x. For the BEEF‐vdW functional, the calculated standard deviation of the dimer interaction energy E _int is given in parenthesis.

Position	E int [eV] for Mg(0001)
	this work		other work
	PBE	BEEF‐vdW	PBE	Ref.
0 & 1	−0.51	−0.40 (0.13)	−0.50	[22,30]
0 & 2	−0.05	−0.02 (0.12)	–	–
0 & 3	−0.04	0.00 (0.09)	–	–
0 & 4[a]	−0.54	−0.43 (0.11)	−0.05	[30]
0 & 5	−0.03	0.01 (0.13)	–	–
0 & 6	−0.54	−0.43 (0.11)	−0.50	[22]
0 & 7[a]	−0.54	−0.43 (0.11)	–	–
0 & 8	−0.04	−0.01 (0.08)	–	–

[a] Not stable; transition into fcc‐hcp configuration (Figure 4b); second atom moves to position 6.

Table 5.

Calculated (PBE/BEEF‐vdW) and theoretical reference dimer interaction energies E _int of two Mg adatoms on (6×3) Mg(10$\bar{1}$ 0)A. E _int was calculated with Equation (3) and the adatoms were initially placed at positions 0 & x. For the BEEF‐vdW functional, the calculated standard deviation of the dimer interaction energy $E_{\mathrm{i}\mathrm{n}\mathrm{t}}$ is given in parenthesis.

Position	E int [eV] for Mg(10$\bar{1}$ 0)A
	this work		other work
	PBE	BEEF‐vdW	PBE	Ref.
0 & 1	−0.28	−0.25 (0.06)	−0.25	[30]
0 & 2	−0.01	−0.02 (0.01)	–	–
0 & 3	0.02	0.02 (0.02)	–	–
0 & 4	0.01	0.01 (0.01)	–	–

Table 6.

Calculated (PBE/BEEF‐vdW) and theoretical reference dimer interaction energies E _int of two Mg adatoms adsorbed on (6×3) Mg(10$\bar{1}$ 1). E _int was calculated with Equation (3) and the adatoms were initially placed at positions 0 & x. For the BEEF‐vdW functional, the calculated standard deviation of the dimer interaction energy E _int is given in parenthesis.

Position	E int [eV] for Mg(10$\bar{1}$ 1)
	this work		other work
	PBE	BEEF‐vdW	PBE	Ref.
0 & 1	−0.31	−0.28 (0.05)	−0.31	[30]
0 & 2	0.01	0.01 (0.02)	–	–
0 & 3	−0.01	0.00 (0.02)	–	–
0 & 4[a]	−0.35	−0.29 (0.07)	–	–
0 & 5	−0.01	−0.01 (0.02)	–	–

[a] Since the adsorption site of atom 4 is not stable outside of the dimer configuration, the adsorption energy for this atom was assumed to be equivalent to an fcc position on Mg(0001) to calculate the interaction energies.

Figure 4.

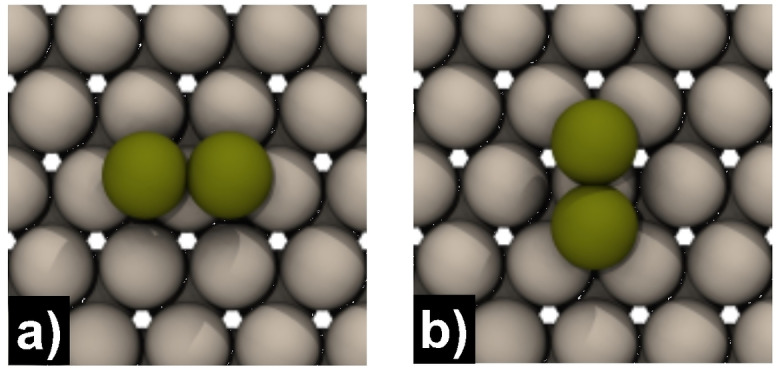
a) One of two possible merged dimer structures on Mg(0001) where both adsorbates are located at bridge‐like positions. b) The second thermodynamically more stable merged dimer structure with one adsorbate at an fcc and a hcp position.

Dimer and trimer self‐diffusion on Mg(0001) and Mg(10$\bar{1}$ 1)

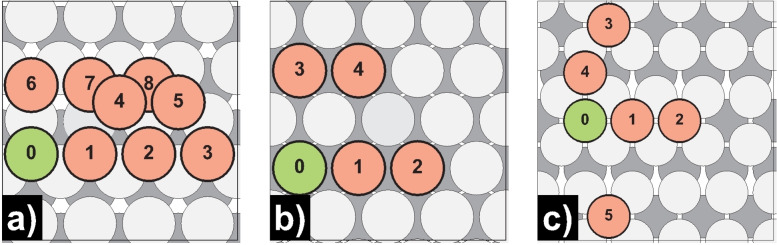
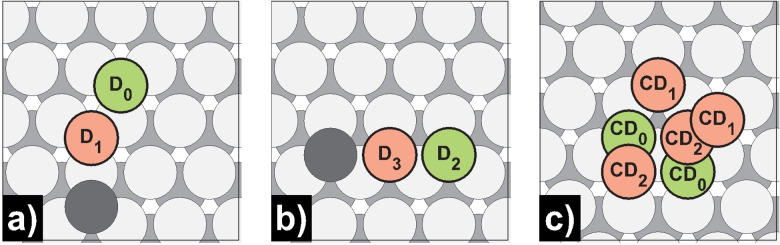
As the interaction energy studies have already indicated, the dimer and trimer diffusion barriers (Figure 5, Figure 6, Table 7) reveal that when two adsorbates meet on Mg(0001), they immediately agglomerate [D_0/2→D_1/3, E _a ^for<0.005 eV]. We could only detect a minor barrier below a certain distance, which we may explain, on the one hand, because of the low terrace self‐diffusion barrier on Mg(0001) (E _a=0.01/0.02 eV) and, on the other hand, the still evident dimer interaction energy at larger distances (e. g., −0.05 eV for adatoms at positions 0 & 2, which is the initial structure for the dimer merge II process). On the contrary, the activation energies for its separation are multiple times higher [D_1/3→D_0/2, E _a ^rev=0.49/0.46 eV], indicating that one dimer can already be considered a center for further island growth. Also noteworthy is that from the time of dimer formation, the propagation as a dimer on Mg(0001) is higher [CD₀↔CD₁, E_a=0.07 eV] than that of the monomer still, the dimer is highly mobile. The transition between the observed dimer configurations occurs almost barrierless [CD₀↔CD₂, E _a=0.01 eV].

Figure 5.

Schematic representation of dimer self‐diffusion processes on Mg(0001): a) dimer merge I; b) dimer merge II; c) dimer concerted. Green‐colored atoms mark the initial, while red‐colored atoms mark the final positions.

Figure 6.

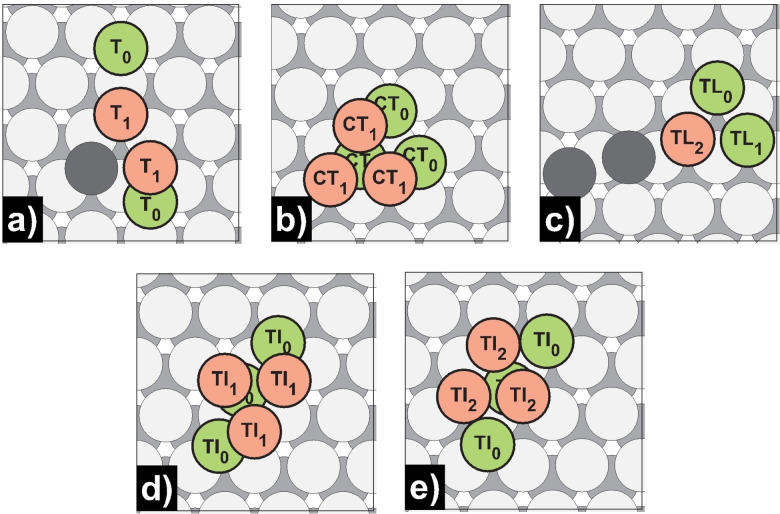
Schematic representation of trimer self‐diffusion processes on Mg(0001): a) trimer merge; b) trimer concerted; c) trimer linear; d) trimer interchange I; e) trimer interchange II. Green‐colored atoms mark the initial, while red‐colored atoms mark the final positions.

Table 7.

Activation energies E _a for forward and backward dimer and trimer self‐diffusion processes on Mg(0001) calculated with Equation (2) (PBE). The forward activation barriers for the dimer and trimer merge processes did not equal exactly 0.00 eV but were below 0.005 eV while rounding to the second decimal place.

Diffusin on Mg(0001)	Path	Pathway	E a for [eV]	E a rev [eV]
dimer	merge	D0↔D1	0.00	0.49
		D2↔D3	0.00	0.46
	concerted	CD0↔CD1	0.07	0.07
		CD0↔CD2	0.01	0.01
trimer	merge	T0↔T1	0.00	0.64
	concerted	CT0↔CT1	0.02	0.12
	linear	TL0↔TL2	0.01	0.47
		TL1↔TL2	0.02	0.46
	interchange	TI0↔TI1	0.06	0.17
		TI0↔TI2	0.07	0.20

On Mg(10$\bar{1}$ 1) (Figure 7 and Table 8), however, there are clearly distinguishable barriers for forward and reverse processes. In the case of two atoms approaching each other within a channel, the forward barrier is about half as large as the reverse barrier [d₀↔d₁, E _a ^for=0.25 eV, E_a ^rev=0.58 eV]. If dimer formation proceeds across the channel along the [10$\bar{1}$ 2]‐direction, diffusion takes place in a two‐step process, but with lower forward barriers in each case [d₂→d₃, E _a ^for=0.19 eV; d₃→d₁, E _a ^for=0.15 eV], making this process very likely to occur. The process across the channel opposite to the [10$\bar{1}$ 2]‐direction exhibits both the highest forward and reverse barrier for all investigated dimer formation processes [d₄↔d₁, E _a ^for=0.37 eV, E _a ^rev=0.67 eV]. Concerted movement of a dimer on Mg(10$\bar{1}$ 1) is again significantly increased compared to Mg(0001) [cd₀↔cd₁, E _a=0.54 eV], as already observed with terrace self‐diffusion.

Figure 7.

Schematic representation of dimer and trimer self‐diffusion processes on Mg(10$\bar{1}$ 1): a) dimer merge; b) dimer concerted; c) trimer merge. Green‐colored atoms mark the initial, while red‐colored atoms mark the final positions.

Table 8.

Activation energies E _a for forward and backward dimer and trimer self‐diffusion processes on Mg(10$\bar{1}$ 1) calculated with Equation (2) (PBE).

Diffusion on Mg(10$\bar{1}$ 1)	Path	Pathway	E a for [eV]	E a rev [eV]
dimer	merge	d0↔d1	0.25	0.58
		d2↔d3	0.19	0.13
		d3↔d1	0.15	0.51
		d4↔d1	0.37	0.67
	concerted	cd0↔cd1	0.54	0.54
trimer	merge	t0↔t1	0.26	0.58
		t2↔t3	0.19	0.20
		t3↔t1	0.27	0.54
		t4↔t5	0.31	0.57
		t5↔t1	0.24	0.28

If a third atom is approaching, a linear or a triangular trimer is formed, depending on the side of the attack. For Mg(0001), no or only extremely low barriers could be determined [T₀→T₁, E _a ^for=0.00 eV; TL_0/1→TL₂, E _a ^for=0.01/0.02 eV], as was already the case for the dimer formation. In turn, the linear form can transform itself into the thermodynamically more stable triangular trimer form. However, from a kinetic point of view, the barrier of the interchange to a hcp trimer is slightly lower [TI₀→TI₁, E _a=0.06 eV] than that of the fcc counterpart [TI₀→TI₂, E _a=0.07 eV]. Nevertheless, at a later stage, the hcp trimer should clearly switch to the thermodynamically preferred fcc position with a minor barrier [CD₀↔CD₁, E _a ^for=0.02 eV, E _a ^rev=0.12 eV].

On the other hand, this contrasts with the hcp packaging series of metallic Mg that should follow the ABABAB‐stacking sequence. Two questions arise, first, why are fcc sites favored over hcp sites for smaller islands, and second, at what critical island size does the original packing order become thermodynamically more stable again. Therefore, for islands up to a size of 7 atoms and full monolayers (MLs) (36 atoms) on (6×6) Mg(0001), the adsorption energies per atom were calculated as shown in Figure S5. Additionally, the exact adsorption energies per atom for the islands and for full hcp and fcc MLs, as well as the stacking fault energies, may be found in Table S9. It turns out that starting from a heptamer adsorption is slightly favored on hcp sites, while tetramers, pentamers, and hexamers are indifferent. This finding is consistent with the results of Ortigoza et al. The group confirmed stacking fault up to the trimer but also used only half of the unit cell size ((3×3) vs. (6×6)). They blame Friedel oscillations for inducing an increased charge density at the fcc pocket, which noticeably stabilizes the bond of the adsorbate to its nearest neighbors. At the same time, however, the increased charge density at adjacent fcc positions vanishes, which explains the renewed preference of the hcp position for larger adislands. ^[40]

On the second studied surface Mg(10$\bar{1}$ 1), the barriers for trimer formation are generally higher than on Mg(0001). In addition, the linear trimer form is thermodynamically more stable with respect to the triangular trimer form. If an atom encounters a dimer within a channel, the barriers are roughly equivalent to those of the dimer formation [t₀↔t₁, E _a ^for=0.26 eV, E _a ^rev=0.58 eV]. Diffusion across the channel proceeds in a two‐step process along [t₂→t₃, E _a ^for=0.19 eV; t₃→t₁, E _a ^for=0.27 eV] and opposite to the [10$\bar{1}$ 2]‐direction [t₄→t₅, E _a ^for=0.31 eV; t₅→t₁, E _a ^for=0.24 eV] with the triangle trimer form as intermediate. The barriers are very similar for all investigated processes, making it difficult to draw accurate predictions about the preferred pathway of trimer formation. However, surface growth should most likely proceed in a line along the hollow sites perpendicular to the [10$\bar{1}$ 2]‐direction. The use of kinetic Monte‐Carlo simulations could provide further insights. ^[41]

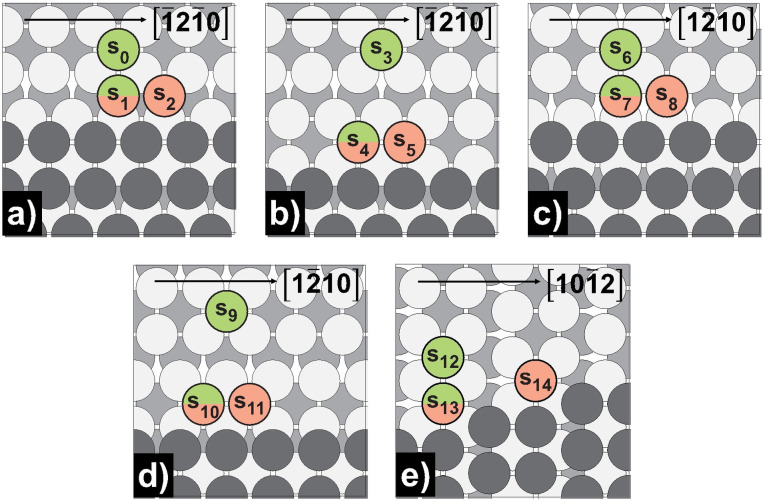
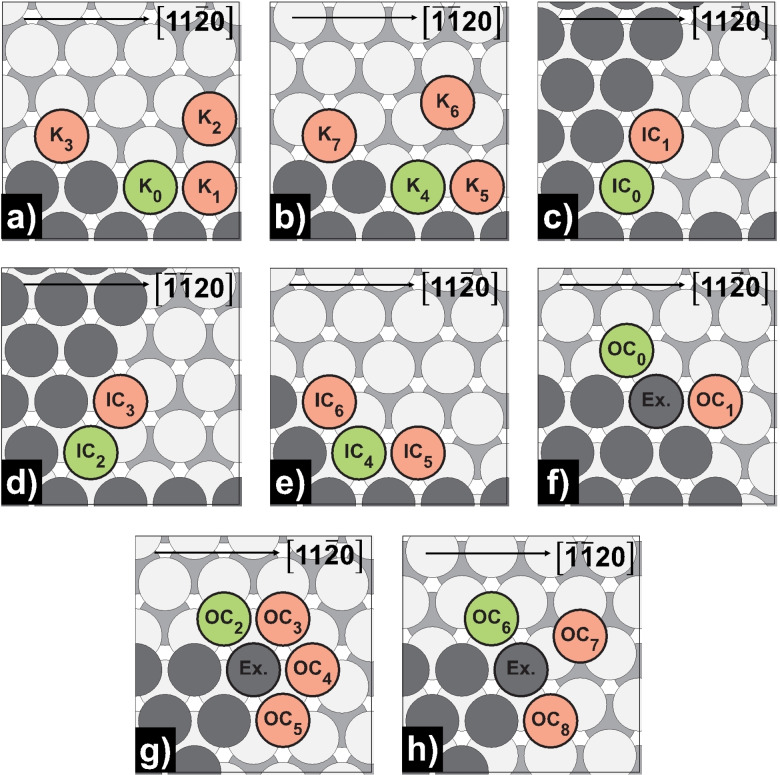
Step, kink, and corner self‐diffusion on Mg(0001) and Mg(10$\bar{1}$ 1)

After the formation of initial polyatomic clusters, we would like to discuss further surface growth, especially island formation, by studying additional processes of the terrace–step‐kink (TSK) model (step‐edge, step‐vacancy, kink, inner‐corner, and outer‐corner). ^[42] The TSK model describes the diffusion processes taking place during surface growth and discusses several growth mechanisms. ^[43] As described previously, islands on Mg(0001) are more stable on hcp sites starting from a heptamer. Thus, only processes at hcp steps, kinks, and corners were investigated, which consist of more than 7 atoms. The activation energies of the processes studied may be found in Table 9 for Mg(0001) and Table 10 for Mg(10$\bar{1}$ 1) with schematic representations shown in Figure 8, Figure 9, and Figure 10.

Table 9.

Activation energies E _a for forward and backward step‐edge, step‐vacancy, kink and corner self‐diffusion processes on Mg(0001) calculated with Equation (2) (PBE).

Diffusion on Mg(0001)	Path	Pathway	E a for [eV]	E a rev [eV]
step‐edge	[11$\bar{2}$ 0]‐step	S0↔S1	0.03	0.70
		S1↔S2	0.22	0.22
	[$\bar{1}$ $\bar{1}$ 20]‐step	S3↔S4	0.02	0.63
		S4↔S5	0.15	0.15
step‐vacancy	[11$\bar{2}$ 0]‐step	SV0↔SV1	0.03	1.15
	[$\bar{1}$ $\bar{1}$ 20]‐step	SV2↔SV3	0.02	1.23
kink	[11$\bar{2}$ 0]‐step	K0↔K1	0.45	0.17
		K0↔K2	0.91	0.02
		K0↔K3	0.51	0.29
	[$\bar{1}$ $\bar{1}$ 20]‐step	K4↔K5	0.46	0.12
		K4↔K6	0.92	0.01
		K4↔K7	0.56	0.22
inner‐corner	60° corner: [11$\bar{2}$ 0]‐step	IC0↔IC1	0.63	0.10
	60° corner: [$\bar{1}$ $\bar{1}$ 20]‐step	IC2↔IC3	0.62	0.08
	120° corner	IC4↔IC5	0.43	0.18
		IC4↔IC6	0.43	0.10
outer‐corner	240° corner	OC0↔OC1	0.29	0.22
		OC0↔OC1 (Ex.)	0.41	0.33
	300° corner: [11$\bar{2}$ 0]‐step	OC2↔OC3 OC5↔OC4	0.24	0.00
		OC3↔OC4	0.03	0.03
		OC2↔OC5 (Ex.)	0.32	0.32
	300° corner: [$\bar{1}$ $\bar{1}$ 20]‐step	OC6↔OC7 OC8↔OC7	0.20	0.03
		OC6↔OC8 (Ex.)	0.16	0.16

Table 10.

Activation energies $E_{\mathrm{a}}$ for forward and backward step‐edge self‐diffusion processes on Mg(10$\bar{1}$ 1) calculated with Equation (2) (PBE).

Diffusion on Mg(10$\bar{1}$ 1)	Path	Pathway	E a for [eV]	E a rev [eV]
step‐edge	[$\bar{1}$ 2$\bar{1}$ 0]A‐step	s 0↔s 1	0.35	0.59
		s 1↔s 2	0.13	0.13
	[$\bar{1}$ 2$\bar{1}$ 0]B‐step	s 3↔s 4	0.44	0.73
		s 4↔s 5	0.16	0.16
	[1$\bar{2}$ 10]A‐step	s 6↔s 7	0.14	0.18
		s 7↔s 8	0.01	0.01
	[1$\bar{2}$ 10]B‐step	s 9↔s 10	0.36	0.95
		s 10↔s 11	0.40	0.40
	[10$\bar{1}$ 2]‐step	s 12↔s 13	0.18	0.71
		s 13↔s 14	0.45	0.45

Figure 8.

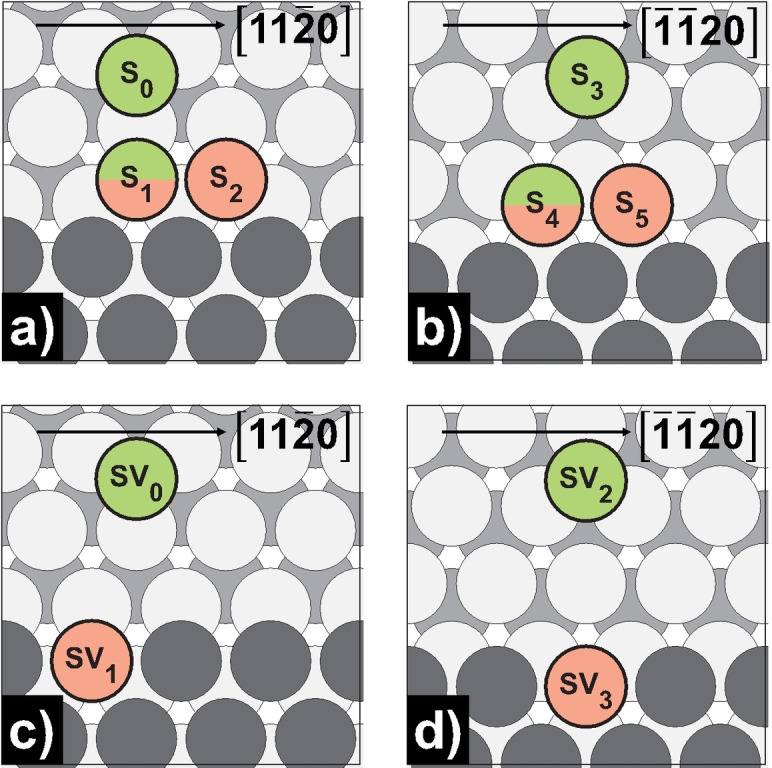
Schematic representation of step‐edge and step‐vacancy self‐diffusion processes on Mg(0001): a) step‐edge [11$\bar{2}$ 0]‐step; b) step‐edge [$\bar{1}$ $\bar{1}$ 20]‐step; c) step‐vacancy [11$\bar{2}$ 0]‐step; d) step‐vacancy [$\bar{1}$ $\bar{1}$ 20]‐step. Green‐colored atoms mark the initial, while red‐colored atoms mark the final positions.

Figure 9.

Schematic representation of step‐edge self‐diffusion processes on Mg(10$\stackrel{-}{1}$ 1): a) step‐edge [$\bar{1}$ 2$\bar{1}$ 0]A‐step; b) step‐edge [$\bar{1}$ 2$\bar{1}$ 0]B‐step; c) step‐edge [1$\bar{2}$ 10]A‐step; d) step‐edge [1$\bar{2}$ 10]B‐step; e) step‐edge [10$\bar{1}$ 2]‐step. Green‐colored atoms mark the initial, while red‐colored atoms mark the final positions.

Figure 10.

Schematic representation of kink, inner‐ and outer‐corner self‐diffusion processes on Mg(0001): a) kink [11$\bar{2}$ 0]‐step; b) kink [$\bar{1}$ $\bar{1}$ 20]‐step; c) 60° inner‐corner [11$\bar{2}$ 0]‐step; d) 60° inner‐corner [$\bar{1}$ $\bar{1}$ 20]‐step; e) 120° inner‐corner; f) 240° outer‐corner; g) 300° outer‐corner [11$\bar{2}$ 0]‐step; h) 300° outer‐corner [$\bar{1}$ $\bar{1}$ 20]‐step. Green‐colored atoms mark the initial, while red‐colored atoms mark the final positions.

Initially, we want to discuss the process of a free atom approaching the step‐edge on Mg(0001). As we have already seen with similar dimer and trimer processes, the forward barrier is negligibly small, but the detachment barrier is many times higher [S_0/3↔S_1/4, E _a ^for=0.03/0.02 eV, E _a ^rev=0.70/0.63 eV]. This observation becomes even more evident with a defect in the edge. Edge‐vacancy formation has the highest barrier of all diffusion processes studied [SV_1/3→SV_0/2, E _a ^rev=1.15/1.23 eV], indicating an extremely low probability of occurrence. It must be added that all fcc and hcp adsorption sites between the initial and the final state of the processes of approaching atoms are unstable and terminate in the initial state during relaxation. Once again, this underlines the high interaction energy on Mg(0001).

On Mg(10$\bar{1}$ 1), it is noticeable that an approaching atom hast to overcome higher forward barriers of at least 0.14 up to 0.44 eV, depending on the direction of the step. However, this behavior is expected since the barriers for terrace self‐diffusion on Mg(10$\bar{1}$ 1) are already at least 0.30 eV. The ratio between forward and reverse barriers is between 1–4 times, significantly lower than for Mg(0001) (25–40 times).

Step‐edge diffusion on Mg(0001) along the [$\bar{1}$ $\bar{1}$ 20] direction [S₄↔S₅, E _a=0.15 eV] is more probable compared to the [11$\bar{2}$ 0] direction [S₄↔S₅, E _a=0.22 eV]. We explain the difference in energy by considering the structure of the respective transition state (TS). In the TS of the [$\bar{1}$ $\bar{1}$ 20]‐directed step, the nearest neighbor atom in the edge row pulls slightly back, leaving a pocket for the diffusing atom to settle in a stabilized fcc‐like position (Figure S10). The step‐edge diffusion barriers are in agreement with results from Jäckle et al., assuming the growth of triangular islands with only <$\bar{1}$ $\bar{1}$ 20>‐directed steps due to the preferred diffusion along the [$\bar{1}$ $\bar{1}$ 20] direction. ^[23] Furthermore, the formation of fractal islands can almost be excluded since the step‐edge barriers are easily overcome at room temperature (see section Activation temperature of diffusion processes on Mg(0001) and Mg(10$\bar{1}$ 1)). Fractal islands are formed when an adatom arrives at an edge, but relaxation to a more favorable position is hindered. ^[43]

Looking at the diffusion along the steps on Mg(10$\bar{1}$ 1), it is noticeable that depending on the directions, the barriers are very heterogeneous. On the one hand, there is barrierless diffusion along the [1$\bar{2}$ 10]A‐directed step [s₇↔s₈, E _a=0.01 eV], while diffusion along the [$\bar{1}$ 2$\bar{1}$ 0]A‐ and [$\bar{1}$ 2$\bar{1}$ 0]B‐directed steps [s_1/4↔s_2/5, E _a=0.13/0.16 eV] is of the same order of magnitude as for Mg(0001) along [$\bar{1}$ $\bar{1}$ 20], and finally, diffusion along [1$\bar{2}$ 10]B and [10$\bar{1}$ 2] [s_10/11↔s_13/14, E _a=0.40/0.45 eV] is about 3 times higher compared to diffusion along the [$\bar{1}$ 2$\bar{1}$ 0]A‐directed step. The reason might be due to different coordination of the diffusing atom in the initial/final sites (hollow vs. fcc‐like sites).

Looking at the 240°‐outer‐corner process [OC₀↔OC₁, E _a ^for=0.29 eV, E _a ^rev=0.22 eV], we notice a thermodynamically favored OC₀ site, strengthening the hypothesis of growth of triangular islands with only <$\bar{1}$ $\bar{1}$ 20>‐ steps on Mg(0001). ^[23] Alternatively, hexagonal islands with alternating <11$\bar{2}$ 0>‐ and <$\bar{1}$ $\bar{1}$ 20>‐steps would be possible at higher temperatures due to vibrational and configurational entropy effects, as assumed for fcc Al(111). ^[44] The competing exchange process at the 240°‐outer‐corner has a higher activation energy and seems unfavorable [OC₀↔OC₁ (Ex.), E _a ^for=0.41 eV, E _a ^rev=0.33 eV]. Equally of interest is the diffusion behavior at the [11$\bar{2}$ 0]‐directed 300°‐corner consisting of three successive hopping steps. First, the adatom jumps from the edge to the tip of the corner [OC_2/4↔OC_3/5, E _a ^for=0.24 eV], switches sides in a symmetrical process [OC₃↔OC₄, E _a=0.03 eV] and finally moves barrierless to its final position [OC_2/4↔OC_3/5, E _a ^rev=0.00 eV]. In contrast, at the [$\bar{1}$ $\bar{1}$ 20]‐directed corner, the exchange process is kinetically preferred with the atom at the tip as exchange partner [OC₆↔OC₈ (Ex.), E _a=0.16 eV]. When looking at the inner corner processes, it becomes clear that in both 60°‐ and 120°‐processes, maximization of the binding partners is associated with lower barriers. In the 120°‐processes, the number of binding partners increases from 2 to 3 [IC₄↔IC_5/6, E _a ^for=0.43 eV, E _a ^rev=0.18/0.10 eV], and in the 60°‐processes from 2 to 4 [IC_0/2↔IC_1/3, E _a ^for=0.63/0.62 eV, E _a ^rev=0.10/0.18 eV], which is associated with forward/reverse barrier ratios of 2–4 and 6–8, respectively. For completion, the processes at the kink sites were studied. The barriers along the steps are similar to the respective 120°‐corner processes [K_0/4↔K_1/5, E_a ^for=0.45/0.46 eV, E _a ^rev=0.17/0.12 eV]. The barriers to leaving the kink position in the direction of the terrace also match the pattern [K_0/4↔K_2/6, E _a ^for=0.91/0.92 eV, E _a ^rev=0.02/0.01 eV]. The barrier height is exactly between the step‐edge and edge‐vacancy activation energy, accompanied by breaking 2 and 4 bonds, respectively. In addition, the process of forming kink sites is favored over the formation of corners [K_0/4↔K_3/7, E _a ^for=0.51/0.56 eV, E _a ^rev=0.29/0.22 eV] indicating compact rather than fractal islands.

Ehrlich‐Schwoebel barrier and upper step self‐diffusion on Mg(0001) and Mg(10$\bar{1}$ 1)

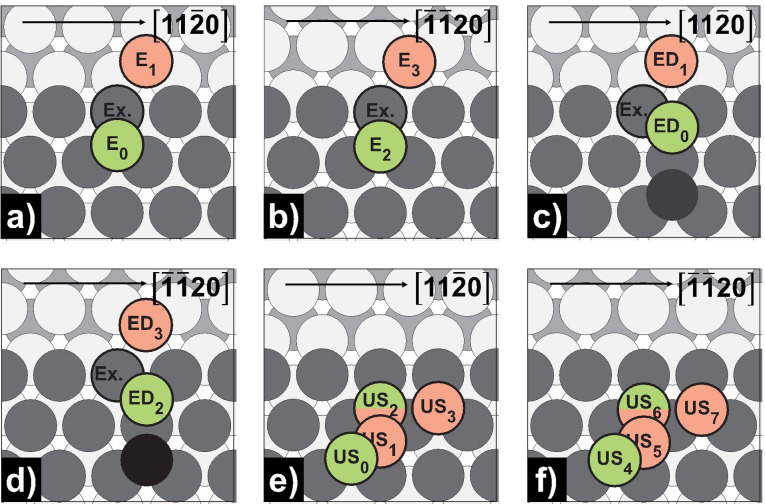
So far, we have only considered 2‐dimensional processes. However, to get a complete picture of surface growth, 3‐dimensional processes such as upper‐step diffusion followed by its descent are particularly important. The activation energies of the respective processes (step‐down, step‐down (dimer), upper‐step) as well as the calculated Ehrlich‐Schwoebel barriers for Mg(0001) and Mg(10$\bar{1}$ 1) are summarized in Table 11 and Table 12. The schematic illustrations of the processes are given in Figure 11 and Figure 12.

Table 11.

Activation energies E _a for forward and backward step‐down, step‐down (dimer) and upper‐step self‐diffusion processes on Mg(0001) were calculated with Equation (2) (PBE). In addition, the Ehrlich‐Schwoebel barriers E _ES were calculated for the step‐down diffusion processes using Equation (4). The forward activation barriers for the upper‐step processes at the [$\bar{1}$ $\bar{1}$ 20]‐step did not equal exactly 0.00 eV but were below 0.005 eV while rounding to the second decimal place.

Diffusion on Mg(0001)	Path	Pathway	E a for [eV]	E a rev [eV]	E ES [eV]
step‐down	[11$\bar{2}$ 0]‐step	E 0↔E 1	0.09	0.75	0.07
		E 0↔E 1 (Ex.)	0.01	0.67	−0.02
	[$\bar{1}$ $\bar{1}$ 20]‐step	E2↔E3	0.16	0.70	0.14
		E2↔E3 (Ex.)	0.02	0.56	−0.01
step‐down (dimer)	[11$\bar{2}$ 0]‐step	ED0↔ED1	0.58	0.74
		ED0↔ED1 (Ex.)	0.21	0.38
	[$\bar{1}$ $\bar{1}$ 20]‐step	ED2↔ED3	0.67	0.68
		ED2↔ED3 (Ex.)	0.11	0.15
upper‐step	[11$\bar{2}$ 0]‐step	US0↔US1	0.02	0.01
		US1↔US2	0.01	0.03
		US2↔US3	0.02	0.02
	[$\bar{1}$ $\bar{1}$ 20]‐step	US4↔US5	0.00	0.03
		US5↔US6	0.00	0.02

Table 12.

Activation energies E _a for forward and backward step‐down self‐diffusion processes on Mg(10$\bar{1}$ 1) were calculated using Equation (2) (PBE) and the Ehrlich–Schwoebel barriers E _ES were calculated using Equation (4).

Diffusion on Mg(10$\bar{1}$ 1)	Path	Pathway	E a for [eV]	E a rev [eV]	E ES [eV]
step‐down	[$\bar{1}$ 2$\bar{1}$ 0]A‐step	e0↔e1	0.44	0.67	0.14
		e0↔e2 (Ex.)	0.11	0.34	−0.19
	[$\bar{1}$ 2$\bar{1}$ 0]B‐step	e3↔e4	0.43	0.75	0.13
		e3↔e4 (Ex.)	0.26	0.58	−0.04
	[1$\bar{2}$ 10]A‐step	e5↔e6	0.29	0.04	–
		e6↔e7	0.12	0.42	−0.18
		e5↔e7 (Ex.)	0.47	0.53	0.17
	[1$\bar{2}$ 10]B‐step	e8↔e9	0.44	0.96	0.14
		e8↔e10 (Ex.)	0.07	0.59	−0.23
	[10$\bar{1}$ 2]‐step	e11↔e12	0.38	0.89	0.08
		e11↔e12 (Ex.)	0.20	0.71	−0.10

Figure 11.

Schematic representation of step‐down, step‐down (dimer) and upper‐step self‐diffusion processes on Mg(0001): a) step‐down [11$\bar{2}$ 0]‐step; b) step‐down [$\bar{1}$ $\bar{1}$ 20]‐step; c) step‐down (dimer) [11$\bar{2}$ 0]‐step; d) step‐down (dimer) [$\bar{1}$ $\bar{1}$ 20]‐step; e) upper‐step [11$\bar{2}$ 0]‐step; f) upper‐step (dimer) [$\bar{1}$ $\bar{1}$ 20]‐step. Green‐colored atoms mark the initial, while red‐colored atoms mark the final positions.

Figure 12.

Schematic representation of step‐down self‐diffusion processes on Mg(10$\bar{1}$ 1): a) step‐down [$\bar{1}$ 2$\bar{1}$ 0]A‐step; b) step‐down [$\bar{1}$ 2$\bar{1}$ 0]B‐step; c) step‐down [1$\bar{2}$ 10]A‐step; d) step‐down [1$\bar{2}$ 10]B‐step; e) step‐down [10$\bar{1}$ 2]‐step. Green‐colored atoms mark the initial, while red‐colored atoms mark the final positions.

Exactly as we have already seen for the terrace self‐diffusion on Mg(0001), the upper‐step diffusion onwards the step‐edge occurs almost barrierless for both facets. Nevertheless, there are small differences from a kinetic and thermodynamic perspective. For example, on [$\bar{1}$ $\bar{1}$ 20]‐ [US_4/5↔US_5/6, E _a ^for=0.00 eV, E _a ^rev=0.03/0.02 eV] as opposed to [11$\bar{2}$ 0]‐steps [US₀↔US₁, E _a ^for=0.02 eV, E _a ^rev=0.01 eV; US₁↔US₂, E _a ^for=0.01 eV, E _a ^rev=0.03 eV], both forward barriers of the two step‐process are lower than the reverse barriers. Moreover, from a thermodynamic point of view, the energy difference between the US₂ and US₀ sites is much smaller (7 meV) than between US₆ and US₄ sites (40 meV), indicating that diffusion occurs preferentially toward the [$\bar{1}$ $\bar{1}$ 20]‐directed step‐edges, followed by the subsequent descent. Likewise, upper‐step diffusion could only be studied along the step‐edge at [11$\bar{2}$ 0]‐steps [US₂↔US₃, E _a=0.02 eV], while at [$\bar{1}$ $\bar{1}$ 20]‐steps [US₆↔US₇] the diffusing atom immediately descends to the lower level (drops down to E ₂ site). In general, the descent takes place via the exchange process [E_0/2↔E_1/3 (Ex.), E _a ^for=0.01/0.02 eV, E _a ^rev=0.69/0.56 eV]. In both cases, this has a significantly reduced barrier compared to the corresponding hopping processes [E_0/2↔E_1/3, E _a ^for=0.09/0.16 eV, E _a ^rev=0.75/0.70 eV]. In addition, the exchange processes show negative Ehrlich‐Schwoebel barriers indicating a uniform and smooth growth due to a high rate of interlayer mass transport. ^[43] Likewise, the descent is clearly preferred to the ascent following the observed increase in coordination partners. All step‐down barriers are in agreement with the literature.[ ²³ , ³⁶ ]

Going one step further, we wanted to investigate the influence of a second adatom on the step‐down barriers. It becomes immediately apparent that the barriers to descent for hopping [ED_0/2↔ED_1/3, E _a ^for=0.58/0.67 eV, E _a ^rev=0.74/0.68 eV] as well as exchange processes [ED_0/2↔ED_1/3 (Ex.), E _a ^for=0.21/0.11 eV, E _a ^rev=0.38/0.15 eV] increase significantly. It can be assumed that the larger the cluster, the stronger the effect. For smooth surface growth, the adatom must reach the step‐edge faster than it reaches another adatom. Thus, the higher the deposition rate, the more likely new islands aggregate on top of existing islands before the bottom layer is fully complete. ^[43] A further interesting case is the exchange process at the [$\bar{1}$ $\bar{1}$ 20]‐step. In this process, the barriers for ascent and descent are very close together. However, it is important to note that the second atom follows the diffusing atom into the fcc position above the exchange atom during descent. This arrangement maintains the dimer conformation until beyond the TS (Figure S11) and lowers the activation energy of the process to half of the corresponding exchange process at the [11$\bar{2}$ 0]‐step.

On Mg(10$\bar{1}$ 1), in almost all cases (except [1$\bar{2}$ 10]A‐step), the exchange process has the lowest barrier on the descent. The smallest step‐down barrier is found at the [1$\bar{2}$ 10]B‐step [e₈↔e₉ (Ex.), E _a ^for=0.07 eV], whereas the lowest ascent barrier is found at the [$\bar{1}$ 2$\bar{1}$ 0]A‐step [e₀↔e₂ (Ex.), E _a ^rev=0.34 eV]. The most frequent descent route is likely to be along the [10$\bar{1}$ 2]‐step [e₁₁↔e₁₂ (Ex.), E _a ^for=0.20 eV]. Here an adatom can diffuse within a channel to the edge, and subsequently descend via the exchange process.

Activation temperature of diffusion processes on Mg(0001) and Mg(10$\bar{1}$ 1)

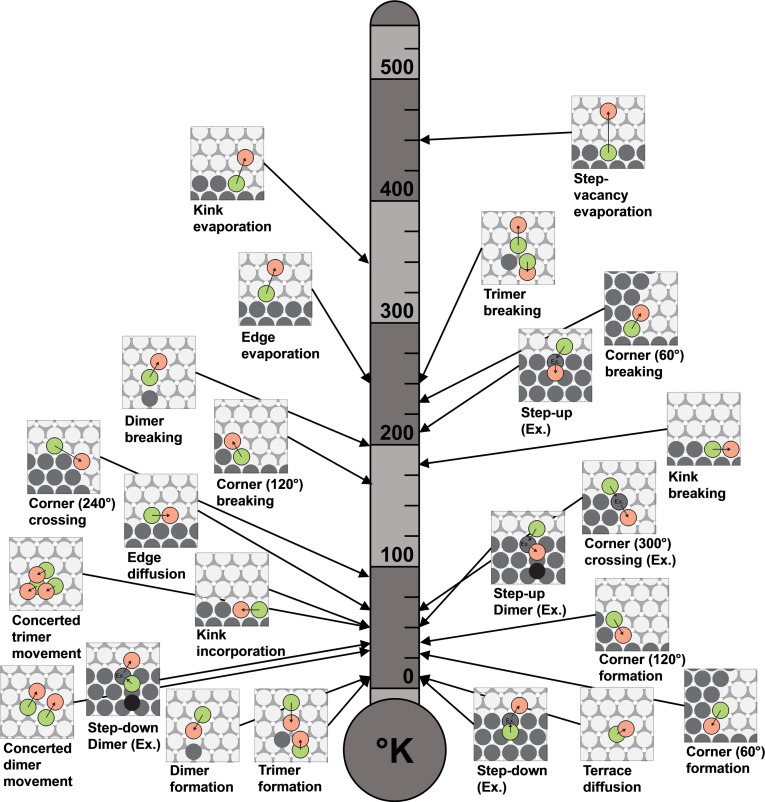
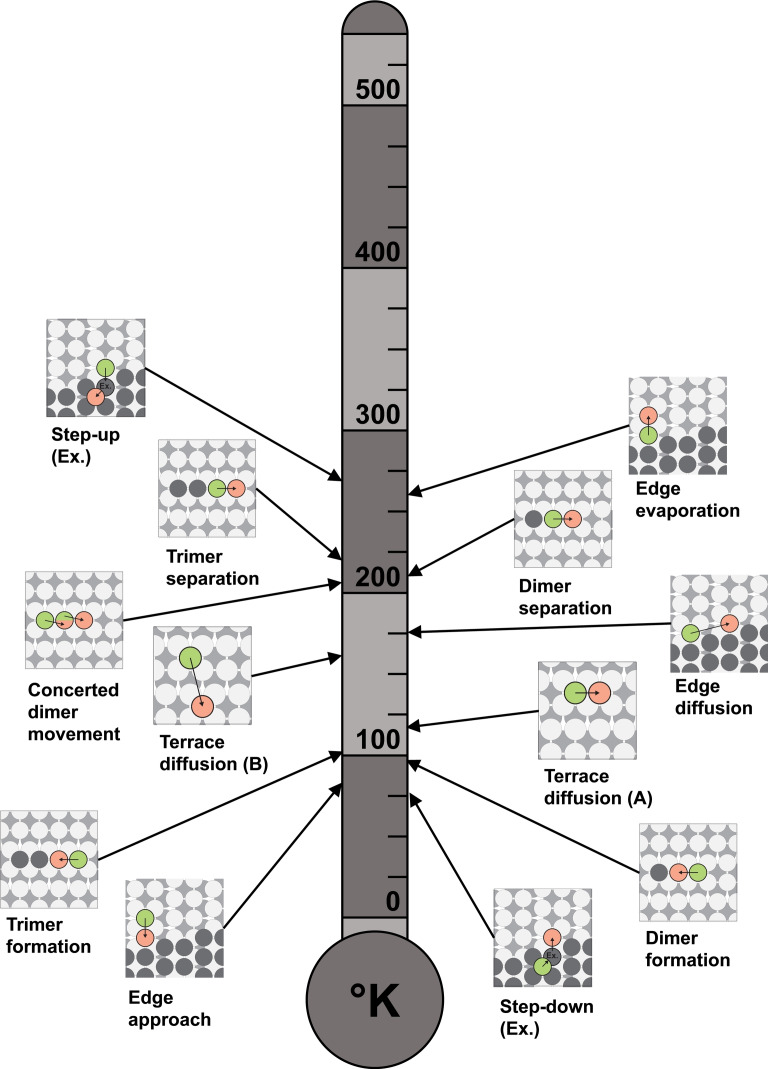
In addition to the diffusion barriers, we calculated the pre‐exponential factors of the Arrhenius equations via the Einstein approximation using Equation (5) to determine the activation temperatures of the processes studied on Mg(0001) and Mg(10$\bar{1}$ 1) using Equation (6). The obtained activation temperatures at which the respective diffusion processes start to contribute to surface growth are shown in Figures 13 and 14.

Figure 13.

Activation temperatures of diffusion processes to impact surface growth on Mg(0001).

Figure 14.

Activation temperatures of diffusion processes to impact surface growth on Mg(10$\bar{1}$ 1).

On Mg(0001), processes such as terrace self‐diffusion, the formation of dimers and trimers, and the step‐down process do not have significant barriers and are already activated at temperatures below 25 K. It must be noted that dimer and trimer formation is highly favored compared to the respective separation processes due to a very high interaction energy. At this point, we would like to address the hypothesis that lower terrace self‐diffusion and step‐down barriers on Mg(0001) vs. Li(100) are responsible for reduced dendrite formation. ^[23] We were able to confirm lower barriers for Mg(0001). However, the corresponding processes for metallic lithium become activated at 16 and 43 K, respectively. ^[24] At room temperature, these processes should run almost equally and have no significant influence on dendrite formation. We believe that to adequately explain dendrite growth, a holistic and more exhaustive model needs to be developed that considers the influence of the SEI interface, the stability of different surface terminations, the diffusion barriers on the respective surfaces, the applied potential, the deposition conditions, and the electrolyte used. It remains an open question to what extent this is already possible with the current theoretical tools. However, the data presented in this work could serve as a reference for future studies where these additional effects are successively accounted for.

At a temperature below 100 K on Mg(0001), a variety of further diffusion processes become active such as dimer and trimer propagation, diffusion along an edge, the formation of 60° and 120° corners, switching sides at 240° and 300° corners and kink incorporation. Especially the activated corner‐crossing barriers contribute to the growth of compact rather than fractal islands. ^[43] Interestingly, both the dimer step‐down and step‐up processes become possible in this temperature range, contrary to uniform and smooth surface growth.

On Mg(10$\bar{1}$ 1), we found that the activation temperatures for diffusion processes are generally higher. Below 100 K, it is only possible for an adatom to step‐down, form a dimer, or diffuse towards an edge. Terrace diffusion within and across a channel and diffusion along an edge on Mg(10$\bar{1}$ 1) becomes possible at elevated temperatures above 100 K.

In the same temperature range, processes in which the coordination number of the diffusing atom is reduced become available on Mg(0001), such as in the 120° corner and kink breaking processes. Above 200 K, the dimer and trimer separation processes, edge evaporation, and 60° corner separation are also enabled, as well as the step‐up process. Despite that, the statement still applies that bond breakages are extremely unlikely for magnesium and that the increase of the coordination number always proceeds preferentially. For example, kink evaporation and the formation of a step‐vacancy are not possible at room temperature for Mg(0001). Nevertheless, activated evaporation and separation processes are necessary for island ripening (redistribution of mass). ^[43] We assume many small islands form in the low‐temperature range, and new adsorbates join existing ones. At higher temperatures, island ripening should begin, and smaller islands dissolve at the expense of larger islands.

On Mg(10$\bar{1}$ 1), all processes studied can occur at ambient conditions. In the temperature range between 200 and 300 K, dimer and trimer separation, edge evaporation, and the exchange step‐up process are activated. In addition, concerted dimer propagation proceeds at about 200 K.

At this point, we would like to refer to the Supporting Information, which summarizes all calculated data. Table S7 and Table S8 show the pre‐exponential factors, activation energies, room‐temperature rate constants, and activation temperatures for the terrace self‐diffusion processes for the PBE and BEEF‐vdW functionals, respectively. Corresponding schematic representations and energy profiles are provided in Figure S4. In addition, overviews of all investigated diffusion processes on Mg(0001) are available in Figure S6 and on Mg(10$\bar{1}$ 1) in Figure S8. The corresponding pre‐exponential factors, activation energies, room temperature rate constants, activation temperatures, and energy profiles may be found in Table S10, Figure S7, Table S11, and Figure S9.

Conclusion

This work aimed to determine and summarize the atomistic properties of magnesium and discuss the initial stages of surface growth in a possible magnesium‐ion battery. Therefore, well‐selected self‐diffusion processes on perfect and imperfect Mg surfaces were investigated to better understand the initial surface growth phenomena at the level of density functional theory. We are aware that in a real battery environment, the operation conditions, the potential, the electrolyte, charge‐ and discharge products, and especially the SEI environment might have a tremendous impact on the atomistic properties of magnesium. For this reason, we do not want to make any statements about possible dendrite growth based on our results, as we believe this is not possible with pure DFT. Nevertheless, we still believe that our studies already provide informative insights into the actual processes taking place.

First, the present calculations confirm the preference of magnesium to crystallize in a hcp crystalline structure at ambient conditions, with surface terminations Mg(0001), Mg(10$\bar{1}$ 0)A, and Mg(10$\bar{1}$ 1) being, in this order, most stable. Interestingly, the surface proportions in a nanocrystal are quite different. According to the Wulff construction, Mg(10$\bar{1}$ 1) has the largest share of the surface with a surface fraction of about 50 %, while the remaining area is distributed evenly between Mg(0001) and Mg(10$\bar{1}$ 0)A, as shown in Figure 1. The Wulff construction clearly illustrates that diffusion properties must be discussed for all three surfaces collectively and cannot be limited to the thermodynamically most stable surface Mg(0001), as done in previous studies.

Terrace self‐diffusion of single atoms runs almost barrier‐free on Mg(0001) but with higher activation energies on Mg(10$\bar{1}$ 1). When adsorbates collide on the surfaces, initial dimer, trimer, and cluster structures are formed, which is highly favored due to high attractive interactions between the adsorbates. The small cluster structures can be seen as seeds for further island growth, which shape on Mg(0001) could be either triangular with only <$\bar{1}$ $\bar{1}$ 20>‐ steps as proposed by Jäckle et al. ^[23] or hexagonal with alternating <11$\bar{2}$ 0>‐ and <$\bar{1}$ $\bar{1}$ 20>‐steps at elevated temperatures. ^[44] However, the island pattern should be compact rather than fractal due to low step‐edge and corner crossing barriers. ^[43] On Mg(10$\bar{1}$ 1), the diffusion barriers are in general higher compared to Mg(0001), but the ratios for bond formation and breakage are closer together. All processes studied on Mg(10$\bar{1}$ 1) can occur at ambient conditions, while on Mg(0001) kink evaporation and the formation of a step‐vacancy are not activated at room temperature. Surface growth on Mg(10$\bar{1}$ 1) could proceed in a line along the hollow sites perpendicular to the [10$\bar{1}$ 2]‐direction.

The three‐dimensional diffusion studies reveal negative Ehrlich‐Schwoebel barriers for all investigated exchange descend processes on Mg(0001) and Mg(10$\bar{1}$ 1) (except [1$\bar{2}$ 10]A‐step), indicating a uniform and smooth surface growth due to a high rate of interlayer mass transport at low deposition rates. ^[43] However, a second adatom significantly increases the descent barriers for hopping and exchange processes, fostering the aggregation of new islands on top of existing islands if the adatom meets another adatom faster than it reaches the step‐edge.

All generated data will be used in a future work as a training set for parameterizing the reactive force field ReaxFF. ReaxFF allows a more realistic investigation of the battery system by including the electrolyte, and at the same time, lowers the computational cost but with similar accuracy.[ ²⁷ , ²⁸ , ⁴⁵ ] Furthermore, the calculated rate constants may be used in kinetic Monte‐Carlo simulations to investigate and visualize the kinetic effects of surface growth. ^[41]

Theoretical Section

Periodic DFT calculations were performed with the plane‐wave based Vienna ab initio simulation package (VASP).[ ⁴⁶ , ⁴⁷ ] The core electrons were described using the projector augmented wave (PAW) ^[48] method of Blöchl as implemented in VASP. ^[49] Exchange correlation effects were described within the generalized gradient approximation (GGA) of Perdew, Burke, and Enzerhof (PBE). ^[50] Additionally, the Bayesian error estimation functional with van der Waals correlation (BEEF‐vdW) was applied to determine the standard deviation of the investigated quantities. ^[51] A plane‐wave cutoff energy of 400 eV was employed after detailed convergence studies (Figure S1 in the Supporting Information), where Mg 2 s electrons were described as valence electrons. Following the scheme of Monkhorst and Pack, a k‐point mesh density of at least 0.14 Å⁻¹ was applied for all total energy calculations. ^[52] Thermal smearing of one‐electron states was allowed using the Gaussian smearing method (σ=0.1 eV) to determine the partial occupancies of each orbital and acquire faster convergence with respect to the number of k‐points. The electronic self‐consistent field (SCF) was considered converged when the total energy difference was less than 10⁻⁵ eV, and the norms of all the forces were smaller than 10⁻³ eV ⋅ Å⁻¹. Surface energies were calculated on symmetrical (1×1) cells with a minimum slab thickness of 30 Å and a minimum vacuum region of 20 Å (Table S1). A single atom in the middle of the slab was fixed to avoid net translations. ^[24] Adsorption energies, dimer interaction, diffusion barriers, and frequencies were generally calculated on converged slabs with 6 surface layers, where the two uttermost layers were fixed to emulate bulk properties. If it became necessary, vicinal slabs were used. The exact surface characteristics are summarized in Table S2. According to a detailed bulk study, the lattice constants used for hcp magnesium were a ₀=3.18 Å and c ₀=5.21 Å for all employed structures (Table S3). A detailed comparison of the bulk properties with literature is also provided in the bulk properties chapter in the Supporting Information. The minimum energy path (MEP) was determined with the climbing image nudged elastic band (CI‐NEB) method as implemented in the transition state tools for VASP (VTST) with generally 7 images between the initial states separated by a spring constant of 5.0 eV Å⁻².[ ⁵³ , ⁵⁴ ] As an initial guess for the MEP the image‐dependent pair potential (IDPP) was applied.[ ⁵⁵ , ⁵⁶ ] To confirm the transition state and to determine rate constants, we calculated vibrational frequencies with the dynamical matrix method from the VTST package. For this purpose, the electronic and ionic convergence criteria were increased to 10⁻⁸ eV and 10⁻⁸ eV Å⁻¹, respectively, and the diffusing as well as the nearest neighbor atoms along the diffusion pathway were symmetrically displaced by 0.007 Å in each spatial direction.

The surface energy γ is defined as the surface excess free energy per unit area and was calculated by subtracting a multiple of the bulk energy N⋅E _bulk from the energy of the slab E _slab, divided by the area of the surface A times two (because of the symmetric slab configuration):

$${\displaystyle \gamma =\frac{1}{2A}\left(E_{\mathrm{s}\mathrm{l}\mathrm{a}\mathrm{b}}-N·E_{\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}}\right)}$$ (1)

All surface energies were employed to carry out the Wulff construction. ^[26] The area fractions of the facets were calculated using the Python package WulffPack for a nanocrystal with 5000 atoms. ^[57]

The activation energies E _a ^for/rev for forward and backward diffusion processes correspond to the energy differences between the energy of the transition state E _TS and the energy of the initial and final structure E _IS/FS, respectively:

$${\displaystyle E_{\mathrm{a}}^{\mathrm{f}\mathrm{o}\mathrm{r}/\mathrm{r}\mathrm{e}\mathrm{v}}=E_{\mathrm{T}\mathrm{S}}-E_{\mathrm{I}\mathrm{S}/\mathrm{F}\mathrm{S}}}$$ (2)

The interaction energy E _int for the dimer configurations was calculated by subtracting two times the adsorption energy of a monomer E _ad ^monomer from the adsorption energy of a dimer E _ad ^dimer:

$${\displaystyle E_{\mathrm{i}\mathrm{n}\mathrm{t}}=E_{\mathrm{a}\mathrm{d}}^{\mathrm{d}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{r}}-{2·E}_{\mathrm{a}\mathrm{d}}^{\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{r}}}$$ (3)

We refer here to the chapter on adsorption energies in the Supporting Information, where the adsorption energies calculated with Equation (S3) for the surfaces Mg(0001), Mg(10$\bar{1}$ 0), and Mg(10$\bar{1}$ 1) are listed in Table S6.

Furthermore, we determined the Ehrlich‐Schwoebel barrier E _ES for all step‐down diffusion processes.[ ⁵⁸ , ⁵⁹ , ⁶⁰ ] E _ES corresponds to the energy barrier that a descending atom must overcome in addition to the terrace self‐diffusion barrier and was calculated by subtracting the terrace self‐diffusion barrier E _a ^for(terrace) from the activation barrier of the step‐down process E _a ^{for(stepdown)}:

$${\displaystyle E_{\mathrm{E}\mathrm{S}}=E_{\mathrm{a}}^{\mathrm{f}\mathrm{o}\mathrm{r}(\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}-\mathrm{d}\mathrm{o}\mathrm{w}\mathrm{n})}-E_{\mathrm{a}}^{\mathrm{f}\mathrm{o}\mathrm{r}\left(\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\right)}}$$ (4)

The reaction rate k _@RT at room temperature (T=293.15 K$)$ was calculated for each diffusion process by means of transition state theory as given by the Arrhenius equation:

$${\displaystyle k_{@\mathrm{R}\mathrm{T}}=\nu ·\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{E_{\mathrm{a}}}{k_{\mathrm{B}}T}\right)}$$ (5)

where the pre‐exponential factor ν was determined based on the Einstein approximation ^[61] with the vibrational frequencies of the diffusing adatom and the nearest surface atoms along the migration pathway for the initial and the transition state. E _a equals the activation energy and k _B is the Boltzmann constant.

The activation temperature T _a above which a process runs at the rate Γ was calculated with the equation used by Bogicevic et al. ^[62] Above T _a, a process is considered to be ‘activated’ following the formula:

$${\displaystyle T_{\mathrm{a}}=\frac{E_{\mathrm{a}}/k_{\mathrm{B}}}{\mathrm{l}\mathrm{n}\left(\nu /\Gamma \right)}}$$ (6)

Since the rate Γ depends on the experimental growth rate, Γ=1 s⁻¹ was set, which is valid for a deposition rate of about 0.001–0.1 ML s⁻¹. As indicated, E _a corresponds to the activation energy, k _B to the Boltzmann constant, and $\nu$ to the pre‐exponential factor. For some processes (D₀↔D₁, D₂↔D₃, T₀↔T₁, E₂↔E₃ (Ex.)) with very small activation barriers (<0.02 eV), the pre‐exponential factor could not be determined due to imaginary frequencies in the TS. In these cases, a value of ν=5.0⋅10¹² s⁻¹ was assumed, which corresponds to the average value of the pre‐exponential factor, usually in the range between 10¹²–10¹³ s⁻¹ $.$

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

F. Fiesinger, D. Gaissmaier, M. van den Borg, T. Jacob, ChemSusChem 2022, 15, e202200414.

Data Availability Statement

The data that support the findings of this study are openly available in zenodo at https://doi.org/10.5281/zenodo.6416097.