Subvoxel Vascular Imaging of the Midbrain Using USPIO-Enhanced MRI

Abstract

There is an urgent need for better detection and understanding of vascular abnormalities at the micro-level, where critical vascular nourishment and cellular metabolic changes occur. This is especially the case for structures such as the midbrain where both the feeding and draining vessels are quite small. Being able to monitor and diagnose vascular changes earlier will aid in better understanding the etiology of the disease and in the development of therapeutics. In this work, thirteen healthy volunteers were scanned with a dual echo susceptibility weighted imaging (SWI) sequence, with a resolution of 0.22×0.44×1mm³ at 3T. Ultra-small superparamagnetic iron oxides (USPIO) were used to induce an increase in susceptibility in both arteries and veins. Although the increased vascular susceptibility enhances the visibility of small subvoxel vessels, the accompanying strong signal loss of the large vessels deteriorates the local tissue contrast. To overcome this problem, the SWI data were acquired at different time points during a gradual administration (final concentration = 4mg/kg) of the USPIO agent, Ferumoxytol, and the data was processed to combine the SWI data dynamically, in order to see through these blooming artifacts. The major vessels and their tributaries (such as the collicular artery, peduncular artery, peduncular vein and the lateral mesencephalic vein) were identified on the combined SWI data using arterio-venous maps. Dynamically combined SWI data was then compared with previous histological work to validate that this protocol was able to detect small vessels on the order of 50μm to 100μm. A complex division-based phase unwrapping was also employed to improve the quality of quantitative susceptibility maps by reducing the artifacts due to aliased voxels at the vessel boundaries. The smallest detectable vessel size was then evaluated by revisiting numerical simulations, using estimated true susceptibilities for the basal vein and the posterior cerebral artery in the presence of Ferumoxytol. These simulations suggest that vessels as small as 50 μm should be visible with the maximum dose of 4mg/kg.

INTRODUCTION

Cerebrovascular diseases affect the circulation of blood to the brain due to abnormal vascular functional hemodynamics (Hu et al., 2017). A growing body of evidence in animal and human studies shows that micro-cerebrovascular abnormalities are the source of many neurological disorders (Desai Bradaric et al., 2012; Iadecola, 2013; Zlokovic, 2008). Although clear pathogenic mechanisms are unknown and may vary among diseases, significant microvasculature involvement has been suggested in many neurodegenerative and inflammatory diseases such as Alzheimer’s disease, Parkinson’s disease (PD), epilepsy, traumatic brain injury and multiple sclerosis (Zlokovic, 2008) to name a few of the major diseases. According to a recent national institutes of health (NIH) workshop, there is an urgent need for better detection and understanding of vascular abnormalities at the micro-level (Bosetti et al., 2016), where critical vascular nourishment and cellular metabolic changes occur. Being able to monitor and diagnose these vascular changes earlier in the disease process will aid in better understanding the etiology of the disease and in the development of therapeutics (Sweeney et al., 2018).

The midbrain, an area of focus in this paper, and its structures, especially the substantia nigra (SN), play a pivotal role in coordinating smooth movements (Guzman et al., 2009). It is not surprising that an ample amount of blood supply is required to meet such an energy demand (Harris et al., 2012; Hofmeijer and van Putten, 2012; Pacelli et al., 2015). It can be inferred that an insufficient blood supply could cause dopaminergic neuronal dysfunction in the SN. Therefore, it is quintessential to trace back the changes in cerebral microvasculature that manifest early in prediagnostic (preclinical and prodromal phases) and follow along ensuing development later in the clinical phase of PD (Noyce et al., 2016).

Magnetic resonance angiography (MRA), as it currently stands, is a powerful practical tool for imaging the major arterial (from M1 to M4) and venous (the dural sinuses and internal cerebral veins) segments. All of these vessels range in size from about 250μm to several millimeters. However, from a total volume perspective, these vessels are just a small part of the vasculature that actually feeds and drains the brain. Susceptibility weighted imaging (SWI) expands the ability on the venous side to image pial veins and medullary veins without the use of contrast agents (Liu et al., 2017). However, if the goal is to image arteries in vivo on the order of 50 to 100μm, then it will be very difficult, if not impossible, to do this with conventional MRA and SWI techniques. And yet it is just at this level where one may find the origin of microvascular disease.

The ability to image the very small veins with SWI without a contrast agent comes from the presence of the susceptibility differences with respect to surrounding tissues induced by the deoxyhemoglobin in the blood. Unfortunately, the arterial blood has no susceptibility difference with the background tissue and, hence, imaging arteries with conventional SWI without the use of a contrast agent has not been possible. Indeed, in previous work, the use of Ferumoxytol was introduced to induce a susceptibility in the arteries (as well as increase the susceptibility in the veins over and above that is caused by deoxyhemoglobin) (Liu et al., 2018; Shen et al., 2020). This new method may be dubbed as MICRO imaging, which stands for “Microvascular In-vivo Contrast Revealed Origins”. Among all the ultrasmall super-paramagnetic iron oxide (USPIO) particles, Ferumoxytol is the one most often used in human studies as an off-label magnetic resonance imaging (MRI) contrast agent. With this USPIO-induced increase in susceptibility comes the potential to make small subvoxel vessels visible (now inclusive of arteries) without having to image at the resolution of the vessel itself. For example, without a contrast agent, small veins can be imaged by using a voxel size equal to twice the diameter of the vessel with SWI (Liu et al., 2017). This is due to both the increased dephasing/blooming artifact as well as to the special processing from SWI that uses phase-enhancing information. By increasing the susceptibility of the vessels, this ratio could be increased to perhaps a factor of four, making it possible to image 50 to 100μm diameter vessels with an imaging resolution of only 200 to 400μm on MRI. However, with this enhancement of the small vessels comes major blooming artifacts from the large vessels and so the challenge is how to collect the imaging data so that the large, medium and small vessels can all be imaged and the arteries separated from the veins. This must be accomplished by having sufficient resolution, signal-to-noise ratio (SNR) and speed to make it clinically viable.

In this work, we introduce a MICRO imaging protocol with the use of Ferumoxytol that enables us to image small vessels in vivo at a subvoxel level (i.e., <200μm) at 3T. Numerical simulations were performed and studied to select the best aspect ratio (testing both symmetric and asymmetric in-plane ratio) and imaging resolution in order to visualize subvoxel vessels. As a demonstration of the potential of MICRO imaging, we focused on studying the anatomy and microvasculature of the midbrain in healthy volunteers with an eye toward future work in studying vascular abnormalities in diseases such as PD. However, as mentioned above, the increase in susceptibility (in the presence of Ferumoxytol) will obscure the regions surrounding the larger vessels due to blooming artifacts. In order to overcome this problem, SWI data were acquired at different time points during the gradual administration of the Ferumoxytol making it possible to see through these blooming artifacts from large vessels by dynamically combining the post-contrast SWI data. The SWI data were used to obtain a map of major arteries and veins, which were then used to classify the smaller vessels as arterial/venous branches. A complex division-based phase unwrapping method was also employed to improve the quality of quantitative susceptibility mapping (QSM) by reducing the artifacts due to aliased voxels at the vessel boundaries. The smallest detectable vessel size was then evaluated by revisiting the simulations, using the estimated true susceptibilities for the basal vein (BV) and the posterior cerebral artery (PCA) in the presence of Ferumoxytol. In addition to the numerical simulations, the diameter of these small vessels was estimated by using the histological sections studied in previous literature.

MATERIALS AND METHODS

Data were acquired with an adapted three-dimensional (3D) gradient echo SWI sequence (Chen et al., 2018a) collected from a 3T MR scanner (Verio, Siemens Healthineers, Erlangen, Germany), with a 32-channel head coil, before and during the administration of Ferumoxytol (Feraheme, AMAG Pharmaceuticals, Inc. Waltham, MA). The post-contrast data were acquired during a gradual increase in dose (final concentration = 4mg/kg). Thirteen healthy volunteers (n = 13, age = 33.5±13.8 years, female/male = 9/4) were scanned after obtaining approval from the institutional review board of Wayne State University, Detroit, Michigan and written informed consent was obtained in all cases.

Optimizing the MRI parameters

The roles of increased susceptibility and R₂’ relaxation were evaluated to visualize arteries and, more specifically, to enhance the visibility of small arteries and veins using a simulation approach. From these simulations, the optimal imaging resolution was chosen to achieve the maximal SNR per unit time and maximal coverage of the brain.

For the numerical simulations, vessels were modeled as an infinite cylinder using a high resolution 2D grid (1024×1024) within which the vasculature could be mimicked at 3T, with an echo time (TE) = 15ms, a flip angle (FA) = 15°, a repetition time (TR) = 27ms and a range of 0.1 to 8mg/kg (with an interval of 0.1mg/kg) for the Ferumoxytol concentration. The dipole fields from an infinitely long cylinder, perpendicular to the main field, were used to simulate the 2D phase images (Brown et al., 2014). The region outside the vein was assumed to be white matter with a T₂* = 53.2ms (Peters et al., 2007) and a T₁ = 838ms (Wright et al., 2008) at 3T, for simulating the corresponding magnitude images. The T₁, T₂* and Δχ values of the cylinder were varied as a function of the Ferumoxytol dose (Knobloch et al., 2018; Liu et al., 2018).

In order to determine the relationship between T₁, T₂* and Δχ with a given Ferumoxytol concentration, the total blood volume was estimated to be 3.75L assuming an average body weight of 50kg (Butterworth et al., 2018). The concentration of Ferumoxytol in blood [cFe] was calculated using [cFe] = dose × (body weight)/(blood volume) in mg/L. The T₁ post-contrast was calculated from: T₁ = 1/(−1.067 × ([cFe]/Fe_M)² + 11.36 × ([cFe]/Fe_M) - 0.09) in sec, where Fe_M is the molar mass of iron (55.8g/mol) (Knobloch et al., 2018). The T₂* was calculated from: T₂* = 1/(1562 × ([cFe]/10³) + 2) in sec and Δχ was calculated using Δχ = 32 × ([cFe]/10³) in ppm (Liu et al., 2018). For a vein, the susceptibility value of 0.45ppm (at ~70% oxygenation) was added to that of the Ferumoxytol-induced susceptibility, to account for the deoxyhemoglobin content. The simulated images for voxel and subvoxel sized objects were generated by first finely sampling the cylinder in the image domain using a large 2D matrix size (1024×1024), where x×y represent the phase×slice dimensions. Then, the image was created by Fourier transforming the central 32×32, 32×16, 16×8 and 16×6 elements of k-space to represent the vessel aspect ratios (VAR), or the ratio of voxel size to the vessel size, of 2:2:2, 2:2:4, 2:4:8 and 2:4:10, respectively, in order to study the partial volume effects and contrast-to-noise ratio (CNR) (Cheng et al., 2009). Here, the frequency encoding dimension was kept constant. Thermal noise was added to simulate the SNRs of 4.2:1, 6:1, 12:1, 12:1 for 2:2:2, 2:2:4, 2:4:8 and 2:4:10, respectively. SWI images were generated by homodyne high-pass filtering (filter size=96×96) the phase images to generate a phase mask (φ_M), which was multiplied with the original magnitude images four times (Haacke et al., 2009). The CNR was calculated over 800 independent repetitions to reduce standard error of the mean estimates. The above steps were repeated with 4:4:4, 4:4:8, 4:8:16 to 4:8:20 VARs. Finally, CNR versus concentration was calculated for the average over two (NEX = 2) adjacent SWI datasets is presented with an SNR of 12√2:1 for the VARs of 2:4:10 and 4:8:20.

Contrast agent administration and data acquisition

All subjects were scanned with a dual echo SWI sequence at four time points: the first was acquired pre-contrast (Fe₀) and the remaining three were acquired post-contrast (Fe₁, Fe₂ and Fe₃) during a gradual increase in dose (final concentration = 4mg/kg). The Ferumoxytol dose was diluted with 60ml of 0.9% sodium chloride (or normal saline). The administration rate was selected between the range of 150–200 ml/hr, which was varied for each subject in order to consistently deliver the complete dose over a target time period of 21–23 minutes. The administration was initiated at the start of the first post-contrast sequence (Fe₁) and the post-contrast scan (Fe₃) began at the end of the infusion time. The blood pressure (BP) was collected before the initiation of the scanning session and within 15 minutes after scanning to monitor any signs of hypotension.

The acquisition time for each of the four sequences was 11 minutes with the imaging parameters: TE1/TE2/TR = 7.5/15/27 ms, bandwidth = 180 Hz/pxl, FOV_read×FOV_phase = 224×182 mm², scanning matrix = 1024×416, number of slices = 96, slice oversampling = 8.3%, flip angle = 15^o (Fe₀ and Fe₃) and 20^o (Fe₁ and Fe₂); with a voxel size = 0.22×0.44×1 mm³ (reconstructed to 0.22×0.22×1 mm³). The generalized autocalibrating partially parallel acquisitions (GRAPPA) was utilized to further accelerate the data acquisition using a GRAPPA factor of 2 with central 36 reference lines.

Data post-processing

Prior to reconstructing the susceptibility maps, phase images need to be unwrapped. But as the concentration of Ferumoxytol increases and the susceptibility likewise increases, the conventional phase unwrapping fails particularly at the vessel boundaries. To overcome this problem, temporal phase unwrapping was employed by complex dividing consecutive time points (Chen et al., 2018b). Unfortunately, the process of co-registration of the images blurs the aliased voxels, making it impossible to unwrap them after registration. Hence, it is imperative to unwrap the phase completely before the registration step. Therefore, we used a ‘step-wise forward registration’ for the phase correction to prevent blurring of the aliased voxels. This was followed by a ‘backward registration’ in order to register the corrected phase to the Fe₀ data. The image registration was performed using the statistical parametric mapping (SPM) package (SPM12, Wellcome Department of Cognitive Neurology, University College London, London, UK) in MATLAB by using the normalized mutual information as the cost function and a 4^th degree spline for interpolation (Ashburner and Friston, 1997; Collignon et al., 1995; Studholme et al., 1999). The transform parameters obtained from magnitude data registration were then applied to the unwrapped phase and SWI data. Data from two volunteers were not included in this study due to major motion during and between scans, leaving data from eleven healthy controls that could be analyzed.

The following pipeline of registration and complex division was used: 1) the phase data from all the time points was unwrapped using the 3D best path method (Abdul-Rahman et al., 2007); 2) Fe_n−1 data was registered to the Fe_n data (or step-wise forward registration) and complex divided phase was calculated (where n = 1 to 3). The complex division was obtained using the short TE data, instead of the long TE, due to the lesser extent of unreliable signal caused by strong phase gradients that are proportional to the TE at the boundaries of the vessels; 3) The complex divided phase contained considerably fewer aliased voxels and was then added to the Fe_n−1 short TE phase data to obtain a corrected short TE Fe_n phase (referred to as φ’_n). For the subsequent time points, φ’_n phase data was used for this correction step; and 4) all the original magnitude and corrected phase data were registered to the Fe₀ data (or backward registration). This process of correcting the aliased voxels surrounding the large vessels before registration is essential to obtain accurate QSM results. The above-mentioned registration process for modified phase unwrapping is illustrated in Figure 1A.

Figure 1.

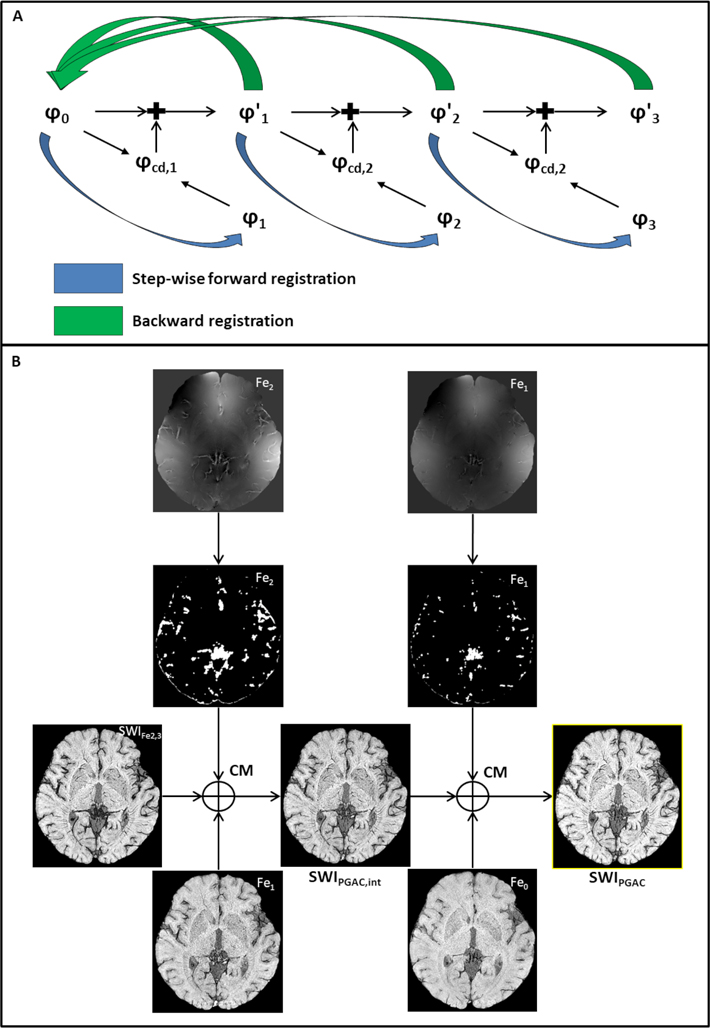
Process of performing complex division-based phase unwrapping and SWI combination. (A) Illustration of the step-wise forward (blue arrows) registration, which is used to reduce the number of aliased voxels (that were remaining after conventional phase unwrapping) in the short TE phase data for post-contrast timepoints (φ_n, where n = 1 to 3). This was done by calculating a complex divided phase (φ_cd,n = φ_n − φ_n-1) between phase data from consecutive timepoints and adding it to the φ_n-1 data to obtain the corrected unwrapped phase (φ′_n = φ_n-1 + φ_cd,n). Backward registration (green arrows) was performed by registering back all the corrected unwrapped phase (φ′_n) to the Fe₀ timepoint (φ₀). (B) Process of reconstructing the phase gradient-based adaptively combined SWI (SWI_PGAC) using the time points: Fe₀, Fe₁, Fe₂ and Fe₃. PQM = phase quality map. SWI Fe_2,3 = average of SWI data at Fe₂ and Fe₃. The combination approach using the SWI mean, which uses the mean of the current and previous timepoint SWI data within the PQM region, was selected using numerical simulation experiments (see also Supplementary Figure S2 for more details). CM = combination method, SWI_PGAC,int = intermediate SWI_PGAC.

For the rest of the QSM processing, the sophisticated harmonic artifact reduction for phase data (SHARP) method was used to estimate the background field and remove it from the unwrapped phase (Schweser et al., 2011). The truncated k-space inverse filter approach with an iterative geometric constraint (also known as iSWIM) was applied to the resultant phase to generate the QSM data (Haacke et al., 2010; Tang et al., 2013). The QSM data was further refined as follows: 1) the strong phase gradients were removed from the long TE phase data using a phase quality mask (PQM) (at a threshold of Δφ > 1.8radians and dilated by a spherical kernel of radius = 5 voxels) and the resultant phase was used to obtain a QSM (QSM_TE2) data set; 2) the QSM of the short TE data (QSM_TE1) was generated without the use of a PQM; since at a low TE, the phase gradients were not as strong; and 3) the missing information on QSM_TE2 was filled-in by applying an inverted quality mask to QSM_TE1. This process reduced the aliasing artifacts surrounding the large vessels by utilizing the QSM_TE1 and helped in revealing the smaller vessels hidden beneath the confounding artifacts by applying a quality mask on the long TE phase data. As mentioned above, the SWI images at each time point were generated by homodyne high-pass filtering the original long TE (15ms) phase data to obtain a φ_M, without any intervention from the PQM and prior to the registration process. Here, φ_M was generated as defined by Haacke et al. (Haacke et al., 2004) and was multiplied into the original long TE magnitude image (multiplication factor = 4). Similarly, the short and long TE magnitude (S(TE)) data were fitted to the monoexponential equation: S(TE) = ρ·e^-(TE·R2*); where ρ is the intrinsic proton density of the tissues, to obtain R₂* maps.

Dynamic combination of SWI data

The main advantage of acquiring multiple time points over the gradual injection of Ferumoxytol was the ability to monitor the blooming artifacts for different levels of vascular diameters. At the Fe₀ time point, the large vessels (diameter ≈ 8 voxels across or 2mm) such as the BV and PCA were clearly visible, with minimal blooming artifact, but the smaller vessels could not be detected. Although these smaller vessels were revealed at the Fe₃ data point, such a high dosage of Ferumoxytol caused the large vessels to appear much larger than in the pre-contrast image, hiding the confluence with the smaller connected vessels. All four time points were combined to create an ideal combined image of SWI, which was obtained by identifying and correcting the regions with strong phase gradients. The resultant SWI data will henceforth be referred to as phase gradient-based adaptively combined SWI (SWI_PGAC) data. First, the TE2 magnitude data of Fe₂ and Fe₃ time points were averaged. This averaged data was then multiplied by the phase mask of the Fe₃image (multiplication factor = 4) to obtain improved SWI data (SWI_Fe2,3) with higher SNR.

The signal from a homogeneous white matter region was obtained from all time points as well as the SWI_Fe2,3 data to determine the effects of different FAs. The difference of mean values, obtained from a homogeneous white matter region, at each time point with respect to the SWI_Fe2,3, data was subtracted from the Fe₀, Fe₁ SWI data to avoid the unwanted signal jumps and improve the quality of SWI_PGAC data. In all cases, the distributions were obtained by manually contouring homogeneous regions, avoiding any hypointense structures that resembled a vessel on Fe₃ SWI data. The contours were then copied to the other SWI datasets.

The regions with strong phase change were masked out on SWI_Fe2,3 data and were updated with that of the previous time points (first, with Fe₁ SWI and then with Fe₀ SWI) using a selected combination method (described in detail further below). A PQM, as defined in the previous sub-section, was used here to identify these regions with strong phase gradients (Δφ > 1.8radians) and dilated by a spherical kernel of radius = 5 voxels, starting from the long TE phase at Fe₂ and then moving to the long TE phase at Fe₁. This process is illustrated in Figure 1B.

The combination method for the dynamic SWI data was evaluated by applying three different methods on numerical simulations: 1) SWI substitution: direct substitution of the current SWI data by the previous timepoint data within the PQM, 2) φ_M substitution: the same as method 1, but instead of SWI data, the φ_M was substituted within the PQM. The resultant φ_M was then multiplied with the pre-contrast TE2 magnitude data; and 3) SWI mean combination: by using the mean of the current and previous timepoint SWI data within the PQM region. The numerical simulation involved a model of three crossing vessels, as shown in Supplementary Figure S1, which made it possible to study how well the above-mentioned methods preserved the contrast at the vessel intersections. The phase data was simulated using the forward filter (Koch et al., 2006; Salomir et al., 2003) on the susceptibility model and the magnitude data was simulated by using the tissue properties as mentioned in ‘Optimizing the MRI parameters’ sub-section. The same imaging parameters were used as the in vivo data and the range of 0 to 4mg/kg was used for simulating the Ferumoxytol concentrations. All three vessels were assumed to be veins. The original simulations were generated with a matrix size of 512×512×256 and, in order to induce Gibbs ringing, partial volume effects and signal loss, the central 32×32×16 k-space elements were cropped.

Producing MRA and MRV maps

The MICRO protocol enables multiple image sources for producing both MRA and MR venograms (MRV). For the MRV, the QSM and R₂* constituted two different representations of veins. The third MRV was generated by dividing the short TE Fe₁ magnitude data by the short TE Fe₀ magnitude data. The T₁-shortening effect of Ferumoxytol increases the signal more dramatically for the veins since the arteries already have high intensity from the time-of-flight (TOF) effect (i.e., even for the pre-contrast data). Hence, the above-mentioned division provides a venous-only map (V_T1). The QSM, R₂* and V_T1 maps were then normalized to values between 0 and 1 and an average of these different MRV sources produced a high quality MRV, referred to as MRV_avg. An MRA image was then calculated using a non-linear subtraction (MRA_nl), as described by Ye et al. (Ye et al., 2013), of the long TE (S’) from the short TE (S) of the Fe₀ magnitude data. This subtraction MRA is obtained via:

$${\text{MRA}}_{\text{nl}}={\text{S}}^2-\lambda {{\text{S}}^{\prime }}^2$$ (1)

where, λ is a constant with an empirically selected value of 1.5. Due to the T₂* effect, this subtraction will also enhance the veins, but to a much smaller extent than the arteries. Nevertheless, any venous enhancement was discarded by using a mask generated from MRV_avg. As the TE2 data were not flow compensated, the arteries on R₂* maps were also hyperintense and were later suppressed using the MRA_nl data.

The MRA_nl and MRV_avg masks were used as overlays for the Fe₃ SWI data to identify whether a newly revealed vessel was an artery or a vein. This was done by confirming the connection of a given subvoxel vessel to the large vessel over several consecutive slices by one of the authors with more than nine years of experience in analyzing MRI images, especially the SWI data. An adaptive vessel tracking method, implemented in SPIN-Research software (SpinTech Inc., Bingham Farms, MI, USA), was used to extract these smaller vessels from SWI_PGAC and overlaid onto the Fe₀ QSM data in order to better visualize the midbrain structures and vasculature (Jiang et al., 2005).

Comparison with histological data

Using previous histology work with vascular ink injection (Salamon, 1971), the ratio of PCA to peduncular artery (PedA) and a collicular artery (ColA) were obtained. This ratio, coupled with the true PCA diameter obtained from the in vivo data, was used to calculate a rough estimate of the true diameters of the PedA and ColA. Using the SWI_PGAC data, PedA and ColA were identified for each volunteer. Similarly, another ex vivo study with methacrylate resin injection into the right internal carotid artery helped reveal deep white matter vessels under the scanning electron microscope (SEM) (Nonaka et al., 2003). The distance (from the ventricular angle, adjacent to the frontal horn of the lateral ventricles) and the diameter of the deep white matter vessels were measured from the SEM image. This distance was compared with the SWI_PGAC data in the same region to obtain an estimate of the vessel size in that region.

Revisiting the numerical simulations

Quantitative values of susceptibility (Δχ) were obtained for large vessels (namely the BV and PCA) at each time point in order to assess the effect of Ferumoxytol. As the concentration of Ferumoxytol increases, the apparent volume of a given vessel increases due to the signal loss surrounding the vessel. This, in turn, causes the apparent Δχ (Δχ_app) to be under-estimated, since the magnetic moment, which is proportional to the product of Δχ and the vessel volume (V) remains invariant. Hence, if the true volume (V_true) is known, the true susceptibility (Δχ_true) of a vessel can be calculated as:

$${△}_{\chi \text{true}}={△}_{\chi \text{app}}\times {\text{V}}_{\text{app}}/{\text{V}}_{\text{true}}$$ (2)

where V_true was obtained by measuring the diameter (d_true) for PCA and basal vein from the MRA_nl and Fe₀ QSM data, respectively. The apparent diameters (d_app) of these vessels were obtained from the short TE magnitude data at each post-contrast time point by measuring the number of voxels across the vessel that were outside the ±3σ range, where σ is the noise level of the image, measured within a homogeneous white matter region. The estimate for the true susceptibility is given by:

$${△}_{\chi true}={△}_{\chi app}\times {\left(d_{app}\right)}^2/{\left(d_{true}\right)}^2$$ (3)

Here, Δχ_app was obtained for each time point using the MRV_avg and MRA_nl masks of the basal vein and PCA and manually correcting these masks to avoid any region that has remnant unreliable phase change and to avoid misalignment between subsequent time points remaining even after image registration. Once Δχ_true was estimated for each post-contrast time point, the simulations were performed, as described above, using a high grid matrix of 1024×1024 and then collapsed to a 16×6 matrix, where x×y represents phase encoding × slice thickness, to obtain a VAR of 4:8:20. These simulated results helped validate whether one-fourth of a voxel-sized vessel could be visualized, especially using the Δχ_true values obtained from our cohort.

Statistical analysis

For the numerical simulations, the CNR values, represented by mean ± standard deviation of the mean (σ_M), were calculated over 800 independent repetitions and were compared with the Rose criterion (CNR > 3:1) to determine whether the simulated vessel would be detectable using the SWI data at a given dosage and imaging resolution. For each subject, using the BP values that were collected before and after the dose delivery, hypotension was defined as a decrease in systolic BP of >20 mmHg, or a decrease in diastolic BP of >15 mmHg (Lu et al., 2010). A paired t-test was used to compare the systolic and diastolic BP values that were acquired before and after Ferumoxytol delivery (statistical significance was set at p<0.05).

The homogeneous white matter signal distributions, obtained from each time point SWI data as well as SWI_Fe2,3 data, were compared using the one-way analysis of variance and the Tukey’s honestly significant difference procedure for multiple comparisons (statistical significance was set at p<0.05) (Brillinger, 2002; Hochberg and Tamhane, 1987; Searle et al., 1980). After the intensity correction, the white matter distribution was obtained from three different regions and the same tests were applied.

Finally, Δχ_app and d_app measurements were summarized as mean and standard error. The profiles of the SWI signal across the large and subvoxel vessels, from all time points, were compared using the root-mean-squared-error (RMSE). For large vessels, Fe₀ SWI was used as the reference for Fe₁, Fe₂, Fe₃ SWI and SWI_PGAC. Practically, the Fe₀ SWI will contain the least blooming artifact surrounding the large vessels and, therefore, will be closest to the true shape and size of the given vessel. Similarly, for the subvoxel vessels (or the vessels which are invisible on Fe₀ data), Fe₃ SWI was used as a reference, since the Ferumoxytol content will be highest at Fe₃ and will induce maximum contrast between the vessel and the surrounding tissue.

RESULTS

Based on the simulation results (Figure 2), the aspect ratio of 1:2:5 (or a VAR of 2:4:10 or 4:8:20) was selected because of: 1) the high CNR between the vessel and the surrounding tissue and 2) the extended brain coverage it offers in the slice-select direction. Therefore, the voxel resolution of 0.22×0.44×1mm³ was selected over other options such as 0.22×0.22×0.44mm³, 0.22×0.22×0.88mm³ and 0.22×0.44×0.88mm³. The acquired 0.22×0.44×1mm³ resolution data was then interpolated by zero filling in k-space along the phase-encode direction to achieve the pseudo-resolution of 0.22×0.22×1mm³. For the vessels on the order of ≈50μm, the trends show a linear increase in CNR for 4:8:16 and 4:8:20. However, with a VAR of 4:8:20 (or an imaging resolution of 0.22×0.44×1mm³ to visualize 50μm-sized vessels), the CNR did not cross the Rose criterion threshold using the estimated Δχ. On the other hand, when NEX = 2 is considered, representing the SWI_Fe2,3 dataset, the CNR improves significantly for VARs of 2:4:10 and 4:8:20, providing the best-case scenario compared to other VARs for detecting the 50μm-100μm vessels with the proposed voxel resolution of 0.22×0.44×1mm³.

Figure 2.

Simulations for a vein and an artery (at TE = 15ms, B₀ = 3T) comparing CNR as a function of Ferumoxytol dose for different vessel aspect ratios (VAR). The values with error bars represent the mean ± standard deviation of the mean, calculated over 800 repetitions. VAR is the aspect ratio of a voxel with respect to the vessel size. The horizontal dotted line (CNR = 3) represents a threshold for detectable vessels based on the Rose criterion. VARs of 2:4:8 and 2:4:10 (frequency:phase:slice) provided the best CNR especially for doses higher than roughly 1.5 mg/kg. SNR used in each case was 4.2:1, 6:1, 12:1, 12:1 for VARs of 2:2:2, 2:2:4, 2:4:8 and 2:4:10 (top row) and, similarly, for VARs of 4:4:4, 4:4:8, 4:8:16 and 4:8:20 (bottom row), respectively. A plot of CNR versus concentration for the average over two (NEX = 2) adjacent SWI datasets is presented with an SNR of 12√2:1 for the VARs of 2:4:10 and 4:8:20. For the vein simulations, the susceptibility induced by the normal venous oxygenation level (Δχ = 0.45ppm at ~70% oxygenation) was added to the overall susceptibility at all Ferumoxytol concentrations. The difference between the venous and arterial simulation trends is mainly observed between the Ferumoxytol doses of 0.5–2.5mg/kg in the top row, where the venous CNR increases faster than that of the arterial case due to the susceptibility difference. If a voxel is (200 μm)³ in size, then a VAR = 2:2:2 represents a 100 μm vessel and a VAR = 4:4:4 represents a 50 μm vessel.

We did not observe any drastic change in BP values that would indicate Ferumoxytol-induced hypotension (Supplementary Table S1). The difference in systolic and diastolic pressures due to Ferumoxytol injection was not statistically significant (p>0.05) for our study population. The SNR, obtained from a homogeneous white matter region, of the original magnitude at Fe₀ was 15:1 for short TE and 12:1 for long TE. The comparisons of the signal distributions for Fe₀, Fe₁ SWI data and SWI_Fe2,3 showed that the mean of the white matter region for Fe₀ SWI data (209.9) was significantly different (p<0.05) than in the Fe₁ (189.9), Fe₂ (187.5), Fe₃ (195.6) and SWI_Fe2,3 (191.4) data. In order to reduce any discontinuities in SWI_PGAC data, the difference of the mean distribution values for Fe₀ and Fe₁ SWI data, with respect to SWI_Fe2,3 data, were obtained and were subtracted from the Fe₀ and Fe₁ SWI data. After this intensity correction, the distributions from three different homogeneous white matter regions were compared and none of the data had means significantly different than the other (p>0.05). Although this step of intensity correction will most likely be required only when the datasets are acquired with different imaging parameters (such as with different FAs), the presence of Ferumoxytol could induce an overall signal loss in white and grey matter for post-contrast data even with the same FAs. This signal loss could be utilized to obtain capillary density measurements. Supplementary Figure S1 demonstrates the reconstruction results of the three combination methods for SWI_PGAC process. The SWI mean combination method was selected over SWI substitution and φ_M substitution methods as it was able to preserve the contrast of the smaller vein passing between the two parallel veins (red arrows in Supplementary Figure S1).

An example of Fe₀ to Fe₃ SWI data (Figure 3) shows gradual enhancement of subvoxel mid-brain vasculature. Ferumoxytol at 4mg/kg in Fe₃ provided much better visualization of the smaller vessels. However, signal around the larger vessels was exacerbated due to the high susceptibility of the Ferumoxytol content (Figure 4C). On the other hand, the SWI_PGAC provided better delineation of the larger vessels and preserved the visibility of the smaller or subvoxel vessels (Figures 4C and 4D). For the profile across the large vessels, SWI_PGAC data exhibited the lowest RMSE value of 11.4 as compared with 79.4 for Fe₃ SWI. Similarly, for small vessels, the RMSE was lowest for SWI_PGAC (10.1) as compared with Fe₀ (70.1), Fe₁ (49.1) and Fe₂ (30.3).

Figure 3.

Revealing the microvasculature of the midbrain using Ferumoxytol. (A) Pre-contrast (Fe₀), post-contrast SWI data (Fe₁, Fe₂, Fe₃) as well as the SWI_PGAC are shown in the top row, whereas the bottom row shows their corresponding zoomed insets, focusing on the midbrain region. Each post-contrast data, starting from Fe₁, was acquired at an interval of 11mins, increasing the dose at a steady rate (rate=150–200ml/hr, final concentration=4mg/kg). The post-contrast data revealed the mid-brain vasculature, which was not visible on the pre-contrast (Fe₀) data. SWI_PGAC was generated using the process illustrated in Figure 1, which reduced the signal loss surrounding the vessels; making it possible to obtain their true size (arrows), as shown in (B). All images were minimum intensity projected (mIP) over 8 sliceswith an effective slice thickness of 8mm.

Figure 4.

Comparing the signal behavior surrounding the large (A) and small (B) vessels on pre-contrast (Fe₀), post-contrast (Fe₁, Fe₂, Fe₃) as well as the SWI_PGAC data. The profile plot in (C), averaged along the four white lines in (A), compares the signal around two neighboring large vessels for Fe₀, Fe₃ and SWI_PGAC data, showing that Fe₃ was not able to separate the two vessels due to the strong extravascular phase gradient. The profile plot in (D), averaged along the four black lines as shown on the zoomed inset in (B), demonstrates the ability to visualize the smaller vessels. These vessels were only visible on the SWI_PGAC and Fe₃.

Supplementary Figure S2 shows the advantage of dynamically acquiring the post-contrast data, where the low levels of Ferumoxytol in the blood makes the intravascular signal hyperintense. The arteries possess identical signal on both Fe₀ and Fe₁ data since the TOF effect pre-contrast is equivalent to the T₁-shortening effect of the Ferumoxytol at Fe₁ (≈11mins post beginning the injection). Hence, the division of Fe₁ by Fe₀ from short TE data suppressed the background tissues as well as the arteries. Additionally, an arterial mask (MRA_nl) was generated by the non-linear subtraction given in Equation 1 and shown in Supplementary Figure S3. Finally, an improved MRV_avg image (Supplementary Figure S4D) was produced by averaging the venous mask generated in Supplementary Figure S2 with the normalized R₂* (Supplementary Figure S4B) and Fe₀ QSM (Supplementary Figure S4C).

The MRA_nl and MRV_avg vessel masks helped visualize the major arteries and draining veins of the midbrain, whereas the QSM and SWI_PGAC data provided a clear picture of the various anatomical structures (Figure 5). The Fe₀ QSM data provided susceptibility-based contrast for structures such as the SN, red nucleus and inferior colliculus (Figure 5A). The vasculature of the midbrain (including the MRA_nl (red), MRV_avg (blue) and tracked smaller vessels (green)) were overlaid on the Fe₀ QSM data (Figure 5C).

Figure 5.

Identifying the various structures of the midbrain using (A) Fe₀ QSM and (B) SWI_PGAC data for one selected participant. The red and blue overlays in (B) represent the MRA_nl (arteries) and MRV_avg (veins) masks. (C) Fe₀ QSM, with the MRA_nl (red) and MRV_avg (blue) overlays. An adaptive vessel tracking algorithm was used to track the small vessels (green in C). SN = substantia nigra, RN = red nucleus, IC = inferior colliculus.

Another advantage of the MRA_nl and MRV_avg overlays was the ability to classify smaller vessels into an arterial or a venous branch (Figure 6). Based on the MRA_nl overlay, the major brainstem arteries such as the anterior choriodal artery, inferior medial mesencephalic artery, medial hippocampal artery, posterior cerebral artery, posterior choroidal artery, posterior communicating artery, posterior hippocampal artery, posterior-medial choriodal artery and superior cerebral artery were identified. Similarly, based on the MRV_avg overlay, the major draining veins of the brainstem such as the basal vein, inferior ventricular vein, interpeduncular vein, vein of Galen were identified. As an example, the PedA and ColA as well as the peduncular vein (PedV) and a branch of the lateral mesencephalic vein (LMV) were identified on the SWI_PGAC data by finding their connections with these overlays in the midbrain region. Minimum intensity projections (mIP) of SWI images with different effective thickness (3mm, 6mm and 9mm) were used to find and confirm the connections of the small vessels to the large ones. The in vivo SWI_PGAC data and the histological data with vascular ink injection, which illustrated small arteries in the midbrain, are shown in Figure 7. SWI_PGAC data shows both arteries and veins due to the presence of Ferumoxytol. Based on the steps shown in Figure 6, PedA and ColA were classified and are identified by yellow and blue arrows, respectively, in Figure 7.

Figure 6.

Mapping the connectivity of the large vessels to the subvoxel level using the overlays of the MRV_avg and MRA_nl maps on SWI_PGAC data in the mid-brain. The SWI_PGAC data, with the overlays, provided an initial condition to map: (1a) the collicular artery (ColA); (2a) peduncular artery (PedA); (1v) peduncular vein (PedV) and (2v) branch of the lateral mesencephalic vein (LMV), arising from the large arteries. The SWI data was minimum intensity projected over 3mm, 6mm and 12mm to visualize and confirm the connectivity. Major brainstem arteries: AChA = anterior choriodal artery, IMA = inferior medial mesencephalic artery, MHA = medial hippocampal artery, PCA = posterior cerebral artery, PChA = posterior choroidal artery, PComA = posterior communicating artery, PHA = posterior hippocampal artery, PmChA = posterior-medial choriodal artery, SCA = superior cerebral artery. Major brainstem veins: BV = basal vein, IVV = inferior ventricular vein, IPV = interpeduncular vein, VofG = vein of Galen.

Figure 7.

SWI_PGAC data of eight different healthy subjects (A-D, F-I) focusing on the midbrain region. All images were minimum intensity projected (mIP) with an effective slice thickness of 8mm. The center image (E) was adapted from Figure 101 of the histology work by Salamon (Salamon, 1971). This histology work is also available online at Salamon’s Neuroanatomy and Neurovasculature Web-Atlas Resource: athttp://www.radnet.ucla.edu/sections/DINR/index.htm. The yellow and blue arrows identify PedA and ColA, respectively. Both vessels were clearly visible in all subjects.

The vessel diameter ratio from histology was calculated to be 7:1 and 18:1 for PCA:PedA and PCA: ColA, respectively (Figure 8A). From the in vivo data, the diameter of the PCA was measured to be 1.96±0.15mm across all subjects (Figure 8B). Based on the histology ratios and the in vivo PCA diameter, the estimated size of PedA and ColA were 280μm and 108μm. Furthermore, another validation was performed in the region near the frontal horn of the lateral ventricles, where the SWI_PGAC data were compared with a panoramic SEM image (Figure 8 in (Nonaka et al., 2003)). Using the SEM, the diameter of the deep white matter vessels (4.7mm from the ventricular angle) was measured to be 46μm. From the ventricular angle, the medullary veins even as far as 16mm from the ventricular angle were clearly visible on the SWI_PGAC data (Figure 8C), validating that the MICRO protocol was able to image vessels at the level of ~50μm.

Figure 8.

Validating the size of the small vessels that were visible after Ferumoxytol administration. (A) The ratio of posterior cerebral artery (PCA) to a peduncular artery (PedA) and collicular artery (ColA) was estimated using the histology work (adapted from Figure 101 in Salamon, 1971) by obtaining the vessel diameters at five different locations, as shown in the green boxes. (B) The true diameter of PCA was also obtained from Fe₀ short TE magnitude data for all subjects. The vessel diameter ratio from the histology photograph was calculated to be 7:1 and 18:1 for PCA:PedA and PCA:ColA, respectively. (C) SWI_PGAC data (with a zoomed inset of the medullary veins as shown by the white box), focusing on the cerebral white matter vessels. In the presence of 4mg/kg Ferumoxytol, the vessels as far as 16mm from the ventricular angle were visible on the SWI_PGAC data. VA = Ventricular angle.

The QSM results were improved by unaliasing the voxels at the vessel boundaries (Supplementary Figure S5). The change in volume of a vessel was determined by measuring the diameter of the vessel on the post-contrast short TE magnitude data and comparing it with Fe₀ QSM for BV and MRA_nl for PCA (Figure 9). The mean and inter-subject variability of the Δχ_app values acquired at Fe₀, Fe₁, Fe₂ and Fe₃ for the BV were 400±48 ppb, 597±131 ppb, 939±90 ppb and 1138±147 ppb, respectively. Similarly, Δχ_app values acquired at Fe₀, Fe₁, Fe₂ and Fe₃ for the PCA were −19±36 ppb, 290±123 ppb, 746±73 ppb and 925±65 ppb, respectively. Based on the d_app value for each subject (Supplementary Table S2), the Δχ_true for each post-contrast time point were obtained (Supplementary Table S2). At a dosage of 4mg/kg of Ferumoxytol, the Δχ_true was estimated as 2340 ppb for the BV and 2157 ppb for the PCA (Figure 9 and Table S1). These calculated Δχ_true values were found to be higher than the estimated values (2156 ppb for veins and 1706 ppb for arteries as derived from Liu et al. 2018) that were used for initial simulation tests. Using the calculated Δχ_true, the numerical simulations were revisited using the VAR of 4:8:20 and we found that CNR exceeded the Rose criterion, for SWI_Fe2,3 data (NEX = 2), to detect the vessels as small as one-fourth the size of a voxel, which corresponds to roughly 50μm based on the imaging resolution undertaken in this study (Supplementary Figure S6).

Figure 9.

Determination of the true diameter (d_true) and apparent diameter (d_app) for (A) the posterior cerebral artery (PCA) and (B) the basal vein (BV). The post-contrast short TE magnitude (Mag) data (Fe₁ to Fe₃) show the increasing signal loss surrounding the vessels due to the presence of Ferumoxytol. MRA_nl and Fe₀ QSM were used to obtain the d_true for PCA and BV, respectively. The diameters were measured by drawing a profile across the vessels, as shown by the red line in the images. The mean Δχ_app (black markers) at each time point increased with the increase in Ferumoxytol dose for both (C) the PCA and (D) BV. The error bars represent the standard deviation of Δχ_app for each subject. The red dots represent the Δχ_true value of blood at each time point derived from Eq. (3) based on the volume change.

DISCUSSION AND CONCLUSION

In this work, we demonstrated the utility of low dose Ferumoxytol in imaging the microvasculature of the midbrain. For large vessels, the high quality MRA_nl and MRV_avg maps were generated to help classify the smaller vessels into an artery or a vein. The SWI_PGAC data helped in revealing the underlying microvasculature and, at the same time, reduced the confounding signal loss surrounding the major vessels. On the quantitative front, the step-wise forward registration was used to unwrap the post-contrast phase data by employing complex division; which in turn improved the quality of the QSM data and reduced the artifacts caused by the aliased voxels (Supplementary Figure S5). QSM data also provided a unique contrast for various structures of the midbrain based on their susceptibility distributions (Figure 5). Using the property of magnetic moment, the change in vessel diameter, caused by signal loss in the presence of Ferumoxytol, was used to calculate the Δχ_true for BV and PCA at all post-contrast time points. The numerical simulations generated Δχ_true values and the previous histological studies (Figure 8) helped validate that, with a dose as low as 4mg/kg, one can image vessels on the order of 50μm to 100μm using the proposed MICRO imaging protocol.

Mapping the vasculature of the brain has immediate implications for understanding the etiology of many neurovascular and neurodegenerative diseases such as PD. It is thought that the loss of dopamine-producing cells of the SN could be related to a hypoxic state brought on by reduced flow and potentially small vessel abnormalities (Guan et al., 2013; Yang et al., 2015). Of course, this vascular hypothesis has not yet been fully validated in PD, but our findings can provide a useful methodology for testing this vascular hypothesis.

MRI has the potential to be the technical choice for investigating the small vessels due to its non-invasive nature and its superb anatomical imaging for differentiating various tissues in the brain, including the level of oxygenation in a blood vessel (Buch et al., 2018, 2016; Haacke et al., 2015, 2010). However, with conventional MRI, there is a limit to the available voxel resolution based on the SNR of the image. SWI is a powerful tool to image the subvoxel veins. However, it is insensitive to arteries in their natural form due to the low level of deoxygenated hemoglobin in arterial blood, which results in no susceptibility contrast with respect to the surrounding tissue. These shortcomings can be circumvented by Ferumoxytol enhanced MRI, such as the MICRO imaging approach discussed herein. By administering a strongly paramagnetic agent, Ferumoxytol, SWI was able to detect both arteries and veins in the same sensitivity; and its sensitivity to detect subvoxel objects increased tremendously.

In order to visualize and determine whether each of these small vessels is a vein or an artery, high quality MRA_nl and MRV_avg were obtained for the major arteries and veins from the pre-contrast data. The overlays of MRV_avg and MRA_nl helped in tracking the smaller tributaries of the major vessels. Studying these smaller vessels and propagating their link with the larger source vessel is key for determining where the problem lies for patients with abnormal vasculature. However, great caution must be used in distinguishing arteries from veins in this way, and numerous errors of interpretation are possible if the vessels are not followed from the boundary of the midbrain, as shown in Figure 6.

The Δχ_app also shows a strong increase for the Fe₁ timepoint (roughly twice for Fe₁ from Fe₀), as compared to the subsequent post-contrast timepoints. Although this sharp increase was expected due to the presence of Ferumoxytol, the blooming artifacts for Fe₂ and Fe₃ timepoints caused the underestimation of the susceptibility measurements due to the preservation of magnetic moment (as explained earlier in the ‘Revisiting the numerical simulations’ sub-section). As seen in Figure 9, the Δχ_true value for Fe₁ timepoint was very similar to the Δχ_app value, but Δχ_true was much higher than Δχ_app for later timepoints, confirming the role of blooming artifacts. In order to reduce the effect of partial volume on measuring the apparent and true values of the vessel volume, only a vessel with diameter greater than or equal to 6 voxels was chosen to obtain Δχ_app. The vessel was then extracted from the MRA_nl and MRV_avg maps by selecting the segments that were not surrounded by other detectable vessels for a distance of 6 voxels. Any presence of a nearby vessel could overestimate the measured volume due to overlapping loss of signal at the vessel boundaries.

Some of the limitations of this study include limited resolution, requirement of Ferumoxytol administration and misalignment of vessels for different scans. It is possible to acquire the data with a higher voxel resolution. However, due to smaller voxel size and, consequently, the need for a higher bandwidth, SNR will be reduced to a point where the CNR will drop dramatically. With strong blooming effects, Ferumoxytol enhanced SWI can circumvent both insufficient spatial resolution and insufficient contrast for very small arterial and venous vessels, thus offering the capability of practically imaging micro-vessels.

The Ferumoxytol dose used in this study (4mg/kg) is a fraction of the usual dose used to treat patients with anemia. Since the rapid injection of Ferumoxytol is not recommended by the FDA (https://www.fda.gov/media/91415/download) to reduce the risk of any adverse reactions, the proposed protocol takes advantage of the gradual injection (over 21–23 mins) by acquiring multiple timepoints of high resolution SWI data. With this low dose and slow injection rate, the post-contrast SWI was able to reveal numerous smaller vessels in the mid brain. One of the known side effects of administering Ferumoxytol is hypotension (Lu et al., 2010). As seen in supplementary table S1, both systolic and diastolic BPs do not show significant changes after the injection of Ferumoxytol over a long scanning session. A possible reason for not seeing any hypotensive changes for this study is the use of low dose and gradual delivery.

Even a small amount of movement between scans or during scanning can deteriorate the temporal comparison of increasing Ferumoxytol content. The image registration mitigates this issue to some extent, but fails in exactly matching the location of the small vessels. For this reason, the registered data for each volunteer was manually examined in order to confirm that the time points were registered adequately to perform the complex divisions. In the end, only two volunteers’ data could not be evaluated because of severe motion and poor image quality.

Another important consideration was to assume that there were no changes between antemortem and postmortem states of the cerebral vasculature. It is known that in the postmortem state, the arterial smooth muscle relaxation and contractility change relative to their in vivo state (Onoue et al., 1993; Patel and Janicki, 1970). This change could have an impact on diameter measurements performed on micro-angiograms, since the dynamic pressure being imposed on the vessel walls is absent. However, we predict that such errors will be minimal for smaller vessels (<100 μm), as there is a lack of significant elastic tissue in their walls (Baker, 1937; Tucker and Mahajan, 2020). In addition, the histological work by Salamon et al, which was used for comparison in this work, does inhibit these changes and other artefacts related to postmortem preparation by injecting the radiopaque injection gradually with the simultaneous gelatin injection to preserve the shape of the vessels and prevent the leakage. The deformation was avoided by placing the cadaver brain slices in a mold on which the cerebral hemispheres rested, in order to reduce the shrinkage of cerebral tissue. Nevertheless, there may still be remnant changes in vascular diameter that cannot be confidently addressed in this work, such as the involvement of the vessel wall in the diameter measurements due to the absence of contrast between the intraluminal space and the vessel wall. In addition, the inter-subject variation in the postmortem vessel size could not be ascertained from the histology work by Salamon et al. Therefore, the numerical simulations based on the previous work (Figure 2) and the data-driven values for Δχ_true were calculated, in order to avoid these unwanted errors related to comparing with postmortem data. These simulations helped in confirming the detectability of 50μm-sized vessels, as shown in Figure 2 and Supplementary Figure S6.

With the help of the proposed MICRO protocol, the subvoxel vascular network can be enhanced at a very high spatial resolution. This will enable the identification of abnormal vasculature throughout the brain in the future and particularly in areas with white matter hyperintensities, which are present in diseases such as multiple sclerosis, dementia, stroke and PD to name a few. Similarly, perfusion weighted imaging and QSM data can be used to assess local cerebral blood flow and oxygenation levels, respectively, especially in areas with reduced vasculature.

In summary, with MICRO imaging, it was possible to image the subvoxel vasculature of the midbrain. With the proposed SWI_PGAC method, the SWI data was improved significantly by reducing the confounding signal loss arising from strong susceptibility structures. Consequently, this approach could be used to study the vasculature of many other important structures such as the hippocampus or basal ganglia and its role in the etiology of different neurological diseases.