Fluid dynamic assessment of positive end-expiratory pressure in a tracheostomy tube connector during respiration

Abstract

High-flow oxygen therapy using a tracheostomy tube is a promising clinical approach to reduce the work of breathing in tracheostomized patients. Positive end-expiratory pressure (PEEP) is usually applied during oxygen inflow to improve oxygenation by preventing end-expiratory lung collapse. However, much is still unknown about the geometrical effects of PEEP, especially regarding tracheostomy tube connectors (or adapters). Quantifying the degree of end-expiratory pressure (EEP) that takes patient-specific spirometry into account would be useful in this regard, but no such framework has been established yet. Thus, a platform to assess PEEP under respiration was developed, wherein three-dimensional simulation of airflow in a tracheostomy tube connector is coupled with a lumped lung model. The numerical model successfully reflected the magnitude of EEP measured experimentally using a lung phantom. Numerical simulations were further performed to quantify the effects of geometrical parameters on PEEP, such as inlet angles and rate of stenosis in the connector. Although sharp inlet angles increased the magnitude of EEP, they cannot be expected to achieve clinically reasonable PEEP. On the other hand, geometrical constriction in the connector can potentially result in PEEP as obtained with conventional nasal cannulae.

Graphical abstract

Introduction

High-flow oxygen therapy, including that administered via high-flow nasal cannula therapy (HFNC), has been applied as a promising treatment for patients with lung injury [8]. One approach to this therapy is to perform tracheostomy by surgically creating an opening through the neck into the trachea to allow direct access to a tracheostomy tube and a connector attached to the tube [10]. The tracheostomized patients can then breathe through the tube rather than through the nose and mouth. Administration of an air-oxygen mixture is required to achieve positive end-expiratory pressure (PEEP) to assist in breathing and avoid pulmonary collapse [21]. HFNC has conventionally been used with an inflow rate between 20–60 L/min [25, 35], because it produces PEEP in the range of 2–8 cmH₂O [6, 26], and can also wash out CO₂ from the upper airways [22, 23]. Furthermore, HFNC can decrease the work of breathing and also enhance neuroventilatory drive [35]. More recently, benchtop experiments were performed with a high-flow tracheostomy circuit, and the so-called potential PEEP, defined as the blow-off pressure of the open gas delivery system, was approximately 0.3–0.9 cmH₂O (≈ 29.4–88.3 Pa) for an inflow rate of 40–60 L/min [38].

The ability to successfully achieve PEEP by tracheostomy cannulae is especially important in ill patients who need long-term (2–3 weeks) ventilation, because such cannulae are used for almost 90% of these patients and also because there is a correlation between high survival rates and short ventilation duration [7]. Hence, providing adequate gas exchange is necessary for early ventilator removal in tracheostomized patients. Considering fast-increasing worldwide incidence of COVID-19, it is currently of paramount importance to identify the mechanical conditions required for PEEP generation in lung therapy. The mechanical conditions necessary to produce PEEP are therefore fundamentally important not only for tracheostomized patients but also for individuals with acute lung injury or acute respiratory distress syndrome (ARDS, the most severe form of acute lung injury) [20] and for patients assisted by extracorporeal membrane oxygenation (ECMO) [28]. Since it is expected that PEEP generation results from the hydrodynamical interplay between pulmonary dynamics (e.g., stress and deformation) and the geometrical characteristics of the tracheostomy tube connector, which can be characterized as a bifurcated tube, understanding the outlet pressure of the connector during respiration is of fundamental importance in high-flow oxygen therapy. However, much is still unknown about the geometrical effects of tracheostomy tube connectors (or adapters) on PEEP.

Along with the aforementioned clinical studies, recent theoretical and computational approaches have successfully been used to investigate aspects of pulmonary dynamics such as stresses and deformation [29, 31], as well as the fully turbulent nature of tracheal flow during inhalation [5, 13, 14, 30, 37, 42]. For instance, Brouns et al. (2007) systematically investigated how pressure drop affected tracheal stenosis in the range between 50 and 90% and showed that the pressure drop over the normal glottis (~ 40% constriction) was negligible with respect to that induced by constrictions greater than 70%, which impaired breathing [5]. Their numerical results suggest that PEEP can be caused by luminal stenosis in the connector. In other numerical studies using a reduced-dimensional (or lumped) model of pulmonary networks that included alveoli, the mechanical effects of downstream regions on airflow in upstream regions were quantified [12, 15, 17]. Such coupled analysis of three-dimensional (3D) fluid flow and reduced-dimensional models of the mechanical pulmonary response will be useful to understand the mechanical conditions of PEEP while considering both airflow in the connector and patient-specific spirometry. However, no such framework has been established yet.

Therefore, the first objective of this study was to develop a computational platform to evaluate PEEP, taking into consideration the 3D nature of the airflow in the tracheostomy tube connector. The second objective was to quantify how luminal stenosis in the connector affected the magnitude of end-expiratory pressure (EEP).

Methods

EEP was calculated as the area-averaged tracheal pressure, which corresponded to the outlet pressure in the connector (P_tr or P_out3) as described below. Calculated EEPs for different inflow rates Q_in were compared with those obtained experimentally. The effects of connector inlet angles θ and luminal stenosis on EEP were further investigated using a newly developed model.

Lumped lung model

In the lumped lung model, the lung tissue is modeled as an isotropic material, and only diagonal components of elastic stress P_e are considered to effectively achieve lung volume change. Alveolar pressure P_al is balanced with pleural pressure P_pl, the latter of which is driven by respiratory muscle contraction as well as pressure (or isotropic elastic stress) P_e due to lung elasticity acting on the lung tissue, i.e.,

$$P_{\mathit{al}}=P_{\mathit{pl}}+P_e.$$ 1

P_pl is given as the sinusoidal function

$$P_{\mathit{pl}}=-P_{\mathit{pl}}^{\mathit{amp}}\sin \left(2,\pi ,t,/,T\right)-P_{\mathit{pl}}^0,$$ 2

where T is the respiratory period (5 s), $P_{\mathrm{pl}}^{\mathrm{amp}}$ is the amplitude of pleural pressure (250 Pa [40]), and $P_{\mathrm{pl}}^0$ is the baseline pleural pressure (750 Pa [40]). Both the inspiration and expiration phases last for T/2 (2.5 s). The isotropic elastic stress P_e can be given as [9]:

$$P_e=4akE\exp \left[2,a,E^2\right],$$ 3

where k is the coefficient of lung elastic stress (10.1 Pa), a is a model coefficient (3.0), and E (= (λ²—1)/2) is Green’s strain defined by the stretch ratio λ (= (V (t)/V₀)^1/3) between the lung volume V(t) at time t and the reference lung volume V₀. The total gas volume in the lung is about 3 × 10^–3 m³, and the volume inspired per breath during quiet breathing is about 0.45 × 10^–3 m³ in a typical man about 40 years old and about 1.7 m tall [27]. Thus, in this study the reference lung volume was defined as V₀ = 1.5 × 10^–3 m³.

Flow model and geometry of tracheostomy tube connectors

Flow was assumed as incompressible, Newtonian viscous fluid flow, and hence, the governing equation of the airflow velocity v in the connector is expressed as

$$\rho \left({\partial }_t,\mathbf{v},+,\mathbf{v},\bullet ,\mathrm{\nabla },\mathbf{v}\right)=-\mathrm{\nabla }p+\mu {\mathrm{\nabla }}^2\mathbf{v},$$ 4

$$\mathrm{\nabla }\bullet \mathbf{v}=0,$$ 5

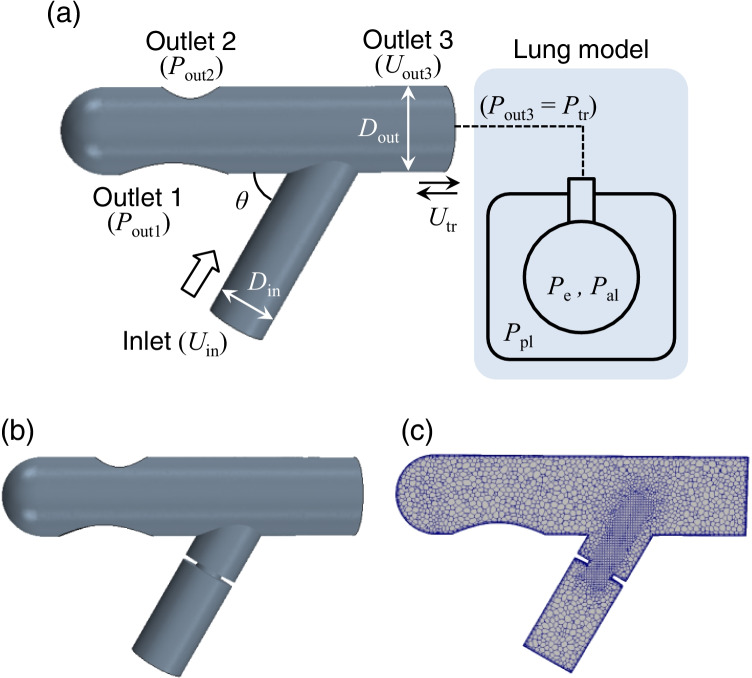
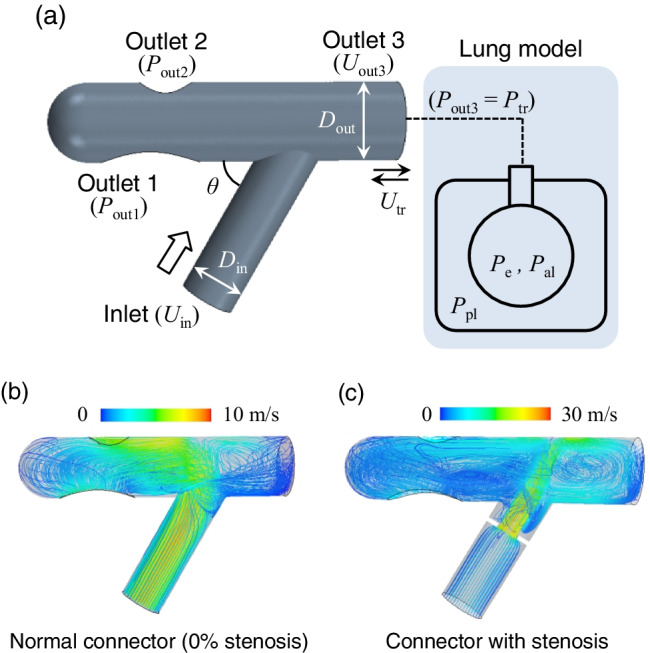
where ρ is the air density (1.18 kg/m³), μ is the viscosity (1.86 × 10^–5 Pa·s), and p is the pressure. The computational domain for 3D computational fluid dynamics (CFD) is shown in Fig. 1a, where the lumped lung model is attached to outlet 3, assuming an open area in the trachea. There are two other outlets (outlet 1 and outlet 2) in the connector, both of which are exposed to the open air (Fig. 1a). The geometry of a connector with 50% stenosis and its internal meshing are also shown in Fig. 1b and 1c. Here, the rate of stenosis was defined as (1—D_min/D_in), where D_in is the inlet diameter (11 mm) and D_min is the minimum connector diameter. The length of the constricted portion of the connectors was set at 1 mm (Fig. 1b and 1c. Unless otherwise specified, we show the results obtained with an inlet angle of θ = 60°.

Fig. 1.

a Computational domain for 3D CFD involving a modeled connector and schematics of a lumped lung model. b 3D CFD computational model with 50% stenosis, and c generated meshes where adaptive mesh refinement and prismatic layers lining the walls are considered in addition to a polyhedral mesh. The boundary conditions of the lumped lung model were set as inlet velocity U_in, outlet pressures P_out1 and P_out2, and outlet velocity U_out3 (= U_tr (t, P_e, P_al, P_pl)). The standard inlet angle was set as θ = 60°. The inlet and outlet diameters in connectors were commonly set as D_in = 11 mm and D_out = 15.4 mm. The rate of stenosis was defined using the minimum connector diameter D_min as (1—D_min/D_in). The length of the constricted portion of each connector was set as 1 mm

Numerical simulation

The clinically relevant range of inlet velocity U_in in the connector could be determined by inlet flow rates Q_in (= U_inπ $D_{\mathrm{in}}^2$/4) = 10, 30, and 50 L/min [24]. Hence, the inflow was characterized by Reynolds number (Re) from 1.2 × 10³ to 6.1 × 10³; Re was defined as ρD_inU_in/μ. Taking into account the connector stenosis and bifurcation, the local Re in the stenotic region was over 10⁴, and it was also expected that laminar, transitional, and turbulent flows would coexist in the flow field. In this study, a realizable k-ε turbulence model [32] was implemented to simulate the turbulence mean flow field. This model was successfully applied to steady inhalation in a simulation of tracheal flow in a human airway [13, 16, 37]. The CFD software Simcenter STAR-CCM + 2020.2 (Siemens Digital Industries Software Inc., Plano, TX) was used for mesh generation and to solve the Navier–Stokes equations. The flow was driven by Dirichlet boundary conditions, where the air velocity in the inlet (U_in), that in the outlet connected to the trachea (U_out3 = U_tr(t, P_e, P_al, P_pl)), and the constant pressure in the outlet (P_out1 = P_out2 = 0 Pa) were defined. A polyhedral mesh was considered for the fluid mesh, and adaptive meshing, including prismatic layers, was also considered in the stenotic region and to line the walls; in total, approximately 40,000 meshes were considered in each airway model. The dependence of the meshes on EEP was also confirmed with double resolution (approximately 80,000 meshes in total) (see result in Sect. 3.1).

Although several lumped models of airways consisting of different types of electrical components (lumped parameters) have been proposed [3, 12], taking into account the structural hierarchy in the human trachea [39, 41], the tracheal velocity U_tr was simply defined as the Dirichlet boundary condition in the 3D CFD model, using the following linear equation:

$${\mathrm{P}}_{\mathit{tr}}-{\mathrm{P}}_{\mathit{al}}=\mathrm{\Gamma }\dot{V}=\mathrm{\Gamma }{\mathrm{U}}_{\mathit{tr}}{\mathrm{A}}_{\mathit{tr}},$$ 6

$$\to {\mathrm{U}}_{\mathit{tr}}=\frac{{\mathrm{P}}_{\mathit{tr}}-{\mathrm{P}}_{\mathit{al}}}{\mathrm{\Gamma }{\mathrm{A}}_{\mathit{tr}}}$$ 7

where P_tr is the tracheal pressure, Γ is the airway resistance (200 kPa/m³), and A_tr (= π $D_{\mathrm{out}}^2$/4) is the opening area in the trachea (or tracheostomy tube) that is given as the outlet diameter of the connector D_out (15.4 mm). In general, the end-expiratory phase was defined as the expiratory flow rate (≥ 0 L/min) reaching zero, as shown in expiratory and inspiratory flow-volume curves [40]. Therefore, in this study, the end of expiration was defined by U_tr = 0. The present lung volume V(t) could be calculated as:

$$\mathrm{V}\left(t,+,\mathrm{\Delta },t\right)={\mathrm{V}}_0+{\int }_0^t\dot{V}d{t}^{{}^{\prime }}\approx {\mathrm{V}}_0+{\mathrm{U}}_{\mathit{tr}}\left(t\right){\mathrm{A}}_{\mathit{tr}}\mathrm{\Delta }t,$$ 8

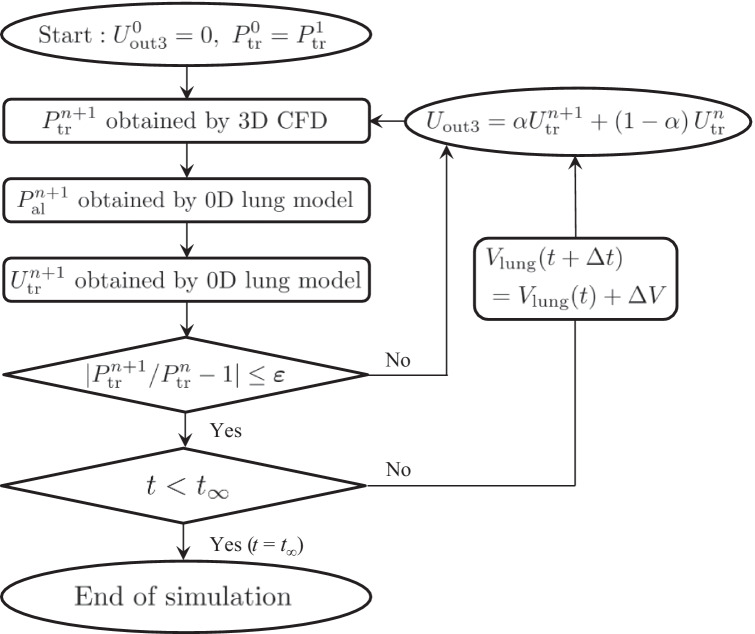
where Δt is set as 0.05 s. 3D CFD was started from temporal tracheal velocity U_tr = 0, and continued while updating U_tr until the tracheal pressure P_tr became almost constant such that |$P_{\mathrm{tr}}^{\mathrm{n}+1}$/$P_{\mathrm{tr}}^{\mathrm{n}}$—1|≤ ε = 0.01, where the superscript n (or n + 1) is the number of trials at time t. The simulation was started with $P_{\mathrm{tr}}^0$ = $P_{\mathrm{tr}}^1$. The boundary velocity U_out3, which changed over time, was determined using a coefficient α (0 ≤ α ≤ 1); U_out3 = α $U_{\mathrm{tr}}^{\mathrm{n}+1}$ + (1—α)$U_{\mathrm{tr}}^{\mathrm{n}}$. In this study, to achieve numerical stability, α was set as 0.3 in a normal connector and 0.8 in a constricted connector. This computational algorithm is summarized in Fig. 2. Simulations lasted for three periods (3 T), during which the calculated variables reached a stable periodicity. As described below, the time history of P_tr was preliminarily checked by experimental measurements as shown in Fig. 3c and found that the time history did not affect the EEP; i.e., the effect of airflow dynamics on EEP was negligible, at least for a physiologically relevant respiratory rate (0.2 Hz). Hence, in the model algorithm to update the flow fields, the steady state under the calculated U_tr in the lumped lung model was considered at each time step.

Fig. 2.

Flow chart for updating the Dirichlet boundary condition U_out3 in 3D CFD, where α is the coefficient for the temporal updating of U_out3 (0 ≤ α ≤ 1), ε and t_∞ are set as ε = 0.01 and t_∞ = 3 T, respectively. The simulation ends at t = t_∞ = 3 T

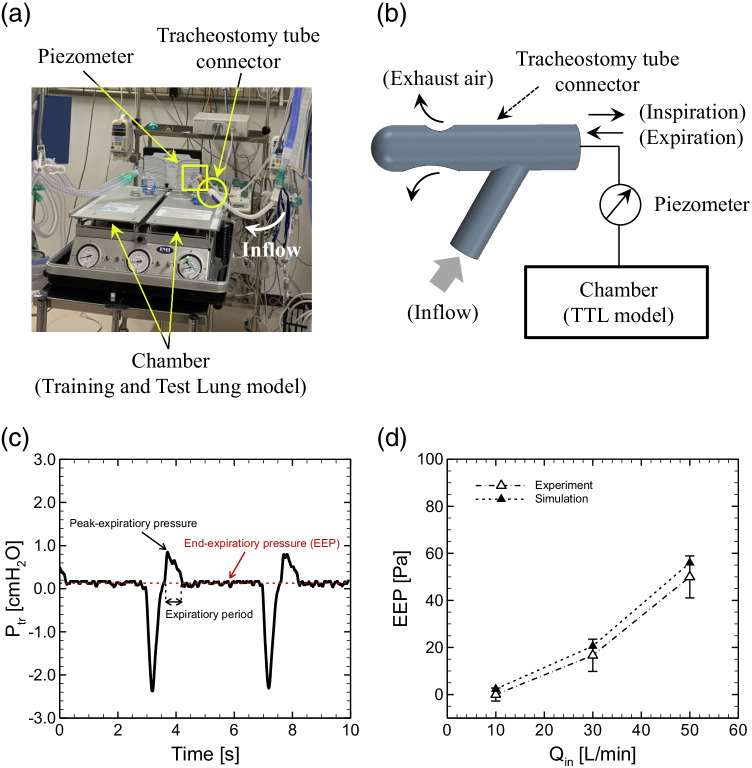
Fig. 3.

a Snapshot of entire experimental setup and b schematic of experiment. c Time history of tracheal pressure P_tr in a normal connector (i.e., inlet angle θ = 60° without stenosis) at Q_in = 30 L/min. d A comparison of EEP obtained with experimental measurements (blank triangles) versus numerical simulations (solid triangles) as a function of inlet flow rate Q_in in a normal connector, where the errors in experimental data represent temporal fluctuations during the end-expiratory phase

Experimental setup

To simulate spontaneous breathing, a double-chamber Training and Test Lung model (TTL) (Michigan Instruments, Grand Rapids, MI) was used, following a previous study [43]. A Puritan- Bennett 840 ventilator (Nellcor Puritan Bennett, Carlsbad, CA) was used as the driving chamber in the TTL model. An Optiflow Plus Tracheostomy Interface Direct Connector (Fisher & Paykel Healthcare, Auckland, New Zealand) was connected to the chamber via an endotracheal tube with an 8-mm internal diameter. Different inflow rates were generated by the Optiflow attached to the connector inlet. The two chambers were connected to each other to stimulate spontaneous breathing during the experiment. The tracheal pressure (P_tr) was measured at the proximal end of the tracheal tube using a pressure transducer (True Wave, Edwards, Irvine, CA). Pressure signals were sampled at a rate of 250 Hz. A surgical support and intensive care management system (Nihon Kohden, Tokyo, Japan) were used to compute P_tr. Considering that patients who require tracheostomy tube connectors are in recovery (i.e., candidates for ventilator withdrawal) but are not fully healed, the compliance of the model lung was set as 0.08 L/cmH₂O, which is slightly smaller than that in healthy subjects (0.094–0.136 L/cmH₂O [18]). The resistance of the model lung was imposed with a parabolic airway resistor (5 cmH₂O/L/s, Pneuflo resistor Rp5, Michigan Instruments). The PB840 ventilator parameters were set as follows: volume control mode, 500 ml of tidal volume; respiratory rate, 15 breaths/min (0.25 Hz); PEEP, 0 cmH₂O; and inspiratory time, 0.7 s. To easily detect EEP from periodic tracheal pressure profiles, the expiratory time was set to be relatively longer (3.3 s) than the inspiratory time (0.7 s). Figure 3a shows the experimental setup. A piezometer was attached to the connector to measure the pressure at the chamber inlet. Figure 3b shows a schematic of the experimental setup. The time history of tracheal pressure P_tr in a normal connector at Q_in = 30 L/min is shown in Fig. 3c, where the moving-average was obtained for the data of P_tr with a window size of 76 ms.

The parameters for the lumped lung model (a, k, Γ, and α) were determined so that the order of magnitude of the calculated EEP was the same as that obtained with experimental measurements (see Fig. 3d), while preserving the physiologically relevant lung deformation ΔV = 500 cm³ [27, 40] and pleural pressure difference ΔP_pl = 500 Pa [19] during respiration under a baseline pleural pressure of 750 Pa [40] with an amplitude of 250 Pa [40]. The model parameters are summarized in Table 1.

Table 1.

Nomenclature of parameters and variables

Symbol	Physical meaning	Value (Dimension)	Reference
Ppl	Pleural pressure		-
$P_{\mathrm{pl}}^{\mathrm{amp}}$	Amplitude of the pleural pressure	250 Pa	[40]
$P_{\mathrm{pl}}^0$	Baseline of the pleural pressure	750 Pa	[40]
Pe	Pressure due to lung elasticity		-
Pal (= Ppl + Pe)	Alveolar pressure		-
Ptr	Tracheal pressure		-
Qin	Inflow rate	10–50 L/min	[24]
Uin	Inflow velocity		-
Utr	Tracheal velocity		-
Din	Inlet diameter of connector	11 mm	-
Dout	Outlet diameter of connector	15.4 mm	-
V	Present lung volume		-
V0	Reference lung volume	1.5 × 10–3 m3	[27]
λ (= (V/V0)1/3)	Stretch ratio		-
E (= (λ2—1)/2)	Green’s strain		-
Γ	Airway resistance	200 kPa/m3	-
T	Respiratory period	5 s	-
a	Model coefficient	3.0	-
k	Coefficient of elastic stress of the lung	10.1 Pa	-
Ρ	Fluid density	1.18 kg/m3	-
µ	Fluid viscosity	1.86 × 10–5 Pa·s	-
θ	Inlet angle	30°, 45°, 60°	-
α	Coefficient for temporal updating of the velocity of outlet3 (Uout3)	0.3 (in normal) 0.8 (in stenosis)	-

Results

Model validation and EEP in a normal connector

Figure 3d shows a comparison of the magnitude of EEP obtained with numerical simulation versus experimental measurements as a function of inlet flow rate Q_in in a normal connector (i.e., inlet angle θ = 60° and without stenosis). It is expected that clinically reasonable PEEP is over 2 cmH₂O (196.2 Pa [6, 26]). Calibrations were performed for the parameters in the lumped lung model (a, k, and Γ) shown in Eqs. (3) and (7), including the coefficient α for the temporal updating of U_tr. The EEP values obtained via experimental measurements (EEP_exp) and numerical simulations (EEP_sim) are summarized in Table 2. For the smallest Q_in = 10 L/min, the EEP value was very small and sometimes became negative. Thus, the EEP value for such small Q_in (≤ 10 L/min) was defined as 0. When these values were evaluated in terms of the difference in the magnitude of EEP per 1 cmH₂O between the numerical and experimental results |EEP_exp—EEP_sim|/cmH₂O, the differences did not exceed than 0.061 for all Q_in, and the calculated magnitudes of EEP_sim were within the range of error of the experimental data (Fig. 3d). The results indicate that the developed model makes it possible to investigate the magnitude of EEP within an accuracy of 1 cmH₂O, and thus, the same model parameters are used hereafter (see Table 1).

Table 2.

EEP values via experimental measurements (EEP_exp) and numerical simulations (EEP_sim)

Qin [L/min]	EEPexp [Pa]	EEPsim [Pa]	|EEPexp – EEPsim|/EEPexp [-]	|EEPexp – EEPsim|/cmH2O [-]
10	0	2.331	-	0.024
30	16.66	20.58	0.235	0.040
50	49.98	55.96	0.120	0.061

The dependence of the meshes on the magnitude of EEP was tested, and the calculated EEP was 20.58 Pa with the present resolution (i.e., 40 000 meshes) and 20.84 Pa with double resolution (approximately 80,000 meshes in total). Because the relative difference in the magnitude of EEP between the present and higher resolutions was less than 1%, it was considered appropriate to examine the numerical results obtained with the present resolution.

A different meshing style, involving increasing the number of prismatic layer and the adaptive meshes in the constricted area, was tested for severe geometry, characterized by 60% stenosis and the sharpest inlet angle (30°). The present model, with a total of ~ 60,000 meshes for this type of constricted connector, is called model C1, while the reconstructed model with a total of over 100,000 meshes is called model C2. The calculated magnitude of EEP obtained with model C1 for Q_in = 30 L/min was 156.5 Pa, and that obtained with model C2 was 172.1 Pa. The relative difference in the magnitude of EEP was 0.098. Hence, the present meshing style still preserves a 1-cmH₂O accuracy for the magnitude of EEP.

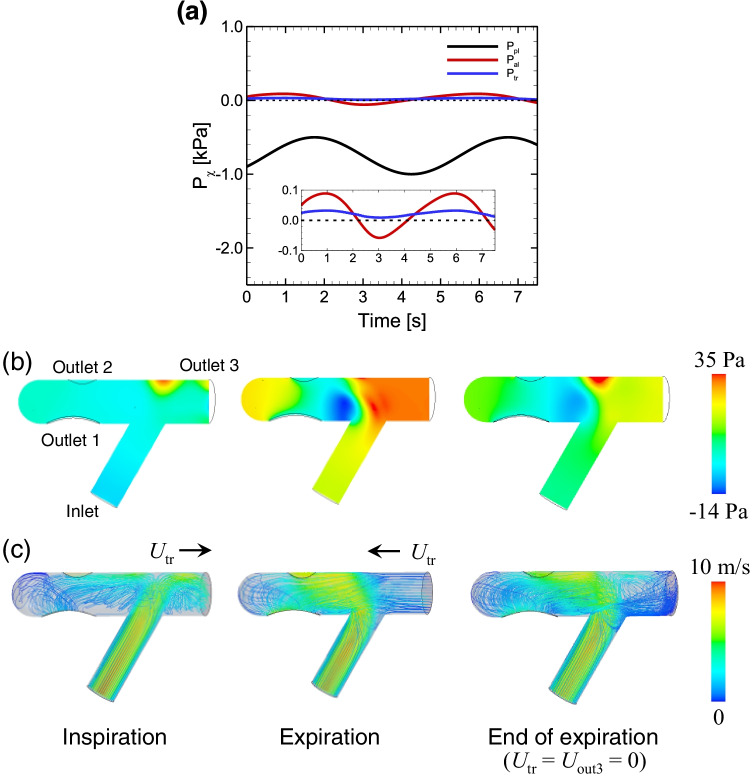
The flow field in a normal connector and the tracheal pressure U_tr during the respiratory period were investigated. Figure 4a shows the time history of the given pleural pressure P_pl, the calculated alveoli pressure P_al obtained with the lumped lung model, and the calculated tracheal pressure P_tr obtained with CFD. Data are shown after P_al and P_tr have reached to the stable periodic phase (t ≥ 2.0 s). All data used hereafter were obtained after these calculated values reached a stable periodicity, in order to avoid the influence of the initial condition ($U_{\mathrm{tr}}^0$ = $U_{\mathrm{out}3}^0$ = 0).

Fig. 4.

a Time history of the pleural pressure P_pl, calculated alveoli pressure P_al, and tracheal pressure P_tr (= P_out3), where data are shown after P_al and P_tr have reached the stable periodic phase. Snapshots of b pressure and c velocity fields in a normal connector in each respiratory phase: (left) inspiration, (middle) expiration, and (right) the end of expiration defined with U_tr = 0. Snapshots of streamlines in each phase are also displayed in c, where the color represents the velocity magnitude. The results were obtained with Q_tr = 30 L/min

Figure 4b and 4c show snapshots of pressure and velocity fields, respectively, in a normal connector for each respiratory state. During inspiration, the pressure in the upper bifurcated area was relatively high because the inlet flow directly reached that location with large momentum and diverged to the tracheal and outlet regions (left in Fig. 4b and 4c. This high-pressure field shifted and expanded toward the tracheal regions during expiration. The direction of the inlet flow was sharply changed by the expiratory flow from outlet 3 (middle in Fig. 4b and 4c. At the end of expiration, defined by U_tr = 0, a high-pressure field again emerged in the upper bifurcated area, and some amount of the inflow moved to the tracheal region, resulting in recirculation there (right in Fig. 4b and 4c.

Figure 5a shows the time history of U_tr and lung volume V during period T (= 5 s) at Q_in = 30 L/min in a normal connector, where the data were obtained only after the stable periodic behavior was achieved. When U_tr reaches zero (i.e., start and end of expiration), the lung volume approaches its maximum and minimum (Fig. 5a). Thus, there is a finite phase difference between the two waves. This phase difference remains the same even for different Q_in (data not shown). Figure 5b shows the tidal volume ΔV_tidal as a function of Q_in. ΔV_tidal was calculated as the volume change from minimum V_min to maximum V_max, i.e., ΔV_tidal = V_max—V_min. The pressure difference between the tracheal pressure and alveolar pressure (P_tr—P_al) in Eq. (7) decreased as Q_in increased, resulting in a decrease in tidal volume; i.e., the magnitude of U_tr decreased. Such passive regulation during exhalation qualitatively agrees with experimental measurements using high-flow nasal ventilation, especially in healthy subjects [4].

Fig. 5.

a Time history of the tracheal velocity U_tr and lung volume V during a period T (= 5 s) at Q_in = 30 L/min. b The tidal volume ΔV_tidal as a function of Q_in. Data were obtained after reaching stable periodic behavior

Figure 6 shows the calculated magnitude of EEP for different inlet angles θ (= 30° and 45°) as a function of inflow rate Q_in. Although the magnitude of EEP increased as the inflow rate Q_in increased and as the inlet angle decreased (Fig. 6), the relative difference in EEP between the normal (θ = 60°) and sharpest angle (θ = 30°) decreased as the inflow rate increased; (EEP|_{θ = 30°}—EEP|_{θ = 60°})/EEP|_{θ = 60°} = 0.47, 0.41, and 0.38 for Q_in = 10, 30, and 50 L/min, respectively.

Fig. 6.

EEP as a function of inlet flow rate Q_in in a normal connector for different inlet angles θ

Effect of connector stenosis on EEP

The effect of connector stenosis on EEP was investigated. Figure 7a shows the time history of the pleural, alveolar, and tracheal pressures (P_pl, P_al, and P_tr) in a connector with 50% stenosis. The baseline of P_al and P_tr values were higher than those in a normal connector, even for the same amplitude of P_pl (Fig. 7a).

Fig. 7.

a Time histories of P_pl, P_al, and P_tr. Snapshots of b pressure and c velocity fields in each respiratory phase in a connector with 50% stenosis: (left) inspiration, (middle) expiration, and (right) end of expiration. The results were obtained with Q_tr = 30 L/min

The mechanism of generating such large EEP involves the pressure field in the connector, as shown in Fig. 7b. The pressure field was constantly high during inspiration. This was especially true in the inlet region (i.e., upstream region before stenosis) and the upper bifurcated area; indeed, in the bifurcated area the pressure reached 250 Pa, which was approximately 7 times higher than that in a normal connector (Fig. 7b). Since a reduced area generates fast flow, flow administrated at the inlet can reach the tracheal region even during and at the end of expiration, as shown in Fig. 7c. These results suggest that connector constriction potentially generates PEEP.

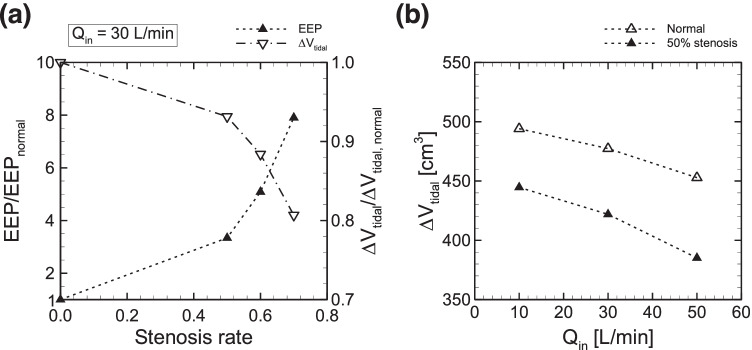
Figure 8a shows the effect of the stenosis rate on EEP and ΔV_tidal at Q_in = 30 L/min. The calculated EEP normalized by the EEP value obtained with a normal connector (0% stenosis) drastically increased for stenosis over 50% (Fig. 8a, left axis). Similar results were also obtained in previous numerical analyses of tracheal flow using the Yang-shih k-ε turbulence model [5], where the simulated pressure drop in the stenotic region dramatically increased only when far more than 70% of the tracheal lumen was obliterated, both for Q_in = 15 and 30 L/min. The calculated EEP at 70% stenosis was almost 8 times higher than that in the normal connector (Fig. 8a, left axis). ΔV_tidal normalized by that obtained with a normal connector sharply decreased for stenosis over 50% (Fig. 8a, right axis). ΔV_tidal was commonly decreased in both a normal and constricted connector when Q_in was increased, while the rate of decrease for Q_in was almost unchanged in the constricted connector (Fig. 8b).

Fig. 8.

a Normalized EEP (left axis) and normalized tidal volume (right axis) by those obtained with a normal connector (0% stenosis) at Q_in = 30 L/min as a function of the degree of stenosis. b Tidal volume ΔV_tidal obtained with the connector with 50% stenosis as a function of Q_in. The results of ΔV_tidal in a normal connector, as shown in Fig. 5, is also displayed

Figure 9 shows calculated EEPs for different degrees of stenosis as a function of Q_in. The EEP obtained with a normal connector, as shown in Fig. 6, is also displayed. Although PEEP at the smallest Q_in (= 10 L/min) was not expected even in the connector with 70% stenosis, the contribution of stenosis to PEEP generation became greater as Q_in increased. At the maximum Q_in (= 50 L/min), PEEP was estimated as 465.8 Pa (≈ 4.7 cmH₂O), which is within the range of PEEP values (2–8 cmH₂O) achieved by high-flow oxygen therapy [6, 26].

Discussion

PEEP attained by high-flow oxygen therapy using a tracheostomy tube in tracheostomized patients has been shown to have various clinical benefits [8, 35]. Although the relationship between the magnitude of EEP and inflow rates was previously investigated experimentally using high-flow tracheostomy [24, 38], it was still unknown whether simple geometrical changes in tracheostomy tube connectors, including the stenosis rate and inlet angles, could potentially generate PEEP. Since it is thought that PEEP is a consequence of the balance between connector fluid flow and lung mechanical responses, the 3D CFD of airflow in the connector during respiration under boundary conditions will be useful to understand the mechanical conditions necessary for PEEP generation. This will also be true while considering geometrical effects on EEP, especially those related to tracheostomy tube connectors. However, such computational frameworks have not yet been established. Thus, a numerical platform was developed in this study to investigate connector airflow and the magnitude of EEP under respiration, as represented by a lumped (0D lung) model. This numerical model made it possible to investigate the flow field in the connector (Figs. 4 and 7) and to quantify the magnitude of EEP (Figs. 3d and 6). Furthermore, the developed model demonstrated passive regulation of tidal volume (Figs. 5 and 8), which was impeded by large inflow rates as reported by previous studies involving experimental measurements using high-flow nasal ventilation [4]. The effect of connector stenosis on EEP was also quantified, and the results showed that PEEP can be expected by simply creating a stenosis, at least for stenosis over 50% and for Q_in ≥ 30 L/min (Fig. 9). The calculated EEP obtained with the largest degree of stenosis (= 70% stenosis) led to an eightfold greater EEP than that in the normal connector at Q_in = 30 L/min (Fig. 8a). This was consistent with the results obtained with the largest inflow rate (Q_in = 50 L/min) (Fig. 9), specifically 55.96 Pa in the normal connector and 465.8 Pa (≈ 4.7 cmH₂O) with 70% stenosis. Since it is expected that clinically reasonable PEEP is over 2 cmH₂O [6, 26], numerical results suggest that geometrical constriction in a connector can potentially produce PEEP, which is conventionally obtained with nasal cannulae [6, 26]. Although sharp inlet angles also increased the magnitude of EEP, they cannot be expected to achieve clinically reasonable PEEP, since the PEEP value was less than 1 cmH₂O even for the sharpest inlet angle θ = 30° and largest inflow rate Q_in = 50 L/min (Fig. 6).

Fig. 9.

EEP for different degrees of stenosis as a function of inlet flow rate Q_in. EEP obtained with a normal connector, as shown in Fig. 6, is also displayed

In experimental measurements using a lung phantom, the expiratory time (3.3 s) was set to be relatively longer than the inspiratory time (0.7 s) so that the EEP could be easily detected from periodic tracheal pressure profiles (Fig. 3c). Thus, comparison between the numerical and experimental measurements was focused on the magnitude of EEP, and they exhibited discrepancies in temporal values such as P_tr and U_tr except in the end-expiration phases. Despite these differences, the developed model makes it possible to investigate the magnitude of EEP within 1-cmH₂O accuracy, since the differences in this magnitude per 1 cmH₂O between the numerical and experimental results |EEP_exp—EEP_sim|/cmH₂O were less than 0.061 for all Q_in, and the numerical results were in the range of errors of the experimental results (Fig. 3d).

Since EEP is thought to depend on the length of the constricted portion of tracheostomy tube connectors, future studies should investigate the effect of this length (10⁰–10¹ mm) on the degree of EEP and also compare the calculated EEP with experimental measurements. The combination of a large degree of stenosis, sharp inlet angle, and large inflow rate may pose a risk of ventilator-associated (or -induced) lung injury [33], caused by a pressure of ≥ 30 cmH₂O (≈ 29.43 kPa) [2]. Furthermore, a previous theoretical analysis by Mead et al. (1970) showed that 30 cmH₂O of alveolar pressure produced 140 cmH₂O of shear stress, which can potentially lead to ARDS [19]. Lesions in such cases are caused by overdistension, collapse and reopening, and oxygen toxicity [33]. Since the change of lung volume was simply modeled by isotropic deformation with isotropic lung tissue [9], prediction of the aforementioned mechanical damage in the lung will be required for more precise modeling that takes into account the viscoelasticity of extra- and intra-parenchymal lung bronchi [29, 31].

Although the material deformability of the connector walls was neglected in this study, it may play important roles, especially for reducing sounds in clinical applications. Expiratory crackles were numerically investigated in terms of the relationship between airway closure dynamics and acoustic fluctuations in a study that considered the elastic deformation of the airway wall [11]. It would be interesting to study how much wall deformability reduces sound, even at high flow rates, while preserving PEEP. Numerical treatment of luminal surfaces may be also important, especially for wet surfaces. It is assumed that the device lumen becomes wet due to patient respiration, especially during long-term application, and therefore, the effect on PEEP of two-phase flow, such as that present at the liquid–air interface, is among the next challenges in terms of future research. Although the tested respiratory rate (0.25 Hz) did not affect the time history of tracheal pressure, as shown in Fig. 3c, more frequent respirations potentially generate harmonic flow behavior in the trachea (i.e., collapsing the airflow during inspiration and expiration). Furthermore, frequent respirations may also cause the pendelluft phenomenon, which decreases gas exchange and is defined as the movement of air within the lung from nondependent to dependent regions without changes in tidal volume during mechanical ventilation [1, 44]. It is known that a humidified and warmed gas mixture favors mucociliary function and reduces upper airway resistance [34, 36]. Thus, it would also be interesting to study whether the synergistic combination of PEEP and pulsatile airflow in the trachea enhance gas exchange or increase the level of oxygen in the blood.

The developed numerical model made it possible to assess both PEEP and tidal volume based on fluid dynamics of the airflow in the connector. Numerical analysis that considers mechanical lung parameters representing patient-specific lung states will be helpful in the clinical care of tracheostomized patients, specifically in decision-making for achieving precise inflow rates while preserving PEEP and determining when to remove the ventilator. Numerical results based on mechanics may also facilitate therapeutic decision-making not only for tracheostomized patients but also for those with lung diseases such as ARDS and those assisted by ECMO.

Conclusion

A computational platform to evaluate PEEP in tracheostomized patients was developed. The airflow in the tracheostomy tube connector was simulated, and the tracheal pressure, which is the outlet pressure of the connector, was calculated by 3D CFD analysis coupled with a lumped lung model. The numerical results for the magnitude of EEP agreed well with experimental measurements and made it possible to investigate the detailed dynamics of airflow in the connector. This suggests that the model can be used to estimate the magnitude of PEEP while taking into account the 3D airflow field in the connector. Although sharp inlet angles increased the magnitude of EEP, they cannot be expected to result in clinically reasonable PEEP. On the other hand, geometrical constriction in a connector can potentially produce PEEP, which is conventionally obtained with nasal cannulae. The numerical results in this study may assist in decision-making regarding the treatment of tracheostomized patients as well as those with other lung diseases such as ARDS and those receiving ECMO.

Biographies

Shiori Kageyama

, M.E., completed her bachelor’s degree and master’s degree at Osaka University, Japan, in 2020 and 2022, respectively.

Naoki Takeishi

, Ph.D., completed his master’s degree and Ph.D. degree at Tohoku University, Japan, in 2013 and 2016, respectively. He is currently an assistant professor at Osaka University. He performs research on computational fluid mechanics and biomechanics, with a particular focus on complex fluid dynamics such as cellular-scale blood flow and biorheology.

Hiroki Taenaka

, M.D., completed his medical degree at Osaka University, Japan, in 2013. He is currently a Ph.D. candidate at the Department of Anesthesiology and Intensive Care Medicine, Osaka University Graduate School of Medicine.

Takeshi Yoshida

, M.D., completed his medical degree and Ph.D. degree at Mie University School of Medicine, Japan, in 2003 and Osaka University, Japan, in 2013, respectively. He is currently a Lecturer at the Department of Anesthesiology and Intensive Care Medicine, Osaka University Graduate School of Medicine.

Shigeo Wada

, Ph.D., received his Ph.D. from Osaka University, Japan, in 1991 and is currently a Professor of Mechanical Science and Bioengineering in Osaka University. His expertise is computational biomechanics involving the respiratory and cardiovascular systems. He is a member of the World Council of Biomechanics.

Author contribution

S.K. and N.T. analyzed data; H.T. and T.Y. performed experiments; S.K., N.T., and S.W. interpreted simulation results; N.T. prepared figures; N.T. drafted the manuscript; N.T. edited and revised the manuscript; S.K., N.T., H.T., T.Y., and S.W. approved the final version of the manuscript; N.T., T.Y., and S.W. contributed to the research conception and design. All authors have read and agreed to the published version of the manuscript.

Declarations

Conflict of interest

The authors declare no competing interests.