Abstract

Here, we report an investigation of the gas–solid reaction between cesium hydroxide (CsOH) and siliceous (calcium silicate) thermal insulation at high temperature, which is postulated as the origin for the formation mechanism of cesium-bearing material emitted from the Fukushima Daiichi nuclear power plant. A developed reaction furnace consisting of two heating compartments was used to study the reaction at temperatures of 873, 973, and 1073 K. Under the influence of hydrogen-steam atmospheric conditions (H2/H2O = 0.2), the reaction between cesium hydroxide vapor and solid thermal insulation was confirmed to occur at temperatures of 973 and 1073 K with the formation of dicalcium silicate (Ca2SiO4) and cesium aluminum silicate (CsAlSiO4). Water-dissolution analyses of the reaction products have demonstrated their stability, in particular, CsAlSiO4. Constituent similarity of the field-observed cesium-bearing materials near the Fukushima Daiichi nuclear power plants with CsAlSiO4 suggests for the first time that gaseous reaction between CsOH with calcium silicate thermal insulation could be one of the original formation mechanisms of the cesium-bearing materials.
1. Introduction
Cesium-bearing materials or more commonly termed as CsMPs (cesium-rich microparticles) are μm-scale particles believed to be emitted from the Fukushima Daiichi nuclear power plants following the aftermath of the March 2011 severe accident.1,2 These particles contain highly concentrated radiocesium as reported in the first successful isolation of CsMPs by Adachi and co-workers1 170 km southwest of the site using aerosol samplers equipped with quartz fiber filters. The particles were characterized to have a spherical shape and consisted of Cs, Fe, Si, Zn, and other trace elements. On other occasions, CsMPs were isolated from different media, including soils,3−7 plant leaves or needles,8−10 non-woven fabric cloth used as ground cover in vegetable cultivation,9,10 and suspended particulate matters in rivers,11 which collectively showed that such particles were heterogeneously shaped with either spherical or non-spherical shapes and consisted of various major elements. Despite their distinct forms, they were commonly classified as type-A or type-B CsMPs particles based on 134Cs/137Cs radioactivity ratios of 0.94, 1.08, and 1.05,2,12 which seemingly reflected their origins: units 1, 2, and 3 of the Fukushima Daiichi nuclear power plant, respectively. The type-A particles were assigned to those observed CsMPs having 134Cs/137Cs ratios similar to that of unit 2 or 3 while type-B particles were given to CsMPs with 134Cs/137Cs similar to that of unit 1. Beyond this 134Cs/137Cs ratio classification, each type of CsMPs was eventually linked to different characteristics such as structures, sizes, and major elements. Type-A CsMPs were found in spherical and non-spherical shapes with a size of 10 μm or less and made of silicate glass4,5,8,9 having Cs, Fe, Si, and Zn (and/or Al) in common. Although partly similar to type-A CsMPs in terms of the shapes and silicate glass structures, type-B CsMPs were found in a much larger size (>50 μm) and consisted of a heterogeneous distribution of various elements.4,6
Because the CsMPs are thought to be attributed to the two major plume events in the Fukushima Daiichi nuclear power plant,1 their formation process could provide a piece of crucial information to unveil the accident progression such as core meltdown.5 Considering that in such accident progressions, the formed CsMPs may not be fully ejected from the power plant but remain inside the reactor containment or reactor building, then their distribution is highly associated with the location of the original material. This means that if such a material could be understood, a well-defined approach for decommissioning and dismantling works in the Fukushima Daiichi nuclear power plant could be realized to protect the workers and to avoid release to the environment. To date, however, the formation process of CsMPs remains elusive, particularly the possible source of silicate. Furuki et al.5 suggested that the origin of SiO2 was siliceous material contained in the concrete of pedestal structures that had been generated during molten core–concrete interaction (MCCI). Zheng et al.13 argued that SiO2 originated from the volatilization of oxide scales of type-304 stainless steel material used in, e.g., control rod claddings. Martin et al.,14 based on their extensive characterization of type-B particles, proposed thermal insulating materials as the origin of such silicates, which are vastly used in the piping system of a nuclear reactor. They continued the assertion by scrutinizing the contained fiber in CsMPs, which showed a strong degree of similarity to those commonly used in thermal insulation. Martin and coworkers’ hypothesis seems more plausible because a recent investigation has indicated favorable retention of cesium in thermal insulation materials through high-temperature interaction.15 Nevertheless, there is a limitation to this reported work15 due to the utilization of powdery starting materials, which could lead to the homogeneous (condensed phases) reaction. It is expected that during an accident progression, the interaction process between cesium and the suspected material occurs in the heterogeneous condition (i.e., a gas–solid reaction). Therefore to confirm the interaction process, a more practical investigation is needed.
Reflecting the above perplexity, the objective of our present study is to report, for the first time, direct evidence of heterogeneous reactions between gaseous cesium with solid siliceous (calcium silicate) thermal insulation at high temperatures, which is expected to shed light on the formation mechanism of cesium-bearing materials and eventually their provenance.
2. Experimental and Calculation Methods
2.1. Experiments
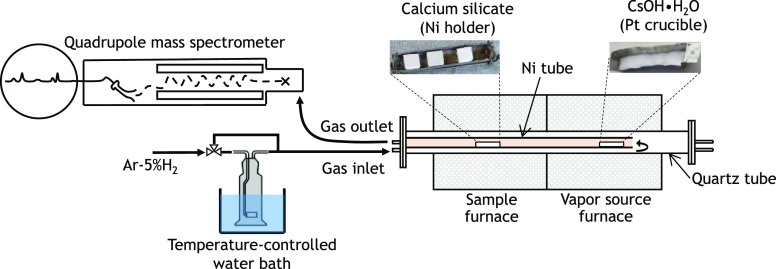
To study the gaseous reaction of cesium with a thermal insulation material, we employed a reaction furnace with 1000 mm in length and comprising two concentric tubes with inner diameters of 50 and 25.4 mm, respectively. The outer tube made of quartz is the passage of feed gas composed of Ar, H2, and H2O to be heated up before entering the inner tube. At the inner tube made of Ni, thermal insulator samples were located 350 mm downstream from the platinum crucible containing a cesium source as depicted in Figure 1. The temperature at the samples and cesium source locations were measured in the separate blank-heating tests using K-type thermocouples. Cesium hydroxide monohydrate (Sigma Aldrich, CsOH·H2O 99.5%) and calcium silicate (Nippon Keical Limited, Keical Ace Super Silica) were used as the cesium source and the thermal insulation material, respectively. Selection of those materials was based on the following facts: (1) cesium hydroxide was regarded as the predominant form of cesium under steam in severe accident conditions,16 and (2) the main steam piping in the Fukushima Daiichi nuclear power plant was vastly equipped with calcium silicate thermal insulation.17 The Keical Ace calcium silicate insulation material consists of CaO (45.09 wt %), SiO2 (52.3 wt %), Al2O3 (0.78 wt %), ZrO2 (0.41 wt %), and other constituents with individual weight percent of less than 0.3 wt %.
Figure 1.
Schematic of the gas–solid reaction test facility.
Three calcium silicate samples were prepared for each test by microcutting the as-received insulation board into smaller blockish forms and were aligned in a nickel holder having a size of 60 mm (length) × 10 mm (width). After inserting the samples and CsOH into the predetermined locations inside the Ni tube, the furnace was degassed and an atmospheric mixture of Ar/H2/H2O was then introduced by means of Ar-5% H2 flow through a temperature-controlled water bath at 333 K and 0.1 MPa. This condition could provide a H2/H2O molar ratio of ca. 0.2. The vapor source furnace with the CsOH source was ramp heated up to 893 K with a heating rate of 10.9 K/min and then brought to 923 K with a rate of 1.5 K/min before being held constant for 3 h at 923 K. Such a heating profile was employed to obtain a constant flow of CsOH as well as to prevent its rapid evaporation. The calcium silicate insulation samples were kept at three different temperatures of 873, 973, and 1073 K (i.e., performed separately) where they were chosen based on the previous thermochemical investigation.15 The study15 showed that the presence or absence of H2O in the atmosphere could induce the formation of a similar kind of Cs compound using thermogravimetry-differential thermal analysis (TG-DTA). Hence in the present study, a steam-containing atmosphere was adopted by considering that the actual event of a nuclear severe accident would be in steam-rich conditions. The mixture of gas was fed at a constant flow rate of 100 cm3/min, and the concentrations of hydrogen and steam were monitored at the outlet of the furnace using a quadrupole mass spectrometer (Canon Anelva Corp., M-101QA-TDM). During the cooling process of the furnace, after a 3 h holding time at target temperatures of samples and CsOH, the steam supply was shut off, leaving only Ar-5% H2 in the gas flow. This was intended to prevent steam condensation on samples, which otherwise could alter the actual mass of deposits formed after gas–solid interaction with CsOH. The mass of deposits was calculated by subtracting the initial mass of calcium silicate samples from the final mass. Furthermore, a ratio between the mass of deposits and the initial mass of calcium silicate could serve not only as the capacity of thermal insulation to retain cesium at high temperatures but also as an indication of the occurrence of a gas–solid reaction. Therefore, the post-test mass and dimension measurements were carefully taken inside the nitrogen inert glovebox with a moisture content of a few ppm to preserve the samples against moisture absorption. After recording such information, samples were pulverized using an agate mortar and pestle and then subjected to post-test analyses.
2.2. Post-test Analyses
The pulverized samples were first dissolved with water before their post-test analyses to mitigate the adverse effect of the condensed CsOH. This is because we encountered large moisture absorption in the previous work,15 which caused the chemical phase identification to be difficult. The dissolution process is as follows: each sample was initially submerged for 72 h in the designated polypropylene tubes containing 20 mL of deionized water and then separated from the supernatant for drying on a ceramic hot plate with a temperature of 383 K. To confirm the adequacy of this process, the 1073 K samples were used and the chemical phase (before and after the treatment) was analyzed using powder X-ray diffractometry (PXRD) (Figure S1). This procedure, in addition to the original intention for removing condensed CsOH, turned out to be able to unveil whether the formed cesium compounds after a gaseous CsOH-solid siliceous thermal insulation reaction are water-soluble or water-insoluble. The solubility of reaction products is important because it could provide a quick grasp of the fate of radiologically important reaction products such as cesium, whether it could remain (insoluble) or could be removed from host material (soluble) that is likely to redistribute further. The cesium phases that could be identified in the final PXRD analysis are classified as insoluble cesium; otherwise, they are classified as soluble cesium. Next, the rest of the samples (873 and 973 K) underwent a similar water dissolution process and were analyzed in their final condition.
A scanning electron microscope equipped with an energy-dispersive X-ray spectrometer (SEM/EDS-silicon drift detector, JSM-IT100, JEOL) was applied to the water-dissolved samples for microstructure and spatial elemental distribution analyses. Double-sided carbon tape was affixed to the sample holder (Al) to place samples without any further coating. The secondary electron images were obtained at 15 kV. For the phase identification of the samples, PXRD analyses with a Rigaku MiniFlex600SC (Cu Kα radiation) were carried out at room temperature in an air-tight sample holder. The diffraction analysis was performed over the scan range 2θ of 10–60° in continuous mode with a step size of 0.01° and scanning speed of 2°/min at the applied voltage and current of 40 kV and 15 mA, respectively.
2.3. Thermodynamic Calculation
To further investigate the reaction involving the Cs-Ca-Al-Si-O-H system, we employed thermodynamic equilibrium calculation using a Thermo-Calc 2021a18 with SGTE (Scientific Group Thermodata Europe) substance database version 5 to predict the stable species of cesium. In the database, however, only cesium silicates (i.e., Cs2SiO3, Cs2Si2O5, and Cs2Si4O9) are available; thus, it is not possible to gain a comprehensive understanding of where cesium aluminosilicates are potentially formed. Therefore, as a first step, we modified the SGTE database of a Cs-Ca-Al-Si-O-H system by incorporating the cesium aluminosilicates. We introduced three cesium aluminosilicates, i.e., CsAlSiO4, CsAlSi2O6, and CsAlSi5O12, that had been reported in the literature regarding their thermodynamic properties,19−22 through the Gibbs energy function based on the following SGTE format:
| 1 |
where ni and HiSER represent the number of atoms and the standard reference enthalpy for each element i in the cesium aluminosilicates, respectively. The polynomial coefficients for CsAlSiO4, CsAlSi2O6, and CsAlSi5O12 were derived in the temperature range of 298–1200 K using the estimated heat capacity functions Cp (T), standard enthalpy formation ΔfH°298, and standard entropy S°298 reported by Yui et al.19Table 1 lists the coefficients for each cesium aluminosilicate.
Table 1. Estimated Gibbs Energy Function of Cesium Aluminosilicates (T = 298–120 0 K).
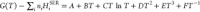 (J/mol) (J/mol) |
||||||
|---|---|---|---|---|---|---|
| A | B | C | D | E | F | |
| CsAlSiO4 | –2.207 × 106 | 8.361 × 102 | –1.447 × 102 | –1.682 × 10–2 | 0 | 1.470 × 106 |
| CsAlSi2O6 | –3.161 × 106 | 1.214 × 103 | –2.068 × 102 | –2.232 × 10–2 | 0 | 2.100 × 106 |
| CsAlSi5O12 | –6.007 × 106 | 2.086 × 103 | –3.481 × 102 | –6.796 × 10–2 | 0 | 3.990 × 106 |
In the first half of thermodynamic equilibrium calculations, the input parameters of reaction temperatures and pressure were set in the range of 673–1173 K and 0.1 MPa, respectively, while the amount of each element (in mole fraction) was thoroughly determined based on the experimental conditions (i.e., CsOH vapor, H2/H2O ratio, and calcium silicate samples) and also on the condition with low steam partial pressure for the sake of phase stability examination. In the second half of the calculations, with the emphasis on cesium abundance (Cs/(Al + Si)), the stable species were examined in an increasing total pressure to foresee them in the event of a nuclear severe accident.
3. Results and Discussion
3.1. Mass and Size Changes
Table 2 lists the size and mass information of the thermal insulation material before and after experiments at the respective temperatures. We noted that almost all samples experienced shrinkage ((V1 – V0)/V0 < 0) but exhibited increases in their masses (ms1 – ms0). The magnitude of shrinkage varied between 21 and 94%, and the largest one occurred in the 1073 K test. To be more precise, if we consider only a linear shrinkage, for instance, sample 2-1 whose magnitude of linear shrinkage (thickness change) of 14% is much greater than the industry-claimed linear shrinkage of 2% at 1273 K and 3 h test (i.e., Keical Ace Super Silica of Nippon Keical Ltd). The 2% shrinkage, considering the crystal structure of the thermal insulation as xonotlite, is consistent with the minute change of xonotlite after dehydration observed by Dent and Taylor.23 They found that the final crystal structure was transformed into low-temperature wollastonite (β-CaSiO3), which had a higher density of 2.75 g/cm3 than that of xonotlite, 2.71 g/cm3. Therefore, in our study, the shrinkage could not be straightforwardly seen as a result of water molecule or hydroxyl group removal alone; instead, it should reflect crystal transformation caused by a reaction with cesium. This is because all samples showed large mass increases after the tests, which are indicative of the coexistence of cesium in thermal insulation.
Table 2. Measurements of Samples and CsOH before and after Gas-Solid Reaction Tests.
| before gas–solid reaction tests | after gas–solid reaction tests | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| group of tests | T (K) | samples, ms0 (g) | samples, V0 (w × l × t) (mm) | CsOH, mc0 (g) | samples, ms1 (g) | samples, V1 (w × l × t) (mm) | mass difference, ms1 – ms0 (g) |
|
|
CsOH, mc1 (g) | ||
| 1-1 | 1073 | 0.0579 | 7.2 × 7.8 × 3.1 | 3.4803 | 0.1068 | 2.6 × 3.5 × 1.1 | 0.0489 | 85 | –94 | 3.1278 | ||
| 1-2 | 1073 | 0.0666 | 7.5 × 7.6 × 3.1 | 0.1157 | 3.8 × 4.2 × 1.8 | 0.0491 | 74 | –84 | ||||
| 1-3 | 1073 | 0.0640 | 6.3 × 8.9 × 3.8 | 0.1090 | 2.9 × 4.6 × 1.6 | 0.0450 | 70 | –90 | ||||
| 2-1 | 973 | 0.0734 | 7.3 × 8.4 × 3.5 | 3.9336 | 0.1066 | 7.0 × 8.0 × 3.0 | 0.0332 | 45 | –21 | 2.7135 | ||
| 2-2 | 973 | 0.0588 | 6.1 × 7.8 × 3.4 | 0.0911 | 5.6 × 7.2 × 2.7 | 0.0323 | 55 | –33 | ||||
| 2-3 | 973 | 0.0577 | 6.2 × 7.5 × 3.4 | 0.1031 | 5.4 × 6.1 × 2.4 | 0.0454 | 79 | –50 | ||||
| 3-1 | 873 | 0.0610 | 5.8 × 7.1 × 3.7 | 3.5114 | 0.1332 | 5.0 × 6.9 × 1.5 | 0.0722 | 118 | –66 | 2.9702 | ||
| 3-2 | 873 | 0.0578 | 5.6 × 8.0 × 3.0 | 0.1352 | 3.5 × 7.2 × 0.4 | 0.0774 | 134 | –92 | ||||
| 3-3 | 873 | 0.0648 | 7.0 × 7.8 × 3.0 | 0.1965 | 5.0 × 5.1 × 1.6 | 0.1317 | 203 | –75 | ||||
At 973 K (group 2) and 1073 K (group 1), the reaction was expected to prevail in the gas–solid interface by considering that at these temperatures, CsOH could be kept in vapor condition due to greater vapor pressure than that in the original/source location (at 923 K). On the other hand, at 873 K (group 3), the reaction was expected to occur in the condensed phase reaction due to lower vapor pressure. The corresponding vapor pressure of CsOH was calculated using thermodynamic data of CsOH (g) and CsOH (s,l) reported by Cordfunke and Konings24 in the temperature range of 615.5–1300 K in the following equation:
| 2 |
Supposing that a homogeneous temperature was attained at each group of the tests, then the estimated CsOH vapor pressures at the sample location would be 6.53 × 10–2 (group 1), 1.52 × 10–2 (group 2), and 2.42 × 10–3 atm (group 3), while the vapor pressure in the source location was estimated to be 6.40 × 10–3 atm. The calculated vapor pressures show that the first two groups have positive pressure differences of 5.89 × 10–2 and 8.78 × 10–3 atm, respectively, as compared to the source location, which are considered important to preserving CsOH in the vapor phase. This indicates that the measured increase in the masses of the thermal insulation materials was not affected by condensation of CsOH, but instead, by the results of gas–solid reactions. Contrarily, due to the negative vapor pressure difference of −3.99 × 10–3 atm, the measured mass of thermal insulation in group 3 was likely affected by the condensation of CsOH, which therefore could not simply suggest the generated amount of product after the condensed phase reaction. In groups 1 and 2, there were average values of 0.0477 and 0.0370 g of the mass increase. Meanwhile, as expected, we found that the mass increase in group 3 was the largest among the group of tests with a value in the range of 0.0722–0.1317 g. This information would be physicochemically meaningful if they are corrected to the initial mass of thermal insulation, as stressed in the latter Section 2.1. The parameter, a ratio between mass of the deposit (or mass change) and the initial mass of thermal insulation, denoted as (ms1 – ms0)/ms0 in Table 2, could provide the information on the capacity of the original calcium silicate material to retain cesium at high temperature and also as an indication for the occurrence of the reaction. If such a presumption is valid, one should obtain a common ratio in both groups 1 and 2. The practically identical samples in these groups, in terms of initial mass, are samples 1-1 and 2-3 (intergroup) and samples 1-2 and 1-3 (intragroup). We found that in intragroup comparison, i.e., the same temperature and initial mass, the ratio was approximately 72 ± 2% while the intergroup counterpart had a ratio of 82 ± 3%. Further, the individual shrinkage for these samples showed a ratio above 50%. Therefore, it could be approximated that the cesium retention capacity of the thermal insulation material above 70% could be used as indirect information on the occurrence of gas–solid reaction when combined with the shrinkage factor of greater than 50%. Otherwise, confirmatory analyses are needed such as for samples 2-1 and 2-2, which possessed a lower shrinkage factor and mass capacity ratio. For group 3, the capacity ratio was much larger than the former groups due to the influences from CsOH condensation. Consequently, it is difficult to indirectly determine whether the reaction had taken place.
3.2. Composition and Morphology
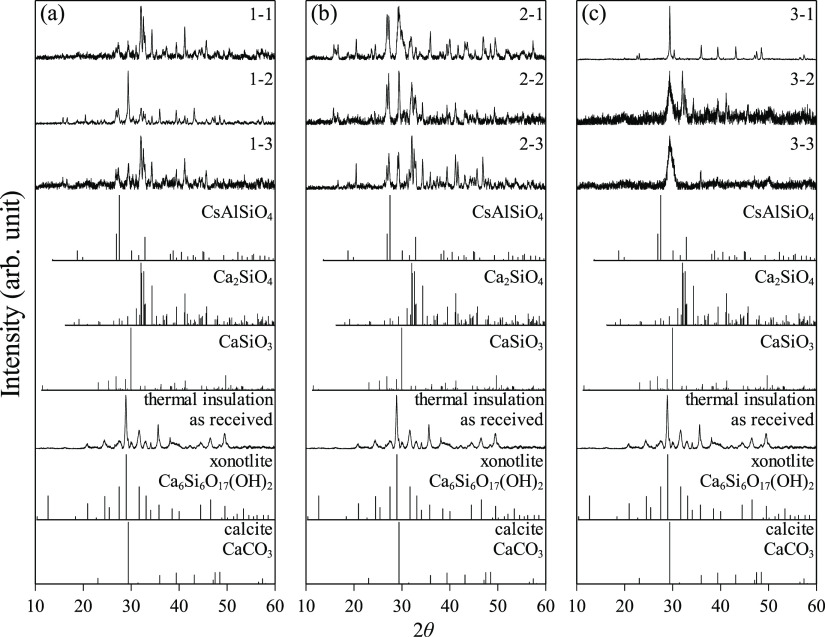
To further investigate, we analyzed the crystal phases of the samples from all groups of tests including the as-received calcium silicate thermal insulation using PXRD. The obtained profiles were baseline-corrected and compared with the ICDD database for identification as shown in Figure 2. After the phase identification, an X-ray diffraction quantitative analysis was performed on each sample using the Rietveld refinement method in Profex 4.3.525 and listed in Table 3. The as-received thermal insulation was found to largely consist of xonotlite (Ca6Si6O17(OH)2) with calcite (CaCO3) as a minor phase. This type of xonotlite-based calcium silicate structure is thermally stable up to the temperature of ca. 1073 K15,23,26 before undergoing crystal transformation into wollastonite (CaSiO3). In this study, however, with the presence of cesium in the system, such an ideal transformation accompanied by the release of water molecules or hydroxyl groups (Ca6Si6O17(OH)2 → 6CaSiO3 + H2O) was restricted; instead, some additional new crystal phases were obtained. Cesium aluminum silicate (CsAlSiO4) and dicalcium silicate (Ca2SiO4) were identified in the samples 1-1, 1-2, and 1-3 of group 1, samples 2-1, 2-2, and 2-3 of group 2, and sample 3-2 of group 3. An exception is sample 3-2, where dicalcium silicate was identified without cesium aluminum silicate. This anomaly could be explained as the consequence of condensed phase reactions prevailing only in group 3 that led to a different reaction path having no CsAlSiO4 in the final product. Such selectivity is analogous to the case of Al exclusion from the reaction system,15 which solely yielded Ca2SiO4. The theoretical approach suggested that a cesium silicate compound Cs2SiO3 (water-soluble) was thermodynamically favorable to form along with Ca2SiO4, while its identification remained unclear.15 The rest of the samples in group 3 showed no formation of new phases, but their predominant crystal structure had changed into calcite. It is considered that this structural alteration was caused by the partial reaction attributed to the formation of Cs2SiO3 and Ca2SiO4 (see Table 3, formation mechanism). The main reaction is described as a two-stage process where xonotlite initially reacts with CsOH to form Cs2SiO3 (i.e., Ca6Si6O17(OH)2(s) + 12CsOH(l) = 6Cs2SiO3(s) + 6CaO (s) + 7H2O(g)) and then the remaining xonotlite in the bulk of thermal insulation interacts with the first-stage reaction product calcium oxide to form Ca2SiO4 (i.e., Ca6Si6O17(OH)2(s) + 6CaO(s) = 6Ca2SiO4(s) + H2O(g)). If the latter formation did not proceed to completion, calcium oxide could readily react with CO2 contained in an air atmosphere (e.g., during sample handling) to form CaCO3. Based on these results of the PXRD analysis, it can be confirmed that the gas–solid reaction occurred between cesium and thermal insulation (groups 1 and 2) and to a lesser extent in the condensed phase (group 3), which are in agreement with the predicted thermal analyses in our previous study.15
Figure 2.
XRD results of water-dissolved samples: (a) group 1 (1073 K), (b) group 2 (973 K), and (c) group 3 (873 K). ICDD card nos. 31-0386 (CsAlSiO4), 80-8935 (Ca2SiO4), 66-0271 (CaSiO3), 23-0125 (Ca6Si6O17(OH)2), and 78-4615 (CaCO3).
Table 3. Quantitative Analysis of Calcium Silicate Thermal Insulation.
| sample/temperature (K) | phases (wt %)a | molar ratio [−] | formation mechanism of new phases |
|---|---|---|---|
| as-received | Ca6Si6O17(OH)2 (87.6), CaCO3 (12.4) | ||
| 1-1/1073 | CaCO3 (5.1), CaSiO3 (17.4), CsAlSiO4 (7.0), Ca2SiO4 (70.5) | CsAlSiO4/Ca2SiO4 = 0.07 | dehydration of xonotlite (eq 3) Ca6Si6O17(OH)2(s) = 6CaSiO3(s) + H2O(g) ΔrG° (900 K) = −188.67 kJ/mol |
| 1-2/1073 | CaCO3 (41.7), CaSiO3 (15.9), CsAlSiO4 (10.9), Ca2SiO4 (31.5) | CsAlSiO4/Ca2SiO4 = 0.24 | |
| 1-3/1073 | CaCO3 (12.7), CaSiO3 (16.2), CsAlSiO4 (9.3), Ca2SiO4 (61.8) | CsAlSiO4/Ca2SiO4 = 0.10 | reaction with CsOH (eq 4) 4CaSiO3(s) + Al2O3(s) + 2CsOH(g) = 2CsAlSiO4(s) + 2Ca2SiO4(s) + H2O(g)ΔrG° (973 – 1073 K) = – 254.38 – –228.75 kJ/mol |
| 2-1/973 | Ca6Si6O17(OH)2 (24.6), CaCO3 (23.1), CsAlSiO4 (12.6),Ca2SiO4 (39.7) | CsAlSiO4/Ca2SiO4 = 0.22 | |
| 2-2/973 | CaCO3 (26.6), CaSiO3 (19.8), CsAlSiO4 (12.9), Ca2SiO4 (40.7) | CsAlSiO4/Ca2SiO4 = 0.22 | reaction with CsOH (eq 5) 2CaSiO3(s) + 2CsOH(g) = Cs2SiO3 (s) + Ca2SiO4(s) + H2O(g) ΔrG° (973–1073 K) = −150.22 – –163.05 kJ/mol |
| 2-3/973 | Ca6Si6O17(OH)2 (12.9), CaCO3 (11.4), CaSiO3 (19.8), CsAlSiO4 (9.9), Ca2SiO4 (65.8) | CsAlSiO4/Ca2SiO4 = 0.10 | |
| 3-1/873 | Ca6Si6O17(OH)2 (13.3), CaCO3 (86.7) | – | reaction with CsOH (eq 6) Ca6Si6O17(OH)2(s) + 6CsOH(l) = 3Cs2SiO3(s) + 3Ca2SiO4(s) + 4H2O(g) ΔrG° (873 K) = −447.47 kJ/mol |
| 3-2/873 | Ca6Si6O17(OH)2 (13.0), CaCO3 (37.3), Ca2SiO4 (49.7) | – | |
| 3-3/873 | Ca6Si6O17(OH)2 (14.2), CaCO3 (85.8) | – |
The newly formed phases are shown in bold-typed texts
Despite its low content (0.78 wt %), aluminum impurity in thermal insulation material had proven to be crucial to yield interaction with cesium in a gas–solid reaction system by forming the cesium aluminum silicate (CsAlSiO4). This might be attributed to the aluminum coordination in calcium silicate layers of the xonotlite structure, where it is arguably to be located in the bridging site (i.e., connected with two other silicate tetrahedra chains) upon its isomorphic substitution of silicon atom,27−29 hence favoring aluminosilicate [AlSiO4]− bonds with foreign cationic ions. The CsAlSiO4 compound is expected to be formed together with dicalcium silicate (Ca2SiO4) when the reaction could proceed to completion, based on an analogous two-stage process of Cs2SiO3-Ca2SiO4 formation described above. According to the results of quantitative analysis, we could calculate the molar ratio of these two compounds. It was found that their molar ratios (Table 3) were generally less than 0.25, which is far from unity if we consider an ideal reaction in eq 4. In other words, the reaction system had produced more dicalcium silicate using not only reaction in eq 4 but also different reaction paths such as reaction in eq 5.15 It should be emphasized that, although a single formation of Ca2SiO4 is possible at a higher Ca/Si ratio such as in hillebrandite,26,30 it is unlikely in our experimental condition where the Ca/Si ratio is one. This means that by taking into account the contribution of Ca2SiO4 content also from the reaction in eq 5, a discrepancy of the CsAlSiO4/Ca2SiO4 ratio from unity was justified.
The Cs2SiO3 phase, on the other hand, as the consequence of reaction in eq 5, could not be confirmed through PXRD prior to the dissolution process (Figure S1), which was considered to be caused by its amorphous structure.15 Nevertheless, a separate study using the developed quantification method on inductively coupled plasma optical emission spectroscopy (ICP-OES) has succeeded to unveil this Cs compound31 by indirect determination of soluble Cs and Si. The developed method is initially tested on an artificial solution with a known solute concentration of Cs and Si, and the findings are compared with similar quantification using conventional methods to confirm whether the measured Cs concentrations have not suffered from the ionization interference. Afterward, the method is applied to determine Cs and Si concentration in the solutions that were previously used to dissolve samples of the cesium-calcium silicate gas–solid reaction test. The results show that all solutions from the 1073 and 973 K tests have an approximately Cs/Si molar ratio of 2, while those of the 873 K test indicate greater ratios.31 It is worth noting that cesium silicate compounds in the pseudo-binary phase diagram of Cs2O-SiO2 comprise Cs2Si4O9, Cs2Si2O5, Cs2SiO3 or its trimer Cs6Si3O9, and Cs6Si2O7,32−34 which correspond to the Cs/Si molar ratio of 0.5, 1, 2, and 3, respectively. In other words, when a dissolution process had been applied to each of these cesium silicates, one should obtain approximate dissolved concentrations of Cs over Si to be relevant to its original silicate compound; otherwise, there is a coexistence of different Cs-containing materials such as CsOH at the 873 K test. To this end, the study31 has corroborated that the Cs2SiO3 phase is unequivocally formed during the gas–solid reaction of cesium and calcium silicate thermal insulation. Furthermore, the thermodynamic analyses provided in Section 3.3 also support this inference where the abundance of Ca2SiO4 (i.e., PXRD quantification) indeed originated from Cs2SiO3 formation.
Figure 3 presents the SEM/EDS results on the as-received materials and the selected water-dissolved samples from each group of tests. The as-received calcium silicate thermal insulation was observed to consist of particles with acicular shapes having a Ca/Si ratio of ca. 1.0, which is a typical xonotlite structure.35−37 This agrees well with the identified xonotlite phase in the X-ray diffraction analysis. Meanwhile, after the high-temperature gas–solid interaction test, the samples showed morphological changes with wide-range Ca/Si ratios. In samples 1-2 (1073 K test) and 2-1 (973 K test), some analytical points indicated that Ca became enriched with a Ca/Si ratio of ca. 2.0, suggesting the presence of the Ca2SiO4 phase. However, we could also find that the Ca/Si ratio in sample 2-1 far exceeded this value at points 6 and 10. This could be caused by the presence of another Ca-rich phase like CaCO3 along with the Ca2SiO4 phase, as what had been identified in XRD. In sample 3-2 (873 K test), the quantitative analysis did not show highly Ca-enriched particles as that in the former two tests, where the Ca/Si ratio was 1.09 on average. It is considered that the Si in such quantification was not only from Ca2SiO4 and unreacted Ca6Si6O17(OH)2 but also from Cs2SiO3 that remained in sample 3-2, as represented by spatial element mapping (Figure S2) having Cs–Si–O congruency. The quantitative analysis showed that the Cs/Si molar ratios were in the range of 0.11–0.22 (Figure 3d). Concerning the Al-containing compound CsAlSiO4, (i.e. confirmed to be formed at 1073 and 973 K by XRD), we obtained a good spatial distribution of its elements only at certain EDS mapping areas as in sample 1-2 (Figure S2), which could be caused by its low concentration as compared to the rest of identified phases in XRD (Ca2SiO4, CaSiO3 or Ca6Si6O17(OH)2, and CaCO3). For details, if we consider the phase contribution conforms to the bulk quantitative XRD, i.e., sample 1-2 (41.7 wt % CaCO3, 15.9 wt % CaSiO3, 10.9 wt % CsAlSiO4, 31.5 wt % Ca2SiO4) and sample 2-1 (23.1 wt % CaCO3, 24.6 wt % Ca6Si6O17(OH)2, 12.6 wt % CsAlSiO4, 39.7 wt % Ca2SiO4), a conservative calculation would result in 0.12 and 0.16 of Cs/Si molar ratio in samples 1-2 and 2-1, respectively. Therefore, it is justified that such low molar ratios, and hence yielding fair Cs-Al spatial distributions, are caused by major influences from other phases. In spite of that, the conservative ratios (0.12 and 0.16) were satisfied in each sample (Figure 3b,c), corroborating the presence of the CsAlSiO4 phase.
Figure 3.

Secondary electron images of calcium silicate thermal insulation: (a) as-received, (b) sample 1-2/1073 K test, (c) sample 2-1/973 K test, and (d) sample 3-2/873 K test. The numbers indicate quantitative point analyses.
3.3. Thermodynamic Stability of Cs–(Al)–Si–O Phases
In the thermodynamic evaluation, 8 cases were analyzed by adjusting the variables: hydrogen to steam ratio, the abundance of cesium (Cs/(Al + Si)), and total pressure. Table 4 summarizes the input parameters for each case. Case 1 is a simulated case for our experimental condition where the mole fractions of elements were derived as follows: Ca, Si, and Al mole fractions were determined by summation of the mass of three calcium silicate samples, averaging them with each group of tests (Table 2), multiplying with weight fraction based on constituents in Keical Ace thermal insulation (i.e., 0.9740 for Ca and Si, 0.0078 for Al), and correcting the results with the molecular weight of xonotlite (Ca6Si6O17(OH)2) and Al2O3, respectively; the Cs mole fraction was obtained by averaging the mass of evaporated CsOH for all group of tests (i.e., 0.5641 g) and correcting it with the molecular weight of CsOH; H and O mole fractions were collectively determined from the amount of gas flow (steam and hydrogen), xonotlite, Al2O3, and CsOH, respectively. Concerning the amount of gas flow, it was approximated by the equation of state starting from the room temperature at the upstream of test apparatus, 923 K on the top of CsOH crucible, and at last the temperature on the top of samples for 3 h (here, 1073 K was chosen for simplification). The remaining seven cases were analyzed for scrutinizing the stability of cesium species in (1) high steam partial pressure but low cesium abundance at standard atmospheric pressure (cases 2 and 3), (2) low steam partial pressure but high cesium abundance at standard atmospheric pressure (case 4), (3) low steam partial pressure and low cesium abundance at standard atmospheric pressure (cases 5 and 6), (4) high steam partial pressure and high cesium abundance at an increasing pressure (case 7), and (5) low steam partial pressure but high cesium abundance at an increasing pressure (case 8).
Table 4. Input Parameters for Thermodynamic Evaluation (T = 673–1173 K).
| case 1a/case 7b | case 2 | case 3 | case 4/case 8c | case 5 | case 6 | |
|---|---|---|---|---|---|---|
| (H2/H2O = 0.20) (Cs/(Al + Si) = 2.75) | (H2/H2O = 0.20) (Cs/(Al + Si) = 5.51 × 10–2) | (H2/H2O = 0.20) (Cs/(Al + Si) = 2.75 × 10–2) | (H2/H2O = 100) (Cs/(Al + Si) = 2.75) | (H2/H2O = 100) (Cs/(Al + Si) = 5.51 × 10–2) | (H2/H2O = 100) (Cs/(Al + Si) = 2.75 × 10–2) | |
| Cs (mole fraction) | 2.43 × 10–3 | 4.89 × 10–5 | 2.43 × 10–5 | 2.43 × 10–3 | 4.89 × 10–5 | 2.43 × 10–5 |
| O (mole fraction) | 2.96 × 10–1 | 2.96 × 10–1 | 2.96 × 10–1 | 1.01 × 10–2 | 7.74 × 10–3 | 7.70 × 10–3 |
| H (mole fraction) | 7.00 × 10–1 | 7.03 × 10–1 | 7.03 × 10–1 | 9.86 × 10–1 | 9.90 × 10–1 | 9.90 × 10–1 |
| Ca (mole fraction) | 8.70 × 10–4 | 8.70 × 10–4 | 8.70 × 10–4 | 8.70 × 10–4 | 8.70 × 10–4 | 8.70 × 10–4 |
| Si (mole fraction) | 8.70 × 10–4 | 8.70 × 10–4 | 8.70 × 10–4 | 8.70 × 10–4 | 8.70 × 10–4 | 8.70 × 10–4 |
| Al (mole fraction) | 1.60 × 10–5 | 1.60 × 10–5 | 1.60 × 10–5 | 1.60 × 10–5 | 1.60 × 10–5 | 1.60 × 10–5 |
| system size (mol) | 1.79 | 1.79 | 1.79 | 1.79 | 1.79 | 1.79 |
| pressure (MPa) | 0.1/0.1–0.7 | 0.1 | 0.1 | 0.1/0.1–0.7 | 0.1 | 0.1 |
Representation of our experimental condition with H2/H2O = 0.20, Cs/(Al + Si) = 2.75, and P = 0.1 MPa.
Extrapolated case in an increasing pressure with the high steam partial pressure and high cesium abundance.
Extrapolated case in an increasing pressure with the low steam partial pressure and high cesium abundance.
The predominance diagram in Figure 4 presents the predicted species of Cs, Ca, Al, and Si in condensed phases as a function of temperature based on the respective input parameters in Table 4. In the diagrams, Cs2SiO3(s), Cs2SiO3(l), CsAlSiO4(s), and Ca2SiO4(s) are predicted to be the stable species in both low and high steam partial pressure above 873 K (Figure 4a,d). These results excellently agree with the experimentally observed water-insoluble phases in our study (i.e., CsAlSiO4(s) and Ca2SiO4(s)), which infers the appropriateness of our modified database through the incorporation of all cesium aluminosilicates in the calculations (elucidated in Section 2.3). However, it should be highlighted that those phases were identified in the experiment at 873–1073 K for Ca2SiO4(s) and 973–1073 K for CsAlSiO4(s). This is considered that at a lower temperature (<973 K), the formation of CsAlSiO4(s) necessitates a much longer equilibration time, which had not been satisfied in our experiment. This might be attributed to a different mode of reaction, i.e., condensed CsOH reaction with solid calcium silicate rather than gas–solid reaction, which depends on the degree of CsOH diffusion/penetration from the surface of calcium silicate sample. Consequently, it could limit the reaction yield with the fractional Al contained in silicate layers in the thermal insulation. Nevertheless, the calculations could foresee the Cs species quite well and particularly CsAlSiO4(s) as the most stable cesium in the reaction system of Cs-Ca-Al-Si-O-H regardless of cesium abundance or steam partial pressure (Figure 4a–f). Furthermore, CsAlSiO4(s) was not singly formed in the system; instead, it was concurrently formed with Ca2SiO4(s). This can be deduced from the equivalent distribution of both species in the less Cs abundance conditions (Figure 4b,c,e,f), which is ca. 1.12 × 10–4 mole fraction. In other words, the presumed two-stage reaction process having cesium aluminum silicate (CsAlSiO4(s)) and dicalcium silicate (Ca2SiO4(s)) in the final products has been corroborated by this thermodynamic calculation. Additionally, at higher total pressure, CsAlSiO4(s) prevailed with its stability regardless of the steam partial pressure (Figure 5a,b).
Figure 4.
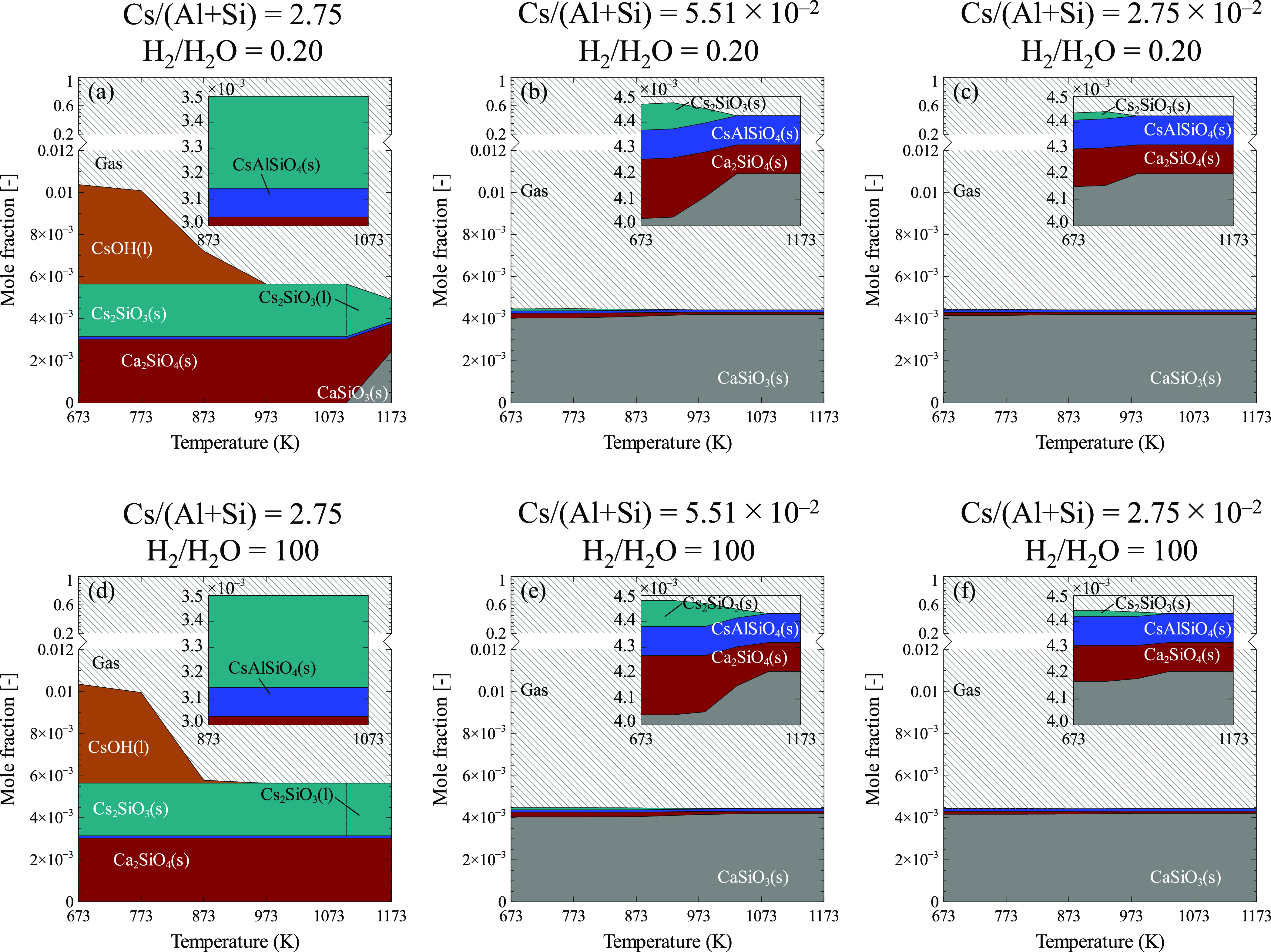
Thermodynamic equilibrium-based temperature-dependent species of Cs, Ca, Al, and Si in (a) case 1, (b) case 2, (c) case 3, (d) case 4, (e) case 5, and (f) case 6. See text for details of each case. The insets depict cesium (alumino)silicates on T = 673–1173 K or 873–1073 K.
Figure 5.
Isobaric temperature-dependent amount of CsAlSiO4(s), Cs2SiO3(s,l), and Ca2SiO4(s) in (a) case 7 and (b) case 8.
Cs2SiO3(s) emerged as another stable phase in high cesium abundance conditions (Figure 4a,d) as well as to the least extent in moderate abundance ones (Figure 4b,c,e,f). In the former conditions, Cs2SiO3(s) was predicted to be stably formed in all temperature ranges of calculation while the latter conditions indicated its formation occurred in the temperature of less than 973 K. The results showed that this phase in the high cesium abundance cases was relatively higher than the CsAlSiO4(s), i.e. approx. 2.50 × 10–3 mole fraction, which implies the favorability of the Cs–Si–O reaction. This turned out to pose a major role in a large formation of Ca2SiO4(s) particularly in low steam partial pressure conditions (Figure 4d). In high steam partial pressure and high-temperature conditions (i.e., H2/H2O = 0.2; T > 1073 K), however, the Cs2SiO3 (s,l) amount was reduced and coincided with the increase of CaSiO3 and gaseous Cs. It is because, above its melting temperature (1100 K32), the dissociation into atomic Cs, O2, and SiO2 could occur,38 which consequently disfavors its formation according to eq 5 in Table 3. Such a hindrance became improved when the total pressure was increased above 0.1 MPa (Figure 5a), where the deviation of Cs2SiO3(s) from its normalized amount had been diminished. Despite its bulk formation, Cs2SiO3 had indicated its large dependence on steam partial pressure, cesium abundance (i.e., Cs/Al + Si), and total pressure to gain its stability in the Cs-Ca-Al-Si-O-H system, which therefore suggests its inferiority as compared to CsAlSiO4 when rapid and unpredicted changes of atmospheric conditions have taken place.
3.4. Implications to the Provenance of Cesium-Bearing Material
We have demonstrated in this study that cesium could chemically react with thermal insulation by forming cesium aluminum silicate (CsAlSiO4) and dicalcium silicate (Ca2SiO4). These reaction products have been confirmed not only to be thermally stable but also water-insoluble in the scope of a 72 h water dissolution process. While Cs2SiO3 was theoretically predicted to be present after such a reaction, it suffered water dissolution. Therefore, it can be inferred that the most stable cesium phase in a reaction system of Cs-Ca-Al-Si-O-H is CsAlSiO4. Our findings have shown experimentally and theoretically that even with only a fractional amount of aluminum in the thermal insulation, the formation of CsAlSiO4 could occur. This means, e.g., in the event of a nuclear severe accident, that the location where radioactive cesium leaks and becomes exposed to Si(Al) materials would be a highly determining factor. In our study, we focused on the origin of Si(Al) materials as calcium silicate thermal insulation, which is based on its bulk use in the nuclear reactor piping system.17 Consequently, the point of encounter between calcium silicate thermal insulation and cesium was centered on any mechanical failure event associated with the piping system, for instance, at safety relief valves (SRVs). Despite no consensus concerning the leakage path of radioactive cesium in the Fukushima Daiichi nuclear power plant,39,40 several research institutes in the framework of the BSAF phase 2 project had predicted the potential SRV leak or failure, to resemble the actual pressure readings in the reactor and containment vessels during the accident. Therefore, in a conservative way, we assume that during the degradation of fuel in the reactor core of Fukushima Daiichi nuclear power plant, a substantial amount of high-pressure and high-temperature steam-containing cesium from the degraded fuels was leaked from SRV components, causing direct exposure to the adjacent thermal insulation of main steam piping and realizing cesium retention by the formation of cesium-bearing materials as CsAlSiO4. Because of the lightweight nature of the formed material (0.20–4.79 g/cm3; derived from (ms1 – ms0)/V1 of 973 and 1073 K tests in Table 2), its release from the plant site in the event of hydrogen explosion41 becomes conceivable. Our candidate cesium-bearing material (CsAlSiO4) is consistent with some recent field-observed water-insoluble cesium-bearing materials,8,42,43 where the coherent elemental distribution of Cs, O, Si, and Al was obtained. Nevertheless, due to the non-negligible incorporation of other constituents such as Fe and Zn in the materials, it is imperative to further investigate whether they originate from the field and hence contaminated the quantitative analyses reported in the works8,42,43 or they are intrinsic to the Si(Al)-material prior to reaction with cesium.
4. Conclusions
A simulated gaseous reaction of cesium with siliceous (calcium silicate) thermal insulation had been investigated at high temperature under the steam atmospheric condition to unveil the unprecedented cesium retention in the event of a nuclear severe accident. Three independent groups of tests were evaluated based on the reaction temperature of 873, 973, and 1073 K, respectively. The 973 and 1073 K tests were targeted to provide an understanding of the intended phenomenon involving the gas–solid reaction between cesium and thermal insulation, while the 873 K test was an extended case to anticipate a condition when gaseous cesium preceding its reaction with thermal insulation was condensed.
Based on the post-test analyses and thermodynamic evaluation, it was found that at 973 and 1073 K, the dehydrated thermal insulation material (i.e. Ca6Si6O17(OH)2(s) → 6CaSiO3(s) + H2O(g)) reacted with cesium in the following two reactions:
and
Large retention of cesium on the thermal insulation material ranging from 45 to 84 wt % initial insulator was observed in these groups of tests. It was comprehended that the majority of retained cesium prevailed as water-soluble Cs2SiO3.
Meanwhile, at 873 K, where condensed phases reaction was expected to occur, it was found that the reaction occurred between the hydrated thermal insulation and cesium as
It was not possible to explicitly determine the amount of retained cesium that belongs to Cs2SiO3 in this group due to influences from unreacted CsOH(l). However, considering a proportion between Cs2SiO3 and Ca2SiO4 in the given reaction, an approximate amount of Cs2SiO3 could be estimated from the results of quantitative XRD on the sample with identified Ca2SiO4 such that in sample 3-2. With an amount of 49.7 wt % Ca2SiO4, it was calculated that Cs2SiO3 could be formed ca. 98.7 wt %.
To this end, many debates arose about the provenance of Si(Al)-containing material be caused by framing the CsMP formation to be valid only on a single event rather than combined or multiple events. This seems plausible because at one time, the assumed formation could explain a portion of CsMP constituents but failed to explain the existence of others. Finally, our study does not rule out those hypotheses of CsMP formation (e.g., concrete origin5 and stainless steel origin13) due to the possible multiple events in nuclear accidents progression; instead, it provides a more realistic approach comprising gas–solid and/or condensed phases reaction, which could be experimentally validated.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c03525.
XRD results of the 1073 K test sample before and after water dissolution and the EDS elemental mapping on selected samples from each group of tests (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Adachi K.; Kajino M.; Zaizen Y.; Igarashi Y. Emission of spherical cesium-bearing particles from an early stage of the Fukushima nuclear accident. Sci. Rep. 2013, 3, 2554. 10.1038/srep02554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Igarashi Y.; Kogure T.; Kurihara Y.; Miura H.; Okumura T.; Satou Y.; Takahashi Y.; Yamaguchi N. A Review of Cs-bearing microparticles in the environment emitted by the Fukushima Dai-Ichi nuclear power plant accident. J. Environ. Radioact. 2019, 205-206, 101–118. 10.1016/j.jenvrad.2019.04.011. [DOI] [PubMed] [Google Scholar]
- Satou Y.; Sueki K.; Sasa K.; Adachi K.; Igarashi Y. First successful isolation of radioactive particles from soil near the Fukushima Daiichi nuclear power plant. Anthropocene 2016, 14, 71–76. 10.1016/j.ancene.2016.05.001. [DOI] [Google Scholar]
- Satou Y.; Sueki K.; Sasa K.; Yoshikawa H.; Nakama S.; Minowa H.; Abe Y.; Nakai I.; Ono T.; Adachi K.; Igarashi Y. Analysis of two forms of radioactive particles emitted during the early stages of the Fukushima Dai-Ichi nuclear power station accident. Geochem. J. 2018, 52, 137–143. 10.2343/geochemj.2.0514. [DOI] [Google Scholar]
- Furuki G.; Imoto J.; Ochiai A.; Yamasaki S.; Nanba K.; Ohnuki T.; Grambow B.; Ewing R. C.; Utsunomiya S. Caesium-rich micro-particles: A window into the meltdown events at the Fukushima Daiichi nuclear power plant. Sci. Rep. 2017, 7, 42731. 10.1038/srep42731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ono T.; Iizawa Y.; Abe Y.; Nakai I.; Terada Y.; Satou Y.; Sueki K.; Adachi K.; Igarashi Y. Investigation of the chemical characteristics of individual radioactive microparticles emitted from reactor 1 by the Fukushima Daiichi nuclear power plant accident by using multiple synchrotron radiation X-ray analyses. Bunseki Kagaku 2017, 66, 251–261. 10.2116/bunsekikagaku.66.251. [DOI] [Google Scholar]
- Ikehara R.; Suetake M.; Komiya T.; Furuki G.; Ochiai A.; Yamasaki S.; Bower W. R.; Law G. T. W.; Ohnuki T.; Grambow B.; Ewing R. C.; Utsunomiya S. Novel method of quantifying radioactive cesium-rich microparticles (CsMPs) in the environment from the Fukushima Daiichi nuclear power plant. Environ. Sci. Technol. 2018, 52, 6390–6398. 10.1021/acs.est.7b06693. [DOI] [PubMed] [Google Scholar]
- Yamaguchi N.; Kogure T.; Mukai H.; Akiyama-Hasegawa K.; Mitome M.; Hara T.; Fujiwara H. Structures of radioactive Cs-bearing microparticles in non-spherical forms collected in Fukushima. Geochem. J. 2018, 52, 123–136. 10.2343/geochemj.2.0483. [DOI] [Google Scholar]
- Yamaguchi N.; Mitome M.; Kotone A.-H.; Asano M.; Adachi K.; Kogure T. Internal structure of cesium-bearing radioactive microparticles released from Fukushima nuclear power plant. Sci. Rep. 2016, 6, 20548. 10.1038/srep20548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kogure T.; Yamaguchi N.; Segawa H.; Mukai H.; Motai S.; Akiyama-Hasegawa K.; Mitome M.; Hara T.; Yaita T. Constituent elements and their distribution in the radioactive Cs-bearing silicate glass microparticles released from Fukushima nuclear plant. Microscopy 2016, 65, 451–459. 10.1093/jmicro/dfw030. [DOI] [PubMed] [Google Scholar]
- Miura H.; Kurihara Y.; Sakaguchi A.; Tanaka K.; Yamaguchi N.; Higaki S.; Takahashi Y. Discovery of radiocesium-bearing microparticles in river water and their influence on the solid-water distribution coefficient (Kd) of radiocesium in the Kuchibuto River in Fukushima. Geochem. J. 2018, 52, 145–154. 10.2343/geochemj.2.0517. [DOI] [Google Scholar]
- Nishihara K.; Iwamoto H.; Suyama K.. Estimation of fuel compositions in Fukushima-Daiichi nuclear power plant; JAEA-Data/Code 2012–018; Japan Atomic Energy Agency: Ibaraki, Japan, 2012. [Google Scholar]
- Zheng L.; Hosoi K.; Ueda S.; Gao X.; Kitamura S.; Kobayashi Y. Si-rich phases and their distributions in the oxide scale formed on 304 stainless steel at high temperatures. J. Nucl. Mater. 2018, 507, 327–338. 10.1016/j.jnucmat.2018.05.018. [DOI] [Google Scholar]
- Martin P. G.; Satou Y.; Griffiths I.; Richards D.; Scott T. Analysis of external surface irregularities on Fukushima-derived fallout particles. Front. Energy Res. 2017, 5, 25. 10.3389/fenrg.2017.00025. [DOI] [Google Scholar]
- Rizaal M.; Nakajima K.; Saito T.; Osaka M.; Okamoto K. Investigation of high-temperature chemical interaction of calcium silicate insulation and cesium hydroxide. J. Nucl. Sci. Technol. 2020, 57, 1062–1073. 10.1080/00223131.2020.1755733. [DOI] [Google Scholar]
- Osborne M. F.; Collins J. L.; Lorenz R. A. Experimental studies of fission product release from commercial light water reactor fuel under accident conditions. Nucl. Technol. 1987, 78, 157–169. 10.13182/NT87-A33994. [DOI] [Google Scholar]
- Nuclear and Industrial Safety Agency. Report on emergency core cooling system strainer and containment vessel recirculation sump screen blocking event and status of measures on boiling water nuclear power plant; 44th Nuclear Safety Commission Report material no. 2 [in Japanese]; Nuclear and Industrial Safety Agency (NISA): Tokyo, Japan, 2006. [Google Scholar]
- Andersson J.-O.; Helander T.; Höglund L.; Shi P.; Sundman B. THERMO-CALC & DICTRA, Computational tools for materials science. Calphad 2002, 26, 273–312. 10.1016/S0364-5916(02)00037-8. [DOI] [Google Scholar]
- Yui K.; Kuramochi H.; Osako M. Understanding the behavior of radioactive cesium during the incineration of contaminated municipal solid waste and sewage sludge by thermodynamic equilibrium calculation. ACS Omega 2018, 3, 15086–15099. 10.1021/acsomega.8b01113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindemer T. B.; Besmann T. M.; Johnson C. E. Thermodynamic review and calculations −alkali-metal oxide systems with nuclear fuels, fission products, and structural materials. J. Nucl. Mater. 1981, 100, 178–226. 10.1016/0022-3115(81)90533-X. [DOI] [Google Scholar]
- Taylor P.; DeVaal S. D.; Owen D. G. Stability relationships between solid cesium aluminosilicates in aqueous solutions at 200 °C. Can. J. Chem. 1989, 67, 76–81. 10.1139/v89-013. [DOI] [Google Scholar]
- Ogorodova L. P.; Melchakova L. V.; Kiseleva I. A.; Belitsky I. A. Thermochemical study of natural pollucite. Thermochim. Acta 2003, 403, 251–256. 10.1016/S0040-6031(03)00048-0. [DOI] [Google Scholar]
- Dent L. S.; Taylor H. F. W. The dehydration of xonotlite. Acta Cryst. 1956, 9, 1002–1004. 10.1107/S0365110X56002916. [DOI] [Google Scholar]
- Cordfunke E. H. P.; Konings R. J. M. M.. The Cs-O-H System. In Thermochemical data for reactor materials and fission products; Cordfunke E. H. P.; Konings R. J. M. M., Eds.; Elsevier Science Publishers B. V.: Amsterdam, 1990; pp. 103–109, ISBN 0–444–88485-8. [Google Scholar]
- Doebelin N.; Kleeberg R. Profex: A graphical user interface for the rietveld refinement program BGMN. J. Appl. Crystallogr. 2015, 48, 1573–1580. 10.1107/S1600576715014685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw S.; Henderson C. M. B.; Komanschek B. U. Dehydration/recrystallization mechanisms, energetics, and kinetics of hydrated calcium silicate minerals: An in situ TGA/DSC and synchrotron radiation SAXS/WAXS study. Chem. Geol. 2000, 167, 141–159. 10.1016/S0009-2541(99)00206-5. [DOI] [Google Scholar]
- Geng G.; Myers R. J.; Qomi M. J. A.; Monteiro P. J. M. Densification of the interlayer spacing governs the nanomechanical properties of calcium-silicate-hydrate. Sci. Rep. 2017, 7, 1–8. 10.1038/s41598-017-11146-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pegado L.; Labbez C.; Churakov S. V. Mechanism of aluminium incorporation into C-S-H from Ab initio calculations. J. Mater. Chem. A 2014, 2, 3477–3483. 10.1039/c3ta14597b. [DOI] [Google Scholar]
- Kunhi Mohamed A.; Moutzouri P.; Berruyer P.; Walder B. J.; Siramanont J.; Harris M.; Negroni M.; Galmarini S. C.; Parker S. C.; Scrivener K. L.; Emsley L.; Bowen P. The atomic-level structure of cementitious calcium aluminate silicate hydrate. J. Am. Chem. Soc. 2020, 142, 11060–11071. 10.1021/jacs.0c02988. [DOI] [PubMed] [Google Scholar]
- Ishida H.; Mabuchi K.; Sasaki K.; Mitsuda T. Low-temperature synthesis of β-Ca2SiO4 from Hillebrandite. J. Am. Ceram. Soc. 1992, 75, 2427–2432. 10.1111/j.1151-2916.1992.tb05595.x. [DOI] [Google Scholar]
- Rizaal M.; Nakajima K.; Saito T.; Osaka M.; Okamoto K.. Determination of soluble Cs compound formed at high temperature in the system of Cs2O-CaO-SiO2; Unpublished research, 2022.
- Spencer P. J.The thermodynamic properties of silicates; NPL Report Chemistry 21; National Physical Laboratory (NPL): London, United Kingdom, 1973. [Google Scholar]
- Ball R. G. J.; Bowsher B. R.; Cordfunke E. H. P.; Dickinson S.; Konings R. J. M. Thermochemistry of selected fission product compounds. J. Nucl. Mater. 1993, 201, 81–91. 10.1016/0022-3115(93)90161-Q. [DOI] [Google Scholar]
- Hoch C.; Röhr C. Alkalimetall-Oxosilicate A6[Si309] und A6[Si207] (A = Rb, Cs): Darstellung und Kristallstruktur. Z. Naturforsch., B 2001, 56, 423–430. 10.1515/znb-2001-4-516. [DOI] [Google Scholar]
- Zheng Q.; Wang W. Calcium silicate based high efficiency thermal insulation. Br. Ceram. Trans. 2000, 99, 187–190. 10.1179/096797800680929. [DOI] [Google Scholar]
- Black L.; Garbev K.; Stumm A. Structure, bonding and morphology of hydrothermally synthesised xonotlite. Adv. Appl. Ceram. 2009, 108, 137–144. 10.1179/174367608X353638. [DOI] [Google Scholar]
- Milestone N. B.; Ahari G. K. Hydrothermal processing of Xonotlite based compositions. Adv. Appl. Ceram. 2007, 106, 302–308. 10.1179/174367607X228124. [DOI] [Google Scholar]
- Stolyarova V. L.; Lopatin S. I.; Belousova O. L.; Grishchenko L. V. Phase equilibria and thermodynamic properties of components in the Cs2O-B2O3-SiO2 system at high Temperatures. Glass Phys. Chem. 2006, 32, 55–62. 10.1134/S108765960601007X. [DOI] [Google Scholar]
- Herranz L. E.; Pellegrini M.; Lind T.; Sonnenkalb M.; Godin-Jacqmin L.; López C.; Dolganov K.; Cousin F.; Tamaki H.; Kim T. W.; Hoshi H.; Andrews N.; Sevon T. Overview and outcomes of the OECD/NEA benchmark study of the accident at the Fukushima Daiichi NPS (BSAF) Phase 2 – Results of severe accident analyses for Unit 1. Nucl. Eng. Des. 2020, 369, 110849 10.1016/j.nucengdes.2020.110849. [DOI] [Google Scholar]
- Sonnenkalb M.; Pellegrini M.; Herranz L. E.; Lind T.; Morreale A. C.; Kanda K.; Tamaki H.; Kim S. I.; Cousin F.; Fernandez Moguel L.; Andrews N.; Sevon T. Overview and outcomes of the OECD/NEA benchmark study of the accident at the Fukushima Daiichi NPS (BSAF) Phase 2 – Results of severe accident analyses for Unit 2. Nucl. Eng. Des. 2020, 369, 110840 10.1016/j.nucengdes.2020.110840. [DOI] [Google Scholar]
- Tokyo Electric Power Company . Evaluation of the situation of cores and containment vessels of Fukushima Daiichi nuclear power station units-1 to 3 and examination into unsolved issues in the accident progression; Progress report no. 5; Tokyo Electric Power Company (TEPCO): Tokyo, Japan, 2017. [Google Scholar]
- Futagami F.; Soliman M.; Takamiya K.; Sekimoto S.; Oki Y.; Kubota T.; Konno M.; Mizuno S.; Ohtsuki T. Isolation, characterization and source analysis of radiocaesium micro-particles in soil sample collected from vicinity of Fukushima Dai-Ichi nuclear power plant. J. Environ. Radioact. 2020, 223-224, 106388 10.1016/j.jenvrad.2020.106388. [DOI] [PubMed] [Google Scholar]
- Fueda K.; Takami R.; Minomo K.; Morooka K.; Horie K.; Takehara M.; Yamasaki S.; Saito T.; Shiotsu H.; Ohnuki T.; Law G. T. W.; Grambow B.; Ewing R. C.; Utsunomiya S. Volatilization of B4C control rods in Fukushima Daiichi nuclear reactors during meltdown: B–Li isotopic signatures in cesium-rich microparticles. J. Hazard. Mater. 2022, 428, 128214 10.1016/j.jhazmat.2022.128214. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.