Abstract

In the current study, the pseudoplastic model is used to analyze the mass and energy transmission through trihybrid nanofluid flow across a stretched permeable surface. The Darcy–Forchheimer relation is employed in the momentum equation to examine the influence of porosity. Energy and mass diffusion expressions are obtained by employing the double diffusion theories, which were proposed by Cattaneo and Christov and is broadly used by several researchers. The thermal efficiency of the trihybrid nanocrystals is evaluated by integrating them with a pseudoplastic substrate. The study of titanium dioxide (TiO2), cobalt ferrite (CoFe2O4), and magnesium oxide (MgO) nanocomposite base hybrid nanofluids across a stretchable sheet is receiving considerable interest in innovation and research due to their extensive spectrum of applicability. For this reason, the phenomena are modeled in the form of a system of PDEs with the effects of a heat source, magnetic field, natural convection, and chemical reaction. Through resemblance substitutions, these are reduced to an ODE system. The resultant first-order differential equations are further processed using the computational approach PCM. For authenticity and reliability, the values are reviewed against the existing literature. The findings are displayed through figures. When compared to the simple nanofluid, the hybrid and trihybrid nanofluid have a greater tendency for fluid energy and velocity propagation rate. The velocity and heat transition rate enhance 11.73% by varying nanoparticles’ values from 0.01 to 0.04, while the thermal conductivity of base fluid boosts with the addition of hybrid and trihybrid nanocomposites, up to 32% and 61%, respectively.
1. Literature Review
The study of simple and hybrid nanofluid flow across a stretching sheet has numerous applications in various fields, i.e., polymer engineering, extrusion of polymer, plastic sheets compression, glass production, fiber, and in metallic furnace.1 Numerical computations were carried out by Gul et al.2 to observe the efficiency of ferrofluid flow over an extending/shrinking slip. Bilal et al.3 utilized a stretchy substance with sucking and intravenous effects to replicate Maxwell NF flow using the PCM approach. Using directly the meshless local Petrov–Galerkin approach and the Dirac function, Wijayanta et al.4 reported the laminar natural convection heat transport in triangular cavities. The quantitative results with the suggested method and those derived with the traditional methods described in the literature were compared. Makarim et al.5 employed the numerical analysis to study the Marangoni convection that occurs when steam is absorbed into an aqueous lithium bromide solution. It was discovered that by including a fixed object at the surface, the convection flow rate can be increased. Shuaib et al.6 revealed the viscous fluid flow with mass and energy communication generated due to the inconsistent wave of an elastic sheet. Ullah et al.7 assessed the heat transference and flow of a liquid containing pseudoplastic nanoparticles through a vertical, narrow cylinder. As the curvature factor, mixed convection, and Weissenberg number are elevated, the flow velocity decreases. Moraveji and Toghraie8 examined the energy and flow patterns in the vortex tube, which are affected by the numbers of inlets, diameter, and tube length. It was determined that as the radius of a cold outflow increases, so does the flow velocity, and that as the length of the vortex tube extended. Alazwari and Safaei9 used a mixture model to simulate a unique design of a spinning tube under the nonisothermal hydrological conditions. It was discovered that raising the Reynolds number would improve the system’s thermal efficiency. Ahmad et al.10 evaluated a 3D MHD Maxwell nanofluid flow across a slendering exponentially stretching sheet with energy dissipation using the bvp4c method. Abu-Hamdeh et al.11 computed the quantity of entropy generation when Powell–Eyring nanofluid flows over permeable media in a horizontal surface under thermal jump conditions. Some further explanations and applications of fluid flow along an extending substrate have been discoursed in refs (12−18).
During energy transfers, a hybrid nanofluid surpasses conventional fluids such as acetone, water, nanofluids, and acetylene. The capacity to freeze at high temperatures is one of the many thermal features of hybrid nanofluids.19−22 Power production, heat exchange, heating systems, air conditioners, the automobile sector, electronic equipment, generators, reactors, and energy transmission in spacecraft are all applications of hybrid nanocomposites.23−25 The working fluid in this study contained titanium dioxide (TiO2), magnesium oxide (MgO), and cobalt ferrite (CoFe2O4) NPs. TiO2 is an inorganic substance that has been utilized in several products for a long period. It relies on it due to its non-noxious, fluorescent, and nonsensitive qualities, which improve the radiance and illumination of materials without causing harm. It is the whitest pigmentation recognized, with insightful properties and scattering abilities, and the capacity to defend against cancer cells. CoFe2O4 is frequently utilized in sensors, catalysts, and microbiology because of these properties.26,27 Chu et al.28 addressed the flow mechanics and heat transference in the context of Al2O3 and TiO2 NPs that were utilized to boost the thermal properties of the base solution. Kristiawan et al.29 conducted an experimental investigation into a hybrid technique using a microfine tunnel and a TiO2/water nanoliquid with different nanoparticulate concentrations. Purnama et al.30 analyzed the molecular binding reaction and excitation energy of a hybrid nanoliquid flow with the inclusion of CoFe2O4 and Fe3O4 NPs. Ullah et al.31 performed a mathematical analysis of the Darcy–Forchheimer flow of magnetized nanoparticles with zero mass flux and observed that endothermic/exothermic reactions raise the thermostat of nanostructures. Purnama et al.32 prepared strontium-substituted cobalt ferrite nanomaterials utilizing the coprecipitation technique and thermogravimetric evaluation. Ullah et al.33 researched the physicochemical parameters of trihybrid CuO/TiO2/SiO2 nanofluids. Depending on the temperature input, it was discovered that the trihybrid liquid had the highest thermal characteristics at roughly 55 °C. Sahu et al.34 analyzed the natural circulatory loop’s transitory and constant features utilizing a variety of water-based trihybrid nanofluids. Using trihybrid nanomaterials improves efficiency while lowering the rate of entropy production. The shape of nanocrystals has a considerable impact and exhibits the best performance. Many researchers have recently scrutinized the physics and use of TiO2, MgO, and CoFe2O4 hybrid NF over various geometries.35−39
The current model is based on the rheological characteristics of a pseudoplastic composite with trihybrid nanocrystals. The steady and incompressible trihybrid (TiO2 + MgO + CoFe2O4/EG) nanofluid flow along a horizontal stretching sheet is addressed. The theories of non- and Fourier’s Darcy’s Forchheimer are examined in the context of heat emission, natural convection, and chemical reaction. PCM is a computational method used for the numerical simulations of the system of PDEs. Our main objective is to examine the characteristics of trihybrid NF flow for industrial and biomedical applications. In the long run, this research could be used to develop an optimal thermal process, such as refrigerants and heat pumps, using appropriate physical sources.
2. Mathematical Formulation
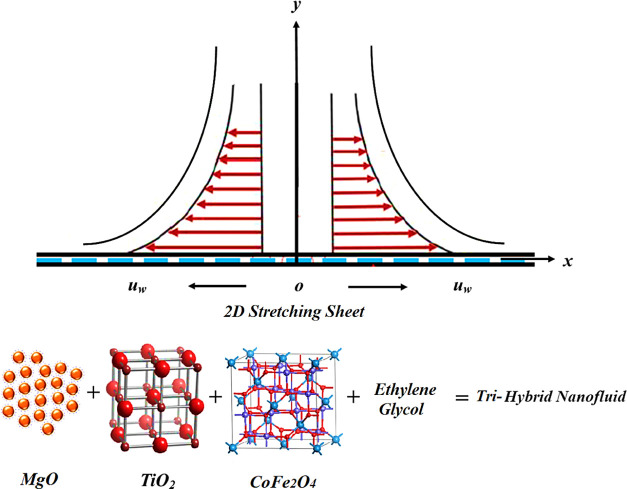
We assumed the fluid flow of trihybrid nanoparticulates in pseudoplastic fluid over a heated stretching surface. The heat energy and particles solute are examined using the CC model theory. Processes of heat generation and chemical reaction are executed in the existence of CC theory. The consequences of Darcy–Forchheimer, natural convection, heat generation are also considered along with velocity and energy equations. The boundary layers associated with thermal and momentum are generated due to the surface stretching. Tables 1 and 2 reveal the experimental outcomes and physical model for the trihybrid nanofluid. A physical illustration of the proposed model is highlighted in Figure 1. The basic equations that control the trihybrid nanofluid flow are characterized as follows40
| 1 |
| 2 |
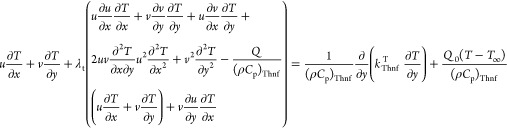 |
3 |
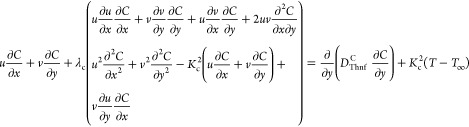 |
4 |
Here, Q0 is the heat source term, Kc2 is the rate of a chemical reaction, D is the mass diffusion, C is the concentration, FD is the inertia coefficient, k* is the porous medium, Thnf is the trihybrid nanofluid, Cp is the specific heat capacity, λt is the time relaxation term, and ρ is the density.
Table 1. Experimental Values of TiO2, MgO, CoFe2O4, and Ethylene Glycol41.
| base fluid and nanoparticles | ρ (kg/m3) | k(W/mK) | σ (S/m) |
|---|---|---|---|
| ethylene glycol C2H6O2 | 1113.1 | 0.253 | 4.3 × 10–5 |
| titanium dioxid TiO2 | 4250 | 8.9538 | 2.38 × 106 |
| cobalt ferrite Fe2O4 | 4907 | 3.7 | 5.51 × 109 |
| magnesium oxide MgO | 3560 | 45 |
Table 2. Thermal Properties of the Hybrid Nanofluid (φ1 = φTiO2, φ2 = φCoFe2O4, φ3 = φMgO)42.
| viscosity |  |
| density |  |
| specific heat |  |
| thermal conduction |  |
| electrical conductivity |  |
Figure 1.
Trihybrid pseudoplastic nanofluid flow over a stretching surface.
The initial and boundary conditions are as follows
| 5 |
The transformation variables are as follows
| 6 |
Variable mass and diffusion and thermal conductivity are defined as follows:
| 7 |
| 8 |
| 9 |
 |
10 |
Here, Pr is the Prandtl number, m is the power-law number, Fr is the Forchheimer number, ε is Darcy’s number, ε1 is the variable thermal conductivity, Sc is the Schmidt number, Ωa is the parameter generated due to non-Fourier’s theory, Ωc is the parameter formulated due to Cattaneo–Christov theory, and Kc2 is the chemical reaction rate. It is assessed that the chemical reaction is a nonreactive reaction for Kc = 0.
The mathematical expression for skin friction is
| 11 |
| 12 |
The temperature gradient is modeled as follows
| 13 |
The rate of mass diffusion is as follows
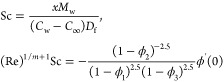 |
14 |
The Reynold number is 
3. Numerical Solution
Several researchers have used different types of numerical procedures for the solution of highly nonlinear PDEs.43−51 The fundamental steps involved in the PCM solution methodology, while dealing with the system of ODEs (8–10), are as follows.52,53
Step 1: Reducing the BVP to a first-order system of ODEs
| 15 |
By putting eqn 13 in eqs 7–9 and 10, we get
| 16 |
| 17 |
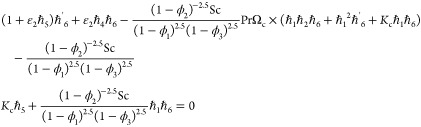 |
18 |
Step 2: Introducing parameter p:
| 19 |
| 20 |
 |
21 |
Step 3: Apply Cauchy Principal and discretizedeqs 19–21.
After discretization, the obtained set of equations are computed through the MATLAB code of PCM.
4. Results and Discussion
This section explains the physics behind each figure and table.
4.1. Velocity Profile f’(η)
Figure 2a–e describes the velocity f′(η) outlines versus Darcy’s number ε, the Forchheimer number Fr, the power-law number m, the thermal Grashof number, and the mass Grashof number, respectively. Figure 2a–c reveals that the field declines with the influence of Darcy’s number ε, the Forchheimer number Fr, and the power-law number, respectively. Physically, greater values of ε generate a frictional effect on fluid flow. So, the frictional effect opposes fluid flow. Hence, an inverse relation occurs among ε and flow, as shown in Figure 2a. The Forchhemier term mathematically appeared as a velocity squared in momentum equations. This offered a retardation effect to the flow motion, as elaborated in Figure 2b. It is assessed that the explanation of m is exhibited due to the addition of the pseudoplastic liquid effect. Furthermore, the grouping of shear thickening, shear thinning, and Newtonian liquid behavior is dependent on the m values. For m > 1 and m < 1, the fluid behaves as shear thinning and thickening among the fluid molecules, respectively. It has been detected that the momentum profile lessens with the increment of m. Figure 2d,e highlights the velocity transfer profile boosts with the rising credit of the thermal and mass Grashof number. The sheet stretching velocity declines with the effect of Gr and Gc, which causes such behavior of the velocity profile.
Figure 2.
Velocity f′(η) outlines versus (a) Darcy’s number ε, (b) Forchheimer number Fr, (c) power-law number m, (d) thermal Grashof number, and (e) mass Grashof number.
4.2. Temperature Profile θ(η)
Figure 3a–d demonstrates the presentation of energy θ(η) outlines versus the variable thermal conductivity ε1, heat absorption/generation Hh, parameter Ωa (generated due to non-Fourier’s theory), and comparative assessment between simple, hybrid, and trihybrid nanofluid φ1 = φ2 = φ3, respectively. Figure 3a–c elucidates that the temperature profile enhances with the significances of variable thermal conductivity ε1, heat absorption/generation Hh, and parameter Ωa, respectively. In terms of physics, ε1 has a linear proportion with the temperature difference. As a result, an intensification in ε1 results in a considerable rise in thermal energy’s capability to transfer excess heat into flowing fluid. When ε1 is elevated, the capacity to conduct energy into hybrid and nanomaterials improves as well. The dualistic function of thermal potential is shown on the thermal energy profile, with negative values of Hh indicating absorption of heat and positive values indicating energy production. When an exterior heat source is installed at the surface, the thermal energy profile is increased. The conduct of boundary layers depends on thermal impact increment. The application of an external entity of thermal potential, which is situated at the surface wall, produces this growing effect of thermal energy, as revealed in Figure 3b. Figure 3d displays the comparative assessment of simple, hybrid, and trihybrid nanofluid. It has been perceived that the trihybrid nanofluid has significantly boosted the energy propagation rate as compared to simple and hybrid nanofluid.
Figure 3.
Comportment of energy θ(η) contour versus (a) variable thermal conductivity ε1, (b) heat absorption/generation Hh, (c) parameter Ωa (generated due to non-Fourier’s theory), (d) comparative assessment between simple, hybrid, and trihybrid nanofluid.
4.3. Concentration Profile ϕ(η)
Figure 4a–d reports the appearance of concentration ϕ(η) outlines versus the parameter Ωc (formulated due to Cattaneo–Christov theory), parameter ε2, chemical reaction Kc, and the Schmidt number Sc, respectively. Figure 3a,b describes that the mass transport φ(η) field enhances with the positive deviation of parameters Ωc and ε2. Elevated quantities Ωc are detected as a massive improvement of species rate when three types of nanostructures are injected into species diffusion. In comparison to the role of Ωc,a significant efficiency of mass species is found. Because of the influence of Cattaneo–Christov theory, the existence of Ωc is defined. When Ωc is increased to include trihybrid nanoparticles, a considerable improvement in solute particles is observed in Figure 4a. The chemical change parameter has a positive impact on mass transport since it pushes fluid molecules to travel quickly, resulting in a positive variation (see Figure 4c). The effect of Sc also diminishes the mass transmission rate because it improves the kinetic viscosity of the fluid, which results in such senior as shown in Figure 4d.
Figure 4.
Concentration ϕ(η) outlines versus (a) parameter Ωc (formulated due to Cattaneo–Christov theory), (b) parameter ε2, (c) chemical reaction Kc, and (d) Schmidt number Sc.
Figure 5 emphasizes the relative analysis of simple (TiO2 or MgO or CoFe2O4), hybrid nanofluid (MgO+TiO2/water), and ternary hybrid nanoliquid (MgO + TiO2 + CoFe2O4/EG) for the energy and velocity profiles. When relative to the simple nanofluid, the trihybrid and hybrid nanofluids have a higher tendency for fluid velocity and energy transmission efficiency. For the numerical approximation of the current model, the parametric continuation method is used. In Figure 6, the convergence of the parametric continuation method is considered. The convergence zones of velocities, energy, and mass profiles of the trihybrid nanofluids are reviewed.
Figure 5.
Percentage (%) comparison between nanofluids. Hybrid and trihybridized nanofluid.
Figure 6.
(a) ℏ-curve for the velocity field, (b) ℏ-curve for the energy profile, (c) ℏ-curve for the concentration distribution.
Table 3 explains the numerical valuation of the Sherwood number, skin friction, and Nusselt number of the existing literature with current outcomes to ensure the authenticity of the current report.
Table 3. Statistical Valuation of Skin Friction, Concentration, and Temperature Gradient of the Current Work with the Existing Literature.
| ref (40) | present work | ref (40) | present work | ref (40) | present work | ||||
|---|---|---|---|---|---|---|---|---|---|
| Fr | Hh | Sc | Kc |  |
 |
 |
 |
 |
 |
| 0.0 | 0.9831194688 | 0.9831195589 | 1.273048742 | 1.2730488451 | 0.1738269697 | 0.1738269788 | |||
| 0.3 | 0.9948702726 | 0.9948703627 | 1.263799787 | 1.263799878 | 0.1636186839 | 0.1636186827 | |||
| 0.6 | 1.0055424430 | 1.005545331 | 1.244465792 | 1.244465883 | 0.1434299640 | 0.1434299731 | |||
| 1.5 | 1.048480792 | 1.048481693 | 2.988980397 | 2.988980886 | 0.1582282354 | 0.1582282445 | |||
| 0.3 | 1.021340103 | 1.021341004 | 2.184136239 | 2.184136348 | 0.1468662589 | 0.1468662677 | |||
| 0.7 | 1.010130191 | 1.010131092 | 2.110134671 | 2.110134762 | 0.1380771772 | 0.1380771863 | |||
| 0.0 | 1.018480792 | 1.018481693 | 1.275290361 | 1.275290452 | 0.1059774514 | 0.1059774605 | |||
| 0.3 | 1.018480792 | 1.018481693 | 1.275290361 | 1.275290452 | 0.2836633481 | 0.2836633573 | |||
| 0.6 | 1.018480792 | 1.018481693 | 1.275290361 | 1.275290450 | 0.6105156610 | 0.6105156700 | |||
| 1.4 | 1.018480792 | 1.018481693 | 1.275290361 | 1.275290450 | 0.08312047671 | 0.08312047762 | |||
| 0.0 | 1.018480792 | 1.018481693 | 1.310199330 | 1.310199441 | 0.09127662373 | 0.09127662464 | |||
| 0.5 | 1.018480792 | 1.018481693 | 1.501284349 | 1.501284457 | 0.29611881081 | 0.29611881173 |
5. Conclusions
The pseudoplastic model is used in the current study to analyze the energy communication through trihybrid nanofluid flow consisting of MgO, TiO2, and CoFe2O4 NPs across a stretched permeable surface. Energy and mass diffusion expressions are obtained by employing the double diffusion theories. The thermal efficiency of the trihybrid nanocrystals is evaluated by integrating them with a pseudoplastic substrate. The problem is solved using the computational approach PCM. The main discoveries are as follows:
The velocity field f′(η) declines with the influence of Darcy’s number ε, Forchheimer’s number Fr, and power law.
The velocity transfer profile boosts with the rising credit of thermal Gr and mass Gc Grashof number.
The temperature profile enhances with the significances of ε1, heat absorption/generation Hh, and parameter Ωa.
The velocity and heat transition rate enhance 11.73% by varying nanoparticle values from 0.01 to 0.04 (see Figure 5), while the thermal conductivity of base fluid boosts with the addition of hybrid and trihybrid nanocomposites, up to 32 and 61%, respectively.
The trihybrid nanofluid has significantly boosted the energy propagation rate as compared to simple and hybrid nanofluid.
The mass transport φ(η) outlines develop with the variation of parameters Ωc and ε2, while the chemical reaction and Schmidt number positively affect the mass transmission.
The skin friction enhances, while the Nusselt number decreases with the variation of Fr.
Glossary
Nomenclature
- ρ
density
- D
mass diffusion
- FD
inertia coefficient
- Q0
heat source term
- λt
time relaxation term
- Pr
Prandtl number
- ε1
variable thermal conductivity
- Thnf
Trihybrid nanofluid
- Cf
skin friction
- Nu
Nusselt number
- ε
Darcy’s number
- ϕ
Dimensionless concentration
- Gr
Thermal Grashof number
- Gc
Mass Grashof number
- σ
electrical conductivity
- k
thermal conduction
- μ
viscosity
- PCM
parametric continuation method
- M
power-law coefficient
- C
concentration
- kc2
chemical reaction
- k*
porous medium
- Cp
specific heat capacity
- Fr
Forchheimer number
- Sc
Schmidt number
- Ωa
generated due to non-Fourier’s theory
- Ωc
generated due to Cattaneo–Christov theory
- Kc = 0
nonreactive chemical reaction
- Re
Reynold number
- θ
dimensionless temperature
- ϕ1 = φTiO2
titanium dioxide nanoparticles
- ϕ2 = φCoFe2O4
cobalt ferrite nanoparticles
- ϕ3 = φMgO
magnesium oxide nanoparticles
- (ρCp)f
specific heat of base fluid
- g
Gravitational acceleration
- EG
(C2H6O2)-ethylene glycol
Author Contributions
M.B. and A.S. wrote the original manuscript and performed the numerical simulation. E.A.A. and H.F.A. reviewed the mathematical results and restructured the manuscript and also responded to the reviewer’s queries. Wajaree Weera has done the data curation and conceptualization and reviewed the manuscript. All of the authors are agreed on the final draft of the submission file.
The authors declare no competing financial interest.
References
- Abdel-Wahed M.; Akl M. Effect of hall current on MHD flow of a nanofluid with variable properties due to a rotating disk with viscous dissipation and nonlinear thermal radiation. AIP Adv. 2016, 6, 095308 10.1063/1.4962961. [DOI] [Google Scholar]
- Gul T.; Khan A.; Bilal M.; Alreshidi N. A.; Mukhtar S.; Shah Z.; Kumam P. Magnetic dipole impact on the hybrid nanofluid flow over an extending surface. Sci. Rep. 2020, 10, 8474 10.1038/s41598-020-65298-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bilal M.; Saeed A.; Selim M. M.; Gul T.; Ali I.; Kumam P. Comparative numerical analysis of Maxwell’s time-dependent thermo-diffusive flow through a stretching cylinder. Case Stud. Therm. Eng. 2021, 27, 101301 10.1016/j.csite.2021.101301. [DOI] [Google Scholar]
- Pranowo; Wijayanta A. T. Numerical solution strategy for natural convection problems in a triangular cavity using a direct meshless local petrov-Galerkin method combined with an implicit artificial-compressibility model. Eng. Anal. Boundary Elem. 2021, 126, 13–29. 10.1016/j.enganabound.2021.02.006. [DOI] [Google Scholar]
- Makarim D. A.; Suami A.; Wijayanta A. T.; Kobayashi N.; Itaya Y. Marangoni convection within thermosolute and absorptive aqueous LiBr solution. Int. J. Heat Mass Transfer 2022, 188, 122621 10.1016/j.ijheatmasstransfer.2022.122621. [DOI] [Google Scholar]
- Shuaib M.; Bilal M.; Khan M. A.; Malebary S. J. Fractional analysis of viscous fluid flow with heat and mass transfer over a flexible rotating disk. Comput. Model. Eng. Sci. 2020, 123, 377–400. 10.32604/cmes.2020.08076. [DOI] [Google Scholar]
- Ullah Z.; Ullah I.; Zaman G.; Sun T. C. A numerical approach to interpret melting and activation energy phenomenon on the magnetized transient flow of Prandtl–Eyring fluid with the application of Cattaneo–Christov theory. Waves Random Complex Media 2022, 0, 1–21. 10.1080/17455030.2022.2032472. [DOI] [Google Scholar]
- Moraveji A.; Toghraie D. Computational fluid dynamics simulation of heat transfer and fluid flow characteristics in a vortex tube by considering the various parameters. Int. J. Heat Mass Transfer 2017, 113, 432–443. 10.1016/j.ijheatmasstransfer.2017.05.095. [DOI] [Google Scholar]
- Alazwari M. A.; Safaei M. R. Non-isothermal hydrodynamic characteristics of a nanofluid in a fin-attached rotating tube bundle. Mathematics 2021, 9, 1153 10.3390/math9101153. [DOI] [Google Scholar]
- Ahmad S.; Khan M. N.; Nadeem S.; Rehman A.; Ahmad H.; Ali R. Impact of Joule heating and multiple slips on a Maxwell nanofluid flow past a slendering surface. Commun. Theor. Phys. 2021, 74, 015001 10.1088/1572-9494/ac3bc8. [DOI] [Google Scholar]
- Abu-Hamdeh N. H.; Alsulami R. A.; Rawa M. J.; Alazwari M. A.; Goodarzi M.; Safaei M. R. A Significant Solar Energy Note on Powell-Eyring Nanofluid with Thermal Jump Conditions: Implementing Cattaneo-Christov Heat Flux Model. Mathematics 2021, 9, 2669 10.3390/math9212669. [DOI] [Google Scholar]
- Ruhani B.; Toghraie D.; Hekmatifar M.; Hadian M. Statistical investigation for developing a new model for rheological behavior of ZnO–Ag (50%–50%)/Water hybrid Newtonian nanofluid using experimental data. Phys. A 2019, 525, 741–751. 10.1016/j.physa.2019.03.118. [DOI] [Google Scholar]
- Ahmadian A.; Bilal M.; Khan M. A.; Asjad M. I. Numerical analysis of thermal conductive hybrid nanofluid flow over the surface of a wavy spinning disk. Sci. Rep. 2020, 10, 18776 10.1038/s41598-020-75905-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lv Y.-P.; Algehyne E. A.; Alshehri M. G.; Alzahrani E.; Bilal M.; Khan M. A.; Shuaib M. Numerical approach towards gyrotactic microorganisms hybrid nanoliquid flow with the hall current and magnetic field over a spinning disk. Sci. Rep. 2021, 11, 8948 10.1038/s41598-021-88269-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mashayekhi R.; Khodabandeh E.; Akbari O. A.; Toghraie D.; Bahiraei M.; Gholami M. CFD analysis of thermal and hydrodynamic characteristics of hybrid nanofluid in a new designed sinusoidal double-layered microchannel heat sink. J. Therm. Anal. Calorim. 2018, 134, 2305–2315. 10.1007/s10973-018-7671-3. [DOI] [Google Scholar]
- Bazdar H.; Toghraie D.; Pourfattah F.; Akbari O. A.; Nguyen H. M.; Asadi A. Numerical investigation of turbulent flow and heat transfer of nanofluid inside a wavy microchannel with different wavelengths. J. Therm. Anal. Calorim. 2020, 139, 2365–2380. 10.1007/s10973-019-08637-3. [DOI] [Google Scholar]
- Rozati S. A.; Montazerifar F.; Ali Akbari O.; Hoseinzadeh S.; Nikkhah V.; Marzban A.; Abdolvand H.; Goodarzi M. Natural convection heat transfer of water/Ag nanofluid inside an elliptical enclosure with different attack angles. Math. Methods Appl. Sci. 2020, 10.1002/mma.7036. [DOI] [Google Scholar]
- Alazwari M. A.; Abu-Hamdeh N. H.; Goodarzi M. Entropy optimization of first-grade viscoelastic nanofluid flow over a stretching sheet by using classical Keller-box scheme. Mathematics 2021, 9, 2563 10.3390/math9202563. [DOI] [Google Scholar]
- Waqas H.; Imran M.; Muhammad T.; Sait S. M.; Ellahi R. Numerical investigation on bioconvection flow of Oldroyd-B nanofluid with nonlinear thermal radiation and motile microorganisms over rotating disk. J. Therm. Anal. Calorim. 2021, 145, 523–539. 10.1007/s10973-020-09728-2. [DOI] [Google Scholar]
- Algarni M.; Alazwari M. A.; Safaei M. R. Optimization of nano-additive characteristics to improve the efficiency of a shell and tube thermal energy storage system using a hybrid procedure: DOE, ANN, MCDM, MOO, and CFD modeling. Mathematics 2021, 9, 3235 10.3390/math9243235. [DOI] [Google Scholar]
- Ahmadi A. A.; Arabbeiki M.; Ali H. M.; Goodarzi M.; Safaei M. R. Configuration and optimization of a minichannel using water–alumina nanofluid by non-dominated sorting genetic algorithm and response surface method. Nanomaterials 2020, 10, 901 10.3390/nano10050901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mostafazadeh A.; Toghraie D.; Mashayekhi R.; Akbari O. A. Effect of radiation on laminar natural convection of nanofluid in a vertical channel with single-and two-phase approaches. J. Therm. Anal. Calorim. 2019, 138, 779–794. 10.1007/s10973-019-08236-2. [DOI] [Google Scholar]
- Kavusi H.; Toghraie D. A comprehensive study of the performance of a heat pipe by using of various nanofluids. Adv. Powder Technol. 2017, 28, 3074–3084. 10.1016/j.apt.2017.09.022. [DOI] [Google Scholar]
- Li Z.; Barnoon P.; Toghraie D.; Dehkordi R. B.; Afrand M. Mixed convection of non-Newtonian nanofluid in an H-shaped cavity with cooler and heater cylinders filled by a porous material: Two phase approach. Adv. Powder Technol. 2019, 30, 2666–2685. 10.1016/j.apt.2019.08.014. [DOI] [Google Scholar]
- Imran M.; Farooq U.; Waqas H.; Anqi A. E.; Safaei M. R. Numerical performance of thermal conductivity in Bioconvection flow of cross nanofluid containing swimming microorganisms over a cylinder with melting phenomenon. Case Stud. Therm. Eng. 2021, 26, 101181 10.1016/j.csite.2021.101181. [DOI] [Google Scholar]
- Ullah I.; Ullah R.; Alqarni M.; Xia W.-F.; Muhammad T. Combined heat source and zero mass flux features on magnetized nanofluid flow by radial disk with the applications of Coriolis force and activation energy. Int. Commun. Heat Mass Transfer 2021, 126, 105416 10.1016/j.icheatmasstransfer.2021.105416. [DOI] [Google Scholar]
- Zhang X.-H.; A Algehyne E.; G Alshehri M.; Bilal M.; Khan M. A.; Muhammad T. The parametric study of hybrid nanofluid flow with heat transition characteristics over a fluctuating spinning disk. PLoS One 2021, 16, e0254457 10.1371/journal.pone.0254457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chu Y.-M.; Nazir U.; Sohail M.; Selim M. M.; Lee J.-R. Enhancement in thermal energy and solute particles using hybrid nanoparticles by engaging activation energy and chemical reaction over a parabolic surface via finite element approach. Fractal Fractional 2021, 5, 119. 10.3390/fractalfract5030119. [DOI] [Google Scholar]
- Kristiawan B.; Rifa’i A. I.; Enoki K.; Wijayanta A. T.; Miyazaki T. Enhancing the thermal performance of TiO2/water nanofluids flowing in a helical microfin tube. Powder Technol. 2020, 376, 254–262. 10.1016/j.powtec.2020.08.020. [DOI] [Google Scholar]
- Purnama B.; Rahmawati R.; Wijayanta A. T.; Suharyana S. Dependence of structural and magnetic properties on annealing times in Co-precipitated cobalt ferrite nanoparticles. J. Magn. 2015, 20, 207–210. 10.4283/JMAG.2015.20.3.207. [DOI] [Google Scholar]
- Ullah I. Activation energy with exothermic/endothermic reaction and Coriolis force effects on magnetized nanomaterials flow through Darcy–Forchheimer porous space with variable features. Waves Random Complex Media 2022, 0, 1–14. 10.1080/17455030.2021.2023779. [DOI] [Google Scholar]
- Purnama B.; Arilasita R.; Rikamukti N.; Budiawanti S.; Wijayanta A. T.; Djuhana D.; Suharyadi E.; Tanaka T.; Matsuyama K. Annealing temperature dependence of crystalline structure and magnetic properties in nano-powder strontium-substituted cobalt ferrite. Nano-Struct. Nano-Objects 2022, 30, 100862 10.1016/j.nanoso.2022.100862. [DOI] [Google Scholar]
- Ullah I.; Hayat T.; Aziz A.; Alsaedi A. Significance of Entropy Generation and the Coriolis Force on the Three-Dimensional Non-Darcy Flow of Ethylene-Glycol Conveying Carbon Nanotubes (SWCNTs and MWCNTs). J. Non-Equilib. Thermodyn. 2022, 47, 61–75. 10.1515/jnet-2021-0012. [DOI] [Google Scholar]
- Sahu M.; Sarkar J.; Chandra L. Steady-state and transient hydrothermal analyses of single-phase natural circulation loop using water-based tri-hybrid nanofluids. AIChE J. 2021, 67, e17179 10.1002/aic.17179. [DOI] [Google Scholar]
- Li Z.; Khaled U.; Al-Rashed A. A.; Goodarzi M.; Sarafraz M.; Meer R. Heat transfer evaluation of a micro heat exchanger cooling with spherical carbon-acetone nanofluid. Int. J. Heat Mass Transfer 2020, 149, 119124 10.1016/j.ijheatmasstransfer.2019.119124. [DOI] [Google Scholar]
- Dhass A. D.; Beemkumar N.; Harikrishnan S.; Ali H. M. A Review on Factors Influencing the Mismatch Losses in Solar Photovoltaic System. Int. J. Photoenergy 2022, 2022, 1–27. 10.1155/2022/2986004. [DOI] [Google Scholar]
- Hadi F.; Ali H. M. Hydro thermal performance evaluation of super hydrophobic pin fin mini channel heat sink. Therm. Sci. 2022, 26, 3627–3640. 10.2298/TSCI210901009H. [DOI] [Google Scholar]
- Habib H. M.; Ali H. M.; Usman M. Investigation of Condensate Retention on Horizontal Pin-Fin Tubes Using Water-Propanol Mixture. Sustainability 2022, 14, 835 10.3390/su14020835. [DOI] [Google Scholar]
- Afshari F.; Sözen A.; Khanlari A.; Tuncer A. D.; Ali H. M. Experimental investigation of effect of refrigerant gases, compressor lubricant and operating conditions on performance of a heat pump. J. Cent. South Univ. 2021, 28, 3556–3568. 10.1007/s11771-021-4875-7. [DOI] [Google Scholar]
- Said Z.; Jamei M.; Sundar L. S.; Pandey A.; Allouhi A.; Li C. Thermophysical properties of water, water and ethylene glycol mixture-based nanodiamond+ Fe3O4 hybrid nanofluids: An experimental assessment and application of data-driven approaches. J. Mol. Liq. 2022, 347, 117944 10.1016/j.molliq.2021.117944. [DOI] [Google Scholar]
- Wang F.; Nazir U.; Sohail M.; El-Zahar E. R.; Park C.; Thounthong P. A Galerkin strategy for tri-hybridized mixture in ethylene glycol comprising variable diffusion and thermal conductivity using non-Fourier’s theory. Nanotechnol. Rev. 2022, 11, 834–845. 10.1515/ntrev-2022-0050. [DOI] [Google Scholar]
- Acharya N.; Maity S.; Kundu P. K. Framing the hydrothermal features of magnetized TiO2–CoFe2O4 water-based steady hybrid nanofluid flow over a radiative revolving disk. Multidiscip. Model. Mater. Struct. 2019, 16, 765–790. 10.1108/MMMS-08-2019-0151. [DOI] [Google Scholar]
- Zhao T.-H.; He Z.-Y.; Chu Y.-M. Sharp bounds for the weighted Hölder mean of the zero-balanced generalized complete elliptic integrals. Comput. Methods Funct. Theory 2021, 21, 413–426. 10.1007/s40315-020-00352-7. [DOI] [Google Scholar]
- Zhao T.-H.; Wang M.-K.; Chu Y.-M. Concavity and bounds involving generalized elliptic integral of the first kind. J. Math. Inequalities 2007, 15, 701–724. 10.7153/jmi-2021-15-50. [DOI] [Google Scholar]
- Chu H.-H.; Zhao T.-H.; Chu Y.-M. Sharp bounds for the Toader mean of order 3 in terms of arithmetic, quadratic and contraharmonic means. Math. Slovaca 2020, 70, 1097–1112. 10.1515/ms-2017-0417. [DOI] [Google Scholar]
- Rashid S.; Sultana S.; Karaca Y.; Khalid A.; Chu Y.-M. Some further extensions considering discrete proportional fractional operators. Fractals 2022, 30, 2240026 10.1142/S0218348X22400266. [DOI] [Google Scholar]
- Jin F.; Qian Z.-S.; Chu Y.-M.; ur Rahman M. On nonlinear evolution model for drinking behavior under Caputo-Fabrizio derivative. J. Appl. Anal. Comput. 2022, 12, 790–806. 10.11948/20210357. [DOI] [Google Scholar]
- Rashid S.; Abouelmagd E. I.; Khalid A.; Farooq F. B.; Chu Y. Some recent developments on dynamical h-discrete fractional type inequalities in the frame of nonsingular and nonlocal kernels. Fractals 2022, 30, 2240110 10.1142/S0218348X22401107. [DOI] [Google Scholar]
- Iqbal S. A.; Hafez M. G.; Chu Y.-M.; Park C. Dynamical Analysis of nonautonomous RLC circuit with the absence and presence of Atangana-Baleanu fractional derivative. J. Appl. Anal. Comput. 2022, 12, 770–789. 10.11948/20210324. [DOI] [Google Scholar]
- Wang F.; Khan M. N.; Ahmad I.; Ahmad H.; Abu-Zinadah H.; Chu Y.-M. Numerical solution of traveling waves in chemical kinetics: time-fractional fishers equations. Fractals 2022, 30, 2240051 10.1142/S0218348X22400515. [DOI] [Google Scholar]
- Chu Y. M.; Bashir S.; Ramzan M.; Malik M. Y. Model-based comparative study of magnetohydrodynamics unsteady hybrid nanofluid flow between two infinite parallel plates with particle shape effects. Math. Methods Appl. Sci. 2022, 10.1002/mma.8234. [DOI] [Google Scholar]
- Shuaib M.; Shah R. A.; Durrani I.; Bilal M. Electrokinetic viscous rotating disk flow of Poisson-Nernst-Planck equation for ion transport. J. Mol. Liq. 2020, 313, 113412 10.1016/j.molliq.2020.113412. [DOI] [Google Scholar]
- Shuaib M.; Shah R. A.; Bilal M. Von-Karman rotating flow in variable magnetic field with variable physical properties. Adv. Mech. Eng. 2021, 13, 1687814021990463 10.1177/1687814021990463. [DOI] [Google Scholar]