Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Aug 9;7(33):28849–28859. doi: 10.1021/acsomega.2c01859

Elongated Rodlike Particle Formation of Methyl Cellulose in Aqueous Solution

Erika Saiki †,‡, Misato Yoshida †,‡, Kei Kurahashi †,‡, Hiroki Iwase §, Toshiyuki Shikata †,‡,*
PMCID: PMC9404515  PMID: 36033728

Abstract

graphic file with name ao2c01859_0010.jpg

The conformation and structure of methyl cellulose (MC) ether samples dissolved in pure water under dilute conditions were carefully reconsidered based on the results obtained using small-to-wide-angle neutron scattering (S-WANS), static light scattering (SLS), dynamic light scattering (DLS), and viscometric techniques. The examined MC samples possessed an average degree of substitution by methyl groups per glucose unit of ca 1.8 and weight average molar masses (Mw), ranging from 23 to 790 kg mol–1. S-WANS experiments clearly demonstrated that the samples possess highly elongated rigid rodlike local structures in deuterium oxide solutions with weak periodicities of ca 0.4 and 1.0 nm on a length scale, which correspond to the average intermolecular distance between molecular chain portions facing each other in the formed rodlike structure and the repeating length of the monomeric cellobiose unit of molecular chains, respectively. Ratios of the particle length (L) to the radius of gyration (Rg) determined by SLS techniques approximately showed the relationship LRg–1 = Inline graphic holding in rigid rods over the entire Mw range examined in this study. However, the folding number, defined as the ratio of the average molecular contour length (l) to L, remained at the value of lL–1 ∼ 2, representing an elongated one-folded hairpin structure, until Mw ∼ 300 kg mol–1 and increased substantially up to ca 4.9 at the highest Mw of 790 kg mol–1. The observed increase in the lL–1 value corresponded well with an increase in the diameter of the formed rod with increasing Mw observed in the S-WANS data. The Mw dependencies of the translational diffusion coefficient determined via DLS measurements and that of the intrinsic viscosity detected via viscometric techniques also distinctly demonstrated that particles formed by the MC samples dissolved in aqueous solution behave as elongated rigid rods irrespective of Mw.

Introduction

Many kinds of plants constantly generate cellulose throughout the year. Thus, cellulose is the most abundant and steadily suppliable natural organic “biomass” resource worldwide.1 However, native cellulose is generally insoluble in most common solvents including water. The reason for this insolubility is the highly developed inter- and intramolecular hydrogen bonds between hydroxy groups and also between hydroxy and ether groups belonging to cellulose molecular chains. Rigid stable crystalline structures called “cellulose-Iα and Iβ” are formed by cellulose molecules in a quite efficient way in native plant cell walls, which are responsible for the insolubility in common solvents.1−4 Although cellulose is a quite eco-friendly biomass and offers great potential as a natural resource to develop a sustainable society, its insolubility in common solvents represents an essential reason for its inapplicability to wide chemical applications in the native state. Many chemically modified cellulose derivatives which are readily soluble in various solvents have been synthesized from natural cellulose to remedy its fatal insolubility.5 Many kinds of water-soluble chemically modified cellulose derivatives have been synthesized and supplied by several chemical manufacureers.5,6 Methyl cellulose (MC), hydroxypropyl cellulose (HpC), hydroxypropyl methyl cellulose (HpMC), hydroxyethyl cellulose (HeC), and sodium carboxymethyl cellulose (NaCMC) ethers are typical water-soluble chemically modified cellulose derivatives, that have been widely distributed in many industries, such as those of food,7 construction,8 and pharmaceutical.9,10

Many macromolecular scientists hypothesize that most water-soluble chemically modified cellulose derivative samples have semi-flexible chain-like conformations and structures in aqueous solution and show random coil-like behavior in a sufficiently high molar mass region, similar to many ordinary synthetic polymer samples dissolved in organic solvents.11 The literature in this field suggests that the idea of the semi-flexible or random coil-like conformation for chemically modified cellulose samples are simply based on the widely observed weight average molar mass (Mw) dependencies of the radius of gyration (Rg) determined by the use of static light scattering (SLS) measurements and of the intrinsic viscosity ([η]), such as Rg ∝ Mwα and [η] ∝ Mwβ with exponents of α ∼ 0.6 and β ∼ 0.8, respectively, which are slightly dependent on chemically modified conditions for tested samples. However, if one examines the previously reported data12−14 of Mw dependencies on Rg or [η] examined over a wide Mw range very carefully, some data cannot be described by the fashion of a simple power law with only one exponent, such as α ∼ 0.6 or β ∼ 0.8 over a wide Mw range. It is therefore possible that the idea of semi-flexible chain or random coil-like conformation is only prejudice to the water-soluble chemically modified cellulose samples.

Very recently, Arai et al.15 clearly demonstrated that some water-soluble MC and HpMC ether samples, which are widely used in many industrially manufactured products, have rigid rodlike structures formed by a one-folded hairpin-like conformation of highly extended cellulose chains in Mw ranges below 100 kg mol–1. They carried out small-to-wide-angle neutron scattering (S-WANS) measurements to determine the local structure of the formed particles in aqueous (deuterium oxide; D2O) solution.15 This striking report was the first evidence to reconsider the conformation and structure of water-soluble chemically modified cellulose samples in aqueous solutions. Bodvik et al.16 captured evidence of the rigid rodlike structures of MC and HpMC with Mw lower than 200 kg mol–1 using small-angle X-ray scattering (SAXS) techniques in a low-temperature range. However, they evaluated the persistence length of 5.8 nm for both the MC and HpMC samples from their SAXS data, which meant that the molecules are semi-flexible polymer chains like the widely accepted view in cellulose derivatives.16 Although Lodge et al.12 also observed rigid rodlike behavior in an aqueous solution of an HpMC sample with the Mw of 370 kg mol–1 using SANS techniques, they mainly paid attention to the gelation mechanism of the solution. It well known that aqueous solutions of MC samples form stable gels at temperatures higher than, for example, 40 °C due to intermolecular interactions that provoke the aggregation formation of individual MC molecules into bundles having a fibril structure. The gelation mechanism is described in detail in recent reviews.17,18

Nevertheless, the investigated Mw range in previous studies was limited to a relatively lower range to reach the general conclusion showing the Mw dependence of conformation and structure for the MC and HpMC samples in aqueous solutions. Thus, we decided to extend the Mw range covered by experiments to lead to clear results proposing the general characteristics of the Mw dependence of conformation and structure for the same MC samples in aqueous solutions. In this study, we employ SLS techniques to precisely determine the weight average molar masses, Mw, and the radii of gyration, Rg, of the MC samples simultaneously, of which scattering vectors (q) cover a much lower range than the S-WANS techniques to provide structural information on a size scale exceeding approximately 20 nm. Thus, the conformation and structure of the MC samples are exactly determined over a wide size scale, ranging from sub-to several hundred nanometers using total curve analysis procedures for the obtained scattering functions using both the S-WANS and SLS experiments. In this study, we reached a surprising conclusion that MC molecules possibly have a rigid rodlike conformation and structure, not semi-flexible polymer chain structure, in aqueous solution over the wide Mw range examined. Then, we will report newly obtained results and conclusions below.

According to a previous report, the temperature dependencies of the hydration numbers and cloud points of MC and HpMC samples possessing similar degrees of substitution (DS) of hydroxy groups by methyl groups, ca 1.8–1.9, are substantially different.19 Thus, it is possible that a small amount of additional substitution by hydroxypropyl groups only at the molar substitution number of MS ∼ 0.25 effectively contributes to changes in the conformation and structure of HpMC samples in aqueous solutions. In the following research, the conformation and structure of the HpMC samples will be discussed over a wide size scale range using similar total curve analysis procedures to the obtained scattering functions using both the S-WANS and SLS experiments used in this study.

Because many kinds of MC and HpMC samples, possessing similar chemically modified conditions to the samples investigated in this study, have been supplied by several chemical manufactures for wide practical applications, understanding the true conformation and structure of the samples in aqueous solution without prejudice would be helpful to reach breakthrough ideas improving processing procedures to effectively introduce solutions to the most desired flow and/or rheological conditions including processing temperatures.

Experimental Section

Materials

All MC ether samples were kindly supplied by Shin-Etsu Chemical Co., Ltd. (Tokyo). The MC samples have a constant degree of substitution (DS) of hydroxy groups per repeating β(1,4) glucopyranose unit by methoxy (M) groups of DS = 1.8, which means the average molar mass of M0 = 0.187 kg mol–1 for the repeating glucopyranose unit. The weight average molar masses (Mw) determined by SLS measurements in this study were Mw = 23, 54, 115, 206, 270, 420, and 790 kg mol–1. The MC samples were coded as eg MC(1.8:23) with numerical values indicating DS and Mw/(kg mol–1), respectively. All the MC samples were used for experiments without any purification procedures. The distributions of molar masses were not exceptionally sharp but rather broad as the polydispersity indices defined by ratios of Mw to the number average molar masses (Mn), MwMn–1 were determined using size exclusion chromatographic techniques and reported to range from approximately 2.0 to Mw ∼ 300 kg mol–1 and increased slightly with Mw values for the MC samples. Highly deionized water obtained by using a Direct-Q UV3 (Merck Milli-Q, Darmstadt) was used as a solvent to prepare sample solutions for SLS, DLS, and viscometric measurements. Deuterium oxide (D2O) (>99.9%) was purchased from Euroisotop (Saint-Aubin) and was used as a solvent to prepare sample solution for S-WANS experiments.

The concentrations (c) of MC samples dissolved in D2O for S-WANS measurements were set at close to the measured [η]−1 values or lower than the values in aqueous solution, which are widely accepted as so-called overlapping concentrations for macromolecules in solution. The c values in the S-WANS measurements were 1.0 × 10–2 g mL–1 for MC(1.8:23), 1.1 × 10–3, 2.1 × 10–3, and 5.0 × 10–3 g mL–1 for MC(1.8:270), and 5.0 × 10–4 and 1.0 × 10–3 g mL–1 for MC(1.8:790). The c values of MC samples in pure aqueous solutions for SLS, DLS, and viscometric measurements ranged from 3 × 10–4 to 6 × 10–2 g mL–1 depending on the sample Mw values.

Methods

S-WANS measurements were carried out at Materials and Life Science Experimental Facility (MLF) in Japan Proton Accelerator Research Complex, J-PARC, (Tokai) using a small-angle neutron scattering instrument (TAIKAN)20 installed on a beamline BL15. The magnitude of the scattering vector (q) covered by the S-WANS experiments ranged from 7.0 × 10–2 to 1.0 × 102 nm–1. Square-type quartz cuvettes with a neutron beam path length of 4.0 mm or banjo-type quartz cuvettes with a path of 2.0 mm were used as sample cells. The standard exposure time was 2 h for each sample solution. S-WANS measurements were carried out at 25 °C. The obtained scattering data were converted to absolute values using the standard material “glassy carbon” for which absolute scattering values had been precisely determined.

SLS and DLS measurements were carried out using a modified DLS7000 (Otsuka Electronics Co. Ltd., Osaka). A continuous-wave solid-state single-frequency laser at a wavelength of λ = 488.0 nm, Sapphire SF488-100 (Coherent, Inc., Santa Clara), was equipped with the modified DLS7000 and was used as a light source for SLS and DLS measurements. A photomultiplier, R9880U-01 (Hamamatsu Photonics K. K., Hamamatsu), was used as a scattered light intensity detector. An LSI correlator (LS Instrument AG, Fribourg) was used to record fluctuations in scattered light intensity as a function of time and to create an autocorrelation function of the scattered light intensity. A Pyrex glass tube with an inner diameter and thickness of 19.0 and 0.5 mm, respectively, was used as a measuring cell. The measuring temperature was set at 25.0 °C, and the scattering angle (θ) was altered from 30 to 150° every 10° step. The magnitude of the scattering vectors, which is given by the equation q = |q|= (4πn/λ)|sin(θ/2)|, where n is the refractive index of water, ranged from 8.86 × 10–3 to 3.31 × 10–2 nm–1 for both the SLS and DLS measurements. Toluene was used as the standard liquid material for scattered light intensities at each θ in the SLS measurements. The refractive index increment (dn/dc) of the MC samples was determined to be 0.134 mL g–1 using an Abbemat MW multiwavelengths refractometer (Anton Paar, Graz) at a wavelength of λ = 486 nm. Because the value of dn/dc = 0.133 mL g–1 was also obtained at λ = 589 nm–1, the λ dependence of dn/dc was quite weak.

The intrinsic viscosities, [η], for each MC and HpMC sample in aqueous solution were determined at 25.0 °C using an Ubbelohde-type capillary viscometer.

Results and Discussion

S-WANS Behaviors for MC Samples

An excess value in the scattering intensity of a solution sample [I(q)] with respect to that of the solvent [Isolv(q)] and a small q independent incoherent component (Iincoh) was normalized by the concentration, c, to obtain the characteristic scattering intensity, ΔI(q)c–1 = (I(q) – Isolv(q) – Iincoh)c–1, for each tested sample. Some S-WANS behaviors such as the q dependence of ΔI(q)c–1, observed in MC sample solutions, are shown in Figure 1a–c with the evaluated error bars to show the accuracy of the experiments. Because the concentration, c, for each MS sample was not higher than the so-called overlap concentration, c* = [η]−1, S-WANS behaviors are almost independent of c and reflect the isolated state in D2O solutions. In the case of the behavior for MC(1.8:23) with the lowest Mw in the examined MC samples, ΔI(q)c–1 data seem to have a plateau region in a q range lower than 0.1 nm–1, an inversely proportional region showing the relationship ΔI(q)c–1 ∝ q–1 in a q range of 0.1 nm–1 < q < 3.0 nm–1, and a steeply decreasing region with q values showing a couple of characteristic interference scatterings, as seen in Figure 1a. The presence of a plateau region in the ΔI(q)c–1 data means that MC(1.8:23) molecules have a characteristic size not far from 10 nm. On the other hand, the relationship ΔI(q)c–1 ∝ q–1 strongly suggests a rigid rodlike structure for the sample. The broad interference scatterings observed at q* ∼ 17 and q** ∼ 6 nm–1, which correspond to the spacing distances of δ* ∼ 0.4 and δ** ∼ 1.0 nm, indicate the presence of loose periodicities in the rigid rodlike structure. There is a broad peak in the S-WANS data of solvent D2O at q = 20 nm–1, which corresponds to 0.3 nm in scale. Because the observed peak value of q* = 17 nm–1 was slightly smaller than the peak q value of D2O and the q dependence of the interference peak observed at q* was obviously sharper than that of D2O, we concluded that the observed peaks at q* result from the periodic structure formed in the particles of MC molecules dissolved in water.15

Figure 1.

Figure 1

Open in a new tab

Dependencies of the concentration reduced excess scattering intensities, ΔI(q)c–1, on the scattering vector, q, for D2O solutions of MC(1.8:23) at c = 1.0 × 10–2 g mL–1 (a), MC(1.8:270) at c = 2.1 × 10–3 and 5.0 × 10–3 g mL–1 (b), and MC(1.8:790) at c = 5.0 × 10–4 g mL–1 (c) in the S-WANS experiments at 25 °C. Solid and broken lines indicate the fit theoretical form factors, P(q) calculated using SasView,22 for rods and rectangular columns with the size parameters shown in each figure on the scale of nanometer.

A solid curve drawn in Figure 1a reveals a theoretically calculated q dependence of the form factor (P(q)) of a rigid rod21 with a length and diameter of L = 39 and d = 0.7 nm, respectively, which was calculated using SasView22 multipurpose open source software for small-angle scattering data analysis and multiplied by a certain adequate value to fit the q dependence of the data. The reason for the L value is described in the later section. Reasonable agreement between the solid curve and ΔI(q)c–1 data convincingly reveals that the MC(1.8:23) molecules have a rigid rod shape with L = 39 and d = 0.7 nm in aqueous solution. Essentially, the same S-WANS behavior except for the presence of a plateau ΔI(q)c–1 region has already been observed in the S-WANS behaviors in the samples of MC(1.8:54) and MS(1.8:115) with Mw higher than MC(1.8:23) in the previous report,15 which are well described by the form factors of rigid rods with the same d value of 0.8 nm and L values longer than 39 nm. Briefly stated, the form factor of a rigid rod, P(q), with L and d exhibits a plateau value ca unity in the q range less than ca (L/3)−1 and is followed by the characteristic relationship P(q) ∝ q–1 up to a q value ca (d/3)−1, then decreases rapidly above the q value. The broken line in Figure 1a indicates the q dependence of the theoretical form factor, P(q), of a rectangular cuboid (rectangular column) calculated by SasView22 with L = 39 nm and major and minor widths of w1 = 0.7 and w2 = 0.3 nm, respectively. Since this form factor for the rectangular column is hardly distinguishable from that for the rod, a rectangular column is also a likely candidate for the structure of MC(1.8:23) molecules in aqueous solution.

Figure 1b,c represents the q dependence of ΔI(q)c–1 data for MC(1.8:270) and MC(1.8:790), respectively, possessing much higher Mw values than MC(1.8:23). In the case of the MC(1.8:270) sample, the c* value is calculated to be 1.9 × 10–3 g mL–1, whereas ΔI(q)c–1 data obtained at c = 5.0 × 10–3 g mL–1, which is approximately 2.6 times as high as c*, appear to follow those determined at c lower than c* even in a low q range. Basically, the essential rigid rod particle characteristics also remain in these longer MC samples in a local structure covered by the S-WANS behaviors. However, a steep decrease in the ΔI(q)c–1 data starts at q ∼ 1.5 nm–1, which is slightly lower than that of MC(1.8:23). Since the solid lines in Figure 1b,c represent the q dependencies of the form factors, P(q), of rigid rods with d = 0.9 and L = 230 nm, and d = 1.1 and L = 430 nm, respectively, calculated using SasView,22 and reasonably fit the ΔI(q)c–1 data, the essential reason for the decrease in ΔI(q)c–1 at lower q values than the MC(1.8:23) sample seems to be an increase in the d value with increasing Mw. These L values are determined in the later section. Agreement between ΔI(q)c–1 data and theoretical form factors for rectangular columns with w1 = 1.0 and w2 ≤ 0.3 nm, as seen in Figure 1b, and w1 = 1.6 and w2 ≤ 0.3 nm, as seen in Figure 1c, is also recognized in the S-WANS behavior as well as that of rods. Any w2 values smaller than 0.3 nm provided the form factor, P(q), which was essentially the same as that obtained with w2 = 0.3 nm in a q range less than 15 nm, for rectangular columnar particles with the fixed L and w1 values. Although one cannot determine which model is more suitable to describe the structure of MC molecules in aqueous solution, the enlargement of the cross-sectional dimension for rodlike particles formed by MC molecules in aqueous solution with increasing Mw values is indubitable.

Chatterjee et al.23 carried out SANS experiments in D2O solutions of MC samples with Mw = 410 and DS = 1.9, and with Mw = 53 kg mol–1 and DS = 1.8 to investigate the gelation mechanisms of MC samples in aqueous solutions. They clearly observed the ΔI(q) ∝ q–1 behavior in a q range from 1.0 × 10–1 to 1.0 nm–1 at temperatures such as 5.8 and 10.9 °C, which were sufficiently lower than gelation temperatures of 43.6 and 57.4 °C, respectively, for the MC samples, as seen in Figure 1a,b. However, they also observed the behavior of ΔI(q) ∝ q∼−2.5 in a lower q range from 1.0 × 10–2 to 5.0 × 10–2 nm–1 in both systems. Although the reasons for such stronger q exponents in their SANS data are not clear at present, the MC sample concentration of c = 1.5 × 10–2 g mL–1 in their experiments is substantially higher than the overlapping concentrations, c*, between MC molecules. The q dependence of structure factors controlled by the interactions between MC molecules at the (not sufficiently low) concentrations would thus be one of the essential reasons for the observed stronger q exponents. Because the SLS experiments cover a q range from 8.86 × 10–3 to 3.31 × 10–2 nm–1 under dilute conditions without the effects of molecular overlap, the exact q dependence of form factors, P(q), for isolated MC molecules describing the overall structure and conformation in aqueous solution will be discussed in detail later.

It is noteworthy that the ΔI(q)c–1 value of the MC(1.8:790)/D2O system, ca 5.0 cm2 g–1, is substantially greater than those of the MC(1.8:23)/D2O, ca 2.0 cm2 g–1, and MC(1.8:270)/D2O, ca 2.5 cm2 g–1, systems at a constant q value of 1.0 nm–1, as seen in Figure 1. If rod particles dissolved in D2O possess the same diameter, d, and different particle lengths, L, the q dependence of ΔI(q)c–1 value does not depend on L (or Mw) in a q range sufficiently higher than L–1. The fact that the ΔI(q)c–1 values for the different MC samples at q = 10 nm–1 (≪ L–1) are not identical to one another, as seen in Figure 1, suggests the variation of d (or w1) depending on the Mw values especially for the high Mw MC samples examined in this study such as MC(1.8:790).

Because the ΔI(q)c–1 data obtained at c values lower than c* are poorly scattered, as shown in Figure 1b,c, the presence of broad interference peaks at q** ∼ 6.0 nm–1 is not obvious. However, the ΔI(q) data for MC(1.8:270) at c = 1.0 × 10–2 g mL–1 clearly demonstrate the existence of the two peaks at the q values identical to that for MC(1.8:23), as seen in Figure 1a. The highly extended conformation of MC molecular chains demonstrating a spacing, δ**, related to the repeating distance of cellobiose of ca 1.0 nm corresponds to q**.15 The distance between two MC molecular chain portions facing each other due to the folding structure formed by the hydrogen bonds between the remaining hydroxy groups, as schematically depicted in Figure 2a, corresponds well to another periodic spacing, δ*, related to q* in MC samples possessing lower Mw value than ca 100 kg mol–1.15 Intermolecular periodicities close to 0.4 nm are usually observed in the reported crystalline structure of cellulose II.24 Because these interference peaks were always observed irrespective of the Mw values, the hairpin-like structure seems to be a fundamental conformation for the MC molecules in aqueous solution for all the samples examined.

Figure 2.

Figure 2

Open in a new tab

Schematic depiction of the particle structure possibly formed by the MC samples in aqueous solution: a one-time folded hairpin-type particle in a lower Mw range (a), a randomly coagulated bundle structure of hairpin-like parts in parallel with lL–1 = 6 (b), and a sequential two dimensional array of hairpin-like parts formed by a highly extended molecular chain with lL–1 = 5 (c). Small rectangular columns constructing each large particle described in (b,c) represent extended molecular chain parts of MC molecules seen in (a).

The cross-sectional enlargement of the formed rodlike structure with increasing Mw results from the increasing molecular chain numbers per the cross section of the formed particles, that is, bundle formation of hairpin-like parts. In the next section, we will determine a ratio between the average molecular contour length (l) and the average particle length (L), lL–1, for each MC sample, assuming the rigid rod model.15 The determined lL–1 value starts from approximately 2 at lower Mw values and increases up to 4.9 at the highest value of Mw = 790 kg mol–1. These results strongly support the one-folded hairpin-like particle structure formation of highly extended molecular chains, as seen in Figure 2a, for MC samples with low Mw values.15 Very recently, the formation of a two dimensional array of hairpin-like parts to construct highly elongated rectangular columnar particles similar to the structure, as seen in Figure 2c, was also found in poly(vinylidene fluoride) (PVDF) solution dissolved in N-methylpyrrolidone (NMP).25 Referring the particle structure formed by PVDF molecules, we speculate that the increase in the lL–1 ratio with increasing Mw leads to at least two possible developments in the formed particle structure: a randomly coagulated bundle structure of a couple of hairpin-like parts in parallel formed by a highly extended molecular chain with some folding points, as schematically depicted in Figure 2b, and a sequential two-dimensional array of hairpin-like parts formed by a highly extended molecular chain, as seen in Figure 2c. The former structure corresponds to the rodlike structure, and the latter corresponds to the rectangular columns assumed above. When the interaction between the formed hairpin-like parts is not so strong as to form the sequential two dimensional arrays shown in Figure 2c, randomly coagulated bundles, as seen in Figure 2b, will be constructed. The reason for the formation of bundles of hairpin-like parts, as seen in Figure 2b,c, is the hydrophobic interactions and hydrogen bond formation between the parts using the remaining hydroxyl groups on the MC molecular chains. The hydrophobic interaction is also important for intermolecular associative behavior of MC molecules in aqueous solution related to the gelation mechanisms of aqueous MC systems.26

Rodlike particles are formed by isolated MC molecules at 25 °C in dilute aqueous solutions, as described in this study. Isolated rodlike MC particles would gather into bundles to make long fibrils due to the hydrophobing of the surface of MC rodlike particles and also interparticle hydrogen bond formation caused by the dehydration of MC molecules at higher temperatures than, for example, 40 °C, as proposed by previous studies.17,18,26 When the formed long fibrils of MC molecules contact each other at high temperatures, the contact points will result in cross-linking points inducing the gelation of the systems due to the hydrogen bond formation.

SLS Behaviors

To probe structure of particles formed by MC molecules on the scale larger than that covered by the S-WANS experiments, SLS measurements were quite useful. The excess Rayleigh ratios (Rθ) from the solvent, water, were determined at each θ in the SLS measurements. The optical constant (K) of the SLS apparatus was determined using a dn/dc value of 0.134 mL g–1. 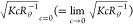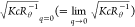As the distributions of the molar masses of the investigated MC and HpMC samples were not exceptionally sharp, the so-called Berry plot,27,28Inline graphic versus q2 and Inline graphic versus c, was used to determine the weight average molar masses, Mw, and the radii of gyration, Rg, of the samples instead of the Zimm plot.29 The Berry plots obtained for aqueous solutions of MC(1.8:270) are shown in Figure 3 as typical results. 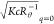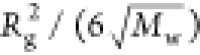The processes in which Inline graphic and Inline graphic data were determined are summarized in the Supporting Information, S1. 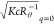According to the standard method, because the intercept and initial slope of a straight line found in Figure 3a indicate the values of Inline graphic and Inline graphic, respectively, Mw and Rg can be determined to be 270 kg mol–1 and 65 nm, respectively. The straight line obviously deviates from the Inline graphic data in a high q range, as observed in Figure 3a. On the other hand, from the intercept of a straight line shown in Figure 3b indicating Mw–0.5, the value of Mw = 270 kg mol–1 was confirmed. Moreover, the second Virial coefficient (A2) can be obtained as 8.8 × 10–4 mol mL g–2 from the slope of a straight line, as seen in Figure 3b, since the slope theoretically represents the value of A2Mw0.5. According to the same procedures, the values of Mw, Rg, and A2 were determined for each MC sample.

Figure 3.

Figure 3

Open in a new tab

Dependencies of 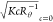Inline graphic data on q2 (a) and Inline graphic on c (b) for aqueous solutions of MC(1.8:270) at 25 °C.

Figure 4a shows the Mw dependence of Rg for the MC samples in aqueous solution. If one would like to approximately describe the relationship between the parameters using a simple power law, such as Rg ∝ Mwα, an Mw exponent, α, could be determined to be ca 0.67. This value is typical for slightly expanded flexible polymer chains in solution.23 However, the validity of the simple power law seems to be doubtful because the Rg data points seem to have a tendency to increase the slope gradually in a low Mw side, as seen in Figure 4a. In particular, the data points on the lower Mw side show the relationship Rg ∝ Mw, which means that the MC molecules with Mw values lower than ca 100 kg mol–1 simply behave as rigid rods in aqueous solution. The widely accepted idea that water-soluble MC samples behave as semi-flexible or random coil-like polymer chains at sufficiently high Mw should be reconsidered, considering the S-WANS experimental fact demonstrating an increase in the diameter of the local rigid-like structure with increasing Mw, as discussed above.

Figure 4.

Figure 4

Open in a new tab

Dependencies of Rg, L, and LRg–1 on Mw (a) and A2 and lL–1 on Mw (b) for aqueous solutions of the MC samples at 25 °C.

A substantial decrease in the A2 data observed at a higher Mw than ca 300 kg mol–1, as seen in Figure 4b, means a decrease in repulsive interparticle interactions, and in other words, an increase in attractive interparticle interactions.27−29 It is interesting to note that the proportional relationship observed between Rg and Mw starts to deviate downwardly in an Mw range similar to that for the beginning of a decrease in the A2 value, as determined from Figure 4a,b.

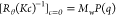Here, we analyze the overall shape of MC molecules in aqueous solution employing a rigid rod particle model21 and a rectangular columnar model30 based on the obtained q dependencies of Inline graphic data that were calculated from the intercepts of Berry plots; Inline graphic. Because the relationship Inline graphic holds theoretically, the q dependence of [Rθ(Kc)−1]c=0 essentially represents that of the particle form factor, P(q). Consequently, if one finds the correct particle form factor, P(q), agreement between [Rθ(Kc)−1]c=0 data and MwP(q) would be confirmed over the entire q range covered by both SLS and S-WANS techniques. In curve fit procedures of the MwP(q) to [Rθ(Kc)−1]c=0 data, assuming the rigid rod and rectangular columnar models, the multipurpose software, SasView, was used again.

The determined best fit MwP(q) curves for each MC sample are shown in Figure 5. The particle lengths, L, necessary to describe the best fit MwP(q) curves are also summarized in Table 1 with the estimated uncertainty of ±5%. The diameters, d, for rods and widths, w1 and w2, for rectangular columns used to calculate the best fit form factors, P(q), were the values that had been determined and are summarized in Table 1 in the S-WANS data analysis section above to discuss the local structure of the formed particles. In fact, if one uses particle diameter and width values that are a few times greater than the values shown in Table 1 to calculate MwP(q) curves, their q dependencies observed in the q range covered by the SLS measurements do not change at all. We only show the q dependencies of the MwP(q) curves calculated with d values, as seen in Table 1. The reasonable agreement between the [Rθ(Kc)−1]c=0 data with error bars and MwP(q) curves, as seen in Figure 5, assuming the rigid rod model for all the MC samples, strongly suggests that MC molecules construct particles possessing elongated rigid rodlike conformations and structures in aqueous solutions over the entire range of examined Mw values.

Figure 5.

Figure 5

Open in a new tab

Dependencies of 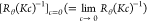Inline graphic data and MwP(q) on q for aqueous solutions of the MC samples at 25 °C. The assumed diameters, d, for the rod models are shown in the figure.

Table 1. Codes, the Weight Average Molar Masses, Mw, the Radii of Gyration, Rg, the Particle Length, L, the Contour Length, l, the Ratio of l/L, the Particle Diameters, d, the Particle Major and Minor Widths, w1 and w2, the Translational and Rotational Diffusion Constants, Dt and Dr, the Intrinsic Viscosity, [η], and the Hydrodynamic Radii, Rh, for the Examined MC Samples.

code Mw/kg mol–1a Rg/nma L/nma l/nm l/L d/nm w1/nm w2/nm Dt/m2 s–1 Dr/s–1 Rh/nm [η]/mL g–1
MC(1.8:23) 23.0 11 39 61.4 1.6 0.7a 0.7a ≤0.3 5.2 × 10–11   4.7 44.0
MC(1.8:54) 54.0 21 75 144 1.9 0.7a 0.7a ≤0.3 3.1 × 10–11   7.9 130
MC(1.8:115) 115 38 135 306 2.3 0.8a 0.8a ≤0.3 2.0 × 10–11   12 260
MC(1.8:206) 206 51 190 550 2.9       1.6 × 10–11   16 360
MC(1.8:270) 270 65 230 720 3.1 0.9b 1.0b ≤0.3 1.2 × 10–11 2.0 × 103 20 530
MC(1.8:420) 420 82 300 1120 3.7       1.0 × 10–11 1.1 × 103 25 610
MC(1.8:790) 790 120 430 2110 4.9 1.1c 1.6c ≤0.3 7.0 × 10–12 3.3 × 102 35 840
Open in a new tab
a

Containing the uncertainty of ±5%.

b

Containing the uncertainty of ±7%.

c

Containing the uncertainty of ±10%.

Figure 4a also shows the Mw dependence of the ratio of LRg–1, which is roughly described to be a constant value close to 3.5 irrespective of the Mw values. Because the relationship L2 = 12Rg2 (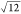Inline graphic = 3.46) holds for rigid long rods, the fact that LRg–1 ∼ 3.5 reveals that the MC samples behave as rigid rods in aqueous solution irrespective of the Mw values from the SLS behavior viewpoint.22 However, we must emphasize another important folding characteristic in the MC molecules related to an increase in the diameters of the formed rigid rod particles with increasing Mw (cf Table 1 and Figure 2). Because the repeating length of the fundamental glucopyranose unit has been known to be ca 0.5 nm, one can calculate the weight average molecular contour length, l, of MC molecules from their Mw values. In accordance with the folding structure of elongated MC molecule chains schematically depicted in Figure 2, a folding number for MC molecules is determined as lL–1, which represents “the average number of MC molecular chains per cross section” of the formed MC particles in aqueous solution. The dependence of the folding number, lL–1, on the Mw value is also plotted in Figure 4b. Because the lL–1 values seem to maintain a constant value of ca 2 in a Mw range lower than 100 kg mol–1 and show steep increase with increasing Mw, the increase in diameter of the formed rigid rods or rectangular columns clearly results from that in the lL–1 values. Therefore, although the MC samples show a change in folding number, lL–1, with increasing Mw, they maintain their rigid rodlike or rectangular column-like structure over the entire range of examined Mw values.

The examined MC samples demonstrate cloud points, for example, 37 °C significantly lower than those of other water-soluble chemically modified cellulose samples. The small A2 values of the MC samples with high Mw observed in this study suggest relatively strong attractive interparticle interactions. It is likely that these observations are induced by the characteristics of the formed rodlike particles. Fortunately, the curve fit analysis could be successfully applied to all the MC samples examined in this study. However, it is possible that the analysis cannot be applied MC samples with Mw > 103 kg mol–1 due to the non-negligible contribution of flexibility in the formed particles, even if rodlike shape particles are formed in the MC samples.

DLS Behaviors

The autocorrelation function of the light electric field (E (q, t)) scattered by dispersed particles in a liquid medium as functions of scattering vector, q, and time (t) defined as g1(t) = ⟨E*(q,0)E(q,t)⟩, where the asterisk indicates complex conjugate, is related to the autocorrelation function of the light intensity (I(q, t)) scattered by dispersed particles defined as g2(t) = ⟨I(q,0)I(q,t)⟩ via the so-called Siegert equation given by g2(t) = 1 + a|g1(t)|2, where a represents a certain constant value depending on the apparatus used.31 According to the standard DLS theory, the first cumulant of 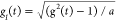Inline graphic defined as 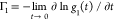Inline graphic is directly related to the average translational diffusion coefficient (Dt) of the dispersed particles in the liquid medium in the manner of Γ1 = q2Dt.31 This consideration is valid only for smaller particles with characteristic sizes less than q–1. In the case of larger anisotropic particles such as rods, one should use the relationship 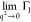Inline graphic=Inline graphicto evaluate Dt values precisely because the contribution of rotational diffusion processes of particles cannot be ignored in a higher q range.

Figure 6a,b demonstrates the typical q2 dependencies of the obtained first cumulants, Γ1, for the short MC(1.8:54) and the longest MC(1.8:790) samples, respectively. Although the Γ1 data of MC(1.8:54) have a constant slope showing a Dt value ca 2.9 × 10–11 m2 s–1 over the entire q2 range examined irrespective of the concentration, c, that of MC(1.8:790) seems to have two straight parts. Dt can be evaluated from the initial slope, 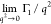Inline graphic, of the Γ1 data to be Dt = 7.0 × 10–12 m2 s–1 for MC(1.8:790). In addition to this initial proportional part, the Γ1 data of MC(1.8:790) possess the second straight part, which has the identical slope to the Dt value, in a higher q2 range, as seen in Figure 6b. Berne et al.31 suggested that the intercept of an extrapolation of the straight part of the Γ1 data found in higher q2 range provides six times the rotational diffusion coefficient (Dr) for large anisotropic particles. Some experimental results verified this idea.32−34 According to them, the Dr value can be evaluated to be 3.3 × 102 s–1 for MC(1.8:790) from the intercept of a broken straight line, as seen in Figure 6b. In all the MC samples, the Dt values could be determined from the (initial) slopes of the Γ1 data, whereas the Dr values were determined only for the longest three MC samples. Although depolarized dynamic light scattering (DLS) experiments31 are known as the most reliable method to determine Dr values for particles with anisotropic structures and were tried in this study, the observed scattering intensities under the depolarized condition were too low to determine Dr values in the aqueous solutions of MC samples examined in this study. All the determined Dt and Dr values and the hydrodynamic radii (Rh) calculated from the Dt values using the Stokes-Einstein relationship, Rh = kBT(6πηwDt)−1, where kB, T, and ηw are the Boltzmann constant, the absolute temperature, and water viscosity, are also summarized in Table 1.

Figure 6.

Figure 6

Open in a new tab

Dependencies of the first cumulants, Γ1, on q2 for aqueous solutions of MC(1.8:54) (a) and MC(1.8:790) (b).

The obtained Mw dependencies of the Dt and Dr values are shown in Figure 7. The Dt value decreases with increasing Mw, approximately demonstrating the relationship Dt ∝ Mw–0.5, as usually observed for many flexible polymers in solutions. However, the so-called shape factor (ρ = Rg/Rh) for the MC samples, which approximately shows proportionality to ln(L/d), as clearly seen in Figure 7b, is greater than that for flexible polymer chains such as the constant value of ca 1.56 in good solvents. According to the theoretical consideration, ρ can be described with an equation ρ = 0.18 + 0.58ln(L/d) for long rods with the ratio of L/d > 10, which is shown in Figure 7b.35 Agreement between the theory and experimental ρ data appears to be reasonable. This consideration of the shape factor, ρ, strongly demonstrates that the particles formed in the aqueous solutions of the MC samples behave as rigid elongated rodlike particles.

Figure 7.

Figure 7

Open in a new tab

(a) Dependencies of the translational, Dt, and rotational diffusion coefficient, Dr, on Mw and (b) dependence of the shape factor, ρ, on ln(L/d), circles, or ln(Lη/d), squares, for the MC samples dissolved in aqueous solution. Solid lines represent theoretical calculations, and broken lines mean theoretical calculations, assuming the hydrodynamic particle length Lη = 0.85L in (a).

Here, we discuss the Mw dependencies of Dt and Dr based on the rigid rod particle model. Ortega and García de la Torre35 proposed simple expression methods for theoretical Dt and Dr including numerical parameters as follows.

graphic file with name ao2c01859_m018.jpg 1
graphic file with name ao2c01859_m019.jpg 2

where Ct and Cr are the numerical factors described by polynomials of the ratio of L/d.35 The solid and broken lines observed in Figure 7a represent the Mw dependencies of theoretically calculated Dt and Dr, respectively, substituting the determined L value for each MC sample into eqs 1 and 2. Although the numbers of Dr data points are not sufficient to discuss the formation of the rigid rod particles in detail, the reasonable agreement between theory and experimental Dt (and Dr) data clearly observed in Figure 7a reveals that the MC samples form elongated rigid rodlike particles irrespective of Mw from the viewpoint of Dt data.

Viscometric Behaviors

The Mw dependence of [η] for the MC samples dissolved in aqueous solution is shown in Figure 8 and Table 1. If one neglects the data of the longest MC(1.8:790) sample, a Mark–Houwink–Sakurada-type expression such as [η] ∝ Mw0.9–1.0 can be approximately obtained forcibly. However, it seems that the classical Mark–Houwink–Sakurada expression does not fit our data as we observe a changing structure with increasing Mw, that is, the folding number, lL–1, and particle diameter, d, change with increasing Mw, as discussed above. On the low Mw side, the [η] data seem to have a large slope close to ca 1.7, that is, [η] ∝ Mw1.7, which is a typical value for rigid rod particles.35,36 Therefore, we analyze the Mw dependence of the [η] data based on the idea that rigid elongated rodlike particles are formed in this system.

Figure 8.

Figure 8

Open in a new tab

Mw dependence of [η] for the MC samples dissolved in aqueous solution. The slope of the straight line is 1.7. Solid and broken curves indicate theoretical calculations using eq 3, assuming Lη = L for [η]cal1 and Lη = 0.85L for [η]cal2, respectively.

According to the theoretical prediction, the intrinsic viscosity [η] of rigid rod particles with the molar mass, Mw, length, L, and a diameter, d, is given using eq 3.35,37

graphic file with name ao2c01859_m020.jpg 3

where NA and Cη represent Avogadro’s number and a numerical constant showing hydrodynamic interactions described by polynomials of the ratio L/d.35 The solid line observed in Figure 8 demonstrates the Mw dependence of the theoretically calculated [η]cal1 by directly substituting the L and d values determined by the SLS measurements into eq 3 at each Mw value. In the case of the examined MC samples, the L/d values were greater than 30 even for the shortest MC(1.8:23) sample. When the L/d value has such large numbers, the numerical parameter, Cη, approaches a constant value of ca −0.93.35 We used the relationship Cη = −0.93 in this study. Although agreement between the theoretical solid line and experimental [η] data is not as good, the solid line has a similar Mw dependence to that qualitatively observed in the [η] data. On the other hand, the broken line, as shown in Figure 8, indicates the [η]cal2 curve theoretically calculated via eq 3, assuming that the hydrodynamically effective particle length (Lη) is not identical to L but 0.85L.25 Because the agreement between the [η]cal2 and [η] data in Figure 8 appears reasonable, the presence of rodlike particles is certain in aqueous solutions of the examined MC samples. If Lη = 0.85L is assumed via eqs 1 and 2, agreement between the theoretical calculations and data is reasonably maintained, as seen in Figure 7a,b. Therefore, it seems that hydrodynamically, the particle length behaves to be shorter than that determined by the SLS techniques by approximately 15%. A similar difference between the Lh and L values was also recently reported in PVDF/NMP solution systems, in which PVDF molecules form highly elongated rigid rodlike particles.25 Consequently, the viscometric data, as well as other experimental techniques such as the SLS and DLS measurements, also revealed the formation of elongated rigid rodlike particles in the MC samples.

Conclusions

S-WANS experiments revealed that the local structure of MC ether samples with a DS of 1.8 dissolved in aqueous solution is reasonably explained with rodlike shape particles, in which MC molecular chains are elongated and folded to show weak periodicities of approximately 0.4 and 1.0 nm. The shorter spacing corresponds to the length of a structural repeating unit, cellobiose, and the other to the distance between facing molecular chain portions in the rodlike structure. The diameter, d, of the formed local rodlike structure increases gradually with increasing average molar mass, Mw.

The results of SLS and DLS measurements were rationally described with the idea that the rodlike local structure is extended to the overall particle structure of the MC samples dissolved in aqueous solution irrespective of Mw over the entire Mw range examined. Because the molecular chain folding number in the formed highly elongated rodlike particles is altered with increasing Mw, the Mw dependence of Rg does not follow the relationship Rg ∝ Mw, which is valid in simple rigid rod particles for which lengths, L, are proportional to Mw. However, the formed particles have a rigid rodlike structure that clearly shows the evidential relationship L2 = 12Rg2 irrespective of Mw.

Reasonable agreement between the intrinsic viscosity, [η], data, and the theoretical calculation, assuming the presence of rigid rods, also supports the formation of elongated rigid rodlike particles in the MC samples irrespective of Mw..

Acknowledgments

All the MC ether samples examined in this study were kindly supplied by Shin-Etsu Chemical Co. Ltd. (Tokyo), and this work was partially supported by the same company. We would like to thank Shingo Niinobe of Shin-Etsu Chemical Co. Ltd. and Dr. Kazuhisa Hayakawa, who previously worked for the same company, for their kind collaboration on this study. The S-WANS experiments at the Materials and Life Science Experimental Facility of the J-PARC were performed under a user program (Proposal no. 2020A00158).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c01859.

  • Procedures to determine Inline graphic data at each q value for some typical MC samples dissolved in aqueous solution and dependencies of Inline graphic data on q2 and Inline graphic on c for aqueous solutions of MC samples at 25 °C other than MC(1.8:270) (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao2c01859_si_001.pdf (297.9KB, pdf)

References

  1. Klemm D.; Heublein B.; Fink H.-P.; Bohn A. Cellulose: Fascinating Biopolymer and Sustainable Raw Material. Angew. Chem., Int. Ed. 2005, 44, 3358–3393. 10.1002/anie.200460587. [DOI] [PubMed] [Google Scholar]
  2. Nishiyama Y.; Langan P.; Chanzy H. Crystal Structure and Hydrogen-Bonding System in Cellulose Iβ from Synchrotron X-ray and Neutron Fiber Diffraction. J. Am. Chem. Soc. 2002, 124, 9074–9082. 10.1021/ja0257319. [DOI] [PubMed] [Google Scholar]
  3. Nishiyama Y.; Sugiyama J.; Chanzy H.; Langan P. Crystal Structure and Hydrogen Bonding System in Cellulose Iα from Synchrotron X-ray and Neutron Fiber Diffraction. J. Am. Chem. Soc. 2003, 125, 14300–14306. 10.1021/ja037055w. [DOI] [PubMed] [Google Scholar]
  4. Li Y.; Liu X.; Zhang Y.; Jiang K.; Wang J.; Zhang S. Why Only Ionic Liquids with Unsaturated Heterocyclic Cations Can Dissolve Cellulose: A Simulation Study. ACS Sustainable Chem. Eng. 2017, 5, 3417–3428. 10.1021/acssuschemeng.7b00073. [DOI] [Google Scholar]
  5. Kamide K.Cellulose and Cellulose Derivatives; Molecular Characterization and its Applications; Elsevier: Amsterdam, 2005; Chapter. 2&3. [Google Scholar]
  6. Klemm D.; Philipp B.; Heinze T., Heinze U.; Wagenknecht W.. Comprehensive Cellulose Chemistry: Volume 2 Functionalization of Cellulose; Wiley-VCH Verlag GmbH: Weinheim: 1998: Chapter 4. [Google Scholar]
  7. Wuestenberg T.Cellulose and Cellulose Derivatives in the Food Industry: Fundamentals and Applications; John Wiley & Sons, 2014; Chapter 5. [Google Scholar]
  8. Knapen E.; Van Gemert D. Cement hydration and microstructure formation in the presence of water-soluble polymers. Cem. Concr. Res. 2009, 39, 6–13. 10.1016/j.cemconres.2008.10.003. [DOI] [Google Scholar]
  9. Seddiqi H.; Oliaei E.; Honarkar H.; Jin J.; Geonzon L. C.; Bacabac R. G.; Klein-Nulend J. Cellulose and its derivatives: towards biomedical applications. Cellulose 2021, 28, 1893–1931. 10.1007/s10570-020-03674-w. [DOI] [Google Scholar]
  10. Podczeck F.; Jones B.. Pharmaceutical Capsules, 2nd ed.; Pharmaceutical Press: London, 2004; Chapter 3. [Google Scholar]
  11. Saito M. Wormlike Chain Parameters of Cellulose and Cellulose Derivatives. Polym. J. 1983, 15, 213–223. 10.1295/polymj.15.213. [DOI] [Google Scholar]
  12. Lodge T. P.; Maxwell A. L.; Lott J. R.; Schmidt P. W.; McAllister J. W.; Morozova S.; Bates F. S.; Li Y.; Sammler R. L. Gelation, Phase Separation, and Fibril Formation in Aqueous Hydroxypropylmethylcellulose Solutions. Biomacromolecules 2018, 19, 816–824. 10.1021/acs.biomac.7b01611. [DOI] [PubMed] [Google Scholar]
  13. McAllister J. W.; Schmidt P. W.; Dorfman K. D.; Lodge T. P.; Bates F. S. Thermodynamics of Aqueous Methylcellulose Solutions. Macromolecules 2015, 48, 7205–7215. 10.1021/acs.macromol.5b01544. [DOI] [Google Scholar]
  14. Keary C. M. Characterization of METHOCEL cellulose ethers by aqueous SEC with multiple detectors. Carbohydr. Polym. 2001, 45, 293–303. 10.1016/s0144-8617(00)00263-0. [DOI] [Google Scholar]
  15. Arai K.; Horikawa Y.; Shikata T.; Iwase H. Reconsideration of the conformation of methyl cellulose and hydroxypropyl methyl cellulose ethers in aqueous solution. RSC Adv. 2020, 10, 19059–19066. 10.1039/d0ra03437a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Bodvik R.; Dedinaite A.; Karlson L.; Bergström M.; Bäverbäck P.; Pedersen J. S.; Edwards K.; Karlsson G.; Varga I.; Claesson P. M. Aggregation and network formation of aqueous methylcellulose and hydroxypropylmethylcellulose solutions. Colloids Surf., A 2010, 354, 162–171. 10.1016/j.colsurfa.2009.09.040. [DOI] [Google Scholar]
  17. Morozova S. Methylcellulose fibrils: a mini review. Polym. Int. 2020, 69, 125–130. 10.1002/pi.5945. [DOI] [Google Scholar]
  18. Coughlin M. L.; Liberman L.; Ertem S. P.; Edmund J.; Bate F. S.; Lodge T. Methyl cellulose solutions and gels: fibril formation and gelation properties. Prog. Polym. Sci. 2021, 112, 101324. 10.1016/j.progpolymsci.2020.101324. [DOI] [Google Scholar]
  19. Arai K.; Shikata T. Hydration/Dehydration Behavior of Cellulose Ethers in Aqueous Solution. Macromolecules 2017, 50, 5920–5928. 10.1021/acs.macromol.7b00848. [DOI] [Google Scholar]
  20. Takata S.; Suzuki J.; Shinohara T.; Oku T.; Tominaga T.; Ohishi K.; Iwase H.; Nakatani T.; Inamura Y.; Ito T.; Suzuki K.; Aizawa K.; Arai M.; Otomo T.; Sugiyama M. The Design and q Resolution of the Small and Wide Angle Neutron Scattering Instrument (TAIKAN) in J-PARC. JPS Conf. Proc. 2015, 8, 036020. [Google Scholar]
  21. Fournet G. Étude théorique et expérimentale de la diffusion des rayons X par les ensembles denses de particules. Bull. Mineral. 1951, 74, 37–172. 10.3406/bulmi.1951.4736. [DOI] [Google Scholar]
  22. Doucet M.et al. SasView Version 5.0.3, Zenodo, 2021, https://www.sasview.org/.
  23. Chatterjee T.; Nakatani A. I.; Adden R.; Brackhagen M.; Redwine D.; Shen H.; Li Y.; Wilson T.; Sammler R. L. Structure and Properties of Aqueous Methylcellulose Gels by Small-Angle Neutron Scattering. Biomacromolecules 2012, 13, 3355–3369. 10.1021/bm301123a. [DOI] [PubMed] [Google Scholar]
  24. Langan P.; Nishiyama Y.; Chanzy H. X-ray Structure of Mercerized Cellulose II at 1 Å Resolution. Biomacromolecules 2001, 2, 410–416. 10.1021/bm005612q. [DOI] [PubMed] [Google Scholar]
  25. Nohara Y.; Saiki E.; Shikata T. Long Two-Dimensional Folding Chain Structure Formation of Poly(vinylidene fluoride) in Solutions of a Polar Solvent, N-Methylpyrrolidone. ACS Appl. Polym. Mater. 2022, 4, 1255–1263. 10.1021/acsapm.1c01630. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Huang W.; Dalal I. S.; Larson R. G. Analysis of Solvation and Gelation Behavior of Methylcellulose Using Atomistic Molecular Dynamics Simulations. J. Phys. Chem. B 2014, 118, 13992–14008. 10.1021/jp509760x. [DOI] [PubMed] [Google Scholar]
  27. Glatter O.Scattering Methods and their Application in Colloid and Interface Science; Elsevier: Amsterdam; 2018, Chapters 9 & 10. [Google Scholar]
  28. Berry G. C. Thermodynamic and Conformational Properties of Polystyrene. I. Light-Scattering Studies on Dilute Solutions of Linear Polystyrenes. J. Chem. Phys. 1966, 44, 4550–4564. 10.1063/1.1726673. [DOI] [Google Scholar]
  29. Zimm H. B. The Scattering of Light and the Radial Distribution Function of High Polymer Solutions. J. Chem. Phys. 1948, 16, 1093–1099. 10.1063/1.1746738. [DOI] [Google Scholar]
  30. Nayuk R.; Huber K. Formfactors of Hollow and Massive Rectangular Parallelepipeds at Variable Degree of Anisometry. Z. Phys. Chem. 2012, 226, 837–854. 10.1524/zpch.2012.0257. [DOI] [Google Scholar]
  31. Berne B.; Pecora R.. Dynamic Light Scattering; Wiley: New York, 1976; Chapter 8. [Google Scholar]
  32. Schillen K.; Brown W.; Johnsen R. M. Micellar Sphere-to-Rod Transition in an Aqueous Triblock Copolymer System. A Dynamic Light Scattering Study of Translational and Rotational Diffusion. Macromolecules 1994, 27, 4825–4832. 10.1021/ma00095a025. [DOI] [Google Scholar]
  33. Arai K.; Horikawa Y.; Shikata T. Transport Properties of Commercial Cellulose Nanocrystals in Aqueous Suspension Prepared from Chemical Pulp via Sulfuric Acid Hydrolysis. ACS Omega 2018, 3, 13944–13951. 10.1021/acsomega.8b01760. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Hasegawa H.; Horikawa Y.; Shikata T. Cellulose Nanocrystals as a Model Substance for Rigid Rod Particle Suspension Rheology. Macromolecules 2020, 53, 2677–2685. 10.1021/acs.macromol.9b02641. [DOI] [Google Scholar]
  35. Ortega A.; García de la Torre J. Hydrodynamic properties of rodlike and disklike particles in dilute solution. J. Chem. Phys. 2003, 119, 9914–9919. 10.1063/1.1615967. [DOI] [Google Scholar]
  36. Yanaki T.; Norisuye T.; Fujita H. Triple Helix of Schirophyllum commune Polysaccharide in Dilute Solution. 3. Hydrodynamic Properties in Water. Macromolecules 1980, 13, 1462–1466. 10.1021/ma60078a019. [DOI] [Google Scholar]
  37. Dio M.; Edwards S. F.. The Theory of Polymer Dynamics; Clarendon Press: Oxford, 1986; Chapter 8. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao2c01859_si_001.pdf (297.9KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES