Significance
Nearly all fluid flows are turbulent, exhibiting diverse spatial and temporal structures. Turbulence is chaotic, where small external disturbances can lead to remarkably different behavior as time evolves. Despite these properties, turbulence can exhibit flow patterns that persist for substantial durations of time, known as coherent structures. Here, we develop a method for detecting when turbulence resembles these coherent flow structures. Using this method, we conclusively show that the organization of turbulence in both space and time is well captured by these structures. These results lay the foundation for representing turbulence in terms of coherent structures and leveraging their persistence in time to overcome the devastating effects of chaos on our ability to predict, control, and engineer fluid flows.
Keywords: turbulence, prediction, coherent structures, nonlinear dynamics
Abstract
Despite a long and rich history of scientific investigation, fluid turbulence remains one of the most challenging problems in science and engineering. One of the key outstanding questions concerns the role of coherent structures that describe frequently observed patterns embedded in turbulence. It has been suggested, but not proved, that coherent structures correspond to unstable, recurrent solutions of the governing equation of fluid dynamics. Here, we present experimental and numerical evidence that three-dimensional turbulent flow tracks, episodically but repeatedly, the spatial and temporal structure of multiple such solutions. Our results provide compelling evidence that coherent structures, grounded in the governing equations, can be harnessed to predict how turbulent flows evolve.
Both engineered and naturally occurring fluid flows are often turbulent and exhibit rich and complicated dynamics. Yet, despite centuries of systematic studies going back to Leonardo da Vinci, numerous open questions remain. Statistical theories (1, 2) brought some success in predicting the universal scaling of energy and momentum transport in high-Reynolds number turbulence, and recent numerical work has observed a scaling to exist even at lower Reynolds numbers (3). Yet quantitative predictions, even for simple properties such as the pressure drop for turbulent pipe flow, remain elusive and require the use of empirical relations (4). Statistical approaches tend to assume isotropic and/or highly symmetric flows, which neglect the important spatial and temporal structure of turbulence (5). In particular, one of the key unexplained mysteries is the role of recurring, recognizable patterns, known as coherent structures (6, 7). Coherent structures can provide a better understanding of turbulence (8), even describing physical mechanisms (9) not captured by statistical distributions. While previous studies have primarily focused on the spatial aspects of coherent structures, coherent structures can be used as building blocks of the temporal behavior of turbulence as well. The attempts to build deterministic models describing the evolution of coherent structures based on various modal decompositions go back many decades (10).
A description of turbulence that incorporates coherent structures requires them to be connected to the governing equations. Development of advanced numerical methods such as Newton–Krylov solvers (11) has enabled the computation of unstable, recurrent solutions of the Navier–Stokes equation. Some of these solutions were found to have spatiotemporal properties similar to the observed coherent structures, which led to the conjecture that coherent structures appear when turbulent flow transiently approaches these solutions. Consequently, such unstable solutions became known as exact coherent structures (ECSs). ECSs provide a direct link between the governing equations and the short-lived patterns frequently observed in turbulent flows. They also make concrete the qualitative picture of turbulence proposed in the 1940s by Eberhard Hopf (12). Inspired by the work of Poincaré on celestial mechanics and chaos (13), Hopf’s picture represents turbulence as coevolving with (shadowing) a repertoire of unstable solutions. Shadowing implies that turbulent flow has spatial and temporal structure mimicking that of (possibly more than one) unstable recurrent solutions to the governing equations.
Most of the prior work exploring the role of exact coherent structures in turbulence focused on traveling waves (TWs) in transitional flows (14), although TWs have been found in flows as high as (15). TWs are equilibria in a comoving reference frame and represent the simplest type of dynamics in systems with continuous spatial symmetries. There is experimental evidence of the role of TWs in the transition from laminar flow to turbulence (16–18); TWs were even found to be visited by turbulent flow in numerical simulations of channel flow (19) and pipe flow (20, 21). However, TWs are too simple to describe the rich temporal dynamics of fluid turbulence. Instead, ECSs that exhibit nontrivial temporal behavior (22, 23) are better suited for this purpose. In particular, relative periodic orbits (RPOs), which are periodic orbits in a comoving reference frame, are thought to play a key role (24). Although previous studies found the flow to instantaneously resemble RPOs in numerical simulation of transitional turbulence (24), it was only recently shown that ECSs describe the temporal evolution as well (25). To date, these findings have not been validated experimentally. We show that unstable, recurrent solutions (i.e., ECSs) play a substantial and persistent role in characterizing the time evolution of experimentally observable turbulence in three spatial dimensions.
To convincingly verify Hopf’s picture of turbulence, it is necessary to compute a collection of ECSs under conditions that fully match those encountered experimentally. This is most conveniently done for a closed flow, where the boundary conditions in the flow direction are naturally periodic. For this reason, the present study focuses on Taylor–Couette flow (TCF) between two concentric, independently rotating cylinders, as shown in Fig. 1. TCF is characterized by four nondimensional parameters. Two are geometrical, and , where h is the height of the fluid annulus and ri and ro are the radii of the inner and outer cylinders, respectively. The other two parameters are the Reynolds numbers, and , where is the gap between the cylinders, ν is the kinematic viscosity of the fluid, and Ωi and Ωo are the angular velocities of the two cylinders.
Fig. 1.
Turbulence is visualized in a laboratory flow between concentric, independently rotating cylinders with radii ri, ro and corresponding angular velocities . Fluid is confined between the cylinders and bounded axially by end caps corotating with the outer cylinder. The red–white–blue colors indicate the fluid’s deviation from the mean azimuthal velocity component at a fixed axial location equidistant () from the axial end caps.
TCF is a canonical flow that has been used to study a wide variety of flow behaviors, including pattern formation (26, 27), transition to turbulence (28–32), and turbulence itself (33–35). The bulk of the previous work was performed in systems with large Γ. In the work presented here, we restrict Γ to be small to allow for direct comparisons between numerics and experiment across the full flow domain. Specifically, we focus on flows driven by counter-rotating cylinders (Rei = 500, ) in a wide-gap (), small-aspect-ratio (Γ = 1) geometry. In the small-aspect-ratio regime () of TCF, there have been several studies with stationary outer cylinder and rotating inner cylinder (36–44); however, only one study examines the co- and counter-rotating scenarios (45), and none investigate turbulence.
As Γ decreases, the end cap effects play a more substantial role than they do at large Γ. In particular, the top and bottom end caps result in a redistribution of angular momentum, which causes the transition away from the laminar base flow to occur at larger values of Rei (46). However, the decrease in Γ does not undermine the three-dimensional nature of the spatiotemporally chaotic flow observed at Reynolds numbers considered in this study, which still exhibits structure over a range of scales in each spatial dimension.
An experimental realization of TCF was constructed with transparent walls, giving optical access to the entire domain of the flow. For visualization, the flow was seeded with neutrally buoyant, fluorescent tracer particles and the plane at was illuminated. Despite having nontrivial structure in the axial direction, we find that shadowing can be characterized sufficiently well by considering the motion in a radial-azimuthal plane at a fixed height along the axis (see Materials and Methods, Experimental Setup for details). The flow was imaged with a camera whose line of sight lies along the cylinders’ axes, and in-plane components of velocity were determined using particle image velocimetry. Direct numerical simulations (DNSs) in the entire flow domain were performed using a pseudospectral solver (47) with boundary conditions exactly matching experiment (48). This correspondence enables a quantitative comparison of numerically computed ECS with experiment.
Rotational symmetry of the Taylor–Couette flow implies that, just like for a pipe or channel flow, most ECSs are expected to take the form of either RPOs or TWs (24). Both types of ECSs satisfy the condition
| [1] |
For RPOs, T is the period of the solution and is the angle by which the solution drifts in the azimuthal direction over one period. The constant angular speed of the comoving frame is then . For TWs, Eq. 1 is satisfied for any and T whose ratio Ω is the drift speed of the solution.
We focused on computing RPOs by analyzing a long, unconstrained turbulent flow obtained through DNS. Nearly recurrent segments of the simulated turbulent trajectory were found by examining minima of the residual,
| [2] |
where . Then, a Newton–Krylov solver is used to converge these segments to solutions of Eq. 1, i.e., exactly recurring flow fields (49).
In general, the set of flow states corresponding to an RPO is a two-torus, Si, in the infinite-dimensional space of flow states (Fig. 2A), known as state space. In the fixed laboratory frame, trajectories lying on Si are quasiperiodic. Any point on the ith RPO (light blue two-torus in Fig. 2B) may be written as , for some and τ. Both coordinates are cyclic, with running from 0 to and τ ranging from 0 to Ti (the solution’s period). To visualize the relationship between the computed ECSs and turbulent flow, we plotted in Fig. 2C each RPO, , using a low-dimensional projection of the state space spanned by the energy and the rate of energy dissipation . Since both and are invariant with respect to rotation, every RPO is represented by a closed curve in this particular projection. Indeed, as we mentioned previously, each RPO becomes a temporally periodic solution in the corotating reference frame.
Fig. 2.
Low-dimensional projections suggest that RPOs, i.e., solutions to the governing equations that recur indefinitely in time, are relevant to turbulence. (A) To demonstrate that RPOs are truly two-tori when rotational symmetry is not reduced, RPO2 is plotted over 80 periods using the coordinates shown, where represents the azimuthal component of the flow velocity and indicates a spatial average. Thus, is the mean azimuthal speed, and [] is the imaginary (real) component of the leading spectral mode. (B) Cartoon depicting how a portion of a turbulent trajectory (solid red curve) shadows, i.e., follows, an RPO (light blue surface) for a period of time. Shown in dark blue is the trajectory belonging to the RPO, which is most similar to the turbulent trajectory. The orange arrow relates a point on the turbulent trajectory to the point closest to it on the torus. (C) Using energy and energy dissipation rate of the flow as projection coordinates, eight RPOs are represented by closed trajectories (shown in color). RPOs appear as closed curves in this projection because both coordinates are rotationally invariant. The chaotic behavior of turbulence is indicated by the distribution (shown in gray) of visits to particular regions of the projection (darker regions have higher likelihood of visitation).
A long turbulent trajectory computed using DNS is shown in Fig. 2C as a histogram, with the grayscale intensity representing the likelihood of visiting different regions of state space. In this low-dimensional projection, we find that the computed RPOs lie in the regions of state space frequently visited by turbulence. Although this fact is consistent with Hopf’s picture of turbulence, it does not by itself demonstrate that turbulent flows evolve similarly to RPOs. If RPOs play an important dynamical role, turbulence will not only approach each RPO, but also shadow it; i.e., the corresponding flows will coevolve in a similar manner for an interval of time before diverging.
The expected duration of shadowing intervals depends on the stability properties of individual RPOs. The more unstable an RPO is compared to its peers, the less frequently its neighborhood is visited by turbulent flow. Moreover, the more unstable a solution is, the shorter the shadowing intervals are. Stability is characterized by the escape rate , where are the unstable Floquet exponents of RPOi. The inverse of the escape rate then gives the characteristic duration of shadowing intervals. The typical value in our system is much shorter than the typical period of an RPO (Table 1), so turbulence is expected to shadow short segments of an RPO before leaving its neighborhood, as illustrated in Fig. 2B.
Table 1.
Properties of RPOs found in TCF for Γ = 1, , and : the temporal period T and shift
| T | Nu | γ | ||
|---|---|---|---|---|
| RPO | 0.196 | 1.043 | 9 | 0.0246 |
| RPO | 0.177 | 0.856 | 7 | 0.0209 |
| RPO | 0.234 | 0.448 | 9 | 0.0260 |
| RPO | 0.200 | 0.199 | 8 | 0.0299 |
| RPO | 0.422 | 0.443 | 7 | 0.0336 |
| RPO | 0.419 | 0.425 | 8 | 0.0358 |
| RPO | 0.164 | 0.481 | 8 | 0.0342 |
| RPO | 0.215 | 5.799 | 8 | 0.0464 |
The dimension of the unstable manifold of each solution, Nu is also shown, as well as the escape time, . Both the period and escape rate have been nondimensionalized using the timescale s, for cylinder gap width d and viscosity ν. Nu includes the 2 marginally stable directions of each solution, along τ and .
We quantify shadowing of RPOi by projecting turbulent flow u onto the coordinate system associated with the corresponding torus Si. We define to be the point on Si closest to a snapshot of turbulent flow at time t, such that
| [3] |
For any initial condition on Si (e.g., any flow field described by the RPO), we will have and with some constant and τ0. For any trajectory passing close to Si, we expect the same relations to be satisfied approximately. Hence, we detect shadowing by searching for intervals where deviations from these two relations are small (specifics can be found in Materials and Methods, Shadowing Criteria).
Shadowing events identified using these criteria are summarized in Fig. 3 for a numerically computed turbulent trajectory over an interval equal to about 300 times the mean RPO period; this interval corresponds to about 270 min in experiment. We find, in validation of Hopf’s picture, that turbulence visits the neighborhoods of all eight RPOs, with each neighborhood visited multiple times. In fact, we observe that turbulence occasionally shadows multiple solutions simultaneously. This should happen, for instance, close to bifurcations in parameter space when two or more distinct but related solutions are themselves almost indistinguishable. Indeed, RPO5 and RPO6 are born from a nearby bifurcation. More generally, turbulence can simultaneously shadow multiple distinct solutions when these solutions also shadow each other for a small portion of their orbits and turbulence shadows these portions. We believe this to be the case for the simultaneous shadowing of solutions other than RPO5 and RPO6. This behavior is often observed in chaotic systems, and here we show it to exist in fluid turbulence as well.
Fig. 3.
Turbulence frequently shadows ECSs. In the graphic, black vertical lines indicate shadowing events—time intervals during which ECSs (RPO1 to RPO8) are being tracked by turbulence obtained from a numerical simulation (Materials and Methods, Shadowing Criteria). The duration of each shadowing event shown is at least one escape time , computed from the unstable Floquet exponents of the corresponding ECS.
To illustrate what shadowing looks like in real space, Fig. 4 illustrates experimentally observed shadowing of RPO1 and RPO7 (Movie S1). For each RPO, Fig. 4 compares four equally spaced snapshots of the flow field in the symmetry midplane that correspond to the RPO and turbulent flow in the experiment. Turbulent flow in this system is characterized by fluctuations that are relatively weak compared to the axisymmetric mean flow . Hence, to visualize the fluctuation, we subtracted this mean from all the flow states. Fig. 4 shows the deviation of the azimuthal flow velocity from its mean. In each observed shadowing event, the turbulent flow’s complex spatial and temporal structure is well characterized by the corresponding RPO.
Fig. 4.
Experimental evidence that turbulence and RPOs, i.e., solutions to the governing equations that recur indefinitely in time, coevolve when our shadowing criteria are met. Turbulence closely follows RPO (Top) and, during a different time interval, tracks RPO (Bottom). In both cases, the color map shows the deviation in the azimuthal component of the velocity from the mean; moreover, the time interval between successive turbulent snapshots is ∼3.5 s, which may be compared to the period, 52 (44) s, and escape time, 6.6 (9.1) s, of RPO (RPO). The flow fields for the RPOs were chosen by first finding the optimal azimuthal orientation and temporal phase τ0 for the entire shadowing event; subsequently, the RPO was evolved in time while holding the azimuthal orientation fixed [i.e., and ].
The results presented here provide the most convincing evidence to date in support of a dynamical description of turbulent flow grounded in the governing equations, as envisioned by Hopf. Turbulent flow does indeed move between neighborhoods of a collection of ECSs, where the evolution of turbulent flow in each neighborhood is well described by corresponding ECSs. Therefore, our work demonstrates that ECSs in the form of RPOs are important in describing the temporal evolution of turbulence.
While a much larger set of ECSs is required for a complete quantitative description of fluid turbulence, even at the relatively low Reynolds numbers considered here, the results of this study are quite significant. They validate several key assumptions of a deterministic description of turbulence that is grounded firmly in the governing equations of fluid dynamics and elucidate the relation of the dynamics of coherent structures to the evolution of turbulent flow. Improved understanding of coherent structures promises to shed additional light on many long-standing problems, including the role and origin of intermittency and the mechanisms of turbulent cascades. Beyond fluid turbulence, a similar framework should be useful for describing complex dynamics in other high-dimensional systems where strong nonlinearities appear, such as plasmas (50), interacting subatomic particles (51), arrhythmic cardiac tissues (52), neural networks (53), and active matter (54).
Materials and Methods
A Quantitative Signature of Shadowing.
To establish the dynamical relevance of an RPO in turbulence, the flows representing both must have similar temporal evolution and spatial orientation. To quantify how closely the RPO is being shadowed, we define two distance metrics
| [4] |
and
| [5] |
whose minima determine the evolution of the coordinates τ and parameterizing the RPO. An example of a turbulent flow in DNSs shadowing an RPO is shown in Fig. 5. In this example, for the range of t where turbulence is shadowing the RPO, there is a clear minimum in that falls along the diagonal and a staircase pattern of minima in , implying the flows are not only similar at one time instant, but both flows have the expected similar orientation and temporal evolution for more than one period. The discrete shifts in the minima of are associated with the rotation of the reference frame by angle once per period of the RPO, so that is expected to be similar to for and .
Fig. 5.
A shadowing event for RPO1 in DNS. The distance metrics (above) and (below) are shown over a time interval including the shadowing event, which corresponds to .
2 Component, Planar Particle Image Velocimetry Is Sufficient.
Unlike TW detection in previous experimental studies, RPO detection requires a measurement that provides spatial structure along the streamwise direction. TWs have spatial and temporal translations that are equivalent, making it possible to detect them by imaging the flow in a fixed plane transverse to the flow and using Taylor’s frozen turbulence hypothesis to reconstruct the spatial variation from the temporal variation. However, RPOs vary independently in space and time, explicitly breaking the Taylor hypothesis. In our system, we find measurement of the streamwise (θ) and radial (r) velocity components in a plane at a fixed height along the axis of rotation provides sufficient spatial and temporal information to detect reliable shadowing events involving RPOs. To illustrate this point, the distance between a turbulent flow in DNS and RPO is shown in Fig. 6. In Fig. 6, a clear correlation exists between distances computed over the entire volume and distances computed with only in-plane velocities obtained from the midplane.
Fig. 6.
The distance D(t) between a turbulent flow in DNS and RPO, during an arbitrary interval, computed using the full, 3 dimensional, 3 components (3D-3C) flow field (solid blue) and the 2 dimensional, 2 components (2D-2C) flow field restricted to the midplane z = 0 (dashed red). Both signals were normalized to allow direct comparison. These normalized signals differ by less than 1% relative error over the interval , indicating that the 2D-2C distance is a good proxy for 3D-3C distances. Here and in main text, time has been nondimensionalized using the timescale , for cylinder gap width d and viscosity ν.
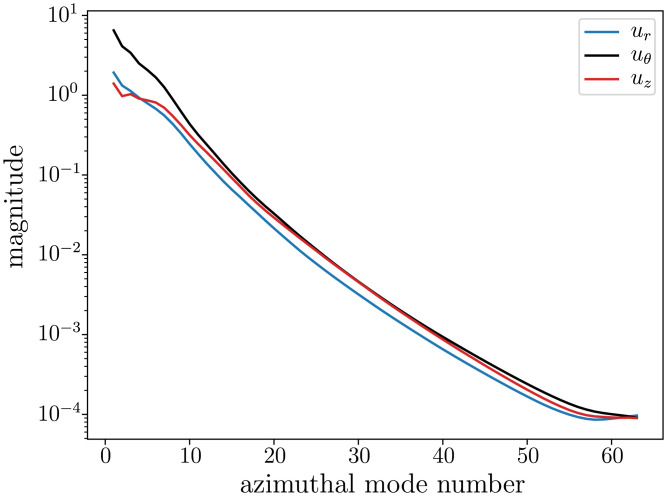
The ability to identify robustly shadowing events with two-dimensional datasets should not be taken to imply that the flow is nearly two-dimensional. Indeed, the small-aspect-ratio Γ implies that end-cap–induced Ekman pumping strongly affects the flow over its entire axial extent. More importantly, as Fig. 7 illustrates, the fluctuations about the mean flow in all three directions have comparable magnitude over a large range of scales, which is typical for three-dimensional turbulent flows. Also, as is typical for turbulent flows, we find the power spectrum to be broadband, without any discernible peaks for any of the three velocity components.
Fig. 7.
Turbulent behavior in all three velocity components is indicated by significant energy in a broad range of azimuthal mode numbers, as illustrated by the time-averaged magnitude of the azimuthal spectral coefficients from numerical simulations at .
Library of Solutions.
Taylor–Couette flow has inherent symmetry with respect to continuous rotations about the z axis, ,
| [6] |
and discrete reflections, Kz,
| [7] |
about the z axis. This implies that the solutions relevant to turbulence are relative solutions, such as RPOs or traveling waves, and preperiodic orbits. A turbulent trajectory was computed for 60 nondimensional time units (equivalent to ), where time is nondimensionalized using the radial momentum diffusion timescale, s. We find that the chaotic set breaks the z-reflection symmetry. That is, there are two z-asymmetric chaotic sets, one the reflected copy of the other, which are observed to be dynamically disconnected. Preperiodic orbits, which would represent orbits lying in both sets, are therefore unlikely to be relevant to turbulent motion. Because of this, we focus on relative solutions exclusively.
Relative solutions were found using an in-house Newton-Generalized Minimum Residual (GMRES) solver (48) that leverages a hookstep algorithm (11). Since Newton’s method is not globally convergent, sufficiently good initial guesses had to be supplied to this solver. To accomplish this, we computed a turbulent trajectory, , and analyzed the recurrence function,
| [8] |
Deep minima of Eq. 8 correspond to moments in which the turbulent trajectory is almost periodic or stationary in the comoving frame. The flow field during these deep minima and their corresponding τ and values are good initial conditions for the solver. These initial conditions are fed into the solver and added to our library of solutions if the relative residual
| [9] |
becomes sufficiently small (. T and represent the period and azimuthal shift of converged solutions. Eight distinct solutions were converged for this parameter regime; their properties are listed in Table 1.
The symmetry-reduced Euclidean distance.
| [10] |
between each of these solutions and the turbulent flow is shown in Fig. 8. The distance was normalized by the radius of the chaotic set
| [11] |
Fig. 8.
The distance between the turbulent DNS trajectory and the eight RPOs, computed using the 3D-3C Euclidean norm. Here, Di is the distance to solution and Σ is the radius of the chaotic set. The threshold below which two flow states are considered close is designated with a dashed black line. While the full dataset spans , only a portion of that interval is shown here, to better illustrate the behavior of the distances, Di.
where denotes a temporal mean. Low (compared with unity) values of indicate instances where turbulence approaches RPO .
Shadowing Criteria.
It has been conjectured that the evolution of turbulent flow over time can be well approximated by a sequence of ECSs. In an effort to validate this picture of fluid turbulence, literature over the past decade has aimed to identify signatures of ECSs in turbulent motion. A large body of work, in both experiment and simulation, has found that the distance Di defined by Eq. 10 generically experiences broad and deep minima (16–18, 21, 23, 55), known as “close passes,” during which turbulence approaches and remains close to a known ECS . While these results support the relevance of ECSs to fluid turbulence, a small value of Di does not automatically imply that the time evolution of turbulence is similar to that of ECS .
In state space, an ECS defines a set Si of all flow states u satisfying . “Shadowing,” which is a stronger condition than “closeness,” requires that turbulence explore Si in a manner consistent with the evolution of a member of the corresponding ECS family when Di is sufficiently small (25). Topologically, Si is a loop (one-torus) for a family of TWs and is naturally parameterized using the angle coordinate . For a family of RPOs , Si is a two-torus that is naturally parameterized using the phase τ and angle . The distance Di from u to Si is a natural transverse coordinate describing the deviation of turbulence from the corresponding family of ECSs. Coordinates τ, , and D then represent a skew-product decomposition (56, 57) of state space in the neighborhood of an RPO, induced by the two continuous symmetry groups: temporal translations and spatial rotations. In this coordinate system, the RPO evolves such that , and Di = 0, where τ0 and are constant for and change discontinuously (by Ti and , respectively) when . Building on Krygier et al. (25), we define shadowing of an RPO using the following three criteria being satisfied simultaneously over a period comparable to solutions’ escape time:
-
•
Turbulent flow remains close to the ECS family ; i.e., is small.
-
•
Turbulent flow follows the same member of the ECS family ; i.e., .
-
•
Turbulent flow evolves at the same rate as the ECS ; i.e., .
Following the notation defined in Krygier et al. (25), Fig. 3 was produced with , and .
Experimental Setup.
The experimental system used in this study was designed and built with the unusual quality of complete optical access to the fully turbulent flow. This makes it possible to directly compare theoretical/numerical predictions with measurements, anywhere in the flow domain. To accomplish this, all surfaces bounding the flow (cylinders, axial end caps) were constructed out of transparent Poly(methyl methacrylate) (PMMA), precision built in house and hand polished to optical quality. The TCF cell is suspended from shafts, allowing both cylinders to rotate independently (shown in Fig. 1) and providing cameras an unobstructed view of the entire TCF cell from below. The cylinders are rotated under computer control using two high-performance stepper motors (Oriental Motors model PKP544N18A with 125,000 steps per revolution), coupled to the cylinders via timing belts. The inner (outer) cylinder radius was chosen to be 50 (70.42) mm; the aspect ratio is set to Γ = 1, such that the height of the cell is equal to the difference in the radii, mm. To remove optical distortion caused by the curved walls, the cell is submerged in a transparent liquid bath. The custom-built, transparent PMMA liquid bath was constructed to encase the inner and outer cylinders, to help stabilize fluctuations in temperature; the temperature is constant to within 10 mK.
Together with careful consideration of the working fluid’s temperature-dependent viscosity, this system provided Re control to better than 1%. Both the working fluid and the liquid bath are index matched to the PMMA walls using an aqueous solution of NH4 SCN, which has a kinematic viscosity close to that of pure water. For the working fluids used in the study, the system dimensions were carefully chosen to minimize the image acquisition sample rate needed to resolve the flow spatially and temporally. This enabled quantitative measurements of the flow using inexpensive machine vision cameras (iDS Model UI-3140CP-M-GL).
Supplementary Material
Acknowledgments
We thank Marc Avila for sharing his Taylor–Couette flow code. We also gratefully acknowledge financial support by Army Research Office under Grants W911NF-15-1-0471 and W911NF-16-10281 and by NSF under Grant CMMI-1725587.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2120665119/-/DCSupplemental.
Data, Materials, and Software Availability
Data that support the key findings of this study (relating to the exact coherent structures and their key properties) have been deposited in Github (https://github.com/cdggt/tcf/tree/main/eta0.71) (49). Some study data are available. Due to their size, experimental datasets and the numerical turbulent trajectory will be available upon request only.
References
- 1.Kolmogorov A. N., The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Cr. Acad. Sci. URSS 30, 301–305 (1941). [Google Scholar]
- 2.Taylor G. I., Statistical theory of turbulence. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 151, 421–444 (1935). [Google Scholar]
- 3.Schumacher J., et al., Small-scale universality in fluid turbulence. Proc. Natl. Acad. Sci. U.S.A. 111, 10961–10965 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Moody L. F., Friction factors for pipe flow. Trans. Asme 66, 671–684 (1944). [Google Scholar]
- 5.Smits A. J., McKeon B. J., Marusic I., High–Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375 (2011). [Google Scholar]
- 6.Hussain A. F., Coherent structures—Reality and myth. Phys. Fluids 26, 2816–2850 (1983). [Google Scholar]
- 7.Jiménez J., Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, 1 (2018). [Google Scholar]
- 8.Schneider T. M., Eckhardt B., Vollmer J., Statistical analysis of coherent structures in transitional pipe flow. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 75, 066313 (2007). [DOI] [PubMed] [Google Scholar]
- 9.Waleffe F., On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900 (1997). [Google Scholar]
- 10.Holmes P., Lumley J. L., Berkooz G., Rowley C. W., Turbulence, Coherent Structures, Dynamical Systems and Symmetry (Cambridge University Press, 2012). [Google Scholar]
- 11.Viswanath D., Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358 (2007). [Google Scholar]
- 12.Hopf E., Abzweigung einer periodischen lösung von einer stationären lösung eines differentialsystems. Ber. Math.-Phys. Kl Sächs. Akad. Wiss. Leipzig 94, 1–22 (1942). [Google Scholar]
- 13.Poincaré H., Les Méthodes Nouvelles de la Mécanique Céleste (Gauthier-Villars, 1899), vol. 3. [Google Scholar]
- 14.Faisst H., Eckhardt B., Traveling waves in pipe flow. Phys. Rev. Lett. 91, 224502 (2003). [DOI] [PubMed] [Google Scholar]
- 15.Eckhardt B., Zammert S., Small scale exact coherent structures at large Reynolds numbers in plane Couette flow. Nonlinearity 31, R66 (2018). [Google Scholar]
- 16.Hof B., et al., Experimental observation of nonlinear traveling waves in turbulent pipe flow. Science 305, 1594–1598 (2004). [DOI] [PubMed] [Google Scholar]
- 17.de Lozar A., Mellibovsky F., Avila M., Hof B., Edge state in pipe flow experiments. Phys. Rev. Lett. 108, 214502 (2012). [DOI] [PubMed] [Google Scholar]
- 18.Lemoult G., Gumowski K., Aider J. L., Wesfreid J. E., Turbulent spots in channel flow: an experimental study: Large-scale flow, inner structure and low-order model. Eur. Phys. J. E Soft Matter 37, 25 (2014). [DOI] [PubMed] [Google Scholar]
- 19.Park J. S., Graham M. D., Exact coherent states and connections to turbulent dynamics in minimal channel flow. J. Fluid Mech. 782, 430–454 (2015). [Google Scholar]
- 20.Kerswell R. R., Tutty O. R., Recurrence of travelling waves in transitional pipe flow. J. Fluid Mech. 584, 69–102 (2007). [Google Scholar]
- 21.Mellibovsky F., Meseguer A., Schneider T. M., Eckhardt B., Transition in localized pipe flow turbulence. Phys. Rev. Lett. 103, 054502 (2009). [DOI] [PubMed] [Google Scholar]
- 22.Cvitanović P., Gibson J., Geometry of the turbulence in wall-bounded shear flows: Periodic orbits. Phys. Scr. 2010, 014007 (2010). [Google Scholar]
- 23.Kawahara G., Kida S., Periodic motion embedded in plane Couette turbulence: Regeneration cycle and burst. J. Fluid Mech. 449, 291 (2001). [Google Scholar]
- 24.Budanur N. B., Short K. Y., Farazmand M., Willis A. P., Cvitanović P., Relative periodic orbits form the backbone of turbulent pipe flow. J. Fluid Mech. 833, 274–301 (2017). [Google Scholar]
- 25.Krygier M. C., Pughe-Sanford J. L., Grigoriev R. O., Exact coherent structures and shadowing in turbulent Taylor–Couette flow. J. Fluid Mech. 923, A7 (2021). [Google Scholar]
- 26.Coles D., Transition in circular Couette flow. J. Fluid Mech. 21, 385 (1965). [Google Scholar]
- 27.Andereck C. D., Liu S. S., Swinney H. L., Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155 (1986). [Google Scholar]
- 28.Gollub J. P., Swinney H. L., Onset of turbulence in a rotating fluid. Phys. Rev. Lett. 35, 927 (1975). [Google Scholar]
- 29.Colovas P. W., Andereck C. D., Turbulent bursting and spatiotemporal intermittency in the counterrotating Taylor-Couette system. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 55, 2736 (1997). [Google Scholar]
- 30.Meseguer A., Mellibovsky F., Avila M., Marques F., Instability mechanisms and transition scenarios of spiral turbulence in Taylor-Couette flow. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 80, 046315 (2009). [DOI] [PubMed] [Google Scholar]
- 31.Borrero-Echeverry D., Schatz M. F., Tagg R., Transient turbulence in Taylor-Couette flow. Phys. Rev. E 81, 025301(R) (2010). [DOI] [PubMed] [Google Scholar]
- 32.Crowley C. J., Krygier M. C., Borrero-Echeverry D., Grigoriev R. O., Schatz M. F., A novel subcritical transition to turbulence in Taylor–Couette flow with counter-rotating cylinders. J. Fluid Mech. 892, A12 (2020). [Google Scholar]
- 33.Huisman S. G., van der Veen R. C., Sun C., Lohse D., Multiple states in highly turbulent Taylor-Couette flow. Nat. Commun. 5, 3820 (2014). [DOI] [PubMed] [Google Scholar]
- 34.van Gils D. P., Huisman S. G., Bruggert G. W., Sun C., Lohse D., Torque scaling in turbulent Taylor-Couette flow with co- and counterrotating cylinders. Phys. Rev. Lett. 106, 024502 (2011). [DOI] [PubMed] [Google Scholar]
- 35.Grossmann S., Lohse D., Sun C., High–Reynolds number Taylor-Couette turbulence. Annu. Rev. Fluid Mech. 48, 53–80 (2016). [Google Scholar]
- 36.Benjamin T. B., Bifurcation phenomena in steady flows of a viscous fluid ii. Experiments. Proc. R. Soc. Lond. A Math. Phys. Sci. 359, 27–43 (1978). [Google Scholar]
- 37.Cliffe K., Numerical calculations of two-cell and single-cell Taylor flows. J. Fluid Mech. 135, 219–233 (1983). [Google Scholar]
- 38.Lücke M., Mihelcic M., Wingerath K., Pfister G., Flow in a small annulus between concentric cylinders. J. Fluid Mech. 140, 343–353 (1984). [Google Scholar]
- 39.Pfister G., Schmidt H., Cliffe K. A., Mullin T., Bifurcation phenomena in Taylor-Couette flow in a very short annulus. J. Fluid Mech. 191, 1 (1988). [Google Scholar]
- 40.Aitta A., Dynamics near a tricritical point in Couette-Taylor flow. Phys. Rev. Lett. 62, 2116–2119 (1989). [DOI] [PubMed] [Google Scholar]
- 41.Nakamura I., Toya Y., Existence of extra vortex and twin vortex of anomalous mode in Taylor vortex flow with a small aspect ratio. Acta Mech. 117, 33–46 (1996). [Google Scholar]
- 42.Mullin T., Toya Y., Tavener S., Symmetry breaking and multiplicity of states in small aspect ratio Taylor–Couette flow. Phys. Fluids 14, 2778–2787 (2002). [Google Scholar]
- 43.Furukawa H., Watanabe T., Toya Y., Nakamura I., Flow pattern exchange in the Taylor-Couette system with a very small aspect ratio. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 65 (3 Pt 2B), 036306 (2002). [DOI] [PubMed] [Google Scholar]
- 44.Marques F., Lopez J., Onset of three-dimensional unsteady states in small-aspect-ratio Taylor–Couette flow. J. Fluid Mech. 561, 255–277 (2006). [Google Scholar]
- 45.Schulz A., Pfister G., Tavener S., The effect of outer cylinder rotation on Taylor–Couette flow at small aspect ratio. Phys. Fluids 15, 417–425 (2003). [Google Scholar]
- 46.Hamill C. F., “Turbulent bursting in the Couette-Taylor system,” Master’s thesis, University of Texas at Austin, Austin, TX: (1995). [Google Scholar]
- 47.Avila M., Grimes M., Lopez J. M., Marques F., Global endwall effects on centrifugally stable flows. Phys. Fluids 20, 104104 (2008). [Google Scholar]
- 48.Krygier M. C., “Turbulent bursting in the Couette-Taylor system,” PhD thesis, Georgia Institute of Technology, Atlanta, GA: (2019). [Google Scholar]
- 49.Crowley C. J., et al., Data for “Turbulence tracks recurrent solutions.” GitHub. https://github.com/cdggt/tcf/tree/main/eta0.71. Deposited 25 April 2022.
- 50.Fredriksen Å., Riccardi C., Cartegni L., Pécseli H., Coherent structures, transport and intermittency in a magnetized plasma. Plasma Phys. Contr. Fusion 45, 721 (2003). [Google Scholar]
- 51.Cvitanović P., Chaotic field theory: A sketch. Physica A 288, 61 (2000). [Google Scholar]
- 52.Marcotte C. D., Grigoriev R. O., Unstable spiral waves and local Euclidean symmetry in a model of cardiac tissue. Chaos 25, 063116 (2015). [DOI] [PubMed] [Google Scholar]
- 53.Amari S., Dynamics of pattern formation in lateral-inhibition type neural fields. Biol. Cybern. 27, 77–87 (1977). [DOI] [PubMed] [Google Scholar]
- 54.Sambelashvili N., Lau A., Cai D., Dynamics of bacterial flow: Emergence of spatiotemporal coherent structures. Phys. Lett. A 360, 507–511 (2007). [Google Scholar]
- 55.Yaln iz G., Hof B., Budanur N. B., Coarse graining the state space of a turbulent flow using periodic orbits. Phys. Rev. Lett. 126, 244502 (2021). [DOI] [PubMed] [Google Scholar]
- 56.Fiedler B., Sandstede B., Scheel A., Wulff C., Bifurcation from relative equilibria of noncompact group actions: Skew products, meanders, and drifts. Doc. Math. 141, 479–505 (1996). [Google Scholar]
- 57.Sandstede B., Scheel A., Wulff C., “Dynamical behavior of patterns with Euclidean symmetry” in Pattern Formation in Continuous and Coupled Systems, Golubitsky M., Luss D., Strogatz S. H., Eds. (Springer, New York, NY, 1999), pp. 249–264. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data that support the key findings of this study (relating to the exact coherent structures and their key properties) have been deposited in Github (https://github.com/cdggt/tcf/tree/main/eta0.71) (49). Some study data are available. Due to their size, experimental datasets and the numerical turbulent trajectory will be available upon request only.