Significance
This paper discusses simulation techniques used to study the formation of organized protein assemblies on cell–cell interfaces. The simulations emphasize the need for a realistic representation of protein structure when studying such cellular phenomena. The results provide a detailed explanation of how many receptor proteins are designed to form one-dimensional zippers and provide a detailed molecular picture of the kinetics of this process. The simulations also reveal the driving force that leads one-dimensional zippers to form two-dimensional arrays. As such, they provide a unified picture of assembly formation of the clustered protocadherins explored in this work and suggest general principles common to many other adhesion proteins.
Keywords: clustered protocadherins, adhesion proteins, ordered protein assemblies, cell–cell interfaces
Abstract
Crystal structures of many cell–cell adhesion receptors reveal the formation of linear “molecular zippers” comprising an ordered one-dimensional array of proteins that form both intercellular (trans) and intracellular (cis) interactions. The clustered protocadherins (cPcdhs) provide an exemplar of this phenomenon and use it as a basis of barcoding of vertebrate neurons. Here, we report both Metropolis and kinetic Monte Carlo simulations of cPcdh zipper formation using simplified models of cPcdhs that nevertheless capture essential features of their three-dimensional structure. The simulations reveal that the formation of long zippers is an implicit feature of cPcdh structure and is driven by their cis and trans interactions that have been quantitatively characterized in previous work. Moreover, in agreement with cryo-electron tomography studies, the zippers are found to organize into two-dimensional arrays even in the absence of attractive interactions between individual zippers. Our results suggest that the formation of ordered two-dimensional arrays of linear zippers of adhesion proteins is a common feature of cell–cell interfaces. From the perspective of simulations, they demonstrate the importance of a realistic depiction of adhesion protein structure and interactions if important biological phenomena are to be properly captured.
The formation of assemblies of adhesive proteins in cell–cell contact regions is a well-characterized phenomenon common to multiple systems (1–5). Some of these assemblies involve the formation of ordered two-dimensional (2D) quasi-crystalline structures that are nearly identical to a single layer formation seen in crystal structures of that protein (6, 7). The more common observation is the presence of one-dimensional (1D) linear “zippers” that also appear to form in cell–cell contact regions (8–11). All adhesion proteins form apposed cell (trans) interactions but ordered structures require a regular arrangement of the same cell (cis) interactions as well (11–16). The evolutionary design of proteins that form lattice-like structures clearly suggests that such structures play a functional role. One possibility is that the regular arrangement of the extracellular domains of adhesion receptors generates ordered assemblies of the cytoplasmic domains that are somehow recognized by intracellular factors to activate downstream signaling. Another possibility suggested by recent studies of adherens junctions is that rigid ordered structures provide a platform for the coupling of forces with the cytoskeleton and for the transmission of force between neighboring cells (8, 17, 18). Perhaps more generally, the existence of ordered structures able to assemble and disassemble under the influence of various cellular factors offers a basis for biological control of multiple cellular processes. In this study, focusing on the clustered protocadherin (cPcdh) family, we describe computer simulations aimed at understanding the mechanism of assembly of adhesion proteins into parallel arrays of linear zippers. The insights we derive from our simulations, in addition to our insights into this important protein family, are likely to be of quite general relevance, in particular the demonstration that linear zippers form 2D structures even in the absence of attractive interactions.
In vertebrates, the cPcdhs comprise the largest family within the cadherin superfamily (19–21). In mice, 58 cPcdhs are organized into three adjacent gene clusters α, β, and γ encoding 14, 22, and 22 protein isoforms, respectively (22, 23). cPcdhs are single-pass transmembrane proteins whose extracellular regions consist of six EC domains that, similar to classical cadherins, are connected by calcium binding linker regions (24–27). However, in contrast to classical cadherins, cPcdh trans binding is mediated by an antiparallel interface involving EC1–EC4 whereas EC5 and EC6 mediate association in cis so that the basic structural unit of cPcdhs is a cis-dimer (24, 26–32). Cell aggregation, as well as structural and biophysical studies, have shown that, with one exception, the extracellular regions of all cPcdh isoforms engage in strict trans homophilic interactions through the membrane distal domains EC1–EC4 (24–26, 28–31, 33). In addition to these trans interactions, cPcdhs form cis-dimers through an additional nonoverlapping interface involving the membrane-proximal EC5–EC6 domains (24, 25, 27, 32–34). In contrast to the strict homophilic recognition of the trans interactions, cis interactions occur between different isoforms (34). A model was proposed for cPcdh-mediated cell–cell interactions where cPcdhs form extended zipper-like oligomers through alternating cis and trans interactions (24). This, in turn, led to the suggestion of the isoform mismatch chain-termination model of cPcdh-mediated neuronal self-recognition, which depends on the formation of such linear chains (24, 28, 32). The crystal structure of the cPcdh-γB4 isoform and cryo-electron tomography (cryo-ET) of the cPcdh-γB6 isoform linked to liposomes (32) reveals zipper-like oligomers as predicted by the model (Fig. 1A). Surprisingly, the cryo-ET structure reveals that these linear protein assemblies pack against each other as parallel arrays to form larger 2D structures between membranes even in the absence of an identifiable attractive interaction between each linear array (32).
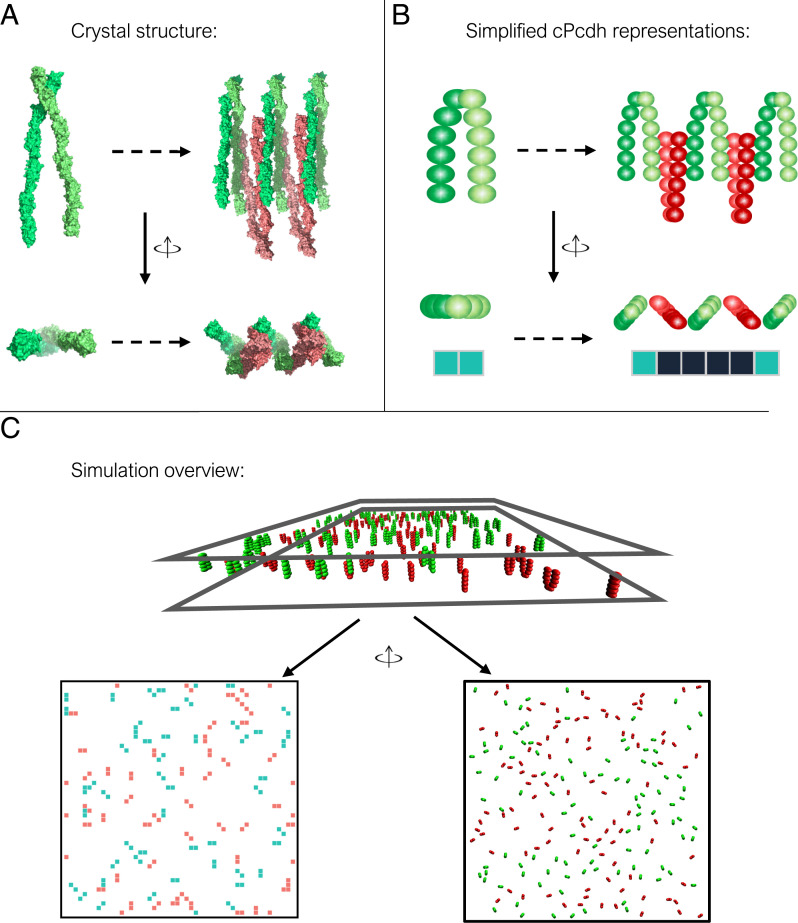
Fig. 1.
Modeling protocadherin structure. (A) cPcdh crystal structures shown in top and side views; Left: cis-dimer with separate monomers indicated by different shades of green; Right: short zipper colored red for cPcdhs from the lower membrane and green for those from the upper membrane. (B) Schematic representation of cPcdh cis-dimer (Left) and zipper-like assembly (Right) as seen from a top and side views of cPcdh crystal structures. For the MC lattice simulations each cPcdh monomer is represented as a square on the lattice (cis-dimer is depicted as a rectangle). The square colors indicate the membrane affiliation with red and green for cPcdhs from the bottom or top membranes, respectively. Black squares represent double occupancies by proteins belonging to apposed membranes. (C) In the initial configuration, cis-dimers are randomly placed on two opposing surfaces shown in a side view and top view for lattice (Left) and kinetic (Right) simulations.
The simulation of protein assemblies on membrane surfaces poses significant challenges. Since the oligomeric structures that are formed depend on the structures and interactions of the proteins involved, it is essential that a model capture the essential features of the relevant proteins. Molecular dynamic (MD) simulations successfully account for protein structure and energetics but their computational demands are too great to allow them to be applied to oligomeric assemblies. On the other hand, theoretical models based, for example, on chemical kinetics or statistical mechanics rarely incorporate the crucial structural features of individual proteins. However, intermediate mesoscopic level simulations can capture important elements of protein structure and are computationally feasible thereby bridging the gap between high-resolution structure-based simulations and pure theoretical analysis (35, 36). As an example, lattice-based models have been widely used to study the clustering of adhesive proteins in different systems. Spatial–temporal resolution beyond lattice models can be improved using a variety of particle-based off-lattice models. For instance, MCell and Smoldyn (37, 38) are both software platforms that exploit off-lattice models. More recently, new platforms such as SpringSaLaD and NERDSS have been applied to the study of receptor clustering in cell signaling and protein self-assembly (39, 40). However, none of these approaches take protein structure into account.
Here, we introduce two computational models to simulate the formation of cPcdh oligomers on cell membranes. Both models are based on the mapping of X-ray structure onto the simulation system thus allowing us to relate protein-specific molecular properties to assembly formation. In the first model, cPcdh proteins are mapped onto a 2D lattice and are allowed to diffuse, associate in cis and/or trans, and dissociate in individual Monte Carlo (MC) simulation steps. In the second model, a higher-resolution domain-based representation of protein structure is used and assembly kinetics are then guided by an off-lattice diffusion-reaction algorithm. We observe: (1) 1D zippers form easily with zipper size dependent on protein concentration and on cis and trans binding free energies; (2) 1D zippers align into 2D assemblies even in the absence of attractive interactions between them; and (3) there is a strong concentration and interaction strength dependence for the formation of 2D arrays of linear zippers. Our methods and results have implications for simulation approaches to study the assembly of other adhesion receptors and, further, suggest that 1D zippers observed in crystal structures are likely to appear as 2D assemblies in cell–cell contact regions.
Results
Lattice Simulations.
cPcdhs form long zippers whose length is affinity and concentration dependent.
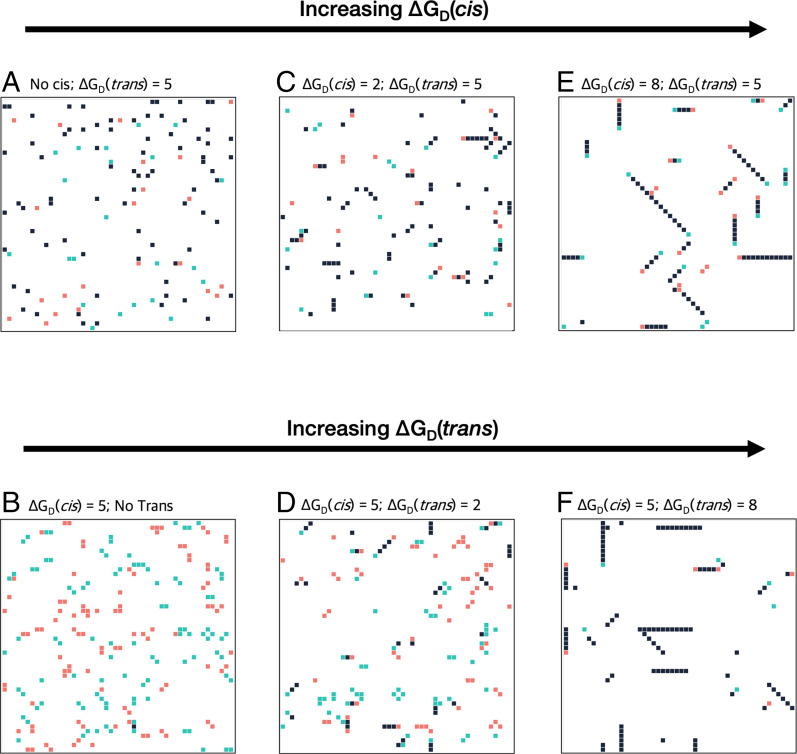
Fig. 2 displays representative snapshots of the last step in simulations for different combinations of cis and trans affinities (using 4% lattice occupancy). We note that biophysical and cell aggregation studies showed that cPcdh proteins forms strong and independent cis and trans interactions that are mediated by two nonoverlapping interfaces (24). Indeed, as is evident from Fig. 2 A and B, in our simulation when only trans or cis interactions are present, many trans- or cis-dimers are formed, respectively, but no zippers are formed. However, when both ΔGD(cis) and ΔGD(trans) are positive, most proteins assembled into zippers (Fig. 2 C–F). Moreover, as can be seen in Fig. 2, increases in either cis or trans affinity drives the formation of longer zippers. We examined the relationship between zipper length (defined as the number of monomers in the zipper) and protein concentrations and dimerization affinities. The average and maximum length were calculated for zippers formed at the last MC step, averaged over 20 simulations (SI Appendix, Figs. 2 and 3A). We found that at lower cis and trans affinities many short zippers were present while long zippers were essentially absent. In contrast, as the cis and trans interactions increase in strength, or as concentration increases, longer zippers are observed while, as a result, the number of short zippers correspondingly decreases (SI Appendix, Fig. 3B).
Fig. 2.
cPcdhs form long zippers whose length is dependent on both cis and trans affinities. Simulation snapshots from the 2D lattice model with green squares representing cPcdhs from top membrane, red squares representing cPcdhs from the lower membrane, and black squares representing double occupancies by proteins belonging to apposed membranes. Protein concentration in each simulation was set to 4% of the total grid size (200 proteins in total). (A and B) snapshots of the grid when either cis or trans interactions are absent, zippers-like arrays do not form. (C–F) An increase in the trans or cis affinities results in longer zipper arrays represented as linear black rectangles.
Zippers form 2D arrays.
A surprising result from the cryo-ET images of the cPcdhγB6 isoform attached to liposomes, is that cPcdhs organize as a 2D array of linear zippers (32). This raised the possibility that, in addition to the known cis and trans interfaces, there is an additional protein–protein interaction responsible for the formation of a 2D array. However, no such interaction could be identified in the cryo-ET images. We therefore examined whether parallel zippers would form in our simulations and under what specific conditions.
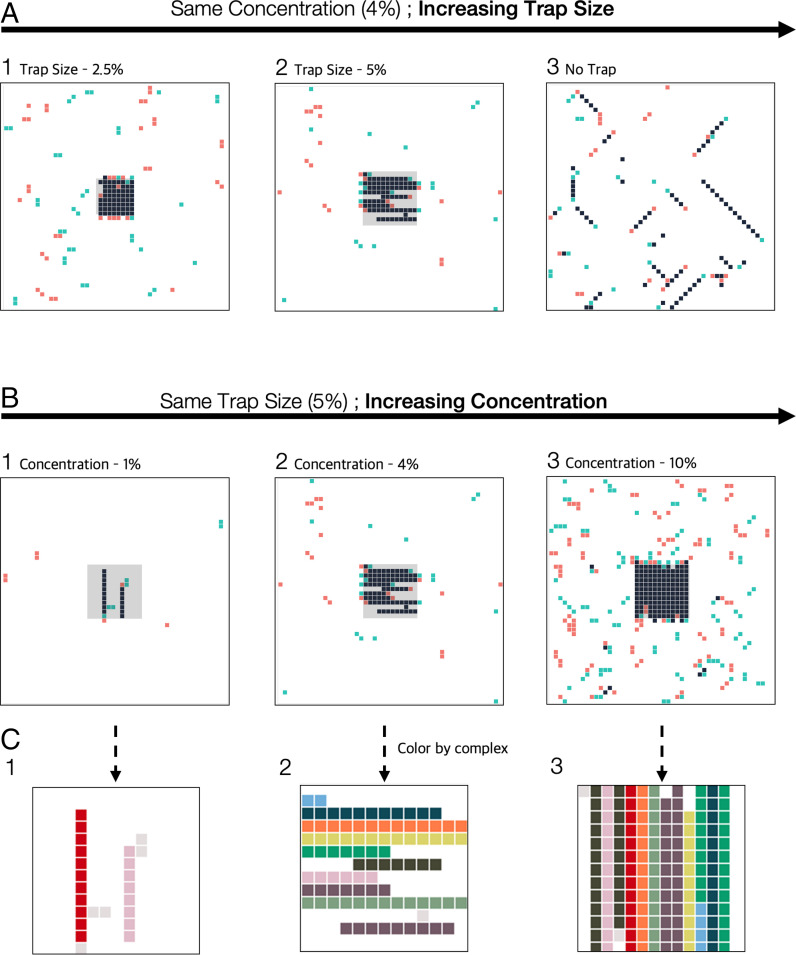
Fig. 3A presents simulation results for 4% lattice occupancy and where trans interactions can form in the full lattice (no diffusion trap), a 5% diffusion trap, and a 2.5% trap. As shown above, long zippers are formed when there is no trap present. In contrast, in the presence of diffusion traps, long zippers are formed whose size is limited only by the dimensions of the trap. Moreover, when the zippers are allowed to rotate as a unit (see Materials and Methods), thereby allowing adjustments in their orientation, they tend to align in parallel to form 2D arrays. Fig. 3B presents results for a 5% trap size for different concentrations. As the bulk concentration increases more zippers are formed with most of them forming a 2D stacked array. Clearly these zippers will form organized 2D arrays even in the absence of interzipper interactions. When we prevented the rotation of zippers on the lattice, during the simulation, zippers still formed 2D stacked arrays, albeit less uniformed (SI Appendix, Fig. 4). The energetic basis of the formation of 2D stacked array will be discussed below.
Fig. 3.
cPcdhs zippers form 2D arrays at high protein concentration. Simulation snapshots of the 2D lattice model. Colors in (A) and (B) represent cPcdhs membrane origins (red, bottom membrane; green, top membrane; black, double occupancies by cPcdhs belonging to apposing membranes). Diffusion traps comprising 8 × 8 lattice sites (A1) or 11 × 11 (A2 and B) is shown in the center of 2D lattice of 50 × 50 lattice sites. When a diffusion trap is present, trans-dimer formation only occurs in this contact zone. In all simulations ΔGD(trans) = 4 kT and ΔGD(cis) = 7 kT. (A) Results of three simulations that differ by diffusion trap size. Long zippers appear in all three simulations, but the size of the zippers is limited by the size of the diffusion trap. In addition, decreasing the cell–cell interaction area (no diffusion trap to 2.5% diffusion trap) prompts zipper cluster formation. (B) Results of three simulations that differ in protein concentration. In all three simulations long zippers appear, however, zippers tend to cluster only at protein concentrations of 4% and more significantly at concentrations of 10% (B2 and B3, respectively). (C) Magnification of the diffusion trap area (gray area) in (B). Each zipper-like assembly is depicted by a different color.
Kinetic MC Simulations.
Dependence of zipper formation on trans-binding affinity.
We tested the dynamics of clustering using different values for on and off rates. Specifically, the association rate of the trans interaction was fixed at 10 ns−1, while the dissociation rate varied from 0.003 ns−1 to 0.000001 ns−1. These values correspond to 2D KDs ranging from 3 × 10−4 to 10−7 corresponding to 2D affinities, ΔGD(trans), of 3.5–7 kT, in the range used in the lattice simulations. A relatively high association rate was used to accelerate the simulations so that results are obtained in computationally feasible times. Lowering the association rate would slow down the kinetics of zipper formation but would not affect other behaviors of the systems. Further, we assume that the association and dissociation rates of a trans interaction are independent of its oligomeric status, (i.e., the dissociation rates of a trans interaction between two cis-dimers in a zipper are the same as when they are not in a zipper). Nevertheless, dissociation of a cis-dimer in the interior of a zipper will be slower than it will be for an isolated cis-dimer since, for dissociation to occur, two trans bonds must be broken in the interior of a zipper—an energetically unlikely event—while only one is broken for cis-dimers not in a zipper.
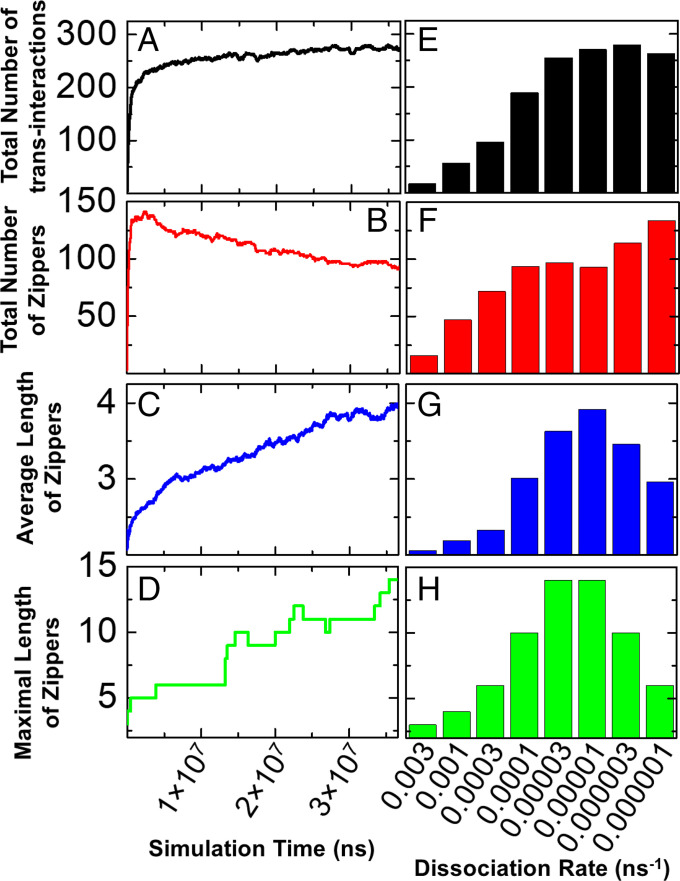
In each simulation, 200 cis-dimers are randomly distributed on each surface of dimension 500 nm × 500 nm. The simulation results under these different conditions are summarized in Fig. 4. Changes over time of the number of trans interactions and zipper properties are shown in Fig. 4 A–D for a representative trajectory with dissociation rate of 0.00001 ns−1, while the dependence of these features on the dissociation constant is shown in Fig. 4 E–H.
Fig. 4.
Kinetic MC simulations were carried out under different trans interaction dissociation rates. The change in total number of trans interactions over time and its dependence on the value of dissociation rate are plotted in (A) and (E), respectively. Similarly, the change in total number of zippers over time and its dependence on the value of dissociation rate are plotted in (B) and (F); the change in average length of zippers over time and its dependence on the value of dissociation rate are plotted in (C) and (G); and finally, the change in maximal length of zippers over time and its dependence on the value of dissociation rate are plotted in (D) and (H).
The total number of trans-dimers increases quickly at the beginning of the simulations but saturates after ∼1.5 × 107 ns (Fig. 4A), while the total number of zippers reaches a maximum at 0.25 × 107 ns and then starts to decrease through the end of the trajectory (Fig. 4B) corresponding to the formation of longer zippers (Fig. 4 C and D), which are still growing at the end of the simulation. Taken together, these kinetic profiles suggest that the clustering of protocadherin is a two-step process. During the first stage of clustering, the total number of zippers in the system increases quickly but the length of each zipper is relatively small. In the second step, the total number of zippers decreases, the total number of trans interactions increases slowly, while zipper length continues to increase. This would appear to result from a process where short zippers dissociate more quickly thus enabling individual cis-dimers and/or monomers to join larger zippers.
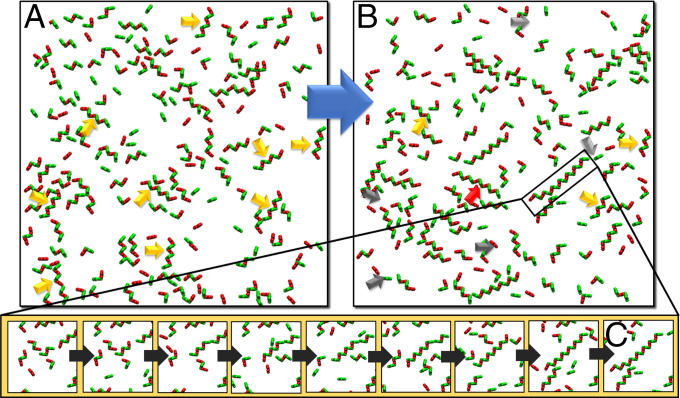
Fig. 5 displays snapshots selected from the simulation trajectories. A large portion of the short zippers (highlighted by orange arrows in Fig. 5A) that formed during the early stage of simulations dissociate into individual cis-dimers (highlighted by gray arrows in Fig. 5B). Concurrently, long zippers, such as the one highlighted by the black rectangle in Fig. 5B, continue to grow through a multistep process where individual cis-dimers are added on to the chain (Fig. 5C). Because zipper growth has not reached equilibrium at the end of the simulations, it is likely that even longer zippers would be observed if our simulations had not terminated.
Fig. 5.
In order to illustrate the mechanism of zipper formation, we selected two snapshots from the early (A) and late (B) stages of the kinetic MC simulation. Some short zippers (orange arrows) later dissociate into individual cis-dimers (gray arrows) that eventually join longer zippers (red arrows). The detailed kinetics of the growth of a long zipper (highlighted by the black frame in B) is further specified by a series of enlarged snapshots shown in (C).
Fig. 4E shows that the number of trans-dimers increases as the binding affinity increases but at dissociation rates greater than 0.00003 ns−1 the number of dimers levels off while the total number of zippers increases slowly (Fig. 4F). As shown in Fig. 4 G and H, zipper size is found to increase for weak trans-binding affinities, reaches a maximum at a dissociation rate of approximately 0.00003 ns−1, and, for the strongest binding affinities (i.e., dissociation rates of 0.000003 ns−1 or 0.000001 ns−1), zipper size decreases. These results suggest that strong trans interactions kinetically trap cPcdhs into small zippers, although thermodynamically, the system still prefers the formation of fewer longer zippers as seen clearly from the lattice simulations described above. However, these processes are beyond the time scales that our current simulations can approach.
Dependence of zipper formation on concentration.
To illustrate the concentration dependence of zipper formation, we fixed the total number of cPcdhs in the system and changed the size of the simulation box. Specifically, three systems were constructed. In each case, 100 cis-dimers are placed on each surface with dimensions 250 nm × 250 nm, 354 nm × 354 nm, and 500 nm × 500 nm, respectively. The association and dissociation rates in all three systems were fixed at 10 ns−1 and 0.00003 ns−1, respectively. At the end of each simulation, we counted the total number of trans-dimers and the total number of zippers formed. The correlation between the area of the simulation box and total number of trans-dimers is plotted as a bar chart in SI Appendix, Fig. 5A while the correlation between the size of the simulation box and total number of zippers is plotted in SI Appendix, Fig. 5B. The figures show that larger numbers of trans interactions were formed under higher concentrations (smaller size of simulation box) while, correspondingly, these assembled into fewer zippers.
We counted the length of each zipper observed at the ends of the simulations in all three systems. SI Appendix, Fig. 5C presents the distributions of zipper length under all three concentrations as a box-whisker plot. The figure indicates that simulations under higher concentrations systematically resulted in longer zippers than the simulations under lower concentrations. Given the distribution of zipper length in these three systems, we further applied one-way ANOVA to test the statistical significance of our observation, which yielded a calculated F-statistic score of 8.5 with a P value of 0.0001, suggesting that variations of zipper length under different concentrations are statistically significant. Based on this statistical result, and consistent with our lattice simulations, a higher concentration of cPcdhs facilitates the formation of zippers with longer length.
Packing of zippers into 2D arrays.
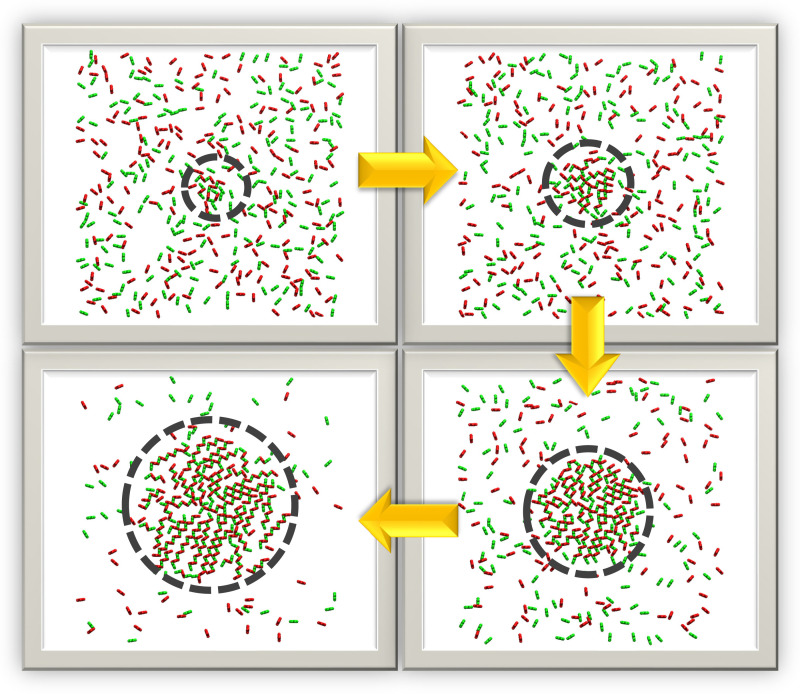
In order to estimate the role of the diffusion trap in regulating cPcdh clustering, we created a circular zone in the center of the simulation box to mimic the contact area between two cells. The size of this region grows dynamically over the course of the simulation with its radius initially set to zero reflecting a state before the two cells are in contact. The radius is increased linearly with the simulation time, mimicking the growth of the contact area between two cells driven by the formation of trans interactions. Cis-dimers were allowed to diffuse anywhere on the 2D surface, but trans interactions are only allowed to form within the circular region.
Fig. 6 shows a few representative snapshots selected from the simulation. It is clear from the figures that the cPcdh concentration gradually increases in the contact zone and, in parallel, long zippers are formed. Moreover, as was observed in the lattice simulations, the zippers tend to pack in parallel into 2D arrays. Although there is no energetic interaction between cPcdhs in different zippers, the simulation clearly demonstrates, in agreement with the lattice simulations, that zippers increasingly align as the contact zone grows in size, leading to the formation of ordered 2D arrays.
Fig. 6.
A circular zone that grows dynamically was created in the center of the simulation box to mimic the contact area between two cells in the kinetic MC simulation. Representative snapshots were selected long the simulation trajectory, as indicated by the yellow arrows. The two cell surfaces in the snapshots are visualized from the top. The contact areas in the figure are defined by the dashed circles in the center of the surface. cPcdh cis-dimers on the top and bottom layers of cell surfaces are displayed in green and red, respectively.
Discussion
Here, we report the development of two distinct models and algorithms that simulate the assembly of cPcdhs into long linear assemblies (zippers) in cell–cell interfaces. One model, involving lattice-based simulations, reaches thermodynamic equilibrium while the other, domain-based off-lattice approach, provides kinetic insights. Both models represent crucial 3D features of the interacting proteins although the domain-based model provides much greater molecular detail. Both simulations reproduce experimental observations and, more generally, reveal general principles that are relevant to the behavior of other adhesion receptors. In the following, we first compare the results of both models which, despite their differences, are seen to provide a consistent and unified picture of zipper formation. We then address specific questions that relate to cellular systems; why and how do long zippers form and why do they stack into ordered 2D arrays. Finally, we discuss the relationship of our findings to the behavior of other cell-surface proteins in cell–cell interfaces.
Comparing Lattice-Based Metropolis MC Simulations to Domain-Based Kinetic MC Simulations.
The lattice-based and domain-based simulation models in this study are complementary. The fewer degrees of freedom in the lattice simulations result in greater computational efficiency allowing us to explore a wider range of binding affinities and concentrations and for the simulations to equilibrate. In contrast, the representation of cPcdhs and their interactions in the kinetic MC simulations is more realistic and, moreover, provides insight into the kinetics of zipper formation not accounted for in the lattice simulations. Together, the two sets of simulations provide a consistent picture of how ordered arrays of linear zippers are formed in cell–cell interfaces.
Both models predict that cPcdhs form long zippers and both predict that increasing cis and/or trans affinities and/or bulk concentration increases the propensity to form long zippers. That zipper formation is driven by larger affinities is of course not surprising, but it is perhaps less clear why fewer long zippers are favored over a greater number of short zippers. This observation is discussed further in the next section. That increasing bulk concentration also drives zipper formation can be understood in terms of any association process; there is a smaller entropic penalty for pulling monomers out of solution (in this case a 2D fluid) as bulk concentration increases. Of note, zippers formed in the lattice-based simulations are much longer than those formed in the domain-based off-lattice model. This is probably due to the fact that the discretized rotations and diffusion in the lattice model make the formation of long one-dimensional structures easier to achieve in the simulations. Indeed, as noted above, the off-lattice simulations have not yet reached equilibrium.
Of particular interest, both methods also show that, under the high concentrations generated within the diffusion trap, linear zippers can laterally stack together into two-dimensional clusters. Moreover, although both models predict that the zippers pack in the diffusion trap region to form 2D arrays, the lattice model predicts a greater extent of parallel packing. Finally, as can be seen by comparing Fig. 3 with Fig. 6, the stacking of zippers in the off-lattice model is not as compact as in the lattice model. This difference arises from inherent features of both models; in the lattice model two zippers can be spatially aligned along the nearest neighbor lattice points, while in the domain-based model, cPcdhs are not allowed to move after they aggregate so that they cannot be further adjusted so as to optimize packing. We anticipate that future improvements in the off-lattice simulations will enable the generation of more compact configurations.
Why Do Long Zippers Form?
When either cis or trans affinities are set to zero while the alternate interaction is significant, individual trans- or cis-dimers are formed, respectively, but no zippers can be formed (Fig. 2 A and B). When both affinities are increased, more zippers are formed with the ratio of the number of long to short zippers increasing with both affinities (Fig. 2 C–F and SI Appendix, Fig. 3B). This behavior can be understood in terms of cis and trans affinities as these are the only driving forces present in the system. Energetic terms will favor the formation of a maximum number of cis and trans interactions while entropy of course opposes assembly processes. A critical feature of the system is that each zipper has two “unsatisfied” trans interactions at each end of the zipper. Thus, long zippers with fewer termini will always be energetically favored over short zippers but entropy will always favor shorter zippers. As the trans affinity increases the tendency to form long zippers will also increase.
The formation of fewer long zippers over many short zippers resembles (at least superficially) the well described phenomenon of Ostwald ripening, the thermodynamically driven dissolution of small crystals in solution and their redeposition on the surfaces of larger crystals (44). In both cases, the driving force results from the minimization of unsatisfied interactions at boundaries where fewer contacts are made than in the crystal interior in one case and at zipper termini in the other.
The kinetic MC simulations provide interesting insights as to how long zippers form from short ones. Fig. 5 reveals rather that short zippers dissociate into isolated cis-dimers that can then undergo rotational and translational diffusions until they encounter and then associate with the terminus of a growing zipper. This process is likely enhanced in our simulations since zippers, once formed, no longer diffuse. In principle, it is possible that short zippers simply add on to the termini of other zippers but, as pointed out above, this would require the concerted motion of an array of cis and trans-dimers constrained by the binding to two apposed membranes. In summary, the formation of long zippers is driven energetically by the minimization of the number of zipper termini and is mediated by the attachment of isolated cis-dimers to these termini.
Why Do Zippers Form 2D Arrays?
At the high protein concentrations formed within the diffusion trap, both sets of simulations reveal the assembly of parallel stacks of 2D arrays (Figs. 3 and 6) that mirror those observed in cryo-ET images of liposomes coated with the ectodomain of cPcdhγB6 (32). As discussed above, these arrays form in the absence of any direct energetic term that might drive the zippers to pack together. Rather, it is clear that the driving force is simply to maximize the number of zippers that can form in the contact zone which in turn maximizes the number of cis and trans interactions. Of note, classical cadherins form ordered crystalline-like 2D lattices in cell–cell interfaces driven by both cis and trans interactions, however, there are few examples of this occurring in other systems. In contrast, there are many examples of the formation of linear zipper-like structures and our simulation results suggest that the assembly of these zippers into stacked 2D arrays, that are crystalline in only one dimension, may well be a common phenomenon.
Zipper-Like Structure and Clustering in Other Systems.
Although the current study focused on cPcdhs interactions, its results represent general principles that can be applied to different proteins that form zipper-like structures. For example, other adhesion proteins such as NCAM, JAM A, and ROBO all form 1D zippers that can be seen in crystal structures (13, 14, 45). Whether and how these proteins form 2D arrays is not yet known. The results of the current study suggest that at high protein concentrations that accumulate in the intercellular contact zone 2D arrays of linear zipper-like structures are likely to form even in the absence of lateral interactions between zippers. In fact, in a recent study of cryo-ET of HEK293 cells over-expressing mouse Downs syndrome cell adhesion molecules (mDSCAM), it was revealed that mDSCAM at the adhesion interface assemble as a 2D pattern composed of linear zippers-like arrays (11). Based on biophysical and cryo-ET data, the authors suggested that the combination of cis and trans interactions between the mDSCAM molecules is crucial to generate the regular pattern found at the adhesion interface (11), which is similar to the patterns discussed here.
The packing of 1D zipper into clusters of higher dimensions might also exist in systems of cell-surface signaling receptors, for example, coregulatory receptors on the surface of T cells that closely control their activation and differentiation. T lymphocyte-associated protein-4 (CTLA-4) is one of the most-studied coregulatory receptors. Binding of the receptors to its corresponding ligand B7 on the antigen-presenting cells triggers the coinhibitory signaling pathways leading to the suppression of T cell functions. Based on the crystal structure of the human CTLA-4/B7-1 costimulatory complex (PDB: 1I8L), CTLA-4 exists as homodimers on T cells through an interface formed by highly conserved residues. Each CTLA-4 in the dimer further binds to a B7 monomer simultaneously, providing the structural basis of a zipper-like oligomerization (10, 46). Using mesoscopic MC simulation, we recently showed that the CTLA-4/B7 ligand-receptor complexes not only form linear oligomers, but these 1D oligomers can also align together into 2D clusters, similar as we observed here for cPcdhs (47).
Materials and Methods
Lattice-Based Metropolis MC Simulations.
Simulation system.
We used a grid with 50 × 50 squares with a periodic boundary to model the 2D interacting membrane surfaces that are represented as two distinct stacked lattices (Fig. 1C). In each lattice, each of the squares can be occupied by only one monomer that we assume approximately occupies ∼120 nm2 so that each square edge is ∼11 nm. For a simple visualization, the two interacting grids are mapped onto a single lattice (Fig. 1C) with different colors representing the proteins' membrane affiliation. Green colored squares denote proteins from the top membrane; red colored squares denote proteins from the bottom membrane; and black colored squares denote squares that have double occupancies by proteins from both membranes (Fig. 1B).
As seen in the X-ray structures (Fig. 1A), cPcdhs combine cis- and trans-dimers to form linear zipper-like arrays (Fig. 1A). The cis interaction is mediated by the membrane proximal domains and result in a V-shape dimer, and the trans interaction is mediated by the membrane distant domains (Fig. 1A). The cis and trans interfaces do not overlap, occupy different sides of the molecule, and are therefore independent of each other. To emulate these interactions properties, each monomer has an angular direction that points to one of eight orientations on the 2D lattice. The angular direction of each monomer also defines the directions of the cis and trans interactions so that the organization of cPcdh complexes on the lattice (black colored squares) resembles their 3D structural organization (Fig. 1B).
cPcdhs are presented on the cell surface as cis-dimers but can dissociate into monomers and reassemble (24, 25, 27). The system was initiated by randomly placing cis-dimers (green and red rectangles) on the 50 × 50 grid. Fig. 1C (Left panel) corresponds to the initiation step in the simulation where the number of molecules is set to a 100 on each membrane for a total of 200 molecules, which are organized as 100 cis-dimers (50 green rectangles and 50 red rectangles in the figure). Each step of the simulation is initiated by randomly selecting a protein from either membrane. The selected molecule can then undergo one of six possible actions: (1) translational motion—by shifting the molecule and its cis/trans partners (if exists) to a neighboring position; (2) a rotation of the protein by 45°; (3) trans association with a molecule on the juxtaposed membrane; (4) trans dissociation; (5) cis association; and (6) cis dissociation.
During the simulation cis-dimers (represented as rectangles) from each membrane shift and rotate on the grid and can interact in trans, with juxtapose molecules, as long as they satisfy four requirements. First, two protomers must occupy the same position (i.e., the same square). Second, both proteins must exhibit a “correct” orientation for interaction, which is based on the crystal structures of cPcdh trans-dimers. Third, a MC probability test that depends on the parameter ΔGD(trans). Fourth, the proteins must be located within a contact zone at the center of the grid (depicted as a gray square). This region corresponds to a “diffusion trap” because once a trans complex is formed, it is trapped within and can only diffuse within the contact zone until it is dissociated. As a result, protein concentrations inside the diffusion trap will exhibit a higher than the average concentration inside the entire cell. In some simulations the entire 50 × 50 lattice is assumed to constitute a contact zone and therefore there is no diffusion trap region. When two cPcdhs satisfy all four requirements and bind following an MC step, the result is either a trans-dimer (consisting of only two proteins) or a zipper (consisting of three or more proteins in a linear-array, Fig. 1B). Cis associations and dissociations were calculated in a similar fashion to trans interactions and dependent on an affinity parameter ΔGD(cis). We analyze both the number of cis and trans interactions and the number and length of zippers defined as the number of cPcdh monomers in a zipper.
Since it is reasonable to assume that on the membrane surface, the rotational motion of long assemblies is restricted, we tested two approaches that take this into account: (a) assume that complexes of three or more proteins are unable to rotate; and (b) reduce the probability of rotation of long assemblies using the sigmoid function, , where Np represents the number of proteins in the assembly.
Trans- and cis-dimerization affinities are treated as parameters, as is the concentration of cPcdh-dimers on each surface. Below, we discuss the values used for these parameters, also summarized in SI Appendix, Table 1.
2D binding free energies.
While binding free energies can be accurately measured in the 3D solution environment, cis interactions of interest take place in the quasi-2D environment of a membrane surface while trans interactions occur in the limited space between these surfaces and are subject to constraints not present in solution. Trans KD in solution (3D environment) for cPcdhs range from 2 to 150 μM (24, 26, 30, 31) and are thus comparable in strength to that of the classical N-cadherin and E-cadherin which have solution KD(3D)s in the range of 20–170 μM (41). Based on theory and simulations of protein flexibility, we have previously estimated free energies, ΔGD(trans), of classical cadherin dissociation at the membrane surface to be in the range of 6.7–7.7 kT (7, 41). In the current simulation, we use similar values for cPcdhs and also tested lower values of ΔGD(trans). Cis KD(3D) for cPcdhs measured in solution has comparable strength to that of cPcdh trans interactions and range between 9–80 μM (24, 27, 30). We therefore use similar values for the free energies of dissociation, ΔGD(cis), as we used in the trans interaction.
Concentrations.
Unfortunately, expression levels of cPcdhs remain unknown. We used a wide range of concentrations that were based on values used in a previous simulation study of classical cadherin interactions (7). Classical cadherins expression range between 25,000–250,000 molecules per cell (7, 42), which for a cell with a 10 μm diameter, corresponds to 80–800 molecules per μm2 which, assuming that each monomer occupies 120 nm2 of surface area, corresponds to 1–10% occupancies on the cell surface (7).
Overall, we ran simulations for 729 parameter combinations: nine combinations of cis and nine combinations of trans interactions (both ranging from 0 to 8 kT), three different protein concentrations (1%, 4%, and 10% occupancy of the grid), and three different contact (diffusion trap) zones (2.5%, 5%, and no-diffusion trap). For each of the 729 sets of parameters, we ran 20 independent MC simulations and analyzed the assemblies that formed. All simulations ran for 30 million MC steps and they all reached equilibrium (SI Appendix, Fig. 1).
Domain-Based Kinetic MC Simulations.
Simulation system.
Our coarse-grain representation of the crystal structure of the cis-dimer of cPcdhγB1 (Fig. 1A) is depicted in Fig. 1B. Each of the six EC domains is represented by a spherical rigid body with a diameter of 4.5 nm, and the entire ectodomain is thus modeled by six sequentially connected rigid bodies. Two protomers from the same cell surface are linked by their EC6 domains to mimic a cis-dimer. Two cis-dimers on apposed cell trans interaction form trans interactions mediated by an anti-parallel interface formed between their EC1 and EC4 domains. The dihedral angle formed between two neighboring cis-dimers in a trans interaction is set to 90°, approximately consistent with crystallographic and electron-tomographic experiments.
The initial configuration of the simulation is shown in Fig. 1C (Right panel). The interface between two cells is modeled as two flat surfaces separated by 39 nm that is the approximate end-to-end distance of classical cadherin and cPcdh trans-dimers. The actual intermembrane spacing is generally smaller, in the 20–30 nm range, because the monomers don’t extend perfectly perpendicular from the membrane plane. Given the surface density and dimensions of the simulation box, a corresponding number of cis-dimers are randomly distributed on each surface.
Starting with the initial configuration (Fig. 1C), the dynamics of the system are simulated with a kinetic MC algorithm. Each time step in this algorithm involves one of two scenarios; nonreactive and reactive. The length of each time step was taken as 0.1 ns, a value that was empirically determined in a previous study to effectively balance accuracy and efficiency (43). In the first scenario, each cis-dimer is chosen in random order to diffuse stochastically in two dimensions using 2D periodic boundary conditions. Rotations of a dimer are with respect to the membrane normal axis, and translational movements are limited to the membrane plane. The amplitude of each translation is 0.2 nm and 5° for each random rotation. The probabilities of movements within each time step depend on the translational and rotational diffusion constants of the dimer and the assigned amplitude of movements (43). A translational diffusion coefficient of 10 μm2/s and a rotational diffusion coefficient of 1° ns−1 were adopted from our previous studies (43). If collisions between any pair of cis-dimers are detected, the new configuration is rejected and a new diffusion trial is carried out. The simulation will not proceed until all the intermolecular clashes are removed.
The second scenario simulates the reaction kinetics of the system. Association between two cis-dimers through their corresponding trans-binding interfaces is triggered by two criteria: (1) the distance between the interfaces of two molecules is below the predefined cutoff value; and (2) the relative dihedral angle formed between two interacting cis-dimers also need to fall below specific ranges around 90°. If both criteria are fulfilled, an on-rate is further assigned to determine the probability of trans-dimerization. The probability of dissociation of a trans-dimer is determined by its off-rate. After dissociation, the corresponding cis-dimers can either reassociate if their distance and dihedral angle are still below the cutoff values, or diffuse farther away from each other. We assume that once a trans interaction has formed, the corresponding zipper, long or short, no longer undergoes diffusive motion. This simplification was made for computational efficiency but is also physically reasonable since the concerted movement of weakly bound molecules connecting two membranes is likely to be much slower than that of a single cis-dimer diffusing on a single cell surface. Finally, the simulation is terminated after the system reaches a predetermined length.
Supplementary Material
Acknowledgments
This work was supported by the Israel Science Foundation (1463/19 to R.R.), the Israel Cancer Research Fund (ICRF 19-203-RCDA to R.R.), the National Science Foundation (MCB-1914542 to B.H.), the NIH (R01GM120238 and R01GM122804 to Y.W. and R01MH114817 to L.S.).
Footnotes
Reviewers: T.C.B., The University of Utah; and S.S., University of California Davis.
The authors declare no competing interest.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2206175119/-/DCSupplemental.
Data, Materials, and Software Availability
All study data are included in the article and/or SI Appendix. The source codes of simulations developed in this work are available for download at https://github.com/Rubinstein-Lab (48).
References
- 1.Harrison O. J., et al. , The extracellular architecture of adherens junctions revealed by crystal structures of type I cadherins. Structure 19, 244–256 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dean C., et al. , Neurexin mediates the assembly of presynaptic terminals. Nat. Neurosci. 6, 708–716 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Grakoui A., et al. , The immunological synapse: A molecular machine controlling T cell activation. Science 285, 221–227 (1999). [DOI] [PubMed] [Google Scholar]
- 4.Hong S., Troyanovsky R. B., Troyanovsky S. M., Spontaneous assembly and active disassembly balance adherens junction homeostasis. Proc. Natl. Acad. Sci. U.S.A. 107, 3528–3533 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yap A. S., Niessen C. M., Gumbiner B. M., The juxtamembrane region of the cadherin cytoplasmic tail supports lateral clustering, adhesive strengthening, and interaction with p120ctn. J. Cell Biol. 141, 779–789 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Al-Amoudi A., et al. , The three-dimensional molecular structure of the desmosomal plaque. Proc. Natl. Acad. Sci. U.S.A. 108, 6480–6485 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wu Y., et al. , Cooperativity between trans and cis interactions in cadherin-mediated junction formation. Proc. Natl. Acad. Sci. U.S.A. 107, 17592–17597 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Honig B., Shapiro L., Adhesion protein structure, molecular affinities, and principles of cell-cell recognition. Cell 181, 520–535 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Aricescu A. R., Jones E. Y., Immunoglobulin superfamily cell adhesion molecules: Zippers and signals. Curr. Opin. Cell Biol. 19, 543–550 (2007). [DOI] [PubMed] [Google Scholar]
- 10.Schwartz J. C., Zhang X., Fedorov A. A., Nathenson S. G., Almo S. C., Structural basis for co-stimulation by the human CTLA-4/B7-2 complex. Nature 410, 604–608 (2001). [DOI] [PubMed] [Google Scholar]
- 11.Guo L., et al. , Structure of cell-cell adhesion mediated by the Down syndrome cell adhesion molecule. Proc. Natl. Acad. Sci. U.S.A. 118, e2022442118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kunz B., et al. , Axonin-1/TAG-1 mediates cell-cell adhesion by a cis-assisted trans-interaction. J. Biol. Chem. 277, 4551–4557 (2002). [DOI] [PubMed] [Google Scholar]
- 13.Kostrewa D., et al. , X-ray structure of junctional adhesion molecule: Structural basis for homophilic adhesion via a novel dimerization motif. EMBO J. 20, 4391–4398 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Soroka V., et al. , Structure and interactions of NCAM Ig1-2-3 suggest a novel zipper mechanism for homophilic adhesion. Structure 11, 1291–1301 (2003). [DOI] [PubMed] [Google Scholar]
- 15.Dong X., et al. , Crystal structure of the V domain of human Nectin-like molecule-1/Syncam3/Tsll1/Igsf4b, a neural tissue-specific immunoglobulin-like cell-cell adhesion molecule. J. Biol. Chem. 281, 10610–10617 (2006). [DOI] [PubMed] [Google Scholar]
- 16.Aricescu A. R., et al. , Molecular analysis of receptor protein tyrosine phosphatase mu-mediated cell adhesion. EMBO J. 25, 701–712 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schlessinger J., Receptor tyrosine kinases: Legacy of the first two decades. Cold Spring Harb. Perspect. Biol. 6, a008912 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Indra I., Troyanovsky R. B., Shapiro L., Honig B., Troyanovsky S. M., Sensing Actin Dynamics through Adherens Junctions. Cell Rep. 30, 2820–2833.e3 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hirano S., Takeichi M., Cadherins in brain morphogenesis and wiring. Physiol. Rev. 92, 597–634 (2012). [DOI] [PubMed] [Google Scholar]
- 20.Halbleib J. M., Nelson W. J., Cadherins in development: Cell adhesion, sorting, and tissue morphogenesis. Genes Dev. 20, 3199–3214 (2006). [DOI] [PubMed] [Google Scholar]
- 21.Nollet F., Kools P., van Roy F., Phylogenetic analysis of the cadherin superfamily allows identification of six major subfamilies besides several solitary members. J. Mol. Biol. 299, 551–572 (2000). [DOI] [PubMed] [Google Scholar]
- 22.Wu Q., Maniatis T., A striking organization of a large family of human neural cadherin-like cell adhesion genes. Cell 97, 779–790 (1999). [DOI] [PubMed] [Google Scholar]
- 23.Wu Q., et al. , Comparative DNA sequence analysis of mouse and human protocadherin gene clusters. Genome Res. 11, 389–404 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rubinstein R., et al. , Molecular logic of neuronal self-recognition through protocadherin domain interactions. Cell 163, 629–642 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Thu C. A., et al. , Single-cell identity generated by combinatorial homophilic interactions between α, β, and γ protocadherins. Cell 158, 1045–1059 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Goodman K. M., et al. , Structural basis of diverse homophilic recognition by clustered α- and β-protocadherins. Neuron 90, 709–723 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Goodman K. M., et al. , Protocadherin cis-dimer architecture and recognition unit diversity. Proc. Natl. Acad. Sci. U.S.A. 114, E9829–E9837 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rubinstein R., Goodman K. M., Maniatis T., Shapiro L., Honig B., Structural origins of clustered protocadherin-mediated neuronal barcoding. Semin. Cell Dev. Biol. 69, 140–150 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nicoludis J. M., et al. , Structure and sequence analyses of clustered protocadherins reveal antiparallel interactions that mediate homophilic specificity. Structure 23, 2087–2098 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Goodman K. M., et al. , γ-Protocadherin structural diversity and functional implications. eLife 5, e20930 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Nicoludis J. M., et al. , Antiparallel protocadherin homodimers use distinct affinity- and specificity-mediating regions in cadherin repeats 1-4. eLife 5, e18449 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Brasch J., et al. , Visualization of clustered protocadherin neuronal self-recognition complexes. Nature 569, 280–283 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Schreiner D., Weiner J. A., Combinatorial homophilic interaction between gamma-protocadherin multimers greatly expands the molecular diversity of cell adhesion. Proc. Natl. Acad. Sci. U.S.A. 107, 14893–14898 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Goodman K. M., et al. , How clustered protocadherin binding specificity is tuned for neuronal self-/nonself-recognition. eLife 11, e72416 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Su Z., Dhusia K., Wu Y., Understand the functions of scaffold proteins in cell signaling by a mesoscopic simulation method. Biophys. J. 119, 2116–2126 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wu Y., Honig B., Ben-Shaul A., Theory and simulations of adhesion receptor dimerization on membrane surfaces. Biophys. J. 104, 1221–1229 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kerr R. A., et al. , Fast monte carlo simulation methods for biological reaction-diffusion systems in solution and on surfaces. SIAM J. Sci. Comput. 30, 3126 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Andrews S. S., Addy N. J., Brent R., Arkin A. P., Detailed simulations of cell biology with Smoldyn 2.1. PLOS Comput. Biol. 6, e1000705 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Michalski P. J., Loew L. M., SpringSaLaD: A spatial, particle-based biochemical simulation platform with excluded volume. Biophys. J. 110, 523–529 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Varga M. J., Fu Y., Loggia S., Yogurtcu O. N., Johnson M. E., NERDSS: A nonequilibrium simulator for multibody self-assembly at the cellular scale. Biophys. J. 118, 3026–3040 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Katsamba P., et al. , Linking molecular affinity and cellular specificity in cadherin-mediated adhesion. Proc. Natl. Acad. Sci. U.S.A. 106, 11594–11599 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Foty R. A., Steinberg M. S., The differential adhesion hypothesis: A direct evaluation. Dev. Biol. 278, 255–263 (2005). [DOI] [PubMed] [Google Scholar]
- 43.Xie Z.-R., Chen J., Wu Y., A coarse-grained model for the simulations of biomolecular interactions in cellular environments. J. Chem. Phys. 140, 054112 (2014). [DOI] [PubMed] [Google Scholar]
- 44.Ostwald W., Studien über die Bildung und Umwandlung fester Körper. Z. Phys. Chem. 22U, 289–330 (1897). [Google Scholar]
- 45.Barak R., et al. , Structural principles in robo activation and auto-inhibition. Cell 177, 272–285.e16 (2019). [DOI] [PubMed] [Google Scholar]
- 46.Stamper C. C., et al. , Crystal structure of the B7-1/CTLA-4 complex that inhibits human immune responses. Nature 410, 608–611 (2001). [DOI] [PubMed] [Google Scholar]
- 47.Su Z., Dhusia K., Wu Y., A computational study of co-inhibitory immune complex assembly at the interface between T cells and antigen presenting cells. PLOS Comput. Biol. 17, e1008825 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Rubinstein-Lab. cPcdh-simulation. https://github.com/Rubinstein-Lab/cPcdh-simulation. Deposited 4 August 2022.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or SI Appendix. The source codes of simulations developed in this work are available for download at https://github.com/Rubinstein-Lab (48).