Achieving the theoretical limit of strength in shell-based carbon nanolattices

Significance

Micro- and nanolattices have recently emerged as a class of mechanical metamaterials that can be designed to achieve remarkable mechanical properties, such as ultralow density, high stiffness, high strength, large deformability, excellent recoverability, and supersonic impact resilience in the lightweight regime. Here, using finite element simulations and additive manufacturing techniques, we designed and created shell-based carbon nanolattices with minimal surface topologies and nanoscale feature sizes to achieve ultrahigh moduli, compressive strengths, and specific strengths, surpassing all existing materials in this category. Our study demonstrates a mechanomaterial approach to creating materials with desirable properties by proactively deploying designed geometries during fabrication.

Abstract

Recent developments in mechanical metamaterials exemplify a new paradigm shift called mechanomaterials, in which mechanical forces and designed geometries are proactively deployed to program material properties at multiple scales. Here, we designed shell-based micro-/nanolattices with I-WP (Schoen’s I-graph–wrapped package) and Neovius minimal surface topologies. Following the designed topologies, polymeric microlattices were fabricated via projection microstereolithography or two-photon lithography, and pyrolytic carbon nanolattices were created through two-photon lithography and subsequent pyrolysis. The shell thickness of created lattice metamaterials varies over three orders of magnitude from a few hundred nanometers to a few hundred micrometers, covering a wider range of relative densities than most plate-based micro-/nanolattices. In situ compression tests showed that the measured modulus and strength of our shell-based micro-/nanolattices with I-WP topology are superior to those of the optimized plate-based lattices with cubic and octet plate unit cells and truss-based lattices. More strikingly, when the density is larger than 0.53 g cm⁻³, the strength of shell-based pyrolytic carbon nanolattices with I-WP topology was found to achieve its theoretical limit. In addition, our shell-based carbon nanolattices exhibited an ultrahigh strength of 3.52 GPa, an ultralarge fracture strain of 23%, and an ultrahigh specific strength of 4.42 GPa g⁻¹ cm³, surpassing all previous micro-/nanolattices at comparable densities. These unprecedented properties can be attributed to the designed topologies inducing relatively uniform strain energy distributions and avoiding stress concentrations as well as the nanoscale feature size. Our study demonstrates a mechanomaterial route to design and synthesize micro-/nanoarchitected materials.

Natural materials with cellular structures are often simultaneously lightweight and mechanically robust (1). Inspired by nature, many artificial cellular materials have been synthesized and are widely used for weight reduction, energy absorption, heat transfer, and vibration control (2). Cellular structures with periodic architectures have been demonstrated to exhibit mechanical properties that are typically superior to those with stochastic architectures at the same density (2). Among different types of cellular materials, of special interest are lattices with periodic architectures (1, 2), which can be classified as truss-, plate-, and shell-based lattices (3) according to their architecture and building block.

Over the past decade, micro-/nanolattices (3–5) with feature sizes of tens of micrometers and below have been created owing to rapid advances in additive manufacturing (AM) techniques. As an emerging class of mechanical metamaterials, micro-/nanolattices exhibit remarkable mechanical properties, such as ultralow density (6–8), high stiffness (8), high strength (9–11), large deformability (12, 13), excellent recoverability (11–14), supersonic impact resilience (15), and tunable acoustic bandgaps (16), which tremendously extend the accessible material property space. In recent years, increasing effort has been devoted to ultralight, ultrastiff, and ultrastrong micro-/nanolattices. Glassy carbon nanolattices with tetrahedral unit cells and strut diameters of ∼200 nm have been fabricated by two-photon lithography (TPL) and high-temperature pyrolysis (9), exhibiting a compressive strength of 310 MPa at a density of 0.35 g cm⁻³. Pyrolytic carbon nanolattices with octet and isotruss unit cells achieved a strength on the order of 1.0 GPa at densities below 1.0 g cm⁻³, which is close to the theoretical strength of pyrolytic carbon (10). The ultrahigh strength of these nanolattices has been attributed to the utilization of an ultrastrong constituent material (high-quality pyrolytic carbon) and reduced feature size comparable with the critical size for flaw insensitivity (5, 10, 17, 18). However, truss-based nanolattices cannot reach the Hashin–Shtrikman (HS) (19) and Suquet (20) upper bounds of the effective Young’s modulus and yield strength of isotropic cellular materials, which can be expressed as (19–23)

$$E^{\text{HSU}}=\frac{2E_s\overline{\rho }\left(7-5{\nu }_s\right)}{15\left(\overline{\rho }-1\right){\nu }_s{}^2+2\left(\overline{\rho }-6\right){\nu }_s-13\overline{\rho }+27}$$ [1]

$${\sigma }_y^{\text{SU}}=\frac{6{\sigma }_{ys}\overline{\rho }}{\sqrt{69-33\overline{\rho }}},$$ [2]

where the superscript “HSU” denotes the HS upper bound; “SU” denotes the Suquet upper bound; $\overline{\rho }$ is the relative density; and E_s, σ_ys, and ν_s are Young’s modulus, yield strength, and Poisson’s ratio of the constituent material, respectively. SI Appendix, Fig. S1 shows that Poisson’s ratio has negligible effect on the HS upper bound of the modulus. The stress concentration or localized deformation at nodes in the truss-based lattices can significantly degrade their mechanical properties up to ∼25 and 20% of the HS and Suquet upper bounds, respectively (23). On the other hand, the effective modulus and strength of porous materials according to the rule of mixtures are

$$E^{\text{VU}}=E_s\overline{\rho }$$ [3]

$${\sigma }_y^{\text{VU}}={\sigma }_{ys}\overline{\rho }.$$ [4]

Eqs. 3 and 4 also represent the theoretical limits of the effective modulus and strength of an anisotropic porous material based on the isostrain assumption. Eq. 3 is commonly referred to as the Voigt upper bound, hence the superscript “VU.” The theoretical limits predicted by Eqs. 3 and 4 are generally higher than those in Eqs. 1 and 2, which are upper bounds for isotropic materials.

Plate-based lattices with a combination of cubic and octet plate unit cells (referred to as cubic + octet plate) have been theoretically predicted to achieve the HS upper bound (21). Recent experimental studies showed that polymeric cubic + octet plate microlattices fabricated by TPL exhibited a modulus three times higher than those of truss-based analogs at the same relative density (22). More remarkably, pyrolytic carbon cubic + octet plate nanolattices fabricated via TPL and pyrolysis have been experimentally demonstrated to reach the HS and Suquet upper bounds (23), with a specific strength of 3.75 GPa g⁻¹ cm³, which outperforms all lightweight truss-based lattices (23) reported previously. However, cubic + octet plate lattices have a closed-cell geometry, which complicates their fabrication process and increases manufacturing costs (23). In particular, when one uses powder-bed or liquid-bath AM techniques to fabricate such a closed-cell plate lattice, holes often need to be introduced to allow for the removal and extraction of unexposed liquid photoresists or nonmolten powder enclosed within cells (22, 23). The stress concentration around the introduced holes or at the intersections of multiple plates can induce large localized deformation or crack nucleation, which reduces the reliability and strength of the overall structure in practical applications.

In addition to truss- and plate-based lattices, shell-based lattices consisting of periodic and nonintersecting smooth surfaces have also emerged in recent years (24–32). Most studies on the shell architecture have focused on triply periodic minimal surfaces (TPMSs; common examples include Schwarz P, Schwarz D, and gyroid surfaces) (33, 34), which have a minimized surface area within a given boundary and zero mean curvature at each point. Recently, Ni–P microlattices with a Schwarz P surface topology and shell thicknesses of 0.20 to 56 μm have been fabricated by self-propagating photopolymer waveguides and electroless plating, achieving ultralow densities of 1.7 × 10⁻³ to 0.29 g cm⁻³ and corresponding compressive strengths of 4.5 × 10⁻⁴ to 5.0 MPa (28). Polymer microlattices with a Schwarz D surface topology and shell thicknesses of ∼1 to 10 μm synthesized via TPL exhibited compressive yield strengths of 5.9 to 11.2 MPa at relative densities of 10 to 25%, which are higher than those of octet truss lattices at similar relative densities (27). CoCrMo lattices with Neovius and I-WP topologies have been synthesized via laser powder-bed fusion. When these lattices have shell thicknesses of 140 to 260 μm and relative densities of 11.4 to 73.6%, they possess tensile yield strengths of 5.4 to 242.6 MPa (29). Ti-6Al-4V lattices with Schwarz P, Neovius, and I-WP topologies have been fabricated through selective laser melting. These lattices have shell thicknesses of 300 to 500 μm, relative densities of 7.5 to 22.3%, and compressive strengths of 10.0 to 73.1 MPa (30). Recent finite element (FE) simulations showed the variations of various elastic and plastic properties (such as elastic constants, Zener ratio, yield strengths, and yield surfaces under different loading) of I-WP lattice with the relative density (31). It was found that for a given relative density, the I-WP lattice has higher modulus and strength than Schwarz P, octet and gyroid lattices, and open-cell foam (31). Since the constituent shell structure is a smooth and continuous curved surface, the stress concentration in shell-based lattices is significantly reduced and even avoided. Moreover, their open-cell topologies allow for easy removal and extraction of uncured powder or liquids after fabrication by AM techniques. These advantages suggest that it might be possible to construct shell-based micro-/nanolattices with unprecedented mechanical properties.

In this paper, we combine smooth architected shell topology, the size strengthening of nanomaterials, and high-resolution AM techniques to design and fabricate shell-based nanolattices with unprecedented mechanical properties. We fabricate polymeric microlattices with octet truss (35), isotropic truss (36), cubic + octet plate (21), and three TPMS [including Schwarz P (33), I-WP (34), and Neovius (37) surfaces] topologies via projection microstereolithography (PμSL) and/or TPL, and we further manufacture pyrolytic carbon shell-based nanolattices using a combination of TPL and high-temperature pyrolysis. In situ compression experiments reveal that pyrolytic carbon nanolattices with I-WP geometry exhibit ultrahigh modulus and strength, superior to those of the most advanced pyrolytic carbon truss-based nanolattices (10) and the cubic + octet plate nanolattices, which are the only isotropic porous materials to experimentally achieve HS and Suquet upper bounds to date (23). It is also found that the normalized strength of the shell-based lattice is sensitive to its feature size. The simulation-guided topology design, the advantage of small-scale size effects, and the fabrication simplicity make the shell-based micro-/nanolattices a promising class of mechanical metamaterials. In contrast to the conventional mechanics of materials approach, which typically focuses on mechanical properties of materials in existing forms, our study exemplifies a paradigm shift called mechanomaterials (38), in which mechanical forces and designed geometries are proactively deployed to program material properties at multiple scales.

Results

Design, Fabrication, and FE Simulations.

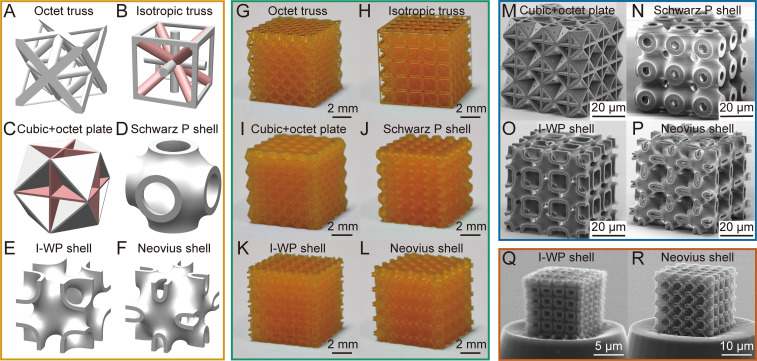
We investigated six types of lattices with truss-, plate-, and shell-based topologies, including representative octet and isotropic trusses; cubic + octet plate; and Schwarz P, I-WP, and Neovius shells. Fig. 1A–F presents the three-dimensional (3D) computer-aided design (CAD) models of various truss-, plate-, and shell-based unit cells. The 3D shell-based unit cells were constructed based on the TPMS via Surface Evolver software (39) and subsequent smoothing/thickening techniques (more details are in Methods). According to the CAD models, we fabricated polymeric truss-, plate-, and shell-based microlattices with 5 × 5 × 5 unit cells and feature sizes (strut diameters of truss-based lattices and plate/shell thicknesses of plate-/shell-based lattices) of 30 to 273 μm via PμSL. Fig. 1G–L shows digital images of the fabricated microlattices with various unit cells. During fabrication, we tailored the relative densities of the microlattices by maintaining the unit cell length as a constant of 1.5 mm and then, scaling their feature sizes. Thus, the octet/isotropic truss-, cubic + octet plate-, and shell-based lattices have controllable relative densities in the ranges from 8.1 to 39.1%, from 31.4 to 46.4%, and from 10.3 to 42.3%, respectively. According to the topological optimization, the ratio d_v/d_s of the isotropic truss unit cell is set as $2/3^{3/4}$ to achieve optimal isotropic stiffness (36), where d_v and d_s are the diameters of the vertical and slanted struts (i.e., the gray and pink parts in Fig. 1B), respectively. Similarly, the ratio t_c/t_o of the cubic + octet plate unit cell is taken as $8\sqrt{3}/9$ for isotropic and maximum stiffness (21), where t_c and t_o are the wall thicknesses of the cubic and octet subgeometries (i.e., the pink and gray parts in Fig. 1C), respectively. To remove/extract the unpolymerized resin after fabrication, we introduced a small hole with a diameter of ∼240 μm at the center of each plate in the plate-based lattice (Fig. 1I). To investigate the influence of the feature size on the mechanical properties of the lattices, we also fabricated plate- and shell-based microlattices from IP-Dip photoresist using TPL. These fabricated microlattices had feature sizes of 0.57 to 4.47 μm, which are approximately two orders of magnitude lower than those manufactured by PμSL. The hole diameter in the plate-based microlattices fabricated via TPL is ∼1.6 μm. Fig. 1M–P shows typical scanning electron microscopy images of the plate- and shell-based microlattices fabricated via TPL. SI Appendix, Fig. S2 shows schematic illustrations of the manufacturing processes of polymeric lattices via PμSL and TPL. Moreover, pyrolytic carbon shell-based nanolattices with I-WP and Neovius surfaces were created using TPL and high-temperature pyrolysis (9, 10). After pyrolysis, the polymeric microlattices transformed into pyrolytic carbon nanolattices with significant volumetric shrinkage and mass loss, resulting in the shell thickness being reduced to 177 to 333 nm. Fig. 1Q and R shows typical scanning electron microscopy images of pyrolytic carbon nanolattices with I-WP and Neovius surfaces, respectively.

Fig. 1.

Topologies and fabricated configurations of truss-, plate-, and shell-based lattices. (A–F) 3D models of various truss-, plate-, and shell-based unit cells. The pink parts in B and C have different sizes from the other gray parts. (G–L) Digital images of various truss-, plate-, and shell-based lattices fabricated by PμSL. (M–P) Scanning electron microscopy images of cubic + octet plate-based microlattices and shell-based microlattices with Schwarz P, I-WP, and Neovius minimal surfaces fabricated by TPL. (Q and R) Scanning electron microscopy images of pyrolytic carbon shell-based nanolattices with I-WP and Neovius topologies fabricated by TPL and high-temperature pyrolysis.

We performed FE simulations to analyze the mechanical properties and behaviors of various designed unit cells with periodic boundary conditions (40, 41). We calculated Young’s moduli, yield strengths, and Zener ratios (42) of these unit cells as a function of relative density. The corresponding results are shown in Fig. 2A and B and SI Appendix, Fig. S3. The Zener ratio is a common measure of the anisotropy of materials with cubic symmetry. It can be expressed as $a=\overline{E}/\left[2\overline{G}\left(1+\overline{\nu }\right)\right]$, where $\overline{E}$, $\overline{G}$, and $\overline{\nu }$ are the effective Young’s modulus, shear modulus, and Poisson’s ratio, respectively. SI Appendix, Fig. S4 shows a comparison of our calculated moduli and Zener ratios of the I-WP lattices with previous FE simulations (31), indicating that our results agree well with those from previous studies (31). Our simulations showed that the shell-based lattices with I-WP and Neovius topologies outperform both truss-based lattices and Schwarz P lattices under uniaxial compression (Fig. 2A and B). As shown in Fig. 2A and B, the modulus and strength of the shell-based lattices with I-WP and Neovius topologies are very close to those of cubic + octet plate lattices. In particular, the moduli of both shell-based lattices with I-WP and Neovius topologies and cubic + octet plate lattices reach the HS upper bound (Fig. 2A), and the strengths of the shell-based lattices with I-WP and Neovius topologies are close to those of the cubic + octet plate lattices and get closer to the Suquet upper bound (Fig. 2B). However, the modulus and strength of both shell- and plate-based lattices have an apparent gap with the bounds predicted by the Voigt limits in Fig. 2A and B, respectively. Note that the lattices with minimal surfaces under investigation are anisotropic (SI Appendix, Fig. S3), where similar to previous studies (23, 24, 35), the HS and Suquet upper bounds for isotropic materials can only serve as loose benchmarks to evaluate how high the modulus and strength of a lattice can reach. The anisotropy of the I-WP and Neovius unit cells was further compared with octet truss and cubic + octet plate unit cells (SI Appendix, Fig. S3). The cubic + octet plate unit cell has a Zener ratio of approximately one, indicating an isotropic behavior consistent with a previous computational study (21). In comparison, the Zener ratios of the I-WP and Neovius shells are larger than one, while that of the octet truss is smaller than one, meaning that the I-WP and Neovius shells and the octet truss are anisotropic. When $\overline{\rho }$ < 30%, the Zener ratio of the I-WP shell is closer to one than that of the Neovius shell, meaning that the I-WP shell is less elastically anisotropic than the Neovius shell.

Fig. 2.

FE simulations of uniaxial compression of various truss-, plate-, and shell-based unit cells. (A) Log–log plots of the normalized Young’s modulus vs. the relative density of different unit cells. (B) Log–log plots of the normalized yield strength vs. the relative density of different unit cells. (C–H) Strain energy distributions. The local strain energy density U_ε is normalized by the macroscopic solid fraction strain energy density ${\overline{U}}_{\epsilon }$ at the 0.2% offset yield point. The result indicates that the cubic + octet, Schwarz P, I-WP, and Neovius unit cells have a more uniform strain energy distribution during deformation than the octet and isotropic truss-based unit cells.

As shown in SI Appendix, Fig. S5, when small holes are introduced in the cubic + octet plate lattices, their moduli decrease by less than 10%, and no significant anisotropy is induced, which is consistent with previous FE modeling (23). However, their strengths are reduced by ∼20% due to the presence of holes and the associated stress concentration. According to the elastic–plastic theory of cellular structures (1), their modulus E and yield strength σ_y generally follow power law scaling with relative density as $E/E_s\hspace{0.17em}\propto \hspace{0.17em}{\overline{\rho }}^m$ and ${\sigma }_y/{\sigma }_{ys}\hspace{0.17em}\propto \hspace{0.17em}{\overline{\rho }}^n$, where m and n are constants dependent on the architecture (1). The scaling exponents m and n are equal to one for ideal stretching-dominated structures and m = 2 and n = 1.5 for bending-dominated structures. Least squares fitting of the data from the FE simulations gave m = 1.16 and n = 1.11 for I-WP (for $\overline{\rho }$ = 5 to 40%), m = 1.21 and n = 1.17 for Neovius (for $\overline{\rho }$ = 5 to 40%), and m = 1.15 and n = 1.16 for the cubic + octet plate (for $\overline{\rho }$ = 20 to 50%) (Fig. 2A and B), implying that the deformation mode in the I-WP shell, Neovius shell, and cubic + octet plate lattices is stretching dominated. Additional analyses of the scaling exponents of different unit cells are supplied in SI Appendix, section S1. Fig. 2C–H shows the strain energy density distributions of various truss-, plate-, and shell-based unit cells from the FE modeling. It is obvious that both shell- and plate-based unit cells exhibit a more uniform strain energy distribution during deformation than the truss-based unit cells, where a high strain energy density localizes and concentrates at the nodes or individual load-bearing struts. SI Appendix, Fig. S6 shows the von Mises stress distributions of various unit cells from the FE modeling, with the result also indicating the apparent stress concentrations near the nodes or intersections of struts or plates. The superior modulus and strength of the shell-based lattices with I-WP and Neovius topologies and cubic + octet plate lattices are closely associated with their uniform strain energy distributions during deformation, which are consistent with previous FE analyses on cubic + octet plate lattices (21).

Mechanical Behaviors and Properties of Polymeric Microlattices from Experiments.

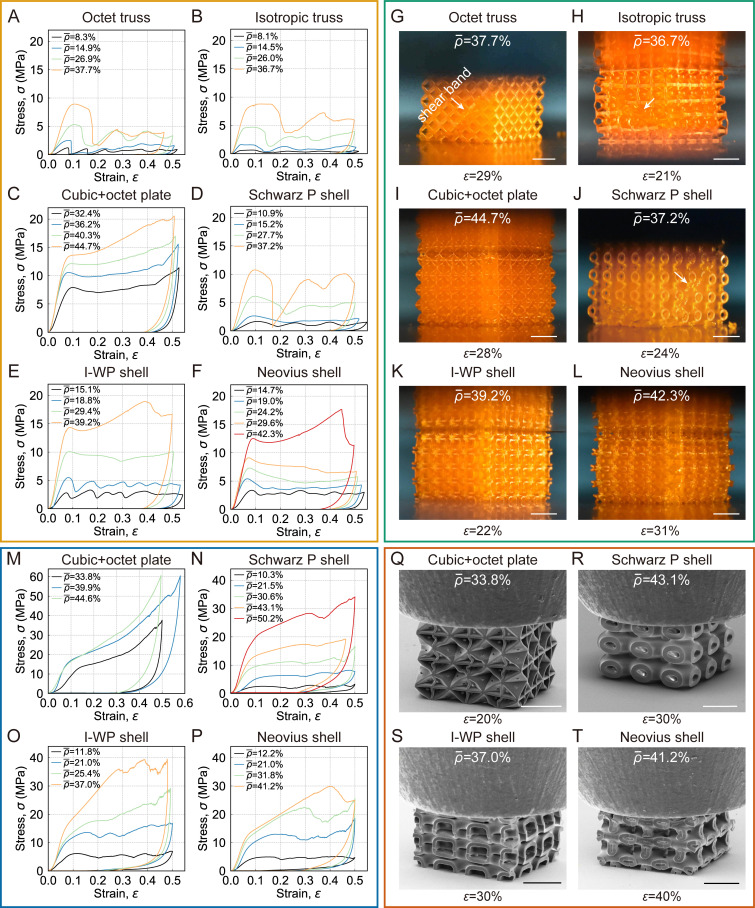
To investigate the actual mechanical properties and behaviors, we performed uniaxial compression tests on all fabricated polymer microlattices (details are in Methods). Fig. 3A–F shows typical stress–strain curves for various truss-, plate-, and shell-based microlattices with different relative densities. All curves exhibit three typical regimes: elastic, plastic, and unloading. In the plastic deformation regime, the stress in the truss-based and Schwarz P lattices fluctuates, while the stress in the cubic + octet plate, I-WP, and Neovius lattices with higher relative densities varies smoothly and increases in the last stage. Typical images in Fig. 3G–L and detailed snapshots in SI Appendix, Fig. S7 show the deformed features of the microlattices with various unit cells during compression. For the octet truss microlattices with $\overline{\rho }$ < ∼10%, the struts near the bottom fractured first, resulting in the first stress drop in the stress–strain curves. As the compressive strain increased, severe deformation propagated from the bottom to the top, leading to layer by layer crushing (SI Appendix, Fig. S7A–D) and associated stress fluctuation in the stress–strain curves (Fig. 3A). For $\overline{\rho }$ > ∼10%, multiple shear bands successively formed and traveled through the overall lattices (Fig. 3G and SI Appendix, Fig. S7E–H), resulting in significant stress drops in the stress–strain curves (Fig. 3A). Isotropic truss microlattices exhibited similar behaviors in the formation and propagation of shear bands at a high relative density (Fig. 3H). However, the isotropic truss microlattice shows a longer stress plateau before the first stress drop than the octet truss (Fig. 3B), which can be attributed to more uniform deformation in the isotropic truss at the initial stage of compression (Fig. 3H). Due to the limitations in the resolution of PμSL and one to two orders of magnitude differences between the unit cell size and plate thickness of the cubic + octet plate unit cell, the lowest relative density of the cubic + octet plate-based polymeric microlattice we fabricated is ∼30%. These high-relative-density plate-based lattices did not undergo localized deformation and exhibited much more uniform deformation (except for a few buckled plates) than the truss-based lattices (Fig. 3I and SI Appendix, Fig. S7I–L). Therefore, their stress–strain curves are quite distinct from those of truss-based lattices and similar to that of the fully dense polymerized resin (Fig. 3C and SI Appendix, Fig. S8A). The Schwarz P shell-based lattices with high relative densities behaved similarly to truss-based lattices, and shear localization occurred during plastic deformation (Fig. 3J and SI Appendix, Fig. S7M–P), leading to the stress drop in the stress–strain curve seen in Fig. 3D. Notably, the deformation of the I-WP and Neovius shell-based lattices with $\overline{\rho }$ > ∼20% is nearly uniform without visible localization at the overall structure level (Fig. 3K and L), which is significantly different from the truss-based lattices but similar to the plate-based lattices. Consequently, these shell-based lattices could sustain higher stress at large strains (even exceeding 40%) without catastrophic failure. For $\overline{\rho }$ < ∼20%, the plastic deformation mainly localized first at the bottom, leading to full compaction of the bottom layer (SI Appendix, Fig. S7Q–T). Subsequently, such behavior repeated and gradually propagated from bottom to top, exhibiting a layer by layer deformation mode (SI Appendix, Fig. S7Q–T). Each localized deformation corresponds to a stress drop in the stress–strain curve (Fig. 3E). However, unlike truss-based lattices, despite severe localized deformation, the I-WP and Neovius shell-based lattices with $\overline{\rho }$ < ∼20% did not exhibit catastrophic brittle fracture since their smooth and continuous topologies avoided stress concentrations (SI Appendix, Fig. S7Q–T). As a result, the stress drops in stress–strain curves of the I-WP and Neovius shell-based lattices with $\overline{\rho }$ < ∼20% are less pronounced compared with their truss-based analogs (Fig. 3A and E).

Fig. 3.

In situ compression experiments of various truss-, plate-, and shell-based microlattices. (A–F) Stress–strain curves of octet truss; isotropic truss; cubic + octet plate; and Schwarz P, I-WP, and Neovius shell large-scale polymeric microlattices with different relative densities (fabricated via PμSL). (G–L) Digital images of octet truss; isotropic truss; cubic + octet plate; and Schwarz P, I-WP, and Neovius shell large-scale microlattices with typical relative densities under compression. The arrows in G, H, and J indicate the shear bands formed during compression. (M–P) Stress–strain curves of the cubic + octet plate and Schwarz P, I-WP, and Neovius shell small-scale polymeric microlattices with different relative densities (fabricated via TPL). (Q–T) Scanning electron microscopy images of the cubic + octet plate and Schwarz P, I-WP, and Neovius shell small-scale microlattices with typical relative densities under compression. (Scale bars: G–L, 2 mm; Q–T, 20 μm.)

In situ scanning electron microscopy compression tests were performed on plate- and shell-based microlattices fabricated via TPL. The feature sizes of these fabricated microlattices are only 0.57 to 4.47 μm and approximately two orders of magnitude lower than those (30 to 273 μm) of the microlattices made by PμSL. Hence, the microlattices fabricated via TPL can be referred to as small-scale microlattices, while those fabricated by PμSL can be referred to as large-scale microlattices. Fig. 3M–T shows some typical stress–strain curves and scanning electron microscopy images of the plate- and shell-based small-scale microlattices. Additional scanning electron microscopy images of the deformed small-scale microlattices are shown in SI Appendix, Fig. S9. These small-scale microlattices exhibited nearly uniform deformation during compression when $\overline{\rho }$ > ∼25%, similar to the large-scale microlattices with high relative density, except that some plates in plate-based lattices buckled. It is noted that a layer by layer deformation mode was observed in the shell-based lattices with $\overline{\rho }$ < ∼25% (SI Appendix, Fig. S9I–L). Fig. 4 shows the variation of the average Young’s modulus and yield strength (normalized by Young’s modulus and yield strength of the constituent materials from SI Appendix, Fig. S8) of the tested polymeric microlattices. The corresponding scatter data are plotted in SI Appendix, Figs. S10 and S11. It is noted that in the scattered-data plot in SI Appendix, Fig. S10, the moduli of the large-scale microlattices are comparable with those of the small-scale ones. As shown in Fig. 4B, the average strengths of the small-scale microlattices are higher than those of their large-scale analogs, indicating a size effect known as “smaller and stronger”. This size effect is attributed to fewer flaws and imperfections in small-scale microlattices fabricated via TPL. More detailed analyses of the size effect will be supplied shortly. Furthermore, at both large and small scales, the moduli and strengths of the microlattices with I-WP unit cells are superior to those of their counterparts with other unit cells, indicating that the I-WP unit cell is mechanically more efficient than truss-based, cubic + octet plate-based, Neovius, and Schwarz P unit cells. We obtained the scaling exponents of the measured modulus and strength vs. the relative density of various unit cells by fitting the corresponding scatter data in SI Appendix, Figs. S10 and S11. The obtained scaling exponents are summarized in SI Appendix, Table S1 and compared with the results from the FE modeling. For large- and small-scale microlattices, most of the scaling exponents obtained from experiments are within 0.8 to 31.4% errors compared to the FE predictions, except that the scaling exponents for the modulus and strength of the small-scale cubic + octet plate microlattices show differences exceeding 37%. Such differences may be associated with the fact that it is difficult to fully eliminate the residual resins or photoresists from the micrometer-sized holes after printing (especially for the small-scale cubic + octet plate microlattices). This reflects the fabrication complexity of cubic + octet plate microlattices. In contrast, the scaling exponents for the modulus and strength of the small-scale microlattices with I-WP and Neovius shells are very close to the classic theoretical value of one, indicating that the small-scale microlattices with I-WP and Neovius shells are nearly stretching-dominated structures. More detailed discussions about the scaling exponents of various unit cells are given in SI Appendix, section S1.

Fig. 4.

Normalized modulus and strength vs. relative density diagrams of polymeric microlattices. (A) Log–log plots of the normalized compressive modulus vs. the relative density of various truss-, plate-, and shell-based microlattices. (B) Log–log plots of normalized yield strength vs. relative density of various truss-, plate-, and shell-based microlattices. In both A and B, the experimental data of the microlattices with feature sizes of 30 to 273 μm fabricated via PμSL are denoted by open markers, while the data of the microlattices with thicknesses of 0.57 to 4.47 μm fabricated via TPL are denoted by solid markers. The error bar of each data point in A and B is the SD from the statistical average for three to six experimental samples.

Mechanical Behaviors and Properties of Pyrolytic Carbon Shell-Based Nanolattices from Experiments.

Our study showed that the I-WP unit cell is optimal among the various topologies we studied and that small-scale polymeric microlattices with I-WP unit cells are closer to the Voigt upper bounds for modulus and strength than other geometries. To further improve the mechanical properties of the shell-based lattices, we fabricated pyrolytic carbon nanolattices with I-WP and Neovius surface topologies with feature size on the order of hundreds of nanometers and relative densities of 12.2 to 56.9% by TPL and subsequent pyrolysis. SI Appendix, Fig. S12 shows a series of scanning electron microscopy images of the polymeric shell-based microlattices before pyrolysis and the corresponding nanolattices obtained after pyrolysis. The obtained pyrolytic carbon shell-based nanolattices underwent significant mass loss and volumetric shrinkage, with shell thicknesses in the range of 177 to 333 nm. The minimum shell thickness of our nanolattices is smaller than the minimum strut size (∼261.2 nm) of pyrolytic carbon truss-based nanolattices (10). For shell-based nanolattices with sufficiently low relative density, some pyrolysis-induced imperfections (i.e., warping/buckling of thin shells) can form at the lattice edges (SI Appendix, Fig. S12). We used focused ion beam milling to cut these nanolattices and to check their interior geometries. SI Appendix, Fig. S13 shows scanning electron microscopy images of the cross-section of I-WP pyrolytic carbon nanolattices with relative densities of ∼52 and ∼13%. It is seen that the interior parts of nanolattices with low relative densities are nearly regular, resembling the designed geometry, and that the porous parts of pyrolytic carbon nanolattices with high relative densities are completely hollow and follow our designed geometry (Movies S1 and S2). We further conducted in situ scanning electron microscopy uniaxial compression tests on these pyrolytic carbon shell-based nanolattices. Fig. 5A and B shows the typical compressive stress–strain curves of I-WP nanolattices with $\overline{\rho }$ = 13 to 55% and Neovius nanolattices with $\overline{\rho }$ = 12 to 30%, respectively. The initial nonlinearity at small strains arises from a slight misalignment between the lattice structure and the flat indenter (10). After linear elastic deformation, pyrolytic carbon I-WP nanolattices with $\overline{\rho }$ > 25% catastrophically failed via brittle fracture, with fracture strain in the range of 7 to 23% (Fig. 5C–E and Movies S3–S5). Such failure behavior is similar to what is observed in pyrolytic carbon truss-based (10) and cubic + octet plate-based (23) nanolattices at higher relative densities. However, the I-WP nanolattices with $\overline{\rho }$ = 13% fractured into small pieces in a layer by layer manner, which is very similar to the progressive failure behavior recently reported in a pyrolytic carbon shell-based nanolattice with random spinodal topology (43) (Fig. 5F–H and Movie S6). The Neovius nanolattices exhibited deformation and failure behaviors similar to those of the I-WP nanolattices, as shown in Fig. 5I–N.

Fig. 5.

In situ compression experiments of pyrolytic carbon shell-based nanolattices. (A and B) Stress–strain curves of pyrolytic carbon shell nanolattices with I-WP and Neovius surfaces, respectively. The inset in A shows the stress–strain curve of I-WP nanolattice with a relative density of 13%. (C–H) Snapshots of I-WP nanolattices with relative densities of 31% (C–E) and 13% (F–H) at different compressive strains. (I–N) Snapshots of Neovius nanolattices with relative densities of 30% (I–K) and 12% (L–N) at different compressive strains. (Scale bars: C–E and I–K, 5 μm; F–H and L–N, 10 μm.)

Fig. 6A and B shows the variation of the modulus and yield strength, respectively, of all tested pyrolytic carbon shell-based nanolattices with relative density. The moduli and strengths of shell-based nanolattices at high relative densities reach the Voigt bounds (i.e., the theoretical limits for anisotropic materials), when the modulus of the constituent pyrolytic carbon is varied from 40 to 62 GPa [these two values represent the range of pyrolytic carbon as reported in two previous studies (44, 45)] and the yield strength of pyrolytic carbon under compression is set from 3.4 to 7.8 GPa as measured from previous experimental studies (18, 44).

Fig. 6.

Mechanical properties of pyrolytic carbon shell-based nanolattices with I-WP and Neovius surface topologies. (A and B) Variations in the compressive Young’s modulus and yield strength with the relative density, respectively. (C and D) Compressive Young’s modulus and fracture strength vs. density maps. Pyrolytic carbon nanolattices with tetrahedral truss (9), octet truss (10), isotropic truss (10), cubic + octet plate (23), and spinodal shell (43) unit cells are included for comparison. The lines of the theoretical limits in C and D are determined by the rule of mixtures and data of real materials (9, 10, 23). The lower bounds are defined by diamond, which has the highest specific strength of all bulk materials, while their upper bounds are determined by graphene, which has the highest strength of all materials so far.

We further compared the modulus and fracture strength of our pyrolytic carbon shell-based nanolattices with those of previous pyrolytic carbon nanolattices with other topologies. As shown in Fig. 6C and D, our I-WP and Neovius nanolattices outperform previously reported truss-based and spinodal shell-based nanolattices. When the density is larger than 0.47 g cm⁻³, our I-WP nanolattices show higher modulus and fracture strength than the state-of-the-art pyrolytic carbon plate-based nanolattices (23). In particular, the highest modulus and fracture strength of the I-WP nanolattices are 25.68 and 3.52 GPa, respectively. This modulus is higher than the maximum modulus (21.56 GPa) of pyrolytic carbon cubic + octet plate-based nanolattices (23) at a higher density of 0.73 g cm⁻³ (Fig. 6C), which is the highest modulus of pyrolytic carbon micro-/nanolattices reported to date (23). The corresponding strength is 18% higher than the highest strength achieved by pyrolytic carbon cubic + octet plate-based nanolattices (23) (Fig. 6D). Notably, due to the manufacturing complexity of cubic + octet plate unit cells, the lowest density of plate-based nanolattices fabricated previously is limited to 0.35 g cm⁻³. In comparison, our fabricated shell-based nanolattices reach a density as low as 0.17 g cm⁻³, which is ∼50% lighter than that of plate-based nanolattices. The highest specific compressive strength of our I-WP nanolattice reaches ∼4.42 GPa g⁻¹ cm³, which is higher than the corresponding highest value (1.90 GPa g⁻¹ cm³) of pyrolytic carbon truss-based nanolattices (10) and that (3.75 GPa g⁻¹ cm³) of pyrolytic carbon cubic + octet plate-based nanolattices (23), even exceeding almost all bulk materials (including certain diamond systems).

Discussion

A recent computational study predicted that cubic + octet plate-based lattices can reach the HS upper bound for the elastic modulus (21). Subsequent experimental studies demonstrated that pyrolytic carbon nanolattices with cubic + octet plate unit cells not only reach the HS upper bound for the modulus but also achieve the Suquet bound for the strength (23). Nevertheless, there exist two challenges in fabricating cubic + octet plate lattices with closed-cell nature by AM techniques (22, 23): removal of unexposed liquid photoresists from the closed cells and utilization of complex printing strategies to ensure high-quality plates with different orientations and thicknesses. Strategies to overcome the above fabrication challenges lead to very expensive manufacturing costs, which restrict the applications of cubic + octet plate-based lattices. Furthermore, the ratio of the unit cell length to feature size of the cubic + octet plate at low relative density is much larger than that of truss-based topologies at the same relative density. For example, this ratio is ∼110 for the cubic + octet plate and ∼11 for the octet truss at $\overline{\rho }$ = 10%. Together with the limitations of print resolution and the maximum print size of existing AM techniques, it is very difficult to fabricate highly voided cubic + octet plate micro-/nanolattices with such a high aspect ratio. Even if cubic + octet plate micro-/nanolattices with such a high ratio can be fabricated, the thin walls in the lattices are very susceptible to buckling/warping, which has a negative influence on both the modulus and the strength of the overall lattices (23). In contrast, our shell-based lattices with I-WP and Neovius topologies can be fabricated with relative ease due to the open-cell nature and geometrical features (such as smooth and continuous shells and interpenetrating void networks). Such fabrication simplicity leads to a larger range of available relative densities (or absolute densities) and less expensive costs for shell-based lattices than cubic + octet plate-based lattices.

Our experimental and numerical results indicated that the I-WP micro-/nanolattices achieve superior modulus and strength compared with the octet truss, isotropic truss, cubic + octet plate, and Schwarz P micro-/nanolattices. The unique, smooth, and continuous topology of the I-WP shell ensures efficient loading transfer between neighboring members and avoids stress concentrations, leading to uniform strain energy and stress distributions during deformation (as shown in Fig. 2G and SI Appendix, Fig. S6E). We estimated all scaling exponents for the modulus and strength vs. the relative density of pyrolytic carbon shell-based nanolattices (SI Appendix, Table S1), with values of 1.86 (I-WP) and 1.85 (Neovius) for Young’s modulus and 2.93 (I-WP) and 2.82 (Neovius) for yield strength. These values deviate from the theoretical predictions for ideal stretching-dominated structures and from our FE modeling for I-WP and Neovius unit cells, which can be attributed to pyrolysis-induced structural imperfections (10, 23) (i.e., warping/buckling of the very thin shell structure). Pyrolysis-induced warping/bulking is only observed in shell-based nanolattices with $\overline{\rho }$ < 25%. These structural imperfections induce deformation localization and even premature failure, eventually reducing the modulus and strength of the shell-based nanolattices at low relative densities. Similar phenomena have been observed in previous experimental studies of pyrolytic carbon cubic + octet plate-based nanolattices (23).

We fabricated three types of I-WP and Neovius micro-/nanolattices by using different AM techniques and constituent materials, including polymeric microlattices fabricated by PμSL, polymeric microlattices fabricated via TPL, and pyrolytic carbon nanolattices synthesized by TPL and pyrolysis. Due to the differences in the AM techniques and associated posttreatment, the feature size (i.e., shell thickness) of the three types of lattices varied in different scale ranges: from hundreds to tens of micrometers for the microlattices fabricated via PμSL, from several micrometers to submicrometers for the microlattices fabricated via TPL, and on the order of hundreds of nanometers for the nanolattices. Note that the three types of micro-/nanolattices were made up of different constituent materials. When we subsequently studied the effects of feature size on the mechanical properties of the shell-based micro-/nanolattices, these properties were normalized by the properties of the constituent materials. SI Appendix, Fig. S14 shows the variation of the normalized Young’s modulus and yield strength of all investigated I-WP and Neovius micro-/nanolattices with their shell thickness and relative density. The result indicates that the normalized Young’s modulus seems to be independent of the shell thickness, while the normalized yield strength increases as the shell thickness decreases. It is noted that as the relative density increases, the effect of the feature size on the normalized yield strength becomes more significant. Such size effect of the normalized yield strength can be attributed to fewer flaws and defects in the lattices with smaller feature sizes. In particular, when the feature size (177 to 333 nm) of our shell-based nanolattices is close to the critical size (239.6 to 550.5 nm) for the flaw insensitivity of the constituent material (i.e., pyrolytic carbon), the stress level of the shell-based nanolattices approaches the theoretical strength of the constituent material, leading to an ultrahigh overall strength reaching the theoretical limit (Fig. 6D). The estimation of the critical size for flaw insensitivity is given in SI Appendix, section S2. Therefore, the ultrahigh strength achieved in our pyrolytic carbon shell-based nanolattices is mainly attributed to a combination of unique topology, nanoscale feature sizes, and strong constituent material.

The Schwarz P, I-WP, and Neovius topologies we investigated are common examples from the TPMS family. These topologies are free of discontinuities and self-intersections, which can significantly reduce and even avoid stress concentrations under loading. Furthermore, the shell-based lattice can be regarded as a single periodic, smooth and connected interface separating two subvolumes, showing promising applications for the integration of structures and multifunctions, such as scaffolds for tissue engineering (46, 47), electrolyte membranes for fuel cells (48), and thermal management devices (49). In our current study, we showed that I-WP shell micro-/nanolattices exhibited enhanced mechanical properties compared with truss- and plate-based micro-/nanolattices due apparently to the unique topological features of the I-WP. It is well known that there exist a large number of different topologies in the TPMS family according to the mathematical representation (26). These abundant TPMS topologies provide a wide design space and inspiration, which allows us to seek more optimized shell structures with superior mechanical properties, performances, and multifunctionality.

Conclusion

We designed shell-based micro-/nanolattices by using I-WP and Neovius minimal surfaces and then fabricated polymeric shell-based microlattices via PμSL or TPL and pyrolytic carbon shell-based nanolattices via TPL and pyrolysis. Polymeric microlattices with truss- and cubic + octet plate-based unit cells were also fabricated for comparison. In situ compression on these fabricated micro-/nanolattices with different feature sizes showed that the I-WP microlattices exhibited moduli and yield strengths superior to truss-based and state-of-the-art plate-based lattices. Taking advantage of the mechanically efficient topology, nanoscale feature sizes, and strong constituent material, the strength of pyrolytic carbon I-WP nanolattices can reach its theoretical limit. With a specific compressive strength up to ∼4.42 GPa g⁻¹ cm³, our I-WP nanolattices outperform all previous micro-/nanoarchitected materials and almost all bulk materials (including certain diamond systems). The experimental results further indicated that the normalized Young’s modulus of the shell-based lattices is insensitive to the shell thickness, while the normalized yield strength increases as the shell thickness decreases. The current work provides a feasible path for the design and fabrication of lightweight architected materials to reach the theoretical limits of cellular materials and sheds light on the connections of the mechanical properties of architected materials with the topology, feature size, and constituent materials.

Methods

Topology Generation.

The TPMS-based shell topologies were generated via a three-step process. First, the TPMS geometries were created by using an open software, Surface Evolver, that can model the evolution of a surface subjected to various constraints toward minimal energy by a gradient descent method. Second, the created surfaces composed of many triangles were transformed into more accurate 3D models (i.e., 3D unit cell) by constructing nonuniform rational basis spline surfaces. Finally, the thickness of the unit cell was assigned a specific value to achieve a desirable relative density via the software package SolidWorks. Using the above process, we generated three types of unit cells with Schwarz P, I-WP, and Neovius topologies.

Fabrication.

Polymeric microlattices with 5 × 5 × 5 unit cells were fabricated from commercial GR resin (BMF Material Technology, Inc.) by using a PμSL instrument (nanoArch S140; BMF Material Technology, Inc.). During fabrication, the printing layer thickness was 10 μm. The diameters of the struts or the thicknesses of the plates or shells in the printed microlattices varied from 30 to 273 μm. Polymeric plate- and shell-based microlattices with 3 × 3 × 3 unit cells and thicknesses of 0.57 to 4.47 μm were fabricated out of IP-Dip photoresist (Nanoscribe, GmbH) by using a TPL direct laser writing system (Photonic Professional GT; Nanoscribe, GmbH). During writing, we used the dip-in laser lithography mode with a 63× objective lens. The laser power and writing speed were set as 21.5 mW and 8,000 μm s⁻¹, respectively. After writing, the samples were submerged in a propylene glycol monomethyl ether acetate (PGMEA) bath for development and in an isopropyl alcohol (IPA) bath for further cleaning. Pyrolytic carbon shell-based nanolattices with 5 × 5 × 5 unit cells were fabricated via a two-step method (9, 10), including high-resolution 3D printing (via TPL) and subsequent high-temperature pyrolysis. To ensure that the unexposed liquid photoresists were completely removed, the printed polymeric lattices with relative densities >35% were developed in the solvent upon heating to 45 °C, with continuous magnetic stirring at a speed of 300 rpm. The sequential development solvents and corresponding durations were PGMEA for 0.5 h, fresh PGMEA for 1.5 h, IPA for 1 h, and fresh IPA for 5 h. During pyrolysis, initial polymeric shell-based lattices were pyrolyzed at 900 °C for 1 h in a vacuum tube furnace with a ramp rate of 3 °C min⁻¹ up to the target temperature and were then cooled to room temperature at a natural rate. After pyrolysis, polymeric lattices suffered a pronounced volume shrinkage of >97.8% (dimensions shrank to 20 to 27% of their original values) and were transformed into pyrolytic carbon lattices with a side length of 5.23 to 32.28 μm and a thickness of 177 to 333 nm. The relative density of tested pyrolytic carbon nanolattices varied in the range from 12.2 to 56.9%.

The relative density of the polymeric microlattices at a larger scale can be obtained directly by dividing the sample mass measured via a balance by the mass of the fully dense polymerized resin with the same volume. For polymeric microlattices at a smaller scale and pyrolytic carbon nanolattices, CAD models were first constructed using scanning electron microscopy–measured dimensions of the fabricated lattices. Their relative densities were then determined by the fraction of volume occupied by the corresponding CAD models. For a specific relative density, we fabricated three to six different samples. Due to limitations in both printing resolution and maximum printing size in AM techniques, the ranges of relative densities of our shell-based microlattices fabricated via PμSL and TPL are from 10 to 42% and from 12 to 53%, respectively. When the relative densities of I-WP lattices fall below 10%, they seem susceptible to initial imperfections (i.e., buckling of the thin shell) (SI Appendix, Fig. S15).

Mechanical Testing.

All fabricated polymeric microlattices and pyrolytic carbon nanolattices were tested under uniaxial compression at a constant nominal strain rate of 10⁻³ s⁻¹. Polymeric microlattices with larger feature sizes (30 to 273 μm) were compressed using a testing machine with a 5-kN load cell (Zwick/Roell). Polymeric microlattices with smaller feature sizes (0.57 to 4.47 μm) and pyrolytic carbon nanolattices were compressed in a nanomechanical testing instrument (PI-85; Hysitron) with a 20- or 100-μm diamond flat punch tip inside an scanning electron microscope (FEI Quanta FEG 450). Calibrations of force sensor were always performed before using the PI-85 instrument. The engineering stress and strain were obtained by normalizing the recorded load and displacement by the cross-sectional footprint area and the initial height of the overall lattice, respectively. During calculation of the strain of pyrolytic carbon nanolattices, the strain was corrected by excluding the compliance of the support and loading system via a method (23) based on information from the in situ scanning electron microscopy videos. SI Appendix, Fig. S16 shows an example of a corrected stress–strain curve of I-WP nanolattice with a relative density of 55%. Young’s modulus was calculated by fitting the slope of the initial linear regime of the corrected stress–strain curve. The compressive yield strength was extracted from the 0.2% yield offset of the engineering stress–strain curve. For the nanolattices with relative density of <15%, the corresponding support after pyrolysis is slightly curved (Fig. 5F–H and L–N). We performed FE simulations to verify that the slightly curved support has negligible influence on the measurement of the modulus of the nanolattices (SI Appendix, Fig. S17).

FE Modeling.

FE simulations were performed via ABAQUS (Dassault Systèmes SE). During simulations, the unit cells were meshed via four-noded linear tetrahedron elements (C3D4), and 4 to 13 elements through the thickness of the shell/plate or through the diameter of the truss were used to ensure high accuracy. Additional simulations using 10-noded quadratic tetrahedron elements (C3D10) were performed on the I-WP and Neovius unit cells to verify the accuracy of the simulations based on C3D4 elements (SI Appendix, Table S2). The material was modeled as an elastic–perfectly plastic material with Young’s modulus of 2.1 GPa and a yield stress of 67.2 MPa (6). The effective properties ($\overline{E}$, $\overline{G}$, and $\overline{\nu }$) of different porous unit cells were computed using a representative volume element (RVE) technique. The open-source EasyPBC tool (40) was used to impose uniform strains on the RVE and to further maintain the unified periodicity by applying the required constraint equations and displacement boundary conditions.

Data, Materials, and Software Availability

All study data are included in the article and/or supporting information.