Subdiffusive hydrodynamics of nearly integrable anisotropic spin chains

Significance

While charge transport is known to be anomalous at low temperature in low-dimensional interacting systems, strong anomalies can be present at high temperature as well. Using the paradigmatic example of the quantum XXZ spin chain, we show that the presence of spin dephasing or generic additional Hamiltonian interactions leads to a broad regime of subdiffusive spin transport due to the interplay of emergent dynamical constraints and the effective screening of the relevant quasiparticle excitations. Although ordinary diffusion is eventually recovered at long times, the diffusion constant is shown to be nonperturbative and a discontinuous function of the strength of the external couplings.

Abstract

We address spin transport in the easy-axis Heisenberg spin chain subject to different integrability-breaking perturbations. We find subdiffusive spin transport characterized by dynamical exponent z = 4 up to a timescale parametrically long in the anisotropy. In the limit of infinite anisotropy, transport is subdiffusive at all times; for finite anisotropy, one eventually recovers diffusion at late times but with a diffusion constant independent of the strength of the perturbation and solely fixed by the value of the anisotropy. We provide numerical evidence for these findings, and we show how they can be understood in terms of the dynamical screening of the relevant quasiparticle excitations and effective dynamical constraints. Our results show that the diffusion constant of near-integrable diffusive spin chains is generically not perturbative in the integrability-breaking strength.

Many strongly interacting one-dimensional and quasione-dimensional experimental systems are approximately described by integrable models, such as the Heisenberg and Hubbard models (1–6). Although integrable systems are in some sense exactly solvable, the problem of characterizing their long-distance, late-time hydrodynamic response at nonzero temperature remained largely open until the recent advent of generalized hydrodynamics (GHD) (7–11) as well as modern numerical methods (12). It was found, remarkably, that although integrable systems possess stable, ballistically propagating quasiparticles, certain quantities (such as spin in the Heisenberg model) are transported diffusively or superdiffusively (11, 13–15). Given that experiments are never described by perfectly integrable systems, it is natural to ask how weak integrability-breaking perturbations affect transport dynamics. Incorporating such perturbations when the unperturbed model is already interacting is a challenging open problem, despite much recent progress (16–20). Qualitatively, integrability-breaking perturbations endow the ballistic quasiparticles with a finite lifetime, after which they scatter or decay. For quantities such as energy that are transported ballistically in the integrable limit, integrability breaking generically renders transport diffusive; the zero-frequency singularity or “Drude peak” associated with ballistic transport broadens into a Lorentzian feature of width set by the strength of the integrability-breaking perturbation or alternatively, by the lifetime of the quasiparticles (15–17, 19–29), in full analogy with the standard quantum Boltzmann equation (30).

In the present work, we address instead what happens to quantities that are diffusive in the unperturbed integrable limit. We shall see that the mechanism at play in this case sharply differs from the usual broadening of Drude weight; transport coefficients are discontinuous functions of the integrability-breaking coupling.

As a concrete example, we consider spin transport in the anisotropic Heisenberg (or XXZ) spin chain, governed by the Hamiltonian

$$H_{\text{XXZ}}=J{\displaystyle \sum _i(S_i^x{S}_{i+1}^x+S_i^y{S}_{i+1}^y+\mathrm{\Delta }{S}_i^z{S}_{i+1}^z)},$$ [1]

where $S_i^{\alpha }={\sigma }_i^{\alpha }/2$ represents the $\alpha =(x,y,z)$ spin-1/2 operator on site i, J is an overall energy scale (set to one in what follows), and Δ is the anisotropy parameter. At nonzero temperature, the equilibrium state is always a paramagnet, and the late-time dynamics is qualitatively the same regardless of the sign of J.

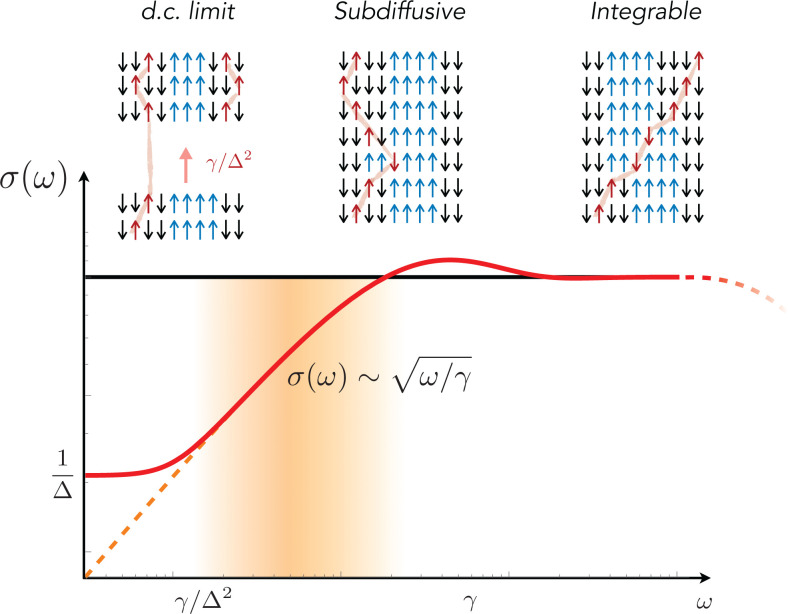
When $\mathrm{\Delta }>1$, transport is diffusive in the purely integrable limit, with a diffusion constant $D_{\text{XXZ}}(\mathrm{\Delta })$ that is exactly known (31, 32); as $\mathrm{\Delta }\to \infty ,\hspace{0.17em}{D}_{\text{XXZ}}(\mathrm{\Delta })$ approaches a nonzero constant when rescaling the temperature so as to keep $\beta \mathrm{\Delta }$ fixed. We address here what happens when integrability is weakly broken, with some generic perturbation of strength γ. Explicitly, we consider the effect of local spin dephasing, described by the Hamiltonian $H=H_{\text{XXZ}}+\sqrt{\gamma }{\displaystyle {\sum }_i{\eta }_i}(t)S_i^z$, with white noise η. Since the integrable and perturbed nonintegrable models are both diffusive, one might expect that the diffusion constant $D_{\text{XXZ}}(\gamma ,\mathrm{\Delta })$ simply picks up γ-dependent corrections $D_{\text{XXZ}}(\gamma ,\mathrm{\Delta })=D_{\text{XXZ}}(\mathrm{\Delta })+O({\gamma }^r)$, with some power r. What we find is much more striking; for arbitrary $\gamma >0$, the true diffusion constant $D(\gamma ,\mathrm{\Delta })$ is strongly suppressed at large Δ and approaches zero as $\mathrm{\Delta }\to \infty$. Moreover, $D(\gamma ,\mathrm{\Delta })$ does not depend on the strength of the integrability-breaking perturbation. In the limit $\mathrm{\Delta }\to \infty$, the dynamics is subdiffusive, with the space-time scaling $x\sim t^{1/4}$. For large finite Δ, subdiffusion occurs over a timescale that grows with Δ before crossing over to diffusion at the latest times. In effect, the integrability-breaking perturbation moves spectral weight from the spin conductivity from very low frequencies to a peak at frequency $\omega \sim \gamma$, as shown in Figs. 1 and 2.

Fig. 1.

Anomalous low-frequency spin conductivity in the noisy XXZ chain (in log–log scale). In the frequency regime $\frac{\gamma }{{\mathrm{\Delta }}^2}\ll \omega \ll \gamma$, spin transport is subdiffusive with $\sigma (\omega )\sim \sqrt{\omega /\gamma }$, corresponding to the dynamical exponent z = 4. At very low frequency, the conductivity eventually saturates to a finite d.c. value proportional to ${\mathrm{\Delta }}^{-1}$ (Fig. 2). The cartoon in Upper illustrates the dominant spin dynamical processes at different timescales; single (mobile) magnons are pictured in red, and strings (frozen) are in blue (in the text).

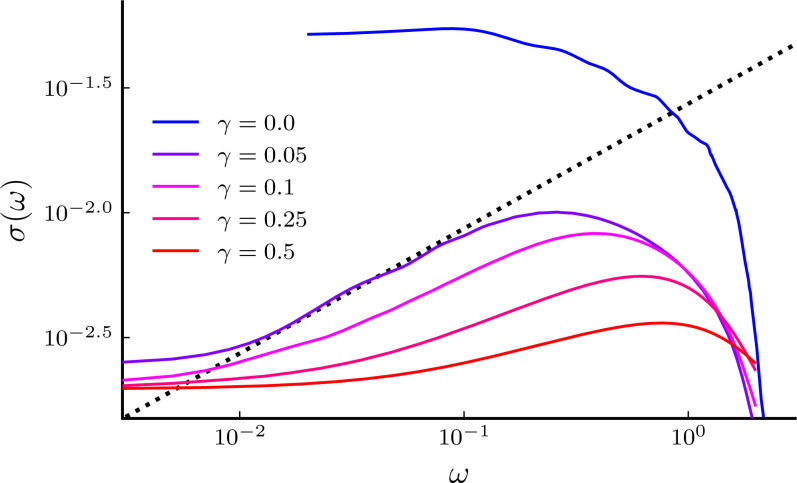
Fig. 2.

Low-frequency spin conductivity in the noisy XXZ chain. Plot of $\sigma (\omega )$ obtained from MPO simulations at Δ = 12 and for various values of the noise strengths γ. The dashed line corresponds to the predicted intermediate subdiffusive behavior $\sim {\omega }^{1/2}$. Note that the plot starts at $\omega =0.005$, and data for $\gamma =0.05$ are expected to converge to lower values at smaller ω. Moreover, the spectral weights are also redistributed by the noise at higher frequencies (not shown in this plot).

Observable

We consider linear-response transport under the Hamiltonian Eq. 1. We expect that our results hold at any nonzero temperature, but for simplicity, we will work in the high-temperature limit, where the frequency-dependent conductivity is simply related to the autocorrelation function of the spin current operator $\widehat{J}(t)={\displaystyle {\sum }_n{\widehat{j}}_n}(t)$, with $j_n=i(S_n^{+}{S}_{n+1}^{-}-S_n^{-}{S}_{n+1}^{+})/2$:

$$T\sigma (\omega )={\displaystyle {\int }_0^{\infty }d}t\hspace{0.17em}\langle \widehat{J}(t){\widehat{j}}_0(0)\rangle e^{i\omega t}.$$ [2]

Under diffusive dynamics (i.e., for Eq. 1 with no integrability-breaking perturbation), the current–current correlator decays on a finite timescale τ; therefore, the conductivity is close to its d.c. value, $\sigma (\omega )\simeq D\chi$ for $\omega \tau \ll 1$, with χ the static susceptibility. For finite γ, remarkably, the correlator overshoots, so the late-time current, on timescales $\gamma t>1$, becomes anticorrelated with the early-time current. Thus, the integrability-breaking perturbation shifts spectral weight from very low frequencies to a peak at $\omega \sim \gamma$ (Figs. 1 and 2).

Quasiparticle Picture

We now explain the origin of this phenomenon in terms of the quasiparticle structure of Eq. 1. For $\mathrm{\Delta }>1$, this model has infinitely many quasiparticle species, called “strings.” These strings are easiest to visualize near the ferromagnetic vacuum (Fig. 1), where they simply correspond to spin domains of various sizes. Under the integrable dynamics, the number of domains of each size is separately conserved. At large Δ, a domain of size s can only move collectively via an $s\hspace{0.17em}\text{th}$-order process in perturbation theory, with an effective tunneling amplitude $\sim {\mathrm{\Delta }}^{1-s}$. Because of integrability, even in a high-temperature thermal state, these strings remain stable, and their characteristic velocity scale does not change appreciably, although their other properties are highly renormalized, as we now discuss.

$\mathbf{\Delta }=\infty$ Limit

It is instructive to consider the $\mathrm{\Delta }=\infty$ limit first; this limit is sometimes called the “folded XXZ model” (33–35). Here, the quasiparticle picture simplifies; all strings with s > 1 are frozen, and the only dynamics is due to the s = 1 strings, or magnons, moving in a static background of spin domains with velocity $v=O(1)$ (36). In the integrable limit, magnons move ballistically. However, as a magnon moves through the system, the spin it carries fluctuates (e.g., when it is moving through a spin-up domain, it does so as a minority spin-down particle, but on passing into a spin-down domain, it becomes a minority spin-up particle). On average, there are equally many up and down domains in a high-temperature state, so the magnon carries no net spin (hence, the absence of ballistic transport). However, over a time t, the region it traverses (of size $\left|vt\right|$) has a net magnetization $1/\sqrt{\left|vt\right|}$ from equilibrium thermal fluctuations. Thus, the effective spin carried by the magnon over this distance is $O(1/\sqrt{\left|vt\right|})$. Since in time t, the magnon transports an amount of spin $\sim t^{-1/2}$ over a distance $\sim t$, spin transport is diffusive with an O(1) diffusion constant. At infinite temperature, this diffusion constant has the closed-form expression $D(T=\infty ,\mathrm{\Delta }=\infty )=4/(3\pi )$ (31, 32).

We now consider, heuristically, what happens when integrability is broken by a generic local perturbation. In principle, the perturbation could either relax the momentum of a magnon or change the number of magnons. As we will discuss below, the latter process becomes impossible for generic, sufficiently local perturbations at $\mathrm{\Delta }=\infty$. Thus, the only thing perturbations can do is scatter magnons. One can easily adapt the previous argument to the case of diffusive magnons; in a time t, they have moved by an amount $\sqrt{Dt}$, over which the net magnetization fluctuations are ${(Dt)}^{-1/4}$; thus, one would spin transport to be subdiffusive, with the scaling $x\sim t^{1/4}$, corresponding to a conductivity scaling as $\sigma (\omega )\sim \sqrt{\omega }.$ As a function of time, spin transport would be diffusive until the mean free time of the magnon (which depends on the integrability-breaking parameter) and subdiffusive thereafter.

Mapping to Constrained Models

This heuristic argument can be put on a firmer footing if one notes that the dynamics at infinite Δ is controlled by the “folded XXZ” Hamiltonian (33), which consists of flip-flop XY interactions acting on a constrained subspace with domain wall number conservation (since creating or destroying domain walls costs infinite energy). This model is interacting and integrable, and the only allowed spin moves are those that conserve the total domain wall number—similar constraints have been considered recently in refs. 33 and 37–41. This constrained model is discussed further in Infinite Δ XXZ Chain, and we have checked numerically that its dynamics is subdiffusive with z = 4 whenever integrability is broken. We have also checked that any perturbations acting on four or fewer sites that conserve the domain wall number also conserve the number of magnons. Thus, as we anticipated, the only process an integrability-breaking perturbation (acting on fewer than five sites) can do is to scatter magnons, supporting the heuristic argument above.

Interestingly, one can go further by considering dynamics that is constrained and conserves magnon number but is otherwise random. This corresponds to the case where integrability is strongly broken. The transport properties of this stochastic model were very recently computed by a Markov-matrix method in ref. 41; the subdiffusive transport exponent $x\sim t^{1/4}$ was computed from the low-energy spectrum of the Markov matrix in that work. To check that the phenomenon we are considering is due specifically to magnon physics [and not a generic consequence of the domain wall conservation law, which holds until exponentially long timescales $\sim {\text{e}}^{\mathrm{\Delta }}$ (42)], we have explored random dynamics that obeys the domain wall constraint but allows for moves on five or more sites. Such gates do not in general conserve magnon number; for example, they connect the configuration $\dots \downarrow \downarrow \uparrow \uparrow \uparrow \downarrow \downarrow \uparrow \downarrow \dots$ to $\dots \downarrow \downarrow \uparrow \uparrow \downarrow \downarrow \uparrow \uparrow \downarrow \dots$, turning two 2-strings into a magnon and a 3-string. We find that the random constrained dynamics is diffusive for all gate sizes greater than or equal to five (Infinite Δ XXZ Chain), highlighting the central role that magnon physics and proximity of integrability play in subdiffusion. In particular, we emphasize that the physics at play here is unrelated to other types of z = 4 dynamics in the presence of the fraction-like constraints recently discussed in the literature (38, 43–45).

Finite $\mathbf{\Delta }$ and Noise

We now turn to finite Δ. To discuss this case, we need to specify the noise model more explicitly. We first consider the simplest integrability-breaking perturbation, namely uncorrelated noise. We take $H=H_{\text{XXZ}}+\sqrt{\gamma }{\displaystyle {\sum }_i{\eta }_i}(t)S_i^z$, where the noise η has the properties $\langle {\eta }_i\rangle =0$ and $\langle {\eta }_i(t){\eta }_j(0)\rangle =\delta (t){\delta }_{ij}$. This noise backscatters magnons at a rate $\sim \gamma$. It can also create magnons out of strings by the following process; one end of a larger string virtually hops away from the rest of the string by one site, with amplitude $1/\mathrm{\Delta }$, and is put on shell by the noise, giving a transition rate $\gamma /{\mathrm{\Delta }}^2$.

The quasiparticle picture is modified in this case as follows (Fig. 1). Magnons that were created at the initial time propagate ballistically, with a vanishing net magnetization due to scattering with larger bound states of magnons (strings) (Fig. 1) until they hit their mean free path, contributing to diffusive spin transport. At later times, they contribute only through subdiffusion due to their randomized velocities. However, new magnons are created at a rate $\gamma /{\mathrm{\Delta }}^2$ and then, propagate for a time $1/\gamma$ before backscattering; thus, at any time, some fraction of magnons are contributing to diffusive transport. In addition to magnons, one should also consider the contribution to transport due to mobile larger strings; however, the velocity of these large strings is exponentially suppressed in Δ, and in any case, they will also contribute subdiffusively to transport by exactly the same reasoning as we used for magnons.

The nature of the transport cross-overs can be understood by a straightforward scaling argument. Let us define a time-dependent diffusion constant via the relation $D(t)=\frac{1}{2}\frac{d\delta x^2}{dt}$ with $\delta x(t)$ the variance of the spin structure factor $\mathcal{C}(x,t)=\langle {\sigma }_z(x,t){\sigma }_z(0,0)\rangle$. If γ is small enough, then on a timescale $1/\gamma ,\hspace{0.17em}D(t)=D_{\text{XXZ}}(\mathrm{\Delta })$ is some well-defined O(1) number, which is approximately independent of Δ for $\mathrm{\Delta }\gg 1$. On timescales $1/\gamma \ll t\ll {\mathrm{\Delta }}^2/\gamma$, the dynamics will be subdiffusive, so $D(t)\sim t^{-1/2}$. Enforcing continuity at $t_{\gamma }=1/\gamma$, we find that $D(t)\sim {(\gamma t)}^{-1/2}$, independently of Δ. Finally, enforcing continuity at the later cross-over timescale $t_{\mathrm{\star }}={\mathrm{\Delta }}^2/\gamma$, we get the asymptotic diffusion constant $D_{\infty }\sim 1/\mathrm{\Delta }$, with no γ dependence. We thus expect the scaling form (valid for $\gamma \ll 1,\hspace{0.17em}\omega \ll \gamma ,\hspace{0.17em}\mathrm{\Delta }\gg 1$, and $\frac{\omega {\mathrm{\Delta }}^2}{\gamma }$ fixed) for the conductivity:

$$\sigma (\omega ,\gamma ,\mathrm{\Delta })=\frac{1}{\mathrm{\Delta }}f\left(\frac{\omega {\mathrm{\Delta }}^2}{\gamma }\right),$$ [3]

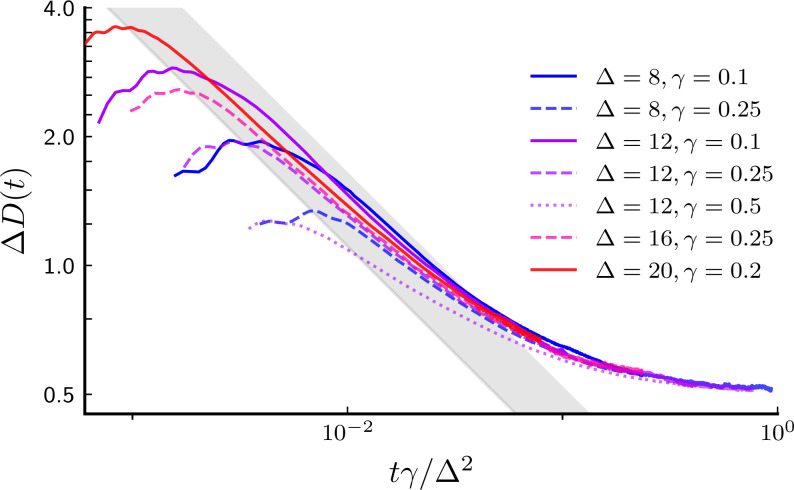
with f(0) as a constant and $f(x)\sim \sqrt{x}$ as $x\gg 1$. Equivalently, we expect a time-dependent diffusion constant scaling as $D=\frac{1}{\mathrm{\Delta }}g\left(\frac{t\gamma }{{\mathrm{\Delta }}^2}\right)$. As shown in Fig. 3, direct numerical calculations of D(t) using matrix product operator (MPO) methods (46) collapse well onto this scaling form even for relatively large γ and intermediate Δ. Curiously, our numerical results suggest that ${\lim }_{y\to \infty }g\left(y\right)=\frac{1}{2}$, although we do not have a theoretical prediction for this value.

Fig. 3.

Cross-over of the time-dependent diffusion in the noisy XXZ spin chain. Diffusion constant D(t) times Δ at infinite temperatures, obtained from MPO simulations, for the time evolution in the presence of on-site noise of strength γ at large anisotropy Δ is shown. The axes are rescaled to test the theoretical prediction in Eq. 3. For small γ and large Δ, we find good agreement; in particular, the diffusion constant saturates to a γ-independent value at long times [up to $O(\gamma /{\mathrm{\Delta }}^2)$ corrections] and is compatible with subdiffusion with $D(t)\sim t^{-1/2}$ (shown as the shaded region) for ${\gamma }^{-1}\ll t\ll {\mathrm{\Delta }}^2/\gamma$.

Hamiltonian Perturbations

So far, we included spin dephasing both to allow for well-converged numerical checks and to simplify the theoretical analysis by allowing us to neglect energy conservation. We now turn to generic Hamiltonian perturbations with perturbation strength $\delta$. Here as well, the timescales for magnon backscattering and for the string number conservation breaking are both expected to scale as $1/{\delta }^2$ but with two different Δ dependences, giving a broad subdiffusive regime. In particular, we can derive general lower bounds on the cross-over timescale to diffusion (or equivalently, upper bounds on the diffusion constant), even if these might not be tight for all perturbations. The first lower bound, which is just a consequence of energy conservation, can be derived as follows. As we saw above, the physics that sets this cross-over timescale is the creation or destruction of magnons. Consider the simplest such process, in which two 2-strings collide to create a magnon and a 3-string. This process must conserve energy; since the initial and final states have the same number of domain walls, it suffices to consider the kinetic energy of the magnons. The bandwidth of the 2-string is suppressed by a factor $1/\mathrm{\Delta }$ (at large Δ) relative to that of the magnon. (The bandwidth of the 3-string is suppressed by yet another factor of Δ and is negligible.) Thus, conservation of energy forces the magnon to lie in a state within an energy window of width $\sim {\mathrm{\Delta }}^{-1}$ measured from the center of the magnon band. This phase space restriction forces the magnon creation/decay rate to scale as $1/\mathrm{\Delta }$ and (by the cross-over time analysis above) implies that $D(\gamma ,\mathrm{\Delta })\sim 1/\sqrt{\mathrm{\Delta }}$.

While our analysis was phrased in terms of a particular scattering process (which we expect to be the leading one), it is clear that any scattering process creating a magnon out of higher strings will acquire the same bandwidth restriction, so this bound applies to all local Hamiltonian perturbations. For the specific subclass of nearest neighbor or on-site perturbations, one can derive a stronger bound that combines the two arguments above. For these, the matrix element for tunneling to a configuration with a broken magnon number is itself suppressed by $1/\mathrm{\Delta }$, as we discussed above for on-site noise. Combining this with the phase space restriction, we find that the cross-over timescale grows at least as ${\mathrm{\Delta }}^3$, giving the upper bound $D(\mathrm{\Delta })\sim 1/{\mathrm{\Delta }}^{3/2}$ and a subdiffusive region within the timescale $1/{\delta }^2\mathrm{\lesssim }t\mathrm{\lesssim }{\mathrm{\Delta }}^3/{\delta }^2$.

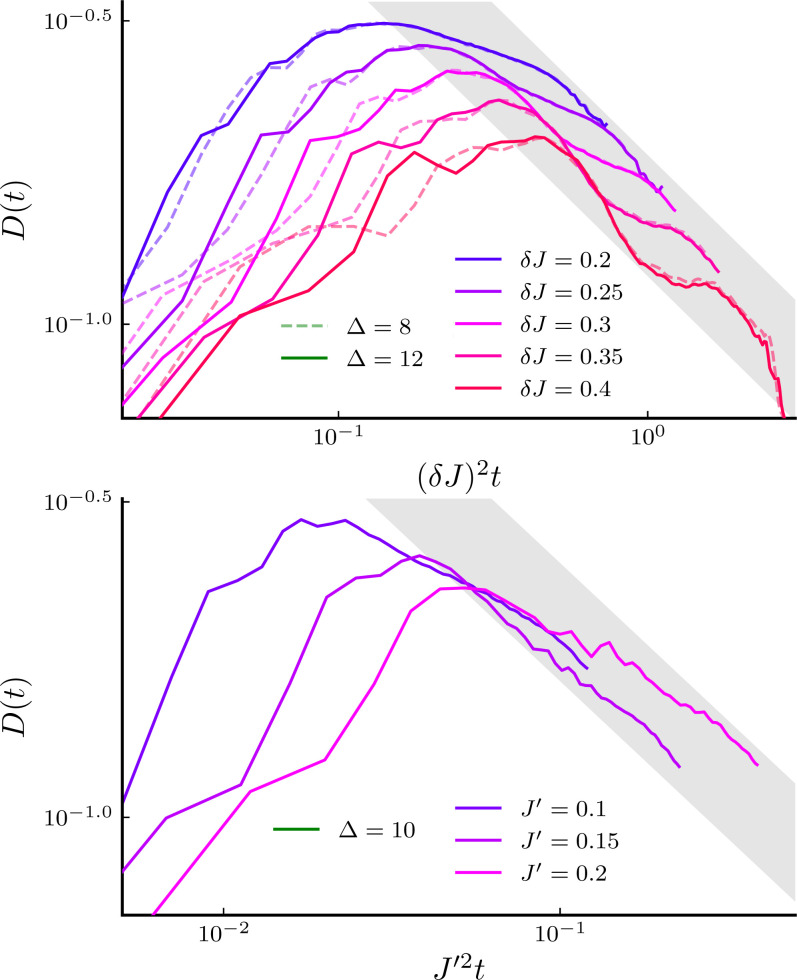
To test these predictions, we have simulated the spin chains given by the Hamiltonian $H=H_{\text{XXZ}}+V$, where the XXZ Hamiltonian is either perturbed with integrability-breaking staggered couplings $V=\delta J{\displaystyle {\sum }_i{(-1)}^i}(S_i^x{S}_{i+1}^x+S_i^y{S}_{i+1}^y+\mathrm{\Delta }{S}_i^z{S}_{i+1}^z)$ or next nearest neighbor couplings $V=J\prime {\displaystyle {\sum }_i(S_i^x{S}_{i+2}^x+S_i^y{S}_{i+2}^y+\mathrm{\Delta }{S}_i^z{S}_{i+2}^z)}$. Again, we simulated the dynamics using MPO methods. For Hamiltonian perturbations as opposed to noisy perturbations, the simulation complexity (captured by the bond dimension of the MPO) grows exponentially in time. Therefore, our simulations are limited to relatively early times and cannot extract the saturated diffusion constant; nevertheless, they clearly display the nonmonotonicity of D(t) and the onset of the subdiffusive regime for $1/{\delta }^2\mathrm{\lesssim }t$, where we indeed correctly predict $D(t)\sim 1/\sqrt{{\delta }^{2}t}$ (Fig. 4).

Fig. 4.

Hamiltonian perturbations. Time-dependent diffusion constant D(t) with the couplings staggered by an amount δJ at large anisotropy $\mathrm{\Delta }\in \{8,12\}$ (Upper) and next nearest neighbor couplings $J\prime$ at Δ = 10 (Lower) obtained from MPO simulations. Consistent with the theoretical prediction, D(t) exhibits a subdiffusive regime consistent with $D(t)\sim t^{-1/2}$ (shown as the shaded regions).

Discussion

In this work, we have presented evidence that integrability breaking has drastic effects on transport in integrable systems where the integrable limit is itself diffusive, in sharp constraint with the ballistic case. For the infinitesimal integrability-breaking parameter γ, the diffusion constant jumps to a value that is independent of γ but is parametrically lower than the integrable diffusion constant at large Δ. The mechanism for this abrupt change in the diffusion constant is the emergence of a large subdiffusive temporal regime, which becomes the asymptotic behavior in the limit of large anisotropy. We presented a kinetic argument for this asymptotic subdiffusive behavior in terms of the diffusive propagation of magnons whose magnetization is screened by thermal fluctuations.

We expect such nonmonotonicity of the diffusion constant and the $\sqrt{\omega }$ dependence of the conductivity at low frequencies to be observable in cold atomic settings with emergent XXZ interaction (40, 47–49) and in anisotropic Heisenberg–Ising compounds (50, 51).

Our findings also clarify the reasons behind the apparent difficulties encountered in evaluating diffusion constants by dissipative truncation schemes, as introduced in ref. 52. One should indeed expect that close to integrability, the diffusion constant is not a continuous function of the dissipation strength, making it hard to extrapolate its value in the limit of small noise. Our results could also be related to the vanishing of the diffusion constant $D\sim {\mathrm{\Delta }}^{-1}$ obtained coupling an XXZ chain to boundary Lindblad spin reservoirs (53).

Materials and Methods

A Stochastic Kinematically Constrained Model with Domain Wall Number Conservation.

In this section, we consider a stochastic kinetically constrained model, where the total number of domain walls is strictly conserved and the only allowed spin moves are those that respect this conservation law in addition to charge conservation. The discrete time evolution can be constructed from a brick-wall pattern of nonunitary gates that implement all possible transitions allowed by symmetries with equal probability.

For interactions acting on M = 4 sites, the allowed moves are flip-flop spin flips between sites j and j + 1 if the spins on sites j – 1 and j + 2 are aligned. Similar constraints have been considered in refs. 33, 37–40, and 54, and this model was studied in detail in ref. 41. The allowed moves constrain the motion of the domain walls themselves so that isolated domain walls are frozen, but adjacent pairs of domain walls (corresponding to isolated magnons in some background) can hop. In that case, the number of magnons (and more generally, the string number) is conserved by the evolution. This corresponds to a form of intermediate integrability breaking where the string number is conserved but magnons move diffusively (while larger strings are frozen). This is the case relevant to integrability breaking in the XXZ spin chain discussed in the text, and this model was shown to have subdiffusive spin dynamics with z = 4 in ref. 41.

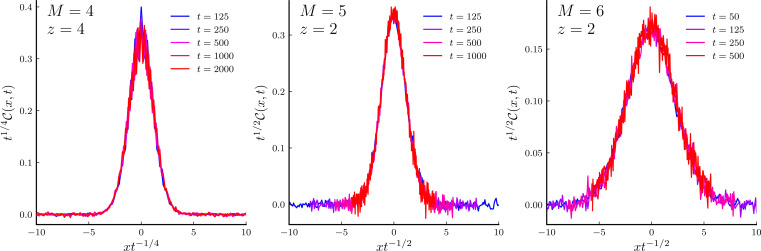
However, subdiffusion does not follow from charge and domain wall conservation alone. To illustrate this point, we classically simulated the stochastic kinetically constrained models with all possible charge and domain wall conserving transitions within an interaction radius of M = 4, 5, and 6 sites. For each model, we computed the average spin structure factor by averaging over $7\times {10}^6$ realizations of the dynamics. As noted in the text, for M > 4, the allowed spin moves do not conserve magnon number; for example, they connect the configurations $\dots \downarrow \downarrow \uparrow \uparrow \uparrow \downarrow \downarrow \uparrow \downarrow \dots$ and $\dots \downarrow \downarrow \uparrow \uparrow \downarrow \downarrow \uparrow \uparrow \downarrow \dots$, turning two 2-strings into a magnon and a 3-string and vice versa while conserving both charge and domain wall number. This breaks integrability strongly, and in that case, our numerical results (Fig. 5) indicate vanilla diffusion with dynamical exponent z = 2.

Fig. 5.

Classical kinetically constrained models. Structure factor $\mathcal{C}(x,t)=\langle {\sigma }^z(x,t){\sigma }^z(0,0)\rangle$ in a stochastic model with charge and domain wall conservation, with local interactions (nonunitary “gates”) acting on M sites. For M = 4, which is the case relevant to the XXZ spin chain with broken integrability, the magnon number is conserved, and we find subdiffusive transport with z = 4 (Left). For higher-range interactions, the magnon number is not conserved, and we find ordinary diffusion z = 2, indicating that domain wall conservation is not enough for subdiffusion to occur.

Infinite Δ XXZ Chain.

The large Δ limit of Hamiltonian Eq. 1 can be taken by projecting out the fast oscillating term and giving an effective projected hopping term, namely

$$\begin{array}{l}{H}_{\text{XXZ},\mathrm{\Delta }=\infty }\to {\displaystyle \sum _i[}{P}_{i-1}^{\text{up}}[S_i^x{S}_{i+1}^x+S_i^y{S}_{i+1}^y]P_{i+2}^{\text{up}}\\ +P_{i-1}^{\text{down}}[S_i^x{S}_{i+1}^x+S_i^y{S}_{i+1}^y]P_{i+2}^{\text{down}}],\end{array}$$ [4]

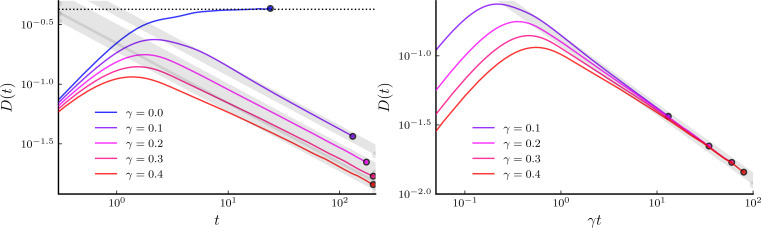
with $P^{\text{up/down}}=(1\pm 2S^z)/2$ the projection on spin up or down. This Hamiltonian is still interacting and integrable (33) and displays spin diffusion with the finite diffusion constant $D_{\mathrm{\Delta }=\infty }=4/(3\pi )$ (32). By perturbing it with a spin dephasing term, it displays spin subdiffusion at all timescales showing a clear dependence $D(t)\sim {(\gamma t)}^{-1/2}$ (Fig. 6) as explained in the text. In this $\mathrm{\Delta }\to \infty$ limit, only magnons are mobile, and bigger domains are strictly frozen. As discussed in the text, larger domains of size s can only move via an $s\hspace{0.17em}\text{th}$-order process in perturbation theory with amplitude $\sim {\mathrm{\Delta }}^{s-1}$. The cross-over to diffusion occurs for finite Δ at the timescale $t_{*}\sim {\mathrm{\Delta }}^2/\gamma$, corresponding to the creation of magnons out of bigger strings (in the text).

Fig. 6.

Projected XXZ chain at infinite Δ. Time evolution of the spin diffusion constant given by the Hamiltonian Eq. 4 coupled to spin dephasing with different values of coupling strength γ is shown. While the γ = 0 case shows diffusion (the dotted horizontal line indicates the value $D=\frac{4}{3\pi }$ predicted by GHD), any finite γ leads to subdiffusion at all times $D(t)\sim t^{-1/2}$ (the shaded regions), with time dependence solely fixed by the rescaled time γt as shown in Right.

Details on the Numerical Calculations.

For the case where the XXZ chain is coupled to a bath, we numerically simulate real-time dynamics of quantum systems with Markovian noise by evolving operators with the Lindblad master equation

$$\dot{\rho }=\mathcal{L}[\rho ]=-i[H,\rho ]+\gamma {\displaystyle \sum _i\left({\sigma }_i^z\rho {\sigma }_i^z-\rho \right)}.$$

We work in the Heisenberg picture, where the density matrix is static and operators evolve as

$$\frac{dA}{dt}={\mathcal{L}}^{*}(A),\hspace{1em}{\mathcal{L}}^{*}=i\overrightarrow{H}-i\overleftarrow{H}-\frac{\gamma }{2}{\displaystyle \sum _j{(\overrightarrow{{\sigma }_{j\prime }^z}-\overleftarrow{{\sigma }_{j\prime }^z})}^2}.$$ [5]

We Trotter decompose the operator evolution

$$A(t+\delta t)=e^{{\mathcal{L}}^{*}\delta t}A(t)\approx e^{{\mathcal{L}}_1^{*}\delta t}{e}^{{\mathcal{L}}_0^{*}\delta t}A(t).$$ [6]

The evolution by H₀ is further decomposed using a standard Trotter scheme, and the noisy evolution is represented as a quantum channel with Kraus operators M_a, where the evolution of an operator is

$$\begin{array}{l}A(t+\delta t)={\displaystyle \sum _a{M}_a^{†}}(\delta t)A(t)M_a(\delta t),\hspace{1em}{\displaystyle \sum _a{M}_a}{M}_a^{†}={\displaystyle \sum _a{M}_a^{†}}{M}_a=\mathbf{1},\\ M_{1,j}=\sqrt{1-\gamma \delta t}·\mathbf{1},\\ M_{2,j}=\sqrt{\gamma \delta t}·{\sigma }_j^z.\end{array}$$

The evolution can then be represented as a product superoperator:

$$e^{{\mathcal{L}}_1\delta t}={\displaystyle \prod _j\left({\displaystyle \sum _a\overrightarrow{M_{a,j}}}{\overleftarrow{M_{a,j}}}^{†}\right)}.$$

We use time steps $\delta t=0.1/\sqrt{\mathrm{\Delta }}$ in the case with finite noise γ and $\delta t=0.1$ for the case of Hamiltonian perturbations (where a fourth-order Trotter scheme is employed). The maximal bond dimension is chosen to be 1,024, which is never saturated in the case of noisy perturbation, due to the loss of quantum entanglement due to dephasing.

Data Availability

All study data are included in the main text.