Method for tissue clearing: temporal tissue optical clearing

Abstract

Light absorption and scattering in biological tissue are significant variables in optical imaging technologies and regulating them enhances optical imaging quality. Optical clearing methods can decrease light scattering and improve optical imaging quality to some extent but owing to their limited efficacy and the potential influence of optical clearing agents on tissue functioning, complementing approaches must be investigated. In this paper, a new strategy of optical clearing proposed as time-dependent or temporal tissue optical clearing (TTOC) is described. The absorption and scattering in light interaction with tissue are regulated in the TTOC technique by altering the pulse width. Here, the dependence of optical properties of matter on the pulse width in a gelatin-based phantom was investigated experimentally. Then, a semi-classical model was introduced to computationally study of Ultra-short laser/matter interaction. After studying phantom, the absorption and scattering probabilities in the interaction of the pulse with modeled human skin tissue were investigated using the proposed model for pulse widths ranging from 1µs to 10fs. The propagation of the pulse through the skin tissue was simulated using the Monte Carlo technique by computing the pulse width-dependent optical properties (absorption coefficient µ_a, scattering coefficient µ_s, and anisotropy factor g). Finally, the penetration depth of light into the tissue and reflectance for different pulse widths was found.

1. Introduction

In recent years, optical imaging techniques have attracted the attention of imaging researchers due to their many advantages, including noninvasiveness, simplicity, and cost-efficiency [1–3]. The absorption and scattering of light in the target tissue, which limits the imaging depth, is one of the primary limitations of these techniques [4]. The absorption of light in matter occurs due to the presence of molecules with resonant frequencies and the scattering occurs due to the refractive indices mismatch between the internal components of matter (for example, the cytoplasm and the nucleus of a cell) [5]. Tissue optical clearing (TOC) is one of the useful techniques that researchers have chosen to address the challenge of light scattering in tissues [6]. TOC, which is performed in diverse ways, is based on dropping the difference in the refractive index of tissue components. Three hypothesized mechanisms of tissue optical clearing were suggested [7]. The first one is the matching of refractive indices between tissue components and interstitial fluid changed by an optical clearing agent (OCA) diffused into the tissue [7,8]. Other mechanisms are related to the interaction of an OCA with the tissue compounds and can be associated with reversible dissociation of collagen fibers [9], and tissue dehydration process induced by hyperosmolality of the applied agent [10]. Due to the refractive index matching phenomena, the OCA can also minimize light scattering from Red blood cells (RBCs), which is useful for detecting malignant cells in whole blood samples. In Ref. [11], the use of glycerol and glucose water solutions reduce the scattering in samples having polystyrene and RBCs. Reference [12] is a successful example of optical clearing in OCT imaging that uses solution of l Iohexol in water as an OCA. A biocompatible Omnipaque (x-ray contrast agent) has also recently been used to detect melanoma cells in phantoms of human melanoma cells and suspensions of mouse melanoma cells of line B16F10 alone and in mixture with blood [13]. The result of TOC methods is a reduction in light scattering in the tissue and an increase in penetration depth of light. One of the weaknesses of conventional TOC methods is the possible toxicity of some clearing agents. Common OCAs such as glycerol and Dimethyl sulfoxide (DMSO) are often nontoxic. However, prolonged treatment with a highly concentrated OCA can produces negative effects on tissue such as local hemostasis, shrinkage, and even tissue necrosis. Glycerol is one of the most common OCA that can cause alteration in skin morphology due to a dissociation of the collagen fibers. It was also found that anhydrous glycerol causes a strong effect on the cutaneous vasculature [14,15]. To overcome this limitation, Ref. [16] presented an ultrasound-based optical cleaning technique that enhances light penetration depth by 1.5 times without the need for a chemical agent. In addition, using focused ultrasound beams, the penetration depth of light into the scattering medium was increased in Ref. [17]. Wave front shaping is another agent-free way for regulating light scattering in tissue. The shaping of the wave front by adaptive optical systems improved the quality and depth of OCT imaging in this method, which was employed in combination with OCAs in Ref. [18]. One of the disadvantages of the wave front shaping method is its intricacy.

Key point about conventional (immersion) TOC methods is that they remove only part of the scattering. This issue has been reported theoretically and experimentally in Refs. [19,20]. To achieve an ideal image, most of the attenuation of light in tissue caused by scattering and absorption must be eliminated, so a combination of alternative TOC methods may be promising. One way to solve the challenges facing optical clearing is to use ultra-short pulses.

Computational studies in recent years have showed that the pulse width influences light absorption and scattering in the target matter [21]. In these investigations, which use quantum and semi-classical approaches to investigate the interaction of light with an atomic and molecular target at different pulse widths, the probability of absorption and scattering in the matter is reported as a function of the pulse width. These findings show that with sufficiently short pulses, the absorption and scattering peaks of matter disappear [22–24]. Experimental studies have also shown that the use of ultra-short pulses leads to an increase in the quality of imaging methods such as photoacoustics (PA). When gold nanostructure colloidal suspensions were excited with time-delayed femtosecond pulses (duration 40 fs, wavelength 800 nm, repetition rate 1 kHz), PA signal amplification was seen (enhancement factor ∼2) enhancement of signal was ascribed to the first stage of thermalization and bubble generation in the nanosecond time scale [25]. In another study, the effect of orientation and shape of nanoparticles on increasing the PA signal produced by femtosecond pulses from nanostructure colloidal suspension was investigated. In this paper, researchers believe that ultra-short pulses can deliver energy deposition faster than the electron-phonon relaxation time (picoseconds) [26]. In Ref. [27], the use of ultra-short pulses in time-resolved imaging improved the image quality. The researchers said that experimental results show that ultrashort pulsed illumination with ultrashort gated detection significantly improve image contrast as compared to any other combinations. Also, in Ref. [28], using ultra-short pulses with the tissue increased the penetration depth (up to 7 cm) of an interference pattern into the tissue without disruption for optical stimulation. While the interference pattern of long pulses is destroyed at short distances in tissue. This report attributed the reduction in attenuation to quantum electrodynamics and avoided commenting further. The use of ultra-short pulses in underwater applications has also reduced the absorption and increased the length of underwater telecommunication links [29,30]. In Ref. [29], using a 60fs pulse with a repetition rate of 1 kHz, they achieved more than 2 orders of magnitude less absorption after propagation through 6-meter in water. In other experimental studies, it has been shown that in addition to increasing laser fluence, within the allowable exposure range and by avoiding tissue and nanoparticle degradation [31], the use of ultrashort pulses improves the PA signal. Due to the ability of ultrashort pulses to reduce the absorption and scattering of tissue and improve the quality of optical imaging and sensing efficiency, these pulses are suitable for optical clearing without agents.

Here, a novel approach termed time-dependent or temporal tissue optical clearing (TTOC) is presented, which can significantly improve optical clearing efficiency. In the TTOC, one can change the width of pulses used in the interaction of light with matter so that it has the least possible absorption and scattering. As a result, altering the pulse width can results in the least amount of absorption and scattering. Instead of decreasing the difference in the refractive index of distinct tissue components, TTOC alters the interaction mechanism of light with matter, reducing light attenuation in the tissue. TTOC, like other TOC methods, enhances the depth of light penetration into the tissue and hence improves optical imaging quality. Simultaneous use of TTOC and conventional TOC methods can make great strides in improving optical images. In this paper, TTOC was investigated experimentally on a gelatin-based phantom and a semi-classical model was proposed to computationally investigate the effect of pulse width on the optical properties of the target matter. For experimental test, two different lasers, the nanosecond laser (808nm, 6ns-129ns) and the femtosecond laser (800nm, 80fs) were used. Comparison of experimental and modeling results showed that the proposed semi-classical model has good accuracy in simulating the propagation of ultra-short pulses in matter. Then, the propagation of ultra-short pulses in the skin tissue was studied. The findings of the computations are presented as pulse width-dependent optical properties of the tissue (µ_a, µ_s and g), reflectance of light from the tissue, and the penetration depth of light into the tissue. One of the important challenges in computational part is pulse broadening during propagation due to multiple scattering. Pulse broadening changes the pulse width and ultimately changes the optical properties, so in pulse propagation modeling should be considered.

In the next section, the experimental test to investigate the dependence of the attenuation coefficient on the pulse width is described and the absorption and scattering probability formulae in terms of the pulse width are introduced. Then, as a function of pulse width, the computation of optical coefficients of human skin tissue will be investigated. Finally, the reflectance and pulse penetration depth will be calculated in terms of the pulse width.

2. Materials and methods

2.1. Experimental study

To study the effect of pulse width on attenuation coefficient in biological targets, a gelatin-based phantom with dimensions of 5cm×5cm×1cm was prepared. To prepare the phantom gelatin dry powder was dissolved in distilled water (65°C) at a ratio of 3:7 (w/w) and the mixture was left to cool down and to set at room temperature.

The attenuation characteristics of the prepared phantom were measured by Double Beam UV-Vis Spectrophotometer (UV-2100, BRAIC, China). The effective attenuation coefficient ( ${\mu }_{\mathit{eff}}$ ) of the phantom at the wavelength of 800 nm is equal to 0.8 mm^-1. The attenuation cross-section of the phantom was found in the wavelength range of 120 nm to 1000 nm, which in the next section was used to model the propagation of light in the phantom.

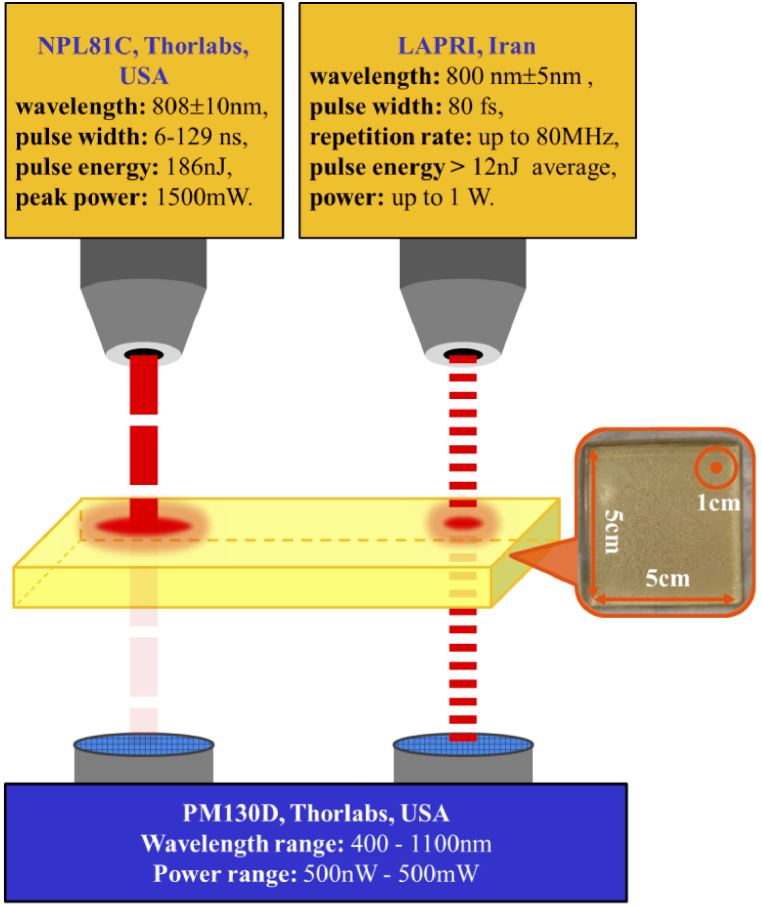
As shown in Fig. 1, two lasers with different pulse widths were used to find the attenuation coefficient in terms of the pulse width. The first is the nanosecond laser diode (NPL81C, Thorlabs, USA) and the second is the Ti: Sapphire laser (LAPRI, Iran). The attenuation coefficient of the phantom was measured using Beer-Lambert law as follows [32]:

$$\frac{I}{I_0}=\exp (-{\mu }_{\text{t}}l).$$ (1)

where, I₀ is the intensity of the laser beam before entering the phantom, I, is the intensity of transmitted laser beam, µ_t, is the attenuation coefficient, and l, is the path length (average optical path length calculated in MC code). We measured I/I₀ for pulse widths of 10ns, 50ns, 100ns, and 80fs with a power meter (PM130D, Thorlabs, USA), and calculated µ_t from Eq. (1). Given that Eq. (1) is valid for collimated beams, the beam is collimated by two lenses and the distance between the tissue and the detector is considered large enough so that the photons in the direct path reach the detector. Also, due to the short distance between the sample and the detector, the beam width was smaller than the size of the detector and there was no need to use an aperture. To compare the experimental results with the presented numerical model, we performed simulations for the phantom with the method described in the next section.

Fig. 1.

Schematic of experimental test.

2.2. Numerical study

Use In general, quantum theory computes the total probability of all optical processes, including absorption and scattering, using the first order of perturbation [33]:

$$W_{\text{tot}}={\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}\sigma (\omega \mathrm{\prime })\frac{I(\omega \mathrm{\prime },t)}{\hslash \omega \mathrm{\prime }}dtd\omega \mathrm{\prime },$$ (2)

where I $(\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{g}\mathrm{a}\mathrm{\prime },t)$ is the Fourier transform of the laser pulse intensity and $\sigma (\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{g}\mathrm{a})$ is the cross section of optical process at the frequency $\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{g}\mathrm{a}$ . The parameter $\sigma (\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{g}\mathrm{a})$ should be replaced by the absorption cross-section when calculating the absorption probability. The scattering cross-section will also be replaced for the scattering probability. Because working with the electric field is more convenient, we replace the intensity in Eq. (2) with the electric field as follows [33]:

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}I(\omega \mathrm{\prime },t)dt=\frac{c}{{(2\pi )}^2}|E(\omega \mathrm{\prime }){|}^2$$ (3)

where c is the speed of light. Here, the temporal profile of the pulse is considered as a function with a Gaussian envelope [33]:

$$E(t)=E_0\exp (-\frac{t^2}{{\tau }^2})\cos (\omega t)$$ (4)

where E₀ is the electric field amplitude, τ is the pulse width, and $\omega$ is the carrier frequency. The Fourier transform of the electrical field takes the following form [33]:

$$E(\omega \mathrm{\prime })=E_0\frac{\sqrt{\pi }}{2}\tau \cdot \text{exp}(-\frac{{(\omega -\omega \mathrm{\prime })}^{\text{2}}{\tau }^{\text{2}}}{\text{4}}).$$ (5)

For long pulses (usually longer than 100ns), the pulse distribution is limited to the central frequency $(\omega \approx {\omega }^{\mathrm{\prime }})$ and the probability of absorption and scattering in Eq. (2) will be simplified as follows [21]:

$$W_{\text{tot}}=\sigma (\omega )\frac{c{E}_0^2}{{(2\pi )}^2\hslash \omega }\tau =\sigma (\omega )\frac{I}{\hslash \omega }\tau .$$ (6)

Equation (6) shows that at long pulse widths, the probability is linearly related to the pulse width. Equation (2) should be used to investigate the relationship between probability and pulse width in short and ultra-short pulses. The application of Eq. (2) to the interaction of ultra-short pulses with atomic and molecular targets revealed a nonlinear relationship between probability and pulse width in the ultra-short pulse regime [21–24]. In fact, in the ultra-short pulse range, target matter may show transition behavior from linear to nonlinear. We must define the absorption and scattering cross-sections of target matter to compute the probability from Eq. (2). Attenuation cross-section for the phantom was measured using the spectrometer, but tissue simulation is necessary to find the absorption and scattering cross-section of the modeled skin tissue. For this purpose, using the information in Ref. [36], we consider the human skin to have four layers (upper epidermis, lower epidermis, dermis, and sub-cutis), each of which is made up of spheres of different radii. Although there are difficulties in approximating the skin to spheres of various sizes, such as the presence of empty space between the spheres and the strong dependence of the optical properties on the size and shape of the particles, tissue modeling with spherical and non-spherical components is a common method that has been used in some papers, and its results have been confirmed by reference models and measurements [34–36]. Because the findings of this technique correspond with Mie theory in Ref. [36], it may be used in Eq. (2) as a simplified model for the absorption and scattering cross-section of the skin. According to Ref. [36], the cross section of absorption and scattering for each layer of skin can be calculated using the sphere size distribution, n(r), the geometric cross section, $\pi$ r², and the absorption/scattering efficiency, Q [36]:

$$\begin{array}{l}{\sigma }_{\text{s}}(\lambda )=\frac{1}{N}{\int }_{r_1}^{r_2}\pi r^2{Q}_{\text{s}}(\lambda ,r)n(r)dr\\ {\sigma }_{\text{a}}(\lambda )=\frac{1}{N}{\int }_{r_1}^{r_2}\pi r^2{Q}_{\text{a}}(\lambda ,r)n(r)dr\end{array}.$$ (7)

N denotes the number of particles in a unit volume, Q_s and Q_a, which are the scattering and absorption efficiencies, are also obtained from Mie theory in terms of wavelength and particle radius [37]. Also, r₁= r_av-3σ and r₂= r_av+3σ which r_av and σ are the mean and standard deviation of radii. Calculating the probability of absorption and scattering (solving Eq. (2)) requires two factors. The first is the pulse intensity distribution, which is obtained from Eq. (3), and the second is the absorption and scattering cross-section, which is obtained from Eq. (7). Therefore, using Eq. (3) and Eq. (7), the probability of absorption and scattering can be calculated. Finally, for each pulse width, the probability of absorption and scattering is obtained numerically.

Three optical parameters of the tissue are necessary to simulate light propagation in the tissue: 1) absorption coefficient, µ_a, which is defined as the absorption probability per unit length; 2) scattering coefficient, µ_s, which is defined as the scattering probability per unit length; 3) anisotropy factor, g, which is the average of the cosine of the scattering angles. Beer's law is used to compute the absorption and scattering coefficients. As a result, the probability of light absorption in tissue with a first intensity of I₀ is as follows [32,38]:

$$W_{\text{abs}}=1-\frac{I}{I_0}=1-\exp (-{\mu }_{\text{a}}l)$$ (8)

where, I denote the intensity of light and l is the path length. Similarly, scattering probability is defined as follows [32,38]:

$$W_{\text{scat}}=1-\frac{I}{I_0}=1-\exp (-{\mu }_{\text{s}}l).$$ (9)

The absorption and scattering coefficients are obtained using Eq. (8) and Eq. (9):

$$\begin{array}{l}{\mu }_{\text{a}}=-\frac{1}{l}\ln (1-W_{\text{abs}})\\ {\mu }_{\text{s}}=-\frac{1}{l}\ln (1-W_{\text{scat}})\end{array}.$$ (10)

To calculate the anisotropy factor, we add the angular function of the scattering cross section from Mie theory to Eq. (2). The angle-dependent scattering probability is calculated as follows [21]:

$$W_{\text{scat}}(\theta )={\int }_0^{\mathrm{\infty }}{\sigma }_{\text{scat}}(\omega \mathrm{\prime },\theta )\frac{I(\omega \mathrm{\prime })}{\hslash \omega \mathrm{\prime }}dtd\omega \mathrm{\prime }.$$ (11)

Using Eq. (11), the phase function, which is defined as the probability of scattering per unit solid angle, is obtained [32,39]:

$$p(\theta )=\frac{d{W}_{\text{scat}}(\theta )}{d\mathrm{\Omega }}.$$ (12)

The MC calculations are based on the phase function calculated in Eq. (12) and no other approximation is used. Finally, the anisotropy factor is defined using the phase function as follows [39]:

$$g={\int }_{4\pi }p(\mathrm{c}\mathrm{o}\mathrm{s}\theta )\mathrm{c}\mathrm{o}\mathrm{s}\theta d\mathrm{\Omega }.$$ (13)

Now that the optical properties of the tissue at different pulse widths have been obtained using Eq. (10) and Eq. (13), simulation of pulse propagation in the tissue is possible. The reflectance and penetration depth of light in skin tissue were studied using Monte Carlo simulation in this work. The depth at which the light intensity reaches 1/e of the first value is assumed as the penetration depth. Penetration depth is usually measured as 1/µ_eff. As a result, for ballistic photons, the penetration depth may be calculated as 1/(µ_s +µ_a) and for diffused photons as 1/ (3µ_a (µ_a +µ′_s)) ^1/2, respectively; which, µ′_s the reduced scattering coefficient (µ′_s= µ_s (1 – g)) [40,41]. The actual penetration depth into the tissue may differ from the predicted penetration depth due to reflection from the top layers [42].

2.3. Considerations for simulations

The Monte Carlo approach was used to conduct a numerical study of light propagation. First, the photon is assigned a weight of one. Then, using random number generation, the propagation direction and step length in the tissue are calculated. Because of absorption, part of the original weight of the photon is decreased after it propagates. Then, using random numbers, a new direction and step length are selected, and the process is repeated until the original weight reaches a specific level and the photon dies. In fact, by emitting photon packet from one point to another, some of the energy of the photon packet is lost due to absorption. The emission of photon packet continues until its energy is less than a certain value and the emission of photons stops. Following the completion of the one-photon propagation stages, the next photon is launched. The accuracy of MC technique improves as the number of photons rises, and it becomes more realistic [32]. A common MC code that runs on MATLAB software is used in this simulation. The optical properties of program were dependent on the pulse width, which distinguished it from non-time-dependent programs. Therefore, by altering the pulse width, new optical properties were computed in parallel and then used in the MC program. In addition, the estimated phase function from scattering probability was employed in the MC run, and photon packet scattering was done using this phase function rather than the Henyey-Greenstein phase function approximation. The next major challenge is the broadening of the pulse as it propagates through the tissue. To investigate broadening of pulse, many photons with Gaussian temporal distribution were launched to the tissue. FWHM of distribution is equal to the first pulse width. Then the arriving time for each photon to a certain depth was estimated in the Monte Carlo code. By measuring the FWHM of new temporal distribution, the pulse width is found. The result, is the pulse width data as a function of light penetration depth. Because the pulse width changes after each scattering, so pulse width is measured at distances about the scattering length (1/µ_s) and by changing the pulse width, new optical properties are replaced the earlier optical properties of the tissue.

The modeled skin in this paper's simulations was divided into four layers with dimensions of 1 mm × 1 mm × 4.1 mm. A Gaussian beam with a beam Waist of 4 mm and a Rayleigh length of 10 mm was employed. Also, 10⁸ photons were employed in each Monte Carlo simulation, which took roughly 8 hours to perform. These simulations are run on a PC with an Intel Xenon E5-2620 12core 2.4GH processor.

Briefly, there are four steps in the numerical part of this study. To begin, Eq. (7) is used to estimate tissue absorption and scattering cross-sections. Following that, the integral of Eq. (2) is numerically solved using the cross-section $\sigma (\omega )$ and the pulse intensity function $I(\omega )$ . One can find the probability as a function of pulse width using Eq. (2), since the pulse intensity function is dependent on it. As a result, we have one absorption probability and one scattering probability for each pulse width at the output of Eq. (2). The absorption and scattering coefficients are found in the third step after placing probability numbers in Beer-Lambert law. Finally, in the fourth step, we apply the Monte Carlo algorithm to simulate the propagation of light with different pulse widths through skin tissue using pulse width-dependent optical properties (optical coefficients and phase function). Although the estimated spectrum width for femtosecond lasers ranges between a few hundred and a few tens of nm, most of the energy of these lasers is spread within a range of around a few ten nanometers. To explore the behavior of the full pulse spectrum in light-tissue interaction, calculations were performed for the three wavelengths present in the spectrum (750 nm, 800 nm, and 850 nm). The actual optical properties for a pulse in the matter are the average of the optical properties for the wavelengths that make up the pulse.

The nonlinear effects of ultra-short pulses are the next crucial subject to consider. The existence or absence of these effects is found by the intensity of the pulse. Nonlinear effects on the pulse interaction with the material can be minimized by lowering the intensity of ultrashort pulses (usually less than 10⁷ W/cm²) [29,30]. Nonlinear effects in imaging can be avoided by using low-intensity ultra-short pulses. As a result, here, nonlinear effects in laser-tissue interaction are disregarded.

3. Results and discussion

In this section, first, the experimental and numerical results for the attenuation coefficient in the phantom are compared. Then, the behavior of optical properties in the context of pulse width for modeled skin tissue is described. Finally, the results of MC simulations including pulse broadening during propagation, reflectance and light penetration depth in skin tissue are presented.

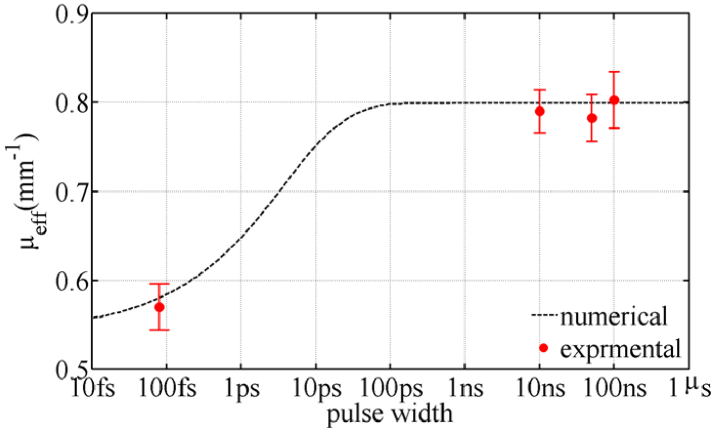
Figure 2 shows the numerical and experimental results for finding the attenuation coefficient (3µ_a (µ_a +µ′_s)) of the phantom. Good agreement between results shows the accuracy of the modeling method. The results show that the attenuation value for pulses longer than 100 ps is a constant value, but it depends on the pulse width for pulses shorter than 100 ps. This important result confirms the results of Refs. [26–30] experimentally seen less attenuation of ultrashort pulses. Therefore, based on the results of Fig. 2, the use of ultrashort pulses in optical imaging improves the depth and quality of the imaging. According to the definition of light penetration depth, which is 1/µ_eff, using the TTOC method with pulses of 80 fs, the light penetration depth has been increased by about 40%.

Fig. 2.

Experimental and numerical results for attenuation coefficient of the gelatin-based phantom in terms of pulse width at wavelength of 800 nm.

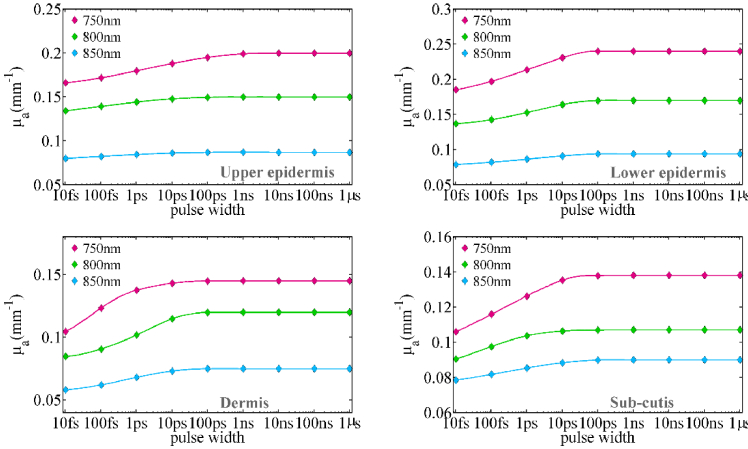
Now that the accuracy of the modeling method for propagation of ultra-short pulses has been set up, it is possible to model temporal optical clearing in skin tissue with proposed method. Figure 3 shows the absorption coefficient of skin layers at different pulse widths for wavelengths of 750 nm, 800 nm, and 850 nm. As can be seen, by reducing the pulse width from 1µs to about 100ps, the absorption coefficient of all skin layers remains almost constant. At pulses shorter than 100ps the absorption coefficient decreases. The reduction slope is steep in the range of 10ps to 10fs. The absorption coefficient varies less as the wavelength increases; hence the absorption coefficient changes more at 750 nm than at the other two wavelengths. The dermis is the layer of the skin that changes the greatest when the pulse width is changed. The value of the dermis absorption coefficient drops by 35% at a wavelength of 750 nm, 30% at a wavelength of 800 nm, and 25% at a wavelength of 850 nm in the 1µs to 10fs range.

Fig. 3.

The absorption coefficient for human skin layers at the wavelengths of 750 nm, 800 nm, and 850 nm as a function of pulse width

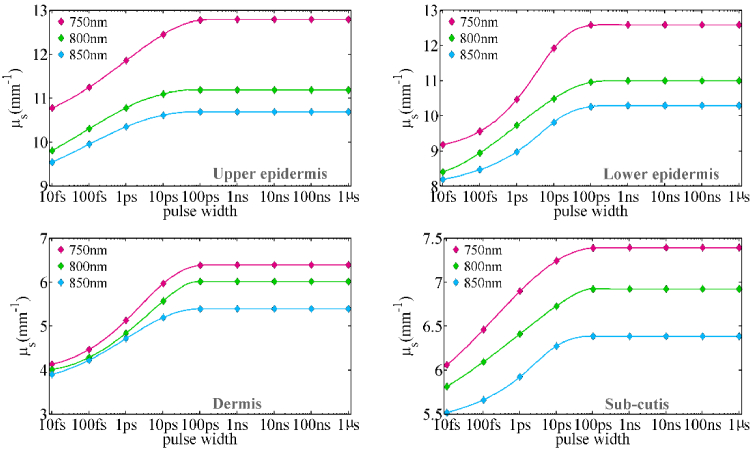
Figure 4 depicts the scattering coefficient of skin layers for three wavelengths and different pulse widths. The scattering coefficient, like the absorption coefficient, decreases rapidly between 10ps and 10fs, and the scattering coefficient changes significantly as the wavelength rises. The dermis’ scattering coefficient drops by 37% at a wavelength of 750 nm, 34% at a wavelength of 800 nm, and 30% at a wavelength of 850 nm (dermis has the most variation of scattering coefficient between skin layers).

Fig. 4.

The scattering coefficient for human skin layers at the wavelengths of 750 nm, 800 nm, and 850 nm as a function of pulse width.

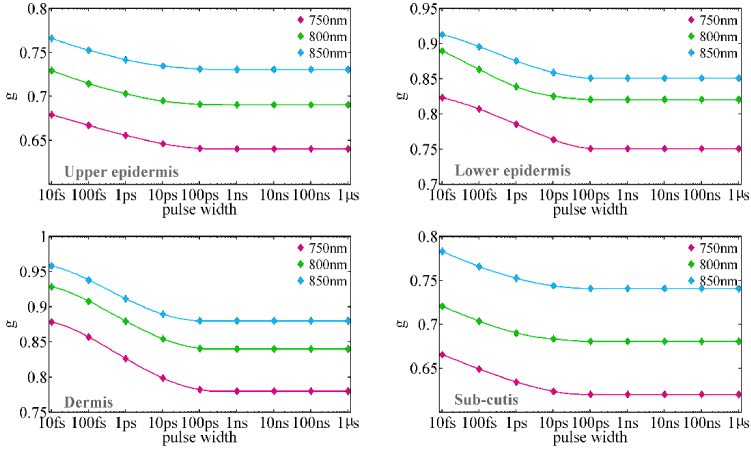
Variations in the parameters finding probability cause changes in absorption and scattering coefficients at various pulse widths. The optical process probability (see Eq. (2)) is the product of two factors: pulse frequency distribution (E $(\omega )$ or I $(\omega )$ ) and cross-section frequency distribution ( $\sigma (\omega )$ ). The pulse frequency distribution varies as the pulse width changes. As a result, the product of E $(\omega )$ and $\sigma (\omega )$ change. The form of the cross-section frequency distribution finds the situation of these changes. Reducing the pulse width generally increases the frequency distribution width of the pulse and reduces the interaction of the pulse with the skin and finally decreases absorption and scattering coefficient, as illustrated in Fig. 3 and 4. Furthermore, differences in the behavior of absorption and scattering coefficients in various layers are attributable to differences in their absorption and scattering cross-sections. The anisotropy factor of skin layers at different pulse widths is shown in Fig. 5. The anisotropy factor begins to grow at a pulse width of around 100ps when the pulse width is reduced. The forward scattering is increased when the anisotropy factor approaches unity. As a result, in the ultra-short pulse region (less than 100ps), reducing the pulse width improves forward scattering on scattering at greater angles, and the pulse is largely transmitted in a straight line. In the case of the anisotropy factor, the largest changes in all three wavelengths are related to the dermis layer.

Fig. 5.

The anisotropy factor for human skin layers at the wavelengths of 750 nm, 800 nm, and 850 nm as a function of pulse width.

The results in long pulses can be compared to the experimental investigations that have been published. Different findings have been reported in measuring the optical properties of the skin due to variations in diverse types of tissues. To confirm, we compare our computational results to a variety of published experimental data. The absorption coefficient of the epidermal layer is around 0.2 mm^-1 at a wavelength of 700 nm, 0.17 mm^-1 at a wavelength of 800 nm, and 0.08 mm^-1 at a wavelength of 900 nm, according to the data presented in Ref. [43]. These values are like those found in the current study: 0.24 mm^-1 at a wavelength of 750 nm, 0.16 mm^-1 at a wavelength of 800 nm, and 0.09 mm^-1 at a wavelength of 850 nm. We only look at the data for the dermis absorption coefficient at a wavelength of 800 nm. The dermis absorption coefficient is given as 0.122 mm^-1 in Ref. [43], which agrees well with the 0.11 mm^-1 found in our computations.

The result published in Ref. [44] for the reduced scattering coefficient for the dermis layer at 800 nm is roughly 2.0 mm^-1, which we calculated to be 1.2 mm^-1. The results presented in Refs. [43,44] also show a reduced scattering coefficient of 2.1 mm^-1 at 800 nm for the epidermis layer, which agrees well with our result (2.0 mm^-1). Separately, the anisotropy factor can be investigated. The anisotropy factor for human skin, according to Ref. [45], is in the range of 0.6 to 0.95 for wavelengths about 800 nm. All the estimated anisotropy factors fall within this range. Although skin optical properties have a broad range of values in reports based on characteristics of the skin, the existence of calculated values in our study for long pulses in the range of reported values shows the correctness of the calculations.

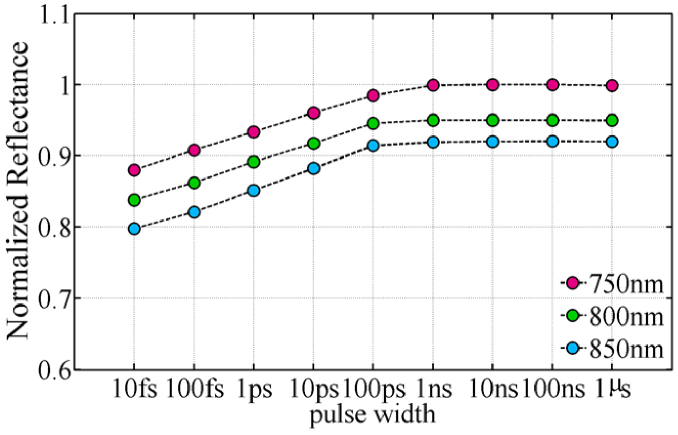
Utilizing the Monte Carlo method, one can simulate the propagation of light in the tissue for different pulse widths using pulse width-dependent optical characteristics. Reflectance is one of the parameters that vary because of changes in skin tissue's optical properties. Reflectance may well be computed directly in the Monte Carlo code and is defined as the fraction of light reflected by the tissue in comparison to incoming light. Because the anisotropy factor approaches one in the ultra-short regime, forward scattering rises compared to scattering at other angles and backward scattering from the tissue decreases. The normalized reflectance for ten different pulse durations and three wavelengths is depicted in Fig. 6. The purpose of figure is to compare the reflections of different wavelengths in the human skin and to see that the reflectance decreases with decreasing pulse width for all wavelengths. Because the reflectance of 750 nm is greater than the other wavelengths, we have normalized all the reflectance to a maximum reflectance of 750 nm. Reflectance in tissue is caused by background backscattering and reflection from the layers’ borders due to refractive index mismatch. In the ultra-short pulse domain, the background scattering decreases as the pulse width decreases, but the amount of reflection from the boundary is still constant. As a result, the reflectance decreases as the pulse width decreases in ultra-short regime.

Fig. 6.

Normalized reflectance of skin tissue for wavelengths of 750 nm, 800 nm, and 850 nm at various pulse widths

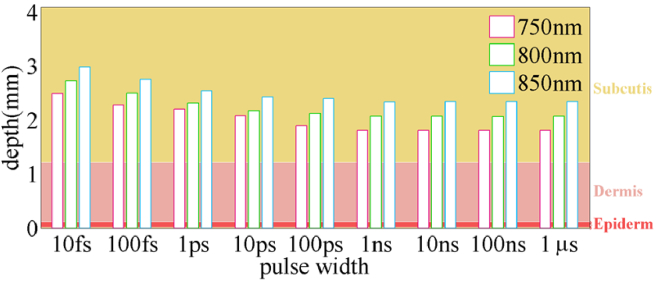
The penetration depth of light in the tissue at various pulse widths is the next quantity to also be studied. Figure 7 depicts the depth of penetration of various pulse widths into skin tissue. The penetration depth of ultrashort pulses in skin tissue rises due to lower absorption and scattering coefficients and a higher anisotropy factor in ultra-short pulses. Due to the lower absorption and scattering for longer wavelengths, the penetration depth of a pulse with a wavelength of 850 nm is greater than other wavelengths. Variations in penetration depth begin at 100ps, the same time as changes in optical properties. The estimated depths for extended pulses are comparable with the observations published by Bashkatov et al. [44]. Even though the energy of the pulses is varied in Fig. 7, and the quantity of energy obtained in the tissue by ultra-short pulses is considerably smaller than that of longer pulses, this picture reveals the important result: ultra-short pulses penetrate deeper into skin tissue at the wavelengths explored. Multiple short or ultra-short pulses, rather than a single long pulse of specific energy, can be used to achieve increased penetration depth. Instead of one pulse with a pulse width of 1ns, a pulse train with a pulse width of 10fs can improve penetration depth by around 40% at wavelengths of 850 nm, comparable to the findings of the phantom study (See Fig. 2), in which 80 fs pulses had a 40% larger penetration depth than nanosecond pulses.

Fig. 7.

The estimation of the penetration depth of different pulse widths in human skin layers at wavelengths of 750 nm, 800 nm, and 850 nm.

It should be noted that not only the average interval between interactions t₂ = l/c(µ_a + µ_s), which is considered as a controllable parameter with a change in the pulse duration but also the function f (t, t’), which describes the temporal deformation of a δ-shaped pulse after single scattering in the temporal equation of the radiative transfer theory, is an exponentially decaying function of the pulse duration f (t, t’) = (1/t₁)exp[–(t – t’)/t₁], where t₁ is the first moment of the distribution function f (t, t’) [38,46]. This function, which can be a function of spatial coordinates, is the time interval of an individual scattering event. When t₁ → 0, f (t, t’) → δ (t – t’). It is important to note that in tissues with a high density of scatterers, the time interval of an individual scattering act, t₁, should be considered since it may be comparable to the average time interval between interactions, t₂ [47]. However, the propagation of shorter pulses is followed by a decreased effect of the diffuse part on radiation transmission in this instance as well, which will contribute to the optical clearing of the scattering.

4. Conclusion

The goal of this study was to present a new, high-efficiency approach for optical clearing of biological tissue that was free of osmotic or mechanical pressure on the tissue. In the experimental section, the attenuation coefficient of a gelatin-based phantom was measured at different pulse widths. The results showed that at pulses shorter than 100 ps, the attenuation of light in the phantom decreases. In phantom study, the penetration depth increases about 40% by reducing the pulse width from nanoseconds to 80 fs. Then, a semi-classical method was used to model the propagation of ultra-short pulses in the phantom. The results of modeling method were in good agreement with the experimental results. Then, calculation method was used to simulate light propagation in human skin tissue. The absorption and scattering coefficients and anisotropy factor of skin layers as a function of pulse width were studied using the semi-classical equation of optical process probability at three wavelengths of 750 nm, 800 nm, and 850 nm. The results revealed that at pulse widths of around 100ps and shorter, the absorption and scattering coefficients dropped while the anisotropy factor rose as the pulse width was reduced. Light is less absorbed, scattered, and transmitted in an advancing direction at ultra-short pulses. Light propagation in the 4-layer human skin tissue was then modeled using time-dependent optical properties using the Monte Carlo technique. According to the findings, pulses less than 100ps exhibit reduced reflectivity and increased penetration depth as the pulse duration decreases. When TTOC is compared to conventional OCAs or ultrasonic-based OC, the results reveal that TTOC alone can enhance penetration depth by the same amount as ultrasonic-based OC and OCA (about 1.5-fold). The distinction is that in TTOC, no external variables are introduced to the light-tissue interaction. The main recommendation of this work is that long pulses be replaced with ultra-short pulse trains (according to the MPE protocol in finding the total energy of the pulse train and the energy per pulse) to obtain better penetration depth and improve optical image quality. TTOC is a novel form of optical clearing that works by changing the time profile of pulses. Using the TTOC method to increase the depth of light penetration into tissues, alone or in combination with traditional TOC methods, would greatly improve optical applications such as optical imaging, spectroscopy, optical monitoring of implant degradation [48], optical nerve stimulation, and laser therapy, which have significant limitations, associated with a small light penetration depth, which reduces their effectiveness.

Funding

Iran National Science Foundation10.13039/501100003968 (98029460); Ministry of Science and Higher Education of the Russian Federation10.13039/501100012190 (13.2251.21.0009).

Disclosures

The authors declare no conflicts of interest.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.