Adaptive Preferential Sampling in Phylodynamics With an Application to SARS-CoV-2

Abstract

Longitudinal molecular data of rapidly evolving viruses and pathogens provide information about disease spread and complement traditional surveillance approaches based on case count data. The coalescent is used to model the genealogy that represents the sample ancestral relationships. The basic assumption is that coalescent events occur at a rate inversely proportional to the effective population size N_e(t), a time-varying measure of genetic diversity. When the sampling process (collection of samples over time) depends on N_e(t), the coalescent and the sampling processes can be jointly modeled to improve estimation of N_e(t). Failing to do so can lead to bias due to model misspecification. However, the way that the sampling process depends on the effective population size may vary over time. We introduce an approach where the sampling process is modeled as an inhomogeneous Poisson process with rate equal to the product of N_e(t) and a time-varying coefficient, making minimal assumptions on their functional shapes via Markov random field priors. We provide efficient algorithms for inference, show the model performance vis-a-vis alternative methods in a simulation study, and apply our model to SARS-CoV-2 sequences from Los Angeles and Santa Clara counties. The methodology is implemented and available in the R package adapref. Supplementary files for this article are available online.

1. Introduction

Molecular sequence data, within the framework of phylodynamics (Grenfell et al. 2004), is increasingly being used to track disease spread caused by rapidly evolving viruses and pathogens such as Influenza viruses (Rambaut et al. 2008), Zika (Faria et al. 2016), and SARS-CoV-2 (Hadfield et al. 2018). The coalescent process (Kingman 1982a, 1982b), a probability model of gene genealogies, depends on a parameter called effective population size N_e(t), which is a time-varying measure of genetic diversity. When disease dynamics can be modeled by simple epidemiological models such as Susceptible-Infected-Recovered, the coalescent effective population size can be expressed in terms of transmission rates and prevalence (Volz et al. 2009; Frost and Volz 2010). Accurate and efficient inference for N_e(t) is thus relevant to estimate epidemiological parameters of great interest in public health. Although this work is motivated by applications in molecular epidemiology of infectious diseases, estimation of N_e(t) is an active area of research with applications ranging across many other scientific domains such as conservation biology and population genetics (e.g., Shapiro et al. 2004; Huff et al. 2010; Lorenzen et al. 2011).

A common feature in these applications is that genetic data are collected sequentially (heterochronous samples). In viral studies, samples are collected and sequenced when infected individuals attend clinics, hospitals, or testing centers. In ancient DNA studies, specimens are dated according to the time they lived, estimated through radiocarbon dating or other techniques. The coalescent typically models the gene genealogy conditionally on sampling dates, that is, the sampling dates are treated as censoring information (Felsenstein and Rodrigo 1999). However, in some situations, it is reasonable to assume that samples are collected at a higher frequency when the population is large and at a lower frequency when the population is small: for example, at the onset of an epidemic, as the viral population grows and more people get infected, more resources may be allocated to monitor the viral spread, possibly leading to more molecular sequence collection. The number of SARS-CoV-2 sequences uploaded daily in GISAID offers some evidence of this claim (Shu and McCauley 2017) (see the histogram in the supplementary material).

Karcher et al. (2016) study the scenario in which the sampling process depends on the population size, and show that an estimator of N_e(t) that does not account for this dependence is biased. This issue was first discussed in the spatial statistics literature by Diggle, Menezes and Su (2010), who term preferential sampling a situation in which the process that determines the data locations and the process under study are dependent. In this article, we will introduce a new model that accounts for preferential sampling in a coalescent framework, while making minimal assumptions on N_e(t), the sampling process, and their dependence.

Three estimators that incorporate preferential sampling into the coalescent framework have been proposed. Volz and Frost (2014) propose an estimator in the case that N_e(t) grows exponentially and samples are collected as an inhomogeneous Poisson process with rate linearly dependent on the effective population size. Karcher et al. (2016) assumed that N_e(t) is a continuous function, and the samples are collected as an inhomogeneous Poisson process with rate $\lambda (t)=\text{exp}\left({\beta }_0\right)N_e{(t)}^{{\beta }_1}$, for β₀, β₁ ≥ 0, that is, the dependence between the sampling process and the effective sample size is described by a parametric model. Recent work by Parag, du Plessis, and Pybus (2020) weakened this assumption substantially, allowing for the dependence between the sampling process and effective population size to vary over time. The key assumption in Parag, du Plessis, and Pybus (2020) is that the sampling rate depends linearly on N_e(t) within a given time interval, but the linear coefficient changes across time intervals. The estimator of Parag, du Plessis, and Pybus (2020), termed Epoch skyline plot (ESP), is an extension of the classic skyline plot estimator for N_e(t) (Pybus, Rambaut, and Harvey 2000), in which the sampling rate and the effective population size are both piecewise-constant, and the location and number of change points (boundary points of the time intervals) are either specified or inferred. As it is typical with skyline plots, the estimates are highly variable, rough, and highly dependent on the specification of change points locations and the number of piecewise-constant pieces used. All three works show that under correct model specification, accounting for preferential sampling leads to a more accurate estimation of N_e(t) (in terms of absolute deviations to the true trajectory), and narrower credible regions.

Other noncoalescent approaches for phylodynamics, such as birth–death processes (Stadler 2010), explicitly incorporate the sampling process by modeling the sampling dates as a partially observed death process where only a fraction of the population is observed. Stadler et al. (2013) extended previous work to allow sampling rates to vary through time. Volz and Frost (2014) show that in both, coalescent and birth-death processes alike, statistical power largely depends on the correct specification of the sampling process rate, rather than on the genealogical model. Hence, the need for a flexible modeling approach of the sampling process, adaptive to any possible scenarios encountered in applications.

There are a plethora of nonparametric estimators of N_e(t) following the skyline plot (Pybus, Rambaut, and Harvey 2000). Among others, the generalized skyline plot (Strimmer and Pybus 2001) and the Bayesian skyline plot (Drummond et al. 2005) reduce the high variance and roughness that characterize the skyline plot estimators. These methodologies require either fixing or estimating change-points in N_e(t). A set of models that do not employ change-points but arbitrary discrete grids is based on Markov random fields (MRF): the Gaussian MRF (GMRF) (Minin, Bloomquist and Suchard 2008; Palacios and Minin 2012) allows for the recovery of smooth continuous trajectories; the Horseshoe MRF (HSMRF) (Faulkner et al. 2020) is an alternative to GMRF which is locally adaptive, that is, it can successfully recover sharp changes in a trajectory and it is adaptive to a varying level of smoothness.

In this article, we borrow from this literature and introduce an adaptive preferential sampling framework for phylodynamics, where the adaptivity follows from the fact that the dependence of the sampling process on N_e(t) changes over time. The effective population size N_e(t) is modeled as a latent parameter included in both, the coalescent and the sampling processes. The latter is assumed to be an inhomogeneous Poisson process with rate λ(t) = β(t)N_e(t), where β(t) is a continuous function controlling the dependence on N_e(t), analogous to that introduced by Parag, du Plessis, and Pybus (2020). We a priori model N_e(t) and β(t) as two Markov random fields (MRF), with the flexibility of using either a GMRF or a HSMRF. The prior choice follows from the properties of the fields. The advantage of the proposed adaptive preferential sampling over the ESP estimator is that there is no need to specify (or estimate) the number and location of the change points of β and N_e. Also, the resulting estimates are smooth and the high variability that characterizes skyline estimates disappears.

We develop the methodology assuming that a genealogy is available to the researcher and develop algorithms for inference under this framework. We test our model on simulated data and compare it to alternative methods, including both, estimators that account for preferential sampling and others that do not. We implement our method in the R package adapref, available at https://github.com/lorenzocapp/adapref, provide two algorithms for posterior approximation: a Hamiltonian MCMC and a Laplace approximation. We apply our method to SARS-CoV-2 sequences from California and study whether there is evidence of preferential sampling.

The rest of the article proceeds as follows. In Section 2, we provide background on the coalescent process, the MRF priors on N_e(t), and previous work on preferential sampling. In Section 3 we introduce the adaptive preferential sampling framework and explain how to approximate the posterior distribution of model parameters. Section 4 includes a simulation study, in which we test our proposal through simulated data and compare it to alternatives. In Section 5, we apply our method to two datasets of SARS-CoV-2 sequences from Santa Clara and Los Angeles counties in California. Section 6 concludes.

2. Background

2.1. Coalescent Model

Coalescent models are continuous-time Markov chains used to model the set of ancestral relationships of a sample of n individuals from a large population. This set of ancestral relationships is called gene genealogy. In the context of molecular epidemiology, a genealogy is a subset of the transmission history among the samples (Figure 1). Starting from the original work of Kingman (1982a), several extensions to the standard coalescent have been developed to incorporate more realistic population and sampling features, such as variable population size (Slatkin and Hudson 1991), longitudinal sampling (also called heterochronous sampling) (Felsenstein and Rodrigo 1999), and population structure (Hudson 1990). Wakeley (2009) provided a good introduction to the subject. Coalescent processes can be characterized by two underlying processes: a jump chain defining the ancestral relationships represented by a binary tree topology and a pure death process that defines the timing of the coalescent events, that is, the times when pairs of lineages meet their common ancestors. This sequence of holding times defines the branch lengths of the corresponding tree topology.

Figure 1.

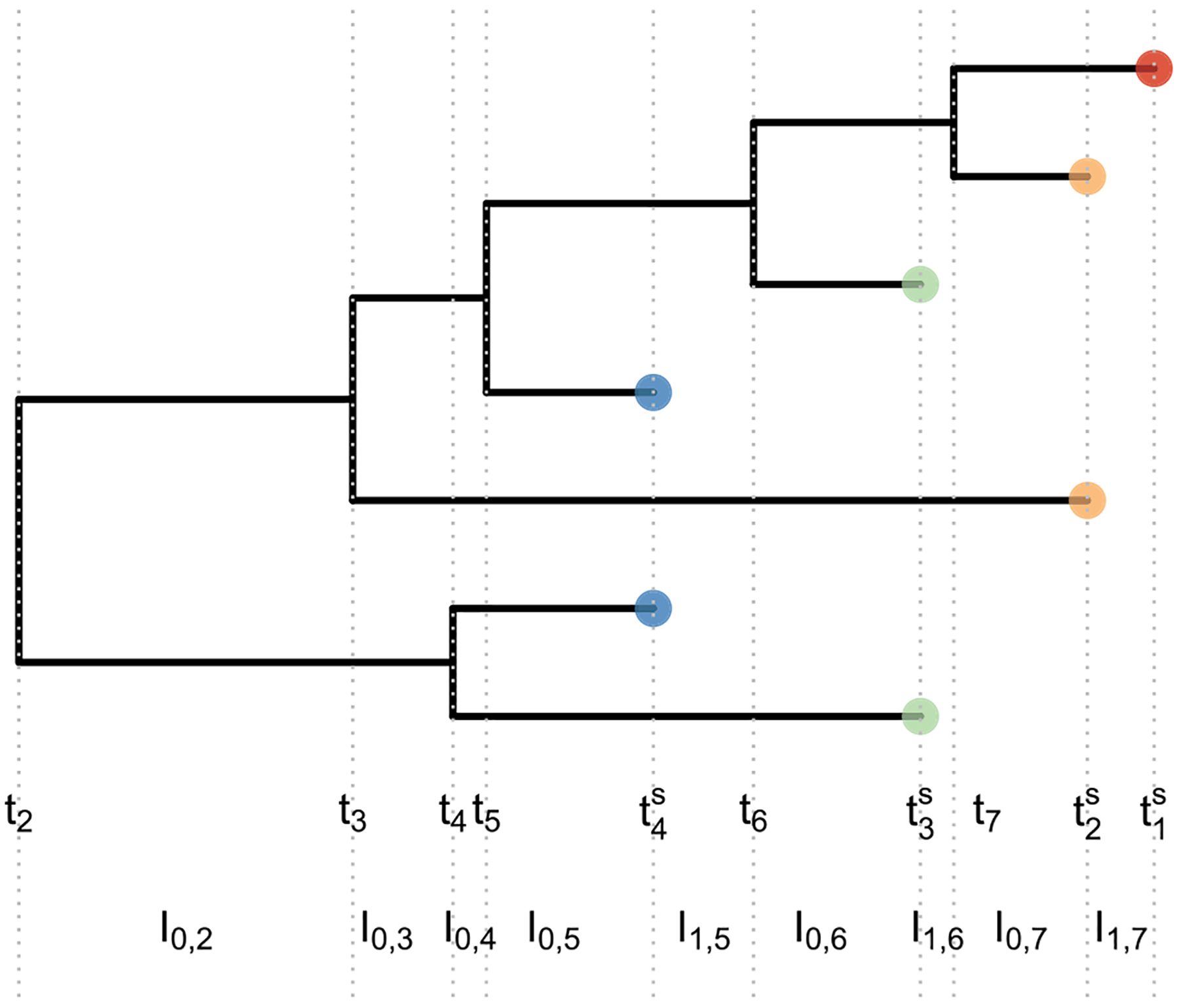
Example of a heterochronous genealogy. A genealogy of 7 individuals sampled at 4 different times (color of tips) with multiplicities (n₁ = 1, n₂ = 2, n₃ = 2, n₄ = 2). Sampling times are denoted by ${\left(t_k^s\right)}_{1:4}$, coalescent times are denoted by (t_k)_2:7 and I_i,j denoted the interval lengths delimited by coalescent times and/or sampling times, that is, every time there is a change in the number of lineages.

Let the vector n = (n₁, …, n_m) denote the sample sizes at times $t^s=\left(t_1^s,\dots ,t_m^s\right)$, with m number of sampling points and n the total sample size. The process goes backward in time (from present toward the past): with $t_1^s=0$ denoting the present time, and $t_j^s>t_{j-1}^s$ for j = 2, …, m. Let = t = (t_n+1, …, t₂) be the vector of coalescent times with t_n+1 = 0 < t_n < ⋯ < t₂. Note that the subscript in t_k is not the current number of extant lineages (often a convention in the coalescent literature) but the number of lineages that have yet to coalesce. Starting from t = 0, the vectors t and t^s partition time into intervals (Figure 1). An interval ending with a coalescent event, say t_k, is denoted by I_0,k; the intervals that end with a sampling time within the interval (t_k+1, t_k) are denoted as I_i,k, where i ≥ 1 indexes all the sampling events in (t_k+1, t_k). Formally, for every k ∈ {2, …, n}, we define

$$I_{0,k}=\left[\max \left\{t_{k+1},t_j^s\right\},t_k\right),\hspace{1em}\text{where}\text{the}\text{maximum}\text{is}\text{taken}\text{over}\text{all}{t}_j^s<t_k,$$

and for every i ≥ 1 we set

$$I_{i,k}=\left[\max \left\{t_{k+1},t_{j-i}^s\right\},t_{j-i+1}^s\right)\text{with}\text{the}\text{max}\text{taken}\text{over}\text{all}{t}_{j-i+1}^s>t_{k+1}\text{and}{t}_j^s<t_k.$$

With n_i,k denoting the number of extant lineages during the time interval I_i,k. Figure 1 plots an example of a heterochronous genealogy with n = (1, 2, 2, 2), at times $t^t=\left(t_1^s,\dots ,,t_4^s\right)$ with $t_1^s=0$. In the interval (t₆, t₅) there are two intervals: $I_{1,5}=\left[t_6,t_4^s\right),I_{0,5}=\left[t_4^s,t_5\right)$.

The vector of coalescent times t is a random vector whose density with respect to the Lebesgue measure on ${ℝ}_{+}^{n-1}$ depends on two quantities: the coalescent factor $C_{i,k}:=\left(\begin{array}{c}{n}_{i,k}\\ 2\end{array}\right)$, and the effective population size N_e(t). The coalescent density can be factorized as the product the of conditional densities of t_k−1 given t_k, that is,

$$p\left(t^s,n,N_e(t)\right)=\prod _{k=n+1}^{3}p\left(t_{k-1}\mid t_k,t^s,n,N_e(t)\right)=\prod _{k=n+1}^3\frac{C_{0,k-1}}{N_e\left(t_{k-1}\right)}\text{exp}\left\{-{\int }_{I_{0,k-1}}\frac{C_{0,k-1}}{N_e(t)}\text{d}t+\sum _{i=1}^m{\int }_{I_{i,k-1}}\frac{C_{i,k-1}}{N_e(t)}\text{d}t\right\},$$ (1)

where the conditional density p(t_k−1|t_k, t^s, n, N_e(t)) is the extension of Kingman n-coalescent holding time density to account for variable effective population size and heterochronous samples (Felsenstein and Rodrigo 1999). The integral over I_i,k−1 accounts for the probability of no coalescence during I_i,k−1. It is zero if there are less than i sampling times between t_k and t_k−1, and t_k appears in the definition of the intervals (either I_0,k−1 or I_1,k−1). In addition, conditionally on t^s, n, and t_k, the coalescent factors can be computed exactly and N_e(t) is the only unknown parameter. Sampling times are assumed fixed.

Coalescent times can be alternatively viewed as the realization of an inhomogeneous point process with rate C(t)N_e(t)⁻¹, with the coalescent factor C(t) being defined for all t ≥ 0 by the notation above. This alternative view allows us to frame the problem of inferring N_e(t) as that of inferring the intensity function of an inhomogeneous point process. Palacios and Minin (2013) is an example of how this representation is useful in inference and simulations.

2.2. Some Priors for the Effective Population Size

Markov random field-based priors on the log effective population trajectory allows the recovery of smooth trajectories. They are computationally tractable thanks to the sparsity assumption in the covariance matrix of the field (Rue and Held 2005). All MRF-based priors for phylodynamic inference share the assumption that the trajectory N_e(t) is an unknown continuous function. The integral in Equation (1) is numerically approximated by the Riemann sum at a regular grid of M + 1 points (k_i)_1:M+1, and one assumes that the trajectory N_e(t) is well approximated by ${\sum }_{i=1}^{M+1}\text{exp}{\theta }_{i}1\left(t\in \left(k_i,k_{i+1}\right)\right)$, with θ = (θ_i)_1:M. We stress that neither the grid cell boundaries (k_i)_1:M+1 nor M depend on t and N_e(t), with the choice of M commonly based on n (Faulkner et al. 2020). A description of the discretized coalescent log-likelihood ℒ(θ|t) is given in detail in Palacios and Minin (2012) and Faulkner et al. (2020).

The Horseshoe Markov random field prior (HSMRF) for θ (Faulkner et al. 2020) assumes that the pth-order forward differences of θ are independent and Horseshoe distributed (Carvalho, Polson, and Scott 2010), that is,

$$\begin{array}{l}{\Delta }^p{\theta }_i\left|{\tau }_i~N\left(0,{\tau }_i^2\right)\hspace{1em}{\tau }_i\right|\gamma ~C^{+}(0,\gamma )\hfill \\ \gamma \mid \zeta ~C^{+}(0,\zeta )\hspace{1em}\text{for}p+1\le i\le M-1,\hfill \end{array}$$ (2)

where C⁺(0, a) is the standard half-Cauchy distribution with positive support with scale parameter a, τ_i are the local shrinkage parameters and γ is the global smoothing parameter. To completely specify the prior, one sets ${\theta }_1~N\left(\mu ,{\sigma }_1^2\right)$, and for p ≥ 2, the first p values of the field have running order q difference priors as follows:

$$\begin{array}{l}{\Delta }^q{\theta }_q\left|a_q{\tau }_q~N\left(0,a_q{\tau }_q^2\right)\hspace{1em}{\tau }_q\right|\gamma ~C^{+}(0,\gamma )\hfill \\ \gamma \mid \zeta ~C^{+}(0,\zeta )\hspace{1em}\text{for}1\le q\le p-1,\hfill \end{array}$$

with a_q = 2^−(p−q)/2. As it is common in the trend filtering literature (Kim et al. 2009), only orders 1 and 2 are typically employed in applications.

A related prior consists in assuming that the pth-order forward difference of θ, more precisely the vector (θ₁, Δ¹θ₁, …, Δ^pθ_p, Δ^pθ_M−1) is distributed as a GMRF

$$\begin{array}{l}{\Delta }^p{\theta }_i\left|\gamma ~N\left(0,{\gamma }^2\right)\hspace{1em}\gamma \right|\zeta ~C^{+}(0,\zeta )\hfill \\ \text{for}p\le i\le M-1,\hfill \end{array}$$ (3)

${\theta }_1~N\left(\mu ,{\sigma }_1^2\right)$, and for 1 ≤ q ≤ p − 1 we set Δ^qθ_q|a_qγ ~ N(0, a_qγ²). That is, the vector (θ₁ Δ¹θ₁, …, Δ^pθp, Δ^pθ_M−1) is normally distributed with a covariance matrix that depends on the order p considered. A common alternative to the half-Cauchy distribution on γ is a Gamma prior, for example, as in Palacios and Minin (2012). We will employ both formulations in our implementations.

A fully nonparametric prior on log N_e(t) has been studied by Palacios and Minin (2013), who proposed a Gaussian process prior on the log effective population size. The advantage of this approach is that no grid needs to be specified a priori. In applications, we believe that the GMRF, the discretized version of this prior, achieves a comparable empirical performance.

2.3. Preferential Sampling

Preferential sampling arises when the process that determines the locations of the data (i.e., sampling process) and the process under study are stochastically dependent. The notion was introduced by Diggle, Menezes and Su (2010) who show that not accounting for this effect leads to biased inference as a result of the model misspecification. On the other hand, a correctly specified sampling model can lead to more accurate estimates.

In phylodynamics, preferential sampling arises when the sampling process depends on N_e(t). Volz and Frost (2014) provide the first evidence that coalescent-based inference under a misspecified sampling process can be biased. They propose a new estimator tailored to a coalescent process with exponentially growing effective population size and a sampling process with rate linearly dependent on N_e(t). They show that the estimator obtained by correctly modeling the sampling process is more accurate than the standard coalescent estimator.

Karcher et al. (2016) assumed that N_e(t) is a continuous function and the sampling process is a Poisson process with rate $\lambda (t)=\text{exp}\left({\beta }_0\right)N_e{(t)}^{{\beta }_1}$, for β₀, β₁ ≥ 0, that is, the rate λ(t) is proportional to the effective population size. This model is parsimonious, capturing a variety of scenarios with two parameters: with β₁ = 1, the rate is a constant times N_e(t), on the opposite side of the spectrum, with β₁ = 0, one models uniform sampling. Another advantage is that little assumptions are made on N_e(t). However, the parametric assumptions on λ(t) make the sampling dates strongly informative about N_e(t). This situation can be problematic in the case of sampling dates errors. Moreover, under no preferential sampling or under a different rate λ(t) (model misspecified), it constitutes a relevant model misspecification, and leads to estimation biases; see, for example, Figure 3 in Section 4. Karcher et al. (2020) addressed some of the limitations of the parametric model by including time-varying covariates into the Poisson process rate: $\lambda (t)=\text{exp}\left({\beta }_0\right)N_e{(t)}^{{\beta }_1}+{\mathit{\beta }}^{\prime }X(t)$, where X is a vector of covariates and β′ the corresponding linear coefficients. Here a covariate can be for example a dummy variable indicating a change in sampling protocols, or when a new sampling center joined the study. The term β′X adds more flexibility to the parametric dependence enforced by $\text{exp}\left({\beta }_0\right)N_e{(t)}^{{\beta }_1}$. Clearly, this extension requires the availability of covariates informative on the sampling design.

Figure 3.

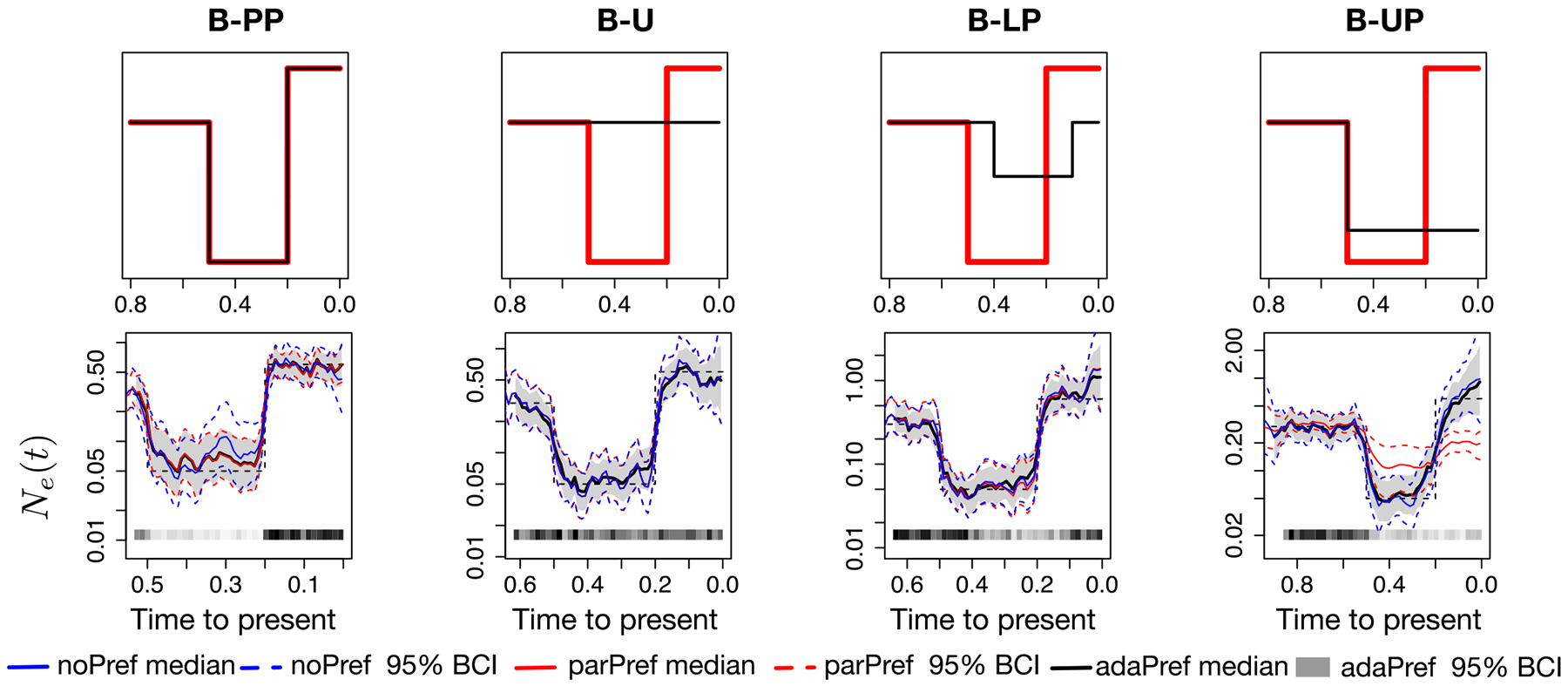
Simulations from bottleneck trajectories and posterior inferences of N_e(t). First row panels depict the simulated log-effective population size (red) and log-sampling intensity (black) trajectories (up to a constant). Second row panels depict posterior estimates for the four simulation scenarios and from a single simulated genealogy picked at random with n = 500 tips. All models used GMRF of order 1 priors and posterior inference is approximated with INLA. The posterior medians of adaPref are depicted as solid black curves and the 95% Bayesian credible regions are depicted by shaded areas. Posterior medians of parPref and noPref are depicted respectively as solid blue and red curves, and the 95% Bayesian credible regions are depicted by the corresponding dashed curves. n and s are depicted by the heat maps at the bottom of the last four panels: the squares along the time axis depict the sampling times, while the intensity of the black color depicts the number of samples. The true trajectories are depicted as a black dashed curves.

Parag, du Plessis, and Pybus (2020) introduced the epoch sampling skyline plot (ESP) estimator that allows for a more flexible dependence of the sampling process on the effective population size. More specifically, the ESP method assumes that N_e(t) is a piecewise-constant function with r segments described by the vector (N₁, …, N_r) of r parameters, and time is further partitioned in d epochs, such that in epoch i and segment r the sampling process is a Poisson process with rate β_iN_j, where (β₁, …, β_d) is a vector of d parameters. The vector (β₁, …, β_d) modulates the dependence of the sampling process on the effective population size, assuming that the dependence changes across d epochs. This is a notable advantage over the parametric model of Karcher et al. (2016): one can model a variety of realistic time-varying sampling protocols, or simply deal with sampling discontinuities typical of outbreaks. We conjecture that the higher flexibility in the ESP preferential model reduces the risk of model misspecification and bias when the preferential sampling assumption does not hold. Furthermore, the model remains identifiable: the authors show that the expected Fisher information matrix is nonsingular, a sufficient condition for parameter identifiability in exponential families (Rothenberg 1971).

In the ESP, the endpoints of the r segments coincide with a subset of the coalescent times t. Similarly, the boundary points of the d epochs are determined by a subset of the sampling times. The number of segments r and epochs d, as well as their lengths, need to be determined or inferred. A downside of this approach is that these choices affect the ESP estimates heavily. The authors implement a frequentist and a Bayesian version with independence assumptions in (N₁, …, N_p) and (β₁, …, β_d), leading to estimates with high variance, a characteristic feature of skyline plot-type estimators.

3. Adaptive Preferential Sampling

In the adaptive preferential sampling framework, the sampling times are determined by the jumps of an inhomogenous Poisson process with rate λ(t) = β(t)N_e(t), with N_e(t) effective population size, and β(t), a function modulating the linear dependence between λ(t) and N_e(t). Let s_i denote the ith sampling time generated by this process, for i = 1, …, n and s₁ fixed to 0. The notation (s_i)_1:n is added to highlight the difference between a realization from the Poisson simple point process (s_i)_1:n of one event at a time, and the observed vector t^s introduced in Section 2 in which multiple events can be observed at a given time point. As we will show later in this section, this discrepancy is resolved by discretizing the observed time window into regular intervals. We assume that both β(t) and N_e(t) are unknown continuous functions. To numerically approximate the integrals in (1), we resort to the approximation sketched in in Section 2.2 and detailed in Palacios and Minin (2012). We employ the regular grid (k_i)_1:M+1 and assume that N_e(t) is governed by parameters θ = (θ_i)_1:M′. Similarly, to model the time-varying rate λ(t), we assume that β(t) is governed by parameters α = (α_i)_1:M′, where M′ = min_i{k_i+1 : k_i+1 > s_n} and β(t) ≈ exp α_i for t ∈ (k_i, k_i+1].

By the independence of nonoverlapping intervals of the Poisson process, we can write the log-likelihood contribution of the sampling process as

$$ℒ(\mathit{\alpha },\mathit{\theta }\mid s)=\sum _{i=1}^{M^{\prime }}\left[\left|\left\{s_i:s_i\in \left(k_i,k_{i+1}\right]\right\}\right|\left({\alpha }_i+{\theta }_i+\text{log\hspace{0.17em}}{\Delta }_i\right)-\text{exp}\left\{{\alpha }_i{\theta }_i\right\}{\Delta }_i\right],$$ (4)

where Δ_i = k_i+1 − k_i and the first interval [k₁, k₂] is closed to include s₁. Equation (4) is the log-likelihood of M′ independent Poisson distributed random variables with rates (exp{α_i θ_i}Δ_i)_1:M′ and number of events (|{s_i : s_i ∈ (k_i, k_i+1)}|)_1:M′.

A few preliminary remarks. M′ is not related to the number of epochs d in ESP: it is solely determined by s_n and the grid (k_i)_1:M+1, which in turn does not depend on t. We have by definition M′ < M to ensure that β(t) is not modeled after the last sampling time (there is no information in the sample to estimate it). In addition, through the term |{s_i : s_i ∈ (k_i, k_i+1]}|, the discretized log-likelihood (4) allows to naturally account for multiple sampling times collected at once, reconciling this model with the description of the heterochronous coalescent given in Section 2.1. Lastly, the identifiability of the model follows by the result in Parag, du Plessis, and Pybus (2020) since our likelihood and the ESP likelihood only differ by the locations of the breakpoints. Intuitively, while the two parameters would not be identifiable from the sampling process alone, the parameter N_e(t) appears in both the coalescent and the sampling likelihoods, making the joint model parameters N_e(t) and β(t) identifiable.

Here, we model both α and θ through Markov random field priors, either HSMRFs or GMRFs. This allows us to make minimal assumptions on N_e(t) and β(t): the choice of the grid practically depends solely on the sample size and no major assumptions are made on the underlying sampling process. The choice of prior for N_e(t) follows from the well-studied characteristics of the two priors discussed in Section 2.2. Under the HSMRF prior on β(t), one can model situations in which there are sharp changes in the sampling design (both first and second orders). Under the GMRF prior on β(t), one favors smooth sampling designs, a situation which is also desirable when one does not have exact knowledge of the underlying sampling protocol. Note that the choice of field and order of the priors can be disjoint: for example, one can place a HSMRF of order 1 prior on N_e(t) and a GMRF of order 2 prior on β(t). We study in details the properties of the prior distributions in the supplementary material.

To formalize, Bayesian phylodynamic inference under adaptive preferential sampling can be written in the most general form as

$$\begin{array}{l}\mathbf{t}\mid \mathit{\theta },\mathbf{n},\mathbf{s}~\text{Coalescent}\text{model}\mathbf{s}\mid \mathit{\theta },\mathbf{\alpha },n~\text{Poisson}\text{process}\hfill \\ \mathit{\theta }\mid \mathit{\tau },\gamma ~\text{HSMRF}-p_1\text{or}\mathit{\theta }\mid \gamma ~\text{GMRF}-p_1\hfill \\ \mathit{\alpha }\mid \mathit{\psi },\xi ~\text{HSMRF}-p_2\text{or}\mathit{\alpha }\mid \xi ~\text{GMRF}-p_2,\hfill \end{array}$$ (5)

where ξ is the global smoothing parameter of the MRF on α, ψ is the vector of local shrinkage parameter of the HSMRF prior on α, p₁, and p₂ are the orders of the respective MRFs. We will refer to any combination of priors above as the adaptive preferential model.

Note that the adaptive preferential model differs notably from the framework of the ESP estimator by the fact that the parameter vectors θ and α are each dependent, the grid at which they are defined does not depend on t, and these priors favor smooth estimates.

3.1. Inference

Posterior distributions.

Under the assumption that t and s are known, and that we place HSMRF priors on both α and θ, the posterior distribution of model parameters could be readily computed

$$\begin{array}{l}\pi (\mathit{\alpha },\mathit{\theta },\mathit{\psi },\mathit{\tau },\gamma ,\xi \mid \mathbf{t},\mathbf{s})\propto ℒ(\mathit{\alpha },\mathit{\theta }\mid \mathbf{s})ℒ(\mathit{\theta }\mid \mathbf{t})\pi (\mathit{\theta }\mid \mathit{\tau })\pi (\mathit{\tau }\mid \gamma )\hfill \\ \pi \left(\gamma \mid {\zeta }_1\right)\pi (\mathit{\alpha }\mid \mathit{\psi })\pi (\mathit{\psi }\mid \xi )\pi \left(\xi \mid {\zeta }_2\right),\hfill \end{array}$$

where ℒ(θ|t) is the discretized coalescent log-likelihood. Under GMRF priors on α and θ, the posterior would be

$$\begin{array}{l}\pi (\mathit{\alpha },\mathit{\theta },\gamma ,\xi \mid \mathbf{t},\mathbf{s})\propto ℒ(\mathit{\alpha },\mathit{\theta }\mid \mathbf{s})ℒ(\mathit{\theta }\mid \mathbf{t})\pi (\mathit{\theta }\mid \gamma )\hfill \\ \pi \left(\gamma \mid {\zeta }_1\right)\pi (\mathit{\alpha }\mid \xi )\pi \left(\xi \mid {\zeta }_2\right).\hfill \end{array}$$

For our analysis, we fixed the pair (g, t), which can be estimated by other methods such as the Maximum clade credibility tree of the posterior distribution of the genealogy. In order to approximate the posterior distribution we use two methods: Hamiltonian MCMC and Integrated Nested Laplace approximation (INLA; Rue, Martino, and Chopin 2009). The choice of the two algorithms is based on the recent results in the phylodynamics literature: Lan et al. (2015) and Faulkner (2020) study the use of HMC in the context of phylodynamics with GP, GMRF, and HSMRF priors on N_e(t); Palacios and Minin (2012) and Karcher et al. (2016) study INLA with a GMRF-1 prior on N_e(t). Both INLA and HMC are shown to accurately approximate the posterior distributions and to efficiently handle large sample sizes (in the order of thousands of samples).

For Hamiltonian MCMC, we rely on Stan (Carpenter et al. 2017). The hyperparameters ζ₁ and ζ₂ are as described in Faulkner et al. (2020, app. B ) (their method is suitably adapted to ζ₂, the global smoothing parameter of the MRF on α).

INLA approximation.

Posterior inference from latent Gaussian models can be achieved by approximating posterior marginal distributions via Laplace approximations. INLA allows us to replace MCMC entirely and approximate the posterior marginals of model parameters when our model is based on GMRF priors. What follows is largely based on Palacios and Minin (2012), who discuss INLA for GMRFs in phylodynamics. We extend it here to include the adaptive preferential sampling priors.

INLA approximates posterior marginals π(γ , ξ |t, s), π(θ_i|t, s) for 1 ≤ i ≤ M, and π(α_j|t, s) for 1 ≤ j ≤ M′. The posterior marginal distribution of hyperparameters is

$${\widehat{\pi }(\gamma ,\xi \mid \mathbf{t},\mathbf{s})\propto \frac{\pi (\gamma ,\xi ,\mathit{\theta },\mathit{\alpha },\mathbf{t},\mathbf{s})}{\widehat{{\pi }_G}(\mathit{\theta },\mathit{\alpha }\mid \gamma ,\xi ,\mathbf{t},\mathbf{s})}|}_{\mathit{\alpha }={\mathit{\alpha }}^{*}(\xi ,\gamma ),\mathit{\theta }={\mathit{\theta }}^{*}(\xi ,\gamma )},$$

where $\widehat{{\pi }_G}(\mathit{\theta },\mathit{\alpha }\mid \gamma ,\xi ,t,s)$ is the Gaussian approximation of π(θ, α|γ, ξ, t, s) obtained from a Taylor expansion around its modes θ*(ξ, γ) and α*(ξ, γ) (modes can be computed through any optimization algorithm, e.g., Newton–Raphson).

The approximation of the marginal distributions of the MRFs π(θ_i|t, s) and π(α_j|t, s) are

$${\widehat{\pi }\left({\theta }_i\mid \gamma ,\xi ,\mathbf{t},\mathbf{s}\right)\propto \frac{\pi (\gamma ,\xi ,\mathit{\theta },\mathit{\alpha },\mathbf{t},\mathbf{s})}{\widehat{{\pi }_{GG}}\left({\mathit{\theta }}_{\mathbf{-}\mathit{i}},\mathit{\alpha }\mid \gamma ,\xi ,\mathbf{t},\mathbf{s}\right)}|}_{\mathit{\alpha }={\mathit{\alpha }}^{*},{\mathit{\theta }}_{\mathbf{-}\mathit{i}}={\mathit{\theta }}_{\mathbf{-}\mathit{i}}*}$$

and

$${\widehat{\pi }\left({\alpha }_i\mid \gamma ,\xi ,\mathbf{t},\mathbf{s}\right)\propto \frac{\pi (\gamma ,\xi ,\mathit{\theta },\mathit{\alpha },\mathbf{t},\mathbf{s})}{\widehat{{\pi }_{GG}}\left(\mathit{\theta },{\mathit{\alpha }}_{\mathbf{-}\mathit{i}}\mid \gamma ,\xi ,\mathbf{t},\mathbf{s}\right)}|}_{{\mathit{\alpha }}_{\mathbf{-}\mathit{i}}\mathbf{=}{\mathit{\alpha }}_{\mathbf{-}\mathit{i}}^{\mathbf{*}},\mathit{\theta }\mathit{=}{\mathit{\theta }}^{*}},$$

where $\widehat{{\pi }_{GG}}\left(\mathit{\theta },{\mathit{\alpha }}_{\mathbf{-}\mathit{i}}\mid \gamma ,\xi ,\mathbf{t},\mathbf{s}\right)$ is the Gaussian approximation of π(θ, α_−i|γ, ξ, t, s) obtained from a Taylor expansion at (α_−i, θ) = E_G[θ, α_−i|γ, ξ, t, s], where E_G denotes the expected value w.r.t. $\widehat{{\pi }_G}(\mathit{\theta },\mathit{\alpha }\mid \gamma ,\xi ,\mathbf{t},\mathbf{s})$. Analogously, we can define the same term for $\widehat{{\pi }_{GG}}\left({\mathit{\theta }}_{\mathbf{-}\mathit{i}},\mathit{\alpha }\mid \gamma ,\xi ,\mathbf{t},\mathbf{s}\right)$. Given $\widehat{\pi }\left({\theta }_i\mid \gamma ,\xi ,\mathbf{t},\mathbf{s}\right)$ and $\widehat{\pi }\left({\alpha }_i\mid \gamma ,\xi ,t,s\right)$, we use $\widehat{\pi }(\gamma ,\xi \mid t,s)$ to obtained out γ and ξ and obtained the desired distributions.

4. Simulations

We rely on simulations to evaluate the performance of the adaptive preferential sampling (adaPref) method in estimating the effective population size trajectory. We compare the performance of adaPref to alternative methods with and without preferential sampling. This simulation study is designed to test the benefit of the adaptive framework. We consider two settings: “strong” preferential sampling (sampling process always depends on N_e(t)), and “weak” preferential sampling (sampling is preferential only during some time periods.

For parsimony, we address the following questions in the supplementary material: (i) we evaluate the sensitivity of adaPref posterior distributions to the choice of the MRF (GMRF vs HSMRF) priors and their orders (1 vs 2), (ii) we study the approximation error incurred using INLA in place of MCMC, (iii) we study how well our model infer β(t).

Simulation setup.

In order to exhibit the benefit of the adaPref framework, we consider adaPref with GMRF order 1 priors (GMRF1) on both N_e(t) and β(t) and posterior distributions approximated by INLA. We compare adaPref with the preferential sampling method of Karcher et al. (2016) (parPref) and the method without preferential sampling of (Palacios and Minin 2012) (noPref), available in the R package phylodyn (Karcher et al. 2017). Both noPref and parPref rely on a GMRF1 prior on N_e(t) and the INLA approximation. All implementations rely on R-INLA (Rue, Martino, and Chopin 2009).

For each dataset, we test the performance of all models through a set of commonly used summary statistics. For a regular grid of time points (v_i)_1:K, as a measure of bias we consider the sum of relative errors: $\text{DEV}={\sum }_{i=1}^K\frac{\left|{\widehat{N}}_e\left(v_i\right)-N_e\left(v_i\right)\right|}{N_e\left(v_i\right)}$, where ${\widehat{N}}_e\left(v_i\right)$ is the posterior median of N_e at time v_i; to quantify the uncertainty in the estimate we use the mean relative width: $\text{RWD}=\frac{1}{K}{\sum }_{i=1}^K\frac{\left|{\widehat{N}}_{97.5}\left(v_i\right)-{\widehat{N}}_{2.5}\left(v_i\right)\right|}{N_e\left(v_i\right)}$, where ${\widehat{N}}_{97.5}\left(v_i\right)$ and ${\widehat{N}}_{2.5}\left(v_i\right)$ are, respectively, the 97.5% and 2.5% quantiles of the posterior distribution of N_e(v_i); last, the envelope measure $\mathit{\text{ENV=}}\frac{1}{K}{\sum }_{i=\mathbf{1}}^K{1}_{\left\{{\widehat{N}}_{2.5}\left(v_i\right)\le N_e\left(v_i\right)\le {\widehat{N}}_{97.5}\left(v_i\right)\right\}}$, which measures the proportion of the curve that is covered by the 95% credible region, that is, it is a proxy for coverage. We fix K = 100, v₁ = 0 and v_K = .8 t₂.

Data.

We simulate genealogies under two population size trajectories: a piece-wise constant and exponential trajectory (CE), and a bottleneck trajectory (B). For the sampling protocols, we simulate sampling trajectories that resemble situations encountered in applications: a sampling protocol proportional to N_e(t) (PP), uniform (U), a “lagged” response to changes in N_e(t) (LP), and a situation where only some segments of the sampling trajectory are preferential (UP). The combination of the two acronyms will be used in the plots, for example, B-U refers to bottleneck trajectory and uniform sampling. The first rows of Figures 2–3 depict the N_e (red) and λ(t) (black) trajectories (up to a scaling constant and in log-scale) of the eight simulation scenarios considered. Exact specifics of the trajectories used are given in the supplementary material.

Figure 2.

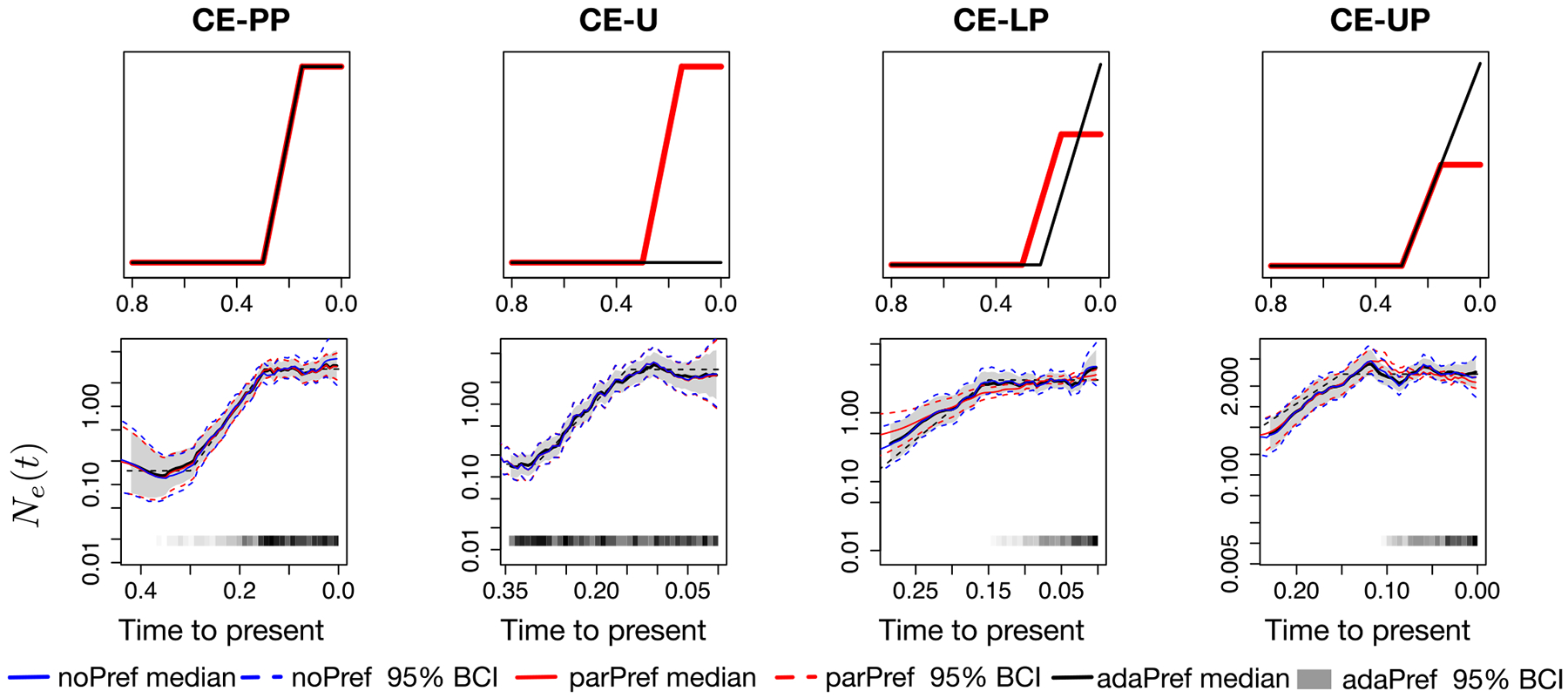
Simulations from constant-exponential trajectories and posterior inferences of N_e(t). First row panels depict the simulated log-effective population size (red) and log-sampling intensity (black) trajectories (up to a constant). Second row panels depict posterior estimates for the four simulation scenarios from a single simulated genealogy picked at random with n = 500 tips. All models used GMRF of order 1 priors and posterior inference is approximated with INLA. The posterior medians of adaPref are depicted as solid black curves and the 95% Bayesian credible regions are depicted as shaded areas. Posterior medians of parPref and noPref are depicted, respectively, as solid blue and red curves, and the 95% Bayesian credible regions are depicted by the corresponding dashed curves. n and s are depicted by the heat maps at the bottom of the last four panels: the squares along the time axis depict the sampling times, while the intensity of the black color depicts the number of samples. The true trajectories are depicted as a black dashed curves.

We consider three sample sizes (n = 100, n = 300, and n = 500) and 50 simulations for each combination of trajectories and sample size. For a fixed n, β(t), and N_e(t), we set n₁ = 2, and simulate n − n₁ sampling locations from a Poisson process with rate β(t)N_e(t). This defines a vector of sampling times and n = (2, 1, …, 1). Conditionally on n, s, and N_e(t), we sample coalescent times t according to Palacios and Minin (2013, algor. 3). Both inhomogeneous Poisson processes are sampled using the Lewis-Shedler thinning algorithm (Lewis and Shedler 1979). Note that there is no need to sample tree topologies because the vector t is a sufficient statistic for N_e(t). Last, we approximate the posterior distribution of N_e(t) conditionally on t, s, and n for the three methods; and the posterior of β(t) conditionally on s and n (only adaPref). The code for reproducing the simulation study is available at https://github.com/lorenzocapp/adapref as a R package.

Results.

We first do a qualitative assessment of the three models considering a single simulated dataset from each simulation scenario (case n = 500). The four panels of Figure 2 second row depict the posterior medians and 95% credible regions of N_e(t) for the constant-exponential trajectory (CE). Our adaPref results are depicted in black and gray scale, the parPref method in red, and the noPref in blue. Each column corresponds to a sampling protocol. All posterior medians of N_e(t) are very similar and close to the truth (black dashed line in the same panel, red line in the panel above) except for parPref (red) in the last two scenarios. Indeed, the last two scenarios correspond to the cases in which the preferential sampling assumption of parPref is violated. ParPref and adaPref show similar credible region widths in the case of proportional preferential sampling (first column), however, adaPref consistently shows narrower credible regions across sampling protocols. Figure 3 shows the same type of comparisons for the bottleneck trajectory (B). The posterior median and credible intervals obtained with parPref are particularly off during the periods of no preferential sampling in the last simulation scenario (fourth column). In all other sampling scenarios, all methods have very similar posterior medians, however again, adaPref shows narrower credible regions while keeping high coverage across sampling protocols.

We now turn to the quantitative comparison of the accuracy of the N_e(t) estimators obtained with the three different models: adaPref, noPref, and parPref considering the 1200 datasets sampled. We use the three metrics described above: ENV as a measure of coverage, RWD as a measure of credible region width, and DEV as a measure of bias. Table 1 reports the average values of the three metrics relative to the value obtained by the adaPref method (grouped by sample size, model, and simulation scenario). A value higher than one means a better performance in terms of ENV, and a worst performance in terms of RWD and DEV. Figure 4 top two rows plot the ENV, RWD, and DEV summary statistics obtained from the CE (first row) and the B (second row) trajectories. In the top two rows, we are not grouping anymore by sample size: a boxplot includes the datasets of all the three sample sizes. Figure 4 last row panels depict the boxplots of the three statistics considered, now grouping simulations by sample size (now, a boxplot includes the datasets of all simulation scenarios).

Table 1.

Simulation: Summary statistics of adaPref posterior inference of N_e(t) grouped by simulation study and sample size.

model	method	n = 100			n = 300			n = 500
		${\overline{\text{ENV}}}^{*}$	${\overline{\text{DEV}}}^{*}$	${\overline{\text{RWD}}}^{*}$	${\overline{\text{ENV}}}^{*}$	${\overline{\text{DEV}}}^{*}$	${\overline{\text{RWD}}}^{*}$	${\overline{\text{ENV}}}^{*}$	${\overline{\text{DEV}}}^{*}$	${\overline{\text{RWD}}}^{*}$
B-LP	adaPref	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	noPref	1.09	1.08	2.02	1.05	1.21	3.02	1.04	1.08	1.33
	parPref	1.08	1.04	1.85	1.05	1.19	2.92	1.04	1.07	1.30
B-PP	adaPref	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	noPref	1.01	1.26	1.77	1.00	1.20	1.92	1.00	1.10	1.20
	parPref	1.00	1.04	1.10	0.99	1.04	1.15	0.99	0.99	0.92
B-U	adaPref	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	noPref	1.06	1.18	2.36	1.04	1.12	1.49	1.03	1.19	1.68
	parPref	1.06	1.15	2.28	1.04	1.11	1.47	1.03	1.19	1.67
B-UP	adaPref	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	noPref	1.04	1.31	3.41	1.05	1.13	1.92	1.04	1.07	1.45
	parPref	1.03	1.27	2.74	0.80	1.32	0.86	0.76	1.40	0.76
CE-LP	adaPref	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	noPref	1.01	0.99	1.49	1.01	1.00	1.11	1.01	0.99	1.10
	parPref	0.90	1.11	0.66	0.84	1.33	0.86	0.59	2.33	1.02
CE-PP	adaPref	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	noPref	1.00	1.11	1.36	1.00	1.15	1.36	1.00	1.19	1.27
	parPref	1.00	1.07	1.16	1.00	1.00	0.99	1.00	1.00	0.99
CE-U	adaPref	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	noPref	1.01	1.20	1.70	1.01	1.12	1.22	1.00	1.12	1.23
	parPref	1.01	1.15	1.56	1.01	1.11	1.21	1.00	1.12	1.22
CE-UP	adaPref	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	noPref	1.01	0.97	1.10	1.01	0.99	1.07	1.01	0.98	1.07
	parPref	0.98	1.01	0.90	0.87	1.25	0.89	0.74	1.60	0.87

NOTES: The bar on top of the criterion means we are considering the average value across the 50 estimated statistics for each simulation trajectory based on N_e(t) posterior, rel refers that the value is relative to the result of adaPref. adaPref (our method), parPref (Karcher et al. 2016), and noPref (Palacios and Minin 2012). A value higher than one means a better performance in terms of ENV, and a worst performance in terms of RWD and DEV.

Figure 4.

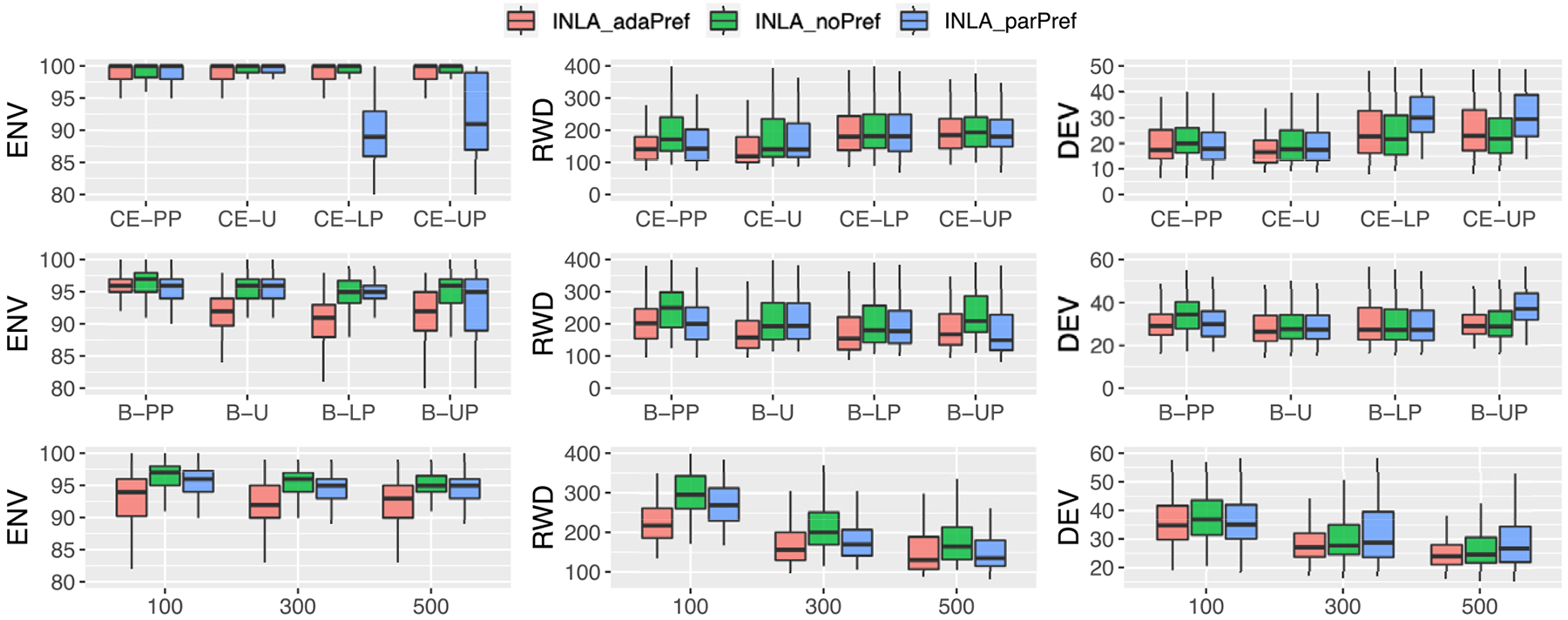
Summary statistics of parPref, noPref and adaPref inference of N_e(t) approximated with INLA. In the first two rows, each box refers to one method (color in the legend) and depicts the distribution of the 150 estimated statistics for each simulation trajectory (50 datasets for each sample size, 150 in total) based on N_e(t) posterior: ENV, first column; RWD, second column; DEV, third column. In the third row, the grouping is done according to the sample size: each box is based on 400 simulated genealogies (50 genealogies for each of the eight trajectories). In the legend, INLA_adaPref is our method, INLA_noPref is the method in Palacios and Minin (2012), INLA_parPref is the method of Karcher et al. (2016). All models used GMRF of order 1 priors.

Table 1 suggests that adaPref has generally a better performance in terms of DEV and RWD. The adaPref model (red boxplots) has the best mean performance in six out of the eight scenarios in terms of both RWD and DEV (B-PP, B-U, all CE scenarios). In the last two scenarios (B-LP, B-UP), the parPref model achieved the lowest mean RWD and noPref the lowest mean DEV. Surprisingly, the adaPref model outperforms parPref also in the CE-PP and B-PP scenarios, where the parametric assumptions are met. noPref is the model that has a slightly better performance in terms of coverage (ENV). However, this is achieved with much wider credible regions. We see how the adaPref coverage is never too different from the noPref ones, while the credible regions are substantially narrower. We judge this as a better performance given that one can always achieve perfect coverage with very wide credible intervals.

The adaPref model is more heavily parameterized and one may be led to think that the performance of the adaPref estimator is affected by the sample size. However, there is no detectable sample size effect: the relative performance of the estimators is roughly similar as n increases. The adaPref estimator is the best performing according to DEV and RWD averaging over all the simulation scenarios jointly. See Table 1 and the last row of Figure 4.

5. SARS-CoV-2 in Los Angeles and Santa Clara counties

SARS-CoV-2 is the virus responsible for the coronavirus disease pandemic in 2019–2020. Molecular surveillance of SARS-CoV-2 complements traditional surveillance methods based on case count data and provides a unique opportunity to retrospectively learn past disease dynamics. Researchers and public health officials agree that a successful response to an outbreak involves the prompt collection, sequencing, and sharing of molecular samples (Gire et al. 2014; Polonsky et al. 2019; WHO 2021). The benefit of a rapid response has been evident in the COVID-19 pandemic; for example, in the Netherlands (Munnink et al. 2020) and in the UK (Meredith et al. 2020). However, the number of sequences collected and shared varied substantially country by country, as can be seen in the GISAID EpiCov database (Shu and McCauley 2017). In addition to a timely response, deciding when, where and how many sequences should be sampled has been receiving attention (Parag and Pybus 2019). The heterogeneity in sampling designs and speed of implementations of genomic surveillance has motivated our work. In this section, we provide a case study to highlight the usefulness of our procedure.

Here, we use the adaPref model for estimating the viral genetic diversity trajectory N_e(t), from currently available viral molecular sequences in GISAID obtained from infected individuals. We analyzed viral whole-genome sequences collected in California in Santa Clara (S.C.) and Los Angeles (L.A.) counties. The GISAID reference numbers of the sequences included in this study, together with data access acknowledgments, are included in the supplementary material.

We downloaded all molecular sequences available on June 27, 2020. The datasets consist of 195 and 134 sequences from S.C and L.A. counties, respectively, with collection dates ranging from mid-February, 2020 to April 13 of 2020. We included only high coverage sequences with more than 25,000 base pairs. Sampling frequency information is depicted in the first and third panels of the last row of Figure 5. We note that the sampling effort varied in the two counties: most of the L.A. samples are concentrated in late March-mid April, while samples have been collected throughout late February-mid April in S.C. county. We consider this case study interesting because the two counties exhibit a different response to the outbreak: S.C. public health officials and researchers promptly responded collecting sequences, while in L.A. country most sequences were collected at the peak of the first outbreak.

Figure 5.

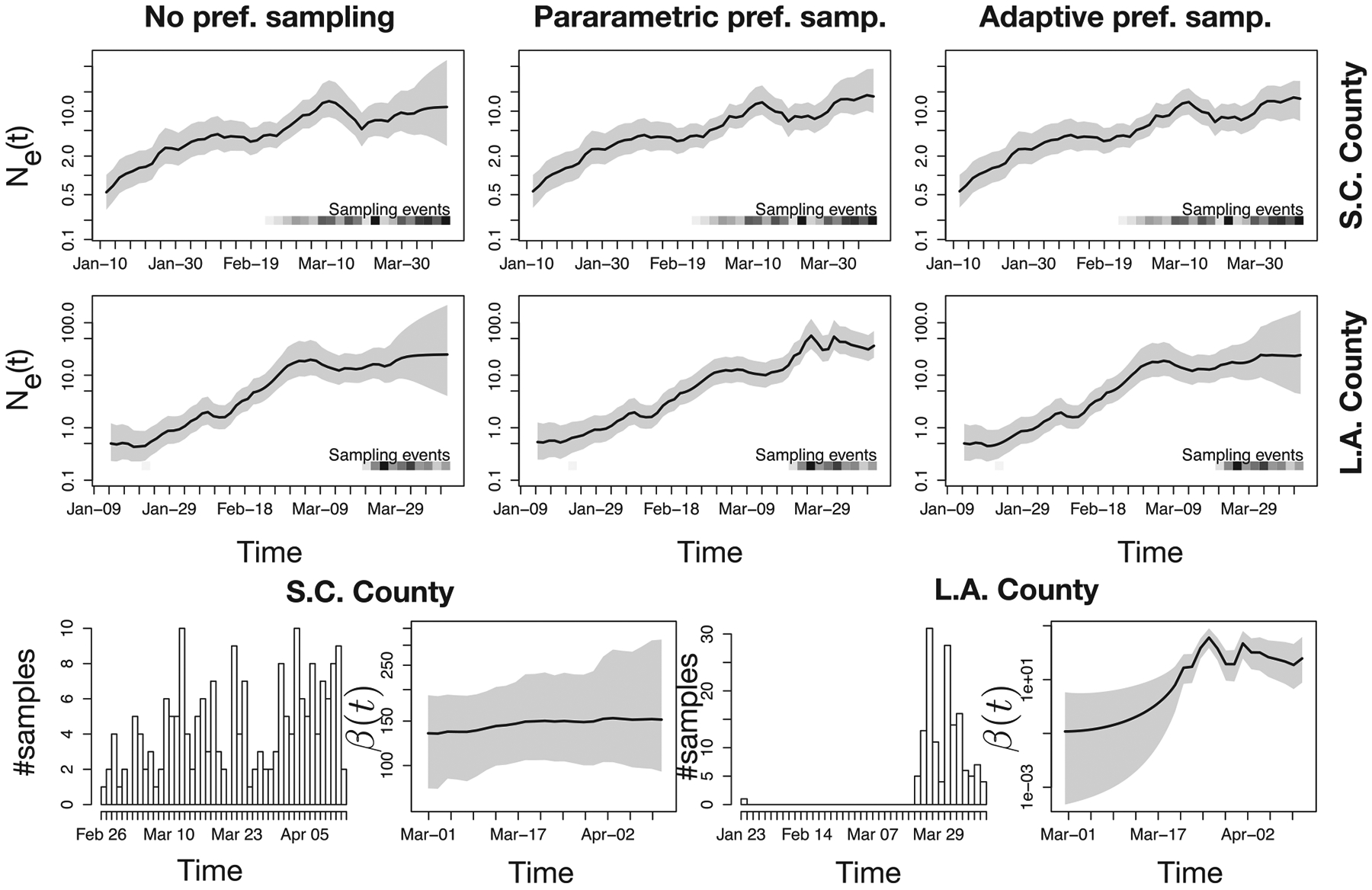
Phylodynamic inference with noPref, parPref and adaPref models from SARS-CoV-2 genealogies inferred from GISAID data obtained from Los Angeles and Santa Clara counties. First two rows panels depict N_e(t) posterior distributions inferred using three possible priors: the noPref (Palacios and Minin 2012), the parPref Karcher et al. (2016), and our adaPref prior. The last row first and third panels depict how many samples are collected each day. The second and fourth panels depict β(t) posterior distribution (only under the adaPref prior). The posterior medians are depicted as solid black lines and the 95% Bayesian credible regions are depicted by shaded areas. Sampling times are also depicted by the heat maps at the bottom of the top two rows panels: the squares along the time axis depicts the sampling time, while the intensity of the black color depicts the number of samples.

The two estimated genealogies employed in the analysis are the maximum clade credibility trees of the posterior distributions obtained with BEAST2 (Bouckaert et al. 2019). The MCMC parameters are 20 × 10⁶ iterations, thinning every 1000 and burnin of 10 × 10⁶ iterations. We selected the following priors: Extended Bayesian Skyline prior on N_e(t) (Heled and Drummond 2008), HKY mutation model with empirically estimated base frequencies (Hasegawa, Kishino and Yano 1985), and uniform prior on the mutation rate with support constrained between 9 × 10⁻⁴ and 1.1 × 10⁻³ substitutions per site per year. The support of the uniform prior was centered around 1 × 10⁻³ mutations per site per year, an estimate obtained by regressing the Hamming distances of the sequences to the ancestral reference sequence (GenBank MN908947; Wu et al. 2020) on the time difference between the sampling times and the reference sampling time.

Given the two estimated genealogies, we approximate posterior marginal distributions of N_e(t) through the INLA approximations of the noPref model (Palacios and Minin 2012), the parPref model (Karcher et al. 2016), and our adaPref model. In the first two rows of Figure 5, we show the estimates of effective population size trajectories with the noPref model (first column), the parPref model (second column), and the adaPref model (third column). Results for S.C. county correspond to the first row and for L.A. county to the second row. Sampling intensity posteriors (computed only through the adaPref model) are given in the third row of Figure 5 in the second and third panels.

The median posteriors of N_e(t) obtained with the noPref and the adaPref models in L.A. county have almost identical trajectories, while the one with the parPref model has a more pronounced maximum later on (around April 1). In the S.C. county dataset, the median posterior estimates of N_e(t) obtained with the parPref and adaPref models are in this case almost identical, with the estimate obtained with noPref not recovering a steep growth at the end of March. The split behavior of the adaPref posterior, once matching with the noPref posterior and once with parPref posterior, can be explained by looking at the posterior of β(t): in the S.C. dataset, β(t) median posterior is practically flat, a situation consistent with the parametric assumption of the parPref model, while the time-varying β(t) accounts for the fact that sampling in L.A. is concentrated in a short time frame.

The average width of the credible regions $\left(\text{RW}=\frac{1}{K}{\sum }_{i=1}^K\left|{\widehat{N}}_{97.5}\left(v_i\right)-{\widehat{N}}_{2.5}\left(v_i\right)\right|\right)$ differ across methods and datasets. In S.C. county, RWD is 8.5 for noPref, 6.6 for parPref, and 4.7 for adaPref inferences. In L.A. county, the RWD is 23.9 for noPref, 13.6 for parPref, and 20.8 for adaPref inferences. We get a general confirmation that preferential sampling estimators lead to narrower credible regions.

We consider the “split performance” of adaPref (in S.C. similar to parPref and in L.A. similar to noPref) a positive feature of our model. The timely response to the outbreak in S.C. county was followed by a sampling collection that spanned the early stages of the pandemic. Here, adaPref detects an association between the sampling and the coalescent processes. In L.A. county, there is one sequence collected on January 23rd, no sequences collected for about 2 months, followed by an intense sampling effort. The preferential sampling assumption “forces N_e(t) down” in February and early March because there are no samples. This is evident in the result of parPref. On the other hand, adaPref does not detect a strong association between the two processes; hence, the estimates are closer to noPref. To understand which model is correct in this setting, we would need to have access to the sampling protocols of L.A. county to know why there are no samples in those two months.

A final remark. The estimates of N_e(t) presented here are representative of genetic diversity over time and do not directly translate to the number of infections. The coalescent we employed ignores recombination, population structure, and selection. Also, we note that observed nucleotide substitutions may be caused by sequencing errors and these are being ignored in our study.

6. Discussion

We have introduced an adaptive preferential sampling model to estimate the effective population size N_e(t) of a coalescent process accounting for a situation in which sampling dates are stochastically dependent on the effective population size. We model sampling dates as an inhomogeneous Poisson process with rate β(t)N_e(t), where β(t) is a time-varying coefficient that modulates how this dependence varies over time. We assume that both N_e(t) and β(t) are continuous functions and model them in a Bayesian framework with Markov random field priors. This methodology allows us to account for preferential sampling while making minimal assumptions on the dependence between the sampling process and the genealogical process. We term the model proposed adaptive preferential sampling.

The adaptive preferential sampling model allows for a situation in which the sampling protocol changes over time but no detailed knowledge on the way samples are collected is available. In particular, the local adaptivity of the Horseshoe Markov random field prior allows also to model abrupt changes in the sampling protocol.

We show through simulation studies that the estimates obtained through the adaptive preferential sampling are more accurate than some of the available alternatives, leading to smaller absolute deviations from the true trajectories and narrower credible regions. The performance is competitive also in a broad set of scenarios in which the parametric assumptions of the alternative methods are met. We provide an application to SARS-CoV-2 monitoring and show the “adaptive nature” of our methodology: in one scenario the estimate was comparable to that of the model without preferential sampling. In a second one, the estimate was matched that of the parametric preferential sampling methodology.

The most direct extension for future work is to include genealogical uncertainty, which is being ignored in the present work. While Kingman heterochronous n-coalescent is the standard coalescent model choice to include genealogical uncertainty, recent works have proposed to infer N_e(t) employing lower resolution coalescent models (Sainudiin, Stadler, and Véber 2015; Cappello, Veber, and Palacios 2020). Our adaptive preferential sampling framework can be paired with any of the ancestral processes.

Another natural extension to the proposed adaptive preferential framework is to incorporate covariates into λ(t), the sampling rate, as it is done in Karcher et al. (2020), to include auxiliary information about the sampling protocols available to the modeler. For example, it is easy to imagine that one may have direct control over the sampling protocol. The resulting rate of the sampling process would be λ(t) = β(t)N_e(t) + β′X(t), where X is a vector of covariates and β′ the corresponding linear coefficients.

In this article, we model jointly the coalescent process and a sampling process depending on N_e(t). An interesting direction of future work is to model jointly the coalescent process with other processes that depend on N_e(t), such as the total number of infected individuals in an epidemic (Volz et al. 2009). The adaptive framework introduced in this article seems to be suitable to such an extension, given that we make limited assumptions on the dependence between the two processes.