Abstract
Parkinson’s disease (PD) is a neurodegenerative disorder with slow progression whose symptoms can be identified at late stages. Early diagnosis and treatment of PD can help to relieve the symptoms and delay progression. However, this is very challenging due to the similarities between the symptoms of PD and other diseases. The current study proposes a generic framework for the diagnosis of PD using handwritten images and (or) speech signals. For the handwriting images, 8 pre-trained convolutional neural networks (CNN) via transfer learning tuned by Aquila Optimizer were trained on the NewHandPD dataset to diagnose PD. For the speech signals, features from the MDVR-KCL dataset are extracted numerically using 16 feature extraction algorithms and fed to 4 different machine learning algorithms tuned by Grid Search algorithm, and graphically using 5 different techniques and fed to the 8 pretrained CNN structures. The authors propose a new technique in extracting the features from the voice dataset based on the segmentation of variable speech-signal-segment-durations, i.e., the use of different durations in the segmentation phase. Using the proposed technique, 5 datasets with 281 numerical features are generated. Results from different experiments are collected and recorded. For the NewHandPD dataset, the best-reported metric is 99.75% using the VGG19 structure. For the MDVR-KCL dataset, the best-reported metrics are 99.94% using the KNN and SVM ML algorithms and the combined numerical features; and 100% using the combined the mel-specgram graphical features and VGG19 structure. These results are better than other state-of-the-art researches.
Keywords: Feature extraction, Hyperparameters optimization, Machine learning (ML), Parkinson disease (PD), Speech segmentation, Transfer learning (TL), Voice segmentation
Introduction
Parkinson’s disease (PD) is a chronic neurological disorder resulting from the diminishment in the levels of dopamine as a result of a shortage of dopamine-producing cells in the brain. As the brain is the control center of the entire human body, any deficiency in the work of its cells affects the signals propagating to the different parts and causes different symptoms. In the case of PD, symptoms can be classified into motors and non-motors (Politis et al. 2010). In the first category, patients suffer from symptoms including (1) tremors, (2) Freezing of Gait (FoG), (3) muscle rigidity, (4) Fear of Falling (FoF), (5) slow movements, (6) impaired posture, (7) micrographia, and (8) voice abnormality (Berus et al. 2019). In the second category, symptoms include (1) depression, (2) dementia, (3) sleep disorders, (4) anxiety, (5) slow thinking, and (6) fatigue (Almeida et al. 2019).
PD mostly affects people after 60 years old. However, it sometimes affects patients in the 40s because of genetic reasons (De Lau and Breteler 2006). PD can affect both genders, but it has been proven that male patients are affected more compared to females (Lamba et al. 2021). The main concern with PD is that symptoms appear clearly after the loss of about of the dopaminergic cells (Sveinbjornsdottir 2016). Till this moment, researchers are unable to specify the reason behind that disease. There is no treatment for PD until the recent moment, but symptoms can be controlled by proper medications (Hireš et al. 2021). Therefore, early detection of PD can help patients have a self-sufficient life (Gupta et al. 2018).
Several diagnostic markers of PD can be used, of which the handwriting and voice signals because of their low cost and less time consumption compared to MRI or other brain tests are selected. Patients with PD have problems in motor skills including those used for writing due to the effect of muscle rigidity, shacking, and slow movement (Dias et al. 2020). Although changes in handwriting are hardly perceivable in the early stages of the disease, it is still an essential biomarker of PD diagnosis (Kamran et al. 2021). With the evolution in deep learning, visual features can be extracted automatically and used to train a network of several layers to correctly classify patients of PD from normal people.
Abnormalities in voice signals are another biomarker of the existence of PD. Patients with PD have their voice turned softer, with fast and monotonous speech. These abnormalities might be unnoticeable to normal people and need experts (Ali et al. 2019). Speech impairments can be observed from either running speech or continuous vowel phonation (Rizvi et al. 2020). Diagnosing PD from voice changes has become very popular in recent research due to its simplicity and time-saving. Therefore, the use of voice tests in the diagnoses of PD is of trending interest (Caliskan et al. 2017).
The application of deep learning (DL) to image classification has guaranteed better accuracy (Xiao et al. 2021b, 2021a; Balaha et al. 2021b). Convolutional neural network (CNN) is the commonly used DL approach in the field of medical imaging because of their robustness in automatic feature extraction (Li et al. 2021; Balaha et al. 2021a; Huynh et al. 2016). Applications of CNN in medical imaging include pancreas segmentation (Roth et al. 2015), brain tumor segmentation (Havaei et al. 2017; Guttman et al. 2003), liver cancer segmentation Li et al. 2018), detection of cerebral microbleeds (Dou et al. 2016), COVID-19 (Balaha et al. 2021e, 2021d; Bahgat et al. 2021), skin cancer detection Połap 2019), and Alzheimer’s disease (Helaly et al. 2021; Khagi et al. 2018). To build a CNN from scratch, big data must be available to train the network efficiently. However, in case of limited available data, it is preferable to use existing models that were previously trained such as ImageNet, and “transfer” all the knowledge in the model targeted to be trained on the new data. This approach is called transfer learning (TL) (Cao et al. 2013; Balaha et al. 2021c).
The use of metaheuristic algorithms (i.e., optimizers) in solving optimization problems is currently the most common approach (Sörensen and Glover 2013). With their flexibility, an optimal solution can be achieved (Yousri et al. 2021). Unfortunately, concerning the no free lunch (NFL) theorem, a single optimization algorithm can outperform other algorithms in some problems, but it can also have bad performance for other problems. Therefore, new algorithms are continuously being built. Examples of the currently available algorithms include Genetic Algorithms (Holland 1992), Particle Swarm Optimization (Kennedy and Eberhart 1995), Bat Algorithm (Yang and Gandomi 2012), Red Fox Optimization Algorithm (Połap and Woźniak 2021), and Marine Predators Algorithm (Faramarzi et al. 2020). The use of metaheuristic algorithms in learning the hyperparameters of CNN is of great interest in recent researches (Singh et al. 2021; Loussaief and Abdelkrim 2018; Wang et al. 2019; Khalid and Javaid 2020; Soon et al. 2018).
Machine learning (ML) algorithms are usually used in data classification problems (Aggarwal et al. 2021; Raheja et al. 2021; Thapliyal et al. 2021; Chakradar et al. 2021). The most important step of ML is to successfully extract the essential features that guarantee robust classification. Different ML algorithms are available such as decision trees (Rokach and Maimon 2005) and support vector machines (Steinwart and Christmann 2008). However, they all have approximately the same principle; i.e., the machine is trained on data for correct classification (Jordan and Mitchell 2015).
In the current study, a comprehensive generic framework for early and accurate detection of PD using both handwritten images and speech signals is proposed. It consists of four phases, namely (1) datasets collection, (2) pre-processing, (3) hyperparameters optimization, and (4) classification, to handle both data types. For handwritten images, patients are required to draw specific shapes. The resulting shapes are then diagnosed by the system. Here, 8 pre-trained CNN models via TL, namely (1) ResNet50 (He et al. 2016), (2) VGG16, (3) VGG19 (Simonyan and Zisserman 2014), (4) MobileNet (Howard et al. 2017), (5) MobileNetV2 (Sandler et al. 2018), (6) MobileNetV3Small, (7) MobileNetV3Large (Howard et al. 2019), and (8) InceptionResNetV2 (Szegedy et al. 2017) are used. To optimize the hyperparameters, an optimization algorithm called Aquila Optimizer (AO) (Abualigah et al. 2021) is utilized. This algorithm is based on the behavior of Aquilas during the hunting process. Due to the limitation of available handwriting data, different data augmentation techniques are applied to increase the diversity dataset to avoid overfitting.
For the speech signals, 16 numerical feature extraction, 5 graphical feature extraction, and 4 machine learning (ML) algorithms are used. The ML algorithms are (1) Decision Tree (DT) (Loh 2011), (2) Support Vector Machine (SVM) (Vapnik 2013), (3) Naïve Bayes (NB) Tsangaratos and Ilia 2016), and (4) K-Nearest Neighbor (KNN) (Zhang et al. 2017). A new approach in the features’ dataset preparation concerning the speech signals’ segmentation is proposed. It involves segmenting the voice signals into segments of different durations and combining them into a heterogeneous dataset. 5 heterogeneous datasets with 281 numerical features each and 5 graphical features are generated. To optimize the hyperparameters, the grid search (GS) (LaValle et al. 2004) is used with the ML algorithms and AO with the pre-trained CNN models.
Contributions
The contributions of the presented work can be summarized in the following points:
Proposing a generic framework for early and accurate diagnosis of PD using a combination of disorders in both handwritten images and speech signals.
Using a combination of disorders in both the handwritten and speech signals.
Using 8 pre-trained CNN models via TL to classify PD using the handwritten images and 4 ML algorithms to diagnose PD from speech signals.
Applying 16 numerical feature extraction and 5 graphical feature extraction algorithms that generated 281 numerical features and 5 graphical features.
Optimizing the CNN and ML hyperparameters using GS and AO.
Proposing a new approach in voice segmentation using different durations to increase the diversity and heterogeneity features.
Paper organization
The rest of the paper is divided into 4 sections. Section 2 presents some state-of-the-art studies about the diagnosis of PD. Section 3 describes the methodology used to build the proposed framework. The experimental results, discussion, and comparative study of the proposed framework are discussed in Sect. 4. Section 5 presents the current study limitations. Section 6 presents the conclusions and future works.
Results
A lot of research has been done to diagnose PD using intelligent techniques. Pereira et al. (2015) made a dataset called HandPD of 55 subjects with 37 PD and 18 healthy subjects. They applied different ML classifiers, i.e., NB, SVM, and optimum-path forest (OPF), on the extracted features. They reported a maximum accuracy of 78.9% using the NB classifier. In their other trial, Pereira et al. (2016b) performed many experiments using CNN. They applied different train/test split ratios and different image resolutions. They could achieve an accuracy of 80.19%.
In their next study, Pereira et al. (2016a) applied different metaheuristic techniques, namely firey algorithm, bat algorithm, and molecule swarm optimization, to extract features from the handwriting dataset. They used CNN in classification. They could achieve an accuracy of 90.385%. In Pereira et al. (2018), Pereira et al. applied CNN to the same dataset and could achieve an accuracy of 95%. Senatore et al. (2019) applied cartesian genetic programming (CGP) for the classification of PD. The authors used the HandPD dataset, and from their results, they could achieve a global accuracy of 72.36%.
PaHaW dataset was also used in many studies. For example, Impedovo (2019) applied an SVM classifier with a linear kernel on it. They could achieve an accuracy of 98.44%. Naseer et al. (2020) used AlexNet architecture via TL in the diagnosis of PD. They applied different augmentation techniques to increase the dataset size and could achieve an accuracy of 98.28%. Kamran et al. (2021) applied different CNN structures via TL on a combination of different datasets, namely HandPD, NewHandPD, and Parkinson’s Drawing datasets. They also applied different augmentation techniques. They could report a maximum accuracy of 99.22% using the AlexNet structure.
Several studies using speech data are also made. For instance, Caliskan et al. (2017) used two speech datasets, namely the Oxford Parkinson’s Disease Detection (OPD) dataset and Parkinson Speech Dataset with Multiple Types of Sound Recordings (PSD). They applied a deep neural network classifier for the detection of PD. They could achieve an average accuracy of 93.79% using the OPD dataset. Sakar et al. (2013) collected voice samples from 20 subjects to create a PD voice dataset. After extracting the essential features, they used SVM and KNN classifiers. They could report a maximum accuracy of 77.5% using the SVM classifier.
Zahid et al. (2020) used AlexNet structure via TL to learn acoustic features and generate spectrograms. They used the pc-Gita dataset and could achieve an accuracy of 99.7%. Tuncer and Dogan (2019) proposed a novel pre-processing technique called the octopus-based pooling technique. They also applied Singular Value Decomposition for feature extraction and Neighborhood Component Analysis for feature selection. They could report a maximum accuracy of 97.62% using the 1-Nearest Neighbor classifier.
These studies are just examples of many other studies (Parziale et al. 2021; Qasim et al. 2021; Orozco-Arroyave et al. 2016; Tsanas et al. 2012; Kurt et al. 2019; Solana-Lavalle et al. 2020; Kurt et al. 2018; Kuresan et al. 2021). The application of IoT has also guaranteed better management and control Sun et al. 2021; Bhardwaj et al. 2021; Połap 2018).
Summarization
Table 1 summarizes the discussed related studies.
Table 1.
Related studies summarization concerning PD
| Reference | Year | Approach | Dataset | Dataset type | Pros. | Cons. | Best accuracy |
|---|---|---|---|---|---|---|---|
| Pereira et al. Pereira et al. 2015) | 2015 | ML using NB, SVM, and OPF | HandPD | Image | Proposing “HandPD” dataset | Achieved accuracy is low | 78.9% using NB |
| Pereira et al. Pereira et al. 2016b) | 2016 | CNN | Proposing an extension to the “HandPD” dataset using signals from a smartpen from meander and spiral drawings | (1) The use of an imbalanced dataset with more healthy samples and (2) the usage of tablet-based devices requires specific conditions for good quality | 80.19% | ||
| Pereira et al. Pereira et al. 2016a) | 2016 | Metaheuristics + CNN | Usage of metaheuristic algorithms to tune the hyperparameters | The usage of imbalanced dataset with more healthy samples | 90.39% | ||
| Pereira et al. Pereira et al. 2018) | 2018 | CNN | (1) CNN is applied for learning features from handwritten dynamics and (2) proposing “NewHandPD” dataset extracted by the use of a smartpen | Process of the time-series data in a black-box manner | 95% | ||
| Senatore et al. Senatore et al. 2019) | 2019 | CGP | The usage of Cartesian Genetic Programming to provide explicit classification rules | Poor results for spiral images | 72.36% | ||
| Impedovo et al. Impedovo 2019) | 2019 | SVM with a linear kernel | PaHaW | Usage of velocity signals | Useful in online handwriting only | 98.44% | |
| Naseer et al. Naseer et al. 2020) | 2020 | CNN using AlexNet | (1) The usage of fine-tuned pretrained models and (2) the usage of k-fold cross-validation | (1) No consideration of dimensionality reduction and (2) vulnerability to acoustic conditions | 98.28% | ||
| Kamran et al. Kamran et al. 2021) | 2021 | CNN using AlexNet, GoogLeNet, VGG, and ResNet | HandPD, NewHandPD, and Parkinson’s Drawing datasets | (1) The usage of several datasets and (2) high achieved accuracy. | Poor accuracy in case of scratch CNN | 99.22% using AlexNet | |
| Sakar et al. Sakar et al. 2013) | 2013 | SVM, KNN | Speech data | Voice | Proposal of voice dataset for Parkinson’s disease | Results are biased | 77.5% |
| Caliskan et al. Caliskan et al. 2017) | 2017 | DNN | OPD and PSD | Remote diagnosis ability | Low accuracy | 93.79% | |
| Tuncer et al. Tuncer and Dogan 2019) | 2019 | SVM, 1NN, DT, and logistic regression | Vowel | Gender classification is taken into account | The usage of small data | 97.62% by 1NN | |
| Zahid et al. Zahid et al. 2020) | 2020 | AlexNet | pc-Gita | (1) The usage of deep features of speech and (2) proving that pronunciation of vowels are sufficient in diagnosis | Poor accuracy for isolated words | 99.7% |
Methodology
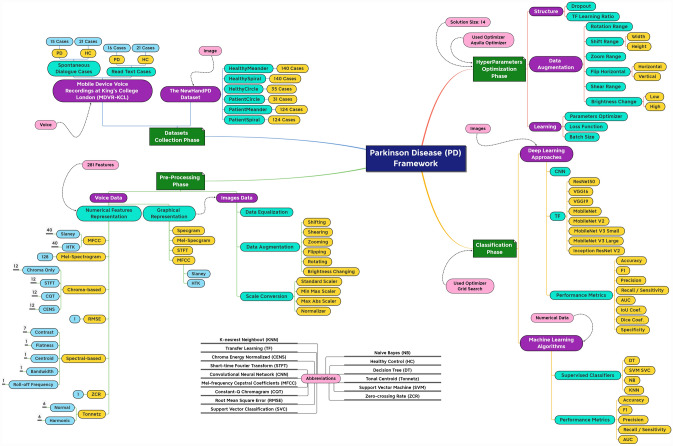
The current study suggests a generic framework (shown in Fig. 1) for Parkinson’s disease learning and optimization. The framework is divided into four major phases. They are (1) datasets collection, (2) pre-processing, (3) classification, and (4) hyperparameters optimization phases. In summary, the data collection phase presents insights into the used Parkinson datasets. The pre-processing phase is responsible for handling the images (and voice) data and preparing them for the classification phase. The classification and hyperparameters optimization phases focus on optimizing a pre-trained CNN model and handling numerical records using ML algorithms. The phases are discussed in the following subsections.
Fig. 1.
The Parkinson diseases learning and optimization framework
Datasets collection phase
The current study works on two public datasets. They are (1) The NewHandPD (Pereira et al. 2016b) and (2) Mobile Device Voice Recordings at King’s College London (MDVR-KCL) (Jaeger et al. 2019). (Check Section 5: Limitations)
The NewHandPD dataset
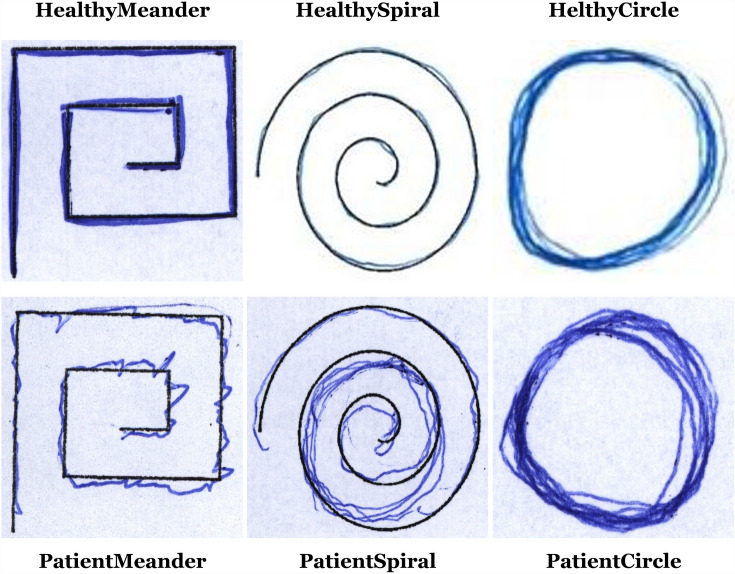
The first dataset consists of 594 images partitioned into 6 classes, where 3 of them belong to healthy people and the remaining three belong to PD patients. They are (1) HealthyMeander (140 images), (2) HealthySpiral (140 images), (3) HelthyCircle (35 images), (4) PatientCircle (31 images), (5) PatientMeander (124 images), and (6) PatientSpiral (124 images) (Pereira et al. 2016b). Samples from it are shown in Fig. 2.
Fig. 2.
Samples from the NewHandPD dataset classes
The MDVR-KCL dataset
The MDVR-KCL dataset consists of “SpontaneousDialogue” and “ReadText” voice records where each of them consists of 2 classes (i.e., PD for sick and HC for healthy people). The number of PD and HC cases are 15 and 21 respectively in the “SpontaneousDialogue” category and 16 and 21 respectively in the “ReadText” category (Jaeger et al. 2019).
Pre-processing phase
The used pre-processing approaches for the images are (1) data equalization, (2) data augmentation, and (3) scale conversion while for the voice records are (1) numerical features representation, (2) graphical representation, and (3) scale conversion.
Images manipulation
The equalization process is applied by finding the highest class concerning the number of records and augmenting the rest of the classes’ records randomly until they reach the highest number. Data augmentation techniques are used to increase the diversity of the images, especially since the available online PD datasets are limited. The followed techniques are (1) shifting, (2) shearing, (3) zooming, (4) flipping, (5) rotation, and (6) brightness changing (Perez and Wang 2017). The augmentation is used in two locations in the current study. The first location is used before the learning process to equalize the number of records in each class. The second location is applied during the optimization and learning process with different ranges. The scale conversion includes four used techniques (1) normalization (Kumar and Verma 2010), (2) min-max scaling (Fulkerson and Wolfe 1962), (3) standard scaling (Fulkerson and Wolfe 1962), and (4) max-abs scaling where in is the input image, is the image mean value, and is the image standard deviation value.
Voice records manipulation
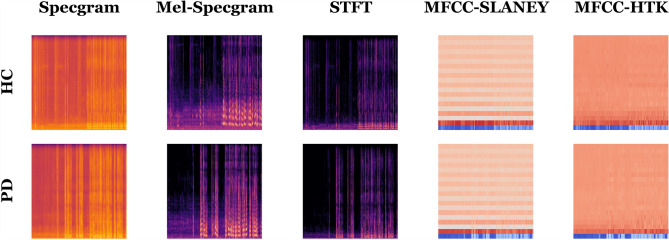
The voice records can be processed numerically and graphically using ML or DL approaches. 16 voice feature extractions techniques are used (1) Mel-frequency Cepstral Coefficients (MFCC) using the Slaney and HTK methods (Sigurdsson et al. 2006), (2) Mel-spectrogram (Kaneko et al. 2020), (3) chroma-based techniques (chroma-only, Short-time Fourier Transform (STFT) Griffin and Lim 1984), Constant-Q Chromagram (CQT) (Liu and Xie 2012), and Chroma Energy Normalized (CENS) Kattel et al. 2019)), (4) spectral-based techniques (contrast, flatness, centroid, bandwidth, and roll-off frequency) (Bou-Ghazale and Hansen 1994), (5) Zero-crossing Rate (ZCR) (Inbar et al. 1986), (6) Tonnetz techniques (normal and harmonic) 2022 2022), and (7) Root Mean Square Error (RMSE) (Chai and Draxler 2014). The voice records are represented graphically using 5 techniques (1) spectrogram, (2) Mel-spectrogram, (3) STFT, and (4) MFCC using the Slaney and HTK methods. The STFT split the signal into time windows and runs the Fourier transform on each window to get the same information (Alsberg et al. 1997). The spectrogram is the frequency change over time. The Mel-spectrogram is the acoustic time-frequency representation. The MFCC describes the overall shape of a spectral envelope (Terasawa et al. 2012). The spectral-contrast describes the differences between the peaks and valleys in the spectrum. The Tonnetz is the tonal centroid features.
How the voice segmentation is applied (one of the study contributions)? The input voice record is read, assuming it is a 95-seconds duration as an example. For a pre-defined segmentation duration, assuming 10 seconds, the voice is cut into 9 segments where each segment is 10-seconds in duration. The remaining 5 seconds are neglected as they are lower than the segmentation duration. This process is run again for another segmentation duration. In the current study, the voices are segmented using 5, 15, 30, and 60 segmentation durations. Also, the output numerical features and graphs from all of them are combined. Hence, the authors generated 5 numerical and graphical datasets from records. Figure 3 shows the proposed voice segmentation approach graphically.
Fig. 3.
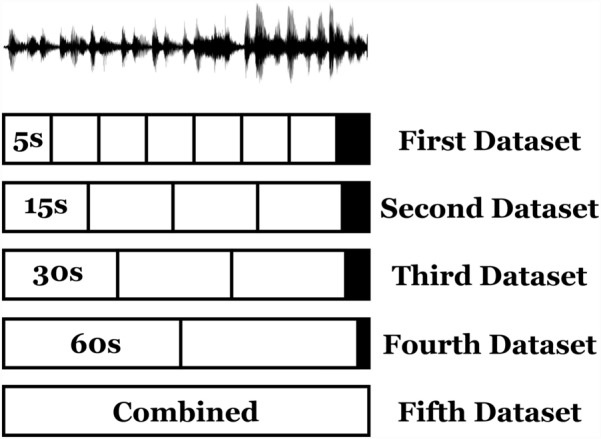
Presentation of the proposed voice records segmentation approach
Current study followed configurations
In the current study, the used pre-defined ranges in the first data augmentation location are shifting in the width (and height), shearing, zooming, horizontal (and vertical) flipping, rotation, and brightness changing with limits of [0.8, 1.2]. For the NewHandPD dataset, the number of total images after equalization is 840 (i.e., 140 images in each class with a size of (100, 100, 3)). For the MDVR-KCL dataset, the “SpontaneousDialogue” and “ReadText” voice records are combined and 281 features are extracted. Each voice record is cut into segments with different time durations (e.g., 10 seconds).
Table 2 shows the number of extracted features using each mentioned technique. Table 3 shows the number of extracted graphs using each segment duration in seconds. Figure 4 shows sample graphs for each technique for the 60-second-segment-duration and they are extracted in the 480 DPI resolution.
Table 2.
Summarization of the number of extracted numerical features for the MDVR-KCL dataset
| Category | Technique | No. features |
|---|---|---|
| MFCC | Slaney | 40 |
| HTK | 40 | |
| Mel-Spectrogram | 128 | |
| Chroma-based | Chroma-only | 12 |
| STFT | 12 | |
| CQT | 12 | |
| CENS | 12 | |
| RMSE | 1 | |
| Spectral-based | Contrast | 7 |
| Flatness | 1 | |
| Centroid | 1 | |
| Bandwidth | 1 | |
| Roll-off Frequency | 1 | |
| ZCR | 1 | |
| Tonnetz | Normal | 6 |
| Harmonic | 6 | |
| Total | 281 |
Table 3.
Summarization of the number of extracted graphs for the MDVR-KCL dataset
| Segment duration (s) | No. PD | No. HC | Total |
|---|---|---|---|
| 5 | 310 | 420 | 730 |
| 15 | 258 | 366 | 624 |
| 30 | 126 | 179 | 305 |
| 60 | 57 | 79 | 136 |
| Total | 751 | 1044 | 1795 |
Fig. 4.
Sample graphs for each technique for the 60-second-segment-duration
Classification and optimization phases
ML algorithms are used to classify the numerical features for the voice records dataset. The convolutional neural network (CNN) (i.e., a DL approach) is used to classify the handwritten images dataset.
Machine learning algorithms
The used ML algorithms are (1) decision trees (DT), (2) support vector machines (SVM), (3) Naïve Bayes (NB), and (4) K-nearest neighbor (KNN). Each ML algorithm is put in a pipeline in the order of (1) a dataset scaler layer, (2) a variance threshold layer, and (3) the ML algorithm.
Pre-trained CNN models
8 pre-trained CNN models on the ImageNet dataset, using the transfer learning approach (TL), are used instead of compiling models from scratch. They are (1) ResNet50, (2) VGG16, (3) VGG19, (4) MobileNet, (5) MobileNetV2, (6) MobileNetV3Small, (7) MobileNetV3Large, and (8) InceptionResNetV2 models. Each model is concatenated with a global average pooling 2D layer, a dropout layer, and an output layer. The output activation function is set to SoftMax and the pre-trained weights’ initialization is set to ImageNet. The input shape is set to (100, 100, 3) in the colored RGB mode.
Hyperparameters optimization
Training the models require specifying a set of hyperparameters such as batch size and dropout. The current study suggests using the grid search (GS) (with the ML algorithms) and injecting the Aquila Optimizer (AO) metaheuristic optimizer (with the CNN models) to find the best combination that will lead to the highest performance metric.
AO depends on four hunting mechanisms (1) high soar with vertical stoop in which the Aquila explores the search space (Equation 1), (2) contour flight with short glide attack in which surrounds the target (Equation 2), (3) a low flight with a slow descent attack in which the Aquila performs a vertical attack (Equation 3), and (4) walking and grab a prey in which the Aquila attacks the target (Eq. 4) Abualigah et al. 2021).
| 1 |
| 2 |
| 3 |
| 4 |
where is the solution of the next iteration , X(t) is the solution of the current iteration t, T is the number of iterations, is the best-obtained solution, is the mean location of the current solutions, D is the dimension value, Levy(D) is the levy flight distribution function, y (and x) are used to present the spiral shape in the search domain, rand is a random uniform value, UB is the upper bound, LB is the lower bound, (and ) are the exploitation adjustment parameters, is a notation of the various motions of the AO, is a decreasing value from 2 to 0, and QF is the quality function used to equilibrium the search techniques.
The word “generic” means that the framework can accept and handle any metaheuristic optimizer and it is not restricted by the specified optimizers in the current study.
Current study followed configurations
The AO population in the current study populates 10 solutions where each solution’s dimension equals 14. The reason behind this number is that each column in the solution is mapped to a specific hyperparameter randomly. These are the target hyperparameters to get optimized.
They are (1) training loss function, (2) training batch size, (3) dropout ratio, (4) TL learning ratio, (5) parameters (i.e., weights) optimizer, (6) augmentation rotation range, (7) augmentation width shift range, (8) augmentation height shift range, (9) augmentation shear range, (10) augmentation zoom range, (11) augmentation horizontal flipping, (12) augmentation vertical flipping, and (13) augmentation brightness change (“from” and “to” ranges).
In the grid search, the hyperparameters are (1) “nNeighbors” is the number of neighbors to use, (2) “leafSize” is the leaf size passed to the tree, (3) “p” is the power parameter for the Minkowski metric, (4) “criterion” is the function to measure the split quality, (5) “maxDepth” is the tree maximum depth, (6) “splitter” is the strategy used to choose the split at each node, (7) “alpha” is the additive (Laplace/Lidstone) smoothing parameter, (8) “C” is the regularization parameter, (9) “kernel” is the kernel type to be used in the algorithm, (10) “degree” is the degree of the polynomial kernel function, (11) “gamma” is the kernel coefficient, and (12) “threshold” is the threshold value used by the variance threshold layer. Table 4 shows the used ranges for each hyperparameter in the current study.
Table 4.
The ranges for each hyperparameter
| Optimizer | Category | Definition | Range |
|---|---|---|---|
| AO | CNN Learning | Loss Function | Categorical Crossentropy, Categorical Hinge, KL Divergence, Poisson, Squared Hinge, and Hinge |
| Batch Size | From 8 to 64 with a step of 8 | ||
| Parameters (i.e., weights) & Optimizer | Adam, Nadam, Adagrad, Adadelta, Adamax, RMSProp, SGD, Ftrl, SGD Nesterov, RMSProp Centered, Adam, and AMSGrad | ||
| CNN Model Structure | Dropout ratio | [0.0, 0.6] | |
| TL learning ratio | From 0 to 100 with a step of 1 | ||
| CNN Data Augmentation | Rotation Range | From 0 to 45 with a step of 1 | |
| Width Shift Range | [0, 0.25] | ||
| Height Shift Range | |||
| Shear Range | |||
| Zoom Range | |||
| Horizontal Flipping | [True, False] | ||
| Vertical Flipping | |||
| Brightness Change (From) | [0.5, 2.0] | ||
| Brightness Change (To) | |||
| GS | KNN | nNeighbors | [1, 2, 3, 5, 7, 10] |
| leafSize | [1, 5, 10, 15] | ||
| p | [1, 2] | ||
| SVM | degree | [1, 2, 3, 4, 5] | |
| C | [0.1, 1, 10, 100, 1000] | ||
| gamma | [1, 0.1, 0.01, 0.001, 0.0001] | ||
| kernel | [Linear, Poly, RBF, Sigmoid, Precomputed] | ||
| DT | criterion | [Gini, Entropy] | |
| splitter | [Best, Random] | ||
| maxDepth | From 3 to 14 with a step of 1 | ||
| NB | alpha | [0, 0.1, 0.5, 1.0, 1.5, 2, 3, 5, 10] | |
| Variance Threshold | threshold | [0, 0.001, 0.005, 0.01, 0.05, 0.1, 0.5] |
Performance metrics
The used performance metrics with the ML algorithms are the accuracy, F1-score, precision, recall (i.e., sensitivity), and AUC; while the used ones with the CNN learning and optimization are loss, accuracy, F1-score, precision, recall (i.e., sensitivity), specificity, AUC, IOU coefficient, and Dice coefficient.
Framework pseudocode
The used framework pseudocode is shown in Algorithm 1. It summarizes the discussed learning and optimization phases in the suggested framework abstractly. Comments are added for illustration purposes.
PD patient diagnosis
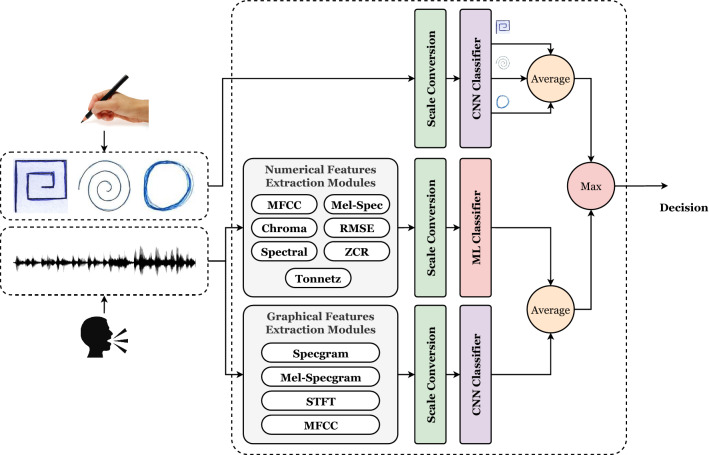
After completing the framework discussion, the question is “how can the patient perform a diagnosis?”. In the suggested generic framework, the patient can apply two tests (1) handwriting test and (2) speech test. In the first test, the patient should draw three graphs while in the second test, the patient should read certain words (or sentences).
The system accepts the drawn three figures as inputs, converts the scale, applies classification of each type, and takes the average of them. The system also accepts the speech record, extract the numerical and graphical features of them, convert the scale, apply classification of each type, and take the average of them. The final decision to the patient is the maximum between the two tests. It is worth mentioning that, the maximum can be changed to the average. This is summarized graphically in Fig. 5.
Fig. 5.
Parkinson disease (PD) patient diagnosis
Experimental results and discussion
The experiments are divided into two categories (1) experiments related to the extracted numerical features and (2) experiments related to the images and extracted graphs.
Environment and configurations
Generally, Python is the used programming language. The learning and optimization environments are Google Colab (with its GPU) and Toshiba Qosmio X70-A with 32 GB RAM and Intel Core i7 Processor (Balaha and Saafan 2021). The NewHandPD (6 classes) and MDVR-KCL (2 classes) are the used datasets. The dataset split ratio is set to 85% (training and validation) and 15% (testing). Dataset shuffling is applied. The images (i.e., graphs) are resized to (100, 100, 3) in RGB. The train and test subsets are different so that there is no data leakage.
First category experiments
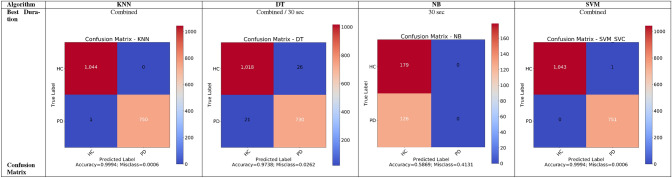
The current subsection presents and discusses the experiments related to the extracted 281 numerical features using the mentioned ML algorithms (i.e., DT, SVM, NB, and KNN). For each ML algorithm, five experiments are applied on the 5, 15, 30, 60, and mixed durations. The algorithms are optimized using the grid search for 10 cross-validation runs, to find the best combinations with the highest metrics. The metrics (i.e., accuracy, precision, recall, F1, and AUC) are captured and reported in Table 5. It reports the best metrics 99.94%, 100%, 100%, 99.93%, and 99.95% for accuracy, precision, recall, F1, and AUC respectively. It shows that the NB algorithm reports the worst metrics. It highlights that the suggested contribution, by combining the features, reports better metrics than the individual uncombined features. The confusion matrices are presented in Table 6.
Table 5.
Summary of the ML numerical experiments (i.e., first category experiments)
| Duration (s) | Algorithm | Accuracy | Precision | Recall | F1 | AUC | Scaler | Variance threshold | Best classifiers parameters |
|---|---|---|---|---|---|---|---|---|---|
| 5 | KNN | 98.36% | 97.76% | 98.39% | 98.07% | 98.36% | Min Max | 0.01 | leafSize = 1, nNeighbors = 1, and p = 1 |
| DT | 83.42% | 89.54% | 69.03% | 77.96% | 81.54% | Normalizer | 0 | criterion = entropy and maxDepth = 5 | |
| NB | 57.53% | 0% | 0% | 0% | 50.00% | Normalizer | 0 | alpha = 0 | |
| SVM | 98.90% | 98.71% | 98.71% | 98.71% | 98.88% | Min Max | 0.01 | C = 0.1, degree = 5, gamma = 1, and kernel = poly | |
| 15 | KNN | 99.04% | 98.84% | 98.84% | 98.84% | 99.01% | Max Abs | 0 | leafSize = 1 and nNeighbors = 1 |
| DT | 96.63% | 96.47% | 95.35% | 95.91% | 96.44% | Normalizer | 0 | criterion = entropy and maxDepth = 13 | |
| NB | 58.65% | 0% | 0% | 0% | 50.00% | Normalizer | 0 | alpha = 0 | |
| SVM | 99.04% | 98.46% | 99.22% | 98.84% | 99.07% | Min Max | 0.01 | C = 100, degree = 1, and gamma = 0.1 | |
| 30 | KNN | 98.03% | 100% | 95.24% | 97.56% | 97.62% | Max Abs | 0.05 | leafSize = 1, nNeighbors = 1, and p = 1 |
| DT | 97.38% | 99.17% | 94.44% | 96.75% | 96.94% | Standardization | 0.10 | maxDepth = 10 and splitter = random | |
| NB | 58.69% | 0% | 0% | 0% | 50.00% | Normalizer | 0 | alpha = 0 | |
| SVM | 98.03% | 100% | 95.24% | 97.56% | 97.62% | Max Abs | 0.05 | C = 0.1, gamma = 1, and kernel = poly | |
| 60 | KNN | 98.53% | 100% | 96.49% | 98.21% | 98.25% | Max Abs | 0.01 | leafSize = 1, nNeighbors = 1, and p = 1 |
| DT | 83.82% | 92.68% | 66.67% | 77.55% | 81.43% | Normalizer | 0 | maxDepth = 3 and splitter = random | |
| NB | 58.09% | 0% | 0% | 0% | 50.00% | Normalizer | 0 | alpha = 0 | |
| SVM | 94.85% | 96.30% | 91.23% | 93.69% | 94.35% | Min Max | 0 | C = 1, degree = 1, and gamma = 0.1 | |
| Combined | KNN | 99.94% | 100% | 99.87% | 99.93% | 99.93% | Max Abs | 0 | leafSize = 1 and nNeighbors = 1 |
| DT | 97.38% | 96.56% | 97.20% | 96.88% | 97.36% | Standardization | 0.50 | criterion = entropy and maxDepth = 14 | |
| NB | 58.16% | 0% | 0% | 0% | 50.00% | Normalizer | 0 | alpha = 0 | |
| SVM | 99.94% | 99.87% | 100% | 99.93% | 99.95% | Max Abs | 0 | C = 100, degree = 1, and gamma = 0.1 |
Table 6.
Summary of the confusion matices (i.e., first category experiments)
Second category experiments
The current subsection presents and discusses the experiments related to the images and extracted graphical features using the mentioned pre-trained CNN models (i.e., ResNet50, VGG16, VGG19, MobileNet, MobileNetV2, MobileNetV3Small, MobileNetV3Large, and InceptionResNetV2) and AO meta-heuristic optimizer. The number of epochs is set to 5. The number of AO iterations and population size are set to 25 and 10 respectively, and hence 250 records are reported. The captured metrics are the loss, accuracy, F1, precision, recall, specificity, AUC, IOU coef., and Dice coef. as mentioned.
The NewHandPD experiments
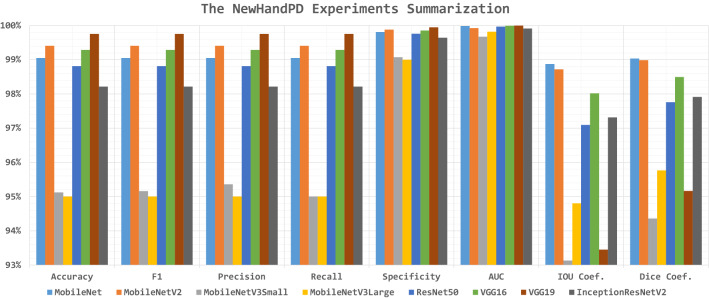
The top-1 record is reported concerning the testing accuracy for each pre-trained CNN model in Table 7. It shows that neglecting the horizontal and vertical flipping is preferable by six and five models respectively. The metrics results are above 93% while the best metrics are 0.029, 99.75%, 99.75%, 99.75%, 99.75%, 99.95%, 100%, 99.75%, 98.87%, and 99.04% for the loss, accuracy, F1, precision, recall, specificity, AUC, IOU coef., and Dice coef. respectively. The KL divergence loss function and SGD Nesterov (and SGD) weights optimizers are the suggested hyperparameters by the experiments. The results are graphically summarized in Fig. 6 and the correlations are reported in Table 8.
Table 7.
The top-1 record concerning the accuracy for the pre-trained models for NewHandPD
| # | MobileNet | MobileNetV2 | MobileNetV3Small | MobileNetV3Large | ResNet50 | VGG16 | VGG19 | InceptionResNetV2 |
|---|---|---|---|---|---|---|---|---|
| Loss function | Categorical crossentropy | Categorical crossentropy | KL divergence | KL divergence | KL divergence | KL divergence | Poisson | Categorical crossentropy |
| Batch size | 24 | 8 | 8 | 24 | 56 | 40 | 48 | 56 |
| Dropout ratio | 0.42 | 0 | 0.37 | 0.20 | 0.41 | 0.26 | 0.33 | 0.35 |
| TL learn ratio | 89% | 0% | 84% | 55% | 22% | 57 | 67 | 58 |
| Weights optimizer | SGD Nesterov | Adam | Adagrad | SGD Nesterov | Adagrad | Adagrad | SGD | SGD Nesterov |
| Rotation range | ||||||||
| Width shift range | 0.24 | 0 | 0.21 | 0.07 | 0.20 | 0.22 | 0.15 | 0.22 |
| Height shift range | 0.24 | 0 | 0.05 | 0.02 | 0.05 | 0.03 | 0.2 | 0.06 |
| Shear range | 0.02 | 0 | 0.21 | 0.23 | 0.19 | 0.15 | 0.15 | 0.13 |
| Zoom range | 0.12 | 0 | 0.22 | 0.25 | 0.01 | 0.19 | 0.22 | 0.20 |
| Horizontal flip | ||||||||
| Vertical flip | ||||||||
| Brightness range (low) | 1.24 | 0.5 | 0.92 | 1.29 | 1.01 | 1.34 | 1.32 | 0.56 |
| Brightness range (high) | 1.28 | 0.5 | 1.08 | 1.52 | 1.67 | 1.76 | 1.46 | 1.3 |
| Loss | 0.038 | 0.032 | 0.152 | 0.107 | 0.049 | 0.029 | 0.180 | 0.049 |
| Accuracy | 99.05% | 99.40% | 95.12% | 95.00% | 98.81% | 99.29% | 99.75% | 98.21% |
| F1-Score | 99.05% | 99.40% | 95.16% | 95.00% | 98.81% | 99.29% | 99.75% | 98.21% |
| Precision | 99.05% | 99.40% | 95.36% | 95.00% | 98.81% | 99.29% | 99.75% | 98.21% |
| Recall | 99.05% | 99.40% | 95.00% | 95.00% | 98.81% | 99.29% | 99.75% | 98.21% |
| Specificity | 99.81% | 99.88% | 99.07% | 99.00% | 99.76% | 99.86% | 99.95% | 99.64% |
| AUC | 99.98% | 99.92% | 99.67% | 99.82% | 99.97% | 99.99% | 100% | 99.91% |
| IOU coefficient | 98.87% | 98.72% | 93.13% | 94.80% | 97.09% | 98.02% | 93.45% | 97.31% |
| Dice coefficient | 99.04% | 98.99% | 94.36% | 95.77% | 97.76% | 98.50% | 95.17% | 97.92% |
Fig. 6.
The NewHandPD experiments summarization
Table 8.
The best hyperparameters correlations for the NewHandPD experiments
| Batch size | Dropout | TL learn ratio | Rotation range | Width shift range | Height shift range | Shear range | Zoom range | Horizontal flip | Vertical flip | Brightness range (low) | Brightness range (high) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Batch size | 1.000 | |||||||||||
| Dropout | 0.488 | 1.000 | ||||||||||
| TL learn ratio | − 0.037 | 0.663 | 1.000 | |||||||||
| Rotation range | 0.112 | 0.543 | 0.817 | 1.000 | ||||||||
| Width shift range | 0.456 | 0.898 | 0.661 | 0.728 | 1.000 | |||||||
| Height shift range | 0.176 | 0.562 | 0.608 | 0.408 | 0.431 | 1.000 | ||||||
| Shear range | 0.271 | 0.342 | 0.231 | 0.142 | 0.203 | − 0.308 | 1.000 | |||||
| Zoom range | 0.047 | 0.251 | 0.731 | 0.646 | 0.259 | 0.144 | 0.558 | 1.000 | ||||
| Horizontal flip | − 0.530 | − 0.365 | − 0.196 | − 0.303 | − 0.315 | 0.271 | − 0.917 | − 0.576 | 1.000 | |||
| Vertical flip | 0.070 | − 0.411 | − 0.766 | − 0.467 | − 0.230 | − 0.511 | − 0.213 | − 0.717 | 0.149 | 1.000 | ||
| Brightness range (low) | 0.149 | 0.365 | 0.512 | 0.266 | 0.293 | 0.443 | 0.371 | 0.446 | − 0.277 | − 0.177 | 1.000 | |
| Brightness range (high) | 0.686 | 0.589 | 0.333 | 0.264 | 0.569 | 0.159 | 0.616 | 0.385 | − 0.669 | − 0.023 | 0.724 | 1.000 |
The MDVR-KCL experiments
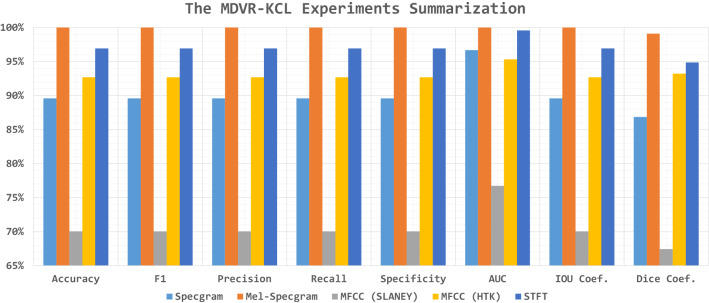
The top-1 record using VGG19 is reported concerning the testing accuracy for each combined dataset (i.e., STFT, MFCC HTK, MFCC Slaney, Specgram, and Mel-Specgram) in Table 9. The reason behind depending on the VGG19, it reported the best metrics in Table 7. It shows that neglecting the horizontal and vertical flipping is preferable by five and three models respectively. The best metrics are 0.090, 100%, 100%, 100%, 100%, 100%, 100%, 100%, 100%, and 99.09% for the loss, accuracy, F1, precision, recall, specificity, AUC, IOU coef., and Dice coef. respectively. The Poisson loss function and Adagrad (and SGD) weights optimizers are the suggested hyperparameters by the experiments. The results are graphically summarized in Fig. 7 and the correlations are reported in Table 10.
Table 9.
The top-1 record concerning the accuracy using VGG19 for MDVR-KCL
| # | Specgram | Mel-Specgram | MFCC (SLANEY) | MFCC (HTK) | STFT |
|---|---|---|---|---|---|
| Loss Function | Poisson | Poisson | Poisson | Squared Hinge | KL Divergence |
| Batch Size | 48 | 40 | 16 | 48 | 40 |
| Dropout Ratio | 0.06 | 0.41 | 0.43 | 0.19 | 0.31 |
| TL Learn Ratio | 86 | 67 | 13 | 59 | 61 |
| Weights Optimizer | Adagrad | SGD | RMSProp Centered | Adagrad | SGD |
| Rotation Range | 29 | 29 | 41 | 41 | 35 |
| Width Shift Range | 0.14 | 0.2 | 0 | 0.09 | 0.16 |
| Height Shift Range | 0.09 | 0.14 | 0.15 | 0.05 | 0.2 |
| Shear Range | 0.01 | 0.14 | 0.22 | 0.13 | 0.14 |
| Zoom Range | 0.13 | 0.13 | 0.01 | 0.13 | 0.17 |
| Horizontal Flip | |||||
| Vertical Flip | |||||
| Brightness Range (Low) | 0.72 | 1.33 | 0.55 | 0.65 | 1.38 |
| Brightness Range (High) | 1.32 | 1.65 | 1.16 | 1.33 | 1.41 |
| Loss | 0.619 | 0.505 | 0.791 | 0.654 | 0.090 |
| Accuracy | 89.58% | 100% | 70.03% | 92.68% | 96.93% |
| F1-Score | 89.58% | 100% | 70.03% | 92.68% | 96.93% |
| Precision | 89.58% | 100% | 70.03% | 92.68% | 96.93% |
| Recall | 89.58% | 100% | 70.03% | 92.68% | 96.93% |
| Specificity | 89.58% | 100% | 70.03% | 92.68% | 96.93% |
| AUC | 96.69% | 100% | 76.72% | 95.33% | 99.55% |
| IOU Coefficient | 89.58% | 100% | 70.03% | 92.68% | 96.93% |
| Dice Coefficient | 86.85% | 99.09% | 67.41% | 93.22% | 94.85% |
Fig. 7.
The MDVR-KCL experiments summarization
Table 10.
The best hyperparameters correlations for the MDVR-KCL experiments
| Batch size | Dropout | TL learn ratio | Rotation range | Width shift range | Height shift range | Shear range | Zoom range | Horizontal flip | Vertical flip | Brightness range (low) | Brightness range (high) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Batch size | 1.000 | |||||||||||
| Dropout | − 0.743 | 1.000 | ||||||||||
| TL learn ratio | 0.923 | − 0.701 | 1.000 | |||||||||
| Rotation range | − 0.456 | 0.241 | − 0.752 | 1.000 | ||||||||
| Width shift range | 0.688 | − 0.169 | 0.816 | − 0.812 | 1.000 | |||||||
| Height shift range | − 0.485 | 0.624 | − 0.292 | − 0.130 | 0.155 | 1.000 | ||||||
| Shear range | − 0.792 | 0.886 | − 0.900 | 0.664 | − 0.519 | 0.423 | 1.000 | |||||
| Zoom range | 0.863 | − 0.445 | 0.836 | − 0.495 | 0.848 | 0.006 | − 0.578 | 1.000 | ||||
| Horizontal flip | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | 1.000 | |||
| Vertical flip | 0.667 | − 0.910 | 0.519 | 0.000 | − 0.036 | − 0.886 | − 0.703 | 0.241 | N/A | 1.000 | ||
| Brightness range (low) | 0.248 | 0.324 | 0.372 | − 0.536 | 0.817 | 0.640 | − 0.005 | 0.657 | N/A | − 0.555 | 1.000 | |
| Brightness range (high) | 0.462 | 0.186 | 0.554 | − 0.671 | 0.898 | 0.162 | − 0.179 | 0.624 | N/A | − 0.250 | 0.816 | 1.000 |
Time complexity remarks
The major objective of the current study was to build a framework for the PD using speech and handwritten datasets. The target was to achieve high performance metrics as reported in the results. The learning and processing time was high and hence was not reported exactly in the study. However, approximate times can be calculated. It is worth noting that the time depended mainly on the working environment. The current study worked on two environments as mentioned in Sect. 4.1. For the ML model, the second environment is used while the first environment is used with the CNN models.
For the first category experiments, the GS and 10-folds CV are used. Assuming that, each ML model takes one second approximately. Table 11 shows the approximate time for each ML model. The total approximate time for the ML models for a single dataset is 7,300 seconds (i.e., 121 minutes or 2 hours). We have 5 datasets as shown in Tables 3 and 5. Hence, we need 10 hours approximately to launch them. Of course, they are approximate times and the ML models may take longer than this.
Table 11.
Approximate times for each ML model
| Model | Hyperparameters # | Total configurations # | With 10 folds | Approximate time (s) |
|---|---|---|---|---|
| KNN | 3 | 480 | 480 | |
| SVM | 4 | 6,250 | 6,250 | |
| DT | 3 | 480 | 480 | |
| NB | 1 | 9 | 90 | 90 |
| 7300 |
By applying the same concept with the pretrained models but with the assumption that each model takes 1 minutes due to the model complexity. There are 14 hyperparameters to optimize using the AO. The number of iterations is set to 10, the population size is set to 25, and the number of epochs is set to 5. Hence, there are runs for each model to complete. The approximate time is 1,250 minutes (i.e., 20 hours) for a single model. We have 8 pretrained models in Table 7 and 5 datasets in Table 9. Hence, there are 14 experiments. The total approximate time can be 291 hours (i.e., 12 days).
Related studies comparisons
Table 12 shows a comparison between the suggested approach and related studies concerning the same used datasets.
Table 12.
Related studies comparisons
| References | Best accuracy | Other metrics |
|---|---|---|
| Pereira et al. 2015) | 78.9% | – |
| Pereira et al. 2016b) | 80.19% | – |
| Pereira et al. 2016a) | 90.39% | – |
| Pereira et al. 2018) | 95% | – |
| Senatore et al. 2019) | 72.36% | – |
| Impedovo 2019) | 98.44% | – |
| Naseer et al. 2020) | 98.28% | 85.98% precision, 67.57% sensitivity, and 76.37% specificity |
| Kamran et al. 2021) | 99.75% (CNN-TL) | – |
| Sakar et al. 2013) | 77.5% | – |
| Caliskan et al. 2017) | 86.09% | 58.27% sensitivity abd 95.39% specificity |
| Goyal et al. 2021) | 99.37% | – |
| Tuncer and Dogan 2019) | 97.62% by 1NN | 97.61% F1 |
| Zahid et al. 2020) | 99.7% | – |
| Proposed approach | 99.94% (ML) | Table 5 |
| Proposed approach | 99.75% (NewHandPD) | Table 7 |
| Proposed approach | 100% (MDVR-KCL) | Table 9 |
Limitations
The major limitation of the current study is the dataset as the PD public and available datasets are limited and there is no dataset that contains handwriting and voice data for the same patient. In the future, data from PD patients can be collected as well to further validate the effect of diversity based on the suggested approach.
Conclusions and future work
Parkinson’s disease is a progressive and chronic disorder that harms the life of the patients. Scientists are still trying to find a suitable treatment for the disease. The main problem of PD is that patients are correctly diagnosed in the late stages. Therefore, a massive effort is done to diagnose PD in its early stages to use the proper medication to control the symptoms as possible. The challenge is that the symptoms of PD are similar to other diseases. In this paper, the authors proposed a comprehensive generic framework for the early diagnosis of PD using a combination of disorders in handwritten and (or) speech signals. For handwriting disorders, 8 pre-trained deep CNNs via TL, namely ResNet50, VGG16, VGG19, MobileNet, MobileNetV2, MobileNetV3Small, MobileNetV3Large, and InceptionResNetV2, are used to diagnose PD using the handwritten spirals drawn by PD patients. To maintain an enhanced performance, the authors used a metaheuristic optimizer, namely the Aquila optimizer, to optimize the hyperparameters in the different CNN structures to achieve the best structure. For voice signals, both numerical and graphical features are extracted. Numerical features are extracted using 16 feature extraction algorithms, namely: (1) MFCC using the Slaney and HTK methods, (2) Mel-spectrogram, (3) chroma-based techniques (chroma-only, STFT, CQT, and CENS), (4) spectral-based techniques (contrast, flatness, centroid, bandwidth, and roll-off frequency), (5) ZCR, (6) Tonnetz techniques (normal and harmonic), and (7) RMSE. These features are used in 4 machine learning (ML) algorithms, namely Decision Tree (DT), Support Vector Machine (SVM), Naïve Bayes (NB), and K-Nearest Neighbor (KNN). The grid search algorithm is applied to optimize the parameters of the different ML algorithms. Graphical features are extracted using 5 techniques, namely (1) spectrogram, (2) Melspectrogram, (3) STFT, and (4) MFCC using the Slaney and HTK methods. These features are applied to the different pretrained CNN structures. One of the major contributions of the current work is proposing a new feature extraction algorithm. The idea of the proposed algorithm is to use a dataset of voice segments divided by different durations to guarantee a variety in the features. For the NewHandPD dataset, the best-reported metrics are 99.75% using the VGG19 structure. For the MDVR-KCL dataset, the best-reported metrics are 99.94% using the KNN and SVM ML algorithms and the combined numerical features; and 100% using the combined the mel-specgram graphical features and VGG19 structure. These results are better than other state-of-the-art researches.
Future work
The proposed framework and suggested approach can be improved by adding other biomarkers and datasets including UPDRS scores for the classification of PD based on severity. Other deep learning classifiers such as recurrent neural networks (RNN) can be used for frequency-time data. The authors plan to apply the proposed framework to other diseases such as Alzheimer’s and heart diseases. Instead of pre-trained models, we also plan to build a CNN model from scratch for the framework. We also plan to use CNN in the pre-processing phase due to its powerful features.
Appendix A: Table of abbreviations
The table of abbreviations is shown in Table 13.
Table 13.
Table of abbreviations
| Abbreviation | Definition |
|---|---|
| PD | Parkinson’s disease |
| CNN | Convolutional neural network |
| TL | Transfer learning |
| ML | Machine learning |
| AO | Aquila optimizer |
| GS | Grid search |
| DL | Deep learning |
| DT | Decision tree |
| SVM | Support vector machine |
| NB | Naive Bayes |
| KNN | K-Nearest neighbor |
| PSD | Parkinson speech dataset |
| OPD | Oxford Parkinson’s disease detection dataset |
| MFCC | Mel-frequency cepstral coefficients |
| STFT | Short-time Fourier transform |
| CQT | Constant-Q chromagram |
| CENS | Chroma energy normalized |
| ZCR | Zero-crossing rate |
| RMSE | Root mean square error |
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB).
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Nada R. Yousif, Email: aserdemo2204@gmail.com
Hossam Magdy Balaha, Email: hossam.m.balaha@mans.edu.eg.
Amira Y. Haikal, Email: amirayh@mans.edu.eg
Eman M. El-Gendy, Email: eman_elgendy@mans.edu.eg
References
- Abualigah L, Yousri D, Abd Elaziz M, Ewees AA, Al-qaness MAA, Gandomi AH. Aquila optimizer: a novel meta-heuristic optimization algorithm. Comput Ind Eng. 2021;157:107250. doi: 10.1016/j.cie.2021.107250. [DOI] [Google Scholar]
- Aggarwal A, Alshehri M, Kumar M, Sharma P, Alfarraj O, Deep V. Principal component analysis, hidden Markov model, and artificial neural network inspired techniques to recognize faces. Concurr Comput Pract Exp. 2021;33(9):e6157. doi: 10.1002/cpe.6157. [DOI] [Google Scholar]
- Ali L, Zhu C, Zhou M, Liu Y. Early diagnosis of Parkinson’s disease from multiple voice recordings by simultaneous sample and feature selection. Expert Syst Appl. 2019;137:22–28. doi: 10.1016/j.eswa.2019.06.052. [DOI] [Google Scholar]
- Almeida JS, Rebouças Filho PP, Carneiro T, Wei W, Damaševičius R, Maskeliūnas R, Hugo C de Albuquerque V. Detecting Parkinson’s disease with sustained phonation and speech signals using machine learning techniques. Pattern Recognit Lett. 2019;125:55–62. doi: 10.1016/j.patrec.2019.04.005. [DOI] [Google Scholar]
- Alsberg BK, Woodward AM, Kell DB. An introduction to wavelet transforms for chemometricians: a time-frequency approach. Chemomet Intell Lab Syst. 1997;37(2):215–239. doi: 10.1016/S0169-7439(97)00029-4. [DOI] [Google Scholar]
- Bahgat WM, Balaha HM, AbdulAzeem Y, Badawy MM. An optimized transfer learning-based approach for automatic diagnosis of covid-19 from chest X-ray images. PeerJ Comput Sci. 2021;7:e555. doi: 10.7717/peerj-cs.555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balaha HM, Saafan MM. Automatic exam correction framework (aecf) for the mcqs, essays, and equations matching. IEEE Access. 2021;9:32368–32389. doi: 10.1109/ACCESS.2021.3060940. [DOI] [Google Scholar]
- Balaha HM, Ali HA, Badawy M. Automatic recognition of handwritten Arabic characters: a comprehensive review. Neural Comput Appl. 2021;33(7):3011–3034. doi: 10.1007/s00521-020-05137-6. [DOI] [Google Scholar]
- Balaha HM, Ali HA, Saraya M, Badawy M. A new arabic handwritten character recognition deep learning system (ahcr-dls) Neural Comput Appl. 2021;33(11):6325–6367. doi: 10.1007/s00521-020-05397-2. [DOI] [Google Scholar]
- Balaha HM, Ali HA, Youssef EK, Elsayed AE, Samak RA, Abdelhaleem MS, Tolba MM, Shehata MR, Mahmoud MR, Abdelhameed MM et al (2021c) Recognizing arabic handwritten characters using deep learning and genetic algorithms. Multim Tools Appl 80(21):32473–32509
- Balaha HM, Balaha MH, Ali HA. Hybrid covid-19 segmentation and recognition framework (hmb-hcf) using deep learning and genetic algorithms. Artif Intell Med. 2021;119:102156. doi: 10.1016/j.artmed.2021.102156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balaha HM, El-Gendy EM. Covh2sd: a covid-19 detection approach based on Harris hawks optimization and stacked deep learning. Expert Syst Appl. 2021;186:115805. doi: 10.1016/j.eswa.2021.115805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berus L, Klancnik S, Brezocnik M, Ficko M. Classifying Parkinson’s disease based on acoustic measures using artificial neural networks. Sensors. 2019;19(1):16. doi: 10.3390/s19010016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhardwaj A, Mohamed AA, Kumar M, Alshehri M, Abugabah A. Real-time privacy preserving framework for covid-19 contact tracing. Comput Mater Continua. 2021;70:1017. doi: 10.32604/cmc.2022.018736. [DOI] [Google Scholar]
- Bou-Ghazale Sahar E, Hansen John HL (1994) Duration and spectral based stress token generation for hmm speech recognition under stress. In: Proceedings of ICASSP’94. IEEE international conference on acoustics, speech and signal processing, vol 1. IEEE, pp I–413
- Caliskan A, Badem H, Basturk A, Yuksel ME. Diagnosis of the Parkinson disease by using deep neural network classifier. IU J Electr Electron Eng. 2017;17(2):3311–3318. [Google Scholar]
- Cao X, David W, Fang W, Genquan D, Jian S (2013) A practical transfer learning algorithm for face verification. In: Proceedings of the IEEE international conference on computer vision, pp 3208–3215
- Chai T, Draxler RR. Root mean square error (rmse) or mean absolute error (mae)?–arguments against avoiding rmse in the literature. Geosci Model Dev. 2014;7(3):1247–1250. doi: 10.5194/gmd-7-1247-2014. [DOI] [Google Scholar]
- Chakradar M, Alok A, Xiaochun C, Anuj R, Manoj K, Achyut S (2021) A non-invasive approach to identify insulin resistance with triglycerides and hdl-c ratio using machine learning. Neural Process Lett 1–21
- De Lau LML, Breteler MMB. Epidemiology of Parkinson’s disease. Lancet Neurol. 2006;5(6):525–535. doi: 10.1016/S1474-4422(06)70471-9. [DOI] [PubMed] [Google Scholar]
- Dias B, Athina G, Alves DJ, Kosmas D, Nikos G, Vicky Z, Theodore S, Evdokimos K, Bamidis Panagiotis D, Hagen J et al (2020) Innovative Parkinson’s disease patients’ motor skills assessment: the i-prognosis paradigm. Front Comput Sci 2:20
- Dou Q, Chen H, Yu L, Zhao L, Qin J, Wang D, Mok VCT, Shi L, Heng P-A. Automatic detection of cerebral microbleeds from mr images via 3d convolutional neural networks. IEEE Trans Med Imaging. 2016;35(5):1182–1195. doi: 10.1109/TMI.2016.2528129. [DOI] [PubMed] [Google Scholar]
- Faramarzi A, Heidarinejad M, Mirjalili S, Gandomi AH. Marine predators algorithm: a nature-inspired metaheuristic. Expert Syst Appl. 2020;152:113377. doi: 10.1016/j.eswa.2020.113377. [DOI] [Google Scholar]
- Fulkerson DoR, Wolfe P. An algorithm for scaling matrices. Siam Rev. 1962;4(2):142–146. doi: 10.1137/1004032. [DOI] [Google Scholar]
- Goyal J, Khandnor P, Aseri TC (2021) A hybrid approach for Parkinson’s disease diagnosis with resonance and time-frequency based features from speech signals. Expert Syst Appl 115283
- Griffin D, Lim J. Signal estimation from modified short-time Fourier transform. IEEE Trans Acoust Speech Signal Process. 1984;32(2):236–243. doi: 10.1109/TASSP.1984.1164317. [DOI] [Google Scholar]
- Gupta D, Julka A, Jain S, Aggarwal T, Khanna A, Arunkumar N, de Albuquerque VHC. Optimized cuttlefish algorithm for diagnosis of Parkinson’s disease. Cogn Syst Res. 2018;52:36–48. doi: 10.1016/j.cogsys.2018.06.006. [DOI] [Google Scholar]
- Guttman M, Kish SJ, Furukawa Y. Current concepts in the diagnosis and management of Parkinson’s disease. Cmaj. 2003;168(3):293–301. [PMC free article] [PubMed] [Google Scholar]
- Havaei M, Davy A, Warde-Farley D, Biard A, Courville A, Bengio Y, Pal C, Jodoin P-M, Larochelle H. Brain tumor segmentation with deep neural networks. Med Image Anal. 2017;35:18–31. doi: 10.1016/j.media.2016.05.004. [DOI] [PubMed] [Google Scholar]
- He K, Zhang X, Ren S, Sun J (2016) Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 770–778
- Helaly HA, Badawy M, Haikal AY (2021) Toward deep mri segmentation for Alzheimer’s disease detection. Neural Comput Appl 1–17
- Hireš M, Gazda M, Drotár P, Pah ND, Motin MA, Kumar DK (2021) Convolutional neural network ensemble for Parkinson’s disease detection from voice recordings. Comput Biol Med 105021 [DOI] [PubMed]
- Holland JH. Genetic algorithms. Sci Am. 1992;267(1):66–73. doi: 10.1038/scientificamerican0792-66. [DOI] [Google Scholar]
- Howard A, Sandler M, Chu G, Chen L-C, Chen B, Tan M, Wang W, Zhu Y, Pang R, Vasudevan V et al (2019) Searching for mobilenetv3. In: Proceedings of the IEEE/CVF international conference on computer vision, pp 1314–1324
- Howard AG, Zhu M, Chen B, Kalenichenko D, Wang W, Weyand T, Andreetto M, Adam H (2017) Mobilenets: efficient convolutional neural networks for mobile vision applications. arXiv:1704.04861
- Huynh BQ, Li H, Giger ML. Digital mammographic tumor classification using transfer learning from deep convolutional neural networks. J Med Imaging. 2016;3(3):034501. doi: 10.1117/1.JMI.3.3.034501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Impedovo D. Velocity-based signal features for the assessment of parkinsonian handwriting. IEEE Signal Process Lett. 2019;26(4):632–636. doi: 10.1109/LSP.2019.2902936. [DOI] [Google Scholar]
- Inbar GF, Paiss O, Allin J, Kranz H. Monitoring surface emg spectral changes by the zero crossing rate. Med Biol Eng Comput. 1986;24(1):10–18. doi: 10.1007/BF02441600. [DOI] [PubMed] [Google Scholar]
- Jaeger H, Trivedi D, Stadtschnitzer M (2019) Mobile device voice recordings at King’s College London (MDVR-KCL) from both early and advanced Parkinson’s disease patients and healthy controls, May 2019. 10.5281/zenodo.2867216
- Jordan MI, Mitchell TM. Machine learning: trends, perspectives, and prospects. Science. 2015;349(6245):255–260. doi: 10.1126/science.aaa8415. [DOI] [PubMed] [Google Scholar]
- Kamran I, Naz S, Razzak I, Imran M. Handwriting dynamics assessment using deep neural network for early identification of Parkinson’s disease. Future Gener Comput Syst. 2021;117:234–244. doi: 10.1016/j.future.2020.11.020. [DOI] [Google Scholar]
- Kaneko T, Kameoka H, Tanaka K, Hojo N (2020) Cyclegan-vc3: examining and improving cyclegan-vcs for mel-spectrogram conversion. arXiv:2010.11672
- Kattel M, Nepal A, Shah AK, Shrestha D (2019) Chroma feature extraction. In: Conference: chroma feature extraction using Fourier transform
- Kennedy J, Eberhart R (1995) Particle swarm optimization. In: Proceedings of ICNN’95-international conference on neural networks, vol 4. IEEE, pp 1942–1948
- Khagi B, Lee CG, Kwon G-R (2018) Alzheimer’s disease classification from brain MRI based on transfer learning from CNN. In: 2018 11th biomedical engineering international conference (BMEiCON). IEEE, pp 1–4
- Khalid Rabiya, Javaid Nadeem. A survey on hyperparameters optimization algorithms of forecasting models in smart grid. Sustainable Cities and Society. 2020;61:102275. doi: 10.1016/j.scs.2020.102275. [DOI] [Google Scholar]
- Kumar T, Verma K. A theory based on conversion of rgb image to gray image. Int J Comput Appl. 2010;7(2):7–10. [Google Scholar]
- Kuresan H, Samiappan D, Ghosh S, Gupta AS (2021) Early diagnosis of Parkinson’s disease based on non-motor symptoms: a descriptive and factor analysis. J Ambient Intell Humaniz Comput 1–15
- Kurt İ, Ulukaya S, Erdem O (2018) Musical feature based classification of Parkinson’s disease using dysphonic speech. In: 2018 41st international conference on telecommunications and signal processing (TSP). IEEE, pp 1–4
- Kurt İUS, Oğuzhan E (2019) Classification of Parkinson’s disease using dynamic time warping. In: 2019 27th telecommunications forum (TELFOR). IEEE, pp 1–4
- Lamba R, Gulati T, Al-Dhlan KA, Jain A (2021) A systematic approach to diagnose Parkinson’s disease through kinematic features extracted from handwritten drawings. J Reliab Intell Environ 1–10
- LaValle SM, Branicky MS, Lindemann SR. On the relationship between classical grid search and probabilistic roadmaps. Int J Robot Res. 2004;23(7–8):673–692. doi: 10.1177/0278364904045481. [DOI] [Google Scholar]
- Li X, Chen H, Qi X, Dou Q, Chi-Wing F, Heng P-A. H-denseunet: hybrid densely connected unet for liver and tumor segmentation from ct volumes. IEEE Trans Med Imaging. 2018;37(12):2663–2674. doi: 10.1109/TMI.2018.2845918. [DOI] [PubMed] [Google Scholar]
- Li X, He M, Li H, Shen H. A combined loss-based multiscale fully convolutional network for high-resolution remote sensing image change detection. IEEE Geosci Remote Sens Lett. 2021;19:1–5. [Google Scholar]
- Liu J, Xie L. Tonal features of Chinese plucked string instruments extracted from constant-q transform spectrum. J Acoust Soc Am. 2012;131(4):3219–3219. doi: 10.1121/1.4708003. [DOI] [Google Scholar]
- Loh W-Y. Classification and regression trees. Wiley Interdiscip Rev Data Min Knowl Discov. 2011;1(1):14–23. doi: 10.1002/widm.8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loussaief S, Abdelkrim A. Convolutional neural network hyper-parameters optimization based on genetic algorithms. Int J Adv Comput Sci Appl. 2018;9(10):252–266. [Google Scholar]
- Milnea AJ, Hollandb S (2022) Empirically testing tonnetz, voice-leading, and spectral models of perceived harmonic distance
- Naseer A, Rani M, Naz S, Razzak MI, Imran M, Xu Guandong. Refining Parkinson’s neurological disorder identification through deep transfer learning. Neural Comput Appl. 2020;32(3):839–854. doi: 10.1007/s00521-019-04069-0. [DOI] [Google Scholar]
- Orozco-Arroyave JR, Hönig F, Arias-Londoño JD, Vargas-Bonilla JF, Daqrouq K, Skodda S, Rusz J, Nöth E. Automatic detection of Parkinson’s disease in running speech spoken in three different languages. J Acoust Soc Am. 2016;139(1):481–500. doi: 10.1121/1.4939739. [DOI] [PubMed] [Google Scholar]
- Parziale A, Senatore R, Della Cioppa A, Marcelli A. Cartesian genetic programming for diagnosis of Parkinson disease through handwriting analysis: performance vs. interpretability issues. Artif Intell Med. 2021;111:101984. doi: 10.1016/j.artmed.2020.101984. [DOI] [PubMed] [Google Scholar]
- Pereira CR, Pereira DR, Da Silva FA, Hook C, Weber SAT, Pereira LAM, Papa JP (2015) A step towards the automated diagnosis of Parkinson’s disease: analyzing handwriting movements. In: 2015 IEEE 28th international symposium on computer-based medical systems, pp 171–176. IEEE
- Pereira CR, Pereira DR, Papa JP, Rosa GH, Yang X-S (2016a) Convolutional neural networks applied for parkinson’s disease identification. In: Machine learning for health informatics, pp 377–390. Springer
- Pereira CR, Weber SAT, Hook C, Rosa GH, Papa JP (2016b) Deep learning-aided Parkinson’s disease diagnosis from handwritten dynamics. In: 2016 29th SIBGRAPI conference on graphics, patterns and images (SIBGRAPI), pp 340–346. IEEE
- Pereira CR, Pereira DR, Rosa GH, Albuquerque VHC, Weber SAT, Hook C, Papa JP (2018) Handwritten dynamics assessment through convolutional neural networks: an application to Parkinson’s disease identification. Artif Intell Med 87:67–77 [DOI] [PubMed]
- Perez L, Wang J (2017) The effectiveness of data augmentation in image classification using deep learning. arXiv:1712.04621
- Połap D. Human-machine interaction in intelligent technologies using the augmented reality. Inf Technol Control. 2018;47(4):691–703. [Google Scholar]
- Połap D. Analysis of skin marks through the use of intelligent things. IEEE Access. 2019;7:149355–149363. doi: 10.1109/ACCESS.2019.2947354. [DOI] [Google Scholar]
- Połap D, Woźniak M. Red fox optimization algorithm. Expert Syst Appl. 2021;166:114107. doi: 10.1016/j.eswa.2020.114107. [DOI] [Google Scholar]
- Politis M, Wu K, Molloy S, G. Bain P, Chaudhuri KR, Piccini P. Parkinson’s disease symptoms: the patient’s perspective. Mov Disord. 2010;25(11):1646–1651. doi: 10.1002/mds.23135. [DOI] [PubMed] [Google Scholar]
- Qasim HM, Ata O, Ansari MA, Alomary MN, Alghamdi S, Almehmadi Mazen. Hybrid feature selection framework for the Parkinson imbalanced dataset prediction problem. Medicina. 2021;57(11):1217. doi: 10.3390/medicina57111217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raheja S, Kasturia S, Cheng X, Kumar M (2021) Machine learning-based diffusion model for prediction of coronavirus-19 outbreak. Neural Comput Appl 1–20 [DOI] [PMC free article] [PubMed]
- Rizvi DR, Iqra N, Sarfaraz M, Mumtaz A, Faiyaz A (2020) An lstm based deep learning model for voice-based detection of Parkinson’s disease. Int J Adv Sci Technol 29(8)
- Rokach L, Maimon O (2005) Decision trees. In: Data mining and knowledge discovery handbook. Springer, pp 165–192
- Roth HR, Farag A, Lu L, Turkbey EB, Summers RM (2015) Deep convolutional networks for pancreas segmentation in ct imaging. In: Medical imaging 2015: image processing, volume 9413, p 94131G. International Society for Optics and Photonics
- Sakar BE, Isenkul ME, Sakar CO, Sertbas A, Gurgen F, Delil S, Apaydin H, Kursun O (2013) Collection and analysis of a Parkinson speech dataset with multiple types of sound recordings. IEEE J Biomed Health Inform 17(4):828–834 [DOI] [PubMed]
- Sandler M, Howard A, Zhu M, Zhmoginov A, Chen L-C (2018) Mobilenetv2: Inverted residuals and linear bottlenecks. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 4510–4520
- Senatore R, Della Cioppa A, Marcelli A (2019) Automatic diagnosis of neurodegenerative diseases: an evolutionary approach for facing the interpretability problem. Information 10(1):30
- Sigurdsson S, Petersen KB, Lehn-Schiøler T (2006) Mel frequency cepstral coefficients: an evaluation of robustness of mp3 encoded music. In: ISMIR, pp 286–289
- Simonyan K, Zisserman A (2014) Very deep convolutional networks for large-scale image recognition. arXiv:1409.1556
- Singh P, Santanu C, Bijaya Ketan P. Hybrid mpso-cnn: multi-level particle swarm optimized hyperparameters of convolutional neural network. Swarm Evol Comput. 2021;63:100863. doi: 10.1016/j.swevo.2021.100863. [DOI] [Google Scholar]
- Solana-Lavalle G, Galán-Hernández J-C, Rosas-Romero R. Automatic Parkinson disease detection at early stages as a pre-diagnosis tool by using classifiers and a small set of vocal features. Biocybern Biomed Eng. 2020;40(1):505–516. doi: 10.1016/j.bbe.2020.01.003. [DOI] [Google Scholar]
- Soon FC, Khaw HY, Chuah JH, Kanesan J (2018) Hyper-parameters optimisation of deep cnn architecture for vehicle logo recognition. IET Intell Transport Syst 12(8):939–946
- Sörensen K, Glover F. Metaheuristics. Encyclop Oper Res Manag Sci. 2013;62:960–970. doi: 10.1007/978-1-4419-1153-7_1167. [DOI] [Google Scholar]
- Steinwart I, Christmann A (2008) Support vector machines. Springer, Berlin
- Sun J, Yuan Y, Tang M, Cheng X, Nie X, Aftab MU (2021) Privacy-preserving bilateral fine-grained access control for cloud-enabled industrial iot healthcare. IEEE Trans Ind Inform
- Sveinbjornsdottir S. The clinical symptoms of Parkinson’s disease. J Neurochem. 2016;139:318–324. doi: 10.1111/jnc.13691. [DOI] [PubMed] [Google Scholar]
- Szegedy C, Ioffe S, Vanhoucke V, Alemi AA (2017) Inception-v4, inception-resnet and the impact of residual connections on learning. In: Thirty-first AAAI conference on artificial intelligence
- Terasawa H, Berger J, Makino S. In search of a perceptual metric for timbre: dissimilarity judgments among synthetic sounds with mfcc-derived spectral envelopes. J Audio Eng Soc. 2012;60(9):674–685. [Google Scholar]
- Thapliyal M, Ahuja NJ, Shankar A, Cheng X, Kumar M (2021) A differentiated learning environment in domain model for learning disabled learners. J Comput Higher Educ 1–23
- Tsanas A, Little MA, McSharry PE, Spielman J, Ramig LO (2012) Novel speech signal processing algorithms for high-accuracy classification of parkinson’s disease. IEEE Trans Biomed Eng 59(5):1264–1271 [DOI] [PubMed]
- Tsangaratos P, Ilia I. Comparison of a logistic regression and naïve bayes classifier in landslide susceptibility assessments: the influence of models complexity and training dataset size. Catena. 2016;145:164–179. doi: 10.1016/j.catena.2016.06.004. [DOI] [Google Scholar]
- Tuncer T, Dogan S. A novel octopus based Parkinson’s disease and gender recognition method using vowels. Appl Acoust. 2019;155:75–83. doi: 10.1016/j.apacoust.2019.05.019. [DOI] [Google Scholar]
- Vapnik V (2013) The nature of statistical learning theory. Springer, Berlin
- Wang Y, Zhang H, Zhang G. cpso-cnn: an efficient pso-based algorithm for fine-tuning hyper-parameters of convolutional neural networks. Swarm Evol Comput. 2019;49:114–123. doi: 10.1016/j.swevo.2019.06.002. [DOI] [Google Scholar]
- Xiao Z, Xin X, Xing H, Luo S, Dai P, Zhan D. Rtfn: a robust temporal feature network for time series classification. Inf Sci. 2021;571:65–86. doi: 10.1016/j.ins.2021.04.053. [DOI] [Google Scholar]
- Xiao Z, Xin X, Xing H, Song F, Wang X, Zhao B. A federated learning system with enhanced feature extraction for human activity recognition. Knowl Based Syst. 2021;229:107338. doi: 10.1016/j.knosys.2021.107338. [DOI] [Google Scholar]
- Yang X-S, Gandomi AH (2012) Bat algorithm: a novel approach for global engineering optimization. Eng Comput
- Yousri D, Abd Elaziz M, Abualigah L, Oliva D, Al-Qaness MAA, Ewees AA (2021) Covid-19 X-ray images classification based on enhanced fractional-order cuckoo search optimizer using heavy-tailed distributions. Appl Soft Comput 101:107052 [DOI] [PMC free article] [PubMed]
- Zahid L, Maqsood M, Durrani MY, Bakhtyar M, Baber J, Jamal H, Mehmood I, Song O-Y (2020) A spectrogram-based deep feature assisted computer-aided diagnostic system for Parkinson’s disease. IEEE Access 8:35482–35495
- Zhang S, Li X, Zong M, Zhu X, Wang R. Efficient knn classification with different numbers of nearest neighbors. IEEE Trans Neural Netw Learn Syst. 2017;29(5):1774–1785. doi: 10.1109/TNNLS.2017.2673241. [DOI] [PubMed] [Google Scholar]