Purcell Enhancement of Erbium Ions in TiO₂ on Silicon Nanocavities

Abstract

Isolated solid-state atomic defects with telecom optical transitions are ideal quantum photon emitters and spin qubits for applications in long-distance quantum communication networks. Prototypical telecom defects, such as erbium, suffer from poor photon emission rates, requiring photonic enhancement using resonant optical cavities. Moreover, many of the traditional hosts for erbium ions are not amenable to direct incorporation with existing integrated photonics platforms, limiting scalable fabrication of qubit-based devices. Here, we present a scalable approach toward CMOS-compatible telecom qubits by using erbium-doped titanium dioxide thin films grown atop silicon-on-insulator substrates. From this heterostructure, we have fabricated one-dimensional photonic crystal cavities demonstrating quality factors in excess of 5 × 10⁴ and corresponding Purcell-enhanced optical emission rates of the erbium ensembles in excess of 200. This easily fabricated materials platform represents an important step toward realizing telecom quantum memories in a scalable qubit architecture compatible with mature silicon technologies.

Rare earth ion defects in solid-state hosts are key candidate qubits for applications in quantum computing and communication owing to their inherent spin–photon interface and long coherence times. These properties have enabled critical demonstrations of optical quantum memory protocols¹ based on light-matter entanglement² and entanglement distribution.³ Quantum technologies geared toward distribution of quantum information over long distances require qubits that interface with telecom photons to avoid huge propagation losses over optical fiber networks. Because the trivalent ion of erbium (Er³⁺) has a ⁴I_15/2 → ⁴I_13/2 transition in the telecom C-band, there has been interest in using erbium ions as optically addressable quantum memories using persistent spectral hole burning techniques⁴⁻⁶ and spin-based⁷ quantum memories in quantum communication, including at the level of single ions.⁸⁻¹⁰ However, significant engineering steps are needed to enhance the low photon emission rates from individual rare earth ions, which tend to have long radiative lifetimes.

One direct way to reduce the radiative lifetime is to use an optical cavity to enhance the emission through the Purcell effect.¹¹ The majority of Purcell enhancement studies on rare earth ions have involved devices derived from rare earth-doped bulk crystals, such as heterogeneous integration with deposited amorphous Si resonators⁵ or bonded Si photonics,^8,12 focused ion beam milling of bulk crystals,^6,13−15 or incorporating relatively small erbium-doped samples into tunable distributed Bragg reflector-based fiber cavities.^16,17 These approaches are all appealing because they leverage the generally good performance of well-studied host materials for Er³⁺ (Y₂SiO₅,^5,6,8,14 YVO₄,¹⁸ CaWO₄^19,20). Furthermore, these prior approaches have led to important cutting-edge demonstrations toward single rare-earth ion quantum memories, including single-shot spin state readout.^10,15,21 However, such approaches may not allow for the on-chip scalability needed for wide deployment of quantum memories in large-scale quantum networks. For instance, estimates for fault-tolerant quantum repeater protocols show that hundreds or thousands of communication qubits are necessary to perform the requisite (operational and loss) error correction for quantum communication over long distances (≥1000 km).²² In addition, the implementation of a fully CMOS-compatible process flow can enable easy integration with filters, phase shifters, and beamsplitters for on-chip photon routing.²³ In the vein of technological scalability with Si, there has also been considerable interest in low concentration implantation of erbium ions into Si nanostructures.²⁴ While this approach might have the greatest technological upside for directly unifying Si photonics with erbium-based quantum memories, early work has shown that the size mismatch between Er³⁺ and the crystalline lattice leads to myriad substitutional and interstitial sites with closely spaced spectral emission,^25,26 and further experiments are needed to resolve the best defects for various applications.

In addition to ease of Si photonic integration—assessed by the ability to grow on Si and perform straightforward fabrication—there are a variety of additional considerations for a candidate material to serve as a high-quality host for Er³⁺. These include a minimal or controlled level of background nuclear spins, a wide bandgap, the number of substitutional sites available, and site symmetries.²⁷⁻²⁹ To that end, previous measurements have suggested that rutile TiO₂ would be a good host for erbium because of narrow optical and spin line widths in implanted bulk crystals owing to the nonpolar symmetry of the substitutional erbium site and the low natural abundance of nuclear spins, respectively.³⁰ Furthermore, TiO₂ thin films can be grown on Si using a variety of deposition techniques,^31,32 are CMOS-compatible, and are amenable to standard fluorine- and chlorine-based dry etch chemistries for top-down device fabrication.³³ Recent work has shown Er-doped TiO₂ thin films grown on Si substrates via molecular beam deposition.³² Some salient findings from that recent work are that the TiO₂ thin films were polycrystalline and the dominant TiO₂ phase (rutile or anatase) could be tuned by varying the substrate temperature during growth. Furthermore, the inhomogeneous line widths for the best buffered devices were as low as 5 GHz, which was substantially narrower than some of the epitaxial thin film control samples grown on better lattice-matched substrates (SrTiO₃ or sapphire). Molecular beam deposition is particularly appealing for these types of heterostructures because of the inherent control of the Er³⁺ doping profile and doping density, in order to spectrally resolve single ions. Moreover, unintentional Er³⁺ doping from the TiO₂ itself is anticipated to be lower than for the more common yttrium-containing oxides because of the relatively high concentrations of trace lanthanides in yttrium precursors.

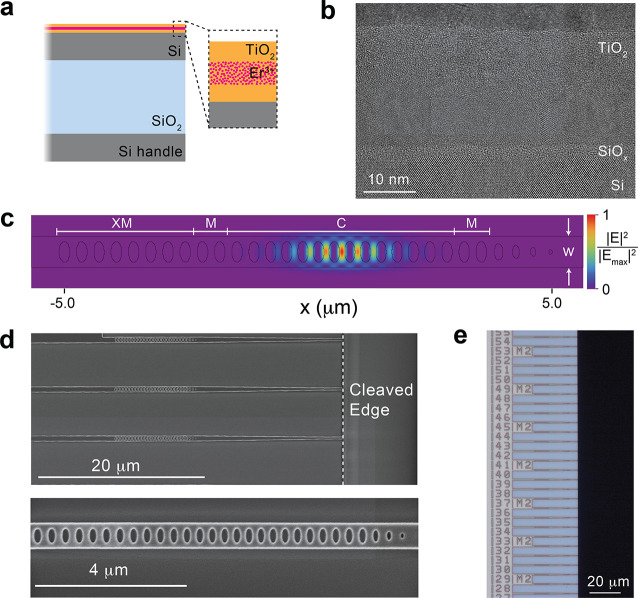
In this Letter, we show early progress on top-down nanofabrication of photonic crystal cavities comprising thin layers of Er-doped TiO₂ grown directly atop Si films. The thin films explored are similar to those discussed previously,³² but consist of an Er-doped TiO₂ heterostructure grown on commercial silicon-on-insulator (SOI) substrates typically used by the Si photonics community: Si device layer thickness of 220 nm atop a 2 μm buried oxide (see Supporting Information (SI)). Within each TiO₂ heterostructure, there are three TiO₂ layers of equal thickness: an erbium-doped layer sandwiched between undoped top and bottom buffer layers, and each layer is ∼7.5 nm, giving a total film thickness of ∼22 nm (Figure 1a). The estimated Er³⁺ density within the doped layer is 35 ppm (see SI). The TiO₂ layers for this sample are grown at a substrate temperature of 520 °C. As shown in Figure 1b, transmission electron microscopy (TEM) cross-sectional imaging reveals that the TiO₂ layer is polycrystalline, and there is a thin oxide layer (∼2 nm) at the Si/TiO₂ interface, as was seen previously for lower temperature growth. However, unlike the previous demonstration, the polycrystalline film has both large and small grains visible, and the grains nearest the Si interface are bigger (13(3) nm) than those near the top of the TiO₂ layer (∼1 nm). The cause of this gradient in grain size and effect on eventual Er properties is currently still under investigation. The roughness of the top surface of the TiO₂ is ∼1 nm according to the cross-sectional TEM.

Figure 1.

Er-doped TiO₂ on SOI device platform. (a) Illustration of the as-grown Er-doped TiO₂ heterostructure. The Er³⁺ layer is sandwiched between nominally undoped layers. The thickness of the SOI layers is not drawn to scale. (b) Cross-sectional TEM image of polycrystalline TiO₂ film atop the Si layer. A modest SiO_x layer of approximately 2 nm thickness develops at the interface during growth. (c) FDTD simulation showing the cross-section of the normalized field intensity within a one-dimensional photonic crystal cavity consisting of a holey waveguide (width, w = 671 nm) etched through the TiO₂ and Si device layers in panel a. This intensity cross-section is in the plane of the Er-doped TiO₂ film, located 10 nm above the surface of the Si. At the simulated resonance (λ = 1536.4 nm), there is strong confinement in the photonic crystal 14-hole cavity defect (C) that is generated by a parabolic taper of the lattice constant between elliptically shaped holes. There are two mirror holes (M) on each side of the cavity region, and extra mirror holes (XM) are included on the left-hand side of the device because all measurements are performed in a one-sided reflection configuration. (d) Top: SEM image of an entire fabricated device showing the tapered waveguide extending from the cleaved edge of the SOI chip. Bottom: An expanded view of the parabolic taper in the lattice constant to generate the cavity defect. (e) Optical image showing an extended view of nearly identical devices, including those in panel d.

Using 3D finite-difference time-domain (FDTD) simulations, we have designed one-dimensional photonic crystal cavities for our Si/TiO₂ heterostructure. The photonic crystal devices consist of a waveguide with identical, elliptically shaped holes and a parabolic reduction of the lattice constant to generate a defect in the photonic bandgap⁸ (see SI). Figure 1c shows the computed fundamental (dielectric) mode with a predominant TE-like polarization in the plane of the TiO₂ film. Our strategy relies on the evanescent field in the Si waveguide coupling to ions in the doped layer of the nearby TiO₂ film. The electric field intensity for a simulated electric dipole oriented normal to the waveguide, parallel to the plane of the TiO₂, and 10 nm above the Si/TiO₂ interface is approximately 37% of the maximum intensity in the center of the Si waveguide (see SI). The photonic crystal cavities (Figure 1d, bottom) are patterned via conventional electron-beam lithography and dry etching through both the TiO₂ and Si device layers (see SI). After etching and hardmask removal, the waveguide is cleaved along alignment marks under a microscope, beyond the inverse-taper (Figure 1d, top). We employ an end-fire measurement configuration, whereby a lensed optical fiber is used to couple light in/out of the device. As a demonstration of the inherent scalability of this scheme, we reliably fabricate hundreds of photonic crystal devices on each chip, a representative array of which is shown in Figure 1e (see SI).

A schematic of our experimental setup used to measure these devices is shown in Figure 2a. We perform our measurements in a closed-cycle cryostat with a base temperature of T = 3.1 K. The sample is fixed to the coldfinger and the lensed fiber is mounted on a 3-axis nanopositioner to enable addressing of different devices. Using a tunable telecom C-band laser, we primarily probe devices with pulse lengths ranging from 1 to 1000 μs and collection times after the pulse that are sufficient to enable decay of the emission (see SI). The pulses are routed to the sample via a fiber circulator and polarization controller to match the polarization of the cavity mode. We then measure the fluorescence from the sample, back through the lensed fiber and circulator, and directed to either a superconducting nanowire single photon detector (SNSPD), a spectrometer with InGaAs camera, or a photodiode. The one-way coupling efficiency (see SI) is fairly poor at approximately 15%, but it is sufficient to probe these particular devices because of the relatively large number of ions in each device. We also have a fiber wavelength division multiplexer (WDM) that can be added into the path of port 2 of the circulator for off-resonant photoluminescence (PL) measurements using a 1480 nm diode laser. Off-resonant PL measurements on a bare waveguide device (no cavity) reveal a variety of peaks from 1520 to 1560 nm, as shown in Figure 2b. The largest peak near 1520.5 nm is attributed to substitutional Er in the rutile phase of TiO₂,³⁰ whereas the other dominant peak near 1533 nm is attributed to substitutional Er in anatase,³⁴ as confirmed previously with electron diffraction measurements.³² This particular sample is polyphase, which has been seen previously for TiO₂ thin films grown at intermediate temperatures.³² The intensity of the substitutional rutile transition—relative to the substitutional anatase peak—is much stronger in this sample compared to previous thin film results when grown near 520 °C.³² The origin of this TiO₂ phase discrepancy is still under investigation. Similarly, the origin of the minor peaks could be due to a variety of factors, such as different localized phases within the TiO₂, Er³⁺ residing in different substitutional/interstitial sites, or crystal field-split transitions, but additional control samples and experiments are needed.

Figure 2.

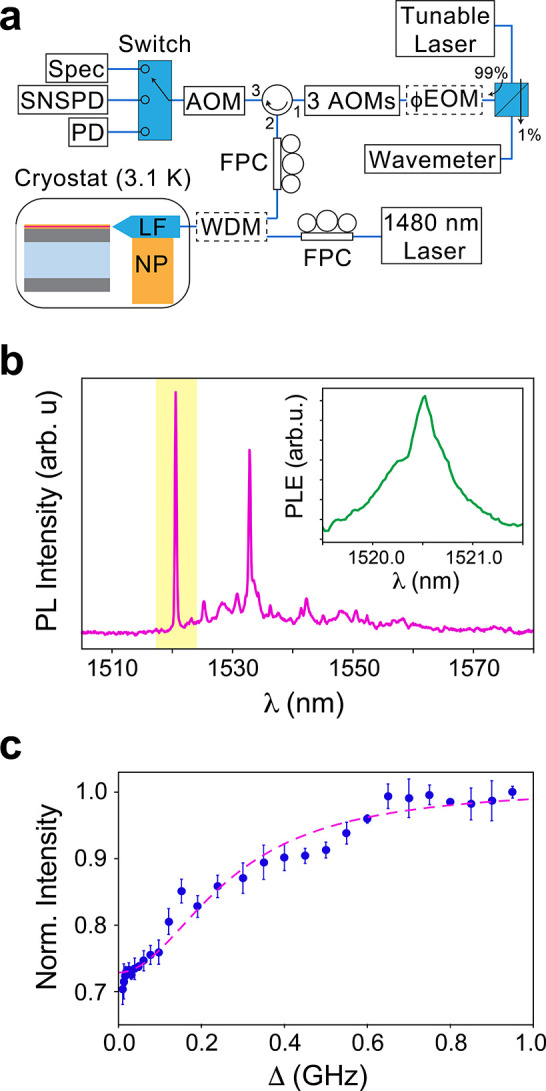
Optical characterization of Er³⁺: TiO₂ on Si waveguides. (a) Schematic of the experimental configuration. The Er³⁺: TiO₂ waveguide device is situated in a cryostat (T = 3.1 K). A tunable laser in combination with three fiber-coupled acousto-optic modulators (AOMs) enable the production of short pulses of light that are directed to the sample through a lensed fiber (LF) mounted on a nanopositioner (NP). The return light can be routed to either a photodiode (PD), IR spectrometer (Spec), or superconducting nanowire single-photon detector (SNSPD). A fiber polarization controller (FPC) is used to rotate the polarization to match that of the cavity. We can insert optional components (dashed boxes), such as an electro-optic phase modulator (ϕEOM) to generate sidebands for transient spectral hole burning and a fiber wavelength division multiplexer (WDM) for off-resonant excitation. Additional details are given in the Supporting Information. (b) PL spectrum of a bare waveguide (no cavity) device pumped with 1480 nm laser light and detected via spectrometer. The tallest peak (highlighted in yellow) is centered at 1520.56 nm and originates from Er³⁺ in the rutile phase of polyphase TiO₂. Inset: A resonant laser scan showing a similar inhomogeneous line width of 0.4 nm (52 GHz) for the rutile peak. (c) Measurement of the spectral diffusion line width for the rutile transition at 1520.56 nm. The inverted Lorentzian fit (dashed magenta line) yields a spectral diffusion line width of 267(17) MHz.

Resonant photoluminescence excitation (PLE) measurements on the bare waveguide device near 1520.56 nm are performed using a narrowband, tunable CW laser and modulated into pulses with emission from the Er³⁺ detected during a collection window following each pulse. The lifetime decay curve and associated total PLE intensity at that pump wavelength are integrated after numerous pulses (see SI). Resonant PLE extracts a line width of 0.4 nm (Figure 2b inset), which is similar to the result from off-resonant pumping. The inhomogeneous line width represents the distribution in Er³⁺ transition energies along the entire device that is over 40 μm long, and this inhomogeneous line width is similar to that measured in predominantly rutile thin film samples using a confocal microscope geometry with a spot size of approximately 1 μm².³² Given that the inhomogeneous line width of the Er³⁺ in rutile transition is relatively broad, it is important to investigate if the homogeneous line width of the emitters is sufficiently narrow to enable cavity-based lifetime enhancement (i.e., the “bad cavity” limit). To that end, we have performed transient spectral hole burning measurements on a bare waveguide device to find an upper bound on the homogeneous line width and spectral diffusion²⁴ for the rutile transition (Figure 2c). Using the pulsed resonant laser PLE scheme described above, we have employed an additional phase modulator (ϕEOM, Figure 2a) to generate two sidebands each with a frequency detuning, Δ, from the carrier frequency. We can then measure the relative PLE intensity change as Δ is swept but the laser carrier wavelength is maintained at the rutile transition, 1520.56 nm, and the total pump power is near saturation for the ensemble. If Δ is larger than the spectral diffusion line width of the erbium ions, the ions are no longer pumped to saturation and the total fluorescence increases. If we plot the normalized intensity as a function of laser sideband-carrier detuning (Figure 2c), we can fit a inverted Lorentzian line shape with a half-width half-maximum (HWHM) of 267(17) MHz, which sets the upper bound on the spectral diffusion-limited homogeneous line width.³⁵ While this homogeneous line width is substantially narrower than the inhomogeneous line width (Figure 2b), it is still quite large compared to the transform-limited line width of Er³⁺ in rutile TiO₂ (sub kHz). It is possible that further optimization of the top capping layer in these devices can reduce the spectral diffusion of the Er emitters.³²

We have the ability to tune the cavity resonance in situ using a combination of controlled gas adsorption and desorption techniques while near base temperature. We use N₂ condensation via a gas nozzle directed at the sample to deposit a thin layer of ice on the cavity, which increases the refractive index of the mode, thereby resulting in a redshift of its resonance.³⁶ We can also deterministically desorb the ice through localized heating, whereby we use relatively strong CW laser excitation tuned directly to the cavity resonance to induce two-photon absorption and heating in the Si, but only at the cavity region, which leads to a blueshift of the cavity resonance (see SI). Furthermore, this heating is sufficiently localized that cavities in neighboring waveguides—separated by only 6 μm—can be tuned independently of one another, which can be useful for future two-cavity interference experiments. We can directly measure the spectral position and line width of the cavity resonance by detecting the wavelength-dependent reflection of the narrowband laser light using a photodiode. If we perform this measurement close to the rutile transition, we typically see cavity quality factors (Q) near 5 × 10⁴. A prototypical cavity reflection scan at T = 3.1 K is shown in Figure 3a. Based on measurements of control devices with and without TiO₂ films, the quality factors in general are currently limited by scattering due to the roughness of the top surface of the TiO₂ rather than sidewall roughness of the waveguide or cavity holes from the dry etching.

Figure 3.

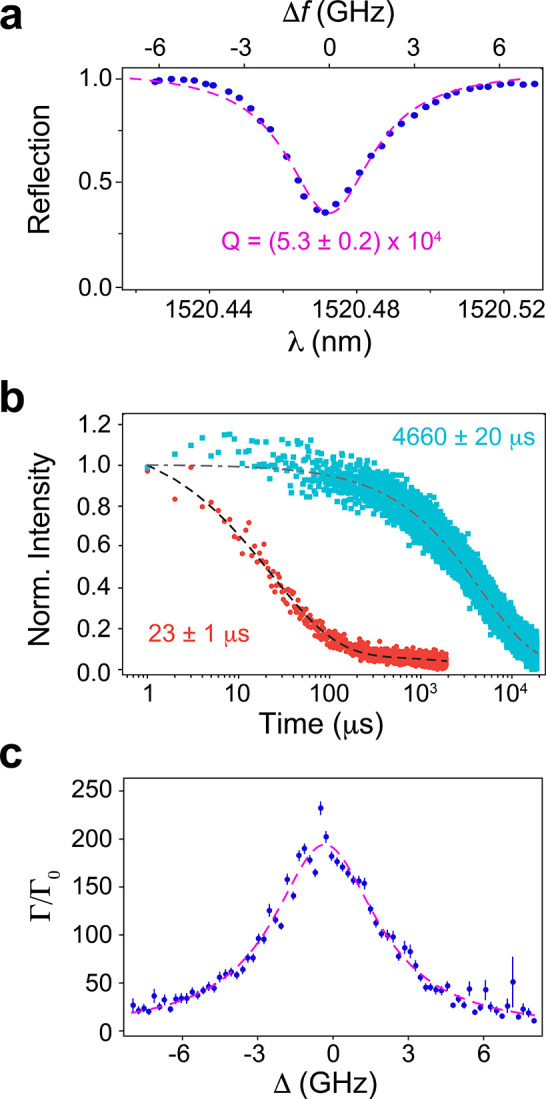
Purcell enhancement of Er³⁺: TiO₂ ensembles on Si photonic crystal cavities. (a) Resonant laser reflection spectrum of a photonic crystal cavity (T = 3.1 K) tuned near the rutile transition, showing a cavity Q near 53 000. The cavity has a corresponding line width (full-width half-maximum, FWHM) of 3.71(0.17) GHz (top axis). (b) Comparison of the ensemble lifetime of Er³⁺ ions coupled in a bare waveguide device (blue squares) versus the cavity-coupled device (red circles) shown in panel a. The corresponding fits give τ = 23(1) μs (black dashed line) and τ = 4660(20) μs (gray dashed-dot line), which is a 200-fold reduction in the decay time. (c) Plot of the increase in the ensemble decay rate as a function of the cavity-laser detuning (Δ) when the laser is fixed at 1520.56 nm. This is the same cavity as in panel a, which was measured at the start of the detuning experiment. The decay rate enhancement line shape is also fit to a Lorentzian with a FWHM line width of 5.06(0.17) GHz.

Our resonant pulsed laser measurements reveal the optical lifetime of all ions that couple to the device. This includes ions well-coupled to the cavity, ions poorly coupled to the cavity—whether because of position or polarization—and ions that couple only to the bare waveguide. Therefore, we use a stretched exponential function to capture the variety of decay times, where the time constant (τ) in the fit represents the fastest time decay within the ensemble.³⁷ Using this approach (see SI), the Er ions coupled to a bare waveguide device give a natural lifetime of τ = 4660(20) μs (Figure 3b), which is close to the time constant of 5.1 ms for Er implanted/annealed bulk TiO₂ measured at low temperature.³⁰ In comparison, the ions which couple most strongly to the cavity—when it is tuned onto the rutile transition at 1520.56 nm—show a greatly decreased decay time of τ = 23(1) μs. This represents a 200-fold decay rate enhancement.

We next measure the emission rate enhancement as a function of the detuning between the cavity resonance and the Er³⁺ rutile transition. To do so, we perform a systematic redshift of the cavity resonance via gas condensation and measure the optical lifetime with the resonant laser fixed at the rutile transition. Figure 3c shows the increase in decay rate relative to the natural decay rate (Γ/Γ₀) as the cavity resonance is tuned across the transition. The cavity-enhanced emission has a Lorentzian line width of 5.06(0.17) GHz, which is modestly broader than the cavity line width measured via reflection of 3.71(0.17) GHz. However, this can be explained by reduction in Q when the cavity is resonant with the Er³⁺ transition versus the reflection scan, which is measured at 90 pm (11.7 GHz) to the blue of the transition (see SI). The general agreement of the decay rate enhancement line shape with that of the cavity suggests that the radiative speedup is due to the cavity rather than nonradiative recombination induced by device fabrication. In addition, the lack of a plateau in Figure 3c confirms that the system is in the bad cavity limit, that is, Γ_h < κ, where Γ_h is the homogeneous line width of the emitters and κ is the cavity line width, in agreement with the transient spectral hole measurement in bare waveguide devices. On the basis of our simulated Purcell factor for the ideally placed TE-oriented electric dipole at the center of the cavity (see SI)—after adjusting for the experimental Q (40 000) of this device at T = 3.1 K at 1526.56 nm—we estimate that the maximum Purcell factor in the ensemble should be 326. The discrepancy between this estimate of the maximum Purcell factor and our experimentally determined value is likely due to a combination of the dipole orientations in the polyphase TiO₂ film and the specific location of erbium ions in the rutile phase grains probed by this experiment.

In this Letter, we have shown optical addressing of Er³⁺ ions in rutile phase TiO₂ grown on commercial SOI wafers. We have fabricated top-down 1D photonic crystal cavities from the Si/TiO₂ heterostructure with Purcell enhancements up to 200. Systematic detuning of the cavity resonance from the Er³⁺ transition in rutile phase TiO₂ reveals a good match of the Purcell enhancement to the Lorentzian cavity line shape, thereby indicating the erbium emission rates are limited by the cavity quality factor, not by the emitters’ homogeneous line widths. The next goal for this platform is to isolate and address individual Er ions as single spin quantum memories by cooling to lower temperatures and applying magnetic fields to address various spin levels. To that end, it is important to push the platform forward in three key areas.

First, it is necessary to reduce the homogeneous and inhomogeneous broadening in this system. The current upper bound of the homogeneous line width and spectral diffusion is estimated to be in the range of a few hundred MHz and could be attributed to a variety of factors, including trapped charges in the interfacial SiO_x, fabrication-induced damage, and the presence of mixed phases of TiO₂. Further improvement of the thin film growth conditions to isolate a single TiO₂ phase and to reduce the interfacial oxide, along with optimization of the buffer layer thicknesses could enable large reductions of the homogeneous and inhomogeneous line widths, as was seen already in predominantly anatase thin films.³² Second, it is important to reduce the number of Er³⁺ coupled to the cavity to spectrally isolate and address single ions. By further reducing the metallic Er source flux and restricting doping to a single delta-doped TiO₂ layer, intentional doping of these films to the single ion level is straightforward via molecular beam deposition. Additional improvements to the homogeneous line width may also be achieved naturally with the reduction in the Er-doping density³² that would be needed to address single ions. Importantly, telecom quantum technologies based on this platform will be enabled by improving the photonic device performance. Most notably, the current fiber-waveguide coupling efficiency will need to be increased through improved mode-matching via cladding layers³⁸ or a full undercut of the Si inverse tapered waveguides.³⁹ Finally, a reduction in the TiO₂ surface roughness during growth can lead to improvements in cavity Q for higher photon rates.

This demonstration represents an exciting first step toward a scalable on-chip quantum light source and memory device platform grown on an SOI wafer. This telecom-ready device architecture can be integrated with standard Si photonics and MEMS foundry process lines, enabling integration with other needed photonic elements such as on-chip filters, phase shifters, and beamsplitters. Furthermore, the Si platform is amenable to combination with other important cryogenic quantum technologies, such as on-chip SNSPDs, superconducting qubits, semiconductor quantum dot qubits, and microwave-to-optical transducers to enable powerful quantum computational and communication nodes. With further improvements to the materials and device fabrication, the scalable nature of this Er-doped TiO₂-on-SOI platform can meet the future demands for large numbers of communication qubits and quantum light sources needed for fault-tolerant long-distance quantum networking.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.2c01561.

• The Supporting Information contains additional simulation, fabrication, and experimental details, including: parameters for 3D FDTD simulations, the expected Purcell factor for dipoles in the TiO₂ layer, a full device fabrication process flow, the cryogenic experimental configuration, rough estimates of the number of ions that couple to the cavity, and characterization of the cavity Q during gas condensation tuning (PDF)

The authors declare no competing financial interest.