Structured sampling of olfactory input by the fly mushroom body

Summary

Associative memory formation and recall in the fruit fly Drosophila melanogaster is subserved by the mushroom body (MB). Upon arrival in the MB, sensory information undergoes a profound transformation, from broadly tuned and stereotyped odorant responses in the olfactory projection neuron (PN) layer, to narrowly tuned and nonstereotyped responses in the Kenyon cells (KCs). Theory and experiment suggest this transformation is implemented by random connectivity between KCs and PNs. However, this hypothesis has been challenging to test, given the difficulty of mapping synaptic connections between large numbers of brain-spanning neurons. Here we used a recent whole-brain electron microscopy volume of the adult fruit fly to map PN-to-KC connectivity at synaptic resolution. The PN-KC connectome revealed unexpected structure, with preponderantly food-responsive PN types converging at above-chance levels on downstream KCs. Axons of the overconvergent PN types tended to arborize near one another in the MB main calyx, making local KC dendrites more likely to receive input from those types. Overconvergent PN types preferentially co-arborize and connect with dendrites of αβ and α’β’ KC subtypes. Computational simulation of the observed network showed degraded discrimination performance compared to a random network, except when all signal flowed through the overconvergent, primarily food-responsive PN types. Additional theory and experiment will be needed to fully characterize the impact of the observed nonrandom network structure on associative memory formation and recall.

Graphical Abstract

In Brief (eTOC Blurb)

By mapping synaptic connectivity in a whole-brain electron microscopy volume of the fruit fly Drosophila melanogaster, Zheng et al. show that sensory input to a canonical associative memory circuit is not sampled at random. Rather, food-responsive olfactory projection neurons converge preferentially onto specific Kenyon cell subtypes.

Introduction

The cellular basis for associative memory formation and recall remains a central mystery of neurobiology. Connectomics, in which synaptic connections are traced between large numbers of neurons to map circuit wiring diagrams,¹ offers a new method by which to explore the topic. The adult fruit fly Drosophila melanogaster is arguably an ideal model system for a connectomics-based investigation of the neuronal networks underpinning learning and memory. Its brain is small enough to have been completely imaged at synaptic resolution by electron microscopy (EM);² it is behaviorally sophisticated;^3–6 and the stereotyped morphology and physiology of its cell types allow ready integration of experimental results across individuals.^7,8 Further, each cell type normally consists of one or a handful of neurons,^9–11 which may be individually addressed using genetic tools, allowing circuits to be functionally imaged and perturbed in a highly specific fashion.^12–15

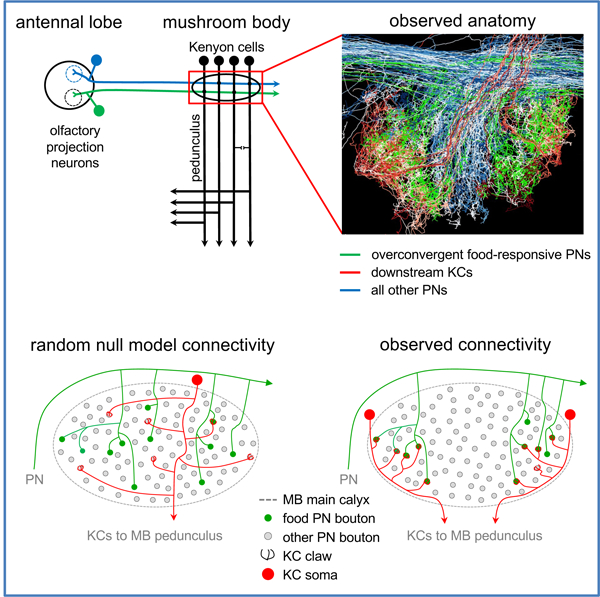
The exception to this norm is the mushroom body (MB; Figure 1A), a bilaterally symmetric structure for associative memory formation and recall.^16–18 The MB contains about 2,200 intrinsic neurons, called Kenyon cells (KCs), on each side of the brain.^19–21 Modification of synapses between KCs and their targets, the MB output neurons (MBONs) likely underlies olfactory learning and memory.^16,18,22 Kenyon cells can be divided into three main subtypes, γ, α’/β’, α/β.^23–25 The axons of each KC subtype project anteriorly to the eponymous MB lobe, where they provide input to 35 cell types comprising ~44 MBONs.^9,26 Sensory input to the MB is dominated by ~150 olfactory projection neurons (PNs), which relay information from the 51 olfactory glomeruli of the antennal lobe (AL).^20,27–29 Olfactory PN type is defined by which AL glomerulus the PN dendrites innervate; PNs of the same type have stereotyped morphology and odorant response profiles across individuals.^7,30 Olfactory PN axons project posteriorly and collateralize in the MB main calyx, where they provide input to KC dendrites, before arborizing extensively in lateral horn (LH), which mediates innate behavioral response to odorants.^29,31 Kenyon cell dendrites terminate in specialized ‘claws’, each of which ensheathes a single PN axonal bouton (Figure 1B). Multiple KC claws commonly ensheath a given PN bouton, and each KC samples input from an average of ~6–8 PNs.^32–35 Multiple input PNs must be coactive in order to evoke an action potential in a given KC,³⁶ and widefield feedback inhibition is preponderant throughout the MB,³⁷ resulting in KC activity that is sparse and sharply tuned compared to that of the input PNs.³⁸

Figure 1. Reconstruction of the PN-to-KC network.

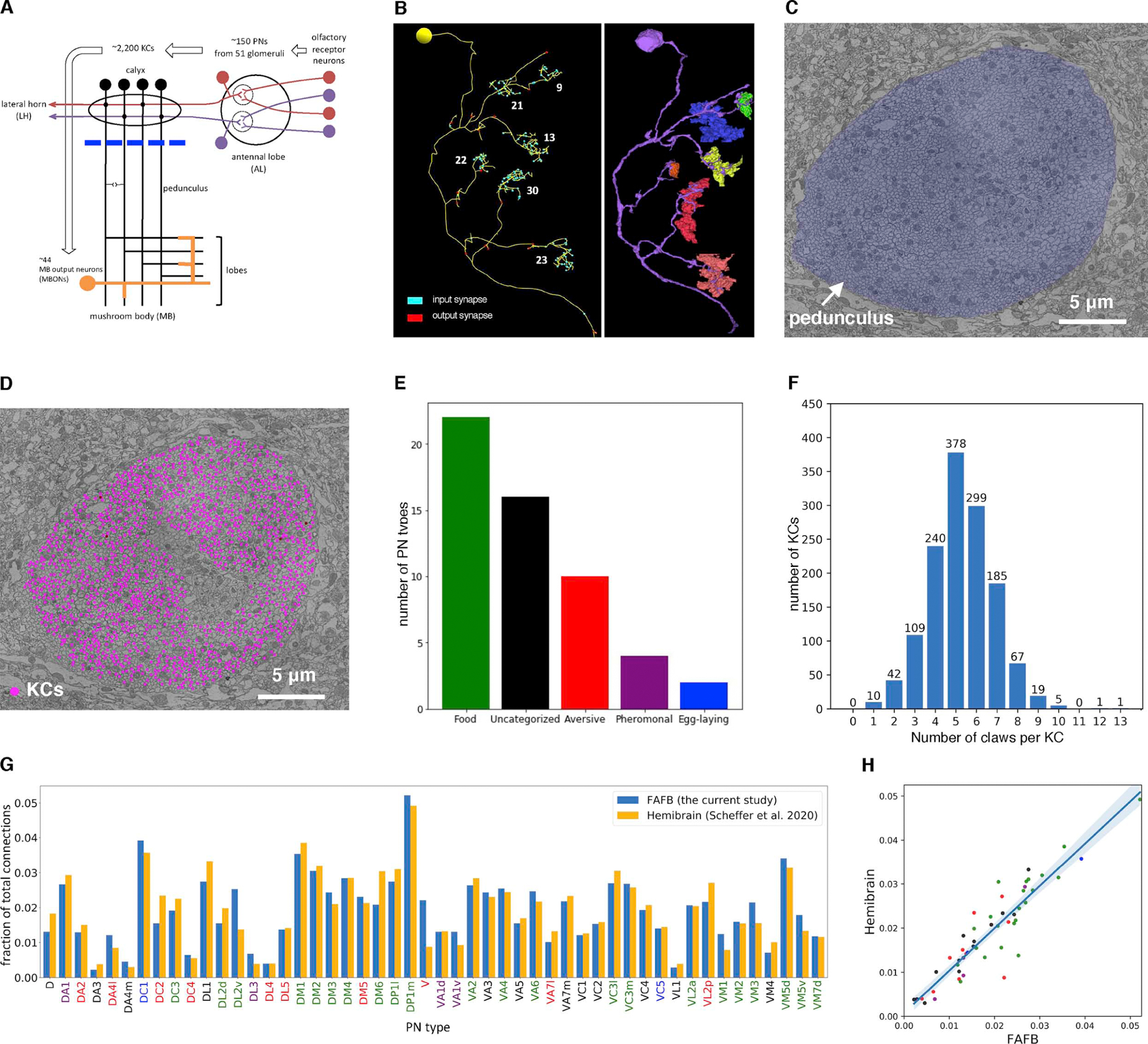
(A) Olfactory pathway schematic. Blue line, the frontal plane where KCs were randomly sampled for reconstruction (C-D).

(B) A representative EM-reconstructed KC. Each claw receives a variable number of synapses (numbers in white) from a single ensheathed PN bouton. Left, skeletonized reconstructions. Right, volumetric segmentation of the same KC (purple) and ensheathed PN boutons (various colors).

(C) Subarea of a frontal section from the whole-brain EM volume, showing the cross-section through pedunculus (blue false color) used for random sampling (D).

(D) Randomly sampled KCs (magenta dots) in the pedunculus. A discrete region in the middle is devoid of magenta points, as it is occupied by other cell classes such as APL and non-olfactory KCs from accessory calyces (i.e. KC-α/βp and KC-γd⁹).

(E) Number of PN types for each category of behavioral significance based on a literature review (Table S1).

(F) Distribution of number of claws per KC for all randomly sampled KCs (mean ± s.d., 5.2 ± 1.6).

(G-H) The number of PN-KC connections per PN type is consistent between the current study and the ‘hemibrain’ dataset.¹⁰ (G), Three or more synapses between each PN-KC pair is counted as a connection. The fraction of connections made by each PN type out of the total number of connections in each dataset is shown. (H), the fraction of output per PN type is highly correlated across the two datasets (r²⁼0.83; blue shade, 95% confidence interval). Bar labels (G) and points (H) are colored according to behavioral category (E).

See also Table S1.

The PN-to-KC layer of MB connectivity therefore implements a transformation of olfactory representation, from broad, stereotyped, and sustained olfactory responses, in a small population of PNs, to sparse, variable, and transient responses, distributed across a large population of KCs. This circuit architecture is an example of a ‘Marr motif’,^39,40 after the theorist David Marr’s foundational work on cerebellar function.^41,42 This motif is found in many brain regions and species, including cerebellum, hippocampus, and piriform cortex in vertebrates, and the vertical lobe of the octopus.^39,43–45 In the fly, it is thought to permit efficient representation of arbitrary combinations of odorants – which may be thought of as points in a high-dimensional olfactory space – for downstream use as a conditioned stimulus during associative memory formation and recall.^17,44,46 Theoretical analyses have argued that randomly mixed input channels, when combined with a nonlinearity such as a spike threshold, increases the dimensionality, and, therefore, the linear separability of activity patterns, making them easier to discriminate.^47–50 Most models of the PN-to-KC network in the fly have therefore assumed that in the Marr motif, input neurons (PNs) are sampled at random by intrinsic neurons (KCs)^{39,40,51,52; but see 53–56}.

Several efforts to test the hypothesis of random PN-to-KC connectivity have been made, using light microscopy, electrophysiology, and, most recently, EM. Single-cell retrograde labeling was used to identify the PN inputs to a single KC in each of 200 individual flies.³⁵ About half the claws for each KC were successfully labeled. No evidence of network structure was found, although some PN types clearly had more downstream targets than others. In another study, electrophysiological recordings of 23 KCs across 27 adult fruit flies revealed highly diverse olfactory responses, with only two KCs exhibiting an identical response profile across individuals.⁵⁷ These studies had relatively small sample sizes and pooled data across individuals, and were sufficient to exclude highly structured and stereotyped PN-to-KC connectivity. However, weaker biases in network structure, or varied structure across individuals, could not be excluded. In contrast, in the fruit fly larva, the complete PN-to-KC connectome of a single individual was mapped using a whole-CNS EM volume.⁵² No evidence of network structure was found, although single claw KCs were found to occur more frequently than a gaussian distribution would predict. However, the larval MB contains only about 100 KCs per hemisphere, all of which are of a single class γ.²⁵ The question of whether network structure might exist in the adult was left open.

Indeed, several studies have indicated that PN-to-KC network structure may be nonrandom. Olfactory PN axonal arbors and KC dendritic arbors are known to occupy stereotyped positions within the MB calyx as a function of cellular subtype,^29,58,59 and EM-based reconstructions showed that the axonal arbors of many PN types occupy more constrained territories within an individual than predicted by LM-based reconstructions pooled across many individuals.² Physiologically, calcium imaging has revealed that KC claws show more correlated responses than would be predicted by chance, and simultaneous optogenetic stimulation of three PN types (comprising ~13 PNs in total) also showed greater-than-chance convergence.³⁶ A recent analysis of MB connectivity in a partial (“hemibrain”) fly connectome¹⁰ showed that the PN-to-KC network exhibits spatial bias and specificity dependent on PN and KC subtypes,²⁶ confirming several findings presented here and in preprint form.⁶⁰ To address this question more thoroughly in the present work, we set out to reconstruct and analyze a large number of PN-to-KC connections, using the previously described Female Adult Fly Brain (“FAFB”) EM volume.²

Results

Reconstruction of the PN-to-KC network

To map the PN-to-KC network, KCs were randomly selected for reconstruction from a cross-section of the MB pedunculus, a tract where KC axons converge after their dendrites receive input in the MB main calyx (Figure 1A–D). The PN bouton innervating each KC claw was then retrogradely traced to the main PN axon trunk, and the PN type was identified, using previously published classifications of PNs in the FAFB dataset.² The broad category of odorants to which each PN type responds was determined through a literature review, blind to the results of the analyses presented below (Figure 1E; Table S1). The intent was to enable analysis of the relationship between the behavioral role of each glomerulus and any observed PN-to-KC network structure. More than half of categorized PN types were responsive to food-related odorants.

Initial KC reconstructions were purely manual; later efforts leveraged an automated segmentation of the full FAFB dataset.⁶¹ In total, all olfactory PN inputs to 7,102 claws arising from 1,356 KCs were mapped and identified (~62% of all claws on the right side of the brain). All PN boutons and KC claws were demarcated during reconstruction, allowing detailed null models of random connectivity to be specified, as described below. In the MB main calyx, all claws from each reconstructed KC were identified, and all dendrites in calyx, including claws, were traced to completion. In the MB lobes, KC axons were traced sufficiently to classify KC subtype as γ, α’/β’, or α/β. Each KC was found to have 5.2 claws on average (Figure 1F), consistent with previous studies.^32,35 The number of KCs postsynaptic to each PN type was also in excellent agreement with counts obtained from a recently released partial (“hemibrain”) connectome of adult fly brain connectivity (Figure 1G–H).¹⁰ The consistency of these metrics across datasets and methods indicates that the PN-to-KC network reconstructed in the present study is of high quality and therefore suitable for detailed analysis.

Non-uniformity of olfactory input to the mushroom body

To assess whether KCs sample PN input at random in the MB calyx, the number of axonal boutons from each PN type must first be quantified. This is a function of the number of PNs per AL glomerulus, and the number of axonal boutons per PN. At both of these levels, different PN types made strikingly different amounts of input to the mushroom body calyx (Figures 2 and S1). For example, glomeruli responsive to sex pheromone (DA1 and VA1v; Table S1) and the microbial odorant geosmin (DA2; Table S1) had many more PNs per glomerulus than other types (Figure 2A), but made relatively few boutons per PN (Figure 2B). For DA1 and DA2, the large number of PNs was enough to offset the low number of boutons per PN; this was not the case for VA1v (Figure 2C). In other cases, such as the acid-sensing PN type (DC4; Table S1), both PN number and boutons per PN were low, resulting in small net input to the MB calyx. Food-responsive PN types provided slightly more total boutons to the calyx, although this effect was small and only reached statistical significance when uncategorized PN types were included (Figures 2C and S1E–F).

Figure 2. Non-uniformity of olfactory input to the mushroom body.

(A-C) For each PN type, the number of PNs (A); average number of boutons per PN (B); and number of boutons (C), in descending order.

See also Figure S1.

Non-random sampling of olfactory PN by KCs

The observed number of PN boutons arising from each glomerulus (Figure 2C) was used to construct a null model for PN-to-KC connectivity, in which each KC claw is assigned a PN bouton at random (Figure 3A). In this “random bouton” model, the probability a claw receives an input from a given PN type is proportional to the number of boutons arising from each PN type. The random bouton model was run 10,000 times to generate the PN-to-KC connectivity that would be expected if PN boutons were sampled at random by KC claws. A conditional input analysis was used to determine whether KCs were more or less likely than expected to get input from a particular PN type (Figure S2A, matrix columns), given input from another PN type (Figure S2A, matrix rows). These pairwise conditional probabilities were quantified as z-scores (i.e., the number of standard deviations of the observed value from the mean of the distribution generated by the random bouton model; Figure S2B), and the order of columns and rows in the resulting matrix was determined using unsupervised k-means clustering.

Figure 3. Non-random sampling of olfactory PN input by KCs.

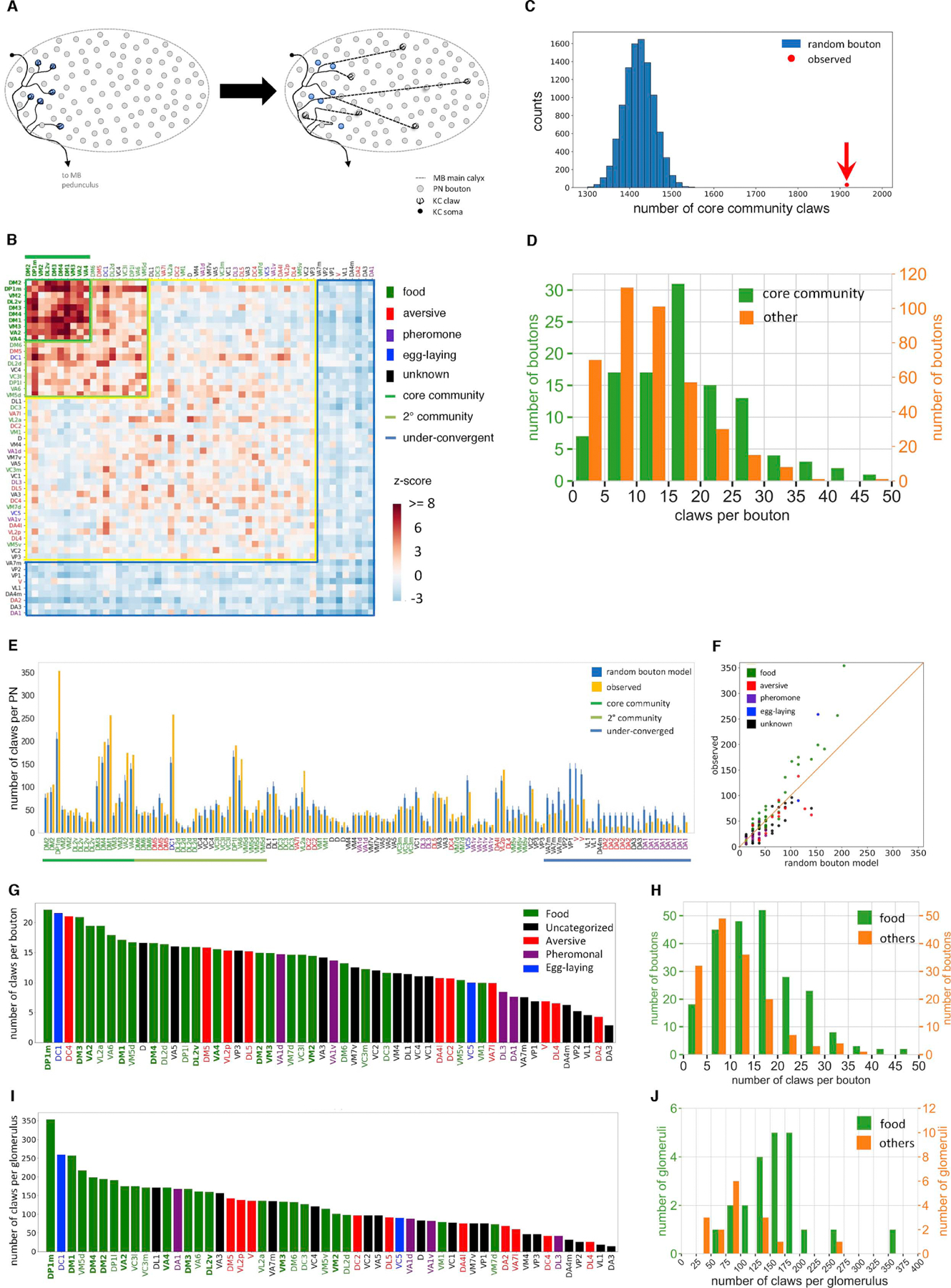
(A) Random bouton null model schematic. Each claw is reassigned to a bouton chosen randomly from all boutons in the MB calyx. This null model ignores the fact that KC dendrites and PN arbors have restricted territories within the calyx, but ensures that the number of claws assigned to a given PN type is proportional to the number of boutons.

(B) Observed PN-to-KC connectivity compared to the random bouton model. Conditional input analysis was applied to 1,356 randomly sampled KCs. A group of PN types (‘community’ PNs, dark and light green lines) provide above-chance levels of convergent input to downstream KCs. All PN types in the core community (dark green with overline), and most in the secondary community (light green), have been reported to primarily respond to food-related odorants (Table S1). In this and subsequent z-score matrices, PN types are color-coded according to behavioral category as in Figure 1E, and core community PN types are decorated with overlines.

(C) Kenyon cells over-sample inputs from core community PN types. The observed number of claws receiving input from core community PNs (1,916; red dot) greatly exceeds the random bouton null model prediction (blue histogram; 10,000 random networks, mean ± s.d., 1,421.7 ± 35.7; z-score, 13.8).

(D) Core community PNs have more claws per bouton than other PNs (mean ± s.d., 17.4 ± 9.3 vs. 11.5 ± 7.4; K-S test p<1×10⁻⁹).

(E-F) Core community PNs in the observed network are presynaptic to more KC claws than predicted by the random bouton model (error bars, s.d. of 10,000 random networks; Chi-square test p<1×10⁻¹⁰). Each bar in (E) and dot in (F) represents a PN. Bar labels (E) and points (H) are colored according to behavioral category (Figure 1E).

(G, I) Number of claws per bouton (G) and number of claws (I) per PN type, in descending order.

(H, J) Food-responsive PNs provided output to more claws than non-food PNs on both a per-bouton (H, mean ± s.d., 15.66 ± 3.08 vs. 10.53 ± 7.3, K-S test p<1.3×10⁻⁹) and per-glomerulus (J, mean ± s.d., 162.95 ± 60.74 vs. 100.06 ± 56.17, K-S test p<2.5×10⁻⁵) basis.

See also Figure S2–4 and Table S2–4.

Conditional input analysis demonstrated that the observed PN-to-KC network structure was qualitatively and quantitatively different from that predicted by the random bouton model (Figures 3B and S2C). Sensory input relayed by olfactory PNs to the MB main calyx is not sampled at random by KCs. To further describe the observed network structure, the most overconvergent cluster (i.e., the one with the highest mean z-score) was termed the “core community.” Less prominent “secondary” and “underconvergent” communities were also delineated based on each cluster’s mean z-score (Figures 3B and S2D). Strikingly, nearly all PN types within the core community were preferentially responsive to food-related odorants (Figure 3B). This result was robust to the clustering method or parameters used (Figures S2E–K and S3), and was the main focus of the following analysis. The observed network structure was dominated by overconvergence onto KCαβ and KCα’β’ subtypes, with little or no apparent structure deriving from input to KCγ neurons (Figure S4A–C).

Preferential ensheathment of food PN boutons by KC claws

How is the overconvergence of food-responsive PN types onto KCs implemented anatomically? The number of claws downstream of core community PNs was far greater than predicted by the random bouton model (Figure 3C), and also greater than the number of claws downstream of other PN types in the observed data (Figure 3D). Consistent with the preponderance of food-responsive PN types in the core community, food-responsive PN boutons were also ensheathed by more KC claws (Figures 3E–J and S2L). The bias toward more claws per core community bouton was greatest for KCαβ and KCα’β’ subtypes, rather than γ KCs (Figure S4D–I), consistent with the elevated z-scores evident for αβ and α’β’ subtypes (Figure S4A–C). Although some PN types were modestly oversampled by γ KCs (e.g. VL2a, D, VA5 in Figure S4H), γ KCs as a population received relatively weak overconvergent input from PNs (Figure S4C).

Underconvergent olfactory PN types had fewer KC claws per bouton (Figure S4J); however, they did not differ in the number of boutons per PN, and their downstream KCs differed by less than a claw, on average, in total claw count (Figure S4K–L). Therefore, underconvergence is likely driven mostly by undersampling of those PN types by KCs, rather than by a reduced number of claws in downstream KCs. The number of boutons per PN type was not significantly greater for core community types than other PN types (Core community vs. others, mean ± s.d., 5.5 ± 4.0 vs. 4.0 ± 2.3; K-S test, p=0.5), but slightly elevated for all (core and secondary) community types (all community vs. others, mean ± s.d., 10.8 ± 2.5 vs. 8.5 ± 4.8; K-S test, p<0.006). Overconvergence could also be generated if core community PN types tend to synapse onto KCs with an unusually large number of claws. Kenyon cells receiving two or more inputs from core community PNs did have an average of one more claw than other KCs (Figure S4M); however, the core community was still evident following random removal of claws from these downstream KCs to equalize total claw numbers (Figure S4N). Therefore, the observed network structure was not substantially driven by an increased number of total claws in downstream KCs.

The above observations suggested that the observed non-random sampling of sensory input was implemented predominantly by greater ensheathment of PN boutons by KC claws for select PN types. To test this hypothesis, a second null model was devised, incorporating the observed distribution of KC claws ensheathing boutons of each PN type. This “random claw” model (Figure 4A) is similar to the random bouton model, except that the number of KC claws assigned to a given PN bouton is held equal to the number of claws ensheathing that bouton in the observed PN-to-KC network. Therefore, in this null model, the number of claws receiving input from a given PN type (i.e. out-degree per PN type; Figure 3G) and the number of claws each KC has (i.e. in-degree per KC) are maintained. Comparison of observed PN-to-KC connectivity to this more realistic null model still revealed the core community of PN types (Figures 4B–C and S5A), indicating that those PN types converge onto KCs even more often than predicted by the observed oversampling of their boutons by KC claws. However, much of the network structure was captured by the random claw model: first, the distribution of z-scores had lower variance than the random bouton model (Figure 4D); second, conditional input analysis of PN connections to each KC subtype revealed greatly diminished clustering (Figure S5B–D; cf. Figure S4A–C); and third, the secondary community (Figure 3B) is eliminated in the random claw model (Figure 4B). In summary, the observed bias in PN-KC network structure is generated by (1) localized overlap of food-responsive PN axonal arbors and downstream αβ and α’β’ KCs, and (2) preferential ensheathment of food-responsive PN boutons by αβ and α’β’ KC claws.

Figure 4. Preferential ensheathment of food-responsive PN boutons by KC claws.

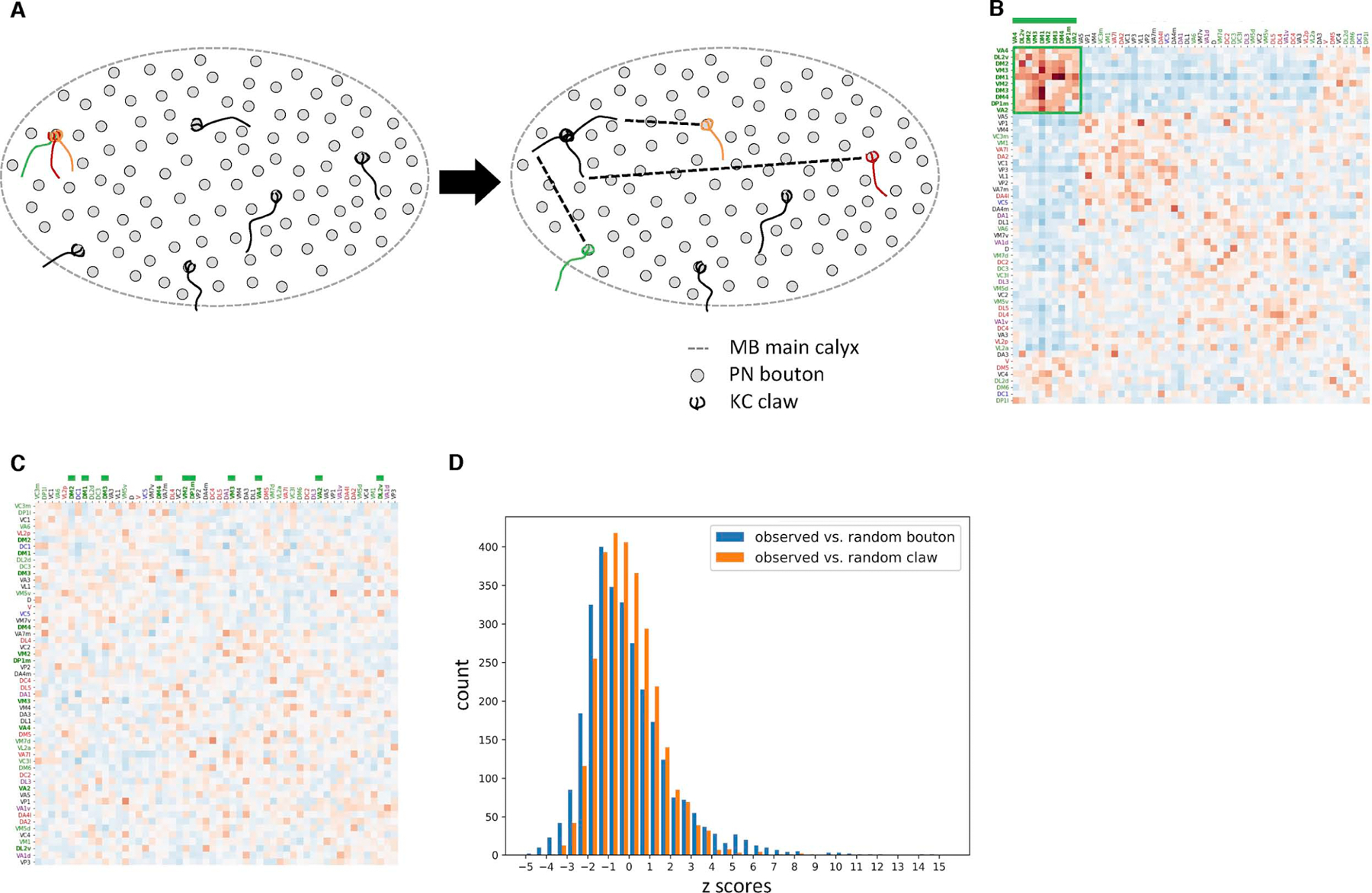
(A) Random claw null model schematic. The biased ensheathment of PN boutons by KCs according to PN subtype is maintained in this null model, while territoriality in the distribution of boutons and claws within the MB calyx is ignored.

(B) Core community PNs types converge more frequently than predicted by the random claw model, suggesting that the preferential ensheathment of their boutons is insufficient to explain the observed network structure.

(C) Conditional input analysis of a single representative network generated using the random claw model shows no clustered structure.

(D) Z-scores for the random claw model (Figure 4B) vary less than for the random bouton model (Figure 3B; mean ± s.d., −0.044 ± 2.11 vs. −0.058 ± 1.47; K-S test p<1×10⁻¹⁰), indicating random claw model captures more of the observed network structure.

See also Figure S5.

Comparison with other PN-to-KC datasets

Application of these analysis methods to PN-to-KC connectivity in the “hemibrain” dataset¹⁰ also revealed a similar core community of mostly food-responsive PN types (Figure S5E–F), suggesting that the presence of such a community may be common across individuals. As with the FAFB dataset, the random claw model more effectively described the observed network structure than the random bouton model (Figure S5G–I). In contrast, reanalysis of PN-to-KC connectivity reported an earlier study³⁵ did not reveal a community of food-responsive PNs (Figure S5J–K), although the non-uniformity of KC sampling reported in their work was detected (Figure S5J; cf. Figure S1 in³⁵). Notably, many fewer PN-to-KC connections were mapped in that study (about half the claws in each of 200 KCs; 1 KC mapped per fly). When connectivity data from the present study were randomly sub-sampled to match this lower number, minimal network structure was detected and the core community could not be discerned (Figure S5L). The sample size of the earlier study was therefore likely insufficient to detect the network structure described here. Finally, an analysis of the 17 PN types preserved between the larva and the adult revealed no overconvergence to γ KCs, the only KC class present in the larva (Figure S5M–N), consistent with the lack of network structure observed in the larva.⁵²

Spatial structure of the PN-to-KC network

Both the random bouton and the random claw models assume that the probability of a PN-to-KC connection is independent of its location in the MB main calyx. However, both PN and KC neuronal arbors are known to occupy stereotyped and circumscribed positions within the calyx as a function of cell type.^2,29,58,59 This suggested that cell type-specific neurogeometry might contribute to the observed nonrandom network structure. Therefore a “local random” model was constructed, in which each KC claw is randomly assigned to one of the five nearest boutons to it within the MB main calyx (Figure 5A). This model preserves the number of claws arising from each KC, the number of boutons arising from each PN, and the localized geometry of connectivity arising from PN axon and KC dendrite arbor extents. Only the number of claws assigned to each PN bouton is allowed to vary.

Figure 5. Neurogeometry of PN and KC arbors best explains the observed network structure.

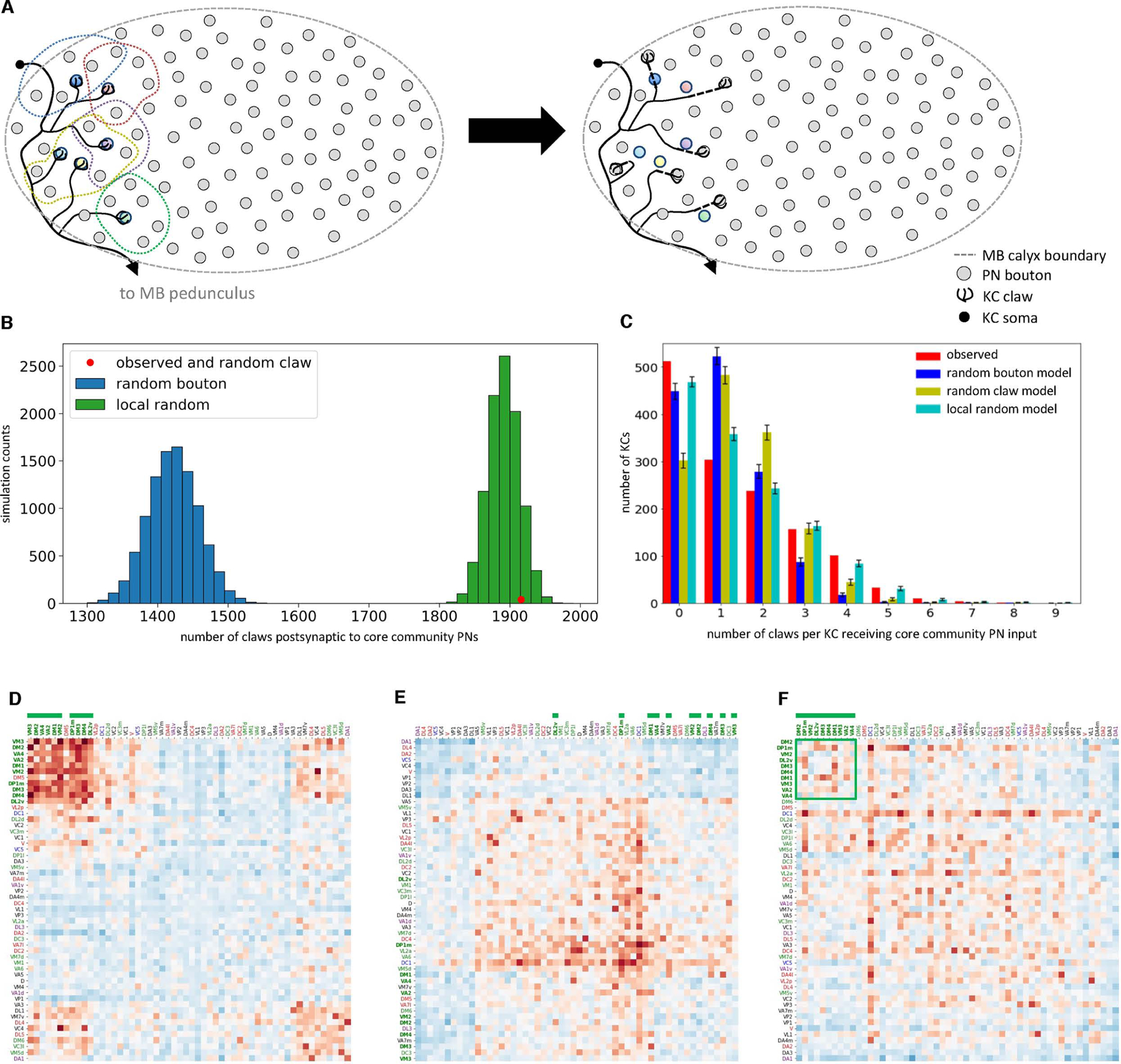
(A) Local random null model schematic. Left: each dashed line circumscribes a claw and its five nearest PN boutons. Right: after randomization, each claw is randomly assigned to one of the five nearest boutons.

(B) The local random model recapitulates the greater number of claws ensheathing core community PN boutons. The observed number of claws receiving inputs from core community PNs (red dot; 1,916 claws) was nearly identical to the mean of the local random model (mean ± s.d., 1,890.6 ± 22.5). By definition, all networks created using the random claw model also have 1,916 claws.

(C) The local random model best recapitulates the number of claws per KC postsynaptic to core community PNs. Observed vs. random bouton, Chi-square test p<1×10⁻¹⁰; observed vs. random claw, Chi-square test p<1×10⁻¹⁰; observed vs. local random, Chi-square test p<0.028 (error bars, ± s.d.).

(D) A single, representative network generated using the local random model recapitulates much of the core community of overconvergent PN types when compared to the random bouton null model.

(E-F) Core community PN types do not converge more often than predicted by the local random model, indicating this more geometrically realistic null model captures much of the observed network structure. (F), Z-scores for the core community PNs (green square) are not elevated compared to other PN types (columns and rows ordered as in Figure 3B).

The local random model better fit the observed network than the other null models, which lacked spatial constraints. In contrast to the random bouton model, it recapitulated the greater number of claws ensheathing core community PN boutons (Figure 5B). It also better recapitulated the overconvergence of core community PNs onto KCs, in particular the number of KCs receiving 4–7 claws of input from core community PNs (Figure 5C). Further, when individual networks generated by the local random model were treated as ‘observed’ networks, and then compared to the random bouton model, the overconvergent PN core community was largely recapitulated (Figure 5D). Conversely, when the observed PN-to-KC network was compared to the local random model, the overconvergent PN core community disappeared (Figure 5E–F), indicating that this model largely captures the observed network structure.

The success of the local random model suggested that much of the observed non-random network structure arises from the specific neurogeometry of PNs and KCs.^29,59,62 Direct visual examination of core community PN axonal arbors and postsynaptic KC dendrites bore out this interpretation. Core community PN axons were tightly clustered in peripheral regions of the MB main calyx (Figure 6A–B). Quantification of pairwise inter-bouton distances revealed that core community PN boutons were significantly closer to one another than non-core-community PNs (Figure 6C). Kenyon cells with the most core community input also showed dendritic arbors localized to four clusters corresponding to core community PN axonal territories (Figure 6D–F). These four clusters of KC dendrites are consistent with four MB neuroblasts.^25,63 The dendritic arbors of αβ and α’β’ (but not γ) KC subtypes were largely constrained to the axonal territories of core community PN types (Figure 6G–I), consistent with the observation that these subtypes receive more convergent input (Figure S4A–I). Complete reconstruction of an arbitrarily selected bundle of KCs fasciculating tightly in the MB pedunculus also showed regional bias toward the dorsolateral quadrant of the MB main calyx (Figure S6A–C), where collaterals of core community PNs tended to ramify. Finally, clustering of core community PNs was qualitatively evident upon inspection of their reconstructed axons (Figure 6J–L). Consistent with this, unsupervised clustering based on NBLAST scores⁷ of PNs in both hemispheres of FAFB (left hemisphere data from ²⁰) and in the hemibrain²⁶ showed co-arborization of core community PNs within the MB calyx (Figure S6D–F); the other clusters did not exhibit systematic per-cluster overconvergence (Figure S6G). Thus, the core community of overconvergent PN types seems to be generated by the overlap of the axonal and dendritic arbors of specific PN and KC subtypes within the MB calyx.

Figure 6. Arbor overlap between core community PNs and KCs.

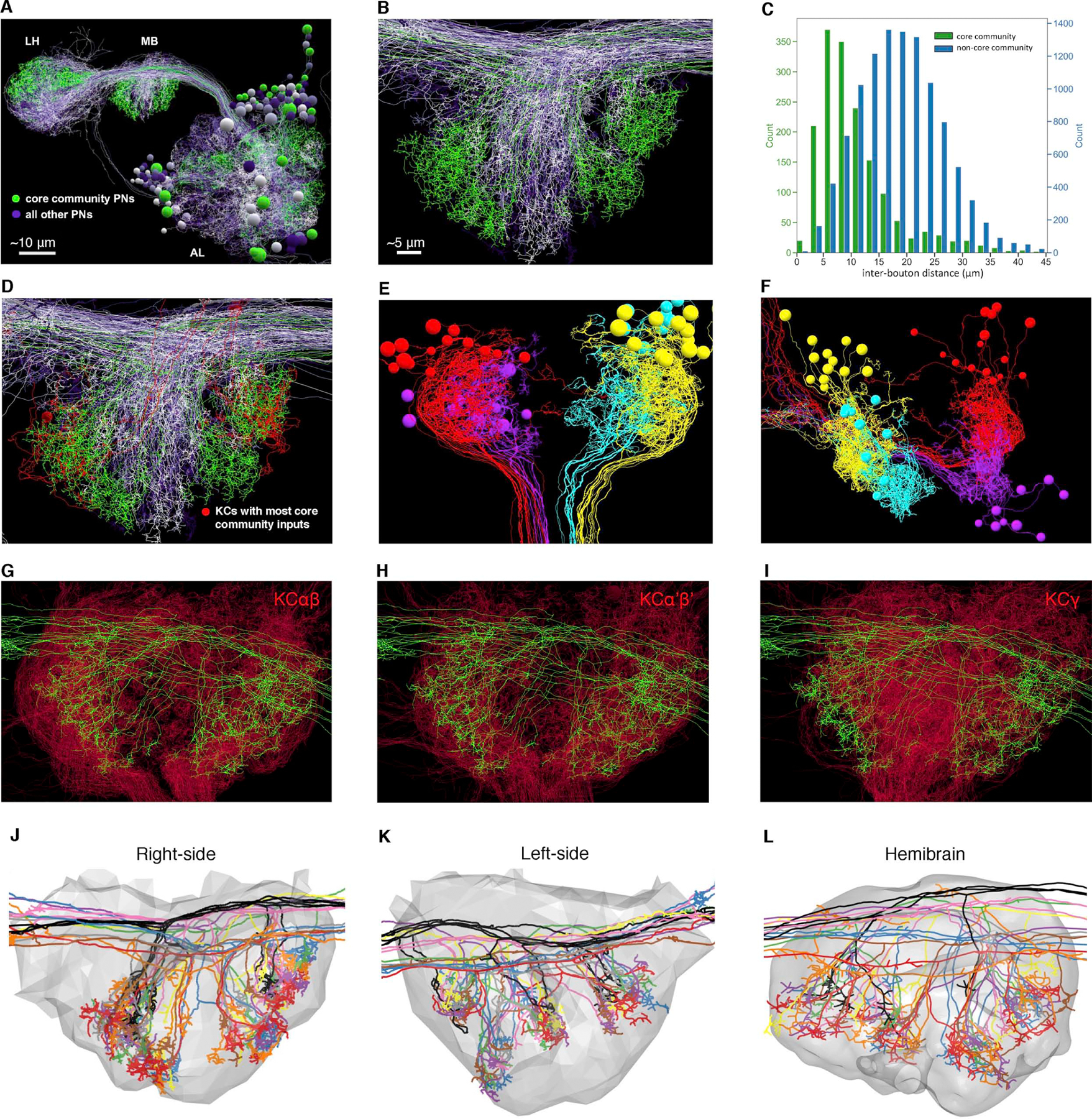
(A-B) Olfactory PNs project from AL to two higher brain centers, MB and LH. Core community PNs (green) have regionalized projection patterns in MB and LH compared to non-core community PNs (varying shades of purple). Scale bar in (B) applies also to (D-L).

(C) Core community PN boutons are closer to each other than to non-core community boutons. Each count represents the distance between a given bouton and the nearest bouton of a PN of a different type (green: core community PN bouton pairs; blue: pairs consisting of a core community PN bouton and a non-core community PN bouton; K-S test p<1×10⁻¹⁰; mean ± s.d., 10.9 ± 6.8 vs. 18.6 ± 7.4)

(D) Core community PN axon territories (green) overlap with the dendritic arbors of the 6 KCs (red) receiving 6 or more bouton inputs from core community PNs (same view as B).

(E-F) Dorsal (E) and posterior (F) view of MB calyx shows the 46 KCs that receive 5 or more inputs from core community PNs. The dendrites, somata, and axonal bundles (proximal pedunculus; see E, bottom) of the KCs, respectively, are segregated into 4 clusters (4 arbitrary colors) that may correspond to the 4 KC neuroblasts in development.^25,63

(G-I) In frontal view of MB calyx, dendritic arbors of KCαβ (G) and KCα’β’ (H) subtypes are more constrained than those of KCγ (I) to territory innervated by core community PN axons. To equalize the number of KC arbors plotted for each subtype, 246 out of 478 αβ KCs and 246 out of 575 γ KCs, were randomly selected for visualization, to be consistent with 246 reconstructed α’β’ KCs.

(J-L) Regionalized arbor distribution of core community PNs in three calyces: right side of FAFB (J), left side of FAFB (K), and hemibrain (L). The PNs are arbitrarily colored by type; colors are consistent across datasets (gray, calyx surface).

See also Figure S6.

Effect of network structure on a simulated discrimination task

To assess the potential effects of nonrandom PN-to-KC network structure on MB function, a simplified, feed-forward computational model of the PN-to-KC network was used in a simulated discrimination task.^40,52 Previous studies using this model have shown that discrimination performance is worse for non-random networks than for random networks in which each PN type (i.e. glomerulus) provides input with equal probability to each KC claw.^26,40 This connectivity scheme, which we term the “random glomerulus” model, is clearly unrealistic, given the nonuniform input of PN types to the MB (Figure 2); unsurprisingly, comparison of the observed PN-to-KC network to this null model strongly recapitulates the core community (Figure S7A–B).

The deviation of the observed, structured network from a theoretically optimal, random network raises the question of how discrimination performance in the computational model is affected by the observed network structure. To address this, PN-to-KC networks were generated using each of the null connectivity models described above – random glomerulus, random bouton, random claw, and local random – which increasingly recapitulate both the observed network structure (Figures 7A and S7C–F) and the observed fraction of convergent core community inputs onto downstream KCs (Figure S7G). These null model-generated PN-to-KC networks, as well as the observed network itself, were then tested in the simulated discrimination task. The fraction of PN input channeled through core and secondary community PN types was also varied systematically. When error rates were compared across network structures and activity patterns, the random glomerulus model performed best, in agreement with previous studies (Figure 7B–G). For the other connectivity models, error rate increased when PN activity was channeled outside community PN types, and recovered if signal was channeled exclusively through the community PN types (Figure 7B–F). Similarly, discrimination performance recovered when activity was channeled through food-responsive PN types, the core community, and PNs known to respond to a natural fruit odor (Figure S7H–J). Consistent with these results, when PN activity was spread across all PN types, overall discrimination performance was worse for more realistic connectivity models (Figure 7G). Thus, the observed network structure compromised performance on the simulated discrimination task, unless all the signal was channeled through the overconvergent PN types. This suggests that the observed PN-to-KC network structure may not be optimal for the simulated discrimination task.

Figure 7. Effect of the observed PN-to-KC network structure on a simulated discrimination task.

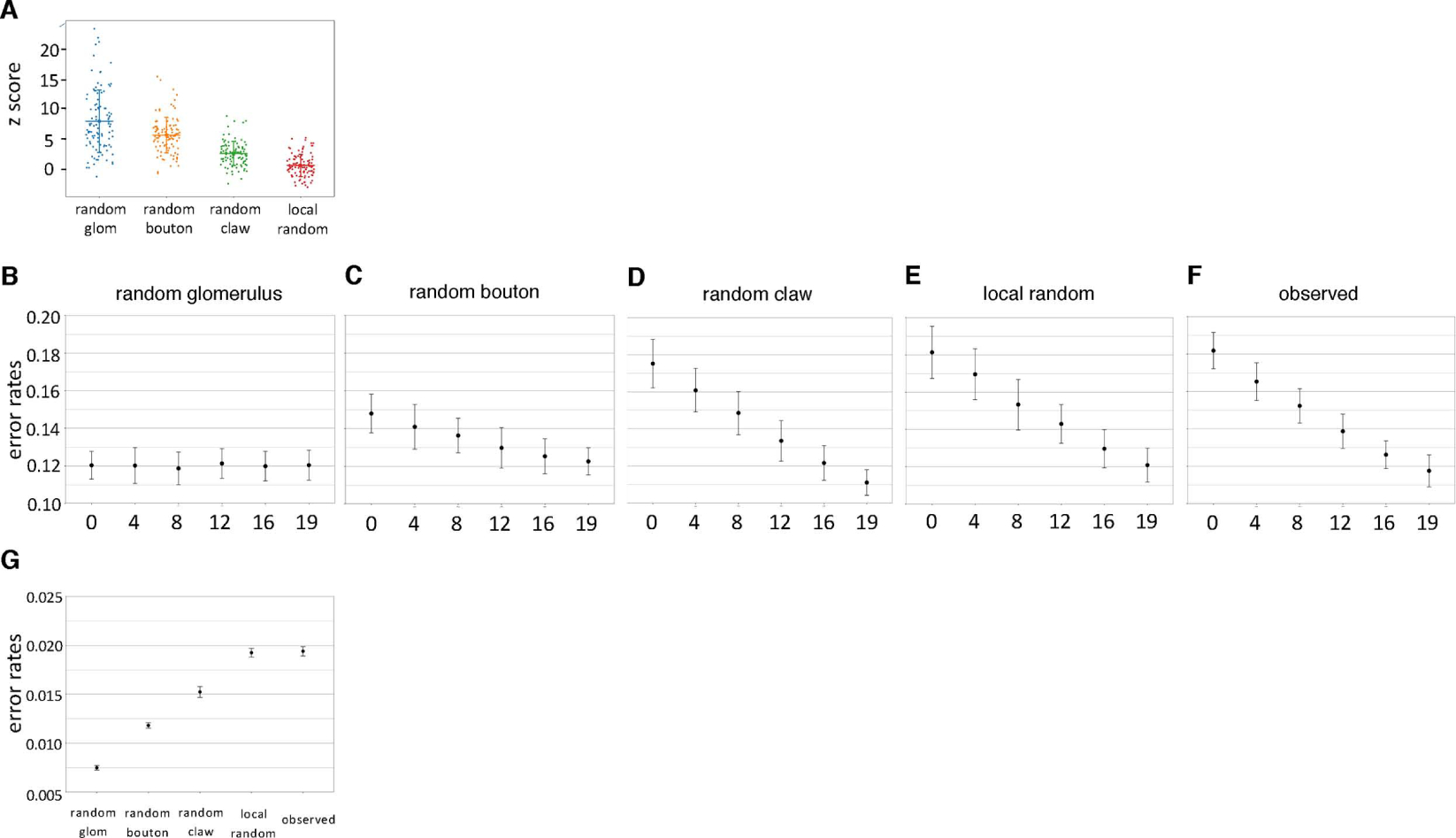
(A) The z-scores of core community PN types compared to the random glomerulus (Figure S7A); random bouton (Figure 3B); random claw (Figure 4B); and local random (Figure 5F) null models. The least realistic null model (random glomerulus) has the highest mean z-score, while the local random model has lowest, indicating it best recapitulates the observed connectivity (horizontal lines: mean; vertical bars: s.d.).

(B-F) Activation of more community PNs (including core and secondary community) leads to rescue of performance in a simulated discrimination task, for all connectivity models incorporating the observed non-uniformity of PN type input to MB calyx. A constant number of PN types (19; i.e., the number of core and secondary PN types) is activated, while the fraction of community PN types activated ranges from 0 to 100%. Error bars: ± s.d.

(G) Overall discrimination performance worsens as with decreasing randomness and increasing connectivity model realism. All 51 PN types provide input to the classifier.

See also Figure S7.

Discussion

The comprehensive EM-based mapping of PN-to-KC connectivity presented here revealed non-random network structure, in which a community of predominantly food-responsive PN types converge at above-chance levels onto downstream KCs (Figure 3B). The network structure is set up anatomically. The axonal boutons of overconvergent PN types are ensheathed by more KC dendrite claws of KCs (Figure 3C–D), and the axons of overconvergent PN types and the dendrites of many postsynaptic KCs arborize in overlapping, restricted regions within the MB main calyx (Figure 6). Available data suggest that this PN community may be stereotyped across individuals: first, the core community PN axonal arbor territories are similar to those obtained in earlier studies based on light microscopy data (cf. Figure 4C–D, cluster 1 in Jefferis et al.²⁹ and Figure 2C, E, green cluster in Tanaka et al.⁵⁸; Seki et al.⁶⁴) and second, re-analysis of the “hemibrain” dataset, acquired from a separate female adult fruit fly,²⁶ also revealed a similar core community of overconvergent PN types (Figure S5E–H). The developmental precision required to achieve this network structure seems within reach of the fly nervous system, given the highly reproducible geometries of most cell types in the fly brain, including those innervating the MB main calyx.^2,9,26,65 Our data showed that the overconvergent input from core community PNs is specific to KCαβ and KCα’β’ subtypes (Figure S4A–I), consistent with the greater overlap of dendritic arbors observed between these subtypes and the axons of core community PNs (Figure 6G–I). Within a given KC subtype, birth order and neuroblast origin may contribute additional specificity to KC arbor territories;⁵⁹ future studies will be required to address the extent to which these fine-scale developmental processes may contribute to the observed network structure.

The extent of overconvergence, and the exact PN types comprising the core community, likely vary to some extent between individuals. It will be of interest to learn whether the observed network structure varies as a function of sex, genetic background, neuronal activity levels, or environmental conditions during development.^66,67 Even if the observed network structure is conserved across individuals, it is likely that synaptic output from food-responsive KCs is variable, given that MBON odorant responses are highly variable across individuals.⁶⁸ Additional datasets and alternative analysis methods^69–71 might also reveal additional network structure.

Past efforts may have missed or deemphasized the observed PN-to-KC network structure for a variety of reasons. Earlier work based on light microscopy or electrophysiology likely lacked sufficient statistical power to detect the PN community. Indeed, subsampling to match the number of samples of the most thorough of these efforts³⁵ renders the community of food-responsive PNs undetectable in our own dataset (Figure S5). Following presentation of these results in preprint form⁶⁰, nonrandom PN-to-KC network structure was detected in an analysis of MB connectivity based on the hemibrain dataset²⁶. There was substantial agreement between the two studies, particularly in the number of connections made by each PN type in the MB calyx (Figure 1G–H); the lack of network structure for the γ KC subtype (Figure S4; c.f. Figure 13A, 14D in²⁶), and the ability of a geometrically constrained null model to recapitulate the observed network structure (Figure 5; c.f. Figure 14 in²⁶). However, the nonrandom network structure was described as relatively modest in extent and effect, possibly because much of the PN-to-KC network structure is generated by non-uniformity of output across PN types (Figure 3G–I); in Li et al., the initial comparison of observed connectivity (Figure 13A in²⁶) was to a null model that already incorporated this non-uniformity (similar to the random claw model described here; Figure 4), reducing the extent of apparent network structure.

Although the network structure we observe is statistically significant, its effect on the operation of the mushroom body remains unknown. There are several reasons to think it may be important. First, the overconvergent PN types were mostly food-responsive, suggesting an ethological role. Second, the overconvergence was detected in two different datasets, suggesting it may be general across individuals. Third, the PN core community we observe in MB calyx is nearly identical to an independently discovered PN subnetwork formed by axo-axonic synapses in the LH (c.f. Figure 3F in²⁰). These axo-axonic synapses are physiologically uncharacterized, but the existence of distinct subnetworks of these PN types in both LH and MB suggests that the information they relay is distinctive.

The effect of the observed nonrandom network structure on associative memory formation and recall in the MB will require additional experimental and theoretical work to determine. Many challenges likely await. The observed network structure is intermingled with extensive recurrent circuitry within the MB calyx, involving both local and extrinsic neurons.^{32,37,72–74} The calyx also includes little-understood and recently discovered cell types² and many physiologically uncharacterized connections, including KC-KC synapses,^52,75–77 PN-PN synapses,²⁰ and KC-to-PN synapses.² It is also unknown whether the cell types involved fire exclusively in all-or-none fashion, or whether synaptic release can be evoked locally at the compartment or even neurite level^78–81. This question becomes especially pertinent given that nearly all neurites in the fly brain (with the exception of the finest dendritic processes) have a mixture of both input and output synapses (our unpublished observations; refs. 20,82–84). The dynamics of MB as a whole during learning and recall are also complex^5,72,85–87 and may affect how local activity within the calyx is read out. Better understanding of MB microcircuitry, as well as richer models incorporating recurrent dynamics,⁸⁸ will likely be required to fully characterize the effect of the observed network structure. Future studies could also incorporate behavioral responses to field-collected odor samples^89,90 potentially allowing exploration of the relationship between neuronal network structure and chemical ecology.

Despite these unknowns, some speculation may be offered. Computational modeling showed that the discrimination performance of the observed network was inferior to that of a random network (Figure 7), as expected.^39,40 However, performance was rescued when simulated PN activity was channeled through overconvergent, predominantly food-responsive PN types. This suggests that the PN-to-KC network structure may be balancing discrimination capacity with other imperatives, for example generalization.^91–93 The rescue of discrimination capacity when activity is channeled through food-responsive PN types calls to mind the efficient coding hypothesis, which states that neuronal resources are allocated to match the distribution of natural stimuli, and that more frequently encountered stimuli (such as food odorants⁹⁴) are sampled more densely.^95,96 In this regard it is attractive to think of the observed network structure as a kind of ‘associational fovea’, in which combinations of input from food-responsive PN types are sampled more densely than combinations from other types.

The present work joins other studies in which quantitative comparison of observed connectivity to null models of neurogeometry has allowed unexpected structure to be detected in neuronal networks.^97–102 A spectrum of null models was used, ranging from the simplistic random glomerulus model to the more sophisticated local random model. The latter incorporates all known nonuniformities in sampling of PN inputs by KCs, as well as the fine-scale territories of each cell type’s axonal and dendritic arbors of each identified cell type. This class of high-resolution model provides a baseline against which additional connectivity datasets can be tested for unexpected network structure. Although connectomics-style synaptic wiring diagrams are by themselves insufficient to explain neuronal circuit function,¹⁰³ they are a useful scaffolding for integrative analysis of network function.

STAR★METHODS

RESOURCE AVAILABILITY

Lead Contact

All queries and requests for resources should be directed to the Lead Contact, Davi D. Bock (dbock@uvm.edu).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

• All neuron reconstructions described in this study will be uploaded to a public CATMAID instance hosted by Virtual Fly Brain (https://fafb.catmaid.virtualflybrain.org/) following publication.

• The full source code is available at https://github.com/bocklab/pn_kc.

• Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

METHOD DETAILS

Neuron tracing

Neurons were reconstructed from the whole brain EM dataset of an adult fly.² Skeleton tracing of neuronal arbors and criteria of synapse annotations are conducted as described previously² with the CATMAID tracing environment.^106,110 To summarize, all the manually traced neurons were reconstructed with an iterative tracing method by at least two tracers, an initial tracer and a subsequent proofreader. The initial tracer reconstructed arbors, followed by systematic review by a different proofreader. When either tracer was not confident about the identifications of a neural process or synapses, they cooperatively examined the image data to reach a consensus. All such sites were further reviewed and resolved by an expert tracer. A chemical synapse was identified if it met at least three of the four following features, with the first as an absolute requirement: 1) an active zone with vesicles; 2) presynaptic specializations such as a ribbon or T-bar with or without a platform; 3) synaptic clefts; and 4) postsynaptic membrane specializations such as postsynaptic densities (PSDs).

Our tracing approach is biased to errors of omission rather than commission. This approach has been shown to have minimal impact on network connectivity in the fly larva.¹¹⁰ In addition, the present study is focused on the connectivity between PNs and KCs at a distinctive structure called the microglomerulus, which contains a multitude of synapses between a given PN bouton and its postsynaptic KC claws.^32–34 It is therefore unlikely that the loss of any particular synapse during reconstruction qualitatively affected the analysis described here.

As in Zheng et al. ² two reconstruction strategies were used: tracing to classification and tracing to completion. In tracing to classification, in general only backbones, and not twigs microtubule-containing, large diameter neurites, and microtubule-free, fine neurites, respecitvely; ¹¹⁰ are reconstructed. Tracing is halted once the reconstructed neuronal morphology unambiguously recapitulates that observed by LM or previous EM reconstruction studies for a given cell class. In tracing to completion, all of a given neurite is reconstructed, along with all of its input and output synapses, unless ambiguities in the data make tracing impossible. In some cases, tracing to completion is done only within a given brain compartment; in the present study, for example, manually reconstructed KCs were traced to completion only within the MB main calyx (see below).

Random sampling of KCs

Kenyon cells were randomly sampled from within MB pedunculus (“Random Draw KCs”) on the right side of the brain. The pedunculus is a tract of fasciculated KC axons projecting from the posterior of the brain, where KC dendrites ramify in the MB calyx, to the lobes of the MB at the anterior of the brain, where synapses are made between KCs, MBONs and DANs.²¹; Figure 1A All neuronal processes in a frontal plane of pedunculus (section #4186 in the FAFB dataset; the “seed node plane”) were labelled with seed nodes (2740 in total; Figure 1C–D). Seed nodes were randomly selected for reconstruction, which proceeded posteriorly (i.e. retrogradely, in the case of KCs) from the seed node plane. In addition to KCs, the anterior paired lateral (APL) neuron a wide-field inhibitory neuron; ⁷⁴ and MB-CP1 an MBON; ²³ were known to have neurites in the pedunculus.² Therefore tracing to classification was done to determine whether the neuron arising from a given seed node was a KC, using the following morphological criteria. Kenyon cell somata are posterior and slightly dorsal to the MB calyx; each KC makes a handful of dendritic specializations called “claws” within the calyx; and has a single axon projecting anteriorly, with few branches, in the pedunculus.⁹ The APL neuron (one within the MB on each side of the brain) has numerous, densely branching and fine neurites ramifying throughout the entire MB. The MB-CP1 neuron similarly branches densely in the pedunculus and calyx. Disambiguating between these neuron types was therefore relatively straightforward, and tracing was halted and discarded from further analysis if the neuron arising from a seed node was determined not to be a KC. The Random Draw KCs were reconstructed either manually (440 KCs) or by an automatic segmentation-assisted approach (916 KCs), described below. The total sample size of 1,356 KCs was constrained by the time and resources available for the effort; the overall goal was to obtain as large a sample as possible to maximize statistical power. The average number of claws per KC, 5.2 ± 1.6 (mean ± s.d., Figure 1F), was within a standard deviation of previously reported numbers: 1) 6.8 ± 1.7 for all KCs;³⁵ 2) 7.3 ± for γ KCs, 5.8 ± 1.8 for α’β’ KCs, and 5.5 ± 1.9 for α’β’ KCs.³²

In a total of 7,102 claws that are reconstructed, ~9% of claws receive inputs from one of the following categories: 1) multi-glomerular PNs, often with inconclusive innervating glomeruli; 2) thermosensory or hygro-sensory PNs; 3) less than 3 synapses per claws identified; and 4) Lateral Horn neurons (LHNs), interneurons (e.g. APL), or MBONs (e.g. MB-CP1). Given each category of these inputs represents a small fraction of the total input, our analysis is focused on 91% of the claws that receive input from uniglomerular olfactory PNs (Table S4).

Sampling of a KC bundle in the pedunculus

To study the arbor pattern of fasciculating KCs (Figure S6A–C), a ‘bundle’ of KCs axons bounded by astrocytic processes in the pendunculus of MB was selected. The calyceal dendrites and peduncular axons of all KCs in the bundle were manually reconstructed (see Manual tracing of KCs). The KCs in the bundle mostly consist of the KCαβ subtype.

Manual tracing of KCs

Each manually reconstructed KC was retrogradely traced to completion from at least section 4,186 (the seed node plane) of the FAFB dataset to the posterior of the brain. This volume spans the posterior ~1/3 of pedunculus, and the entire MB calyx, where the dendrites of the three main KC types (γ, αβ, and α’β’) and their claws ramify. In previous work,² the boutons of all PNs in calyx as well as the glomerular types of all PNs were identified. Typically, each dendritic claw received input from a single bouton.^33,34 To facilitate downstream analysis (see below), “claw border” tags were applied to each KC at a node between the “arm” and distal fingers of each KC claw. The “claw border” tags therefore delineated KC claws post-synaptic to distinct PN boutons. Similarly, “bouton border” tags were applied to the PN arbors within MB main calyx.

The majority of reconstructed KCs received olfactory inputs from PNs within MB main calyx. There are 3 main KC classes, γ, α’/β’, α/β, named according to which of the eponymous lobes at the anterior MB the KC axon projects.^9,23–25 Two additional, numerically fewer types of KC (α/βp and γd) receive non-olfactory inputs such as visual, gustatory, and temperature information, via dendritic arbors within MB accessory calyces.¹¹¹ These were excluded from analysis. All Random Draw KCs were traced to classification anterior to the seed node plane. Subtype was assigned depending on which MB lobe the KC axon ramified within.

Automated segmentation-assisted tracing of KCs

During the KC reconstruction effort, a segmentation of the FAFB dataset became available.⁶¹ A tracing workflow using this segmentation was therefore adopted. Automated segmentation-derived skeleton fragments were manually concatenated, and the entire resulting arbor was proofread as described above. While all claws from each KC were identified, KC claws were only partially reconstructed, sufficient to define which PN bouton was contained and to identify and annotate at least 3 synapses from the bouton to the claw. Control experiments in which one tracing team manually reconstructed KCs to completion and another independently used the automated segmentation to map PN-to-KC connectivity demonstrated the consistency of results between both approaches in quantifying PN bouton/KC claw connection counts (data not shown). Volume reconstruction of the KC and the PN boutons in Figure 1B (right panel) are generated directly from another recently completed segmentation of the FAFB image data “FlyWire”; ¹⁰⁵ with minor proofreading. The axonal branches of input PNs in this figure were removed for better visualization of boutons.

Connectivity matrix analysis

To determine whether input to KCs from PNs was independent or conditional on PN type, a new method was devised which we termed “conditional input analysis” (Figure S2A). The result is a matrix that indicates whether, given input from the row PN type, a given KC is more (or less) likely than chance to get input from the column PN type. Each observed PN bouton-KC claw connection is treated as a single count. The observed number of counts for a given pair of PN types is compared to the distribution of counts generated using a null model. Several null models were used in this study (described below). For each combination of PN types, a z-score is computed, i.e., how many standard deviations from the mean of the null distribution the observed number of counts is (Figure S2B). Unsupervised k-means clustering of the z-score matrix was used to group matrix entries.

A summary of the steps in conditional input analysis follows.

Projection neuron types are named after the glomerulus (‘Glom’) in the antennal lobe that PN’s dendrites innervate. Consider types Glom A, B, C, and so on. For a given connectivity matrix,

1. Select all KCs having at least one claw receiving input from a bouton of Glom A.

2. The number of inputs to these KCs from Glom B, C, D, and so on are counted. This provides a count of the number of inputs to the KC cell population from Glom B-D, given input from Glom A.

3. Repeat (1) – (2) for Glom B, C, D, and so on.

4. For each null model (see below), repeat (1)-(3) above on 10,000 in silico randomizations of the observed PN-to-KC network. This generates the null distributions from which a z-score can be generated for observed connectivity for each PN type pair. All z-score matrices in the study use the same color scale as in Figure 3B.

5. Apply k-means clustering to the z-score matrix. The k-means algorithm¹¹² clustered PN types into groups such that within-group z-score variance is minimized, and the cluster number of each PN type is used to re-order both the columns and rows of the z-score matrix. All z-score matrices are ordered based on the k-means clustering procedure with two exceptions: (1) Figure S2H (hierarchical clustering); (2) Figure S3E, Figure S4A–C, Figure S5B–E, G, Figure 5F, Figure S6G, Figure S7A (to facilitate comparison with other z-score matrices).

K-means clustering of the z-score matrix groups glomeruli with similar z-scores together, and therefore reveals subsets of PNs that as a group provide more (or less) convergent input onto KCs than predicted by a given null model. Overconvergence (red in our figures) is more strongly detected by this approach, since pairs of PN types with low probability of being selected during randomization (e.g. small numbers of boutons in the random bouton model) can have minimal or zero convergence onto common KCs. This, in turn, lowers the magnitude of negative z-scores (since the mean of the null model values is already low).

The key parameter in k-means clustering is the number of clusters (i.e. the parameter ‘k’) sought in the data. Although objective methods for determining k have been devised, the ‘best’ value is largely subjective. The three most commonly used methods to determine k are the average silhouette method;¹¹³ the elbow method;¹¹⁴ and the gap statistic method.¹¹⁵ Silhouette coefficients are a measure of how close each data point in one cluster is to points in neighboring clusters. The average silhouette method identifies the value of k that maximizes the average of silhouette coefficients. The elbow method computes the total within-cluster sum of square (total WSS), a quantification of the compactness of the clustering, for a range of potential k values. The optimal k is that for which WSS cannot be improved further by adding another cluster, often shown as an “elbow” point in the plot of WSS as a function of k. The gap statistic method generates a uniform distribution of z-scores as a null model, and maximizes total intra-cluster variations between observed values and the null model, for different values of k.

For the main z-score matrix (Figure 3B), objective methods yielded an optimal k value of 2–3 (Figure S2E–G); nonetheless, we opted for k = 4, since four clusters better separated underconvergent PNs, and gave results more consistent with hierarchical clustering (Figure S2H–K; Table S3). For consistency, a k=4 was used for all other z-score matrices (Figure S2C; Figure 4B–C; Figure S5F, H–N; Figure 5D–E; Figure S7B). For most matrices, clustering results did not differ qualitatively even when the objectively determined optimal k value differed from 4 (data not shown). However, in four cases (Figures 4B, 5E, S5F, and S7B), the gap statistic method determined that no cluster was present in the data (i.e. k=1), and the other objective methods returned k values of 2 or 3. In this situation, k=4 was still used, to maintain consistency with the rest of the analyses.

To identify overconvergent and underconvergent PN “communities”, clusters were first ranked by the average z-score for each k-means cluster. The PN types most frequently found in the most overconvergent cluster (highest average z-score) were defined as comprising a “core community” (Figure 3B, dark green area; Table S2), and types most frequently found in the second-highest z-score cluster were defined as comprising a “secondary community” (Figure 3B, light green area). Similarly, PN types most frequently appearing in the lowest z-score cluster were defined as the “underconvergent” set of PNs (Figure 3B, blue area; Table S3). Note that the conclusion that most overconvergent PNs tend to respond to food odorants did not depend on membership in “core” or “secondary” communities, nor on the parameter k for number of clusters (Figure S2I–J; Table S2).

Z-score matrix can also be clustered by hierarchical clustering algorithm (Figure S2H). This hierarchy of clusters is represented as a dendrogram and the dendrogram and matrix are reordered such that the Euclidean distance (dendrogram height) between successive entries is minimal.¹¹⁶

Connectivity matrices can also be analyzed with principal component analysis (PCA).^26,35 The fraction of variance between the observed network and a given null model explained by each component can then be visualized, allowing comparison of different null models (Figure S7C–F). While useful and generally powerful, this approach does not allow easy attribution of effect to specific glomeruli. In contrast, the conditional input analysis used here allows for visualization of overconvergence or underconvergence by any given pair of glomeruli.

Connectivity matrices can also be analyzed using covariance analysis.¹¹⁷ Unlike covariance analysis, conditional input analysis allows asymmetries in conditional input to be detected (the case where, e.g., KCs on average get more input from type B, given input from type A; but less input from type A, given input from type B). The results, however, indicate that most overconvergent inputs are symmetric (Figure 3B). Covariance analysis is therefore a reasonable alternative to the conditional input analysis described above. For each pair of PN types, the covariance measured in the observed network was compared to the distribution of covariances generated from 1,000 runs of a given null model of connectivity (see below). The null hypothesis is the observed covariance is equal to or less than 95% of the covariances in the null model distribution for that pair of PN types. When the observed covariance is larger than 95% of the null model distribution, the null hypothesis is rejected (i.e. p < 0.05), and we say there’s an above-chance correlation in the output to common KCs for this pair of PN types.

A p value of less than 0.05 (significance level) implies the probability of obtaining such a covariance in a random network is low, and the alternative hypothesis of seeing such an observed value in a null model is therefore rejected. The results are shown in a p-value matrix (Figure S3A–D) in which each cell represents a p value for a given pair of glomeruli indicated in the corresponding row and column labels.

The p-value matrix was re-ordered either using the Figure 3B clustering order (Figure S3A, C) or using order given by k-means clustering (Figure S3B, D). To aid k-means clustering of very low p-values, the p-value matrix was binarized such that all p values less than 0.05 were set to 1, and otherwise to 0.

For the analysis of synaptic connectivity (Figure S3C–D), covariance measures were directly calculated from synapse counts, using only the manually reconstructed Random Draw KCs (whose dendritic arbors in MB calyx were reconstructed to completion; see Manual Tracing of KCs, above). To generate the null model of synaptic connectivity, the bouton-claw binary network is randomized and each bouton-claw connection is assigned a synapse count that was randomly drawn (with replacement) from the distribution of number of synapses per claw.

Null models of PN-to-KC connectivity

Nonrandom PN-to-KC connectivity can in principle arise from various anatomical parameters, such as: variable numbers of PNs per glomerulus; variable numbers of boutons per PN type; non-uniform sampling of PN boutons by KCs; and regionalized distribution of PN boutons and KC claws. By testing observed connectivity against a range of null models, incorporating none, some, or all of the observed values of these parameters, the relative contribution of each parameter to the observed network structure can be assessed.

In the random glomerulus model (Figure S7A–B), each claw of each KC is randomly assigned to a PN with equal probability per PN type (i.e. glomerulus). The observed values of all the other parameters listed above are ignored. As a result, in this null model, each PN type provides input to equal number of claws, on average.

In the random bouton model (Figure 3A), each KC claw is reassigned to a randomly selected PN bouton in the calyx. All boutons in the calyx are available to be assigned to any given claw with equal probability per bouton. On average, the number of outputs provided by a given PN type (i.e. out-degree per PN type) will be proportional to the number of boutons that belong to that type. Since the number of boutons per PN type is the product of the number of PNs per glomerulus and the number of boutons per PN, the observed value of these anatomical parameters is incorporated into the random bouton null model. The number of claws for each KC (i.e. in-degree per KC) is also maintained. To apply conditional input analysis to the data of Caron et al. ³⁵ using this null model (Figure S5J, L), the bouton counts per PN type obtained from our work were used, since bouton counts per PN type were not generated in that study. Similarly, when the PN-to-KC network in Li et al. ²⁶ is analyzed using this null model (Figure S5E–H), values of bouton counts per PN type from our dataset were used. A caveat of this approach is that bouton counts per PN type may not be consistent across animals. However, the broad consistency of outputs for PN types (Figure 1G) suggests the result may be robust to this parameter.

The random claw model (Figure 4A) is similar to the random bouton model, except that the number of KC claws assigned to a given PN bouton is held equal to the number of claws ensheathing that bouton in the observed PN-to-KC network. Therefore, in this null model, the number of claws receiving input from a given PN type (i.e. out-degree per PN type) and the number of claws each KC has (i.e. in-degree per KC) are maintained.

In the local random model (Figure 5A), each claw of each KC is randomly assigned to one of the five nearest PN boutons (including the one it ensheathed in the observed network). Distances were measured between claw and bouton centroids. The number of claws assigned to each bouton is allowed to deviate from the observed value (unlike the random claw model). Therefore in this model, both KC in-degree and geometric constraints on connectivity are preserved, and out-degree per PN type is allowed to vary.

Morphological clustering of PNs using NBLAST

The complete set of reconstructed PNs and all reconstructed KCs used in the analysis of conditional input are on the right hemisphere of the FAFB brain. On the right side, each PN type was classified and the subset of PN arbors contained in the MB calyx surface mesh was extracted, as described in previous work.² The boundaries of MB calyx were generated from an nc82 (synapse)-stained template brain aligned to the FAFB image volume as described in Zheng et al. ² PNs on the left side of the FAFB brain were reconstructed in a separate study.²⁰ In the current work, the subset of PN arbors innervating the left-side MB main calyx were obtained through intersection with the left-side MB calyx surface mesh. The reconstructed PNs and calyx mesh of the hemibrain dataset¹⁰ were obtained from the neuprint server (neuprint.janelia.org) using the neuprintr R package (github.com/natverse/neuprintr).^20,109 The reconstructed skeletons were re-sampled evenly at 1 μm intervals to reduce the sensitivity of NBLAST to local differences between small branches. For PNs in each of the three data sources (right-side FAFB, left-side FAFB, and hemibrain), hierarchical clustering was performed based on Euclidean distance (dendrogram height) matrices of NBLAST scores,⁷ using Ward’s algorithm.¹¹⁸

Comparison of postsynaptic KC counts between FAFB and hemibrain datasets

During preparation of this manuscript, a segmentation of a portion of a second adult fly brain was published (the ‘hemibrain’).¹⁰ In the hemibrain dataset, all PNs and ~2,000 KCs on the right side of the brain were segmented as part of a large-scale proofreading effort (50 person-years over ~2 calendar years).²⁶ In this hemibrain connectome, we analyzed synaptic connections only at the cell level, rather than individually demarcating PN boutons and KC claws as was done for the right-side of the brain in the FAFB dataset. We used the hemibrainr package (github.com/natverse/hemibrainr)¹⁰⁹ to download the connectivity matrix between all PNs and KCs (hemibrain v. 1.0.1, from https://neuprint.janelia.org). Comparison of PN-to-KC connectivity to the random bouton and random claw null models (Figure S5E–H) was done by (1) assuming that all synapses between a given PN-KC pair were the result of a single PN bouton-KC claw interaction (true for ~ 92% of connections in observed FAFB PN-KC pairs); and (2) using the number of boutons per PN type as measured in the FAFB dataset in null models of connectivity in the hemibrain dataset. The hemibrain PN-to-KC connectivity matrix was then binarized, such that each unique pair of PN and KC with 3 or more synapses is defined as one connection and otherwise zero. For a given PN, the number of connections is therefore equivalent to the number of KCs postsynaptic to the PN. Because the total number of reconstructed neurons is different between the FAFB and the hemibrain dataset, the number of connections for each PN type is divided by the total number of connections in each dataset. This results in a normalized percentage of connections for each PN type, enabling comparison between FAFB and hemibrain datasets (Figure 1G–H).

Modeling of a Discrimination Task

The PN-to-KC network computational model is based on earlier models used in the larval⁵² and adult fly with minimal modifications.⁴⁰ In these models, simulated activities across all PN types are created for each of ten stimulus odors. Each stimulus is randomly assigned one of two categories with equal probability. The PN activity (signal) is generated by drawing independently from a rectified unit Gaussian distribution and then corrupted by Gaussian noise. The PN activity is simulated per PN type (i.e. glomerulus), such that all PNs of the same type have identical activity. Here, the publicly available source code for these earlier models (lk.zuckermaninstitute.columbia.edu/#code^40,52) was minimally modified to allow for channeling of PN activity through subsets of different PN types. To probe the effect of the observed overconvergence of all community PN types (19 PN types, including core and secondary community PN types; Figure 3B), for each stimulus, rectified Gaussian activity patterns were generated for 19 PN types. The fraction of activated community PN types was varied between 0 (19 non-community PN types) and 1 (all 19 community PN types), with intervening fractions of 4/19, 8/19, 12/19, and 16/19 (Figure 7B–F). For fractional values less than 1, activated PNs were randomly selected from the 19 community PN types and non-community PN types were randomly selected from the set of 35 non-community PN types. Gaussian noise with standard deviation 0.4 was then added to the activity levels of all PNs. Kenyon cell activity was calculated by multiplying PN activity with the observed matrix of PN-to-KC synapse counts, without thresholding. In the original model,⁴⁰ simulated activities across all PN types were created for each stimulus odor, and the KC activity was thresholded such that each KC is activated by 5% of odor stimuli, consistent with the general sparseness of KC activity.¹¹⁹ In the event that a given KC does not exceed this threshold, its activity was set to zero. In the current work, the effect of PN noise on classification capability was assessed by making all KC activity available to the classifier, including weak activity inherited from simulated noise of PN input. This change did not qualitatively alter the results (data not shown). Kenyon cell activity patterns were used to train a maximum-margin classifier to predict the pre-assigned category assigned to each PN activity pattern. In the testing phase, the PN activity patterns used during training were corrupted with Gaussian noise, and the resulting KC activities were calculated and used as input to the trained classifier.

The model requires synapse counts between each connected PN-KC cell pair. For each PN-to-KC network generated using one of the null models, each connection is assigned number of synapses drawn from the observed dataset. All generated networks had 2,200 KCs. Since the observed network has only 1,356 KCs, each model of the observed network required an additional 844 KCs, with their number of input synapses, to be drawn from the manually traced KC population.

In Figure S7G–I, the same model is implemented except that 22 food PN types (Table S1), 10 core community PN types (Table S2), 4 PN types that are activated by banana odors ¹²⁰ are chosen to be activated, respectively. In the null model distribution, for each simulation (one count in the histogram), a random set of the same number of PN types are drawn from the remaining PNs and are picked to be activated.

In this class of discrimination task,⁴⁰ the more PNs that are activated, the more information (signal) is available for the classifier to solve the task. Since there are more food PN types (22 PN types) than core community PN types (10 PN types), simulating activity in all food PNs results in lower error rates than core community PNs (Figure S7G vs. Figure S7H).

QUANTIFICATION AND STATISTICAL ANALYSIS

All statistical analyses were performed in Python using the scipy package (https://www.scipy.org).¹²¹ In each of all z-score matrices, 10,000 random networks were generated for a given null connectivity model (random glomerulus, random bouton, random claw, local random). Z-score was defined as the number of standard deviations of the observed value from the mean of the distribution generated by the null model. For modeling of the PN-KC networks in Figure 7B–G and Figure S7H–J, error rates are first averaged over random input patterns (10,000 trials) for an instance of a randomized network, then averaged over 100 instantiations of null-model network architectures, as in⁴⁰. The standard deviations of the mean across network architectures for the error rates are used. The expected error rate for chance performance is 50%.

Supplementary Material

9

Table S4. The connectivity between PNs and KCs at bouton-claw level. Related to Figure 3.

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
The Full Adult Fly Brain (FAFB) ssTEM dataset	Zheng et al.2	https://temca2data.org/
FAFB manual neuronal reconstructions: right-side PNs	Zheng et al.2	https://fafb.catmaid.virtualflybrain.org/
FAFB manual neuronal reconstructions: KCs and others	This paper	https://fafb.catmaid.virtualflybrain.org/
FAFB manual neuronal reconstructions: left-side PNs	Bates et al.20	https://fafb.catmaid.virtualflybrain.org/
Partial auto-segmentation of FAFB	Li et al.104	http://fafb-ffn1.storage.googleapis.com/data.html
Hemibrain	Scheffer et al.10	https://neuprint.janelia.org/
FlyWire	Dorkenwald et al.105	https://flywire.ai/
Software and Algorithms
CATMAID	Saalfeld et al.106 Schneider-Mizell et al.107	https://github.com/catmaid/CATMAID
NBLAST	Costa et al.108	https://github.com/jefferislab/nat.nblast
Pymaid	Bates et al.20	https://github.com/schlegelp/pymaid
Natverse	Bates et al.109	http://natverse.org/
PN-KC model	Litwin-Kumar et al.40 Eichler et al.52	lk.zuckermaninstitute.columbia.edu/#code

Highlights.

• Mushroom body Kenyon cells sample olfactory projection neuron input nonrandomly

• Network structure arises from axon and dendrite overlap between specific cell types

• Food-responsive projection neurons converge preferentially onto αβ and α’β’ KCs

• Activation of overconvergent PNs rescues MB discrimination in a computational model