IMPROVING PHASE-RECTIFIED SIGNAL AVERAGING FOR FETAL HEART RATE ANALYSIS

Abstract

Low umbilical artery pH is a marker for neonatal acidosis and is associated with an increased risk for neonatal complications. The phase-rectified signal averaging (PRSA) features have demonstrated superior discriminatory or diagnostic ability and good interpretability in many biomedical applications including fetal heart rate analysis. However, the performance of PRSA method is sensitive to values of the selected parameters which are usually either chosen based on a grid search or empirically in the literature. In this paper, we examine PRSA method through the lens of dynamical systems theory and reveal the intrinsic connection between state space reconstruction and PRSA. From this perspective, we then introduce a new feature that can better characterize dynamical systems comparing with PRSA. Our experimental results on an open-access intrapartum Cardiotocography database demonstrate that the proposed feature outperforms state-of-the-art PRSA features in pH-based fetal heart rate analysis.

1. INTRODUCTION

The most well-accepted method for monitoring fetal well-being during labor is using Cardiotocography (CTG) where both fetal heart rate (FHR) and uterine activity are simultaneously recorded [1]. Although various clinical guidelines are available [2], the evaluation of FHR recordings by obstetricians suffers from high inter- and intra-variability [3]. In the computerized analysis of FHR, the gold standard for labeling FHR recordings is using the pH values of umbilical cord blood at birth, as low umbilical artery pH is a marker for neonatal acidosis and is associated with an increased risk for neonatal complications [4], and a typical choice of threshold is pH ⩽ 7.05. Although advanced machine learning methods, e.g., deep learning, are able to perform end-to-end learning and learn the features from data automatically, such learned features and embeddings often lack interpretability. On the other hand, despite the good interpretability of conventional FHR features such as heart rate variability features, they are usually not well correlated with the pH value [5] and have limited discriminatory ability, which is often measured by the area under the receiver operating characteristic curve (AUC-ROC).

The phase-rectified signal averaging (PRSA) method was first proposed in [6, 7] for assessing deceleration-related and acceleration-related modulations of heart rate using electrocardiogram (ECG) recordings. PRSA is robust to noise and capable of detecting quasi-periodic oscillations in nonstationary signals [8]. Therefore it has been applied to a variety of biomedical applications including pH-based FHR analysis [9, 10], and it has been found to have superior discriminatory capability. However, the performance of PRSA is sensitive to the choice of parameters which are generally selected empirically or using a grid search. Furthermore, even for the same task, there is no consensus on appropriate values of its parameters.

In dynamical system modeling, each state of a studied system is represented by a (state) vector within its state space where all the possible states are represented. Another powerful concept is the attractor of a system, which is a collection of states toward which a system tends to evolve. In reality, the attractor manifold and the mathematical description of a dynamical system are often latent, and one can only obtain some noisy, partial observations generated by the underlying system. Estimating or reconstructing an attractor manifold, i.e., state space reconstruction (SSR), is of great importance in characterizing the dynamical system and has been well studied in the literature [11]. Unlike the parameters in PRSA, well-established methods are available for selecting the parameters for SSR.

This work reveals, for the first time, the inherent connection between the PRSA and the SSR framework. To be more specific, PRSA is virtually characterizing the underlying dynamical system by averaging state vectors sampled from the reconstructed attractor manifold. This intrinsic connection is illustrated using the well-known Lorenz system. From this viewpoint, we propose a new feature, named average state distance (ASD) that is able to characterize the system in a natural manner by directly working with the reconstructed attractor manifold. In our experiments on an open access intrapartum CTG database, ASD outperformed state-of-the-art PRSA features in pH-based FHR analysis and achieved better diagnostic ability in detecting neonatal acidosis.

2. BACKGROUND

2.1. Phase-Rectified Signal Averaging

The main idea of PRSA method is to quantify the average acceleration capacity (AC) and deceleration capacity (DC) of the signal. The method comprises three steps. The first step is the anchor point selection, where the AC anchor points (corresponding to increase events) and the DC anchor points (corresponding to decrease events) are identified. Specifically, let x[i] denote the ith sample in the time series x_t, i = 1, …, N, and x[i] is an AC anchor point if

$$\frac{1}{T}\sum _{j=0}^{T-1}x[i+j]>\frac{1}{T}\sum _{j=1}^{T}x[i-j],$$ (1)

and it is a DC anchor point if

$$\frac{1}{T}\sum _{j=0}^{T-1}x[i+j]<\frac{1}{T}\sum _{j=1}^{T}x[i-j],$$ (2)

where T is a parameter for anchor points selection, and T ≪ N. Note that, in our experiments, we adopted the definition of anchor points from [6] because, instead of converting FHR signal to RR series [10], which is the time elapsed between successive heartbeats, we directly worked with FHR signals.

In the second step, known as phase rectifying or signal averaging step, for each anchor point, a window of length 2L is constructed by taking L consecutive samples before the anchor point and L − 1 consecutive samples after the anchor points. Then the PRSA curves for AC and DC, denoted as ${\overline{x}}_{\text{AC}}$ and ${\overline{x}}_{\text{DC}}$, respectively, are obtained by aligning and averaging all windows that are framed around the corresponding type of anchor points,

$$\overline{x}[k]=\frac{1}{M}\sum _{m=1}^{M}x\left[i_m+k\right],$$ (3)

where M is the total number of windows associated with a specific type of anchor points, AC or DC, and k = −L, −L +1, …, 0, …, L − 2, L − 1 is the shift from the position of anchor point i_m in the mth window.

In the third step, named capacity calculation step, the AC and DC are computed by

$$\begin{array}{l}\text{AC}=\frac{1}{2s}\sum _{i=L+1}^{L+s}{\overline{x}}_{\text{AC}}[i]-\frac{1}{2s}\sum _{i=L}^{L-s+1}{\overline{x}}_{\text{AC}}[i],\\ \text{DC}=\frac{1}{2s}\sum _{i=L+1}^{L+s}{\overline{x}}_{\text{DC}}[i]-\frac{1}{2s}\sum _{i=L}^{L-s+1}{\overline{x}}_{\text{DC}}[i],\end{array}$$ (4)

where s is a parameter for summarizing the phase-rectified curves.

2.2. The State-of-the-art of PRSA in FHR Analysis

The PRSA method has demonstrated superior performance and great potential for surveillance of intrauterine growth restriction and intrapartum FHR analysis [12]. In [9], the authors adopted the PRSA feature DC for pH-based FHR classification using the last 30 minutes tracings and achieved AUC-ROC of 0.665 on a large private database that contains 7568 Oxford deliveries. Recently, a new PRSA feature named deceleration reserve (DR), as a combination of DC and AC, was proposed in [10] where DR achieved AUC-ROC of 0.65 for pH-base FHR classification using the last one hour tracings on an open access intrapartum CTG database. We also adopted the same open access intrapartum CTG database in our experiments. Despite the similar performance, the parameters used in [9] and [10] are quite different. In [9], T = 5 and L = 45 (s was not reported) were selected after a grid search, whereas in [10], T = 1, L = 50, and s = 2 were set empirically. From a theoretical perspective, in [7], the connection between the PRSA method and wavelet analysis was established. In [10], the authors studied the PRSA method for stationary stochastic Gaussian processes and showed AC = −DC under such assumption.

3. MODEL DESCRIPTION

3.1. State Space Reconstruction

The Takens’ theorem, proposed by Floris Takens in [13], provides theoretical guarantees that one can actually reconstruct the state space using a single observation variable of the system, when some mild conditions are satisfied. Conventionally, a reconstructed attractor manifold is called a shadow manifold.

Theorem 1 (Takens’ theorem)

Let $\mathcal{M}$ be a compact manifold of (integer) dimension d. Then for generic pairs (ϕ, y), where

• $\varphi :\mathcal{M}\to \mathcal{M}$is a C²-diffeomorphism of $\mathcal{M}$ in itself,

• $\text{y}:\mathcal{M}\to ℝ$ is a C²-differentiable function, the map ${\mathrm{\Phi }}_{(\varphi ,\text{y})}:\mathcal{M}\to {ℝ}^{2d+1}$ given by

$${\mathrm{\Phi }}_{(\varphi ,\text{y})}(x):=\left(y(x),y(\varphi (x)),y\left({\varphi }^2(x)\right),\dots ,y\left({\varphi }^{2d}(x)\right)\right)$$

is an embedding of $\mathcal{M}$ in ${ℝ}^{2d+1}$.

In practice, a simple and popular choice of ϕ is delay-coordinate map or delay embedding. Specifically, for a time series x_t of length N, the diffeomorphic shadow manifold reconstructed from x_t with delay embedding with properly selected parameters E and τ (defined below) is denoted as $M_x:={\left\{m_x[n]\right\}}_{n=1+\tau (E-1)}^N$, where

$$m_x[n]=[x[n],x[n-\tau ],\dots ,x[n-(E-1)\tau ]]$$ (5)

is the E-dimensional (state) vector on M_x corresponding to the nth observation in x_t, i.e., x[n].

It can be seen that SSR and PRSA are inherently connected. The first step in PRSA, i.e., selecting anchor points, in a time series x_t can be seen as irregularly sampling the shadow manifold M_x reconstructed with E = 2L and τ = 1. The second step in PRSA, i.e., the phase rectifying or signal averaging step, can be seen as calculating the averaged AC and DC system state vectors denoted as $m_x^{\text{AC}}\in {ℝ}^{2L}$ and $m_x^{\text{DC}}\in {ℝ}^{2L}$, respectively. Finally, capacity calculation step of PRSA is essentially characterizing shadow manifold by summarizing the system state vectors $m_x^{\text{AC}}$ and $m_x^{\text{DC}}$.

The delay embedding dimension E is usually determined with false-nearest-neighbors (FNN) algorithm by examining how the number of neighbors (of a point along a signal trajectory) changes as a function of embedding dimension [14]. FNN selects E as the smallest embedding dimension that minimizes the number of false neighbors. The delay τ is a free parameter, and in theory, its value can be arbitrarily selected. However, in reality, since time series are of finite length, the choice of τ also affects the SSR quality. If τ is small, the dimensions in the shadow manifold will be highly correlated, whereas if τ is too large, dynamical information may be missed. In practice, τ is often selected to be the delay that achieves the first local minimum of the average mutual information (AMI) [15] or cross correlation between the original time series and its delayed version. In this work, we utilized delay embedding for SSR, where E and τ were selected using FNN [14] and AMI-based method [15], respectively.

3.2. State Vector Clustering

In PRSA, the anchor points are selected with criteria (specified by the value of T) on a given time series x_t. In the literature, T is often selected to be relatively small, e.g., T = 1, for capturing oscillations. As a result, the majority of observations in x_t are either AC or DC anchor points. Since there is an one-to-one mapping from x[n] to m_x[n], PRSA essentially assigns majority of system states to have either AC or DC status. Despite efforts for theoretical analysis of PRSA, selecting an appropriate T (especially jointly with L and s) for a specific task and dataset remains challenging. Besides, anchor points that are of the same type are not necessarily having similar system states. Therefore, instead of designing and optimizing the AC or DC anchor points selection criteria for different tasks and datasets, we directly work with state space using shadow manifold M_x and cluster the state vectors in M_x (i.e., rows of M_x) into two classes so that the similarity in state space is properly preserved. Essentially, M_x is partitioned into $M_x^{\text{cluster}1}\in {ℝ}^{N_1\times E}$ (denotes the collection of states vectors in cluster 1) and $M_x^{\text{cluster}2}\in {ℝ}^{N_2\times E}$ (denotes the collection of states vectors in cluster 2). In this work, we adopted K-mean clustering [16] with euclidean distance as distance measure for its simplicity, although more sophisticated clustering methods can readily be applied.

3.3. Average State Distance

The average state vector of cluster 1 denoted as $m_x^{\text{cluster}1}\in {ℝ}^E$, can be constructed by the mean value of each column in $M_x^{\text{cluster 1 }}$. Similarly, $m_x^{\text{cluster }2}\in {ℝ}^E$ is calculated by averaging each column of $M_x^{\text{cluster }2}$. Finally, we define the average state distance (ASD) of x_t as in (6) to characterize M_x, which is the Euclidean distance between $m_x^{\text{cluster}\hspace{0.17em}1}$ and $m_x^{\text{cluster 2}}$,

$$\mathrm{ASD}\left(x_t\right)=\Vert m_x^{\text{cluster }1}-m_x^{\text{cluster }2}\Vert .$$ (6)

4. EXPERIMENTS AND RESULTS

4.1. Simulated Data: Lorenz System

To demonstrate the intrinsic connection between PRSA method and SSR, we adopted the well-studied Lorenz system [17], described by

$$\begin{array}{l}dx/dt=\sigma (y-x),\\ dy/dt=x(\rho -z)-y,\\ dz/dt=xy-\beta z.\end{array}$$ (7)

A Lorenz attractor $\mathcal{M}$ of length N = 921 was simulated with (7) using a classic set of parameter values $\sigma =10,\rho =\frac{8}{3}$, and β = 28. We assumed only x_t was observed.

We implemented the anchor point selection of PRSA method on x_t (with T = 5 and L = 20) and K-mean clustering on shadow manifold M_x (reconstructed with τ = 1 and E = 40), respectively. We set E = 40 and L = 20 so that the window length in PRSA and SSR are the same. Since the observation x_t is tested one by one in anchor point selection, τ = 1 was used to match with this behavior of PRSA. Since a high dimensional shadow manifold $M_x\in {ℝ}^{882\times 40}$ cannot be plotted directly, it was visualized with Gaussian process latent variable model (GPLVM), which is capable of visualizing high dimensional data using nonlinear dimensionality reduction [18]. Specifically, M_x was compressed or reduced to $M_x^{\text{GP}}\in {ℝ}^{882\times 3}$ and the nonlinear mapping between M_x and $M_x^{\text{GP}}$ was governed by a Gaussian process (GP). More details for GPLVM can be found in [18].

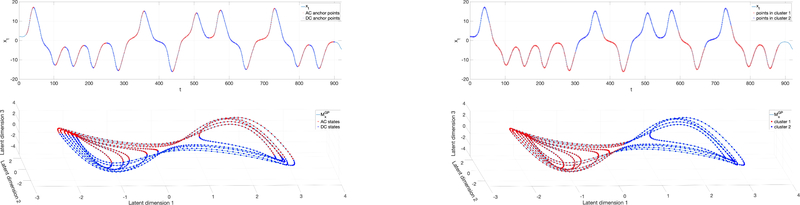
The connection between PRSA and SSR is illustrated in Fig. 1. For the PRSA method (Fig. 1a), the anchor points in x_t were selected first, and then for each anchor point, we colored its corresponding state vector in shadow manifold based on its type (AC or DC). In contrast, for our method (Fig. 1b), we directly applied clustering of the state vectors in the shadow manifold, and then colored the observations in x_t based on the clustering results of their corresponding state vectors. It can be seen that selecting the anchor points in x_t is essentially (irregularly) sampling and clustering the state vectors in M_x. By directly working with state vectors in the shadow manifold, the similarity of states can be better preserved, which is often of better interpretability. For example, in Fig. 1b, the state vectors on the left lobe were assigned to one class and the ones on the right lobe were assigned to the other class.

Fig. 1: Comparison between PRSA and proposed approach using simulated data.

(a) DC and AC anchor points selected in x_t with T = 5 and L = 20 (top) and their corresponding states vectors in shadow manifold (bottom) where the state vectors were colored based on the type of their corresponding anchor points selected using PRSA.

(b) Different from PRSA, in our method, we first applied K-mean clustering of state vectors in the shadow manifold and colored them based on which cluster they belong to (bottom). Then the observations in x_t were colored based on the clustering results (top).

4.2. Real Data: Open Access Intrapartum CTG Database

In this section, we adopted the same open access intrapartum CTG database [19] that was used in [10], and compared the performance of ASD and state-of-the-art PRSA features in [9] and [10]. This database contains 552 recordings as well as the corresponding pH values of umbilical cord blood at birth. Both FHR and UA signals were sampled at 4Hz. We used the same labeling approach as in [9] and [10], where the positive cases are the FHR recordings associated with pH ⩽ 7.05.

In our experiments, similar to [9], the last 30 minutes of FHR recordings were used. Since RR series were employed in [10], we computed PRSA features on both FHR recordings and RR series (in milliseconds). For benchmarking purposes, we extracted AC and DC using the parameters mentioned in [9, 10], and additionally computed DR proposed in [10]. Similar to [9,10], AUC-ROC was used as a performance metric. The performance of the PRSA features is summarized in Table 1. Note that, the parameter s was not specified in [9], so a grid search was performed for s and the highest AUC-ROC score and the corresponding s are reported.

Table 1:

Summary of performance of PRSA features

		AUC-ROC
		FHR		RR series (in ms)
T = 5, L = 45 [9]	AC	s = 45	0.5963	s = 2	0.4872
	DC	s = 2	0.4732	s = 45	0.6066
	DR	s = 2	0.4827	s = 40	0.5661
T = 1, L = 50, s = 2 [10]	AC	0.5325		0.4901
	DC	0.4787		0.5054
	DR	0.5069		0.4932

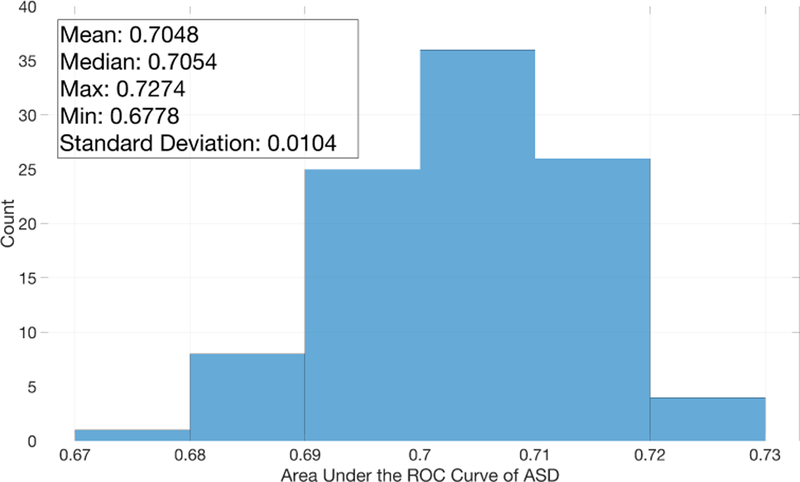
To properly account for the randomness introduced by K-mean clustering (as it initializes centroids randomly), we repeated the experiment of ASD on the open access intrapartum CTG database 100 times. The histogram of AUC-ROC of ASD over 100 runs and some statistics are shown in Fig. 2. The result clearly shows that ASD outperformed the state-of-the-art PRSA features summarized in Table 1 and demonstrated better diagnostic ability for neonatal acidosis; the mean and median of AUC-ROC of ASD are both around 0.705, and the standard deviation is only around 0.01.

Fig. 2:

Histogram of AUC-ROC of ASD over 100 runs on the open access intrapartum CTG database.

5. CONCLUSIONS

In this work, we generalize PRSA method by casting it in the SSR framework and show that the PRSA method is essentially sampling shadow manifold and summarizing certain states vectors. Then we propose a new feature, named ASD, that is able to summarize the shadow manifold more naturally. Our results show that ASD is of superior diagnostic ability for neonatal acidosis compared to state-of-the-art PRSA features. Further, the proposed approach can be readily applied for signal analysis in other fields. Natural signals are generated by low dimensional systems [20], and the proposed method can be combined with a dimensionality reduction method when high dimensional shadow manifolds are encountered.