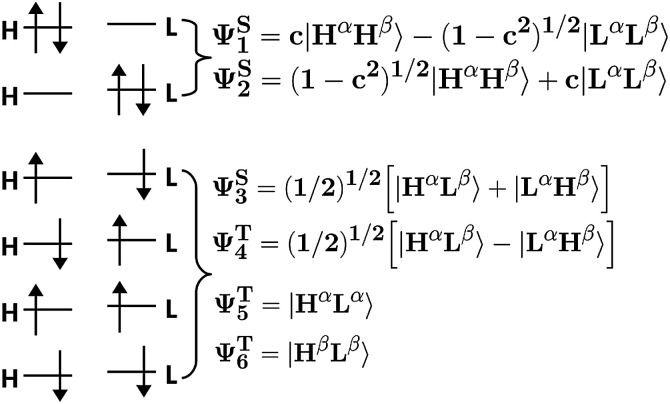Anti-ohmic single molecule electron transport: is it feasible?

Abstract

Hitherto, only molecular wires with a regular ohmic behavior in which the electric conductance decreases with the wire length have been synthesized. Implementation of molecular conductors with reversed conductance/length trend (anti-ohmic) might revolutionize the field of molecular electronics, allowing the development of electronic devices with extraordinary properties. It is for this reason that, recently, theoretical efforts have been focused on this topic and different structures have been proposed to show reversed conductance/length behavior on the basis of density functional theory non-equilibrium Green function approach (DFT-NEGF) and topological models. From the previous works, it can be stated that an anti-ohmic molecular wire must display a very small HOMO–LUMO gap and a reversed bond alternation pattern in the case of polyenes and related conjugated systems. In this work, the pursuit of a mechanism by which the anti-ohmic electron transport may arise was carried out by studying the paradigmatic anti-ohmic p-xylylene chain (pX2) at the DFT level in combination with topological models. It has been found that the electron transport in the anti-ohmic regime is favored by a long-range superexchange mechanism, which, contrary to what is expected, is reinforced by the increase in the length of the chain. Moreover, strong links between anti-ohmic character in molecular wires and one-dimensional topological insulator models have been established. Due to the small HOMO–LUMO gap predicted at DFT level, the anti-ohmic character has been put to the proof using a multireference scenario. Preliminary results point out to the presence of different ohmic and anti-ohmic electronic states. In the particular case of pX2 the anti-ohmic states do not correspond to the ground state. These findings require a reconsideration of previous studies on the reversed conductance/length behavior using single reference methodologies.

Feasibility of anti-ohmic transport in the ground state of molecular wires, intrinsically related to superexchange, is called into question.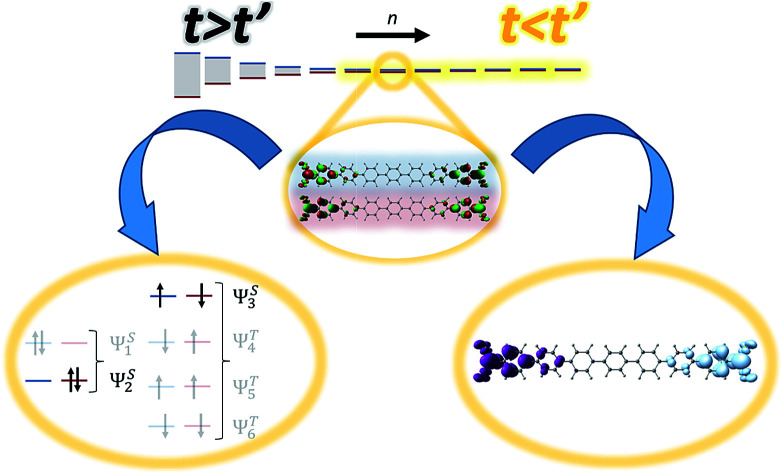

1. Introduction

REDOX reactions in biochemical systems, charge transfer in organic solar cells or electron conduction in molecular junctions^1–5 are processes that involve the rapid transport of electrons through a molecular environment. However, the mechanisms or models proposed to explain them differ significantly from one process to another. This is the case of the electron transference occurring in a donor–bridge–acceptor system which can be understood in terms of the so-called superexchange. This mechanism occurs within an electron exchange coupling between non-bonded electron donor and acceptor moieties without assistance of the bridging molecular region. The mechanism has been, however, restricted to relatively near units and expected to rapidly decay when the donor–acceptor distance increases.⁶ Thus, long-range electron transport in molecular systems is explained by a hopping model where the electrons transferred “hop” between intermediate bonded units instead of a direct donor–acceptor transfer.⁷

In spite of the analogies found between charge transport processes in donor–bridge–acceptor molecules and electron conduction in molecular junctions, superexchange and hopping models have not found place within the theory of molecular conductors. This is mainly due to the fundamental differences between the Marcus theory,^8,9 employed to rationalize charge transfer in chemical processes, and the Landauer–Büttiker approach,^10,11 applied to explain the electron transport physical processes in molecules subjected to finite bias voltages. However, the origin of the two processes is actually the same; electrons are transferred across molecular environments due to a chemical potential gradient between two different regions. It is then expected that concepts successfully employed to rationalize one of them may also work to explain the other under certain conditions. These fundamental differences stem from the gap existing between chemical and physical formalisms, where we could encompass, respectively, the Marcus theory and the Landauer–Büttiker approach.

This back and forth journey between chemistry and physics is fortunately well known. This is the case of concepts such as aromaticity or electron delocalization, which have been recently related to, respectively, quantum interference effects in molecular junctions^12–23 and formation of soliton states²⁴ in one-dimensional topological insulators, TIs. Namely, it has been predicted theoretically and later confirmed experimentally that aromaticity may exert a positive/negative effect on the conducting ability of organic conjugated chains. Therefore, increasing/decreasing the aromatic character of a given ring in a molecular chain^15,22 may be used to tune the conducting character of the entire system. On the other hand, the formation of soliton states or topologically protected edge states has been shown to be reflected on a particular electron delocalization pattern using the polyacetylene chain as model.²⁵

Herein, as the number of theoretical and experimental works on electron conduction in molecular systems have increased over the years, the intuitive expected behavior of the molecular junctions involving an exponential decay of conductivity with the size of the molecular chain, has started to be challenged. For instance, Tsuji et al.²⁶ suggested, from very simple tight binding models, that in the unphysical case where the bond alternation pattern in a polyene was reversed, the conductance would increase with the size of the chain, evidencing an anti-ohmic behavior. More recently, Garner et al.²³ suggested a experimental realization of this reverse bond alternation using cumulenes. Slowly, but steadily, indications pointing toward new possible interesting phenomena accumulate and once more chemical concepts, like bond alternation, acquire through these findings a new physical bright.

A paradigmatic example of the control exerted by aromaticity and bond alternation pattern on the electron transport in organic chains is the simple oligophenyl chain (pP) compared with that terminated by methylene groups (pX2).¹⁶ Whereas in the former the electric conductance shows the expected exponential decay, the later exhibits an anti-ohmic regime, where the electric conductance increases up to reach a maximum. Only qualitative explanations based on valence bond (VB) models were proposed to explain this opposite behavior. Ramos-Berdullas et al.¹⁶ found the unexpected trend observed for pX2 was rooted in the particular electric response of this system, where the electric perturbation reinforces the aromaticity of the chain. A simple VB model showed the aromaticity in pX2 arises from resonance forms polarized at the terminal methylene groups, which are favored by the perturbation. On the contrary, the electric perturbation favors polarized quinoid-like resonance forms in pP, provoking a decrease of the aromatic stabilization. Stuyver et al.^12,27,28 further explained the extraordinary conductance shown by the pX2 chains in terms of an increasing diradical character with the chain length, which comes along with the formation of aromatic resonance forms.

A similar polarized resonance form to that proposed by Ramos-Berdullas et al.¹⁶ to explain the increasing conductance of pX2 chains has been employed by Pinilla et al.²⁹ in polyacetylene to give a chemical interpretation of the topological phase in TIs. The topological phase is refereed to the one displaying reversed bond alternation pattern. As this form gains weight by increasing the chain length, the frontier orbital states become polarized at the edges and degenerated, leading to a system with conducting edges but isolating bulk.

In this work, we establish a link between the particular electron delocalization patterns found in one-dimensional topological insulators and the normal or reverse response of single-molecule conductance with molecular length. We think that this link is considerably more general than the reverse bond-length alternation mechanism exploited up to now, and that it opens a new avenue that deserves being fully explored. We show that the presence of a topological-like phase in molecular chains is linked to an exceptional long-range electronic coupling (dubbed as long-range superexchange). Moreover, it is shown how the transition to the topological-like phase can be controlled by introducing aromatic rings along the chain. The aromatic character of these rings allows shortening/lengthening the length at which this transition occurs, leading even to one-dimensional TI-like behavior at molecular scale. In the following sections, the methodologies employed in this work to account for the long-range electronic coupling, conducting ability and TI character in molecular chains are reviewed and applied on pP and pX2 like chains formed by different aromatic units.

Being the closeness in energy of the HOMO–LUMO orbitals and its localization at the edges of the conducting structure a necessary condition to find a molecular junction within this anti-ohmic behavior,^30–32 one may think about the problematic arising from the single-reference treatment. As a consequence of this fact, at the end of this work, a multireference scenario is proposed in which the different possible configurations are taken into account leading to a set of conducting and isolating states. This evidences nothing more than the doubtless requirement of analyzing each proposed system carefully in order to consider if the extraordinary behavior found within the single-reference context is kept within a multireference scenario.

2. Methodology

2.1. Molecular electric conductance from electron deformation orbitals (EDOs)

In the Landauer–Büttiker approach the electric conductance, G, is obtained from the product of the quantum conductance, G₀, and the transmission function, T,

G = G₀T 1

where G₀ = 2e²/h. Even though the equation given above was originally obtained from scattering theory,¹⁰ it can be also derived from linear-response theory using the Kubo formalism.³³ Thus, eqn (1) represents a general expression to quantify electron conduction and it can be applied within the context of different theoretical approaches. As recently demonstrated,³⁴ this is the case of the time-energy uncertainty relation approach to the electric conductance. This approach is rooted in the origin of the quantum conductance and its relationship with the time-energy uncertainty principle. Batra^35,36 derived the expression of G₀ by applying the uncertainty relation to the case of a free electron crossing a monodimensional conductor under the action of a finite bias voltage, ΔV. Recently, a generalization to interacting electrons subjected to the external potential created by the nuclei in a molecule was proposed,³⁴ giving rise to the following expression,

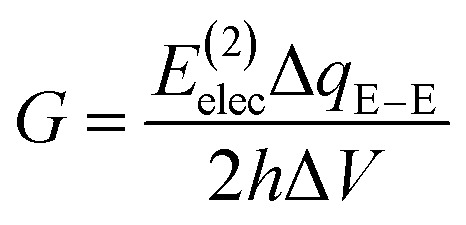2

where, Δq_E–E represents the net electronic charge transferred between electrodes upon the action of the electric voltage and E_elec is the second order electrostatic energy. To get both quantities, the electron deformation density (ρ^def), the difference between the electron density in the electrically perturbed and unperturbed states, has to be obtained. Eqn (3) and (4) provide expressions of Δq_E–E and E_elec in terms of ρ^def, the latter including also higher order terms which are expected to be unimportant.

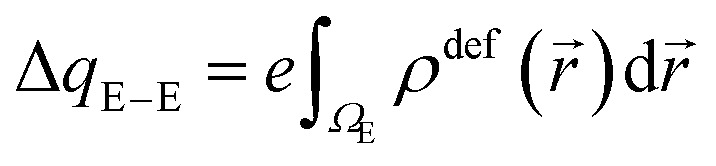3

E⁽²⁾_elec ≈ E_elec = e∫ρ^defV(r⃑)dr⃑ 4

It was proven that eqn (2) can be transformed into eqn (1) by expressing ρ^def with the so-called electron deformation orbitals (EDOs).³⁷ For a system perturbed by a constant electric field, EDOs can be obtained by diagonalization of the electron deformation density matrix. The electron deformation density matrix is defined as,

D^def = D^l − D⁰ 5

where, D^l and D⁰ are, respectively, density matrices for the perturbed and unperturbed systems on the basis of the unperturbed molecular orbitals. Then, the EDOs represent the eigenfunctions of D^def, each with its corresponding eigenvalue. Denoting the eigenvector matrix by U and the set of unperturbed molecular orbitals by χ_i, each EDO is given by,

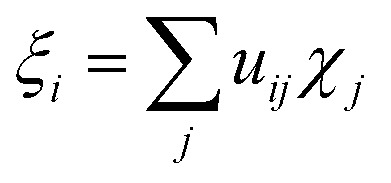6

These functions are conceptually similar to the deformation natural orbitals (DNOs)³⁸ or the natural orbitals for chemical valence (NOCVs),^39–41 employed to study the bond formation in complexes and covalent intramolecular interactions, respectively, and the natural transition orbitals,⁴² extensively applied to analyze the orbital contributions in electronic transitions. In this case of EDOs, they represent the eigenchannels for the electrically induced electron transport in molecules.

EDOs can be grouped in pairs of eigenfunctions with the same absolute eigenvalue but opposite sign. Positive and negative EDOs of a given pair, ξ⁺_k and ξ⁻_k, are, respectively, electron and hole functions within the same electron transport channel, which is mathematically represented by the 2 × 2 matrix Θ_k,

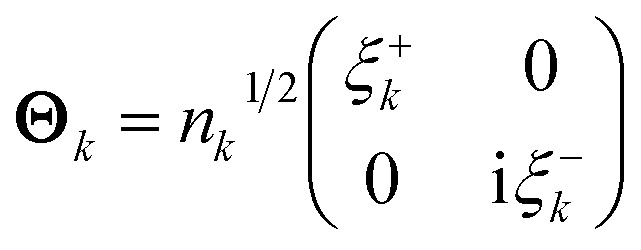7

Thus, the total electron deformation density can be obtained from the traces of the Θ_k matrix products,

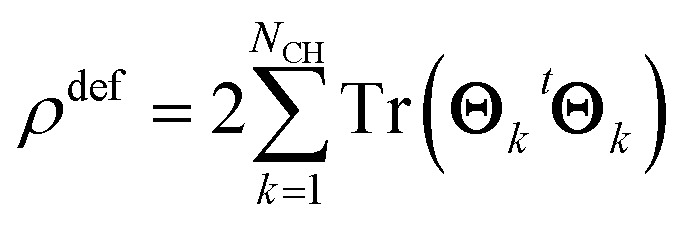8

Previous eqn (2)–(4) and (8) lead, after some algebraic manipulations (see ref. 34 for details), to the following expression for the electric conductance,

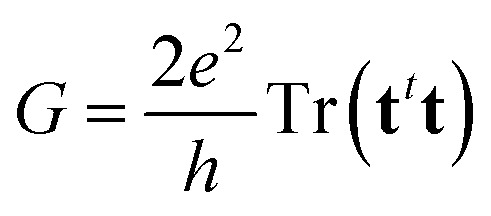9

with the elements of the matrix t given by,

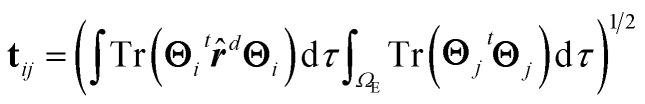10

In eqn (10), r̂^d represents the position operator scaled to the distance, d, between the two points where the bias voltage is applied and the second integral on the rhs is restricted to the electrode region.

Since the EDOs are constructed as linear combinations of MOs, the role played by occupied and virtual states on the electron transport can be evaluated. For instance, the amount of electrons promoted from valence to conduction bands upon the electric perturbation can be obtained,¹⁴ and simple orbital symmetry rules for the formation of transmission channels can be inferred.³⁴

Another appealing feature of using EDOs is that electron and hole densities associated to a given transmission channel can be represented in real space. This provides, as will be shown in the next section, a visual tool to understand the conducting/insulating character of molecular wires by means of the electron and hole density distributions along the transport region.

2.2. Electrical conductivity from ground state properties

A ground state account of electrical conductivity was provided by Kohn⁴³ and reformulated by Resta^44,45 in what it is known as the modern theory of polarization. Succinctly, the localization properties of the wave function of conductors and insulators differ in an essential way, quantified through the so-called localization tensor (LT or λ):

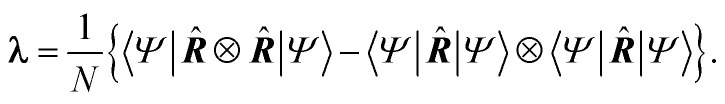11

This object diverges in the thermodynamic limit for conductors and converges for insulators. Since electron localization/delocalization lies behind all chemical intuition regarding the nature of electrical conductivity, a link between the LT and chemical concepts should exist. This was reported recently⁴⁶ by partitioning the LT in real space into intra- and inter-atomic contributions. It is the decay rate of the interatomic terms that may render the global LT divergent. Even more interestingly, at large distances these interatomic contributions scale as,

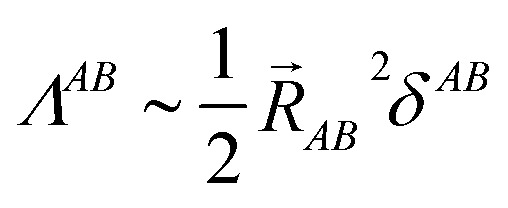12

where A, B are two atoms, R_AB their separation, and δ^AB is their delocalization index (DI),⁴⁷ the real space analogue of the standard covalent bond order. For a one-dimensional chain, for instance, δ^AB must decay faster than R⃑_AB² for the system to be an insulator. Bond orders become in this unexpected way important actors in the chemical understanding of molecular conductivity.

The delocalization index measures the number of electrons that delocalize between two regions through a double domain-restricted integration of the exchange–correlation density, ρ_xc(r₁, r₂) = ρ(r₁)ρ(r₂) − ρ₂(r₁, r₂), where ρ(r₁) is the standard electron density at point r₁ and ρ₂(r₁, r₂) is the pair density:

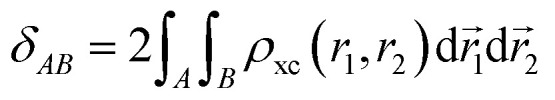13

DIs can be obtained once a partition of the space into chemically meaningful fragments is achieved. This is a full discipline in its own, and over the years many recipes have been proposed. In some formulations, like in the quantum theory of atoms in molecules (QTAIM), space is partitioned exhaustively using the topology induced by the gradient field of the electron density scalar. This partition, proposed and developed by Bader and coworkers,⁴⁸ has deep theoretical foundations, and is widely used. There are nevertheless many other proposals, both exhaustive and fuzzy.⁴⁹ Whenever the interatomic distance R_AB is large enough, the DIs obtained from most of these methods tend to the same value, although the computational cost does not. This is the reason why a very fast, otherwise criticizingly partition like Mulliken's can be safely used to obtain long-range delocalization indices. We will take profit of this trick here.

Even further simplifications are possible if a lattice Hückel (or tight binding) approach is used. This is equivalent to a condensation of the physical space into the lattice positions. In this framework, tight binding orbitals ϕ_μ are expanded over the primitive functions at lattice sites i as 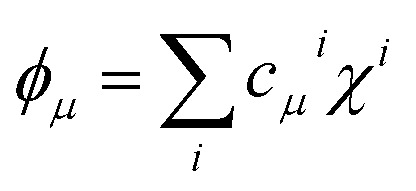, and the DI between sites i and j may be trivially shown to be

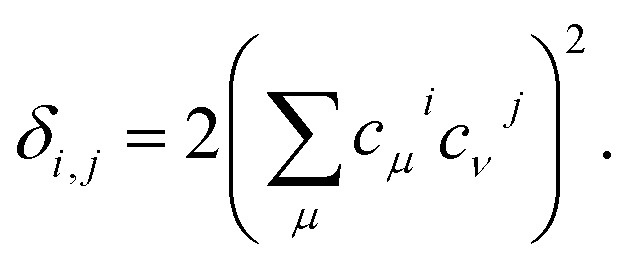14

Two-center DIs are used widely in high-level computational molecular chemistry, but have also found their way to fill the language gap between the chemical and physical languages when applied to models. For instance, it has been shown^50,51 that DIs decay exponentially for insulators and in a power-law manner for metals, and this relation is analytical in the case of tight binding (or Hückel) models.

2.3. Electron delocalization in one-dimensional models

As we will show, many of our results become easy to rationalize from the behavior of extremely simple one-dimensional models. Since electrical conductivity in molecular junctions is basically a one-dimensional problem, it is natural to turn back to polyacetylene, one of the most intensely studied conducting polymers,^25,52 and to the Nobel prize winner Su, Schrieffer and Heeger (SSH) tight binding model that first explained many of its properties. It starts with a Hückel type parameterization where only one p orbital ϕ per carbon atom (or lattice site) is allowed. In the simplest bond equalization regime with all C–C distances equal, only two parameters are needed to describe the effective one-electron Hamiltonian: the diagonal (on-site energies) terms H_ii = α = 〈ϕ_i|H|ϕ_i〉 and the intersite couplings, which are only allowed between first neighbors: H_i,i+1 = t = 〈ϕ_i|H|ϕ_i+1〉. These are also called the hopping constants. The tight binding solution is analytical and easy to take to the infinite n limit.⁵⁰ The delocalization indices between sites i and j for a chain with n sites turn out to be

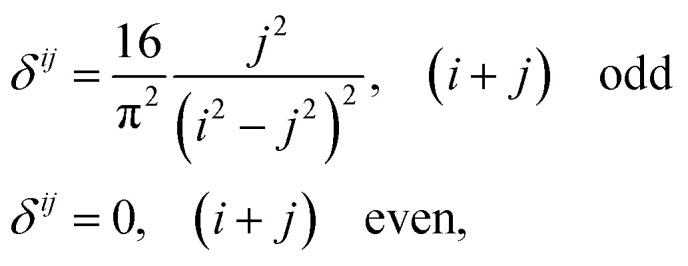15

and the HOMO–LUMO gap closes as

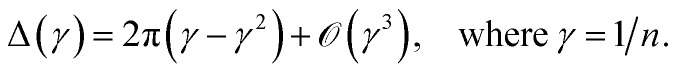16

Bond equalized infinite chains are metals with DIs between sites that decay as R², in agreement with the results obtained from the LT. The vanishing of the DIs for i + j even is only valid in this simple model, but sophisticated calculations keep showing large DI oscillations.⁵⁰ Notice that the power-law (not exponential) decay of the DI is an indication of long-range exchange-channels, see below.

Since polyacetylene shows bond alternation, a better yet simple model is easily constructed by doubling the unit cell, i.e. by considering two carbon atoms in the repeating unit, C_a and C_b. In this way we may introduce two different nearest-neighbor interactions t and t′,

t = 〈ϕ_i,a|H|ϕ_i,b〉, t′ = 〈ϕ_i,b|H|ϕ_i+1,a〉. 17

By altering the t, t′ values we can tune the strength of the two different C–C interactions. Although the problem is not analytical anymore, numerical solutions are straightforward. One can show that whenever |t − t′| ≠ 0 the gap is non-zero and the chain is an insulator.

However, a surprise arises, since two topologically distinct classes of solutions appear when t > t′ and when t < t′. In the first case the occupied manifold is separated by a simple gap from the virtual manifold. This corresponds to the C C–C … chemical motif, with a first double bond (t) followed by a single bond (t′ < t), and is called the trivial class (or phase). All the occupied molecular orbitals are canonically delocalized, with DIs showing an exponentially damped alternating pattern. Interestingly, when the situation is reversed and t < t′, which corresponds to the C–C C–… motif, a pair of non-bonding molecular orbitals, with energies tending to zero in the n → ∞ limit appear in the gap. These states are exponentially localized at the edges, and are called edge states. Their presence is topologically protected, in the sense that they remain unless some symmetry of the system is broken, resisting lattice distortions, doping, etc. This is the topological phase, and the system is now called a topological insulator (TI).⁵³ Only through closing the gap, i.e. by passing through the metallic state, can a trivial system be transformed into its topological counterpart or vice versa.

3D topological insulators have become the subject of intense research, thanks to their unusual conducting behavior: topologically protected conducting surfaces and insulating bulks. They promise a new generation of materials for advanced electronics.⁵⁴ It is particularly important for our purposes that one can inject charge into one end of a TI and extract it from the other end in a quantized way trough a process called charge pumping.⁵³ This exploits the protected character of the localized edge states. An important insight is that charge pumping involves in the case of molecular junctions the polarized structures already defined which control the behavior of a junction in the presence of an electric field. As we will show, this links the conductivity properties of anti-ohmic molecular junctions with the delocalization behavior of TIs.

DIs in the SSH model can be obtained by numerical diagonalization of the model Hamiltonian and direct application of eqn (14). While the bulk DIs in the TI phase do not differ essentially from those of the trivial one, the edge to edge delocalization does. Whenever the two edge states are appropriately entangled the DI between the edges becomes much larger in the TI phase than in the trivial insulator. This provides a link between the primary transport eigenchannel and the edge states of a TI.

3. Results

3.1. Anti-ohmic transport in oligophenyl chains

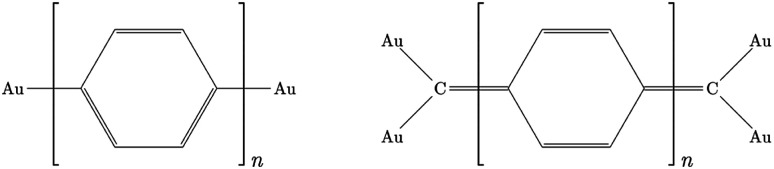
The different electron transport ability observed in oligophenyl chains attached to gold contacts and subjected to finite bias voltages has been previously investigated in a theoretical context.¹⁶ Two different junctions differing in the molecule-metal contacts were evaluated, named pP and pX2 in Fig. 1, the former being a simple chain composed by phenyl rings attached covalently to one gold per side, and the latter, the same chain but with terminal methylene groups. Due to the computational demands of the largest chains studied in this work, we have explored the properties of these junctions using this simple model for the metal contacts, which includes only the contact atoms. In a previous study,³⁴ the effect of different models and different linkers for the gold electrodes on the electron transport of pX2 and pP chains was investigated. The results showed that, even though the total electric conductance may change, the relative values between pX2 and pP chains do not change significantly. DFT calculations of the pX2 structures showed an unexpected increase in the electric conductance as the number of phenyl units in the chain (n) increased from 1 to 5 (anti-ohmic regime).¹⁶ Conversely, the common decrease of the electric conductance with the conductor length was found in pP structures. As discussed in the Introduction section, this behavior was explained using a simple VB model. In this model the strong electron delocalization within the phenyl rings in pP, evidenced by significant multicenter electron delocalization and torsional angles between neighbor rings, is partially destroyed upon the external electric perturbation, whereas the weaker electron delocalization within the phenyl rings in pX2, evidenced by smaller multicenter delocalization and torsional angles, is reinforced upon the perturbation. This disruption/reinforcement of the electron delocalization in pP/pX2 was supported by the changes observed in the multicenter electron delocalization and torsional angles upon the application of an external voltage.

Fig. 1. Molecular junctions with pP (left) and pX2 (right) like linker.

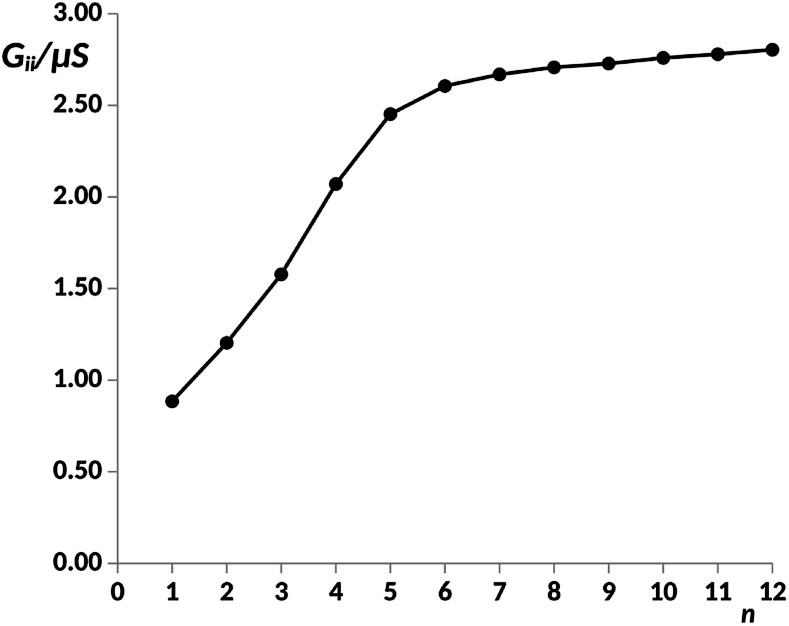
In order to explore the limit of the anti-ohmic regime in pX2, herein, the analysis of the electron transport properties was extended to structures containing up to 12 phenyl units. The same level of theory previously chosen was employed in this study, obtaining the full geometry optimizations and wave functions with the density functional theory (DFT) at the B3PW91/LANLD2Z level as implemented in the Gaussian 09 program.⁵⁵ The obtained values for the electric conductance under a bias voltage of 2 V are collected in Fig. 2, these conductance values and their corresponding transport channels were obtained using an own Fortran code.³⁴ This is a proper voltage value, since larger voltages are unfeasible for experiments using molecular junctions, and smaller ones force the use of quite small cutoffs for representing the transmission channels. Since for pX2 chains most of the conductance corresponds to the main transmission channel, in Fig. 2 only the conductance corresponding to this channel is represented against n (number of phenyl units).

Fig. 2. Electric conductance in the main transport channel, G_ii, in μS, under a bias voltage of 2 V vs. number of phenyl units, n, in the pX2 chain as represented in Fig. 1. Data for n = 1–8 taken from ref. 34.

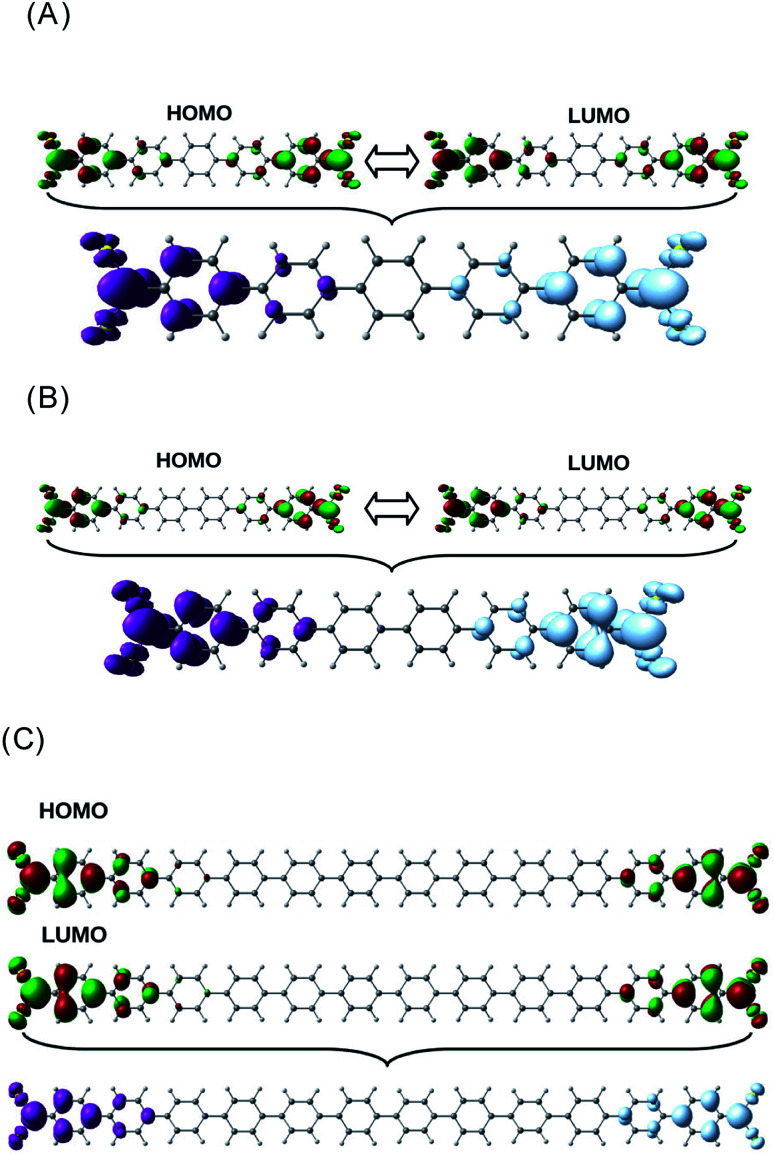
As it can be observed, the G vs. n plot in pX2 shows a remarkable change of trend around n = 6. For n < 6 the conductance displays a sharp increase with the number of phenyl units, however, it can be observed that the conductance rise becomes really slight for n > 6, reaching an almost constant value. Visualizing the transmission channels one can get relevant chemical information. The main channel is formed by the pair of EDOs with the largest absolute eigenvalues, which in turn are constructed as linear combinations of close in energy occupied and virtual molecular orbitals.^34,37 In Fig. 3(A), the channel is represented for the pX2 structure with n = 5, where the mixed occupied and virtual orbitals correspond mainly to the HOMO and LUMO. This representation shows that the electron and hole densities are mainly localized at the ends of the junction, involving the outer rings of the chain and the gold contacts, although there is also non-negligible contributions on the inner rings.

Fig. 3. Distribution of the HOMO–LUMO orbitals and the main transmission channel in the pX2 chain as represented in Fig. 1 with n = 5 (A) n = 6 (B) and n = 12 (C). The isosurface values were 2.5 × 10⁻² for the HOMO–LUMO orbitals and 2.5 × 10⁻³ for the transmission channels. (A) Taken from ref. 16.

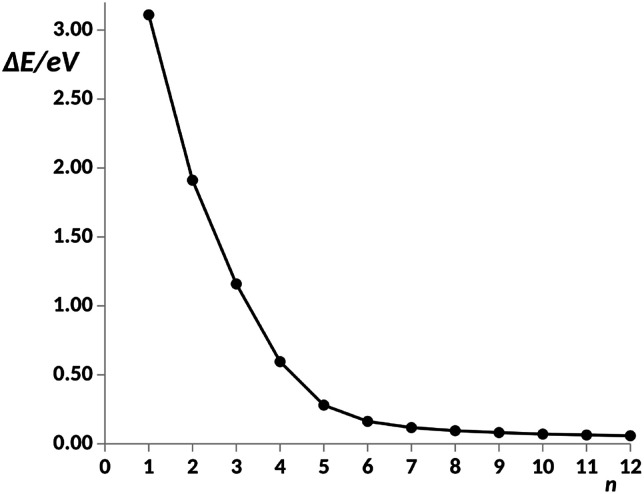
For n = 6, the main transmission channel is even more localized at the ends of the junction (see Fig. 3(B)), allowing for an almost direct electron transfer between the contacts. The same distribution is found when increasing the chain length, this is the case of the n = 12 structure, as shown in Fig. 3(C), where the localization of the main transmission channel at the ends is clearly enhanced. This subtle increase of channel localization at the contacts may explain the slight increase of the conductance with the number of phenyl units for larger chains. In order to shed some light on the change of trend mentioned above, the energy gap between the main occupied and virtual MOs involved in the channel has been represented against the number of phenyl units in Fig. 4. It can be observed in this plot how the gap decreases very quickly as the number of rings increases from n = 1 to n = 6. Once n = 6 is reached, the energy gap is almost null, therefore, from this point the conductance displays an almost constant value, which only changes due to a slight decrease in ΔE. Then, for long chains, the HOMO–LUMO orbitals are almost degenerate and strongly localized at the contacts, allowing for an optimal electron transfer. Notice that the gap closing is already contained in the tight-binding model as in eqn (16). Whether the true behavior leads to a true zero gap in the thermodynamic limit or not is of no relevance here.

Fig. 4. Energy gap, ΔE, in a.u. between the main occupied and virtual orbitals involved in the electron transfer vs. number of phenyl units, n, in the pX2 chain as represented in Fig. 1. Data for n = 1–8 taken from ref. 34.

3.2. Long-range exchange channels

The idea of a direct electron transfer between molecular ends, without assistance of the intermediate atoms, recalls the concepts of hopping and superexchange extensively employed to explain REDOX processes in large biological systems. The superexchange mechanism requires the electron charge to be localized at the donor and acceptor centers, as happens in pX2, so that a strong direct long-range electron exchange may occur. On the contrary, hopping needs from transmission channels with non-negligible inner ring contributions. These disappear as n increases. The electron exchange between two centers in a molecule can be accounted for by the electron delocalization index, DI, which, as mentioned in the methodological section, is obtained from the integration of the exchange–correlation density within the corresponding centers. Non-vanishing long-range DIs signal direct non-mediated exchange, the so-called superexchange. We have evaluated the electron delocalization between the phenyl rings along the pX2 chains, the DIs of one of the terminal rings with the rest are collected in Table 1. Ring–ring DIs measure the total delocalization of all the atoms of one ring with all the atoms of the other. As said in the methodology, the Mulliken partitioning scheme is suitable for long-range delocalization indices, then, the calculation of the DIs was performed under this scheme as implemented in the NDELOC Fortran code (available upon request). The values evidence the role played by superexchange or long-range electron delocalization in the electron transport as the chain length increases. Unexpectedly, the electron delocalization between terminal rings rises as the distance between them increases. Concurrently, the electron delocalization between a terminal ring and the intermediate rings drops to zero more rapidly in longer chains. Thus, the mechanism evolves from hopping to long-range superexchange as the length of the chain increases.

DIs of a terminal ring, R₁, with the rest of rings, R_i (2 ≤ i ≤ n), of pX2 chains as represented in Fig. 1 with n = 3–12.

	n = 3	n = 4	n = 5	n = 6	n = 7	n = 8	n = 9	n = 10	n = 11	n = 12
R1–R2	1.5229	1.3835	1.2841	1.2457	1.2336	1.2291	1.2276	1.2268	1.2268	1.2263
R1–R3	0.1508	0.0823	0.0296	0.0130	0.0093	0.0083	0.0081	0.0079	0.0079	0.0078
R1–R4		0.1307	0.0486	0.0103	0.0024	0.0010	0.0007	0.0006	0.0006	0.0006
R1–R5			0.1414	0.0405	0.0074	0.0013	0.0003	0.0001	0.0001	0.0001
R1–R6				0.1477	0.0381	0.0066	0.0011	0.0002	0.0000	0.0000
R1–R7					0.1500	0.0373	0.0065	0.0010	0.0001	0.0000
R1–R8						0.1499	0.0370	0.0063	0.0010	0.0001
R1–R9							0.1500	0.0368	0.0063	0.0009
R1–R10								0.1502	0.0368	0.0062
R1–R11									0.1501	0.0367
R1–R12										0.1502

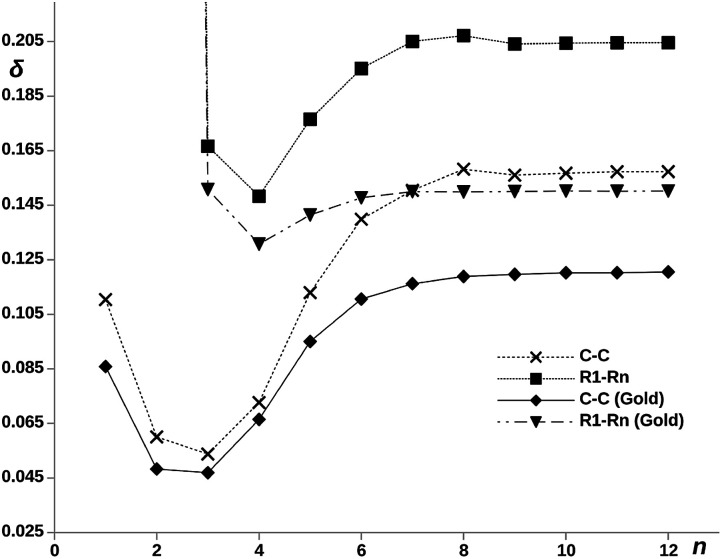
On the other hand, the electron delocalization between the two terminal rings is represented against n in Fig. 5, noted as δ_R1–Rn (Gold), for the pX2 chains. The value obtained for the chain with n = 2 is not shown as the direct covalent contact between the bridge atoms leads to a much larger value of the DI compared to the rest of chains. The plot shows an increase of the delocalization between terminal rings with the number of units, reaching a constant value for n ≥ 6. It is remarkable how this plot matches that obtained for the conductance. The explanation is straightforward, as the MOs involved in the main transmission channel (the frontier orbitals when n > 2) get more localized at the terminal rings, the electron exchange channel connecting them is reinforced, giving rise to the perfect conditions for a direct electron transport between them.

Fig. 5. DI, δ, between terminal rings, denoted as R₁–R_n, and the methylene carbons denoted as C–C with and without gold electrodes vs. number of phenyl units, n, in the pX2 chains. δ_R1–R2, being a direct covalent interaction between rings, is out of the bounds of the scale and has been left out of the plot.

The influence of the covalent metallic links on the long-range electron exchange through the organic chain has been also analyzed. Therefore, DIs were recalculated for the pX2 structures shown in Fig. 1 but substituting the gold atoms by hydrogens. In addition to the calculation of the electron delocalization between terminal rings, DIs were calculated between just the methylene carbons directly attached to gold/hydrogen. Since the rings contain more than one atom, we must expect in general larger ring–ring than atom–atom DIs. The results obtained for chains with n = 1–12 are collected in Fig. 5. As can be observed, the significant long-range electron exchange between terminal rings displayed by chains including gold is reinforced in the hydrogenated chains. Moreover, when the electron delocalization between methylene carbons instead of terminal rings is compared, the trends are even more unequivocal, which is a direct result of orbital localization at the chain ends. The effect of the terminal gold atoms, which spread the transmission channels in an out of phase manner, is clearly deleterious for direct superexchange. This effect is so large for big n values that the single-atom ungolded C–C DI becomes even larger than the ring–ring golded DI. On the other hand, one can also observe the differences in the HOMO–LUMO orbital localization between hydrogenated and golded pX2 chains in the ESI.† The same localization of the orbitals at the edges is observed for both chains. This is an evidence that the superexchange transport is an intrinsic property of the molecule, independent of the metallic link.

This heuristic relationship between electron delocalization and conductance established above has, however, a solid theoretical foundation. The bridge between both magnitudes is the LT. As discussed in the theoretical section, the LT can be partitioned into intra- and interatomic contributions. The mathematical relationship of LT with electric conductivity and electron delocalization explains why the electron transfer is favored when the donor and acceptor centers are connected by direct electron-exchange channels. In the orbital picture extensively employed in the theory of molecular conductors and semiconductors these channels are constructed from occupied and virtual MOs.

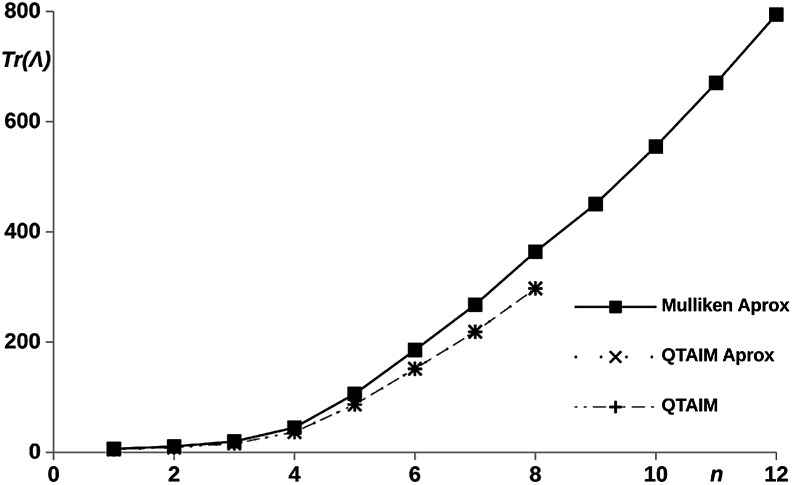
With the aim of understanding the connection between the edges of the molecule (methylene carbons), the interatomic terms of the LT were evaluated within the quantum theory of atoms in molecules (QTAIM) and the Mulliken scheme.⁴⁸ In order to reduce the computational cost, the partition of the LT was performed only for the hydrogenated chains. The results are shown in Fig. 6, we can observe how the QTAIM values calculated with the explicit definition of the LT⁵⁶ (eqn (11)) fully overlap with those obtained with the approximated expression give by eqn (12). This results guarantees the use of eqn (12) in larger chains. In order to make the calculation cheaper, eqn (12) was applied to all the proposed chains n = 1–12 using Mulliken DIs. As showed in Fig. 6, we can observed how, although the Mulliken–QTAIM curves do not overlap, their shapes are quite similar, and show two clear tendencies, where for n = 6 a almost constant value of δ_C1–Cn is reached, making the LT variable only with the centers distances. Then, these results evidence a clear relation of the delocalization between the centers and the electron transport ability, allowing an intuitive analysis of the electric conductance of a system with electron delocalization measures.

Fig. 6. Trace of the LT calculated for the methylene carbons with the Mulliken and QTAIM atomic partitionings, using eqn (11) and (12)vs. number of phenyl units, n, in the pX2 chains.

3.3. One-dimensional topological insulators

These unusual high conductances have been previously observed in other conjugated polymeric chains. This is the case of polyacetylene chains, whose conducting properties are explained by the SSH model, intimately linked to TIs. Recently, Pinilla et al.²⁹ used the Hückel formalism to establish a bridge between the physical concepts behind the theory of TIs and key concepts of the chemical bonding theory. A brief review of the chemical view of TIs is found in the ESI.†

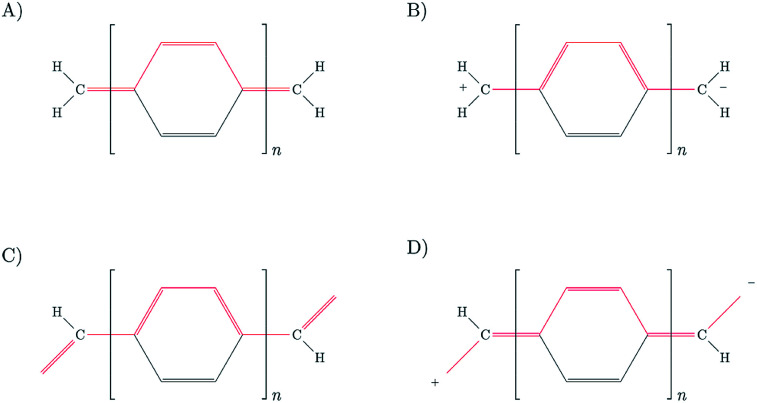
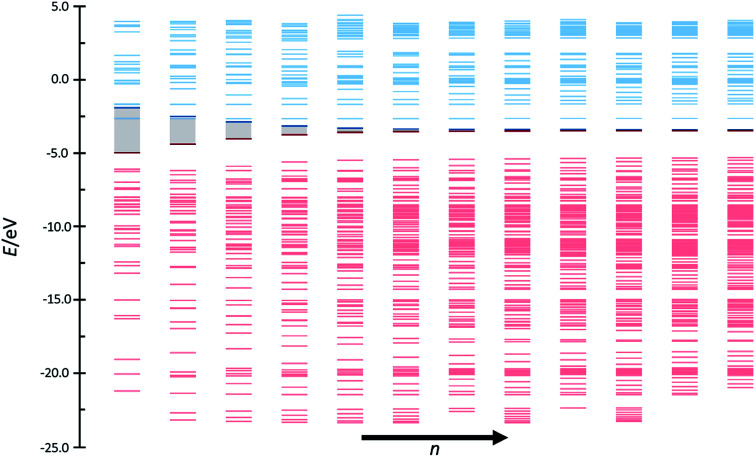
The analogies between the behavior observed and discussed in the previous subsections for pX2 chains and that predicted by the Hückel model for polyacetylene are more than meaningful. In fact, pX2 and polyacetylene chains can be directly compared considering the former as a main polyacetylene structure of alternating trans–cis isomery (highlighted red in Fig. 7) where bridging ethylene units have been incorporated to this main structure (drawn in black in Fig. 7). For the pX2 chains with n < 6, the resonant structure shown in Fig. 7(A) prevails over that shown in Fig. 7(B), so that we are in the situation where t > t′. This situation leads to delocalized orbitals so as large energy gaps. However, as the chain length increases (n > 6) the resonant structure of Fig. 7(B), with a π-sextet on each phenyl ring, rapidly gets weight due to the extra stabilization provided by the formation of these aromatic rings. In this situation, the relative values of t and t′ are inverted and the frontier molecular orbitals tend to localize at the edges and the corresponding energy gap to reduce drastically. Distributions of the orbital energy levels represented in Fig. 8 for pX2 chains certainly confirm the expectations and allows identifying chains with n > 6 as one-dimensional TIs. This explains the shape of the electron transfer channels obtained by ab initio calculations, strongly localized at the terminal rings for n > 6, and the conductance and electron delocalization profiles previously discussed.

Fig. 7. Resonant forms of pX2 structures: (A) trivial, (B) topological and pP structures: (C) trivial, (D) topological. The main polyacetylene structures are depicted in red and the bridging ethylene units in black.

Fig. 8. Orbital bands of the phenyl pX2 structures as represented in Fig. 1 from n = 1–12. Red and blue colors represent occupied and virtual bands, respectively, whereas the occupied and virtual orbitals involved in the main transmission channel are represented by bold lines.

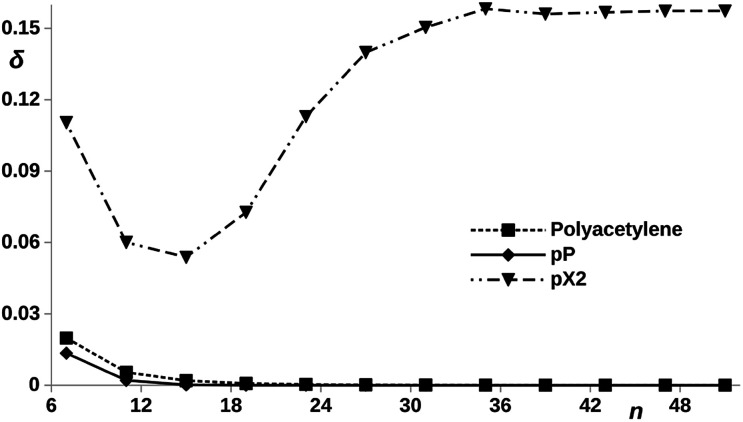
Now, let us compare the pX2 chains with a given number of carbon atoms in the main polyacetylene structure with real polyacetylene chains of the same length. Since the magnitude of the electron delocalization between the terminal methylene carbons is a direct measure of the frontier orbital localization at the edges, a representation of this electron delocalization vs. the number of carbon atoms may give us an idea of the length of the chain in which the TI character emerges. It is also interesting to check what happens when the bridging ethylene units are incorporated to the polyacetylene chain at positions where aromaticity stabilize the trivial case instead of the topological case. In such situation, the system is expected to behave as an insulator where the conductance decreases rapidly with the number of phenyl units. Fig. 7 represents the trivial and topological phases for pX2 and this new proposed chain, which corresponds to a pP chain with two terminal ethylene fragments. In Fig. 9, the electron delocalization between the terminal methylene carbons is represented vs. the number of carbons in the main polyacetylene chain for pX2, pP and polyacetylene. The plot is very clear about the strong TI character of pX2 chains with respect to the other two. Whereas in the former the electron delocalization starts to increase with the chain length relatively soon, it drops to zero in both pP and polyacetylene chains very rapidly and, as expected, the decay is more pronounced in pP, reaching a zero value at shorter lengths. This result is very relevant, even though pristine pX2 chains may not be stable experimentally, stable derivatives that keep similar electron delocalization patterns may be employed to construct chemically stable one-dimensional TIs to be exploited in the field of molecular electronics. Then, pX2 represents a model for the development of reliable one-dimensional TIs.

Fig. 9. DI, δ, between the outer carbon atoms vs. number of carbon atoms, n, contained in the polyacetylene (see ESI, Fig. S1†), pX2 and pP chains, as represented in Fig. 7.

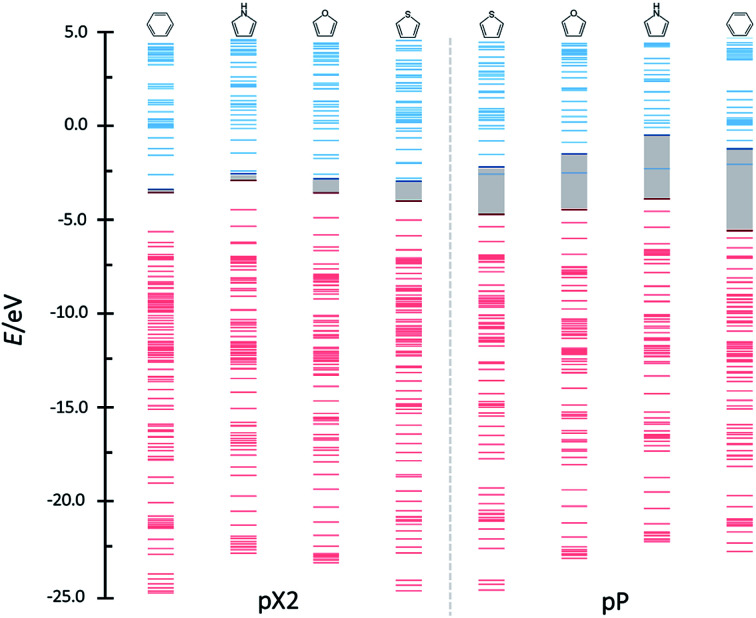
Above, the conducting properties of pX2 and pP and their TI character were related to the aromatic stabilization of the topological and trivial forms, respectively. Thus, it is reasonable to expect that tuning the aromaticity of the rings one may control the shift from trivial to topological forms in pX2. Since a remarkable feature of chains that behave as one-dimensional TIs is an almost zero HOMO–LUMO gap, the orbital energy diagrams for chains with n = 6 and formed by different aromatic rings are compared in Fig. 10. As can be observed, the HOMO–LUMO energy gap certainly increases as the aromaticity of the ring decreases in pX2, following the order phenyl < pyrrole < furan < thiophene. On the contrary, the inverse relationship is found in pP chains, which reflects the control exerted by aromaticity on the relative weight of trivial and topological forms.

Fig. 10. Orbital bands for the phenyl, pyrrole, furan and thiophene pX2 and pP like chains as represented in Fig. 1 with n = 6. Red and blue colors represent occupied and virtual bands, respectively, whereas the occupied and virtual orbitals involved in the main transmission channel are represented by bold lines.

3.4. Topological and trivial phases in a multireference scenario

The fact that HOMO and LUMO orbitals are so close in energy in the one-determinant solution given by HF or KS-DFT, points out the possible multireference character of pX2 like chains. In this section, the effect of multireference character on the formation of trivial and topological phases is analyzed using a simple model where the active space is described by frontier orbitals. Taking into account that remaining occupied and virtual orbitals are quite far in energy from the frontier orbitals when topological phase arises, such a reduced active space is a good approximation when n ≥ 7 in pX2 chains. Moreover, the electron delocalization between terminal methylene groups is mainly (almost exclusively) due to the HOMO orbital in the one-determinant picture since only this occupied orbital is concentrated at the methylene groups. As for the electron–hole delocalization obtained from the virtual orbital space, for the same reason as before, only the LUMO orbital contributes to the delocalization between methylene groups. Then, the electron delocalization in our model is very well described using only the density matrix within the active space.

The wave function in our model is formed by a linear combination of the six possible configurations depicted in Fig. 11. These are the configurations with two electrons occupying the HOMO orbital (H²), two electrons occupying the LUMO orbital (L²), and the electrons occupying different orbitals with different spin configurations (H^αL^β, H^βL^α, H^αL^α and H^βL^β). Taking into account spatial and spin symmetry, H² and L² may be combined to form two closed-shell singlet states (Ψ^S₁ and Ψ^S₂), whereas HL configurations give rise to an open-shell singlet (Ψ^S₃) and the three components of a triplet state (Ψ^T₄, Ψ^T₅ and Ψ^T₆). Introducing normalization conditions, only one coefficient, c, is required to represent the relative weight of configurations H² and L² in Ψ^S₁ and Ψ^S₂.

Fig. 11. Pictorial representation of all the possible configurations and states using an active space that includes only frontier orbitals.

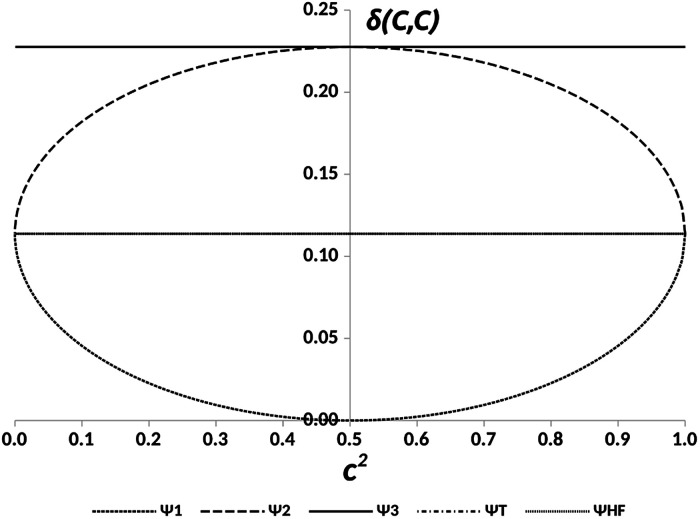
The representation of the electron delocalization in the four states against the square of the coefficient c using HF orbitals is shown in Fig. 12 for pX2 with n = 7. The delocalization indices of all these states can be found after straightforward algebra, see the ESI.† The plot in Fig. 12 reflects that when mixing of configurations H² and L² is null (c² = 0 or 1), the result is basically the one-determinant result. This is due to the fact that HOMO and LUMO orbitals are equally delocalized at the chain ends. As c² lies between the limit values, the electron delocalization decreases and increases for states 1 and 2, respectively. When mixing of configurations H² and L² is maximum (c² = 0.5), the electron delocalization in states 1 and 2 reaches minimum and maximum values, respectively, corresponding to trivial and enhanced topological phases. The label enhanced topological is introduced to distinguish with the topological phase in the one-determinant solution, where the electron delocalization is half reduced. On the other hand, according to the electron delocalization index, state 3 and the triplet state correspond to enhanced topological and trivial phases, respectively. In these cases, the value of the delocalization index in Fig. 12 is represented by a horizontal line as it does not depend on c.

Fig. 12. DIs between the methylene carbon atoms, δ(C, C), in the pX2 chain with n = 7 vs. the relative weight of the H² and L² configurations, c², for the states represented in Fig. 11 and the Hartree–Fock (HF) result.

From this model, one can predict that in a multireference scenario two trivial, and two enhanced topological phases arise, each of them represented by a different electronic state. The stability of these phases depends on the relative energies of the corresponding states.

The quantitative study of these states requires the application of ab initio multireference electronic structure methods, such as the complete active space self-consistent field method (CASSCF). However, besides the large computational demand of these calculations with respect to single reference, several convergence problems are arising when systems like pP and pX2 are subjected to external electric perturbations and simple metal clusters are included for the simulation of the electrodes. Thus, application of CASSCF to the study of the long-range superexchange mechanism, including calculation of electron delocalization indices and electric conductance using electron deformation orbitals, is currently in progress in our lab. Preliminary results at CASSCF(2,2)/6-31G(d,p) level carried out with Gaussian 09 (ref. 55) for the n = 7 hydrogenated pX2 structure (see Table 2), evidenced that the ground state is an insulator triplet state, X, corresponding to the Ψ^T state of the model. The lowest energy singlet state is the insulator state Ψ^S₁, (A¹). However, the second (A²) and the third (A³) excited states were found to be conductor states which correspond to Ψ^S₃ and Ψ^S₂, respectively. The DIs between the terminal methylene carbons are also collected for each state in Table 2. Herein, relying on the stated relation between electron delocalization and conductance a new scenario is obtained, where the conducting character correspond to excited states.

Energies and DIs between the terminal methylene carbons obtained at the CASSCF(2,2)/6-31G(d,p) level for the four different states of pX2 with n = 7.

State	Energy (a.u.)	δ C–C
X	−1684.94838	0.0000
A1	−1684.82707	0.0000
A2	−1684.62903	0.1724
A3	−1684.62902	0.1723

It can be inferred that the impact of the results presented above may be significant in anti-ohmic molecular wires, where a small HOMO–LUMO gap is expected. Thus, the model foresees the conducting character predicted by approaches based on single reference electronic structure calculations (DFT, HF or semiempirical Hückel-like methods), may be significantly affected by the interaction between ground and low-lying excited configurations. This indicates that, for instance, methodologies employed extensively in the study of the electron transport, such as the density functional non-equilibrium Green's function approach (DFT-NEGF), must be applied with care in highly conducting molecules characterized by small HOMO–LUMO gaps. This, on the contrary, is not applicable to the study of semiconductor structures with a remarkable gap.

4. Conclusions

The recent theoretical research on the modelling of conjugated anti-ohmic conducting wires at molecular scale has been substantiated on two equivalent qualitative ideas, namely, a large weight of polarized or diradical forms at the metal–molecule contacts within the ground state wave function of the molecule. The presence of these polarized or diradical forms has been related to well-known concepts in chemical bonding theory like bond alternation and aromatic stabilization. Thus, previous works concluded that these forms lead to a reversed bond alternation and an extra aromatic stabilization, and push the energy gap between frontier orbitals to negligible values.

In this work, we explore in detail the properties of these anti-ohmic molecular wires, using the paradigmatic example of oligophenyl chains as model. We scrutinize point by point the previous qualitative findings at quantitative level, employing rigorous tools derived from quantum theory. Herein, we have concluded that the extraordinary electron transport ability displayed by these anti-ohmic wires is driven by a long-range superexchange mechanism, not previously described, that surprisingly does not attenuate with the chain length. This mechanism is fundamentally associated to the localization of frontier orbitals at the metal-molecule contacts, which makes the large anti-ohmic wires to be conducting at these points but isolating in the bulk. This finding allows relating these anti-ohmic wires with one-dimensional topological insulator models like the Su–Schrieffer–Heeger. As far as we know, this is the first time that a link between concepts used in the theory of topological insulators and anti-ohmic behavior in molecular conductors has been put forward.

Moreover, replacing the phenyl units by other aromatic rings such as pyrrole, furan and thiophene, in this new topological insulator model, has revealed the control exerted by aromaticity in the transition from the trivial to the topological phase, leading to the polarized forms described in previous works. Since aromaticity is reinforced in the topological phase, the larger the aromaticity the faster this transition.

However, the very small HOMO–LUMO gap characteristic of anti-ohmic molecular chains at single-reference level, forces to reconsider the study of these systems at multireference level. A simple model using an active space restricted to frontier orbitals allows concluding that trivial and topological like phases certainly persist in a multireference scenario. The relative stability of each depends on the relative stability of the electronic states in which these phases appear. Preliminary calculations using CASSCF on the oligophenyl chains point out the topological phase and then, the anti-ohmic behaviour, occurs in electronic excited states only. It is necessary to extend this analysis to other recently proposed candidates to show reversed conductance/length trend. The analysis based on electron delocalization measures, rooted on the relation between localization tensor, conductivity and delocalization indices, may serve to check the electron transport ability at multireference level, where explicit calculations of the molecular electric conductance are not readily available. In this sense, this work is also intended to serve as a guideline for experimental and theoretical research on the design of future candidates for anti-ohmic molecular wires. Experimental efforts must be guided by solid theoretical predictions. The theoretical tools provided herein allow characterizing molecular wires as anti-ohmic or not without restriction to single reference models.

Overall, our results show that anti-ohmic electron transport may be deeply related to the topological properties of the electronic states of the molecular junction. By relating those properties to well-known chemical bonding descriptors, which can be taylored through standard techniques in rational chemical design, we believe that a possible new collaborative avenue mixing chemists and physicists opens to build anti-ohmic devices. Some clouds over this horizon appear, though. Our analysis also evidences that anti-ohmic behavior might be an excited state, and not a ground-state property. If this finding is finally found to be common-place, a warning sign over density functional theory simulations, widely spread in the field, should be taken into account. The answer to the question posed in the title of the paper is a possibly yes, but possibly not exactly as expected up to now.

Conflicts of interest

There are no conflicts to declare.