Thermal Hall effect in insulating quantum materials

The emerging field of quantum materials involves an exciting new class of materials in which charge, spin, orbital, and lattice degrees of freedom are intertwined, exhibiting a plethora of exotic physical properties. Quantum materials include, but are not limited to, superconductors, topological quantum matter, and systems with frustrated spins, which enable a wide range of potential applications in biomedicine, energy transport and conversion, quantum sensing, and quantum information processing.

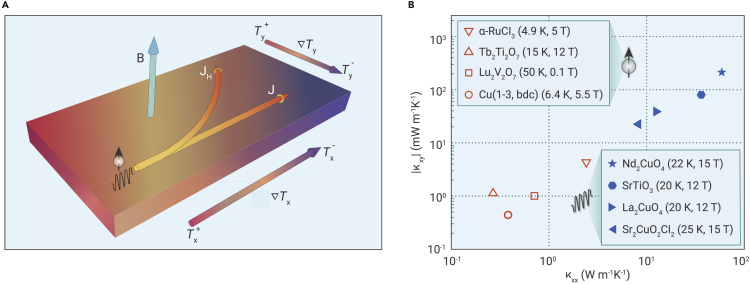
Thermal transport measurement is a powerful method to uncover the unique physical properties in quantum materials. Compared with electrical methods, an apparent advantage of thermal transport measurement is that it can detect charge-neutral excitations, such as lattice vibrations (phonons) and spin excitations. In particular, the thermal Hall effect has become an effective probe of heat carriers due to its sensitivity to the chirality of quasi-particles in the presence of a magnetic field (here, chirality refers to the handedness of heat carriers such as the direction of atomic rotations and spin precessions). In insulators where conduction electrons are absent, the thermal Hall effect provides an exclusive access to the physical nature of charge-neutral heat carriers. The thermal Hall effect is a transport phenomenon in which a longitudinal thermal gradient $\nabla T_x$ induces a transverse heat flow $J_{\text{H}}$ (hence, establishing a transverse temperature gradient $\nabla T_y$) under a magnetic field applied along the third vertical direction ($\text{B}$), as illustrated in Figure 1A. The thermal Hall conductivity (${\kappa }_{xy}$) is obtained by the formula

$${\kappa }_{xy}={\kappa }_{yy}\frac{\Delta T_y/W}{\Delta T_x/L},$$

where ${\kappa }_{yy}$ is the longitudinal thermal conductivity along the y axis, $L$ is the distance between the thermometers placed along the x axis where $\Delta T_x$ is measured, $W$ is the sample width, $\Delta T_x=T_x^{+}-T_x^{-}$, and $\Delta T_y=T_y^{+}-T_y^{-}$. If the heat conduction is isotropic, the following formula is satisfied:

$${\kappa }_{yy}={\kappa }_{xx}=\frac{QL}{\Delta T_{x}Wt},$$

where ${\kappa }_{xx}$ is the longitudinal thermal conductivity along the x axis, $Q$ is the heater power, and $t$ is the sample thickness. In this editorial, we introduce selected recent progress of experimental studies on ${\kappa }_{xy}$ in oxides and two-dimensional (2D) magnetic materials (Figure 1B).1, 2, 3, 4, 5, 6, 7 The mechanisms and insights behind the experimental observations are discussed.

Figure 1.

Thermal Hall effect of charge-neutral excitations

(A) Schematic illustration of the thermal Hall effect.

(B) Measured ${\kappa }_{xy}$ as a function of ${\kappa }_{xx}$ for several quantum materials, in which solid and open symbols represent ${\kappa }_{xy}$ due to phonons1, 2, 3 and spins,4, 5, 6, 7 respectively.

Thermal Hall effect of phonons

The thermal Hall effect of phonons was first discovered in the paramagnetic insulator Tb₃Ga₅O₁₂ by Strohm et al. in 2005,⁸ which was later explained by resonant skew scattering of phonons by rare-earth impurities. This is an extrinsic mechanism referring to the asymmetric scattering of phonons due to the coupling between the quadrupole moment of Tb³⁺ cations and the lattice strain, resulting in a directional motion of the phonons deviating from their original path and generating a transverse heat flow. In general, the iconic signature of the strong resonant skew scattering by rare-earth impurities is a finite increase in ${\kappa }_{xy}$ accompanied by an enormous reduction of ${\kappa }_{xx}$.

Recently, a large phononic ${\kappa }_{xy}$ has been detected in the nonmagnetic insulator SrTiO₃, which is a quantum paraelectric, and has been interpreted by another extrinsic mechanism: scattering of phonons by structural domain boundaries.¹ Compared with another quantum paraelectric KTaO₃, whose ${\kappa }_{xy}$ is almost negligible, the authors inferred that the sizable ${\kappa }_{xy}$ in SrTiO₃ is not a generic feature of quantum paraelectrics. Since SrTiO₃ undergoes an antiferrodistortive structural transition at 105 K, while KTaO₃ always remains cubic, the large ${\kappa }_{xy}$ in SrTiO₃ is closely tied to the polar domain walls resulted from the structural transition.

Apart from these extrinsic mechanisms, intrinsic mechanisms can also play a critical role in ${\kappa }_{xy}$. A prominent intrinsic mechanism is the Berry curvature, which arises from the nontrivial phase relation between quantum states in the momentum space. The Berry curvature acts as an artificial magnetic field generating lateral drift velocities to phonons.

Another intrinsic mechanism for ${\kappa }_{xy}$ pertains to the coupling between phonons and spins. For example, large negative phonon Hall signals with $\Delta T_y<0$ have been observed in some cuprates at low temperatures inside the pseudogap phase,² suggesting the presence of neutral excitations that acquire chirality owing to the interaction with the electronic state in the pseudogap phase of cuprates. Through a comparative study of La₂CuO₄, Nd₂CuO₄, and Sr₂CuO₂Cl₂, potential extrinsic mechanisms of the thermal Hall effect have been ruled out.³ Although these three cuprates have different crystal structures and cations, both the ratio ${\kappa }_{xy}/{\kappa }_{xx}$ and their ${\kappa }_{xy}$ exhibit a high similarity. Therefore, in these cuprates, phonons coupling to the intrinsic spin excitations of the common CuO₂ planes was found to be the dominant mechanism whereby phonons acquire chirality. These results show that ${\kappa }_{xy}$ is an effective probe for subtle phonon–spin interactions in these cuprates.

Thermal Hall effect of magnons

Besides phonons, pure spin excitations can serve as heat carriers as well. But different from phonons, they carry quantized spin angular momenta, which, by definition, naturally come with chirality. When spins couple to momenta, their intrinsic chirality will generate a transverse motion of heat carriers, leading to a thermal Hall effect of spins. In general, measuring ${\kappa }_{xy}$ can reveal various spin excitations in insulating quantum materials. Among these, what has been particularly interesting is the thermal Hall effect of magnons—the quanta of collective precessions of magnetic moments in magnetically ordered materials. First predicted by Katsura et al.,⁹ the thermal Hall effect of magnons is believed to be a magnonic counterpart of the phenomena associate with Berry curvature, similar to the intrinsic thermal Hall effect of phonons. The Dzyaloshinskii–Moriya interaction can act as an effective spin–orbit coupling for magnons, inducing non-zero Berry curvature in the magnonic bands.

The Magnon Hall effect has been observed experimentally in pyrochlore⁴ and kagome⁵ lattices without inversion center. Onose et al. observed a weak but finite ${\kappa }_{xy}$ signal in the ferromagnetic insulator Lu₂V₂O₇ with a pyrochlore lattice in 2010.⁴ The crystal structure of this material can be represented as a stacking of alternating kagome and triangular lattices along the $\left[111\right]$ direction. The authors were able to rule out the electron and phonon origins for the observed ${\kappa }_{xy}$. As such, the observation corroborates the thermal Hall effect of magnons. Later, a finite ${\kappa }_{xy}$ was found in the kagome magnet Cu(1–3, bdc), which is consistent with the predicted magnon Hall effect due to the Berry curvature.⁵ In particular, the observed sign reversal of ${\kappa }_{xy}$ with changes in temperature or magnetic field is associated with the sign alternation of the Chern flux between magnon bands, confirming the magnon origin for the observed ${\kappa }_{xy}$.

Besides magnons, the thermal Hall effect can also be caused by other charge-neutral spin excitations. Hirschberger et al. investigated ${\kappa }_{xy}$ in the pyrochlore compound Tb₂Ti₂O₇,⁶ which is a frustrated magnet remaining disordered even at the lowest attainable temperatures. In this material, ${\kappa }_{xy}$ rapidly falls after peak magnetic field, which is contradictory to the phonon skew-scattering mechanism. The short correlation length and constant ${\kappa }_{xy}/T$ at low temperatures also exclude the magnon origin. Therefore, neutral spin excitations subject to a Lorentz-like force must be the origin of the observed ${\kappa }_{xy}$.

$\alpha$-RuCl₃ is an insulating quantum magnet with a dominant Kitaev interaction on its 2D honeycomb lattice. Recently, Kasahara et al. found that applying a magnetic field can destroy the long-range magnetic order and induce the quantum spin liquid ground state in $\alpha$-RuCl₃.⁷ In the low-temperature regime of this ground state, the 2D thermal Hall conductance reaches a plateau as a function of the applied magnetic field. The quantization value was found to be half of the 2D thermal Hall conductance of the integer quantum Hall effect, which is attributed to the presentence of charge-neutral Majorana fermions (ie, particles that are their own antiparticles). These experimental findings are consistent with theoretical predication, which suggests fractionalization of spins into itinerant Majorana fermions and Z₂ fluxes in Kitaev quantum spin liquids. However, a recent study by Czajka et al. indicated that the ${\kappa }_{xy}$ in $\alpha$-RuCl₃ is not half-quantized.¹⁰ Therefore, the presentence of charge-neutral Majorana fermions in $\alpha$-RuCl₃ is still an open question.

Summary and outlook

The thermal Hall effect, by virtue of its sensitivity to the chirality of heat carriers, plays and will continue to play a major role in characterizing insulating quantum materials. Both phonons and pure spin excitations can contribute to ${\kappa }_{xy}$, where the underlying mechanisms vary, but a common feature is that heat carriers are subject to chirality in one way or another. Phonons can be conferred chirality through various extrinsic and intrinsic mechanisms. The extrinsic mechanisms are related to the scattering by rare-earth impurities and by structural domain boundaries, while the intrinsic mechanisms include the Berry curvature and coupling of phonons to spins. Besides phonons, spin excitations such as magnons also play a critical role in the thermal Hall effect in insulating magnets. Currently, the Berry curvature induced by the Dzyaloshinskii–Moriya interaction is a dominant mechanism of the magnon Hall effect.

Despite remarkable advances in research, the mechanisms for thermal Hall effect still need to be better understood. For example, a predication is that the highly entangled motion of the lattice and spin degrees of freedom can induce the thermal Hall effect. Meanwhile, the physical origins of observed thermal Hall effect in some materials, such as in $\alpha$-RuCl₃, remain controversial. It should also be noted that magnon and phonon Hall effects may coexist in some materials. These mechanisms need to be further verified experimentally. Thus, well-designed experiments are required to reveal the nature of the thermal Hall effect in various quantum materials. In addition, magnetocaloric effect in quantum magnets can affect the accuracy of the measured ${\kappa }_{xy}$ at low temperatures. The current measurement technologies need to be further improved to obtain reliable ${\kappa }_{xy}$ and delineate among different mechanisms.

Further efforts are needed to realize practical applications based on the thermal Hall effect. Since the thermal Hall effect bridges the thermal gradient and the magnetic field, insulators with large ${\kappa }_{xy}$ signals can be used as magnetically operated heat switches. Furthermore, the ability to control spin transport through thermal gradients lays the foundation of spin caloritronics, offering a means of generating high spin current densities for quantum information processing.

Published Online: July 21, 2022