Abstract
The revolutionary technique cryoelectron tomography (cryo-ET) enables imaging of cellular structure and organization in a near-native environment at submolecular resolution, which is vital to subsequent data analysis and modeling. The conventional structure detection process first reconstructs the three-dimensional (3D) tomogram from a series of two-dimensional (2D) projections and then directly detects subcellular components found within the tomogram. However, this process is challenging due to potential structural information loss during the tomographic reconstruction and the limited scope of existing methods since most major state-of-the-art object detection methods are designed for 2D rather than 3D images. Therefore, in this article, as an alternative approach to complement the conventional process, we propose a novel 2D-to-3D framework that detects structures within 2D projection images before reconstructing the results back to 3D. We implemented the proposed framework as three specific algorithms for three individual tasks: semantic segmentation, edge detection, and object localization. As experimental validation of the 2D-to-3D framework for cryo-ET data, we applied the algorithms to the segmentation of mitochondrial calcium phosphate granules, detection of spherical edges, and localization of mitochondria. Quantitative and qualitative results show better performance for prediction tasks of segmentation on the 2D projections and promising performance on object localization and edge detection, paving the way for future studies in the exploration of cryo-ET for in situ structural biology.
Keywords: backward projection, cryoelectron tomography, edge detection, object localization, semantic segmentation
1. INTRODUCTION
Cryoelectron tomography (cryo-ET) is an important tool for the study of macromolecular structures in near-native states. Consequently, cryo-ET plays a key role in establishing structural cell biology as a discipline by producing fundamental insights into cellular organization and ultrastructure (McIntosh et al., 2005; Lučić et al., 2013). A cellular cryoelectron tomogram contains structural information of all the cellular components inside the field of view through imaging the vitrified cell specimen from varying tilt angles through electron microscopy.
The raw data, two-dimensional (2D) projection images, are processed and aligned to reconstruct the three-dimensional (3D) tomogram. After a tomogram is reconstructed, semantic segmentation and object localization methods can be applied to facilitate the discovery of various cellular components from large ultrastructures such as mitochondria and nuclear membrane (Hagen et al., 2015) to macromolecular complexes such as ribosomes and expressomes (OReilly et al., 2020).
Several computational approaches and software have been proposed for the computationally difficult cryo-ET 3D reconstruction task. Basic algorithms that have been studied include backprojection algorithms and iterative algorithms (Kupsch et al., 2016). Backprojection algorithms backward project each projection separately and refine them with filters. In comparison, iterative algorithms transfer the reconstruction task to a linear regression model and use iterative optimization methods to improve the reconstruction performance. More advanced algorithms in popular software packages such as IMOD (Mastronarde, 2006) and AuTom (Han et al., 2017) that involve both the alignment of projections and iterative reconstruction have also been designed.
However, 3D cryo-ET data processing and modeling tasks face possible errors occurred in the 3D reconstruction process related to the approach of generating the 3D image data. The 3D tomogram is reconstructed by aligning a tilt series of 2D projection images. Nevertheless, the reconstruction process may suffer from a number of inaccuracies caused by imperfect alignment, the instability of sample structures during imaging, and the existence of missing values in the Fourier space (known as the missing wedge effect) due to the limited tilt angle ranges (Kawase et al., 2007; Genc et al., 2016).
Although the missing wedge effect can be partially compensated by optimization algorithms (Paavolainen et al., 2014; Yan et al., 2019; Moebel and Kervrann, 2020; Zhai et al., 2020; Liu et al., 2021), the 3D reconstruction is never perfect. Therefore, it is beneficial to have the alternative approach of annotating directly on the 2D tilt series. In addition, other related cryo-ET data analysis challenges include (1) the quality of data: due to the imprecise alignment and missing wedge effects, the reconstructed 3D tomogram may have less ideal structural details compared with 2D projection images, especially for cellular tomograms with complex content and large sample thickness (Behrendt et al., 2009; Irobalieva et al., 2016). (2) the quantity of data: suppose we need to train a convolutional neural network (CNN) for a cryo-ET data analysis task, enough training data need to be obtained. A tomogram is usually reconstructed by a tilt series of >100 projection images (typically ±60° at 0.5–5° [mostly 1°] tilt-angle step) (Hagen et al., 2017).
Therefore, the task of training on one labeled 3D tomogram sample could be decomposed to training on >100 2D projection image samples. Moreover, a 3D tomogram is usually too large to be processed by neural networks due to memory storage issues. (3) The scope of the existing techniques: most state-of-the-art techniques are designed for 2D images (Girshick, 2015; Krizhevsky et al., 2012). To apply on a 3D tomogram, there is a need to extend such methods to the 3D domain. In such case, the existing powerful 2D pretrained models (Tan and Le, 2019; Chen et al., 2021) cannot be applied.
In this article, we propose a 2D-to-3D framework to perform structure detection tasks on 2D projection images and then reconstruct the results back to 3D tomograms. The 2D projection images contain all the structural information of a tomogram without the aforementioned challenges: (1) a 3D tomogram is usually reconstructed from more than a 100 projection images. If we train a neural network for semantic segmentation, we could train on many 2D samples rather than just one 3D sample. (2) Two-dimensional projection images have a relatively better structural details than reconstructed 3D tomograms partly due to information loss during the reconstruction process. (3) Available 2D techniques can be readily applied. We demonstrated the performance of the 2D-to-3D framework on three important cryo-ET data analysis tasks: semantic segmentation, object localization, and edge detection.
2. MATERIALS AND METHODS
In this section, we introduce the proposed 2D-to-3D framework for the three specific cryo-ET structural detection tasks. We denote a task of 3D tomogram analysis as , and our backward projection algorithm as . A tomogram V is reconstructed from a set of projections , where indicates the 2D image of V projected at angle . A structural detection task can be directly performed on the 3D tomogram V. The 3D tomogram analysis task can be formulated as follows:
| (1) |
where Y is the output of task on tomogram V. However, inspired by the potentially better properties of 2D projection images, we propose an alternative approach. The 2D-to-3D framework will perform a task on 2D projection images directly and reconstruct the results back, which is formulated as follows:
| (2) |
Backward projection: The backward projection algorithm is a basic function in our 2D-to-3D framework. We introduce it here that will be used in the three algorithms. It projects 2D images back to the 3D tomogram and is formulated in the discrete domain for matrix operation. Although the back projection direction is opposite to the forward projection direction, but for convenience, we define the back projection direction the same as the forward projection direction. Also, in this article we only use binary backward projection. Hence, we use backward projection to indicate the binary backward projection.
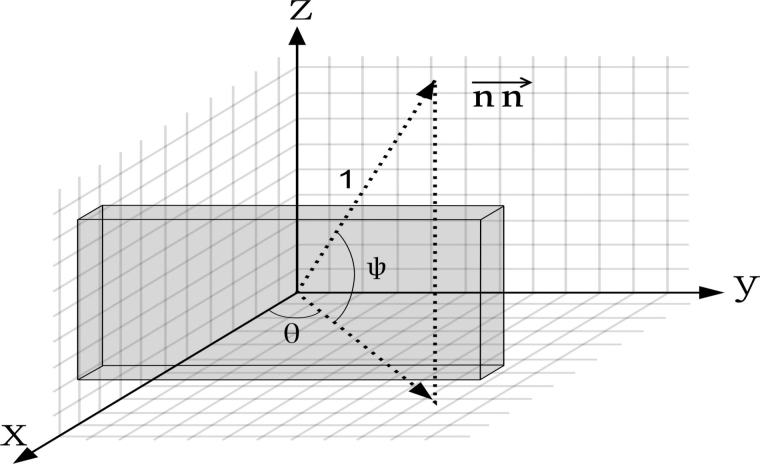
When using the annotated result, we refine the backward projection algorithm for binary backward projection, that is, the 2D images to be backward projected are binary segmentation or object localization maps with value 1 indicating structural regions and value 0 indicating background regions. First, assuming the sample is in a 3D coordinate system, parallel to the coordinate axis and centered at the origin, we define the backward projection angles as Figure 1: The vector of projection direction is a unit vector as formulated as
FIG. 1.
The direction of forward projection and its corresponding angles.
| (3) |
We use S to denote the 3D sample in 3D XYZ coordinates and P to denote the 2D projection image in 2D MN coordinate. Let the origin of XYZ coordinates face toward the origin of MN coordinate through . The backward projection value of voxel in 3D coordinate from pixel in the projection image can be computed as shown in Figure 1. The direction of forward projection vector is the opposite of backward projection vector direction.
| (4) |
where indicates the direction of N-axis of MN coordinate and indicates the direction of M-axis of MN coordinate in the XYZ coordinates, Where indicates the direction of M-axis of MN coordinate in the XYZ coordinates. Then we can find the voxels corresponding to pixel . Let [] denote the nearest integer function, these voxels are along a straight line where .
| (5) |
Unlike the continuous domain, different pixels in a 2D image may be backward projected to the same voxel due to rounding. To deal with this problem, if one or more pixels with value 1 are backward projected to the same voxel in the 3D image, this voxel will be set to 1.
2.1. Semantic segmentation
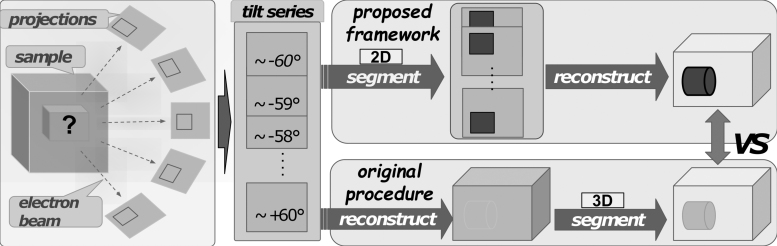
Semantic segmentation seeks to classify different cellular components voxel-wise in an image. Similarly, we aim to segment out known cellular components in tomograms. As shown in Figure 2, the original process reconstructs the 3D tomogram first and then performs the segmentation task. The proposed 2D-to-3D framework performs segmentation on 2D projection images before 3D reconstruction.
FIG. 2.
2D-to-3D framework for semantic segmentation. 2D, two-dimensional; 3D, three-dimensional.
2.1.1. Two-dimensional segmentation and reconstruction algorithm
We first apply a CNN (Szegedy et al., 2017) to the 2D projection images to obtain a 2D binary segmentation map of a particular structure. After training the 2D classification model using training data of projections, we can use the trained model to predict 2D segmentation results on testing data of projections. Then, the 3D segmentation result is reconstructed from the predicted results by our algorithm. The algorithm is mainly based on backward projection. Using backward projection, we give each voxel in the tomogram a score from the 2D segmented projections, and then we use an autocalculated threshold to decide whether it is in an object.
We use the backward projection defined to assign each voxel in the reconstructed 3D tomogram a binary value. Algorithm 1 aims to optimize the Intersection over Union (IoU) between the 2D segmentation maps and the forward projection images from the 3D segmentation map, which ensures the highest consistency between a set of segmented 2D projection images and the reconstructed 3D segmentation map. We use to denote the backward projection function and to denote the forward projection function.
| Algorithm 1: 2D-to-3D framework for semantic segmentation |
|---|
| Input: Segmented projection tilt series |
| Initialization: (L,W,H) |
| Procedure Backward projection |
| For each do |
| end |
| Procedure Threshold autoselection |
| For each proposed threshold do |
| ; |
| score(i) = |
| end |
| return segmented tomogram with the highest score(i). |
2.2. Edge detection
Although edge detection can be seen as a specific case of semantic segmentation, edge detection is notably important in cryo-ET when applied to the detection of cellular membrane, microtubules, and actin filaments structure (Martinez-Sanchez et al., 2014). Many edge detection-based algorithms have been developed for the segmentation of membrane structures in cryo-ET. Therefore, we described edge detection as a separate task in cryo-ET. To achieve the highest consistency between a series of backward projections, we apply an iterative refinement process between backward projection of adjacent 2D projection images to reduce the noise by summation and thresholding.
Assuming that we have obtained the edge detection results of projections, each labeled pixel in projections corresponds to a line in the 3D reconstructed image. To eliminate bias and noise, we propose the iterative refine method to limit the line's impact region to a reasonable range. In each iteration, the backprojection of each projection is refined by adjacent projections, leading to better reconstruction. The algorithm is shown in Algorithm 2.
| Algorithm 2: 2D-to-3D framework for edge detection |
|---|
| Input: Projections with detected edges , threshold T |
| Initialization: |
| Procedure Backward projection |
| for each do |
| end |
| Refine B for m iterations; |
| return tomogram with detected edges |
2.3. Object localization
Object detection is an important research area in computer vision. Compared with semantic segmentation, it has the advantage of being more efficient and not requiring voxel-level dense training annotation. Different from semantic segmentation that segments objects pixel-wise or voxel-wise, object localization is a more general task that aims to localize objects with bounding boxes for further analysis or interpretation. For localization of cellular ultrastructures, past studies employed Faster Regions with Convolutional Neural Network features (Faster R-CNN) (Li et al., 2019) with labeled 2D projection images as training data. Then, the trained Faster R-CNN was applied to 2D slices (breaking from the z-axis) of 3D tomograms to detect the cellular mitochondria.
However, we note that the image intensity, missing wedge limits, and difference in structural details between a 2D projection image and a 2D slice of a 3D tomogram will lead to low prediction accuracy. To our knowledge, there is no existing studies that directly detect cellular ultrastructures in 3D tomograms so far. Therefore, as an extension to the 2D cryo-ET object detection in Li et al. (2019), we propose to reconstruct 2D projection image bounding boxes results accurately on 3D tomograms as 3D bounding boxes. The algorithm is shown in Algorithm 3.
| Algorithm 3: 2D-to-3D framework for object localization |
|---|
| Input: Projections , threshold T |
| Initialization: |
| Procedure Backward projection |
| for each do |
| end |
| ; |
| Compute the set of object bounding boxes {v} from ; |
| return {v} |
We note that the algorithms can be easily extended to multiple classes. For edge detection, there is typically just one class. For object detection, it is simple to run the algorithm multiple times for multiple classes because the bounding box of different classes can have overlaps between them. For semantic segmentation, the algorithm shown can be easily extended to segment multiple semantic classes as long as the input 2D projection image segmentation map has multiple classes annotated.
3. EXPERIMENTS AND RESULTS
3.1. Semantic segmentation
Data set: We applied our 2D-to-3D semantic segmentation algorithm on two experimentally obtained tomograms from the rat neuron culture (Guo et al., 2018). Our data consist of two aligned tilt-series projection image stacks and their corresponding reconstructed tomograms. Our target was to segment out calcium phosphate granules in mitochondria (Malyala et al., 2019). Therefore, we manually segmented these granules found within the mitochondrial matrix on both 2D tilt-series projection images and the 3D reconstructed tomograms as the ground truth for evaluation. One tomogram was used for training the neural network, and the other was used for testing purposes. For comparison between the conventional 3D segmentation process and our proposed 2D-to-3D framework, we used IoU to measure the accuracy of the results.
For the conventional 3D segmentation process, we trained a 3D CheXNet (Rajpurkar et al., 2017) on the training 3D tomogram and predicted on the testing 3D tomogram. For our proposed 2D-to-3D segmentation approach, we trained a ResNet (Szegedy et al., 2017) on the segmented projection images of the training tomogram (Figure 3), predicted on the projection images of the testing tomogram, and reconstructed a 3D segmentation map using Algorithm 1. The segmentation accuracy is measured by IoU compared with the 3D ground truth, the 2D-to-3D segmentation achieves an IoU of 0.523, improved from the 3D segmentation IoU of 0.459.
FIG. 3.
(a) An example 2D projection image and the segmentation map of mitochondrial phosphate precipitates. (b) An example slice of the testing tomogram with predicted mitochondrial phosphate precipitates region highlighted (none of the example images were high-pass or low-pass filtered).
3.2. Edge detection
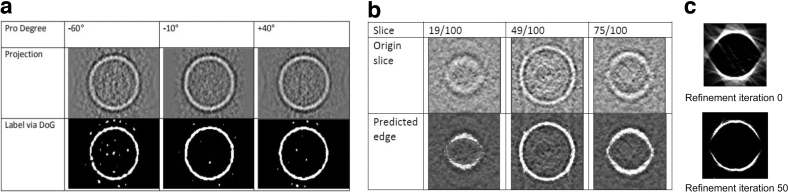
For evaluation of the 2D-to-3D edge detection algorithm, we simulated a small tomogram (size: 100 × 100 × 100 voxels) of an empty sphere structure similar to the cellular membrane with limited tilt angle range from −50° to +50°. On the 2D projection images, difference of Gaussian (DoG) method was applied to detect peaks of potential structural regions. Then, a threshold T is calculated based on the minimum and maximum values of the peaks and applied to detect the membrane structure.
With projections with detected edges and threshold T, we use Algorithm 2 to detect edge structure in the 3D tomogram. As shown in Figure 4, the labeled membrane structure by DoG on 2D projection images can be successfully reconstructed to the 3D tomograms. Regarding the different back projections of different iterations, it can be observed that with adjacent information, the back projections became increasingly precise. In other words, the precise back projections based on iterative refinement will result in precise edge detection.
FIG. 4.
(a) Projection images with the detected edge. (b) Example slices with the predicted edge. (c) Iterative refinement result for reducing backward projection noise.
In this study, we demonstrated edge detection on 3D tomograms through 2D-to-3D framework using the results from the simplest edge detection method. Results from more advanced edge detection methods (He et al., 2019; Mittal et al., 2019; Versaci and Morabito, 2021) can also be integrated into the framework. In addition, the low electron dosage used in cryo-ET imaging results in the low Signal-to-Noise Ratio (SNR) of edges. Denoising is usually a necessary preprocessing step in performing edge detection on 3D tomograms. Similarly, our generic 2D-to-3D approach can also incorporate the denoising step before performing edge detection on 2D projection images to optimize the final 3D results.
3.3. Object localization
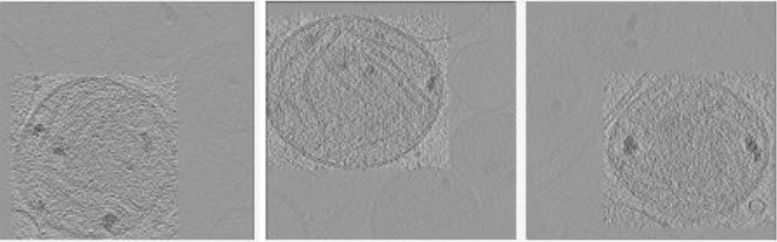
We directly applied the 2D-to-3D objection localization method to the results from Li et al. (2019). They predicted the bounding boxes of mitochondria on 2D projection images of nine tomograms of fibroblasts from a patient with Leigh syndrome, a mitochondrial disease (Siegmund et al., 2018). We successfully reconstructed their results to 3D bounding boxes. Example slices of localized mitochondria in three tomograms are shown in Figure 5, demonstrating the utility of our 2D-to-3D framework in transforming object localization results on 2D cryo-ET projection images to object localization results on 3D reconstructed tomograms.
FIG. 5.
Example 2D slices of localized mitochondria (inside the bounding boxes) in three 3D tomograms.
4. DISCUSSION
We propose a routine 2D-to-3D framework for conducting structure detection tasks in cellular cryo-ET. Unlike performing directly on the 3D reconstructed tomogram, which is limited by the low SNR, the low number of training samples, and the scope of existing techniques, the 2D-to-3D framework detects structures on the 2D projection images and reconstructs the results back to the 3D tomogram. We demonstrated the framework on three important structure detection tasks: semantic segmentation, edge detection, and object localization. We achieved better IoU accuracy and further extended an existing deep learning-based study (Li et al., 2019).
Because the volume of a 3D tomogram is too large to be processed by a neural network, existing deep learning-based cryo-ET annotation methods usually operate on 2D slices (Chen et al., 2017) or small 3D volume patches (Moebel et al., 2021). This will lead to inconsistencies at the border between predictions. In the three algorithms, we optimize the IoU between the final 3D segmentation map or object bounding box and the reprojections of the 2D annotations to minimize the inconsistency between different projections. In the future, we will continue to test the 2D-to-3D framework on more tasks such as particle picking (Burt et al., 2021) and saliency detection (Zhou et al., 2018) to obtain more quantitative validation of this framework.
Our proposed 2D-to-3D framework provides new insights into 3D segmentation and detection in cryo-ET. As 2D projection images are directly obtained from cryo-ET experiments and the quality of reconstructed cryoelectron tomograms depends on the reconstruction algorithm, the prediction tasks conducted directly on the 2D projections before reconstruction show promising performances to complement the conventional 3D prediction approach. Recently, unsupervised methods have been developed for cryo-ET tasks including subtomogram clustering, subtomogram alignment, and tomogram denoising. Since subtomogram clustering and subtomogram alignment are performed on the subtomogram level, our 2D-to-3D framework cannot be applied.
For tomogram denoising, it is feasible to directly extend state-of-the-art 2D denoising methods (Abdelhamed et al., 2019; Thakur et al., 2019) and integrated with the 2D-to-3D framework by performing the denoising task on 2D projection images and project the results back in a similar way as tomographic reconstruction. Hence, designing new methods to integrate the prediction on 2D and 3D images has many important applications in in situ. Admittedly, this is an interesting direction that is yet to be explored largely by the structural biology community. Therefore, a substantial optimization on these algorithms can be done in the future.
ACKNOWLEDGMENT
We thank Dr. Qiang Guo for providing testing data sets. None of the views expressed here should be attributed to the funding organizations. Neither did they play any role in the decision to publish or in the process of publication.
AUTHORS' CONTRIBUTIONS
M.X. and X.Z. conceived of the project. X.Z. designed the methods. Z.L. and X.Z. conducted the experiments and wrote the initial draft. M.R.U., B.Z., C.C., J.Z., and Z.F. provided suggestions. All authors participated in the writing of the article.
AUTHOR DISCLOSURE STATEMENT
The authors declare they have no conflicting financial interests.
FUNDING INFORMATION
This study was supported in part by U.S. NSF grants DBI-1949629 and IIS-2007595, NIH grants R01GM134020 and P41GM103712, and Mark Foundation for Cancer Research 19-044-ASP. The computational resources were supported by AMD COVID-19 HPC Fund. Z.F. received support from U.S. DoD grant PR2192466, U.S. NIH grants R01DK124219, R21DA052419, and the Commonwealth of Pennsylvania Formula Fund. X.Z. was supported in part by a fellowship from Center of Machine Learning and Health at Carnegie Mellon University.
REFERENCES
- Abdelhamed, A., Timofte, R., Brown, M.S., et al. . 2019. NTIRE 2019 challenge on real image denoising: Methods and results, 2197–2210. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. IEEE Computer Society. Long Beach, CA. [Google Scholar]
- Behrendt, F.F., Schmidt, B., Plumhans, C., et al. . 2009. Image fusion in dual energy computed tomography: effect on contrast enhancement, signal-to-noise ratio and image quality in computed tomography angiography. Investig. Radiol. 44, 1–6. [DOI] [PubMed] [Google Scholar]
- Burt, A., Gaifas, L., Dendooven, T., et al. . 2021. A flexible framework for multi-particle refinement in cryo-electron tomography. PLoS Biol. 19, e3001319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, H., Wang, Y., Guo, T., et al. . 2021. Pre-trained image processing transformer, 12299–12310. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. IEEE. Nashville, TN. [Google Scholar]
- Chen, M., Dai, W., Sun, S.Y., et al. . 2017. Convolutional neural networks for automated annotation of cellular cryo-electron tomograms. Nat. Methods 14, 983–985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genc, A., Kovarik, L., Pullan, L., et al. . 2016. Reducing the missing wedge in tem tomography. Microsc. Microanal. 22(S3), 26–27. [Google Scholar]
- Girshick, R. 2015. Fast R-CNN, 1440–1448. In Proceedings of the IEEE International Conference on Computer Vision. IEEE Computer Society. Santiago, Chile. [Google Scholar]
- Guo, Q., Lehmer, C., Martínez-Sánchez, A., et al. . 2018. In situ structure of neuronal C9orf72 poly-GA aggregates reveals proteasome recruitment. Cell 172, 696–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagen, C., Dent, K.C., Zeev-Ben-Mordehai, T., et al. . 2015. Structural basis of vesicle formation at the inner nuclear membrane. Cell 163, 1692–1701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagen, W.J., Wan, W., and Briggs, J.A.. 2017. Implementation of a cryo-electron tomography tilt-scheme optimized for high resolution subtomogram averaging. J. Struct. Biol. 197, 191–198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han, R., Wan, X., Wang, Z., et al. . 2017. AuTom: A novel automatic platform for electron tomography reconstruction. J. Struct. Biol. 199, 196–208. [DOI] [PubMed] [Google Scholar]
- He, J., Zhang, S., Yang, M., et al. . 2019. Bi-directional cascade network for perceptual edge detection, 3828–3837. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. IEEE. Long beach, CA. [Google Scholar]
- Irobalieva, R.N., Martins, B., and Medalia, O.. 2016. Cellular structural biology as revealed by cryo-electron tomography. J. Cell Sci. 129, 469–476. [DOI] [PubMed] [Google Scholar]
- Kawase, N., Kato, M., Nishioka, H., et al. . 2007. Transmission electron microtomography without the missing wedge for quantitative structural analysis. Ultramicroscopy 107, 8–15. [DOI] [PubMed] [Google Scholar]
- Krizhevsky, A., Sutskever, I., and Hinton, G.E.. 2012. Imagenet classification with deep convolutional neural networks, 1097–1105. In Advances in Neural Information Processing Systems. [Google Scholar]
- Kupsch, A., Lange, A., Hentschel, M.P., et al. . 2016. Missing wedge computed tomography by iterative algorithm directt. J. Microsc. 261, 36–45. [DOI] [PubMed] [Google Scholar]
- Li, R., Zeng, X., Sigmund, S.E., et al. . 2019. Automatic localization and identification of mitochondria in cellular electron cryo-tomography using faster-RCNN. BMC Bioinformatics 20, 75–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, Y.-T., Zhang, H., Wang, H., et al. . 2021. Isotropic reconstruction of electron tomograms with deep learning. bioRxiv number: 2021.07.17.452128. [Google Scholar]
- Lučić, V., Rigort, A., and Baumeister, W.. 2013. Cryo-electron tomography: The challenge of doing structural biology in situ. J. Cell Biol. 202, 407–419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malyala, S., Zhang, Y., Strubbe, J.O., et al. . 2019. Calcium phosphate precipitation inhibits mitochondrial energy metabolism. PLoS Comput. Biol. 15, e1006719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez-Sanchez, A., Garcia, I., Asano, S., et al. . 2014. Robust membrane detection based on tensor voting for electron tomography. J. Struct. Biol. 186, 49–61. [DOI] [PubMed] [Google Scholar]
- Mastronarde, D. 2006. Tomographic reconstruction with the imod software package. Microsc. Microanal. 12(S02), 178–179.17481355 [Google Scholar]
- McIntosh, R., Nicastro, D., and Mastronarde, D.. 2005. New views of cells in 3D: An introduction to electron tomography. Trends Cell Biol. 15, 43–51. [DOI] [PubMed] [Google Scholar]
- Mittal, M., Verma, A., Kaur, I., et al. . 2019. An efficient edge detection approach to provide better edge connectivity for image analysis. IEEE Access 7, 33240–33255. [Google Scholar]
- Moebel, E., and Kervrann, C.. 2020. A Monte Carlo framework for missing wedge restoration and noise removal in cryo-electron tomography. J. Struct. Biol. X. 4, 100013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moebel, E., Martinez-Sanchez, A., Lamm, L., et al. . 2021. Deep learning improves macromolecule identification in 3D cellular cryo-electron tomograms. Nat. Methods 18, 1386–1394. [DOI] [PubMed] [Google Scholar]
- OReilly, F.J., Xue, L., Graziadei, A., et al. . 2020. In-cell architecture of an actively transcribing-translating expressome. Science 369, 554–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paavolainen, L., Acar, E., Tuna, U., et al. . 2014. Compensation of missing wedge effects with sequential statistical reconstruction in electron tomography. PLoS One 9, e108978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajpurkar, P., Irvin, J., Zhu, K., et al. CheXNet: Radiologist-level pneumonia detection on chest X-rays with deep learning.. arXiv preprint arXiv:1711.05225, 2017.
- Siegmund, S.E., Grassucci, R., Carter, S.D., et al. . 2018. Three-dimensional analysis of mitochondrial crista ultrastructure in a patient with Leigh syndrome by in situ cryoelectron tomography. iScience 6, 83–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szegedy, C., Ioffe, S., Vanhoucke, V., et al. . 2017. Inception-v4, inception-ResNet and the impact of residual connections on learning. In Thirty-First AAAI Conference on Artificial Intelligence. AAAI. San Francisco, CA. [Google Scholar]
- Tan, M., and Le, Q.. 2019. EfficientNet: Rethinking model scaling for convolutional neural networks, 6105–6114. In International Conference on Machine Learning. PMLR, Long Beach, CA. [Google Scholar]
- Thakur, R.S., Yadav, R.N., and Gupta, L.. 2019. State-of-art analysis of image denoising methods using convolutional neural networks. IET Image Process. 13, 2367–2380. [Google Scholar]
- Versaci, M., and Morabito, F.C.. 2021. Image edge detection: A new approach based on fuzzy entropy and fuzzy divergence. Int. J. Fuzzy Syst. 23, 918–936. [Google Scholar]
- Yan, R., Venkatakrishnan, S.V., Liu, J., et al. . 2019. MBIR: A cryo-ET 3D reconstruction method that effectively minimizes missing wedge artifacts and restores missing information. J. Struct. Biol. 206, 183–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhai, X., Lei, D., Zhang, M., et al. . 2020. LoTToR: An algorithm for missing-wedge correction of the low-tilt tomographic 3D reconstruction of a single-molecule structure. Sci. Rep. 10, 1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou, B., Guo, Q., Wang, K., et al. . 2018. Feature decomposition based saliency detection in electron cryo-tomograms, 2467–2473. In 2018 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). IEEE, Madrid, Spain. [DOI] [PMC free article] [PubMed] [Google Scholar]