Pre-hospital prediction of adverse outcomes in patients with suspected COVID-19: Development, application and comparison of machine learning and deep learning methods

Abstract

Background:

COVID-19 infected millions of people and increased mortality worldwide. Patients with suspected COVID-19 utilised emergency medical services (EMS) and attended emergency departments, resulting in increased pressures and waiting times. Rapid and accurate decision-making is required to identify patients at high-risk of clinical deterioration following COVID-19 infection, whilst also avoiding unnecessary hospital admissions. Our study aimed to develop artificial intelligence models to predict adverse outcomes in suspected COVID-19 patients attended by EMS clinicians.

Method:

Linked ambulance service data were obtained for 7,549 adult patients with suspected COVID-19 infection attended by EMS clinicians in the Yorkshire and Humber region (England) from 18-03-2020 to 29-06-2020. We used support vector machines (SVM), extreme gradient boosting, artificial neural network (ANN) models, ensemble learning methods and logistic regression to predict the primary outcome (death or need for organ support within 30 days). Models were compared with two baselines: the decision made by EMS clinicians to convey patients to hospital, and the PRIEST clinical severity score.

Results:

Of the 7,549 patients attended by EMS clinicians, 1,330 (17.6%) experienced the primary outcome. Machine Learning methods showed slight improvements in sensitivity over baseline results. Further improvements were obtained using stacking ensemble methods, the best geometric mean (GM) results were obtained using SVM and ANN as base learners when maximising sensitivity and specificity.

Conclusions:

These methods could potentially reduce the numbers of patients conveyed to hospital without a concomitant increase in adverse outcomes. Further work is required to test the models externally and develop an automated system for use in clinical settings.

1. Introduction and background

Following the first occurrence of the SARS-CoV-2 virus in late 2019, the virus spread quickly and led to the global COVID-19 pandemic, threatening the health and lives of millions of people world-wide. Emergency medical services (EMS) in the UK reported up to three times the expected number of emergency calls during the first and second waves of the pandemic, an increase also observed in other parts of Europe [1], [2]. Surges in demand led to some EMS in the UK declaring major incidents and warning of care being compromised by overwhelming demand. In order to manage and meet the demands on these services during such times, and to optimise the use of limited available health care resources, risk assessment tools are required. These tools identify patients at greatest risk of adverse outcomes whilst simultaneously avoiding overwhelming emergency and hospital services with patients who will not deteriorate or require hospital treatment. Managing this clinical risk for patients with COVID-19 infection is complex, and currently relies on rapid assessment by health care professionals: machine learning (ML) and artificial intelligence (AI) have the potential to support health care professions with their clinical decision-making.

Advances in ML and AI methods have enabled more accurate predictive models to be developed to improve decision-making relating to the treatment and management of patients, as well as improving the organisation and delivery of health services [3], [4], [5]. Developing and applying such tools for use during the COVID-19 pandemic, as well as for future pandemics, could help create better tools to support decision-making, helping alleviate pressures on EMS and prioritise care requirements. Early reviews of the use of AI for tackling COVID-19, by Nguyen et al. [6] and Abd-Alrazaq et al. [7], identified five main uses of AI against the disease: diagnosis, treatment and vaccines, epidemiology, patient outcomes and infodemiology. ML and AI methods offer advantages over traditional methods of analysis [8] that may be of particular benefit for tackling the problems arising from the pandemic.

The rapid spread of the virus and dramatic increase in infections around the world, generated a significant volume of patient-related data. AI methods are particularly suited to handling and analysing large datasets [7], [8], and are adept at learning from patterns in data as they emerge over time. In recent years, AI methods have been developed and applied in a variety of clinical contexts to improve decision-making when accuracy and speed of decision-making is vital: the COVID-19 pandemic also requires accurate and rapid decision making to reduce the risk of complications and mortality in patients.

Jamshidi et al. [8] and Nguyen et al. [6] reviewed the use of AI for medical diagnosis using imaging and value-based data. Whilst the former paper discusses the potential of AI approaches for overcoming COVID-19 related challenges using a variety of strategies, the latter paper focused on the use of AI for analysing data from medical images, text from public conversations (e.g., Twitter) and news feeds, and smartphone-based data such as location.

In order to prioritise the treatment of COVID-19 patients by EMS, efforts have been made to improve methods of diagnosing the condition and of identifying patients at greatest risk of deterioration and adverse health outcomes. Abd-Alrazaq et al. [7] identified 14 early studies that had used AI for outcome-related functions, including assessing the severity of the disease (n $=$ 9), predicting progression to severe COVID-19 (n $=$ 4), predicting hospital length of stay (n $=$ 1) and mortality (n $=$ 2) and identifying predictors of mortality (n $=$ 1). Given the need for prioritising EMS during the COVID-19 pandemic, we were interested in developing models to predict adverse health outcomes, which could be used to triage the need for hospitalisation, among patients for whom suspected or confirmed COVID-19 infection had been recorded by EMS clinicians.

Despite the work demonstrating the potential of AI in combating the COVID-19 pandemic, there have been challenges in relation to the available data. An important limitation of using AI for developing predictive models in medicine is that many of these models are at high risk of bias [9], due to the small size of the datasets that may be available for training, and then testing, the classification models. For example, in a recent review by [10], it was reported that the median number of cases in datasets that use AI to make clinical scores was 214. The review of the use of AI for tackling COVID-19 by Abd-Alrazaq et al. [7] reported that half of the datasets considered in their review included fewer than 1000 patients. Training predictive models using small numbers of cases makes the classification models more prone to overfitting and leads to a high risk of bias. Studies utilising a greater number of cases are therefore required in order to develop better predictive models: our study utilised data from over 7500 patients, based on a priori sample size calculations outlined below [11], to reduce the risk of overfitting and bias.

The aim of our study was to use statistical and AI methods to develop models that would help predict whether patients with suspected COVID-19 would experience adverse health outcomes within 30 days of an initial assessment by EMS staff, and compare these with decisions made using an existing tool and by EMS staff. We propose a hybrid model, which merges the benefits of: (a) statistical, (b) machine learning and (c) deep learning methods, using a stacking ensemble approach. The proposed approach was useful for predicting patients at high risk and suggested that the performance of the stacking ensemble models outperform the individual models. We utilised a data set containing sufficient cases to develop appropriate predictive models. More specifically, the objectives were to use a range of AI and statistical approaches to (i) predict which patients with suspected COVID-19 would require in-hospital organ support or would die from COVID-19 within 30 days of their initial assessment, (ii) identify which features/variables from patient records would support this decision-making, and (iii) identify which models/methods offer improved performances under different operating points.

We applied the prediction model risk of bias assessment tool (PROBAST, Moons et al. [12]) to assess the risk of bias and verify that our proposed models were at low risk of bias. Additionally, the TRIPOD guidelines [13] for reporting prediction models performance were followed to evaluate the machine learning methods and logistic regression. In summary, the main contributions and novel aspects of this paper are that it describes:

• •The application of statistical and machine learning based models to predict adverse outcomes in patients with suspected COVID-19, using data from clinical assessments of patients by EMS clinicians.
• •The integration of classical and deep learning models in an ensemble framework to determine the benefit of both types of models and demonstrate how the proposed framework helps in improving the predictions of high risk patients.
• •A comparative evaluation of the different proposed models, based on TRIPOD guideline recommendations for model development.
• •The potential for these to models to be deployed and used by EMS to aid rapid risk assessment of COVID-19 patients.

The remainder of this paper is organised as follows: the proposed methods are presented in Section 2, including a description of the data and the problem definition. This section discuss the data used in this work and the prediction models used to build the proposed classifiers. Model performance and feature importance are presented in Section 3 and discussed in Section 4. Finally, a summary of the work is provided in Section 5.

2. Method

In this section we describe the methods used in the study. First, we describe the data sources used (2.1), before presenting the problem definition, i.e., the outcome of interest in our study (2.2). Section 2.3 briefly describes the range of methods of imputation for handling missing data, before describing the method (Section 2.4). Details of our sample size estimates and how predictor variables were selected are presented in 2.5. Section 2.6 describes the prediction models we developed for the analyses, including logistic regression (2.6.1), support vector machines (2.6.2), gradient boosted decision trees (2.6.3), neural networks (2.6.4), and the stacking ensemble method (2.6.5). The metrics used for evaluating the performance of the models are described in Section 2.7. Details of ethical approval are provided in Section 2.8.

2.1. Data

Access to anonymised patient-level data from electronic health care records was provided by Yorkshire Ambulance Service (YAS) NHS Trust in the UK. YAS serves a population of 5.5 million citizens in Yorkshire and Humber and in 2020/2021 received more than 1,000,000 emergency (999) calls.

EMS clinicians complete an electronic patient care record (ePCR) each time they attend an emergency call, which records presenting patient characteristics and clinical care in a standardised manner. YAS provided a dataset of ePCR data for EMS responses between the 26th March 2020 and 25th June 2020 where a clinical impression of suspected or confirmed COVID-19 infection had been recorded. The dataset consisted of patient identifiers, demographic data, measured physiological parameters and other available clinical information. In order to measure outcomes (i.e., 30-day mortality/organ support) following the visits, EMS attendances were linked to routinely collected COVID-related general practice (GP) records, emergency department attendance and hospital inpatient admission, including critical care, by the NHS Digital service in England. This service manages health and social care data on behalf of the UK National Health Service (NHS) (NHS Digital, 2022). Death registration data were obtained from the UK Office of National Statistics (ONS). The final cohort consisted of all adult patients (aged 16 years and over) at the time of first (index) attendance by EMS during the study period with a clinical assessment of suspected or confirmed COVID-19 infection, and who had been successfully traced by NHS Digital. We purposively identified a cohort of patients with suspected COVID-19 infection because, in the absence of universal accurate rapid COVID-19 tests for patients with symptoms indicating possible infection at that time, this is the population that EMS clinicians had to clinically risk-stratify.

2.2. Outcome

In terms of the problem definition, we defined the primary outcome as death, or requirement for renal, respiratory, or cardiovascular organ support within 30 days of the index attendance. Information on outcomes, $y$, was obtained from death registration and critical care data in the patient record. The outcome prediction was modelled as a binary classification problem, in which an event is to be predicted as either an adverse outcome $(y=1)$ or no adverse outcome $(y=0)$. Prediction of the outcome was undertaken using four algorithms, namely logistic regression (LR), support vector machine (SVM), gradient boosting decision trees (XGBoost) and artificial neural networks (ANNs). Brief descriptions of each of these algorithms are provided in Section 2.6.

2.3. Managing missing data

Clinical/medical data can be limited by the number within the samples and/or the amount of data that are missing. Removing cases from the sample due to there being missing values is not considered good practice, because this further reduces the number of cases for analysis. As an alternative, data imputation algorithms can be applied to replace the missing values with reasonable values. Data imputation methods can be generally grouped into three categories: statistical methods, which estimate the underlying data distribution and replace missing values by drawing values from the estimated distribution; machine learning based methods, which learn the data distribution from the training samples in order to reconstruct the training samples; and hybrid combinations of both statistical and machine learning methods.

Genetic algorithms (GA) [14] are optimisation algorithms, inspired by biological evolution, to find a good approximation to search problems. They have been developed in the computational sciences and used, in conjunction with imputation methods, to find optimal sets of values to replace the missing data and have been used. In this study we employed a standard approach within health/medical sciences for handling missing data: Multiple imputation by chained equations (MICE). Multiple imputation is considered superior to more basic methods such as complete-case analysis, missing indicator and single imputation methods [15]. The MICE approach uses the observed data to estimate a set of plausible values for the missing data, reflecting the uncertainty in missing value estimation, reducing bias and giving more accurate standard errors. The approach relies on the correct specification of imputation models and assumes data are missing at random.

The MICE algorithm imputes missing values by modelling each variable with missing values as a function of other variables in a round-robin style, by which all variables with missing values are equally chosen in a rotational order. This usually starts with the variable with the least number of missing values. Let the set of sorted variables be $v_1,v_2,v_3,\dots ,v_{k-1},v_k$; with $v1$ and $v2$ complete variables and $v3$ having the least number of missing values. Initially, all missing values are randomly filled. The first variable with the least number of missing values, $v_3$, is then regressed on the other variables, and their values are estimated from the posterior predictive distribution of $v_3$. This process is repeated in turn for all other variables with missing values in one cycle. The imputation rounds are repeated for k rounds/cycle (in this work k $=$ 50), or until the stopping criterion is met ($max\left(abs(v_t-v_{t-1})\right)/max\left(abs\left(v\left[know{n}_{values}\right]\right)\right)<toleranc{e}_{value}$). The Imputation package from SKlearn [16] and the Mice package in R [17] were used to implement the MICE algorithm.

2.4. Predictor variables

Physiological parameters were extracted from the first set of clinical observations recorded by the EMS clinicians. Comorbidities were included if recorded within 12 months before the first EMS attendance. Immunosuppressant drug prescriptions documented in GP records within 30 days before the index attendance, contributed to the immunosuppression comorbidity variable. Frailty in patients older than 65 years was derived from the latest recorded Clinical Frailty Scale (CFS) score [18] (where it was recorded) in the electronic GP records prior to index attendance. Patients under the age of 65 years were not given a CFS score since it this not validated in this age group.

2.5. Sample size estimate and variable selection

A priori, and for the original analyses [11], we assessed the required sample size on the estimated precision of the area under the receiver operating characteristic (AUC) curve based on a likely 5% event rate in a cohort of 6000 patients [19].

A priori sample size estimation suggested around 30 predictors could be assessed for inclusion. Candidate predictor variables were selected using both statistical and clinical judgement. Expert clinicians within the project team reviewed the list of candidate predictors for clinical feasibility. Variables were excluded if they had a high proportion of missing data ($>$50%) or high collinearity. Predictor selection for logistic regression modelling was conducted using least absolute shrinkage and selection operator (LASSO) analysis. The final set of predictors corresponded to $\sim$50 events per predictor parameter [20].

2.6. Prediction models

The aim of our research was to apply statistical and AI methods to determine how they might improve the performance of predictive models, both on their own and when the predictions are combined using ensemble methods. We therefore employed the following established statistical and machine learning methods to predict the adverse outcome for patients: logistic regression, support vector machine, gradient boosting decision trees and artificial neural networks. This section briefly describes these classification techniques and how their predictions are combined using a stacking ensemble framework. To enable us to measure the performance of the models more reliably, we used 10 fold cross-validation with 50 rounds of imputations was employed to develop the models discussed above. Finally, the average classification performance metrics from all of the 10-fold cross-validations were obtained.

2.6.1. Logistic regression

Logistic regression (LR) models have been used frequently in prediction and analysis for several clinical applications and injury severity [21]. They can estimate the probability of an adverse outcome event as a prediction result (1, adverse outcome; 0, no adverse outcome). Moreover, the coefficients of the logistic regression reflect the contribution of each predictive feature to the adverse outcome event (the target). Thus, one will be able to get an estimated prediction, and identify the most important contributing factors related to the adverse outcome. Logistic regression models can be presented as:

$$p\left(\mathbf{y}\right)=f(\mathbf{aX}+c)$$

where $p\left(\mathbf{y}\right)$ is the probability of having an adverse outcome, $y\in \{0,1\}$, $c$ is the model constant, $\mathbf{X}$ is the vector of the predictor variables and $\mathbf{a}$ is the vector of the regression coefficient of these variables. In this study 26 predictor parameters were used (Table 1, Table 2). The probability, $p\left(y_i\right)$, should be close to either $0$ or $1$, therefore it is best to use a sigmoid function. Thus the probability of adverse outcome and no adverse outcome events can respectively be described by $p_{y=1}=\pi$ and $p_{y=0}=1-\pi$, where $\pi =\frac{e^{c+\mathbf{aX}}}{1+e^{c+\mathbf{aX}}}$

Table 1.

Patient characteristics.

Characteristic	Statistic/level	Adverse	No adverse	Total,
		outcome, n (%)	outcome, n (%)	n (%)
	N	1330 (17.6)a	6220 (82.4)a	7549
Age (years)a	Mean (SD)	74.5 (15.4)	56.9 (19.4)	60 (20)
	Median (IQR)	78 (65,86)	56 (42,73)	59 (45,77)
	Range	19 to 103	16 to 105	16 to 105
Gendera	Male	760 (57.3)	2825 (45.4)	3590 (47.5)
	Female	570 (42.7)	3390 (54.6)	3960 (52.5)
Number of	N	1330	6220	7549
current	Mean (SD)	4.5 (3.3)	3.2 (3.3)	3.4 (3.3)
medicationsa	Median (IQR)	4 (2,7)	2 (0,5)	3 (0,6)
	Range	0 to 19	0 to19	0 to19
Comorbiditiesa	Cardiovascular disease	95 (7)	290 (4.6)	380 (5.1)
	Chronic respiratory disease	375 (28)	1855 (29.8)	2230 (29.5)
	Diabetes	390 (29.2)	995 (16)	1380 (18.3)
	Hypertension	610 (45.8)	1765 (28.4)	2375 (31.4)
	Immunosuppression	280 (21.1)	930 (15)	1215 (16.1)
	Active malignancy	60 (4.6)	115 (1.9)	180 (2.3)
	Renal impairment	55 (4.1)	125 (2)	180 (2.4)
	Stroke	30 (2.3)	85 (1.4)	115 (1.5)
Clinical frailtya	N/A (age $<$65 years)	330 (47.5)	3985 (86.4)	4310 (81.3)
	Missing	645	1605	2250
	1–3	20 (4.7)	40 (6.4)	60 (5.8)
	4–6	75 (20.5)	240 (37.7)	310 (31.4)
	7–9	270 (74.8)	350 (55.9)	620 (62.8)
Glasgow Coma	N	1297	6085	7382
Scale	Mean (SD)	13.7 (2.4)	14.8 (0.8)	14.6 (1.3)
	Median (IQR)	15 (14,15)	15 (15,15)	15 (15,15)
	Range	3 to 15	3 to 15	3 to 15

^aTo comply with NHS digital disclosure guidance totals for these variables are rounded to the nearest 5,

which may result in apparent disparities in the overall totals.

Table 2.

Patient characteristics (continued).

Characteristic	Statistic/level	Adverse	No adverse	Total,
		outcome, n (%)	outcome, n (%)	n (%)
ACVPU	Missing	13	58	71
	Alert	1002 (76)	5860 (95.1)	6862 (91.8)
	Confusion	125 (9.5)	188 (3.1)	313 (4.2)
	Voice	100 (7.6)	84 (1.4)	184 (2.5)
	Pain	64 (4.9)	21 (0.3)	85 (1.1)
	Unresponsive	27 (2)	7 (0.1)	34 (0.5)
Diastolic BP	N	1278	6029	7307
(mmHg)	Mean (SD)	76.7 (17.7)	84.5 (15.9)	83.1 (16.5)
	Median (IQR)	76 (65,87)	84 (74,94)	83 (72,93)
	Range	0 to 193	22 to 167	0 to 193
Systolic BP	N	1277	6032	7309
(mmHg)	Mean (SD)	133.2 (25.8)	140.2 (23.2)	139 (23.9)
	Median (IQR)	132 (116,148)	139 (124,153)	138 (123,152)
	Range	65 to 238	33 to 237	33 to 238
Pulse rate	N	1303	6130	7433
(beats/min)	Mean (SD)	100.2 (22.5)	96 (19.5)	96.7 (20.1)
	Median (IQR)	99 (84,115)	94 (82,109)	95 (82,110)
	Range	38 to 194	7 to 190	7 to 194
Respiratory rate	N	1315	6145	7460
(breaths/min)	Mean (SD)	30.1 (10)	23.1 (6.9)	24.4 (8)
	Median (IQR)	28 (22,36)	20 (18,26)	22 (18,28)
	Range	0 to 76	0 to 84	0 to 84
Oxygen saturation	Missing	36	109	145
	$>$95 on air	142 (11)	3532 (57.8)	3674 (49.6)
	94–95 on air	134 (10.3)	854 (14)	988 (13.3)
	92%–93% on air	109 (8.4)	449 (7.3)	558 (7.5)
	$<$92% on air or O2 given	910 (70.3)	1274 (20.9)	2184 (29.5)
Blood glucose	N	982	4021	5003
(mmol/L)	Mean (SD)	8.1 (4)	6.9 (3.2)	7.2 (3.4)
	Median (IQR)	6.8 (5.6,9)	6 (5.2,7.3)	6.2 (5.2,7.7)
	Range	0.9 to 35	1.1 to 33.8	0.9 to 35
Temperature (°C)	N	1301	6115	7416
	Mean (SD)	38.1 (1.2)	37.8 (1.1)	37.8 (1.1)
	Median (IQR)	38.2 (37.4,38.9)	37.7 (37,38.5)	37.8 (37,38.6)
	Range	32 to 42	34 to 41.7

Logistic regression assumes linearity in the logit for continuous predictors. Where this was not the case, fractional polynomial transformations were used. The method also relies on low multicollinearity. Where variables were highly correlated, clinical experts were consulted and only the recommended variable was entered into the variable selection process. In our implementation of LR, shrinkage and internal bootstrap validation processes were employed to reduce the likelihood of over-fitting.

2.6.2. Support vector machine

Support Vector Machine (SVM) [22] is one of the most commonly-used machine learning models in supervised learning for classification problems, due to its ability to handle non-linear data and its reduced tendency for overfitting compared to other techniques [23]. To predict the outcome, the algorithm classifies the data into the two classes utilising the optimal hyperplane. The hyperplane is selected based on the maximum margin from the nearest points. Let the training instances be expressed as $(x_i,y_i)$ where $i=1,2,\dots ,N$, $y_i$ denotes the class of instance $x_i$, and $N$ indicates the number of instances. The algorithm finds two parallel hyperplanes that can separate the data, and maximise their distance. This distance is calculated by dual formulation using Lagrange’s multiplier $\alpha$:

$$\text{Minimise }L=\sum _{i=1}^l{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^l{\alpha }_i{\alpha }_j{y}_i{y}_{j}k\left({\mathbf{x}}_i{\mathbf{x}}_j\right)$$

where $k\left({\mathbf{x}}_i{\mathbf{x}}_j\right)$ is the kernel function of SVM. Appropriate parameters for the SVM, namely the kernel function, cost, and gamma were set for this analysis based on the performance on a small development set. It was observed that a linear kernel suits this application more than the non-linear kernel and therefore it has been used in this work.

2.6.3. Gradient boosted decision trees

XGBoost (XGB, Chen and Guestrin [24]) is an improved version of Gradient Boosted Decision Trees (GBDT), which is a machine learning method that works by combining an ensemble of $K$ weak models $f_k\left(\mathbf{x}\right)$ from a space of regression trees $\mathcal{F}=\{f\left(x\right)=wq\left(x\right)\}$, to create more accurate models [25]. Each $f_k$ is a function with weight $w\in R^T$ and independent tree structure $q$ with $T$ leaves, such that $q:R^m\leftarrow T$ maps a set of features $\mathbf{x}$ into the corresponding leaf index. In particular, for a set of data with $m$ features, $K$ additive functions are used to predict the $i$th output:

$${\hat{y}}_i=\varphi \left(x_i\right)=\sum _k^K{f}_k\left({\mathbf{x}}_i\right),f_k\in \mathcal{F},$$

where ${\mathbf{x}}_i\in R^m$, is the feature vector of the $i$th input. The core of the algorithm is based on learning the set of functions with the objective that minimises the difference between the actual outcome $y$ and the predicted outcome $\hat{y}$ via the following loss function $\mathcal{L}$:

$$\mathcal{L}\left(\varphi \left(x_i\right)\right)=\sum _k(y_i,{\hat{y}}_i)+\sum \Omega \left(f_k\right),$$

where $\Omega \left(f_k\right)$ is a regularisation term that helps smooth the learning of the weights to prevent over-fitting.

2.6.4. Artificial neural networks (ANNs)

Artificial Neural networks (ANNs), often referred to as “neural networks” or “networks”, are well known for their self-learning, using self-error correction mechanisms and nonlinear mapping abilities, to achieve high performance. They can potentially improve the prediction of adverse outcomes by learning and exploiting non-linear relationships between the various patient characteristics and the adverse outcome. In our neural network implementation, four-layer feed-forward networks, was used, with a back-propagation supervised learning algorithm [26]. The training parameters included a batch size of 80 and 100 epochs. Batch size indicates the total number of training samples processed in a single batch and the number of epochs indicates the number of times all of the training data have been used to train the neural network. The patient characteristics were fed into the input layer of the neural network, where a collection of neurons processed it and passed it to the next hidden layer sequentially, until it reached the output layer. As such, the neural network implements a mapping between our input vectors and output vectors, with layers of intermediate nodes. During the training process, at the output layer, the processed data were compared with the ground truth outcomes (i.e., the actual observations) and the error was fed back to the network to update its weights/parameters. This is the process of back-propagation, which fine-tunes the weights of the neural network based on the error rate obtained in the previous epoch, with the ultimate aim of minimising the error, E, in achieving the target values.

$$E=\sum _{\mu }{E}_{\mu }=\sum _{\mu ,j}(t_j^{\mu }-o_j^{\mu })$$ (1)

where $o_j^{\mu }$ is the output of the $j$th node when a set of input vectors $s_i^{\mu }$ and target values $t_j^u$ are introduced into the neural network. The initial set of weights used in back-propagation ($w_{ij}$) are randomly selected, and hence, there is a risk of reaching a locally optimal set of weights. In addition to this risk, neural networks also have other limitations, the primary ones being the need for very large volumes of data and the computing resources required. In our specific applied scenario, resource limitations did not have an impact on the performance of our model, as we used a dedicated high performance machine. However, a discussion of the impact of different sizes of data sets on our model performance is outside the scope of this paper. In our model, there were four layers, the input layer, two dense-ReLU hidden layers and an output layer. The input layer contained 26 nodes corresponding for the 26 patient characteristics features, while the output layer had one node, to represent whether the output was an adverse case or not. The overall network therefore had a 26:128:64:1 architecture, i.e., that it had 26 input nodes for the independent variables, 128 and 64 nodes in the first and second hidden layers respectively, and one output, Sigmoid-activated, node in the final layer for the dependent variable. The neural network was implemented in Python, using the Keras library [27].

2.6.5. Stacking ensemble method

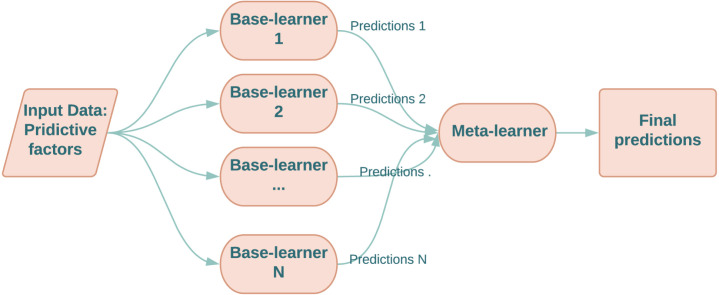
Ensemble learning is a mechanism for collaborative decision-making that aggregates the decisions (predictions) of multiple models to produce new (probably better) predictions. There are several ensemble learning techniques in literature however, the most common ones are: (a) Bagging [28], (b) Boosting [29], Stacking [30] and Mixture of Experts [31], [32], [33]. Despite of several ensemble methods are presented in literature, finding a good ensemble configuration is still not a trivial task and depends on the target application. In this work, the stacking ensemble learning technique is used. Stacking, also called stacking generalisation, was first proposed by Wolpert [30], and is a hierarchical ensemble technique that aims to combine the strengths of multiple prediction methods to boost the prediction accuracy. In particular, the predictions of multiple models, referred to as base-models, are fed into a second-level model, referred to as a meta-learner. The meta-learner is then trained to optimally combine the predictions of base-learners, to form a final set of predictions. An example of its use in medical research is to predict occurrences of major adverse cardiovascular events in patients with acute coronary syndromes [34]. A simplified diagram of stacking is shown in Fig. 1.

Fig. 1.

A sketch of stacking ensemble framework.

With regards to selecting the meta-learner, Wolpert [30] stated that a simple linear model could do very well since all the classification efforts were completed by the base-learners.

In this study, a logistic regression model was used as the meta-learner, and different combinations of SVM, XGB and ANNs were used as base-learners, resulting in four different instances of stacking ensemble models.

2.7. Evaluation metrics

The accuracy of the predictions of the adverse outcome was assessed using the AUC, also referred to as the c-statistic, a measure of the goodness fit of the model. This gives the probability of a model correctly predicting the patients with higher risk. Unlike other metrics, it does not require a particular threshold value. However, the AUC is not enough on its own to evaluate performance on imbalanced data [35], [36]. Thus, typically, the negative predictive value (NPV) and positive predictive value (PPV) measures are also reported together with the sensitivity (the % of true positive cases [i.e., that experienced an adverse outcome] that were correctly identified by each method), and specificity (the % of true negative cases [i.e., that did not observe the adverse outcome] that were correctly identified as false cases), and the geometric mean, GM, of the sensitivity and specificity:

$$\text{Sensitivity}=\frac{TP}{TP+FN}$$

$$\text{Specificity}=\frac{TN}{FP+TN}$$

$$GM=\sqrt{\text{sensitivity}x\text{specificity}}$$

$$NPV=\frac{TN}{TN+FN}$$

$$PPV=\frac{TP}{TP+FP}$$

where TN (the number of true negatives), FN (the number of false negatives), TP (the number of true positives) and FP (the number of false positives) were calculated for a particular operating point (also referred to as cut-off point) on the AUC curve. The operating point can be adjusted to alter the sensitivity, and this is usually set by clinical experts based on the requirements of the application. Choosing an operating point that has a high sensitivity is common practice in several clinical applications [37], [38], [39], as this minimises the number of false negatives. This is particularly desirable for the COVID-19 pandemic, because cases treated earlier were more likely to survive. However, there is inevitably a trade-off between increasing the sensitivity, which is typically associated with a decrease in specificity. We therefore used two operating points in separate models for each algorithm, the first to maximise the sensitivity and the second to maximise the specificity.

In the research literature, setting the operating points is varied according to the application. For example, Abràmoff et al. [38] chose a pre-selected set point on the AUC at which a sensitivity of 96.8% was reported for detecting referable diabetic retinopathy on the publicly available Messidor-2 data set. This point was associated with a specificity of 59.4%, PPV of 39.8% and NPV of 98.5%. Valente et al. [40] considered a cut-off threshold that achieved a sensitivity of 80% in predicting the level of mortality risk after acute coronary syndrome. This cut-off was associated with NPV and PPV values of 99% and 17% respectively. In developing the PRIEST tool, Marincowitz et al. [41] selected a predicted probability threshold that led to high NPV (this also implies high sensitivity), but with a relatively high PPV (i.e., at least 96.5% NPV and a minimum PPV of 28%). These restrictions were associated with a sensitivity of 99% but the specificity was reduced to 7%.

Other studies have selected operating points at which the $F1$ measure (the harmonic mean of sensitivity and precision) was maximum, as used by Vaid et al. [42], and where the cut-off was calculated separately for each folder to maximise the $F1$ measure. The threshold for the final model was then computed as the median of those per-fold thresholds.

Using the baseline PRIEST scoring tool [11], the best performance achieved on the same data set used in this study was: sensitivity 97%, specificity 41%, NPV 98%, PPV 26%. In this study, a cut-off that achieved an NPV of at least 98% and a PPV of at least 26% was used as the operating point for the developed classification models for predicting adverse outcomes.

2.8. Ethical approval

The North West-Haydock Research Ethics Committee gave a favourable opinion on the PAINTED study on 25th June 2012 (reference 12/NW/0303) and on the updated PRIEST study on 23rd March 2020, including the analysis presented here. The Confidentiality Advisory Group of the NHS Health Research Authority granted approval to collect data without patient consent in line with Section 251 of the National Health Service Act 2006. Access to data collected by NHS Digital was recommended for approval by its Independent Group Advising on the Release of Data (IGARD) on 11th September 2021 having received additional recommendation for access to GP records from the Profession Advisory Group (PAG) on 19th August 2021.

3. Results

3.1. Sample characteristics

The study cohort derivation and the characteristics of the 7549 adult patients are summarised in Table 1, Table 2, for the overall sample and according to whether the patients experienced the adverse outcome or not. The sample is described in further detail elsewhere. Marincowitz et al. [11]. In brief, the mean age of patients was 60 years (SD $=$ 20) and 52.5% of the sample was female (n $=$ 3960). The mean number of medications being taken was 3.4 (SD $=$ 3.3). In total, 1330 patients (17.6%, 95% CI:16.8% to 18.5%) experienced one or more of the primary outcomes (i.e., death or organ support). Patients who experienced adverse outcomes were generally older than those who did not, and were taking higher numbers of medications. A higher proportion of those who experienced an adverse outcome were males (57.3%; n $=$ 760).

The variables listed in Table 1, Table 2 form the predictors (e.g., gender, number of current medications, comorbidities and clinical frailty scores, etc.) used in the proposed prediction models. All reported results are based on the average of ten cycles of ten-fold cross-validation experiments.

3.2. Model performance

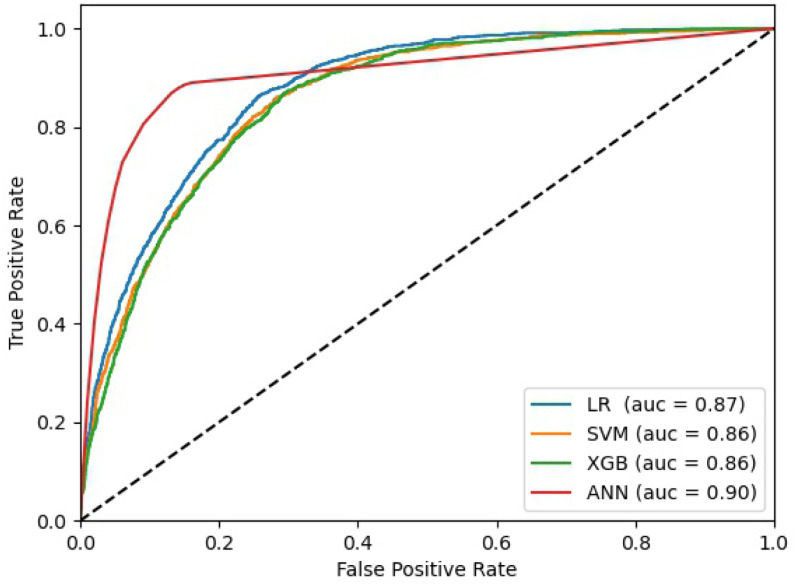
Table 3 presents the results for the four separate prediction methods in comparison with the baseline results, i.e., EMS clinician and PRIEST clinical severity score [11], at the two different operating points, i.e., to maximise sensitivity (3a) and specificity (3b), whilst also restricting the region of performance to have NPV and PPV values of at least 0.98 and 0.26 respectively. Three of the methods (LR, SVM and XGB) showed slight improvements in sensitivity over the study baseline results reported previously [11] with no major differences among these methods: they all achieved AUC scores between 0.86-0.87 and geometric means (GM) of sensitivity and specificity between 0.62–0.65. These three methods also showed improved performance compared to the baseline when maximising specificity (3b). However, the ANN model performed better overall when compared to these methods at both operating points with much a higher specificity, geometric mean and AUC. It achieved GMs of 0.83 and 0.86 at the first and second operating points respectively, and AUC of 0.90 and 0.86, albeit with greater variability at both operating points. Fig. 2 shows the Receiver Operating Characteristic (ROC) curves for the individual LR, SVM, XGB and ANN models.

Table 3.

Performance of individual algorithms using the first (high sensitivity) and second (high specificity) operating points. The baseline models were the decision by the EMS clinicians whether to convey the patient to hospital or not and the recommendation arising from the use of the PRIEST clinical severity score [11].

	Model	Sensitivity	Specificity	npv	ppv	GM	AUC
Baseline	EMS clinician	0.84	0.39	0.92	0.23	0.57	NA
	PRIEST score	0.97	0.41	0.98	0.26	0.63	0.83 ± 0.01
(a) High sensitivity	LR	0.98	0.43	0.99	0.27	0.65	0.87 ± 0.01
	XGB	0.98	0.39	0.99	0.26	0.62	0.86 ± 0.02
	SVM	0.98	0.41	0.99	0.26	0.63	0.86 ± 0.01
	ANN	0.96	0.72	0.99	0.43	0.80	0.90 ± 0.09
(b) High specificity	LR	0.93	0.64	0.98	0.37	0.77	0.87 ± 0.01
	XGB	0.95	0.56	0.98	0.31	0.72	0.86 ± 0.02
	SVM	0.94	0.60	0.98	0.33	0.75	0.86 ± 0.01
	ANN	0.95	0.77	0.98	0.48	0.86	0.90 ± 0.09

Fig. 2.

The ROC curves of the individual models.

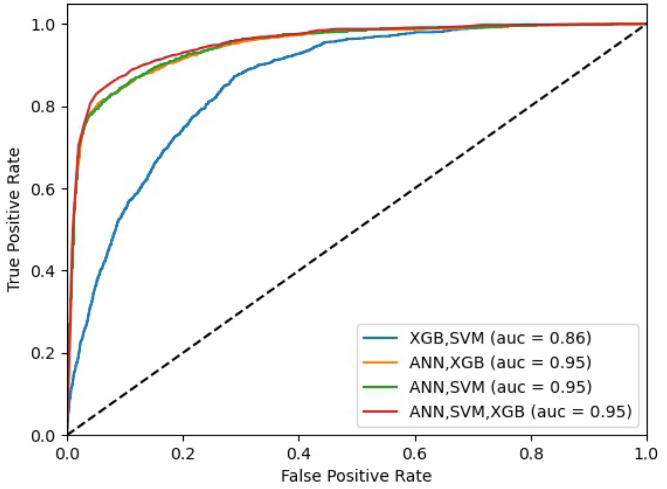
In order to improve the prediction of patients with high risk of adverse outcome, we combined the predictions of these classifiers to produce optimal predictive models using the stacking ensemble method (as discussed in Section 2.6.5). Table 4 shows the results for the four ensemble methods in comparison with the baseline results (i.e., EMS clinician assessment and PRIEST clinical severity score). Overall, the ensemble models showed clear improvements and consistent increase in the prediction measures when compared to the individual models, with AUC values of 0.95 for three of the four stacked ensemble models at both operating points. The best GM results were obtained when stacking SVM and ANN as base learners at both operating points. The best GM was achieved at the second operating point for this ensemble with a relative difference of 4%, compared to the performance of the same model operating at the first operating point. Fig. 3 shows the ROC curves for the ensembled models presented in Table 4.

Table 4.

Performance of stacked ensemble algorithms using the first (high sensitivity) and second (high specificity) operating points. The baseline models were the decision by the EMS clinician whether to convey the patient to hospital or not and the recommendation arising from the use of the PRIEST clinical severity score [11].

	Model	Sensitivity	Specificity	npv	ppv	GM	AUC
Baseline	EMS clinician	0.84	0.39	0.92	0.23	0.57	NA
	PRIEST score	0.97	0.41	0.98	0.26	0.63	0.83 ± 0.01
(a) High sensitivity	SVM,XGB	0.98	0.42	0.99	0.26	0.64	0.86 ± 0.01
	ANN,SVM	0.96	0.73	0.99	0.45	0.84	0.95 ± 0.01
	ANN,XGB	0.95	0.73	0.98	0.43	0.83	0.95 ± 0.01
	ANN,SVM,XGB	0.99	0.47	0.99	0.29	0.68	0.95 ± 0.01
(b) High specificity	SVM,XGB	0.93	0.60	0.98	0.33	0.74	0.86 ± 0.01
	ANN,SVM	0.92	0.83	0.98	0.57	0.88	0.95 ± 0.01
	ANN,XGB	0.90	0.83	0.98	0.53	0.86	0.95 ± 0.01
	ANN,SVM,XGB	0.90	0.83	0.98	0.53	0.86	0.95 ± 0.01

Fig. 3.

The ROC curves of the stacking models.

3.3. Feature importance

Feature importance ranking is important to help develop understandable and interpretable ML models. However, this is very challenging for deep learning methods due to the nature of combinatorial optimisation and the nested non-linear structure within these methods. Although recently several attempts have been made to understand the importance of features within deep learning methods [43], [44], they are still in their initial stages of development and beyond the scope of this study. In this section, we therefore only discuss the feature importance of the linear models.

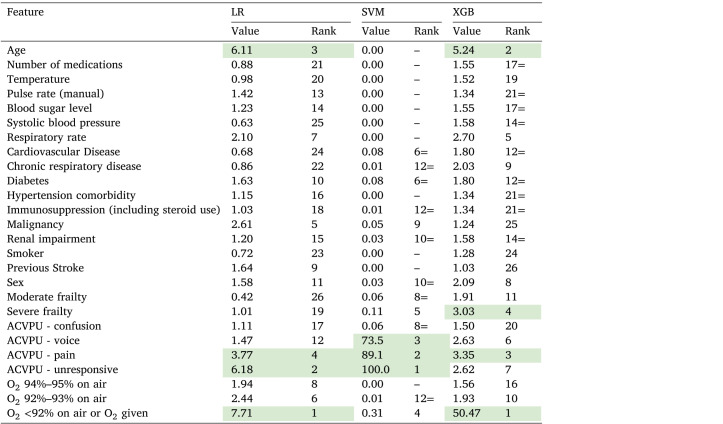
Table 5 lists the coefficients/weights considered by the linear models LR, SVM and XGB. The LR coefficients are exponentiated standardised coefficients. The weights given for the different features by the SVM classifier are normalised by the largest weight, to reduce the effect of the high variation among those weights. The coefficients of the XGB, however, are normalised by their count and multiplied by a 100, such that the column sum is 100%.

Table 5.

Feature importance for LR, SVM and XGB Models (the higher levels of importance within each model are highlighted in green for emphasis).

It can clearly be seen from Table 5 that the distribution of feature relevance varies considerably according to the three different classifiers and is unbalanced across the individual features. While SVM mainly considered the patient’s level of consciousness (ACVPU), XGB gave most weight to oxygen saturation, with much lower weights to other variables, including age and severe frailty. Overall, while the XGB selected all features, the SVM classifier selected (in a descending order) ACVPU, oxygen saturation, frailty, comorbidity and sex. Logistic regression (LR) highlighted oxygen saturation, level of consciousness and age as the most important features. The importance of these features was also reported by the papers reviewed in [9].

4. Discussion

The aim of this study was to develop and improve prediction models for identifying adverse health outcomes for patients with suspected COVID-19 in a pre-hospital setting. A cohort of patients with suspected, as opposed to confirmed, infection was used as this reflects the population that EMS clinicians had to risk stratify clinically. We used a composite health outcome measure of in-hospital organ support or death within 30 days of initial assessment by EMS clinicians. While predicting inpatient admission or oxygen therapy is likely to vary in different settings, developing more accurate predictive models using AI methods could help ensure necessary care is provided for those most at risk of serious adverse outcomes, whilst reducing unnecessary transfers and the risk of hospitals and EMS services being overwhelmed by demand, which was an important problem during the COVID-19 pandemic. To the best of our knowledge, this is the first study of its kind to investigate applying ML methods to enhance the predictive ability of decision-making by EMS clinicians for patients with suspected COVID-19. Our use of ensemble methods in this respect is novel and adds to the knowledge base on using ML methods for decision-making in clinical practice.

The use of risk prediction models in clinical decision-making requires trade-offs. The first is between overall accuracy, sensitivity and specificity. Given the serious consequence of not transporting a patient with suspected COVID-19 to hospital, e.g., who subsequently dies or requires intensive care support, we aimed for our machine learning models to achieve the same sensitivity (0.97) as the PRIEST clinical severity score [11] for decision-making alone and corresponded to a non-conveyed patient having a 1/50 (NPV 0.98) risk of subsequent deterioration, without sacrificing the specificity of current practice and leading to large increase in patients transported to hospital. Although a useful comparator for performance of developed predictive models, EMS decision-making to transfer patients to hospital is not made solely on the basis of the risk of deterioration. Decisions may need to account for clinical best interest decisions not to convey patients to hospital who subsequently deteriorate, especially at the end-of-life, when palliation may be appropriate, or the patient wishes not to be conveyed.

XGB, LR and SVM models could achieve theoretical gains in the sensitivity of prediction, whilst maintaining specificity, leading to overall gains in discrimination. Stacking of methods led to further gains in accuracy and their use in clinical settings could lead to reductions in hospital conveyance with a reduced risk of non-conveyed patients deteriorating. Stacking of ANN, SVM and XGB achieved a sensitivity 0.99, specificity of 0.47 and an AUC of 0.95. However, increased accuracy of these methods comes at the cost of increased complexity and reduced interpretability. The PRIEST clinical severity score can be manually calculated and is based on physiological parameters already used by EMS clinicians to risk assess patients as part of the National Early Warning Score (NEWS2), alongside age, sex and performance. Logistic regression modelling used to develop the PRIEST clinical severity score achieved similar measures of accuracy and calibration to LR, SVM and XGB modelling in this study [45]. However, following consultation with clinical stakeholders, a simplified scoring system based on NEWS2 was derived in order to improve clinical usability at the cost of accuracy. ANN and stacked prediction methods offer significant gains in accuracy, but use a greater number of variables and the prediction methods are not transparent and would require automation of individual prediction to allow implementation. The ‘black box’ nature of prediction may have implications for acceptability for both patients and clinicians. In addition, the PRIEST clinical severity score has been externally validated in different settings [11], [46]. Our machine learning models would require both the ability to be practically implemented by EMS clinicians and external validation before they could be used clinically.

A strength of our study is in the relatively large numbers of cases ($>$7500) available for the analyses, including 1330 cases with adverse outcomes (17.6%). This compares favourably with other studies developing prediction models for COVID-19 using AI methods. In a recent review, Abd-Alrazaq et al. [7] reported that half of the included studies had fewer than 1000 patients. Having small numbers of cases can lead to overfitting and increased risk of bias. Our a priori sample size calculations were based on an estimated precision of the area under the ROC curve based on a likely 5% event rate in a cohort of 6000 patients [19]. The sample size estimation suggested 30 predictors could be assessed for inclusion in the models (we included 26). The number of included variables were reduced on the basis of clinical feasibility, the level of missing data or high collinearity.

However, our machine learning models have only been internally validated and due to (potential) over-fitting, may not perform as well when applied to new datasets. The data we obtained were from a single region in the UK (Yorkshire and Humber) and features used by the models may be less applicable to other settings. Further testing of our models on other data would therefore be required to validate the models externally, and to assess the clinical impact of using these methods for triage alongside clinical judgement. Additionally, these data were collected during the first lockdown period in the UK (March–June 2020), a period before the COVID-19 virus had mutated significantly, and before vaccinations and universal reliable COVID tests were available. Further testing of the models on data collected from patients in more recent phases of the pandemic is required to test the durability of our models in the light of changes in the virus and the pandemic.

As described previously, our study used a combined adverse outcome of a patient dying or requiring organ support within 30 days of their initial visit by the EMS. It is possible that the model performance and feature importance may have differed if these outcomes had been assessed separately: however, our aim was to develop models that predicted an outcome which identified patients in definite need of hospital care. This would prioritise care for those who need it most and help to minimise the risk of hospitals and EMS being overwhelmed during the pandemic. Further research could develop predictive models for these separate outcomes and compare the features (variables) contributing to the predictions.

Our study focused on the effectiveness of the machine learning models and compared these with clinical decision-making and existing triage tools: our aim was not to examine the efficiency of these methods, and clearly this would require further work, i.e., to compare the computation times of the developed approaches. Further work is required for these ML models to be implemented into routine practice, and more research would be needed to demonstrate how such models can be operationalised effectively and efficiently. A robust prospective evaluation would be needed to demonstrate the effectiveness and safety in a pre-hospital clinical setting.

Further work could also usefully explore what other forms of data collected by EMS might help improve the effectiveness of these algorithms. For example, the textual notes that EMS clinicians record could potentially be a rich source of data, as well as other patient details. These records might yield insights into the possibilities of patients developing complications that require hospital admission, the need for organ support, as well as risk of death during COVID-19 infection. The use of text mining methods, such as Natural Language Processing (NLP), could be used to extract features to refine predictive models further.

5. Conclusion

This study provides new evidence regarding the potential of machine learning methods to develop models for prediction of adverse health outcomes in patients with suspected COVID-19 within 30 days of being assessed by an EMS clinician. When compared with transfer decisions made by EMS clinicians at the time of assessment, and the previously reported PRIEST tool [11], the proposed models performed better at predicting who was at risk of requiring organ support and/or dying, and therefore who was in most need of hospital care. Compared with the PRIEST tool, the XGB method demonstrated a relative improvement in performance by 3.6%, SVM by 3.5%, ANNs by 8.4% and LR by 4.8%. When the models were stacked, there was further improvement in performance: the best overall performance was obtained when stacking the ANN and SVM models, which showed an improved relative performance over the PRIEST tool by 14.5%.

The work demonstrates the potential of ML methods to support the decision-making of front-line EMS clinicians in assessing the severity of patients with suspected COVID-19. The proposed ML methods could be applied to help clinicians in identifying patients at high risk of adverse outcomes using data gathered from patients with high PPV rates (ranging from 31%–48%), considerably higher than the PRIEST tool or the EMS clinicians.

The developed models could therefore help both identify patients most likely to need treatment in hospital whilst avoiding overwhelming hospital and emergency services with large numbers of patients. In other words, these models could potentially lead to reductions in the numbers of patients conveyed to hospital without a concomitant increase in adverse outcomes. The research is also important in that it provides an understanding of the relative importance of specific patient features in the decision-making process within the predictive models, overcoming the problems traditionally associated with ‘black box’ technologies. Across the methods for which the importance of these features could be ranked, oxygen saturation, the patient’s level of consciousness, their level of frailty and age appeared the most important. These features concurred with those previously identified in [9] and those in the PRIEST tool [11].

Further research is required to validate the findings externally, and to develop and test a tool to automate the prediction of the risk of adverse outcome, so that the methods can be utilised by EMS clinicians in practice. This would also require the computational efficiency of the algorithms to be compared, and optimised, in order to balance both accurate and timely decision-making. Further work could also investigate the use of NLP for extracting features from the textual notes of EMS clinicians within electronic records and to investigate other methods (e.g., genetic algorithms) for dealing with missing data, a common problem when utilising data from clinical records.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.