Abstract
The coronavirus disease 2019 (COVID-19) epidemic has spread worldwide, posing a great threat to human beings. The stay-home quarantine is an effective way to reduce physical contacts and the associated COVID-19 transmission risk, which requires the support of efficient living materials (such as meats, vegetables, grain, and oil) delivery. Notably, the presence of potential infected individuals increases the COVID-19 transmission risk during the delivery. The deliveryman may be the medium through which the virus spreads among urban residents. However, traditional delivery route optimization methods don’t take the virus transmission risk into account. Here, we propose a novel living material delivery route approach considering the possible COVID-19 transmission during the delivery. A complex network-based virus transmission model is developed to simulate the possible COVID-19 infection between urban residents and the deliverymen. A bi-objective model considering the COVID-19 transmission risk and the total route length is proposed and solved by the hybrid meta-heuristics integrating the adaptive large neighborhood search and simulated annealing. The experiment was conducted in Wuhan, China to assess the performance of the proposed approach. The results demonstrate that 935 vehicles will totally travel 56,424.55 km to deliver necessary living materials to 3,154 neighborhoods, with total risk
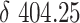 . The presented approach reduces the risk of COVID-19 transmission by 67.55% compared to traditional distance-based optimization methods. The presented approach can facilitate a well response to the COVID-19 in the transportation sector.
. The presented approach reduces the risk of COVID-19 transmission by 67.55% compared to traditional distance-based optimization methods. The presented approach can facilitate a well response to the COVID-19 in the transportation sector.
Keywords: COVID-19, virus transmission, emergency logistics, hybrid meta-heuristics, living materials
I. Introduction
Humans have long been afflicted by epidemics, such as, the Black Death, the “Spanish Influenza”, etc [1]. Since 2000, there have been several outbreaks of multiple coronaviruses, including SARS(2003), MERS(2012), etc. In December 2019, the coronavirus disease 2019 (COVID-19) outbreak began and had since spread worldwide. On May 23, 2020, it was reported 5.1 million people had been infected, 0.33 million of which has been dead [2]. COVID-19 is now posing a great threat to human beings, wreaking havoc on socio-economic development. Restricting travel and crowding is effective to cut off COVID-19 transmission [3]. The department of epidemic prevention and control of Wuhan encouraged people to stay at home to reduce the infection risk. On January 23, 2020, Wuhan was “locked down”. Public transportation, such as bus, subway, and ferry, was stopped. Airports and railway stations were temporarily shut down. On February 14, 2020, the neighborhood close policy was suggested to strengthen the home quarantine [4]. This situation calls for emergent living material (such as meats, vegetables, grain, and oil) for basic home living. Governments and enterprises closely cooperated in collecting residents’ demands, organizing living material, and distributing them.
The distribution of living materials is the key to the home quarantine. About 3 million delivery drivers were encouraged to distribute living material to ensure the success of the home quarantine [5]. However, the COVID-19 can transmit along with the living material delivery. The deliverymen confront a high infection risk because they frequently touch with living materials, some of which may be attached to the COVID-19. Many cases in Beijing and Dalian, China have been reported that the package surface of living materials (i.e., frozen food) can cause the COVID-19 infection [6]. Furthermore, a deliveryman may contact other persons. If one deliveryman is infected, he/she will become the super spreader of the COVID-19. For example, a pizza delivery boy in Malvia Nagar, Delhi, India has reported with the positive COVID-19, leading 72 families he delivered food to be quarantined [7]. Similar cases were also reported in BeiJing and Shenzhen, China [8]. Therefore, the necessary living material delivery will increase the COVID-19 transmission risk.
The COVID-19 may transmit between neighborhoods due to necessary living material delivery. Although the contactless delivery, such as express cabinets, will reduce physical contact between the deliveryman and urban residents, there is still an un-ignorable risk for the delivery because of the necessary human-things-human interactions. Fig. 1 shows the lifecycles of the living material delivery. The residents firstly order their living material in the online B2C platform. The supermarkets will accept orders, prepare the goods, and assign the deliveryman. During the early COVID-19 period, there are many confirmed and suspected COVID-19 cases in the neighborhoods. These cases are not timely checked and token care because of the limited health resources and fast virus transmission. Therefore, when the deliveryman directly or indirectly contacts these COVID-19 cases, they would bring the COVID-19 virus to the following delivered neighborhoods. For example, if one neighborhood has some COVID-19 cases, i.e., n1, the deliveryman may be infected and bring the COVID-19 virus to the following neighborhood, n2.
Fig. 1.
Living materials delivery during the home quarantine.
Measuring the COVID-19 transmission risk during the delivery process is the prerequisite. Several popular models, e.g., the susceptible-infectious (SI), the susceptible-infectious-recovered (SIR), and the susceptible-exposed-infectious-recovered (SEIR) model have been developed to simulate and predict the virus transmission [9]. These models focus on the viral infection status transition and incubation, assuming that contacts among people are homogeneous. But this assumption is challenged, as some persons’ daily travels are quite different [10]. Especially, the deliveryman travels the most in the city. Generally, human movements can be characterized by complex network, which represents the connections and interactions among nodes. The complex network-based virus transmission can well describe the group-based virus spreading process [11]. In this study, we propose a virus transmission risk indicator,
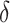 , to investigate the risk because of the living material delivery. A complex network-based approach is developed to quantify the COVID-19 transmission risk for different distribution schemes.
, to investigate the risk because of the living material delivery. A complex network-based approach is developed to quantify the COVID-19 transmission risk for different distribution schemes.
Optimizing the living material delivery routes during the epidemic falls into the domain of emergency logistics. Previous emergency logistics studies mainly address the design of the emergency logistic network [12] or the planning of goods movement [13] to respond to emergent incidents, such as earthquakes, rainstorms, and typhoons. These studies generally pay much attention to the efficiency and unreliability of emergency logistics. Notably, the virus transmission risk during the distribution in the epidemic event has rarely been considered.
Taking the virus transmission risk into account, we propose a novel living material Delivery Route Optimization approach considering the Virus Transmission (DROVT) to support the essential home quarantine. A complex network-based virus transmission model is developed to simulate the possible COVID-19 transmission among residents and the deliverymen. A bi-objective model considering the COVID-19 transmission risk and the total route length is proposed and solved by the hybrid meta-heuristics integrating the adaptive large neighborhood search (ALNS) and simulated annealing (SA). An experiment in Wuhan was conducted to assess the performance of the DROVT. The results demonstrate that the proposed approach well balance between the virus transmission prevention and the efficiency of the living material delivery. Specifically, the main contributions of this study are summarized below:
-
•
A complex network-based virus transmission dynamics model is proposed to evaluate the COVID-19 transmission risk of the deliverymen and the neighborhoods.
-
•
A delivery route optimization framework considering both the virus transmission and the distribution efficiency is developed.
-
•
A hybrid meta-heuristics method integrating ALNS and SA is proposed to find a high-quality living material delivery scheme.
-
•
A set of experiments in Wuhan are designed to verify the effectiveness of the proposed approach. The effect of several factors, including vehicle capacity, travel control, and personal protection, are explored.
The rest of this paper is organized as follows. Section II reviews related literature. Section III introduces the study area and the dataset. Section IVdescribes the proposed approach. Section V reports the experiment and the results. The last section VI concludes this study.
II. Related Work
A. Epidemic Spreading Models
Modeling epidemic spreads refer to analyze and predict the disease spreading process and patterns [13]. The most typical epidemic spreading models is the compartment model, SIR, which was firstly applied to investigate the spreading of the Black Death pandemic [14]. The SIR generally assumes that the population is divided into several compartments, such as the susceptible (S), the infectious (I), and the recovered (R) individuals. The evolution of the disease is simulated and predicted according to the disease characteristics, i.e., the basic reproduction number, R0. Various models following the principle of the SIR have been developed, including the SEIR, SIQR, and SEIQR [15]. Noted that these models assume that the individuals are homogeneous in space, they ignore the complex spatial and topological structures of real-world epidemic spreading processes, especially in high-density cities.
The contacts between the crowds show some complex network characteristics, such as small-world, scale-free, etc [11], [16]. Complex network-based models have been proposed to simulate and predict the epidemics spreading. Generally, complex network-based epidemic spreading models could be classified into two categories: (1) individual contact-based network models (ICNM), in which nodes represent individuals, and edges represents physical contacts between individuals. By walking along the edges, the virus infects healthy individuals and spreads among the population. For example, zhang et al. [15] improved the SIR model based on social contact network, simulated the virus outbreak on social contact network, and presented some immunization strategies. (2) Meta-population network models (MNM), in which the nodes denote a group of people and the edges denote the inter-group contacts [17]. The MNM simulates and predicts at the group level rather than the individual level, therefore it is suitable for the modeling epidemic spreading from one geographical zone to another. For example, Calvetti et al. [18] built the complex network to predict the COVID-19 in Michigan and Ohio, USA by characterizing the nodes with the contact frequency and the connectivity with other nodes. Following the MNM approach, we regard the neighborhood as a meta-population and simulate the COVID-19 transmission between neighborhoods along with the delivery. The DROVT approach considering the virus transmission is developed to provide effective living material delivery to support the essential home quarantine.
B. Emergency Logistics
Emergency logistics refers to specialized transport activities aimed at providing necessary humanistic services during the events, such as pandemic, rainstorms, and typhoons [19], [20]. Emergency logistics emphasizes the humanitarian relief by providing the necessary daily living materials, i.e., water, food, and medicines. Previous studies on emergency logistics can be divided into three categories: (1) siting emergency logistics facilities to provide effective emergency services, e.g., locating emergency material supply center for post-earthquake rescuing and siting emergency ambulance depots [21], [22]; (2) designing emergency logistics network to improve the response efficiency or strengthen the reliability of the logistics [23], [24]. and (3) optimizing emergency distribution to design the best delivery routes by considering the uncertain road traffic, or the limited material supply [25], [26]. These emergency logistics tasks are with high computing complexity; therefore, they are hard to find the best solution. Heuristics are developed to find high-quality solution in a reasonable time. Meta-heuristics, including intelligent search (i.e., genetic algorithm (GA) [24], ant colony optimization (ACO) [27], etc) and local search, (i.e., large neighborhood search (LNS) [28], SA, tabu search (TS), etc. [29]–[31], are proposed to find a near-optimal solution by keeping the equilibrium of the intensification and the diversification of solution search [32]. In particular, the ALNS meta-heuristics extends the LNS framework, which destroys current solution and repairs it to iteratively explore neighborhood solutions. ALNS has achieved success in VRP and scheduling problem [33], [34].
The emergency logistics for the epidemic has also attracted some attention. For example, Zaric and Brandeau [35] investigated the allocation of medical resources for epidemic prevention and control using the cost-effectiveness analysis. Recently, a few studies examined the optimization of emergency medical logistics services. Dasaklis et al. [12] presented an emergency supplies distribution network optimization model to provide mass vaccination service to fight with a Smallpox Outbreak. For living material distribution, Ekici et al. [13] modeled the Influenza pandemic and planned food distribution with a heuristics algorithm. These studies provide useful insights into fighting with the medical emergency. However, the virus transmission risk because of the distribution activities under epidemics has often been ignored. To fill this gap, this study develops the DROVT approach considering the virus transmission along with the living material delivery. A hybrid meta-heuristics method integrating the ALNS and SA is proposed to find a high-quality solution.
III. Study Area and Data
The study was conducted in Wuhan, China, a city with a total area of 8,569.15
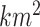 and a population of 14.2 million [36]. This city has 13 administrative districts, seven of which are core urban area, i.e., Jiang’an, Jianghan, Qiaokou, Hanyang, Qingshan, Wuchang, and Hongshan. In Decmber 2019, several unexplained pneumonia cases were reported in Wuhan. In the following month, Wuhan has been the epicenter of China. During the COVID-19 outbreak, about 5 million population had already left Wuhan, while approximately 9 million population stayed in the city [37].
and a population of 14.2 million [36]. This city has 13 administrative districts, seven of which are core urban area, i.e., Jiang’an, Jianghan, Qiaokou, Hanyang, Qingshan, Wuchang, and Hongshan. In Decmber 2019, several unexplained pneumonia cases were reported in Wuhan. In the following month, Wuhan has been the epicenter of China. During the COVID-19 outbreak, about 5 million population had already left Wuhan, while approximately 9 million population stayed in the city [37].
The COVID-19 cases dataset was collected in the core districts of Wuhan covering the period February 3 to March 3, 2020. It includes the numbers of confirmed and suspected COVID-19 cases as Table I reports. Generally, 3,154 neighborhoods were collected, of which 2,349 neighborhoods reported confirmed or suspected cases. About living material supply support, 26 depots, 526 material supply supermarkets, and 935 vehicles are available. The road network is from open street map (OSM). The average speed of vehicles is set to
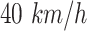 .
.
TABLE I. COVID-19 Data of Residential Neighborhoods.
| ID | District | Neighborhoods Name | Population | COVID-19 cases | |
|---|---|---|---|---|---|
| Confirmed | Suspected | ||||
| 1 | Hongshan | Donghu Jingyuan Area A | 3,391 | 64 | 33 |
| 2 | Jiangan | Yisongting, Hankou Garden | 6,377 | 51 | 7 |
| 3 | Qingshan | Biyuan Neighborhood | 4,067 | 36 | 21 |
| 4 |
 |
 |
 |
 |
 |
Fig. 2 shows the spatial distribution of the reported COVID-19 cases at the neighborhood level. It shows some neighborhoods in Jianghan, Hanyang, and Hongshan, were heavily infected, while the sub-urban areas including Huangpi and Xinzhou are with few infected cases. It also demonstrates that the COVID-19 cases gradually decreases from the core urban area to the suburbs.
Fig. 2.
Spatial distribution of COVID-19 infected neighborhoods in Wuhan.
To support the home quarantine, governments, enterprises, and neighborhoods cooperated in providing living services. The supermarkets, i.e., Wu Shang Liang Fan, Zhong Bai Chao Shi, Walmart, and Carrefour, were selected as the supply centers. To estimate daily living material demands, we collected residential gross floor area to estimate the population. Generally, according to the Chinese Dietary Guidelines (CDG) [38], three types of essential living materials, including vegetables, meats, grain, are considered. As shown in Table II, their quantities are also set with the suggestion of CDG.
TABLE II. Essential Daily Living Material Demands for a Person.
| Living materials | Vegetables | Meats | Grain and oil |
|---|---|---|---|
| Quantity (gram) | 350 | 125 | 340 |
IV. Methodology
We developed the DROVT approach to provide effective and efficient living material delivery service under the threat of the COVID-19. The framework of the DROVT is shown in Fig. 3. First, daily living material demand is estimated. Then, the virus transmission risk along the delivery is measured with the complex network-based virus transmission model. Finally, a delivery route optimization model considering the virus transmission risk is developed and solved with a hybrid meta-heuristics integrating the ALNS and SA. Details of the framework are described below.
Fig. 3.
The framework of the DROVT approach.
A. Estimating Daily Living Material Demands
We estimate the daily living material demands by the residential gross floor area data. The population is calculated according to the Per Capita Living Space,
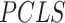 ,
,
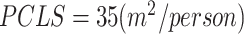 in Wuhan. The population per home unit is set according to the household structure. The total daily living materials demand of a neighborhood,
in Wuhan. The population per home unit is set according to the household structure. The total daily living materials demand of a neighborhood,
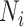 , is equal to the sum of the product of the number of family (
, is equal to the sum of the product of the number of family (
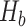 ) and the daily living material demand per person (
) and the daily living material demand per person (
 ), as Eq. (1), where
), as Eq. (1), where
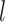 is a type of living materials,
is a type of living materials,
 is a building,
is a building,
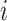 is a neighborhood.
is a neighborhood.
 |
After data processing, every day 8,601.55 tons living materials are necessary, including vegetables 3,693.92 tons, meats 1,319.26 tons, and grain and oil 3,588.38 tons in Wuhan. Fig. 4 shows the spatial distribution of daily living materials demands. It demonstrates that the living material demand of a neighborhood varies from 0.01 to 12.2 tons. By assigning one neighborhood to the nearest supermarket, the necessary living material delivery will be modeled as below.
Fig. 4.
Spatial distribution of the estimated living material demands.
B. Complex Network-Based Virus Transmission Model
The essential living material delivery service would impose virus transmission from people to people. Complex network simulates the grouping and the interaction of the crowds, therefore can well describe the epidemic transmission process. It addresses the setting of the epidemic’s outbreak threshold as well as the evolutionary characteristics of the infected people over time. A complex network contains two elements: nodes and edges. For the living material delivery process, the node represents the neighborhood, the supermarket, or the depot. The edge represents the travel between neighborhoods, supermarkets, or depots.
The MNM is used to describe the dynamic processes of the COVID-19 transmission between neighborhoods because of the living material delivery, as Fig. 5 shows. Generally, a neighborhood,
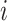 , contains a set of people with some infected and suspected COVID-19 cases. Considering the different transmission ability of these COVID cases, we set them with different virus transmission risk. Consequently, a neighborhood can be described with an initial COVID probability,
, contains a set of people with some infected and suspected COVID-19 cases. Considering the different transmission ability of these COVID cases, we set them with different virus transmission risk. Consequently, a neighborhood can be described with an initial COVID probability,
 , as Eq. (2), where
, as Eq. (2), where
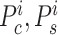 , denotes the number of the confirmed and the suspected COVID-19 cases.
, denotes the number of the confirmed and the suspected COVID-19 cases.
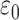 and
and
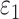 ,are the corresponding transmission probabilities of these two cases. According to Yang et al.
[39], they are set to 1 and 0.15 respectively. By normalizing the probability of neighborhoods, we unify the COVID infection risk in a neighborhood,
,are the corresponding transmission probabilities of these two cases. According to Yang et al.
[39], they are set to 1 and 0.15 respectively. By normalizing the probability of neighborhoods, we unify the COVID infection risk in a neighborhood,
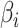 , as Eq. (3), where
, as Eq. (3), where
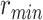 and
and
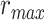 are the minimum and the maximum risk value of all neighborhoods in the city. As Fig. 5 shows, the more the COVID-19 cases, the greater the value of
are the minimum and the maximum risk value of all neighborhoods in the city. As Fig. 5 shows, the more the COVID-19 cases, the greater the value of
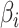 .
.
 |
Fig. 5.
Complex-network-based virus transmission.
When the deliveryman travels in the city, the COVID-19 was transmited because of the necessary contact of human-to-human or human-to-things. Generally, the living material distribution from the supermarkets to the neighborhoods can be described with the directed graph
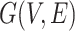 , in which
, in which
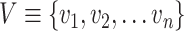 is the set of all nodes and
is the set of all nodes and
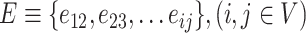 is the set of all edges. In this study, the node represents the neighborhoods, the supermarkets, and the depots. The edge represents a travel route segment from one neighborhood to another.
is the set of all edges. In this study, the node represents the neighborhoods, the supermarkets, and the depots. The edge represents a travel route segment from one neighborhood to another.
The virus are transmitted in two situations during the delivery. One situation is that when the deliveryman distribute living materials, the COVID-19 may transmit from the neighborhood residents to the deliveryman, depending on the contact and the virus prevention level. Here, the virus transmission risk of the delivery is presented by
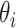 , which indicates the contact manner in the delivery. The range of
, which indicates the contact manner in the delivery. The range of
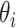 is between 0 and 1. Formally, the transmission probability of one delivery action, can be calculated as (4), where
is between 0 and 1. Formally, the transmission probability of one delivery action, can be calculated as (4), where
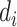 is the protection level of the neighborhood
is the protection level of the neighborhood
 , and
, and
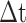 is the duration the deliveryman stayed at neighborhoods
is the duration the deliveryman stayed at neighborhoods
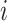 , determined by loading and unloading time. The longer the loading and unloading action, the more contacts between the packages, the deliveryman, and the residents, the higher the virus transmission probability,
, determined by loading and unloading time. The longer the loading and unloading action, the more contacts between the packages, the deliveryman, and the residents, the higher the virus transmission probability,
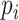 . In this study, we set the value of
. In this study, we set the value of
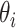 equal to 1 by assuming the contact delivery as we don’t know the contact or contact-less context in the delivery.
equal to 1 by assuming the contact delivery as we don’t know the contact or contact-less context in the delivery.
 |
The other situation is that the virus may be transmitted from the deliveryman to the residents. Generally, the more neighborhood the deliveryman serves, the higher the virus transmission risk is. Hence, the virus transmission risk should accumulate along the route of the deliveryman, as Fig. 6 shows. The infection risk at the neighborhood after one delivery action,
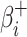 , is equal to the risk before the delivery,
, is equal to the risk before the delivery,
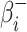 , and the added risk of this delivery,
, and the added risk of this delivery,
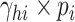 , as Eq. (5). For the deliveryman, the virus transmission risk after one delivery action,
, as Eq. (5). For the deliveryman, the virus transmission risk after one delivery action,
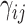 , is equal to the risk before plus that of the visiting node, as Eq. (6), where
, is equal to the risk before plus that of the visiting node, as Eq. (6), where
 and
and
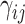 are the risk of the edge
are the risk of the edge
 and
and
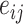 respectively,
respectively,
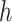 is a neighborhood visited before.
is a neighborhood visited before.
Fig. 6.

The COVID-19 risk along one delivery route.
The risk of the distribution network is finally represented by an indicator,
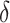 , as shown in Eq. (7), which is equal to the cumulative risk of all neighborhoods and the cumulative risk of the deliverymen after the distribution. The time when all delivery finished is represented by
, as shown in Eq. (7), which is equal to the cumulative risk of all neighborhoods and the cumulative risk of the deliverymen after the distribution. The time when all delivery finished is represented by
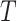 .
.
 |
C. The Delivery Route Optimization Model Considering the COVID-19 Transmission
As the COVID-19 may be transmitted during the living material delivery, we presented a delivery route optimization problem (DROP) below. The goal of the DROP is to reduce the virus transmission risk due to necessary living material delivery. Here, we assume that enough logistics vehicles will be located at depots. Neighborhoods’ living material orders are assigned to the nearest supermarket. One vehicle departs from the depot, picks up the living materials at the supermarket, delivers it to the corresponding neighborhood, and then returns to the departing depot. Vehicles travel around in the city to deliver living material packages until all orders of neighborhoods are delivered. Formally, the developed DROP is formulated as follows. Four sets and three constraints are firstly given.
-
(1)
the set of vehicle depots is
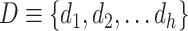 ,
, -
(2)
the set of vehicles is
 ,
, -
(3)
the set of supermarkets is
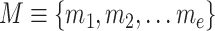 ,
, -
(4)
the set of neighborhoods’ living material orders is
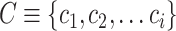 .
. -
(5)
all vehicles depart from their respective depots and finally return to the depot,
-
(6)
the load of the vehicle must not exceed its load capacity
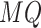 ,
, -
(7)
the working hours of the deliveryman do not exceed the prescribed working hours
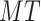 .
.
The DROP can be represented as a directed graph
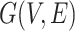 . The nodes of the graph
. The nodes of the graph
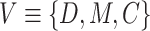 is the union of the vehicle depots, the supermarkets, and neighborhoods. The edge
is the union of the vehicle depots, the supermarkets, and neighborhoods. The edge
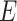 represents route segments traveling from one node to another. Each edge
represents route segments traveling from one node to another. Each edge
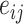 denotes a route segment from node
denotes a route segment from node
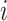 to node
to node
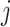 , with travel distance
, with travel distance
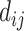 .
.
The DROP involves two components: the COVID-19 transmission risk and the travel distance. Here, the total transmission risk includes the risk of all neighborhoods and the risk of all deliverymen. Generally, the direct delivery from one supermarket to one neighborhood will produce the minimum virus transmission risk as there is no indirect virus transmission from neighborhood to neighborhood. However, it will require thousands of vehicles and deliverymen, which expose more deliverymen to the COVID-19. Hence, two objectives should be coordinated. Here, using a weighting parameter,
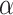 , we transform the DROP to a single objective problem. Formally, a mixed-integer programming model is proposed to describe the DROP.
, we transform the DROP to a single objective problem. Formally, a mixed-integer programming model is proposed to describe the DROP.
Decision Variables:
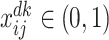 : a binary variable that is equal to 1 if vehicle
: a binary variable that is equal to 1 if vehicle
 departing from depot
departing from depot
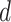 travels from the node
travels from the node
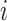 to node
to node
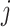 ;
;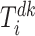 : arrival time of vehicle
: arrival time of vehicle
 departing from depot
departing from depot
 at node
at node
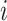 ;
;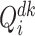 : the load of vehicle
: the load of vehicle
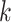 from depot
from depot
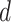 when leaving node
when leaving node
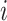 ;
;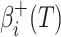 ,
,
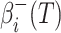 : the virus transmission risk at node
: the virus transmission risk at node
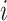 after
after
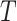 and before
and before
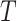 respectively;
respectively;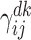 : the virus transmission risk for vehicle
: the virus transmission risk for vehicle
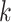 from depot
from depot
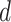 traveling from node
traveling from node
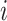 to node
to node
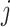 .
.
Objective:
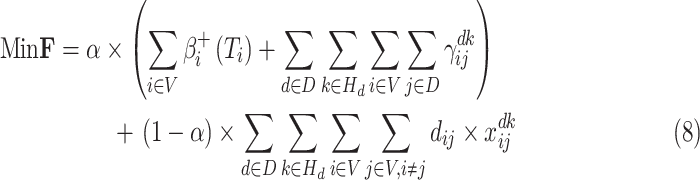 |
Constraints:
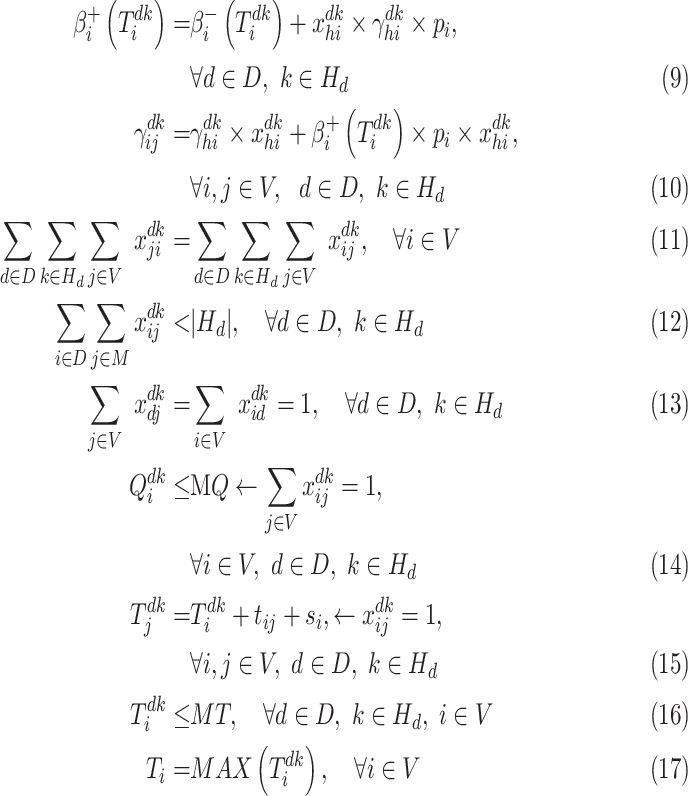 |
The first part of Eq. (8) denotes the total virus transmission risk, includes the cumulative risks of all neighborhoods and all deliverymen. The second part of Eq. (8) denotes the total length of all delivery routes.
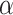 and
and
 are the corresponding weights of two objectives. Eq. (9) and (10) state that the risk of neighborhoods and the risk of the deliveryman are updated after one living material delivery action. Eq. (11) states that the number of arrival vehicles at neighborhood
are the corresponding weights of two objectives. Eq. (9) and (10) state that the risk of neighborhoods and the risk of the deliveryman are updated after one living material delivery action. Eq. (11) states that the number of arrival vehicles at neighborhood
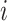 is equal to the number of left vehicles. Eq. (12) requires that the number of vehicles departing from one depot is less than the number of the located vehicles at the depot,
is equal to the number of left vehicles. Eq. (12) requires that the number of vehicles departing from one depot is less than the number of the located vehicles at the depot,
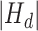 . Eq. (13) states that one vehicle must return to the departing depot. (14) ensures that total delivered living materials of one vehicle is less than the vehicle capacity,
. Eq. (13) states that one vehicle must return to the departing depot. (14) ensures that total delivered living materials of one vehicle is less than the vehicle capacity,
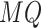 . Eq. (15) states that the vehicle arrival time at node
. Eq. (15) states that the vehicle arrival time at node
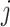 is equal to the arrival time at the previous node
is equal to the arrival time at the previous node
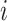 plus the service time at node
plus the service time at node
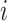 and the travel time from node
and the travel time from node
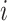 to
to
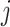 . Eq. (16) restricts that the total working time for one deliveryman must less the prescribed maximum operation time,
. Eq. (16) restricts that the total working time for one deliveryman must less the prescribed maximum operation time,
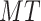 . Eq. (17) denotes that the living material delivery process ends at the node
. Eq. (17) denotes that the living material delivery process ends at the node
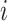 ,
,
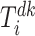 , is equal to the arrival time of the last delivery vehicle.
, is equal to the arrival time of the last delivery vehicle.
D. Hybrid Meta-Heuristic Algorithm
The proposed DROP is a variant of multi-depot vehicle routing problem [40], therefore it is NP-hard. When thousands of nodes are involved, it is difficult to get the global optimal solution in a reasonable time. Here, we develop a hybrid meta-heuristic algorithm integrating ALNS and SA to solve this problem. The hybrid meta-heuristics contains two steps: (1) construct a good initial solution; (2) iteratively improve the current solution by ALNS and SA.
1). Initial Solution:
The initial solution generation method iteratively insert living material orders to routes. The workflow is shown in Algorithm 1. Firstly, the initial empty route starting at the depot are generated for all vehicles in
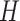 (Line 1). Then, an order
(Line 1). Then, an order
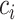 is randomly selected. one delivery route
is randomly selected. one delivery route
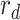 will be chosen to insert this order. The best-inserted position
will be chosen to insert this order. The best-inserted position
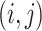 in the route
in the route
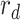 is that with the least insert cost (Lines 3–9). The insertion will repeat until all orders are inserted.
is that with the least insert cost (Lines 3–9). The insertion will repeat until all orders are inserted.
Algorithm 1 Construct the Initial Solution
Input:
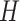 : the vehicle set;
: the vehicle set;
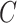 : the neighborhood demand order set
: the neighborhood demand order setOutput: the initial solution
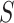
-
1:
 initialize route for
initialize route for
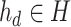
-
2:
for all
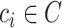 do
do -
3:
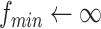
-
4:
for all
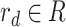 do
do -
5:
if
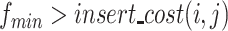 and
and
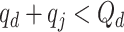 then
then -
6:
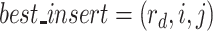
-
7:
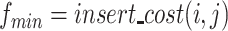
-
8:
end if
-
9:
end for
-
10:
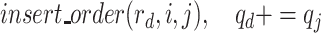
-
11:
end for
2). The ALNS:
The ALNS algorithm was first proposed by Pisinger and Ropke (2006) to solve vehicle routing problems [41]. The core principle of ALNS is to iteratively destroy and repair current solutions to find a high-quality solution. Algorithm 2 shows the ALNS framework for improving the living material delivery solution. Firstly, parameters, current solution, best solution are initialized (Line 1). A destroying operator is randomly select to remove a set of nodes from the current solution
 , which are then re-inserted back to obtain a new solution
, which are then re-inserted back to obtain a new solution
 (Lines 2 to 5). The new solution will be accepted by the SA criterion. According to the performance of the destroying operators, the weights of the destroying operator are dynamically adjusted (Lines 7 to 12). The remove-insertion iteration will repeat until the maximum iteration. Finally, the found best solution will be reported.
(Lines 2 to 5). The new solution will be accepted by the SA criterion. According to the performance of the destroying operators, the weights of the destroying operator are dynamically adjusted (Lines 7 to 12). The remove-insertion iteration will repeat until the maximum iteration. Finally, the found best solution will be reported.
Algorithm 2 ALNS
Input:
 Supermarkets set;
Supermarkets set;
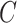 Neighborhoods set;
Neighborhoods set;
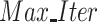 Maximum iterations;
Maximum iterations;
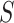 initial solution.
initial solution.Output: Best solution
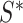
-
1:
Initialize parameters, set
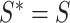
-
2:
for k = 1 to
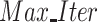 do
do -
3:
Choose a destroying operator
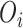
-
4:
Remove
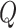 nodes from
nodes from
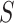 by
by
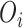
-
5:
Reinsert
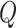 nodes by the repair operator, produce a new solution
nodes by the repair operator, produce a new solution
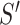 ,
, -
6:
Accept current solution
 by simulated annealing
by simulated annealing -
7:
if If accept
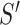 then
then -
8:
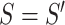
-
9:
if
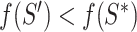 then
then -
10:
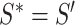
-
11:
end if
-
12:
Update the weight of destroying operators
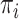
-
13:
end if
-
14:
end for
a). Destroying Operators:
The destroying operators remove a set of nodes (in other words, neighborhoods, supermarkets) from current delivery routes to perturb the current solution. In this study, four destroying operators are designed. One destroying operator will be randomly selected by the roulette strategy.
-
•
Random Removal (RR):
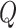 nodes are randomly removed from the current solution.
nodes are randomly removed from the current solution. -
•
High-Risk Removal (HRR): The nodes with the
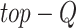 highest risk will be removed. This operator ejects the nodes forming the edges with higher virus transmission risk values.
highest risk will be removed. This operator ejects the nodes forming the edges with higher virus transmission risk values. -
•
The Longest Route Segment Removal (LR): A long delivery travel between two nodes may induce unreasonable delivery; therefore, the nodes connected by the longest route segment in the current solution will be ejected from the current solution.
-
•
The Clustering Removal (CR): When a destroying operation removes a set of quite different nodes, these nodes are possibly re-inserted at the same positions. Here, the K-Means clustering is applied to all neighborhoods. A cluster of neighborhoods will be removed from the solution. The value of
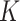 is set as the
is set as the
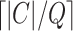 .
.
b). Repairing Operator:
The repairing operator reinserts the ejected
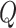 nodes into the delivery routes to produce a new viable delivery scheme without violating the vehicle capacity and the working hour constraint. Essentially, the repairing operator uses the insertion heuristic to repair the solution. The insertion sequence will influence the quality of the re-inserted solution. Following Tu et al.
[30], we randomly sort the removed nodes and re-insert them into the proper places. To avoid some bad repairing operations, we repeat the sorting-reinsertion
nodes into the delivery routes to produce a new viable delivery scheme without violating the vehicle capacity and the working hour constraint. Essentially, the repairing operator uses the insertion heuristic to repair the solution. The insertion sequence will influence the quality of the re-inserted solution. Following Tu et al.
[30], we randomly sort the removed nodes and re-insert them into the proper places. To avoid some bad repairing operations, we repeat the sorting-reinsertion
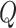 times and evaluate the performance. The re-insertion with the best performance will be conducted.
times and evaluate the performance. The re-insertion with the best performance will be conducted.
c). Adaptive Weighting Strategy:
After one destroying and repairing operation, the weight of one destroying operator,
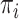 , will be updated according to the new solution obtained, as Eq. (18), where
, will be updated according to the new solution obtained, as Eq. (18), where
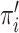 is the weight after one iteration,
is the weight after one iteration,
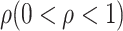 is the parameter controlling the weight changing speed. The
is the parameter controlling the weight changing speed. The
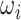 is the got improvement cost of the current solution by the corresponding operator,
is the got improvement cost of the current solution by the corresponding operator,
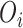 , in the iteration. So, the operator achieving greater performance will be used more.
, in the iteration. So, the operator achieving greater performance will be used more.
 |
3). The SA:
SA is used to accept the new solution. The SA criterion is adopted to possibly accept a worse solution with the Metropolis criterion [42]. It escapes from local optimum effectively and increases the search depth to generate a better solution.
E. The DROVT Prototype System
An online DROVT prototype system was developed to provide efficient living material delivery service. One Wechat Mini Program was developed to collect the living material orders, as Fig. 7(a) shows. It is easily developed and shared among residents by the widely used Wechat. The proposed DROVT model and the solving hybrid meta-heuristics algorithm were implemented and deployed in a cloud server. Fig. 7(c) displays the delivery routes in a day. The routes would be sent to the drivers for the route navigation and the loading and unloading action as Fig. 7(b).
Fig. 7.
The DROVT prototype system.
V. Experiment and Result Analysis
The experiment was conducted in Wuhan. The methods was implemented in python on a PC with Intel Core i5-3470 @3.2 GHz, 16 GB memory, and 64-bit Windows 10 operating system. To evaluate the performance of the proposed approach, we compared the results of the conventional ALNS method and the hybrid ALNS + SA meta-heuristic method. In addition, we analyzed the living material delivery strategies with different the vehicle capacities, traffic control, and personal protection.
The vehilce capacity,
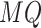 , is set to 3 tons. The maximum working hours,
, is set to 3 tons. The maximum working hours,
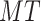 , is set to 8 hours. There are several parameters to be set in the hybrid meta-heuristics. After pre-experiments, we multiplied the total travel distance objective by 0.01 to match the value with the total virus transmission risk objective. We set
, is set to 8 hours. There are several parameters to be set in the hybrid meta-heuristics. After pre-experiments, we multiplied the total travel distance objective by 0.01 to match the value with the total virus transmission risk objective. We set
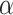 to 0.5 to assign equal weights to two objectives. Following Tu et al.
[33], the initial temperature of the SA,
to 0.5 to assign equal weights to two objectives. Following Tu et al.
[33], the initial temperature of the SA,
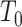 , is set the objectives of the initial solution. The cooling ratio is set as the 0.95. Regarding the number of removed nodes in ALNS,
, is set the objectives of the initial solution. The cooling ratio is set as the 0.95. Regarding the number of removed nodes in ALNS,
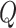 , we set it to
, we set it to
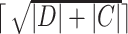 . The weight updating speed controlling parameter in ALNS,
. The weight updating speed controlling parameter in ALNS,
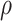 , is set to 0.5.
, is set to 0.5.
A. The Results of the Proposed Approach
The hybrid meta-heuristic algorithm and ALNS are used to solve the DROVT model in Wuhan dataset. The total objective, the total risk, the total distance, and the computing time are reported. The gap between the ALNS and hybrid meta-heuristics is evaluated as
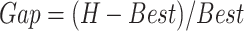 , where
, where
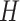 denotes the objective value of the hybrid meta-heuristics solution. The results are reported in Table III.
denotes the objective value of the hybrid meta-heuristics solution. The results are reported in Table III.
TABLE III. The Results of the DROVT.
| Methods | Total objective | Total risk | Total distance (/km) | Computing time (/s) |
|---|---|---|---|---|
| Hybrid meta-heuristics | 484.25 | 404.25 | 56,424.55 | 5,875.3 |
| ALNS | 498.25 | 407.28 | 58,923.14 | 5,580.5 |
| Gap | −2.89% | −0.75% | −4.43% | 5.02% |
The results demonstrate that 935 vehicles will totally travel 56,424.55 km to deliver necessary living materials to 3,154 neighborhoods, with total virus transmission risk
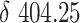 . The obtained delivery solution balance the virus transmission risk and travel cost. Fig. 8 shows three indices of one solution. It demonstrates that the virus transmission risk varies from neighborhood to neighborhood. The median risk of all neighborhoods is 0.05. 90 percents of neighborhoods are with the risk less than 0.26. The median risk of deliverymen is 0.19. 90 percents of deliverymen are with the risk less than 0.37. Fig. 9 shows delivery routes solved by hybrid meta-heuristic in the core urban area of Wuhan, as well as the virus transmission risk on each route segment. The darker the color, the greater the risk value. It verifies that the virus transmission risk increases along the delivery routes.
. The obtained delivery solution balance the virus transmission risk and travel cost. Fig. 8 shows three indices of one solution. It demonstrates that the virus transmission risk varies from neighborhood to neighborhood. The median risk of all neighborhoods is 0.05. 90 percents of neighborhoods are with the risk less than 0.26. The median risk of deliverymen is 0.19. 90 percents of deliverymen are with the risk less than 0.37. Fig. 9 shows delivery routes solved by hybrid meta-heuristic in the core urban area of Wuhan, as well as the virus transmission risk on each route segment. The darker the color, the greater the risk value. It verifies that the virus transmission risk increases along the delivery routes.
Fig. 8.
The statistics of the DROVT results.
Fig. 9.
The delivery routes of the DROVT.
The hybrid meta-heuristic results outperform the ALNS results as Table III describes. In terms of the total risk, the hybrid meta-heuristics results (404.25) are superior to the ALNS solution (407.28) by 0.75%. For the total travel distance, the hybrid meta-heuristics results (56,424.55) is better than that of the ALNS (58,923.14). But the hybrid meta-heuristics also cost more computing efforts, with only 5.02 percent increases.
Fig. 10 shows the weight change of four destroying operators, including the RR, the HRR, the LR, and the CR operator. At the first stage of the ALNS, all operators are with the same weight, 0.25. As the HRR operator gain more improvement of the objectives, its weight increases while the weights of three other operators decrease. Finally, the weight of the HRR operator achieved about 0.6. This variation of the weights demonstrates the good performance of the proposed HRR operator.
Fig. 10.
The weights change of four destroying operators.
B. Comparison With Distance-Based Delivery Routing Optimization
The effectiveness of the proposed DROVT approach was further evaluated by comparing with Distance-based Delivery Routing Optimization (DDRO), in which the virus transmission along the living material is not considered. In other words, the parameter,
 , is set to 0.0. We implemented these methods 30 times and compared the got results. The distribution of these results are displayed in Fig. 11. It demonstrates that the median of total risk
, is set to 0.0. We implemented these methods 30 times and compared the got results. The distribution of these results are displayed in Fig. 11. It demonstrates that the median of total risk
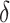 of DDRO is 598.39. When considering the virus transmission, the DROVT results achieve a lower COVID-19 transmission risk
of DDRO is 598.39. When considering the virus transmission, the DROVT results achieve a lower COVID-19 transmission risk
 , 404.24, about 67.5% of the DDRO results. In terms of the total distance, the median total distance of DDRO results is 45,543.02 km, less than those of the DROVT results, 56,424.55 km. This result shows the DROVT trades off travel distance against lower virus transmission risk by taking reasonably detours.
, 404.24, about 67.5% of the DDRO results. In terms of the total distance, the median total distance of DDRO results is 45,543.02 km, less than those of the DROVT results, 56,424.55 km. This result shows the DROVT trades off travel distance against lower virus transmission risk by taking reasonably detours.
Fig. 11.
Comparisons of the results of the DROVT and the DDRO.
Fig. 12 displays the spatial distribution of neighborhoods risk of the DROVT and DDRO results. The neighborhood risk values are between 0 and 4.689. The number of neighborhoods with high virus transmission risk in the DROVT result was significantly less than those in the DDRO results. Especially, in the northwest Wuhan with many confirmed COVID-19 cases, the virus transmission risk is significantly reduced.
Fig. 12.
Spatial distribution of the neighborhood-level risk.
C. Analysis of Materials Distribution Strategies
1). Effects of the Vehicle Capacities:
The capacity of the vehicles may have a great impact on living material delivery routes. Small vehicles will require more travels therefore possibly increase the virus transmission risk. By setting different values to the vehicle capacity, we examined the effect. The objectives of the got results are presented as Fig. 13. With vehicle capacities of 1 ton, 3 tons, and 5 tons, the total virus transmission risk
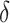 is 648.92, 404.25 and 336.35, respectively, and the corresponding total distances are 124,796.49 km, 56,424.55 km and 43,961.99 km respectively. When the vehicle capacities increased from 1 ton to 5 tons, the risk of virus transmission was reduced by 92.92%, and the total transportation distance was reduced by 121.17%. These results demonstrate that large vehicle does reduce virus transmission risk.
is 648.92, 404.25 and 336.35, respectively, and the corresponding total distances are 124,796.49 km, 56,424.55 km and 43,961.99 km respectively. When the vehicle capacities increased from 1 ton to 5 tons, the risk of virus transmission was reduced by 92.92%, and the total transportation distance was reduced by 121.17%. These results demonstrate that large vehicle does reduce virus transmission risk.
Fig. 13.
Comparison of risk for vehicles with different load capacities.
The delivery routes of a solution forms a complex network. The delivery network structure changes due to the different vehicle capacities. By summarizing the node degree, which indicates the number of route segment connected with the node, the necessary contact between the deliverymen and the neighborhoods are measured. Fig. 14 displays the node degree distribution of the delivery route-based network with different capacities. The proportion of nodes in the same degree of 1 ton is significantly higher than 5 tons, in other words, it contains more contacts.
Fig. 14.
The node degree distribution of the delivery network.
2). Effect of Traffic Control:
Due to the epidemiological characteristics, confirmed COVID-19 cases will be concentrated in certain areas of a city. Implementing traffic control, which cutts off the travels between these high-risk areas, may be an effective means to reduce the risk of COVID-19 transmission. Here, we chose two high-risk administrative districts, Dongxihu and Hanyang, to implement the travel control. In other words, vehicles in these districts can’t go to other districts, and vice versa. The obtained results are presented in Fig. 15. Under traffic control, the median virus transmission risk
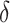 will decline from 404.25 to 385.52 with a 4.63 percent decrease. While the total route length increases from 56,424.55 km to 58,928.58 km. These results demonstrate that the traffic control strategy can effectively reduce the risk of COVID-19 transmission among urban residents and the deliveryman.
will decline from 404.25 to 385.52 with a 4.63 percent decrease. While the total route length increases from 56,424.55 km to 58,928.58 km. These results demonstrate that the traffic control strategy can effectively reduce the risk of COVID-19 transmission among urban residents and the deliveryman.
Fig. 15.
Comparison of the results with travel control and free travel.
3). Effect of the Personal Protection of the Deliveryman:
The level of personal protection also influences the COVID-19 infection risk during the living material delivery. By setting the protection level in Eq. 5 with different values, 0.8, 0.95, and 0.99, the effect of personal protection is evaluated. The results are shown in Fig. 16. With the protection level increase from 0.80 to 0.99, the total COVID transmission risk declines from 105.36 to 70.1. Meanwhile, the median total route length also decreases from 60,620.6 km to 46,866.9 km. It suggests higher personal protection will significantly reduce the infection risk of both the residents and the deliverymen. It also improves the delivery efficiency by reducing the total travel route length.
Fig. 16.
Comparison of the results with different protection levels.
VI. Conclusion
During the COVID-19 outbreak, the living materials delivery is essential for the success of the necessary home quarantine. Traditional emergency logistics ignore the virus transmission risk along with the delivery. This study presents a novel living material delivery route optimization approach considering the possible COVID-19 transmission during the delivery. A complex network-based virus transmission model is developed to simulate the possible COVID-19 infection between residents and the deliverymen. A bi-objective model considering the COVID-19 infection risk and the total route length is proposed and solved by the hybrid meta-heuristics. The results of the experiments in Wuhan demonstrate that 935 vehicles will totally travel 56,424.55 km to deliver necessary living materials to 3,154 neighborhoods, with total risk 404.25, which reduce the risk of COVID-19 transmission by 67.55% compared to traditional distance-based optimization methods.
There are still some limitations in this study, i.e., the asymptomatic COVID-19 case, living material is delivered day by day. In the future, we will extend the complex network-based virus transmission model to consider the infection due to the asymptomatic COVID-19 case. On the other hand, the proposed approach will be extended to adopt to multi-day living material delivery.
Biographies

Tianhong Zhao is currently pursuing the Ph.D. degree with the Department of Urban Informatics, School of Architecture and Urban Planning, Shenzhen University, Shenzhen, China. His current research interests include spatio-temporal optimization and spatio-temporal big data analysis.

Wei Tu (Member, IEEE) received the Ph.D. degree in photogrammetry and remote sensing from Wuhan University, Wuhan, China, in 2013. He is currently an Associate Professor with the Department of Urban Informatics, Shenzhen University, Shenzhen, China. He is also a Visiting Scholar with the Senseable City Laboratory, Massachusetts Institute of Technology, Cambridge, MA, USA. His research interests include urban informatics, big data driven human activity and mobility, and trajectory analytic.

Zhixiang Fang received the M.Sc. and Ph.D. degrees from Wuhan University, in 2002 and 2005, respectively. He is currently a Professor with the State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University. His research interests include spatio-temporal modeling in transport geography and human activity.

Xiaofan Wang is currently a Graduate Student with the State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University. Her research interest includes spatio-temporal data models.

Zhengdong Huang received the Ph.D. degree in human geography from Utrecht University, Utrecht, The Netherlands, in 2003. He is currently a Professor with the School of Architecture and Urban Planning and the Guangdong Key Laboratory of Urban Informatics, Shenzhen University, Shenzhen, China. His research interests include GIS and urban traffic, transportation and environment, urban spatial analysis, and smart city.

Shengwu Xiong received the B.Sc. degree in computational mathematics and the M.Sc. and Ph.D. degrees in computer software and theory from Wuhan University, Wuhan, China, in 1987, 1997, and 2003, respectively. He is currently a Professor with the School of Computer Science and Technology, Wuhan University of Technology, China. His research interests include intelligent computing, machine learning, and pattern recognition.

Meng Zheng received the M.E. degree from Wuhan University in 2011. He is currently a Senior Engineer and the Director of Research Department with the Wuhan Transportation Development Strategy Institute. His research interests include tour-based model, traffic simulation, urban spatial analysis, and smart city.
Funding Statement
This work was supported in part by the National Key Research and Development Program of China under Grant 2019YFB2103104, in part by the Natural Science Foundation of Guangdong Province under Grant 2019A1515011049, and in part by the Fundamental Research Funds for the Central Universities under Grant 2042020kfxg24.
Contributor Information
Tianhong Zhao, Email: zhaotianhong2016@email.szu.edu.cn.
Wei Tu, Email: tuwei@szu.edu.cn.
Zhixiang Fang, Email: zxfang@whu.edu.cn.
Xiaofan Wang, Email: 2018206190027@whu.edu.cn.
Zhengdong Huang, Email: zdhuang@szu.edu.cn.
Shengwu Xiong, Email: xiongsw@whut.edu.cn.
Meng Zheng, Email: zmfly@163.com.
References
- [1].Tillett H. E., “Infectious diseases of humans; dynamics and control,” Epidemiol. Infection, vol. 108, no. 1, p. 211, Feb. 1992. [Google Scholar]
- [2].WHO. COVID-19 Situation Reports. Accessed: Jun. 28, 2020. [Online]. Available: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports
- [3].Wu F., Zhao S., Yu B., Chen Y. M., Wang W., and Song Z. G., “A new coronavirus associated with human respiratory disease in China,” Nature, vol. 579, no. 7798, pp. 265–269, Mar. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Jia J. S., Lu X., Yuan Y., Xu G., Jia J., and Christakis N. A., “Population flow drives spatio-temporal distribution of COVID-19 in China,” Nature, vol. 582, no. 7812, pp. 389–394, 2020. [DOI] [PubMed] [Google Scholar]
- [5].Charlie C.. These Delivery Drivers are Risking Their Health to Keep China Running During the Coronavirus Epidemic. Accessed: Oct. 19, 2020. [Online]. Available: https://time.com/5803803/china-delivery-driver-ecommerce-covid19 [Google Scholar]
- [6].Fisher D., Reilly A., Zheng A. K. E., Cook A. R., and Anderson D. E., “Seeding of outbreaks of COVID-19 by contaminated fresh and frozen food,” BioRxiv, Aug. 2020, Art. no. 2020.08.17.255166. Accessed: Mar. 12, 2021. [Online]. Available: https://www.biorxiv.org/content/10.1101/2020.08.17.255166v1, doi: 10.1101/2020.08.17.255166. [DOI] [Google Scholar]
- [7].Mallica J.. COVID-19 in Delhi: Pizza Delivery Man Tests Positive 72 Quarantined. Accessed: Oct. 19, 2020. [Online]. Available: https://indianexpress.com/article/cities/delhi/delhi-pizza-coronavirus-covid-19-6364606/ [Google Scholar]
- [8].Caiyu L. and Siqi C.. Beijing Deliveryman who Sends 50 Orders Per Day Confirmed With COVID-19. Accessed: Oct. 22, 2020. [Online]. Available: https://www.globaltimes.cn/content/1192565.shtml [Google Scholar]
- [9].Kang H., Sun M., Yu Y., Fu X., and Bao B., “Spreading dynamics of an SEIR model with delay on scale-free networks,” IEEE Trans. Netw. Sci. Eng., vol. 7, no. 1, pp. 489–496, Jan. 2020. [Google Scholar]
- [10].Tu W., Cao R., Yue Y., Zhou B., Li Q., and Li Q., “Spatial variations in urban public ridership derived from GPS trajectories and smart card data,” J. Transp. Geography, vol. 69, pp. 45–57, May 2018. [Google Scholar]
- [11].Stegehuis C., van der Hofstad R., and van Leeuwaarden J. S. H., “Epidemic spreading on complex networks with community structures,” Sci. Rep., vol. 6, no. 1, Sep. 2016, Art. no. 029748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Dasaklis T. K., Rachaniotis N., and Pappis C., “Emergency supply chain management for controlling a smallpox outbreak: The case for regional mass vaccination,” Int. J. Syst. Sci., Oper. Logistics, vol. 4, no. 1, pp. 27–40, Jan. 2017. [Google Scholar]
- [13].Ekici A., Keskinocak P., and Swann J. L., “Modeling influenza pandemic and planning food distribution,” Manuf. Service Oper. Manage., vol. 16, no. 1, pp. 11–27, Feb. 2014. [Google Scholar]
- [14].Kermack W. O. and McKendrick A. G., “A contribution to the mathematical theory of epidemics,” Proc. Roy. Soc. London A, Containing Papers Math. Phys. Character, vol. 115, no. 772, pp. 700–721, 1927. [Google Scholar]
- [15].Zhang Z., Wang H., Wang C., and Fang H., “Modeling epidemics spreading on social contact networks,” IEEE Trans. Emerg. Topics Comput., vol. 3, no. 3, pp. 410–419, Sep. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Saramäki J. and Kaski K., “Modelling development of epidemics with dynamic small-world networks,” J. Theor. Biol., vol. 234, no. 3, pp. 413–421, Jun. 2005. [DOI] [PubMed] [Google Scholar]
- [17].Wang J.-B. and Li X., “Uncovering spatial invasion on metapopulation networks with SIR epidemics,” IEEE Trans. Netw. Sci. Eng., vol. 6, no. 4, pp. 788–800, Oct. 2019. [Google Scholar]
- [18].Calvetti D., Hoover A., Rose J., and Somersalo E., “Metapopulation network models for understanding, predicting and managing the coronavirus disease COVID-19,” 2020, arXiv:2005.06137. [Online]. Available: http://arxiv.org/abs/2005.06137 [Google Scholar]
- [19].Tufekci S. and Wallace W. A., “The emerging area of emergency management and engineering,” IEEE Trans. Eng. Manag., vol. 45, no. 2, pp. 103–105, May 1998. [Google Scholar]
- [20].Lei C., Lin W.-H., and Miao L., “A stochastic emergency vehicle redeployment model for an effective response to traffic incidents,” IEEE Trans. Intell. Transp. Syst., vol. 16, no. 2, pp. 898–909, Apr. 2015. [Google Scholar]
- [21].Zhen L., Wang K., and Liu H.-C., “Disaster relief facility network design in metropolises,” IEEE Trans. Syst., Man, Cybern. Syst., vol. 45, no. 5, pp. 751–761, May 2015. [Google Scholar]
- [22].Lan Y.-L., Liu F.-G., Huang Z., Ng W. W. Y., and Zhong J., “Two-echelon dispatching problem with mobile satellites in city logistics,” IEEE Trans. Intell. Transp. Syst., early access, Jun. 30, 2020, doi: 10.1109/TITS.2020.3003598. [DOI] [Google Scholar]
- [23].Sheu J.-B., “Challenges of emergency logistics management,” Transp. Res. E, Logistics Transp. Rev., vol. 43, no. 6, pp. 655–659, Nov. 2007. [Google Scholar]
- [24].Li Q., Zhong S., Fang Z., Liu L., Tu W., and Chen B., “Optimizing mixed pedestrian-vehicle evacuation via adaptive network reconfiguration,” IEEE Trans. Intell. Transp. Syst., vol. 21, no. 3, pp. 1023–1033, Mar. 2020. [Google Scholar]
- [25].Xiang X., Tian Y., Xiao J., and Zhang X., “A clustering-based surrogate-assisted multiobjective evolutionary algorithm for shelter location problem under uncertainty of road networks,” IEEE Trans. Ind. Informat., vol. 16, no. 12, pp. 7544–7555, Dec. 2020. [Google Scholar]
- [26].Li Q., Tu W., and Zhuo L., “Reliable rescue routing optimization for urban emergency logistics under travel time uncertainty,” ISPRS Int. J. Geo-Inf., vol. 7, no. 2, p. 77, Feb. 2018. [Google Scholar]
- [27].Wang X., Choi T.-M., Liu H., and Yue X., “Novel ant colony optimization methods for simplifying solution construction in vehicle routing problems,” IEEE Trans. Intell. Transp. Syst., vol. 17, no. 11, pp. 3132–3141, Nov. 2016. [Google Scholar]
- [28].Shaw P., “Using constraint programming and local search methods to solve vehicle routing problems,” in Proc. Int. Conf. Princ. Pract. Constraint Program. Berlin, Germany: Springer, 1998, pp. 417–431. [Google Scholar]
- [29].Ho S. C. and Szeto W. Y., “A hybrid large neighborhood search for the static multi-vehicle bike-repositioning problem,” Transp. Res. B, Methodol., vol. 95, pp. 340–363, Jan. 2017. [Google Scholar]
- [30].Tu W., Fang Z., Li Q., Shaw S.-L., and Chen B., “A bi-level Voronoi diagram-based metaheuristic for a large-scale multi-depot vehicle routing problem,” Transp. Res. E, Logistics Transp. Rev., vol. 61, pp. 84–97, Jan. 2014. [Google Scholar]
- [31].Xie Y., Zeng G., Kurachi R., Peng X., Xie G., and Takada H., “Balancing bandwidth utilization and interrupts: Two heuristic algorithms for the optimized design of automotive CPS,” IEEE Trans. Ind. Informat., vol. 16, no. 4, pp. 2382–2392, Apr. 2020. [Google Scholar]
- [32].Gendreau M., and Potvin J. Y., Handbook of Metaheuristics. New York, NY, USA: Springer, 2019. [Google Scholar]
- [33].Tu W., Zhao T., Zhou B., Jiang J., Xia J., and Li Q., “OCD: Online crowdsourced delivery for on-demand food,” IEEE Internet Things J., vol. 7, no. 8, pp. 6842–6854, Aug. 2020. [Google Scholar]
- [34].Ji B., Yuan X., Yuan Y., Lei X., and Iu H. H. C., “An adaptive large neighborhood search for solving generalized lock scheduling problem: Comparative study with exact methods,” IEEE Trans. Intell. Transp. Syst., vol. 21, no. 8, pp. 3344–3356, Aug. 2020. [Google Scholar]
- [35].Zaric G. S. and Brandeau M. L., “Resource allocation for epidemic control over short time horizons,” Math. Biosci., vol. 171, no. 1, pp. 33–58, May 2001. [DOI] [PubMed] [Google Scholar]
- [36].Statistics Bureau of Wuhan Municipality, “Wuhan statistical yearbook,” Wuhan Municipal Government, Wuhan, China, Tech. Rep. 2018, 2018. [Online]. Available: http://tjj.wuhan.gov.cn [Google Scholar]
- [37].Phelan A. L., Katz R., and Gostin L. O., “The novel coronavirus originating in Wuhan, China: Challenges for global health governance,” J. Amer. Med. Assoc., vol. 323, no. 8, pp. 709–710, 2020. [DOI] [PubMed] [Google Scholar]
- [38].CNSOC. (2016). The Chinese Dietary Guidelines. [Online]. Available: http://dg.en.cnsoc.org
- [39].Yang Z.et al. , “Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions,” J. Thoracic Disease, vol. 12, no. 3, pp. 165–174, Mar. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Mancini S., “A real-life multi depot multi period vehicle routing problem with a heterogeneous fleet: Formulation and adaptive large neighborhood search based matheuristic,” Transp. Res. C, Emerg. Technol., vol. 70, pp. 100–112, Sep. 2016. [Google Scholar]
- [41].Ropke S. and Pisinger D., “An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows,” Transp. Sci., vol. 40, no. 4, pp. 455–472, Nov. 2006. [Google Scholar]
- [42].Tarantilis C. D., Zachariadis E. E., and Kiranoudis C. T., “A hybrid metaheuristic algorithm for the integrated vehicle routing and three-dimensional container-loading problem,” IEEE Trans. Intell. Transp. Syst., vol. 10, no. 2, pp. 255–271, Jun. 2009. [Google Scholar]

















