A Permutation Test-Based Approach to Strengthening Inference on the Effects of Environmental Mixtures: Comparison between Single-Index Analytic Methods

Abstract

Background:

Optimization of mixture analyses is critical to assess potential impacts of human exposures to multiple pollutants. Single-index regression methods quantify total mixture association and chemical component contributions. Single-index methods include several variants of quantile g-computation (QGC) and weighted quantile sum regression (WQSr), though each has limitations.

Objectives:

We developed a novel permutation test for WQSr and compared its performance to extant versions of WQSr and QGC in simulation studies and an analysis of prenatal phthalates and childhood cognition.

Methods:

WQSr uses ensemble nonlinear optimization to identify weights for mixture exposures in an index associated with the outcome in a prespecified direction, with ensembles based on bootstrap resampling (WQSBS) or random subsetting of exposures (WQSRS). Statistical significance can be assessed without splitting the data (Nosplit), by splitting the data into training and test sets (Split), by repeatedly holding out test sets (RH), or by using a novel permutation test (PT) to obtain a more accurate $p$-value. QGC instead provides a sum mixture coefficient and component coefficients with no constraints on direction. In simulations, we compared false positive rates (FPR) and power to detect true associations and accuracy in estimating mixture weights. We also estimated associations between prenatal phthalate mixtures and childhood IQ in the Conditions Affecting Neurocognitive Development and Learning in Early Childhood cohort using each method.

Results:

FPR was well controlled at $\le 7\%$ in all but the Nosplit WQSr variants. Among these methods, the WQSBS and WQSRS PT variants had the highest power (89%–98%), with lower power for QGC (85%–93%) and RH (60%–97%) or Split WQSr variants (40%–78%). WQSr methods estimated mixture weights 2–4 times more accurately than the QGC method. Coefficients for mixture associations with full scale IQ varied 3- to 4-fold across analytic methods.

Discussion:

WQSr paired with our novel permutation test best balanced power and false positive rate when assessing a mixture effect. As new methods develop, each should be examined for performance and applicability. https://doi.org/10.1289/EHP10570

Introduction

Traditionally, epidemiology and toxicology have both focused on evaluating the potential effects of individual exposures, though in reality environmental exposures occur in complex mixtures.¹ Given that the diseases with the highest global burden are primarily predicted by environmental exposures rather than genetics, there has been a paradigm shift away from a “single exposure” framework to attempt to evaluate the health effects of the “exposome,” which is the sum total mixture of all environmental exposures over an individual’s lifetime.^2,3 Inferring relationships between health outcomes and multiple simultaneous exposures can provide benefits over the more traditional approach of analyzing each exposure individually, such as the ability to estimate cumulative health effects, to more accurately model the effects of codependent mixture components in real-world exposures, and to inform interventions that are both more realistic and potentially more efficient.⁴ When evaluating a mixture, one can not only assess the effect of some aggregate mixture measure treated as a single exposure such as the molar sum of all mixture component exposure concentrations, but also the sum of the individual and/or joint effects of each mixture component.⁵ A popular approach to address the latter question is to model a single index that represents the sum of linear effects of each mixture component.

Weighted quantile sum regression (WQSr) is a single-index method that estimates a combined mixture sum effect as well as weights determining each individual mixture component’s contributions to that sum effect.^6,7 WQSr estimates a mixture effect in only one direction at a time, which is done to avoid any apparent canceling out of mixture associations in the case of competing, bidirectional mixture effects.⁶ The authors of this method provide an illustrative example in which one can consume both alcohol to impair alertness and then consume coffee to nullify that deficit in alertness, but the individual is not the same as before the consumption of those agents. Therefore estimating a zero effect overall would be erroneous and would differ from conclusions when evaluating the effects of both alcohol and coffee in each direction sequentially.⁸ However, WQSr features a statistical power and Type I error (i.e., false positive) rate trade-off that is common to all ensemble statistical methods, because there are separate stages to estimate the mixture weights and the sum effect. If all data are used to estimate both the mixture component weights and the regression coefficients, there is high power but also a high false positive rate because coefficient $p$-values are calculated for a weighted mixture independent variable calculated using weights that have already been optimized to find a large effect. As a result, it is recommended to split the data into training and validation sets,^6,7 but this approach reduces statistical power in estimating the linear model coefficients since the sample size being used in the linear model is reduced. One proposed method for addressing this issue is the repeated holdout WQSr, which repeatedly splits the data into training and validation sets, obtaining a series of iterative weight and coefficient estimates.⁹

We recently proposed an alternative method based on a permutation test that should reliably allow for both higher power and lower false positive rate when using the WQSr.^10,11 Permutation tests are a class of nonparametric statistical tests that were first introduced by Sir Ronald Fisher, who demonstrated that one could flexibly test for a difference in means by permuting observations and observing how many times the observed difference in means exceeded the original observed difference, in effect directly testing the null hypothesis.¹² For multivariate linear regression models, several variations on permutation tests have been proposed, with multiple simulation comparisons finding that the method proposed by Freedman and Lane¹³ performs among the best in preserving statistical power and low false positive rate.^14,15 The Freedman and Lane method involves first obtaining a test statistic for the independent variable of interest, such as a $t$- or z-statistic, from a regression of the full model. Then the dependent variable is regressed only on the covariates, obtaining predicted dependent variable values and residuals. The residuals are then permuted and added to the predicted dependent variable values to obtain new dependent variable values, which are regressed on the full model again. These steps are performed iteratively to obtain a null distribution of test statistics for the coefficient of interest. Our approach is similar, but in each iteration the full WQSr is performed without splitting the data into training and validation data sets, and because the test statistic will be biased due to the lack of splitting the data, we instead iteratively sample from a null distribution of mixture coefficient estimates.

Another recently proposed single-index model is quantile g-computation (QGC), which constructs an overall mixture effect coefficient that is the sum of the mixture effect in both directions combined.¹⁶ This overall mixture effect is limited in that competing mixture effects are zeroed out, which the unidirectional approach of WQSr explicitly aims to avoid.⁸ QGC involves performing an ordinary least squares multiple linear regression including all mixture exposure components and covariates as independent variables. The bidirectional mixture coefficient is then the sum of the individual coefficients for the mixture components and the variance of this mixture coefficient derived from the variances and covariances of coefficient estimates for all mixture components. Initial simulations suggest strong performance for the overall mixture coefficient in models with no covariates and having at most two mixture components with nonnull coefficients.

Though previous studies have provided simulations validating and comparing the performance of at least one form of WQSr against one or more other related models,^16,17 to our knowledge, no study has systematically validated and compared the most current forms of WQSr and QGC in the context of their most important model output. We aimed to address this gap by using simulations to compare our novel permutation test WQSr method against the other similar single-index mixture methods currently in the literature, including recent advancements not previously directly compared against each other. In addition to the standard implementations of WQSr with and without the permutation test, we included the recently introduced random subset WQSr models,¹⁷ which provide an alternate strategy for mixture component weight estimation, as well as repeated holdout WQSr models, which were never evaluated for model performance in simulations,⁹ as well as quantile g-computation models. To highlight how results from these different methods can vary, we used real data from the Environmental Influences on Child Health Outcomes (ECHO) PATHWAYS Conditions Affecting Neurocognitive Development and Learning in Early Childhood (CANDLE) cohort to assess prenatal phthalate mixture exposure associations with age 4–6 y full scale IQ (FSIQ) using all assessed single-index mixture methods. These simulations will allow us to determine which methods perform best in detecting and quantifying an additive mixture effect under realistic modeling scenarios, thereby choosing a method best suited to improving our understanding of how real-world mixtures impact health.

Methods

Weighted Quantile Sum Regressions

Mathematical formulation.

Weighted quantile sum (WQS) regressions were developed to assess the additive linear mixture association in either the positive or negative direction of an exposure mixture with an outcome.⁶ A simplified form of this model is shown in Equation 1. Weights for each mixture component $w$ are combined with quantile-transformed exposure data $X_q$ to form a weighted index called a weighted quantile sum ($WQS$) [Equation 1 (2)]. The outcome variable $y$ is then regressed on the $WQS$ and covariates $Z$ to obtain model coefficients [Equation 1 (1)]. Model estimation is accomplished in two stages. This first stage uses bootstrapping of observations and a nonlinear optimization algorithm to determine mixture component weights that, when combined with the exposure data to generate a WQS, maximize the likelihood of the model shown in Equation 1 (1). The second stage selects the weights from the first stage that resulted in either a positive or negative mixture coefficient, then combines a weighted sum of that vector of weights with the exposure data to get a final $WQS$ that is then fed into a final linear model [Equation 1 (1)] to obtain a mixture coefficient ${\mathrm{\beta }}_1$.

If there is little or no signal in the specified direction and a strong signal in the opposite direction, the first stage may return no mixture coefficients in the specified direction and thus the model will return no estimates. This model “failure” is not due to the algorithm not converging, but rather the aforementioned lack of iterated mixture coefficients in the specified direction, making it impossible to derive weights in that direction when using this algorithm. We interpret this as equivalent to the model returning a zero ${\mathrm{\beta }}_1$ coefficient. Directionality in the model is controlled by two inputs in the gWQS R package implementation of the WQSr. The “b1_pos” input chooses the direction by determining whether positive or negative bootstrapped mixture coefficient values and their associated mixture weights are selected for calculating the $WQS$ for the second stage. There is also an additional constraint parameter “b1_constr” that does not constrain all bootstrapped mixture coefficients to be in a particular direction but instead increases the probability that bootstrapped mixture coefficients will be in the direction specified by “b1_pos”; therefore, setting “b1_constr” to be true decreases the probability that the first stage of the model will return no estimates in the specified direction and fail to return estimates. An illustration of the effect of the “b1_constr” parameter on bootstrapped mixture coefficient values is shown in Figure S1, and additional technical details are described in supplemental material section titled, “Additional Information about Bootstrap Weighted Quantile Sum Regressions (WQSBS).”

$$\begin{array}{c}\left(1\right)y={\mathrm{\beta }}_0+WQS\cdot {\mathrm{\beta }}_1+Z\cdot \mathrm{\gamma }+\mathrm{\epsilon }\\ \left(2\right)WQS=X_q\cdot w\end{array}$$ (1)

Approaches to Assessing Uncertainty

Estimation of statistical uncertainty for ${\mathrm{\beta }}_1$ is complicated by the fact that the data are used twice, once to optimize the WQS weights and a second time to estimate ${\mathrm{\beta }}_1$. A naïve approach (which we refer to as WQSBS_Nosplit) treats the weights as fixed and uses model-based or robust sandwich standard errors (SEs) to estimate $p$-values and 95% confidence intervals (CIs) for ${\mathrm{\beta }}_1$.¹⁸ This approach is expected to underestimate uncertainty and result in inflated Type 1 error rates, and it is explicitly advised against by the authors of the WQS regression.^6,19 Nevertheless, this approach has been used in several studies, and so it is worthwhile to estimate the extent of the Type 1 error issues with this approach.^20–22 Data can be split into a training set for the first stage and a validation set for the second stage (WQSBS_Split), which should result in nominal confidence interval coverage and false positive rate, though at the cost of reduced power. Which data are selected randomly into the training and validation data sets can impact model weight and coefficient estimates,²³ and so an alternate strategy proposed is to repeatedly perform random splits in a process known as repeated holdout WQSr, which we refer to as WQSBS_RH.⁹ The mean of the WQS coefficient (${\mathrm{\beta }}_1$) values across all repeated holdout iterations is the point estimate, and the standard deviation of these values is the corresponding SE estimate. For situations in which any iterated model run fails to return estimates in the specified direction as previously described, the entire repeated holdout model also will not return estimates in that direction, which we treat as returning a ${\mathrm{\beta }}_1$ coefficient of zero. For greater numbers of mixture components, an innovation on bootstrapped WQSr called random subset WQSr (WQSRS) was proposed in which, instead of bootstrapping observations, random subsets of mixture components (i.e., columns of $X_q$) are selected for each iteration during the weight estimation stage.¹⁷

We hypothesized that we could preserve the statistical power or low Type II error rate of Nosplit WQSr along with the nominal false positive rate of split WQSr by using a modified form of the permutation test to calculate $p$-values for the mixture coefficient. The permutation test is a method of obtaining a $p$-value by simulating the null distribution through permutations of the data. We modified the Freedman and Lane method for applying permutation tests to coefficients in multiple linear regressions.¹³ The modified Freedman and Lane permutation test algorithm we employed is as follows:

1. Run a WQS regression in the specified direction without splitting the data (i.e., a Nosplit WQSr), thereby obtaining a WQS coefficient estimate for the WQS coefficient, ${\mathrm{\beta }}_{ref}$.

2. Using an ordinary least squares linear regression, regress the outcome on all covariates Z but not the WQS variable, and then obtain the predicted outcome values $\left(\widehat{y}\right)$ and their residuals ($r_{y|Z}$) from this regression.

3. Randomly permute the residual values $r_{y|Z}^{*}$ and then add them to the unpermuted predicted outcome values $\widehat{y}$ to get the new outcome variable vector $y^{*}$ ($y^{*}=\widehat{y}+r_{y|Z}^{*}$).

4. Run a WQS regression in the specified direction without splitting the data in which $y^{*}$ replaces the vector of observed outcome variables, obtaining a WQS coefficient $b^{*}$.

5. Repeat steps 3 and 4 $n_p$ times to obtain a distribution of $b^{*}$ values.

6. WQS regressions can at times fail to obtain a coefficient in the specified direction when there is little or no signal in that direction, and so we treat those iterations that don’t return a $b^{*}$ value as zero values.

7. Calculate the $p$-value for the WQS coefficient obtained in step 1 as the proportion of $b^{*}$ values $>{\mathrm{\beta }}_{ref}$ (length($b^{*}>{\mathrm{\beta }}_{ref}$)/$n_p$) if the specified direction is positive or the proportion of $b^{*}$ values $<{\mathrm{\beta }}_{ref}$ (length($b^{*}<{\mathrm{\beta }}_{ref}$)/$n_p$) if the specified direction is negative.

We chose the WQS coefficient value as the reference value for the permutation test $p$-value rather than a pivotal value such as the $t$-statistic¹⁴ because the latter value relies on a proper SE estimate, which WQS regression does not give when the data are not split into training and validation sets. For each model, we repeated this process 200 times ($n_p=200$), and each WQS regression repeated for step 4 was run with 100 bootstraps, the default number in the gWQS R package (version 3.0.4; https://cran.r-project.org/web/packages/gWQS). Iterations in which the WQSr does not return any WQS coefficients from the first stage in the specified direction are treated as having a zero ${\mathrm{\beta }}_1$ value for that iteration, and the $p$-value is calculated accordingly. This permutation test is used in combination with the Nosplit WQSr to obtain a new $p$-value for the mixture coefficient, and the other estimates such as coefficients and mixture weights from this model are identical to those of the Nosplit WQSr. The accompanying R package wqspt implements this permutation test for the WQS regression.

Quantile G-Computation

QGC models are proposed as alternatives to WQSr, in which quantile-transformed exposure variables are treated as independent variables in a multiple linear regression, and the sum mixture effect of the exposure mixture is the sum of all individual mixture coefficients $\mathrm{\beta }$.¹⁶ As shown in Equation 2, this overall mixture coefficient $\mathrm{\psi }$ is bidirectional in that it is the sum mixture effect in both positive and negative directions. This differs from WQSr in that WQSr gives directional, i.e., positive or negative, mixture coefficients but lacks a mechanism for estimating the overall mixture effect. However, the WQS coefficient from WQSr and $\mathrm{\psi }$ from QGC regression should be comparable if mixture effects are unidirectional. The confidence intervals for $\mathrm{\psi }$ are either bootstrapped (QGC_Boot) or based on a normal confidence interval calculation, where the variance of $\mathrm{\psi }$ is derived from the covariance matrix for all coefficients of the quantile-transformed mixture exposure variables in the matrix $X_q$ (QGC_Noboot).

$$\begin{array}{c}\left(1\right)y={\mathrm{\beta }}_0+X_q\cdot \mathrm{\beta }+Z\cdot \mathrm{\gamma }+\mathrm{\epsilon }\\ \left(2\right)\mathrm{\psi }={\sum }_{i=1}^m{\mathrm{\beta }}_i\end{array}$$ (2)

Simulation Parameters

Data were simulated based on Equation 1, where $X$ and $Z$ were randomly generated as a single multivariate normally distributed matrix of 10 mixture components ($X$) and 10 covariates ($Z$) with means of zero, variances of 1, and covariances of either 0 (uncorrelated) or a correlation matrix derived from 10 urinary phthalate exposure variables and 10 covariates in the TIDES study¹⁰ (correlated; see supplemental material, “TIDES Correlation Matrix” and Figure S2). $X$ was then separately quintile-transformed to get $X_q$. Five of the mixture weights $w$ were set to be high (0.15), and the other five were set to be low (0.05). The intercept ${\mathrm{\beta }}_0$ was set to 2. ${\mathrm{\beta }}_1$ was set to either 0 (when testing false positive rate), 0.2 (when testing statistical power for the correlated data), or 0.3 (when testing power for the uncorrelated data) based on values that gave clear differences in power and false positive rate in repeated simulations. The covariate coefficients $\mathrm{\gamma }$ were half noise ($\text{values}=0$) and half signal ($\text{values}=\left[-0.63,0.18,-0.84,1.60,0.33\right]$ based on the first five values provided by the R random normal deviate algorithm with a standard normal distribution and when setting the random seed to 1), and finally the error vector $\mathrm{\epsilon }$ was randomly selected each time based on a standard normal distribution. We ran 500 simulations for each scenario with a different random seed leading to random differences in $X_q$, $Z$, and $\mathrm{\epsilon }$ based on the aforementioned distributions. All WQSBS regressions were performed using the default 100 bootstraps. The size of the WQSRS regression subsets was the default value of the closest integer less than or equal to the square root of the number of mixture components, which for these simulations equaled 3. Given the small size of these subsets, we doubled the default number of random subsets for all WQSRS regressions to 200 to better allow for parameter estimation comparable to the 100 bootstrap WQSBS models. Repeated holdout WQSr used the default 100 iterations of 100 bootstraps or 200 random subsets each, and permutation test WQSr used 200 iterations of 100 bootstraps or 200 random subsets each for a minimal quantifiable $p$-value of 0.005. All WQSr models were run in the positive direction and with the additional direction constraint “b1_constr” set to be its default value of false. This constraint is used to reduce the number of WQSr models failing to return estimates in the specified direction, and results from identical simulations with this constraint set to be true are presented in the supplemental materials. We chose the default value of 200 bootstraps for the QGC_Boot confidence intervals.

Measures chosen to evaluate simulation-derived WQS coefficient estimation performance included statistical power, the false positive or Type I error rate (“FPR”), mean absolute percent error when the true coefficient was nonzero ($=0.3\text{\hspace{0.17em}or\hspace{0.17em}}0.2$ for the uncorrelated or correlated simulation, respectively; “MAPE”), coverage of the 95% CIs when the true coefficient was nonzero, and finally mean absolute error and 95% CI coverage when the true coefficient was zero (“${\text{MAE}}_0$” and “ ${\text{Coverage}}_0$”). For simulation-derived weight estimates, weights were rescaled as component-specific coefficients and MAPE was determined for all simulations with nonzero WQS coefficients. For the QGC models, only component-specific coefficient estimates $>0$ were considered in calculations to provide a more direct comparison with the unidirectional estimates of the WQSr models. These mixture component coefficient performance measures were separately evaluated for high (0.15) and low (0.05) weights to evaluate how component-specific coefficient effect size impacted performance. All calculations were performed with the R statistical computing software (version 3.6.3; https://cran.r-project.org) using the packages gWQS (version 3.0.4; https://cran.r-project.org/web/packages/gWQS) and qgcomp (version 2.7.0; https://cran.r-project.org/web/packages/qgcomp). The high-performance computing cluster at the Seattle Children’s Research Institute was utilized for parallel computation of all simulations using two 28-core $2\times 2.6\text{\hspace{0.17em}GHz}$ processors, each with 512 GB RAM. Simulation and permutation test WQSr R code is provided at https://github.com/drewdstat/WQSPermutationTest.

CANDLE Gestational Phthalate and IQ Data

To test each model on real data, we used CANDLE Study implemented in Memphis, Tennessee, to associate gestational phthalate exposure with age 4–6 y FSIQ in female children as previously reported.¹¹ CANDLE study procedures were approved by the University of Tennessee Health Sciences Center institutional review board, and all participants provided written informed consent prior to engaging in study activities. Analyses for this study were conducted as part of the ECHO PATHWAYS Consortium and were approved by the University of Washington institutional review board. We chose this outcome and the stratified female population because initial WQS_Nosplit model results indicated significant results in both the positive and negative directions, providing an interesting case for comparing results between models. A total of 444 mother–daughter dyads had complete data for 13 maternal third-trimester gestational urinary specific gravity-adjusted phthalate concentrations, which we treated as exposure mixture components, including, monomethyl phthalate (MMP), monoethyl phthalate (MEP), monobutyl phthalate (MBP), monoisobutyl phthalate (MiBP), monobenzyl phthalate (MBzP), mono(2-ethylhexyl) phthalate (MEHP), mono(2-ethyl-5-oxohexyl) phthalate (MEOHP), mono(2-ethyl-5-hydroxyhexyl) phthalate (MEHHP), mono(2-ethyl-5-carboxypentyl) phthalate (MECPP), mono(2-carboxymethylhexyl) phthalate (MCMHP), mono(3-carboxypropyl) phthalate (MCPP), monocarboxyisooctyl phthalate (MCIOP), and monocarboxyisononyl phthalate (MCINP). The correlation matrix for these metabolites is shown in Figure S3.

Following the primary analysis in Loftus et al., each of our models included 19 covariates, which were selected a priori for having known associations with both pediatric cognitive development and phthalate exposure but not being on the causal pathway.¹¹ Several of these covariates were collected during pregnancy, including study site, maternal psychopathology score as assessed by the Brief Symptom Inventory; maternal childcare knowledge score as assessed by the Knowledge of Infant Development Inventory; and maternal self-reported age, race, education, marital status, medical insurance, prepregnancy body mass index, parity, tobacco smoking, and income adjusted by household size, region, and inflation. Addresses collected during pregnancy were used to obtain educational, health and environment, and social and economic Childhood Opportunity Index scores,²⁴ each of which were included as 3-degree of freedom cubic splines in the models. Year of birth as abstracted from birth records was also included. Additional covariates collected at the age 4–6 y visit included maternal IQ as assessed by the Weschler Abbreviated Scales of Intelligence, child age, and child breastfeeding history. In this study population, 93% of participants identified as either Black or White, and we dichotomized race as Black or non-Black to be consistent with the published results that we are reanalyzing.¹¹ Categorizations and collection timing for these covariates are shown in Table S1. When covariates were expanded with dummy variables into a model matrix, these represented 34 covariate columns. Model estimates were compared across model types, using the same numbers of bootstraps, random subsets, and/or iterations used in the simulations for each respective model. A 28-core $2\times 2.6\text{\hspace{0.17em}GHz}$ processor with 512 GB RAM was used to run models on the CANDLE data.

Results

Simulation Results—Mixture Coefficients

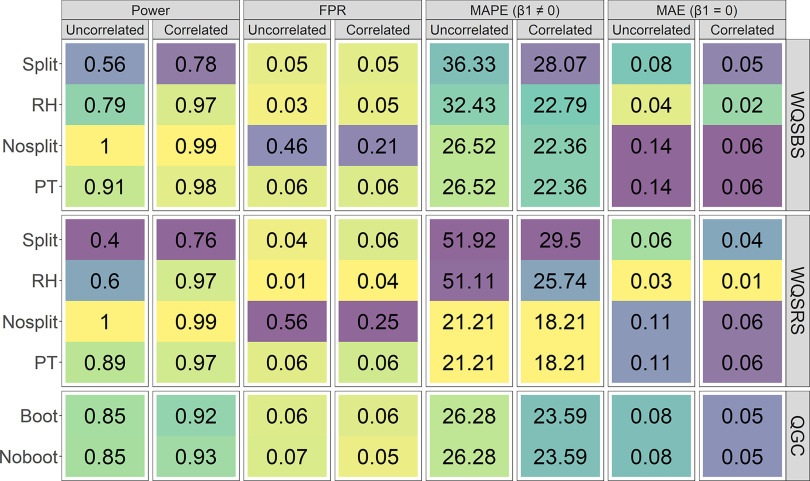
Figure 1 shows various performance measures of each model in terms of the mixture coefficient, which is the positive WQS coefficient for the WQSr models and the overall coefficient $\mathrm{\psi }$ for the QGC models, when WQSr models had the “b1_constr” parameter set to be false. Models were compared across simulations with either uncorrelated or correlated exposure mixtures and covariates. Nosplit forms of WQSBS and WQSRS had high false positive rates ($\text{FPR}=0.21–0.46$ and 0.25–0.56, respectively), whereas FPRs for the other models were between 0.01 and 0.07. Of those models with approximately nominal FPRs, power was highest for the WQSBS_PT (0.91–0.98) and WQSRS_PT (0.89–0.97) models. The QGC models with the nonbootstrapped CIs had similar power to the bootstrapped versions (0.85–0.93 vs. 0.85–0.92). The WQSr versions based on splitting the data had lower power, which in order of descending power were the WQSBS_RH (0.79–0.97), WQSRS_RH (0.60–0.97), WQSBS_Split (0.56–0.78), and WQSRS_Split (0.40–0.76) models.

Figure 1.

Model performance measures for mixture coefficient estimates in 500 simulations for nonzero or zero mixture coefficients between correlation conditions. Within each performance measure and simulation exposure correlation condition (i.e., uncorrelated predictors or correlated predictors with a variance-covariate matrix derived from a real data set), lighter (yellow) tiles indicate better performance, whereas darker (purple) tiles indicate worse performance. Note: FPR, false positive rate; MAPE, mean absolute percent error (when ${\mathrm{\beta }}_1$ is nonzero); MAE, mean absolute error (when ${\mathrm{\beta }}_1$ is zero); PT, permutation test; QGC, quantile g-computation; RH, repeated holdout; WQSBS, bootstrap weighted quantile sum regression; WQSRS, random subset weighted quantile sum regression.

For true nonzero coefficients, error was similar across all models, though slightly higher for Split ($\text{MAPE}=28.07–51.92\%$) and RH WQSr models (22.79%–51.14%). These models had lower error when the true coefficient was zero, with higher error in this case being observed for the WQSBS_PT and WQSBS_Nosplit models ($\text{MAE}=0.06–0.14$) and slightly lower for the WQSRS_PT and WQSRS_Nosplit models (0.06–0.11). The coverage measures for both true nonzero and zero coefficients suggest improper 95% CIs for at least one simulation scenario for all models except the QGC models (see supplemental material, “Confidence Interval Coverage Results from Simulations” and Figure S4).

Cases in which models failed to return any estimates in the positive direction were rare (0%–2%) for all models except the WQSBS_RH models (35% under all true zero ${\mathrm{\beta }}_1$ scenarios), WQSRS_RH models (26%–86%), and all other forms of WQSRS models when in the scenario with true zero ${\mathrm{\beta }}_1$ and correlated predictors (11%–14%; see supplemental material, “Rates of WQSr Models Failing to Estimate a Coefficient in the Desired Direction” and Table S2). Internal PT model WQSr iterations failed to return estimates in the positive direction in 0%–4% of iterations for all scenarios except for WQSRS_PT models, for which this occurred in 5%–19% of iterations with correlated predictors.

Mixture coefficient simulation results for models when the “b1_constr” parameter was set to be true are shown in Figure S5. Results were largely similar with slightly lower power for the Split (0.39–0.77 vs. 0.40–0.78) and WQSBS_PT models (0.90–0.97 vs. 0.91–0.98), as well as slightly higher FPR for the WQSBS_RH (0.07–0.08 vs. 0.03–0.05) and WQSRS_RH models (0.02–0.04 vs. 0.01–0.03). CI coverage raters were similar when using the “b1_constr” constraint (Figure S5), except coverage for WQSBS_RH models, when the true mixture coefficient was zero increased from 0.60–0.62 to 0.92–0.93. Failure rates also dropped when the “b1_constr” parameter was true as shown in Table S4, with no WQSBS_RH model failures and WQSRS_RH failures dropping to 7.6%–72% under true zero ${\mathrm{\beta }}_1$ conditions. There were no internal WQSBS_PT model failures with the “b1_constr” constraint parameter, and WQSRS_PT internal failures were 0%–18%.

Simulation Results—Mixture Component Coefficients

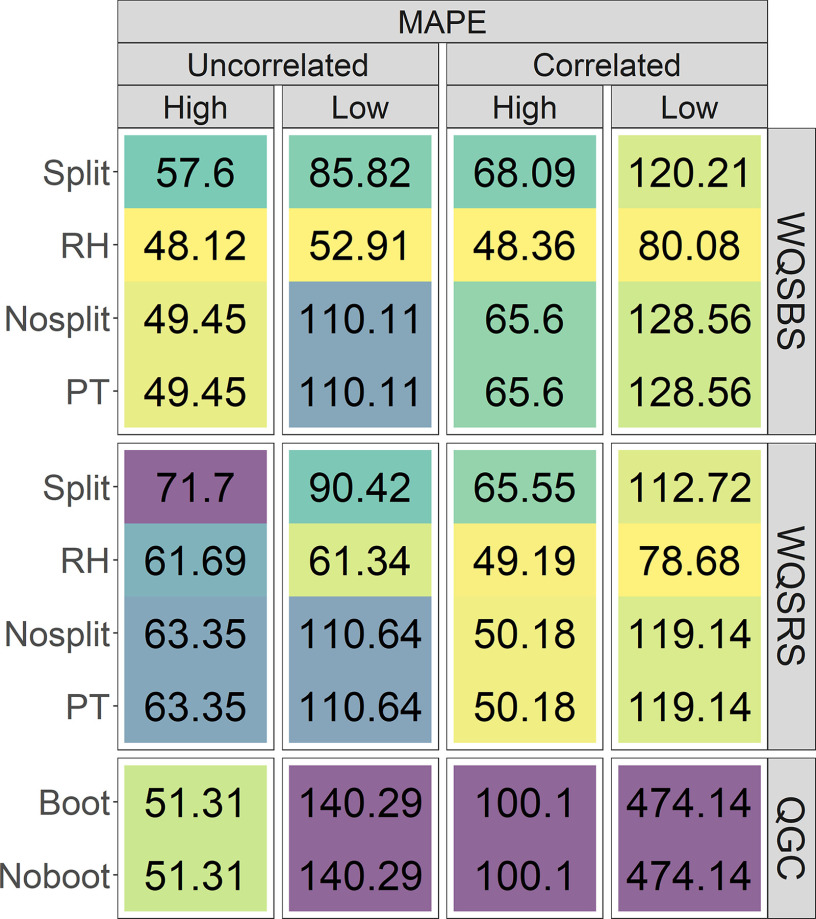
Figure 2 shows MAPE for the mixture weights rescaled as component-specific coefficients from simulations with either correlated or uncorrelated predictors, separately evaluated for the higher weights ($\text{weight}=0.15$) and the lower weights ($\text{weight}=0.05$) when ${\mathrm{\beta }}_1$ is nonzero. Note that nonsplit and permutation test WQSr component-specific coefficients are identical because the permutation test only provides a $p$-value for the WQS coefficient. Similarly, the QGC_Boot and QGC_Noboot models only differ in their estimates of the $\mathrm{\psi }$ overall mixture coefficient error, which does not affect the component-specific coefficient values. WQSr mixture component coefficient values were treated as zeros when the model did not return estimates in the positive direction.

Figure 2.

MAPE for high and low mixture weight estimates rescaled as component-specific coefficients in 500 simulations for nonzero mixture coefficients between correlation conditions. Within each simulation exposure correlation condition (i.e., uncorrelated predictors or correlated predictors with a variance-covariate matrix derived from a real data set) and class of weights (i.e., high or low), lighter (yellow/green) tiles indicate better performance, whereas darker (blue/purple) tiles indicate worse performance. Note: FPR, false positive rate; MAPE, mean absolute percent error (when ${\mathrm{\beta }}_1$ is nonzero); MAE, mean absolute error (when ${\mathrm{\beta }}_1$ is zero); PT, permutation test; QGC, quantile g-computation; RH, repeated holdout; WQSBS, bootstrap weighted quantile sum regression; WQSRS, random subset weighted quantile sum regression.

In general, error was lower for the more highly weighted mixture components than for those with lower weights, and error increased as correlations between the mixture components increased with the exception of WQSRS model error for the higher weights. The WQSRS models tended to have lower error when predictors were correlated but higher error when predictors were uncorrelated. For the higher weights and among the WQSr models, the RH forms consistently had the lowest error ($\text{MAPE}=48.12\%–61.69\%$), followed by the Nosplit/PT models (49.45%–65.60%), and finally the Split models (57.60%–71.70%). For the higher weights, the QGC models had low error (51.31%) for high weights when predictors were uncorrelated but the highest error (100.1%) when predictors were correlated. For the lower weights, the RH WQSr models also returned more accurate estimates of the component-specific coefficient values for lower weights ($\text{MAPE}=52.91\%–80.08\%$), followed by the Split models (85.82%–120.21%), the Nosplit/PT models (110.11%–128.56%), and finally the QGC models had particularly inaccurate estimates (140.29%–474.14%). Simulations with the “b1_constr” constraint showed similar error values (Figure S6).

Prenatal Maternal Phthalate Mixtures and Child FSIQ in the CANDLE Cohort

Model results in either the negative or positive direction or both directions combined without the “b1_constr” constraint for all WQSr are shown in Figure 3, whereas the results with that constraint are shown in Figure S7. Numeric values for the coefficients displayed in these figures are shown in Table S3. The models with the best balance of power and FPR from the simulation analyses, namely both forms of PT WQSr models, suggested nonsignificant results. The Nosplit WQSr models as well as the WQSRS_Split model provided significant mixture associations. For the negative direction, there was an adverse, negative 1.7-point association between the phthalate mixture and FSIQ with high weights for MBZP, MiBP, MMP, MCMHP, MEP, and MBP provided by the WQSBS_Nosplit model with a $p$-value of 0.08 after the PT, and the WQSRS_Nosplit model had only a slightly different 1.5-point negative association with a PT $p$-value of 0.08 and similar weights except for a lower component-specific coefficient for MEP. The significant positive associations all had high weight only for MCINP and had magnitudes of 1.2, 1.1, and 1.4 for WQSBS_Nosplit, WQSRS_Nosplit, and WQSRS_Split, respectively, with the two Nosplit WQSr models having $p$-values of 0.30 and 0.36 after the PT, respectively. The other models varied in estimate value, though the WQSRS_RH model failed to return any estimates in the positive direction. The overall mixture coefficient estimates for both directions combined provided by the QGC models trended negative but were also nonsignificant. Internal iterations of the PT WQSr models did not return any estimates in the specified direction 1%–2% of the time for WQSBS_PT and 17%–18% of the time for WQSRS_PT. Results were similar when the “b1_constr” constraint was set to be false (Figure S7), though the internal failure rate decreased to 0% for WQSBS_PT and 4.5%–5.0% for WQSRS_PT.

Figure 3.

Mixture coefficient and component coefficient results for all models evaluating associations between prenatal maternal phthalate mixtures and female child FSIQ in the CANDLE Cohort. The top forest plot shows means and 95% CIs for mixture coefficient estimates in the negative and positive directions for WQSr models or for both directions for the QGC models. The bottom heat map shows the corresponding mixture component-specific coefficients for each model, direction, and measured phthalate metabolite. These mixture component-specific coefficient values are color coded by value with darker red values being more negative and darker blue values being more positive. These colors highlight the coefficient values in the bottom heat map; they do not contain any information beyond the printed numeric values. Numeric values for the top forest plot are provided in Table S3. Note: CI, confidence interval; FSIQ, full scale IQ; MBP, monobutyl phthalate; MBzP, monobenzyl phthalate; MCINP, monocarboxyisononyl phthalate; MCIOP, monocarboxyisooctyl phthalate; MCMHP, mono(2-carboxymethylhexyl) phthalate; MCPP, mono(3-carboxypropyl) phthalate; MECPP, mono(2-ethyl-5-carboxypentyl) phthalate; MEHP, mono(2-ethylhexyl) phthalate; MEHHP, mono(2-ethyl-5-hydroxyhexyl) phthalate; MEOHP, mono(2-ethyl-5-oxohexyl) phthalate; MEP, monoethyl phthalate; MiBP, monoisobutyl phthalate; MMP, monomethyl phthalate; QGC, quantile g-computation; WQSR, weighted quantile sums regression.

The QGC models consistently had much larger mixture component coefficient estimates than other models, corresponding to total estimates of the mixture association in the positive direction (${\mathrm{\psi }}^{+}$) of 3.2 and in the negative direction (${\mathrm{\psi }}^{-}$) of $-4.2$, far greater than the directional mixture coefficient estimates from the WQSr models (WQS negative $\text{coefficient}=-1.7–0.4$ and positive $\text{coefficient}=0.4–1.4$). Those metabolites with higher coefficients in the QGC models did not necessarily correspond with more heavily weighted metabolites in the other models. Differences between mixture coefficient estimates returned by the QGC and WQSr models were greater in the negative direction than in the positive direction.

Discussion

Overall Summary of Results across Models

After directly comparing model performance between most current single mixture index regression models, our findings suggest that the novel permutation test form of WQSr was best able to balance high power and a nominal FPR under multiple simulation scenarios. The PT WQSr models will enhance the field of mixture exposure analysis by providing a more reliable means of assessing mixture effects. Mixture exposure analysis improves on analyzing each exposure in individual models by modeling the cumulative impacts of exposures that occur simultaneously in real life, reframing the effects of a given exposure in the context of its coexposures and providing inference on how interventions that can simultaneously impact multiple chemical concentrations may improve public health.⁴ The WQSr permutation test better achieves these objectives by a) providing a more sensitive and specific way of determining the mixture effect and b) providing better estimates of individual component effects with its nonlinear optimization step than methods relying on nonregularized multiple regression, such as those observed in our simulations for the QGC models. The CANDLE data analysis shows that model choice can affect the results and conclusions drawn from exposure mixture analysis. In particular, these results highlighted how unidirectional mixture effect estimates may be more informative, because the WQSr results suggested at least some evidence of negative and positive effects for different mixture components, whereas the overall mixture effect estimate of the QGC models suggested neither.

The PT WQSr models are a preferable modeling choice for multiple analytic contexts. They provide benefits over QGC models when a unidirectional coefficient is desired and when researchers want more accurate estimates of mixture component weights. They can also provide benefits over the split WQSr models by providing much more power and by avoiding stochastic drift in model estimates caused by random splits in the data, which are not performed in the PT WQSr method. The permutation test WQSr method also has several advantages over the repeated holdout method, including that the PT WQSr models maintain higher power than repeated holdout models in the case of uncorrelated mixture components, and there is also a lower frequency of models failing to return estimates when using the current algorithms for those models. The PT WQSr method also has a shorter overall computational time than the repeated holdout WQSr because the permutation test need only be run for models with significant mixture coefficients after the initial nonsplit WQSr, whereas the iterative repeated holdout method must be run each time. This is because the permutation test $p$-value will almost always be more conservative than the nonsplit WQSr mixture coefficient $p$-value, and therefore one could just run permutation tests on the subset of results that are significant during the much quicker nonsplit WQSr step. In many cases this would require running only a few models, which would allow time for more accurate estimates because we would recommend increasing the number of bootstraps and the number of permutations when using the WQSBS_PT model, such as doing 200 permutations of 200-bootstrap models. For comparability, the test coefficient against which all permuted coefficients are compared should also be from a WQSr run with 200 bootstraps. In short, the PT WQSr are applicable to and preferable for any mixture exposure analysis seeking to evaluate unidirectional, additive, and linear mixture effects.

There was similar performance between WQSBS_PT and WQSRS_PT models, with the slight differences likely being primarily stochastic, though the increased probability of WQSRS_PT model failure suggests using the bootstrap model when possible. We expect that this performance would be even better when increasing the number of WQSBS bootstraps or WQSRS random subsets well beyond the default setting. The additional directionality constraint “b1_constr” tended to make model performance measures slightly worse, but this may have been in part stochastic, and differences were negligible.

Comparing Simulation Results to Prior Evaluations of Mixture Exposure Model Performance

Our simulations involved several novel comparisons of exposure mixtures analytical methods, as well as expanded on some comparisons already implemented in prior analyses. For instance, though introduced in 2019⁹ and since used in dozens of publications,^25,26 repeated holdout WQSBS model performance has to our knowledge never been assessed using simulated data before. Our assessment of model performance under realistic simulation parameters shows that though WQSBS_RH models have a nominal FPR, they are underpowered in the case of uncorrelated predictors and frequently failed to return estimates in the specified direction. Our results suggests that the WQSBS_PT models outperform WQSBS_RH models in terms of assessing the WQS coefficient. However, the WQSBS_RH models do perform favorably in comparison with WQSBS_PT models in terms of mixture component weight estimation, though the difference in error for the more heavily weighted mixture components was small.

Simulations have previously compared the performance of WQSRS_Split and WQSBS_Split models in evaluating larger numbers of mixture components, namely 34 or 59, but the performance of applying the random subset form of WQSr to the more novel RH or PT models had not been previously tested.¹⁷ Our findings suggest similar top performance for the WQSRS and WQSBS forms of the PT WQSr models, though power and FPR are slightly better for the WQSBS form when predictors were uncorrelated. We also observed that the Split, Nosplit, and RH forms of WQSRS perform worse in balancing power and FPR than the WQSBS forms in all tested models and scenarios, perhaps in part because the random subset method was introduced specifically for larger sets of mixture components. These novel findings suggest that the random subset method will perform similarly well to the bootstrap method when combined with the permutation test, even when being applied to smaller numbers of mixture components than it was originally designed to evaluate.

Quantile g-computation was introduced as an alternative to WQSr, and when introduced it was directly compared against WQSBS_Split models using several different simulation conditions.¹⁶ There has been some criticism that these simulations may have incorrectly assessed WQSr bias under certain simulation conditions,⁸ and Keil et al. have since responded to that criticism defending their methods.²⁷ Similar to the Keil et al. findings when assessing unidirectional simulations, quantile g-computation is more powerful and less biased than the WQSBS_Split models in determining a mixture coefficient. However, they were slightly underpowered in comparison with the PT WQSr models, whereas both had comparably low bias and FPRs. Furthermore, the mixture component-specific coefficients estimated by quantile g-computation were far less accurate than those of any of the WQSr models. This may be due to the QGC model relying on a linear regression without regularization, whereas the WQSr is able to return more accurate mixture component coefficient estimates due to the internal optimization algorithm. Our findings may differ from the Keil et al. findings because we tested alternative forms of WQSr and included a higher number of nonnoise exposure variables and also covariates in our simulated models. Our results suggest caution when interpreting quantile g-computation coefficients beyond the $\mathrm{\psi }$ total mixture effect parameter. Additional simulations are needed to test the relative performance of quantile g-computation with the various forms of WQSr under different mixture scenarios.

Strengths and Limitations

Strengths of this study include demonstrating the viability and advantages of using the permutation test WQSr using simulations with realistic numbers of observations, variables, and correlation structures, as well as comparing the model performance of several recent advancements in mixture analysis that had not previously been directly compared. We have created an R package wqspt that implements the permutation test method described here as well as versions for logistic WQS regression and other generalized linear model forms of WQS regression.

There are however some limitations of the permutation test WQSr method as well as the simulations used in this study. First, the permutation test WQSr takes a considerable amount of computational time, comparable to the repeated holdout WQSr, because one must repeat the entire WQSr process many times. For the simulations performed in this study, a single-core computational unit in our computing cluster (roughly analogous to an individual computer), WQSr permutation tests each took approximately 9 h to compute, which is similar to repeated holdout WQSr. When using our 28-core computational unit for the CANDLE data, which would otherwise take more time than the simulated data due to the higher number of mixture components and covariates, this process took approximately 3–4 h. The number of models requiring long run times with the permutation test will be low for the aforementioned reason that only mixture components significant in the Nosplit WQSr estimates need to undergo the permutation test.

Another limitation of the permutation test is that it does not produce CIs. It should be noted that our simulation results suggest that no WQSr consistently produces valid 95% CIs, although QGC models do, as is evidenced by only QGC showing 95% coverage for its mixture coefficient CIs across simulation conditions (Figure S4). Regarding the simulations, they are sufficient to ascertain the relative performance of the permutation test WQS regressions under a unidirectional mixture effect scenario, but it is unclear how well our other WQSr methods would perform when the true mixture effect is bidirectional or if nonlinear mixture effects exist. This and other potential features of mixtures analysis, such as unmeasured confounding, remain to be tested in additional simulations. Furthermore, our simulations assume that the quantile structure applied to the exposure mixture is accurate, and so our simulations are unable to reveal how improper quantization may bias results. Future simulations may also incorporate additional comparisons, because we have excluded mixture methods that are less comparable to single-index methods such as Bayesian kernel machine regression, which models a flexible response surface allowing for nonlinear and interactive effects and does not lend itself to frequentist evaluations of statistical power and other related measures.²⁸ Another related method that we excluded is the Bayesian WQSr, which differs substantially from other WQSr methods by combining an overall, bidirectional mixture effect coefficient with a simplex of weights.²⁹ We did not include this model in our comparisons because this method only returns interpretable mixture weights under strict assumptions of unidirectionality, which is not true for the other methods and limits the utility of this model. An alternative form of WQSr was recently published that replaces bootstrapping with L1 or L2 penalization to induce sparsity in mixture weights, in addition to utilizing a different version of the permutation test for sampling the null distribution.³⁰ Simulations from that study suggest favorable performance in comparison with Split WQSr, but future analyses will be necessary to determine how the Lyden et al. method compares with our own permutation test method or the other models we tested in our study.

Conclusions

Adding a permutation test step to the bootstrap WQSr balanced high statistical power and a low FPR in detecting a directional, additive mixture effect. In our simulations this model outperformed other existing models in terms of these parameters, suggesting that it should be adopted to most reliably detect cumulative, additive associations between mixture exposures and outcomes. Continued refinement of mixture exposure models will improve our ability to understand and mitigate the health impacts of exposure to complex mixtures, and we believe this permutation test method for the WQSr advances our ability to characterize mixture exposure health effects.