Diminishing returns from ultra-hypofractionated radiation therapy for prostate cancer

Abstract

Introduction:

More than a decade of randomized controlled trials in prostate cancer have established a positive radiation dose response at moderate doses and a consistently low α/β ratio in the linear quadratic model for moderate hypofractionation. The recently published large randomized trial of ultra-hypofractionated prostate cancer radiotherapy adds substantially to our current knowledge of dose-response and fractionation sensitivity.

Methods and Materials:

Randomized trials of dose-escalation and hypofractionation of radiotherapy are meta-analyzed to yield the overall best estimate of the α/β ratio. Additionally, a putative saturation of dose effect previously reported at approximately 80 Gy EQD2 is investigated by mapping the relative effectiveness assessed at five years onto a single reference dose-response curve.

Results:

Meta-analysis of 14 randomized trials including 13,384 patients yields a best estimate of α/β=1.6 Gy [95% CI: 1.3 to 2.0 Gy], but with highly significant heterogeneity (I²=70%, P=0.0005). Further analysis indicates an association between increasing dose per fraction in the experimental arm and increasing α/β ratio (slope: 0.6 Gy increase in α/β per Gy increase in fraction size, p=0.017). This deviation from the linear quadratic model could, however, also be explained by biochemical control maxing out at doses above approximately 80 Gy.

Conclusions:

Biochemical control data from randomized controlled trials of dose-per-fraction escalation in prostate cancer radiotherapy are inconsistent with the presence of a constant fractionation sensitivity in the LQ model and/or a monotonic dose response for biochemical control beyond 80 Gy equivalent dose. These observations have potential impact on the optimal doses in future trials as well as the interpretation of ongoing trials of ultra-hypofractionation.

Introduction

Evidence-based dose-time-fractionation regimens in radiation therapy for prostate cancer have developed substantially through a whole string of large randomized trials, first testing the effect of dose escalation [1–5] and subsequently testing hypofractionated regimens based on a putative high fractionation sensitivity of prostate cancer [6–14]. The ASTRO evidence-based guideline now supports the use of moderate hypofractionation in certain patient groups with good consensus and high level of evidence, but points to lack of evidence behind ultra-hypofractionated RT in the absence of data from randomized comparisons at the time of writing the report[15].

In light of the increased understanding of the complexity of tumor-host interactions and updated hallmarks of cancer, it may even be surprising that the linear-quadratic model (LQ model) has provided such a good description of clinical data up till now. It has been questioned, however, whether the LQ model remains a reliable description of the time-dose-fractionation problem when moving beyond the moderately hypofractionated regimens towards ultra-hypofractionated schedules or even stereotactic doses. Widmark and colleagues pushed the experimental arm to 6.1 Gy times 7 over 1–2 weeks in a large trial opened in 2005[6]. Initially, the trial was designed to show superiority of the test arm over a control arm delivering 78 Gy in 2-Gy fractions. However, after a blinded interim analysis, the statistical analysis plan was revised to test for non-inferiority of the test arm within a margin of 4%. The recent publication suggests that this margin of non-inferior biochemical control was met and with acceptable toxicity and is indeed the first large randomized trial venturing beyond the widely accepted range of applicability of the LQ model. In the following, we will discuss the added insights from the Widmark trial compared with the existing body of clinical trials.

Methods and material

The previous search for randomized trials of prostate cancer radiotherapy[16] is updated to October 2019. In short, trials were included if they enrolled patients with any-risk prostate cancer; and if they randomized patients between two fractionation schedules delivered with External Beam Radiotherapy (EBRT) only. Finally, the trials should report the outcome measures of overall survival (OS) and prostate-specific antigen (PSA) control in sufficient detail to be included in the quantitative data synthesis. Studies of brachytherapy were excluded from the analysis. See the previous report for further details [16].

A logistic dose-response function, $bNED=\frac{1}{1+exp(4{\gamma }_{50}\left(1-\frac{EQD2}{D_{50}}\right)}$, is assumed for the original dose-response studies and a steepness was extracted in [16] to yield γ50= 0.62 (95% CI 0.37–0.87) assuming no effect of overall treatment time (no new data). Here EQD2 is the fraction-size corrected prescribed radiation dose and D50 is the dose required for 50% biochemical control. Here we use the LQ model, $EQD2=D\left(\frac{d+\alpha /\beta }{2+\alpha /\beta }\right)$ with D denoting the total prescribed physical dose and d the dose per fraction. Subsequently, the steepness of the dose-response was used to estimate the α/β ratio for each included study and these were summarized in a forest plot using review manager[17]. The heterogeneity of the observed α/β estimates is quantified by the I² statistics which describes the percentage of variation that is not explained by random sampling [18].

The observed α/β estimate in each study is plotted against dose per fraction in the experimental arm of the study in order to assess a possible systematic deviation indicating a potential limitation to the validity of the linear-quadratic model over the range of fraction doses applied in the trials. A linear regression of α/β estimate versus fraction dose is performed and the p-value for non-zero slope is used to test the dependence of α/β on fraction dose. The linear regression is weighted by the inverse variance of the study-specific α/β estimates, see [16] for details re. derivation of the standard errors of the estimates.

Finally, we provide an estimate of an overall dose-response relationship for 5-year freedom from biochemical failure. As we have previously investigated, a simple plot of direct observed control probabilities on a single graph breaks the randomized comparisons in the trials and lead to an exaggerated steepness of the dose-response relationship - probably due to different case-mix and treatment support in newer series [19]. Here, we assume a logistic dose response as above with γ50= 0.62 and implement a dose-modifying offset, δDose, estimated from the control arm in each trial to adjust for case mix etc. In this way, all control-arm outcomes fall on a curve with γ50= 0.62. D50 is adjusted until the mean value of δDose is zero to achieve a representative curve; this curve is illustrative only as the D50 of each study is assumed to be different according to case-mix. Experimental arms are plotted on this curve with confidence intervals using $bNE{D}_{exp}={\left(bNE{D}_{ctrl}\right)}^{HR}$, where bNEDctrl denotes the 5-year biochemical control in the control arm and HR is the reported Hazard ratio between the arms of the study. The confidence interval of HR is used to estimate the 95% confidence limits of bNEDexp. A linear fit weighted by the inverse variance of bNEDexp estimates for observations with EQD2>80 Gy is performed to quantitatively discuss the previous hypothesis that the dose-response relationship flattens at such high doses[16].

Results

The ultra-fractionated study by Widmark et al[6] is the only study added to the previous list of 13 randomized trials, yielding a total of nine randomized trials of altered fractionation [6–14] involving 9,146 patients and five of dose escalation [1–5] involving 2,238 patients.

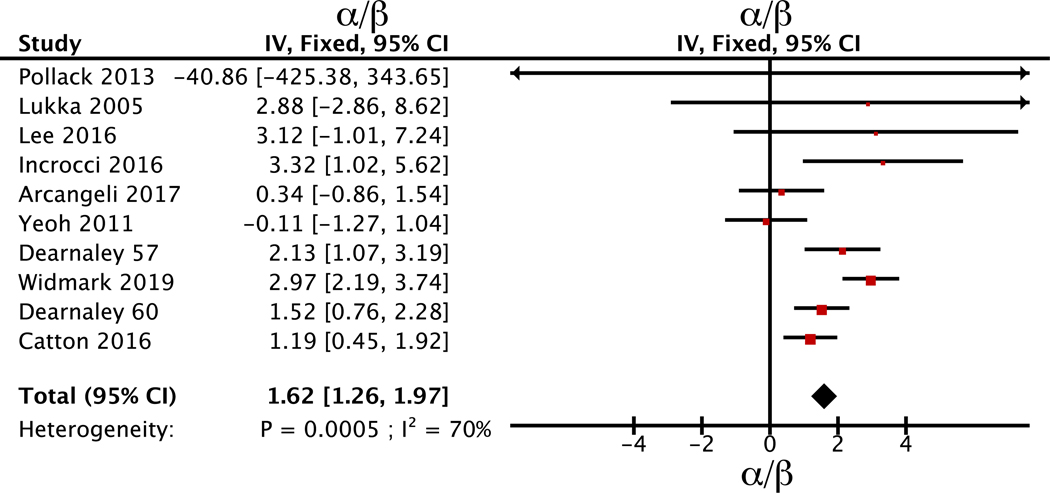
The updated meta-analysis of the α/β ratio is still consistent with a low value and tight confidence interval at α/β=1.6 Gy (95% CI: 1.3 to 2.0 Gy). Figure 1 shows the individual study estimates sorted by the inverse variance of each study. The heterogeneity is qualitatively visible and the p-value for heterogeneity is p<0.001 and I² is high at 70%. Random effects modeling yield slightly wider confidence interval at α/β=1.6 Gy (95% CI: 0.8 to 2.4 Gy). The Widmark study, testing the only ultra-fractionated schedule so far, yields a higher α/β estimate than the remaining studies, α/β=3 Gy (2.2 Gy to 3.7 Gy) vs α/β=1.3 Gy (0.9 to 1.7 Gy), with a highly significant p=0.0001 for difference between estimates.

Figure 1.

Forest plot of estimated α/β value of the included studies with 95% confidence interval. Studies are ordered according to inverse variance (IV) of the estimate. Nine studies of altered fractionation are included. The two experimental arms by Dearnaley et al from 2016 are included as individual studies and denoted by experimental arm dose rather than date of publication.

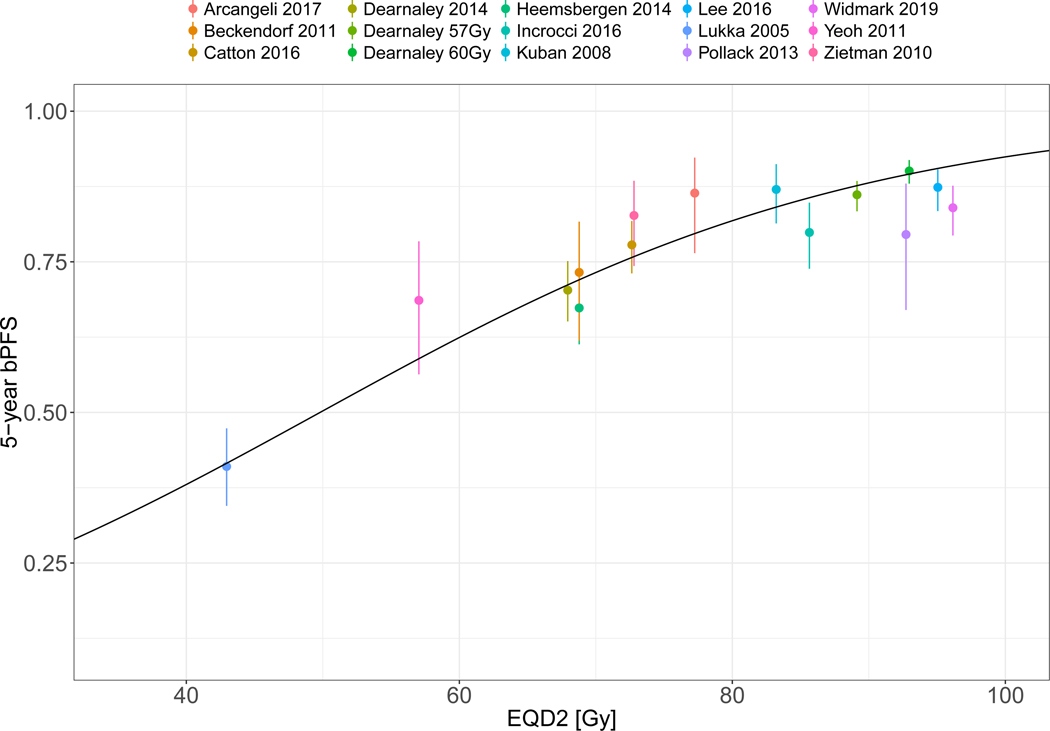
The presence of heterogeneity might be interpreted as an indication that the linear quadratic fit to the entire range of fractionation schemes is not appropriate. In other words that the effective dose is not well described by the single formula, $EQD2=D\left(\frac{d+\alpha /\beta }{2+\alpha /\beta }\right)$ and constant α/β throughout the full range of studies. Figure 2 shows a re-plot of the individual study estimates of Figure 1, but as function of the experimental arm fraction dose to explore this suggestion quantitatively. Linear regression shows a trend towards an increasing value of the study estimate of α/β with a slope of 0.57 Gy (of estimated α/β) per Gy increase in experimental arm fraction dose (95% CI: 0.2 to 0.9 Gy per Gy), p=0.02. Figure 2 also illustrates the large information content of the Widmark trial in this context due to the choice of the investigators to select a radically different fraction size.

Figure 2.

Estimated α/β value and 95% confidence interval as function of experimental arm fraction size. Linear regression model with 95% confidence (dashed) and prediction (dotted) bounds are shown for the best fitting model with slope=0.57 Gy/Gy (SEE=0.19, p=0.017). The linear regression is weighted by the inverse variance of the individual α/β estimates from 9 included studies. The two experimental arms by Dearnaley et al from 2016 are included as individual studies and denoted by experimental arm dose rather than date of publication.

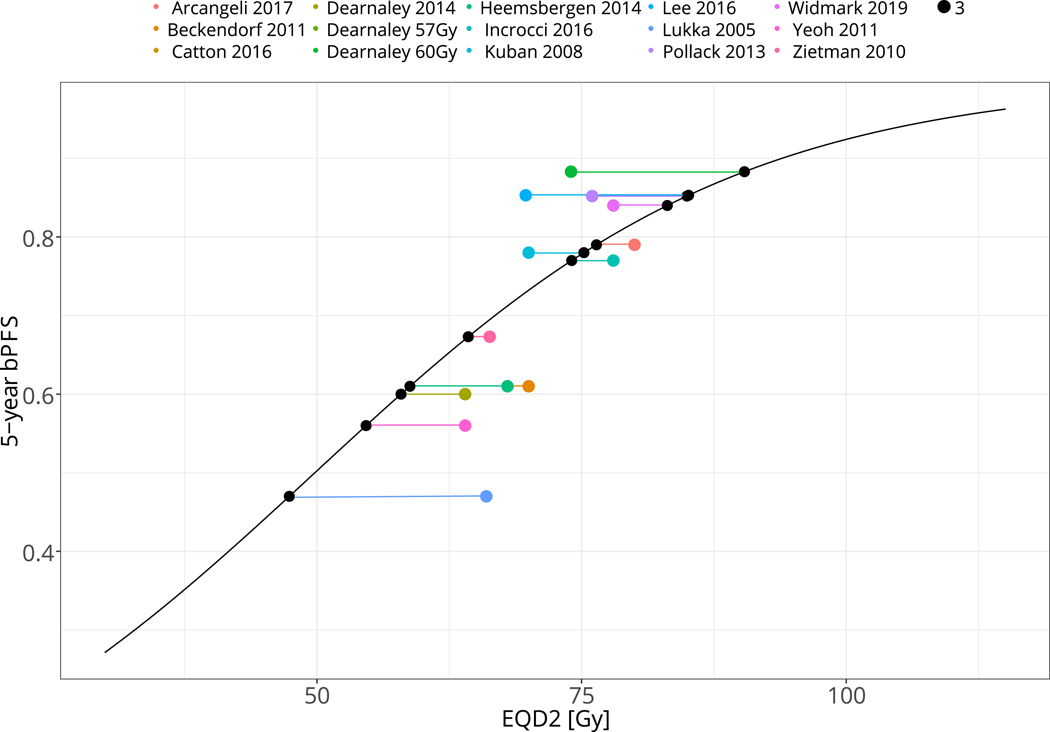
Another possible cause of the heterogeneity in Figure 1 would be the breakdown of the dose-response assumption, rather than the LQ fraction size correction. This hypothesis was discussed in Vogelius & Bentzen 2018[16] where the positive effect on the HR for dose escalation vanished when the experimental arm exceeded 80 Gy EQD2. Figure 3A shows the application of a dose-modifying offset, δDose, to each individual study control arm in order to arrange all studies on a representative dose-response curve in accordance with the overall best estimate of γ50 as derived from the five dose-escalation studies. Subsequently, Figure 3B shows the position of the experimental arms in relationship to the common dose-response curve after applying the same study-specific δDose. The maneuver allows visualization of a deviation from the sigmoid shape at doses exceeding ~80 Gy EQD2. Indeed, the data is consistent with a flat dose-response for all points exceeding 80 Gy EQD2 when fitted with a linear model (slope: 0.3% per Gy increase in EQD2, 95% CI: −0.5% to 1% per Gy EQD2, p=0.48).

Figure 3.

A: Illustration of the study-specific dose offset, δDose, required for the control arm outcome to fall on a reference sigmoid dose-response curve with the steepness defined by meta-analysis of the normofractionated randomized dose-escalation studies.

B: Experimental arm EQD2 and control probabilities after applying δDose, Note signs of systematic deviation from sigmoid shape at high doses. Error bars show 95% CI of the bPFS estimate as detailed in Methods and Materials. Nine studies of altered fractionation and five studies of dose escalation are included. The two experimental arms by Dearnaley et al from 2016 are included as individual studies and denoted by experimental arm dose rather than date of publication.

Discussion

Credit should go to Brenner and Hall for first suggesting a high fractionation sensitivity of prostate cancer with an estimated α/β=1.5Gy (95% CI: 0.8 to 2.2 Gy) [20] based on a fairly complex comparison of outcome after brachytherapy vs. external beam radiation therapy. Nevertheless, their α/β estimate is in remarkable agreement with the estimate presented here, which builds on the subsequent 20 years of systematic scientific effort to improve prostate cancer radiotherapy through dose escalation and hypofractionation in randomized controlled clinical trials.

In 2018 it was argued that the number of high-quality clinical trials of moderate hypofractionation was enough that the “question of the sensitivity of prostate cancer towards moderate hypofractionation was well elucidated” [16] by the existing body of trials with more than 10,000 patients. The question remained, however, if the low value of α/β would apply regimens with more extreme hypofractionation. To this end, the ultra-hypofractionated trial of Widmark et al is highly informative in terms of answering the question of sensitivity to fraction size beyond 3 Gy/fraction. Clearly, this also comes with the caution of only having a single data point, so further ongoing data from ongoing studies are still eagerly awaited [21]. For example, the PACE-B trial, which recently reported early toxicity data [22] tests fraction doses of 7.3 Gy cf. Figure 2.

Figure 2 would seem to be in conflict with the presence of a constant, i.e. dose-per-fraction-independent, value of α/β across the entire range of fraction sizes studied. In other words, one possible conclusion of the heterogeneous results presented here would be that at extreme hypofractionation, the effective doses are lower than expected (albeit not catastrophically so). The experimental arm of the Widmark trial was dosed high enough, however, to maintain disease control, probably due to the heritage from an originally planned superiority design,

Figure 3 presents a different hypothesis, namely that the fraction size corrected dose may be precise, but the biochemical control simply maxes out at or about level of 87% biochemical control at five years/80 Gy EQD2. This would be analogous to f.ex. the historical experience in Hodgkin Lymphoma where attempts to show a positive dose-response for tumor control above 30 Gy [23] was driven by the shape of the mathematical dose-response function rather than by the observed data points from published studies[24]. In Hodgkin lymphoma, subsequent studies have demonstrated the detriment of further dose escalation to clinical outcome.

If indeed the biochemical control saturates at 80 Gy EQD2, the conclusion would be quite different with respect to the study by Widmark et al: In that case, the increased acute toxicity reported [6] could possibly have been avoided by decreasing the dose to effective 78 Gy to make the arms more balanced in intensity without a loss of biochemical control in the test arm.

Unfortunately, the coupling of dose intensification and hypofractionation in the current trials does not allow separating the two hypotheses; the putative effect of non-constant α/β versus saturation of disease control. However, in either case we conclude that superiority designs using dose intensification above 78–80 Gy by means of extreme hypofractionation run a high risk of failing. That said, even if ultra-hypofractionated therapy is not superior, but non-inferior, it could be of value due to the impact on patient convenience and resources.

In terms of endpoints, it deserves mention that the endpoint of biochemical control has yet to be proven as clinically relevant intermediate clinical endpoint [25,26] and previous attempts to couple effects on biochemical control to an effect on overall survival have failed[16]. Further, it may be argued that putative benefits of dose-intensification may be delayed by the use of androgen deprivation therapy, but this would not impact the Widmark trial, as ADT was not allowed.

The present analysis excluded studies of brachytherapy due to the challenge of clearly defining dose-time-fractionation from literature reports as result of the inhomogeneous dose. The recent Ascende-RT trial lends some support to the value of brachytherapy in improving biochemical control rates [27]. Unfortunately, the large number of patients treated on trials of EBRT is not matched by brachytherapy combinations, so definitive estimates are not available yet.

In terms of the effect of overall treatment time, we now know that the overall treatment time impacts toxicity by increasing the acute reactions if dose is delivered in very short schedules[28], which may also affect the Widmark results. When we turn to disease control there is some suggestions of a moderate detrimental effect of protracting the overall treatment time[29,30], but it is unclear if such an effect would extend to the short schedules of ultra-hypofractionation. We therefore analyzed the current data without an assumed effect of overall treatment time. If the previously reported effect of overall treatment time is included (data not shown), the Widmark study loses weight in the meta-analysis of α/β but the study outcome is in agreement with the predicted effect from studies above 80 Gy EQD2 in the experimental arm of [16].

Conclusions

The addition of data from the ultra-fractionated schedule tried in the Widmark trial adds to our knowledge of the fractionation biology of prostate cancer. The data appears in disagreement with the presence of a single, constant α/β ratio and/or a sigmoid dose-response curve with improved biochemical control from exceeding 80Gy EQD2 prescriptions. It appears that either the validity of the LQ model is challenged when extended to the ultra-hypofractionated dose-per-fraction range or that the expectation of continued improvements in biochemical control with dose-per-fraction intensification is likely to be unfulfilled.