Beyond COVID-19: Do biothermodynamic properties allow predicting the future evolution of SARS-CoV-2 variants?

Abstract

During the COVID-19 pandemic, many statistical and epidemiological studies have been published, trying to predict the future development of the SARS-CoV-2 pandemic. However, it would be beneficial to have a specific, mechanistic biophysical model, based on the driving forces of processes performed during virus-host interactions and fundamental laws of nature, allowing prediction of future evolution of SARS-CoV-2 and other viruses. In this paper, an attempt was made to predict the development of the pandemic, based on biothermodynamic parameters: Gibbs energy of binding and Gibbs energy of growth. Based on analysis of biothermodynamic parameters of various variants of SARS-CoV-2, SARS-CoV and MERS-CoV that appeared during evolution, an attempt was made to predict the future directions of evolution of SARS-CoV-2 and potential occurrence of new strains that could lead to new pandemic waves. Possible new mutations that could appear in the future could lead to changes in chemical composition, biothermodynamic properties (driving forces of new virus strains) and biological properties of SARS CoV-2 that represent a risk for humanity.

1. Introduction

During the COVID-19 pandemic, many statistical and epidemiological studies have been published, trying to predict the future development of the SARS-CoV-2 pandemic (Chen, 2022; Šušteršič et al., 2021; Chu, 2021). Both statistical and epidemiological models are not based on the physical driving forces and mechanistic models of SARS-CoV-2 – Human host interactions occurring on membrane and in the cytoplasm. Thus, it would be beneficial to have a mechanistic model, based on the driving forces of processes performed during virus-host interactions, allowing prediction of future evolution of SARS-CoV-2 and other viruses. An attempt was made to use statistical mechanics and thermodynamics to analyze viral evolution (Jones et al., 2015).

All live matter represents biological, but also open nonequilibrium thermodynamic systems (von Bertalanffy, 1950; Popovic, 2019; Demirel, 2014; von Stockar, 2013a, 2013b; Balmer, 2010; Popovic, 2017a). Thus, nonequilibrium thermodynamics should be used in analysis of processes performed by living matter (Popovic, 2018; von Stockar, 2013a, 2013b; Balmer, 2010; Demirel, 2014; Popovic and Minceva, 2021b). Indeed, the human organism represents an open thermodynamic system characterized by an empirical formula (Forbes, 2012, Heymsfield et al., 1997) and thermodynamic properties (Popovic and Minceva, 2020c). Humans represent host organisms for many virus species (Riedel et al., 2019). Viruses also represent open thermodynamic systems (Popovic and Minceva, 2020a; Katen et al, 2009; Lucia et al, 2020b). A biothermodynamic system performs thermodynamic processes, including interactions with other systems (Moerman et al, 2016). Viruses interact with their host both biologically and chemically (Popovic, 2021, 2022a, 2022b). Moreover, viruses can interact with other viruses (Da Palma et al., 2010; Nickbakhsh et al., 2019; Popovic and Minceva, 2021a). This interaction results in interference or coinfection (Popovic and Minceva, 2021a).

Even though thermodynamics is scientific discipline usually associated with engineering and technology, it is not widely known that the origin of thermodynamics is closely related to analysis of living organisms. The steam engine has not been the primary subject of thermodynamics, but organisms. The founders of thermodynamics, Lavoisier and Laplace were the first to measure heat released by a mouse using a calorimeter (Lavoisier and marquis de Laplace, 1783; Müller, 2010). After 50 years of intense application of thermodynamics in technology, thermodynamics has returned to its routes, in the works of Boltzmann (1974). Schrödinger has in the mid-20th century contributed to application of biothermodynamics to research of function of organisms (Schrödinger, 1944). A great contribution to studying biological processes was given by nonequilibrium thermodynamics developed by Prigogine (Glansdorff and Prigogine, 1971; Prigogine, 1977, 1947; Prigogine and Wiame, 1946). A great contribution to development of biological thermodynamics (biothermodynamics) was given by Morowitz (1992, 1968). Von Stockar answered the question of the thermodynamic driving force of growth of organisms (von Stockar, 2013a, 2013b; von Stockar and Liu, 1999). Hansen et al. (2018) has analysed the role of the laws of thermodynamics in Darwinian evolution . Recently, Lucia insists on applying thermodynamic methodology in research on biological processes, including viral life cycle and epidemiology (Lucia and Grisolia, 2020; Lucia, 2015; Lucia et al., 2021, 2020a, 2020b; Kaniadakis et al., 2020). Maskow has used thermodynamics and calorimetry to study microorganisms and viruses (Maskow, 2013; Maskow et al., 2010a, 2010b).

Several issues concerning the origin, time of introduction to humans, evolutionary patterns, and underlying force driving the SARS-CoV-2 outbreak remain unclear for now (Chaw et al., 2020). Physical and chemical processes in nature are driven by physical driving forces (von Stockar, 2013a, 2013b; Balmer, 2010; Demirel, 2014; Popovic and Popovic, 2022; Popovic, 2022a, 2022b). The driving force of virus entry into a host is Gibbs energy of binding (Popovic and Popovic, 2022; Popovic, 2022a, 2022b; Gale, 2021, 2020, 2019, 2018; Ridgway et al, 2022). Similarly, Gibbs energy of growth represents the driving force of virus multiplication (Popovic, 2022b; Popovic and Minceva, 2020b). Energetics determines the outcome of virus-host interactions (Mahmoudabadi et al., 2017). Thus, Gibbs energy of binding is responsible for virus attachment and entry into the host (Casasnovas and Springer, 1995; Gale, 2021, 2020, 2019, 2018; Popovic and Popovic 2022, Popovic 2022a, 2022b), while Gibbs energy of growth is responsible for virus multiplication inside the host (Popovic and Minceva, 2020a, 2020b). The two thermodynamic properties represent the basis of biological properties: infectivity and pathogenicity (Popovic, 2022b). To enable a thermodynamic analysis of virus-host interactions, standard thermodynamic properties of human host tissues have been reported (Popovic and Minceva, 2020c).

Recently, there has been an increasing call for integrating mechanistic perspectives in evolutionary considerations, but it is not clear whether and how mechanisms affect the course and outcome of evolution (van den Berg and Weissing, 2015). Mutation is the engine (driving force) of evolution in that it generates the genetic variation on which the evolutionary process depends (Hershberg, 2015; Roossinck 1997). Mutations are not just biological phenomena. The result of mutation is the change in elemental composition of the virus, cell and organism (Popovic and Popovic, 2022; Popovic, 2022a, 2022b, 2022c) and change in information content (Hansen et al., 2018). This change is represented by change in empirical formula of the organism (Popovic and Popovic, 2022; Popovic, 2022a, 2022b, 2022c). Change in elemental composition of an organism leads to change in its thermodynamic properties (Battley, 1998, 1999, 2013, 1992; Patel and Erickson, 1981; Roels, 1989; Sandler and Orbey, 1991). The change in thermodynamic properties influences virus-virus and virus-host interaction. SARS-CoV-2 has evolved rapidly into new variants throughout the pandemic through acquisition of more than 50 mutations from Hu-1 to BA.2 (Sun et al, 2022, Magazine et al, 2022). The energetics of a viral infection are in medias res of broader evolutionary and biophysical questions in virology (Mahmoudabadi et al., 2017).

The aim of this paper is to relate one of the known evolutionary mechanisms – mutation to the subsequent change in chemical composition (empirical formula), thermodynamic properties (entropy, enthalpy and Gibbs energy), as well as the driving forces guiding the chemical and thermodynamic changes leading to evolution. Hopefully, this could help us to predict the future of COVID-19 pandemic.

2. Methodology

A mechanistic model of coronavirus evolution includes an analysis of two thermodynamic properties: Gibbs energy of binding and Gibbs energy of growth. During analysis of the virus evolution, a comparison was made of thermodynamic properties of different strains, which appeared through mutations of SARS-CoV, MERS-CoV and SARS-CoV-2. The missing data for Gibbs energies of binding for SARS-CoV and MERS-CoV had to be determined. Thermodynamic properties of SARS-CoV-2 were taken from the literature.

2.1. Data sources

Li et al. (2005) reported standard thermodynamic and kinetic data for SARS-CoV strains TOR2 and SZ3, including dissociation equilibrium constant, K_d, binding equilibrium constant, K_B, on-rate constant, k_on, and off-rate constant, k_off. Lu et al. (2013) reported dissociation equilibrium constant, forward rate constant and off-rate constant for MERS-CoV. Standard Gibbs energies of binding of SARS-CoV-2 strains were taken from (Popovic, 2022b). Empirical formulas and standard thermodynamic properties of growth were taken from (Popovic and Minceva, 2020b; Popovic, 2022b).

2.2. Binding reaction and rate constants

SARS-CoV enters the host cell, in a process where the viral spike glycoprotein (SGP) binds to the host cell ACE2 receptor (Li et al., 2005). Similarly, MERS-CoV enters by attachment of its spike glycoprotein to the CD26 (also known as DPP4) protein of the host cell (Lu et al., 2013). The antigen-receptor binding can be described by the chemical reaction

$$A+R\rightleftarrows AR$$ (1)

Where A is the free virus antigen (SGP), R the host cell receptor (ACE2 or CD26) and AR the antigen-receptor complex. Antigen-receptor binding is a reversible chemical process, consisting of a forward and a backward part. In the forward part the antigen and receptor bind to form the antigen receptor complex, in a second order reaction. The concentrations of the free antigen, [A], and free receptor, [R], determine the rate of the forward reaction, r_on, which is described by the law of mass action

$$r_{on}=k_{on}\left[A\right]\left[R\right]$$ (2)

where k_on is the forward rate constant, also known as the on-rate or association rate constant (Du et al., 2016). On the other hand, in the backward reaction, the antigen-receptor complex dissociates into the free antigen and receptor. The rate of the backward reaction, r_off, depends only on the concentration of the antigen-receptor complex, [AR], and follows first order kinetics

$$r_{off}=k_{off}\left[AR\right]$$ (3)

where k_off is the first order rate constant for dissociation of the antigen-receptor complex, also known as the off-rate constant (Du et al., 2016). Therefore, the overall binding rate, r_B, is the difference of the forward and backward rates.

$$r_B=r_{on}-r_{off}$$ (4)

The overall binding rate, r_B, becomes zero at equilibrium, implying that the equilibrium forward, r_on^eq, and backward, r_off^eq, rates are equal (Demirel, 2014).

$$r_{on}^{eq}=r_{off}^{eq}$$ (5)

This represents the kinetic perspective on antigen-receptor binding. A similar complementary perspective is given by nonequilibrium thermodynamics.

2.3. Thermodynamics of virus binding

Binding of the spike protein to the host cell receptor represents a chemical reaction, similar to protein-ligand binding (Du et al., 2016). The rate of the antigen-receptor binding reaction, r_B, is related to Gibbs energy of binding, Δ_BG, by the binding phenomenological equation

$$r_B=-\frac{L_B}{T}{\Delta }_{B}G$$ (6)

where L_B is the binding phenomenological coefficient and T is temperature (Demirel, 2014; Popovic and Popovic, 2022). Since all the analyzed coronaviruses infect the same host, the temperature is the same for all the strains. However, every strain has its own L_B and Δ_BG. Thus, r_B of every virus species or variant depends on their L_B and Δ_BG values. The Δ_BG values vary between viruses, depending on mutations (and chemical change) in their spike glycoprotein (SGP). The binding phenomenological coefficient depends on binding kinetic parameters.

For chemical reactions the binding phenomenological coefficient is proportional the equilibrium forward reaction rate, r_on^eq, divided by the universal gas constant R_g (Demirel, 2014).

$$L_B=\frac{r_{on}^{eq}}{R_g}$$ (7)

Combining Eqs. (7) and (2) gives

$$L_B=\frac{k_{on}{K}_D{\left[AR\right]}^{eq}}{R_g}$$ (8)

The dissociation equilibrium constant is given by the equation (Du et al., 2016)

$$K_D=\frac{{\left[A\right]}^{eq}{\left[R\right]}^{eq}}{{\left[AR\right]}^{eq}}$$ (9)

Combining Eqs. (7) and (8) results in

$$L_B=\frac{k_{on}{K}_D{\left[AR\right]}^{eq}}{R_g}$$ (10)

Since the reported K_D values are very small, the equilibrium is shifted towards antigen-receptor binding. Thus, most virus particles in the body will be bound to host cells, implying that the equilibrium antigen-receptor complex concentration is approximately equal to the total virus particle (virion) concentration in the organism [AR]^eq ≈ [V]_tot. Thus, Eq. (10) becomes

$$L_B=\frac{k_{on}{K}_D{\left[V\right]}_{tot}}{R_g}$$ (11)

The value of [V]_tot was reported by Sender et al. (2021), to be 1 · 10⁷ RNA copies per gram of tissue. It seems reasonable to assume that one RNA copy corresponds to one virion. In that case, the concentration of virions is 1 · 10⁷ per gram of tissue. The density of tissues is 1050 g/dm³ (IT'IS Foundation, 2021). Thus, the concentration of virions is 1.74· 10⁻¹⁴ M.

2.4. Standard thermodynamic properties of binding

The dissociation process is the opposite of binding, meaning that dissociation equilibrium constants are reciprocal of binding equilibrium constants (Du et al., 2016). Thus, dissociation equilibrium constants were used to calculate binding equilibrium constants, K_B, using the equation (Du et al., 2016)

$$K_B=\frac{1}{K_D}$$ (12)

The binding constants were used to find standard Gibbs energy of binding, Δ_BG⁰, using the equation (Du et al., 2016)

$${\Delta }_B{G}^0=-R_{g}T\ln K_B$$ (13)

2.5. Virus binding rate

Virus binding rates have been determined in three ways: kinetic, linear and exponential. The kinetic method uses the law of mass action. The overall binding rate is the difference of the forward and backward reaction rate and is given by Eq. (4). The forward and backward reaction rates are found by multiplying the appropriate reaction rate constants with concentrations of the reactants, using Eqs. (2) and (3), respectively. The rate constants, k_on and k_off, were taken from (Lu et al., 2013).

The linear method uses linear nonequilibrium thermodynamics. Linear nonequilibrium thermodynamics states that the rate of a process is a linear function of its driving force, to which it is related by the linear phenomenological Eq. (6). Thus, the linear method determines binding rate through Eq. (6), using binding phenomenological coefficients and standard Gibbs energies of binding. Standard Gibbs energies of binding, Δ_BG⁰, are converted into Gibbs energies of binding, Δ_BG, using the equation (Atkins and de Paula, 2011, 2014)

$${\Delta }_{B}G={\Delta }_B{G}^0+R_{g}T\ln Q$$ (14)

where Q is the quotient of reaction (1) defined as

$$Q=\frac{\left[AR\right]}{\left[A\right]\left[R\right]}$$ (15)

The exponential method uses a more general nonequilibrium thermodynamic equation, which is valid outside the linear region. In general, chemical reaction rate is proportional to the exponent of the driving force, according to the equation (Demirel, 2014)

$$r_B=r_{on}\left(1-e^{{\Delta }_{B}G/R_{g}T}\right)$$ (16)

This equation reduces into phenomenological Eq. (6) in case of small values of Gibbs energy (since then the exponent can be approximated as e^x ≈ 1 + x, where x = Δ_BG /R_gT and r_on/R_g = L_B) (Demirel, 2014).

2.5. Growth rate and driving force

Standard Gibbs energies of growth of the analyzed viruses have been taken from (Popovic and Minceva, 2020b; Popovic, 2022b). Growth rate of microorganisms, r_g, is proportional to their Gibbs energy of growth, Δ_gG, according to the growth phenomenological equation

$$r_g=-\frac{L_g}{T}{\Delta }_{g}G$$ (17)

where L_g is the growth phenomenological coefficient (different than the binding phenomenological coefficient) Westerhoff et al., 1982; Hellingwerf et al., 1982; von Stockar, 2013a; Demirel, 2014; Popovic and Minceva, 2020a, 2020b, 2021a). Notice that Eqs. (6) and ((17) have the same form, but apply to two different reactions. Both Eqs. (6) and (17) belong to the family of phenomenological equations (Demirel, 2014). However, they apply for different processes, namely binding and multiplication, respectively. Eq. (6) gives the rate of the antigen-receptor binding reaction (1). On the other hand, Eq. (17) applies to virus growth reactions, describing virus multiplication inside the host cell cytoplasm (Popovic, 2022b).

3. Results

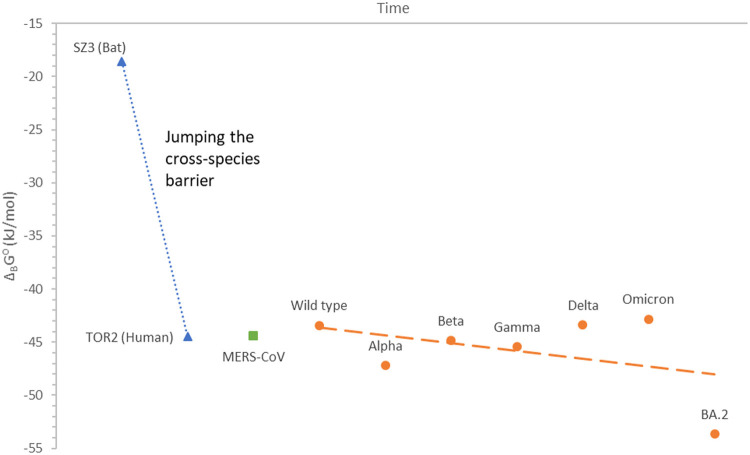
For the first time, standard Gibbs energy of binding has been determined for SZ3 (bat) and TOR2 (human) variants of SARS-CoV, as well as MERS-CoV. They are shown in Table 1 and Fig. 1 . Standard Gibbs energy of binding of SZ3 was found to be -18.6 kJ/mol, while that of TOR2 was found to be -44.5 kJ/mol (Table 1). Standard Gibbs energy of binding of MERS-CoV was found to be -44.4 kJ/mol (Table 1). Moreover, the binding phenomenological coefficient has been determined for MERS-CoV, L_B = 6.27 · 10⁻¹⁸ (mol² K / J s dm³). The L_B and Δ_BG⁰ values of MERS-CoV were combined to find the antigen-receptor binding rate for the first time, using the kinetic method (5.19 · 10⁻¹⁸ M/s), linear method (4.97 · 10⁻¹⁸ M/s) and exponential method (5.20 · 10⁻¹⁸ M/s).

Table 1.

Gibbs energies of binding of SARS-CoV, MERS-CoV and SARS-CoV-2 variants. For each virus variant, the date of first isolation was provided.

Virus	Variant	Appeared in	ΔBG (kJ/mol)
SARS-CoV	SZ3	Before Nov-02	-18.6
	TOR2	Nov-02	-44.5
MERS-CoV	MERS-CoV	Jun-12	-44.4
SARS-CoV-2	Wild type	Dec-19	-43.4
	Alpha	Jan-21	-47.2
	Beta	May-20	-44.9
	Gamma	Nov-20	-45.4
	Delta	Oct-20	-43.4
	Omicron	Nov-21	-42.8
	BA.2	Mar-22	-53.6

Fig. 1.

Standard Gibbs energy of binding of SARS-CoV and SARS-CoV-2 variants, as a function of time. Data for SARS-CoV variants are with blue triangles (▲), while the blue dotted line (·····) is a linear fit through the SARS-CoV data. MERS-CoV is represented by the green square (■). The SARS-CoV-2 variants are represented with orange circles (●), while the dashed orange line (—————) represents a linear fit through the SARS-CoV-2 data. Each data point is labelled with the name of the variant. Between the SARS-CoV epidemic, MERS-CoV epidemic and SARS-CoV-2 pandemic, time has passed, which was not presented in the graph for better clarity.

4. Discussion

Some biological agents are eliminated and some diseases are eradicated (i.e. variola vera; Smallpox) through time. However, some biological agents survived through millennia, adapted, and are still with us causing endemics, epidemics and pandemics. Adaptation represents a complex phenomenon. It consists of continuous changes of a virus in several directions. Biological agents causing epidemics have evolved towards decrease in pathogenicity according to our experience. However, at the same time, microorganisms noticeably increase their infectivity. At the end, but not less important is evasion of immune response. These three biological mechanisms enable both a microorganism and its host to survive through balance between their life driving forces. However, the first two biological mechanisms have their biophysical and chemical background. To understand biophysical mechanism of evolutionary adaptation it is necessary to understand both changes in infectivity and pathogenicity. Both are driven by physical driving forces. Hypothetically, the driving force for change in infectivity is Gibbs energy of binding, but change in pathogenicity is driven by its driving force – Gibbs energy of biosynthesis. Thus, both processes, change in infectivity and pathogenicity will be analyzed in this paper in order to get as much as possible complete mechanism of virus adaptation process. Change in driving force of binding can explain change in infectivity, but cannot explain change in pathogenicity. Thus, change in pathogenicity are caused by its own driving force, and should be analyzed separately from infectivity. Notice that mutations acquired through time, which resulted in new variants, are located mostly on the region responsible for SGP synthesis, but significant number of mutations appear in other regions responsible for synthesis of other structural proteins. These mutations are responsible for changes in Gibbs energy of biosynthesis – driving force of growth. Unfortunately, due to lack of immunological data and a biophysical model of immune response, the evasion of immune response not analyzed in this paper.

Our current understanding of virulence evolution is based on insights drawn from two perspectives that have developed largely independently: long-standing evolutionary theory based on limited real data examples, and experimental studies of virulence-determining mutations using cell culture or animal models. A more comprehensive understanding of virulence mutations and their evolution can be achieved by bridging the gap between these two research pathways through the phylogenomic analysis of virus genome sequence data as a guide to experimental study (Geoghegan, et al.2018) and biothermodynamic studies of changes in chemical, kinetic and biothermodynamic properties of viruses (Popovic, 2022).

One of the basic mechanisms of evolution is mutation, providing the genetic variation for the evolution process (Hershberg, 2015; Carlin, 2011). However, a question appears, in which way does this mechanism function? In other words, to know the virus-host interaction well, we must understand its mechanisms and driving force(s). The driving force for most chemical processes is Gibbs energy (Atkins and de Paula, 2011, 2014; Demirel, 2014). Virus multiplication represents a chemical process of polymerization of nucleotides into nucleic acid and amino acids into proteins. Thus, the driving force for virus multiplication is Gibbs energy of growth (polymerization). This means that Gibbs energy of growth is the driving force of microbial growth (Von Stockar, 2013a, 2013b). Mutations occur during virus multiplication (Sanjuán and Domingo-Calap, 2016; Cann, 2012; Domingo, 2019, Peck et al, 2018). RNA viruses mutate faster than DNA viruses, single-stranded viruses mutate faster than double-strand viruses (Sanjuán and Domingo-Calap, 2016).

Virus entry into host cells depends on Gibbs energy of binding (Gale, 2021, 2020, 2019, 2018; Casasnovas and Springer, 1995; de Andrade et al., 2020). Thus, Gibbs energy of binding represents the driving force for virus–host interaction appearing on membrane (antigen-receptor binding). Mutations that influence Gibbs energy of binding occur on the sequence encoding spike glycoprotein (SGP). Mutations in the SGP of SARS-CoV-2 are well described in the literature (Harvey et al., 2021; Wei et al., 2021; Song and Masaki, 2021). The BA.1 Omicron variant has 45 mutations (Wei et al., 2021), of which 32 are on the SGP (Song and Masaki, 2021), while the remaining 13 mutations are on other parts of the genome and hence do not influence binding energetics, but can influence virus multiplication rate.

In this paper, we will attempt to explain the thermodynamic backgrounds of the mechanism through which mutations influence the antigen-receptor binding rate and multiplication rate of viruses. A greater antigen-receptor binding rate leads to increased infectivity. Greater multiplication rate leads to greater damage to host cells and hence greater pathogenicity (Popovic 2022). Both processes are described using phenomenological equations, which belong to nonequilibrium thermodynamics (Demire, 2014; Balmer, 2010; Westerhoff et al., 1982; Hellingwerf et al., 1982). Antigen-receptor binding is described by the binding phenomenological equation

$$r_B=-\frac{L_B}{T}{\Delta }_{B}G$$ (18)

where r_B is the binding rate, L_B binding phenomenological coefficient, T temperature and Δ_BG Gibbs energy of binding (Popovic, 2022b).

Virus multiplication rate is given by the growth phenomenological equation

$$r_g=-\frac{L_g}{T}{\Delta }_{g}G$$ (19)

where r_g is the virus multiplication (growth) rate, L_g growth phenomenological coefficient, T temperature and Δ_gG Gibbs energy of growth (Popovic, 2022b).

As viruses are obligate intracellular pathogens they cannot replicate without the machinery and metabolism of a host cell. Thus, viruses compete for host biosynthesis machinery and metabolism Popovic and Minceva, 2020a). Viruses have an advantage over the host, given to them by their driving force of biosynthesis – Gibbs energy of growth. Gibbs energy of growth depends on chemical composition of the microorganism, including virus particle (Popovic and Minceva, 2020a; Batley, 1999, 1998, 1992). Mutations lead to change in information sequence and aminoacid sequence. Replacement one amino acid with another leads to significant change in protein structure and function. Change in SGP significantly changes receptor binding affinity (Popovic, 2022e). Change in other structural proteins, and changes in SGP together significantly change virus multiplication rate. Indeed, empirical formula of Hu-1 is CH_1.5708O_0.3452N_0.3125P_0.0060S_0.0033, while the Gibbs energy of growth of Hu-1 is -222.2 kJ/C-mol (Popovic and Minceva, 2020b). The empirical formula of the Delta strain nucleocapsid is CH_1.569O_0.343N_0.311P_0.0060S_0.0043, while its Gibbs energy of growth is -216.54 kJ/C-mol (Popovic, 2022d). The empirical formula of the Omicron BA.1 strain nucleocapsid is CH_1.5734O_0.3442N_0.3122P_0.0060S_0.0033, while its Gibbs energy of growth is -221.10 kJ/C-mol (Popovic, 2022d). Mutations had led to differences in elemental compositions of various strains, which led to different empirical formulas of the strains. Thus, the net effect of mutations is difference in Gibbs energies of growth of various coronavirus strains. Eqs. (18) and ((19) belong to the family of phenomenological equations, which proved themselves as an efficient tool in research (Demirel, 2014; von Stockar, 2013a; Hellingwerf et al., 1982; Westerhoff et al., 1982). Phenomenological equations relate the rate of a process to its driving force (Demirel, 2014; Balmer, 2010). Thus, changes in caused by mutations lead to changes in elemental composition and thermodynamic properties, including the driving force – Gibbs energy of growth. The final result is change in multiplication rate of the virus, which leads to better adaptation of the virus to its environment. Thus, the influence of Gibbs energy of growth on virus adaptation should be taken into account. However, adaptation of a virus to its environment is a complex process, which also includes the immune response. Thermodynamic background of the immune response has not yet been considered, first of all due to lack of literature data. Analysis of the thermodynamic background of immune response remains a goal for the future.

Parallel molecular evolution and adaptation are important phenomena commonly observed in viruses (Escalera-Zamudio et al, 2020). Mutations are common in RNA viruses (Sanjuán and Domingo-Calap, 2016; Cann, 2012), including SARS-CoV-2 (Harvey et al., 2021; Callaway 2022). Mutations that increase binding rate are favorable in the evolutionary sense (Holmes, 2020). The increased binding rate is a consequence of more negative Gibbs energy of binding (Popovic and Popovic, 2022). Change in binding rate is a consequence of changed chemical composition of the virus. Every nucleotide has its own characteristic elemental composition. Change in nucleotide sequence leads to change in elemental composition of the spike glycoprotein, which in turn changes the composition of the entire virus particle. Thus, change in genetic sequence during mutations leads to changes in chemical composition, thermodynamic properties, kinetic properties (binding rate, biosynthesis rate) (Popovic, 2022) and biological properties (infectivity and pathogenicity) (Ortega et al., 2020).

Some mutations are favorable and enable better accommodation of the virus to its environment, for example faster virus entry, faster multiplication, or avoiding immune response (Barton et al., 2021; Cann, 2012). Unfavorable mutations are lost in subsequent generations. During mutations, changes occur in nucleotide sequences, which lead to change in amino acid sequences in proteins. Every amino acid has a characteristic elemental composition. Change in the type of amino acid in a protein chain, leads to change in elemental composition of the protein. Change in elemental composition of the protein leads to change in thermodynamic properties of the protein. Changes in thermodynamic properties of proteins and nucleic acid, lead to change in thermodynamic properties of the entire virus particle. The change in thermodynamic properties of the entire virus particle influences both binding and multiplication properties of viruses. Thus in general, mutation (biological property) leads to change in elemental composition (chemical property), that leads to change in entropy, enthalpy and Gibbs energy (biothermodynamic properties), leading to change in binding and multiplication rate (kinetic properties), and finally results in change in infectivity and pathogenicity (biological properties). Therefore, bridging the gap between evolutionary theory and experimental studies of virulence-determining mutations we can reach the full picture from the microscopic to the macroscopic, from biological, through chemical, biothermodynamic, kinetic and back to biological observation.

A virus variant characterized by more negative Gibbs energies of binding and growth, has an advantage over the original virus in multiplication, spreading and survival. And opposite, a virus particle characterized by a less negative Gibbs energy exhibits lower binding affinity, slower multiplication, lower infectivity and lower pathogenicity.

Fig. 1 shows Gibbs energies of binding of the SZ3 and TOR2 variants of SARS-CoV. The figure clearly shows that SARS-CoV has evolved from SZ3 through mutations that led to more negative Gibbs energy of binding, from -18.6 kJ/mol to -44.5 kJ/mol. SZ3, a bat virus, has a much less negative Gibbs energy of binding to the human ACE2 receptor, than the human coronaviruses (Fig. 1). Thus, it must become more negative for the virus to jump cross-species barrier, transitioning from bat to human. More than two times more negative value of Gibbs energy of binding of TOR2 could have allowed the transition to humans. The huge change in Gibbs energy of binding appears due to mutations leading to change in elemental composition, thermodynamic properties, kinetic properties and biological properties.

Gibbs energy of growth of SARS-CoV is -230.3 kJ/C-mol (Popovic and Minceva, 2020b). The highly negative value of Gibbs energy of growth of SARS-CoV indicates a great rate of virus multiplication, greater damage to host tissues and hence great pathogenicity. The great pathogenicity has resulted in shorter duration and lower intensity of the SARS-CoV epidemic by limiting its spread. To compare, SARS-CoV-2 is characterized by a less negative Gibbs energy of growth: -222.2 kJ/C-mol for the original Hu-1 strain (Popovic and Minceva, 2020b). More negative Gibbs energy of growth of SARS-CoV compared to that of SARS-CoV-2 resulted in a severe clinical picture, greater mortality, but also more difficult and limited transmission. Thus, SARS-CoV-2 has survived longer in population and turned into a pandemic. The high pathogenicity of SARS-CoV, as well as the epidemiological measures taken, resulted in a relatively fast confinement and ending of the epidemic. Several years later, MERS-CoV appeared. MERS-CoV is characterized by a Gibbs energy of binding of -44.4 kJ/mol and Gibbs energy of growth of -208.5 kJ/C-mol (Popovic and Minceva, 2020b). Thus, Gibbs energy of growth of MERS-CoV is much less negative than that of SARS-CoV. MERS-CoV has evolved through less negative Gibbs energy of growth (decreasing pathogenicity) and slight change in Gibbs energy of binding (retaining infectivity).

Theory of evolution predicts that an organism evolves towards better adaptation to its environment. In case of coronaviruses, this would mean that evolution would progress towards greater infectivity and decrease in pathogenicity (Domingo, 2019). In practice, Fig. 1 shows that SARS-CoV-2 has evolved towards more negative Gibbs energy of binding, leading to increase in binding rate and greater infectivity. This is in complete agreement with the prediction of the theory of evolution (Cohen et al., 2020). On the other hand, Gibbs energy of growth has not changed to a great extent, during the evolution of SARS-CoV-2 strains through time. It seems that the second attempt (MERS) of coronaviruses to enter the human population was not successful. Possible reason may be that the virus evolved towards a too strong decrease in pathogenicity followed by approximately constant infectivity. It seems that the properties for successful pathogenicity lay between those of SARS-CoV (as a maximum) and MERS-CoV (as a minimum). This means that Gibbs energy of growth should be in the interval from -230.3 kJ/C-mol to -208.5 kJ/C-mol for successful survival. Indeed, SARS-CoV-2 strains are characterized by Gibbs energy of growth in this order of magnitude (Fig. 2 ). Now we have some numbers that we can use the predict the future of SARS-CoV-2 evolution. Actually Gibbs energies of SARS-CoV and MERS-CoV represent two extremes.

Fig. 2.

Gibbs energy of growth of coronaviruses through time. SARS-CoV is represented by the blue triangle (▲), while MERS-CoV is represented by the green square (■). Data for SARS-CoV-2 are represented by orange circles (●). The orange dashed line (—————) represents a line fitted through the SARS-CoV-2 data. Between the SARS-CoV epidemic, MERS-CoV epidemic and SARS-CoV-2 pandemic, time has passed, which was not presented in the graph for better clarity.

Notice that 32 mutations in the BA.1 Omicron variant of SARS-CoV-2 appeared on the SGP and are related to binding, while only 13 are related to multiplication (Wei et al., 2021; Song and Masaki, 2021). Thus, Gibbs energy of binding has changed more through evolution, compared to Gibbs energy of growth. Thus, infectivity has changed more through virus time evolution, compared to pathogenicity.

Fig. 2 shows Gibbs energies of growth of coronaviruses from SARS-CoV to the BA.2 strain of SARS-CoV-2. Gibbs energy of growth of SARS-CoV is the most negative of all coronaviruses. This leads to the conclusion that multiplication rate and tissue damage is the greatest for SARS-CoV. For MERS-CoV, Gibbs energy of growth has the least negative value. This implies the lowest multiplication rate, tissue damage and pathogenicity. During the evolution of SARS-CoV-2 variants, from Hu-1 to BA.2, change in Gibbs energy of growth (multiplication) has been very small. However, a slight tendency towards more negative Gibbs energy of growth can be noticed, during evolution of SARS-CoV-2 variants. Thus, we can conclude that pathogenicity has changed very little during evolution of SARS-CoV-2. However, Gibbs energy of binding and therefore infectivity has changed significantly (Fig. 1).

Now we can ask the question from the title of this paper. Will SARS-CoV-2 continue to evolve and remain with us or will the pandemic end like those of SARS and MERS? Historia magistra vitae est. The history of time evolution of various SARS strains could help us to understand and predict the direction of virus evolution in the future.

Mutations acquired by SZ3 (Bat) resulted in change in elemental composition and thermodynamic properties of SZ3 strain and lead to jump through the cross-species barrier, leading to the appearance of new, human host adapted strain TOR2. It seems that SARS-CoV (TOR2) is characterized by a by far the most negative Gibbs energy of growth (Fig. 2) and hence greatest host tissue damage and pathogenicity. Coronaviruses should evolve in the direction of decrease in pathogenicity in order to survive long enough to spread in the population. Gibbs energy of growth -230.3 kJ/C-mol is not favorable because it leads to high rate of multiplication and hence high damage to host organism. Thus, the next strain has evolved towards less negative Gibbs energy of growth to reduce pathogenicity. MERS-CoV, which appeared after SARS-CoV, had a much less negative Gibbs energy of growth than SARS-CoV. MERS has evolved towards decreased pathogenicity, trying to survive longer in the population. The increase in pathogenicity is not favorable in the context of evolution (Domingo, 2019). However, the less negative Gibbs energy of growth can lead to slow virus multiplication. This can result in more effective immune response leading to the restriction of epidemic. In the third attempt, coronaviruses have appeared as SARS-CoV-2, characterized by intermediate values of Gibbs energy of growth between SARS-CoV and MERS. Thus, the replication rate of various strains of SARS-CoV-2 lay in the intermediate region, leaving enough space for various strains to spread and evolve through 2,5 years (Fig. 2). During this relatively long period, SARS-CoV-2 has mutated several times, but Gibbs energy of binding oscillates very little. The general trend of change in Gibbs energy of growth is presented on Fig. 2. We can notice a slow decreasing slope towards more negative Gibbs energy of growth. It means that pathogenicity has not been changed significantly. Especially, it has not decreased.

TOR2 (SARS-CoV) epidemic has ended at a much less negative Gibbs energy of binding than SARS-CoV-2. SARS-CoV-2 has evolved towards mutations leading to more negative Gibbs energy of binding (Fig. 1). This has lead to an increase in binding rate and hence infectivity. Indeed, the number of new cases of COVID-19 has increased during time (Worldometer, 2022) and each wave of the pandemic became more serious even though massive vaccination and rigorous epidemiological measures were applied. However, in the future, we can expect coronaviruses to evolve towards new strains, which would be characterized by more negative Gibbs energy of binding, but less negative, or constant Gibbs energy of growth. In the biological sense, this coincides with the expectation of appearance of viruses characterized by greater infectivity and equal or lower pathogenicity. The risk of transmission of SARS-CoV-2 still remain high (Karan et al, 2022; European Centre for Disease Prevention and Control, 2022).

5. Conclusions

A virus evolves through mutations. RNA viruses, including coronaviruses, mutate very fast. Mutations lead to change in the order of nucleotides, changing the information content of the nucleic acid. Mutations are favorable if they lead to better adaptation of the microorganism to its environment. In case of virus evolution, mutations can lead to change in infectivity and pathogenicity. Replacement of one nucleotide by another one leads to change in elemental composition of the virus particle. Change in elemental composition leads to change in thermodynamic properties. If a mutation has occurred on a part of the nucleic acid that encodes the spike glycoprotein, changes occur in its chemical composition, binding thermodynamic properties and infectivity. On the other hand, if the mutation occurred in the part of the nucleic acid that encodes other proteins, there is change in chemical composition and thermodynamic properties of growth (multiplication) of the virus, which lead to change in pathogenicity. Changes in thermodynamic properties of binding and growth towards more negative Gibbs energy lead to greater spontaneity of the process (binding or multiplication), which implies a change in the rate of the process. Thus, Gibbs energies are driving forces for both processes, representing the basic mechanism of better adaptation of a virus to its environment. Therefore, the tendency towards more negative Gibbs energy represents the fundamental mechanism and driving force for evolution.

Concerning the survival of SARS-CoV-2, it seems that there is a space for further evolution towards further decrease in Gibbs energy of growth. Having in mind that Gibbs energy of growth of SARS-CoV is much more negative than Gibbs energy of all known SARS-CoV-2 variants. On the other hand, it seems that Gibbs energy of binding can also decrease. In biological terms, SARS-CoV-2 could slightly increase its pathogenicity, but the infectivity of BA.2 will most likely increase significantly in the future.

CRediT authorship contribution statement

Marko Popovic: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Writing – original draft, Writing – review & editing, Visualization.

Declaration of Competing Interest

The author declares no conflict of interest.