Abstract
Ratcliff, Voskuilen, and McKoon (2018) presented data and model-based analyses that provided strong evidence for across-trial variability in evidence entering the decision process in several perceptual tasks. They did this using a double-pass procedure in which exactly the same stimuli are presented on two widely-separated trials. If there were only random variability (i.e., the first and second presentations of a stimulus were independent), then the agreement in the choice made on the two trials would be a function of accuracy: as accuracy increases from chance to 100% correct, then the probability of agreement increases. In the experiments, agreement was greater than that predicted from independence which means that there was systematic variability in items from trial to trial. Evans, Tillman, and Wagenmakers (2020) criticized this by arguing that because of possible tradeoffs among parameters, the evidence did not support two sources of across-trial variability, but rather the results could be explained by only a systematic (item) component of variability. However, their own analysis showed that parameter estimates were accurate enough to support identification of the two sources of variability. We present a new analysis of possible sources of across-trial variability in evidence and show that systematic variability can be estimated from accuracy-agreement functions with a functional form that depends on only two diffusion model parameters. We also point out that size of the estimates of these two sources are model-dependent.
Keywords: double-pass procedure, diffusion decision model, response time and accuracy, trial-to-trial variability
Noise is a fundamental theoretical construct in many models of human decision-making that is used to explain why decision outcomes (accuracy) and response times (RTs) vary across experimental trials. There is an ongoing debate in the psychology and neuroscience literature about the nature and the number of sources of noise. In the diffusion model (Ratcliff, 1978), both within-trial and across-trial noise in the decision process are assumed. These allow the model to predict the shapes of RT distributions and the ordering of RTs for correct responses and errors as a function of experimental conditions (Ratcliff & McKoon, 2008; Ratcliff, Van Zandt, & McKoon, 1999).
There are three sources of across-trial noise in the current version of the diffusion model but the oldest one historically, and the one that concerns us here, is variability in the rate at which evidence accumulates in the decision process, represented mathematically by the drift rate of a Wiener or Brownian motion diffusion process. In the earliest application of the model, in which it was used to model retrieval from memory (Ratcliff, 1978), drift rate was assumed to be a function of the strength of the match or the “relatedness” between a test item and an item stored in memory. Ratcliff stated that “relatedness will be assumed to vary over items because whenever a group of nominally equivalent items is memorized some items are better remembered than others” (Ratcliff, 1978, p. 63). The idea that drift rate varies across trials linked the model theoretically with signal detection theory and allowed it to predict error responses slower than correct responses, as is often found in difficult tasks in which accuracy is stressed (Luce, 1986; Swensson, 1972).
Despite the success of the diffusion model in explaining data from a wide variety of experimental paradigms (Ratcliff, Smith, Brown, & McKoon, 2016), and despite the theoretical basis of variability in stimulus encoding (e.g., signal detection theory), the issue of drift-rate variability has remained controversial, particularly in neuroscience where its utility and necessity have both been questioned. As alternatives, researchers have argued either for a combination of leakage and lateral inhibition in the evidence accumulation process (Usher & McClelland, 2001) or for time-dependent “collapsing” decision bounds (Ditterich, 2006a, 2006b), both of which can also predict slow error responses (for recent arguments, see O’Connell, Shadlen, Wong-Lin, & Kelly, 2018).
In response to concerns about the existence of across-trial variability in drift rate, Ratcliff, Voskuilen, and McKoon (2018) (hereafter RVM) carried out a study designed to demonstrate the necessity for across-trial variability in drift rate for explaining data. To do so, they used the double-pass procedure (Burgess & Colborne, 1988; Green, 1964; Lu & Dosher, 2008; Swets, Shipley, McKey, & Green, 1959), in which exactly the same stimuli are presented on two widely-separated trials. In RVM’s study, stimuli were re-presented 96–100 trials after the first presentation (the double-pass). If the two stimulus presentations are independent, then the agreement in the choice made on the two trials will be a function of accuracy and is easily calculated. If the accuracy is p, then the probability of agreement is p×p+(1-p)×(1-p), that is, the probability of random occurrence of two correct responses plus the probability of random occurrence of two errors (e.g., for p=.75, agreement is .625). If the agreement is higher than this baseline, then processing of the stimuli is not independent (RVM, Appendix B): the greater the agreement between them, the more similar is the evidence driving the decision process (the drift rate) on the two trials.
RVM reported data and model fits from five tasks and six experiments using perceptual tasks performed with the double-pass procedure in order to show the necessity of across-trial variability in drift rate in diffusion models. A secondary aim was to characterize how much of the across-trial variability was attributable to variability among the stimuli themselves and how much was attributable to variability in the way in which stimuli are encoded. RVM referred to the first kind of variability as external noise (p. 33) and the second as internal across-trial variability (p. 36). This terminology was intended to distinguish the latter source of variability from internal within-trial variability associated with noise in the evidence accumulation process itself.
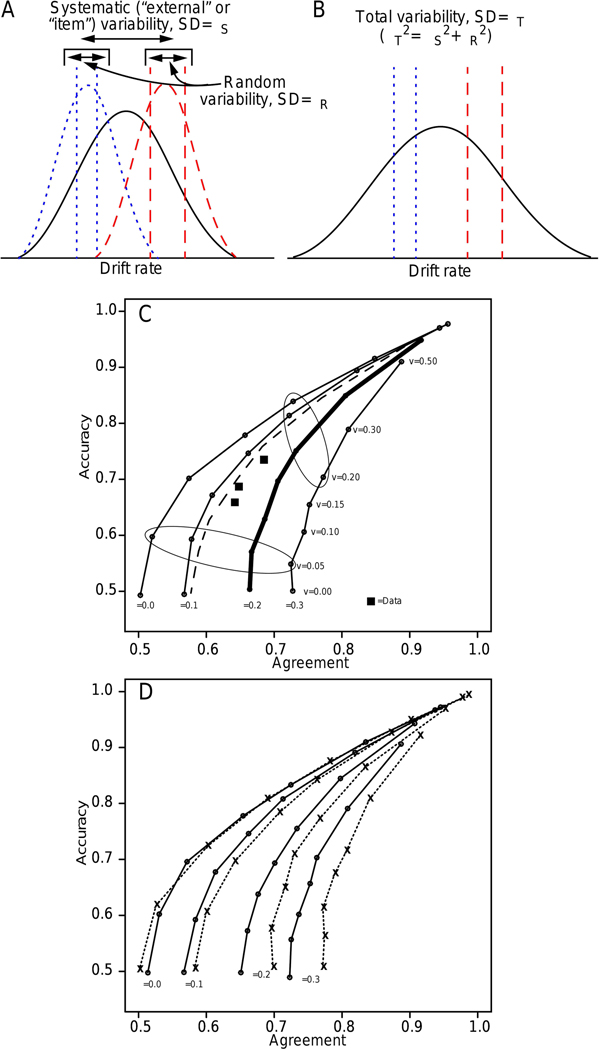
The diffusion model was fit to the data from each experiment and parameter values, including the across-trial standard deviation (SD) in drift rate, η, were estimated for each subject. Predictions were generated using these parameter values and under the assumption that drift rates were equal for the two presentations of each stimulus (i.e., perfect agreement) but the pair of drift rates varied from stimulus pair to stimulus pair with SD η (Figure 1A and 1B). This produced a family of accuracy-agreement functions (Figure 1C) with lines drawn between the different values of drift rate (v) for the same value of η. In Figure 1C, the ellipses show points with the same values of drift rate. The thick dark line shows the accuracy-agreement function from the model with a value of η close to that estimated from fits to data. (The other parameter values were from Experiment 11, Ratcliff & McKoon, 2018 and are close to those from Experiment 3, RVM.) From the data, experimental values of accuracy and agreement for the three conditions of the experiment that differed in difficulty were plotted, shown as squares in Figure 1C. Then these derived empirical values were compared with the function representing perfect agreement with the value of η derived from fits to the data. If the two coincided, then the drift rates for the original stimulus and the repetition would have been exactly the same. However, in four of the five experiments, the exception being the random-dot-motion task, the empirical functions lay between chance and perfect agreement (RVM, Figure 4) showing that only some, but not all of the variability from trial to trial in drift rate is systematic from presentation to presentation of the same stimuli.
Figure 1.
A: An illustration of systematic (item) variability (solid curve) and random variability around specific items (the dotted and dashed curves are two examples). B: These distributions are combined to produce the solid curve and the variance (η2 is the sum of the individual variances. C: A plot of accuracy against agreement between the two responses in the double-pass procedure. Seven values of drift rate were used to produce each function (shown as the small dots on the lines) and 4 values of the SD in drift rate across trials (η) were used to generate the different functions. The assumption was that the drift rates on the two passes were identical. The other model parameters were the means from the fits to the data for Experiment 11 from Ratcliff & McKoon (2018) which are almost identical to those from the motion discrimination task in RVM. Boundary separation a=0.097 (and the starting point z=a/2), and the across-trial range in starting point sz=0.057. Nondecision time and across-trial range in nondecision time do not affect these functions. The squares are values of accuracy plotted against agreement for the conditions of the experiment. The dashed line shows the function with η=0.2 but with a 0.5 correlation between the two drift rates. Note that it falls close to the value with perfectly correlated drift rates with η=0.1. The ellipses encircle points with the same values of drift rate. The thick dark line shows the accuracy-agreement function from the model with a value of η close to the average estimated from fits to data. D: The solid line shows accuracy-agreement functions for a=0.098 and sz=0.062 and the dotted line shows functions for a=0.098 and sz=0.0 (these values are from Experiment 3, RVM).
This analysis is important because most of the other evidence supporting the need for trial-to-trial variability in model components in the diffusion model comes from the rather subtle behavior of correct versus error RTs. The across-trial sources of variability have relatively small effects on overall accuracy, overall correct RTs, and their distributions; their effect is the slowing (for variability in drift rate) or speeding up of errors relative to correct responses (for variability in starting point). For researchers who ignore error RTs and those who do not regard mispredictions of error RTs as serious, it is possible to argue that trial-to-trial variability in drift rate is not needed in modeling. Furthermore, it has sometimes been suggested to us that drift rate variability may play a role in higher-order cognitive tasks like recognition memory but it cannot explain the ordering of correct and error RTs in perceptual tasks like the random-dot motion task because differences among stimuli will average out over successive frames and so be negligible. Consequently, other explanations of RT ordering in this task, such as collapsing decision boundaries, have been seen as more plausible. Thus the focus of RVM’s study was to give a different kind of evidence for the assumptions of trial-to-trial variability in drift rate, evidence that makes it difficult to ignore trial-to-trial variability in processing.
The results of Ratcliff et al. (2018) were sharply criticized by Evans, Tillman, and Wagenmakers (2020) (hereafter ETW) who asserted that RVM’s study led to “misleading conclusions,” and that their results “contradicted the central claim of their article.” These assertions by ETW depend critically on how “external noise” is defined and interpreted. ETW chose to define external noise differently than RVM and differently than it has been defined in prior research with the double-pass paradigm. They then criticized RWM for failing to demonstrate the necessity of external noise in their preferred sense. In response to ETW, we make four main points. First, we remind readers of the central claims of RVM’s article, which were not as they are represented by ETW, and show they demonstrated the necessity of external noise in the way in which they defined it. Second, we show that RVM also provided strong evidence for the necessity of external noise in the alternative sense in which it was defined by ETW. Third, we provide an alternative quantitative interpretation of the relationship between the different components of across-trial variability in drift rate that is simpler than the one in ETW. Fourth, we point out that estimates of the relative proportions of systematic and random variability are model dependent, a point that was also emphasized by RVM.
External Noise
RVM followed Green (1964) and Swets et al. (1959) and defined external noise as noise “from variability in the representations encoded from stimuli.” In the terminology of ETW, they defined external noise as item noise. They noted that in perceptual experiments, like the classical auditory signal detection experiments of Swets, Green, and colleagues, or in studies of noise in visual decision making like those of Lu and Dosher (2008), noise is added to stimuli to limit their discriminability. Because each sample of noise is physically different from every other sample of noise, the combination of a fixed signal and a random sample of noise results in a set of stimuli that, while nominally equivalent, will differ from one other another in their discriminability because of differences in the added noise.
In addition to external noise, RVM also identified a second source of internal across-trial noise (or variability) in drift rate. Such variability can arise for many different reasons. In near-threshold vision tasks it can arise from differences in the quantum catch of retinal photoreceptors (i.e., photon noise; Geisler, 1989) which results in the same stimulus being encoded differently on different trials. Also, the way in which a stimulus is processed will depend on the state of the neural system that processes it and that state is unlikely to be the same at different times. Psychologically, this kind of variability can reflect momentary fluctuations of alertness or arousal in a subject and fluctuations in the focus of attention to the stimulus display. Ratcliff’s (1978) reason for including across-trial variability in drift rate in the diffusion model was intended to encompass both of these sources of noise. Items in a studied list may vary in memorability because of objective, external, item properties -- they may differ for a host of reasons that an experimenter might conceivably have controlled for but did not -- but they also may vary because of momentary variations in the state of the participant, for example, thinking about relationships to other items in the study list. The variations in memorability of items in a memory experiment used by Ratcliff (1978) to motivate drift rate variability in the original formulation of the diffusion model could arise from either of these sources of noise.
In contrast, ETW defined external noise in a different way. They stated that “external noise refers to random between-trial variability in drift rate, where ‘random variability’ is variability that cannot be modeled deterministically and instead must be modeled as a random variable from a probability distribution.” In making this definition, they specifically exclude variability due to differences among items, stating that “between-trial variability in drift rate can be due to random sources (e.g., external noise) or systematic sources (e.g., item effects), and … a non-zero η parameter does not indicate the necessity of external noise” (their italics). They then state: “we argue that RVM failed to distinguish between two different potential sources of between-trial variability: random (i.e., “external noise”) and systematic (e.g., item effects).” They make this claim despite the statement in RVM’s abstract that “the double-pass procedure provided estimates of how much of this total variability was systematic and dependent on the stimulus.” The basis of ETW’s critique is that the agreement measure in the double-pass procedure only identifies systematic sources of noise attributable to differences among items. But this was precisely the sense in which RVM used the term “external noise” and their reason for using the double-pass paradigm was in order to identify variability of this kind. In claiming that RVM’s method only identified systematic noise due to differences among items ETW are in fact acknowledging that RVM showed the need for external noise in the way RVM defined it.
Internal, Across-Trial Noise
Much of ETW’s critique, which they pursued through several simulations, is focused on whether RVM also provided evidence for external noise in ETW’s sense, which RVM called internal, across-trial variability -- that is, variability not due to differences among items. RVM argued that, as well as providing an estimate of variability due to items (external variability in their sense), the double-pass procedure also provides a way to estimate internal, across-trial variability, because the variability due to items can be estimated independently of the total across-trial variability in fits of the diffusion model. To the extent that the external variability is less than the total variability, the difference can be attributed to internal variability.
In RVM’s Figure 4, in four of their five tasks, the degree of agreement found in the double-pass task was less than predicted from the estimated η parameter from fitting the diffusion model as shown in Figure 1C here. If all of the estimated across-trial variability in drift rate represented by the estimated parameter η were due to external (item) variability, then the predicted and observed double-pass agreement would have been the same. This was indeed so in the random-dot motion task, but in the other four tasks (numerosity discrimination, brightness discrimination, letter discrimination, dynamic brightness discrimination), the observed agreement was less than the predicted agreement, leading RVM to attribute the difference to internal across-trial variability. Unlike estimates of external variability, RVM emphasized that estimates of internal, across-trial variability obtained in this way were model-dependent: “measuring the various internal and external sources of noise requires a model that makes explicit assumptions about their contributions to performance as the diffusion model does” (p. 39).
The model dependency was highlighted in a recent reanalysis of the RVM data by Kang, Ratcliff, and Voskuilen (2020) using the linear ballistic accumulator (LBA) model (Brown & Heathcote, 2008). They showed that the estimates of systematic variability were lower in the LBA model than in the diffusion model because the LBA model has no within-trial variability, so all variability in RT and accuracy must by explained with across-trial variability in starting point and drift rate.
Identifying Different Sources of Across-Trial Variability In Drift Rate
Most of ETW’s article focuses on how accurately random and systematic sources of variability can be estimated from the double-pass method. They proposed a bivariate-normal model of across-trial variability in which the agreement in drift rates on the two passes is determined by a free correlation parameter. They investigated the properties of this model in several simulations and showed that across-trial SD in drift rate can trade off with the correlation to produce almost identical accuracy-agreement functions. Consequently, unless the across-trial SD in drift rate can be measured accurately, the parameters of the general bivariate normal model are not well identified and it cannot be used to estimate internal across-trial variability with any reliability.
However, there is a more direct and accurate way of estimating the systematic component of across-trial SD in η that avoids the problem of the unknown correlation if one assumes, as RVM did, that the systematic and random components of variance in η are independent. Let the SDs for the random internal across-trial variability be ηR and for the systematic (item) across-trial variability be ηS. If they are independent, then the accuracy-agreement functions are indexed by the systematic SD, ηS. RVM demonstrated this in the simulation on page 37 of their article in which they added different amounts of ηR to make the total η=0.15 and found that the accuracy agreement functions fell on the function indexed by ηS.
This means that ηS can be estimated empirically by identifying the accuracy agreement function on which it falls. If ηR and ηS are independent, then the total variance is simply ηT2=ηR2+ηS2, and the internal across-trial variance can be obtained as the difference in the two estimates. The predicted accuracy agreement functions depend on only two parameters of the model, the boundary separation a and the starting point range sz. Boundary separation is estimated reliably from data but the starting point range is not (Ratcliff & Tuerlinckx, 2002). However, the predicted accuracy agreement function is not much affected by starting point variability unless drift rate variability is also large. Figure 1D shows predicted accuracy agreement functions for two different values of starting point variability, sz=0.062 (solid lines) and sz=0.0 (dotted lines). The two sets of functions are in reasonably close agreement unless η is much larger than 0.1.
For Experiments 1–6 in RVM, the SD’s in accuracy are between 0.004 and 0.006 (using the binomial probability expression) and the SD’s in agreement are between 0.022 and 0.028 (using a bootstrap re-sampling method). Thus if the two or three points representing accuracy and agreement fall on a curve indexed by a single value of η, then this will be a reasonably accurate estimate of ηS (to within .02) if it lies on a line with η not a lot greater than 0.1 irrespective of the accuracy in estimating sz. And as argued later, with more sessions of data, this variability could be reduced considerably.
The relationship between ETW’s bivariate normal approach and RVM’s independent variance-components approach is that, in the latter, the square of the correlation is simply the ratio of the systematic variance to the total variance: ρ2=ηS2/ηT2. This means that uncertainty in estimation of η (ηT) from fits to the behavioral data lead to uncertainty in ηR. ETW performed a simulation to show how ρ and ηT trade off against each other and if the independent variance components assumption is valid, then ρ×ηT (the estimate of the systematic component) should be invariant. Using the values from ETW’s simulation (ETW’s Figure 2), the values of ρ×ηT are 0.6, 0.72, 0.72, and 0.6 (in ETW’s scaling, within-trial SD=1) and these values are close to invariant. This shows ETW’s bivariate representation (assuming independence) is consistent with the simpler additive variance representation.
Parameter Recovery
As described above, the main focus of the analyses in ETW was the relationship and tradeoff between η and the correlation between the two passes of a stimulus. To identify ηR, accurate recovery of ηT is needed. ETW argued that ηT can never be measured accurately enough to allow identification of it and the correlation ρ. In their Appendix E, ETW presented parameter recovery studies of ηT and they correctly noted that when ηT is small, parameter recovery is poor. But they also showed (in the top right hand corners of the panels in their Figure E1) that when ηT is large and drift rate is large, parameter recovery is quite good. This is because ηT is largely determined by the relative speed of correct and error RTs and larger values of both ηT and drift rate produces larger differences in correct and error RTs which leads to better estimates of ηT. These values in the upper right hand corner of Figure E1 are similar to the higher-accuracy values in the Experiments of RVM and so instead of demonstrating problems for the modeling and interpretation, they actually support RVM’s analysis.
The problem in estimating ηT is not an in-principle limitation but is a matter of sample size. A number of studies have examined parameter recovery in the diffusion model focussing on low numbers of observations (Boehm, Annis, et al., 2018; Lerche & Voss, 2016; Ratcliff & Childers, 2015). These are important in cases in which one might have access to a clinical or a neuropsychological data set with relatively few observations or when a limited amount of data can be obtained because of limited testing time in the context of a large battery of tests, or limited testing time because of the availability of a subject or fatigue. However, using Monte Carlo studies, Ratcliff and Tuerlinckx (2002) showed that the SD’s in η were less than 10% of the value with four conditions and 1000 observations per condition (with values of η that are typical in experiments). Thus, if it is critical to obtain point estimates of η with a SD smaller than 10% of the value of η, multiple sessions should be run per subject (as in Ratcliff, 2008, 20,000 observations with 38 subjects; Ratcliff, Thapar, & McKoon, 2010, 4,000 observations per subject with 138 subjects, etc.).
ETW also argue that two-step methods (in which point estimates of parameters are estimated from fits to individuals followed by hypothesis testing) are flawed when precise point estimates of parameters cannot be obtained. But this two-step “problem” needs to be shown to be a problem in the exact context of the sample sizes of the data and analyses in the RVM experiments. In the article by Boehm, Marsman, et al. (2018) cited by ETW, samples of 30 observations or less were used. Practical problems might be found if precise hypotheses about systematic and random sources of across-trial variability are developed followed by the demonstration of a failure of estimation of ηT or the two-step method for reasonable sample sizes and numbers of subjects. But this needs to be demonstrated. We are not arguing that methodology is unimportant; good methodology, fitting methods, etc. are critical and good methods should be used, but if the focus is on psychological issues, high quality data should be of primary concern.
ETW make an extraordinary assertion that all trial-to-trial variability is systematic: “we believe that future research should aim to eventually discard these ‘noise’ terms, and replace them with actual explanations of the process.” For both theoretical and practical reasons, it is unlikely that noise terms can be replaced by deterministic explanations of processing. Indeed, ETW investigated a fixed-effects model of item variability in drift rates and, unsurprisingly, were unable to recover the parameters of the model. More generally, the neural system is inherently stochastic and a given stimulus produces different neural responses on exact repetitions which means that it is likely that random across-trial variability will be present in encoding identical stimuli. Systematic across-trial variability occurs because stimuli from a single condition in the perceptual tasks in RVM (p. 34) differ in their configurations (and so are not identical) which means that processing must be different for the different items. We believe that modeling these differences is significantly beyond current theory. Even for identical items, attention is highly likely directed to (slightly) different parts of the display for the two presentations of a stimulus (especially for the RVM stimuli) resulting in different encoding for the two presentations of a stimulus leading to random across-trial variability.
We are not arguing that estimating the magnitudes of the sources of variance is a worthless enterprise, even though the estimates of the sizes are model-dependent. We are arguing that in the context of the stimuli in the experiments in RVM, such modeling would involve a complicated interaction between the subject and stimuli, the specific details of which seem beyond our current understanding.
Many two-choice decision tasks show sequential effects in choice probabilities (Treisman & Williams, 1984) or RT (Luce, 1984, Chap. 6.6) and there is a literature dating back to the 1970s that has attempted to characterize sequential effects in decision making using additive, or Markov, learning models (e.g., Jones, Curran, Mozer, & Wilder, 2013). Potentially, some part of the across-trial variability in the diffusion model could be attributed to sequential learning processes of this kind, but there is currently no satisfactory theory of these effects. The challenges in developing such a theory were highlighted by Laming (1969). Absent such a theory, the double pass experiments in RVM provide at least a rough idea of how much of the across-trial variability is random and how much is systematic.
ETW’s Suggested Solutions
ETW present what they see as possible solutions to this problem of unexplained variability and in the following, we present arguments and examples from the research in our laboratories. The first method they suggest is to use experimental designs to tightly constrain the predictions of models. Four examples are the joint modeling of speed and accuracy instructions on the standard RT task along with response signal data (Ratcliff 2006, 2008), modeling two-choice and go/no-go tasks jointly (Gomez, Ratcliff, & Perea, 2007; Ratcliff, Huang-Pollack, & McKoon, 2018), modeling manipulations of contrast, attention, and stimulus presentation duration in perceptual discrimination tasks (Smith & Ratcliff, 2009), and using EEG data to model drift rate in a recognition memory task (Ratcliff, Sederberg, Smith, & Childers, 2016).
A second method of identifying sources of variability proposed by ETW is to create a direct mapping between stimulus features and evidence used to drive the decision process. Most of the examples in the seven references that ETW provide would fail to account for double-pass results because they do not specifically implement across-trial variability in evidence (we are not arguing that could not be done, but the studies in their published form do not provide a way to characterize the sources of variability in the double-pass task).
Examples that do explicitly model across-trial variability in drift rate are the numerosity and perceptual discrimination models (Ratcliff & McKoon, 2018; Kang & Ratcliff, 2020; Ratcliff, Voskuilen, & Teodorescu, 2018). These models assume that numerosity or perceptual strength is represented on either a log or linear drift-rate scale with normally distributed across-trial variability in drift rate derived from a constant and the numerosities or perceptual strengths in the stimuli. These assumptions allow the models to account for a counterintuitive finding that for a constant small numerosity difference, as overall numerosity increases, accuracy falls, but RT decreases instead of the usual pattern of RT increasing as accuracy decreases. Other models from our laboratories that provide front-ends are presented in Smith and Ratcliff (2009) mentioned above, Ratcliff (1981) for perceptual matching, and White et al. (2011) for the flanker task.
ETW cite models that are “neurally inspired” as a third way of identifying different sources of variability, in particular, the Usher and McClelland (2001) and the Verdonck and Tuerlinckx (2014) models. Once again, these models do not have systematic sources of across-trial variability in evidence and because of this, these models cannot account for the double-pass results which makes is puzzling why these specific neurally inspired models were cited as a method for identifying sources of variability. Other examples that relate diffusion model predictions to neural firing rate data are Ratcliff, Cherian, and Segraves (2003) and Ratcliff, Hasegawa et al. (2007).
Conclusions
In this note we have addressed the main issues in the commentary of ETW. We pointed out that ETW redefined external noise to be what RVM termed internal across-trial noise and then argued that external noise is not needed to account for their results. ETW showed that the correlation between the two presentations of items trades off with across-trial variability in drift rate and because across-trial SD in drift rate is poorly measured, identifying the sources of variability is impossible. But we showed that for values of parameters and numbers of observations in RVM’s experiments, this parameter is identified well enough to provide reasonably good estimates of the two sources of across-trial variability in drift rate.
We have to ask two questions that ETW left open. First, when would accurate estimates of the amount of systematic versus random across-trial variability in drift rate be necessary? For example, if we estimated 50% but it could have been between 30% and 70%, what theoretical issues would critically hinge on such a discrepancy? This is also an issue because different models produce different relative proportions of the two components (Kang et al., 2020) and so there are no model-independent measures of these quantities. Second, what kinds of theories would specify item effects in these simple perceptual tasks? As an aside, application of double-pass experiments would not be convincing in cognitive experiments with pictures or words because it could be argued that subjects would remember the first presentation in many cases and that would produce different processing from the first presentation. Experiments of this kind potentially could be characterized using ETW’s bivariate normal model but, as they showed, the tradeoffs in this model make parameter recovery difficult. The perceptual experiments do not have this problem because the stimuli are not memorable (Figure 2, RVM) and the delay between presentations is large (96–100 trials).
More generally, the estimates in RVM’s Figure 4 show that double-pass agreement varies smoothly and regularly as a function of stimulus discriminability and, for four of the five tasks, shows maximum separation from the predictions of the diffusion model at intermediate levels of task performance, as one would expect. This separation is consistent with the presence of a second, internal source of across-trial variability in drift rates (or external noise, as ETW chose to define it). It was not part of RVM’s purpose to precisely quantify the relative magnitudes of the two components of across-trial variability, for which very large samples would be needed, which could be collected if required. Their aim was instead to demonstrate the necessity for external noise, or across-trial variability, in drift rates in the diffusion model. ETW agreed that they did so.
References
- Boehm U, Annis J, Frank MJ, Hawkins GE, Heathcote A, van der Kellen Mendes D, Krypotos AM, Lerche V, Logan GD, Palmeri TJ, van Ravenzwaaij D, Servant M, Singmann H, Starns JJ, Voss A, Wiecki TV, Matzke D, & Wagenmakers EJ (2018). Estimating across-trial variability parameters of the Diffusion Decision Model: Expert advice and recommendations. Journal of Mathematical Psychology, 87, 46–75. [Google Scholar]
- Boehm U, Marsman M, Matzke D, & Wagenmakers E-J (2018). On the importance of avoiding shortcuts in applying cognitive models to hierarchical data. Behavior Research Methods, 50, 1614–1631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown SD, & Heathcote AJ (2008). The simplest complete model of choice response time: Linear ballistic accumulation. Cognitive Psychology, 57, 153–178. [DOI] [PubMed] [Google Scholar]
- Burgess AE, & Colborne B. (1988). Visual signal detection. IV. Observer inconsistency. Journal of the Optical Society of America A, 5(4), 617–627. [DOI] [PubMed] [Google Scholar]
- Ditterich J, (2006a). Evidence for time-variant decision making. European Journal of Neuroscience, 24, 3628–3641. [DOI] [PubMed] [Google Scholar]
- Ditterich J. (2006b). Stochastic models of decisions about motion direction: Behavior and physiology. Neural Networks, 19, 981–1012. [DOI] [PubMed] [Google Scholar]
- Evans NJ, Tillman G, & Wagenmakers E-J (2020). Systematic and random sources of variability in perceptual decision-making: Comment on Ratcliff, Voskuilen, and McKoon (2018). Psychological Review. [DOI] [PubMed] [Google Scholar]
- Geisler WS (1989). Sequential ideal-observer analysis of visual discriminations. Psychological Review, 96, 267–314. [DOI] [PubMed] [Google Scholar]
- Gomez P, Ratcliff R, & Perea M. (2007). A model of the go/no-go task. Journal of Experimental Psychology: General, 136, 347–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green DM (1964). Consistency of auditory detection judgments. Psychological Review, 71, 392–407. [DOI] [PubMed] [Google Scholar]
- Jones M, Curran T, Mozer MC, & Wilder MH (2013). Sequential effects in response time reveal learning mechanisms and event representations. Psychological Review, 120, 628–666. [DOI] [PubMed] [Google Scholar]
- Kang I, & Ratcliff R. (2020). Modeling the interaction of numerosity and perceptual variables with the diffusion model. Cognitive Psychology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang I, Ratcliff R, & Voskuilen C. (2020). A note on decomposition of sources of variability in perceptual decision-making. Journal of Mathematical Psychology, 98, 102431. 10.1016/j.jmp.2020.102431 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerche V, & Voss A. (2016). Model complexity in diffusion modeling: Benefits of making the model more parsimonious. Frontiers in Psychology, 7, Article 1324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laming DRJ (1969). Subjective probability in choice-reaction experiments. Journal of Mathematical Psychology, 6, 81–120. [Google Scholar]
- Lu Z-L, & Dosher BA (2008). Characterizing observer states using external noise and observer models: Assessing internal representations with external noise. Psychological Review, 115, 44–82. [DOI] [PubMed] [Google Scholar]
- Luce RD (1986). Response times. New York: Oxford University Press. [Google Scholar]
- O’Connell RG, Shadlen MN, Wong-Lin K, & Kelly SP (2018). Bridging neural and computational viewpoints on perceptual decision-making. Trends in Neurosciences, 41, 838–852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R. (1978). A theory of memory retrieval. Psychological Review, 85, 59–108. [Google Scholar]
- Ratcliff R. (1981). A theory of order relations in perceptual matching. Psychological Review, 88, 552–572. [Google Scholar]
- Ratcliff R. (2006). Modeling response signal and response time data. Cognitive Psychology, 53, 195–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R. (2008). Modeling aging effects on two-choice tasks: response signal and response time data. Psychology and Aging, 23, 900–916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Cherian A, & Segraves M. (2003). A comparison of macaque behavior and superior colliculus neuronal activity to predictions from models of simple two-choice decisions. Journal of Neurophysiology, 90, 1392–1407. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. & Childers R. (2015). Individual differences and fitting methods for the two-choice diffusion model. Decision, 2, 237–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Hasegawa YT, Hasegawa YP, Smith PL, & Segraves MA (2007). Dual diffusion model for single-cell recording data from the superior colliculus in a brightness-discrimination task. Journal of Neurophysiology, 97, 1756–1774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Huang-Pollock C, & McKoon G. (2018). Modeling individual differences in the go/ no-go task with a diffusion model. Decision, 5, 42–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & McKoon G. (2008). The diffusion decision model: Theory and data for two-choice decision tasks. Neural Computation, 20, 873–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & McKoon G. (2018). Modeling numeracy representation with an integrated diffusion model. Psychological Review, 125, 183–217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Sederberg P, Smith T, & Childers R. (2016). A single trial analysis of EEG in recognition memory: Tracking the neural correlates of memory strength. Neuropsychologia, 93, 128–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Smith PL, Brown SD, & McKoon G. (2016). Diffusion decision model: Current issues and history. Trends in Cognitive Science, 20, 260–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, & McKoon G. (2010). Individual differences, aging, and IQ in two-choice tasks. Cognitive Psychology, 60, 127–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & Tuerlinckx F. (2002). Estimating the parameters of the diffusion model: Approaches to dealing with contaminant reaction times and parameter variability. Psychonomic Bulletin and Review, 9, 438–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Van Zandt T, & McKoon G. (1999). Connectionist and diffusion models of reaction time. Psychological Review, 106, 261–300. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Voskuilen C, & McKoon G. (2018). Internal and external sources of variability in perceptual decision-making. Psychological Review, 125, 33–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Voskuilen C, & Teodorescu A. (2018). Modeling 2-alternative forced-choice tasks: Accounting for both magnitude and difference effects. Cognitive Psychology, 103, 1–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith PL, & Ratcliff R. (2009). An integrated theory of attention and decision making in visual signal detection. Psychological Review, 116, 283–317. [DOI] [PubMed] [Google Scholar]
- Swensson RG (1972). The elusive tradeoff: Speed versus accuracy in visual discrimination tasks. Perception and Psychophysics, 12, 16–32. [Google Scholar]
- Swets JA, Shipley EF, McKey MJ, & Green DM (1959). Multiple observations of signals in noise. Journal of the Acoustical Society of America, 31, 514–521. [Google Scholar]
- Treisman M. & Williams TC (1984). A theory of criterion setting with an application to sequential dependencies. Psychological Review, 91, 68–111. [Google Scholar]
- Usher M. & McClelland JL (2001). The time course of perceptual choice: The leaky, competing accumulator model. Psychological Review, 108, 550–592. [DOI] [PubMed] [Google Scholar]
- Verdonck S, & Tuerlinckx F. (2014). The Ising Decision Maker: A binary stochastic network for choice response time. Psychological Review, 121, 422–462. [DOI] [PubMed] [Google Scholar]
- White CN, Ratcliff R, & Starns JJ (2011). Diffusion models of the flanker task: Discrete versus gradual attentional selection. Cognitive Psychology, 63, 210–238. [DOI] [PMC free article] [PubMed] [Google Scholar]