Deep learning models fail to capture the configural nature of human shape perception

Summary

A hallmark of human object perception is sensitivity to the holistic configuration of the local shape features of an object. Deep convolutional neural networks (DCNNs) are currently the dominant models for object recognition processing in the visual cortex, but do they capture this configural sensitivity? To answer this question, we employed a dataset of animal silhouettes and created a variant of this dataset that disrupts the configuration of each object while preserving local features. While human performance was impacted by this manipulation, DCNN performance was not, indicating insensitivity to object configuration. Modifications to training and architecture to make networks more brain-like did not lead to configural processing, and none of the networks were able to accurately predict trial-by-trial human object judgements. We speculate that to match human configural sensitivity, networks must be trained to solve a broader range of object tasks beyond category recognition.

Graphical abstract

Highlights

• •Humans rely on configural relations between local shape features to recognize objects
• •Networks trained to recognize objects are insensitive to these configural relations
• •Training and architecture innovations do not lead to configural processing
• •Networks remain unable to account for human object shape perception

Biological sciences; Neuroscience; Sensory neuroscience.

Introduction

Deep convolutional neural networks (DCNNs) represent the state of the art in computer vision artificial intelligence systems for image recognition (He et al., 2016; Hu et al., 2018; Gao et al., 2021; Dai et al., 2021). These networks are also quantitatively predictive of neural response in object-selective visual areas of both human and nonhuman primate cortex (Cadieu et al., 2014; Khaligh-Razavi and Kriegeskorte, 2014; Yamins et al., 2014; Mehrer et al., 2017), although deviations between these models and brain response have been noted (Spoerer et al., 2017; Schrimpf et al., 2018).

A better understanding of the potential of DCNNs as models of human object perception requires an analysis of the visual features underlying object recognition, which can include color, texture, and shape. Shape cues are known to be the foundation for object recognition in human perception (Biederman and Ju, 1988; Landau et al., 1988; Xu et al., 2004; Elder and Velisavljević, 2009). Although prior work (Baker et al., 2018; Geirhos et al., 2018) suggests that DCNNs may rely less on shape and more on color and texture than humans, these networks do still use shape cues to support object recognition (Kubilius et al., 2016). Here, we wish to understand how the use of shape cues by these networks compares to the use of shape cues by the human visual system.

Local versus configural shape properties

Objects have both local and configural shape properties. A local shape property manifests in a confined region of the object and can be interpreted without reference to more distant shape features on the object. Local shape properties can play an important role in recognition for both humans and artificial systems (a rabbit may be identified by its ears alone), and multiple weak local object properties can potentially be accumulated to yield relatively strong classifiers.

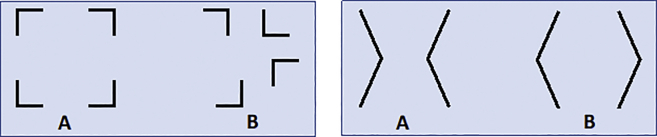
In contrast, a configural shape property is a function not just of one or more specific local features but also of how those features are related spatially (Wagemans et al., 2012a, 2012b) – Figure 1.

Figure 1.

Local versus configural properties

In both examples, objects A and B are made up of the same locally connected features in the same orientations, but their spatial arrangement is different. Whereas humans perceive objects A and B as highly dissimilar, an algorithm that lacks configural sensitivity and relies only on a sum over local features will judge the objects to be highly similar.

Many of the shape properties that are most salient to humans (e.g., convexity, closure, and symmetry; Wertheimer, 1923; Harrower, 1936) are configural, not apparent locally but only through a holistic computation that takes into account the spatial arrangement of local features over the shape. Early work of Gestalt psychologists (Koffka, 1935; Wagemans et al., 2012a) emphasized the primacy of configural shape perception and argued that it could not be reduced to a “sum” of parts. Research in the intervening decades has reinforced the importance of human configural perception not only through many rigorous behavioral studies (e.g., Pomerantz et al., 1977; Elder and Zucker, 1993, 1994; Kubovy and Wagemans, 1995; Drewes et al., 2016; Elder et al., 2018; Baker and Kellman, 2018; Elder, 2018) but also through fMRI and other physiological measures that relate Gestalt percepts to underlying neural processing and representation (e.g., Kubilius et al., 2011) and through more quantitative work that relates configural processing to ecological statistics and Bayesian decision theory (Geisler et al., 2001; Elder and Goldberg, 2002).

Local versus configural processing in computational object recognition models

Prior to the ascendance of deep networks for image recognition, leading computer vision recognition algorithms, e.g., SIFT (Lowe, 2004), bag-of-features (Zhang et al., 2007), semantic texton forests (Shotton et al., 2008), relied primarily on summing evidence from local features, largely ignoring spatial configural relationships between these features. DCNN models vastly outperform these earlier recognition systems (He et al., 2016; Hu et al., 2018; Gao et al., 2021): What is the basis for this superior performance? Because units in higher convolutional and fully connected layers have large receptive fields that combine information from widely separated pixels through a complex nonlinear mapping, these networks could potentially go beyond a sum of evidence over local features to incorporate configural information.

Despite this potential, Brendel and Bethge (2019) have argued that in fact ImageNet-trained DCNNs may behave like bag-of-features classifiers. While their findings could reflect the dominance of texture cues rather than the processing of shape per se, results from Baker and colleagues suggest that DCNNs do weight local shape cues higher than global shape cues relative to humans, at least for simple geometric shapes (Baker et al., 2020), and seem relatively insensitive to rearrangements in the configuration of local parts (Baker et al., 2018).

These prior studies raise the question of whether deep network models are at all sensitive to configural shape properties. This is important because if these networks did exhibit human-like configural sensitivity, they could be a good family of models for human object perception, and we could expect that incremental research will lead to increased capacity to predict human brain response and behavior. If, on the other hand, these network models fail to exhibit configural sensitivity, they would be missing what is perhaps the most salient feature of human object perception, and this would motivate a search for fundamentally different models. To distinguish these possibilities, we introduce here a methodology that isolates configural sensitivity from sensitivity to local shape cues and apply it jointly to human observers and a broad range of deep neural architectures.

Results

Experiment 1: Configural sensitivity of humans and feedforward DCNNs

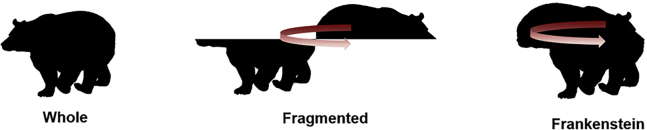
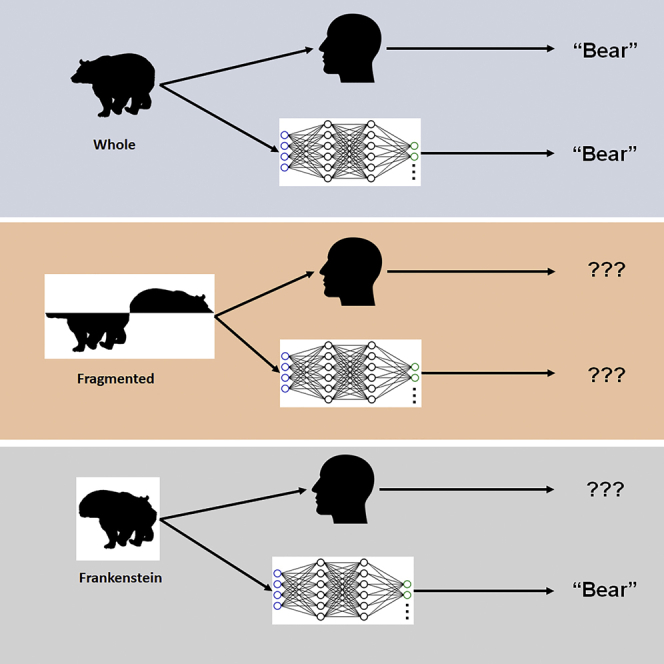
To compare configural sensitivity of humans and DCNNs, we measured performance on a 9-alternative animal classification task. Animal objects were rendered as silhouettes, thus isolating shape as a cue to object category. To dissociate configural shape from local shape cues, we applied two separate manipulations to these silhouette stimuli that disrupt global configuration while leaving local shape features largely intact (Figure 2) and then compared performance on these disrupted stimuli to performance on the original, whole silhouettes. In the fragmented condition, we flipped the top half of the object from left to right at a point on the extreme left or right of the shape. This manipulation fragments the configuration into two separate abutting objects but largely preserves local shape features. In the Frankenstein condition, we slid this top portion back to align with the bottom. Unlike the fragmented condition, this manipulation preserves the stimulus as a single object while still disrupting the configural relationship between shape features on the top of the object and shape features on the bottom of the object.

Figure 2.

Example animal silhouette stimulus in our three configural conditions

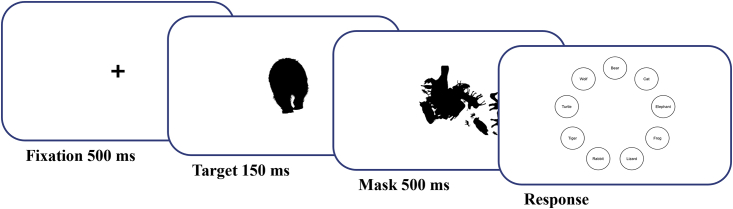
We measured the ability of both humans and ImageNet-trained DCNNs (VGG-19, Simonyan and Zisserman, 2014; ResNet-50, He et al., 2016) to identify the correct category of the animal for each of these three stimulus conditions and analyzed the results using a generalized linear mixed-effects analysis with participant and animal category as random effects and system (Human, VGG-19, ResNet-50) and configural condition (whole, fragmented, Frankenstein) as fixed effects. In Figure 3, we show a sample trial schematic. (See STAR methods for details.).

Figure 3.

Sample psychophysical trial

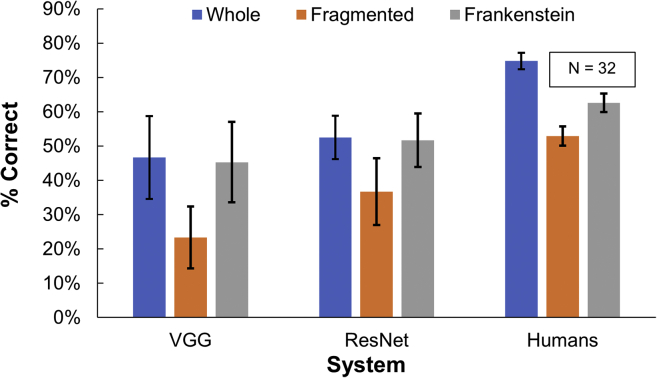
Overall, ResNet-50 performed somewhat better than VGG-19 (Figure 4, M_ResNet = 0.47, M_VGG = 0.38, Δ = 0.09, t(2158) = 4.99, p<0.001), but both were substantially worse than humans (M_humans = 0.64, M_ResNet = 0.47, Δ = 0.17, t(4898) = 10.87, p<0.001; M_humans = 0.64, M_VGG = 0.38, Δ = 0.25, t(4898) = 16.43, p<0.001).

Figure 4.

Experiment 1: Configural sensitivity of humans and feedforward DCNNs

Chance performance is 11% for this 9-alternative task. DCNN results: mean and SE over 9 ground truth animal categories. Human results: mean and SE over 32 participants.

We found that fragmentation impaired recognition for both humans and networks (Humans: M_whole = 0.74, M_fragmented = 0.53, Δ = 0.21, t(3817) = 12.63, p<0.001; ResNet-50: M_whole = 0.53, M_fragmented = 0.37, Δ = 0.16, t(1077) = 5.64, p<0.001; VGG-19: M_whole = 0.47, M_fragmented = 0.24, Δ = 0.23, t(1077) = 8.01, p<0.001). What exactly causes this impairment? While it could be a disruption of the configural relationship between features on the top and bottom of the objects, it could also be the salient but distracting local artifacts (strong horizontal edge and sharp tangent discontinuities) introduced by this manipulation, or the perception of the fragmented stimulus as two separate objects.

The Frankenstein condition discriminates between these explanations, disrupting configural relationships while minimizing the introduction of new salient local features and preserving the appearance of the stimulus as a single object. We found that while human performance was still profoundly impacted by the Frankenstein manipulation (M_whole = 0.75, M_Frankenstein = 0.63, Δ = 0.12, t(3817) = 6.84, p<0.001), the networks were unaffected (VGG-19: M_whole = 0.47, M_Frankenstein = 0.46, Δ = 0.01, t(1077) = 0.48, p = 0.66; Resnet-50: M_whole = 0.53, M_Frankenstein = 0.52, Δ = 0.008, t(1077) = 0.30, p = 0.77). This result shows that representative ImageNet-trained DCNNs fail to capture the configural sensitivity of human object perception.

Experiment 2: Can upweighting shape cues lead to configural shape perception?

Prior research suggests that, relative to humans, ImageNet-trained DCNNs rely more on texture than shape information for object recognition (Baker et al., 2018; Geirhos et al., 2018). Geirhos et al. found that by lowering the reliability of texture information during training, a DCNN can be trained to upweight shape cues toward human levels. But what are the shape cues used by this retrained network? Is it processing shapes configurally like humans, or has retraining simply substituted local shape cues for local texture cues?

To address this question, we repeated our experiment on the shape-biased version of ResNet-50 trained by Geirhos et al.(2018) on Stylized ImageNet (SIN), a transformation of ImageNet in which image texture is rendered less reliable as a cue to object category.

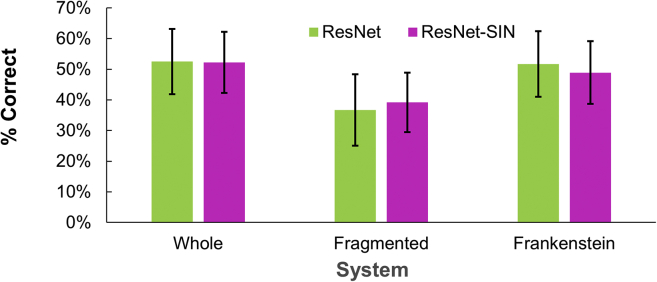
While Geirhos et al. reported that this training improved classification performance on silhouettes, we failed to find such an improvement on our animal silhouette dataset (Figure 5) (M_ImageNet = 0.47, M_SIN = 0.47, Δ= 0.002, t(2158) = 0.16, p = 0.88) or indeed a change in performance for any of the three configural conditions (M_{ImageNet whole} = 0.53, M_{SIN whole} = 0.52, Δ= 0.003, t(718) = 0.09, p = 0.93; M_{ImageNet fragmented} = 0.37, M_{SIN fragmented} = 0.39, Δ= 0.02, t(718) = 0.78, p = 0.44; M_{ImageNet Frankenstein} = 0.52, M_{SIN Frankenstein} = 0.49, Δ = 0.03, t(718) = 0.88, p = 0.38).

Figure 5.

Experiment 2: Can upweighting shape cues lead to configural shape perception?

Classification performance for ImageNet-trained ResNet-50 (as reported in Figure 3) and ResNet-50-SIN, trained jointly on standard ImageNet images and ImageNet images transformed by StyleNet (Gan et al., 2017) to reduce the reliability of texture as a cue to image category. Mean and SE over 9 animal categories.

We conclude that retraining a network to upweight shape information does not lead to human-like configural processing and conjecture that the improved performance on silhouette recognition observed by Geirhos et al. may be driven by local shape features that are more informative for their silhouette dataset, which contains not only animal objects but also artifactual objects.

Experiment 3: Can other network architectures lead to configural processing?

The architecture of standard DCNNs is much simpler than that of the visual cortex. Processing is feedforward, proceeding systematically from fine to coarse scales, with global interactions limited to the final layers. In contrast, the visual cortex features massive recurrent and skip connections that have the potential to fuse global and local information early in processing, which could be critical to configural perception.

Indeed, evidence suggests that recurrent connections in the visual cortex are important for object recognition (Spoerer et al., 2017; Schrimpf et al., 2018; Kar et al., 2019; Kar and DiCarlo, 2021) and for capturing the long-range spatial dependencies underlying configural perception (Linsley et al., 2018; Linsley et al., 2020). To test whether recurrence can lead to configural shape processing, we repeated our experiment on CORnet (Kubilius et al., 2019), a recurrent DCNN inspired by the architecture of the primate ventral stream. CORnet comprises four layers roughly corresponding to ventral stream areas V1, V2, V4, and IT of primate visual cortex. Unlike standard feedforward DCNNs, CORnet includes recurrent connections that recycle the output of each layer back to its input several times before passing on to the next layer. This produces a nonlinear expansion of the effective receptive field size in each visual layer that may facilitate long-range configural processing. CORnet is also a top performer on the Schrimpf et al. (2018) Brain-Score metric, a measure that includes several neural and behavioral tests to compare artificial networks to the primate brain.

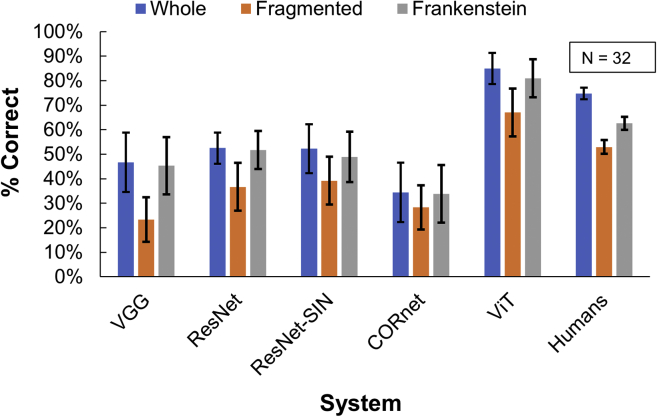
Figure 6 shows CORnet performance on our shape recognition task alongside humans and the other networks we have tested. Overall, CORnet failed to match human performance (M_humans = 0.64, M_CORnet = 0.32, Δ = 0.32, t(4898) = 20.85, p<0.001) and performed significantly worse than ResNet-50 (M_ResNet = 0.47, M_CORnet = 0.32, Δ = 0.15, t(2158) = 9.22, p<0.001). As for DCNNs, the fragmentation manipulation led to impaired recognition (M_whole = 0.34, M_fragmented = 0.28, Δ = 0.061, t(1077) = 2.42, p = 0.02), but the Frankenstein manipulation had no significant effect (M_whole = 0.344, M_Frankenstein= 0.338, Δ = 0.006, t(1077) = 0.22, p = 0.83).

Figure 6.

Comparison of network and human performance on shape recognition task

Performance for all 5 networks tested and for humans. Chance performance is 11% for this 9-alternative task. Network results: mean and SE over 9 ground truth animal categories. Human results: mean and SE over 32 participants.

An alternative computational approach to capturing long-range dependencies early in processing is to forsake the convolutional architecture altogether in favor of a transformer architecture, first introduced by Vaswani et al and now dominant in the natural language processing community (Vaswani et al., 2017). Transformers have recently become popular for many computer vision problems, including object recognition. Here, we assess the Vision Transformer (ViT) architecture (Dosovitskiy et al., 2020), which learns an embedding of local image patches and uses multiplicative “self-attention” between all pairs of these embedded patches to capture long-range dependencies. This architecture has been found to yield long-range interactions even at the earliest layers and leads to superior performance/speed balance relative to the convolutional ResNet architecture (He et al., 2016).

Figure 6 compares the performance of this transformer architecture with humans and the other networks tested. Interestingly, we find that overall the ViT network outperforms the DCNN and recurrent CORnet architectures (M_ResNet = 0.47, M_ViT = 0.79, Δ = 0.32, t(2158) = 15.22, p<0.001; M_CORnet = 0.32, M_ViT = 0.79, Δ = 0.47, t(2158) = 25.42, p<0.001) and even outperforms humans (M_humans = 0.63, M_ViT = 0.79, Δ = 0.16, t(4898) = 9.14, p<0.001). While this improvement could be due to the transformer architecture, it may also be due to the way ViT was trained: while the DCNN and CORnet models were initialized randomly prior to training on ImageNet, ViT was pretrained on the very large proprietary JFT-300M dataset (Sun et al., 2017) prior to fine-tuning on ImageNet.

As for humans and the other networks, fragmentation had a negative impact on ViT performance (M_whole = 0.85, M_ragmented = 0.67, Δ= 0.18, t(1077) = 7.28, p<0.001). Although the Frankenstein manipulation led to a slightly larger drop in performance than for the other networks, this drop did not reach significance (M_whole = 0.85, M_Frankenstein = 0.81, Δ = 0.04, t(1077) = 1.79, p = 0.07).

These results suggest that human-like sensitivity to configural shape may not be achievable solely through the introduction of recurrence or attention operations.

Experiment 4: Effects of stimulus inversion

In Experiments 1–3, we manipulated the configural relationship between features in the top and bottom halves of objects to probe configural sensitivity of humans and deep network models, finding that while humans rely on configural information for object perception, deep network models do not.

Our methodology bears some resemblance to methods used to probe holistic sensitivity to human faces. The basic face inversion effect is that faces are harder to recognize when turned upside down (Yin, 1969). Inversion effects for other classes of object tend to be smaller but do occur (Gauthier andTarr2002; Rousselet et al., 2003). However, this basic inversion effect is not a reliable indicator of configural processing because inversion changes not just the spatial relationship between local features but also the orientation of those local features themselves. Thus, both a system that relies upon configural processing and a system that relies upon an independent processing of local features (e.g., a bag-of-features model) may show a basic inversion effect.

A more diagnostic test of configural processing assesses whether there is an interaction between widely separated features on an object. An example of such a test is the composite-face task (Young et al., 1987; Rossion, 2008, 2009, 2013), in which a participant is shown the upper half of one face together with the lower half of a different face. If asked to ignore one half (e.g., the bottom) and report identity based only on the other half (e.g., the top), judgements are still strongly influenced by both halves, indicating an involuntary holistic integration of information from the top and bottom of the stimulus. Interestingly, this effect is greatly diminished for inverted faces, indicating an attenuation of configural processing. This composite-face method has also been applied to simple pseudo-random line drawings (Zhao et al., 2016), with similar results for upright stimuli.

In both this composite task and our whole-Frankenstein task, objects are split in half horizontally. A key difference is that in our Frankenstein condition, both halves still come from the same object and are thus still relevant to the task, despite the mirror reversal applied to one-half relative to the other. Nevertheless, assessing the impact of stimulus inversion on our configural manipulations could improve our understanding of how configural processing of our animal silhouette stimuli compares with configural processing of faces.

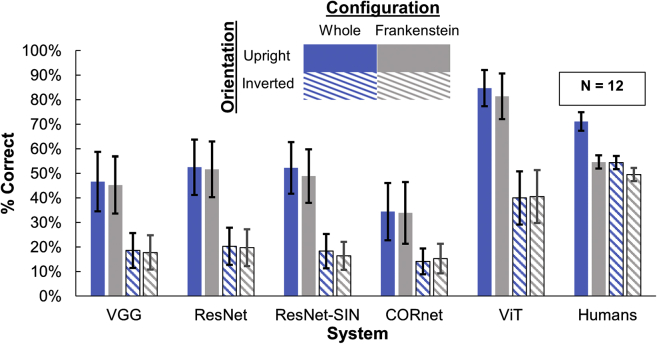
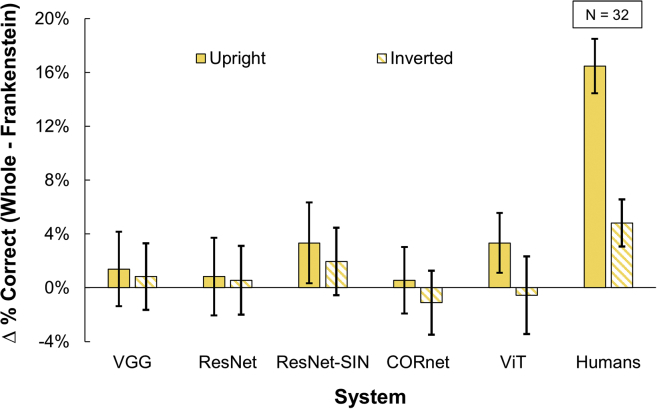
To this end, we conducted a new experiment in which we measured human and network recognition performance for both whole and Frankenstein stimuli in both upright and inverted conditions (Figure 7). Results (Figure 8) reveal that for the whole condition, inversion lowers recognition performance substantially for both humans and networks. Interestingly, the impact on the networks was even greater than that on humans. This result shows that both humans and networks are orientation sensitive. For the Frankenstein condition, inversion also lowers performance for both humans and networks, but the effect on humans is reduced by a factor of 3.4 (Figure 9), indicating a strong attenuation of configural processing and highly consistent with the composite task criteria for holistic processing (Gauthier, 2020). Generalized linear modeling confirms a significant interaction between orientation and configuration in humans (t(4316) = 4.2, p<0.001). For the networks, on the other hand, the minor and nonsignificant differences in performance for whole and Frankenstein conditions remain highly stable across upright and inverted objects, indicating an absence of configural processing. Analyses confirmed no significant interaction between orientation and configuration for any of the networks (lowest pvalue = 0.31).

Figure 7.

Example stimuli for Experiment 4

Figure 8.

Recognition performance for upright and inverted objects

Chance performance is 11% for this 9-alternative task. Network results: mean and SE over 9 ground truth animal categories. Human results: mean and SE over 12 participants.

Figure 9.

Frankenstein effect for upright and inverted images, as represented by the difference in recognition performance between whole and Frankenstein objects

Network results: mean and SE over 9 ground truth animal categories. Human results: mean and SE over 12 participants.

Is the human configurality effect transient in nature?

Unlike our network models, humans can adapt to stimuli and tasks over time even without feedback. Given the unfamiliar nature of the fragmented and Frankenstein stimuli, it is possible that the observed decrement in performance relative to the whole condition is transient and could disappear with practice. To assess this possibility, we compared mean human performance over the first 50% of trials with mean human performance over the second 50% of trials for each of the three conditions. We found no significant improvement between first and second halves for any of the three conditions (whole: M_{first half} = 0.69 M_{second half} = 0.74, t(33) = 2.01, p = 0.052; fragmented: M_{first half} = 0.49 M_{second half} = 0.52, t(33) = 0.91, p = 0.37; Frankenstein: M_{first half} = 0.59 M_{second half} = 0.61, t(33) = 0.63, p = 0.53), and in fact the gap between whole and Frankenstein conditions was found to widen in the second half, suggesting that the observed configurality effect is not transient in nature.

Stimulus scaling

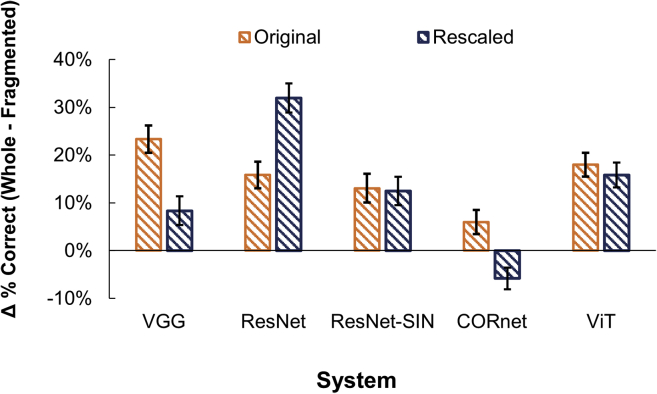
For both our psychophysical and network experiments, stimuli were scaled to have the same maximum dimension (width or height, whichever was larger). Because fragmenting the stimuli doubled the width, this resulted in the upper and lower halves of the stimuli being smaller in the fragmented condition than in the other conditions.

To test the effect of this difference on network performance, we performed a control experiment in which we scaled down each of the whole stimuli so that the two-halves of each stimulus were matched in size to the two-halves of the corresponding fragmented stimulus.

While some effects of rescaling the whole stimuli were observed (Figure 10), for all networks but CORnet, fragmenting the stimuli still resulted in a significant decline in performance (all p values <0.006). For CORnet, the pattern reversed: fragmenting the stimuli resulted in a significant improvement in performance (p = 0.01). We speculate that this may reflect a reduced sensitivity to large stimuli peculiar to CORnet. Aside from this exception, it appears that the drop in network performance for fragmented stimuli was not caused by scaling effects.

Figure 10.

Difference between whole and fragmented condition with and without size matching

Bars and error bars indicate mean and SEM.

Limitations of the stimulus dataset

Because the number of stimuli employed for the three conditions was small (40 instances per animal category) relative to most DCNN test sets, we created an expanded test set, increasing the number of stimuli by 50% (60 instances per category), in order to assess whether the observed insensitivity of the DCNN models to configurality remained stable. For this expanded test set, we again found no significant difference in accuracy between whole and Frankenstein stimuli in any of the networks tested (VGG-19: M_whole = 0.47, M_Frankenstein = 0.47, Δ <0.01, t(1617) = 0.23, p = 0.82; ResNet: M_whole = 0.55, M_Frankenstein = 0.54, Δ = 0.01, t(1617) = 0.47, p = 0.64; ResNet-SIN: M_whole = 0.53, M_Frankenstein = 0.49, Δ = 0.04, t(1617) = 1.79, p = 0.09; CORnet: M_whole = 0.344, M_Frankenstein= 0.326, Δ = 0.014, t(1617) = 0.90, p = 0.37; ViT: M_whole = 0.84, M_Frankenstein= 0.80, Δ = 0.04, t(1617) = 1.50, p = 0.13).

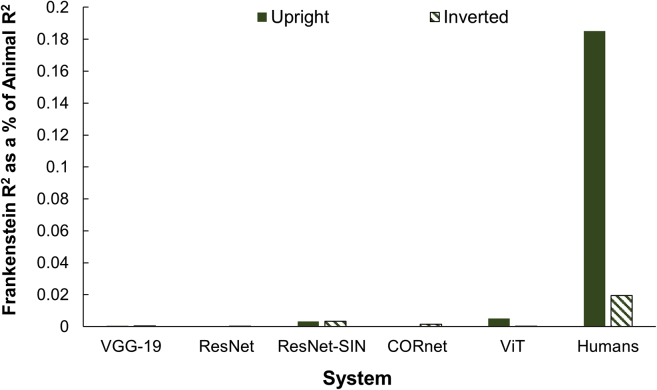
Effect size

When comparing human and network performance across conditions, it is important to analyze not only statistical significance but also the size of the effect. We measured effect size by comparing the proportion of variance explained by the Frankenstein manipulation relative to the variance explained by animal category in both humans and the network models. We found a large difference in effect size for humans and networks (Figure 11): The proportion of variance explained by the Frankenstein manipulation relative to the variance explained by animal category was 18.52% for humans and ranged from 0.01% to 0.54% for the networks.

Figure 11.

Configurality effect size: Proportion of variance explained by the Frankenstein manipulation, relative to the variance explained by animal category

For humans, the Frankenstein effect size was nearly ten times smaller when the objects were inverted, while for the networks, the effect sizes were insignificant and very similar for both orientations. These results show that while the human brain is acutely sensitive to configural shape, the network models are not.

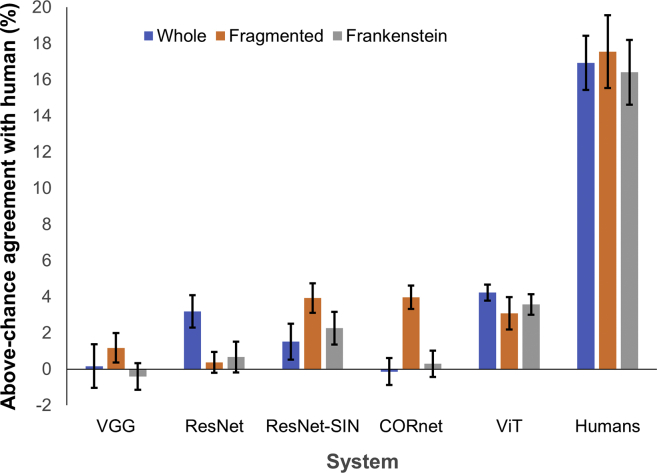
Trial-by-trial agreement analysis

While none of the network models capture the configural sensitivity of the human visual system, performance on the task does vary over models, and it would be nice to know whether any of the models are more predictive of human behavior than the others. To this end, we report the trial-by-trial above-chance agreement (ACA) between each of the DCNN models and the human data. To compute the ACA for a given DCNN model, we take each of our 32 observers and each configurality condition in turn and step through each of the 9 animal categories. For each animal category, we determine the proportion $p_a$ of stimulus instances for which the human observer and the DCNN model generated the same response.

While the mean of $p_a$ could potentially be used directly as a measure of agreement, note that it will depend strongly on the performance and biases of the human observer and model. To eliminate this dependence, we subtract the proportion agreement $p_0$ that would be expected for two systems that match the observed performance and bias of the human observer and model but which are otherwise independent. Note that $p_0={\mathit{p}}_m^T{\mathit{p}}_h$, where ${\mathit{p}}_m$ and ${\mathit{p}}_h$ are the 9-vectors representing the empirical probability distribution over model and human responses, respectively, for each configural condition and animal category.

We note that this ACA measure of agreement $p_a-p_0$ is the numerator of the well-established Cohen’s kappa coefficient (Cohen, 1960) used to measure inter-rater reliability:

$$\kappa =\frac{p_a-p_0}{1-p_0}$$

Cohen’s kappa is formed by normalizing the ACA measure of agreement by the maximum ACA attainable. Because this leads to instability when $p_0$ approaches 1, we omit the normalization here and just report the numerator, $p_a-p_0$. To estimate an upper bound on the ACA attainable by a model, we also compute the ACA between each human observer and the mode response of all other human observers who saw the same stimulus instance in the same configural condition.

The results of this analysis are shown in Figure 12. We find that all models except VGG exhibit some degree of above-chance agreement with the human data and that this agreement is most consistent for the ViT transformer model. While this result suggests that of the five models ViT is the most human-like, we note that agreement with the human observers remains in the 20%–25% range of what is in principle attainable, based upon the mode of the human data. It is thus fair to conclude that most aspects of human behavior on this task, including configural sensitivity, remain unaccounted for by all network models.

Figure 12.

Above-chance trial-by-trial agreement with human observers

Bars and error bars indicate means and standard errors over 32 human observers. Human agreement with human observers is computed by comparing the responses of each human observer with the mode response of other human observers who performed the same task with the same stimulus instance and configural condition.

Discussion

Animal silhouette recognition performance

All the networks we tested performed well above chance on our animal silhouette recognition task, for all three configuration conditions. While most of the networks did not perform as well as our human participants, the ViT network actually exceeded the mean human performance. As noted, this superior performance could not only derive in part from the transformer architecture but could also derive in part from the proprietary JFT-300M dataset (Sun et al., 2017) used to train the ViT network prior to fine-tuning on ImageNet.

However, comparing the absolute performance of humans and networks is of limited value for two reasons. First, to conduct the human experiments, we had to make specific choices regarding the stimulus duration and the nature of the poststimulus mask (see STAR methods); modifying these parameters might change the absolute performance of our human participants relative to the networks. But second and more important, our interest here is not in whether the networks can do the task but whether they do it in the same way as humans. Our configural manipulation reveals an enormous difference in how humans and networks recognize the objects: while humans rely profoundly on configural cues, networks do not.

Configural shape templates?

Our fourth experiment revealed that human configural processing as measured here is almost extinguished when the stimuli are presented in an unfamiliar orientation, consistent with prior work on face perception (Tanaka and Farah, 1993; Hill et al., 1997; Valentine, 1998; Leder and Bruce, 2000; Tanaka and Simonyi, 2016). This suggests that for humans, configural processing may to some degree be based on templates of familiar configurations (Cavanagh, 1991), rather than more general geometric properties.

What is needed for deep network models to become sensitive to configural object properties?

We consider three possible factors that could determine the configural sensitivity of a deep network model: training stimuli, architecture, and task. Our second experiment assessed the configural sensitivity of a network trained with an altered training dataset shown in prior work to increase shape sensitivity (Geirhos et al., 2018). We found that this shift in training stimuli did not improve performance on our shape recognition task and did not increase configural sensitivity. Our third experiment assessed whether architectural innovations could lead to configural processing. Considering the known importance of recurrent cortical connections (Spoerer et al., 2017; Linsley et al., 2018; Kar et al., 2019; Kar and DiCarlo, 2021) and attention mechanisms (Peters et al., 2005; Womelsdorf and Fries, 2007) in capturing long-range spatial interactions for human object processing, we evaluated recent recurrent (CORnet[Kubilius et al., 2019]) and attention-based transformer (ViT[Dosovitskiy et al., 2020]) architectures. However, we found that neither of these networks exhibited human-like configural processing.

To summarize, our experiments with altered training datasets and architectures have not led to configural sensitivity. While it is certainly possible that different alterations to datasets and architectures could produce different results, these innovations may not be enough. Rather, we suspect that a core factor limiting the configural sensitivity of these networks might be the limited nature of the task on which they were trained.

The ImageNet task is to classify the dominant object in an image. In many cases, the correct answer might be easily computed from a simple sum of local features, a calculation that is easy for a network to learn. In contrast, object processing in the primate cortex is likely to support not only recognition of the object class but also diverse physical judgements about the object, including its 3D location and orientation relative to the observer and the objects around it, its 3D shape and size, and its physical condition (e.g., intact or fragmented). These kinds of spatial tasks are likely not as easy to solve by summing local features, instead requiring more global reasoning about the object. Modeling this more general form of object processing could potentially involve discriminative multitask learning paradigms (Li and Hoiem, 2017; Zheng et al., 2017) or generative inverse-rendering approaches (Yu and Smith, 2019; Sengupta et al., 2019; Li et al., 2020), and we hypothesize that training networks to deliver this broader form of object understanding could lead to a more human-like configural sensitivity to object shape.

Limitations of the study

We selected the recurrent CORnet architecture for evaluation of recurrent architectures in part because of its high Brain Score (Schrimpf et al., 2018). However, it is a relatively simple architecture and its performance on ImageNet falls below the state of the art for feedforward architectures. It is possible that more advanced recurrent architectures might show increased configural processing for shape recognition tasks, especially if combined with training that explicitly demands configural processing (e.g., Linsley et al., 2018; Linsley et al., 2020).

Funding sources

All funding sources for this study are listed in the “acknowledgments” section of the manuscript.

Competing financial interests

We, the authors and our immediate family members, have no financial interests to declare.

Advisory/management and consulting positions

We, the authors and our immediate family members, have no positions to declare and are not members of the journal’s advisory board.

Patents

We, the authors and our immediate family members, have no related patents to declare.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Human data	https://osf.io/2j74f/	Deidentified human data
Network data	https://osf.io/q834p/	Network data

Resource availability

Lead contact

Further information should be directed to and will be fulfilled by the lead contact, Nicholas Baker (nbaker1@luc.edu).

Materials availability

All images used to test humans and networks in this experiment will be freely shared upon request. Please email Nicholas Baker (nbaker1@luc.edu) for any such requests.

Experimental model and subject details

All experimental methods involving human participants were approved by the York University Office of Research Ethics underCertificate #: 2019-265 for the project Recurrent Computations for the Perceptual Organization of Shape and Experiment 4, which was conducted at Loyola University was approved by the Loyola University of Chicago Internal Review Board underCertificate # 3447 for the project Human Recognition of Images.

All participants gave informed consent before beginning the study. In Experiment 1, 32 participants (19 male, 13 female, M_age = 28.6) were shown 40 randomly-selected animal silhouettes (four to five instances per animal category) for each of the three experimental conditions (Whole, Fragmented, Frankenstein). In Experiment 4, 12 participants (six male, six female, M_age = 25.1) were shown 90 randomly-selected animal silhouettes (10 instances per animal category) for each of the four experimental conditions (Whole, Frankenstein, Whole Inverted, Frankenstein Inverted).

Computational methods

We downloaded trained networks from: https://download.pytorch.org/models/resnet50-19c8e357.pth (ResNet-50), https://github.com/rgeirhos/texture-vs-shape (ResNet-50 trained on ImageNet and Stylized ImageNet), https://github.com/dicarlolab/cornet (CORnet), and https://github.com/google-research/vision_transformer (Vision Transformer).

Method details

Stimulus generation

To create the animal dataset we used Google Image, searching on each of 9 animal category names: Bear, cat, elephant, frog, lizard, rabbit, tiger, turtle, wolf. In this way we obtained 40 (and later an additional 20 for our expanded dataset) photographs of real animals with blank backgrounds, either segmented by hand or photographed in a white room, for each of the 9 categories, for a total of 360 images. The pose of the animals varied substantially within each category. We converted each raster image into a binary silhouette by thresholding the image. We converted to vector graphics using Potrace (http://potrace.sourceforge.net/) to reduce pixel aliasing and then mapped back to a raster representation.

To create the Fragmented and Frankenstein versions of each binary animal silhouette, we first identified the subset of image rows that contained a single black interval. We then determined the maximum length of these intervals and selected the subset of rows with intervals at least half this length. Finally, we selected the median height of these rows as the dividing line between top and bottom fragments of the shape. This served to divide each shape at roughly the middle of its major body region.

To create the fragmented stimuli, we flipped the top portion about a vertical axis passing through either the rightmost or the leftmost point on the shape. To create the Frankenstein stimuli, we shifted the top portion back to sit exactly on the bottom portion of the shape.

Psychophysical methods

Experiments 1 and 4 involved psychophysical tests on human participants. Participants performed the experiment remotely online through Prolific and were compensated for their participation. To standardize the retinal size of the stimuli, participants were asked to measure and enter the width of their screen and their viewing distance, which were used to adjust the stimuli to subtend 8.8 degrees of visual angle (maximum of horizontal and vertical dimensions).

Stimuli from our 360 animal shapes were randomly assigned to conditions, independently for each participant. Each participant saw an animal instance at most once - there were no repeats across conditions. Trials from all conditions were randomly interleaved.

Each trial sequence (Figure 3) consisted of a central fixation mark (500 ms), silhouette stimulus (150 ms), pattern mask consisting of a collage of animal silhouettes created from other animal categories (500 ms) and finally a response screen (until response). Participants completed nine random practice trials with feedback to become familiar with the procedure before data collection began.

A buffer of 20 white pixels was placed around input images so that the edge of the silhouette did not touch the edge of the image frame at any location. Images were transformed for presentation to the networks by resizing them to 224×224 pixels and normalizing the color channels. No other transformations or manipulations were applied to the images.

For all networks, we first computed a normalized confidence vector over the 1,000 ImageNet categories. For ResNet-50, ResNet-50-SIN, CORnet, and Vision Transformer, we used Python’s PyTorch library. For VGG-19, we used MATLAB’s Deep Networks toolbox.

While we used entry-level categories to define our 9-animal category task (ranging from species to order under the standard taxonomic ranking system), ImageNet contains finer-grained categories, generally species and sub-species, so that between 3 and 11 ImageNet categories map to each of our 9 animal categories. The mapping of ImageNet categories to our response categories is given below, with the response in bold and followed by the corresponding ImageNet categories:

Bear: Brown bear, American black bear, Polar bear, Sloth bear

Cat: Tabby cat, Tiger cat, Persian cat, Siamese cat, Egyptian cat

Elephant: Tusker, Indian elephant, African elephant

Frog: Bullfrog, Tree frog, Tailed frog

Lizard: Banded gecko, Common iguana, American chameleon, Whiptail lizard, Agama, Frilled lizard, Alligator lizard, Gila monster, Green lizard, African chameleon, Komodo dragon

Rabbit: Wood rabbit, Hare, Angora

Tiger: Cougar, Lynx, Leopard, Snow leopard, Jaguar, Lion, Tiger, Cheetah

Turtle: Loggerhead turtle, Leatherback turtle, Mud turtle, Terrapin, Box turtle

Wolf: Timber wolf, White wolf, Red wolf, Coyote, Dingo, Dhole, African hunting dog

We identified the network response to each of our stimuli by finding the maximum network confidence over ImageNet categories within each of our 9 entry-level categories and then taking the maximum across these 9 categories. ImageNet categories other than the 49 mentioned above were ignored.

Quantification and statistical analysis

We analyzed the results of our shape recognition experiments using a generalized linear mixed-effects approach. To assess human configural sensitivity, Participant $z_p$ and Animal Category $z_a$ were incorporated as random effects, and Configural Condition ${\mathit{x}}_c$ (Whole, Fragmented, Frankenstein) was incorporated as a fixed effect. The model was thus

$$g\left(\text{μ}\right)=g\left(E\left[y|{\mathit{u}}_p,{\mathit{u}}_a\right]\right)={\text{β}}_0+{{\mathit{u}}_p}^{\top }{\mathit{z}}_p+{{\mathit{u}}_a}^{\top }{\mathit{z}}_a+{\text{β}}_c{\mathit{x}}_c+ϵ$$

Here $y$ is the outcome (category decision incorrect/correct, represented as 0 and 1, respectively) and $\text{μ}=E\left[y|{\mathit{u}}_p,{\mathit{u}}_a\right]$ is its expectation. $g\left(\text{μ}\right)$ is the logistic link function $g\left(\text{μ}\right)=\ln \frac{\text{μ}}{1-\text{μ}}$. ${\mathit{z}}_p$ is a 31-dimensional indicator vector for our 32 participants, with the 0 vector indicating the base participant. Similarly, ${\mathit{z}}_a$ is an 8-dimensional indicator vector for our 9 animal categories and ${\mathit{x}}_c$ is a 2-dimensional indicator vector for our 3 configural conditions. ${\mathit{u}}_p$ and ${\mathit{u}}_a$ and ${\beta }_c$ are corresponding vectors of unknown parameters encoding effects for each participant, animal category and configural condition.

To assess the configural sensitivity of each network, we employed the same model, without the Participant effect. The model was thus,

$$g\left(\text{μ}\right)=g\left(E\left[y|{\mathit{u}}_a\right]\right)={\text{β}}_0+{{\mathit{u}}_a}^{\top }{\mathit{z}}_a+{\text{β}}_c{\mathit{x}}_c+ϵ$$

To compare overall shape recognition performance between pairs of networks and between individual networks and humans, we used the same model augmented with a fixed System effect $x_s$, contrasting two systems drawn from {Human, VGG-19, ResNet-50, ResNet-50-SIN, CORnet, ViT}. (Note that here we collapsed the human data across participants.). The model was thus,

$$g\left(\text{μ}\right)=g\left(E\left[y|{\mathit{u}}_a\right]\right)={\text{β}}_0+{{\mathit{u}}_a}^{\top }{\mathit{z}}_a+{\text{β}}_c{\mathit{x}}_c+{\text{β}}_s{x}_s+ϵ$$

To compare shape recognition performance between the ResNet-50 and ResNet-50-SIN network for specific configural conditions, we selected only the data for those conditions and eliminated configural condition from the model. The resulting simplified model was thus

$$g\left(\text{μ}\right)=g\left(E\left[y|{\mathit{u}}_a\right]\right)={\text{β}}_0+{{\mathit{u}}_a}^{\top }{\mathit{z}}_a+{\text{β}}_s{x}_s+ϵ$$

To measure the effect size for the Frankenstein manipulation, we selected only the data for Whole and Frankenstein conditions and then measured the proportion of variance explained (R²) by Frankenstein manipulation as a proportion of the variance explained by the animal category. Effect sizes therefore express how much the Frankenstein manipulation explains variance relative to the amount of variance explained by the animal category.

Published: September 16, 2022

Data and code availability

Data availability

• •Data from de-identified human participants is publicly available on Open Science Framework: https://doi.org/10.17605/OSF.IO/ZHVG7.
• •Data from DCNNs is shared as .mat files on Open Science Framework: https://doi.org/10.17605/OSF.IO/ZHVG7. Please email Nicholas Baker (nbaker1@luc.edu) if you have any trouble using these data.

Code availability

• •This paper does not report original code.