A Deep Invertible 3D Facial Shape Model For Interpretable Genetic Syndrome Diagnosis

Abstract

One of the primary difficulties in treating patients with genetic syndromes is diagnosing their condition. Many syndromes are associated with characteristic facial features that can be imaged and utilized by computer-assisted diagnosis systems. In this work, we develop a novel 3D facial surface modeling approach with the objective of maximizing diagnostic model interpretability within a flexible deep learning framework. Therefore, an invertible normalizing flow architecture is introduced to enable both inferential and generative tasks in a unified and efficient manner. The proposed model can be used (1) to infer syndrome diagnosis and other demographic variables given a 3D facial surface scan and (2) to explain model inferences to non-technical users via multiple interpretability mechanisms. The model was trained and evaluated on more than 4700 facial surface scans from subjects with 47 different syndromes. For the challenging task of predicting syndrome diagnosis given a new 3D facial surface scan, age, and sex of a subject, the model achieves a competitive overall top-1 accuracy of 71%, and a mean sensitivity of 43% across all syndrome classes. We believe that invertible models such as the one presented in this work can achieve competitive inferential performance while greatly increasing model interpretability in the domain of medical diagnosis.

I. Introduction

Diagnosing human genetic syndromes is a complex and difficult process due to their diversity, subtle differences between subjects with different syndromes, and their rarity. Genetic testing is the ideal way to diagnose afflicted subjects, but these tests are expensive, genetic experts are often scarce, and many syndromes exist for which the genetic profile is not yet known. As a supplement to genetic testing, computer-assisted phenotyping based on facial images or scans has been proposed as a low-cost, easy to utilize, and entirely non-invasive strategy for genetic syndrome screening [1].

The facial morphology associated with a syndrome can be quite distinctive and it has been shown that facial shape features are useful diagnostic indicators for many syndromes [1]–[4]. Experienced clinical geneticists will often use facial morphology as a preliminary diagnostic indicator prior to genetic testing. The development of robust and fully automatic computational pipelines to analyze facial morphology would, therefore, allow non-expert clinicians all across the globe to utilize a unified quantitative understanding of syndromic facial morphology to support clinical decision making processes at a very low cost.

Face-based syndrome detection models have been developed for both 2D facial images and 3D facial surface scans. State-of-the-art 2D approaches such as [5], [6] commonly use deep learning-based discrimintative models. However, single uncalibrated 2D images cannot capture facial morphology with the fidelity of 3D surface imaging [4]. Furthermore, deep discriminative models often lack interpretability, which makes it difficult for clinicians to understand what information a model uses to make inferences. Model interpretability is particularly important in medical applications as many clinicians hesitate to introduce black box models into their decision making process. On the other hand, state-of-the-art approaches relying on more informative 3D surface scans like [4] commonly utilize point-based generative shape models [7] that are equipped with an inference mechanism (e.g., a regularized discriminant analysis variant as proposed in [4]). While these models are more interpretable than solely discriminative ones, they usually rely on simplified facial representations (e.g., a sparse set of landmarks) and simplified probabilistic assumptions (e.g., Gaussian distributions). Both of those properties restrict model flexibility in ways that may impact model performance. 3D facial morphology may not follow a Gaussian distribution, and sparse landmarks may be incapable of capturing important, subtle shape details.

In this work, we propose a novel deep learning-based, invertible 3D facial surface modeling approach. The main novelty of our method is two-fold: (1) In contrast to standard facial shape analysis methods used for syndrome data modeling (often limited to Gaussian distributions), our NF model can learn complex non-Gaussian conditional face distributions. (2) Our model is fully invertible and, as a result of this, is highly multi-functional. Specifically, the proposed model is the first non-Gaussian 3D facial shape model with the ability to (1) infer syndrome diagnosis and other demographic variables given a high-resolution 3D facial surface scan, (2) generate modal, randomly sampled, and counterfactual 3D faces using demographic information, and (3) analyze the magnitude of facial variation between and within demographic groups (e.g., males vs. females) in a fully probabilistic way. The proposed normalizing flow approach efficiently handles all tasks within a single unified probabilistic model. The results of the evaluation show how this multi-functionality can help non-technical clinicians to intuitively understand and gain confidence in the model and its inference process through, for example, counterfactual visualizations. To the best of our knowledge, a deep invertible model of 3D syndromic facial morphology has not been proposed before.

(A). Related Work

1). Face-based Syndrome Classification:

In contrast to the volumes of work on general facial shape modeling and recognition [8], approaches specifically designed to diagnose genetic syndromes are scarce. Many available machine learning-based syndrome classification methods [5], [6], [9]–[12] rely on 2D frontal facial images of the subject as they are widely available in a clinical setting. However, this usually restricts the set of input features to projected geometric information and texture data, which may limit the achievable classification accuracy [9]. This problem can be alleviated by using 3D geometric information from 3D surface scans [3], [4] directly acquired via 3D scanning techniques [1]. As a low-cost alternative to real 3D data acquisition, some authors propose to infer 3D shape information for diagnostic purposes from 2D images [13], [14] by fitting a 3D face model [15]. Most approaches were developed and evaluated using a small number of syndrome classes.

2). Generative 3D Facial Shape Modelling:

Facial shape modelling generally aims at estimating a low-dimensional manifold of typical shape variations together with a probability density based on available high-dimensional training data (e.g., contours or meshes). Historically, this has been mostly achieved by linear approaches [7], [16] that define linear subspaces and use simple (often Gaussian) densities (see [8] for an overview). Over the years, those efforts have led to a multitude of so-called 3D morphable face models (3DMMs; e.g., [15], [17], [18]). While many 3DMMs successfully disentangle certain semantically meaningful factors of variation like identity and expressions, conditioning them on additional demographic variables is not common or straightforward (e.g., in [18] several 3DMMs are built to independently capture age and sex variations) and available solutions for conditional shape modeling [19] typically rely on Gaussian distributions.

3). Deep Learning-based 3D Facial Shape Modelling:

More recently, the first deep learning-based 3DMMs have been proposed [20]–[25] that make use of specifically adapted versions of variational auto-encoders (VAE) and generative adversarial networks (GAN). In contrast to traditional 3DMMs, their inherent non-linearity allows them to represent more complex manifolds and probability densities, which may lead to models that better capture the data [21]. A unique challenge associated with processing 3D surface meshes is their special graph-like structure. Hence, popular operations widely used in imaged-based deep learning solutions either need to be specifically adapted (e.g., spectral graph convolutions [21]–[23]) or the data needs to be reparameterized accordingly [25]. Although VAEs and GANs are excellent for generating visually convincing synthetic data samples, they are not well suited for tasks that involve evaluating the likelihood of samples. Both GANs and VAEs require computationally expensive Monte-Carlo integration, which can be intractable for high dimensional data, or lower-bound approximations to estimate likelihood values [26], [27]. In contrast, invertible normalizing flow models are designed to support efficient and exact likelihood evaluation.

4). Normalizing Flows:

Normalizing flows (NF) are a recently proposed class of deep learning model. A NF model represents a learnable bijective function (see reviews in [28], [29]). NFs are most commonly applied to generative manifold and density estimation tasks much like VAEs and GANs [30]. However, in contrast to VAEs where two separate models (encoder and decoder) are trained to map to and from a latent variable space, NFs are able to perform encoding and decoding using the forward and inverse directions of a single unified model. This avoids consistency issues often seen when modeling both directions independently. Furthermore, unlike GANs and VAEs, the likelihood of a NF model can be evaluated efficiently and exactly. This allows for direct maximum likelihood-based training, Bayesian inference of condition variables, and estimation of information theoretic measures like KL-divergence and differential entropy.

Recently, the first NF models operating on point clouds or mesh data were described (e.g., [31], [32]), but we are not aware of any work specifically using NFs to build syndromic 3D face models.

II. Methods

In this section, we will first introduce our notation and describe necessary data pre-processing steps before our NF architecture is described in Sec. II-C. We then describe in Sec. II-D how the model can be used to perform Bayesian inference of syndrome classes and demographic variables before different probabilistic interpretability mechanisms are described in Secs. II-E and II-F.

The overarching goal of our modelling approach is to efficiently approximate the distribution of human facial surface morphology conditioned on genetic syndrome diagnosis, age, and sex. For model training, we assume a population ${\left\{\left(S_i,y_i\right)\right\}}_{i=1}^{n_{pop}}$ of n_pop subjects to be given. Each tuple (S_i, y_i) consists of a subject’s 3D facial surface mesh S_i and a set of associated factors y_i = {age_i, sex_i, synd_i} with $ag{e}_i\in {ℝ}^{+}$, sex_i ∈ {male, female}, and syndrome diagnosis synd_i ∈ Γ, where Γ is a set of clinical genetic syndrome classes including a class for unaffected (non-syndromic) people.

A. Reference Surface and Registration

Depending on the actual 3D scanning and reconstruction techniques employed to capture the facial scans S_i of the training population, the number of vertices to represent each discrete surface and their topology may vary considerably between subjects. We, therefore, normalize all scans to a reference topology with a fixed number of vertices located at corresponding locations for each subject. This is done by first registering a fixed template mesh $\overline{S}:V\to {ℝ}^3$ with |V | = n_vert vertices to all n_pop scans S_i (see Sec. III-B for details). This results in non-linear transformations that are used to propagate the template’s vertices to the subject scans. Finally, positional and rotational information is removed and each surface is vectorized by stacking the 3D point coordinates of all n_vert vertices to obtain vectors ${\text{s}}_i\in {ℝ}^{3n_{\text{vert}}}$.

B. Manifold Estimation

Facial surface meshes produced by modern scanners commonly contain tens of thousands of vertices resulting in very high-dimensional surface vectors ${\mathbf{s}}_i\in {ℝ}^{3n_{\text{vert}}}$. Estimating a probability density on this very high-dimensional space is both computationally challenging and unnecessary since the positions of neighboring points on densely sampled facial surfaces will naturally have high mutual information. Therefore, we construct our model as a probability density on a sub-manifold of the ambient data space (see [30] for a description of how manifold and density estimation relate within a NF framework).

As in standard linear shape modeling approaches [7], we assume that the surface vectors s_i can be accurately represented by a n_sub-dimensional Euclidean manifold of maximum data variation F estimated using principal components analysis (PCA) of the training samples. F is then spanned by the first n_sub principal components with descending eigenvalue magnitude and centered at the training sample mean $\overline{\mathbf{s}}\in {ℝ}^{3n_{\text{vert}}}$. More specifically, all elements of sub-manifold F are identified by the set $\overline{\mathbf{s}}+\mathbf{s}|s\in \text{span}\left(F\right)$. Surface vectors s_i are projected to F in a least squares sense [7], which results in low-dimensional vectors ${\mathbf{f}}_i={\mathbf{F}}^T\left({\text{s}}_i-\overline{s}\right)$ with ${\mathbf{f}}_i\in {ℝ}^{n_{\text{sub}}}$. n_sub is selected to be as low as possible without negatively impacting syndrome classification performance so that the manifold projection removes only diagnostically unimportant information. The manifold projection can be easily inverted as in standard shape models [7] via ${\mathbf{s}}_i\approx \overline{\mathbf{s}}\hspace{0.17em}+\mathbf{F}{\mathbf{f}}_i$.

C. Model Architecture

Let ${\left\{\left({\mathbf{f}}_i,y_i\right)\right\}}_{i=1}^{n_{pop}}$ denote the training tuples consisting of the dimensionality-reduced face representations and the associated conditioning factors. We now aim to estimate the conditional probability distribution p_F (f |y) of facial surface morphology on manifold F. Mathematically, our NF model represents a bijective function $g\left(\mathbf{z}\hspace{0.17em};y,\theta \right):{ℝ}^{n_{\text{sub}}}\to {ℝ}^{n_{\text{sub}}}$ with trainable parameters θ that maps elements z of a n_sub-dimensional latent space Z to a n_sub-dimensional space F of facial morphology f while imposing conditions y. We chose a simple Gaussian base distribution p_Z (z) = p_Z (z|y) = N (0, I) for the latent variable space Z. This allows us to express the the potentially non-Gaussian conditional distribution of interest p_F (f |y) using the change of variables theorem [33]:

$$p_F\left(\mathbf{f}|y\right)=p_Z\left(g^{-1}\left(\mathbf{f}\hspace{0.17em};y,\theta \right)\right)\cdot \left|\det \left(\nabla g^{-1}\left(\mathbf{f}\hspace{0.17em};y,\theta \right)\right)\right|$$

Here, $\left|\det \left(\nabla g^{-1}\left(\mathbf{f}\hspace{0.17em};y,\theta \right)\right)\right|$ denotes the Jacobian determinant of g⁻¹ (f; y, θ). To convert Eq. (1) into a tractable NF model, function g(·; y, θ) must be specified such that it is efficiently invertible and possesses a tractable jacobian determinant. We first split $g\left(\cdot ;y,\theta \right)=g_{n_{\text{lay}}}\circ \cdots \circ g_i\circ \cdots \circ g_1\left(\cdot ;y,{\theta }_1\right)$ into a chain of n_lay simpler sub-functions (called layers in NF models). The different types of layers used in our model will be described first, followed by a summary of how the layers are composed to create the full NF model (see also Fig. 1).

Fig. 1.

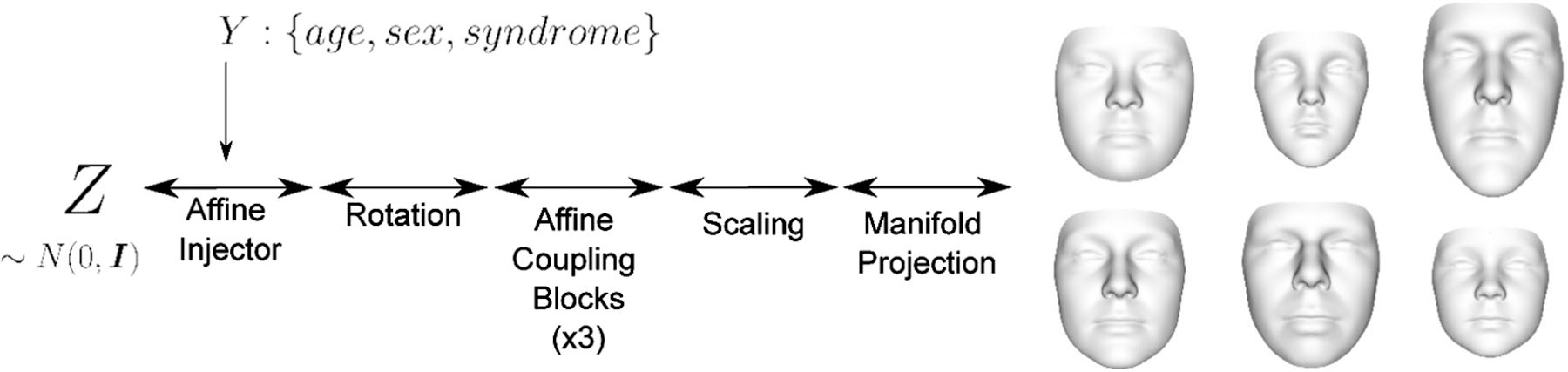
The proposed normalizing flow-based 3D facial shape model is a non-linear, invertible bijection (indicated by bidirectional arrows) between a normally distributed latent space Z and a linear manifold embedded in a space of 3D facial surfaces. The bijection is modeled as a composition of bijective layers (affine injector, rotation, …) that successively transform the normal latent density p_Z (z) to match the complex density on the manifold of 3D faces. Furthermore, the bijection is conditional on demographic variables age, sex, and genetic syndrome diagnosis. The synthetic faces on the right represent maximally probable faces (modes) on the linear manifold that are produced by the model for different combinations of demographic variables. The characteristic Down syndrome facial phenotype is clearly recognizable in the first column, first row. See sections II-B and II-C for a detailed explanation of the model architecture and mathematical notation.

1). Affine Injector:

Within our NF model, the first layer is the only conditional layer. It applies an affine transformation w =g_i(u; y, θ_i) determined by the conditions y to each dimension of the layer’s input $\mathbf{u}\in {ℝ}^{n_{\text{sub}}}$ to generate the output $\mathbf{w}\in {ℝ}^{n_{\text{sub}}}$:

$$\mathbf{w}=\exp \left(s\left(y;{\theta }_i\right)\right)\odot \mathbf{u}+t\left(y;{\theta }_i\right).$$

The scaling s(·; θ_i) and translation t(·; θ_i) functions can be complex neural networks as the inverse of the layer can be computed without having to invert s(·; θ_i) or t(·; θ_i) via

$$\mathbf{u}=\exp \left(-s\left(y;{\theta }_i\right)\right)\odot \left(\mathbf{w}-t\left(y;{\theta }_i\right)\right)$$

and its Jacobian has a simple triangular structure [34]. We will refer to this type of layer as an affine injector following [35]. We choose s(·; θ_i) and t(·; θ_i) to be fully-connected neural networks (two hidden layers, 100 neurons per layer and ELU activations) with partially shared weights θ_i. In consideration of the available training data, we also encode the assumption that the magnitude of facial shape variation along each dimension of the latent space does not depend on syndrome class by excluding synd as an input to the scaling network s(·; θ_i).

2). Rotation:

The second layer in our model is a trainable rotation layer. Rotation is an appealing transformation in this context due to its close relation to PCA and related methods for learning linear bases of data spaces. We use the Cayley transform to produce a smooth parameterization of the special orthogonal group SO(n_sub) as discussed in [36]. Later in the model, we also use fixed random rotations to mix information between dimensions. Rotations are easily invertible and always have a Jacobian determinant of unity.

3). Affine Coupling Blocks:

The next layers of our NF model are affine coupling layers that were first introduced in [34]. Affine coupling layers also define an invertible affine transformation w = g_i(u; θ_i) between their inputs $\mathbf{u}=\left[{\mathbf{u}}_1,{\mathbf{u}}_2\right]\in {ℝ}^{n_{\text{sub}}}$ and their outputs $\mathbf{w}=\left[{\mathbf{w}}_1,{\mathbf{w}}_2\right]\in {ℝ}^{n_{\text{sub}}}$. Here, u₁ and w₁ denote the first n_sub/2 dimensions and u₂ and w₂ represent the second half of the input and output vectors, respectively. The element-wise affine transformation is then defined as:

$${\mathbf{w}}_1=\exp \left(s\left({\mathbf{u}}_2;{\theta }_i\right)\right)\odot {\mathbf{u}}_1+t\left({\mathbf{u}}_2;{\theta }_i\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{w}}_2={\mathbf{u}}_2.$$

In our model, we use a volume preserving (and differential entropy preserving) variant of affine coupling layers where the Jacobian determinant of each layer is constrained to unity (see [37] for details). In practice, this constraint has a strong regularizing effect and can be enforced by subtracting the mean from the vector produced by the scaling function s(·, θ_i) such that it sums to zero. We choose s(·; θ_i) and t(·; θ_i) to be fully-connected neural networks (two hidden layers, 32 neurons per layer and ELU activations) with shared weights θ_i.

Permuting or mixing the inputs after each affine coupling layer is necessary because otherwise interactions between dimensions would be restricted. Therefore, we create affine coupling blocks consisting of two affine coupling layers separated by a permutation that reverses dimension order. At the end of each affine coupling block, we also place a random, fixed rotation that mixes the data as proposed in [33].

4). Scaling:

The final layer of our model is a fixed scaling layer. The fixed parameters of the layer are set once at the start of training according to the standard deviation of each dimension of the dimensionality reduced training data. The purpose of the final layer is to ensure that data representations are normalized as they pass through the other layers of the model while maintaining the information associated with data magnitude in the loss function via the Jacobian determinant of the scaling layer.

5). Layer Composition:

The composition order of the various flow layers used to create g(·; y, θ) is shown in Fig 1. The trainable layer parameters $\theta =\left\{{\theta }_1,\dots ,{\theta }_{n_{\text{lay}}}\right\}$ can be optimized using maximum likelihood training. We chose a multivariate Gaussian distribution with identity covariance as a prior for p_Z (z) resulting in the negative log-likelihood loss

$$\begin{gathered} 𝓛\left(\theta \right)=-\sum _{i=1}^{n_{\text{pop}}}\text{log}\left(p_Z\left(g^{-1}\left({\mathbf{f}}_i;y_i,\theta \right)\right)\right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\log \left|\det \left(\nabla g^{-1}\left({\mathbf{f}}_i;y_i,\theta \right)\right)\right| \end{gathered}$$

for training data ${\left\{\left({\mathbf{f}}_i,y_i\right)\right\}}_{i=1}^{n_{pop}}$. Although the optimization is carried out on the low-dimensional shape representations f_i, it is equivalent to an optimization on manifold F in the high-dimensional ambient data space. This is due to the definition of F as a Euclidean manifold; the manifold projection described in Sec. II-B has a constant Jacobian determinant independent of the input data. [30], [38].

D. Bayesian Inference

To infer the syndrome class synd_i of a subject i from facial surface morphology f_i and demographic variables age_i and sex_i, the flow model can be used along with Bayes’ theorem to compute a posterior distribution:

$$\begin{gathered} p_{synd}\left(synd|{\mathbf{f}}_i,ag{e}_i,se{x}_i\right)= \\ \frac{p_F\left({\mathbf{f}}_i|ag{e}_i,se{x}_i,synd\right)p_{synd}\left(synd|ag{e}_i,se{x}_i\right)}{p_F\left({\mathbf{f}}_i|ag{e}_i,se{x}_i\right)} \end{gathered}$$

Here, we can see that the inclusion of age and sex as conditioning variables enables our model to account for the effects of age and sex on facial morphology when making inferences. Furthermore, an identical approach can be used to infer subject age or sex. Although this is less relevant for clinical applications, it nicely demonstrates the multi-functionality of the proposed model. In addition to a trained flow model, we require a joint distribution for the condition variables p(age, sex, synd) in order to perform inference. In this work, we use a naïve prior that assumes condition variable independence:

$$\begin{gathered} p\left(age,sex,synd\right)=p\left(age\right)\cdot p\left(sex\right)\cdot p\left(synd\right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}p\left(age\right)=\text{Uniform}\left(0,80\right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}p\left(sex\right)\hspace{0.17em}\hspace{0.17em}=\text{Bernoulli}\left(0.5\right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}p\left(synd\right)=\text{Uniform}\left(\Gamma \right) \end{gathered}$$

In a clinical application the joint distribution of condition variables could be set and manipulated by the clinician using prior knowledge about the application context.

E. Face Generation

Data generation capabilities improve interpretability by enabling a model to visually answer questions about what information it has learned and what information it uses to make inferences. Two of the three interpretablity mechanisms of the proposed NF model demonstrated in this work involve data generation.

1). Demographic Specific Face Generation:

The first type of interpretability mechanism is intended to answer questions about what facial representations the model has learned for a particular demographic (e.g., “What do 8 year old males with Down syndrome look like?”). To address this, the model can be used to generate randomly sampled and maximally probable faces (modes) to exemplify general trends and typical variability. Clinicians can then visually assess the facial characteristics the model has learned.

For this task, our NF model can be used in the same way as a conditional VAE or GAN without requiring any additional training. First, a latent sample is drawn from the latent prior. The sample is then mapped using the NF and the specified condition variables from the latent space to the data space and rendered as a 3D surface mesh. Our model can also generate modes (maximally probable faces) for specific demographics by mapping the origin of the latent space (the mode of the latent prior) to the data space in the same way. This property of mode preservation is a consequence of our model architecture enabled through use of the affine injector layer and volume preserving coupling layers.

2). Counterfactual Face Generation:

The second interpretability mechanism is intended to answer questions about what facial information the model uses to justify particular inferences (e.g., “Why did the model infer the syndrome class of this subject as unaffected instead of Down syndrome?”). To address this, the model can be used to generate a counterfactual face, which represents what the model would expect a given subject to look like if they belonged, hypothetically, to a counterfactual demographic group. This counterfactual face visually shows, by contrast with the subjects true face, what facial information was used by the model to justify that particular inference. Counterfactual representations have been shown to be highly effective when explaining a models decision making process to non-technical users [39].

For this task, the original subject face is first mapped to the latent space using the NF and the predicted (or true) condition variables. Next, the subject’s latent representation is mapped back to the data space using the inverse direction of the flow and a different set of counterfactual condition variables. The original and counterfactual faces can then be visually compared.

F. Variation Analysis

The third interpretability mechanism is intended to answer questions about the magnitude of inter- and intra-demographic facial variation as captured by the model (e.g., “How much overlap is there between the facial morphology of males and females?”). This information can be presented to clinicians to help them assess and evaluate the model’s internal understanding of facial variation within and between demographic groups. Variance, co-variance, and variance-based statistics are commonly used within Gaussian modelling approaches to compute standardized effect sizes and magnitudes of variation. To address these questions using a non-Gaussian model such as the one presented in this work, we propose a more general information-based approach.

For this task, we compute Monte Carlo estimates of differential entropy

$$h\left(p_F\left(\mathbf{f}|y_i\right)\right)=-{\int }_F{p}_F\left(\mathbf{f}|y_i\right)\log p_F\left(\mathbf{f}|y_i\right)d\mathbf{f}$$

and KL divergence

$$D_{KL}\left(p_F\left(\mathbf{f}|y_i\right)\left|\right|p_F\left(\mathbf{f}|y_j\right)\right)=-{\int }_F{p}_F\left(\mathbf{f}|y_i\right)\log \frac{p_F\left(\mathbf{f}|y_j\right)}{p_F\left(\mathbf{f}|y_i\right)}d\mathbf{f}$$

for and between different demographic groups. Integration over F weighted by a probability distribution p_F (f |y_i) can be numerically approximated by sampling from the model, and the likelihood of samples under different demographic conditions can be efficiently evaluated using Eq. (1).

III. Experiments

The first aim of the evaluation is to show that the developed NF model can accurately infer syndrome diagnosis, age, and sex from 3D faces. We then use the same model to generate interpretability results that can be used by clinicians to evaluate whether the model bases its inferences on reasonable facial shape information, or noise and other imaging artefacts. Since the exact same NF model is used for a multitude of tasks, the results of various evaluation procedures are mutually supportive.

A. Data Description

The 4727 3D facial scans used to train and evaluate our model were acquired using 3DMD facial imaging systems¹ and are available through the FaceBase Consortium². Patients with cranio-facial syndromes were recruited through clinical geneticists at different sites across North America and have a clinical or molecular diagnosis. Each of the 47 syndromes in this analysis is represented by 20 or more subjects. 2600 of the 4727 subjects are presumed to be unaffected by a genetic syndrome. Ethics approval for this study was granted by the Conjoint Health Research Ethics Board (Id #: REB14-0340 REN4) at the University of Calgary

B. Data Pre-Processing

Each subject scan was landmarked with a set of eight guide points using a combination of manual landmarking and an image-based automatic algorithm [40]. An averaged template mesh (see Fig. 2) was then registered to each scan. This template mesh was initially non-linearly mapped to each subject scan using a thin plate spline transformation anchored by the corresponding guide points. Next, the non-rigid iterative closest point algorithm [41] was used to relax the template mesh completely onto the surface of the scan (see Fig. 2 for an example).

Fig. 2.

Top Left: the average template mesh annotated with eight guide points. Bottom Left: an example subject scan annotated with the same eight guide points. Top Right: the subject mesh (with color) overlaid with transformed template (white mesh). Bottom Right: the transformed template.

The topology of the template was designed so that there is a bijective mapping between bilaterally (across the median plane of the template) corresponding vertices. This bijection was used to produce a mirrored and symmetric version of each subject face as a form of data augmentation. Finally, information associated with facial position and rotation was removed from the template registration transformations and a data manifold was estimated using the approach described in Sec. II-B. For this analysis, we chose n_sub = 100, which produced a manifold capturing 99.8% of the total variance in the training data.

C. Training and Evaluation

All NF models evaluated were trained for 1500 epochs using the NAdam optimizer with a learning rate of 10⁻³ and a batch size of 2056 using a Python-based implementation (Tensorflow 2.2.0 and Tensorflow-Probability 0.10.1) and a 2070 Super NVIDIA GPU with 8 GB memory. The full NF model has 68428 trainable parameters in total. Training a single NF model takes less than 1 hour. Mapping individual faces to and from the latent space is very fast (less than a second) and on par with a VAE comparison model. Importantly, the time to evaluate the conditional likelihood p_F (f_i|y_i) of a 3D face f_i using the NF model is comparable to performing a forward or inverse transformation. This is essential for efficient Bayesian inference and analysis of variation. Comparatively, approximating the conditional likelihood of a single sample using a cVAE model requires expensive Monte Carlo integration. The time to perform inference using the NF model is slightly longer compared to discriminative comparison models (MLP, PointNet) due to the need to sample multiple conditional likelihood values when computing a posterior distribution. The time to perform an analysis of variation varies with the number of random samples used to produce Monte Carlo estimates of the information-based statistics. The full analysis performed in this work completes in approximately one hour.

1). Inference:

For all inference experiments, model training was performed as described above using Monte Carlo cross validation with ten random train/test splits of the 4727 scans. Maximum a posteriori (MAP) estimates from posterior distributions as defined in Eq. (3) are used for all inference tasks and integer age values are sampled at an interval of one year during inference.

For the sake of comparison with baseline non-linear discriminative models, we also trained and evaluated a multi-layer perceptron (MLP) model (two hidden layers, 100 neurons per layer, and ELU activations) and a PointNet (PN) model [42] following the implementation of keras.io/examples/vision/pointnet/ on the same data splits as used for the proposed NF model. The MLP model uses the same dimensionality reduced data as the NF model while the PN model is applied to a randomly sampled subset of 3038 3D points from the dense surface meshes.

In order to compare the proposed model to previously proposed Gaussian modelling approaches, and to test if non-Gaussian models are valuable in this application, NF models were trained and evaluated with the affine coupling blocks removed from the architecture shown in Fig 1. This ablated architecture (LinearNF) has a bijection g(·; y, θ) that is linear with respect to the input (though not with respect to the condition variable y) so that the induced distribution p_F (f |y) is always Gaussian.

2). Face Generation:

The NF model used to generate qualitative face generation results (Figures 3, 4) as well as for analysis of variation results (Sec. IV-C) was trained as described above but using the full set of scans described in Sec.III-A.

Fig. 3.

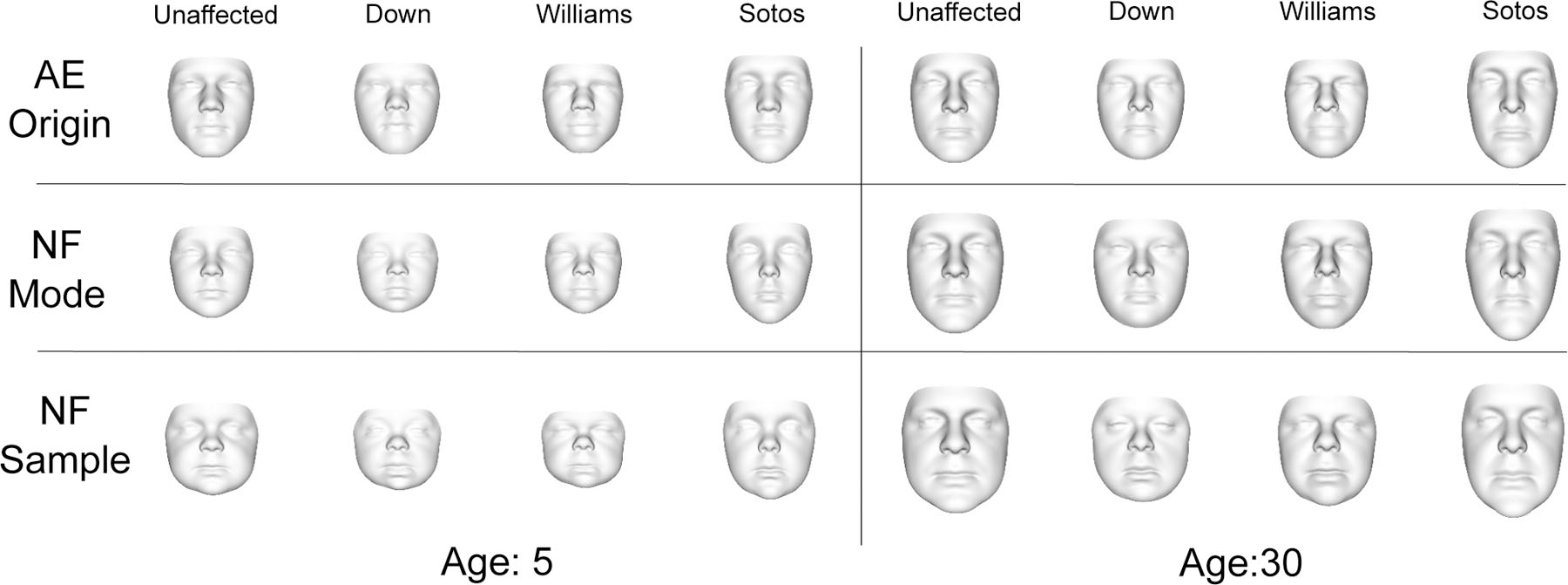
Top Row: Faces corresponding to the origin of the latent space of a cVAE which, unlike the proposed NF model, may not represent the mode of the conditional distribution. Middle Row: modal faces for different syndrome classes at different ages produced by the NF model. Bottom Row: a random sample from the latent space z_rand mapped forward through the NF using different syndrome and age conditions. The sex condition was fixed to male.

Fig. 4.

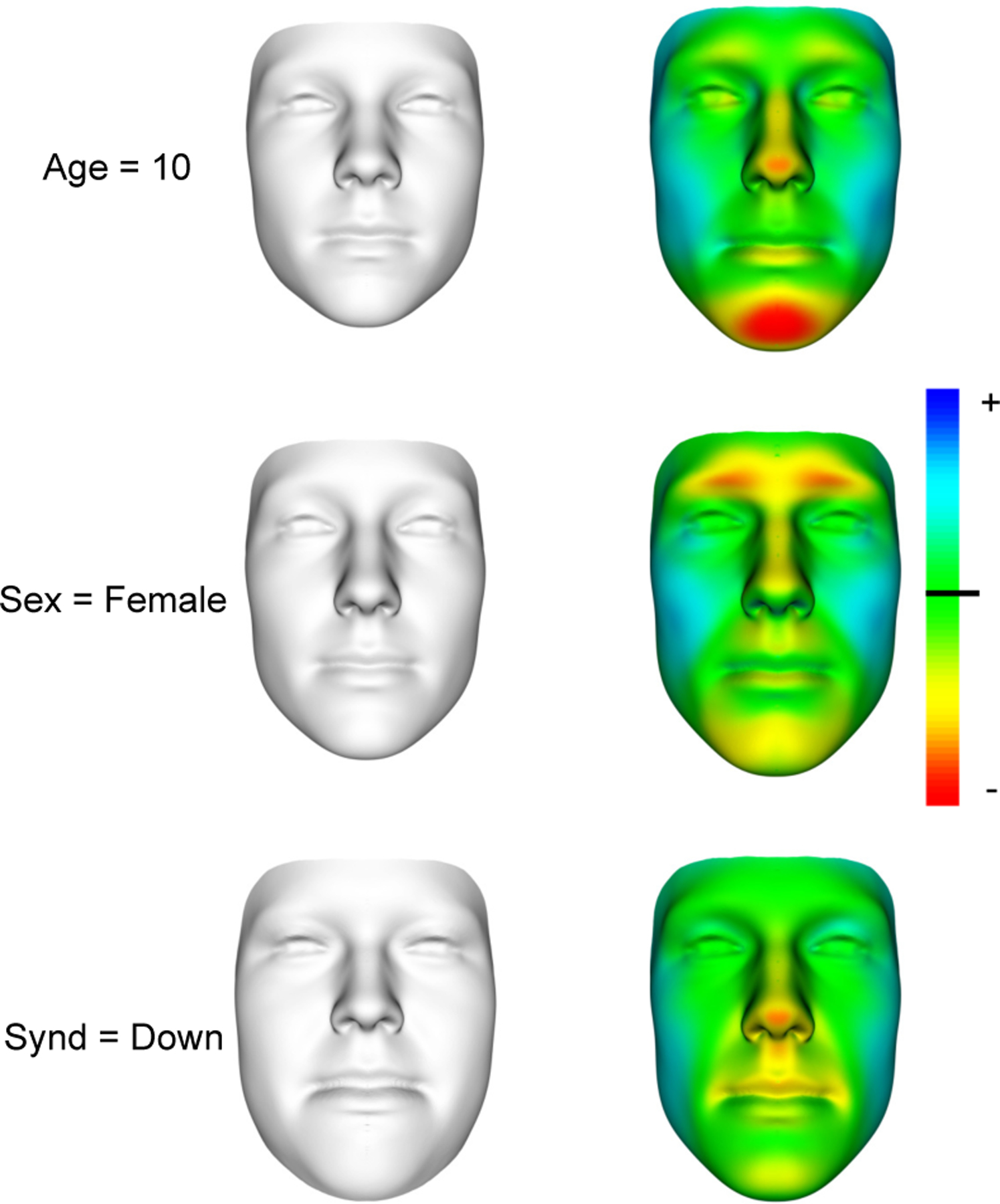
Left column: counterfactual faces for the example subject shown in Fig. 2. Right column: A color map of the shape differences (excluding size information) between original and counterfactual faces overlaid on the original face. Blue indicates an area where the counterfactual shape protrudes outwards compared to the original shape, and red indicates the opposite. The true demographics of the subject are y_true ={27, Male, Unaffected}. The counterfactual demographics shown in each row are y_top ={10, Male, Unaffected}, y_middle ={27, Female, Unaffected}, and y_bottom ={27, Male, Down}.

For a quantitative comparison with another non-linear generative model, we trained a conditional variational auto-encoder (cVAE) on the same, dimensionality reduced, face data as the proposed NF model to represent the same conditional distribution of facial morphology p_F (f |y). The auto-encoder has a latent space dimensionality of n_sub and an isotropic Gaussian latent prior (the same as the NF model). The encoder and decoder are densely connected neural networks (two hidden layers, 100 neurons per layer, and ELU activations).

We quantitatively compared the generative capabilities in terms of cross-validated likeness scores. Likeness scores are calculated by comparing the distributions of intra-class Euclidean distances, and between-class distances (where class indicates whether the data is real or model generated) using the Komolgorov-Smirnov (KS) distance. The larger of the two KS distances between intra-class Euclidean distances and between class Euclidean distances is subtracted from 1 to compute the likeness score. Therefore, a score closer to 1 is better. Likeness scores have been shown to capture important performance aspects of generative models such as creativity, diversity, and inheritance [43]. We compute likeness scores for different demographics using the first of the ten random train/test data splits. All scores were computed using 10,000 random samples.

3). Variation Analysis:

All estimates of KL divergence and differential entropy (Eqs. (5) and (6)) were produced using 50,000 random samples from the latent prior p_Z (z), which we found sufficient to produce stable results. KL divergence and differential entropy are always expressed in units of nats/dim. Units of information (nats or bits) per dimension are commonly used to evaluate non-Gaussian generative models [34], [44].

Unlike the case of discrete entropy where there is a natural canonical reference measure (the counting measure), there is no canonical reference measure for differential entropy. Here, we use the Lebesque measure over ${ℝ}^{n_{\text{sub}}}$ and express all facial measurements f using units of millimeters. Despite this added complexity, differential entropy can still be interpreted as a measure of relative uncertainty or magnitude of variation. A uniform distribution over a unit cube in ${ℝ}^{n_{\text{sub}}}$ with volume 1 $m{m}^{n_{\text{sub}}}$ will have a differential entropy of 0 nats/dim. More localized distributions will have a smaller (negative) differential entropy and less localized distributions will have a larger (positive) differential entropy. KL divergence has the same interpretation (relative entropy or information gain) for both continuous and discrete probability distributions.

IV. Results

A. Inference

1). Syndrome Inference:

Table I summarizes the results of the inference experiments. The overall accuracy of the NF model is 71%. For 92% of unaffected subjects, the correct unaffected class was selected by the model. Results vary widely for the syndrome classes, which is an effect regularly seen in studies that include a large number of syndrome classes [4]. Averaged across all 47 syndrome classes in the analysis (excluding unaffected subjects), the mean sensitivity was 43%. Compared to the Gaussian model (LinearNF), the non-Gaussian model (NF) showed improved overall accuracy (71% vs. 69%) and mean syndrome sensitivity (43% vs. 38%).

TABLE I.

Top-1 overall accuracy and per-syndrome sensitivities for the syndrome inference task (%).

	NF	LinearNF	MLP	PointNet
Overall accuracy	71	69	72	47
Mean syndrome sensitivity	43	38	41	9
1p36 Del	20	14	23	2
22q 11 2 Del	36	43	35	7
4p Del Wolff-Hirschhorn	53	32	56	11
5p Del Cri du Chat	51	47	57	9
Achondroplasia	68	61	62	14
Angelman	17	19	26	2
CHARGE	44	41	56	5
Cardiofaciocutaneous	19	25	34	7
Cleft Lip Palate	36	27	27	10
Cockayne	75	67	71	44
Coffin Siris	0	25	0	0
Cohen	57	67	43	4
Cornelia de Lange	52	59	56	8
Costello	43	41	54	6
Crouzon	34	21	33	13
Down	81	66	79	20
Ehlers Danlos	40	34	35	9
Fragile X	25	3	32	0
Goldenhar	23	35	27	11
Jacobsen	28	21	24	1
Joubert	35	17	22	1
Kabuki	23	33	30	5
Klinefelter	58	67	50	13
Loeys Dietz	22	22	23	0
Marfan	40	41	35	11
Moebius	9	0	7	0
Mucopolysaccharidosis	32	27	39	4
Neurofibromatosis	35	31	26	2
Noonan	38	39	34	4
Osteogenesis Imperfecta	26	17	24	7
Pallister Killian	40	41	35	10
Phelan McDermid	48	34	42	2
Pierre Robin Sequence	4	9	7	0
Pitt Hopkins	38	35	40	1
Prader-Willi	30	12	24	5
Rett	40	45	32	5
Rhizomelic Chondro Punctata	72	86	59	26
Rubinstein Taybi	43	22	43	17
Russell Silver	68	51	62	12
Smith Lemli Opitz	13	24	28	2
Sotos	60	38	58	9
Stickler	42	21	21	6
Treacher Collins	63	65	64	12
Trisomy 18	74	26	68	13
Turner	71	69	58	8
Unaffected	93	94	96	79
Williams	78	71	64	12
X Linked Hypohidrotic Ectodermal	47	51	31	1

The MLP results were generally similar to those of the NF model, but come without the additional interpretability and multi-functionality of the proposed NF model. Overall accuracy and mean syndrome sensitivity were both within two percentage points. The MLP model struggled with the same syndromes as the NF model (Coffin Siris sensitivity 0% and Pierre Robin Sequence sensitivity 7%), and performed well on similar syndromes (Down sensitivity 79%, Cockayne sensitivity 71%, Williams sensitivity 64%). The sensitivity of the MLP model identifying unaffected individuals was slightly better (96%).

The PointNet model performed the worst overall as well as for each individual syndrome. We believe this is primarily an issue of the high input dimensionality and low sample size (as low as 20 subjects for some syndromes). The comparison between the PointNet model and the MLP model (which uses dimensionality reduced data) suggests that the manifold projection step in our approach provides useful regularization for this setup. Furthermore, the PointNet model and other similar models [45] were designed for more challenging tasks in which mesh vertex ordering is unknown and variable. Mesh topology and vertex order are fixed in our dataset using registration to a reference mesh (see section II-A). This property of vertex permutation invariance may also contribute to the inferior performance of PointNet. Like the MLP and most other discriminative models, PointNet has no ability to generate 3D facial surfaces, and no ability to analyze inter- or intra-demographic facial variation.

2). Age Inference:

The mean absolute error between predicted and true age was 4.4 years for unaffected subjects and 11.9 years for patients with syndromes. For unaffected subjects, the mean standard deviation of the posterior age distribution was 3.5 years, indicating that the model tends to be slightly overconfident in its age estimates. In general, age estimation was more accurate for younger subjects. This trend was also mirrored in the variation analysis results (see Fig. 6).

Fig. 6.

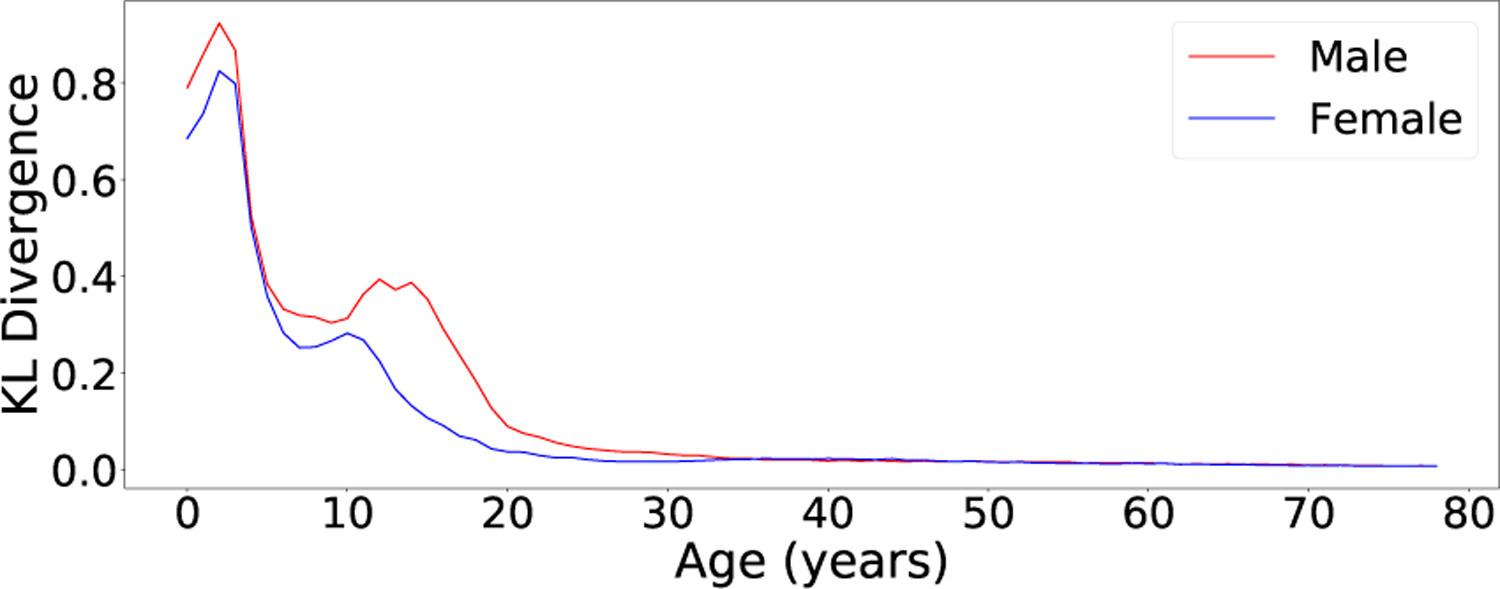
The KL divergences D_KL(p_F (f|y_i)||p_F (f|y_j)) for different values of age_i with age_j = age_i +1. The syndrome condition was fixed (synd_i = synd_j = Unaffected). In general, facial morphology changes fastest at very young ages and during puberty.

3). Sex Inference:

91% of unaffected subjects and 66% of patients with syndromes were classified as the correct sex using MAP estimation. Sex estimation was more accurate for older subjects most likely because sex-specific facial features develop later in life. This trend was also mirrored in the variation analysis results (see Fig. 7).

Fig. 7.

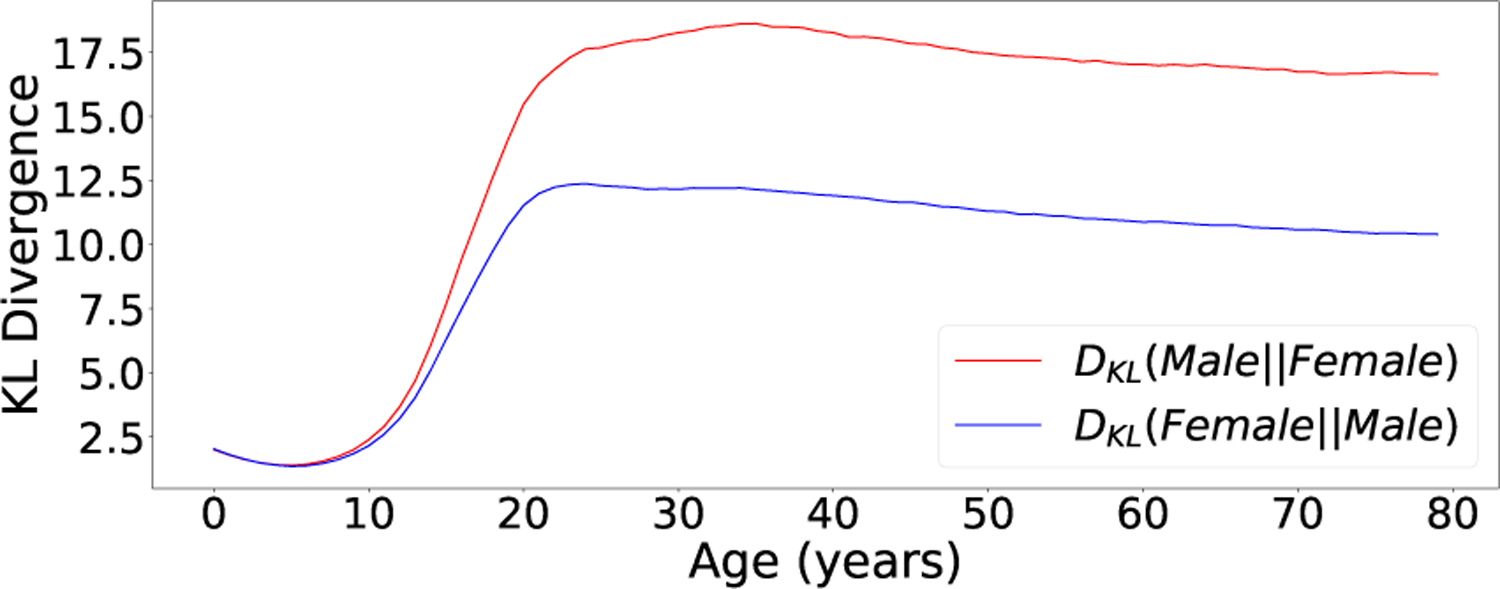
The KL divergences D_KL(p_F (f|y_i)||p_F (f|y_j)) between sex specific distributions at different ages (age_i = age_j ). The syndrome condition was fixed (synd_i = synd_j = Unaffected). In general, sex divergences increase with age until adulthood.

B. Face Generation

1). Demographic Specific Face Generation:

Fig. 3 shows maximally probable faces (modes) and random samples produced by the NF model for a selection of different syndrome and age conditions. The modes and samples exhibit facial features characteristic of the different syndromes and age groups (e.g., small faces for young ages, wide faces for Down syndrome, long faces for Sotos syndrome). Additional visualizations of samples and modes from the NF model are provided as supplementary files (see Appendix II).

Fig. 3 also shows faces generated using a cVAE model. These faces correspond to the origin of the latent space which, unlike the proposed NF model, may not represent the mode of the conditional distribution. Although these faces lack a probabilistic interpretation, they also exhibit features characteristic of the different syndrome classes. The effect of age appears to be less prominent compared to the NF modes.

Table II shows cross-validated likeness scores for selected demographics that are well represented within our data. Both NF models outperform the cVAE model for all demographics included in our evaluation. The Gaussian (LinearNF) and non-Gaussian (NF) flow models performed similarly overall. NF showed small improvements over LinearNF in some demographics and was slightly outperformed in other demographics. In general, likeness scores are better for demographics with more training and evaluation subjects.

TABLE II.

Likeness scores for different generative models and different demographics.

Demographic (# of evaluation subjects)	NF	LinearNF	cVAE
Unaffected, 5–10 yrs (48)	0.66	0.61	0.10
Unaffected, 10–20 yrs (117)	0.89	0.82	0.65
Unaffected, 20–30 yrs (321)	0.94	0.94	0.74
Unaffected, 30–40 yrs (134)	0.87	0.89	0.70
Marfan, 5–40 yrs (21)	0.81	0.83	0.51
Down, 5–40 yrs (9)	0.40	0.39	0.44

2). Counterfactual Face Generation:

Fig. 4 shows counterfactual faces produced using an example subject previously unseen by the model. By contrasting the counterfactual faces with the original face, we can see what information the model uses to make inferences. With respect to this example subject (y_true ={27 yrs, Male, Unaffected}), the model expects that: a younger subject would have a smaller face with a less pronounced nose and chin, a female subject would have a smaller face and less pronounced brow, nose, and chin, and a Down syndrome patient would have a wider, flatter face.

C. Variation Analysis

1). Differential Entropy Analysis:

We first calculated the differential entropy of the marginal distribution of facial morphology h(p_F (f )) = 483 nats/dim, marginalizing the condition variables by integration with respect to the naïve joint distribution of condition variables (see Eq. (4)). Next, we calculated the conditional differential entropy of facial morphology given all condition variables h(p_F (f |y)) = 424 nats/dim. Thus, differential entropy decreased by 12% on average when age, sex, and syndrome diagnosis are specified. This result indicates that intra-demographic facial variation is larger than inter-demographic variation with respect to age, sex, and syndrome class. Furthermore, we computed partially conditional entropies h(p_F (f |synd)) = 460 nats/dim, h(p_F (f |age)) = 463 nats/dim, and h(p_F (f |sex)) = 478 nats/dim. These results indicate that the sex condition has the least effect on facial morphology compared to the other condition variables.

Fig. 5 shows the differential entropies of age- and sex-specific distributions. In general, total facial morphological variation was greater for males and older demographics. Our model architecture assumes that differential entropy is invariant with respect to syndrome class.

Fig. 5.

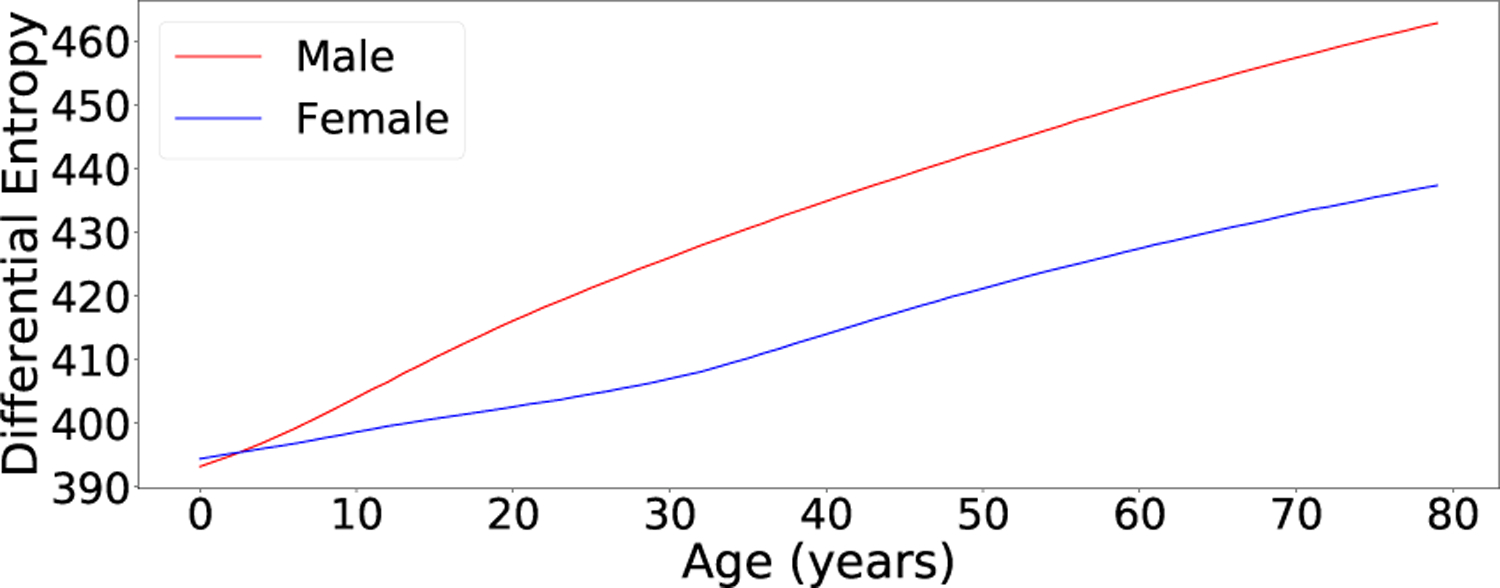
The differential entropies h(p_F (f|y_i)) for different values of age_i and sex_i with synd_i fixed (our model assumes that differential entropy is invariant with respect to syndrome class). In general, total facial morphological variation is greater for males and older demographics.

2). KL Divergence Analysis:

Fig. 6 shows the KL-divergences induced by increasing the age condition by 1 year for unaffected subjects of both sexes at different ages. These values reflect the rate at which the distribution of facial morphology changes at different ages across both sexes. In general, facial morphology changes faster at younger ages. This pattern is also mirrored in the age inference experiments where the MAP age estimates are more accurate for younger subjects. Some other interesting patterns are the spikes in KL divergence that occur around 10–15 years. These are likely attributable to the onset of puberty; the female spike happens slightly earlier and the male spike continues more into the late teens and early twenties.

Fig. 7 shows KL-divergences between sex-specific distributions at different ages. In general, sex divergences increase with age up until 25 to 30 years after which they gradually decline. This pattern is also mirrored in the sex inference experiments where the MAP sex estimates are more accurate for older subjects.

Overall, the variation analysis results quantitatively show that the model has learned patterns of facial variation that are in agreement with what is generally known about syndromic facial morphology, facial development, and sexual dimorphism. The results provide an additional perspective from which clinicians can evaluate patterns (e.g., the development of sexually dimorphic facial features with age) that are also observed in the inference and generation results.

V. Discussion

For the task of predicting genetic syndrome diagnosis from a 3D facial surface scan in a challenging setup with 48 classes, the model performed very well (overall top-1 accuracy of 71%, and a mean sensitivity of 43% across all syndrome classes). It is important to note that the face-based computer-assisted diagnosis of genetic syndromes is an extremely difficult problem as there is a large number of syndrome classes and there often exists a considerable overlap between the facial morphological distributions associated with different genetic syndromes. A particularly useful property of our probabilistic model is its inherent ability to directly quantify and visualize those overlaps (see Figs. 6 and 7).

Aside from the domain-specific challenges mentioned above, we believe that the classification results are also affected by the sample sizes within our training data. For some classes, only twenty patients were available (e.g., Coffin Siris), which is a very small sample for deep learning applications. Performance for those minority classes could likely be improved by collecting additional data. Due to the rarity of genetic syndromes and the large number of different syndromes, data collection is challenging within this domain.

As a result of patient anonymization processes, we do not have the ability to perform a direct comparison with 2D image-based approaches using this data. We believe that a future study comparing 2D and 3D facial representations for syndrome diagnosis would be highly valuable.

Despite these limitations, we believe that our results are highly clinically relevant and the models very useful. Compared to discriminative baseline models, the syndrome classification performance of the proposed NF model is similar (MLP) or better (PointNet) while being far more interpretable and multi-functional. In addition to inferential tasks, the NF model is able to perform multiple generative tasks (sample, mode, and counterfactual generation) as well as extensive analyses of inter- and intra-demographic facial variation that the MLP and PointNet models cannot perform. Compared to a Gaussian generative model (LinearNF), our non-Gaussian architecture achieves a higher overall accuracy and mean syndrome class sensitivity. We also expect the more flexible, non-Gaussian model to benefit more from a larger training sample size. Compared to the limited number of previous studies also specifically aiming at differentiating a large number of syndrome classes using 3D facial data such as [4], the syndrome inference results are competitive. However, it is very challenging to compare scores that are generated using different training and validation data. Furthermore, the generative results and information-based statistics produced by our models provide additional insight into demographic-specific facial morphological variation that may be useful to clinicians to study characteristics of different syndromes.

VI. Conclusion

In this work, we proposed a novel 3D facial surface model, which can be used to infer syndrome diagnosis and other demographic variables given a high-resolution 3D facial scan. With the goal of maximizing model interpretability within a single, flexible deep learning framework, an invertible normalizing flow architecture was designed that discards the commonly employed Gaussian assumption and can seamlessly handle high dimensional 3D data as well as a large number of syndrome classes. The proposed model is the first non-Gaussian 3D facial shape model with the ability to (1) infer syndrome diagnosis and other demographic variables given a high-resolution 3D facial surface scan, (2) generate modal, randomly sampled and counterfactual 3D faces using demographic information, and (3) analyze the magnitude of facial variation between and within demographic groups (e.g., males vs. females) in a fully probabilistic way. Our evaluation demonstrates that a unified invertible architecture achieves competitive inferential performance while enabling much greater interpretability through multiple mechanisms that do not require any additional model training or modification. To the best of our knowledge, a deep invertible model of 3D facial morphology has never been proposed before, neither for general purposes in computer vision nor specifically for genetic syndromes. Furthermore, this work, for the first time, describes the use of invertible flow models to analyze the magnitude of inter- and intra-demographic morphological variation using entropy-based statistics. We believe that invertible models such as the one presented in this work have the potential to greatly increase model interpretability in the domain of medical diagnosis.