A Guide to Estimating the Reference Range From a Meta-Analysis Using Aggregate or Individual Participant Data

Abstract

Clinicians frequently must decide whether a patient’s measurement reflects that of a healthy “normal” individual. Thus, the reference range is defined as the interval in which some proportion (frequently 95%) of measurements from a healthy population is expected to fall. One can estimate it from a single study or preferably from a meta-analysis of multiple studies to increase generalizability. This range differs from the confidence interval for the pooled mean and the prediction interval for a new study mean in a meta-analysis, which do not capture natural variation across healthy individuals. Methods for estimating the reference range from a meta-analysis of aggregate data that incorporates both within- and between-study variations were recently proposed. In this guide, we present 3 approaches for estimating the reference range: one frequentist, one Bayesian, and one empirical. Each method can be applied to either aggregate or individual-participant data meta-analysis, with the latter being the gold standard when available. We illustrate the application of these approaches to data from a previously published individual-participant data meta-analysis of studies measuring liver stiffness by transient elastography in healthy individuals between 2006 and 2016.

Abbreviations

CI

confidence interval

IPD

individual participant data

kPa

kilopascal

CLINICAL SCENARIO

A 50-year-old apparently healthy man presents for a preventive health examination. He is concerned because his sister was diagnosed with “liver fibrosis.” A liver biopsy, the gold standard diagnostic tool, is too invasive and costly to perform on an asymptomatic individual. A noninvasive ultrasound-based test called transient elastography was introduced in 2003. The test measures stiffness of the liver, which is a surrogate of liver scarring (fibrosis). However, the normal range for this test is not known and has only been reported in studies with heterogeneous populations in terms of clinical and demographic characteristics. Bazerbachi et al. (1) conducted an individual participant data (IPD) meta-analysis and estimated the mean stiffness in healthy nonobese individuals with a confidence interval (CI). This CI only reflects uncertainty in the pooled mean rather than the variation across individuals; thus, it is not a reference range. We have revisited this analysis to construct a reference range that incorporates natural variability across healthy individuals.

INTRODUCTION

Often clinicians would like to know whether a patient’s measurement falls within some “normal” range for healthy individuals. While meta-analysis most frequently involves summarizing 1 or more treatment effects on an outcome, many examples exist of meta-analyses of normative data (1–13). Normative data are assumed to be drawn from a predefined healthy population (e.g., with certain inclusion and exclusion criteria) that serves as a reference for future comparison (14). These data may be drawn from normative studies of healthy individuals, cohort studies, the control arms of case-control studies, or baseline values from randomized-controlled trials in healthy populations (1, 9, 11). A reference range, or an interval in which we would expect the measurements of a specified proportion of a healthy population (e.g., 95%) to fall (15, 16), provides important information in determining whether a patient’s measurement is “normal.” This can also be defined as a prediction interval for the value of a new healthy individual conditional on the normative data from existing evidence (15). While several studies in the biomedical literature have used ad-hoc methods to report reference ranges estimated from meta-analyses (6, 7, 10, 11), Siegel et al. (17) recently proposed 3 methods for estimating the reference range from a meta-analysis with aggregated data. To provide some practical guidance, we describe how to calculate the reference range from a meta-analysis and outline how it differs from the CI for the pooled mean and the prediction interval for the mean of a new study (18, 19). We applied these methods to a systematic review and meta-analysis of studies measuring normative liver stiffness in adults. We considered using aggregate data from publications but also extended these methods to IPD.

WHAT AGGREGATE DATA ARE TYPICALLY NEEDED?

Often, when conducting a meta-analysis of multiple studies to estimate the reference range, only aggregate data are available from published studies. The required aggregate data typically include the observed means, standard deviations, and sample sizes from each study. Studies may also report demographic information, such as the proportion of males and females or the mean age of participants in the study.

DEFINING THE POPULATION OF INTEREST

To determine whether the studies included in a meta-analysis have enrolled participants who belong to the prespecified target population, we suggest evaluating 2 sources of information. First, the inclusion and exclusion criteria of the meta-analysis. Second, the observed demographic information provided in the manuscripts of included studies. Based on these 2 sources of data, a judgment needs to be made about whether the studies include representative participants from the target population for the reference range. One should also consider whether some studies have enrolled participants with occult disease and exclude such studies. For example, healthy volunteers with occult fatty liver disease enrolling in hepatology studies is a well-recognized phenomenon (20).

Each of the proposed methods for estimating the reference range allows the underlying means of each study included in the meta-analysis to differ (a “random effects” assumption). In other words, variation in the observed means across studies can be attributed to both actual differences and sampling variability (19). We assume that the studies included in the meta-analysis form a representative or random sample from a greater “superpopulation” of potential studies and are interested in the marginal (overall) distribution of individuals across these studies (Figure 1). Determining whether this sample is representative requires investigating possible heterogeneity sources, as described in the next section. We focus on the overall distribution, rather than conditioning on a specific study, since it may be unclear which theoretical study population a patient would belong to in practice.

Figure 1.

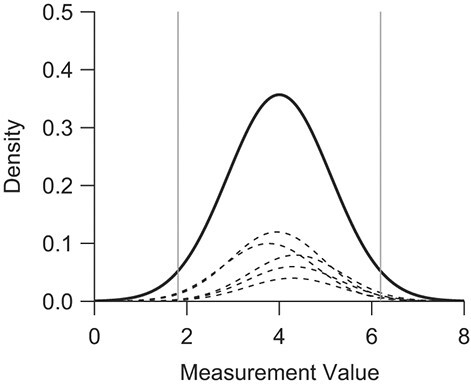
Marginal (overall) distribution and a selection of hypothetical study distributions according to a random-effects model where . The distributions of study means and individuals within each study are all normal. The vertical lines represent the 2.5th and 97.5th quantiles of the marginal distribution. Each of the meta-analysis methods presented allows for true differences between subpopulations, and the target population is the overall distribution that captures each of these.

In the clinical scenario described previously, the target population consists of healthy nonobese individuals without evidence of liver steatosis or fibrosis across all potential studies, as we aim to characterize liver stiffness measurements that would be extreme for patients with healthy livers while incorporating the total variability found across different populations of healthy patients.

INVESTIGATING SOURCES OF HETEROGENEITY

The random-effects assumption described earlier to account for between-study heterogeneity assumes many possible studies whose underlying study means follow a distribution, typically a normal distribution. This assumption is consistent with small variations across studies such as those due to slightly different but overlapping study populations, similar but not identical equipment, or different personnel collecting measurements. If it is believed that the overall population can be partitioned into several distinct subpopulations with different measurements, separate reference ranges corresponding to each population would be more informative. Hypothesized sources of heterogeneity could be investigated using subgroup analyses or meta-regression methods (21), although this often lacks precision or power (with meta-regression) due to a small number of studies. This emphasizes the importance of clear and well-defined inclusion criteria, so that studies in the meta-analysis are applicable to the population of interest.

Because the overall mean and variance across individual participants are of equal interest when estimating the reference range, heterogeneity in the within-study variances should be carefully explored. Differences in the within-study variances can be investigated visually using a forest plot of the observed study standard deviations and their corresponding CIs.

META-ANALYSIS METHODS FOR ESTIMATING THE REFERENCE RANGE

We previously proposed 3 methods for estimating the reference range using aggregate data (17); these methods are described in detail in Web Appendix 1 (available at https://doi.org/10.1093/aje/kwac013) and summarized in Web Tables 1 and 2. The first 2 methods, the frequentist method and the Bayesian posterior predictive interval, assume that 1) values of the variable of interest follow a normal distribution for each study population; 2) the variances of individual measurements within each study are equal across studies; and 3) that the true study means are also normally distributed. These assumptions then imply that the overall distribution across studies is also normal.

The frequentist approach involves estimating the shared within-study variance, fitting a random-effects model on the aggregate data, and then using the estimated pooled mean and within- and between-study variances to approximate the overall distribution of individuals. The bounds of the estimated 95% reference range are then given the 2.5th and 97.5th quantiles of this overall normal distribution, assuming the estimated parameters are fixed quantities (i.e., ignoring their uncertainty).

The Bayesian method requires fitting a random-effects model on the aggregate data where the shared within-study variance is estimated using the sampling distribution of the sample variance. The bounds of the 95% reference range are then given by the 2.5th and 97.5th quantiles of the posterior predictive distribution for a new individual. This differs from the other 2 methods in that the reference range becomes wider with greater uncertainty by considering the variation of parameters, consistent with the definition of the reference range as a prediction interval. While it may be possible to introduce this behavior with the frequentist approach using a t-distribution, the appropriate degrees of freedom are unclear and likely require approximation. Furthermore, the degrees of freedom will depend on both the estimated within- and between-study variances and will be high when the number of studies is large or when the between-study variance is small relative to the total variance. Under those conditions, the t-distribution will strongly resemble that of a normal distribution.

The frequentist and Bayesian methods also make the usual random-effects assumption that the study means (random effects) follow a normal distribution (18). It is often incorrectly assumed that the central limit theorem (CLT) guarantees this (22). The CLT only guarantees normality of the sampling distribution of the mean from a single study, not the overall collection of study means. Instead, this assumption should also be visually assessed. Methods have also been developed for estimating prediction intervals for a new study effect that do not require this normality assumption, such as those based on bootstrap sampling methods (22, 23). Future work could expand these methods to prediction on the individual level.

The third aggregate data approach, the empirical approach, does not require the data within each study to be normally distributed or assume equal within-study variances, only that the overall distribution across all studies is normal. Instead, the pooled mean is estimated as a weighted average of the study means, and the total variance is estimated as the sum of a weighted average of the sample variances and the sample variance of the study means. This empirical method could also likely be used when the overall distribution is assumed to be any other distribution that is entirely determined by its mean and variance. The different interpretations of the reference ranges, the CI for the pooled mean, and the prediction interval for a new study are summarized in Web Table 2. Furthermore, while the methods mentioned thus far assume that the overall distribution is normal, we also describe in Web Appendix 2 how to handle aggregate data that are believed to follow a lognormal distribution.

Simulation results suggest that each of the proposed aggregate data approaches perform similarly when the between-study heterogeneity is relatively small and the number of studies in the meta-analysis is large (at least 20) (17). However, some caution should be used in cases of large between-study heterogeneity or very few studies. In particular, if unexplained between-study heterogeneity comprises approximately 30%–50% or more of the total estimated variance, one should carefully consider the interpretability of the estimated reference range. While the equal within-study variation assumption made by the frequentist and Bayesian methods is arguably strong, Siegel et al. (17) demonstrated through simulations that these methods might be robust to small differences in the true variances across studies. However, if the within-study variances plausibly differ according to some characteristic of the studies, separate reference ranges for these groups may be more clinically meaningful regardless of the distributional assumptions of the method used.

APPLIED EXAMPLE

We reanalyzed the data used in the clinical scenario (1) to construct a reference range that reflects natural variability across healthy individuals.

Defining the population of interest

Individuals were included in the original analysis if they had a body mass index less than 30 and did not have hypertension, dyslipidemia, hepatic steatosis on ultrasound, or diabetes mellitus. The authors of 1 study withheld permission for use of the data in further analyses, leaving 3,652 individuals across 20 studies. Because one of these studies contained only 4 individuals meeting the inclusion criteria, we further excluded these 4 patients. This resulted in a final data set containing 3,648 individuals across 19 studies.

Derivation of aggregate data

To replicate the scenario where only aggregate data were available, we summarized the data within each study by the mean, standard deviation, and sample size. These data are shown in Web Table 3; the R code (R Foundation for Statistical Computing, Vienna, Austria) used in the aggregate data analysis is presented in Web Appendixes 3–5.

Application of methods

We present a forest plot for the study-specific means and pooled mean in Figure 2. The pooled mean was estimated using the aggregate data and a frequentist random-effects model (using restricted maximum likelihood estimation) implemented in the R package “meta” (24).

Figure 2.

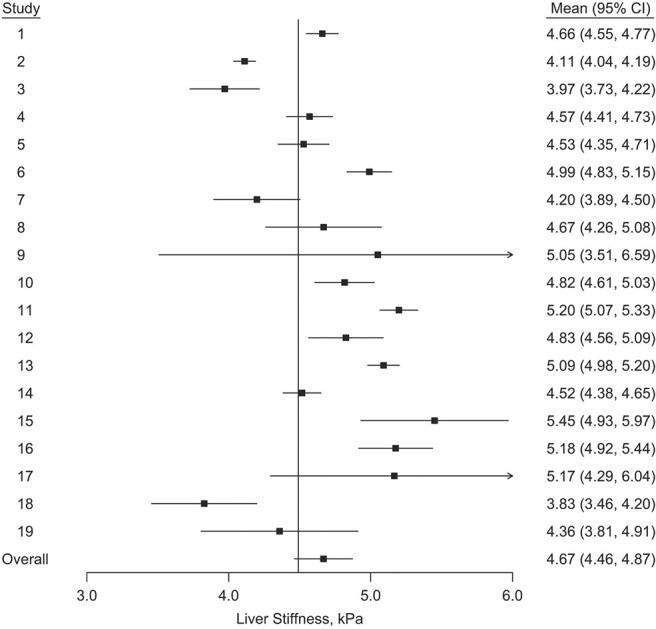
Estimated mean and 95% confidence interval (CI) for each transient elastography liver-stiffness measurement study and estimated pooled mean (95% CI) based on aggregate data from a previously published meta-analysis of liver stiffness measurements collected between 2006–2016 (1). kPa, kilopascal.

We next applied each of the proposed methods for estimating the 95% reference range (Table 1) using the aggregate data. Because liver stiffness measurements must be positive, and the observed distribution of measurements was slightly right-skewed, we first log-transformed the liver stiffness measurements and then exponentiated the results for the estimated 95% reference ranges. With only aggregate data available, this log-transformation required using the approximation described in Web Appendix 2.

Table 1.

Estimated 95% Reference Ranges for Liver Stiffness Measurement Using Each of the Methods Presented With Aggregate Data From a Previously Published Meta-Analysis of Liver Stiffness Measurements Collected Between 2006–2016^a

Method	Estimated 95% Reference Range, kPa b
Frequentist	2.55, 7.90
Bayesian	2.52, 7.94
Empirical	2.57, 7.86

Abbreviation: kPa, kilopascal.

^a Bazerbachi et al. (1).

^b The reference ranges were estimated on the log-scale, and the resulting intervals were exponentiated.

We implemented the Bayesian models in JAGS (https://mcmc-jags.sourceforge.io/) using the R packages “rjags” and “coda” (25, 26). For the Bayesian models, we ran 2 chains with 100,000 iterations each and a burn-in period of 5,000 iterations and assessed convergence based on trace plots, the Markov chain Monte Carlo error, and the potential scale reduction factor. All analyses were conducted using R, version 3.6.3.

The estimated reference ranges were similar across each of the methods used (Table 1, Figure 3). The Bayesian posterior predictive interval was slightly wider, followed by the frequentist method, then the empirical approach. We would expect the Bayesian method to give a wider reference range as it incorporates uncertainty in the parameter estimates. Web Appendix 5, which includes Web Figure 1, shows a normal quantile-quantile (Q-Q) plot of the study means on the log-scale; this shows no clear deviations from the assumption in the frequentist and Bayesian methods that these follow a normal distribution. Web Figure 2 displays the observed standard deviations of the log of liver stiffness within each study and their respective 95% CIs. We use this to assess the equal within-study variance assumption imposed by the frequentist and Bayesian methods. Most of the observed study standard deviations are similar, with a high degree of overlap in their respective CIs, with the possible exceptions of studies 9 and 16. We therefore performed a sensitivity analysis where we removed studies 9 and 16, which gave estimated reference ranges similar to the original results (Web Table 4).

Figure 3.

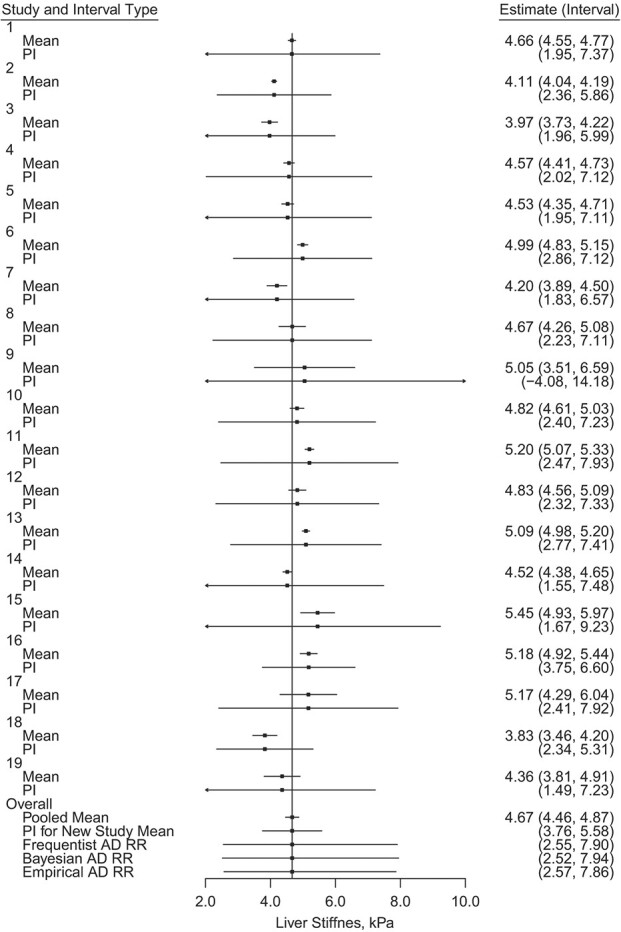
Estimated mean, 95% confidence interval (CI), and 95% frequentist prediction interval (PI) for a new individual’s transient elastography liver stiffness measurement by study, 95% CI for the pooled mean, 95% PI for a new study mean, and estimated 95% reference ranges (RRs) using the 3 methods presented, based on aggregate data (AD) from a previously published meta-analysis of liver stiffness measurements collected between 2006–2016 (1). Each reference range was estimated on the log-scale and the resulting bounds were exponentiated. kPa, kilopascal.

Each of the estimated reference ranges can be interpreted as the predicted interval in which we would expect 95% of liver stiffness measurements of healthy individuals to fall. For example, based on the Bayesian reference range, we would expect 95% of healthy patients to have liver stiffness measurements between 2.52 kilopascals (kPa) and 7.94 kPa. If our hypothetical patient has a liver stiffness measurement of 9.00 kPa, this may necessitate further investigation, as this degree of liver stiffness is atypical of a healthy individual.

The 95% CI for the pooled mean (4.46 kPa, 4.87 kPa), is much narrower than any of the estimated reference ranges (Figure 3). This demonstrates the difference that incorporating natural variability across all individuals makes when constructing the reference range. This is also true when comparing the estimated reference ranges with the frequentist 95% prediction interval for the mean of a new study, (3.76 kPa, 5.58 kPa), instead of the measurement of an individual (19, 22). We can also compare the results with the 2.5th and 97.5th quantiles of the individual measurements, ignoring study assignment: (2.70 kPa, 7.49 kPa). The estimated reference ranges that incorporate study assignment are slightly wider than this because they allow for between-study variation and the possibility of more extreme measurements in a future study. The CI for the pooled mean and the prediction interval for a new study mean are far narrower and do not capture healthy individuals’ full variation.

INDIVIDUAL PARTICIPANT DATA

All 3 approaches are designed for the meta-analysis of aggregate data, where only the study means, standard deviations, and sample sizes are known. Because of this, we also include how the reference range could be calculated using IPD without first aggregating the data (i.e., a 1-step approach) (Web Table 1). These approaches are 1-step analogues of each of the 3 approaches described previously; the estimated reference ranges based on IPD ultimately serve as a “gold standard.”

IPD allows for a more detailed exploration of the modeling assumptions. Each of the methods previously discussed assumes that the individuals across all studies follow an overall normal distribution. Both the Bayesian and frequentist approaches also assume that the data within each study are normally distributed and the within-study variances are equal across studies. If IPD are available, these normality assumptions can be visually assessed using methods such as histograms and normal Q-Q plots. Because of this, access to IPD even for 1 or 2 studies could be valuable in investigating these distributional assumptions before using an aggregate data method to estimate the reference range. Similarly, with aggregate data, we cannot directly log-transform the individual measurements. Instead, the approximation given in Web Appendix 2 must be used.

We present the results for the clinical scenario using both the aggregate (2-step) approaches and the 1-step approaches using IPD in Table 2. The code for the IPD analysis is presented in Web Appendixes 6 and 7. In all cases, the data are first log-transformed (before aggregating), and the resulting ranges are exponentiated. As expected, the frequentist and empirical IPD methods gave slightly narrower estimated reference ranges than the Bayesian IPD method (Table 2, Web Figure 3). With IPD available, we directly obtained the mean and standard deviation on the log scale for each study rather than estimating these using the methods presented in Web Appendix 2. Because the log-transformation differed between this analysis and the aggregate data analysis presented previously in Table 1, we would expect slightly different results even among the aggregate data approaches. However, the results using the aggregate data are comparable to those based on the IPD (Table 2). This supports the validity of the aggregate data approaches in this case, an important point since IPD are rarely available for all studies included in a meta-analysis. Web Appendix 6 includes histograms of the liver stiffness measurements both by study and pooled across studies on both the original and log-scales (Web Figures 4–7). These were used to assess the within-study and overall normality assumptions imposed by the frequentist and Bayesian methods. We also plotted the study standard deviations and their CIs on the log-scale based on the IPD (Web Figure 8) and repeated the sensitivity analysis described in the previous section; we observed similar results with and without studies 9 and 16, as shown in Web Table 5.

Table 2.

Estimated 95% Reference Ranges for Liver Stiffness Measurement Using IPD From a Previously Published Meta-Analysis of Liver Stiffness Measurements Collected Between 2006–2016^a

Method	Estimated 95% Reference Range, kPa b
Frequentist AD	2.62, 7.74
Bayesian AD	2.61, 7.79
Empirical AD	2.64, 7.69
Frequentist IPD	2.63, 7.72
Bayesian IPD	2.52, 7.94
Empirical IPD	2.64, 7.69

Abbreviations: AD, aggregate data; kPa, kilopascal; IPD, individual participant data.

^a Bazerbachi et al. (1).

^b The reference ranges were estimated on the log-scale and the resulting intervals were exponentiated.

INTERPRETATION OF RESULTS

Because there has been little guidance in the literature on estimating reference ranges from a meta-analysis, many meta-analytical studies have reported the pooled mean as a “reference value” (8, 9, 12). While the pooled mean can establish a point of reference, it does not capture natural variation across healthy individuals. As a result, some studies have also reported the 95% CI for the pooled mean as a “reference range” (1, 3, 5), although this better reflects the uncertainty in the estimated pooled mean, not the range of predicted values for a new individual. For example, as the number of studies included in the meta-analysis increases, we would expect the CI for the pooled mean to narrow, reflecting increased precision in the estimate. However, we would not expect the width of the estimated reference range to approach zero as the total sample size increases.

Similarly, some have recently advocated for the reporting of a prediction interval for the mean or effect size of a new study when conducting meta-analyses in order to better describe between-study heterogeneity (19, 22, 27, 28). Riley et al. (19) describe a random-effects meta-analysis example with a statistically significant pooled treatment effect but with a prediction interval for the treatment effect in a new study of (−0.79, 0.09). They explain that the small amount of the interval falling above zero indicates that the treatment may not be effective in some situations (19). This example clearly illustrates how the CI for the pooled mean does not necessarily represent the variation across study populations. However, the prediction interval for the mean of a new study still does not reflect the total variation on the individual participant level and would therefore not be suitable as a reference range either.

The differences in these intervals are illustrated in Figure 4, which shows the 95% CI for the pooled mean, 95% prediction interval for a new study, and the estimated 95% reference range based on the same estimates of the pooled mean and within- and between-study variances, but varying the numbers of studies included in the meta-analysis (N) and the number of individuals within each study (n). As the number of studies or number of participants within each study increases, the CI for the pooled mean narrows. The prediction interval for a new study mean also narrows slightly, but this is due to greater perceived precision in the estimated parameters. Figure 4 also shows the estimated 95% reference ranges for each of these meta-analyses when using the frequentist method proposed by Siegel et al. (17). This method does not incorporate uncertainty in the estimated parameters, so the width of the reference range remains fixed for different sample sizes. However, the Bayesian posterior predictive reference range interval, also proposed by Siegel et al. (17), can naturally incorporate the uncertainty in the estimated parameters. Despite this difference, the estimated reference ranges in Figure 4 are still wider than other intervals. This is because they reflect both the estimated within-study and between-study variances, rather than only the between-study variance, as does the prediction interval for the mean of a new study, or neither as does the CI for the pooled mean (Web Table 2).

Figure 4.

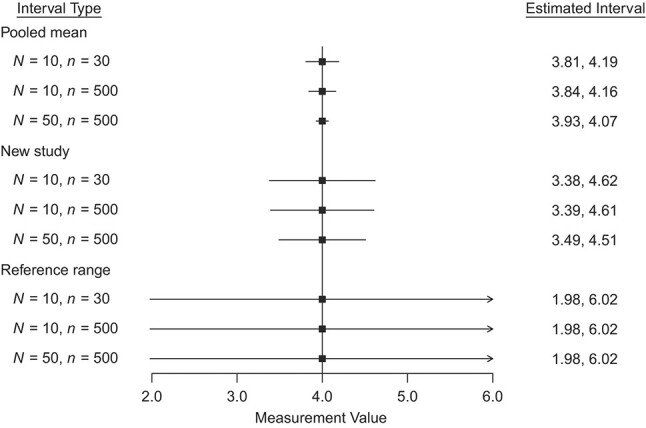
95% confidence interval for the pooled mean, 95% prediction interval for the mean of a new study, and estimated 95% reference range for hypothetical data where 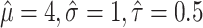and for different within-study sample size (n) and number of studies (N).

CERTAINTY ABOUT THE ESTIMATED REFERENCE RANGE

To apply research evidence to patient care properly, evidence users (clinicians, patients, and guideline developers) need to know how certain or trustworthy the evidence is. Therefore, when a reference range is estimated, we need to consider applicability, risk of bias, heterogeneity, and precision (29). If possible, studies at high risk of bias (e.g., due to poor ascertainment of the measured laboratory test or because of a large proportion of patients lost to follow up) (30) could be excluded from the reference range estimation. If excluding these studies is not feasible, and we are left with a reference range estimated from studies at high risk of bias, certainty in this range will be low. If heterogeneity between the studies used to estimate the range was high and not explained by subgroup analyses, certainty will also be low. If the total sample size of included studies was small, the estimation of this range will also be imprecise and warrants lower certainty.

The Bayesian method for estimating the reference range incorporates the estimation uncertainty of parameters into the width of the interval. However, depending on the application, it may be more prudent to flag a truly healthy individual as abnormal, thus necessitating further investigation, rather than fail to discern pathology in a sick patient. In such a scenario, it may be preferable to omit the estimation uncertainty of parameters from the width of the interval, because, under the Bayesian approach, the estimated interval may contain greater than 95% of measurements in the case of large estimation uncertainty (e.g., when the number of studies is small, the between-study variance may be estimated with greater uncertainty). Conversely, if avoiding overdiagnosis is of greater concern, the estimated interval from the Bayesian approach may be preferred. If overdiagnosis is of paramount concern, a tolerance interval (31–33), which limits the probability that the interval will cover less than the prespecified proportion (e.g., 95%) of the distribution, may be appropriate. Further work is needed to estimate tolerance intervals for individual measurements from a meta-analysis.

DISCUSSION

This empirical application introduces the aggregate data approaches to estimating reference ranges proposed by Siegel et al. (17) and their IPD analogues. Each of the proposed methods is relatively easy to use, and R code is provided in Web Appendix 3 (aggregate data) and Web Appendix 6 (IPD). The Bayesian methods (both 1- and 2-step) differ from the other methods in that the width of the estimated ranges increases with greater uncertainty. The frequentist and empirical approaches also do not require setting prior distributions for the model parameters and may be easier to implement in practice than the Bayesian methods. The frequentist methods can be implemented using existing software packages, while the empirical approaches use only simple formulas. When implementing these methods, one should consider the target population and possible subgroup heterogeneity, using methods such as stratified analyses or meta-regression, to ensure applicability of the estimated range.

The modeling assumptions used by each of the proposed methods should also be considered when estimating the reference range, preferably by investigating distributional assumptions using IPD from at least 1–2 data sets, and further work is needed to address situations where the normality or equal within-study variance assumptions are not met. However, our applied example using liver stiffness measurements illustrates how each method more accurately describes variation across healthy individuals than the CI for the pooled mean or the prediction interval for the mean of a new study.