Reference-Relation Guided Autoencoder with Deep CCA Restriction for Awake-to-Sleep Brain Functional Connectome Prediction

Abstract

The difficulty of acquiring resting-state fMRI of early developing children under the same condition leads to a dedicated protocol, i.e., scanning younger infants during sleep and older children during being awake, respectively. However, the obviously different brain activities of sleep and awake states arouse a new challenge of awake-to-sleep connectome prediction/translation, which remains unexplored despite its importance in the longitudinally-consistent delineation of brain functional development. Due to the data scarcity and huge differences between natural images and geometric data (e.g., brain connectome), existing methods tailored for image translation generally fail in predicting functional connectome from awake to sleep. To fill this critical gap, we unprecedentedly propose a novel reference-relation guided autoencoder with deep CCA restriction (R²AE-dCCA) for awake-to-sleep connectome prediction. Specifically, 1) A reference-autoencoder (RAE) is proposed to realize a guided generation from the source domain to the target domain. The limited paired data are thus greatly augmented by including the combinations of all the age-restricted neighboring subjects as the references, while the target-specific pattern is fully learned; 2) A relation network is then designed and embedded into RAE, which utilizes the similarity in the source domain to determine the belief-strength of the reference during prediction; 3) To ensure that the learned relation in the source domain can effectively guide the generation in the target domain, a deep CCA restriction is further employed to maintain the neighboring relation during translation; 4) New validation metrics dedicated for connectome prediction are also proposed. Experimental results showed that our proposed R²AE-dCCA produces better prediction accuracy and well maintains the modular structure of brain functional connectome in comparison with state-of-the-art methods.

1. Introduction

During the first few years of life, the human brain undergoes exceptionally dynamic development that could largely shape later behavioral and cognitive performance [1–3]. Delineating the functional developmental trajectories through this stage with resting-state fMRI (rs-fMRI) is of great importance in understanding the normal brain and diagnosing neurodevelopmental disorders [4, 5]. However, there are unique challenges associated with acquiring rs-fMRI for early developing children under a unified condition (sleep or awake), i.e., 1) it is impossible to request younger infants to be awake while remaining still during scanning; 2) it is difficult to persuade older children (>24 months) to sleep during the daytime and also the brain activity in the deep sleep during the night is significantly different from normal resting state. This dilemma generally leads to a dedicated protocol, i.e., scanning younger infants during sleep, while scanning older children during being awake and keeping them still by watching movies [4, 6]. However, there are big differences lying in the hemodynamic responses of sleep and awake that will be reflected in fMRI and the corresponding brain functional connectome. Thus, to realize meaningful and consistent cross-age studies under different scan conditions, predicting the functional connectome obtained during sleep from that during being awake is critical, which, however, remains unexplored to the best of our knowledge and challenging. Due to the difficulties in image acquisition and recruitment, training the model for awake-to-sleep brain connectome prediction usually confronts the problem of data scarcity. Moreover, although deep generative adversarial networks based domain translation have been successfully developed for image translation [7–9], these methods generally fail in predicting functional connectome because of the huge difference between natural images and geometric data (e.g., brain connectome). In addition, the multi-view brain graph synthesis method [10, 11] may not perform well in awake-to-sleep prediction, as it was designed for connectomes obtained by cortical morphological measures, which usually have smaller distribution differences between the source and target domains.

To address these issues, we unprecedentedly propose a Reference-Relation guided AutoEncoder with deep Canonical Correlation Analysis restriction (R²AE-dCCA) for awake-to-sleep connectome prediction. First, a reference-autoencoder (RAE) is proposed to realize a guided generation from the source domain to the target domain. During the training stage, reference-couples from the target domain will be used to guide the prediction, which are constructed by the combinations of all the age-restricted neighboring subjects of the ones to be predicted. Merging with the individualized patterns learned from the source domain in the latent space, reference-couples not only provide the sleep-specific patterns but also greatly augment the limited data by random coupling. Then, a relation network is designed and embedded into RAE, which learns the similarity of the reference-couples to the subject to be predicted in the source domain and determine the belief-strength of reference in the process of target connectome generation. To guarantee that that similarity in the source domain will be maintained in the target domain, a deep CCA (Canonical Correlation Analysis) restriction is further employed in the coupled latent space to keep the neighboring relation from the source domain to the target domain. Finally, in the testing stage, all the samples in the target domain will be used as references and the corresponding reference-strengths are co-determined by the relation network and age distance. Our R²AE-dCCA was implemented on a developing children rs-fMRI dataset and compared with state-of-the-art methods. The superiority of our proposed R²AE-dCCA was validated not only on the overall accuracy but also on our proposed three new validation metrics dedicated for connectome prediction.

2. Method

2.1. Model description

The framework of our proposed model, reference-relation guided autoencoder with deep CCA restriction (R²AE-dCCA), is depicted in Fig. 1 and detailed below.

Fig. 1.

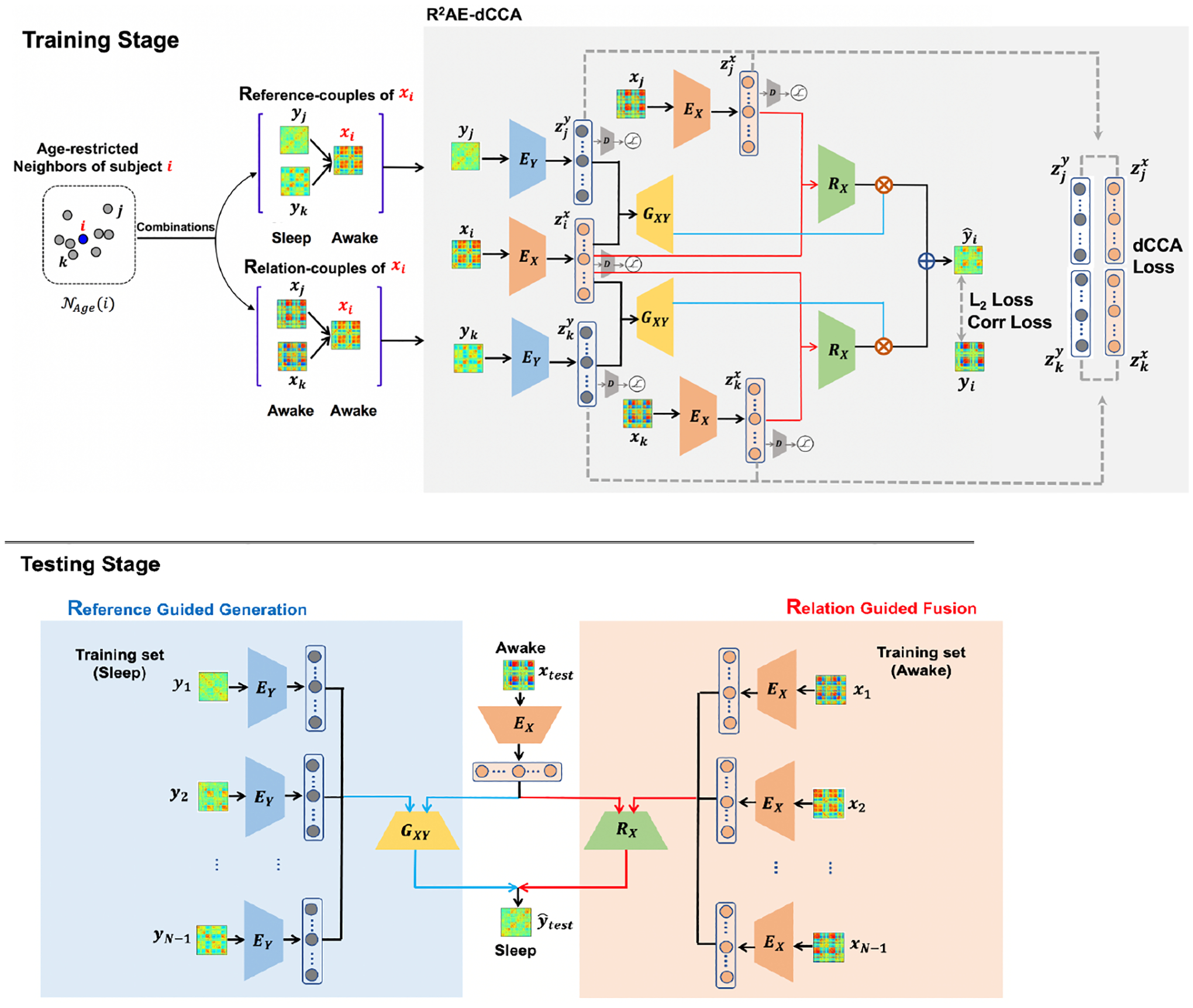
The framework of our proposed R²AE-dCCA model.

Our goal is to learn the mapping from the awake domain X to the sleep domain Y, f:X→Y, given paired samples {(x_i, y_i, Age_i)|x_i ∈ X, y_i ∈ Y}, where i =1, ⋯, N. N is the number of subjects, Age_i is the scan age of subject i, x_i and y_i are brain functional connectome represented by functional connectivity matrix and usually vectorized as the corresponding off-diagonal upper triangular elements for computation.

There are four main steps in training stage: (1) Reference-couples and relation-couples construction based on age-restricted neighborhood; (2) Reference guided target connectome generation; (3) Deep-CCA based source domain to target domain correlation; (4) Relation guided fusion.

Reference-couples and relation-couples construction.

For each connectome x_i in the awake domain, except for the paired y_i, other connectomes in the sleep domain Y could also provide rich information of how the brain connectivity patterns look like during sleep. Since the infant brain undergoes exceptionally dynamic development in both structure and function during early childhood [1–3, 28, 29], we only leverage the subjects within a neighboring age range to guide the learning of prediction. For a subject i, the age-restricted neighborhood of i is defined as ${\mathcal{N}}_{Age}(i)=\left\{j|\left|Ag{e}_i-Ag{e}_j\right|<\theta \right\}$, θ is the user-defined threshold and set as 30 days in our experiments. Then, the relation-couples and reference-couples are constructed as $\left\{\left(x_j,x_i,x_k\right)\mid x_i,x_j,x_k\in X,j,k\in {\mathcal{N}}_{Age}(i)\right\}$ and $\left\{\left(y_j,x_i,y_k\right)\mid x_i\in X,y_j,y_k\in Y,j,k\in {\mathcal{N}}_{Age}(i)\right\}$, respectively.

Encoding.

The inputs x_i, x_j, and x_k employ a multilayer perceptron neural network, denoted as E_X, as the encoder for the source domain to learn the individualized information, while y_j and y_k employ another multi-layer perceptron neural network, E_Y, as the encoder for the target domain to learn the domain-specific pattern. The outputs of the encoders are latent variables, which denoted as $z_i^x$, $z_j^x$, $z_k^x$, $z_j^y$, and $z_k^y$, respectively.

Reference guided target connectome generation.

In the latent space, $z_j^y$ and $z_k^y$ encoded from the target domain are leveraged as the reference information to guide the generation of the target connectome. Here a multi-layer perceptron neural network, denoted as G_XY, is employed for the generation with the inputs, which are the concatenations of the individualized information $z_i^x$ from the source domain and the sleep-specific information $\left(z_j^y,z_k^y\right)$ from the target domain. Thus, ${\widehat{y}}_{ij}=G_{XY}\left(\left[z_i^x;z_j^y\right]\right)$ and ${\widehat{y}}_{ik}=G_{XY}\left(\left[z_i^x;z_k^y\right]\right)$ are the predicted sleep connectome corresponding to x_i based on the reference of y_i and y_k, respectively. Together with the encoding process, a reference autoencoder (RAE) is designed.

Relation guided fusion.

Since more than one ${\widehat{y}}_{i*}$ are obtained from the multiple reference couples and the RAE, a relation network is further designed to guide the fusion. Specifically, according to the relation-couples, a multi-layer perceptron neural network, denoted as R_X, is embedded into RAE and employed to learn the reference-strength that y_j and y_k should contribute to the prediction of y_i. That is, based on the latent variables $z_i^x$, $z_j^x$, and $z_k^x$,

$${\widehat{y}}_i=\frac{e^{R_X\left(z_i^x,z_j^x\right)}\cdot {\widehat{y}}_{ij}}{e^{R_X\left(z_i^x,z_j^x\right)}+e^{R_X\left(z_i^x,z_k^x\right)}}+\frac{e^{R_X\left(z_i^x,z_k^x\right)}\cdot {\widehat{y}}_{ik}}{e^{R_X\left(z_i^x,z_j^x\right)}+e^{R_X\left(z_i^x,z_k^x\right)}}$$ (1)

Deep-CCA based source domain to target domain correlation.

From Equation (1), ${\widehat{y}}_i$ is estimated based on the assumption that the similarity relationship in the source domain maintains in the target domain. Therefore, the correlation between the learned embedding of the source domain and the target domain should be maximized during the training, thus ensuring the effectiveness of the fusion by preserving the neighboring relationship cross domains. Suppose $z_j^x,z_k^x,z_j^y,z_k^y\in {ℝ}^{l\times s}$, l is the dimension of the latent space, s is the batch size of training, $Z_x=\left[z_j^x,z_k^x\right]$ and $Z_y=\left[z_j^y,z_k^y\right]$ are the column-wise concatenation of $\left(z_j^x,z_k^x\right)$ and $\left(z_j^y,z_k^y\right)$, respectively. Let ${\overline{Z}}_x=Z_x-\frac{1}{2s}{Z}_{x}1$ and ${\overline{Z}}_y=Z_y-\frac{1}{2s}{Z}_{y}1$ be the centered matrix, 1 is an all-1s matrix, and ${\widehat{\Sigma }}_{xy}=\frac{1}{2s-1}{\overline{Z}}_x{\overline{Z}}_y^{\prime }$, ${\widehat{\Sigma }}_{xx}=\frac{1}{2s-1}{\overline{Z}}_x{\overline{Z}}_x^{\prime }+{\delta }_{1}I$, ${\widehat{\Sigma }}_{yy}=\frac{1}{2s-1}{\overline{Z}}_y{\overline{Z}}_y^{\prime }+{\delta }_{2}I$, δ₁, δ₂ > 0 are constants to ensure ${\widehat{\Sigma }}_{xx}$ and ${\widehat{\Sigma }}_{yy}$ to be positive definite. As for the classical CCA, the total correlation of the top m components of Z_x and Z_y is the sum of the top m singular values of the matrix $T={\widehat{\Sigma }}_{xx}^{-1/2}{\widehat{\Sigma }}_{xy}{\widehat{\Sigma }}_{yy}^{-1/2}$. In our case, m is set as l, then the correlation of Z_x and Z_y is the matrix trace norm of T, i.e.,

$${\mathcal{L}}_{\mathit{\text{dCCA}}}=\mathit{\text{corr}}\left(Z_x,Z_y\right)=\parallel T{\parallel }_{tr}=tr{\left(T^{\prime }T\right)}^{1/2}$$ (2)

Taking ${\mathcal{L}}_{\mathit{\text{dCCA}}}$ as one term of the loss function, the embeddings of the source domain and target domain are required to be maximally correlated.

Adversarial loss.

To enforce the stability of the training, a distribution regularization is imposed to the latent space and realized by a shared discriminator D [12]. Let p(z) be the prior distribution imposing on the latent variable z, q(z|x) be the encoding distribution. Training the autoencoder with distribution regularization requires the aggregated posterior distribution $q(z)={\int }_{x_i}q(z\mid x)p_d(x)\text{d}x$ matching the predefined prior p(z), where p_d(x) is the distribution of the input data. Here, this regularization is realized by an adversarial procedure, which leads to a ${\text{min}}_E{\text{max}}_D{\mathcal{L}}_{adv}$ problem, where

$${\mathcal{L}}_{adv}={\mathcal{L}}_{ad{v}_{-}{E}_X}+{\mathcal{L}}_{ad{v}_{-}{E}_Y}$$ (3)

$${\mathcal{L}}_{ad{v}_{-}{E}_X}={\sum }_{x=x_i,x_j,x_k}{\mathbb{E}}_x\text{log}\left(1-D\left(E_X(x)\right)\right)+{\mathbb{E}}_z\text{\hspace{0.17em}log}(D(z))$$ (4)

$${\mathcal{L}}_{ad{v}_{-}{E}_Y}={\sum }_{y=y_j,y_k}{\mathbb{E}}_y\text{log}\left(1-D\left(E_Y(y)\right)\right)+{\mathbb{E}}_z\text{\hspace{0.17em}log}(D(z))$$ (5)

Target connectome prediction loss.

L² norm and Pearson’s correlation are adopted as our generation loss for the target connectome prediction:

$${\mathcal{L}}_{\mathit{\text{element}}}={\mathbb{E}}_{x_i}{\Vert y_i-{\widehat{y}}_i\Vert }_2^2$$ (6)

$${\mathcal{L}}_{\mathit{\text{corr}}}={\mathbb{E}}_{x_i}\text{corr}\left(y_i,{\widehat{y}}_i\right)$$ (7)

Full objective.

The objective functions to optimize E_X, E_Y, G_XY, and D are written as:

$${\mathcal{L}}_D={\mathcal{L}}_{adv}$$ (8)

$${\mathcal{L}}_{E_X,E_Y,G_{XY}}=-{\lambda }_1{\mathcal{L}}_{\mathit{\text{corr}}}+{\lambda }_2{\mathcal{L}}_{\mathit{\text{element}}}+{\lambda }_3{\mathcal{L}}_{ad{v}_{-}E}-{\mathcal{L}}_{\mathit{\text{dCCA}}}$$ (9)

where ${\mathcal{L}}_{ad{v}_{-}E}={\mathbb{E}}_x\text{log\hspace{0.17em}}\left(1-D\left(E_X(x)\right)\right)+{\mathbb{E}}_y\text{log\hspace{0.17em}}\left(1-D\left(E_Y(y)\right)\right)$, λ₁, λ₂, and λ₃ are trade off parameters. The model alternatively updates E_X, E_Y, G_XY, and D with ${\mathcal{L}}_{E_X,E_Y,G_{XY}}$ and ${\mathcal{L}}_D$.

Testing stage.

For each x_test, with the age of refence connectome being considered into the relation guided fusion, all the connectome y_Tr in the training set are used as reference to avoid the lack of variability. With RAE obtaining corresponding sleep connectome ${\widehat{y}}_{\mathit{\text{test}},Tr}$ and relation network providing the reference-strength of each reference, the final prediction of y_test is estimated as

$${\widehat{y}}_{\mathit{\text{test}}}={\sum }_{y_{Tr}}\sigma \left(W_{y_{Tr}}\cdot R_X\left(E_X\left(x_{\mathit{\text{test}}}\right),E_X\left(x_{Tr}\right)\right)\right)\cdot G_{XY}\left(\left[E_X\left(x_{\mathit{\text{test}}}\right),E_Y\left(y_{Tr}\right)\right]\right)$$ (10)

where $W_{y_{Tr}}=e^{-\left|Ag{e}_{\mathit{\text{test}}}-Ag{e}_{y_{Tr}}\right|}$, $\sigma (*)=\frac{\text{exp}(*)}{{\sum }_{y_{Tr}}\text{exp}(*)}$ is the Softmax function, (x_Tr, y_Tr) is the paired connectomes obtained during sleep and being awake of the same subject.

2.2. Validation of functional connectome prediction

Although Pearson’s correlation coefficient (r) and mean absolute error (MAE) are usually taken as the evaluation metrics, they are general measures without any characteristics of specific applications. Taking the practical requirement of functional connectome prediction into consideration, we propose three new metrics dedicated for the validation of functional connectome prediction, i.e., correlation of top percentile connections (Corr_percl), normalized variation of information (VIn), and normalized mutual information (MIn) of the induced modular structure.

Correlation of top percentile connections (Corr_percl).

For a functional connectome, the connections with top percentile of strength are usually the focus of functional graph or network construction [13, 14]. Thus, Corr_percl is the Pearson’s correlation coefficient merely counted within the connections with top percentile of strength, i.e.,

$${\text{Corr}}_{\text{percl}}=\mathit{\text{corr}}\left(y^{\text{percl }},{\widehat{y}}^{\text{percl }}\right)$$ (11)

where y^percl and ${\widehat{y}}^{\text{percl }}$ are consisting of connections with top percentile of strength in the expected connectome y. The percentile was set as 95% in our experiments.

Normalized variation of information (VIn) and mutual information (MIn).

The modular structure based on graph theory is one of the most important analyses for functional brain networks [15, 16]. Here we introduce the capability of maintaining the modular structure of the expected connectome y as one metric to validate the predicted connectome. Let A = {a₁, a₂, ⋯, a_c} and b = {b₁, b₂, ⋯, b_c} be the modular partition induced by y and $\widehat{y}$, respectively. The VIn and MIn [17] between A and B are defined as follow:

$$\text{VIn}(A,B)=-\frac{1}{\text{log}\mathbb{N}}\sum _{t_1,t_2=1,\dots ,c}\frac{\left|a_{t_1}\cap b_{t_2}\right|}{\mathbb{N}}\left(\text{log}\frac{\left|a_{t_1}\cap b_{t_2}\right|}{\left|a_{t_1}\right|}+\text{log}\frac{\left|a_{t_1}\cap b_{t_2}\right|}{\left|b_{t_2}\right|}\right)$$ (12)

$$\text{MIn}(A,B)=1+\frac{\text{VIn}(A,B)\cdot \text{log}\mathbb{N}}{{\sum }_{t_1}\frac{\left|a_{t_1}\right|}{\mathbb{N}}log\frac{\left|a_{t_1}\right|}{\mathbb{N}}+{\sum }_{t_2}\frac{\left|b_{t_2}\right|}{\mathbb{N}}log\frac{\left|b_{t_2}\right|}{\mathbb{N}}}$$ (13)

where $\mathbb{N}$ is the number of connections in y_i, and | · | in Equations (12) and (13) represents the numbers of connections in the module. In our experiments, A and B are obtained by finding the modular structure with the maximal between-class and within-class ratio within 100 repetition of k-means clustering [18]. The number of clusters is set as 10.

3. Experiments

3.1. Data description

We verified the effectiveness of the proposed R²AE-dCCA model on a high-resolution resting-state fMRI (rs-fMRI) data including 20 paired sleep and awake scans in the UNC/UMN Baby Connectome Project [6]. All paired rs-fMRI data were acquired during natural sleeping and video watching on a 3T Siemens Prisma MRI scanner using a 32-channel head coil. T1-weighted and T2-weighted MR images were obtained with the resolution = 0.8×0.8×0.8 mm³. The rs-fMRIs scans were acquired with TR/TE = 800/37 ms, FA = 80°, FOV = 220 mm, resolution = 2×2×2 mm³, and total volumes = 420 (5 min 47 sec). All structural and functional MR images were preprocessed by a state-of-the-art infant-tailored in-house pipeline [23–27]. Each rs-fMRI was finally parcellated based on the automated anatomical labeling template [19], thus obtaining 116 anatomical regions. The average time series within each ROI was correlated with those from all others. The functional connectivity matrix was derived by calculating the Pearson’s correlation coefficient between time series of each pair of ROIs. Fishers r-to-z transformation was conducted to improve the normality of the functional connectivity.

3.2. Validation of R²AE-dCCA

With the metrics of MAE, r, Corr_percl, VIn, and MIn, we compared the proposed R²AE-dCCA model by leave-one-out cross-validation with the following five methods: (1) Connectome prediction with linear model (GLM) [20]; (2) Multi-kernel manifold learning (MKML) [21]; (3) CCA-based MKML (CCA-TSW)[10]; (4) Pixel2Pixel GAN [22]; (5) R²AE-dCCA without relation network (R²AE-dCCA no R-Net);

In R²AE-dCCA, the encoder E_X and E_Y constitute of 3 densely connected layers of dimension (50, 50, 100) with (LeakyReLU, Sigmoid, Linear) as the corresponding activation function. G_XY constitutes of 4 densely connected layers of dimension (30, 30, 30, 30) with LeakyReLU as the activation function. The discriminator D constitutes of 4 densely connected layers of dimension (50, 50, 25, 1) with LeakyReLU as the activation function of the first 3 layers and Sigmoid as the activation function of the last layer. R²AE-dCCA was implemented with Pytorch and optimized with Adamax by a fixed learning rate as 0.001. The batch size was set as 400. λ₁ = 0.1, λ₂ = 0.8, and λ₃ = 0.1. Methods (4) and (5) share the similar architecture with R²AE-dCCA for the fairness of the comparison. The means and standard deviations of the leave-one-out cross-validation are reported in Table 1. Our method achieves lowest MAE, VIn, highest r, Corr_percl, and MIn among all comparison methods, indicating the superior performance of our method. Fig. 2 shows the scatter plots of the expected and predicted connection strength on a representative subject. It can be seen that our method achieved better prediction especially for the connections with strength greater than 1, i.e., the top percentile connections. Fig. 3 shows how the predicted connectome maintains the obtained modular structures induced from the expected functional connectome of a representative subject. In Fig. 3, the order of the brain regions are the same in the subfigures, while the values are the corresponding predicted connection strengthes based on different methods. The results obtained by our method shows higher similarity with the groud truth. In summary, our R²AE-dCCA model outperformed the other five state-of-the-art methods not only on overall prediction accuracy but also on maintaining the modular structure.

Table 1.

The comparison of R²AE-dCCA with other five methods.

Methods╲Metrics	Conventional		Connectome Specific
	MAE	r	Corrpercl	VIn	MIn
GLM [20]	.272 ± .040	.304 ± .086	.302 ± .090	.553 ± .055	.213 ± .072
MKML [21]	.257 ± .046	.534 ± .081	.542 ± .079	.460 ± .044	.338 ± .066
CCA-TSW [10]	.247 ± .048	.549 ± .083	.546 ± .056	.451 ± .057	.349 ± .085
Pixel2Pixel GAN [22]	.316 ± .088	.426 ± .076	.212 ± .093	.448 ± .051	.330 ± .070
R2AE-dCCA no R-Net	.239 ± .050	.592 ± .089	.568 ± .095	.442 ± .056	.365 ± .066
R2AE-dCCA (proposed)	.227 ± .050	.614 ± .084	.583 ± .010	.427 ± 0.51	.379 ± .062

Fig. 2.

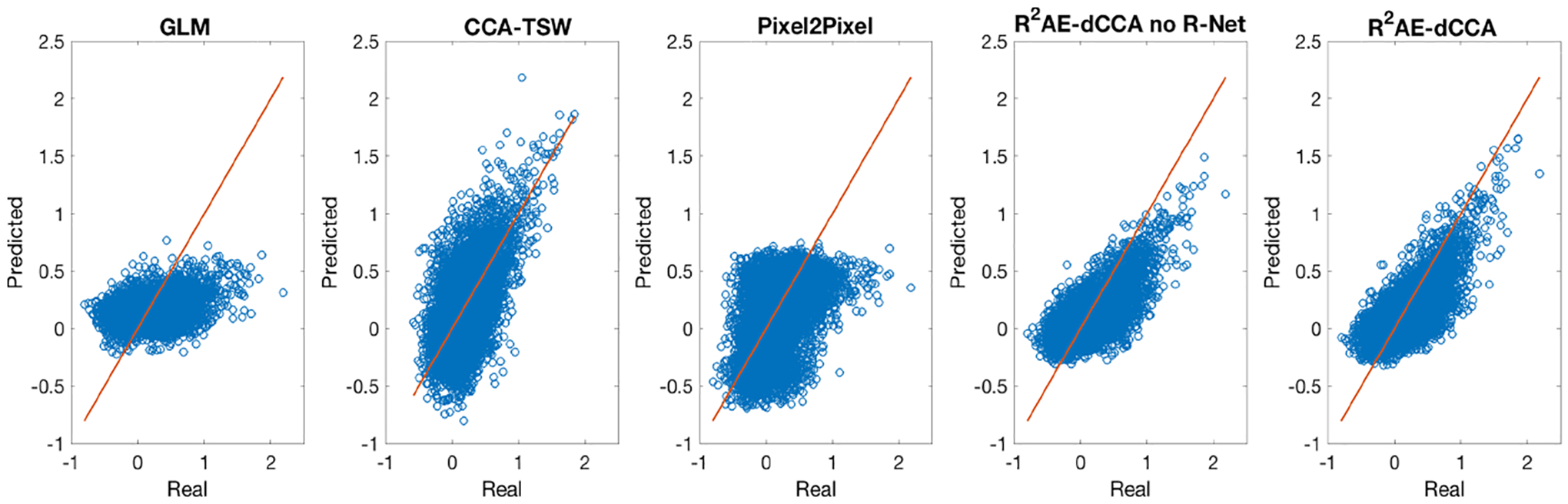
The scatter plots of our proposed R²AE-dCCA model in comparison with GLM, CCA-TSW, Pixel2Pixel, and R²AE-dCCA no R-Net in terms of connection strength.

Fig. 3.

Comparison of modular structures obtained by different methods.

4. Conclusion

In this paper, to fill the gap of awake-to-sleep connectome prediction for longitudinal study of early brain functional development, we proposed a reference-relation guided autoencoder with deep CCA restriction (R²AE-dCCA). With the framework of reference guided generation and relation guided fusion, R²AE-dCCA reaches the superior prediction accuracy by effectively augmenting the severely limited data, utilizing the domain specific pattern from the target domain, and maintaining neighboring relationship from the source domain. As a generalized model for connectome translation, our model and the proposed connectome-dedicated validation metrics have high potential in other connectome prediction related fields.