Membrane tension propagation couples axon growth and collateral branching

Abstract

Neuronal axons must navigate a mechanically heterogeneous environment to reach their targets, but the biophysical mechanisms coupling mechanosensation, growth, and branching are not fully understood. Here, we show that local changes in membrane tension propagate along axons at approximately 20 μm/s, more than 1000-fold faster than in most other nonmotile cells where this property has been measured. Local perturbations to tension decay along the axon with a length constant of approximately 41 μm. This rapid and long-range mechanical signaling mediates bidirectional competition between axonal branch initiation and growth cone extension. Our data suggest a mechanism by which mechanical cues at one part of a growing axon can affect growth dynamics remotely.

Membrane tension in axons drives competition between extension of the growth cone and nucleation of collateral branches.

INTRODUCTION

Mechanical forces play an important role in modulating axon growth and branching (1, 2). An intriguing aspect of axon guidance is the presence of long-range coordination between growth of different axon branches and apparent competition between elongation versus branching (3). In cultured rat hippocampal neurons, growth rates of distinct axonal branches are anticorrelated (4). In cultured locust neurons, anchoring of individual branches caused retraction of neighboring unanchored branches (5). The signals coordinating these dynamics across long distances have not been identified. We explored whether plasma membrane tension could be such a signal.

For membrane tension to mediate long-range coordination of axon growth and branching, tension must satisfy two criteria. First, changes in membrane tension induced by local mechanical perturbations must propagate to distal parts of the growing axon. Second, the membrane tension must then modulate the local growth or branching rate. We briefly review the literature around each of these criteria.

Experiments on tension propagation in cells have yielded hugely diverse outcomes. In a comparison of tether-pulling experiments on different cell types, Brochard-Wyart and co-workers inferred that flow resistances varied by at least a factor of 10⁴ (6), while theoretical estimates have varied by as much as 10⁶ (7). We recently measured plasma membrane tension propagation in several nonmotile mammalian cell types and found that local perturbations to tension remained localized for many minutes and that the membrane tension could be highly heterogeneous within a single cell (8). This absence of tension propagation was attributed to the flow resistance of membrane-cortex attachments (MCAs). Because of the long-range influence of obstacles on two-dimensional flows, a cell membrane punctuated by a high density of MCAs was shown to behave rheologically more like a gel than a fluid (7, 9, 10).

On the other hand, substantial evidence has accumulated that tension propagation in axonal membranes can be qualitatively different from our measurements in other cell types. Dai and Sheetz (11) showed that in chick dorsal root ganglion (DRG) axons, membrane flowed from the growth cone toward the soma, driven by a gradient in membrane tension. Tethers pulled from the middle of an axon-induced membrane flows along the axon, primarily from the direction of the growth cone (11, 12). Gomis Perez et al. (13) recently performed dual-tether measurements on goldfish retinal bipolar neuron presynaptic terminals, a specialized secretory structure, and observed rapid coupling of tension over distances up to 11 μm within the terminal and rapid, but substantially less efficient, propagation of changes in tension over distances up to 17 μm within the soma and between the nerve terminal and the axon.

In both chick DRG and goldfish retinal bipolar neurons, the viscoelastic properties of the membrane were profoundly sensitive to perturbations to the underlying actin cytoskeleton, showing that resistance to membrane flow is dominated by membrane-cytoskeleton interactions (which could comprise specific MCAs or other transient or nonspecific interactions) (12–14). The peak force to nucleate a tether was recently reported to be ~2-fold lower in Xenopus retinal ganglion cell axons than in fibroblasts (15), and tracer diffusion studies reported a ~2-fold difference in diffusion coefficient between chromaffin cells and goldfish retinal bipolar neuron axon terminals (13). Together, these results suggest a modestly lower density of MCAs in axons compared to other cells. It has not been clear how to reconcile these modest differences in MCA density with the dramatic differences in membrane flow between axons and other plasma membrane structures.

Membrane flow depends not only on the density of MCA obstacles but also on their arrangement. Tether-sliding assays provide a rough measure of the spacing between MCA obstacles: A membrane tether’s attachment point on a cell can only move freely if the spacing between obstacles exceeds the tether diameter (typically 50 to 100 nm) (16). Facile tether sliding has been reported in chick sensory neuron axons (17) and in goldfish retinal bipolar neuron presynaptic terminals (13). In contrast, for tethers pulled on HeLa cells (17), neutrophils (18), endocrine chromaffin cells (13), fibroblasts, epithelial cells, and endothelial cells (8), the attachment point remains largely pinned, implying a much smaller MCA spacing than on axons.

Given the unusual properties of tension propagation in axons, one might expect this property to play a role in axonal biology. In mouse hippocampal axons, local tension propagation has been proposed to mediate ultrafast coupling of vesicle fusion and nearby vesicle endocytosis (19). In goldfish retinal bipolar neurons, synaptic vesicle cycling can cause global changes in membrane tension, and this mechanism was proposed as a means of coupling exocytosis and endocytosis over distances up to ~10 μm (13). Several lines of evidence further suggest that membrane tension could also play a role, at least locally, in axon growth dynamics. The mechanical pushing force of the growth cone is closely balanced with the local membrane tension, both having values of order 10 pN/μm (20), and very small forces (<10 pN) exerted by magnetic nanoparticles can speed axon growth (21). Membrane addition at the growth cone is essential for growth, and blocking membrane addition at the growth cone stops elongation (22, 23). Membrane tension also appears to play a role in inhibiting collateral branch nucleation. Overcoming the tension barrier by mechanically pulling a lateral membrane tether from an axon can nucleate growth of new functional axonal branches (24). The combination of rapid tension propagation in axons and sensitivity of axonal growth to membrane tension motivated our hypothesis that tension propagation could couple nucleation and growth of distinct axonal branches.

Here, we quantify the time-dependent propagation of tension changes in axons of rat hippocampal neurons. We then compare tracer diffusion and tether sliding on axons versus on dendrites. We propose a model of the axon membrane in which MCA obstacles are in clusters spaced by ~180 nm. This model provides a parsimonious explanation for our disparate transport measurements (tension propagation, tracer diffusion, and tether sliding) as well as for previously published results on axon membrane rheology. Last, we study how perturbations to tension at the growth cone or along the axon shaft affect branching and growth dynamics at locations up to ~100 μm from the site of perturbation.

RESULTS

Membrane tension propagates along the axon but not dendrites

We used membrane tethers to both perturb and measure membrane tension in axons of cultured rat hippocampal neurons. We expressed cytosolic enhanced green fluorescent protein (eGFP) and used the fluorescence density of the tether (fluorescence per unit length; Materials and Methods) as a proxy for the tether’s cross-sectional area. Tether area is inversely proportional to local membrane tension and inversely proportional to the square of the tether-pulling force (25). To validate this approach, we pulled tethers from axons with optical tweezers and verified the expected relation between tether fluorescence and pulling force (fig. S1). Subsequent measurements used tether fluorescence rather than force because of the greater ease of pulling tethers from axons using micromanipulators instead of optical tweezers.

Using two micromanipulators, we pulled a pair of tethers from a single axon in a neuron expressing cytosolic eGFP (Fig. 1A and movie S1; Materials and Methods). We then dynamically stretched tether 1 and monitored the fluorescence in both tethers (Fig. 1B). Stretching tether 1 led to a clear response in tether 2, 40 μm away (Fig. 1C). This observation established that membrane tension propagated along the axon. We quantified the strength of the coupling as a function of distance between the tethers by measuring the ratio of the fluorescence changes in tether 2 to the changes in tether 1 for many tether pairs (n = 10 tether pairs, 10 neurons). The tension coupling was nearly perfect when the tethers were within 5 μm and decayed with a length constant of 41 ± 7 μm (Fig. 1E).

Fig. 1. Membrane tension propagates in axons but not in dendrites.

(A) Double tether experiment to probe tension propagation in an axon. (B) Two tethers, 40 μm apart, were pulled from an axon in a neuron expressing cytosolic eGFP. White boxes indicate regions used to analyze tether brightness and dashed boxes were used for background correction. Scale bar, 10 μm. (C) Length (top) and fluorescence (bottom) of tether 1 (red) and tether 2 (blue) as tether 1 was stretched. (D) Fluorescence of tether 2 as a function of fluorescence in tether 1. The fluorescence of tether 2 was time-shifted by 2 s to account for the tension propagation delay. Dashed and solid lines represent idealized responses for perfect tension coupling and zero coupling, respectively. (E) Ratio of fluorescence response in tether 2 to fluorescence response in tether 1 as a function of the separation between the tethers (n = 10 tethers, 10 neurons). Line is a fit to an exponential decay with length constant 41 ± 7 μm (95% confidence interval). (F) Double tether experiment to probe tension propagation on a proximal dendrite. (G) Two tethers, 12 μm apart, were pulled from a dendrite in a neuron expressing cytosolic eGFP. Scale bar, 10 μm. (H) Length (top) and fluorescence (bottom) of tether 1 (red) and tether 2 (blue) as tether 1 was stretched. (I) Fluorescence of tether 2 as a function of fluorescence in tether 1. Dashed and solid lines represent idealized responses for perfect tension coupling and zero coupling, respectively. Data are representative of experiments on n = 12 neurons.

In contrast, no tension propagation was observed between two tethers pulled from proximal dendrites even when the tethers were less than 20 μm apart (Fig. 1, F to I, and movie S2). In separate experiments, we expressed a membrane label, glycosylphosphatidylinositol (GPI)–eGFP, and an actin tag, mCherry-UtrCH (26), and did not observe any actin polymerization within the tethers pulled from dendrites (fig. S2 and Materials and Methods). In cases where tethers broke, the piece of tether attached to cells retracted in about 1 min. Together, these observations confirm that the tethers in dendrites were not stabilized by internal cytoskeletal elements. The absence of tension propagation between tethers pulled from dendrites is consistent with our earlier observations of no coupling of tension between tethers in HeLa cells, and also lack of tension propagation in many other nonmotile mammalian cells (8).

Axon pearls report membrane tension propagation speed

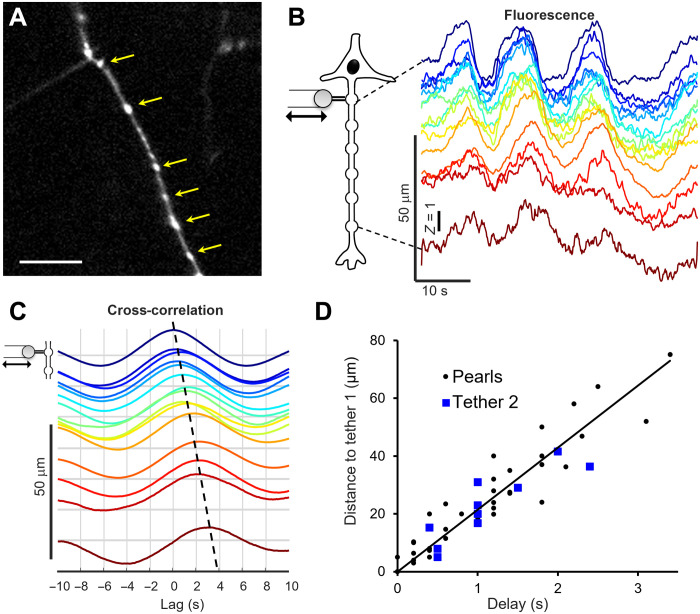
We found that tether-induced increases in local membrane tension could induce a pearling instability in the axon (Fig. 2 and movie S3), similar to the pearling instability previously observed in axons under osmotic shock (27) and in synthetic membrane tubes under high membrane tension (28, 29). The pearling was reversible, disappearing when the tension was relaxed.

Fig. 2. Membrane tension propagation triggers reversible pearling along the axon.

(A) Image of an axon expressing cytosolic eGFP, where pulling a tether induced pearls (yellow arrows). Scale bar, 10 μm. (B) Time-dependent fluorescence of the pearls as the tether was alternately stretched and relaxed. Here, each fluorescence trace has been Z-scaled (mean subtracted and divided by SD; thus, Z = 1 corresponds to 1 SD). The dark blue trace was recorded at the tether attachment point; the vertical offsets of the other traces correspond to their distance from the tether attachment point. (C) Cross-correlation between fluorescence of the pearl at the tether attachment point and of all other pearls. The vertical offset of the curves indicates the distance between each pearl and the tether attachment point. The time of the peak near zero delay gives the time delay of each pearl. The curves have all been scaled to have the same amplitude. (D) Delay for response of each pearl (black) or of a second tether (blue) as a function of distance to tether 1. A linear fit to the pearl data gives a velocity of 20.1 μm/s, R² = 0.9.

Compared to the dual-tether assay, the pearling transition was a more convenient means to monitor tension propagation because pearling reported the tension dynamics all along the axon as opposed to at a single probe point. We alternately stretched and relaxed single tethers at a pulling speed of approximately 5 μm/s and monitored the amplitude of the pearling as a function of distance and time (Fig. 2B). The pearling response lagged behind the tether stretch with a delay that increased with distance from the tether (Fig. 2C and Materials and Methods). The relation between time lag and pearl distance gave a propagation speed of membrane tension of 22 ± 6 μm/s (means ± SD, n = 31 tethers, 30 neurons; Fig. 2D).

We validated this estimate of tension propagation speed using pairs of tethers pulled at a few discrete separations. The fluorescence of tether 2 responded to stretch of tether 1 with a lag that increased as a function of the separation, giving a similar tension propagation velocity to the pearl measurements (Fig. 2D).

Tension propagation does not depend on calcium signaling

High mechanical stress at the growth cone has been shown to activate mechanosensitive ion channels, leading to a calcium influx that led to axonal retraction (30). We thus hypothesized that rapid diffusion of Ca²⁺ within the lumen of the axon might mediate changes in tension that followed the local Ca²⁺ dynamics.

We expressed an axon-targeted variant of the genetically encoded calcium indicator GCaMP6s in cultured rat hippocampal neurons (31). Breaking the axon led to a large increase in fluorescence, confirming proper expression and function of the Ca²⁺ indicator (fig. S3). However, we did not observe any Ca²⁺ signal during tether pulling. Even when tethers were pulled enough to elicit pearling, there was no observable Ca²⁺ signal (fig. S3). These findings indicate that membrane tension propagation could occur without Ca²⁺ influx.

Clustering of MCAs can explain axon membrane rheology

Hydrodynamic models of membrane flow have shown that tension propagation is impeded by immobile MCAs (7, 8, 32–35). We used transport measurements to probe the MCA distribution in the axon. Three aspects of the MCA distribution contribute to flow resistance: (i) the area fraction, ϕ, occupied by the MCAs; (ii) the characteristic radius, a, of the MCAs; and (iii) the geometrical arrangement of the MCAs, i.e., how they are distributed spatially in the membrane. Specifying ϕ and a also sets the mean spacing between MCAs.

If a membrane is subjected to a linear gradient in tension, ∇σ, then, the membrane will flow at a velocity

$$\mathbf{v}=-\frac{k}{\mathrm{\eta }}\nabla \mathrm{\sigma }$$ (1)

where η is the intrinsic bilayer viscosity (typically 0.001 to 0.01 pN s/μm) (36, 37) and k is the Darcy permeability of the network of MCAs or other obstacles to flow (the quantity $\frac{\mathrm{\eta }}{k}$ is the membrane drag coefficient). Dimensional analysis shows that

$$k=a^{2}f(\mathrm{\varphi })$$ (2)

where a is the radius of the immobile obstacles and f(ϕ) is a dimensionless function of their area fraction, ϕ, and possibly their geometrical arrangement. If each MCA contributed a fixed amount of drag irrespective of the presence of other MCAs, then f(ϕ) would scale as 1/ϕ. However, because of long-range hydrodynamic coupling between MCAs, the function f(ϕ) has more complex dependence on ϕ. For randomly distributed obstacles, f(ϕ) is approximately given by (7, 38)

$$f(\mathrm{\varphi })\approx -\frac{[1+\text{ln}(\mathrm{\varphi })]}{8\mathrm{\varphi }}$$ (3)

Diffusion of tracer particles is also impeded by MCA obstacles (7, 32); thus, we sought to use measurements of tracer diffusion to infer the relative values of ϕ in the axon and dendrites. We performed fluorescence recovery after photobleaching experiments on rat hippocampal neurons expressing GPI-anchored eGFP (fig. S4). In paired measurements on dendrites and axons of the same cells, we observed that the diffusion coefficient in the axons was 1.5-fold higher than on the dendrites (D_axon = 0.29 ± 0.05 μm²/s, D_dendrite = 0.19 ± 0.05 μm²/s, means ± SEM, n = 8 cells, P = 0.018, paired t test). This result is consistent with a recent finding from Gomis Perez et al. (13), who reported a 1.7-fold difference in tracer diffusion between retinal bipolar neuron axons and soma.

The modestly faster tracer diffusion on axons indicates fewer obstacles in the axonal membrane (39). At low ϕ, the tracer diffusion coefficient, D_T scales as $D_T\propto \text{ln}\frac{1}{\mathrm{\varphi }}$, assuming that the tracer and the MCAs have a similar size. Tracer diffusion is much less sensitive to MCA density than is Darcy permeability (which scales as $k\propto \frac{1}{\mathrm{\varphi }}\text{ln}\frac{1}{\mathrm{\varphi }}$ for small ϕ); thus, small changes in tracer diffusion could correspond to big changes in Darcy permeability. For example, if a membrane has MCAs at an area fraction of ϕ₁ = 0.15 and a tracer diffusion coefficient D₁, and another membrane has tracer diffusion coefficient D₂ = 2 D₁, then the obstacle density in the other membrane is ${\mathrm{\varphi }}_2={\mathrm{\varphi }}_1^{D_2/D_1}=0.023$, and the Darcy permeability in the second membrane is $k_2=k_1\frac{D_2}{D_1}{\mathrm{\varphi }}_1^{1-D_2/D_1}=13.3 k_1$ (Supplementary Calculation, table S1) (7, 32). Such a difference in flow resistance is substantial but not big enough to account for the >1,000-fold difference in membrane flow resistance between, e.g., HeLa cells and axons.

Next, we asked whether arrangement of the MCAs could account for the unusual fluidity of axon membranes. Our previous models of tension propagation assumed a random array of MCA obstacles (7, 8). Would periodicity of MCAs in axons affect resistance to membrane flow? Sangani and Acrivos (40) analyzed viscous two-dimensional flows past periodic arrays of obstacles. We compared their solutions to predictions of various models of flow past random arrays of obstacles that we analyzed previously (7). For both square and hexagonal lattices, at MCA area fractions ϕ < 0.3, the dimensionless Darcy permeability k/a² for periodic obstacles differed by <40% from any of the models of random obstacle arrangements that accounted for hydrodynamic coupling (fig. S5). Thus, periodicity per se does not explain the dramatic difference in membrane flow between axons and other cell types. Furthermore, rheological measurements provide no information on whether the MCAs are in a regular array or randomly dispersed. Last, we examined the effect of clustering of MCAs. Clustering into compact islands effectively increases a (where a now represents the radius of the island), without changing ϕ. Since k = a²f(ϕ), clustering can dramatically increase the Darcy permeability without substantially affecting tracer diffusion. Specifically, if MCAs of radius a₁ and Darcy permeability k₁ are clustered in groups of N, the radius of each cluster is approximately a_N = N^1/2a₁, and the Darcy permeability becomes k_N = Nk₁.

The relatively modest differences in tracer diffusion between axon and dendrites suggested that the primary difference between these structures was in MCA clustering. This hypothesis was supported by measurements of tether sliding. We pulled short tethers from axons and then translated the pipette parallel to the axon axis (Materials and Methods). In 14 of 23 tethers, the tether slid along the axon until it was perpendicular to the axon axis, minimizing the tether length (fig. S4 and movie S4). Similar tether sliding has been observed in axons of chicken sensory neurons (17) and in axon terminals of goldfish retinal bipolar neurons (13). In contrast, tethers pulled from the soma remained pinned at their initial spots (fig. S4), and others reported tether pinning in neutrophils (18), HeLa cells (17), and adrenal chromaffin cells (13). This finding suggests that the spacing between MCAs in the axon exceeds the tether diameter (estimated to be 50 to 100 nm; Materials and Methods), whereas in most other nonmotile cells, the spacing between MCAs was estimated to be approximately 4 to 5 nm (7). MCA clustering provides a means to increase MCA spacing without affecting mean (i.e., averaged over a distance large compared to the cluster spacing) MCA density.

Membrane tension coordinates axon growth and branching

Growth and branching of the axon are required for the axon to navigate through the mechanically heterogeneous brain and form a properly connected network (2). Actin filaments push on the growth cone membrane to elongate the axon, and actin filaments deform the membrane on the axon shaft to initiate new branches. Could membrane tension play a role in coordinating the dynamics of growth and branching?

We hypothesized that a decrease in tension at the growth cone, triggered, for example, by a mechanical barrier that blocked growth cone extension, could propagate toward the soma along the axon and facilitate collateral branching. We used localized perfusion to lower tension at the growth cone and monitored upstream tension and branching.

First, in a neuron expressing cytosolic eGFP, we pulled a tether 75 μm upstream of the growth cone and locally perfused the growth cone with deoxycholate (500 μM; Materials and Methods), which has been shown to lower local membrane tension (41). Application of deoxycholate at the growth cone led to a 50% drop in membrane tension at the upstream tether (Fig. 3, A and B).

Fig. 3. Lowering membrane tension at the growth cone triggers upstream collateral branching.

(A) Composite image showing local perfusion of deoxycholate, traced by Alexa 647 (magenta) and the growth cone (green) in a neuron expressing cytosolic eGFP. White arrow, perfusion pipette. Yellow arrow, membrane tether for tension sensing. (B) Changes in tether fluorescence, inversely proportional to membrane tension (blue), in response to deoxycholate perfusion of the growth cone (magenta). (C) Fluorescence and transmitted-light image of a neuron, with a deoxycholate-loaded pipette next to the growth cone (arrow). (D) Perfusion of the growth cone with deoxycholate-triggered formation of a new branch (arrow) in a distant section of the axon. Inset, close-up view of the new branch. (E) Perfusion of deoxycholate (+SDC) at the growth cone increased the density of branches along the axon compared to before injection (−SDC). The same trend was observed close to (<50 μm) and far from (50 to 150 μm) the growth cone (n = 23 neurons). (F) Fluorescence image of an axon before perfusion with hypertonic buffer. Arrow indicates the perfusion pipette. (G) Hypertonic perfusion at the growth cone–triggered collateral branching (arrows) in distant sections of the axon. Insets show magnified views of the change in fluorescence (after − before perfusion) highlighting new branches. (H) Perfusion of hypertonic buffer (Hyper) at the growth cone increased the density of branches along the axon compared to before perfusion (Iso). The same trend was observed close to (<50 μm) and far from (50 to 150 μm) the growth cone (n = 8 neurons). P values calculated from two-tailed paired t-test after Kolmogorov-Smirnov test for normality. Data that did not pass the normality test were evaluated by the Wilcoxon rank-sum test. Scale bars, 10 μm.

Local perfusion of the growth cone with deoxycholate also triggered initiation of new axonal protrusions outside the perfused region in 12 of 23 neurons (Fig. 3, C and D, and fig. S6). The number density of protrusions along the axon significantly increased upon deoxycholate perfusion of the growth cone, with a similar effect on axon segments close to the growth cone (<50 μm, protrusion density from 19 ± 5 to 30 ± 6 mm⁻¹, means ± SD, P = 0.008) and far from the growth cone (50 to 150 μm, protrusion density from 8 ± 2 to 22 ± 4 mm⁻¹, P = 0.001) (Fig. 3E). Similar increases in protrusion density were observed when we perfused hypertonic buffer to the growth cone (+350 mM mannitol; Materials and Methods), which reduces membrane tension through osmosis (Fig. 3, F to H) (42). Perfusion with dye alone did not lead to any new protrusion formation in n = 15 neurons (fig. S6G). These experiments confirmed our hypothesis that lowering membrane tension at the growth cone increased formation of axon collateral protrusions upstream.

Next, we asked whether an increase in axonal membrane tension, such as might occur because of new branching events, could inhibit extension of the growth cone or of other branches. To address this question, we pulled tethers on the axon at distances 25 to 110 μm from the growth cone and monitored the motion of the growth cone and of other branches as we changed the length of the tether (Fig. 4A). The growth cone stalled and then slightly shrank during tether pulling and recovered after relaxing the tether (Fig. 4, B and C). Short protrusions near the growth cone also disappeared during the pulling period (Fig. 4B). On average, the growth cone shrank to 95.3 ± 1.3% of its original surface area during tether pulling and fully recovered (100.5 ± 1.3%) upon releasing the tether tension (means ± SEM, n = 14 neurons; Fig. 4D). When we pulled a tether 110 μm from the growth cone, a clear 6-s delay in the growth cone response was observed (fig. S7), consistent with our earlier measurements of membrane tension propagation speed ~20 μm/s. The density of protrusions along the axon also decreased during tether pulling, from 22 ± 3 to 11 ± 3 mm⁻¹ (means ± SD, P = 0.003). The density of protrusions partially recovered to 17 ± 3 mm⁻¹ within 1 min of releasing the tether (Fig. 4E).

Fig. 4. Increases of axonal membrane tension lead to retraction of growth cone and of collateral branches.

(A) Fluorescence and transmitted light image of a pipette holding a bead in contact with an axon expressing superecliptic pHluorin-neurexin (SEP-NXN). Blue box, growth cone. (B) Left, change in fluorescence after stretching the tether. Dark indicates a decrease in fluorescence; light represents an increase. Arrow points to the disappearance of one branch. Right, change in fluorescence after relaxing the tether. (C) Top, tether length. Time windows show before (T1), during (T2), and after (T3) stretching. Bottom, fluorescence of the tether (red) and the growth cone (blue). A.U., arbitrary units. (D) The growth cone shrank during tether pulling (n = 16 neurons) and regrew after tether relaxation (n = 14 neurons). (E) Number of branches on the axon decreased during tether pulling (n = 9 neurons) and partially recovered after tether relaxation (n = 7 neurons). In (E), only axons with existing branches were chosen for tether pulling. P values calculated from two-tailed paired t test after Kolmogorov-Smirnov test for normality [in (D), the test was done on growth cone areas instead of the normalized areas]. Scale bars, 10 μm.

DISCUSSION

Our experiments show that tension readily propagates along axons of rat hippocampal neurons, that changes in tension at the growth cone modulate the rate at which protrusions emerge from the parent axon, and that artificial induction of tethers along the axon can trigger growth cone stalling and slight retraction. Together, these results suggest that the growth cone and collateral branches compete for membrane area, and that perturbations to the growth of one branch can be conveyed by changes in membrane tension to modulate the growth of distal branches. Figure 5 summarizes these ideas in a speculative model of how tension propagation might function in axon branching and guidance.

Fig. 5. Model of membrane tension propagation in axons and its role in branching.

(A) Schematic representation showing how dispersed MCAs (blue circles) obstruct membrane flow (black arrows), while clustered MCAs create channels permitting membrane flow. This model provides a parsimonious explanation for the comparatively similar (<2-fold different) tracer diffusion coefficients and membrane-cortex adhesion energies of non-axons versus axons, and also the dramatic differences in tether sliding and membrane flow between non-axons and axons. Membrane rheology is almost indistinguishable between periodic and random obstacle arrangements (fig. S5); thus, the schematic representation of an ordered array overlaid on the membrane periodic cytoskeleton is speculative. (B) Hypothesized role of tension propagation in axon branching and growth. During rapid growth cone advancement, membrane tension suppresses branching. Obstacles or mechanical heterogeneities that impede growth cone progress are proposed to create a local imbalance between membrane addition and area expansion, leading to a propagating front of lower tension that enhances nucleation and growth of collaterals. As the collaterals grow, each broadcasts information about its progress to the others via long-range changes in membrane tension.

It is instructive to compare our results with previous measurements of membrane flow in axons. In a study on chick sensory axons, Dai and Sheetz (11) reported a spontaneous retrograde membrane flow with a typical speed of 7 μm/min. (This mass-flow rate is a physically distinct quantity from the tension propagation rate of 20 μm/s we measured here.) Dai and Sheetz ascribed the retrograde membrane flow to a tension differential between the soma and the growth cone of ~2.25 pN/μm. By combining the tension differential (2.25 pN/μm), the flow speed (7 μm/min), and the axon length [60 to 100 μm in (11)], one obtains a membrane drag coefficient of ~0.24 pN s/μm³ along the axon. In comparison, the drag coefficient in HeLa cells was reported to be ~1670 pN s/μm³ (7), a difference of almost 10⁴. Brochard-Wyart and co-workers collated data on the relation between tether-pulling speed and tether force in multiple cell types and also inferred that the membrane flow resistance in neurons was ~10²-fold lower than in neutrophils, ~10³-fold lower than in outer hair cells, and ~10⁴-fold lower than in red blood cells. Consistent with these results, our measurements in the present work and in (8) together suggest a ~10⁴-fold lower drag coefficient in axons than in HeLa cells.

By combining our results with prior literature, we propose that a microscopic model of axonal membrane flows should account for four different and seemingly inconsistent observations (Fig. 5A): (i) Tracer diffusion is less than twofold higher in axons compared to most other plasma membranes [fig. S4 and (13)]; (ii) membrane-cortex adhesion is approximately twofold lower in axons compared to fibroblasts (15); (iii) membrane tethers slide easily on axons but are typically pinned on other plasma membranes [fig. S4 and refs. (13, 17)]; and (iv) membrane flow resistance on axons is up to ~10⁴-fold lower than on other plasma membranes [Figs. 1 and 2 and (6, 13)]. Can these disparate observations be reconciled in a consistent microscopic model of axon membrane flow?

The first two observations imply a relatively modest difference in the density of MCA obstacles in axons versus most other cell plasma membranes. How can we reconcile this with the third and fourth observations, which imply the existence of large (>100 nm) fluid channels in axon membranes? The key insight is that tracer diffusion and mean membrane-cortex adhesion energy are largely insensitive to the arrangement of MCAs but rather depend mainly on the density (ϕ). In contrast, tether sliding and membrane flow are exquisitely sensitive to MCA spatial arrangement. Periodic versus random arrangements of MCAs have nearly identical flow resistances, but clustering of MCAs can create channels that permit facile tether sliding and membrane flow (Fig. 5A).

We can make quantitative estimates to test the prediction that MCAs are finely dispersed in most cell types but clustered in axons. Inserting reasonable values for a HeLa cell (a = 1 nm, ϕ = 0.12, η = 0.002 pN s/μm) into Eqs. 1 to 3 gives a drag coefficient $\frac{\mathrm{\eta }}{k}=1700$ pN s/μm³, in close agreement with the experimental estimate for HeLa cells of ~1670 pN s/μm³ (7). This value for the drag coefficient can be converted into an effective membrane viscosity, as defined in Brochard-Wyart, of η_e = 1.6 × 10⁻⁶ Pa s m, which is between the values they reported for neutrophils and outer hair cells (6). Thus, randomly distributed MCAs with typical molecular radii of a ~ 1 nm can cause substantial resistance to membrane flow (8, 9).

To adapt this model to axons, we can consider clusters of MCAs with a ~ 100 nm while keeping all other parameters constant. This clustering decreases the membrane drag coefficient by a factor of (1/100)², implying $\frac{\mathrm{\eta }}{k}=0.17$ pN s/μm³, in reasonable agreement with the drag coefficient 0.24 pN s/μm³ inferred from the Dai and Sheetz measurements (11). This clustering would also create channels large enough for tethers to slide. While there is substantial uncertainty in the microscopic parameters for this model, these estimates show that MCA clustering in axons can reconcile diverse experimental results.

In axons, super-resolution imaging has revealed coaxial actin rings with 180-nm periodicity, underlying the axonal membrane (43). The actin rings are linked by spectrin tetramers that bind to membrane proteins through ankyrin (44, 45). This membrane periodic skeleton (MPS) interacts with hundreds of proteins and imposes its periodicity on the distribution of at least 20 proteins (46), strongly suggesting that the MCA obstacles may be clustered in axons. While the relation of our membrane flow measurements to clustering by the MPS remains speculative, the similar length scales are suggestive and merit further investigation.

Membrane tension is an important regulator in cell migration, mechanosensing, intracellular vesicle trafficking (47), and even propagation of cortical waves in immune cells (48). Synaptic vesicle fusion adds lipids to, and lowers the membrane tension of, the presynaptic plasma membrane. Watanabe et al. (19) proposed that this tension drop can quickly travel across the active zone, triggering a mode of ultrafast endocytosis within 50 ms. Assuming a 500-nm size for the active zone, the speed of tension propagation must exceed 10 μm/s for this effect to occur, consistent with our estimates of tension propagation speed. Gomis Perez et al. (13) directly observed rapid membrane tension propagation in axon terminals over distances >10 μm but did not quantify the speed of tension propagation. They proposed that tension propagation couples exo- and endocytosis over the whole axon terminal. Our results suggest an additional role for axonal tension propagation over developmental time scales. The critical role of tension propagation in axon growth and branching suggests that this parameter should be studied during axonal growth in vivo.

Long-range tension propagation has been proposed to play a central role in coordinating the shape and motions of motile cells. For example, in neutrophils, actin polymerization at the leading edge is thought to cause global increases in membrane tension, which suppress formation of secondary growth fronts (49). The long and slender geometry of the axon leads to qualitatively different dynamics. Since perturbations to tension attenuate over a ~40-μm length scale in rat hippocampal axons (Fig. 1E), the winner-takes-all growth rule seen in neutrophils is not absolute in axons. Rather, branches may nucleate if far enough apart, but tension coupling maintains a competition between extension of the growth cone and of nearby branches.

MATERIALS AND METHODS

Neuron culture

All procedures involving animals were in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and were approved by the Institutional Animal Care and Use Committee at Harvard. Hippocampal neurons from P0 rat pups were purchased from BrainBits and cultured in NBActiv4 medium at a density of 5000 to 30,000 cells/cm² on glass-bottom dishes precoated with poly-d-lysine and Matrigel. At 1 day in vitro (DIV), glia cells were plated on top of the neurons at a density of 7000 cells/cm². At 3 to 5 DIV, neurons were transfected following the calcium phosphate protocol (Jiang and Chen, 2006). Imaging was performed on DIV 7 to 14, with neuron culture medium replaced with extracellular (XC) imaging buffer (125 mM NaCl, 2.5 mM KCl, 15 mM Hepes, 30 mM glucose, 1 mM MgCl₂, 3 mM CaCl₂, and pH 7.3).

Neuron labeling

For experiments in Figs. 1 and 2 and figs. S1, S3 (A to D), and S4, neurons were labeled with cytosolic eGFP to maximize sensitivity to changes in tether radius. To visualize native membrane branches, we found that a membrane tag was preferable. Neurexin (NXN) is an axon-enriched transmembrane protein; thus, we used NXN to label axonal membranes. To minimize fluorescence from proteins in intracellular vesicles, which have an acidic lumen, we fused NXN to a pH-sensitive fluorescent protein, superecliptic pHluorin (SEP), to create SEP-NXN (construct ZS090). For experiments in Fig. 3 (F to H) and figs. S4, S6, and S7, we labeled neurons with SEP-NXN.

Tether pulling

Micropipettes were pulled from glass capillaries (World Precision Instrument, 1B150F-4) using a pipette puller (Sutter P1000). The tip of the pipette was cut to an opening diameter of ∼3 μm and bent to ∼40° using a microforge (WPI, DMF1000). Tethers were pulled with a 4-μm-diameter polystyrene bead (Spherotech #DIGP-40-2) held at the tip of a micropipette and controlled by micromanipulators.

Cloning and constructs

SEP-NXN (ZS090, Addgene #186631): To facilitate the identification of growth cones, we switched the axon marker from cytosolic eGFP to the axon-specific rat NXN-1β, tagged with an SEP at the N terminus. SEP from Addgene #24000 (50) and NXN from Addgene #44968, (51) were ligated together via Gibson cloning. GPI-eGFP was from Addgene #32601 (52). Cytosolic eGFP was used for most of the tether imaging. Axon GCaMP6s (Addgene #112005) was from (31). To test whether actin polymerized in the tethers, we cotransfected neurons with GPI-eGFP and mCherry fused to Utrophin (mCherry-UtrCH), a gift from W. Bement (Addgene #26740).

Perfusion experiments

A micropipette was loaded with XC buffer supplemented with either sodium deoxycholate (500 μM, Sigma-Aldrich, 30970) or d-Mannitol (350 mM, Sigma-Aldrich, M4125). The deoxycholate concentration was chosen to be well below the critical micellar concentration of 2 mM (53). The micropipette was then positioned ~10 μm from the growth cone (see fig. S6). A slight suction pressure was used to minimize the leakage of the solution inside the pipette before experiments. While imaging of the axon, a pressure ~0.1 atm was used to inject the solution inside the pipette for 10 to 30 s, aiming at the growth cone. The axon was continuously monitored until >1 min after stopping the injection.

Estimate of tether diameter

Experiments were performed on a home-built epifluorescence microscope with a 60× objective and an electron-multiplying charge-coupled device (EMCCD) camera (Andor iXon, DU-897). A digital micromirror device (DMD) restricted illumination to the tethers to avoid overwhelming fluorescence from much brighter objects (e.g., cell bodies) in the vicinity. Fluorescence intensity values of membrane tethers were extracted as follows. A narrow rectangular region of interest (ROI) was defined along the tether, selected to be free of other fluorescent structures, not too close to the attachment points to the cell or the pipette, and positioned such that the tether spanned the length of the entire ROI for all tether-pulling extensions. Fluorescence in the ROI was averaged along the tether axis to create a profile of fluorescence transverse to the tether. This profile was then fit to a Gaussian function with variable offset to accommodate background fluorescence. The offset was determined in nominally fluorescence-free regions that bracketed the ROI (see Fig. 1B for an example). The integral of the Gaussian function was used to estimate the tether fluorescence, F. For tethers containing cytosolic markers, the tether radius r scales as r ∝ F^1/2. For membrane-labeled tethers, r ∝ F. In dual-tether experiments when one tether was stretched, the other tether was held still. Illumination intensities were low enough that photobleaching was negligible during tether-pulling experiments.

Estimate of diffusion coefficients

Localized photobleaching was performed using a 488 nm laser focused on a small spot on the face of a DMD. The DMD was used to restrict the illuminated spot to a 1 μm circle aligned on the axon or dendrite of a rat hippocampal neuron expressing GPI-eGFP. The spot was bleached for 15 s, and recovery was monitored for 5 min, with most of the recovery occurring within the first ~30 s. The fluorescence intensity profile F (r, t) was extracted along the profile of the axon or dendrite. To correct for slight photobleaching during the recovery period, fluorescence values were normalized by fluorescence of a region of the cell far from the initial bleaching spot. The first 50 s of recovery of the photobleaching-corrected trace were fit to a one-dimensional diffusion model

$$F(r,t)={\displaystyle {\int }_{-L}^L}F(r\prime ,0)G(r-r\prime ,t)dr\prime$$

where the Gaussian diffusion kernel is

$$G(r,t)=\frac{1}{\sqrt{4\mathrm{\pi }\mathit{Dt}}}{e}^{-\frac{r^2}{4\mathit{Dt}}}$$

with D as the only free parameter. Image analysis and nonlinear least squares fitting were carried out in MATLAB.

Estimate of changes in growth cone area

The growth cone was labeled with a membrane tag, SEP-NXN; thus, we used fluorescence in an ROI around the growth cone as a proxy for changes in growth cone area. We used a cell-free ROI near the growth cone for background correction.

Statistical methods

In paired statistical tests, the underlying distribution was tested for normality by the Kolmogorov-Smirnov test. In cases where the data were normally distributed, P values were calculated from two-tailed paired t test. In cases that were not normally distributed, P values were calculated from the Wilcoxon rank-sum test.

Supplementary Materials

This PDF file includes:

Supplementary Calculation

Figs. S1 to S7

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S4

View/request a protocol for this paper from Bio-protocol.