Learning 4D Infant Cortical Surface Atlas with Unsupervised Spherical Networks

Abstract

Spatiotemporal (4D) cortical surface atlas during infancy plays an important role for surface-based visualization, normalization and analysis of the dynamic early brain development. Conventional atlas construction methods typically rely on classical group-wise registration on sub-populations and ignore longitudinal constraints, thus having three main issues: 1) constructing templates at discrete time points; 2) resulting in longitudinal inconsistency among different age’s atlases; and 3) taking extremely long runtime. To address these issues, in this paper, we propose a fast unsupervised learning-based surface atlas construction framework incorporating longitudinal constraints to enforce the within-subject temporal correspondence in the atlas space. To well handle the difficulties of learning large deformations, we propose a multi-level multimodal spherical registration network to perform cortical surface registration in a coarse-to-fine manner. Thus, only small deformations need to be estimated at each resolution level using the registration network, which further improves registration accuracy and atlas quality. Our constructed 4D infant cortical surface atlas based on 625 longitudinal scans from 291 infants is temporally continuous, in contrast to the state-of-the-art UNC 4D Infant Surface Atlas, which only provides the atlases at a few discrete sparse time points. By evaluating the intra- and inter-subject spatial normalization accuracy after alignment onto the atlas, our atlas demonstrates more detailed and fine-grained cortical patterns, thus leading to higher accuracy in surface registration.

1. Introduction

Cortical surface atlases play an important role in neuroimaging studies by providing a common space for normalizing, comparing, and analyzing brain structure and function across different individuals and studies [19,14]. Considering the rapid growth of the cerebral cortex during early brain development, spatiotemporal (4D) surface atlases are essential to characterize and model such dynamic development of infant brains [22] and are typically constructed on the spherical space by taking advantage of the intrinsic spherical typology of the cortex [9]. Conventional 4D atlas construction methods [22,12,9,10,1,16] generally perform several rounds of template estimation and individual-to-template registration, and finally average (based on Euclidean distance [9], Wasserstein distance [2], or sparse representation [22,17]) the cortical features in each age group to obtain the atlas for each age. Although these methods and their constructed infant cortical surface atlases are popular and widely used to investigate early brain development in the past decade, they have three main issues. First, these methods require an extremely long runtime due to the iterative group-wise registration process. Second, they create the atlas at each age based on a subset of the data without exploiting the rich information from the whole dataset, leading to suboptimal atlases. Accordingly, the resulting 4D atlases are constructed at discrete, sparse time points based on subpopulations scanned by predefined concentrated ages, e.g., 1, 3, 6, 9, 12, 18 and 24 months of age. These atlases are thus temporally discontinuous and cannot cover many important ages during infancy. Although the kernel regression approach [12,1,16] could be applied to interpolate the uncovered ages’ atlases with specific kernel designs, it was not fully investigated and developed for infants, due to the difficulties in modeling the complicated, regionally-heterogeneous and nonlinear early brain development. Third, the methods [1,16] constructing atlases for each age independently based on the subset of the data may cause longitudinal inconsistency among different ages’ atlases when longitudinal subjects are involved. The reason is that, as revealed by previous works [22,12,9], without considering the longitudinal information, the longitudinally-corresponding anatomical points at different ages of the same subject are independently deformed to different locations in the atlas space, consequently leading to a longitudinally-inconsistent 4D atlas.

To address these issues, we propose an unsupervised learning framework to learn a continuous 4D infant cortical surface atlas, inspired by the recent spherical networks developed on cortical surfaces [25] and an unsupervised atlas construction method [3]. Our approach jointly learns an age-conditional atlas synthesis network and an unsupervised registration network from the entire dataset without manually partitioning the dataset into subgroups, thus is computationally more efficient and powerful in learning rich, useful information from the whole dataset than conventional methods. Moreover, since learning large deformations is difficult [13,28], we propose a deep multi-level multi-modal spherical registration network (MM-SRegNet) to decompose the large deformations into small ones at each resolution step and perform cortical surface registration in a coarse-to-fine manner. Further considering the subject-specific longitudinal information of longitudinal subjects frequently seen in large-scale studies, we design a novel longitudinal constraint (LC) loss to enforce the within-subject temporal correspondence after registration to the atlas space, which is important for establishing longitudinally consistent 4D atlases [9]. To sum up, our contributions in this paper are:

1. We propose an unsupervised learning-based 4D cortical surface atlas construction framework to jointly learn an atlas synthesis network and MM-SRegNet for generating the age-conditional atlas and the deformation field registering the cortical surfaces to the age-matched atlases simultaneously. Besides, our MM-SRegNet enables flexible and accurate cortical surface registration using multiple cortical features in a coarse-to-fine manner.

2. We efficiently and effectively incorporate longitudinal constraints into our atlas learning framework, which is essential for establishing within-subject longitudinally-consistent correspondences, thus obtaining longitudinally more consistent atlas with higher quality.

3. Leveraging our proposed method, we construct the first longitudinally-consistent temporally-continuous 4D infant cortical surface atlas based on 625 longitudinal scans from 291 infants and show that our generated 4D atlas preserves more details of cortical folding patterns compared to the state-of-the-art [22].

2. Method

As shown in Fig. 1, our goal is to jointly train a generative model G_t that can synthesize atlas given on-demand ages, and a registration model that registers the synthesized atlas to each input surface, thus avoiding the expensive time cost of conventional multi-round registration and iterative template refinement process. Let $S=\left\{S_1^1,\dots ,S_1^{n_1},\dots ,S_i^j,\dots ,S_N^{n_N}\right\}$ denote a longitudinal cortical surface dataset with N subjects and each subject i (i = 1,...,N) has n_i longitudinal scans, $S_i^j$ denotes the jth time point cortical surface of subject i and $t_i^j$ is the age of subject i at jth time point. Note that the number of longitudinal scans and the time points of each subject are not necessarily to be the same. Then a baseline framework aims to minimize the loss ${\mathcal{L}}_{BL}$ on the whole dataset:

$${\mathcal{L}}_{BL}={\mathcal{L}}_{sim}\left(S_i^j,A_{t_i^j}\circ {\varphi }_i^j\right)+{\lambda }_c\parallel \overline{u}{\parallel }^2+{\lambda }_d{\sum }_{i,j}{\Vert u_i^j\Vert }^2+{\lambda }_s{\sum }_{i,j}{\Vert {\nabla }_s{u}_i^j\Vert }^2$$ (1)

Fig.1.

Overview of our unsupervised learning framework for 4D infant cortical surface atlas construction. The atlas synthesis network G_t takes age attributes as input and outputs the conditional atlases, which are then registered to each surface in the input minibatch by MM-SRegNet (Fig. 2). Cortical surfaces of the same subject are grouped together to build the longitudinal constraint loss highlighted in orange color. The blank spheres indicate unavailable data at those time points.

Where ${\mathcal{L}}_{sim}\left(S_i^j,A_{t_i^j}\circ {\varphi }_i^j\right)=1-\frac{cov\left(S_i^j,A_{t_i^j}\circ {\varphi }_i^j\right)}{\sqrt{{\sigma }_{S_i^j}\cdot {\sigma }_{A_{t_i^j}}\circ {\varphi }_i^j}}$ is the correlation coefficient loss for enforcing the similarity between the moved atlas and individual cortical surface maps, $A_{t_i^j}=G_t\left(t_i^j\right)$ is the synthesized atlas at age $t_i^j,{\varphi }_i^j$ is the deformation field aligning atlas to jth surface of subject i and $\varphi =exp(v)$ is computed using 6 “scaling and squaring” layers as in [24], which is an effective extension of diffeomorphic deformation from Euclidean space to spherical space. $u=\frac{\varphi (x)}{x\cdot \varphi (x)}-x$ is the tangent displacement vector on a unit sphere from x to ϕ(x). Hence, the rest terms in Eq. 1 regularize the unbiasedness, extent and smoothness of u, respectively. Note that we use the same ${\nabla }_s$ operator as in [26] on the spherical surface to approximate the tangent displacement field’s gradients and accordingly penalize it to encourage a smooth deformation field on the spherical surface.

2.1. Longitudinal Constraint

Since the above baseline framework ignores the within-subject longitudinal consistency constraint when involving longitudinal subjects, we are motivated to incorporate it into our framework. To achieve this, we first group the longitudinal surfaces from the same subject in one minibatch, as shown in Fig. 1. Then we can explicitly enforce the longitudinal correspondence among the surfaces of the same subject after moving them to the atlas space, which is formulated as the longitudinal constraint (LC) loss:

$${\mathcal{L}}_{LC}={\sum }_i{\sum }_{j=0}^{n_i-1}{\mathcal{L}}_{sim}\left(S_i^j\circ {\left({\varphi }_i^j\right)}^{-1},S_i^{j+1}\circ {\left({\varphi }_i^{j+1}\right)}^{-1}\right)$$ (2)

where ${(\varphi )}^{-1}$ denotes the inverse deformation of ϕ, which can be conveniently computed using the method in [23]. This novel ${\mathcal{L}}_{LC}$ is very efficient to integrate, as it adds 0 parameters and only a small overhead over computation to the baseline framework.

2.2. Multi-level Multi-modal Spherical Registration Network

In unsupervised registration framework, it is known that large deformations are difficult to learn [13,28]. To address this issue, a typical method is stacking multiple networks in a pyramid fashion and perform the registration in a coarse-to-fine manner [20,13,28]. Inspired by these networks, we propose the MM-SRegNet to perform the coarse-to-fine cortical surface registration. A recent unsupervised cortical surface registration framework [26] employs three Spherical U-Nets [27] to predict spherical deformation fields for three equatorial regions at three orthogonal orientations, thus addressing the polar-distortion issue in spherical surface registration. We build on this method and incorporate the novel spherical “scaling and squaring” layers [23] to ensure diffeomorphic (invertible and topology-preserving) deformations to construct SRegNet and further stack it to construct MM-SRegNet, as shown in Fig. 2. Note that multimodal cortical features (such as geometry, myelin or functional gradient) are imperfectly correlated [15], therefore our MM-SRegNet also offers much flexibility in the choice of cortical features and thus can provide on-demand atlas flexibly.

Fig.2.

Illustration of our MM-SRegNet. The superscript (6c) indicates the level 6 and the feature (‘s’ for sulc, ‘c’ for curv). ‘A’ denotes the atlas surface and ‘S’ is the individual surface. Note that this only provides a brief overview of our method, which can be flexibly extended to other levels and cortical features.

In this paper, to obtain 4D atlas with fine cortical folding patterns, we follow the popular registration configuration [23,15] to align geometric features, i.e., ‘sulc’ (average convexity) and ‘curv’ (mean curvature), measuring cortical folding in a coarse and fine view, respectively. We stack 4 SRegNets at 4 levels (4, 5, 6, 6, with 2,562, 10,242, 40,962, 40,962 vertices, respectively) for aligning sulc, sulc, sulc, curv, respectively. Finally, we deform the generated sulc atlas to the final curv atlas space using the learned deformation field at the last level.

2.3. Network and Implementation Details

The generative model G_t for synthesizing the atlas consists of a fully connected layer with 10242*3 neurons, a reshape layer and an upsampling layer followed by 3 “batch normalization [7] + spherical 1-ring convolution [25] + ReLU” blocks each with [16, 32, 1] channels. Herein, G_t takes age $t_i^j$ as a scalar value input and outputs the age-conditional atlas (40962×1). For the registration network, since we stack multiple SRegNets to perform the coarse-to-fine registration, we create a smaller version of Spherical U-Net [25] used in SRegNet, with 3 resolution steps and [8, 16, 32] channels, resulting in only 0.5M parameters in each SRegNet.

We implemented our method using PyTorch. We trained the atlas synthesis network G_t and registration network MM-SRegNet jointly by minimizing the full objective ${\mathcal{L}}_{BL}+{\lambda }_{LC}{\mathcal{L}}_{LC}$ in a minibatch style. We trained the network using Adam optimizer with learning rate 5e-4 for 50 epochs. λ_c=1.0, λ_d=0.2, λ_s=1.5, 2.5 and 4.0 at 4th, 5th and 6th level, respectively, and λ_LC=1.0.

Note that although looking bigger, our final model is compact with only a small number of parameters, G_t with 66K, and MM-SRegNet with 6M parameters in total. Taking about 10 hours to fully train the networks on a PC with an NVIDIA RTX2080 Ti GPU and an Intel Core i7–9700K CPU, it only needs 5 seconds for one forward inference, including atlas generation and individual-to-atlas registration, which is much faster than conventional atlas construction and registration methods, where the whole process can take several days.

3. Experiments

3.1. Dataset and Preprocessing

We used a longitudinal infant dataset [6] with 625 scans from 291 subjects, with ages ranging from 0 to 5 years. The distribution of the number of longitudinal scans is, 44% infants with only 1 scan, 24% with 2 scans, 14% with 3, 10% with 4 and 8% with 5 or more scans. Cortical surfaces were reconstructed via iBEAT V2.0 Cloud (http://www.ibeat.cloud/) [21,11,18,8] and then mapped onto the sphere using FreeSurfer [5]. Each surface is then represented as a spherical map with 2 features at each vertex, i.e., ‘sulc’ and ‘curv’, and a parcellation map is also generated based on [4]. We randomly split the dataset into a training set with 418 scans from 185 subjects, and a test set with 207 scans from 106 subjects. In testing stage, we generate the age-matched atlas for each test surface and the corresponding deformation field aligning it to the age-specific atlas simultaneously.

To quantitatively validate the atlas, we calculate the widely-used within-group spatial normalization accuracy, which is measured by the Pearson correlation coefficient (PCC) of feature maps and Dice overlap metric of parcellation maps as in [22,9,15,26]. Generally, sharper atlases lead to higher registration accuracy and thus better spatial normalization performance. Therefore, a higher PCC and Dice indicate better within-group alignment and thus a better atlas.

3.2. Ablation Studies

MM-SRegNet.

To demonstrate the effectiveness of our MM-SRegNet, we trained two baseline models on the 6th level, named B-Sulc, B-Curv for generating two baseline sulc and curv atlas with single level SRegNet. Since they use single-modal feature, the most critical problem of these two baselines is that the constructed atlases may not be in the same space, which causes trouble in neuroimaging analysis. As shown in Table 1, the B-M model using our MM-SRegNet as the registration network leads to a higher correlation and Dice for both within-subject and across-subject alignment. This is important for building atlases with other cortical features accurately and flexibly in the future study.

Table 1.

Within-subject and inter-subject alignment performance of different models.

	Within-subject alignment			Inter-subject alignment
	PCC sulc	PCC curv	Dice (%)	PCC sulc	PCC curv	Dice (%)
B-Sulc	0.879±0.051	-	83.45±5.76	0.672±0.062	-	70.92±4.40
B-Curv	-	0.557±0.088	83.31±5.79	-	0.337±0.053	69.39±6.16
B-M	0.907±0.044	0.677±0.100	85.02±5.32	0.728±0.060	0.484±0.046	74.91±5.46
B-M+LC	0.927±0.040	0.743±0.067	86.52±5.10	0.751±0.052	0.528±0.057	76.12±4.85

Longitudinal Constraint (LC).

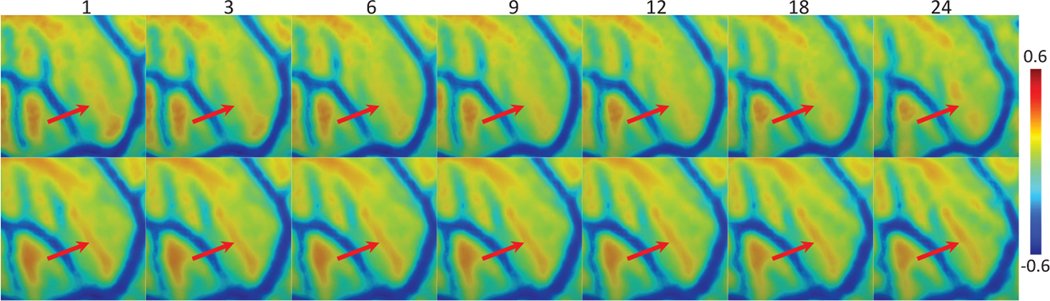
As shown in Table 1, adding LC loss to the baseline model (named B-M+LC) significantly improve the performance, which is reasonable for correlation metrics, since we directly add the within-subject correlation as an additional loss to train the model. As a more unbiased metric, the Dice improvement is a compelling evidence that incorporating LC strengthens the within-subject temporal correspondence and thus enhances the longitudinal consistency and the quality of the synthesized 4D atlas. Fig. 3 provides a typical example of the curv atlases learned without LC and with LC. As we can see, the LC encourages longitudinally more consistent 4D cortical surface atlases along with much shaper cortical folding patterns, than the model without LC.

Fig.3.

Comparison of the learned 4D surface curv atlases using B-M (upper row) and B-M+LC (lower row) at discrete ages (months) in the first two postnatal years.

3.3. Comparison with State-of-the-art

Visual Inspection.

We used the B-M+LC model to generate the infant cortical surface atlases at corresponding discrete ages with the state-of-the-art UNC 4D infant cortical surface atlas [22] for comparison. Fig. 4 shows the two atlases only in the first two postnatal years because of the most dynamic postnatal development during this period [11]. We can see that our atlas preserves more detailed cortical folding patterns than UNC atlas in most regions, e.g., insula, inferior parietal and lateral temporal cortex. More importantly, as indicated by arrows, minor cortical folds, which are still developing rapidly during infancy, are well captured by our atlas, but absent in UNC 4D atlas.

Fig.4.

Comparison of UNC 4D surface atlas and ours. Note that though limited time points are shown, our method offers continuous 4D atlas at arbitrary time points from 0 to 5 years of age.

Quantitative Evaluation.

We used a third-party registration tool, Spherical Demons [23], a conventional method solving registration problem using Gauss-Newton method, to fairly register the hold-out test surfaces to our atlas and UNC atlas, respectively. Note that we choose the age-matched UNC atlas that are closest to the individual surface’s age for each individual surface (11 instances available in UNC atlas, i.e., 1, 3, 6, 9, 12, 18, 24, 36, 48, 60, and 72 months), while our method generates on-demand age-specific atlas at arbitrary time points and thus can provide more accurate and matched atlas to guide the registration. The average PCC of sulc, PCC of curv, and Dice is 0.706±0.039, 0.373±0.063, 0.812±0.049 for UNC atlas, and 0.720±0.043, 0.382±0.058, 0.821±0.030 for our atlas. Detailed results in the first two years are shown in Fig. 5. We can see that our atlas outperforms UNC atlas in most age groups and shows no significantly differences if not better, except PCC of curv and Dice at 1 month likely because of the limited samples in this group, demonstrating the practical usefulness of our higher-quality atlas in improving surface registration and parcellation accuracy.

Fig.5.

Spatial normalization accuracy at each age group based on different atlases.

4. Conclusion

In this paper, we present three methodological contributions to efficiently and accurately build the first longitudinally-consistent temporally-continuous 4D infant cortical surface atlas. First, we propose an unsupervised learning framework for simultaneously atlas synthesis and individual-to-atlas registration. Taking advantage of the deep learning ability of neural networks, our method can efficiently learn the atlas from the whole dataset and rapidly warp the new surfaces to the generated atlas. Second, our novel MM-SRegNet can accurately perform cortical surface registration in a coarse-to-fine manner flexibly using multiple cortical features. Third, incorporating the longitudinal constraint further improves within-subject longitudinal consistency and thus the quality of 4D atlas. Compared with the state-of-the-art UNC 4D atlas both visually and quantitatively, our atlas exhibits sharper and much more detailed patterns for more accurately mapping infant brain development. In future, we will release our model and atlas to the community to advance the neuroimaging studies of infants.