Optimal Two-Stage Phase II Survival Trial Design

Abstract

Recently molecularly targeted agents and immunotherapy have been advanced for the treatment of relapse or refractory cancer patients, where disease progression-free survival or event-free survival is often a primary endpoint for the trial design. However, methods to evaluate two-stage single-arm phase II trials with a time-to-event endpoint are currently processed under an exponential distribution, which limits application of real trial designs. In this paper, we developed an optimal two-stage design, which is applied to the four commonly used parametric survival distributions and a non-parametric logspline distribution. The proposed method has advantages compared to existing methods in that the choice of underlying survival model is more flexible and the power of the study is more adequately addressed. Therefore, the proposed optimal two-stage design can be routinely used for single-arm phase II trial designs with a time-to-event endpoint as a complement to the commonly used Simon’s two-stage design for the binary outcome.

1. Introduction

Traditional phase II cancer trials are often conducted as single-arm studies to determine whether new treatment agents have sufficient antitumor activities to warrant further investigation in randomized phase III trials. The antitumor activity for evaluating cytotoxic compounds might be quantified by tumor response which is often categorized as a binary endpoint: responder or non-responder. The two-stage procedures proposed by Simon [1] are commonly used for these trial designs.

However, there are some situations in which tumor response may not be an appropriate endpoint. These circumstances occur with agents such as cytostatic, molecularly targeted agents and immunotherapy that can prevent the tumor growth but may not kill the tumor cells and/or lead to tumor shrinkage. In such cases, time-to-event (TTE), e.g., disease progression-free survival or event-free survival, is an alternative endpoint for the trial design. Due to limited methods available to design single-arm phase II trial with a TTE endpoint, the TTE endpoint is often dichotomized as a binary endpoint and the trial is designed using Simon’s two-stage approach. However, efficiency is greatly compromised by dichotomizing the TTE at a fixed landmark time point.

Researchers have proposed a variety of methods for single-arm phase II trial designs with TTE as the primary endpoint. To test survival probability at a fixed time point, Case and Morgan [2] and Huang et al. [3] developed optimal two-stage designs. Huang and Thomas [4] extended their methodology to include three-stage designs. In addition, Lin et al. [5], and Wu and Xiong [6] proposed multiple-stage designs. However, one issue for such trial designs is the choice of the landmark time point. Furthermore, none of these designs are fully efficient. Finkelstein et al. [7], Sun et al. [8], Wu [9,10] and Schmidt et al. [11] proposed single-stage designs by using the one-sample log-rank test (OSLRT) which evaluates the treatment effect based on the entire survival distribution. Kwak and Jung [12] and Belin et al. [13] developed an optimal two-stage design without and with restricted follow-up, respectively. However, both Kwak and Jung, and Belin’s two-stage designs are implemented under the exponential distribution which limits application for real trial designs. Furthermore, the sample size calculations in both Kwak and Jung, and Belin’s designs could be underpowered [9].

Motivated by an institutional small-cell lung cancer trial, we developed a flexible and accurate optimal two-stage single-arm trial design with a TTE endpoint. The proposed method can be applied to the four commonly used parametric survival distributions: Weibull, log-normal, gamma and log-logistic. If none of the four parametric survival distributions fit the null distribution well, then a non-parametric logspline distribution can be used to fit historical data and applied to the trial design. Thus, the choice of the underlying survival model is flexible. Furthermore, the exact variance estimate of the OSLRT proposed by Wu [9] is used for the two-stage design, thus, the power of the study is adequately provided. Therefore, the proposed method can be routinely used for two-stage single-arm phase II trials designed with a TTE endpoint that complements the Simon’s two-stage design for a binary endpoint.

2. One-Sample Log-Rank Test

The OSLRT was first introduced by Breslow [14], and its applications to the single-arm phase II trial designs were discussed by Sun et al. [15], Kwak and Jung [12], Wu [9,10], Schmidt et al. [11] and Belin et al. [13]. The study design based on the OSLRT requires each patient to be followed until an event occurs or until the end of study. In real practice, however, the full follow-up information for a phase II trial is often difficult to obtain in the late period of trial, particularly when the accrual duration is long; obtaining the status of each patient within a restricted period is more realistic [13].

In this article, a restricted follow-up time period for each patient is assumed up to a clinically meaningful time-point x. Thus, the hypothesis of interest for the trial design is given as follows:

$$H_0:S(u)\le S_0(u)\text{vs}.S(u)>S_0(u)\text{,}\text{for}\text{all}u\le x$$

or equivalent to the hypothesis, in terms of cumulative hazard function,

$$H_0:\mathrm{\Lambda }(u)\ge {\mathrm{\Lambda }}_0(u)\text{vs}\mathrm{\Lambda }(u)<{\mathrm{\Lambda }}_0(u),\text{for}\text{all}u\le x$$

where S(·) and Λ(·) are the true survival distribution and cumulative hazard function for the experimental group, respectively; S₀(·) and Λ₀(·) are the known survival distribution and cumulative hazard function under the null hypothesis, respectively. An alternative survival distribution S₁(u), or cumulative hazard function Λ₁(u) for all u ≤ x needs to be specified for the sample size or power calculation.

We assume that the failure time T_i and censoring time C_i are independent and {T_i, C_i, i = 1, . . ., n} are independent and identically distributed. The observed failure time and failure indicator are X_i = T_i ∧ C_i and Δ_i = I(T_i ≤ C_i), respectively, for the i^th subject. On the basis of observed data {X_i, Δ_i, i = 1, · · ·, n}, we define $O={\sum }_{i=1}^n{\mathrm{\Delta }}_i$ as the observed number of events, and $E={\sum }_{i=1}^n{\mathrm{\Lambda }}_0\left(X_i\right)$ as the expected number of events (asymptotically), then the OSLRT is defined by

$$L=\frac{E-O}{\sqrt{E}}.$$ (1)

Note: We reversed the order O and E in the test statistic L so that reducing the number of events compared to the null hypothesis provides a positive value of L.

It has been shown that L is asymptotically standard normal distributed under the null hypothesis [14]. Hence, we reject null hypothesis H₀ with one-sided type I error rate α if L > z_1−α, where z_1−α is the 100(1 − α) percentile of the standard normal distribution.

3. Single-Stage Design

With restricted follow-up, that is each patient is followed for a fixed length of period x, and assuming no loss to follow-up during the follow-up time of x, then, censoring time C_i is fixed to x, and the survival function of censoring time C_i is G(u) = I(u ≤ x), where I(·) is an indicator function. Thus, the sample size for a single-stage design using the OSLRT derived with restricted follow-up time x can be simplified as follows:

$$n_0=\frac{{\left({\sigma }_0{z}_{1-\alpha }+\sigma z_{1-\beta }\right)}^2}{{\omega }^2},$$

where ω = v₀ − v₁, ${\sigma }_0^2=v_0$ and ${\sigma }^2=v_1-v_1^2+2v_{00}-v_0^2-2v_{01}+2v_0{v}_1$, with v₀, v₁, v₀₀ and v₀₁ given as follows:

$$v_0={\int }_0^x{S}_1(u)d{\mathrm{\Lambda }}_0(u),$$

$$v_1={\int }_0^x{S}_1(x)d{\mathrm{\Lambda }}_1(u),$$

$$v_{00}={\int }_0^x{S}_1(u){\mathrm{\Lambda }}_0(u)d{\mathrm{\Lambda }}_0(u),$$

$$v_{01}={\int }_0^x{S}_1(u){\mathrm{\Lambda }}_0(u)d{\mathrm{\Lambda }}_1(u).$$

3.1. Optimal Two-Stage Design

Single-arm phase II trials are often designed with an interim analysis so that they can be stopped early if a drug or treatment is ineffective. The data are examined at calendar time t ≤ τ, where t is measured from the start of study and τ is the duration of a period of enrollment t_a plus a fixed follow-up time x, i.e. τ = t_a + x. Further assuming no loss to follow-up during the follow-up period of x, then, we observe the time-to-failure X_i(t) = T_i ∧ x ∧ (t − A_i)⁺ and the failure indicator Δ_i(t) = I(T_i ≤ x ∧ (t − A_i)⁺), i = 1, · · ·, n, where A_i is the entry time of the i^th subject which is assumed to be uniform on [0, t_a]. Based on the observed data {X_i(t), Δ_i(t), i = 1, · · ·, n}, let N_i(t, u) = Δ_i(t)I(X_i(t) ≤ u) and Y_i(t, u) = I(X_i(t) ≥ u) be the failure and at-risk processes, respectively. To consider a two-stage design with an interim analysis at calendar time t₁ and final analysis at calendar time τ, the corresponding sample sizes are n₁ and n for the interim analysis and final analysis, respectively. Let $Z_1=W_1/{\widehat{\sigma }}_1$ and $Z=W/\widehat{\sigma }$ be the OSLRT statistics for the first stage and second stage, respectively [16], where

$$W_1=n_1^{-1/2}\sum _{i=1}^{n_1}{\int }_0^{\infty }\left\{Y_i\left(t_1,u\right)d{\mathrm{\Lambda }}_0(u)-N_i\left(t_1,du\right)\right\},$$

$$W=n^{-1/2}\sum _{i=1}^n{\int }_0^{\infty }\left\{Y_i(\tau ,u)d{\mathrm{\Lambda }}_0(u)-N_i(\tau ,du)\right\}$$

and

$${\widehat{\sigma }}_1^2=n_1^{-1}\sum _{i=1}^{n_1}{\int }_0^{\infty }{Y}_i\left(t_1,u\right)d{\mathrm{\Lambda }}_0(u),$$

$${\widehat{\sigma }}^2=n^{-1}\sum _{i=1}^n{\int }_0^{\infty }{Y}_i(\tau ,u)d{\mathrm{\Lambda }}_0(u).$$

Under the null hypothesis H₀, the means E(W₁|H₀) = E(W|H₀) = 0 and variances var(W₁|H₁) = ν₁ and var(W|H₁) = ν, where ν₁ and ν are given as follows:

$${\nu }_1={\int }_0^{x}G\left(u,t_1\right)S_0(u)d{\mathrm{\Lambda }}_0(u),$$

$$\nu ={\int }_0^x{S}_0(u)d{\mathrm{\Lambda }}_0(u),$$

and G(u, t₁) = P(t₁ − A₁ > u) = P(A₁ < t₁ − u) with A₁ is uniformly distributed on [0, t_a]. Thus, G(u, t₁) is given as follows:

$$G\left(u,t_1\right)=\{\begin{array}{ll}1\hfill & u\le t_1-t_a\hfill \\ \left(t_1-u\right)/t_a\hfill & t_1-t_a<u\le t_1\hfill \\ 0\hfill & u>t_1\hfill \end{array}$$

Under the null hypothesis H₀, we can show that correlation between W₁ and W is ${\rho }_0=\mathrm{corr}\left(W_1,W\mid H_0\right)=\sqrt{{\nu }_1/\nu }$. Furthermore, $n_1^{-1}{\sum }_{i=1}^{n_1}{Y}_i\left(t_1,u\right)$ and $n^{-1}{\sum }_{i=1}^{n_1}{Y}_i\left(t_2,u\right)$ uniformly converge to S₀(u)G(u, t₁)I(u ≤ x) and S₀(u)I(u ≤ x), respectively, then, ${\widehat{\sigma }}_1^2\to {\nu }_1$ and ${\widehat{\sigma }}^2\to \nu$. Thus, under the null hypothesis, (Z₁, Z) is approximately bivariate normal distributed with mean μ = (0, 0)′ and variance matrix

$$\mathrm{\Sigma }=\left(\begin{array}{ll}1\hfill & {\rho }_0\hfill \\ {\rho }_0\hfill & 1\hfill \end{array}\right)$$

Under the alternative H₁, we have $E\left(W_1\mid H_1\right)=\sqrt{n_1}{\omega }_1$ and $E\left(W\mid H_1\right)=\sqrt{n}\omega$, where ω₁ and ω are given as follows:

$${\omega }_1={\int }_0^{x}G\left(u,t_1\right)S_1(u)d{\mathrm{\Lambda }}_0(u)-{\int }_0^{x}G\left(u,t_1\right)S_1(u)d{\mathrm{\Lambda }}_1(u)$$

and

$$\omega ={\int }_0^x{S}_1(u)d{\mathrm{\Lambda }}_0(u)-{\int }_0^x{S}_1(u)d{\mathrm{\Lambda }}_1(u)$$

and the exact variance of W₁ under H₁ is given by ${\sigma }_{11}^2=p_1-p_1^2+2p_{00}-p_0^2-2p_{01}+2p_0{p}_1$ with p₀, p₁, p₀₀ and p₀₁ given as follows:

$$p_0={\int }_0^{x}G\left(u,t_1\right)S_1(u)d{\mathrm{\Lambda }}_0(u),$$

$$p_1={\int }_0^{x}G\left(u,t_1\right)S_1(u)d{\mathrm{\Lambda }}_1(u),$$

$$p_{00}={\int }_0^{x}G\left(u,t_1\right)S_1(u){\mathrm{\Lambda }}_0(u)d{\mathrm{\Lambda }}_0(u),$$

$$p_{01}={\int }_0^{x}G\left(u,t_1\right)S_1(u){\mathrm{\Lambda }}_0(u)d{\mathrm{\Lambda }}_1(u).$$

Similarly the exact variance of W under H₁ is given by ${\sigma }_{21}^2=v_1-v_1^2+2v_{00}-v_0^2-2v_{01}+2v_0{v}_1$, with v₀, v₁, v₀₀ and v₀₁ given by equations (3-6).

The correlation between W₁ and W is given by ρ₁ = σ₁₁/σ₂₁. Furthermore, it can be shown that ${\widehat{\sigma }}_1^2\to {\sigma }_{01}^2={\int }_0^{x}G\left(u,t_1\right)S_1(u)d{\mathrm{\Lambda }}_0(u)$ and ${\widehat{\sigma }}^2\to {\sigma }_0^2={\int }_0^x{S}_1(u)d{\mathrm{\Lambda }}_0(u)$. Therefore, under the alternative, (Z₁, Z) is approximately bivariate normal distributed with a mean $\mu ={\left(\sqrt{n_1}{\omega }_1/{\sigma }_{01},\sqrt{n}\omega /{\sigma }_0\right)}^{\prime }$ and variance matrix

$$\mathrm{\Sigma }=\left(\begin{array}{cc}{\sigma }_{11}^2/{\sigma }_{01}^2& {\rho }_1{\sigma }_{11}{\sigma }_1/{\sigma }_{01}{\sigma }_0\\ {\rho }_1{\sigma }_{11}{\sigma }_1/{\sigma }_{01}{\sigma }_0& {\sigma }_1^2/{\sigma }_0^2\end{array}\right)$$

For a two-stage design, we consider stopping for futility only at the first interim analysis. We suppose that the stopping boundaries are c₁ and c for the first stage and final analysis. At the first stage we stop for futility if Z₁ ≤ c₁. Otherwise, the trial continues to the second stage and we accept futility or reject futility according to Z ≤ c or Z > c, respectively, where the boundaries c₁ and c satisfy following type I error α and power 1 − β constrains:

$$P\left(Z_1>c_1,Z>c\mid H_0\right)=\alpha ,$$ (2)

$$P\left(Z_1>c_1,Z>c\mid H_1\right)=1-\beta .$$ (3)

The two-stage design parameters (n₁, c₁, n, c) are unknown. An iterative algorithm will be implemented to determine (n₁, c₁, n, c) under the following set up of the design parameters. (1) Uniform accrual with a constant accrual rate r. (2) Survival probability S₀ at fixed time point x₀ under the null hypothesis. (3) Survival distribution function under the null hypothesis or a shape parameter for a parametric survival distribution. (4) Hazard ratio δ, here a proportional hazard model is assumed under the alternative. (5) The restricted follow-up time x for each patient.

The procedure of an optimal two-stage can be summarized as follows.

1. Given (α, β, r, S₀, x₀, δ, x, dist, data), calculate sample size n₀ and accrual period $t_a^0=n_0/r$ required for a single-stage design, where r is a constant accrual rate; S₀ is the survival probability under the null hypothesis at a fixed time point x₀; x is the follow-up duration specified for the trial; “dist” augment is used to specify the underlying survival distribution under the null hypothesis. In our algorithm, we implemented four parametric distributions: Weibull (WB), log-normal (LN), gamma (GM), log-logistic (LG) and a non-parametric logspline distribution (LS) (see Table 1). With a parametric distribution, we need only to specify the shape parameter; “data” augment is used to fit logspline distribution when user inputs data to fit logspline survival distribution under the null hypothesis; survival distribution under the alternative is determined by a proportional hazard assumption.

2. Initial algorithm with n₁ = n = n₀, and c₁ = 0.25, and given c, calculate α (call it α_c) by using the following equation (see Appendix 1)

   $$\alpha ={\int }_c^{\infty }\varphi (z)\mathrm{\Phi }\left(\frac{{\rho }_{0}z-c_1}{\sqrt{1-{\rho }_0^2}}\right)dz$$ (4)

   and iterate the expression until α_c is close to the nominal type I error α.
3. Calculate the power of a given design (n₁, c₁, n, c) using the following equation (see Appendix 1)

   $$\text{power}={\int }_{\overline{c}}^{\infty }\varphi (z)\mathrm{\Phi }\left(\frac{{\rho }_{1}z-{\overline{c}}_1}{\sqrt{1-{\rho }_1^2}}\right)dz$$ (5)

   where

   $${\overline{c}}_1=\frac{{\sigma }_{01}}{{\sigma }_{11}}\left(c_1-\frac{\sqrt{n_1}{\omega }_1}{{\sigma }_{01}}\right)\text{and}\overline{c}=\frac{{\sigma }_0}{{\sigma }_1}\left(c-\frac{\sqrt{n}\omega }{{\sigma }_0}\right)$$

4. If the power is smaller than 1 − β, then (n₁, c₁, n, c) is left and a new triplet (n₁, c₁, n) is tested by repeating step 2 and 3, otherwise, (n₁, c₁, n, c) is selected.

Table 1:

Four parametric distributions: Weibull (WB), log-normal (LN), gamma (GM) and log-logistic (LG) with shape parameter a and scale parameter b.

	Surv. function	Density	Cumu. hazard	Hazard
Dist.	S(t)	f(t)	Λ(t)	h(t)
WB	$e^{-{(t/b)}^a}$	$\left(\frac{a}{b}\right){\left(\frac{t}{b}\right)}^{a-1}{e}^{-{(t/b)}^{a-1}}$	(t/b)a	$\left(\frac{a}{b}\right){\left(\frac{t}{b}\right)}^{a-1}$
LN	$1-\mathrm{\Phi }(\frac{\log t-b}{a})$	$\frac{1}{\sqrt{2\pi }at}{e}^{-\frac{(\log t-b)}{2a^2}}$	−log S(t)	$\frac{f(t)}{S(t)}$
GM	1 − Ia(t/b)	$\frac{{(t/b)}^{a-1}{e}^{-t/b}}{\mathrm{\Gamma }(a)b}$	−log S(t)	$\frac{f(t)}{S(t)}$
LG	$\frac{1}{1+{(t/b)}^a}$	$\frac{(a/b){(t/b)}^{a-1}}{{\left(1+{(t/b)}^a\right)}^2}$	log(1 + (t/b)a)	$\frac{(a/b){(t/b)}^{a-1}}{1+{(t/b)}^a}$

I_a(·) is the incomplete gamma function and Φ(·) is the cumulative standard normal distribution function. Abbreviations: Dist.: distribution; Cumu.: cumulative.

For each selected candidate design (n₁, c₁, n, c), the expected sample size under H₀ is calculated by ES = E(n|H₀) = n₁ + (1 − PS)(n − n₁), where PS is the probability of an early stop under H₀, that is PS = Φ(c₁) and the maximum total study length is MTSL = t_a + x. Thus, the optimal design is the (n₁, c₁, n, c) which minimizes E(n|H₀). The R function ‘Optimal.rKJ’ which implements the above optimal algorithm is given in Appendix 2, where ‘Optimal.rKJ’ refers to optimal restricted-Kwak and Jung’s design.

4. Example

Small-cell lung cancer (SCLC) is the most aggressive type of lung cancer. Unfortunately, little progress has been made in improving survival rates for this malignancy over the last 30 years. Most patients experience relapse or disease progression after first-line therapy, thus a second line therapy is often required. Recently immunotherapy shows some advantages for treating relapse or refractory SCLC disease in patients. In this example, we will illustrate a single-arm phase II trial design using immunotherapy as second-line treatment for patients with SCLC. The primary endpoint of the trial is the progression-free survival (PFS). The PFS distribution of a randomized phase III trial using Topotecan as second-line treatment for patients with SCLC [17] is used as the null distribution for the trial design. The Weibull distribution is fitted to the PFS distribution with a shape parameter a=1.47327 and median survival time m₀ = 3.5 (months). Therefore, the survival distribution under the null hypothesis is $S_0(u)=e^{-\log (2){\left(u/m_0\right)}^a}$ and the cumulative hazard function is Λ₀(u) = log(2)(u/m₀)^a (Figure 1). Investigators expect that the immunotherapy could increase the median PFS from 3.5 to 5 months. Thus, the trial design is to detect a hazard ratio of (3.5/5)^1.47327 = 0.5913 under the proportional hazard model, with one-sided type I error of α = 0.05 and power of 1 − β = 80%. We assume that patients are uniformly recruited with a constant accrual rate of 2 subjects per month. We suppose the restricted follow-up period is 5 months (Figure 1), and no patients are lost to follow-up within the restricted follow-up period.

Figure 1:

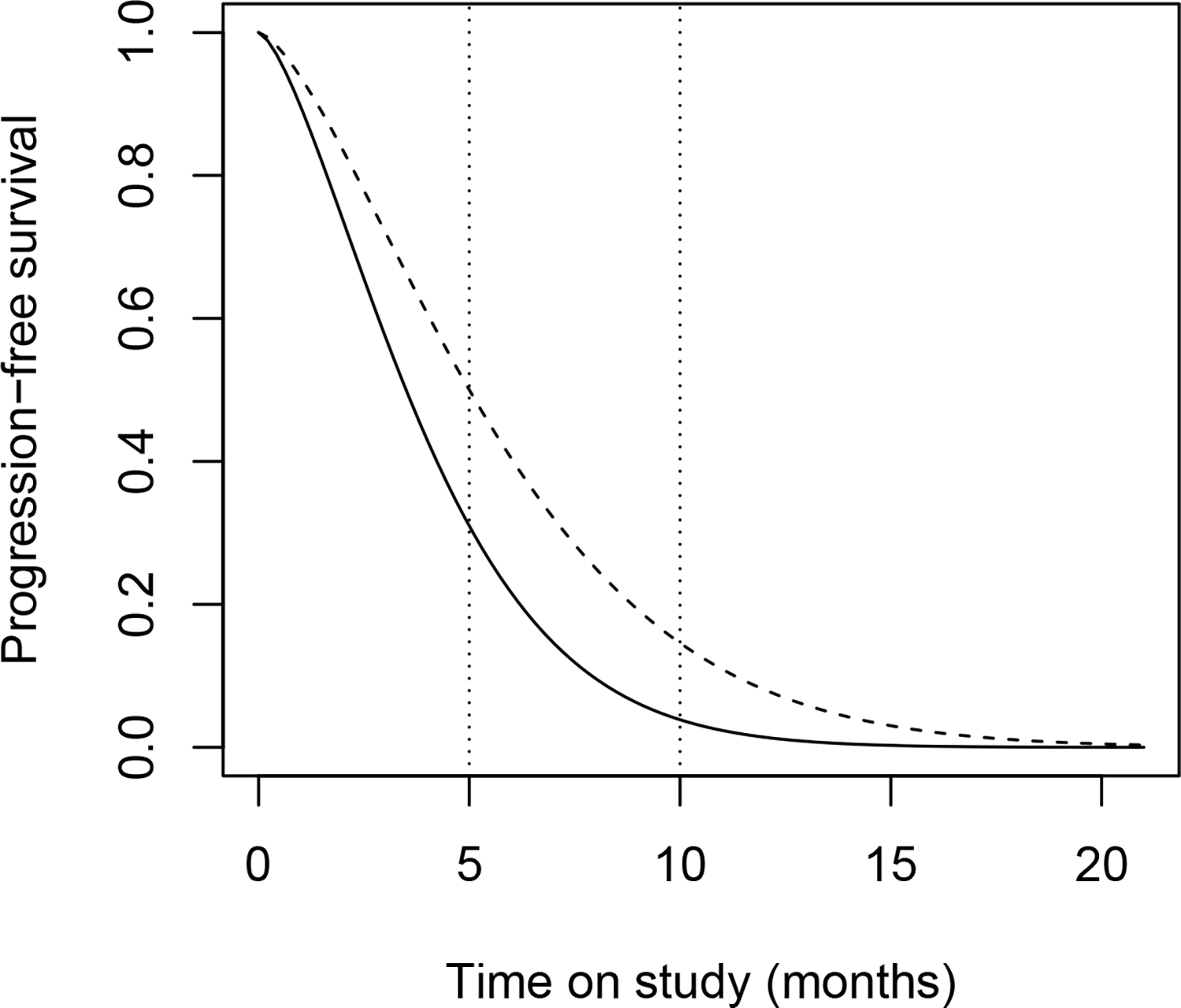
The solid curve is the fitted Weibull distribution under the null hypothesis. The dash curve is the hypothetic survival distribution under the proportional hazard alternative. The two dot lines are the restricted follow-up for 5 and 10 months, respectively.

Using the R function ‘Optimal.rKJ’ (see Appendix 2), two-stage designs under the Weibull distribution with 5 months restricted follow-up are derived as follows:

Optimal.rKJ(shape=1.47327,S0=0.5,x0=3.5,hr=0.5913,x=5,rate=2,alpha=0.05, beta=0.2,dist=“WB”)
$param
shape S0 hr alpha beta rate x0 x 
1.47327 0.5 0.5914 0.05 0.2 2 3.5 5
$Single_stage
nsingle tasingle csingle 
42 21 1.644854
$Two_stage
n1 c1 n c t1 MTSL ES PS 
28 0.0936 45 1.6269 13.6537 27.5 35.4937 0.5373

Based on this design, we will enroll 28 patients during the first stage. After all 28 patients are enrolled, we will conduct an interim analysis. At the interim analysis, each patient is followed until an event (disease progression or death) before the end of study at 5 months, or censored at the time of the interim analysis (approximately t₁ = 13.7 months) if the patient is free of an event. If the first stage test statistic Z₁ < 0.0936, we would stop the trial for futility. Otherwise, the trial would continue to the second stage and a total of 45 patients would be enrolled on the study. The final analysis would be conducted after the last patient on the study was followed for 5 months. If the second stage test statistic Z < 1.6269, we don’t reject the null hypothesis and conclude no efficacy by the treatment. If Z ≥ 1.6269, we conclude that the treatment is promising.

If the restricted follow-up is extended to 10 months (Figure 1), then the two-stage designs are given as follows:

Optimal.rKJ(shape=1.47327,S0=0.5,x0=3.5,hr=0.5913,x=10,rate=2,alpha=0.05, beta=0.2,dist=“WB”)
$param
shape S0 hr alpha beta rate x0 x 
1.47327 0.5 0.5913 0.05 0.2 2 3.5 10
$Single_stage
nsingle tasingle csingle 
28 14 1.644854
$Two_stage
n1 c1 n c t1 MTSL ES PS 
21 −0.2642 30 1.6354 10.2367 25 26.2294 0.3958

With a longer follow-up of 10 months, the total sample size would be reduced to 30 patients with 21 patients at first stage. If the first stage test statistic Z₁ < −0.2642, we would stop the trial for futility. Otherwise, the trial would continue to the second stage with a total of 30 patients. If the second stage test statistic Z < 1.6354, we conclude no efficacy by the treatment, otherwise we conclude that the treatment is promising.

5. Simulation

To study the operating characteristics of the proposed optimal two-stage design with restricted follow-up, we conducted simulation studies under various scenarios. In the simulations, the survival distribution under the null hypothesis is taken as the Weibull distribution (WB), log-normal (LN), gamma (GM) and log-logistic (LG) distributions (Table 1) with shape parameter to be 0.5, 1 and 2. The survival probabilities under null S₀ at fixed time point x₀ = 1 is set to be 0.3. The scale parameter under the null hypothesis is determined by the value of S₀(1) for each corresponding survival distribution. We assume a proportional hazard model under the alternative with a hazard ratio of δ = 0.65. The restricted follow-up time is set to x = 1 or 2, and assuming a constant accrual rate r = 10 per month, type I error of α = 0.05 and power of 80%.

The optimal two-stage designs were calculated using the R function ‘Optimal.rKJ’. Overall empirical type I errors and powers for the optimal two-stage designs were estimated based on 10,000 simulation runs (Table 2). From simulation results, we can make following conclusions. The proposed optimal two-stage design preserves type I error and power well but was slightly conservative. The optimal two-stage design increases the maximum sample size from single-stage design by a small amount and the critical value (c) for the final test is closer to that of the single stage design (z_1−α = 1.645). The two-stage designs for different scenarios were similar across the different survival distributions for a relatively short restricted follow-up period (x = 1). However more differences for the two-stage designs across the different parametric survival distributions were observed for a relatively longer restricted follow-up period (x = 2). Table 3 gives results for the comparison between proposed design to Belin’s design under the exponential model. The proposed design preserves power while Belin’s design did not preserve power for some scenarios because Belin’s design uses an approximate variance estimate that could either underestimate or overestimate the exact variance of the OSLRT [10].

Table 2:

The characteristics for optimal two-stage design with restricted follow-up x = 1, 2 under Weibull (WB), log-normal (LN), gamma (GM) and log-logistic (LG) distributions with nominal type I error 5%, power of 80%, accrual rate r = 10. Overall empirical type I error and power for the two-stage designs were estimated from 10,000 simulated trials.

Dist.	Shape	S 0	δ	x	t 1	c 1	c	n 1	n	$\widehat{\alpha }$	$1-\widehat{\beta }$
WB	0.5	.3	.65	1	3.71	0.169	1.631	38	63	.039	.796
		.3	.65	2	3.25	0.109	1.632	33	53	.038	.803
	1	.3	.65	1	3.76	0.141	1.629	38	63	.039	.796
		.3	.65	2	3.01	−0.042	1.635	31	46	.038	.813
	2	.3	.65	1	3.74	0.068	1.629	38	63	.039	.797
		.3	.65	2	2.88	−0.180	1.639	29	41	.037	.821
LN	0.5	.3	.65	1	3.84	0.110	1.628	39	63	.040	.801
		.3	.65	2	2.93	−0.160	1.638	30	42	.038	.818
	1	.3	.65	1	3.78	0.143	1.629	38	63	.040	.800
		.3	.65	2	3.12	0.046	1.632	32	48	.038	.810
	2	.3	.65	1	3.74	0.178	1.631	38	63	.040	.799
		.3	.65	2	3.25	0.098	1.631	33	54	.038	.804
GM	0.5	.3	.65	1	3.71	0.151	1.631	38	63	.040	.801
		.3	.65	2	3.13	0.055	1.633	32	50	.038	.808
	1	.3	.65	1	3.76	0.141	1.629	38	63	.040	.800
		.3	.65	2	3.01	−0.042	1.635	31	46	.037	.813
	2	.3	.65	1	3.72	0.084	1.629	38	63	.040	.801
		.3	.65	2	2.96	−0.109	1.637	30	43	.038	.815
LG	0.5	.3	.65	1	3.71	0.196	1.631	38	63	.040	.800
		.3	.65	2	3.33	0.102	1.632	34	57	.039	.803
	1	.3	.65	1	3.75	0.165	1.630	38	63	.040	.800
		.3	.65	2	3.29	0.084	1.633	33	52	.038	.805
	2	.3	.65	1	3.86	0.168	1.628	39	63	.040	.800
		.3	.65	2	3.12	0.045	1.632	32	47	.037	.810

S₀ is the survival probability at x₀ under the null hypothesis; δ is the hazard ratio; x is the restricted follow-up period; t₁ is the calendar time for the first-stage interim analysis; c₁ and c are the boundaries for the first-stage and final analysis; n₁ and n are the sample sizes for the first-stage and final analysis; Abbreviations: Dist.: distribution.

Table 3:

Comparison between the proposed optimal two-stage and Belin’s design under the exponential distribution with nominal type I error 5% and power of 80%, a constant accrual rate r = 10, a restricted follow-up x = 1 and x₀ = 1. Overall empirical type I error ($\widehat{\alpha }$) and power ($1-\widehat{\beta }$) for the two-stage designs were estimated from 10,000 simulated trials.

(S0, S1)	t 1	c 1	c	ES	ETSL	n 1	n	PS	$\widehat{\alpha }$	$1-\widehat{\beta }$
Belin’s two-stage design under exponential model
(.1, .3)	1.11	0.068	1.615	14.8	2.9	12	19	0.53	.033	.727
(.1, .25)	1.67	0.097	1.673	22.9	4.0	17	30	0.54	.035	.722
(.2, .4)	1.72	0.082	1.621	23.2	4.0	18	30	0.53	.036	.748
(.2, .35)	2.84	0.150	1.623	37.9	6.0	29	50	0.56	.037	.750
(.3, .5)	2.16	0.107	1.621	29.1	4.8	22	38	0.54	.037	.764
(.3, .45)	3.68	0.358	1.627	49.0	7.4	37	64	0.55	.039	.765
(.4, .6)	2.50	0.167	1.622	32.4	5.2	25	42	0.57	.039	.780
(.4, .55)	4.11	0.137	1.626	55.3	8.3	42	73	0.55	.040	.777
(.5, .7)	2.44	0.114	1.621	32.9	5.3	25	43	0.55	.038	.797
(.5, .65)	4.27	0.149	1.626	56.9	8.5	43	75	0.56	.039	.789
(.6, .8)	2.28	0.106	1.620	30.7	5.0	23	40	0.54	.037	.814
(.6, .75)	3.93	0.122	1.624	53.6	8.1	40	71	0.55	.039	.802
(.7, .85)	3.42	0.191	1.618	45.6	7.1	35	61	0.58	.040	.827
Proposed two-stage design under exponential model
(.1, .3)	1.48	−0.106	1.638	18.7	3.2	15	22	0.46	.032	.786
(.1, .25)	2.21	0.054	1.634	28.3	4.5	23	35	0.52	.038	.810
(.2, .4)	2.12	0.052	1.633	26.8	4.3	22	33	0.52	.036	.784
(.2, .35)	3.33	0.110	1.632	43.2	6.5	34	55	0.54	.038	.801
(.3, .5)	2.48	0.082	1.631	31.9	5.0	26	40	0.53	.038	.800
(.3, .45)	4.12	0.130	1.632	53.2	7.8	42	68	0.55	.039	.798
(.4, .6)	2.56	0.129	1.623	33.9	5.4	26	44	0.55	.039	.797
(.4, .55)	4.46	0.185	1.627	58.0	8.6	45	76	0.57	.040	.797
(.5, .7)	2.54	0.184	1.620	32.9	5.3	26	43	0.57	.038	.798
(.5, .65)	4.45	0.202	1.625	57.7	8.6	45	76	0.58	.039	.797
(.6, .8)	2.14	0.121	1.616	28.9	4.8	22	38	0.55	.038	.795
(.6, .75)	3.87	0.135	1.617	52.2	7.9	39	69	0.55	.039	.793
(.7, .85)	2.98	0.126	1.682	41.6	6.6	30	56	0.55	.040	.791

S₀ and S₁ are the survival probabilities at x₀ under the null hypothesis and alternative, respectively; t₁ is the calendar time for the first-stage interim analysis; c₁ and c are the boundaries for the first-stage and final analysis; n₁ and n are the sample sizes for the first-stage and final analysis; PS is the stopping probability of first stage under the null hypothesis; ES is the expected sample size under the null hypothesis; ETSL is expected total study duration.

6. Conclusion

An optimal two-stage design is developed for single-arm phase II trial with a time-to-event endpoint. Four commonly used parametric survival distributions: Weibull, log-normal, gamma, log-logistic have been implemented in the R function ‘Optimal.rKJ’. If none of the four parametric survival distributions fit the null distribution, then, a non-parametric logspline distribution can be applied for the trial design. Simulations were conducted to study the operating characteristics of the proposed two-stage design with restricted follow-up. The simulation results showed that the proposed design preserved the overall type I error and power well but was slightly conservative. The two-stage designs are very similar across the four parametric survival distributions for a relatively shorter restricted follow-up period and more differences are expected for a relatively longer restricted follow-up period. Because of the flexibility, the proposed method can be routinely used for two-stage design for single-arm phase II trial as the counterpart of Simon’s two-stage design for TTE endpoint.

Appendix 1: Derivation of equations (4) and (5).

If (X, Y) is a bivariate normal random vector with mean μ = (μ₁, μ₂) and variance matrix

$$\mathrm{\Sigma }=\left(\begin{array}{cc}{\sigma }_1^2& \rho {\sigma }_1{\sigma }_2\\ \rho {\sigma }_1{\sigma }_2& {\sigma }_2^2\end{array}\right)$$

then, the conditional distribution of X given Y = y is normal with mean μ₁ + (ρσ₁/σ₂)(y − μ₂) and variance ${\sigma }_1^2\left(1-{\rho }^2\right)$.

As under the null hypothesis H₀, (Z₁, Z) is approximately bivariate normal distributed with mean μ = (0, 0)′ and variance matrix

$$\mathrm{\Sigma }=\left(\begin{array}{ll}1\hfill & {\rho }_0\hfill \\ {\rho }_0\hfill & 1\hfill \end{array}\right)$$

Thus, by conditional distribution integration, we obtain

$$\begin{array}{l}\alpha =P\left(Z_1>c_1,Z>c\mid H_0\right)\\ ={\int }_{-\infty }^{\infty }\varphi (z)P\left(Z_1>c_1,Z>c\mid Z=z,H_0\right)dz\\ ={\int }_c^{\infty }\varphi (z)P\left(Z_1>c_1\mid Z=z,H_0\right)dz\\ ={\int }_c^{\infty }\varphi (z)\mathrm{\Phi }\left(\frac{{\rho }_{0}z-c_1}{\sqrt{1-{\rho }_0^2}}\right)dz.\end{array}$$

Similarly, under the alternative H₁, (Z₁, Z) is approximately bivariate normal distributed with mean $\mu ={\left(\sqrt{n_1}{\omega }_1/{\sigma }_{01},\sqrt{n}\omega /{\sigma }_0\right)}^{\prime }$ and variance matrix

$$\mathrm{\Sigma }=\left(\begin{array}{cc}{\sigma }_{11}^2/{\sigma }_{01}^2& {\rho }_1{\sigma }_{11}{\sigma }_1/{\sigma }_{01}{\sigma }_0\\ {\rho }_1{\sigma }_{11}{\sigma }_1/{\sigma }_{01}{\sigma }_0& {\sigma }_1^2/{\sigma }_0^2\end{array}\right)$$

Thus, after standardization, we have

$$\text{power}=P\left({\overline{Z}}_1>\overline{c_1},\overline{Z}>\overline{c}\mid H_1\right)$$

where ${\overline{Z}}_1=\frac{{\sigma }_{01}}{{\sigma }_{11}}(Z_1-\frac{\sqrt{n_1}{\omega }_1}{{\sigma }_{01}})$ and ${\overline{c}}_1=\frac{{\sigma }_{01}}{{\sigma }_{11}}(c_1-\frac{\sqrt{n_1}{\omega }_1}{{\sigma }_{01}})$ and $\overline{Z}=\frac{{\sigma }_0}{{\sigma }_1}(Z-\frac{\sqrt{n}\omega }{{\sigma }_0})$ and $\overline{c}=\frac{{\sigma }_0}{{\sigma }_1}(c-\frac{\sqrt{n}\omega }{{\sigma }_0})$. Thus, $({\overline{Z}}_1,\overline{Z})$ is bivariate normal with zero means, unit variances and correlation ρ₁. Again by conditional distribution integration, we have

$$\begin{array}{l}\text{power}=P\left({\overline{Z}}_1>{\overline{c}}_1,\overline{Z}>\overline{c}\mid H_1\right)\\ ={\int }_{-\infty }^{\infty }\varphi (z)P\left({\overline{Z}}_1>{\overline{c}}_1,\overline{Z}>\overline{c}\mid \overline{Z}=z,H_1\right)dz\\ ={\int }_c^{\infty }\varphi (z)P\left({\overline{Z}}_1>{\overline{c}}_1\mid \overline{Z}=z,H_0\right)dz\\ ={\int }_{\overline{c}}^{\infty }\varphi (z)\mathrm{\Phi }\left(\frac{{\rho }_{1}z-{\overline{c}}_1}{\sqrt{1-{\rho }_1^2}}\right)dz.\end{array}$$

Appendix 2: R code for optimal two-stage design with restricted follow-up and PBC data

#################### Optimal.rKJ Input parameters #############################
### shape is the shape parameter for one the four parametric distributions;###
### S0 is the survival probability at fixed time point x0 under the null; ###
### hr is inverse of hazard ratio; x is fixed follow-up time period; ###
### rate is constant accrual rate; alpha and beta are type I and II errors ### ### 
dist is distribution option with ‘WB’ as Weibull, ‘GM’ as Gamma,’LN’ as###
### log-normal, ‘LG’ as log-logistic, ‘SP’ as logspline; data is used for ###
### fit logspline; if dist=‘SP’, there is no need to input shape,S0, x0 ###
############################################################################### 
library(survival) 
library(logspline)
Optimal.rKJ<-function(shape,S0,x0,hr,x,rate,alpha,beta,dist,data)
{ 
calculate_alpha<-function(c2, c1, rho0){ 
fun1<-function(z, c1, rho0){ 
f<-dnorm(z)*pnorm((rho0*z-c1)/sqrt(1-rho0^2)) 
return(f) 
} 
alpha<-integrate(fun1, lower= c2, upper= Inf, c1, rho0)$value 
return(alpha)
}
calculate_power<-function(cb, cb1, rho1){ 
fun2<-function(z, cb1, rho1){ 
f<-dnorm(z)*pnorm((rho1*z-cb1)/sqrt(1-rho1^2)) 
return(f) 
} 
pwr<-integrate(fun2,lower=cb,upper=Inf,cb1=cb1,rho1=rho1)$value 
return(pwr)
}
fct<-function(zi, ceps=0.0001,alphaeps=0.0001,nbmaxiter=100,dist){ 
ta<-as.numeric(zi[1]) 
t1<-as.numeric(zi[2]) 
c1<-as.numeric(zi[3])
if (dist==“WB”){ 
s0=function(u){1-pweibull(u,shape,scale0)} 
f0=function(u){dweibull(u,shape,scale0)} 
h0=function(u){f0(u)/s0(u)} 
H0=function(u){-log(s0(u))} 
s=function(b,u) {s0(u)^b} 
h=function(b,u){b*f0(u)/s0(u)} 
H=function(b,u){-b*log(s0(u))} 
scale0=x0/(−log(S0))^(1/shape) 
scale1=hr 
}
if (dist==“LN”){ 
s0=function(u){1-plnorm(u,scale0,shape)} 
f0=function(u){dlnorm(u,scale0,shape)} 
h0=function(u){f0(u)/s0(u)} 
H0=function(u){-log(s0(u))} 
s=function(b,u) {s0(u)^b} 
h=function(b,u){b*f0(u)/s0(u)} 
H=function(b,u){-b*log(s0(u))} 
scale0=log(x0)-shape*qnorm(1-S0) 
scale1=hr 
}
if (dist==“LG”){ 
s0=function(u){1/(1+(u/scale0)ŝhape)} 
f0=function(u){(shape/scale0)*(u/scale0)^(shape-1)/(1+(u/scale0)ŝhape)^2} 
h0=function(u){f0(u)/s0(u)} 
H0=function(u){-log(s0(u))} 
s=function(b,u) {s0(u)^b} 
h=function(b,u){b*f0(u)/s0(u)} 
H=function(b,u){-b*log(s0(u))} 
scale0=x0/(1/S0–1)^(1/shape) 
scale1=hr 
}
if (dist==“GM”){ 
s0=function(u){1-pgamma(u,shape,scale0)} 
f0=function(u){dgamma(u,shape,scale0)} 
h0=function(u){f0(u)/s0(u)} 
H0=function(u){-log(s0(u))} 
s=function(b,u) {s0(u)^b} 
h=function(b,u){b*f0(u)/s0(u)} 
H=function(b,u){-b*log(s0(u))} 
root0=function(t){1-pgamma(x0,shape,t)-S0} 
scale0=uniroot(root0,c(0,10))$root 
scale1=hr 
}
if (dist==“SP”){ 
time=data$time 
status=data$status 
fitSP=oldlogspline(time[status==1],time[status==0],lbound=0) 
s0=function(u){1-poldlogspline(u, fitSP)} 
f0=function(u){doldlogspline(u, fitSP)} 
h0=function(u){f0(u)/s0(u)} 
H0=function(u){-log(s0(u))} 
s=function(b,u) {s0(u)^b} 
f=function(b,u){b*f0(u)/s0(u)^(1-b)} 
h=function(b,u){b*f0(u)/s0(u)} 
H=function(b,u){-b*log(s0(u))} 
scale1=hr 
}
g0=function(t){s(scale1,t)*h0(t)} 
g1=function(t){s(scale1,t)*h(scale1,t)} 
g00=function(t){s(scale1,t)*H0(t)*h0(t)} 
g01=function(t){s(scale1,t)*H0(t)*h(scale1,t)} 
p0=integrate(g0, 0, x)$value 
p1=integrate(g1, 0, x)$value 
p00=integrate(g00, 0, x)$value 
p01=integrate(g01, 0, x)$value 
sigma2.1=p1-p1^2+2*p00-p0^2–2*p01+2*p0*p1 
sigma2.0=p0 
om=p0-p1
G1=function(t){1-punif(t, t1-ta, t1)} 
g0=function(t){s(scale1,t)*h0(t)*G1(t)} 
g1=function(t){s(scale1,t)*h(scale1,t)*G1(t)} 
g00=function(t){s(scale1,t)*H0(t)*h0(t)*G1(t)} 
g01=function(t){s(scale1,t)*H0(t)*h(scale1,t)*G1(t)} 
p0=integrate(g0, 0, x)$value 
p1=integrate(g1, 0, x)$value 
p00=integrate(g00, 0, x)$value 
p01=integrate(g01, 0, x)$value 
sigma2.11=p1-p1^2+2*p00-p0^2–2*p01+2*p0*p1 
sigma2.01=p0 
om1=p0-p1
q1=function(t){s0(t)*h0(t)*G1(t)} 
q=function(t){s0(t)*h0(t)} 
v1=integrate(q1, 0, x)$value 
v=integrate(q, 0, x)$value 
rho0=sqrt(v1/v) 
rho1<-sqrt(sigma2.11/sigma2.1)
cL<-(−10) 
cU<-(10) 
alphac<−100 
iter<−0 
while ((abs(alphac-alpha)>alphaeps|cU-cL>ceps)&iter<nbmaxiter){ 
iter<-iter+1 
c<-(cL+cU)/2 
alphac<-calculate_alpha(c, c1, rho0) 
if (alphac>alpha) { 
cL<-c
} else {
cU<-c
} 
}
cb1<-sqrt((sigma2.01/sigma2.11))*(c1-(om1*sqrt(rate*t1)/sqrt(sigma2.01)))
cb<-sqrt((sigma2.0/sigma2.1))*(c-(om*sqrt(rate*ta))/sqrt(sigma2.0)) 
pwrc<-calculate_power(cb=cb, cb1=cb1, rho1=rho1) 
res<-c(cL, cU, alphac, 1-pwrc, rho0, rho1, cb1, cb) 
return(res)
}
c1<−0 ; rho0<−0; cb1<−0; rho1<−0 ; hz<-c(0,0); 
ceps<−0.001;alphaeps<−0.001;nbmaxiter<−100
if (dist==“WB”){ 
s0=function(u){1-pweibull(u,shape,scale0)} 
f0=function(u){dweibull(u,shape,scale0)} 
h0=function(u){f0(u)/s0(u)} 
H0=function(u){-log(s0(u))} 
s=function(b,u) {s0(u)^b} 
h=function(b,u){b*f0(u)/s0(u)} 
H=function(b,u){-b*log(s0(u))} 
scale0=x0/(−log(S0))^(1/shape) 
scale1=hr 
}
if (dist==“LN”){ 
s0=function(u){1-plnorm(u,scale0,shape)} 
f0=function(u){dlnorm(u,scale0,shape)} 
h0=function(u){f0(u)/s0(u)} 
H0=function(u){-log(s0(u))} 
s=function(b,u) {s0(u)^b} 
h=function(b,u){b*f0(u)/s0(u)} 
H=function(b,u){-b*log(s0(u))} 
scale0=log(x0)-shape*qnorm(1-S0) 
scale1=hr 
}
if (dist==“LG”){ 
s0=function(u){1/(1+(u/scale0)ŝhape)} 
f0=function(u){(shape/scale0)*(u/scale0)^(shape-1)/(1+(u/scale0)ŝhape)^2}
h0=function(u){f0(u)/s0(u)} 
H0=function(u){-log(s0(u))} 
s=function(b,u) {s0(u)^b} 
h=function(b,u){b*f0(u)/s0(u)} 
H=function(b,u){-b*log(s0(u))} 
scale0=x0/(1/S0–1)^(1/shape) 
scale1=hr 
}
if (dist==“GM”){
s0=function(u){1-pgamma(u,shape,scale0)} 
f0=function(u){dgamma(u,shape,scale0)} 
h0=function(u){f0(u)/s0(u)} 
H0=function(u){-log(s0(u))} 
s=function(b,u) {s0(u)^b} 
h=function(b,u){b*f0(u)/s0(u)} 
H=function(b,u){-b*log(s0(u))} 
root0=function(t){1-pgamma(x0,shape,t)-S0} 
scale0=uniroot(root0,c(0,10))$root 
scale1=hr 
}
if (dist==“SP”){ 
time=data$time 
status=data$status 
fitSP=oldlogspline(time[status==1],time[status==0],lbound=0) 
s0=function(u){1-poldlogspline(u, fitSP)} 
f0=function(u){doldlogspline(u, fitSP)} 
h0=function(u){f0(u)/s0(u)} 
H0=function(u){-log(s0(u))} 
s=function(b,u) {s0(u)^b} 
f=function(b,u){b*f0(u)/s0(u)^(1-b)} 
h=function(b,u){b*f0(u)/s0(u)} 
H=function(b,u){-b*log(s0(u))} 
scale1=hr 
}
g0=function(t){s(scale1,t)*h0(t)} 
g1=function(t){s(scale1,t)*h(scale1,t)} 
g00=function(t){s(scale1,t)*H0(t)*h0(t)} 
g01=function(t){s(scale1,t)*H0(t)*h(scale1,t)} 
p0=integrate(g0, 0, x)$value 
p1=integrate(g1, 0, x)$value 
p00=integrate(g00, 0, x)$value 
p01=integrate(g01, 0, x)$value 
s1=sqrt(p1-p1^2+2*p00-p0^2–2*p01+2*p0*p1) 
s0=sqrt(p0) 
om=p0-p1 
nsingle<-(s0*qnorm(1-alpha)+s1*qnorm(1-beta))^2/om^2 
nsingle<-ceiling(nsingle) 
tasingle<-nsingle/rate
Single_stage<-data.frame(nsingle=nsingle,tasingle=tasingle, csingle=qnorm(1-alpha))
atc0<-data.frame(n=nsingle, t1=tasingle, c1=0.25) 
nbpt<−11 
pascote<−1.26 
cote<−1*pascote 
c1.lim<-nbpt*c(−1,1) 
EnH0<−10000 
iter<−0
while (iter<nbmaxiter & diff(c1.lim)/nbpt>0.001){
iter<-iter+1 
cat(“iter=“,iter,”&EnH0=“,round(EnH0, 2),”& Dc1/nbpt=“, round(diff(c1.lim)/nbpt,5),”\n”,sep=““)
if (iter%%2==0) nbpt<-nbpt+1 
cote<-cote/pascote
n.lim<-atc0$n+c(−1, 1)*nsingle*cote 
t1.lim<-atc0$t1+c(−1, 1)*tasingle*cote 
c1.lim<-atc0$c1+c(−1, 1)*cote 
ta.lim<-n.lim/rate 
t1.lim<-pmax(0, t1.lim) 
n<-seq(n.lim[1], n.lim[2], l=nbpt) 
n<-ceiling(n)
n<-unique(n) 
ta<-n/rate 
t1<-seq(t1.lim[1], t1.lim[2], l=nbpt) 
c1<-seq(c1.lim[1], c1.lim[2], l=nbpt) 
ta<-ta[ta>0] 
t1<-t1[t1>=0.2*tasingle & t1<=1.2*tasingle] 
z<-expand.grid(list(ta=ta, t1=t1, c1=c1)) 
z<-z[z$ta>z$t1,] 
nz<-dim(z)[1] 
z$pap<-pnorm(z$c1) 
z$eta<-z$ta-pmax(0, z$ta-z$t1)*z$pap 
z$enh0<-z$eta*rate 
z<-z[z$enh0<=EnH0,] 
nz1<-dim(z)[1]
resz<-t(apply(z,1,fct,ceps=ceps,alphaeps=alphaeps,nbmaxiter=nbmaxiter, dist=dist)) 
resz<-as.data.frame(resz) 
names(resz)<-c(“cL”,”cU”,”alphac”,”betac”,”rho0”,”rho1”,”cb1”,”cb”) 
r<-cbind(z, resz) 
r$pap<-pnorm(r$c1) 
r$eta<-r$ta-pmax(0, r$ta-r$t1)*r$pap 
r$etar<-r$eta*rate 
r$tar<-r$ta*rate 
r$c<-r$cL+(r$cU-resz$cL)/2 
r$diffc<-r$cU-r$cL 
r$diffc<-ifelse(r$diffc<=ceps, 1, 0) 
r<-r[1-r$betac>=1-beta,] 
r<-r[order(r$enh0),] 
r$n<-r$ta*rate
if (dim(r)[1]>0) { 
atc<-r[, c(“ta”, “t1”, “c1”, “n”)][1,] 
r1<-r[1,] 
if (r1$enh0<EnH0) { 
EnH0<-r1$enh0 
atc0<-atc
}
} else {
atc<-data.frame(ta=NA, t1=NA, c1=NA, n=NA)
} 
atc$iter<-iter 
atc$enh0<-r$enh0[1] 
atc$EnH0<-EnH0 
atc$tai<-ta.lim[1] 
atc$tas<-ta.lim[2] 
atc$ti<-t1.lim[1] 
atc$ts<-t1.lim[2] 
atc$ci<-c1.lim[1] 
atc$cs<-c1.lim[2] 
atc$cote<-cote
if (iter==1) { 
atcs<-atc
} else {
atcs<-rbind(atcs, atc)
} 
} 
atcs$i<−1:dim(atcs)[1] 
a<-atcs[!is.na(atcs$n),]
p<-t(apply(a,1,fct,ceps=ceps,alphaeps=alphaeps,nbmaxiter=nbmaxiter, dist=dist)) 
p<-as.data.frame(p) 
names(p)<-c(“cL”,”cU”,”alphac”,”betac”,”rho0”,”rho1”,”cb1”,”cb”) 
p$i<-a$i
res<-merge(atcs, p, by=“i”, all=T) 
res$pap<-round(pnorm(res$c1),4) ## stopping prob of stage 1 ##
res$ta<-res$n/rate 
res$Enh0<-(res$ta-pmax(0, res$ta-res$t1)*res$pap)*rate 
res$diffc<-res$cU-res$cL
res$c<-round(res$cL+(res$cU-res$cL)/2,4) 
res$diffc<-ifelse(res$diffc<=ceps, 1, 0) 
res<-res[order(res$enh0),]
des<-round(res[1,],4)
if (dist==“SP”){ 
param<-data.frame(hr=hr, alpha=alpha, beta=beta, rate=rate, x=x)} 
else { 
param<-data.frame(shape=shape,S0=S0,hr=hr,alpha=alpha,beta=beta, rate=rate, x0=x0, x=x) }
Two_stage<- data.frame(n1= ceiling(des$t1*param$rate), c1=des$c1, n=ceiling(des$ta*param$rate), c=des$c, t1=des$t1, MTSL=des$ta+param$x, ES=des$Enh0, PS=des$pap) 
DESIGN<-list(param=param,Single_stage=Single_stage,Two_stage=Two_stage) 
return(DESIGN)}