Abstract
Cemented paste backfill (CPB) is wildly used in mines production practices around the world. The strength of CPB is the core of research which is affected by factors such as slurry concentration and cement content. In this paper, a research on the UCS is conducted by means of a combination of laboratory experiments and machine learning. BPNN, RBFNN, GRNN and LSTM are trained and used for UCS prediction based on 180 sets of experimental UCS data. The simulation results show that LSTM is the neural network with the optimal prediction performance (The total rank is 11). The trial-and-error, PSO, GWO and SSA are used to optimize the learning rate and the hidden layer nodes for LSTM. The comparison results show that GWO-LSTM is the optimal model which can effectively express the non-linear relationship between underflow productivity, slurry concentration, cement content and UCS in experiments (, RMSE = 0.0204, VAF = 98.2847 and T = 16.37 s). The correction coefficient (k) is defined to adjust the error between predicted UCS in laboratory (UCSM) and predicted UCS in actual engineering (UCSA) based on extensive engineering and experimental experience. Using GWO-LSTM combined with k, the strength of the filling body is successfully predicted for 153 different filled stopes with different stowing gradient at different curing times. This study provides both effective guidance and a new intelligent method for the support of safety mining.
Keywords: Backfill, Uniaxial compressive strength, Cemented paste backfill, Neural network, Optimization
Backfill; Uniaxial compressive strength; Cemented paste backfill; Neural network; Optimization
1. Introduction
Filling mining is a green and efficient mining method that can both recycle solid waste in mine and improve the safety of underground mining operations [1], [2], [3], [4]. It is widely used in mines all around the world because it can effectively solve the safety hazards from the mined-out areas and tailings reservoir [5], [6], [7], [8]. Cemented paste backfill (CPB) is an important technology in filling mining methods which uses tailings, waste rock or river sand as aggregate and mixed it with binder to make a filling slurry and then filled it into the mined-out area [9], [10], [11], [12], [13], [14]. CPB forms a filling body with strength and can effectively support the mined-out area. Uniaxial compressive strength (UCS) is the essential strength metric for CPB, which is affected by slurry concentration, binder content, curing time and particle size for tailings [15], [16], [17], [18], [19], [20]. Many scholars have conducted mechanistic modeling of UCS based on different affecting factors and have achieved instructive results [21], [22], [23], [24], [25]. However, the CPB is a complex multiphase mixture and the formation of UCS depends on the hydration of the binder and the coupling effect of different factors. Therefore, the use of simple mechanistic modeling cannot construct a valid mapping relationship between UCS and different affecting factors.
In the age of artificial intelligence, many scholars have done prospective and innovative studies on predicting UCS in recent years, as detailed in Table 1 [1], [20], [26], [27], [28], [29], [30], [31]. Artificial neural networks (ANN), a popular branch of machine learning technology, have been widely used in various engineering practices and modeling. ANN processes complex information by simulating the nervous system of the human brain and have a unique knowledge representation and intelligent adaptive learning capability. Meanwhile, intelligent optimization algorithms (IOA) as the core of artificial intelligence have also gained popularity in engineering, especially in the field of optimization in engineering design. IOA can rapidly solve optimization problems in multidimensional spaces that are difficult to solve by traditional computational methods. In filling mining, ANN and IOA are combined and applied in the strength design of the CPB. This is because IOA can be used to optimize ANN for parameters such as hidden layer nodes and learning rate. Many researchers have done a lot of research on the application of ANN and IOA in filling mining.
Table 1.
Summary of ANN and IOA applications in filling mining.
| Authors | Publish time | Main methods | Input | Output |
|---|---|---|---|---|
| Sivakugan et al. [29] | 2005 | ANN | Cement content, solids content, curing time and grain size distribution | Strength |
| Orejarena et al. [31] | 2010 | ANN | Water-cement ratios, binder composition and binder content | 150d UCS |
| Qi et al. [28] | 2018 | PSO, ANN | Tailings type, cement-tailings ratio, solids content, and curing time | 3d, 7d, 28d UCS |
| Qi et al. [26] | 2018 | PSO | Physical and chemical characteristics of tailings, cement-tailings ratio, solids content, and curing time. | 7d, 28d UCS |
| Qi et al. [27] | 2018 | GA | Physical and chemical characteristics of tailings, the cement-tailings ratio, the solids content, and the curing time | 28d UCS |
| Xiao et al. [30] | 2020 | ANN | Proportion of OPC, CG, CFA, and YS, solids content, and curing time | 1d, 3d, 28d UCS |
| Yu et al. [20] | 2021 | ELM, SSA | Cement-to-tailing mass ratio, solid mass concentration, fiber content, fiber length, and curing time | 3d. 7d, 28d, and 56d UCS |
| Li et al. [1] | 2021 | GA, PSO, SSA | Fiber properties, cement type, curing time, cement–tailings ratio and concentration | 3d, 7d, 28d UCS |
As can be seen in Table 1, ANN and IOA have been shown to have excellent application in filling mining, especially in predicting the UCS of CPB, in previous researches. However, traditional ANNs suffer from gradient disappearance and gradient explosion in predicting UCS [26], [27], [28]. In addition, the neurons of the hidden layer in a traditional ANN are independent and do not affect each other, which makes the ANN lack the memory and storage function of data when processing information [32]. In filling mining, different materials and multiple factors have different degrees of effect on the strength of the filling body. Besides, force majeure factors such as uneven slurry mixing and impurity mixing during the experimental process can also affect UCS. This can lead to outliers in the UCS obtained from laboratory experiments [15], [16], [17], [18], [19], [20]. In the conditions of above problems, the weakness of traditional ANNs without data storage and memory mechanisms is exposed, which makes the accuracy of the constructed UCS prediction models also suffer. This not only affect the accuracy of ANN in predicting UCS, but also limit the in-depth application of ANN in filling mining. In a word, the traditional ANN in predicting UCS needs to be improved to suit the requirements of future mine intelligence development.
Long short-term memory neural network (LSTM), as a new neural network with excellent generalization ability and robustness, is currently less used in fill mining [33], [34]. Its unique gating mechanism changed the structure of the traditional ANN, which gives ANN the function of memorializing and forgetting information [35]. The core of this study is to explore and construct the prediction model for UCS of CPB with LSTM as the fundamental model and IOA as the optimization method.
In this paper, section 2 and section 3 explain that underflow productivity for tailings, slurry concentration, cement content and curing time are used as affecting factors to design the mix proportion experiments of the filling slurry and 180 sets of experimental data are obtained after the UCS test. Section 4 presents four neural networks, four optimization algorithms, and the performance metrics in this study. Section 5 illustrates the process of selecting LSTM as the basic model for this study by comparing the prediction accuracy of different neural networks. Section 6 illustrates the accuracy of the improved LSTM prediction of UCS of CPB using different optimization algorithms and determines the LSTM improved by grey wolf optimization (GWO-LSTM) model as the optimal prediction model. In section 7, GWO-LSTM that is the optimal model, is combined with the correction coefficient (k) to predict the strength of the filling body of 153 approaches in filled stope. This study not only provides guidance for safety mining, but also bring new tools for the intelligent development of mines.
2. Materials
The material used to prepare CPB is generally composed of two parts: aggregate and binder. Aggregate, an inert material, is used to form the skeleton structure of CPB to enhance durability and effectively inhibit crack expansion. Commonly used aggregates are tailings, river sand and wind sand, etc. The binder mainly plays the role of gelling effect, which triggers the hydration reaction after mixing with water and generates hydration products to fill the gaps between the aggregates. Commonly used binders are cement, fly ash, slag powder, etc. The combination of the skeletal structure formed by the aggregates and the gelling effect of the binder gives CPB its strength. In this study, tailings and cement are used as aggregate and binder, respectively.
2.1. Tailings
The tailings used in this study are from the Jinfeng Mining Limited (Gold Mine), Southwest of Guizhou province, China. The composition of the tailings by using X-ray fluorescence (XRF) is shown in Table 2. From the Table 2, the main composition of the tailings is SiO2, which indicates that the tailings is an inert material and can be used as an aggregate to produce the filling slurry. Due to the fine size of the tailings, the hydrocyclone is used to classify the tailings and obtained classified tailings with underflow productivity of 45%, 55%, 65% and 75% respectively. The comparison of particle size for tailings of different underflow productivity is shown in Table 3.
Table 2.
The main chemical composition of the tailings.
| Composition | SiO2 | CaO | MgO | Fe2O3 | Al2O3 | Others |
|---|---|---|---|---|---|---|
| Content (%) | 69.3 | 2.47 | 0.59 | 2.03 | 18.84 | 6.77 |
Table 3.
The comparison of particle size for tailings of different underflow productivity.
| Underflow productivity | Main particle size and cumulative proportion |
|||||
|---|---|---|---|---|---|---|
| −5 μm | −10 μm | −20 μm | −30 μm | −45 μm | −75 μm | |
| 100% | 30.07% | 44.44% | 58.92% | 70.73% | 79.31% | 96.08% |
| 75% | 30.53% | 41.30% | 52.81% | 64.44% | 74.62% | 96.14% |
| 65% | 23.92% | 33.20% | 43.87% | 58.65% | 72.08% | 94.09% |
| 55% | 18.76% | 26.80% | 36.32% | 50.86% | 65.39% | 93.82% |
| 45% | 13.24% | 20.36% | 29.52% | 42.55% | 57.38% | 83.67% |
2.2. Binder
The binder is the Portland cement (P.O42.5). The density of cement is 3.1 g/cm3 and the 28d compressive strength is higher than 45 MPa. The cement performance parameter is shown in Table 4.
Table 4.
The cement performance parameter.
| Level | Fineness | Bending strength | Compressive strength | Setting time | |||
|---|---|---|---|---|---|---|---|
| P.O42.5 | ≤6.0% | 3d | 28d | 3d | 28d | Initial | Final |
| 17 MPa | 20 MPa | ≥25 MPa | ≥45 MPa | 2.0h | 4.0h | ||
3. Experiments
UCS is an important indicator used to evaluate whether CPB fulfills engineering standards. The level of UCS affects whether CPB satisfies the requirements of mine safety production. The current methods of measuring the UCS of CPB are mainly mix proportion experiments in the laboratory and the UCS test using a hydraulic testing machine.
3.1. Mix proportion of materials
In this study, proportional tests are conducted with underflow productivity, slurry concentration, cement content and curing time as the main affecting factors of UCS of CPB. The mix proportions are shown in Table 5.
Table 5.
The mix proportion of materials.
| Affecting factors | Mix proportion | ||||
|---|---|---|---|---|---|
| Underflow productivity | 45% | 55% | 65% | 75% | ﹨ |
| Slurry concentration | 63% | 64% | 65% | ﹨ | ﹨ |
| Cement content | 5% | 5.5% | 6% | 6.5% | 7% |
| Curing time | 5d | 7d | 28d | ﹨ | ﹨ |
3.2. Experimental process
The tailings and cement used in the experiment are weighed according to the different mix proportions in section 3.1 and the backfill slurry is prepared according to Chinese standards GBT17671-1999. First, the solid materials are mixed according to above proportions for not less than 5 minutes. Then, put the mixture into a bucket with water and blend for 5 min by using a handheld electric mixer. Lastly, the prepared slurry is poured into a mold with a size of 70.7 mm × 70.7 mm × 70.7 mm. After the specimen is shaped, the mold is dismantled and the specimen is placed in the standard curing room (the temperature is 20 °C and the humidity range is 90-95%) to cure until the predetermined curing time. In addition, 3 specimens are made for each mix proportion and the UCS is taken as their average. Finally, the cured specimens are tested with a press for UCS and 180 sets of UCS data are obtained. The flow of the experiments is shown in Fig. 1
Figure 1.

The flow of the experiments (preparing materials, mixing slurry, making and curing specimen).
3.3. Experiment results
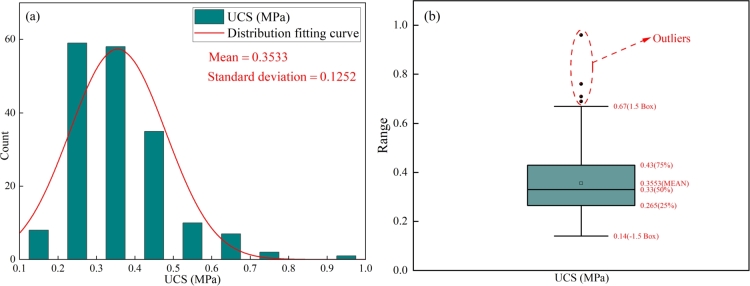
The experimental results of UCS are shown in Fig. 2. From Fig. 2(a), the mean of UCS obtained from the experiment is 0.3533 and the standard deviation is 0.1252. From Fig. 2(b), the minimum, maximum, first quartile (Q1), third quartile (Q2) and median of UCS are 0.14, 0.96, 0.265, 0.43 and 0.33, respectively. Set the two values of Q3 and Q1 plus or minus 1.5 times the interquartile distance (Q1-1.5 IQR and Q3+1.5 IQR) as the truncation points of the outliers. There are 4 outliers in the experimental UCS and they are all distributed in the upper side of Q3+1.5 IQR, which is the reason for the rightward bias of the distribution of UCS in Fig. 2(a). From Fig. 2, the experimental UCS is concentrated between 0.265 MPa and 0.43 MPa. Although there are a very few outliers in the experimental UCS, this is normal in the UCS test.
Figure 2.
Distribution of experimental UCS (a) distribution curve of UCS; (b) box line diagram of UCS.
4. Methodology
This section introduces 4 neural networks (BPNN, RBFNN, GRNN and LSTM), 3 intelligent optimization algorithms (GWO, PSO and SSA) and 4 performance metrics (RMSE, R, VAF and T). Neural networks are used to construct mapping relationships between inputs (underflow productivity) and output (UCS); intelligent optimization algorithms are used to optimize the neural networks that obtain the best mapping relationships; and performance metrics are used to compare the performance of different models.
4.1. Neural network
Neural network is an algorithmic mathematical model that imitates the behavioral characteristics of animal neural networks and performs distributed parallel information processing. It relies on the complexity of the system and by adjusting the interconnections between internal nodes for the purpose of processing information. This section introduces 4 neural networks for searching and constructing the relationship between inputs and outputs in this study.
For the fairness of the comparison of different neural networks, the hidden layer nodes, the learning rate and the maximum iterations are set to 5, 0.1 and 100 for all neural networks. At the same time, the number of hidden layers is set to 1 for both BPNN and RBFNN; the number of pattern layer and summation layer of GRNN are both set to 1. In addition, the important parameter spread factor of RBF and GRNN is set to 5. The above parameter settings are based on relevant researches and modeling experience [20], [36], [37], [38], [39].
4.1.1. Back propagation neural network
Back Propagation neural network (BPNN) is a multilayer feedforward neural network [40], [41]. It is characterized by the forward transmission of the signal while the error is reverse transmitted. In forward transmission, the input signal is processed layer by layer from the input layer through the hidden layer to the output layer. In this process, the state of neurons in each layer affects only the state of neurons in the next layer [42], [43]. If the desired output is not obtained in the output layer, the network is back-propagated and the weights and thresholds are adjusted according to the prediction error, which enables the predicted output of the BPNN to continuously approach the desired output. The network structure of BPNN is shown in Fig. 3. The neuronal structure of the BPNN in this study is set according to the literatures [26], [27], [28] as 4-8-1.
Figure 3.
The network structure of BPNN.
4.1.2. Radial basis function neural network
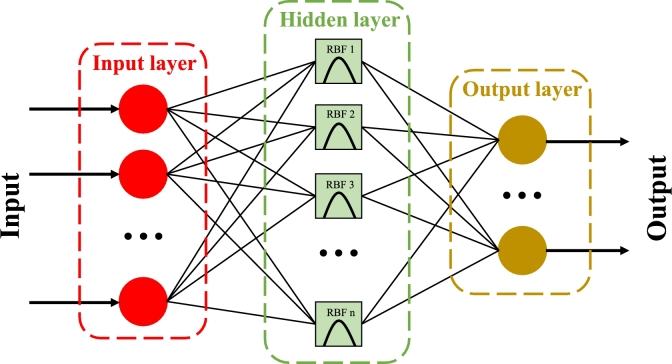
Similar to BPNN, Radial basis function neural network (RBFNN) is also a forward neural network, which has a network structure consisting of input layer, hidden layer and output layer [44]. RBFNN is characterized by the introduction of RBF as the transform function of neurons in its hidden layer. This enables the hidden layer unit to transform the input vector from low-dimensional and linearly inseparable to high-dimensional and linearly separable to improve generalizability and robustness [45], [46]. The network structure of RBFNN is shown in Fig. 4. To make the comparison fair, the neuronal structure of RBFNN is set to 4-8-1.
Figure 4.
The network structure of RBFNN.
4.1.3. General regression neural network
General regression neural network (GRNN) is a modified RBFNN. Unlike RBFNN, the structure of GRNN has 4 layers: input layer, pattern layer, summation layer and output layer [47], [48]. The regression of GRNN on the inputs is different from the least-square superposition of Gaussian weights in RBF, which uses the density function to predict the output by using the calculation of the pattern layer and the summation layer [49], [50], [51]. The network structure of GRNN is shown in Fig. 5. The number of neurons in the pattern layer of GRNN is the number of variables in the input layer. In addition, two types of neurons are used in the summation layer for summation. Therefore, the neuronal structure of GRNN is 4-144-2-1. The setting of the neuron structure of GRNN is referred to the literatures [47], [48], [49], [50], [51] and is not described here due to the limitation of space.
Figure 5.
The network structure of GRNN.
4.1.4. Long short-term memory neural network
Long short-term memory neural network (LSTM) is an improved recurrent neural network (RNN). The difference between LSTM and traditional RNN is its addition of memory units to the network structure [52], [53], [54]. The memory cell structure of LSTM is shown in Fig. 6. The LSTM processes information through a four-part gating mechanism consisting of forget gate f, input gate i, output gate o, and memory cell c [55]. The structure of LSTM is as follows.
Figure 6.
The memory cell structure of LSTM.
(1) There are two parts of input at moment t: the output result at the previous moment and the new input information at this moment. The forget gate f is used to control the amount of input information that would be forgotten. Its calculation equation is as follows.
| (1) |
(2) The input gate i is used to control the amount of input information that would be engaged in the update of the cell. Its calculation equation is as follows.
| (2) |
(3) Calculate the state of the cell at this moment for the current information. Its calculation equation is as follows.
| (3) |
(4) The cell state c is the key to the LSTM model. Updates to the previous cell state . Its calculation equation is as follows.
| (4) |
(5) Calculate the output gate o and calculate how the amount of information under the output gate control would be used to generate . Its calculation equation is as follows.
| (5) |
| (6) |
(6) Transfer to the output layer and output y. The equation is calculated as follows.
| (7) |
In equations (1)–(7), σ is the sigmoid function; tanh is the hyperbolic cosine function; W and U are the weight matrices; b is the bias vector; ⊗ is the sign of the convolution operation; y is the output at time t.
4.2. Optimization algorithm
The optimization algorithm is a heuristic optimizer, which is an algorithm that imitates the laws of the biological world to solve the problem. It is used for solving the optimal solution of the problem under complex conditions. This section presents 3 bionic algorithms to solve the parameters of a neural network with optimal mapping relationship.
4.2.1. Grey wolf optimization
Grey wolf optimization (GWO) is a new intelligent algorithm that imitates the hunting behavior of gray wolves in nature to optimize objectives [56], [57], [58]. Wolves are classified into 4 classes of α, β, δ and ω according to their fitness degree during hunting. Their ranks are ordered from highest to lowest: . In addition, α is called the head wolf which leads the other wolves in the hunting process and ω is the bottom wolf which is dominated by the other three classes of wolves in the hunting process. The hunting process is as follows.
(1) Search for and surround prey. Its calculation equation is as follows.
| (8) |
| (9) |
In equations (8)–(9), t is the current number of iterations; A and C are coefficient vectors; is the position vector of the prey; X is the position vector of the grey wolf; D is the distance vector between the gray wolf and the prey. A and C are calculated as follows.
| (10) |
| (11) |
In equations (10)–(11), a decreases from 2 to 0 as the number of iterations increases; and R are vectors of random numbers in the range .
(2) Attacking the prey. Suppose that α is the gray wolf closest to the prey and β and δ are the next closest. Use equation (12) to calculate their distance to the prey and updating the positions of α, β and δ by equation (13). Finally, other gray wolves gradually approach prey through equation (14). Its calculation equation is as follows.
| (12) |
| (13) |
| (14) |
In equations (12)–(14), , and are the positions of α, β and δ at the t-th iteration.
4.2.2. Particle swarm optimization
Particle swarm optimization (PSO) is an intelligent algorithm designed by simulating the hunting behavior of a group of birds [59], [60], [61]. It uses the sharing of information by individuals in a population to make the entire movement of the group in the problem solution space from disorder to order evolutionary process to obtain the optimal solution. PSO is mainly implemented by the following 2 core equations.
| (15) |
| (16) |
In equations (15)–(16), and R are random numbers uniformly distributed within ; and are learning factors; w is inertia weight; is the i-th particle optimal position; is the population optimal position; is the current position of the particle; is the current speed of the particle.
4.2.3. Sparrow search algorithm
The sparrow search algorithm (SSA) was proposed as a new algorithm to solve optimization problems in 2020 [62], [63]. The core principle of SSA is from the group predatory behavior of sparrows in nature [63], [64], [65]. SSA divides sparrow group into finder and follower. The function of the finder is to guide the entire sparrow group to search and hunt. Its position equation is as follows.
| (17) |
In equations (17), i is iteration; j is the individual dimension; is the position of the sparrow; itermax is the maximum iteration; is a random number; and are the alarm value and the security threshold respectively. Q is random number.
The role of a follower is to follow the finder in order to acquire better adaptive ability. The equation for its position is as follows.
| (18) |
In equations (18), is the worst position of finder; is the best position the producer; A is a matrix with each element being −1 or 1; n is the number of individual sparrows. In the above equation, .
Some finders can act as vigilantes to help the finder with foraging. When danger is present, the vigilantes would counter-trap or approach other sparrows. The equation for its position is as follows.
| (19) |
In equation (19), is the global best position; is the parameter used to control the step size; is a random number; is adaptation degree of current sparrow; and are the global best adaptation degree value and the global worst adaptation degree value, respectively; ε is a constant close to 0 to avoid the denominator being 0.
4.3. Performance metrics
To construct the optimal LSTM, the prediction results of different models are compared in this paper. The root mean square error (RMSE), correlation coefficient (R), variance account for (VAF) and running time of model (T/s) are used as evaluation metrics [66], [67]. The equations of the first three metrics are as follows.
| (20) |
| (21) |
| (22) |
In equation (20)–(22), and f () are the measured values and predicted values; is the mean of the measured values; VAF is used to indicate the degree of fit between the measured and predicted values. In addition, VAR is the variance of the dataset and the range is . The closer the RMSE is to 0, the closer the R is to 1 and the closer the VAF is to 100, the higher the prediction accuracy of the model.
Moreover, statistical evaluation of measured and predicted values using 95% confidence interval in this paper. The narrower the confidence interval and the more sample points included, the more significant the accuracy of the prediction results in the regression fitting fig.
5. Comparison and selection of networks
This section constructs 4 neural networks to characterize the mapping relationships between inputs and output based on data set in section 4 in conjunction with section 2. Also, the LSTM with the best mapping relationship is optimized using 4 optimized methods and the model with the best prediction effect applicable to this study is obtained.
In this paper, 4 neural networks are trained based on the experimental data in section 3. 80% of the experimental data is used as the training set to train networks and 20% is used as the validation set to test the reliability of the output of the neural networks.
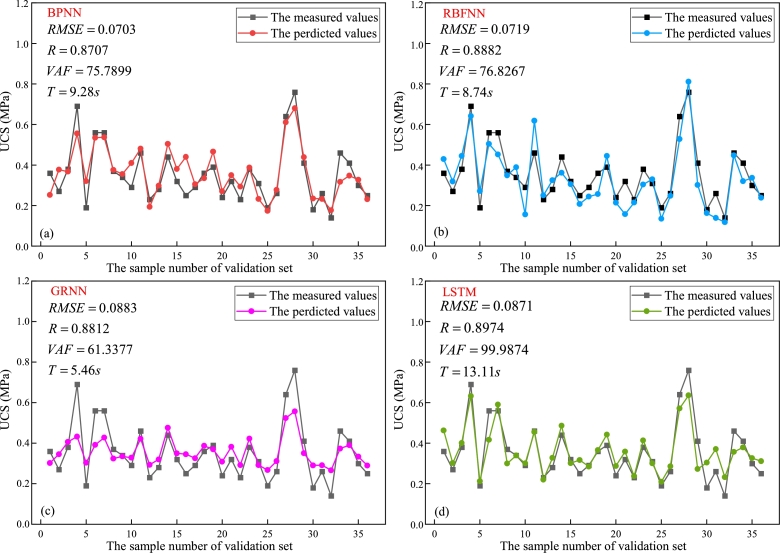
The comparison of the results for validation set of the 4 networks is shown in Fig. 7. From Fig. 7, the RMSE of BPNN, RBFNN, GRNN and LSTM are 0.0703, 0.0719, 0.0883 and 0.0871, respectively. The R of BPNN, RBFNN, GRNN and LSTM are 0.8707, 0.8882, 0.8812 and 0.8974, respectively. The VAF of BPNN, RBFNN, GRNN and LSTM are 75.7899, 76.8267, 61.3377 and 99.9874, respectively. The T of BPNN, RBFNN, GRNN and LSTM are 9.28 s, 8.74 s, 5.46 s and 13.11 s, respectively. The LSTM has a better fit of the predicted values to the measured values but the longest running time, which is because the complex structure of LSTM increases the amount of computation while enhancing the understanding of the data. Moreover, a ranking method for the performance of different models proposed by Zorlu is utilized as shown in Table 6 [68]. From Fig. 7 and Table 6, LSTM and RBFNN have relatively better prediction performance (the total rank are both 11) for UCS of CPB compared with BPNN and GRNN (the total rank are both 10). For the prediction of UCS of CPB, the main focus in practical application is on prediction accuracy and error. Although the running time of LSTM is longest, it is still the optimal model in this study. Therefore, LSTM is selected as the basic model and the next step of the research is conducted.
Figure 7.
The prediction results of networks for validation set (a) BPNN; (b) RBFNN; (c) GRNN; (d) LSTM.
Table 6.
The performance indices of different networks.
| Network | Results |
Rank values |
Total rank | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R | RMSE | VAF | T | R | RMSE | VAF | T | ||
| BPNN | 0.8707 | 0.0703 | 75.7899 | 9.28 s | 1 | 4 | 2 | 1 | 10 |
| RBFNN | 0.8882 | 0.0719 | 76.8267 | 8.74 s | 3 | 3 | 3 | 2 | 11 |
| GRNN | 0.8812 | 0.0883 | 61.3377 | 5.46 s | 2 | 1 | 1 | 4 | 10 |
| LSTM | 0.8974 | 0.0871 | 99.9874 | 13.11 s | 4 | 2 | 4 | 1 | 11 |
6. Optimization of LSTM and results
Two parameters, the hidden layer nodes and the learning rate, have important effects on the performance of LSTM [69], [70], [71]. Generally, the higher the hidden layer codes, the higher the computational accuracy and complexity of the LSTM. Therefore, selecting the appropriate the hidden layer codes is essential for LSTM. Similarly, the learning rate has a significant effect on the output of the LSTM. The learning rate is used to control the step size during gradient descent in order to optimize the output of the LSTM. So, selecting an appropriate learning rate can prevent the LSTM from missing the optimal solution and improve its robustness. For LSTM, the values of the above two parameters were usually determined using trial-and-error or some experimental equations, which leads to an unstable performance of LSTM in practical applications. To improve the performance of LSTM and apply it to this study, the hidden layer nodes and the learning rate are optimized using trial-and-error, GWO, PSO and SSA. The optimization and modeling process is shown in Fig. 8. From Fig. 8, experimental data is randomly classified into training set and validation set. The training set is used to train the LSTM improved by different optimization methods to obtain the optimal hyperparameters and to construct the mapping relationship between input and output. The validation set is used to validate whether the trained LSTM has generalizability and prediction accuracy. Moreover, the maximum iterations of LSTM and each optimization algorithm are set to 100 and the population size of each optimization algorithm is set to 20 according to related literatures to ensure fairness in the comparison.
Figure 8.
The optimization and modeling process.
6.1. Results of trial-and-error-LSTM
Some researches have shown that the optimal performance can be achieved when the hidden layer nodes do not exceed 2 times the input plus 1. Similarly, the learning rate is set to a range of 0.1 to 1 (in steps of 0.1) according to previous researches [35], [72], [73]. Therefore, various LSTM with the hidden layer nodes is from 1 to 9 and the range of learning rate is be constructed to select the optimal parameters for LSTM. In this process, the 10-fold cross-validation method is used to evaluate the generalization performance of the LSTM and to guide the selection of the parameters of the optimal LSTM. Using the mean absolute error (MAE) as an evaluation metric, the performance of the LSTM with different combinations of the above parameters is shown in Fig. 9. From the Fig. 9, it can be seen that the effect of learning rate on MAE is more significant than that of hidden layer nodes. When the learning rate is lower than 0.65, MAE is low and basically in the interval ; when the learning rate is higher than 0.65, MAE increases significantly and is basically higher than 0.1. When the learning rate is between 0.4 and 0.65, the overall trend of MAE increases and then decreases with the increase of hidden layer nodes and shows a fluctuating change. Also, when the learning rate is between 0.9 and 1, the change of MAE is characterized by fluctuations. MAE obtains minimum when the hidden layer nodes is 8 and the learning rate is 0.1.
Figure 9.
The performance of the LSTM using trial-and-error.
The results of the prediction of the validation set using trial-and-error-LSTM are shown in Fig. 10. From the Fig. 10(a), the LSTM yield a prediction performance of , RMSE = 0.0657, VAF = 79.5911 and T = 18.61 s for validation set. From the Fig. 10(b), the narrowest and widest confidence intervals are and , respectively; the narrowest and widest prediction intervals are and , respectively. This shows that the width of the prediction band is far wider than the confidence band, which indicates that the error between the predicted and measured values is high using trial-and-error-LSTM for the validation set.
Figure 10.
The prediction performance of the trial-and-error-LSTM (a) the measured and predicted results of trial-and-error-LSTM; (b) the confidence band and prediction band of trial-and-error-LSTM.
6.2. Results of GWO-LSTM
To search for the optimal parameters of the LSTM, the search space of the hidden layer nodes and the learning rate are expanded to and , respectively. Same settings in both PSO-LSTM and SSA-LSTM as above. The hidden layer nodes obtained using GWO is 25 and the learning rate is 0.0785.
The results of the prediction of the validation set using GWO-LSTM are shown in Fig. 11. From the Fig. 11(a), the GWO-LSTM yield a prediction performance of , RMSE = 0.0204, VAF = 98.2847 and T = 16.37 s for validation set. From the Fig. 11(b), the narrowest and widest confidence intervals are and , respectively; the narrowest and widest prediction intervals are and , respectively. This shows that both the prediction and confidence bands are narrow and overlap highly, which indicates the high prediction accuracy of GWO-LSTM for the validation set.
Figure 11.
The prediction performance of the GWO-LSTM (a) the measured and predicted results of GWO-LSTM; (b) the confidence band and prediction band of GWO-LSTM.
6.3. Results of PSO-LSTM
The hidden layer nodes obtained using PSO is 29 and the learning rate is 0.1475. The results of the prediction of the validation set using PSO-LSTM are shown in Fig. 12. From the Fig. 12(a), the PSO-LSTM yield a prediction performance of , RMSE = 0.0507, VAF = 88.3365 and T = 21.31 s for validation set. From the Fig. 12(b), the narrowest and widest confidence intervals are and , respectively; the narrowest and widest prediction intervals are and , respectively. This shows that the width of the prediction band is wider than the confidence band, which indicates that the prediction error using PSO-LSTM for the validation set is higher than GWO-LSTM. In addition, the presence of misfit points outside the prediction band also demonstrates that the prediction accuracy of PSO-LSTM is lower than that of GWO-LSTM. In PSO, the learning factors and inertia weights of PSO are referred to some related research results to obtain the optimal optimization performance [63], [74], [75].
Figure 12.
The prediction performance of the PSO-LSTM (a) the measured and predicted results of PSO-LSTM; (b) the confidence band and prediction band of PSO-LSTM.
6.4. Results of SSA-LSTM
The hidden layer nodes obtained using SSA is 6 and the learning rate is 0.0378. The results of the prediction of the validation set using SSA-LSTM are shown in Fig. 13. From the Fig. 13(a), the SSA-LSTM yield a prediction performance of , RMSE = 0.0586, VAF = 83.0121 and T = 15.19 s for validation data. From the Fig. 13(b), the narrowest and widest confidence intervals are and , respectively; the narrowest and widest prediction intervals are and , respectively. This shows that the width of the prediction band is wider than the confidence band, which indicates that the prediction error using SSA-LSTM for the validation set is higher than GWO-LSTM. In addition, the presence of misfit points outside the prediction band also demonstrates that the prediction accuracy of SSA-LSTM is lower than that of GWO-LSTM. In SSA, the values of ST and PD in SSA are taken with reference to the relevant literature [76].
Figure 13.
The prediction performance of the SSA-LSTM (a) the measured and predicted results of SSA-LSTM; (b) the confidence band and prediction band of SSA-LSTM.
6.5. Analysis of results
The running time of the 4 improved LSTMs and neural networks in section 5 are shown in Table 7. From Table 7, it can be seen that the running time of LSTM is significantly higher than that of other neural networks and the running time of the improved LSTM is higher than that of the original LSTM. The reasons for this phenomenon are analyzed as follows. First, the core of LSTM is a gating mechanism, which means that the network structure of LSTM is complex and requires many parameters to be calculated. Second, LSTM is a time series model, which means that when processing data the results of the later moment are dependent on the information of the previous moment and cannot be executed in parallel. Lastly, the use of optimization algorithms to improve the LSTM increases the amount of operations, which can increase the running time. Although running time is an important metric in machine learning, the prediction accuracy and error of the model are of more important in this study and in practical engineering applications.
Table 7.
The running time of different models.
| Model | T | Model | T |
|---|---|---|---|
| BPNN | 9.28 s | trial-and-error-LSTM | 18.61 s |
| RBFNN | 8.74 s | GWO-LSTM | 16.37 s |
| GRNN | 5.46 s | PSO-LSTM | 21.31 s |
| LSTM | 13.11 s | SSA-LSTM | 22.19 s |
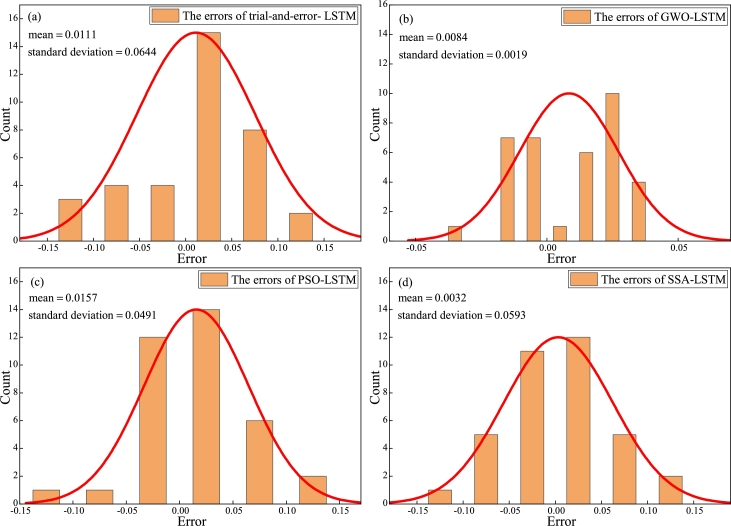
An analysis of the errors distribution between the measured and predicted values of the 4 models is shown in Fig. 14. From the Fig. 14(a), the errors of trail-and-error-LSTM are concentrated between 0.25 and 0.75 with mean and standard deviation of 0.0111 and 0.0644, respectively. From the Fig. 14(b), the errors of GWO-LSTM are concentrated between −0.02 and 0.03 with mean and standard deviation of 0.0084 and 0.0019, respectively. From the Fig. 14(c), it can be seen that the errors of PSO-LSTM are concentrated between −0.025 and 0.075 with mean and standard deviation of 0.0157 and 0.0491, respectively. From the Fig. 14(d), it can be seen that the errors of SSA-LSTM are concentrated between −0.075 and 0.075 with mean and standard deviation of 0.0032 and 0.0593, respectively. The absolute value of the center error of GWO-LSTM is almost 0 (mean = 0.0084) and the minimum value of width value (standard deviation = 0.0019). All of above analysis indicate that the GWO-LSTM has the lowest error between the predicted and measured values and the highest prediction accuracy.
Figure 14.
The comparison of errors distribution from different models (a) trail-and-error-LSTM; (b) GWO-LSTM; (c) PSO-LSTM; (d) SSA-LSTM.
In addition, Taylor diagrams with standard deviation, R and RMSE as the core are plotted in Fig. 15. In the Taylor diagram, each model corresponds to a measured point according to the 3 metrics mentioned above. The radial line represents R, the solid arc represents standard deviation and the red dashed line represents RMSE in Fig. 15. From the Fig. 15, GWO-LSTM has not only the lowest RMSE and standard deviation but also the highest R, which indicates that GWO-LSTM has the highest prediction accuracy among the 4 optimized LSTMs.
Figure 15.
The Taylor Diagram for performance from different model.
According to the no free lunch theorem, the performance of the optimization algorithm is equivalent due to the mutual compensation of all possible functions. This means that one algorithm (Algorithm A) outperforms another algorithm (Algorithm B) on a specific dataset and must be associated with Algorithm A outperforming Algorithm B on another specific dataset. Without certain assumptions about the prior distribution of training set in the feature space, there are as many cases of better performance as there are cases of worse performance, which means that if the algorithm wants to get a positive performance improvement on problems, a negative performance degradation on problems must to be paid. In this study, the prediction accuracy of LSTM for UCS is higher than other neural networks but the running time is long. In addition, the predictions of UCS using trial-and-error, GWO, PSO, and SSA optimized LSTM get higher accuracy but they have longer running time. Although GWO-LSTM is the optimal model in this study, this optimal effect exists at the sacrifice of running time. Therefore, it can only be said that GWO-LSTM has excellent performance in this research and it still has much room for improvement.
7. Engineering applications
In this section, the GWO-LSTM constructed in section 6 is used as the core model and combined with filling body of 153 underground approaches for 3 filled stopes to predict the UCS of CPB.
7.1. Engineering background
The transportation with gravity by pipelines is generally used to transport the filling slurry to the mining stope. The stowing gradient is applied to describe the filling range that the gravity system can reach. The stowing gradient characterizes the engineering characteristics of the filling pipeline, which is one of the critical factors for the transportation with gravity of the filling slurry and is essential for the design and production management of the transportation system for the filling slurry. The stowing gradient is calculated and represented as shown in equation (23) and Fig. 16.
| (23) |
In equation (23), N is the stowing gradient; H is the height difference from start and finish points of filling pipeline; L is the total length of the filling pipeline including the converted length of fittings such as elbows and joints ().
Figure 16.
The schematic representation for stowing gradient.
Due to the different stopes and depths of underground mining, the stowing gradients of different filled stopes are variant. If the filling slurry concentration is adjusted blindly under the above conditions, the strength of the filling body would be unstable. The gold mine studied in this paper is mined using the drift fill stopping and cemented filling method. The filling slurry is transported by gravity to the mined-out area and the stowing gradient of each filled stope ranges from 3 to 7. Filled stope with the range of stowing gradient of 3 to 4.5 are set up as filled stope A; the range of 4.5 to 6 are set up as filled stope B; the range of 6 to 7 are set up as filled stope C. The different filled stopes are zoned according to the stowing gradient as shown in Fig. 17.
Figure 17.
Filled stope zoning based on stowing gradient (a) the diagram of stowing gradient; (b) the filled stopes divided by different stowing gradient.
7.2. Correction coefficient
Related researches have shown that the actual values of strength for the filling body in the filled stope with the same slurry mix proportion is significantly lower than the laboratory measured values. Although many of UCS prediction studies have been conducted by researchers, the predicted UCS measured in laboratory (UCSM) rather than the predicted UCS in actual engineering (UCSA) with engineering guidance. This means that the above studies have limitations in engineering applications. To accurately obtain the UCS of the filled stope and to provide guidance for safe production, a core machine is used to drill the filling body in filled stope and process it into standard specimens. The final UCS of filling body is obtained for different filled stopes and different curing time.
For the error between UCSM and UCSA, a correction coefficient (k) is introduced to adjust for this error and is used to guide production. The correction coefficient is defined and calculated by the following equation.
| (24) |
The correction coefficients for the strength of different filled stopes are obtained by comparing UCSM and UCSA, which is as shown in Fig. 18. From the Fig. 18(a)-(c), k for 5d, 7d and 28d in filled stope A are 1.63, 1.51 and 1.48, respectively; k for 5d, 7d and 28d in filled stope B are 1.57, 1.46 and 1.41, respectively; k for 5d, 7d and 28d in filled stope C are 1.48, 1.37 and 1.33, respectively. The is the maximum value, which is found in stope A with a curing time of 5d; is the minimum value, which is found in stope C with a curing time of 28d. This indicates that there is still a certain error between UCSM and UCSA when using GWO-LSTM for prediction but the distribution of error is regular, which can be seen from the range of distribution of k (). On the other hand, this can also demonstrate the rationality of using k to correct error. From the Fig. 18(d), the minimum value of k is obtained in the filled stope C regardless of the curing time, which indicates that the error between UCSM and UCSA in filled stope C is lowest. In addition, k of different filled stopes show a decreasing trend when the curing time is extended. This means that with the stowing gradient increases, the k increases gradually for different curing times. The reasons for the phenomenon above are analyzed as follows. The filling slurry in filled stope with high stowing gradient (e.g. filled stope C) is less fluid during gravity transport. To ensure the filling slurry can be transported to the filling stope by gravity, water is added to the stirred tank for the slurry to dilute in engineering practice. This leads to a decrease in filling slurry concentration and causes a decrease in UCS. Therefore, the larger the stowing gradient for filled stope, the larger the error between UCSM and UCSA and the larger the k.
Figure 18.
The correction coefficients in different filled stopes (a) the results of UCSM and UCSA in stope A; (b) the results of UCSM and UCSA in stope B; (c) the results of UCSM and UCSA in stope C; (d) the correction coefficient of different stopes.
7.3. Strength prediction of CPB in filled stope
In the production of mines using the filling mining, the strength of the filling body in the underground is directly determined by the safety of the mining work. Based on the high-precision UCS prediction model constructed in this paper, the strength of filling body in 153 filling approaches in filled stopes filled with a horizontal height from 330 m to 430 m is predicted to provide guidance for the safe mining. The slurry mix proportions for the 153 filling approaches (A:48, B:42 and C:63) are input into GWO-LSTM to obtain the UCSM. Then UCSM is divided by k and the UCSA is obtained. According to safety standard of the mine, 5d UCS must not be lower than 0.3 MPa, 7d UCS must not be than 0.35 MPa and 28d UCS must not be lower than 0.5 MPa. The statistical distribution of the UCSA is shown in Fig. 19.
Figure 19.
The statistical distribution of the UCSA (a) 5d; (b) 7d; (c) 28d.
From the Fig. 19(a), there are 44, 34 and 2 UCSA at 5d higher than 0.3 MPa in filled stope A, B and C respectively. From the Fig. 19(b), there are 47, 36 and 5 UCSA at 7d higher than 0.35 MPa in filled stope A, B and C respectively. From the Fig. 19(c), there are 45, 33 and 41 UCSA at 28d higher than 0.5 MPa in filled stope A, B and C respectively. This shows that the percent of UCSA compliant with safety standards obtained using GWO-LSTM in combination with k are 97.3%, 80.9% and 65.1% at 5d, 7d and 28d in three filled stope, respectively. In addition, the strength of 3, 9 and 22 approaches in filled stope A, B and C respectively cannot reach the safety standard and need to conduct some safety measures.
Although this study has made some progress in engineering applications, it still has some limitations. First, the dataset composed of UCS of CPB is usually homogeneous and heterogeneous, which makes it more difficult to perceive the working conditions in the engineering applications of the constructed models. Second, the mechanism of hydration reaction and mechanical properties of filling materials is extremely complex and have not been understood and recognized uniformly, which makes the modeling process lack of theoretical knowledge to guide. Lastly, it is difficult for the model to balance real-time and dynamic with limited data sets, which can affect the reliability and robustness of the constructed model. Therefore, there is still room for progress in this study.
8. Conclusion
(1) The UCS database include 180 sets of mix proportion experiments for filling slurry is constructed using tailings as aggregate and cement (PO.42.5) as binder from a gold mine in Guizhou, China. In the above database, the underflow productivity for tailings, slurry concentration, cement content and curing time are set as input and UCS as output. The experimental values of UCS were concentrated between 0.265 MPa and 0.43 MPa (maximum value of 0.96 MPa and minimum value of 0.14 MPa).
(2) Four neural networks, BPNN, RBFNN, GRNN and LSTM, are trained to construct mapping relationships between input and output variables and are used to predict the UCS based on the constructed database. Although RMSE is not the lowest and the running time is higher than the other three neural networks, the LSTM is the optimal model in the prediction of UCS of CPB based on engineering practice. (, RMSE = 0.0871, VAF = 99.9874, T = 13.11 s and Total rank = 11).
(3) The learning rate and the hidden layer nodes in the LSTM are optimized using trial-and-error, PSO, GWO, and SSA to improve the prediction performance of the LSTM. The simulation results show that the prediction performance of the GWO-LSTM (learning rate = 0.0785 and hidden layer nodes = 25) is optimal (, RMSE = 0.0204, VAF = 98.2847 and T = 16.37 s).
(4) The correction coefficient (k) is defined to correct for the errors of UCSM and UCSA. The k and GWO-LSTM are combined and successfully predict the strength of the filling body in 153 approaches for 3 filled stopes with different stowing gradient. The results in section 7 demonstrate the rationality of k and the high prediction accuracy of GWO-LSTM for UCS of CPB. This provides guidance for the safety mining of filled stopes.
(5) Future studies will focus on the processing of multi-source heterogeneous data sets in machine learning modeling and the mechanistic modeling of hydration reactions of filling materials.
Declarations
Author contribution statement
Bo Zhang: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Keqing Li, Siqi Zhang, Bin Han: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Yafei Hu: Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
Professor Bin Han was supported by the National Key Research and Development Program of China [2018YFC1900603]. Keqing Li was supported by the National Key Research and Development Program of China [2018YFC0604604].
Data availability statement
The authors do not have permission to share data.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Contributor Information
Bo Zhang, Email: zszhangbo210@163.com.
Bin Han, Email: hanbin_ustb@163.com.
References
- 1.Li E., Zhou J., Shi X., Jahed Armaghani D., Yu Z., Chen X., Huang P. Developing a hybrid model of salp swarm algorithm-based support vector machine to predict the strength of fiber-reinforced cemented paste backfill. Eng. Comput. 2021;37(4):3519–3540. [Google Scholar]
- 2.Qi C., Fourie A. Cemented paste backfill for mineral tailings management: review and future perspectives. Miner. Eng. 2019;144 [Google Scholar]
- 3.Zhang S., Shi T., Ni W., Li K., Gao W., Wang K., Zhang Y. The mechanism of hydrating and solidifying green mine fill materials using circulating fluidized bed fly ash-slag-based agent. J. Hazard. Mater. 2021;415 doi: 10.1016/j.jhazmat.2021.125625. [DOI] [PubMed] [Google Scholar]
- 4.Sun W., Wang H., Hou K. Control of waste rock-tailings paste backfill for active mining subsidence areas. J. Clean. Prod. 2018;171:567–579. [Google Scholar]
- 5.Tian J., Qi C., Sun Y., Yaseen Z.M., Pham B.T. Permeability prediction of porous media using a combination of computational fluid dynamics and hybrid machine learning methods. Eng. Comput. 2021;37(4):3455–3471. [Google Scholar]
- 6.Fourie A. Preventing catastrophic failures and mitigating environmental impacts of tailings storage facilities. Proc. Earth Planet. Sci. 2009;1(1):1067–1071. [Google Scholar]
- 7.Lu H., Qi C., Chen Q., Gan D., Xue Z., Hu Y. A new procedure for recycling waste tailings as cemented paste backfill to underground stopes and open pits. J. Clean. Prod. 2018;188:601–612. [Google Scholar]
- 8.Sun W., Wu D., Liu H., Qu C. Thermal, mechanical and ultrasonic properties of cemented tailings backfill subjected to microwave radiation. Constr. Build. Mater. 2021;313 [Google Scholar]
- 9.Qiu J., Guo Z., Yang L., Jiang H., Zhao Y. Effects of packing density and water film thickness on the fluidity behaviour of cemented paste backfill. Powder Technol. 2020;359:27–35. [Google Scholar]
- 10.Qi C., Chen Q., Dong X., Zhang Q., Yaseen Z.M. Pressure drops of fresh cemented paste backfills through coupled test loop experiments and machine learning techniques. Powder Technol. 2020;361:748–758. [Google Scholar]
- 11.Zhao X., Zhang H., Zhu W. Fracture evolution around pre-existing cylindrical cavities in brittle rocks under uniaxial compression. Trans. Nonferr. Met. Soc. China. 2014;24(3):806–815. [Google Scholar]
- 12.Wang C., Hou X., Liao Z., Chen Z., Lu Z. Experimental investigation of predicting coal failure using acoustic emission energy and load-unload response ratio theory. J. Appl. Geophys. 2019;161:76–83. [Google Scholar]
- 13.He Y., Zhang Q., Chen Q., Bian J., Qi C., Kang Q., Feng Y. Mechanical and environmental characteristics of cemented paste backfill containing lithium slag-blended binder. Constr. Build. Mater. 2021;271 [Google Scholar]
- 14.Wu D., Sun W., Liu S., Qu C. Effect of microwave heating on thermo-mechanical behavior of cemented tailings backfill. Constr. Build. Mater. 2021;266 [Google Scholar]
- 15.Hettiarachchi H.A.C.K., Mampearachchi W.K. Effect of vibration frequency, size ratio and large particle volume fraction on packing density of binary spherical mixtures. Powder Technol. 2018;336:150–160. [Google Scholar]
- 16.Zhang Y., Gao W., Ni W., Zhang S., Li Y., Wang K., Huang X., Fu P., Hu W. Influence of calcium hydroxide addition on arsenic leaching and solidification/stabilisation behaviour of metallurgical-slag-based green mining fill. J. Hazard. Mater. 2020;390 doi: 10.1016/j.jhazmat.2020.122161. [DOI] [PubMed] [Google Scholar]
- 17.Qiu J., Guo Z., Yang L., Jiang H., Zhao Y. Effect of tailings fineness on flow, strength, ultrasonic and microstructure characteristics of cemented paste backfill. Constr. Build. Mater. 2020;263 [Google Scholar]
- 18.Zhang Q., Hu G., Wang X. Hydraulic calculation of gravity transportation pipeline system for backfill slurry. J. Cent. South Univ. Technol. 2008;15(5):645–649. [Google Scholar]
- 19.Chen Q., Zhang Q., Wang X., Xiao C., Hu Q. A hydraulic gradient model of paste-like crude tailings backfill slurry transported by a pipeline system. Environ. Earth Sci. 2016;75(14):1099. [Google Scholar]
- 20.Yu Z., Shi X., Chen X., Zhou J., Qi C., Chen Q., Rao D. Artificial intelligence model for studying unconfined compressive performance of fiber-reinforced cemented paste backfill. Trans. Nonferr. Met. Soc. China. 2021;31(4):1087–1102. [Google Scholar]
- 21.Yan B., Zhu W., Hou C., Yilmaz E., Saadat M. Characterization of early age behavior of cemented paste backfill through the magnitude and frequency spectrum of ultrasonic P-wave. Constr. Build. Mater. 2020;249 [Google Scholar]
- 22.Jiang H., Fall M., Li Y., Han J. An experimental study on compressive behaviour of cemented rockfill. Constr. Build. Mater. 2019;213:10–19. [Google Scholar]
- 23.Shi Y., Cheng L., Tao M., Tong S., Yao X., Liu Y. Using modified quartz sand for phosphate pollution control in cemented phosphogypsum (PG) backfill. J. Clean. Prod. 2021;283 [Google Scholar]
- 24.Wu J., Jing H., Yin Q., Meng B., Han G. Strength and ultrasonic properties of cemented waste rock backfill considering confining pressure, dosage and particle size effects. Constr. Build. Mater. 2020;242 [Google Scholar]
- 25.Mohammed A., Mahmood W., Ghafor K. TGA, rheological properties with maximum shear stress and compressive strength of cement-based grout modified with polycarboxylate polymers. Constr. Build. Mater. 2020;235 [Google Scholar]
- 26.Qi C., Fourie A., Chen Q., Zhang Q. A strength prediction model using artificial intelligence for recycling waste tailings as cemented paste backfill. J. Clean. Prod. 2018;183:566–578. [Google Scholar]
- 27.Qi C., Chen Q., Fourie A., Zhang Q. An intelligent modelling framework for mechanical properties of cemented paste backfill. Miner. Eng. 2018;123:16–27. [Google Scholar]
- 28.Qi C., Fourie A., Chen Q. Neural network and particle swarm optimization for predicting the unconfined compressive strength of cemented paste backfill. Constr. Build. Mater. 2018;159:473–478. [Google Scholar]
- 29.Sivakugan R.R.N. Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering. 2005. Prediction of paste backfill performance using artificial neural networks; pp. 1107–1110. [Google Scholar]
- 30.Xiao C., Wang X., Chen Q., Bin F., Wang Y., Wei W. Strength investigation of the silt-based cemented paste backfill using lab experiments and deep neural network. Adv. Mater. Sci. Eng. 2020;2020:1–12. [Google Scholar]
- 31.Orejarena L., Fall M. The use of artificial neural networks to predict the effect of sulphate attack on the strength of cemented paste backfill. Bull. Eng. Geol. Environ. 2010;69(4):659–670. [Google Scholar]
- 32.Altan A., Karasu S., Zio E. A new hybrid model for wind speed forecasting combining long short-term memory neural network, decomposition methods and grey wolf optimizer. Appl. Soft Comput. 2021;100 [Google Scholar]
- 33.Xing L., Liu W. A data fusion powered bi-directional long short term memory model for predicting multi-lane short term traffic flow. IEEE Trans. Intell. Transp. Syst. 2021:1–10. [Google Scholar]
- 34.Zhou W., Liu M., Zheng Y., Dai Y. 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC) 2020. Online error correction method of PMU data based on LSTM model and Kalman filter; pp. 1–6. [Google Scholar]
- 35.Kumar K., Haider M.T.U. Enhanced prediction of intra-day stock market using metaheuristic optimization on RNN–LSTM network. New Gener. Comput. 2021;39(1):231–272. [Google Scholar]
- 36.Zhou N., Zhang J., Ouyang S., Deng X., Dong C., Du E. Feasibility study and performance optimization of sand-based cemented paste backfill materials. J. Clean. Prod. 2020;259 [Google Scholar]
- 37.Cao W., Zhu W., Wang W., Demazeau Y., Zhang C. A deep coupled LSTM approach for USD/CNY exchange rate forecasting. IEEE Intell. Syst. 2020;35(2):43–53. [Google Scholar]
- 38.Qi C., Chen Q., Fourie A., Tang X., Zhang Q., Dong X., Feng Y. Constitutive modelling of cemented paste backfill: a data-mining approach. Constr. Build. Mater. 2019;197:262–270. [Google Scholar]
- 39.Wu D., Deng T., Zhao R. A coupled THMC modeling application of cemented coal gangue-fly ash backfill. Constr. Build. Mater. 2018;158:326–336. [Google Scholar]
- 40.Wang Y., Cao Y., Cui L., Si Z., Wang H. Effect of external sulfate attack on the mechanical behavior of cemented paste backfill. Constr. Build. Mater. 2020;263 [Google Scholar]
- 41.Zhou W., Sun G., Yang Z., Wang H., Fang L., Wang J. BP neural network based reconstruction method for radiation field applications. Nucl. Eng. Des. 2021;380 [Google Scholar]
- 42.Xue H., Cui H. Research on image restoration algorithms based on BP neural network. J. Vis. Commun. Image Represent. 2019;59:204–209. [Google Scholar]
- 43.Liang W., Wang G., Ning X., Zhang J., Li Y., Jiang C., Zhang N. Application of BP neural network to the prediction of coal ash melting characteristic temperature. Fuel. 2020;260 [Google Scholar]
- 44.Reiner P., Wilamowski B.M. Efficient incremental construction of RBF networks using quasi-gradient method. Neurocomputing. 2015;150:349–356. [Google Scholar]
- 45.Xu X., Shan D., Li S., Sun T., Xiao P., Fan J. Multi-label learning method based on ML-RBF and Laplacian ELM. Neurocomputing. 2019;331:213–219. [Google Scholar]
- 46.Zhang N., Ding S., Zhang J. Multi layer ELM-RBF for multi-label learning. Appl. Soft Comput. 2016;43:535–545. [Google Scholar]
- 47.Xiao X., Zhao X. Retraction note: evaluation of mangrove wetland potential based on convolutional neural network and development of film and television cultural creative industry. Arab. J. Geosci. 2021;14(21):2247. [Google Scholar]
- 48.Rui H., Gao C. Retraction note to: neural network-based urban green vegetation coverage detection and smart home system optimization. Arab. J. Geosci. 2021;14(22):2424. [Google Scholar]
- 49.Khatter H., Kumar Ahlawat A. Correction to: an intelligent personalized web blog searching technique using fuzzy-based feedback recurrent neural network. Soft Comput. 2020;24(12):9335. [Google Scholar]
- 50.Rohit S., Chakravarthy S. A convolutional neural network model of the neural responses of inferotemporal cortex to complex visual objects. BMC Neurosci. 2011;12(1):P35. [Google Scholar]
- 51.Cheng Y. Retraction note: rainfall trend and supply chain network management in mountainous areas based on dynamic neural network. Arab. J. Geosci. 2021;14(24):2779. [Google Scholar]
- 52.Hajiaghayi M., Vahedi E. 2019 IEEE Fifth International Conference on Big Data Computing Service and Applications (BigDataService) 2019. Code failure prediction and pattern extraction using LSTM networks; pp. 55–62. [Google Scholar]
- 53.Guo Y. 2020 2nd International Conference on Economic Management and Model Engineering (ICEMME) 2020. Stock price prediction based on LSTM neural network: the effectiveness of news sentiment analysis; pp. 1018–1024. [Google Scholar]
- 54.van de Leemput S.C., Prokop M., van Ginneken B., Manniesing R. Stacked bidirectional convolutional LSTMs for deriving 3D non-contrast CT from spatiotemporal 4D CT. IEEE Trans. Med. Imaging. 2020;39(4):985–996. doi: 10.1109/TMI.2019.2939044. [DOI] [PubMed] [Google Scholar]
- 55.Hochreiter S., Schmidhuber J. Long short-term memory. Neural Comput. 1997;9(8):1735–1780. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- 56.Siddavaatam P., Sedaghat R. Grey wolf optimizer driven design space exploration: a novel framework for multi-objective trade-off in architectural synthesis. Swarm Evol. Comput. 2019;49:44–61. [Google Scholar]
- 57.Maroufpoor S., Maroufpoor E., Bozorg-Haddad O., Shiri J., Mundher Yaseen Z. Soil moisture simulation using hybrid artificial intelligent model: hybridization of adaptive neuro fuzzy inference system with grey wolf optimizer algorithm. J. Hydrol. 2019;575:544–556. [Google Scholar]
- 58.Mirjalili S., Mirjalili S.M., Lewis A. Grey wolf optimizer. Adv. Eng. Softw. 2014;69:46–61. [Google Scholar]
- 59.Deepa G., Mary G.L.R., Karthikeyan A., Rajalakshmi P., Hemavathi K., Dharanisri M. Detection of brain tumor using modified particle swarm optimization (MPSO) segmentation via Haralick features extraction and subsequent classification by KNN algorithm. Mater. Today Proc. 2021 [Google Scholar]
- 60.Wang N., Liu J., Lu J., Zeng X., Zhao X. Low-delay layout planning based on improved particle swarm optimization algorithm in 5G optical fronthaul network. Opt. Fiber Technol. 2021;67 [Google Scholar]
- 61.Peng J., Li Y., Kang H., Shen Y., Sun X., Chen Q. Impact of population topology on particle swarm optimization and its variants: an information propagation perspective. Swarm Evol. Comput. 2021 [Google Scholar]
- 62.Xue J., Shen B. A novel swarm intelligence optimization approach: sparrow search algorithm. Syst. Sci. Control Eng. 2020;8(1):22–34. [Google Scholar]
- 63.Zhang H., Peng Z., Tang J., Dong M., Wang K., Li W. A multi-layer extreme learning machine refined by sparrow search algorithm and weighted mean filter for short-term multi-step wind speed forecasting. Sustain. Energy Technol. Assess. 2022;50 [Google Scholar]
- 64.Zhou S., Xie H., Zhang C., Hua Y., Zhang W., Chen Q., Gu G., Sui X. Wavefront-shaping focusing based on a modified sparrow search algorithm. Optik. 2021;244 [Google Scholar]
- 65.Kathiroli P., Selvadurai K. Energy efficient cluster head selection using improved sparrow search algorithm in wireless sensor networks. J. King Saud Univ, Comput. Inf. Sci. 2021 [Google Scholar]
- 66.Zorlu K., Gokceoglu C., Ocakoglu F., Nefeslioglu H.A., Acikalin S. Prediction of uniaxial compressive strength of sandstones using petrography-based models. Eng. Geol. 2008;96(3–4):141–158. [Google Scholar]
- 67.Borna K., Ghanbari R. Hierarchical LSTM network for text classification. SN Appl. Sci. 2019;1(9):1124. [Google Scholar]
- 68.Song J., Tang S., Xiao J., Wu F., Zhang Z.M. LSTM-in-LSTM for generating long descriptions of images. Comput. Vis. Media. 2016;2(4):379–388. [Google Scholar]
- 69.Yuan X., Chen C., Lei X., Yuan Y., Muhammad Adnan R. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018;32(8):2199–2212. [Google Scholar]
- 70.Rybalkin V., Sudarshan C., Weis C., Lappas J., Wehn N., Cheng L. Correction to: efficient hardware architectures for 1D- and MD-LSTM networks. J. Signal Process. Syst. 2021;93(12):1467. [Google Scholar]
- 71.Wang L., Zhong X., Wang S., Liu Y. Correction to: ncDLRES: a novel method for non-coding RNAs family prediction based on dynamic LSTM and ResNet. BMC Bioinform. 2021;22(1):583. doi: 10.1186/s12859-021-04495-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Rezaei S., Behnamian J. Benders decomposition-based particle swarm optimization for competitive supply networks with a sustainable multi-agent platform and virtual alliances. Appl. Soft Comput. 2022;114 [Google Scholar]
- 73.Ben Hmamou D., Elyaqouti M., Arjdal E., Chaoufi J., Saadaoui D., Lidaighbi S., Aqel R. Particle swarm optimization approach to determine all parameters of the photovoltaic cell. Mater. Today Proc. 2021 [Google Scholar]
- 74.Kumar R. Fuzzy particle swarm optimization control algorithm implementation in photovoltaic integrated shunt active power filter for power quality improvement using hardware-in-the-loop. Sustain. Energy Technol. Assess. 2022;50 [Google Scholar]
- 75.Ma J., Hao Z., Sun W. Enhancing sparrow search algorithm via multi-strategies for continuous optimization problems. Inf. Process. Manag. 2022;59(2) [Google Scholar]
- 76.Hui X.U., Guangbin C., Shengxiu Z., Xiaogang Y., Mingzhe H. Hypersonic reentry trajectory optimization by using improved sparrow search algorithm and control parametrization method. Adv. Space Res. 2021 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The authors do not have permission to share data.