Abstract
The BGLR-R package implements various types of single-trait shrinkage/variable selection Bayesian regressions. The package was first released in 2014, since then it has become a software very often used in genomic studies. We recently develop functionality for multitrait models. The implementation allows users to include an arbitrary number of random-effects terms. For each set of predictors, users can choose diffuse, Gaussian, and Gaussian–spike–slab multivariate priors. Unlike other software packages for multitrait genomic regressions, BGLR offers many specifications for (co)variance parameters (unstructured, diagonal, factor analytic, and recursive). Samples from the posterior distribution of the models implemented in the multitrait function are generated using a Gibbs sampler, which is implemented by combining code written in the R and C programming languages. In this article, we provide an overview of the models and methods implemented BGLR’s multitrait function, present examples that illustrate the use of the package, and benchmark the performance of the software.
Keywords: Bayesian, high-dimensional regression, multivariate models, multitrait models, Gibbs sampling, genomic regressions, pedigree regressions, Genomic Prediction, GenPred, Shared Data Resource
Introduction
High-dimensional regression problems are ubiquitous in many research areas. To confront the “curse” of dimensionality, a common approach is to use regularized regression procedures such as penalized, reduced rank, or Bayesian methods. In genetics, the continued development of genotyping and sequencing technologies has led to the development of large volumes of genomic data. Genomic prediction (GP) models have been adopted in plant and animal breeding for genomic selection (GS) (Meuwissen et al. 2001) and are used for complex trait prediction in human as well (de los Campos et al. 2010; Yang et al. 2010). Several software packages offer implementations to fit Bayesian (de los Campos et al. 2013; Pérez and de los Campos 2014) and non-Bayesian (Friedman et al. 2010; Endelman 2011) models for single-trait genomic models.
In most genomic data set, genotypes are evaluated for multiple traits; likewise, in experimental settings genotypes are often evaluated in multiple environments. Thus, soon after GS received attention, it becomes clear that extensions to multitrait/multienvironment settings were needed (Burgueño et al. 2012). Several software packages implement multivariate mixed-effects Gaussian models using likelihood/restricted maximum likelihood (REML) methods (Gilmour et al. 1995; Meyer 2007; Lippert et al. 2014; Covarrubias-Pazaran 2016) or within a Bayesian setting (Hadfield 2010; Cheng et al. 2018; Montesinos-López et al. 2019). However, the extension of GP to multitrait settings within the context of Bayesian variable selection models is more challenging; thus, the availability of multitrait Bayesian variable selection models is much more limited. Within the open-source domain, we are only aware of 1 software package that implements multitrait Bayesian variable selection and shrinkage methods for the Julia language (Cheng et al. 2018).
The BGLR-R package (Pérez and de los Campos 2014) was originally developed for single-trait models; recently, we developed the multitrait function, which implements shrinkage and variable selection models for multitrait analysis. The software combines features of the single-trait “BGLR” function (a similar user interface, and similar programming strategies, and similar default rules for setting hyperparameters) with some of the features of the MTM R package, a software that we developed and maintained in GitHub (https://github.com/QuantGen/MTM) since 2013 (de los Campos and Grueneberg 2013). MTM implements Bayesian Gaussian multivariate models with structured and unstructured (co)variance matrix using the methods described in de los Campos and Gianola (2007). However, MTM was fully developed using the R language and, thus, it does not scale for problems involving large numbers of samples. Moreover, MTM does not implement variable selection methods.
In the multitrait function of the BGLR-R package, users can specify models for an arbitrary number of random effects. For each random effect, users can choose between diffuse, Gaussian, and spike–slab priors. For (co)variance parameters, the software offers the possibility of using either structured (e.g. diagonal, factor analytic, or recursive structures) or completely unstructured specifications. Inputs for each of the random effects could be relationship matrices (aka kernels, e.g. pedigree- or SNP-derived genomic relationship matrices), eigenvectors and eigenvalue values from those matrices, or numeric matrices, which would be used to provide SNP genotypes, factorizations of relationship matrices (e.g. scaled eigenvectors or Cholesky factors), environmental covariates, and other quantitative predictors. Importantly, the trait matrix can have arbitrary patterns of missing values.
In what remains of this article, we describe the statistical models and the algorithms implemented in the multitrait function, present examples that illustrate the use of the software, and provide an overview of the computational time required for analyses involving various sample sizes, number of predictors (e.g. number of SNPs), and number of traits.
Materials and methods
The data equation of the multitrait function can include various types of effects, in matrix form, and the data equation can be represented as follows:
| (1) |
where is an n × t matrix (individuals in rows, traits in columns) of phenotypes (missing values are allowed), is a vector of trait-specific intercepts, is an incidence matrix for effects of a set of predictors (e.g. SNPs in columns), is a matrix of effects (predictors in rows, effects on each of the traits in columns), is a matrix of random effects (individuals in rows, traits in columns), and is a matrix with error terms (individuals in rows, traits in columns). The error terms are assumed to be independent and identically distributed (IID), each row following a multivariate normal (MVN) distribution with zero mean and covariance matrix ; therefore, the conditional distribution of the data given the regression parameters and the error covariance matrix is
| (2) |
where , where is a t-dimensional vector containing the conditional mean of the ith observation for each of the t traits, and are the ith rows of the corresponding and matrices, and .
Prior distribution
The software assumes independent priors for each set of predictors; therefore,
| (3) |
Intercepts are assigned diffuse priors , with equal to 1,000 times the maximum of the variance of each of the phenotypes.
The random-effects matrices are each assigned MVN distributions of the form
| (4) |
where is a vector with the columns of stacked, is a t × t (unknown) covariance matrix, is a n × n covariance structure (e.g. a genomic relationship matrix), and is the Kronecker product operator (more information about the prior on is provided below).
Regression coefficients can be either assigned MVN priors or priors from the spike–slab family. In the MVN prior,
| (5) |
where is the jth row of and is a t × t (unknown) covariance matrix describing covariance among the effects of the jth predictor on each of the traits.
For variable selection models, users can choose a multivariate spike–slab priors with a point of mass at zero and an MVN slab (this is one possible multivariate extension of the model known as BayesC in the animal breeding literature, e.g. Habier et al. 2011). For the spike–slab prior, we represent each of the entries of as the product of a normal random variable () and a dummy variable () which controls whether the jth predictor enters in the equation for the kth trait; thus,
| (6) |
Above represent the proportion of nonzero effects in each of the traits. By default, each of these parameters are treated as unknown and they are assigned independent Beta priors, that is: , where and are the prior shape1 and shape2 parameters for the kth trait.
Table 1 describes for each type of random effects ( and ) the priors implemented and how to specify it.
Table 1.
Specification of regression terms in the linear predictor.
| Component | Options |
|---|---|
| Regression functions ( |
|
| Random-intercept matrices ( |
|
Finally, for each of the covariance matrices involved in the model ( and each of the ) the software offers the option to modeled it as unstructured [in which case and Inverse-Wishart (IW) prior is used], or structured (with 3 options in this case, see Table 2). Covariance structures are specified using a list, the entry $type of the list specifies the type of the structure (unstructured, diagonal, factor analytic structure, or recursive model, see Table 2), other arguments include the hyperparameters for the structure (e.g. scale and degree of freedom parameters). In the case of recursive and Factor Analytic (FA) structures, an entry labeled as M (logical matrix) is also needed. For FA models this matrix must have dimensions number of factors and each cell (TRUE/FALSE) indicates whether the trait (row) loads on the corresponding factor (column). For recursive models, the matrix M has dimensions , and the cells (also TRUE/FALSE) indicate whether the trait in column enters for the equation of the trait in row, typically the diagonal entries of M will be FALSE, except for simultaneous equation models, but this requires fixed-effects exclusion restrictions (e.g. Goldberger 1972). Fully recursive models (those with an M matrix with TRUE in all cells below the diagonal and FALSE everywhere else) lead to an UN covariance matrix.
Table 2.
Covariance structures.
| Structure | Prior and hyperparameters | Specification |
|---|---|---|
| Unstructured |
|
Cov=list(type=“UN”, df0=,S0=) |
| Diagonal |
|
Cov=list(type=“DIAG”, df0=,S0=) |
| Factor analytic |
|
Cov=list(type=“FA”,df0=,S0=, M=, var=) |
| Recursive |
|
Cov=list(type=“REC”,df0=,S0=, M=, var=) |
Default rules for hyperparameters
To simplify the use of the software we have implemented default rules to set these parameters; therefore, when the user does not specify 1 or several of the hyperparameters involved in the model, the rules described in Supplementary File 1 are used to set default values. The hyperparameter values selected using these rules always lead to proper priors with scale parameters chosen considering the variance of the phenotype, the number of terms in the linear predictor, and the number of covariates in each of them.
Algorithms
The joint prior distribution of the model defined by expressions (2)–(6) does not have a closed form; however, with the likelihood and prior specifications used, all the fully conditionals have closed form; therefore, the software generates samples from the joint posterior distribution using a Gibbs sampler (e.g. Casella and George 1992).
In our implementation, most of the model unknowns are updated sampling from univariate fully conditionals; the only exception are the unstructured covariance matrices for which a sample for the matrix is obtained from an IW fully conditional. Describing each of the fully conditionals in detail is beyond the scope of this article; for location parameters (intercepts and regression coefficients), most of the fully conditional distributions are standard and have been previously described for Gaussian multitrait models with conjugate priors (e.g. Sorensen and Gianola 2002). The fully conditional distribution of the parameters involved in structured covariance matrices are borrowed from de los Campos and Gianola (2007), and from the implementation of the MTM software (de los Campos and Grueneberg 2013).
Sampling regression coefficients (and the dummy variables () in the case of the terms with spike–slab priors) is computationally the most demanding step. Therefore, we update all these unknowns using a routine implemented in the C programming language (Kernighan and Ritchie 1988). For hyperparameters and for covariance matrices, we collect samples using code implemented in the R language (R Core Team 2019).
Missing values
The phenotype matrix (Y in (1)) can contain missing values (NAs); when this is the case, at each iteration of the sampler, the missing values are “imputed” with samples from the fully conditional distribution (see Sorensen and Gianola 2002). Missing values in the linear predictor (e.g. X or K matrices) are not allowed.
User interface and outputs
The main arguments of the multitrait function are the phenotype matrix (y: a matrix of dimensions , where is the number of individuals and is the number of traits), the linear predictor (ETA: a 2-level list, each elements of the regression function (1), either a regression term of the form , or random intercepts (, see Table 1), and error covariance structure (resCov: A list that specifies the structure and the hyperparameters for ). A complete list of arguments can be found in the help included in the package.
The software returns a list with the estimated posterior means, estimated posterior deviations, together with all the elements of model specification (priors and hyperparameters). In the case of covariance matrices, only lower-triangular elements are stored; the corresponding matrices can be recreated using the function “xpnd,” also included originally in the MCMCpack package (Martin et al. 2011).
Data sets
The BGLR-R package includes 2 data sets (these data sets were also included in earlier versions of the package). The wheat data set (data(wheat)) was first made available by Crossa et al. (2010). This data set contains least-square means (average of 2 years) of grain yield (wheat.Y) for 599 wheat lines which were evaluated in 4 environments, a kinship matrix derived from a pedigree (wheat.A) and 1,279 Diversity Array Technology markers (wheat.X, since these are inbreed lines, genotypes are coded as 0/1). The mice data set (data(mice)) comes from mice experiments conducted by the Wellcome Trust (Valdar, Solberg, Gauguier, Burnett, et al. 2006; Valdar, Solberg, Gauguier, Cookson, et al. 2006). The phenotypes consist of traits related to diabetes and biochemistry for 1,814 mice (mice.pheno), a kinship matrix derived from pedigree (mice.A) and 10,346 SNP markers (mice.X).
Results
In this section, we introduce examples of various models that can be implemented with the multitrait function. We present in the article snippets with concise scripts that illustrate how to fit models and how to retrieve results. The complete set of scripts used to simulate and analyze data is provided in an R-Markdown as a Supplementary material and is also available at BGLR’s GitHub repository.
Gaussian (kernel) models
The example in Box 1 illustrates how to fit a single-kernel multitrait (GBLUP) model with unstructured (co)variance matrices. Lines 13–18 show how to retrieve parameter estimates and the corresponding posterior SD. The code in line 20 shows how to retrieve the predicted genomic values. Samples from the posterior distribution of model parameters can be found in files UN_mu.dat (intercepts), UN_R.dat (residual covariance matrix), and UN_Omega_1.dat (genomic covariance matrix). Supplementary Box 1 (File 2) provides scripts that illustrate how to create trace plots and posterior samples for genetic and residual dispersion parameters and the resulting plots are shown in Supplementary Figs. 1 and 2 (File 3). By default, the software fits unstructured (co)variance matrices; the examples in Box 2 illustrate how to specify structured covariance matrices. The first model (fmRD) uses a fully recursive model for the genomic covariance matrix and a diagonal structure for the error terms. In the recursive structure, there are regressions of traits 3 and 4 on trait 2 and of trait 4 on trait 3. This is specified with the matrix M (logical), which is used to specify recursions between traits. In the example, M is specified in a way that makes the genetic values of trait 1 independent from the genetic values on the other 3 traits (i.e. the resulting structure is block diagonal). The second example uses a 1-factor model for the genomic covariance matrix and a diagonal structure for the error terms (fmFD). The parameter M, which in this case links traits with common factors, links traits 2–4 with a common factor, thus, also leading to a block diagonal structure. In models with structured covariance matrices, the covariance matrices are nonlinear functions of the model parameters. For instance, in a GBLUP model with a FA structure for the genetic covariance, ; likewise, for a recursive model, the covariance matrix is (see Table 2). At each iteration of the sampler, the software computes these covariances and returns not only the posterior means of the parameters involved in the covariance structure (, in the preceding examples), but also the posterior means of the corresponding covariance matrix () (see lines 17–21 and 34–38). Supplementary Boxes 2a and 2b (File 2) provide code that can be used to produce posterior plots and summaries of the parameters of recursive and FA covariance structures, the resulting plots are shown in Supplementary Figs. 3–5 (File 3). In genetic models, upon appropriate scaling, parameters and can be interpreted as genetic and environmental (co)variance components. However, we will discuss later in the document approaches drawn from Lehermeier et al. (2017), which account for linkage disequilibrium and yield estimates, which often have smaller biases than those of the posterior means of and .
Box 1: Multitrait GBLUP with unstructured and structured covariances.
1 library(BGLR)
2 data(wheat)
3 K<-tcrossprod(scale(wheat.X, center=TRUE))
4 K<-K/mean(diag(K))
5 Y<-wheat.Y # 4 traits
6
7 # Fitting a GBLUP un-structured cov-matrices
8 LP<-list(mar=list(K = K, model=“RKHS”))
9 set.seed(123)
10 fmUN<-Multitrait(y = Y, ETA=LP, nIter = 10000, burnIn = 5000,
11 saveAt=“UN_”,verbose=FALSE)
12
13 # Retrieving estimates and posterior SD
14 fmUN$resCov$R # residual covariance matrix
15 fmUN$resCov$SD.R
16
17 fmUN$ETA$mar$Cov$Omega # genomic covariance matrix
18 fmUN$ETA$mar$Cov$SD.Omega
19
20 fmUN$ETA$mar$u # predicted random effects
Box 2: Multitrait GBLUP with structured covariance matrices.
1 #(continued from Box 1)
2
3 # Omega-recursive, R-diagonal
4 # Matrix specifying loadings among traits 2=>3,2=>4,3=>4
5 M1<-matrix(nrow = 4, ncol = 4, FALSE)
6 M1[3,2]<-M1[4,2]<-M1[4,3]<-TRUE
7 CovREC<-list(type=“REC”,M=M1)
8 LP<-list(mar=list(K = K, model=“RKHS”,Cov=CovREC))
9
10 CovDIAG<-list(type=“DIAG”)
11
12 set.seed(456)
13 fmRD<-Multitrait(y = Y, ETA=LP, nIter = 10000, burnIn = 5000,
14 resCov=CovDIAG, saveAt= “REC_DIAG_”,
15 verbose=FALSE)
16
17 fmRD$resCov$R
18 fmRD$ETA$mar$Cov$Omega # genomic covariance
19 fmRD$ETA$mar$Cov$W # recursive effects
20 fmRD$ETA$mar$u # predicted genetic effects
21 fmRD$ETA$mar$Cov$PSI # scaling factors
22
23
24 # Omega-FA(2), R-diagonal
25 M2<-matrix(nrow = 4, ncol = 1, FALSE)
26 M2[2:4,1]<-TRUE
27 CovFA<-list(type=“FA”,M=M2)
28 LP<-list(mar=list(K = K, model=“RKHS”,Cov=CovFA))
29
30 set.seed(789)
31 fmFAD<-Multitrait(y = Y, ETA=LP, nIter = 10000, burnIn = 5000,
32 resCov=CovDIAG, saveAt= “FA_DIAG_”,
33 verbose=FALSE)
34 fmFAD$resCov$R
35 fmFAD$ETA$mar$Cov$Omega # genomic covariance
36 fmFAD$ETA$mar$Cov$W # recursive effects
37 fmFAD$ETA$mar$u # predicted genetic effects
38 fmFAD$ETA$mar$Cov$PSI # scaling factors
Multikernel models
The Gaussian models described above can be extended by adding fixed effects and other random effects (e.g. pedigree + SNP models). The scripts in Supplementary Boxes 3a and 3b (File 2) implements a model with a genomic and a pedigree relationship matrix for the wheat data set, the script implements the unstructured and structured (diagonal, recursive, and FA) covariance matrices.
Bayesian variable selection models
We turn now into models using priors that can perform variable selection. To illustrate the use of these models, we simulated 3 traits using the genomes available in the mice data set (data(mice)). The script used to simulate data is presented in Supplementary Box 4a (File 2). Briefly, the simulation has a sample size of 1,814, and 1,000 SNPs, 12 of which had nonzero effect. Each trait had 6 QTL. Traits 1 and 3 had 3 “private” QTL and 3 shared with trait 2. All the QTL affecting trait 2 were shared with either trait 1 or trait 2. The trait heritabilities were 0.1, 0.05, and 0.1 for traits 1, 2, and 3, respectively. For illustration purposes, we present results from a single Monte Carlo replicate; we emphasize that assessing mapping power and FDR would require running multiple replicates and more complex simulation settings.
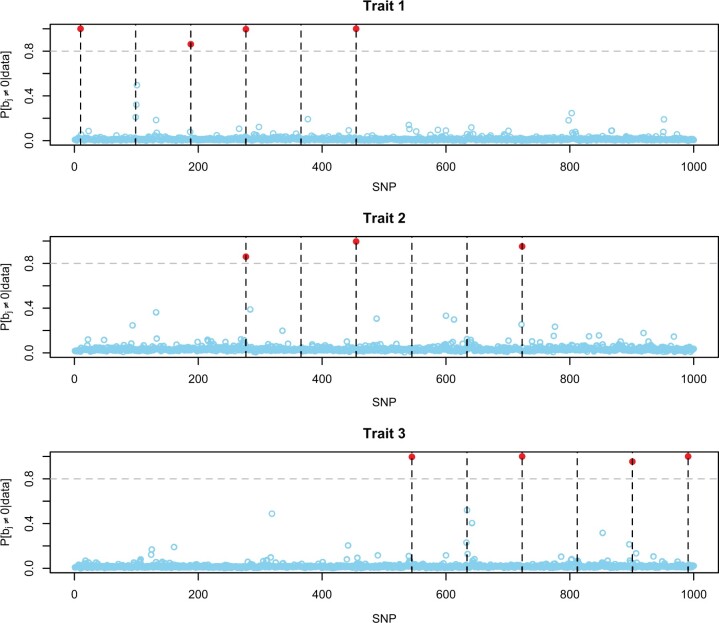
Box 3 shows how to fit a multitrait Bayesian regression model with a spike–slab prior. As before, Y is a matrix with traits in columns and subjects in rows, and X is a matrix with subjects in rows and SNPs in columns. For regression models, the multitrait function supports 3 priors (see Table 1). The argument saveEffects=TRUE can be used to save the samples of effects into a binary file. Figure 1 shows the posterior probability of inclusion by SNP and trait (the code used to produce the plot are given in Supplementary Box 4b, File 2). The model correctly identified 8 of the 12 QTL. Trait 2 had the lowest heritability and the lowest proportion of QTL detected. Some QTL are not individually detected because of high LD in the QTL region. This happened, for example, for QTL2, which was located (position 99) in a region with high LD. In this region, there were 3 SNPs (position 99, 100, and 101) with elevated probability of inclusion in the QTL region. The R-squared between the causal variant and SNP 100 and 101 is 0.999 and 0.937. Clearly, when SNPs are in high LD, variable selection algorithms cannot discern which SNP is associated with the phenotype—this also happens in single-trait models. When this situation happens, there are at least 2 possible remedies: (1) filter SNPs based on LD or (2) use all the SNPs and make inferences using credible sets (i.e. groups of SNPs). For example, in the region in question (positions 99–101) the joint posterior probability of inclusion (i.e. the proportion of times that at least one of the SNPs in the region was active) was 99.75 (see code in Supplementary Box 4c, File 2). Thus, for this region, we can be confident that there is an association with the phenotype, but we are uncertain as to which SNP has an effect.
Box 3: Fitting a multitrait spike–slab model.
1 # Run the code in Box S4a before runing this code
2 fmSS<-Multitrait(y = Y, ETA=list(list(X = X, model=”SpikeSlab”,
3 saveEffects=TRUE)),nIter = 12000, burnIn = 2000,
4 verbose=FALSE)
Fig. 1.
Posterior probability of nonzero effect by SNP and trait. Each dot/circle represents an SNP, red circles had posterior probability of inclusion greater than 0.8, and the dashed vertical lines show the position of the causal variants.
A more general approach to identify credible sets is demonstrated in Supplementary Box 4d (File 2). The function “segments” of the BGData R package (Grueneberg and de los Campos 2019) is used to identify segments with local FDR smaller than 0.7 (that is SNP inclusion probability greater than 0.3), and then we used the samples from the posterior distribution to estimate the joint probability of inclusion of each segment (i.e. the probability that at least 1 SNP in the segment is active in the model). The result is a table with discoveries, which includes both individual SNP and credible sets and their posterior probability of inclusion.
For comparison with the multitrait model, we fitted 4 separate single-trait models using the BayesC implementation available in BGLR function (see Supplementary Box 4e, File 2). The results are presented in Supplementary Fig. 6 (File 3). The single-trait analysis identified 2 QTL less than the corresponding multitrait model. In particular, the single-trait model did not identify (from left to right) the 3rd QTL of trait 1 and the first QTL of trait 2; the last 1 was shared between traits 1 and 2. This example illustrates some potential benefits of using a multitrait model for mapping variants with pleiotropic effects; however, as we will see below, in some cases, single-trait models may be more powerful.
The previous example used a stylized simulation, to illustrate the application of multitrait variable selection models in a more complex scenario, we used the function multitrait to map risk loci for 6 blood biomarkers (glucose, total cholesterol, HDL and LDL cholesterol, creatinine, and triglycerides) using the mice data set. The results are presented in Supplementary Fig. 7 and Supplementary Table 1 (File 3). In this case, the combination of small effects, small sample size, and high LD leads to no individual variants with a probability of inclusion greater than 0.8. However, for each of the biomarkers there are multiple regions with clearly elevated inclusion probabilities. Using the function “segments” of the BGData R package (Grueneberg and de los Campos 2019), we identified 25 regions with joint posterior probability greater than 0.8 (Supplementary Fig. 7, File 3). We identified 5 of such regions for glucose and 5 for HDL cholesterol, 9 regions for LDL cholesterol, 1 for creatinine, 3 regions for triglycerides, and 2 regions for total cholesterol. Some of the regions identified for different traits overlap (e.g. chromosome 1, mbp 89–98, chromosome 4, mbp 62–67, and chromosome 12, mbp 0–3) suggesting pleiotropy. For completeness, we also analyzed the same traits using single-trait models (Supplementary Fig. 8, File 3); most of the regions with elevated posterior probability of inclusion detected using with the multitrait model also showed elevated posterior probability of inclusion in the single-trait models.
We repeated the analysis of mice blood biomarkers using a sequence of 5 single-trait analyses using BGLR with a variable selection prior (BayesC) prior. Interestingly, the number of regions that cleared a joint inclusion probability of 0.8 was similar for glucose but more significant for the other traits (Supplementary Table 2 and Supplementary Fig. 8, File 3). Overall, there was a substantial overlap in findings between the single-trait and multitrait analyses. However, many regions identified by the single-trait models were not identified by the multitrait analysis. Conversely, the single-trait model did not identify a few regions discovered through a multitrait analysis (Supplementary Table 3, File 3). Because these analyses are based on real data, we cannot discern which discoveries were true and which ones are false discoveries. However, the example illustrates that multitrait analyses, which borrow information between traits, may not always lead to a higher power and more discoveries.
Estimation of variance components
Dissecting the phenotypic (co)variance into genetic and nongenetic components is an important goal of many genetic studies. Maximum likelihood, REML, and Bayesian estimates of (co)variance parameters are not guaranteed to be unbiased. In our experience, environmental (co)variances are often estimated with relatively small biases using the estimated posterior mean of . However, this is not always the case for genetic (co)variances. There is an extensive literature on biases that may emerge when using genomic models to estimate genetic variances (e.g. de los Campos et al. 2015; Krishna Kumar et al. 2016; Lehermeier et al. 2017). The amount of information at the likelihood about covariances is often smaller than the information provided for variances; therefore, presumably, there may be also sizable biases in estimate of genetic covariances.
The literature on genetic (co)variance estimates is largely focused on GBLUP-type models; however, at least in principle, those parameters should be estimable in variable selection models. In this section, we present a simulation study in which we assess the bias of (co)variance estimates derived from multitrait GBLUP and spike–slab models. For residual covariance matrix, we use as estimator the posterior mean of .
For estimating genetic covariances in models not involving variable selection (e.g. “RKHS” or “BRR”) we consider 2 estimation methods: the posterior mean of the (co)variance parameter (, method 1) and a second method (method 2) based on an approach described in Lehermeier et al. (2017), which account for covariances between predictors (e.g. LD between SNPs). Briefly, for method 2, at each iteration of the sampler, we compute for each trait the vectors of genomic values (i.e. the columns of in GBLUP models or in regression on SNPs, ) and compute the sample covariance between the columns of .
In models involving variable selection (“SpikeSlab”), only a fraction of the SNPs are active in the equation of each trait. Therefore, the (co)variance matrix of effects, , cannot be directly used to estimate the contribution of the regression. Therefore, to estimate genetic covariances in these models we consider 3 methods: method 1, at each iteration of the Gibbs sampler, we compute and then compute the sample covariance between the columns ; the estimate is then the posterior mean of cov(B). For method 2, we computed genomic values () at each iteration of the sampling process and form there we computed the sample variance–covariance matrix of the realized genomic values (var(U)). This approach, which accounts for LD between markers, extends the method described for single-trait models by Lehermeier et al. (2017) to multitrait analyses. Finally, we consider a 3rd method, which was proposed by Cheng et al. (2018). In method 3, at each iteration of the Gibbs sampler, we compute the following variance–covariance parameters:
where is the sum of the variances of the markers (), is the proportion of markers with non-null effect on trait and is the proportion of markers with non-null effects for traits and .
We evaluated the bias of each of the estimation methods above described using 200 MC replicates of the simulation described in the previous section (see Supplementary Box 4a for the simulation code, File 2). The code for estimating genetic covariance matrixes is given in Supplementary Box 5 (File 2).
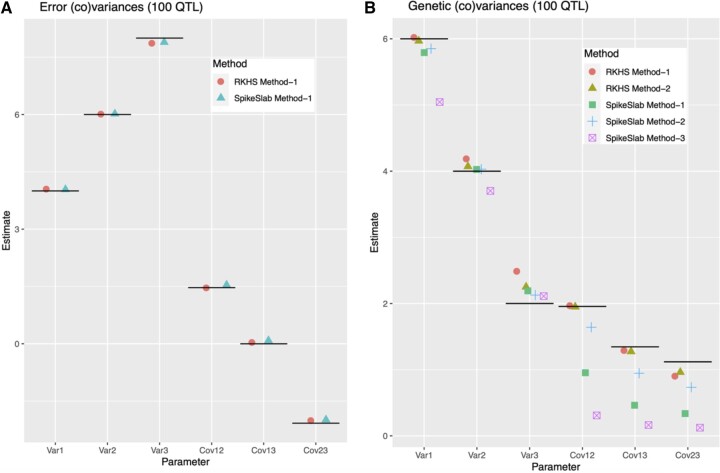
The error (co)variance parameters were estimated without any noticeable bias by both the GBLUP and spike–slab model (Fig. 2a). The genetic variances were estimated with small biases by the GBLUP, with method 2 having slightly smaller bias than method 1 (Fig. 2b, see Supplementary Table 4, File 3 for average estimates and SEs). The spike–slab model gave estimates with noticeable bias with methods 1 and 3; however, these biases were reduced when method 2 was used. In summary, at least for this specific data set and simulation setting, it seems that regardless of the prior used, the residual (co)variance parameters can be estimated with small biases, and estimation of genetic (co)variances seem to be better with method 2.
Fig. 2.
Average Monte Carlo estimates of error (a) and genetic (b) (co)variance parameter, by model and estimation method. The horizontal line gives the true parameter value (for SEs see Supplementary Table 4, File 3).
Prediction
For the entries of the phenotype matrix containing missing values, at each iteration of the sampler, the software samples the missing phenotypes from the corresponding fully conditional distributions (which in the models implemented is MVN). This process leads to inferences that average over possible values of the missing phenotypes. To make the sampling of missing phenotypes more efficient, we identify missing value patterns and impute them (with samples) jointly (missing_patterns contain the patterns identified and labeled missing_records indicate the rows of Y, which map to each of the patterns).
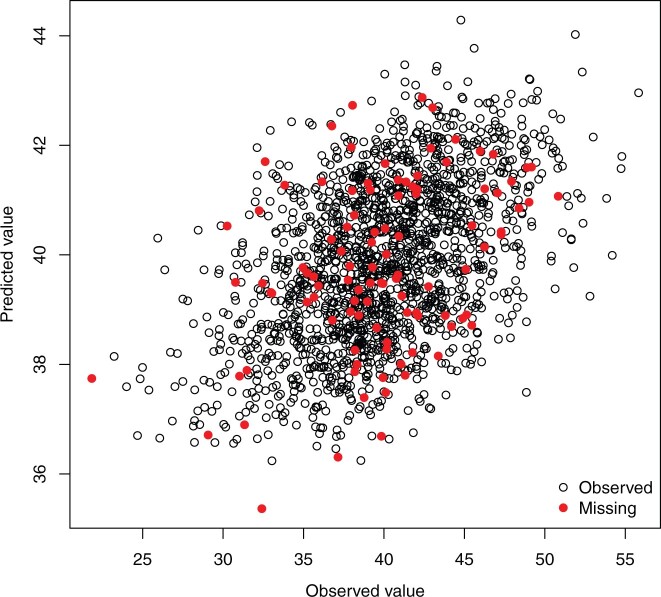
The multitrait function returns estimates of the posterior mean of the linear predictor (, named ETAHat in the returned object), these are estimates of the expected value of the phenotypes given the predictors. Box 4 shows how to retrieve these predictions (the missing value patterns in YNa were generated using the script in Supplementary Box 6, File 2). The plot in Fig. 3 shows the simulated phenotype vs the posterior mean of for entries that were observed and missing, using trait 3 as an example (see Supplementary Box 6, File 2).
Box 4: Prediction.
1
2 K<-tcrossprod(X)
3 K<-K/mean(diag(K))
4
5 LP<-list(list(K = K, model=“RKHS”))
6
7 #Fit multivariate GBLUP with UN-structured covariance matrixes
8 fmG<-Multitrait(y=YNa, ETA=LP, nIter = 10000, burnIn = 5000, thin = 10,
9 verbose=FALSE)
10
11 #Missing values for trait 3
12 whichNa3<-fmG$missing_records[fmG$patterns[ , 3]]
13 Y[whichNa3,3] #Observed values
14 fmG$ETAHat[whichNa3,3] #Predicted values
Fig. 3.
Predicted (posterior mean of the linear predictor) vs observed phenotypes for trait 3 (see Supplementary Box 6, File 2).
Benchmark
We evaluated the computational time it takes for the multitrait function to generate 1,000 posterior samples for data sets with a sample size ranging from 10,000 to 500,000 individuals and with 5,000 to 50,000 SNPs. The data used for this benchmark were from the UK-Biobank; we fitted models to 2 and 4 traits (body mass index total cholesterol, glucose, and height, all adjusted by sex, age, center, and 10 SNP-derived PCs) using either Gaussian or spike–slab priors. The analyses were performed in MSU’s high-performance computing cluster using nodes equipped with Intel Xeon Gold 6148 processors at 2.40 GHz. We used R 4.2.0 compiled from source and the reference BLAS implementation was substituted with OpenBLAS version 0.3.17 (https://www.openblas.net). Jobs were run using 4 computing threads. To benchmark our software, we compared the computational performance of BGLR’s multitrait function with that of Julia’s JWAS package (Cheng et al. 2018), which also uses OpenBLAS for matrix operations. We provide the scripts to produce the benchmarks in the case of a Gaussian prior in Supplementary Boxes 7 and 8 (File 2).
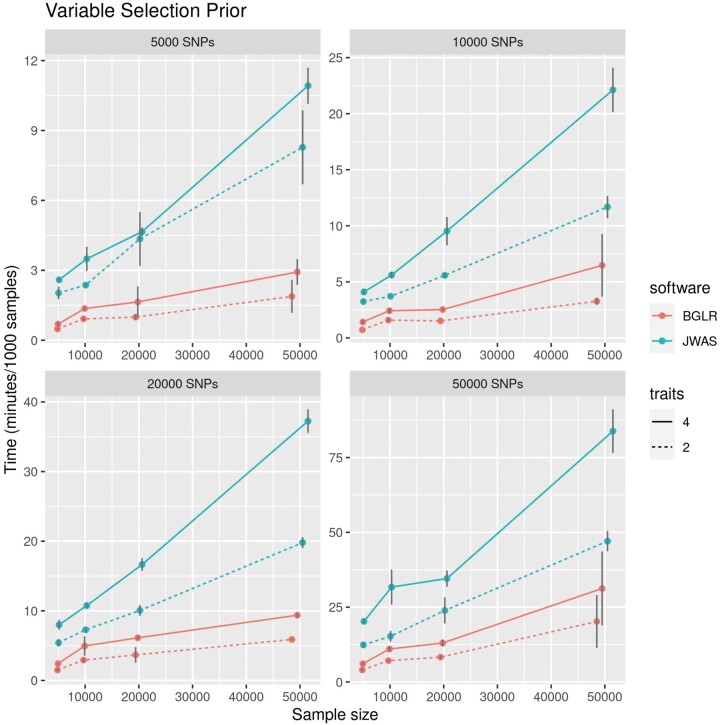
Figure 4 shows the time (in minutes) required to generate 1,000 Gibbs samples for models using variable selection priors. We found that JWAS performed slightly better using just 1 thread; therefore, the results in Fig. 4 are for multitrait running with 4 threads and JWAS running with 1 thread (for results with both software using 4 threads, see Supplementary Fig. 9, File 3). Both software scaled approximately linearly with sample size, but the slope of the lines representing computational time vs sample size was smaller for the multitrait function. Likewise, while in both packages, the computational time increased with the number of traits, the increase in computational time that occurred when increasing the number of traits from 2 to 4 was more important for JWAS. The results for models using a Gaussian prior are presented in Supplementary Figs. 10 and 11 (File 3). The overall trends were very similar to those obtained with the variable selection priors (Fig. 4).
Fig. 4.
Average time (in minutes, ± SD) to collect 1,000 posterior samples for variable selection models, by the number of SNPs (panels), the number of traits (horizontal axis), and the software used. Results for Gaussian prior are presented in Supplementary Figs. 10 and 11 (File 3).
The computational time required for implementing a GBLUP (or any other kernel model) depends on sample size, this without considering the time it takes to compute the genomic relationship matrix. The BGLR and multitrait functions fit GBLUP model by first factorizing kernel matrices using an eigenvalue decomposition; then, the software runs a random regression (with Gaussian IID priors) on the scaled eigenvectors (de los Campos et al. 2009). Therefore, the computational time it takes to collect samples for kernel models is the same as the computing time it takes for a Gaussian model with a sample size of n and n SNPs (which can be inferred from the results just presented), plus the time it takes to factorize the genomic relationship matrix. We present in Supplementary Fig. 12 (File 3) the computational time required to perform eigenvalue decomposition. The computational time increases exponentially with the dimensions of the kernel matrix; for 30,000 subjects it took approximately 25 min to compute the eigenvalue decomposition. In general, the option of using a genomic relationship matrix is recommended (relative to an equivalent model implemented as a random regression on SNPs) only when n is not too large, and sample size is considerably smaller than the number of SNPs.
Discussion
We presented the newly developed multitrait function of the BGLR-R package. The software allows the user to include fixed effects (i.e. effects with a diffuse prior), shrinkage, and variable selection priors in multitrait models. These methods can be used to fit models commonly used in genomic analysis of complex traits, including parametric genomic and pedigree models, variable selection models, and semiparametric regressions (e.g. RKHS). The interface allows users to specify models with multiple terms, each having their own priors.
The architecture of the software was designed to take advantage of interpreted code written in R and compiled code written in C. The MCMC algorithms (Metropolis and Gibbs sampler) implemented are computationally intensive. We make an effort to optimize computations without losing much flexibility in terms of the types of models that users can implement. As a result, the software can be used with a very large sample size, large numbers of SNPs, and multiple traits. However, users must be aware that the computational time grows linearly with sample size and with the number of SNPs; thus, fitting models to very large data sets and hundreds of thousands of SNPs will have a very high memory requirement and it will be time consuming. The programming strategy we adopted makes intensive use of level-1 BLAS functions “ddot” and “daxpy.” For large problems, we strongly recommend using an optimized version of BLAS for the hardware and running the software on multiple threads.
The possibility of specifying structured (co)variance matrices for both Gaussian and variable selection priors is a distinctive feature of multitrait. Users should be aware that priors on (co)variance matrices can be influential; this is particularly the case of the IW prior, which can be highly influential if sample size is small, and the number of traits is large. To remediate this problem, we described in this study an approach (referred as to method 2 in Fig. 2) for estimating the variances and covariances that are less influenced by the prior; however, even with this approach, the IW prior can be influential. This method, which extend the ideas discussed in Lehermeier et al. (2017) to multitrait models, accounts for the contribution of linkage disequilibrium to (co)variance and, importantly, can be used with any prior (including diffuse, Gaussian, and variable selection priors). Another approach that may be less influential is to use a fully recursive model which also leads to an unstructured (co)variance matrix. In this case, the prior specification involves defining priors over variances and over recursive effects. The priors on the recursive effects (which in the multitrait are by default Gaussian) can be made effectively diffuse and this may lead to less influence of the prior on inferences.
Although the software was originally developed for genomic and pedigree model, like BGLR, the multitrait function can also be used to implement models for other omics (including metabolomic, microbiome, and gene expression data) and environmental information (e.g. models for environmental covariates). We look forward to continuing improving BGLR and welcome users’ feedback. Future updates will be shared in BGLR’s GitHub repository (https://github.com/gdlc/BGLR-R) and in the CRAN (https://cran.r-project.org/web/packages/BGLR/index.html).
The reader may wonder: For what problems, or under what conditions, is a multitrait analysis preferred relative to a sequence of single-trait analyses? Of course, the answer to that question is problem specific; however, some guidelines can be provided for parameter estimation, mapping, and prediction problems. Obviously, multitrait analyses are needed to estimate genetic and environmental correlations between traits (or environments).
Depending on the problem, the multitrait model may offer higher or lower power than the single-trait analysis. Standard multitrait models assume a homogeneous covariance of effects across the genome. In regions of the genome where the correlation of effects aligns with the average correlation of effects of the genome, borrowing information between traits may increase power. However, in regions where the correlation of effects is markedly different than the average correlation of effects in the genome, the multitrait model may reduce power because multitrait models tend to shrink effects toward a common covariance pattern. Variable selection priors may mitigate this problem because the model, as implemented in the multitrait function, has separate variable selection dummy variables for each SNP-trait combination. This allows for an SNP to affect some traits but not others. However, even considering the flexibility that variable selection priors offer for mapping, we strongly encourage considering both the multitrait and the single-trait models.
For GP, there is evidence showing that for some prediction problems (Burgueño et al. 2012), the multitrait model can offer higher prediction accuracy than predictions derived from single-trait models. The superiority of the multitrait model over single-trait analyses occurs when the prediction problem enables borrowing of information within-subject between traits and environments. This happens, for example, when predicting genetic values for an unmeasured trait for individuals with records for other traits (or environments, this was labeled as CV2 in Burgueño et al. 2012). On the other hand, for the prediction of genetic values for subjects that do not have any records (labeled as CV1 in Burgueño et al. 2012), multitrait models do not consistently outperform predictions derived from single-trait models.
Data availability
The data sets are included with the BGLR package, which is freely available in the CRAN website, https://cran.r-project.org/web/packages/BGLR/index.html and also in our GitHub web site, https://github.com/gdlc/BGLR-R.
Supplemental material is available at GENETICS online.
Funding
The development and maintenance of BGLR has been founded by NIH grant GM R01 101219. The authors also acknowledge financial support from Michigan State University.
Conflicts of interest
None declared.
Supplementary Material
Contributor Information
Paulino Pérez-Rodríguez, Colegio de Postgraduados, Montecillo, Estado de México 56230, Mexico; Department of Epidemiology and Biostatistics, Michigan State University, East Lansing, MI 48824, USA.
Gustavo de los Campos, Department of Epidemiology and Biostatistics, Michigan State University, East Lansing, MI 48824, USA; Department of Statistics and Probability, Michigan State University, East Lansing, MI 48824, USA; Institute for Quantitative Health Science and Engineering, Michigan State University, East Lansing, MI 48824, USA.
Literature cited
- Burgueño J, de los Campos G, Weigel K, Crossa J.. Genomic prediction of breeding values when modeling genotype × environment interaction using pedigree and dense molecular markers. Crop Sci. 2012;52(2):707–719. 10.2135/cropsci2011.06.0299. [DOI] [Google Scholar]
- Casella G, George EI.. Explaining the Gibbs sampler. Am Stat. 1992;46(3):167–174. 10.1080/00031305.1992.10475878. [DOI] [Google Scholar]
- Cheng H, Fernando R, Garrick D.. 2018. JWAS: Julia implementation of whole-genome analyses software. Proceedings of the World Congress on Genetics Applied to Livestock Production Methods and Tools-Software. 859.
- Cheng H, Kizilkaya K, Zeng J, Garrick D, Fernando R.. Genomic prediction from multiple-trait Bayesian regression methods using mixture priors. Genetics. 2018;209(1):89–103. 10.1534/genetics.118.300650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Covarrubias-Pazaran G. Genome-assisted prediction of quantitative traits using the R Package Sommer. PLoS One. 2016;11(6):e0156744. 10.1371/journal.pone.0156744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossa J, Campos GdL, Pérez P, Gianola D, Burgueño J, Araus JL, Makumbi D, Singh RP, Dreisigacker S, Yan J, et al. Prediction of genetic values of quantitative traits in plant breeding using pedigree and molecular markers. Genetics. 2010;186(2):713–724. 10.1534/genetics.110.118521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de los Campos G, Gianola D, Rosa GJM.. Reproducing Kernel Hilbert spaces regression: a general framework for genetic evaluation. J Anim Sci. 2009;87(6):1883–1887. 10.2527/jas.2008-1259. [DOI] [PubMed] [Google Scholar]
- de los Campos G, Gianola D.. Factor analysis models for structuring covariance matrices of additive genetic effects: a Bayesian implementation. Genet Sel Evol. 2007;39(5):481–494. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- de los Campos G, Gianola D, Allison DB.. Predicting genetic predisposition in humans: the promise of whole-genome markers. Nat Rev Genet. 2010;11(12):880–886. 10.1038/nrg2898. [DOI] [PubMed] [Google Scholar]
- de los Campos G, Grueneberg A. MTM: An R-Package for Genetic Multi-Trait Recursive and Factor Analyses Models (version 1.0); 2013. https://github.com/QuantGen/MTM
- de los Campos G, Hickey JM, Pong-Wong R, Daetwyler HD, Calus MPL.. Whole-genome regression and prediction methods applied to plant and animal breeding. Genetics. 2013;193(2):327–345. 10.1534/genetics.112.143313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Los Campos G, Sorensen D, Gianola D.. Genomic heritability: what is it? PLoS Genet. 2015;11(5):e1005048. 10.1371/journal.pgen.1005048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endelman JB. Ridge regression and other kernels for genomic selection with R Package RrBLUP. Plant Genome. 2011;4(3):250–255. 10.3835/plantgenome2011.08.0024. [DOI] [Google Scholar]
- Friedman J, Hastie T, Tibshirani R.. Regularization paths for generalized linear models via coordinate descent. J Stat Softw. 2010;33(1):1–22. 10.18637/jss.v033.i01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmour AR, Thompson R, Cullis BR.. Average information REML: an efficient algorithm for variance parameter estimation in linear mixed models. Biometrics. 1995;51(4):1440. 10.2307/2533274. [DOI] [Google Scholar]
- Goldberger AS. Structural equation methods in the social sciences. Econometrica. 1972;40(6):979–1001. [Google Scholar]
- Grueneberg A, de los Campos G.. BGData—a suite of R packages for genomic analysis with big data. G3 (Bethesda). 2019;9(5):1377–1383. 10.1534/g3.119.400018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habier D, Fernando RL, Kizilkaya K, Garrick DJ.. Extension of the Bayesian alphabet for genomic selection. BMC Bioinformatics. 2011;12(1):186. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hadfield JD. MCMC methods for multi-response generalized linear mixed models: the MCMCglmm R package. J Stat Softw. 2010;33(2):1–22. 10.18637/jss.v033.i02.20808728 [DOI] [Google Scholar]
- Kernighan BW, Ritchie DM.. The C Programming Language. 2nd ed. Englewood Cliffs (NJ: ): Prentice Hall; 1988. [Google Scholar]
- Krishna Kumar S, Feldman MW, Rehkopf DH, Tuljapurkar S.. Limitations of GCTA as a solution to the missing heritability problem. Proc Natl Acad Sci U S A. 2016;113(1):E61–70. 10.1073/pnas.1520109113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehermeier C, de los Campos G, Wimmer V, Schön C-C.. Genomic variance estimates: with or without disequilibrium covariances? J Anim Breed Genet. 2017;134(3):232–241. 10.1111/jbg.12268. [DOI] [PubMed] [Google Scholar]
- Lippert C, Paolo Casale F, Rakitsch B, Stegle O. LIMIX: genetic analysis of multiple traits. 10.1101/003905, 2014, preprint. [DOI]
- Martin AD, Quinn KM, Park JH.. MCMCpack: Markov Chain Monte Carlo in R. J Stat Softw. 2011;42(9):22. [Google Scholar]
- Meuwissen THE, Hayes BJB, Goddard MEM.. Prediction of total genetic value using genome-wide dense marker maps. Genetics. 2001;157(4):1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer K. WOMBAT—a tool for mixed model analyses in quantitative genetics by Restricted Maximum Likelihood (REML). J Zhejiang Univ Sci B. 2007;8(11):815–821. 10.1631/jzus.2007.B0815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montesinos-López OA, Montesinos-López A, Luna-Vázquez FJ, Toledo FH, Pérez-Rodríguez P, Lillemo M, Crossa J.. An R package for Bayesian analysis of multi-environment and multi-trait multi-environment data for genome-based prediction. G3 (Bethesda). 2019;9(5):1355–1369. 10.1534/g3.119.400126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez P, de los Campos G.. Genome-wide regression and prediction with the BGLR statistical package. Genetics. 2014;198(2):483–495. 10.1534/genetics.114.164442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2019. [accessed 2022 May 10]. https://www.R-project.org/. [Google Scholar]
- Sorensen D, Gianola D.. Likelihood, Bayesian and MCMC Methods in Quantitative Genetics. Statistics for Biology and Health. New York: Springer-Verlag; 2002. [Google Scholar]
- Valdar W, Solberg LC, Gauguier D, Burnett S, Klenerman P, Cookson WO, Taylor MS, Rawlins JNP, Mott R, Flint J.. Genome-wide genetic association of complex traits in heterogeneous stock mice. Nat Genet. 2006;38(8):879–887. 10.1038/ng1840. [DOI] [PubMed] [Google Scholar]
- Valdar W, Solberg LC, Gauguier D, Cookson WO, Rawlins JNP, Mott R, Flint J.. Genetic and environmental effects on complex traits in mice. Genetics. 2006;174(2):959–984. 10.1534/genetics.106.060004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR, Madden PA, Heath AC, Martin NG, Montgomery GW, et al. Common SNPs explain a large proportion of the heritability for human height. Nat Genet. 2010;42(7):565–569. 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data sets are included with the BGLR package, which is freely available in the CRAN website, https://cran.r-project.org/web/packages/BGLR/index.html and also in our GitHub web site, https://github.com/gdlc/BGLR-R.
Supplemental material is available at GENETICS online.