Biomechanical origins of inherent tension in fibrin networks

Abstract

Blood clots form at the site of vascular injury to seal the wound and prevent bleeding. Clots are in tension as they perform their biological functions and withstand hydrodynamic forces of blood flow, vessel wall fluctuations, extravascular muscle contraction and other forces. There are several mechanisms that generate tension in a blood clot, of which the most well-known is the contraction/retraction caused by activated platelets. Here we show through experiments and modeling that clot tension is generated by the polymerization of fibrin. Our mathematical model is built on the hypothesis that the shape of fibrin monomers having two-fold symmetry and off-axis binding sites is ultimately the source of inherent tension in individual fibers and the clot. As the diameter of a fiber grows during polymerization the fibrin monomers must suffer axial twisting deformation so that they remain in register to form the half-staggered arrangement characteristic of fibrin protofibrils. This deformation results in a pre-strain that causes fiber and network tension. Our results for the pre-strain in single fibrin fibers is in agreement with experiments that measured it by cutting fibers and measuring their relaxed length. We connect the mechanics of a fiber to that of the network using the 8-chain model of polymer elasticity. By combining this with a continuum model of swellable elastomers we can compute the evolution of tension in a constrained fibrin gel. The temporal evolution and tensile stresses predicted by this model are in qualitative agreement with experimental measurements of the inherent tension of fibrin clots polymerized between two fixed rheometer plates. These experiments also revealed that increasing thrombin concentration leads to increasing internal tension in the fibrin network. Our model may be extended to account for other mechanisms that generate pre-strains in individual fibers and cause tension in three-dimensional proteinaceous polymeric networks.

1. Introduction

Blood clots are formed at the sites of vessel wall injuries to seal or plug the damage and stem bleeding. Clots result from multiple reactions that involve blood cells and plasma components, including fibrinogen, the soluble protein converted enzymatically to insoluble fibrin (Weisel and Litvinov, 2017). A three-dimensional polymeric fibrin network comprises the scaffold of a blood clot and, in combination with embedded platelets and red blood cells (Chernysh et al., 2020), largely determines the clot’s biological and mechanical properties.

To fulfill its biomechanical function and prevent or stop bleeding, the blood clot and the fibrin scaffold must have certain mechanical resilience to be able to withstand hydrodynamic forces of blood flow, pulsation of a vessel wall, extravascular muscle contraction, and more (Litvinov and Weisel, 2017). Among many factors that contribute to the mechanical behavior of fibrin, one of the least studied is the physiological tension of the fibrin network generated by at least two mechanisms. The most apparent and well-studied is the external traction and compression of fibrin clots driven by activated platelets, with each individual platelet exerting contractile forces on the order of tens of nano-Newtons on adjacent fibrin fibers (Kim et al., 2017; Lam et al., 2011; Pathare et al., 2021; Sun et al., 2022). However, there is strong evidence that fibrin clots generate inherent (internal or intrinsic) tension unrelated to platelet contractility or any other external mechanical perturbations. For example, the individual hydrated fibrin fibers observed in a light microscope are straight, not sinuous, suggesting that each fiber is under inherent tension (Britton et al., 2019). Tension of individual fibrin fibers was introduced in Weisel et al. (1987), and their elasticity has been shown and quantified in AFM pulling experiments (Liu et al., 2010) and by active flexing or stretching a separate fibrin fiber using optical tweezers (Collet et al., 2005). Finally, the inherent fibrin fiber tension has been established directly by severing these fibers and watching them retract (Cone et al., 2020). If a great number of such taut individual fibers form a three-dimensional network, then the entire network must also be under tension. From the general theory of polymer mechanics, tension is self-generated in the polymers that possess some degree of non-uniformity and thermodynamic instability of the major structural elements (Zhang et al., 1991; Li et al., 2014). The complex spatial axial and lateral packing of the fibrin monomers and oligomers dictates their deviation (stretching) from the relaxed and stable conformational state that provides a fundamental structural and thermodynamic basis for the existence of inherent tension of fibrin networks (Torbet et al., 1981; Caracciolo et al., 2003; Yeromonahos et al., 2010; Portale and Torbet, 2018; Jansen et al., 2020; Weisel et al., 1983; Weisel, 1986).

The inherent tension of fibrin clots has a number of conceivable biological implications. First, it may comprise a thermodynamic mechanism to control the diameter of fibrin fibers, as the lateral aggregation of protofibrils stops when the protofibril stretching energy surpasses the energy of bonding (Weisel et al., 1987). Since fiber diameter is related to network porosity, fiber length, branch point density, etc., the inherent tension of fibrin clots may modulate the overall network structure. Second, the inherent tension in fibrin fibers can affect the rate of fibrinolysis both at the individual fiber level (Hudson, 2017; Li et al., 2017a; Cone et al., 2020) and in whole clot (Varjú et al., 2011) because susceptibility of fibrin to fibrinolytic enzymes depends strongly on the mechanical tension of the proteinaceous fibrous substrate. In aggregate, modulation of the structure of a fibrin network along with the tension of fibers can affect the mechanical and enzymatic stability of entire blood clots and thrombi that determine the course and outcomes of various hemostatic disorders (Litvinov and Weisel, 2017; Feller et al., 2022). Notably, the magnitude of inherent tension in fibrin networks should be quite variable since it must depend on multiple local and systemic influences that determine fibrin polymerization, including physiological and pathological variations in blood composition.

Here, our goal is to construct a mathematical model for the evolution of tension in isotropic fibrin networks by accounting for the kinetics of the fibrin polymerization reaction that regulates the size and structure of the fibrin fibers in a network model, accounting for the idea in Weisel et al. (1987) that monomers make a twisted protofibril, and the aggregation in register with a 22.5 nm repeat introduces tension. In the following we first describe experiments for the measurement of tension in fibrin networks during polymerization and a model for capturing the evolution of tension in a fibrin gel. We show how tension develops in a polymerizing fibrin fiber as its diameter increases, then use this information in a continuum model to predict the evolution of tension in a constrained fibrin clot.

2. Materials and methods

2.1. Sample preparation

Citrated apheresis platelet poor plasma (PPP) was obtained from 25 de-identified donors from discarded blood bank donations. Donors were consented in accordance with the University of Pennsylvania and State University of New York Stony Brook Blood Blank guidelines. Individual PPP samples were frozen at −65 °C, thawed (only once), pooled, filtered, and then aliquoted and refrozen at −80 °C. The fibrinogen concentration in the final PPP was 2.7 ± 0.2 mg/mL. For each testing method, a PPP aliquote was warmed to 37 °C and clots were formed, through the addition of 20 mM calcium chloride and 0.2 U/mL or 1 U/mL human thrombin (final concentration, Sigma Aldrich). Immediately after initiation of clotting, the plasma was used in dynamic mechanical rheometer testing or optical turbidity testing to follow clot formation.

2.2. Mechanical rheometer testing

A Malvern Kinexus Ultra rheometer was used to analyze the inherent tensile force generated during fibrin polymerization in clotting plasma. Plasma samples were activated, mixed, and 960 μL of the sample was quickly transferred to the surface of the lower horizontal plate of the rheometer. After the upper plate came into contact with the activated plasma sample, the sample was surrounded with 300 μL of mineral oil to prevent drying during the test (see Fig. 1). An oscillation shear strain test was performed on each plasma clot sample, at 0.001 Hz and 0.001% shear strain using a 40-mm parallel plate, a 0.70 mm gap and 2 s sampling rate for 1 h. The rheometer was equipped with a normal force sensor with a minimum detectable force of 0.001 N and a resolution of 0.5 mN. The normal/perpendicular force generated during formation of a plasma clot was measured as the force pushing (positive) or pulling (negative or tensile force) on the upper plate of the rheometer as a function of time. Normal force was converted to normal pressure using the area of the 40-mm diameter upper plate, then data was shifted to start at zero pascals at the start of the experiment. Pressure leveled off at ~1000 s, and was then normalized to zero or to the unclotted control plasma sample at this point to examine differences in the tensile pressure generated by each sample after this time point. At least four replicates were run for each sample.

Fig. 1.

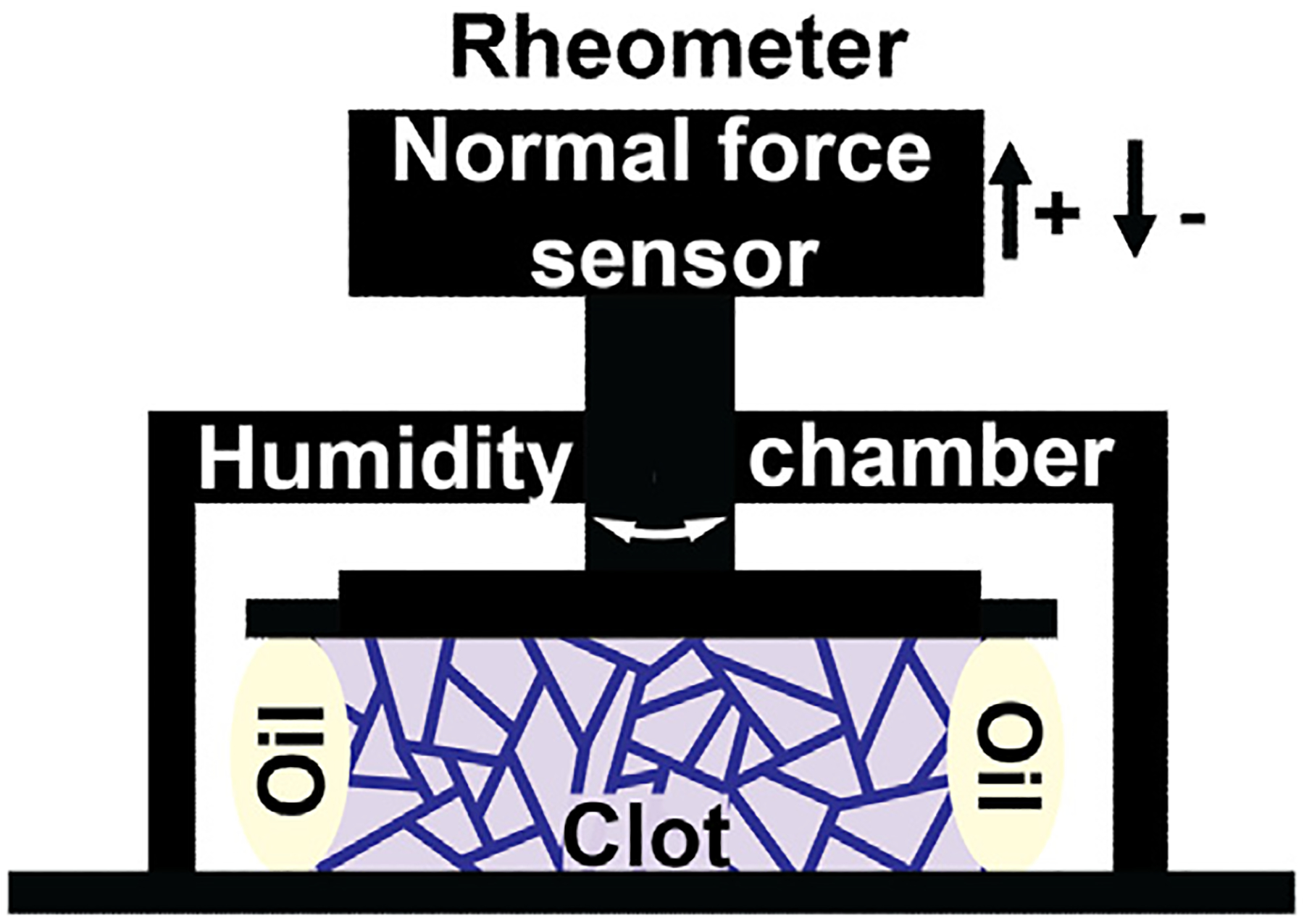
Cartoon depicting the experimental setup using a rheometer. Testing apparatus, including rheometer plates, force sensor, and humidity chamber, are shown in black. The light purple shape represents the fibrin network material, the purple lines in the fibrin network represent the isotropic fiber network, and the off-white ovals next to the clot represent the mineral oil added to prevent sample drying during testing. Platelet poor plasma (PPP) was activated with 20 mM CaCl2 and 0.2 U/mL or 1 U/mL thrombin and placed between rheometer plates, which leads to a polymerization reaction that forms a fibrin network. The rheometer plates are held fixed such that a tension in the network results in pulling on the upper plate. The tensile force on the rheometer plates generated by the polymerizing fibrin clot is measured as a function of time.

2.3. Data analysis

To ascertain the inherent tensile force generated during the clot formation process, the normal pressure measured by the rheometer must be corrected for some artifacts and adjusted to 0 at time = 0. To make these corrections, we used unclotted plasma (without thrombin) as a control, since there will be no force generated. In order to isolate the changes in normal pressure due to the inherent tension and remove effects related to surface tension of the liquid phase of the sample, the average normal pressure values for unclotted plasma were subtracted from the individual clotted samples. Normal pressure was shifted to 0 for time = 0 and the relative changes in normal pressure we assessed over the course of time. The normalized pressure was relatively unchanged until ~ 1000 s. At this time point, a change in magnitude in the negative direction was observed, representing the inherent tension developed as the clot forms. First order differential for each sample was calculated with GraphPad prism. The point at which the first order differential first crossed the x-axis indicated the beginning of decreasing normal pressure (tension generation) in each sample. The green shaded region in Fig. 2(a) includes the time points where each sample crossed the x-axis first (between 0–1000 s). The second point at which they crossed the x-axis indicates when the slope became 0 and normal pressure plateaued for the samples and no more tension was generated. The red shaded region in Fig. 2(a) includes the time points where each sample crossed the x-axis the second time (between 1800–2700 s). Each sample was individually analyzed to determine the change in pressure across this time period as well as the rate of pressure generation during the period. The absolute pressure generated was calculated by taking the difference between the beginning pressure values within the initial no-tension region and the final pressure values in the plateau region. A linear regression analysis was performed in this region to determine the rate of force generation.

Fig. 2.

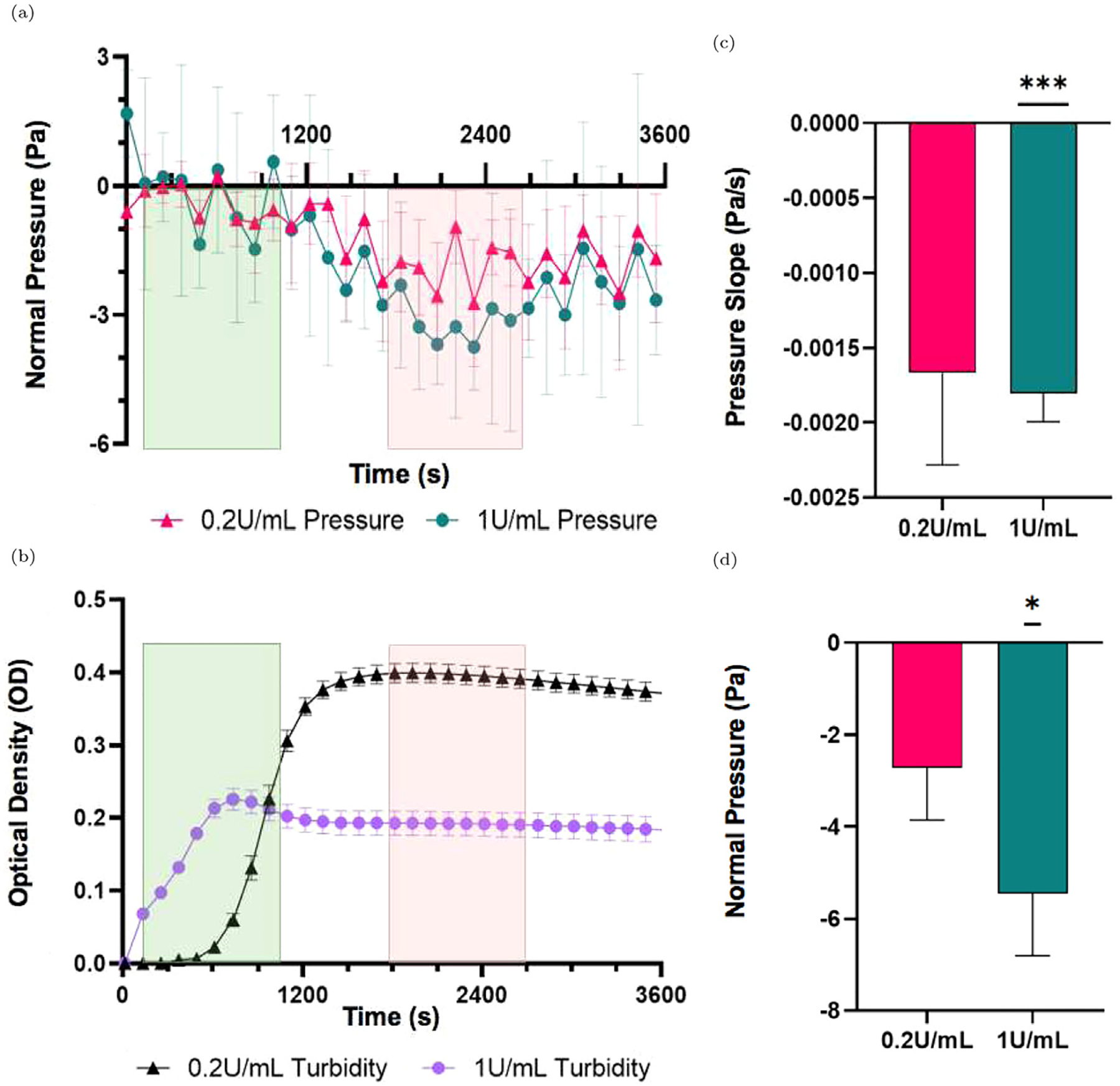
(a) Average normal pressure for 0.2 U/mL thrombin (pink, triangles) and 1 U/mL thrombin samples (teal, circles) profile in plasma samples after activation of clotting. Green shaded regions on the left indicate the range of time where first order derivatives were negative, indicating decreasing normal pressure. Red shaded regions on the right indicate where the first order derivative crosses the x axis indicating a plateau of normal pressure across each sample. (b) Average optical density measurements of 0.2 U/mL thrombin (black, triangles) and 1 U/mL thrombin (purple, circles) samples. Green and red ranges indicate the same as in (a). (c) Comparison of the slope of normal pressure in clotting plasma after normalization to unclotted plasma, as negative normal pressure is generated in samples activated with 0.2 U/mL (pink, left) and 1 U/mL (teal, right) thrombin. (d) Comparison of the change in normal pressure in clotting plasma after normalization to unclotted plasma, as negative normal pressure is generated in the samples. All data are represented as mean ± standard error of the mean unless otherwise noted. Subfigures (c) and (d) show comparison to the unclotted plasma slope and pressure at 0 Pa/s and 0 Pa respectively. *p ≤ 0.05, ***p < 0.001, and lack of significant differences between samples is indicated by no bar above the samples graphed. Analysis was completed using a one sample t-test relative to a theoretical 0 value, as the samples were normalized to the unclotted control.

2.4. Dynamic optical turbidity testing

A Molecular Devices Spectramax Plus plate reader was used to analyze the dynamic optical density of clotting plasma. Following initiation of clotting 100 μL plasma samples were transferred to a clear bottom 96-well plate, where surrounding wells were filled with distilled water to prevent drying of the clots. Turbidity measurements were taken at 405 nm and 37 °C every 15 s to track clot formation over the course of 90 min. Four replicates were run for each sample.

2.5. Statistical analyses

All statistical analyses were performed using GraphPad Prism 9.0. One sample t-test was used to determine the significance of the slope of force generation and amount of normal force produced by clotted blood plasma compared to an unclotted control at zero force. All data are represented as mean ± standard error of the mean unless otherwise noted. * p < 0.05, ***p ≤ 0.01, and lack of significant differences between samples is indicated by no bar above the samples graphed.

3. Experimental results

The generation of normal (tensile) stress was measured in activated plasma to determine the inherent tension that is produced by the fibrin network during the clotting process. The clot formation kinetics, measured with turbidity, showed that clotting began at near 0 s with thrombin added at 1.0 U/mL and 600 s with 0.2 U/mL thrombin with both clots fully formed near 1000 s (Fig. 2(b)). The rate of tensile stress generation was higher in 1 U/mL thrombin samples (−0.001804 Pa/s, p < 0.001) than 0.2 U/mL thrombin samples (−0.001667 Pa/s) (Fig. 2(c)). The directionality of these slopes indicates the generation of a negative normal pressure, which corresponds to the inherent tension of the polymerizing fibrin network. The inherent tension was determined as the absolute magnitude of this force for samples normalized to the unclotted plasma. Our results reveal that clots formed at a higher thrombin concentration (1 U/mL) generated a higher inherent tensile force (−5.45 Pa relative to the unclotted plasma sample, p < 0.05) compared to the clots formed with 0.2 U/mL thrombin (−2.72 Pa) (Fig. 2(d)).

4. Theoretical model

Here we give a brief overview of the mathematical model that will be developed in the following sections, as well as some of the underlying motivation. The basis of this mathematical model is that each fiber making up the fibrin network is under tension, and the tension increases as the fiber diameter increases due to polymerization. The existence of tension in fibrin fibers has been demonstrated by cutting individual fibers and observing their retraction (Cone et al., 2020). The origin of tension in fibrin fibers may have to do with the spatial geometry of monomeric fibrin and oligomeric protofibrils (Weisel et al., 1987; Weisel, 1987). The protofibrils making up a fibrin fiber are twisted into a helical shape in their stress-free state due to the spatial arrangement of the symmetrical rod-like fibrin monomers that polymerize axially and laterally (see Figs. 3(a) and 3(b)). When the protofibrils come together to form a fiber, the molecules making up a protofibril must be in register (Weisel et al., 1987; Medved et al., 1990), or properly aligned perpendicularly, in order for the linkages between them to form properly (see Figs. 3(c) and 3(d)). However, as the diameter of the fiber increases, the stress-free helix must deform in order for the molecules to be in register (see Fig. 3(d)), leading to some geometric frustration from the opposing forces (Grason, 2013; Atkinson et al., 2021). This causes strain in the helical protofibrils and induces stress. This stress is ultimately responsible for the tension in a fibrin fiber.

Fig. 3.

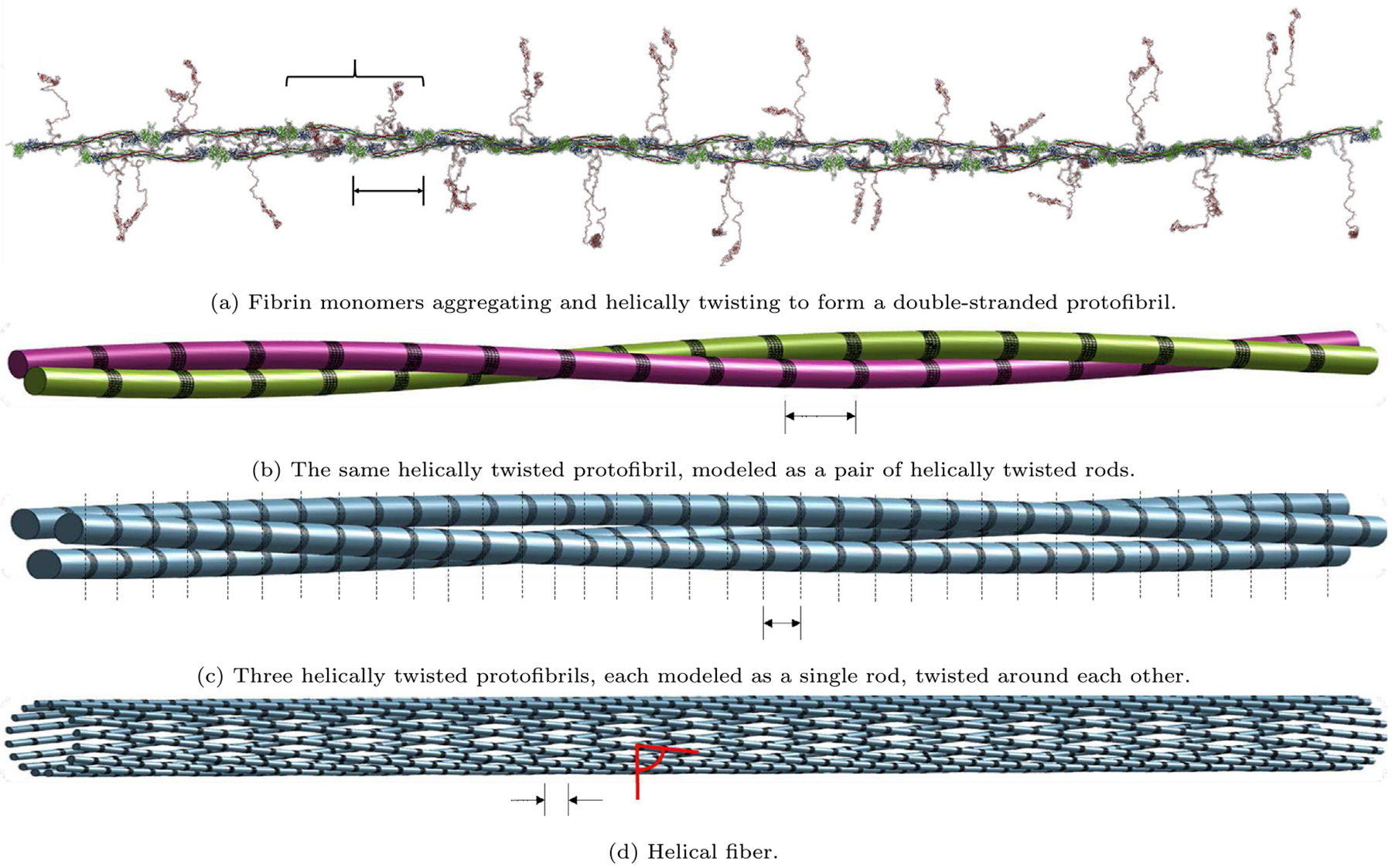
Schematic representations of fibrin fibers. (a) A protofibril constructed from fibrin monomers (Zhmurov et al., 2018), having two-fold axis of symmetry and off-axis binding sites (Weisel, 1987), depicting the 22.5 nm half-staggered periodicity. Brace indicates one full monomer. (b) A protofibril modeled as a pair of helical rods. Each rod of the protofibril is comprised of fibrin monomers stacked end to end, twisting around the other rod in a helical fashion. (c) Three helically twisted protofibrils, each formed of the same structure as (b) but depicted and modeled here as a single rod instead, twisted around each other. Dashed lines emphasize the 22.5 nm vertical striation necessitated to maintain longitudinal periodicity. (d) The outer shell of a helical fiber modeled as a collection of protofibrils helically twisted around the fiber core (not shown). Each protofibril is depicted and modeled here as a single rod. All scale bars are 22.5 nm. All black areas of protein densification (Yermolenko et al., 2011) correspond to the DED structures in the half-staggered packing. All red angular measures represent the pitch angle α.

No models exist for quantifying the tension in a fibrin fiber, let alone as a function of its diameter. Here we build such a model by analyzing the deformation of helical protofibrils and considering the change in radius and pitch of a helical rod. The evolution of the diameter of a fiber is given by a system of ordinary differential equations, based on Weisel and Nagaswami (1992), which track the concentrations of various species as the polymerization reaction proceeds. The helical rod model for a fibrin fiber then outputs the tension in an individual constrained fiber as a function of its (evolving) diameter. We show how a single fiber under tension relaxes when the constraint is removed; this mimics recent experiments in which individual fibers are cut and allowed to relax to determine their pre-strain (Cone et al., 2020). Next, we connect the mechanics of a single fiber to the constitutive response of a network using the 8-chain model of polymer elasticity (Arruda and Boyce, 1993; Qi et al., 2006; Brown et al., 2009; Purohit et al., 2011). We then use a continuum mechanical model of swellable elastomers (Chester and Anand, 2010) to predict the network tension as a function of time in a constrained fibrin gel. Initially we let the network solid volume fraction increase while holding constant the number of fibers per unit reference volume, and then we hold constant the network solid volume fraction to better mimic experiments.

4.1. Fibrin network polymerization model

Based on the paper of Weisel and Nagaswami (1992), the set of differential equations modeling the polymerization of a fibrin network, beginning with a concentration of fibrinogen, is

$$\frac{d\left[f_A\right]}{dt}=-k_A\left[f_A\right]$$ (1)

$$\frac{d\left[f_1\right]}{dt}=-k_{pi}\left(\left[f_1\right]\left[f_1\right]+\left[f_1\right]\sum _{i=1}^{l_{agg}}\left[f_i\right]\right)-k_{pg}[f]\left[f_n\right]+k_A\left[f_A\right]$$ (2)

$$\frac{d\left[f_j\right]}{dt}=k_{pi}\left(\sum _{i=1}^{\lfloor \frac{j}{2}\rfloor }\left[f_i\right]\left[f_{j-i}\right]-\left[f_j\right]\left[f_j\right]-\left[f_j\right]\sum _{i=1}^{l_{agg}}\left[f_i\right]\right)-k_{pg}\left[f_n\right]\left[f_j\right]\forall j\in \left[2,l_{agg}\right]$$ (3)

$$\frac{d\left[f_n\right]}{dt}=k_{pi}\left(\sum _{j=1}^{\lfloor \frac{l_{agg}+1}{2}\rfloor }\left(\left(\left[f_j\right]+\left[f_{l_{agg}+1-j}\right]\right)\sum _{i=l_{agg}+1-j}^{l_{agg}}\left[f_i\right]\right)\right)-2k_{fi}\left[f_n\right]\left[f_n\right]-k_{fg}\left[f_r\right]\left[f_n\right]$$ (4)

$$\frac{d\left[f_r\right]}{dt}=k_{fi}\left[f_n\right]\left[f_n\right]-k_{fA}\left[f_r\right]\left[f_r\right]$$ (5)

$$\frac{d\left[f_n^{tot}\right]}{dt}=2k_{fi}\left[f_n\right]\left[f_n\right]+k_{fg}\left[f_r\right]\left[f_n\right]+k_{fA}\left[f_r\right]\left[f_r\right]$$ (6)

$$\frac{d\left[c_{f_n}\right]}{dt}=k_{pi}\sum _{i=1}^{l_{agg}}\left(\left(l_{agg}+i\right)\sum _{j=i}^{\lfloor \frac{l_{agg}+i}{2}\rfloor }\left[f_j\right]\left[f_{l_{agg}+i-j}\right]\right)+k_{pg}\left[f_n\right]\sum _{i=1}^{l_{agg}}\left[f_i\right]-k_{fi}\left[f_n\right]\left[c_{f_n}\right]-k_{fg}\left[f_r\right]\left[c_{f_n}\right]$$ (7)

$$\frac{d\left[c_{f_r}\right]}{dt}=2k_{fi}\left[f_n\right]\left[c_{f_n}\right]+k_{fg}\left[f_r\right]\left[c_{f_n}\right]+k_{fA}\left[f_r\right]\left[f_r\right]$$ (8)

$$m=\frac{\left[f_n^{tot}\right]}{\left[f_r\right]},$$ (9)

where f_A represents fibrinogen, f₁ represents fibrin monomers, f_i represent fibrin oligomers comprised of i monomers, f_n represent protofibrils, f_r represent fibrin fibers, $\left[f_n^{tot}\right]$ represents total protofibrils in fibers, $\left[c_{f_n}\right]$ represents total fibrin (monomers) in protofibrils, $\left[c_{f_r}\right]$ represents total fibrin in fibers, and, m is the average number of protofibrils per fiber cross-sectional area (see Appendix A).

The parameters in this system are as follows:

• l_agg + 1, the minimum length for protofibrils to be capable of lateral aggregation: Since the length of protofibrils is about 500 nm (Weisel and Litvinov, 2017; Chernysh et al., 2011) and the half-staggered length of monomers is about 22.5 nm (Weisel et al., 1987; Weisel and Litvinov, 2017; Chernysh et al., 2011; Erickson and Fowler, 1983; Yermolenko et al., 2011), and thus the number of fibrin monomers in protofibrils are about 20 (Weisel and Litvinov, 2017), l_agg = 20 is chosen.

• $f_{A_0}$, the initial concentration of fibrin(ogen): $f_{A_0}$ = 2.8229 mg/mL is chosen to match the initial fibrin(ogen) concentration value of 5 × 10¹⁸ molecules/L of Weisel and Nagaswami (1992) (the experimental concentration used in Section 2.1 was 2.7 mg/mL, but as can be seen from Fig. 5(a), this difference does not have a large effect on the results).

• k_A, the rate of fibrinopeptide A cleavage to convert fibrinogen to fibrin monomers: k_A = 1 s⁻¹.

• k_pi, the rate of association of fibrin monomers to yield small oligomers and initiate protofibril formation: k_pi = 6.0 × 10⁻²⁰ L/molecule s.

• k_pg, the rate of protofibril growth in length by longitudinal association with monomers or shorter oligomers: k_pg = 1.4 × 10⁻¹⁷ L/molecule s.

• k_fi, the rate of protofibril lateral aggregation to initiate a fiber: k_fi = 1.0 × 10⁻²⁰ L/molecule s.

• k_fg, the rate of fiber growth by association with additional protofibrils: k_fg = 2.0 × 10⁻¹⁶ L/molecule s.

• k_fA, the rate of lateral aggregation of fibers: the value k_fA = 1.0 × 10⁻¹⁹ L/molecule s is chosen to be in a similar range as the other rate constants.

The rate constants were selected to be similarly valued to those used by Weisel and Nagaswami (1992), and the conditions k_pi < k_pg and k_fi < k_fg in Weisel and Nagaswami (1992) were ensured.

Fig. 5.

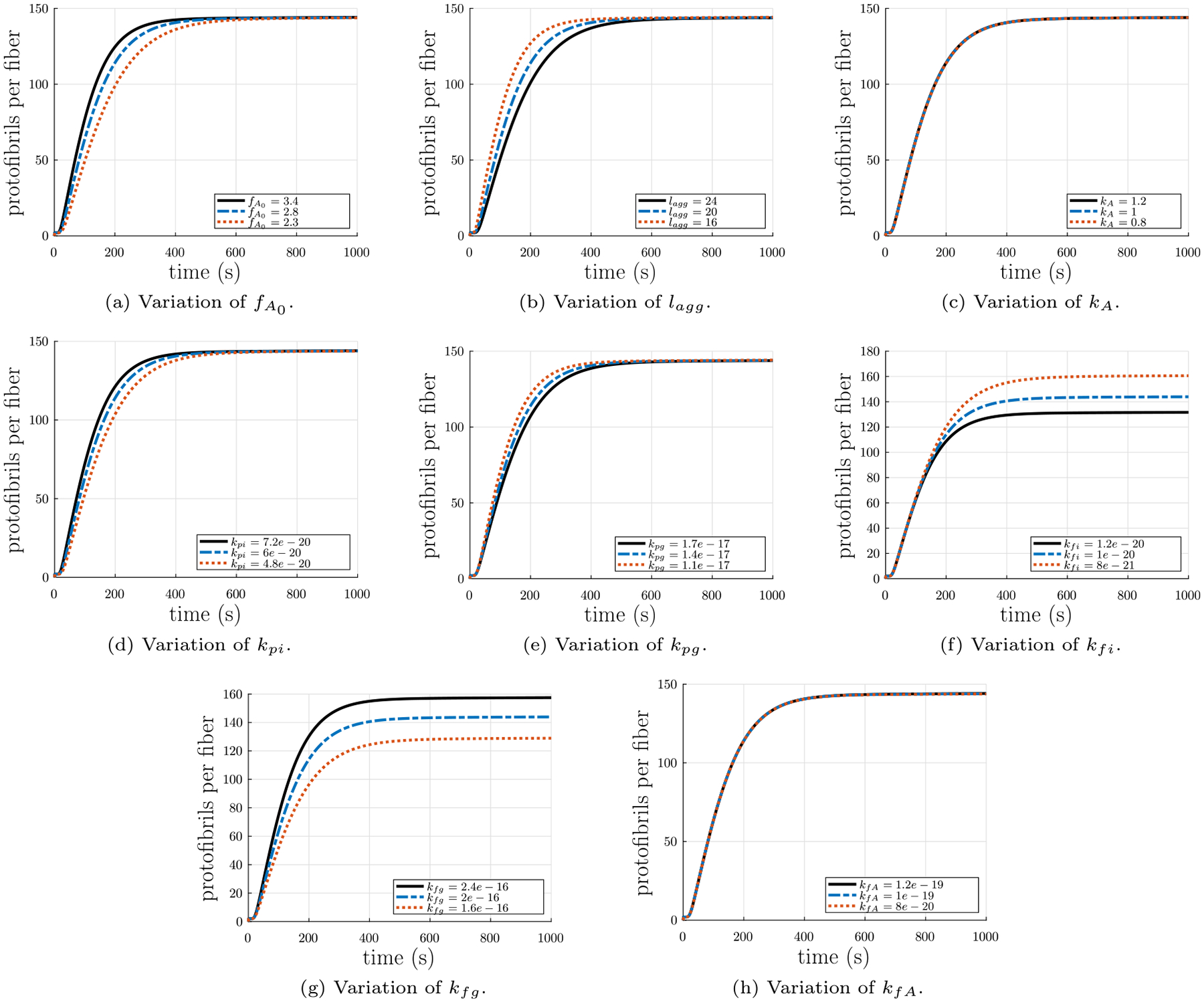
Parameter study of the input parameters in the fiber formation model. Each parameter was both increased and decreased by 20%. (a) Variation of initial concentration of fibrinogen $f_{A_0}\left(\frac{mg}{mL}\right)$. (b) Variation of the minimum length for protofibrils to be capable of lateral aggregation l_agg + 1 (number of monomers). (c) Variation of the rate of fibrinopeptide A cleavage to convert fibrinogen to fibrin monomers $k_A\left(\frac{1}{ \text{s}}\right)$. (d) Variation of the rate of association of fibrin monomers to yield small oligomers and initiate protofibril formation $k_{pi}\left(\frac{\text{L}}{\text{molecule s}}\right)$. (e) Variation of the rate of protofibril growth in length by association with oligomers $k_{pg}\left(\frac{\text{L}}{\text{molecule s}}\right)$. (f) Variation of the rate of protofibril lateral aggregation to initiate a fiber $k_{fi}\left(\frac{\text{L}}{\text{molecule s}}\right)$. (g) Variation of the rate of fiber growth in diameter by association with additional protofibrils $k_{f_g}\left(\frac{\text{L}}{\text{molecule s}}\right)$. (h) Variation of the rate of lateral aggregation of fibers $k_{fA}\left(\frac{\text{L}}{\text{molecule s}}\right)$.

The output parameter that is most important for this context is m, the average number of protofibrils per fiber cross-sectional area, since that is the one from which the radius of the fiber is estimated (see Section 4.2). For the parameter choice given above, the evolution of m over time can be seen in Fig. 4.

Fig. 4.

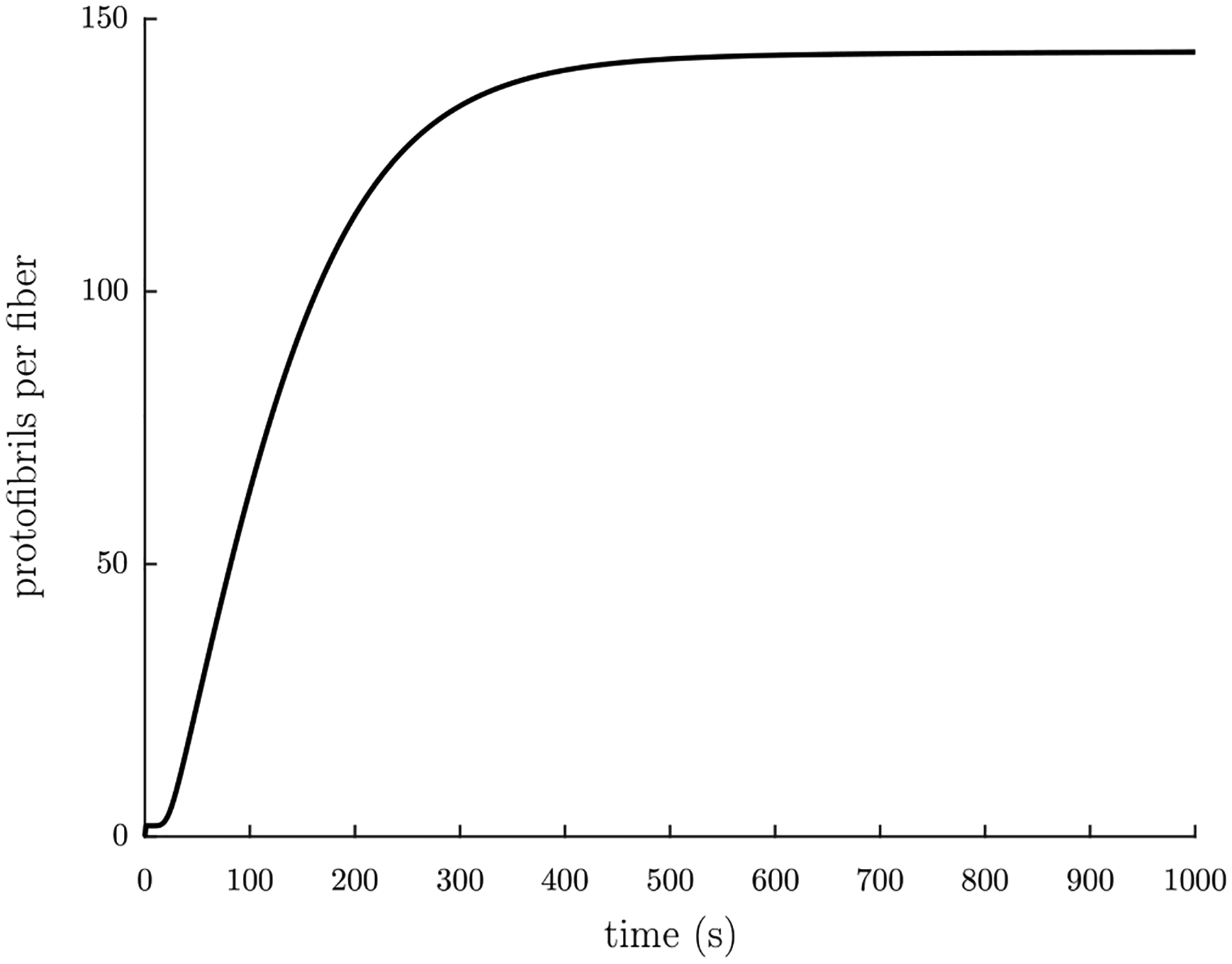
The average number of protofibrils per fiber cross-section m over time t, given the input parameters $f_{A_0}=2.8229\text{ mg}/\text{mL}$, l_agg = 20, k_A = 1 s⁻¹, k_pi = 6.0 × 10⁻²⁰ L/molecule s, k_pg = 1.4 × 10⁻¹⁷ L/molecule s, k_fi = 1.0 × 10⁻²⁰ L/molecule s, k_fg = 2.0 × 10⁻¹⁶ L/molecule s, and k_fA = 1.0 × 10⁻¹⁹ L/molecule s.

To study the effect of each parameter on the evolution of m over time, we ran the calculations for a 20% change in each parameter and plotted the results together (see Fig. 5). As can be seen in Fig. 5(a), a 20% change in the initial concentration of fibrin(ogen) affects the slope of the increase in thickness: a larger $f_{A_0}$ causes a greater slope. Similarly, as can be seen in Fig. 5(b), l_agg also affects the slope of the increase in thickness, but in the opposite way: a larger l_agg results in a smaller slope. In Fig. 5(c), it can be seen that small changes in k_A have only a very small effect similar to l_agg. Fig. 5(d) shows that small changes in k_pi have a similar effect as $f_{A_0}$, whereas Fig. 5(e) depicts that small changes in k_pg have a similar effect as l_agg. Fig. 5(f) demonstrates that small changes in k_fi result in changes in the value of the asymptotic limit plateau region of the average number of protofibrils per fiber m: smaller values of k_fi yield larger values of the limit. In contrast, Fig. 5(g) shows that k_fg has the opposite effect: smaller values of k_fg yield smaller values of the limit. Finally, Fig. 5(h) depicts that k_fA has a small affect on the slope of the asymptotic limit plateau region of m: larger values of k_fA result in larger slopes in the asymptotic limit plateau region of m.

As noted above, the rate constants k_fi and k_fg control the value of the asymptotic limit plateau region. These rate constants are likely related to the energy barrier that must be surmounted by protofibrils laterally attaching to each other and to existing fibers. Protofibrils must deform in order for their bonding sites to align with those on the perimeter of a fiber, and the protofibrils must deform more as the fiber radius increases (as shown later). Once the energy required to deform the protofibril to align its binding sites exceeds the energy binding the protofibril to the fiber, protofibrils will no longer laterally aggregate onto the fiber. As these binding energies are likely related to the rate constant k_fg for growing fibers through lateral aggregation of protofibrils, the rate of lateral aggregation of protofibrils onto a fiber will decrease as the fiber radius increases, and the rate of increase of the number of protofibrils per fiber cross-section will also be reduced. Thus, in theory, the rate constant k_fg should decrease as the fiber radius increases, but we leave it as a constant here because our main focus is on the development of tension in a polymerizing fibrin gel.

4.2. Fiber radius as a function of fibrin polymerization time

If the radius of the region occupied by a single protofibril is given as r_m, then the cross-sectional area occupied by a single protofibril is

$$a_0=\pi r_m^2.$$ (10)

Similarly, if the radius of a fiber is R, then the cross-sectional area of a fiber is given by

$$A_{\mathit{\text{fiber}}}=\pi R^2.$$ (11)

Since the average number of protofibrils per fiber is given above as m,

$$A_{\mathit{\text{fiber}}}=a_{0}m,$$ (12)

which gives us

$$\pi R^2=\pi r_m^{2}m,$$ (13)

or

$$R(t)=r_m\sqrt{m(t)}.$$ (14)

This is similar to the expression derived in Palmer and Boyce (2008). This derivation assumes a uniform density of protofibrils per fiber cross-sectional area. The simplicity of this assumption enables concrete calculations, but there is evidence of non-uniform protofibril density (Yeromonahos et al., 2010; Yermolenko et al., 2011; Yang et al., 2000; Guthold et al., 2004; Li et al., 2016, 2017b) in the fiber cross-section. See Appendix B for a quantitative discussion of the ramifications of non-uniform protofibril density. The polymerization parameters (see Section 4.1) which most directly control the plateau value of R(t) are $k_{f_i}$ and $k_{f_g}$.

4.3. Tensile force in a fiber

It has been observed (Weisel et al., 1987; Medved et al., 1990; Zhmurov et al., 2016, 2018) that protofibrils and fibrin fibers are comprised of smaller longitudinal units helically twisted around a central stem. Thus, the theory developed in Appendix C is applicable to the components of both fibrin fibers and protofibrils. For a helix of radius r and pitch p, the pitch angle is given by

$$\text{tan }\alpha =\left|\frac{\tau }{\kappa }\right|=\frac{p}{2\pi r}$$ (15)

where τ is the torsion of and κ is the curvature of the helical curve. Additionally, since the adjacent helical protofibrils must maintain register required for the 22.5 nm half-staggered longitudinal band pattern (Weisel et al., 1987; Weisel and Litvinov, 2017; Chernysh et al., 2011), the pitch angle must remain constant through the cross-section of the fiber at different values of the radius r. As r evolves in time the pitch angle also evolves. For example, the pitch angle α = 80.8° calculated from the measured quantities r = 50 nm and p = 1930 nm for fibrin fibers (Weisel et al., 1987). The pitch angle α = 85.5° calculated from the extracted quantities r = 5 nm and p = 400 nm from simulations of equilibrated molecular structures (Zhmurov et al., 2018). Assuming also that there is no twisting moment, so that κ₃ = κ₀₃, the magnitude of the force in a protofibril can be written as (see Appendix C)

$$n(r)=\left|-K_b\text{ sin }\alpha \frac{1}{r}\left(\frac{{\text{cos}}^2\alpha }{r}-{\kappa }_0\right)\right|,$$ (16)

where K_b is a bending modulus and κ₀ is a spontaneous curvature, both material properties of the helical protofibrils. In a tension-free state with pitch angle α_s (for example, in a hypothetical free-floating twisted but unstretched fiber) the total force on the fiber is F = 0. Since the radial distribution of protofibrils is disordered (Weisel et al., 1987), the number density of protofibrils per unit cross-sectional area is assumed to be constant (see Appendix B for a discussion of the ramifications of a non-uniform density) and the fiber cross-section is taken as being circular of radius R. Then, the force balance in the tension-free fiber cross-section is

$${\int }_{r_m}^R\frac{2\pi r}{a_0}n(r)dr=0,$$ (17)

where again

$$a_0=\pi r_m^2$$ (18)

is the area occupied by one protofibril. Since K_b, a₀, and α_s are constant, the integral simplifies to

$${\int }_{r_m}^R\frac{{\text{cos}}^2{\alpha }_s}{r}dr={\int }_{r_m}^R{\kappa }_{0}dr,$$ (19)

which gives

$${\text{cos}}^2{\alpha }_s=\frac{{\kappa }_0\left(R-r_m\right)}{\text{ln}\left(\frac{R}{r_m}\right)}.$$ (20)

This sets the pitch angle of the fiber as a function of the radius R in a stress-free state.

For a fiber of pitch angle α_e ≠ α_s both twisted and stretched to connect to a network, the total force on the fiber is F ≠ 0. In this case, the force balance for the cross-section of a fiber under tension is

$${\int }_{r_m}^R\frac{2\pi r}{a_0}n(r)dr=F.$$ (21)

This time, the solution of the integral for the force on the fiber is

$$F=\frac{2\pi }{a_0}{K}_b\text{ sin }{\alpha }_e\left({\kappa }_0\left(R-r_m\right)-{\text{cos}}^2{\alpha }_e\text{ ln }\left(\frac{R}{r_m}\right)\right).$$ (22)

If we define

$${\lambda }_e=\frac{\text{tan }{\alpha }_e}{\text{tan }{\alpha }_s}$$ (23)

as the elastic stretch of the fiber between the twisted but unstretched state with pitch angle α_s and the twisted and stretched state with pitch angle α_e, then the force on the fiber Eq. (22) can be considered as a function of λ_e and α_s(R), where α_s(R) is known from Eq. (20), and R(t) from Eq. (14) can be calculated from the fiber polymerization equations in Section 4.1. The result from Eq. (22) for different values of R, in line with previously reported range of fibrin fiber radii of 25 – 115 nm (Tutwiler et al., 2020), are shown in Fig. 6 for parameter values discussed below. Note that F = 0 at λ_e = 1 for all values of R. This will be useful when we define a stress-free intermediate configuration in the continuum model (see Section 4.5).

Fig. 6.

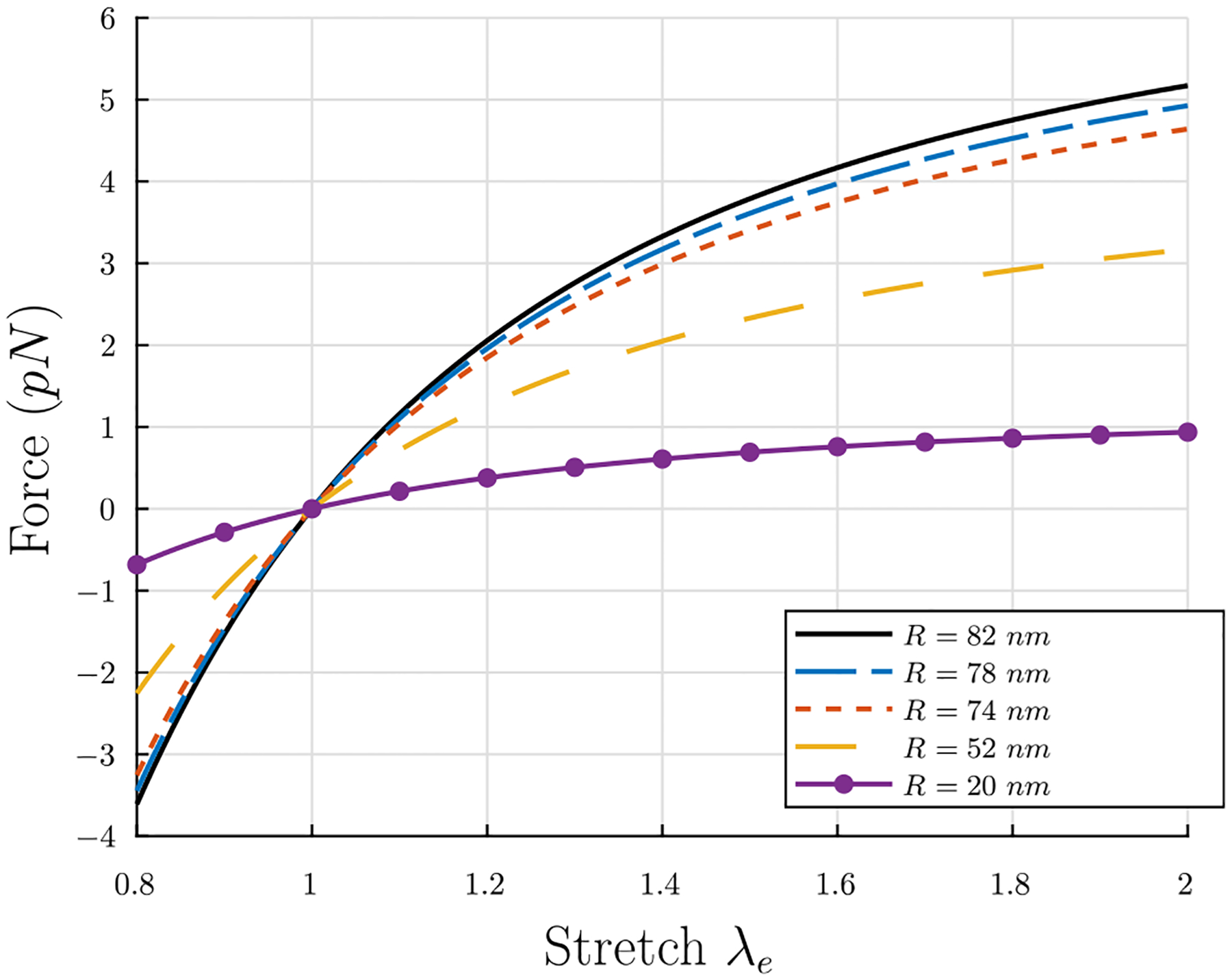
Tensile force F vs. stretch λ_e in an individual fiber for different fiber radii. Thicker fibers develop higher tensile forces.

The parameters in Eq. (22) are as follows: $a_0=\pi r_m^2$, the area of a circular region of radius r_m occupied by one protofibril (plus surrounding fluid); K_b, the bending modulus of the fiber; λ_e, the stretch of the fiber between the twisted but unstretched state with pitch angle α_s and the twisted and stretched state with pitch angle α_e; and κ₀, the spontaneous curvature in the stress-free state. The radius of the area occupied by a single protofibril is known to be r_m = 6.5 nm (Zhmurov et al., 2016, 2018; Jansen et al., 2020). With an estimate of the persistence length of protofibrils of L_p = 400 nm (Zhmurov et al., 2018) and a room temperature of T = 290 K, the bending modulus can be estimated as K_b = k_BTL_p ≈ 1600 pN nm², where k_B is the Boltzmann constant. κ₀ can be estimated in two ways: the first way utilizes the relationship between curvature and the radius and pitch of a helix Eq. (C.52), and the extracted quantities r₀ = 5 nm and p₀ = 400 nm from simulations of equilibrated molecular structures of free protofibrils (Zhmurov et al., 2018), which gives a value κ₀ ≈ 1.226 × 10⁻³ nm⁻¹; the second way rearranges Eq. (20), uses $\text{tan }{\alpha }_s=\frac{p}{2\pi R}$, and takes the average value of κ₀ for the values of R = 50 nm and the range p = 1930±280 nm from Weisel et al. (1987), which gives a value ⟨κ₀⟩ ≈ 1.235 × 10⁻³ nm⁻¹. These two estimates are in excellent agreement, so the value κ₀ = 1.23×10⁻³ nm⁻¹ is chosen. Using these values, the tensile force F in a fiber vs. time t in polymerization can be seen in Fig. 7 with λ_e = 1.501 held fixed.

Fig. 7.

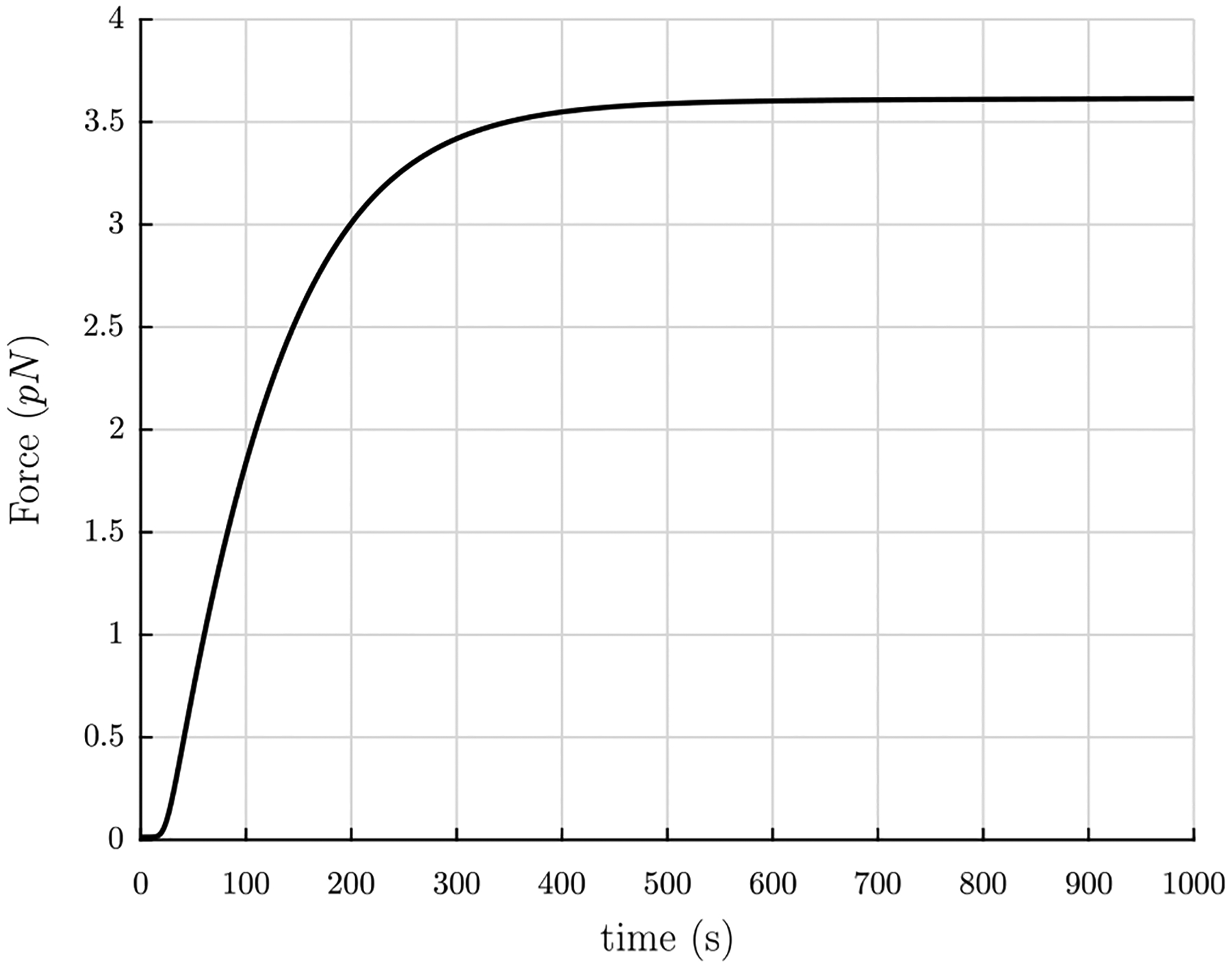
Tensile force F in individual fibers vs. time t in polymerization for the values r_m = 6.5 nm, K_b = 1600 pN nm², λ_e = 1.501, and κ₀ = 1.23 × 10⁻³ nm⁻¹.

Fig. 7 shows that the force in a fiber is on the order of a few pN while the scale of thermal energy k_BT at T = 300 K is 4.1 pN nm. However, thermal fluctuations of the fibers turn out to be negligible, as can be seen from the following calculation. Thermal fluctuations are largest at the center of a fiber fixed at both ends. With hinged–hinged boundary conditions and taking the origin of coordinates as the center of the fiber, the thermal fluctuations can be calculated from eqn. (20) of Purohit et al. (2008):

$$\langle d^2\rangle =\frac{2k_{B}T}{FL}\left[\frac{L^2}{4}-L\sqrt{\frac{K_b}{F}}\frac{{\text{sinh}}^2\left(\frac{L}{2}\sqrt{\frac{F}{K_b}}\right)}{\text{sinh }\left(L\sqrt{\frac{F}{K_b}}\right)}\right].$$ (24)

Suppose the length of the fiber is taken as L = 1 μm and the radius is R = 75 nm. The Young’s modulus of a fiber can be approximated as E = 15 MPa (Collet et al., 2005) (note that this is different from the Young’s modulus estimated in Section 5 where important factors in the modulus, such as fiber cross-linking, the packing density of protofibrils in fibers, all lateral forces, and the long and largely unstructured αC regions, are neglected). Then, the bending modulus of the fiber is K_b = EI, with $I=\frac{\pi }{4}{r}^4$ for a cylindrical cross-section. There will be more fluctuations if the fiber is not as taut, so it is logical to use a force on the lower end, F = 1 pN. Doing so, the thermal fluctuations are $\sqrt{\langle d^2\rangle }\approx 0.672\text{ nm}$. Therefore, thermal fluctuations here are not so significant. This is consistent with the relatively straight fibers seen in confocal images of clots (Litvinov and Weisel, 2017).

4.4. Kinematics of fiber relaxation after transverse cutting

According to the theory presented in Section 4.3, a fiber of length l in a network will relax to an equilibrium length l/λ_e when cut transversely. This assertion can be confirmed by solving for the length of a fiber over time as it relaxes. Here, the fiber will be modeled as a rod relaxing through a fluid. Similar to Raj and Purohit (2011), the kinematics over time t are developed for a rod-like structure of length l in one spatial dimension characterized by the reference configuration variable ς. All relevant vectors have the same direction along the length of the fiber from ς = 0 to l, so they will be treated as scalars with unit vector direction along the length of the fiber. The fiber is assumed to be moving in a fluid, which itself is flowing with velocity ν, which causes a drag force. Thus, the spatial position of a material point ς at time t is z(t, ς), the velocity of the spatial point is $\frac{\partial z}{\partial t}$, and the stretch

$$\lambda =\left|\frac{\partial z}{\partial \varsigma }\right|=\frac{\text{tan }\alpha }{\text{tan }{\alpha }_e}$$ (25)

depends on both position and time. Here α(ς, t) is the current pitch angle and we have chosen the reference state to be the one with uniform stretch λ_e everywhere. The balance of linear momentum for a segment of the fiber in this reference configuration can be written

$$\frac{d}{dt}{\int }_{{\varsigma }_1}^{{\varsigma }_2}\rho \frac{\partial z}{\partial t}d\varsigma =F\left(t,{\varsigma }_2\right)-F\left(t,{\varsigma }_1\right)+{\int }_{{\varsigma }_1}^{{\varsigma }_2}b(t,\varsigma )d\varsigma ,$$ (26)

where the linear density ρ is mass per unit length of the fiber, F = F(t, ς) is the force at time t acting on material point ς, and b = b(t, ς) is a distributed load per unit length at ς. Here, the inertia force is negligible, so ρ = 0. The distributed body force

$$b(t,\varsigma )=-d_w\left(\frac{\partial z(t,\varsigma )}{\partial t}-v\right)$$ (27)

where d_w is the effective drag coefficient caused by the drag force exerted on the fiber by the surrounding fluid. The effective drag coefficient d_w is estimated using results proposed by Brennen and Winet (1977) for thin bodies in flow with low Reynolds’ number. These results take advantage of thinness to make simplifications to approximate solutions for the flow around these bodies, and superimpose fundamental singularities around the body to solve for complex flows. Exact solutions can be obtained for mathematically simple bodies in mathematically simple flows. Their expression for the axial drag coefficient is

$$d_w=\frac{2\pi \mu }{\text{ln}\left(\frac{l}{R}\right)+c},$$ (28)

where μ is the fluid viscosity, l is the length of the body, R is the radius of gyration of the body, and c depends on the shape of the body. For a uniform cylinder,

$$c=\text{ln }2-\frac{3}{2}.$$ (29)

As such, the linear momentum equation becomes

$$F\left(t,{\varsigma }_2\right)-F\left(t,{\varsigma }_1\right)-{\int }_{{\varsigma }_1}^{{\varsigma }_2}{d}_w\left(\frac{\partial z(t,\varsigma )}{\partial t}-v\right)d\varsigma ,$$ (30)

which can be localized to

$$\frac{\partial F(t,\varsigma )}{\partial \varsigma }=d_w\left(\frac{\partial z(t,\varsigma )}{\partial t}-v\right)$$ (31)

since there are no discontinuities. In this case, the fluid is not flowing, so ν = 0. Therefore, the localized balance of linear momentum becomes

$$\frac{\partial F(t,\varsigma )}{\partial \zeta }=d_w\left(\frac{\partial z(t,\varsigma )}{\partial t}\right).$$ (32)

We take the constitutive law for the force F to be the same as in Eq. (22),

$$F(t,\varsigma )=\frac{2\pi }{a_0}{K}_b\text{ sin }\alpha \left({\kappa }_0\left(R-r_m\right)-\text{ln }\left(\frac{R}{r_m}\right){\text{ cos}}^2\alpha \right),$$ (33)

with

$$\text{tan }\alpha =\frac{\partial z}{\partial \zeta }\text{tan }{\alpha }_e.$$ (34)

For the fiber in question, one end is assumed fixed and the free end has no force. Therefore, the boundary conditions are

$$z(t,\varsigma =0)=0,$$ (35)

$$F(t,\varsigma =l)=0.$$ (36)

The initial condition at time t = 0+ is that z(ς) = ς everywhere except very close to the end which is severed. At the severed end the tension instantaneously goes to zero. Since we integrate the PDE for the relaxation numerically by a finite difference method we give the initial condition in discrete form as:

$$z(t=0,\varsigma )=\{\begin{array}{ll}\varsigma ,\hfill & 0\le \varsigma \le 0.99l,\hfill \\ \frac{\text{tan }{\alpha }_s}{\text{tan }{\alpha }_e}(\varsigma -0.99l)+0.99l,\hfill & 0.99l<\varsigma \le l,\hfill \end{array}$$ (37)

where the last (100th) element is assumed to be at zero force.

Eq. (32) can be solved using a finite difference method. Eq. (32) is discretized for numerical calculation as

$$\frac{F_{i,j+\frac{1}{2}}-F_{i,j-\frac{1}{2}}}{\Delta \varsigma }=d_w\frac{z_{i+1,j}-z_{i,j}}{\Delta t},$$ (38)

where j denotes the jth node and i denotes the ith time step, Δς is the element length, and Δt is the time step. From this, the position of the fiber at the next time increment can be calculated by

$$z_{i+1,j}=\frac{F_{i,j+\frac{1}{2}}-F_{i,j-\frac{1}{2}}}{\Delta \zeta }\frac{\Delta t}{d_w}+z_{i,j}.$$ (39)

The condition

$$\Delta t\le \frac{d_w}{2k_a}{(\Delta \varsigma )}^2,$$ (40)

with the largest slope of the force-stretch relation curve

$$k_a=\frac{2\pi }{a_0}{K}_b\text{ tan }{\alpha }_e{\text{ cos}}^3{\alpha }_s\left({\kappa }_0\left(R-r_m\right)+\left(1+{\text{sin}}^2{\alpha }_s\right)\text{ ln }\left(\frac{R}{r_m}\right)\right),$$ (41)

must be satisfied to ensure stability of the method.

The inputs to this partial differential equation are as follows: the fiber radius, R; the pitch angle of the fiber in the stress-free state, α_s; the pitch angle of the fiber in the state in which it is twisted, stretched, and connected to the network, α_e; the fluid viscosity, μ; and the length of the fiber l when it is connected to the network. The fiber radius R is chosen from the final value calculated from the polymerization over time t, Eq. (14), which is in line with our previously reported range of fibrin fiber radii of 25–115 nm (Tutwiler et al., 2020). The pitch angle in the stress-free state α_s is calculated as in Eq. (20), and the pitch angle of the fiber α_e in its connected state is computed from Eq. (23) with the fixed value λ_e = 1.501 used above in Section 4.3. Since the fluid in which the rod resides predominantly behaves like water, μ = 1.002 × 10⁻³ Pa s, the fluid viscosity of water. The probability density function of the fiber lengths P(l) in a network is a log-normal distribution function of l with parameters μ = 0.53 and σ = 0.78, as found in Kim et al. (2014). The most probable value is l = 0.9 μm, with a likely range of about 0.5 μm ≤ l ≤ 2 μm (see also Appendix D). Fig. 8 depicts the length z(t, ς = l) of the fiber relaxing over time t, with R = 78 nm, tan α_s = 5.22, tan α_e = 7.84, λ_e = 1.501, and l = 0.5 μm. For λ_e = 1.501, the fiber relaxes to the length 0.34 μm in time t_f = 0.12 ms from Eq. (32), in excellent agreement with the length l/λ_e = 0.33 μm from the theory proposed in Section 4.3. Relaxation time t_f was taken as the amount of time required to reach the expected length l/λ_e ±1% from the theory proposed in Section 4.3. Relaxation times and lengths, both calculated from Eq. (32) and from l/λ_e from the theory proposed in Section 4.3, for different initial lengths l are presented in table Table 1.

Fig. 8.

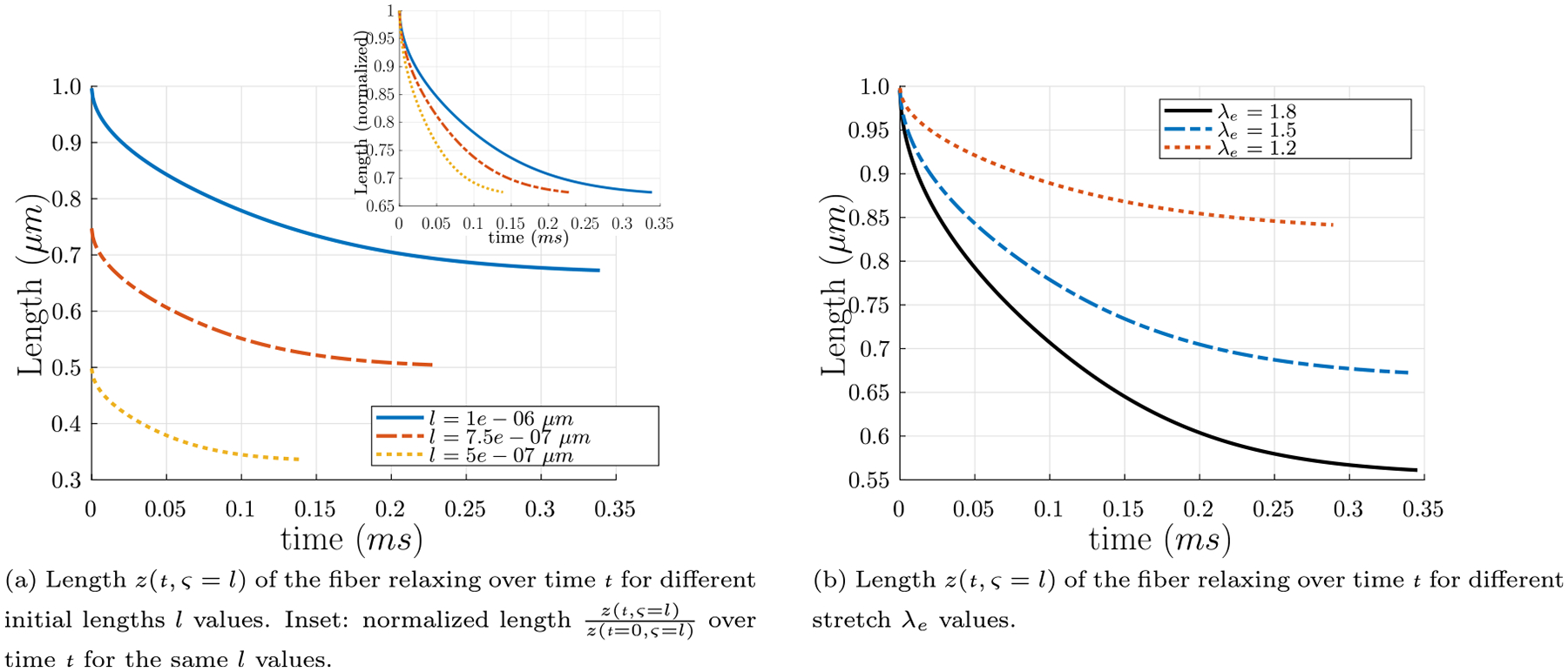
Length z(t, ς = l) of the fiber relaxing over time t for different initial lengths l and different stretch λ_e values. (a) Length z(t, ς = l) of the fiber relaxing over time t, with R = 78 nm, tan α_s = 5.22, tan α_e = 7.84, λ_e = 1.501, and the initial length values l = 0.5 μm, l = 0.75 μm, and l = 1.0 μm. Inset: the same curves with y-axis normalized by the initial lengths of the fibers z(t = 0, ς = l). For λ_e = 1.501, the fibers relax to the lengths 0.34 μm, 0.50 μm, and 0.67 μm, respectively, from Eq. (32), in excellent agreement with the lengths l/λ_e = 0.33 μm, l/λ_e = 0.50 μm, and l/λ_e = 0.67 μm from the theory proposed in Section 4.3. (b) Length z(t, ς = l) of the fiber relaxing over time t for different stretch λ_e values, with R = 78 nm, tan α_s = 5.22, l = 1.0 μm, and the stretch and pitch angle values λ_e = 1.2 and tan α_e = 6.27, λ_e = 1.501 and tan α_e = 7.84, and λ_e = 1.8 and tan α_e = 9.40..

Table 1.

Relaxation times t_f and lengths, both calculated from Eq. (32) and from l/λ_e from the theory proposed in Section 4.3, for different initial lengths z(t = 0, ς = l) = l. Relaxation time t_f was taken as the amount of time required to reach the expected length l/λ_e±1% from the theory proposed in Section 4.3.

z(t = 0, ς = l) = l	t f	z(t = tf, ς = l)	$\frac{l}{{\lambda }_e}$	$L=\frac{l}{{\lambda }_e{\lambda }_s}$
0.5 μm	0.12 ms	0.34 μm	0.33 μm	0.81 μm
0.75 μm	0.23 ms	0.50 μm	0.50 μm	1.22 μm
1.0 μm	0.34 ms	0.67 μm	0.67 μm	1.62 μm
1.5 μm	0.62 ms	1.01 μm	1.00 μm	2.44 μm
2.0 μm	0.98 ms	1.35 μm	1.33 μm	3.25 μm

Studies such as Hudson et al. (2013) (specifically as interpreted by Cone et al. (2020)) demonstrate that fibrin fibers recoil in a timescale on the order of milliseconds or even submilliseconds. The relaxation times t_f given by the theory developed here agree with the millisecond and submillisecond recoil times presented by Hudson et al. (2013). Additionally, recent works of Cone et al. (2020) have also measured lengths of individual fibers from fibrin networks prior to cleavage and the subsequent fragments, and calculated the average prestrain value as ⟨ε⟩ = 23 ± 11%. The prestrain from the model presented here can be calculated as

$$\epsilon =1-\frac{1}{{\lambda }_e}.$$ (42)

With the value of λ_e = 1.501 calculated from the mechanisms in Section 4.5, the prestrain is ε = 33%. This value is in excellent agreement with the prestrain measured by Cone et al. (2020). This suggests that our assumption that λ_e ≈ 1.5 is reasonable.

4.5. Continuum model of fibrin gel

Consider a hypothetical free fibrin fiber polymerizing in space, beginning as a string of length L of protofibrils in this initial configuration. As it is not attached to any other fibers, such an imaginary fiber would not be constrained by outside agents (note that an actual fibrin fiber would polymerize attached to other fibers in a network and would thus be under tension). As polymerization of this imaginary fiber proceeds, protofibrils aggregate laterally around the initial protofibril. If the fiber is not constrained in any way, the length of the fiber will decrease as the radius increases, as outer protofibrils stretch and protofibrils near the center contract in order for the protofibrils to maintain register required for the 22.5 nm half-staggered pattern (Weisel et al., 1987; Weisel and Litvinov, 2017; Chernysh et al., 2011; Weisel, 1986). Let us assume that the stretch of this fiber (with respect to the initial configuration of length L) is

$${\lambda }_s(t)\le 1,$$ (43)

where t is the elapsed time since the start of polymerization (see Section 4.1). If there was an unconstrained isotropic network of such fibers which we describe as a continuum then this network will shrink compared to its configuration at t = 0 and the deformation gradient will be given by:

$$F_s(t)={\lambda }_s(t)I.$$ (44)

Following the framework developed in Chester and Anand (2010) we will call this state of the continuum as an intermediate stress-free configuration. In this state, the length of the fibers is λ_sL, and the fibers are twisted helically but are not under tension. Imagine next that the network was actually formed between two rheometer plates whose normals are in the z-direction. If the distance between the plates is not allowed to change then the network is constrained and it will pull on the plates as the fiber diameter increases. Accordingly, there is a force along the e_z direction, and there are zero forces in the e_x and e_y directions. Thus, due to this constraint, the fibers will be in a twisted and stretched state and the continuum representing the network has stretches λ_ex(t), λ_ey(t), and λ_ez(t) measured with respect to the intermediate state, giving a deformation gradient

$$F_e(t)=\frac{\partial x_e}{\partial x_s},$$ (45)

where x_e is the position in the fully deformed configuration of a particle whose position in the intermediate configuration is x_s, and the elastic right Cauchy–Green tensor is

$$C_e=F_e^T{F}_e=\left[\begin{array}{ccc}{\lambda }_{ex}^2& 0& 0\\ 0& {\lambda }_{ey}^2& 0\\ 0& 0& {\lambda }_{ez}^2\end{array}\right].$$ (46)

The total deformation gradient is then

$$F(t)=F_e(t)F_s(t).$$ (47)

Next, we need to give an expression for the stored energy density in the continuum as a function of F. To this end, we will use the 8-chain model proposed in Arruda and Boyce (1993), Qi et al. (2006) and Bischoff et al. (2001). This model was shown to describe fibrin networks (Brown et al., 2009; Purohit et al., 2011), rubbers and elastomers (Arruda and Boyce, 1993; Bischoff et al., 2001), actin filament networks (Palmer and Boyce, 2008), and other random networks. In Brown et al. (2009) the stored energy density had two parts — (a) due to the deformation of the fibrin fibers, for which we use the Arruda–Boyce 8-chain model (Arruda and Boyce, 1993), and (b) due to volumetric deformation that the 8-chain model cannot capture for which we use a bulk-modulus. In the 8-chain model, the network is represented by a cube of length a in the reference (undeformed) configuration with eight fibers (or chains) of length

$$L=\frac{\sqrt{3}}{2}a$$ (48)

connecting each of the vertices to the center of the cube.

If the sides of the cube are parallel to the principal coordinates of the deformation, then after the deformation the length of each fiber is λ_e(t)λ_s(t)L, where

$${\lambda }_e=\sqrt{\frac{{\lambda }_{ex}^2+{\lambda }_{ey}^2+{\lambda }_{ez}^2}{3}}.$$ (49)

If the strain energy per unit reference length of the fiber in the intermediate configuration due to the elastic deformation is G(λ_e), then the stored energy in each fiber is G(λ_e)λ_sL, and the force–extension relation of a fiber is

$$F\left({\lambda }_e\right)=\frac{dG\left({\lambda }_e\right)}{d{\lambda }_e}.$$ (50)

The contribution of fiber deformation to the total strain energy per unit volume is $\frac{v}{{\lambda }_s^3}{\lambda }_{s}LG\left({\lambda }_e\right)$, where

$$v=v_{nd}=\frac{3\sqrt{3}}{L^3}$$ (51)

is the density of fibers in the reference configuration. Next, we need to account for the energy of volumetric deformation that is not captured by the 8-chain model. If the volume of the cube in the intermediate configuration is V_s and the volume change of the cube to the final configuration is ΔV, then

$$\frac{\Delta V}{V_s}={\lambda }_{ex}{\lambda }_{ey}{\lambda }_{ez}-1.$$ (52)

The strain energy per unit intermediate volume due to this volumetric deformation is denoted as g(λ_exλ_eyλ_ez). Thus, the strain energy density per unit volume of the cube in the intermediate configuration is given by

$$U_e\left({\lambda }_{ex},{\lambda }_{ey},{\lambda }_{ez}\right)=\frac{v}{{\lambda }_s^3}{\lambda }_{s}LG\left({\lambda }_e\right)+g\left({\lambda }_{ex}{\lambda }_{ey}{\lambda }_{ez}\right).$$ (53)

By observing that the strain energy density in the reference configuration U is related to the strain energy density in the intermediate configuration by

$$U={\lambda }_s^3{U}_e,$$ (54)

the strain energy density in the intermediate configuration can be converted into the strain energy density in the reference configuration as

$$U\left({\lambda }_{ex},{\lambda }_{ey},{\lambda }_{ez},{\lambda }_s\right)=v{\lambda }_{s}LG\left({\lambda }_e\right)+{\lambda }_s^{3}g\left({\lambda }_{ex}{\lambda }_{ey}{\lambda }_{ez}\right).$$ (55)

Having described the kinematics and energetics of the continuum in this way we now want to enforce equilibrium. A comprehensive continuum mechanical theory to do this exercise for gels is given in Chester and Anand (2010). We refer the reader to Chester and Anand (2010) for detailed derivations of the equations used below. Similar to the analyses in Chester and Anand (2010), the second Piola–Kirchhoff stress can be written

$$T_e=2F_e\frac{\partial U}{\partial C_e}$$ (56)

$$T_R=2F_e\frac{\partial U}{\partial C_e}{F}_s^{-T},$$ (57)

where T_R is the reference Piola–Kirchhoff stress that satisfies the equilibrium equation

$$\text{Div }{T}_R=0$$ (58)

in the reference configuration. Using our expression for the stored energy function we get,

$$T_e=\frac{v{\lambda }_{s}L}{3{\lambda }_e}\left[\begin{array}{ccc}{\lambda }_{ex}& 0& 0\\ 0& {\lambda }_{ey}& 0\\ 0& 0& {\lambda }_{ez}\end{array}\right]F\left({\lambda }_e\right)+{\lambda }_s^{3}f\left({\lambda }_{ex}{\lambda }_{ey}{\lambda }_{ez}\right)\times \left[\begin{array}{ccc}\frac{1}{{\lambda }_{ex}}& 0& 0\\ 0& \frac{1}{{\lambda }_{ey}}& 0\\ 0& 0& \frac{1}{{\lambda }_{ez}}\end{array}\right]{\lambda }_{ex}{\lambda }_{ey}{\lambda }_{ez}$$ (59)

$$T_R=\frac{vL}{3{\lambda }_e}\left[\begin{array}{ccc}{\lambda }_{ex}& 0& 0\\ 0& {\lambda }_{ey}& 0\\ 0& 0& {\lambda }_{ez}\end{array}\right]F\left({\lambda }_e\right)+{\lambda }_s^{2}f\left({\lambda }_{ex}{\lambda }_{ey}{\lambda }_{ez}\right)\times \left[\begin{array}{ccc}\frac{1}{{\lambda }_{ex}}& 0& 0\\ 0& \frac{1}{{\lambda }_{ey}}& 0\\ 0& 0& \frac{1}{{\lambda }_{ez}}\end{array}\right]{\lambda }_{ex}{\lambda }_{ey}{\lambda }_{ez}.$$ (60)

where $f\left(\frac{\Delta V}{V_s}\right)=g^{\prime }\left(\frac{\Delta V}{V_s}\right)$. It should be noted that the shear components of T_e and T_R are all 0 in principal coordinates. Since there are no forces or constraints applied on the fibers in the intermediate configuration, it is reasonable to assume F(1) = f(1) = 0.

In the present case with a network polymerizing in between fixed rheometer plates with surfaces perpendicular to the axial e_z direction, forces are applied only in the axial e_z direction, and

$$T_{Rxx}=T_{Ryy}=0.$$ (61)

Due to isotropy,

$${\lambda }_{ex}={\lambda }_{ey}={\lambda }_{*}$$ (62)

are also expected, and so

$${\lambda }_x={\lambda }_y={\lambda }_{*}{\lambda }_s$$ (63)

$${\lambda }_z={\lambda }_{ez}{\lambda }_s.$$ (64)

Since during polymerization the rheometer plates are fixed,

$${\lambda }_z=1.$$ (65)

Hence,

$${\lambda }_{ez}=\frac{1}{{\lambda }_s}.$$ (66)

As such, equilibrium in terms of the Piola–Kirchhoff stresses reduce to the following two equations:

$$0=\frac{vL}{3{\lambda }_e}{\lambda }_{*}F\left({\lambda }_e\right)+{\lambda }_s{\lambda }_{*}f\left(\frac{{\lambda }_{*}^2}{{\lambda }_s}\right)$$ (67)

$$T_{Rzz}=\frac{vL}{3{\lambda }_e{\lambda }_s}F\left({\lambda }_e\right)+{\lambda }_s^2{\lambda }_{*}^{2}f\left(\frac{{\lambda }_{*}^2}{{\lambda }_s}\right),$$ (68)

for the two unknowns λ_* and T_Rzz, where now

$${\lambda }_e=\sqrt{\frac{2{\lambda }_{*}^2{\lambda }_s^2+1}{3{\lambda }_s^2}}.$$ (69)

The network stress T_Rzz can be multiplied by the area of the rheometer plate to get the force exerted on the network due to polymerization.

The unknowns in this model are as follows: L, the length of the fiber in the imaginary reference configuration; F(λ_e), the force-stretch relation of a fiber; f, the relationship between volumetric strain and pressure; λ_s, the stretch between the imaginary reference configuration and the intermediate configuration; λ_*, the stretches between the intermediate configuration and the final configuration in the directions other than that in the axial e_Z direction; and, in the fixed solid volume fraction formulation, the solid volume fraction ϕ_s. The length of the fiber L in the imaginary reference configuration can be found by calculating

$$L=\frac{l}{{\lambda }_e{\lambda }_s},$$ (70)

from the distribution found in Kim et al. (2014), as discussed in Section 4.4. The force-stretch relation of a fiber F(λ_e) is the same as the force in a fiber Eq. (22) derived in Section 4.3. The relationship between volumetric strain and pressure is taken to be

$$f\left(\frac{{\lambda }_{*}^2}{{\lambda }_s}\right)=K\left(\frac{{\lambda }_{*}^2}{{\lambda }_s}-1\right),$$ (71)

where K = 1314.67 Pa is a bulk modulus as found in Punter et al. (2020). We have verified that a higher bulk modulus value of K = 100 kPa has little effect on the results. The stretch between the imaginary reference configuration and the intermediate configuration is taken to be

$${\lambda }_s(R(t))=\frac{\text{tan }{\alpha }_s(R(t))}{\text{tan }{\alpha }_0},$$ (72)

where tan α_s(R(t)) is given by Eq. (20), and $\text{tan }{\alpha }_0=\frac{400}{2\pi \times 5}$ for a single protofibril based on Zhmurov et al. (2018). The stretches λ_* between the intermediate configuration and the final configuration in the directions other than that in the axial e_z direction can be solved for each elapsed polymerization time t from Eq. (67). This calculated value of λ_*, along with the λ_s value, can be used to calculate λ_e in Eq. (69). In solving these equations, we use λ_e = 1.501. Finally, the network Piola–Kirchhoff stress T_Rzz can be computed from Eq. (68).

Using the above values and choosing l = 0.5 μm, the Piola–Kirchhoff stress T_Rzz as a function of polymerization time t can be seen in Fig. 9. As the clot polymerizes the tension increases, as expected. Steady state is reached by about 1000 s, in qualitative agreement with experiments.

Fig. 9.

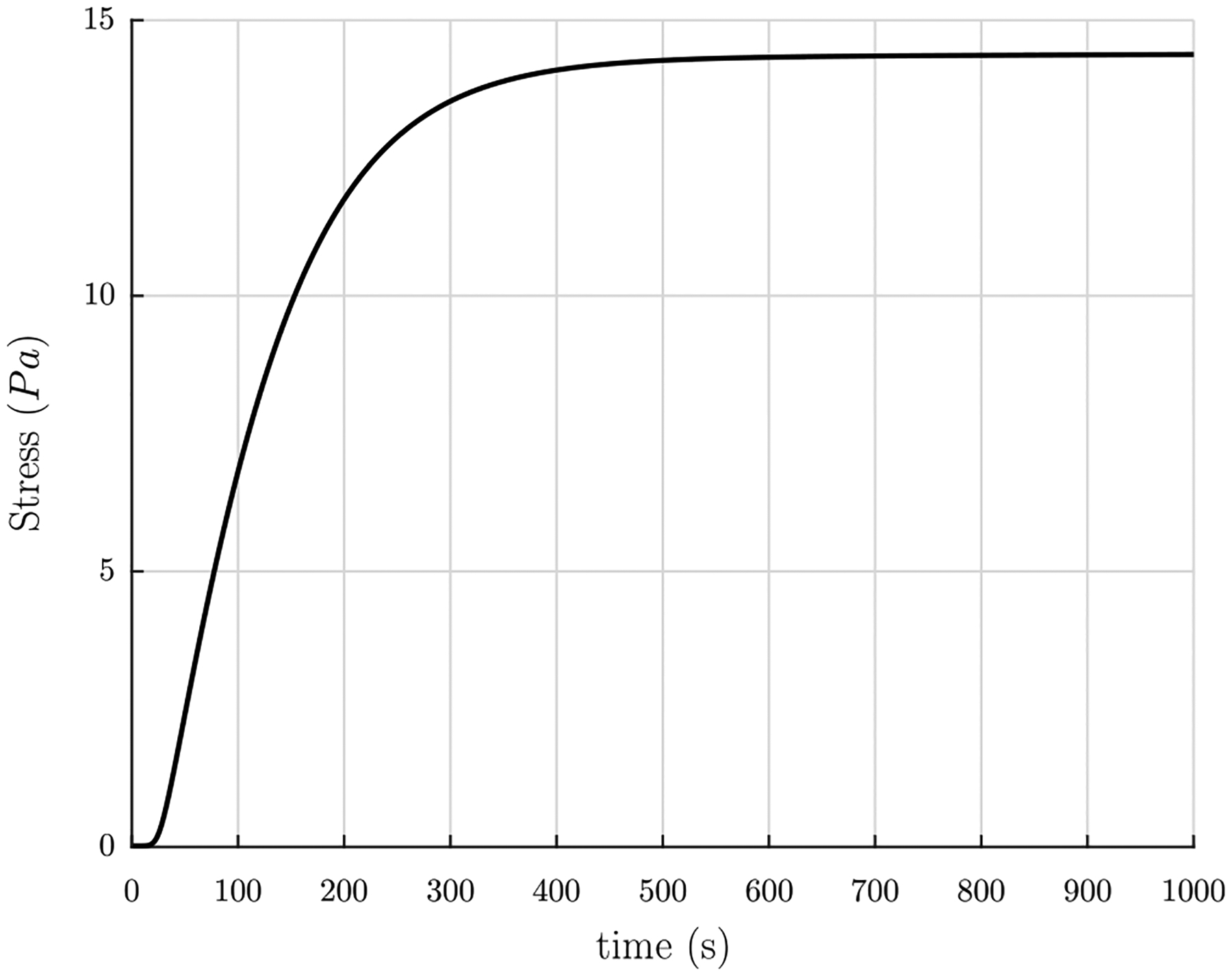
Piola–Kirchhoff stress T_Rzz in the network in the fixed number density formulation as a function of polymerization time t, using the length of the fiber connected in a network l = 0.5 μm.

To study the effect of the estimated parameter length l and final fiber radius R on the network Piola stress T_Rzz, we ran simulations with different values for each and compared the results. Fig. 10(a) depicts the change in Piola stress T_Rzz for fiber length l values in the range 0.5 μm ≤ l ≤ 2.0 μm. As can be seen in Fig. 10(a), larger fiber lengths produce smaller network Piola stresses T_Rzz. Additionally, as can be seen in Fig. 10(b), thicker fibers of the same length produce larger network Piola stresses T_Rzz.

Fig. 10.

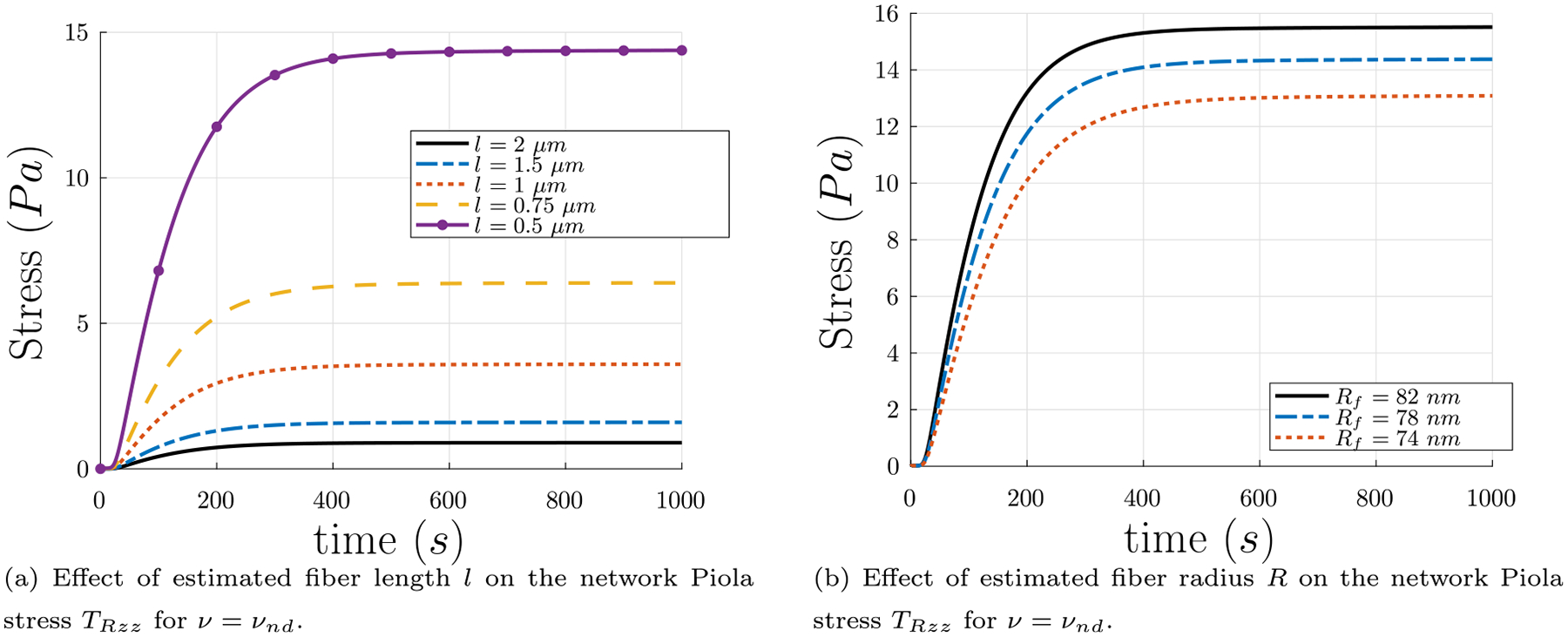
(a) Effect of estimated fiber length l on the network Piola stress T_Rzz using five values of l from the most likely range of l from the experimental probability distribution found in Kim et al. (2014), as discussed in Section 4.4. These plots assume that l remains fixed as solid volume fraction ϕ_s evolves with time. (b) Network Piola stress T_Rzz vs. polymerization time t for constant fiber length l = 0.5 μm, for different final values of fiber radius R_f. Thicker fibers contribute more network Piola stress T_Rzz.

The above discussion held the number of fibers per unit reference volume constant, giving a density ν_nd. If, instead, as in our experiments (see Section 3) and in other experiments (Tutwiler et al., 2020), the solid volume fraction ϕ_s is held constant at ϕ_s = 0.01 or 1%, a value previously estimated for plasma clot fibrin networks (see Figures S3 and S4 in the supplement of Tutwiler et al. (2020)), the density becomes

$$v=v_{vf}=\frac{{\varphi }_s}{\pi R^2{\lambda }_e{\lambda }_{s}L}.$$ (73)

In this formulation, the number density of fibers varies as the solid volume fraction is held fixed, such that in a given volume there will be fewer but thicker fibers or more but thinner fibers to yield the same protein concentration. When using this density in the calculations of network stress, results for varying different input parameters are more consistent. As can be seen in Fig. 11(a), fibers of different lengths produced the same network stress T_Rzz; this is not the same effect as in Fig. 10(a) which held the number density of fibers fixed, where larger fiber lengths produce smaller network Piola stresses T_Rzz. Also, the estimated final values of the tensile stress are in agreement with experimental results in Fig. 2. Additionally, as can be observed in Fig. 11(b), thinner fibers of the same length produce larger network Piola stresses T_Rzz, which is also different from the trend observed in Fig. 10(b) which held the number density fixed. Recall from our experiments that increased thrombin concentration causes decrease in turbidity, which is related to the average protofibrils per fiber m (Weisel and Nagaswami, 1992), leading to a decrease in R. Thus, these results for ν = ν_υf are in agreement with the trend expected from Weisel and Nagaswami (1992) and the results from our experiments where increased thrombin concentration yields increased magnitude of network stress (see Section 3). In a real network there is a distribution of fiber lengths, so we accounted for this in rudimentary way in Appendix D and showed that the resulting values of final tensile stress are not very different from those reported in Fig. 11.

Fig. 11.

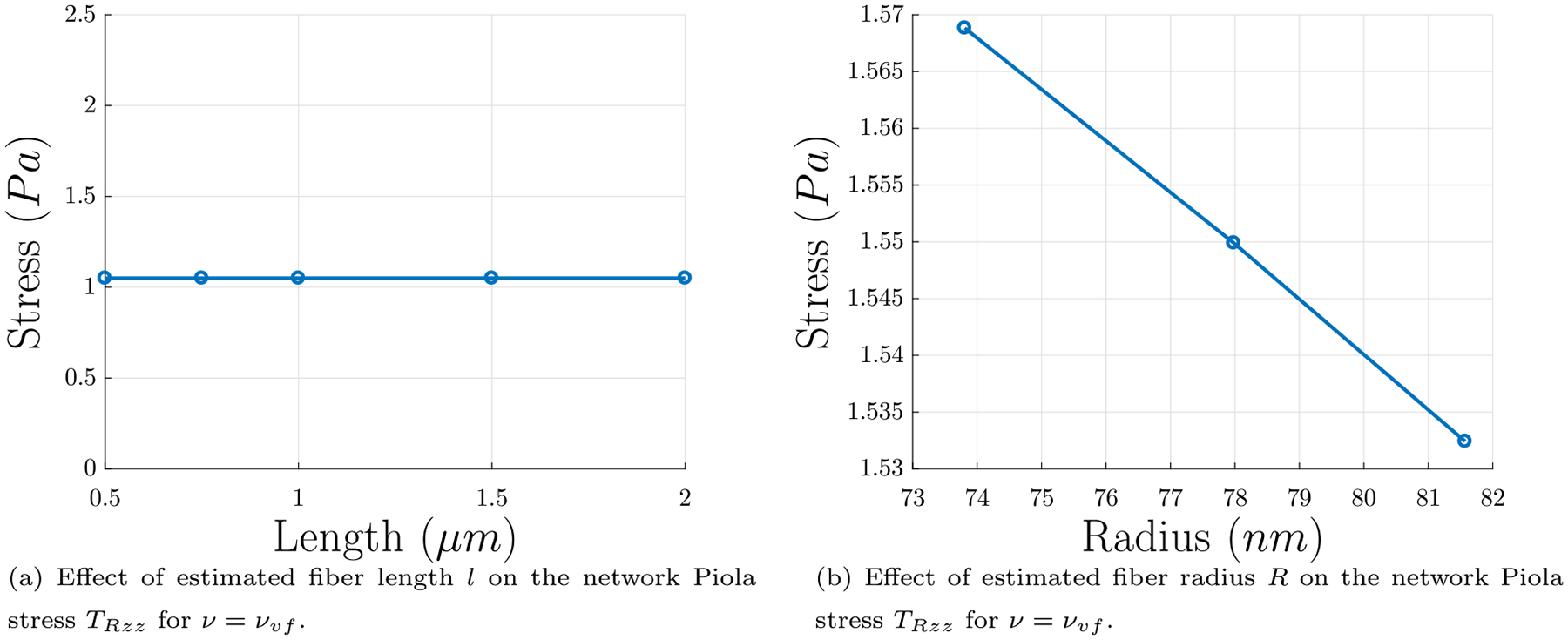
Results for network Piola stress using the fixed solid volume fraction formulation. In this formulation, the number density of fibers varies as the solid volume concentration is held fixed, such that in a given volume there will be fewer but thicker fibers or more but thinner fibers to yield the same protein concentration. (a) Effect of estimated fiber length l on the final network Piola stress T_Rzz using five values of l from the most likely range of l from the probability distribution found in Kim et al. (2014), as discussed in Section 4.4. (b) Effect of final fiber radius R on final network Piola stress T_Rzz, for constant fiber length l = 0.5 μm. Thinner fibers contribute more network Piola stress T_Rzz. Since the solid volume fraction during polymerization is not constant, only the values calculated from the final time in the polymerization have been included. The final solid volume fraction for each of these points is ϕ_s = 0.01..

4.6. Summary of full mathematical model

The model can be summarized as follows: The system of ODEs, resulting from the chemical rate equations governing fiber polymerization, are as follows:

$$\frac{d\left[f_A\right]}{dt}=-k_A\left[f_A\right]$$ (74)

$$\frac{d\left[f_1\right]}{dt}=-k_{pi}\left(\left[f_1\right]\left[f_1\right]+\left[f_1\right]\sum _{i=1}^{l_{agg}}\left[f_i\right]\right)-k_{pg}[f]\left[f_n\right]+k_A\left[f_A\right]$$ (75)

$$\frac{d\left[f_j\right]}{dt}=k_{pi}\left(\sum _{i=1}^{\lfloor \frac{j}{2}\rfloor }\left[f_i\right]\left[f_{j-i}\right]-\left[f_j\right]\left[f_j\right]-\left[f_j\right]\sum _{i=1}^{l_{agg}}\left[f_i\right]\right)-k_{pg}\left[f_n\right]\left[f_j\right]\forall j\in \left[2,l_{agg}\right]$$ (76)

$$\frac{d\left[f_n\right]}{dt}=k_{pi}\left(\sum _{j=1}^{\lfloor \frac{l_{aag}+1}{2}\rfloor }\left(\left(\left[f_j\right]+\left[f_{l_{agg}+1-j}\right]\right)\sum _{i=l_{agg}+1-j}^{l_{agg}}\left[f_i\right]\right)\right)-2k_{fi}\left[f_n\right]\left[f_n\right]-k_{fg}\left[f_r\right]\left[f_n\right]$$ (77)

$$\frac{d\left[f_r\right]}{dt}=k_{fi}\left[f_n\right]\left[f_n\right]-k_{fA}\left[f_r\right]\left[f_r\right]$$ (78)

$$\frac{d\left[f_n^{tot}\right]}{dt}=2k_{fi}\left[f_n\right]\left[f_n\right]+k_{fg}\left[f_r\right]\left[f_n\right]+k_{fA}\left[f_r\right]\left[f_r\right]$$ (79)

$$\frac{d\left[c_{f_n}\right]}{dt}=k_{pi}\sum _{i=1}^{l_{agg}}\left(\left(l_{agg}+i\right)\sum _{j=i}^{\lfloor \frac{l_{agg}+i}{2}\rfloor }\left[f_j\right]\left[f_{l_{agg}+i-j}\right]\right)+k_{pg}\left[f_n\right]\sum _{i=1}^{l_{agg}}\left[f_i\right]-k_{fi}\left[f_n\right]\left[c_{f_n}\right]-k_{fg}\left[f_r\right]\left[c_{f_n}\right]$$ (80)

$$\frac{d\left[c_{f_r}\right]}{dt}=2k_{fi}\left[f_n\right]\left[c_{f_n}\right]+k_{fg}\left[f_r\right]\left[c_{f_n}\right]+k_{fA}\left[f_r\right]\left[f_r\right].$$ (81)

with

$$m=\frac{\left[f_n^{tot}\right]}{\left[f_r\right]}.$$ (82)

The fiber radius R as a function of the average number of protofibrils per fiber cross-section m is

$$R(t)=r_m\sqrt{m(t)}.$$ (83)

The stretch connecting the imaginary reference configuration and the intermediate configuration of a fiber, as a function of fiber radius R, is given by

$${\lambda }_s(R(t))=\frac{\text{tan }{\alpha }_s(R(t))}{\text{tan }{\alpha }_0}=\frac{\sqrt{\frac{\text{ln}\left(\frac{R(t)}{r_m}\right)}{{\kappa }_0\left(R(t)-r_m\right)}-1}}{\frac{400}{2\pi \times 5}}.$$ (84)

The stretch between the intermediate configuration and the final configuration of the whole network in the directions other than that in the axial e_z direction λ_* is calculated by solving

$$0=\frac{vL}{3{\lambda }_e}{\lambda }_{*}F\left({\lambda }_e\right)+{\lambda }_s{\lambda }_{*}f\left(\frac{{\lambda }_{*}^2}{{\lambda }_s}\right)$$ (85)

using the force in a fiber

$$F=\frac{2\pi }{a_0}{K}_b\text{ sin }\alpha \left({\kappa }_0\left(R-r_m\right)-{\text{cos}}^2\alpha \text{ ln }\left(\frac{R}{r_m}\right)\right)$$ (86)

with

$$\text{tan }\alpha ={\lambda }_e\text{ tan }{\alpha }_s={\lambda }_e\sqrt{\frac{\text{ln }\left(\frac{R(t)}{r_m}\right)}{{\kappa }_0\left(R(t)-r_m\right)}-1},$$ (87)

the stretch between the intermediate configuration and the final configuration

$${\lambda }_e=\sqrt{\frac{2{\lambda }_{*}^2{\lambda }_s^2+1}{3{\lambda }_s^2}},$$ (88)

and the relationship between volumetric strain and pressure

$$f\left(\frac{{\lambda }_{*}^2}{{\lambda }_s}\right)=K\left(\frac{{\lambda }_{*}^2}{{\lambda }_s}-1\right).$$ (89)

Then, the network Piola stress can be computed from

$$T_{Rzz}=\frac{vL}{3{\lambda }_e{\lambda }_s}F\left({\lambda }_e\right)+{\lambda }_s^2{\lambda }_{*}{f}^2\left(\frac{{\lambda }_{*}^2}{{\lambda }_s}\right).$$ (90)

The model takes the unknown input parameters initial concentration of fibrinogen $f_{A_0}$, rate of fibrinopeptide A cleavage to convert fibrinogen to fibrin monomers k_A, the rate of association of fibrin monomers to yield small oligomers and initiate protofibril formation k_pi, the rate of protofibril growth in length by association with oligomers k_pg, the rate of protofibril aggregation to initiate a fiber k_fi, the rate of fiber growth by association with additional protofibrils k_fg, the rate of interactions between fibers k_fA, and initial length of a fiber connected in a network l. The model outputs the radius of a polymerizing fiber R(t), force on a fiber F, the stretches λ_s and λ_e, the relaxed length of a fiber l/λ_e, and the network Piola stress T_Rzz.

5. Discussion

In this paper we have followed Weisel et al. (1987) and Weisel and Nagaswami (1992) and modeled fibrin clot formation – from fibrinogen to fibrin monomers and oligomers to protofibrils to fiber formation – by a set of ODEs for the chemical rate of change in concentration of the reacting structures of each individual stage. The solution of that system of ODEs gives the average number of protofibrils per fiber cross-section as a function of polymerization time. Variation of the rate constants involved in the intermediary biochemical reactions demonstrates that the two most important stages determining final fiber radius are fiber initiation by lateral aggregation of protofibrils and fiber growth by transverse association with additional protofibrils. The resulting (final value of) average number of protofibrils per fiber cross-sectional area is directly related to the radius of a fiber. Therefore, we can calculate how the radius of a fiber evolves in time. This radius is used as an input to calculate the evolving tensile force in a fiber, which ultimately determines the tensile force in a network constrained between two rheometer plates.

We assumed that since the radial distribution of protofibrils is disordered (Weisel et al., 1987; Weisel, 1986), the number density of protofibrils per unit fiber cross-sectional area is constant. In particular, we assumed that a single protofibril occupies a circle of radius 6.5 nm in the fiber cross-section. Thus, if the number of protofibrils in a fiber is known (from the solution of the ODEs), the radius of the fiber as a function of time can be calculated. The resulting values of the fiber radius are in line with the previously reported range of fibrin fiber radii of 25–115 nm (Tutwiler et al., 2020). However, we note that other works suggest that the density of protofibrils per fiber cross-sectional area is not constant (Yang et al., 2000; Guthold et al., 2004; Yeromonahos et al., 2010; Yermolenko et al., 2011; Li et al., 2016, 2017b); the number of protofibrils per fiber cross sectional area is proportional to D^1.3 (Guthold et al., 2004) or D^1.4±0.2 (Li et al., 2017b), and not D² as we have used. It has also been suggested that the fiber core is more dense than the periphery layers (Li et al., 2017b). We used the constant number density assumption in our calculations due to its simplicity and also because a specific numerical value (6.5 nm) for the inter-protofibril distance was available (Jansen et al., 2020; Zhmurov et al., 2016, 2018). On the other hand, other works (Guthold et al., 2004; Li et al., 2017b) provide scaling laws which do not furnish enough information to compute actual numerical values of the fiber radius. Additionally, even if a more accurate relationship between the number of protofibrils per fiber cross sectional area is specified, it will only change the computation of the radius from the average number of protofibrils in a fiber and some details of the force in a fiber computation (see additional details discussed in Appendix B). Our overall approach of computing the fiber tension and the network tension will still remain the same. Furthermore, our simple assumption of constant number density of protofibrils per fiber cross-sectional area is able to capture a crucial experimental observation that the Young’s modulus of a fibrin fiber decreases with increasing radius, as demonstrated below.

Our equation (see Eq. (22)) for the force-stretch relation of a single fiber is derived by mathematically describing ideas in Weisel et al. (1987), which trace the origin of tension in fibrin fibers to the two-fold axis of symmetry and off-axis binding sites of individual fibrin monomers. This causes protofibrils to be helical as clearly seen in the simulations of Zhmurov et al. (2018) and images of Medved et al. (1990). If a number of such helical protofibrils are to form a fibrin fiber by lateral aggregation then it is necessary that the individual monomers be properly aligned. This causes some protofibrils to stretch and others to shorten so that there is overall force balance in the cross-section (Weisel et al., 1987). We have enforced this force balance in a fiber cross-section by considering the equilibrium of each individual helical protofibril, which may have stretched or shortened depending on its location in the fiber cross-section. This force balance is expressed as Eq. (22) and the radius R of a fiber enters as a parameter in this equation. Starting with the force F in Eq. (22) and dividing by the assumed cross sectional area πR², we get the stress σ in a fiber due to external force F. Then, since this stress and the stretch in Eq. (23) are both functions of the variable tan α_e, the Young’s modulus E of a fiber may be calculated as

$$E={\frac{d\sigma /d{\alpha }_e}{d{\lambda }_e/d{\alpha }_e}|}_{{\lambda }_e=1}=\frac{4}{a_0{R}^2}{K}_b{\kappa }_0\left(R-r_m\right){\text{sin}}^3{\alpha }_s.$$ (91)

The results of this equation can be found in Fig. 12, and the trend of decreasing Young’s modulus with increasing radius is similar to the trend in Li et al. (2016). There are additional contributions to individual fiber modulus, for example fiber cross-linking, the packing density of protofibrils in fibers, all lateral forces, and the long and largely unstructured αC regions may have significant contribution as well (Li et al., 2016), but we have captured the general trend in Fig. 12. While the model is not yet entirely quantitative, incorporating neglected factors mentioned above and the dependence of rate constants on the mechanical deformations of protofibrils is likely to improve the predictive ability of the model.

Fig. 12.

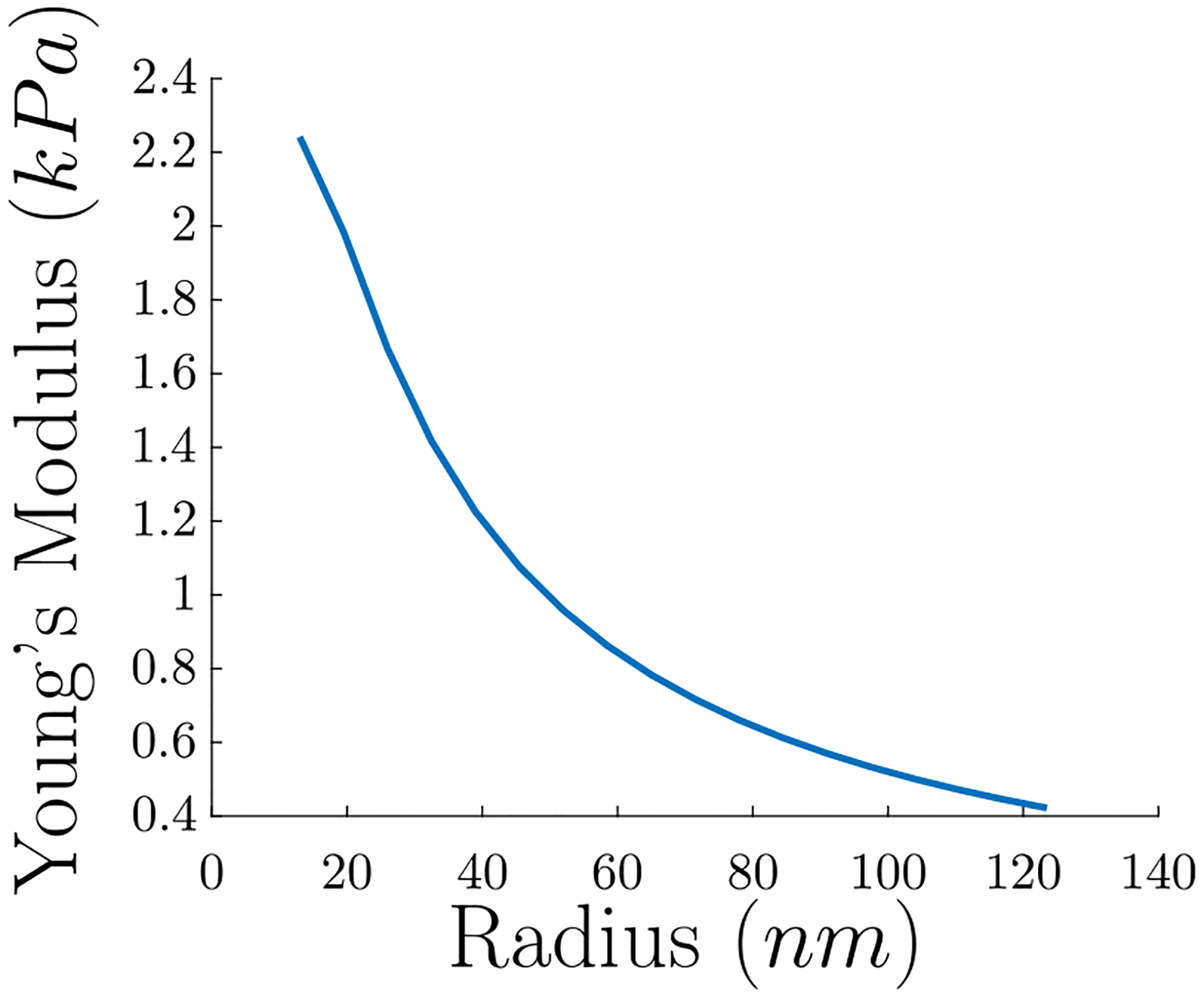
Calculated Young’s modulus of an individual fiber in a fibrin network vs. fiber radius. Note the trend that the Young’s modulus decreases with increasing radius.

The force-stretch relation given by Eqs. (22) and (23) can be combined with the equation of motion of a fiber subject to fluid drag to predict the relaxation to equilibrium of a severed fibrin fiber. Here we have shown that the relaxation time depends on the fiber length and radius and the resulting time scales as well as fiber pre-strains are in excellent agreement with the cutting experiments of Cone et al. (2020). Importantly, we made no attempt to compare the forces (or stresses) in our calculations with those documented in Cone et al. (2020) because the experimental values of the forces are obtained from the strains using a Young’s modulus that is different from those calculated in Fig. 12. Also, a simple linear relation between stress and strain in a single fibrin fiber may not be appropriate at large strains. Finally, we acknowledge that the process of enzymatic cleavage of a fibrin fiber (as in Lynch et al. (2022)) is quite complex since one would have to also model the diffusion and binding/unbinding of the enzyme together with mechanics of cleavage of individual protofibrils. As a fiber is digested, it at least partially maintains its inherent tension (Lynch et al., 2022) likely because some of the protofibrils break, but others remain intact. This can be accounted for in the balance of forces by having fewer protofibrils in the fiber. However, the coupling of fiber mechanics, cleavage kinetics, and enzyme diffusion is a complex problem that is beyond the scope of this work.

Finally, we connect the mechanical behavior of a fibrin network to that of individual fibers by using the 8-chain model (Arruda and Boyce, 1993; Qi et al., 2006) together with the continuum mechanics of swellable gels (Chester and Anand, 2010). We show that the inherent tensile stress in polymerizing fibrin networks depends on fiber length, radius, solid volume fractions, etc. Our results from the continuum model in Section 4.5 are in agreement with the results from experiments in Section 3. The order of magnitude of the inherent tension is the same in both experiments and continuum model and steady state is reached by around 1000 s in both the model and the experiments. Additionally, our continuum model can recover the trend that thinner fibers produce larger network stress for fixed solid volume fraction as observed in our experiments coupled with the study of the effect of thrombin concentration on turbidity in Weisel and Nagaswami (1992), although the predicted trends from the model are weaker than those from experiments.

This trend in Fig. 11(b) that thinner fibers produce larger network stress is not obvious. One hypothesis to explain this phenomenon involves the following simplified scenario: imagine that two fixed horizontal plates are connected by a “network” consisting of only vertical fibers of uniform thickness. Since the fibrin volume fraction is constant irrespective of the fiber radius, the total sum of the cross-sectional area of all those fibers will be the same whether the fibers are thinner or thicker, but there will be more thinner fibers in such a scenario than if the fibers were thicker. Now, from Eq. (22), the force in a fiber can be calculated as a function of the fiber radius, from which the inherent stress in the fiber can be computed by dividing by the cross-sectional area of a fiber πR². If the cross-sectional area of a fiber increases faster as the radius increases than does the force in the fiber, the inherent stress in the fiber will decrease with radius, and the total “network” stress will decrease with fiber radius as well.

This can be better illustrated by the use of concrete examples, such as the three radii in Fig. 11(b), namely, R = 74 nm, R = 78 nm, and R = 82 nm. For these radii and choosing the same fiber length l = 0.5 μm, the resulting fiber stretches λ_e from using Eq. (73) in Eq. (67) are λ_e = 1.48, λ_e = 1.50, and λ_e = 1.52, respectively. With these values and computing the pitch angle α_e from Eq. (23), the inherent forces in each fiber are, F = 0.78 pN, F = 0.83 pN, and F = 0.88 pN, respectively. The cross-sectional area of each fiber is, A_fiber = 17200 nm², A_fiber = 19100 nm², and A_fiber = 21100 nm², respectively, which, combined with the inherent forces in the fibers, yields the fiber inherent stresses, σ = 45.4 Pa, σ = 43.5 Pa, and 41.7 Pa, respectively (see Table 2). It should be noted that these calculations were performed in a simplified scenario to illustrate one possible hypothesis, and they do not take into account confounding factors such as the isotropic nature of fibrin gels or branch points, although they give some physical intuition for the phenomenon.

Table 2.

Computed values for fiber (and network) stresses, given a fixed and uniform fiber radius for a “network” of fibers vertically connected between two horizontal plates with a fixed separation distance 0.5 μm. The fiber stretches λ_e are calculated using Eq. (73) in Eq. (67). Inherent forces in fibers F are computed from Eq. (22), using pitch angles calculated from Eq. (23). The cross-sectional area of each fiber A_fiber = πR². Inherent fiber stresses σ are computed by dividing the force F by the fiber cross-sectional area A_fiber.

R (nm)	λ e	F (pN)	Afiber (nm2)	σ (Pa)
74	1.48	0.78	17,200	45.4
78	1.50	0.83	19,100	43.5
82	1.52	0.88	21,100	41.7

Our calculation based on the 8-chain model assumes a given constant length of all fibers, but this is not the case for real fibrin networks. The constant length we use to compute pre-tension should really be interpreted as the average fiber length in a network. We may be able to do slightly better by using the probability density function for the fiber lengths and computing a probability density for the pre-tension values obtained (see Appendix D). However, this still does not account exactly for the different values of pre-tension in each fiber of a real fibrin gel, although it does utilize known information about the structure of a true fibrin network. A proper accounting of the variation of fiber lengths to predict pre-tension in a network will likely require computations that are beyond the scope of the research presented in this paper.

Pre-tension in fibrin networks specifically is important because it contributes to the stability of the material. Fibrin fiber networks, as well as many other biological networks, have connectivity (average number of fibers connected at a junction) below the Maxwell isostatic threshold, which, for networks with a large number of elements, is twice the dimensionality (Maxwell and Clerk, 1864; Vahabi et al., 2016; Arzash et al., 2019). Thus, if the fiber interactions were limited to tension and compression central forces, the network materials would be unstable for small deformations and would be floppy rather than rigid (Vahabi et al., 2016; Arzash et al., 2019). The presence of pre-tension in fibrin networks, similar to the presence of fiber bending in F-actin networks in cytoskeletons (Head et al., 2003), active stresses generated by myosin motors in cytoskeletal networks (Koenderink et al., 2009) and in fibrin networks in blood clots (Jansen et al., 2013), thermal fluctuations (Qi et al., 2006; Su and Purohit, 2012), and osmotic pressure in actin networks (Palmer and Boyce, 2008), stabilizes and rigidifies the network material (Vahabi et al., 2016; Arzash et al., 2019).

Estimations of inherent stress in a fibrin fiber network, as well as of other network material properties, will be useful in interpreting experiments performed on blood clots and thrombi, in the use of fibrin as a biomaterial – for example, the inherent tension may comprise a thermodynamic mechanism to control fiber diameter, and thus modulate the overall network structure – and in the application and development of novel methods of treatment of thrombotic states such as in mechanical thrombectomy since the susceptibility of fibrin to fibrinolytic enzymes depends strongly on the mechanical tension of the proteinaceous fibrous substrate (Hudson, 2017; Li et al., 2017a; Cone et al., 2020; Varjú et al., 2011). Thus, variation of the tension in fibers and the structure of the fibrin network can affect mechanical and enzymatic stability of entire blood clots and thrombi, which determines the course and outcome of hemostatic disorders (Litvinov and Weisel, 2017; Feller et al., 2022).

Appendix A. Expanded fibrin network polymerization model

Weisel and Nagaswami (1992) propose a system of ordinary differential equations (ODEs), to describe the polymerization of fibrin fibers, comprising fibrin network, from a fibrinogen solution. The polymerization process they describe consists of the following steps — beginning with a concentration of fibrinogen and thrombin (which cleaves the A fibrinopeptides from the fibrinogen to create fibrin monomers), association of fibrin monomers to form double-stranded half-staggered protofibrils, and then aggregation of protofibrils into fibrin fibers, which branch and grow to create the fibrin network gel. Their polymerization process includes a minimum length requirement (which we will call l_agg + 1) for protofibrils to be capable of aggregation, which produces the observed lag period in the number of protofibrils per fiber. Their model, including the polymerization chemical reaction equations and the resulting system of ODEs, for the example of l_agg = 10, is given as follows (with some modification of the explanatory text only, to better reflect our current understanding of fibrin polymerization):

$$\begin{array}{cc}{f}_A\stackrel{k_A}{\to }f& \text{fibrinopeptide A cleavage to convert fibrinogen to monomeric fibrin}\end{array}$$ (A.1)

$$\begin{array}{cc}f+f\stackrel{k_{pi}}{\to }{f}_2& \text{fibrin monomers associate to yield small longitudinal oligomers},\text{ protofibril precursors}\end{array}$$ (A.2)

$$f_2+f\stackrel{k_{pi}}{\to }{f}_3$$ (A.3)

$$f_3+f\stackrel{k_{pi}}{\to }{f}_4$$ (A.4)

$$\begin{array}{c}⋮\\ f_9+f\stackrel{k_{pi}}{\to }{f}_{10}\end{array}$$ (A.5)

$$\begin{array}{cc}{f}_{10}+f\stackrel{k_{pi}}{\to }{f}_n& \text{longer oligomers are formed until they reach the length of protofibrils capable of lateral association}\end{array}$$ (A.6)

$$\begin{array}{cc}{f}_n+f\stackrel{k_{pg}}{\to }{f}_n& \text{protofibrils grow in length}\end{array}$$ (A.7)

$$\begin{array}{cc}{f}_n+f_n\stackrel{k_{fi}}{\to }{f}_r& \text{two protofibrils aggregate laterally to initiate a fiber}\end{array}$$ (A.8)

$$\begin{array}{cc}{f}_r+f_n\stackrel{k_{fg}}{\to }{f}_r& \text{additional protofibrils add to a transversely growing fiber}\end{array}$$ (A.9)

$$\frac{d\left[f_A\right]}{dt}=-k_A\left[f_A\right]$$ (A.10)

$$\frac{d[f]}{dt}=k_A\left[f_A\right]-k_{pi}[f]\left(2[f]+\left[f_2\right]+\left[f_3\right]+\cdots +\left[f_{10}\right]\right)-k_{pg}[f]\left[f_n\right]$$ (A.11)

$$\frac{d\left[f_2\right]}{dt}=k_{pi}[f]\left([f]-\left[f_2\right]\right)$$ (A.12)

$$\frac{d\left[f_3\right]}{dt}=k_{pi}[f]\left(\left[f_2\right]-\left[f_3\right]\right)$$ (A.13)

$$\begin{array}{c}⋮\\ \frac{d\left[f_{10}\right]}{dt}=k_{pi}[f]\left(\left[f_9\right]-\left[f_{10}\right]\right)\end{array}$$ (A.14)

$$\frac{d\left[f_n\right]}{dt}=k_{pi}[f]\left[f_{10}\right]-2k_{fi}\left[f_n\right]\left[f_n\right]-k_{fg}\left[f_r\right]\left[f_n\right]$$ (A.15)

$$\frac{d\left[f_r\right]}{dt}=k_{fi}\left[f_n\right]\left[f_n\right]$$ (A.16)

$$\frac{d\left[f_n^{tot}\right]}{dt}=2k_{fi}\left[f_n\right]\left[f_n\right]+k_{fg}\left[f_r\right]\left[f_n\right]$$ (A.17)

$$\frac{d\left[c_{f_n}\right]}{dt}=11k_{pi}[f]\left[f_{10}\right]+k_{pg}\left[f_n\right][f]-2k_{fi}\left[f_n\right]\left[c_{f_n}\right]-k_{fg}\left[f_r\right]\left[c_{f_n}\right]$$ (A.18)

$$\frac{d\left[c_{f_r}\right]}{dt}=2k_{fi}\left[f_n\right]\left[c_{f_n}\right]+k_{fg}\left[f_r\right]\left[c_{f_n}\right]$$ (A.19)

$$n=\frac{\left[c_{f_n}\right]}{\left[f_n\right]}$$ (A.20)

$$m=\frac{\left[f_n^{tot}\right]}{\left[f_r\right]}$$ (A.21)

$$l=\frac{\left[c_{f_r}\right]}{\left[f_n^{tot}\right]},$$ (A.22)

where f_A represents fibrinogen, f represents fibrin monomers, f₂ through f₁₀ represent fibrin oligomers comprised of 2 through 10 monomers, f_n represent protofibrils, f_r represent fibrin fibers, $\left[f_n^{tot}\right]$ represents total protofibrils in fibers, $\left[c_{f_n}\right]$ represents total fibrin [monomers] in protofibrils, $\left[c_{f_r}\right]$ represents total fibrin in fibers, n is the average number of fibrin per protofibril, m is the average number of protofibrils per fiber, and l is the average length of fibers.

Weisel and Nagaswami (1992) also mention that the model should also account for longitudinal oligomer–monomer and oligomer–oligomer interactions in the intermediate stages of protofibril formation, which are not explicitly accounted for in the above model. A logical extension to this, which is also mentioned by Weisel and Nagaswami (1992), would be to include protofibril growth due to interactions with oligomers, which is also not included in the above model. They additionally describe that a reaction can be included to account for fiber–fiber interactions. Taking these additions into account, we can write the following chemical polymerization reactions:

$$f_A\stackrel{k_A}{\to }{f}_1$$ (A.23)

$$f_i+f_j\stackrel{k_{pi}}{\to }\{\begin{array}{ll}{f}_{i+j}\hfill & i+j<l_{agg}+1\hfill \\ f_n\hfill & i+j\ge l_{agg}+1,\hfill \end{array}\forall j\in \left[i,l_{agg}\right]\forall i\in \left[1,l_{agg}\right]$$ (A.24)

$$f_n+f_i\stackrel{k_{pg}}{\to }{f}_n\forall i\in \left[1,l_{agg}\right]$$ (A.25)

$$f_n+f_n\stackrel{k_{fi}}{\to }{f}_r$$ (A.26)

$$f_r+f_n\stackrel{k_{fg}}{\to }{f}_r$$ (A.27)

$$f_r+f_r\stackrel{k_{fA}}{\to }{f}_r$$ (A.28)

These polymerization reactions result in the following system of ODEs:

$$\frac{d\left[f_A\right]}{dt}=-k_A\left[f_A\right]$$ (A.29)

$$\frac{d\left[f_1\right]}{dt}=-k_{pi}\left(\left[f_1\right]\left[f_1\right]+\left[f_1\right]\sum _{i=1}^{l_{agg}}\left[f_i\right]\right)-k_{pg}[f]\left[f_n\right]+k_A\left[f_A\right]$$ (A.30)

$$\frac{d\left[f_j\right]}{dt}=k_{pi}\left(\sum _{i=1}^{\lfloor \frac{j}{2}\rfloor }\left[f_i\right]\left[f_{j-i}\right]-\left[f_j\right]\left[f_j\right]-\left[f_j\right]\sum _{i=1}^{l_{agg}}\left[f_i\right]\right)-k_{pg}\left[f_n\right]\left[f_j\right]\forall j\in \left[2,l_{agg}\right]$$ (A.31)

$$\frac{d\left[f_n\right]}{dt}=k_{pi}\left(\sum _{j=1}^{\lfloor \frac{l_{aag}+1}{2}\rfloor }\left(\left(\left[f_j\right]+\left[f_{l_{agg}+1-j}\right]\right)\sum _{i=l_{agg}+1-j}^{l_{agg}}\left[f_i\right]\right)\right)-2k_{f_i}\left[f_n\right]\left[f_n\right]-k_{fg}\left[f_r\right]\left[f_n\right]$$ (A.32)

$$\frac{d\left[f_r\right]}{dt}=k_{fi}\left[f_n\right]\left[f_n\right]-k_{fA}\left[f_r\right]\left[f_r\right]$$ (A.33)

$$\frac{d\left[f_n^{tot}\right]}{dt}=2k_{fi}\left[f_n\right]\left[f_n\right]+k_{fg}\left[f_r\right]\left[f_n\right]+k_{fA}\left[f_r\right]\left[f_r\right]$$ (A.34)

$$\frac{d\left[c_{f_n}\right]}{dt}=k_{pi}\sum _{i=1}^{l_{agg}}\left(\left(l_{agg}+i\right)\sum _{j=i}^{\lfloor \frac{l_{agg}+i}{2}\rfloor }\left[f_j\right]\left[f_{l_{agg}+i-j}\right]\right)+k_{pg}\left[f_n\right]\sum _{i=1}^{l_{agg}}\left[f_i\right]-k_{fi}\left[f_n\right]\left[c_{f_n}\right]-k_{fg}\left[f_r\right]\left[c_{f_n}\right]$$ (A.35)

$$\frac{d\left[c_{f_r}\right]}{dt}=2k_{fi}\left[f_n\right]\left[c_{f_n}\right]+k_{fg}\left[f_r\right]\left[c_{f_n}\right]+k_{fA}\left[f_r\right]\left[f_r\right].$$ (A.36)

We retain the same definitions

$$n=\frac{\left[c_{f_n}\right]}{\left[f_n\right]}$$ (A.37)

$$m=\frac{\left[f_n^{tot}\right]}{\left[f_r\right]}$$ (A.38)

$$l=\frac{\left[c_{f_r}\right]}{\left[f_n^{tot}\right]}.$$ (A.39)

The parameters in this system are as follows: l_agg + 1, the minimum length for protofibrils to be capable of aggregation; $f_{A_0}$, the initial concentration of fibrinogen; k_A, the rate of fibrinopeptide A cleavage to convert fibrinogen to fibrin monomers; k_pi, the rate of association of fibrin monomers to yield small oligomers and initiate protofibril formation; k_pg, the rate of protofibril growth in length by association with oligomers; k_fi, the rate of protofibril aggregation to initiate a fiber; k_fg, the rate of fiber growth by association with additional protofibrils; and k_fA, the rate of lateral interactions between fibers.

Appendix B. Non-uniform protofibril density

The results presented earlier assumed a uniform density of protofibrils in the fiber cross-section, which is known to be inaccurate (Yeromonahos et al., 2010; Yermolenko et al., 2011; Yang et al., 2000; Guthold et al., 2004; Li et al., 2016, 2017b). Here, the modifications to the above theory to include a non-uniform density, and the changes in the results caused by these modifications, will be discussed. The necessary modifications appear in two primary locations: first, the relationship Eq. (14) between fiber radius R and average number of protofibrils per fiber cross-section m, will be different; and second, a density function must be included in the force balance equations Eqs. (17) and (21), which would also change the results from those equations. Since it is known that the density of protofibrils decreases closer to the perimeter of a fiber (Yeromonahos et al., 2010; Yermolenko et al., 2011; Yang et al., 2000; Guthold et al., 2004; Li et al., 2016, 2017b), this fact must be incorporated into the theory.

To generalize the theory to include non-uniform densities of protofibrils per fiber cross-section, the density can be described as having a power law relationship:

$$\varrho (r)=\frac{1}{a_0}{\left(\frac{r}{r_{pc}}\right)}^{-h},$$ (B.1)

where r_pc is a proportionality constant with the same units as r, which, for the purposes of this derivation, will be taken as r_pc = 20 nm in order for the calculated fiber radii to be in the correct range, but must be determined from experiment (and may also depend on h). h = 0 represents uniform density. Recall that $a_0=\pi r_m^2$ is the area occupied by one protofibril under the assumption of constant density. Since it is known that the density of protofibrils decreases closer to the perimeter of a fiber (Yeromonahos et al., 2010; Yermolenko et al., 2011; Yang et al., 2000; Guthold et al., 2004; Li et al., 2016, 2017b), h ≥ 0.

Next, the relationship Eq. (14) between the fiber radius R and the average number of protofibrils per fiber cross-section m can be rewritten as

$$m(t)=\frac{1}{\pi r_m^2}{\int }_0^{R(t)}\varrho (r)2\pi rdr.$$ (B.2)

This yields

$$m(t)=\frac{2r_{pc}^h}{r_m^2}{\int }_0^{R(t)}{r}^{1-h}dr,$$ (B.3)

which reduces to

$$m(t)=\frac{2r_{pc}^h}{r_m^2}\frac{R^{2-h}}{2-h}.$$ (B.4)

Since we want m > 0, we will take 0 ≤ h < 2, then

$$R(t)={\left(\frac{1-\frac{h}{2}}{r_{pc}^h}\right)}^{\frac{1}{2-h}}{r}_m^{\frac{2}{2-h}}{(m(t))}^{\frac{1}{2-h}}.$$ (B.5)

When h = 0 the result Eq. (14) is recovered. As an example, some experimental results showed m ∝ R^0.4 as a minimum exponent (Li et al., 2016) which corresponds to h = 1.6. Results for selected values of 0 ≤ h < 2 are depicted in Fig. B.13. Note that, as discussed in Section 4.1, the polymerization reaction rate constants k_fi and k_fg can be adjusted to account for this change in fiber radius.

Next, the new density function Eq. (B.1) must be included in Eq. (17):

$${\int }_{r_m}^R\frac{2\pi r}{a_0}\varrho (r)n(r)dr=0.$$ (B.6)

Then, the equation becomes

$${\text{cos}}^2\alpha {\int }_{r_m}^R{r}^{-1-h}dr={\kappa }_0{\int }_{r_m}^R{r}^{-h}dr.$$ (B.7)

Now, the solution to this integral equation also will depend on the value of h > 0. If h = 0, then the integral on the left would become

$${\int }_{r_m}^R{r}^{-1}dr=\text{ln }\left(\frac{R}{r_m}\right);$$ (B.8)

if h = 1, the above would be the solution for the integral on the right; and if h is anything else, then the integral would become

$${\int }_{r_m}^R{r}^{-h}dr=R^{1-h}-r_m^{1-h}.$$ (B.9)

Thus, the solution is

$${\text{cos}}^2{\alpha }_s=\{\begin{array}{ll}{\kappa }_0\frac{R-r_m}{\text{ln}\left(\frac{R}{r_m}\right)},\hfill & h=0\hfill \\ {\kappa }_0\frac{\text{ln}\left(\frac{R}{r_m}\right)}{R^{-1}-r_m^{-1}},\hfill & h=1\hfill \\ {\kappa }_0\frac{R^{1-h}-r_m^{1-h}}{R^{-h}-r_m^{-h}},\hfill & \text{otherwise}.\hfill \end{array}$$ (B.10)

For the value of h = 0, the uniform density assumed previously, this reduces to Eq. (20).

Fig. B.13.

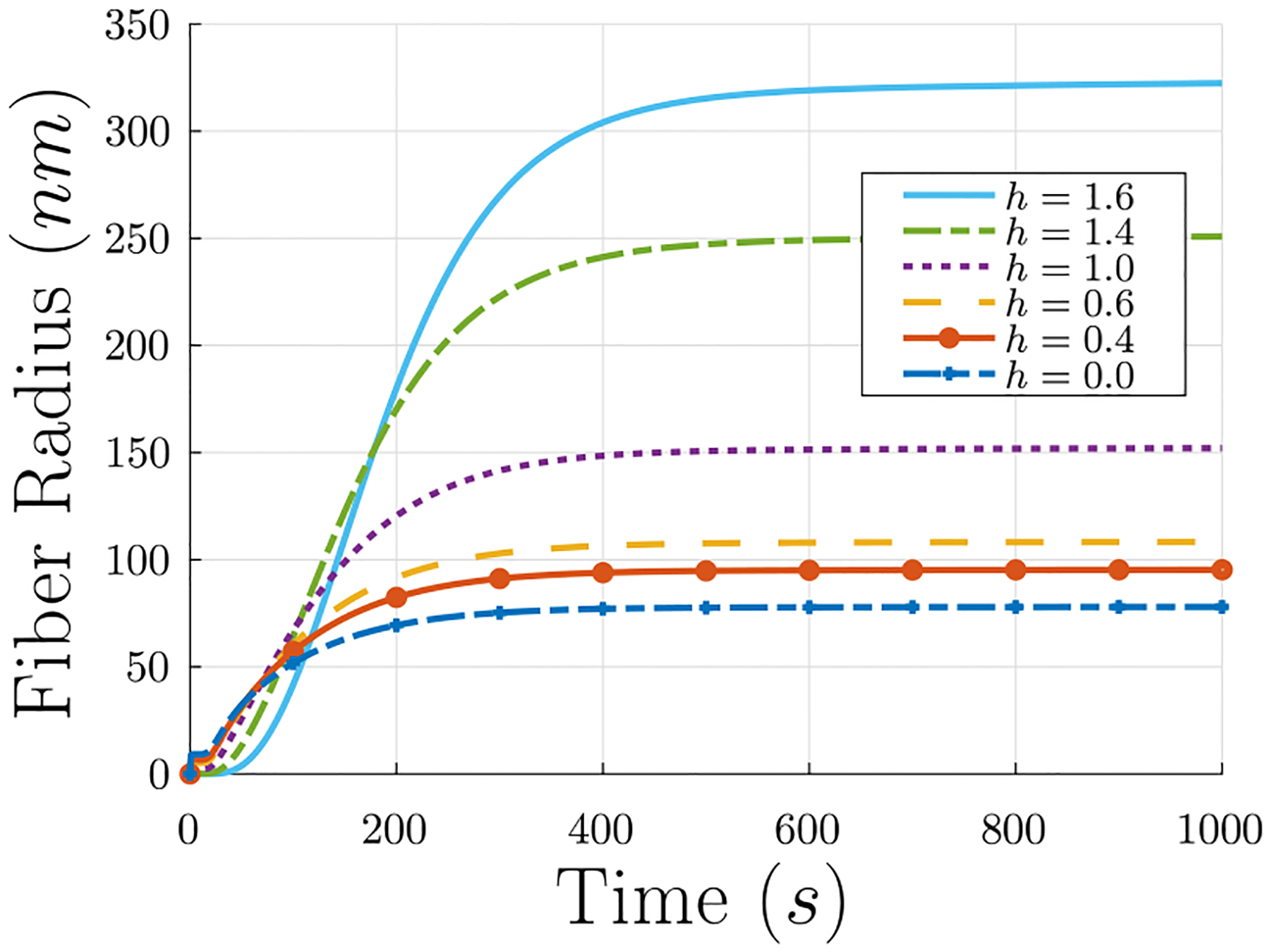
Effect of modifying the assumption of uniform density of protofibrils per fiber cross-section to be non-uniform. Effect on the fiber radius R. Recall that h = 0 is the uniform density assumed in the main text.

Similarly, Eq. (21) would become

$$F={\int }_{r_m}^R\frac{2\pi r}{a_0}\varrho (r)n(r)dr,$$ (B.11)

for which the solution is

$$F\left({\lambda }_e,R(t)\right)=\frac{2\pi }{a_0}{K}_b\text{ sin }{\alpha }_e\times \{\begin{array}{ll}{r}_{pc}^h\left({\kappa }_0\left(R-r_m\right)-{\text{cos}}^2{\alpha }_e\text{ ln }\left(\frac{R}{r_m}\right)\right),\hfill & h=0\hfill \\ r_{pc}^h\left({\kappa }_0\text{ ln }\left(\frac{R}{r_m}\right)-{\text{cos}}^2{\alpha }_e\left(R^{-1}-r_m^{-1}\right)\right),\hfill & h=1\hfill \\ r_{pc}^h\left({\kappa }_0\left(R^{1-h}-r_m^{1-h}\right)-{\text{cos}}^2{\alpha }_e\left(R^{-h}-r_m^{-h}\right)\right),\hfill & \text{otherwise}.\hfill \end{array}$$ (B.12)

Again, for h = 0, the uniform density assumed previously, this reduces to Eq. (22).

Appendix C. Force in helical rods

Since it has been observed (Weisel et al., 1987; Zhmurov et al., 2018) that both protofibrils and fibrin fibers are comprised of smaller units helically twisted around a central stem, the derivation for the force in a helical fiber is presented here.

A circular helix of radius r and pitch p with right-handed chirality can be described in lab-frame Cartesian coordinates as

$$r(\zeta )=r\text{ cos}(\zeta )e_1+r\text{ sin}(\zeta )e_2+\left(\frac{p}{2\pi }\right)\zeta e_3,$$ (C.1)

and we denote

$$\frac{1}{\eta }=\left|\frac{dr(\zeta )}{d\zeta }\right|=\sqrt{r^2+{\left(\frac{p}{2\pi }\right)}^2}$$ (C.2)

for simplicity. If s(ζ) is an arc-length coordinate along the contour of the helix, then

$$s(\zeta )={\int }_0^{\zeta }\left|\frac{dr(\sigma )}{d\sigma }\right|d\sigma =\frac{\zeta }{\eta },$$ (C.3)

and the helix can be rewritten as

$$r(s)=r\text{ cos}(\eta s)e_1+r\text{ sin}(\eta s)e_2+\left(\frac{p}{2\pi }\right)\eta s{e}_3.$$ (C.4)

The tangent to the helix is given as

$$\widehat{t}(s)=\frac{dr(s)}{ds}=-r\eta \text{ sin}(\eta s)e_1+r\eta \text{ cos}(\eta s)e_2+\left(\frac{p}{2\pi }\right)\eta e_3,$$ (C.5)

which is clearly a unit vector since

$$|\widehat{t}(s){|}^2={\eta }^2\left(r^2+{\left(\frac{p}{2\pi }\right)}^2\right)=1.$$ (C.6)

We can define the curvature

$$\kappa =\left|\frac{d\widehat{t}(s)}{ds}\right|=r{\eta }^2$$ (C.7)

and unit normal vector

$$\widehat{v}(s)=\frac{1}{\kappa }\left(\frac{d\widehat{t}(s)}{ds}\right)=-\text{cos}(\eta s)e_1-\text{sin}(\eta s)e_2+0e_3,$$ (C.8)

from which we can also define the unit binormal vector

$$\widehat{\beta }(s)=\widehat{t}(s)\times \widehat{v}(s)=\left(\frac{p}{2\pi }\right)\eta \text{ sin}(\eta s)e_1-\left(\frac{p}{2\pi }\right)\eta \text{ cos}(\eta s)e_2+r\eta e_3$$ (C.9)

and right-handed torsion

$$\tau =(\widehat{t}\times \widehat{v})\cdot \frac{d\widehat{v}}{ds}=\left(\frac{p}{2\pi }\right){\eta }^2.$$ (C.10)

(Note that for a helix with left chirality, for example $r(s)=r\text{ sin}(\eta s)e_1+r\text{ cos}(\eta s)e_2+\left(\frac{p}{2\pi }\right)\eta s{e}_3$, the right-handed torsion is $\tau =-\left(\frac{p}{2\pi }\right){\eta }^2$, but with the given definitions the difference has no other effect.) From here it is clear that

$${\kappa }^2+{\tau }^2={\eta }^2$$ (C.11)

and thus

$$r=\frac{\kappa }{{\kappa }^2+{\tau }^2}$$ (C.12)

$$\left(\frac{p}{2\pi }\right)=\frac{\tau }{{\kappa }^2+{\tau }^2}.$$ (C.13)

It can be verified that the three vectors $\widehat{t}(s)$, $\widehat{v}(s)$, and $\widehat{\beta }(s)$ are orthonormal, and that the Frenet–Serret theorem

$$\frac{d}{ds}\left[\begin{array}{l}\widehat{t}(s)\hfill \\ \widehat{v}(s)\hfill \\ \widehat{\beta }(s)\hfill \end{array}\right]=\left[\begin{array}{ccc}0& \kappa & 0\\ -\kappa & 0& \tau \\ 0& -\tau & 0\end{array}\right]\left[\begin{array}{l}\widehat{t}(s)\hfill \\ \widehat{v}(s)\hfill \\ \widehat{\beta }(s)\hfill \end{array}\right]$$ (C.14)

holds. As such, it is logical to express the lab-frame in the Frenet frame, using the transformations

$$\left[\begin{array}{l}\widehat{t}(s)\hfill \\ \widehat{v}(s)\hfill \\ \widehat{\beta }(s)\hfill \end{array}\right]=\left[\begin{array}{ccc}-r\eta \text{ sin}(\eta s)& r\eta \text{ cos}(\eta s)& \left(\frac{p}{2\pi }\right)\eta \\ -\text{cos}(\eta s)& -\text{sin}(\eta s)& 0\\ \left(\frac{p}{2\pi }\right)\eta \text{ sin}(\eta s)& -\left(\frac{p}{2\pi }\right)\eta \text{ cos}(\eta s)& r\eta \end{array}\right]\left[\begin{array}{l}{e}_1\hfill \\ e_2\hfill \\ e_3\hfill \end{array}\right]$$ (C.15)

$$\left[\begin{array}{l}{e}_1\hfill \\ e_2\hfill \\ e_3\hfill \end{array}\right]=\left[\begin{array}{ccc}-r\eta \text{ sin}(\eta s)& -\text{cos}(\eta s)& \left(\frac{p}{2\pi }\right)\eta \text{ sin}(\eta s)\\ r\eta \text{ cos}(\eta s)& -\text{sin}(\eta s)& -\left(\frac{p}{2\pi }\right)\eta \text{ cos}(\eta s)\\ \left(\frac{p}{2\pi }\right)\eta & 0& r\eta \end{array}\right]\left[\begin{array}{c}\widehat{t}(s)\\ \widehat{v}(s)\\ \widehat{\beta }(s)\end{array}\right].$$ (C.16)

Having described the kinematics of a helical rod we now want to examine equilibria with curvature κ and torsion τ, both independent of s. It is assumed that the helical rod can carry forces and moments and that it is acted upon by body forces and body moments. The goal is to find the force and moment in the helical rod, given κ, τ, and the body forces and body moments. In the Frenet frame, the body force per unit length on the helix, assumed independent of position on the helix s, can be written

$$f=f_t\widehat{t}+f_v\widehat{v}+f_{\beta }\widehat{\beta },$$ (C.17)

and the force vector at any point s in the helix can be written

$$n(s)=n_t\widehat{t}+n_v\widehat{v}+n_{\beta }\widehat{\beta }.$$ (C.18)

The balance of forces requires

$$\frac{dn(s)}{ds}+f=0,$$ (C.19)

which, using the Frenet–Serret theorem Eq. (C.14), reduces to

$$\frac{d{n}_t}{ds}-n_v\kappa +f_t=0$$ (C.20)

$$\frac{d{n}_v}{ds}-n_{\beta }\tau +n_t\kappa +f_v=0$$ (C.21)

$$\frac{d{n}_{\beta }}{ds}+n_v\tau +f_{\beta }=0.$$ (C.22)

Differentiating Eq. (C.21) with respect to s, and substituting in for $\frac{d{n}_t}{ds}$ from Eq. (C.20) and $\frac{d{n}_{\beta }}{ds}$ from Eq. (C.22), results in

$$\frac{d^2{n}_v}{d{s}^2}+{\eta }^2{n}_v+\left(\tau f_{\beta }-\kappa f_t\right)=0,$$ (C.23)

which has solution

$$n_v(s)=A\text{ cos}(\eta s)+B\text{ sin}(\eta s)-\frac{1}{{\eta }^2}\left(\tau f_{\beta }-\kappa f_t\right),$$ (C.24)

where A and B are two constants. Putting Eq. (C.24) into Eqs. (C.20) and (C.22), we have

$$\frac{d{n}_t}{ds}=A\kappa \text{ cos}(\eta s)+B\kappa \text{ sin}(\eta s)-\frac{\kappa }{{\eta }^2}\left(\tau f_{\beta }-\kappa f_t\right)-f_t$$ (C.25)

$$\frac{d{n}_{\beta }}{ds}=-A\tau \text{ cos}(\eta s)-B\tau \text{ sin}(\eta s)+\frac{\tau }{{\eta }^2}\left(\tau f_{\beta }-\kappa f_t\right)-f_{\beta },$$ (C.26)

which can be integrated with respect to s to get

$$n_t=\frac{A\kappa }{\eta }\text{sin}(\eta s)-\frac{B\kappa }{\eta }\text{cos}(\eta s)-\frac{\kappa s}{{\eta }^2}\left(\tau f_{\beta }-\kappa f_t\right)-f_{t}s+D_t$$ (C.27)

$$n_{\beta }=-\frac{A\tau }{\eta }\text{sin}(\eta s)+\frac{B\tau }{\eta }\text{cos}(\eta s)+\frac{\tau s}{{\eta }^2}\left(\tau f_{\beta }-\kappa f_t\right)-f_{\beta }s+D_{\beta },$$ (C.28)

where D_t and D_β are arbitrary constants. Substituting Eqs. (C.27), (C.24), and (C.28) into Eq. (C.21) yields

$$f_v=\tau D_{\beta }-\kappa D_t.$$ (C.29)

It is useful to recast the force balance in the directors d_i, i = 1, 2, 3 of a material frame in the reference configuration of the circular cross-section of the rod comprising the helix. This frame is a rotation by an angle

$$\varphi (s)=\left({\kappa }_3-\tau \right)s$$ (C.30)

about the normal vector $\widehat{t}$, where κ₃ is a constant. In this frame,

$$\left[\begin{array}{l}{d}_1(s)\hfill \\ d_2(s)\hfill \\ d_3(s)\hfill \end{array}\right]=\left[\begin{array}{ccc}0& \text{cos }\varphi & \text{sin }\varphi \\ 0& -\text{sin }\varphi & \text{cos }\varphi \\ 1& 0& 0\end{array}\right]\left[\begin{array}{l}\widehat{t}(s)\hfill \\ \widehat{v}(s)\hfill \\ \widehat{\beta }(s)\hfill \end{array}\right],$$ (C.31)

and

$$\left[\begin{array}{l}\widehat{t}(s)\hfill \\ \widehat{v}(s)\hfill \\ \widehat{\beta }(s)\hfill \end{array}\right]=\left[\begin{array}{ccc}0& 0& 1\\ \text{cos }\varphi & -\text{sin }\varphi & 0\\ \text{sin }\varphi & \text{cos }\varphi & 0\end{array}\right]\left[\begin{array}{l}{d}_1(s)\hfill \\ d_2(s)\hfill \\ d_3(s)\hfill \end{array}\right].$$ (C.32)

The material frame also has the property

$$\frac{d{d}_i}{ds}=\kappa \times d_i,i=1,2,3,$$ (C.33)

where the curvature vector can be represented

$$\kappa ={\kappa }_1{d}_1+{\kappa }_2{d}_2+{\kappa }_3{d}_3,$$ (C.34)

or, in the Frenet frame, as

$$\kappa =\left({\kappa }_1\text{ cos }\varphi -{\kappa }_2\text{ sin }\varphi \right)\widehat{v}+\left({\kappa }_1\text{ sin }\varphi +{\kappa }_2\text{ cos }\varphi \right)\widehat{\beta }+{\kappa }_3\widehat{t}$$ (C.35)

$$={\kappa }_3\widehat{t}+\kappa \widehat{\beta },$$ (C.36)

with

$${\kappa }_1=\kappa \text{ sin }\left(\left({\kappa }_3-\tau \right)s\right)$$ (C.37)

$${\kappa }_2=\kappa \text{ cos }\left(\left({\kappa }_3-\tau \right)s\right)$$ (C.38)

$${\kappa }_3=\text{constant}.$$ (C.39)

We next analyze the moments. The balance of moments can be expressed as

$$\frac{dm}{ds}+\widehat{t}\times n+\mathit{\ell }=0,$$ (C.40)

where m is the moment at any point on the helix and ℓ is a body moment per unit arc length. Following the example of Nizette and Goriely (1999), to relate the moment m and the curvature vector κ, we use the constitutive relation from linear elasticity for a rod of circular cross section

$$m=K_b\left({\kappa }_1-{\kappa }_{01}\right)d_1+K_b\left({\kappa }_2-{\kappa }_{02}\right)d_2+K_t\left({\kappa }_3-{\kappa }_{03}\right)d_3,$$ (C.41)

where

$$K_b=E\frac{\pi r^4}{4}$$ (C.42)

is the bending modulus with E the Young’s modulus of the rod,

$$K_t=G\frac{\pi r^4}{2}$$ (C.43)

is the twisting modulus with G the shear modulus of the rod, and

$${\kappa }_{01}={\kappa }_0\text{ sin }\left(\left({\kappa }_3-\tau \right)s\right),$$ (C.44)

$${\kappa }_{02}={\kappa }_0\text{ cos }\left(\left({\kappa }_3-\tau \right)s\right),$$ (C.45)

κ₀₃, and κ₀ are the spontaneous curvatures of the helix in the stress-free state. In the Frenet frame, the constitutive relation giving the moment m can be written

$$m=K_b\left(\kappa -{\kappa }_0\right)\widehat{\beta }+K_t\left({\kappa }_3-{\kappa }_{03}\right)\widehat{t}.$$ (C.46)

As in Nizette and Goriely (1999), we also take the body moment

$$\mathit{\ell }=0.$$ (C.47)

Now, the balance of moments reduces to the following three equations:

$$K_t\frac{d{\kappa }_3}{ds}=0$$ (C.48)

$$K_t\left({\kappa }_3-{\kappa }_{03}\right)\kappa -K_b\left(\kappa -{\kappa }_0\right)\tau -n_{\beta }=0$$ (C.49)

$$n_v=0,$$ (C.50)

recalling that

$$\kappa =\frac{r}{r^2+{\left(\frac{p}{2\pi }\right)}^2},$$ (C.51)

$${\kappa }_0=\frac{r_0}{r_0^2+{\left(\frac{p_0}{2\pi }\right)}^2},$$ (C.52)

and κ₀₃ are constants. Eq. (C.48) shows that κ₃ is constant, and Eq. (C.49) shows that

$$n_{\beta }=K_t\left({\kappa }_3-{\kappa }_{03}\right)\kappa -K_b\left(\kappa -{\kappa }_0\right)\tau ,$$ (C.53)

which is therefore also a constant. Combining Eq. (C.50) with Eq. (C.24), we have

$$0=A\text{ cos}(\eta s)+B\text{ sin}(\eta s)-\frac{1}{{\eta }^2}\left(\tau f_{\beta }-\kappa f_t\right)\forall s.$$ (C.54)

In order for this equation to be true for all s, we must conclude that

$$A=B=0,$$ (C.55)

$$\tau f_{\beta }=\kappa f_t.$$ (C.56)

Using these conclusions, Eqs. (C.27) and (C.28) become

$$n_t=D_t-f_{t}s$$ (C.57)

$$n_{\beta }=D_{\beta }-f_{\beta }s.$$ (C.58)

However, since we have also Eq. (C.53) independent of s, from the last equation we must conclude also that

$$f_{\beta }=0$$ (C.59)

$$D_{\beta }=n_{\beta }=K_t\left({\kappa }_3-{\kappa }_{03}\right)\kappa -K_b\left(\kappa -{\kappa }_0\right)\tau .$$ (C.60)

Since we also have Eq. (C.56), if f_β = 0, we must also have

$$f_t=0,$$ (C.61)

and therefore

$$n_t=D_t$$ (C.62)

is also a constant. Thus, we have

$$n=D_t\widehat{t}+\left(K_t\left({\kappa }_3-{\kappa }_{03}\right)\kappa -K_b\left(\kappa -{\kappa }_0\right)\tau \right)\widehat{\beta }$$ (C.63)

$$f=\left(K_t\left({\kappa }_3-{\kappa }_{03}\right)\kappa \tau -K_b\left(\kappa -{\kappa }_0\right){\tau }^2-\kappa D_t\right)\widehat{v}.$$ (C.64)

Fig. D.14.

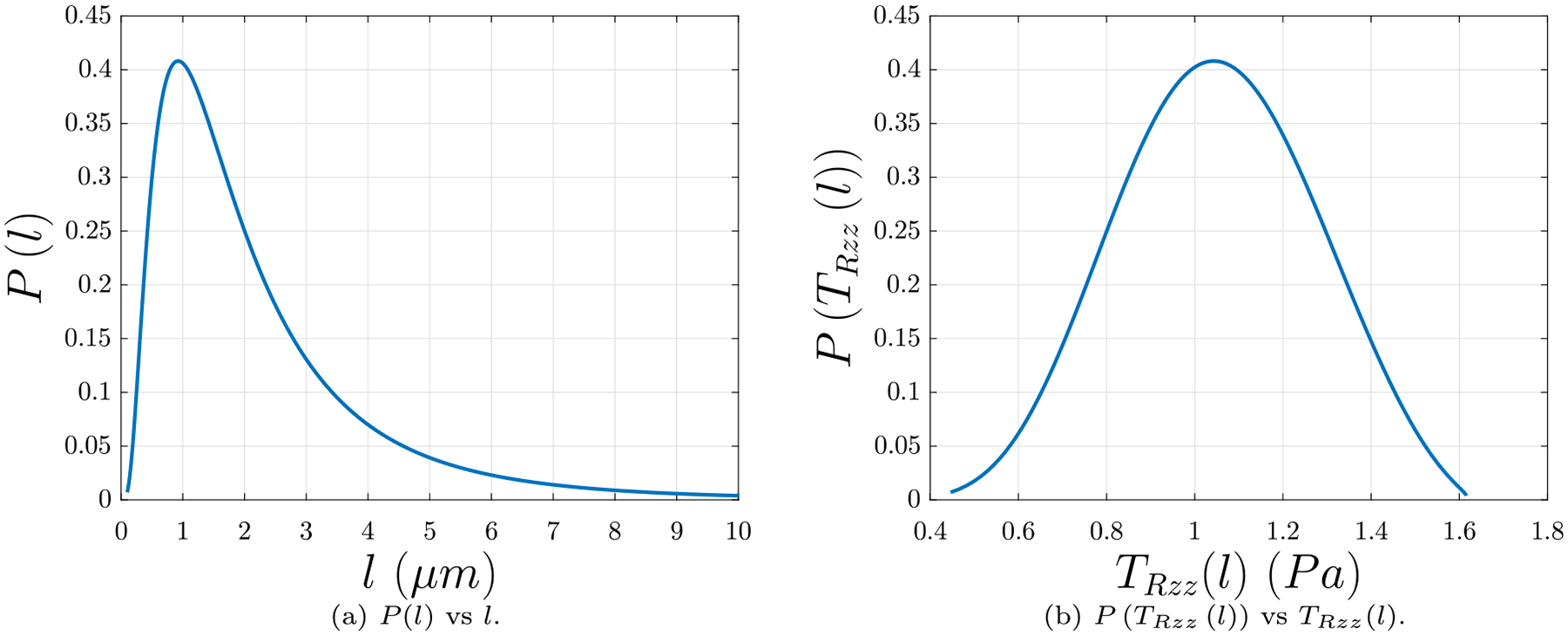
Probability distributions of (b) fiber lengths as found in Kim et al. (2014), and (b) network stresses based on the fiber lengths and holding constant the solid volume fraction ϕ_s = 0.01 as estimated in Tutwiler et al. (2020).

In the material frame, the body force per unit length on the helix can be written

$$f=f_1{d}_1+f_2{d}_2+f_3{d}_3,$$ (C.65)

and the force vector at any point s in the helix can be written

$$n(s)=n_1{d}_1+n_2{d}_2+n_3{d}_3.$$ (C.66)

From our previous analysis, we have

$$n=\left(K_t\left({\kappa }_3-{\kappa }_{03}\right)-K_b\left(\kappa -{\kappa }_0\right)\frac{\tau }{\kappa }\right)\left({\kappa }_1{d}_1+{\kappa }_2{d}_2\right)+D_t{d}_3$$ (C.67)

$$f=\left(K_t\left({\kappa }_3-{\kappa }_{03}\right)\tau -K_b\left(\kappa -{\kappa }_0\right)\frac{{\tau }^2}{\kappa }-D_t\right)\left({\kappa }_2{d}_1-{\kappa }_1{d}_2\right),$$ (C.68)

which gives us

$$n_1=\left(K_t\left({\kappa }_3-{\kappa }_{03}\right)-K_b\left(\kappa -{\kappa }_0\right)\frac{\tau }{\kappa }\right){\kappa }_1$$ (C.69)

$$n_2=\left(K_t\left({\kappa }_3-{\kappa }_{03}\right)-K_b\left(\kappa -{\kappa }_0\right)\frac{\tau }{\kappa }\right){\kappa }_2$$ (C.70)

$$n_3=D_t$$ (C.71)

$$f_1=\left(K_t\left({\kappa }_3-{\kappa }_{03}\right)\tau -K_b\left(\kappa -{\kappa }_0\right)\frac{{\tau }^2}{\kappa }-D_t\right){\kappa }_2$$ (C.72)

$$f_2=-\left(K_t\left({\kappa }_3-{\kappa }_{03}\right)\tau -K_b\left(\kappa -{\kappa }_0\right)\frac{{\tau }^2}{\kappa }-D_t\right){\kappa }_1$$ (C.73)

$$f_3=0.$$ (C.74)

Suppose there is a force F = Fe₃ applied on the helical filament along its axis. This applied force in the Frenet frame can be expressed

$$F=F{e}_3=F\left(\left(\frac{p}{2\pi }\right)\eta \widehat{t}+r\eta \widehat{\beta }\right).$$ (C.75)

The filament will carry the force as the force vector n = F. Thus, in the Frenet frame, we have

$$D_t=F\left(\frac{p}{2\pi }\right)\eta$$ (C.76)

$$K_t\left({\kappa }_3-{\kappa }_{03}\right)\kappa -K_b\left(\kappa -{\kappa }_0\right)\tau =Fr\eta .$$ (C.77)

Solving the second of these two equations for F and substituting back into the first, we arrive at

$$D_t=\left(K_t\left({\kappa }_3-{\kappa }_{03}\right)-K_b\left(\kappa -{\kappa }_0\right)\frac{\tau }{\kappa }\right)\tau .$$ (C.78)

Thus, the body force per unit length on the helix and the force vector at any point s on the helix become

$$f=0$$ (C.79)

$$n=\left(K_t\left({\kappa }_3-{\kappa }_{03}\right)-K_b\left(\kappa -{\kappa }_0\right)\frac{\tau }{\kappa }\right)\left({\kappa }_1{d}_1+{\kappa }_2{d}_2+\tau d_3\right).$$ (C.80)

In the case when κ₀ = κ₀₃ = 0, the force vector

$$\frac{n}{K_b}=\left(\frac{K_t}{K_b}{\kappa }_3-\tau \right)\left[\kappa -\left({\kappa }_3-\tau \right)d_3\right]$$ (C.81)

from Nizette and Goriely (1999) is recovered.

The magnitude of the force vector is

$$n=\left|\left(K_t\left({\kappa }_3-{\kappa }_{03}\right)-K_b\left(\kappa -{\kappa }_0\right)\frac{\tau }{\kappa }\right)\right|\eta .$$ (C.82)

In the main text we assume there is no twisting moment acting on the helix, so K_t(κ₃ − κ₀₃) = 0.

Appendix D. Distribution of fibrin fiber lengths

Fig. D.14(a) depicts the probability distribution of fiber lengths in a fibrin network, as found in Kim et al. (2014). The probability density function is a log-normal distribution function of l with parameters μ = 0.53 and σ = 0.78, as found in Kim et al. (2014). Fig. D.14(b) depicts the probability density of l vs. the peak stress T_Rzz from the simulations utilizing that l as an input parameter, with the radius for that given l calculated by

$$R=\sqrt{\frac{{\varphi }_s}{v\pi l}},$$ (D.1)

where the density ν = 0.1 μm⁻³, as measured in Kim et al. (2016), and T_Rzz is also calculated using ν = 0.1 μm⁻³ from Kim et al. (2016). The mean value of T_Rzz is 1.21 Pa. This mean value is roughly of the same order of magnitude as the network Piola stresses T_Rzz calculated from the simulations in Fig. 9. The stress values resulting from these computations are also of the same order of magnitude as the values produced by the experiments in Section 3.

Data availability

Data will be made available on request.